Insulation Condition Assessment of High-Voltage Single-Core Cables Via Zero-Crossing Frequency Analysis of Impedance Phase Angle
Abstract
1. Introduction
2. Methods
2.1. Circuit Model of a HV Cable
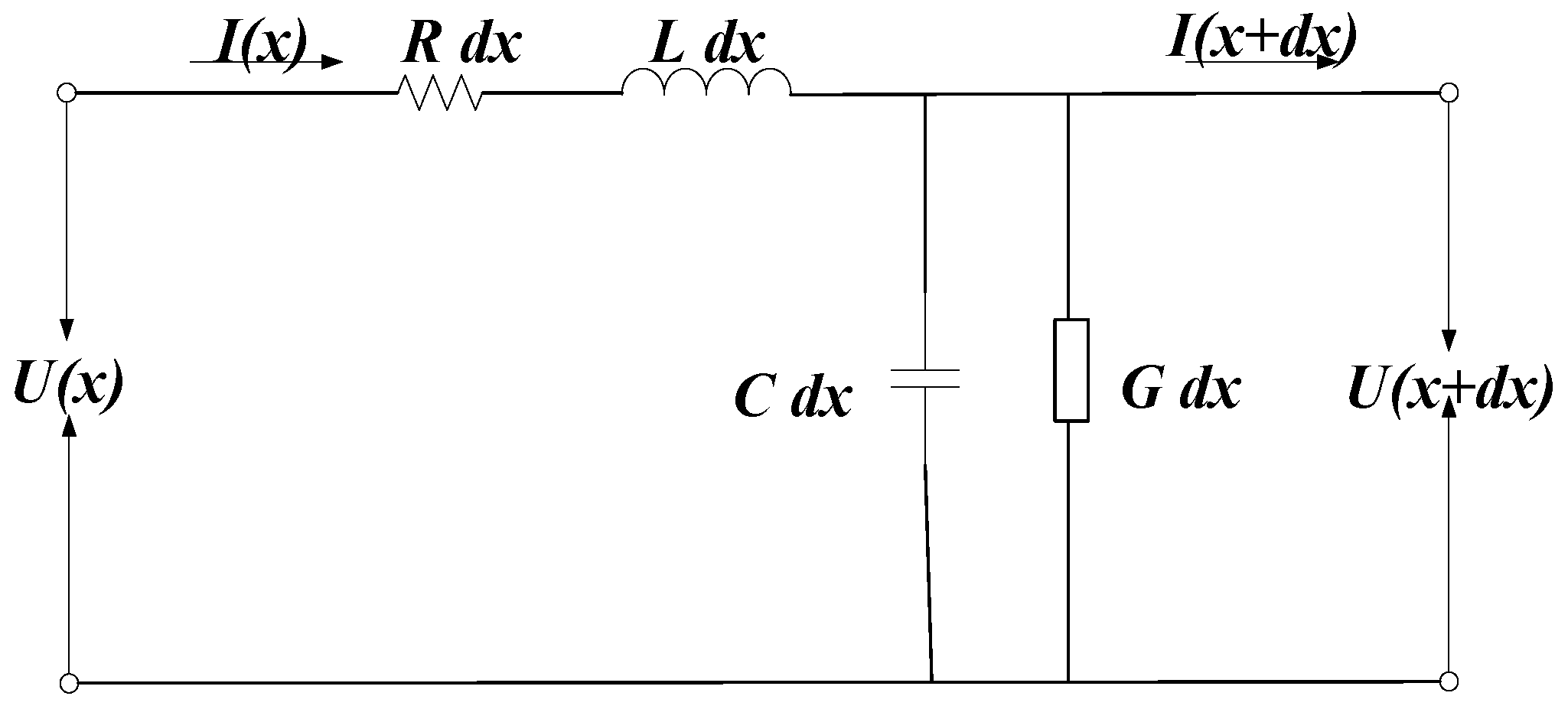
2.2. Distributed Parameters of HV Cables
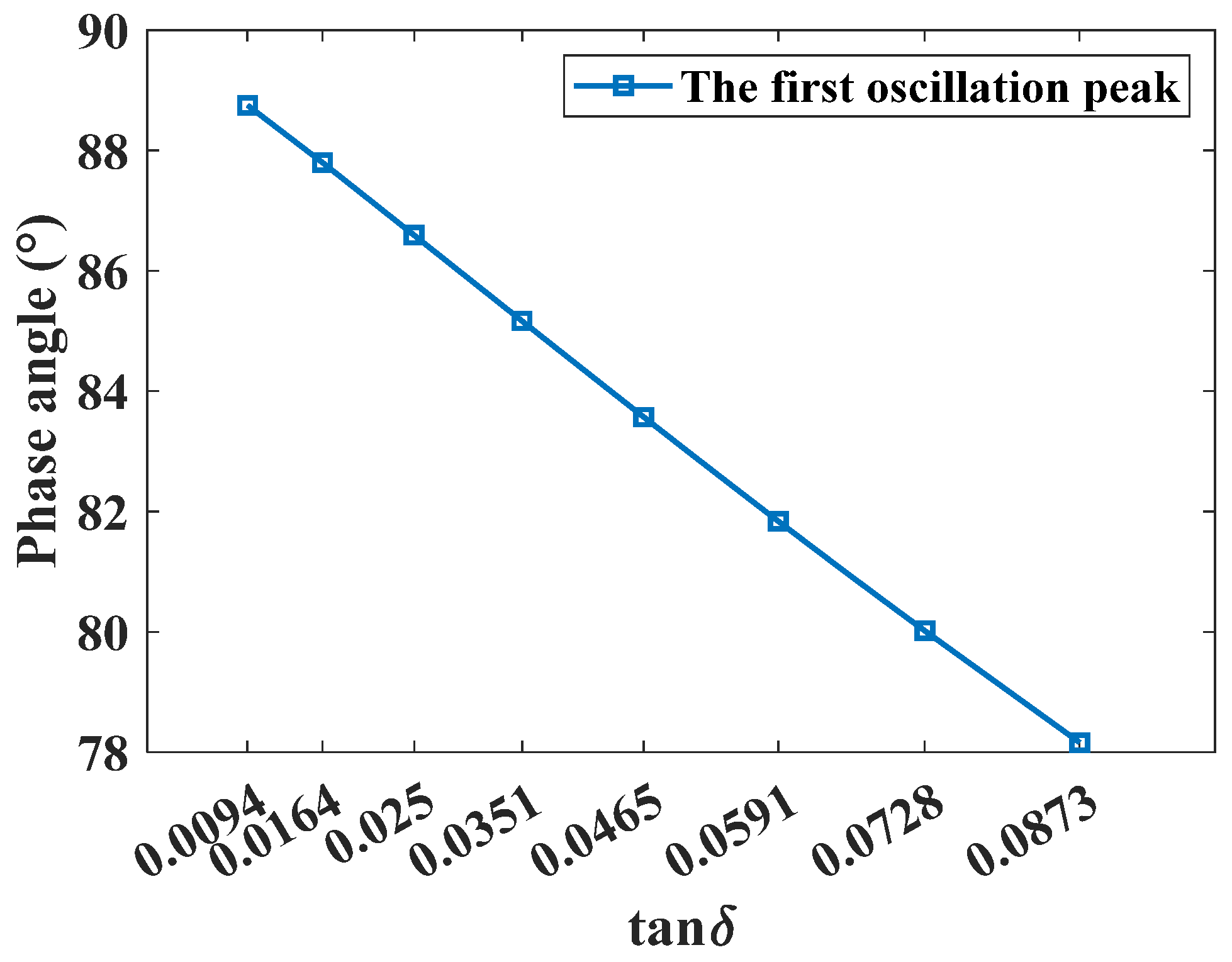
2.3. Correlation Between Dielectric Loss Tangent and Aging Condition
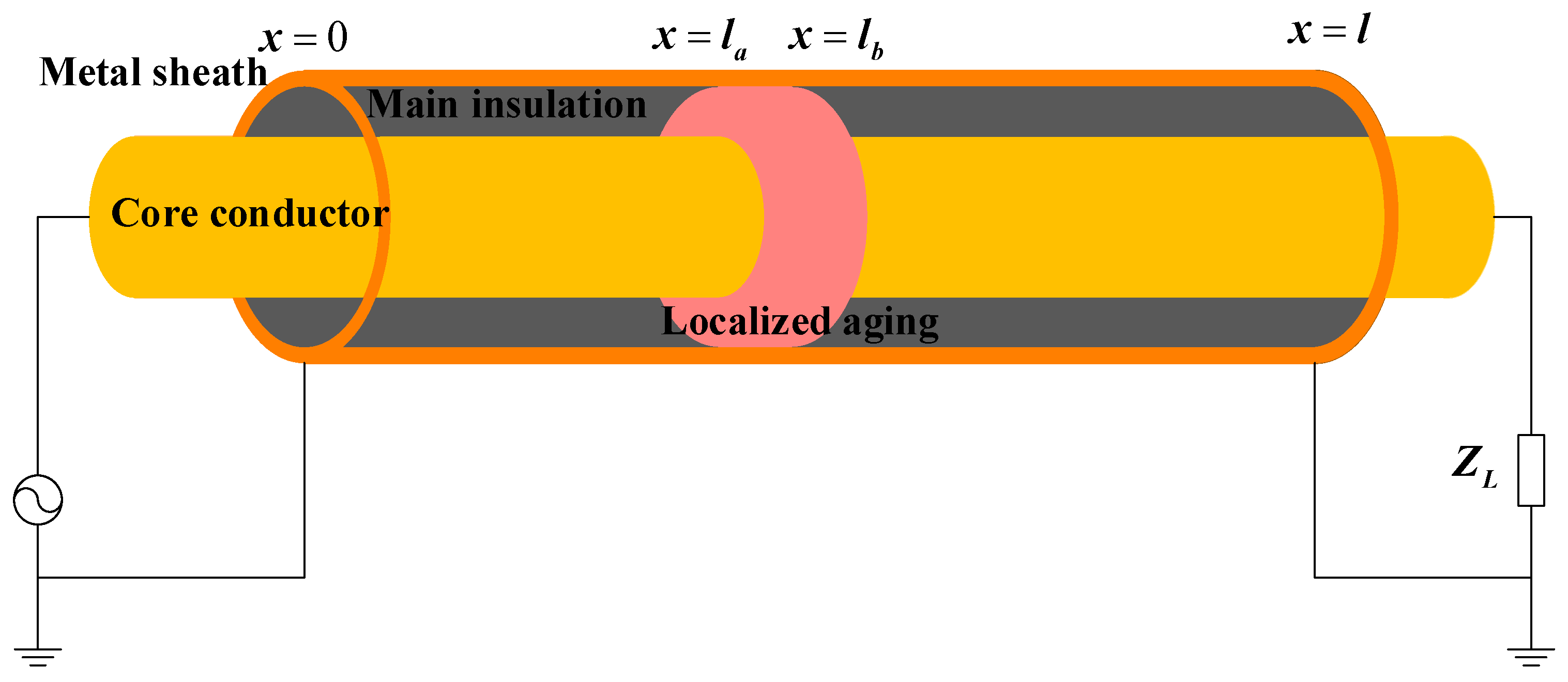
2.4. Input Impedance at the Source End of the Localized Aging Cable
3. Simulation and Analysis
3.1. Background of Simulation
3.2. Simulation and Results
3.2.1. Impedance Spectroscopy of Cables Under Different Conditions
3.2.2. Influence of Overall Aging on Impedance Spectroscopy
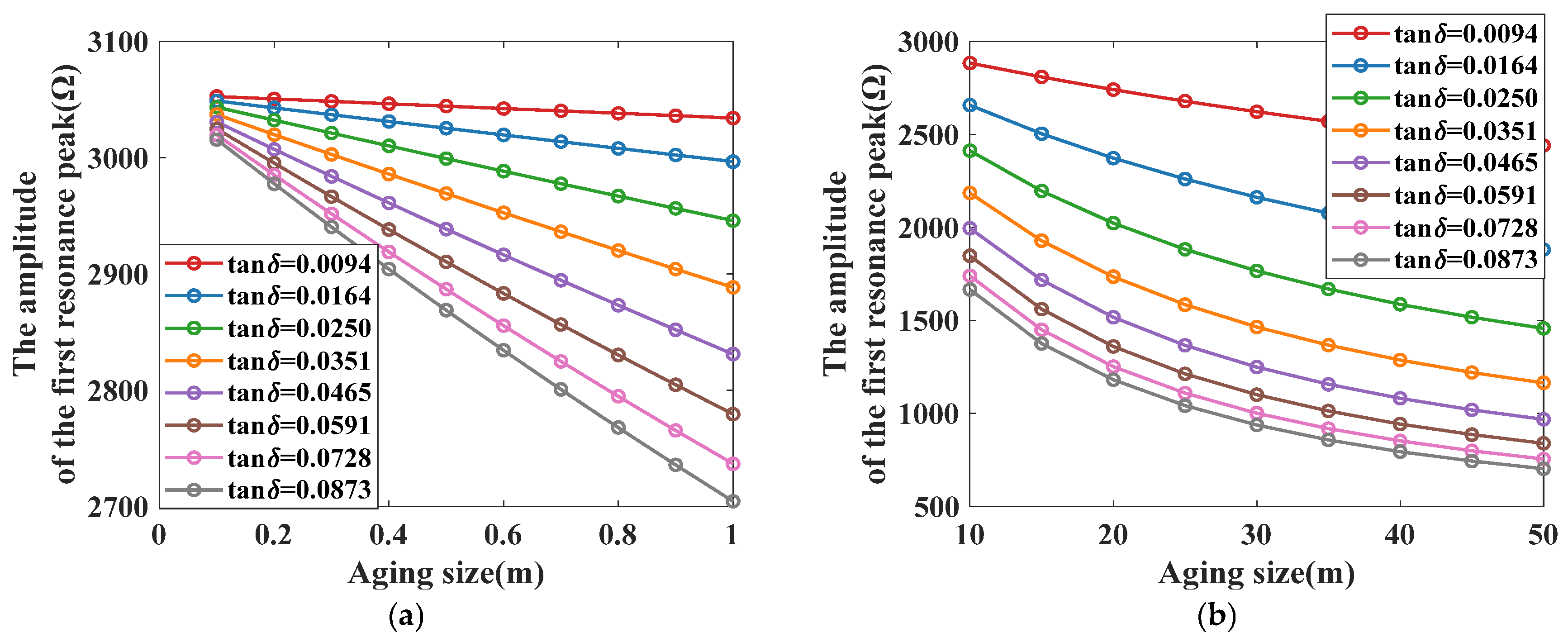
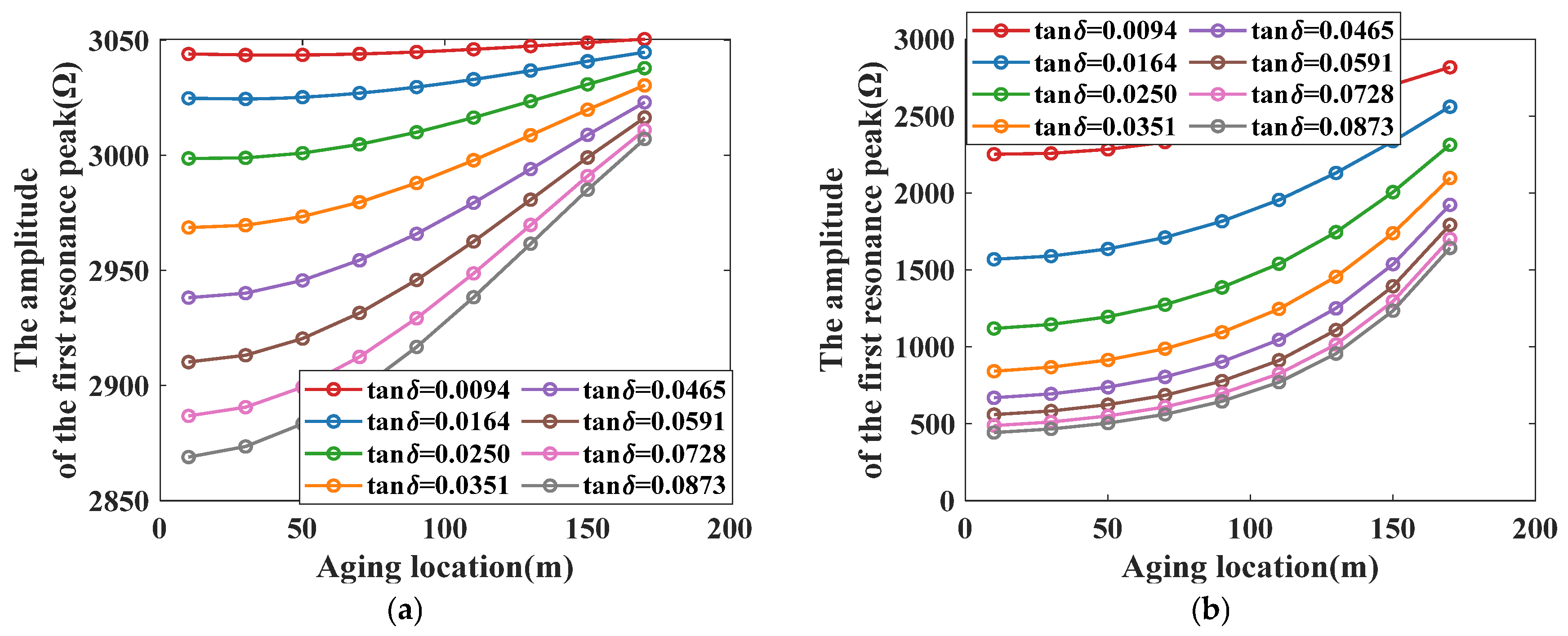
3.2.3. Influence of Localized Aging on the Impedance Spectroscopy
3.2.4. Impedance Spectroscopy-Based Diagnostic Framework for Assessing the Insulation Condition of HV Single-Core Cables
3.3. Analysis of Factors Influencing the Impedance Spectroscopy
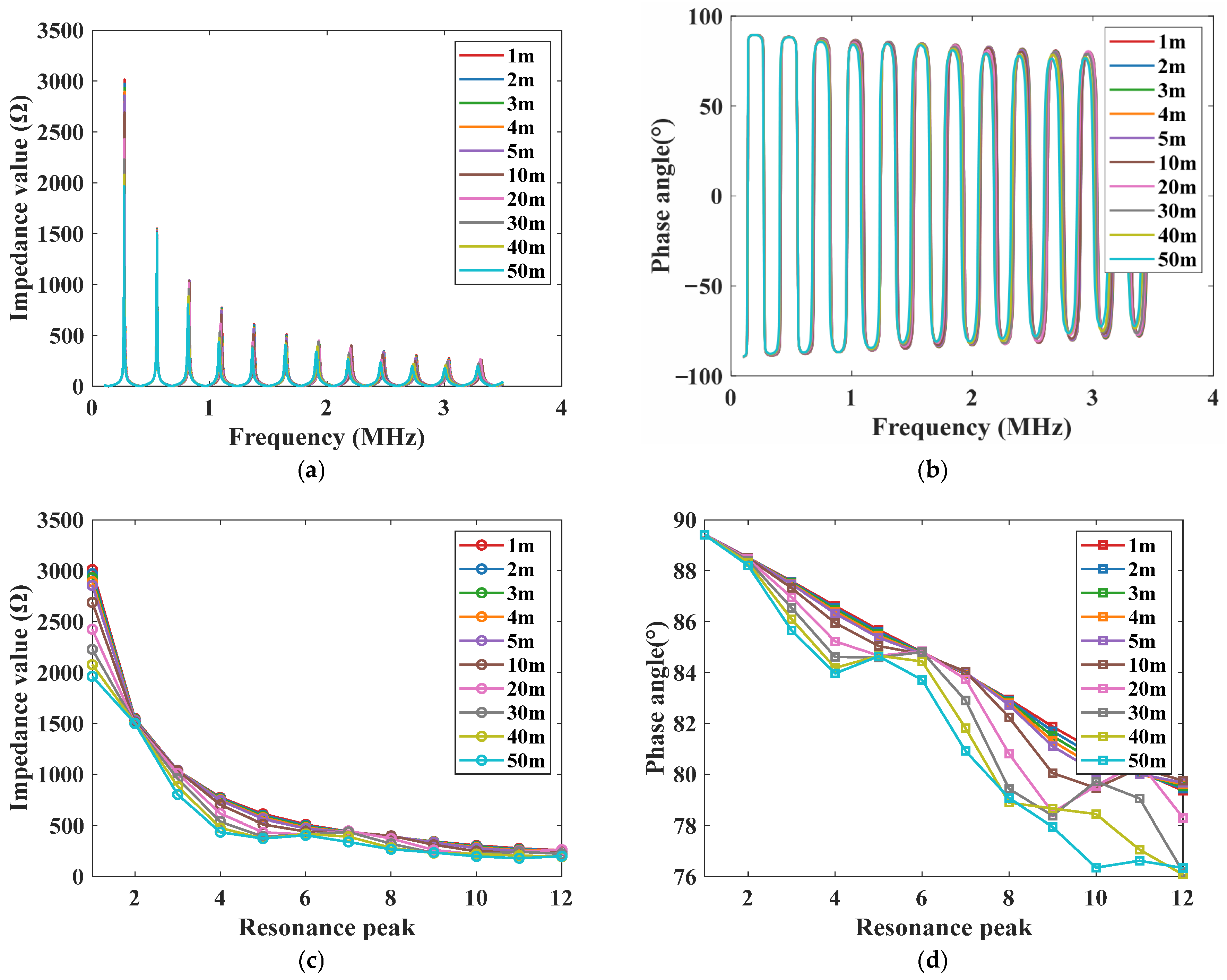
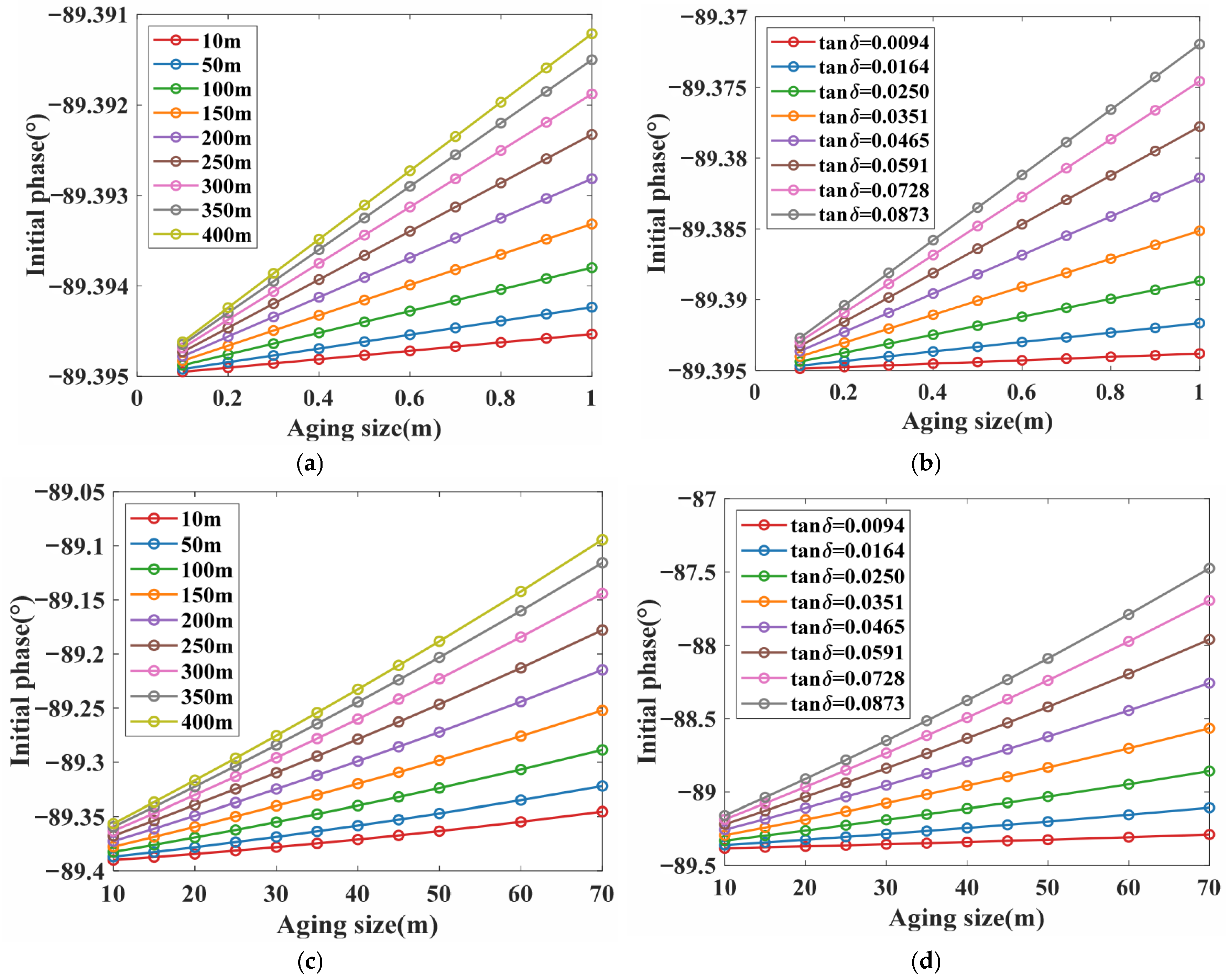
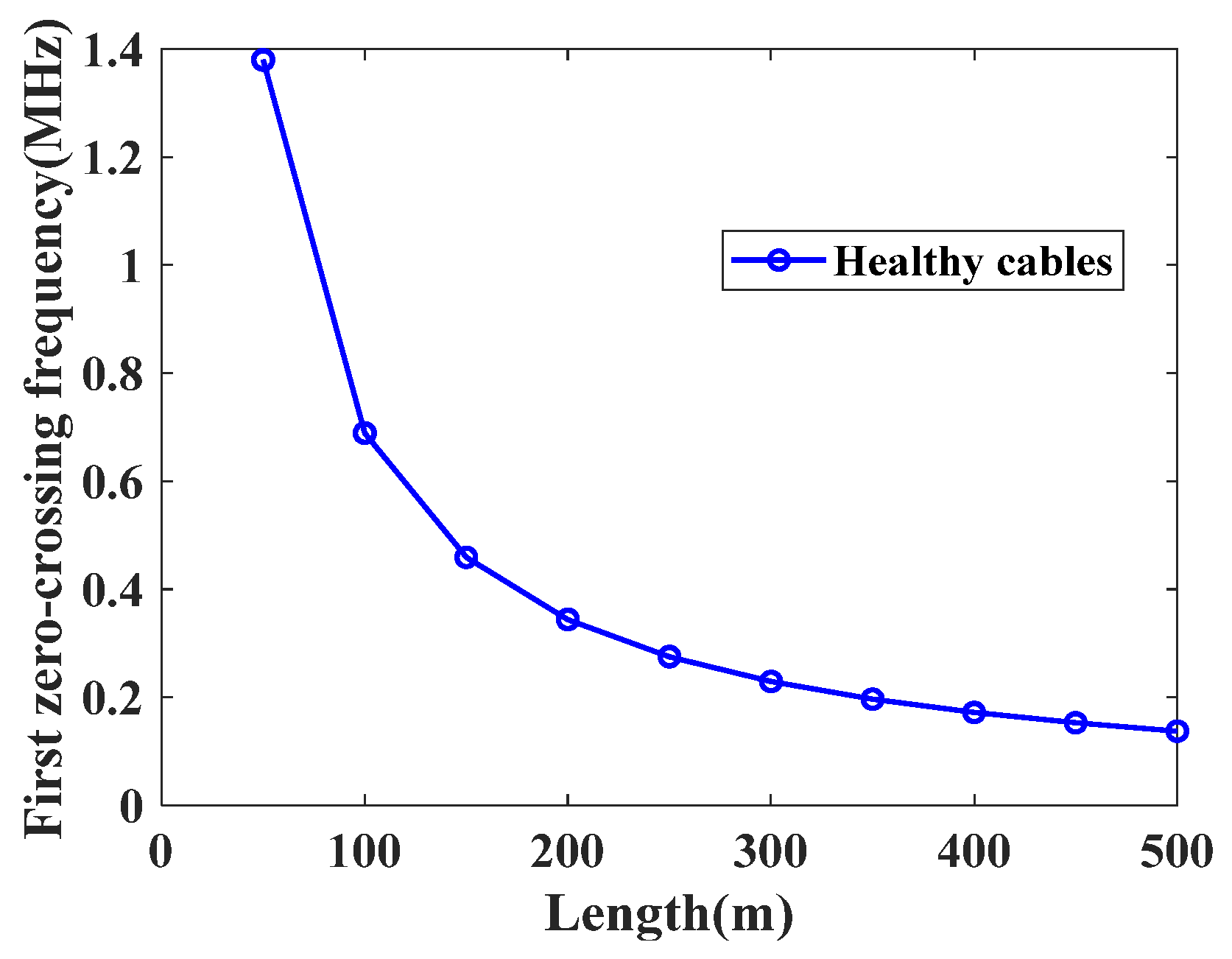
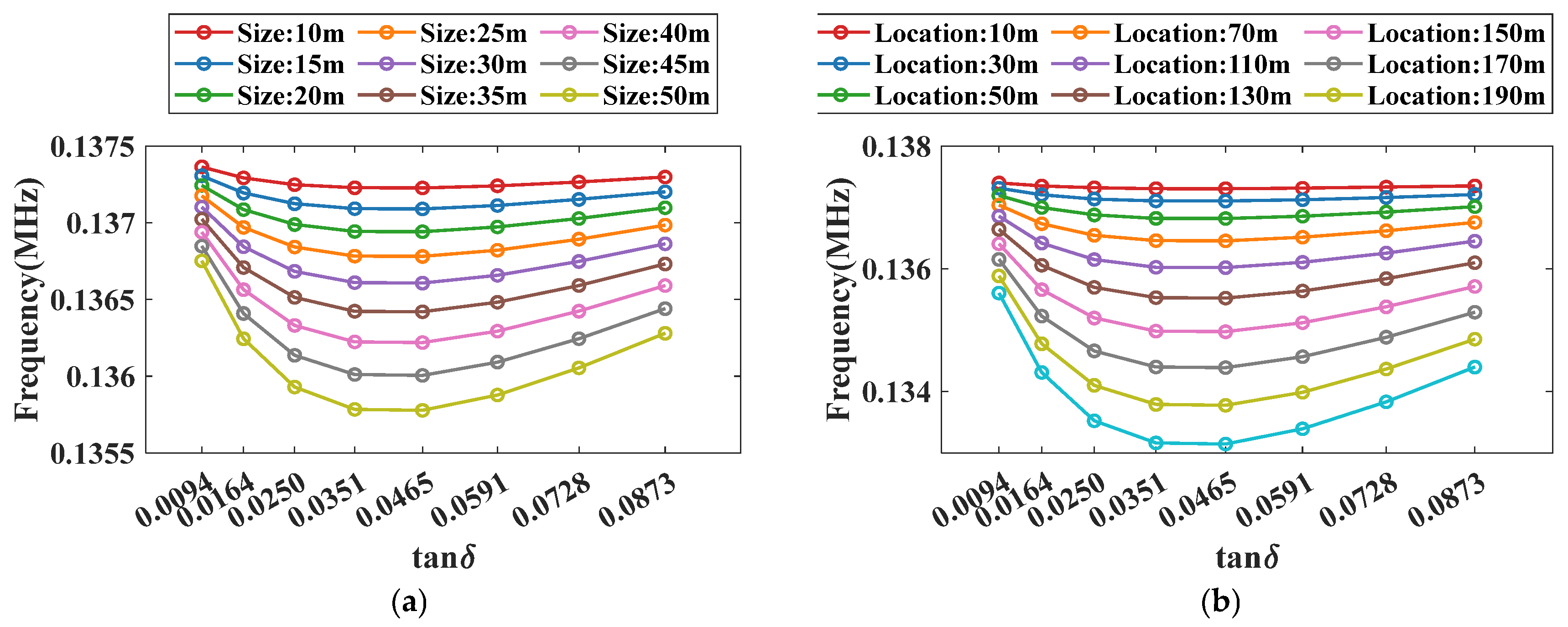
3.3.1. Impact of Cable Length
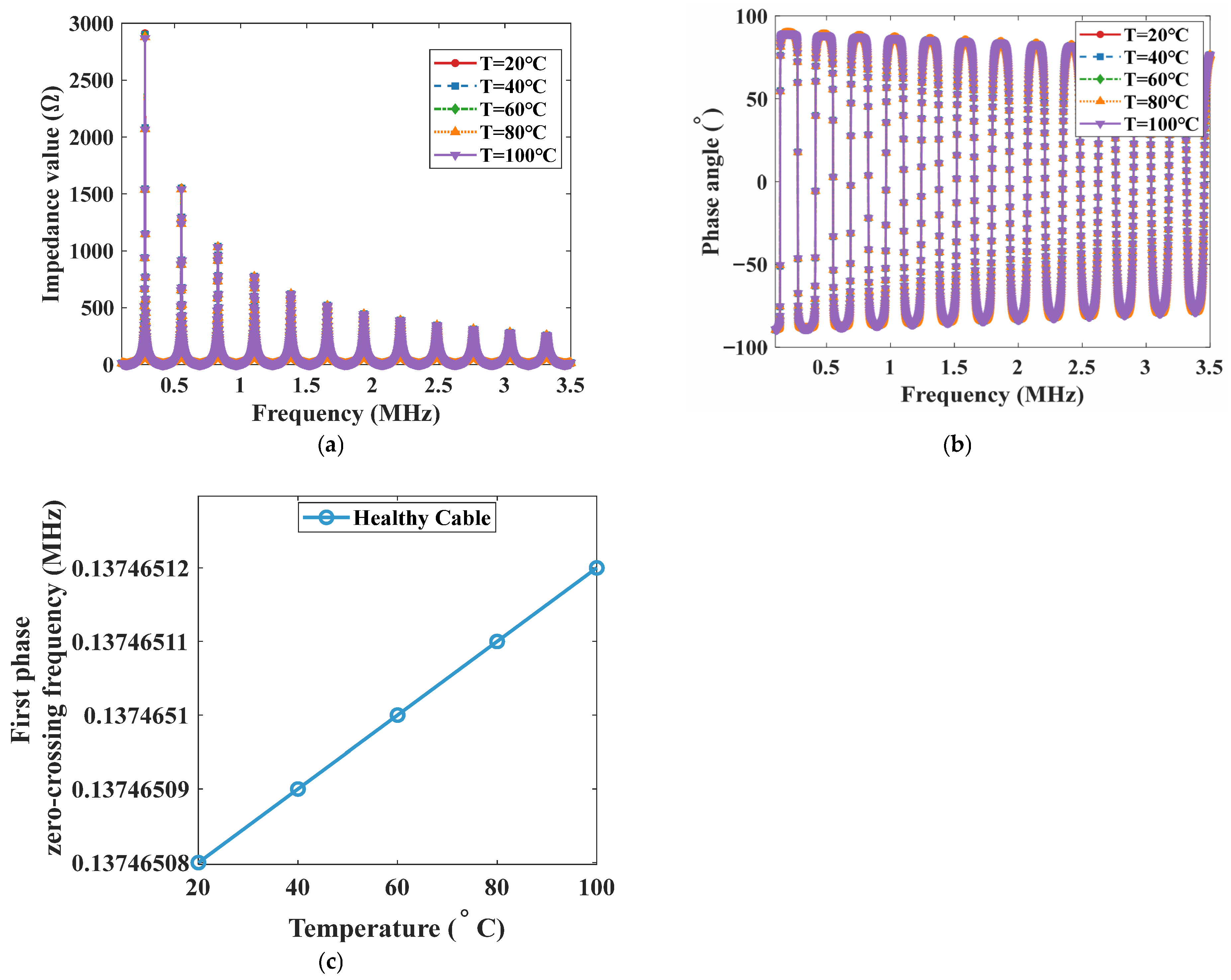
3.3.2. Impact of Instantaneous Temperature
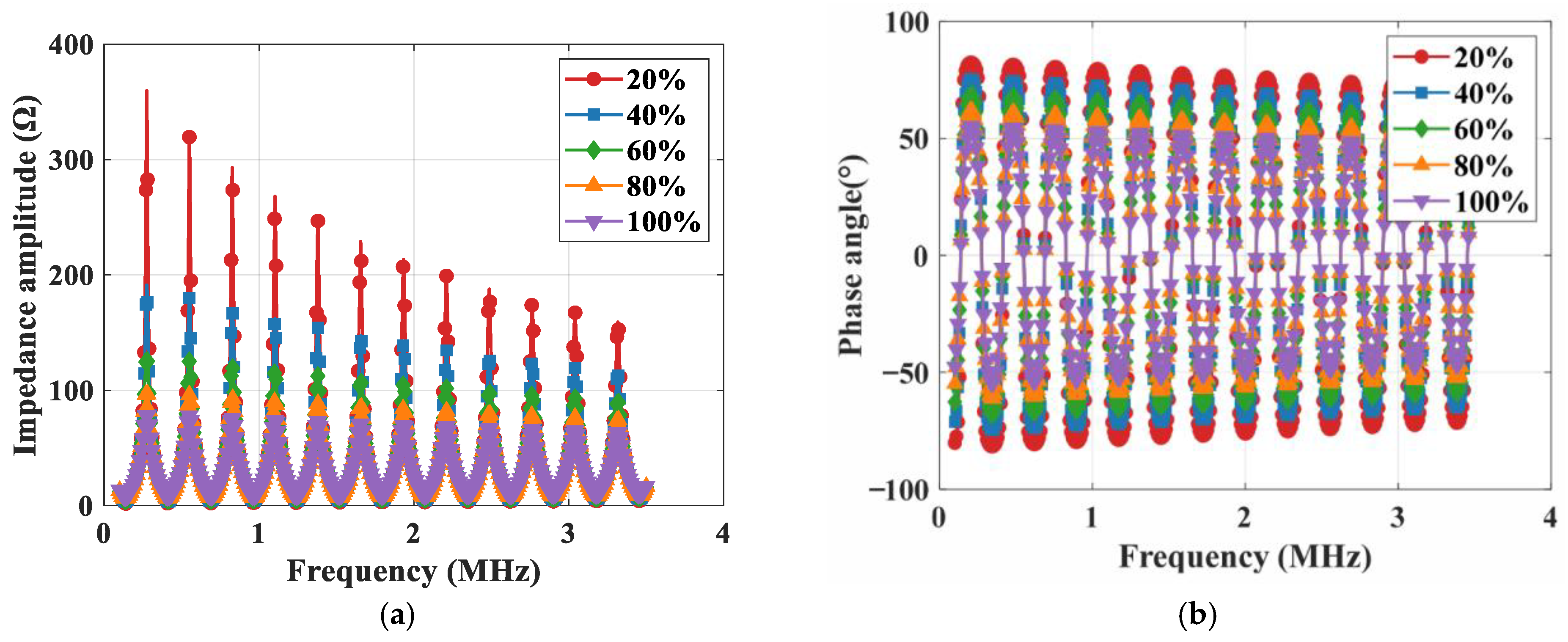
3.3.3. Impact of Load Rate
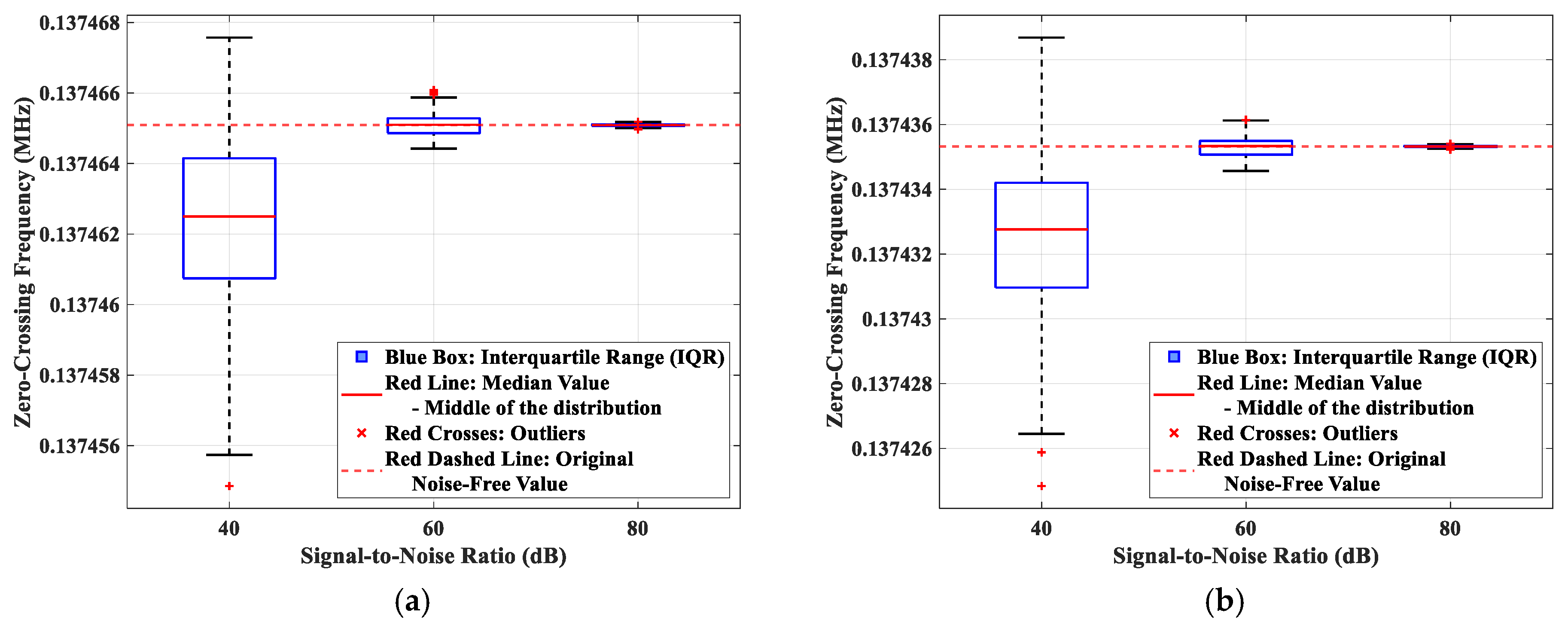
3.4. Sensitivity Analysis of the Proposed Method to Random Noise
4. Discussion
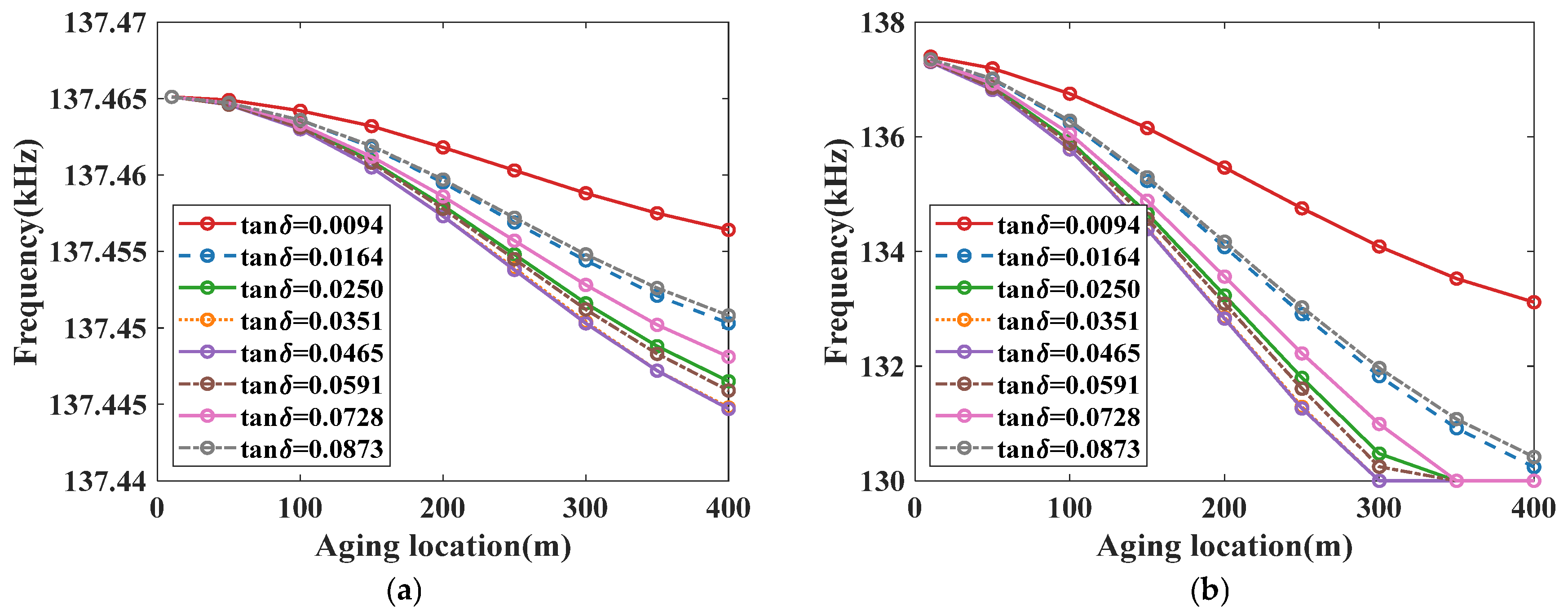
4.1. The Cause of the Dual-Frequency Offset Phenomenon
4.2. Comparison
4.3. Future Work Prospects: Hardware-Software System Design for Engineering Applications
4.3.1. Selection of High-Precision Impedance Sensing Probes
4.3.2. Hardware-Software Integrated System Architecture
4.3.3. Measurement Strategy and Data Reliability Assurance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, L.; Li, B.; Zhao, L.; Xu, L.; Zhu, F. High Voltage Cable Insulation Aging Mechanism and Prevention Measures Research. Brand Stand. 2024, 2, 76–78. [Google Scholar]
- Wang, J.; Li, W.; Zhang, W.; Wan, B.; Zha, J. Aging and Lifetime Regulation of Cross-Linked Polyethylene for Cable Insulation Materials. Acta Phys. Sin. 2024, 73, 363–374. [Google Scholar]
- Chen, Y.; Hui, B.; Cheng, Y.; Hao, Y.; Fu, M.; Yang, L.; Hou, S.; Li, L. Failure investigation of buffer layers in high-voltage XLPE cables. Eng. Fail. Anal. 2020, 113, 104546. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, K.; Wang, C.; Meng, P.; Li, Y.; Lin, S.; Fu, Y.; Yuan, H. Failure of Cable Accessory: Interface Breakdown Under the Effect of Moisture. IEEE Trans. Power Deliv. 2024, 39, 2644–2652. [Google Scholar] [CrossRef]
- Kruizinga, B.; Wouters, P.A.A.F.; Steennis, E.F. Fault development upon water ingress in damaged low voltage underground power cables with polymer insulation. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 808–816. [Google Scholar] [CrossRef]
- Ge, X.; Fan, F.; Given, M.J.; Stewart, B.G. Insulation Resistance Measurements of Medium-Voltage Cross-Linked Polyethylene Cables under Thermal Stresses. In Proceedings of the 2024 IEEE Electrical Insulation Conference, EIC 2024, Minneapolis, MN, USA, 2–5 June 2024; Institute of Electrical and Electronics Engineers Inc.: Minneapolis, MN, USA, 2024; pp. 34–37. [Google Scholar]
- Um, K.H.; Lee, K.W. Development of Equipment to Measure Insulation Resistance and Evaluate the Lifetime of High-voltage Cable in Operation. J. Inst. Internet Broadcast. Commun. 2014, 14, 237–242. [Google Scholar] [CrossRef]
- Geng, P.; Song, J.; Tian, M.; Lei, Z.; Du, Y. Influence of thermal aging on AC leakage current in XLPE insulation. Aip Adv. 2018, 8, 025115. [Google Scholar] [CrossRef]
- Noske, S.; Rakowska, A.; Siodla, K. Measurements of partial discharges as source of management knowledge improvement of the power cable network. Prz. Elektrotechniczny 2008, 84, 12–15. [Google Scholar]
- Zhang, X.; Zhang, Y. Analysis of Partial Discharge Characteristics of Power Cable and Research on Operation and Maintenance Strategy. Electr. Technol. 2022, 11, 95–98. [Google Scholar]
- Montanari, G.C.; Cavallini, A.; Pulettli, F. A new approach to partial discharge testing of HV cable systems. IEEE Electr. Insul. Mag. 2006, 22, 14–23. [Google Scholar] [CrossRef]
- Wester, F.J.; Gulski, E.; Smit, J.J. Detection of partial discharges at different AC voltage stresses in power cables. IEEE Electr. Insul. Mag. 2007, 23, 28–43. [Google Scholar] [CrossRef]
- Hong, S.; Son, W.; Cheon, H.; Kang, D.; Park, J. Detection and localization of partial discharge in high-voltage direct current cables using a high-frequency current transformer. J. Sens. Sci. Technol. 2021, 30, 105–108. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, J.; Luo, C.; Zhang, J. A Study on Aging Characteristics of Silicone Oil in HV Oil-filled Cable Termination Based on Infrared Thermal Imaging Test. In Proceedings of the International Conference on Engineering Technology and Application, ICETA 2015, Xiamen, China, 29–30 May 2015; EDP Sciences: Xiamen, China, 2015. [Google Scholar]
- Yu, G. Three-Dimensional Point Cloud Stitching Method for Infrared Images of High-Voltage Cables Based on Improved Feature Point Matching. 2024. Available online: https://ssrn.com/abstract=4813623 (accessed on 2 March 2025).
- Wang, D.; Liu, J.; Hou, M. Novel travelling wave fault location approach for overhead transmission lines. Int. J. Electr. Power Energy Syst. 2024, 155, 109617. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.A.; Liu, Y. Travelling Wave Based Velocity-Free Single-Ended Fault Location Method for Transmission Lines. IEEE Trans. Power Deliv. 2025, 40, 1874–1888. [Google Scholar] [CrossRef]
- Walczak, K. Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors. Energies 2023, 16, 2297. [Google Scholar] [CrossRef]
- Su, J.; Wei, L.; Zhang, P.; Li, Y.; Liu, Y. Multi-type defect detection and location based on non-destructive impedance spectrum measurement for underground power cables. High Volt. 2023, 8, 977–985. [Google Scholar] [CrossRef]
- Toman, G.J.; Fantoni, P.F. Cable aging assessment and condition monitoring using line resonance analysis (LIRA). In Proceedings of the 16th International Conference on Nuclear Engineering, ICONE16 2008, Orlando, FL, USA, 11–15 May 2008; American Society of Mechanical Engineers (ASME): Orlando, FL, USA, 2008; pp. 177–186. [Google Scholar]
- Ohki, Y.; Hirai, N. Location feasibility of degradation in cable through Fourier transform analysis of broadband impedance spectra. Electr. Eng. Jpn. 2013, 183, 1–8. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, D.; He, J.; Li, M. Local degradation diagnosis for cable insulation based on broadband impedance spectroscopy. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2097–2107. [Google Scholar] [CrossRef]
- Clayton, R.P. The Transmission Line Equations for Multiconductor Lines. In Analysis of Multiconductor Transmission Lines; IEEE: New York, NY, USA, 2008; pp. 89–109. [Google Scholar]
- Wedepohl, L.M.; Wilcox, D.J. Transient analysis of underground power-transmission systems. System-model and wave-propagation characteristics. Proc. Inst. Electr. Eng. 1973, 120, 253–260. [Google Scholar] [CrossRef]
- Fothergill, J.C.; Dodd, S.J.; Dissado, L.A.; Liu, T.; Nilsson, U.H. The Measurement of Very Low Conductivity and Dielectric Loss in XLPE Cables: A Possible Method to Detect Degradation Due to Thermal Aging. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1544–1553. [Google Scholar] [CrossRef]
- Ojha, S.K.; Purkait, P.; Chatterjee, B.; Chakravorti, S. Application of Cole-Cole model to transformer oil-paper insulation considering distributed dielectric relaxation. High Volt. 2019, 4, 72–79. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Y.; Liu, H.; Dong, S.; Lv, Y.; Ma, J. Dielectric Variations of Potato Induced by Irreversible Electroporation under Different Pulses Based on the Cole-Cole Model. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2225–2233. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, K.; Yang, M.; Zhan, W.; Tao, W.; Yao, G. A Novel Water Electrode Method for Accelerating Water Tree Aging of XLPE Cables. Insul. Mater. 2015, 48, 45–50. [Google Scholar]
- Bezprozvannych, A.V.; Kessaev, A.G.; Shcherba, M.A. Frequency dependence of dielectric loss tangent on the degree of humidification of polyethylene cable insulation. Tech. Electrodyn. 2016, 2016, 18–24. [Google Scholar] [CrossRef]
- Li, H.; Xi, Z.; Xu, L.; Shan, C.; Nan, M.; Zhao, L. Research on the degradation in micro-structure and dielectric performance of XLPE cable insulation in service. J. Mater. Sci. Mater. Electron. 2023, 34, 1449. [Google Scholar] [CrossRef]
- Li, G.; Chen, J.; Li, H.; Hu, L.; Zhou, W.; Zhou, C.; Li, M. Diagnosis and Location of Power Cable Faults Based on Characteristic Frequencies of Impedance Spectroscopy. Energies 2022, 15, 5617. [Google Scholar] [CrossRef]
- Bade, T.G.; Roudet, J.; Guichon, J.-M.; Kuo-Peng, P.; Sartori, C.A.F. Analysis of the resonance phenomenon in unmatched power cables with the resonance surface response. Electr. Power Syst. Res. 2021, 200, 107466. [Google Scholar] [CrossRef]
- Wang, H.; Sun, M.; Zhao, K.; Wang, X.; Wang, W.; Li, C. Diagnostic Evaluation Method for Cable Insulation Aging Using High-Voltage Frequency Domain Dielectric Spectroscopy. Proc. CSEE 2023, 43, 3630–3642. [Google Scholar]
- Chukwu, R.; Mugisa, J.; Brogioli, D.; La Mantia, F. Statistical Analysis of the Measurement Noise in Dynamic Impedance Spectra. Chemelectrochem 2022, 9, e202200109. [Google Scholar] [CrossRef] [PubMed]
- Py, B.; Maradesa, A.; Ciucci, F. Gaussian processes for the analysis of electrochemical impedance spectroscopy data: Prediction, filtering, and active learning. Electrochim. Acta 2023, 439, 141688. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, C.J.; Gao, B.B.; Zhao, L.X. A Fast Measurement Method for Electrochemical Impedance Spectroscopy Based on White Noise. Min. Metall. 2020, 29, 57–62. [Google Scholar]
- Elsoe, K.; Kraglund, M.R.; Grahl-Madsen, L.; Scherer, G.G.; Hjelm, J.; Jensen, S.H.; Jacobsen, T.; Mogensen, M.B. Noise Phenomena in Electrochemical Impedance Spectroscopy of Polymer Electrolyte Membrane Electrolysis Cells. Fuel Cells 2018, 18, 640–648. [Google Scholar] [CrossRef]
- Gao, L.; Hu, Q.; Gao, X.; Liu, Y.; Yuan, Y. Review of Diagnostic and Detection Technologies for Power Cables. Electr. Wire Cable 2025, 68, 1–11. [Google Scholar]
- Jin, C. Design of Distributed Monitoring System for Cable Partial Discharge Based on Internet of Things. China New Telecommun. 2025, 27, 14–16. [Google Scholar]
- Gao, Q.; Yang, J. Review of Power Cable Fault Diagnosis Research. Guizhou Electr. Power Technol. 2016, 19, 54–58. [Google Scholar]
- Dong, Y. Application of Low Frequency Impedance Analyzer in Metrology and Testing. Mod. Meas. Lab. Manag. 2002, 10, 25–27. [Google Scholar]
- Yang, X.; He, G. Design and Implementation of an Ultra-Low-Cost Impedance Analyzer. In Proceedings of the 16th IEEE International Conference on Electronic Measurement and Instruments, ICEMI 2023, Harbin, China, 9–11 August 2023; Institute of Electrical and Electronics Engineers Inc.: Harbin, China, 2023; pp. 33–38. [Google Scholar]
- Zhou, Z. Research on Cable Local Defect Diagnosis Method Based on Broadband Impedance Spectrum. Ph.D. Thesis, Tianjin University, Tianjin, China, 2015. [Google Scholar]
- Zhang, F.; Yuan, H.; Zhang, F. Signals and Systems, 1st ed.; Chemical Industry Press: Beijing, China, 2015; p. 233. [Google Scholar]
- Lin, J.; Xu, D. Brief Discussion on Kelvin Four-Wire Testing Technology and Its Application in ATE Testing. Equip. Electron. Prod. Manuf. 2017, 46, 22–25. [Google Scholar]
- Zhao, M.; Ding, X. Research on Compensation Algorithm for Impedance Analyzer Adapter Fixture. Electron. Product Reliab. Environ. Test 2021, 39, 69–73. [Google Scholar]






| Diagnostic Method | Major Limitations |
|---|---|
| Insulation Resistance | Low sensitivity to localized defects; highly sensitive to environmental conditions |
| PD | Susceptible to EMI; signal attenuation |
| Infrared Thermography | Limited to surface |
| Traveling Wave | Environmentally influenced wave velocity |
| Capacitive Sensor Array | Limited by cable structure complexity |
| LIRA | Undisclosed algorithms |
| IFFT | Constrained by practical high-frequency limitations |
| Integral Transform | Requires model recalibration |
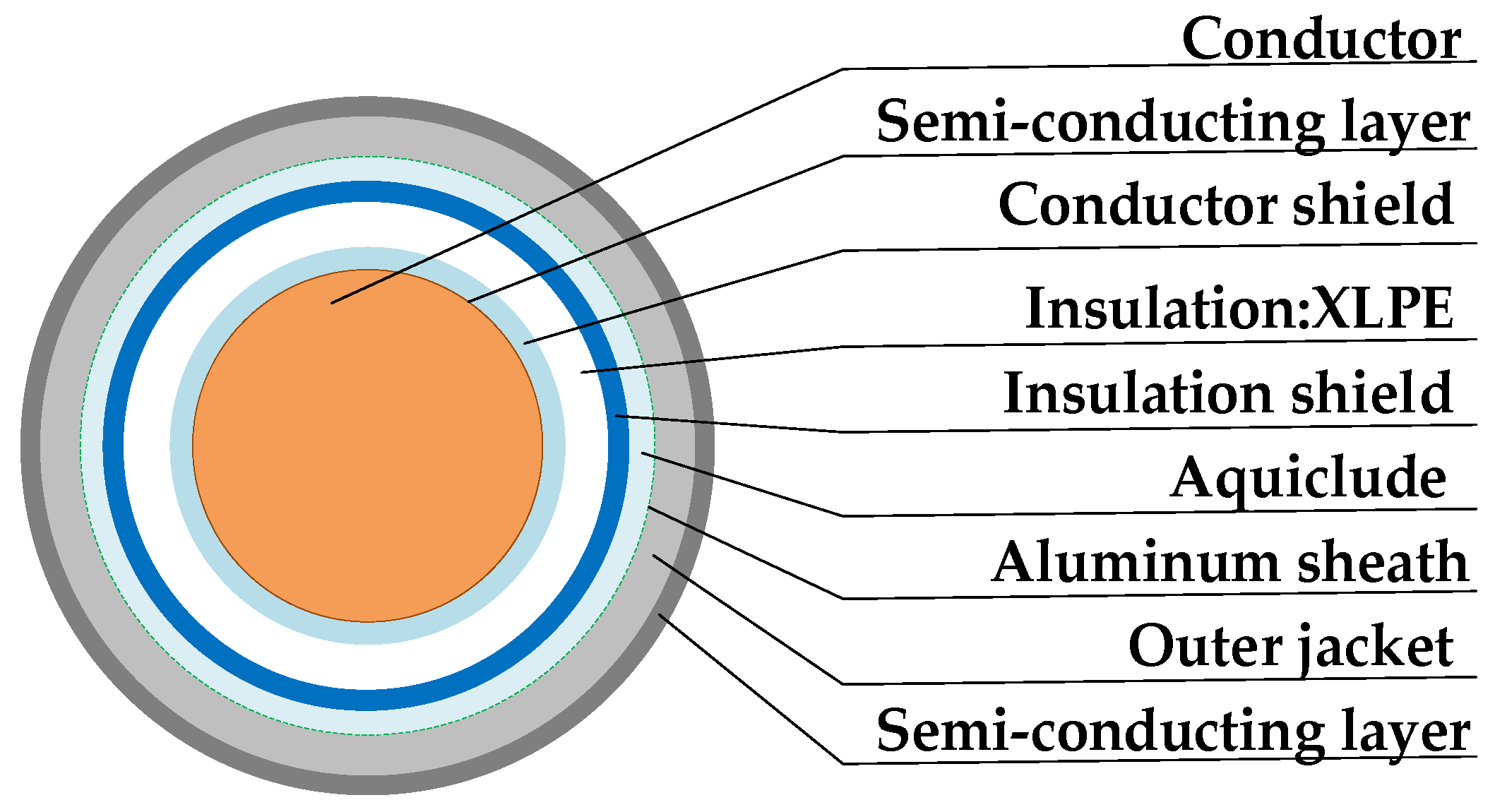
| Structure | Radius/Thickness (mm) |
|---|---|
| Conductor | 14.9 |
| Semi-conducting layer | 2 |
| Insulation | 16.5 |
| Aquiclude | 2 |
| Aluminum sheath | 2 |
| Outer jacket | 4 |
| Parameters Related to Impedance Spectroscopy | Value |
|---|---|
| r1 | 14.9 mm |
| r2 | 35.4 mm |
| r3 | 41.4 mm |
| ρc | 1.68 × 10−8 (Ω·m) |
| ρs | 2.83 × 10−8 (Ω·m) |
| Method | The Proposed Method | Traditional Electrical Test | Partial Discharge (PD) |
|---|---|---|---|
| Dimension | |||
| Detection principle | Impedance spectroscopy | Insulation resistance | Partial discharge signal |
| Non-destructiveness | Excellent | Moderate | Good |
| Condition discrimination | Excellent (Healthy/Overall/Localized) | Poor | Excellent |
| Sensitivity to localized aging | Excellent | Poor | Excellent |
| Quantification of overall aging | Good | - | - |
| Robustness | Excellent | Moderate | Moderate |
| Convenience | Excellent | Moderate | Poor |
| Cost-effectiveness | Good | Moderate | Poor |
| Method | The Proposed Method | IFFT Localization Method | Integral Diagnostic Function Method |
|---|---|---|---|
| Dimension | |||
| Key feature extraction | Fine structure of phase spectroscopy and multiple characteristic points | Time-domain reflected waveform | Integrated value |
| Condition discrimination | Healthy/Overall/Localized | Defect location | Single health index |
| Computational Complexity | Low | High | Medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Tang, Z.; Song, Z.; Zhou, E.; Li, M.; Zhang, X. Insulation Condition Assessment of High-Voltage Single-Core Cables Via Zero-Crossing Frequency Analysis of Impedance Phase Angle. Energies 2025, 18, 3985. https://doi.org/10.3390/en18153985
Wang F, Tang Z, Song Z, Zhou E, Li M, Zhang X. Insulation Condition Assessment of High-Voltage Single-Core Cables Via Zero-Crossing Frequency Analysis of Impedance Phase Angle. Energies. 2025; 18(15):3985. https://doi.org/10.3390/en18153985
Chicago/Turabian StyleWang, Fang, Zeyang Tang, Zaixin Song, Enci Zhou, Mingzhen Li, and Xinsong Zhang. 2025. "Insulation Condition Assessment of High-Voltage Single-Core Cables Via Zero-Crossing Frequency Analysis of Impedance Phase Angle" Energies 18, no. 15: 3985. https://doi.org/10.3390/en18153985
APA StyleWang, F., Tang, Z., Song, Z., Zhou, E., Li, M., & Zhang, X. (2025). Insulation Condition Assessment of High-Voltage Single-Core Cables Via Zero-Crossing Frequency Analysis of Impedance Phase Angle. Energies, 18(15), 3985. https://doi.org/10.3390/en18153985







