An Additional Damping Control Strategy for Grid-Forming Energy Storage to Address Low-Frequency Oscillation
Abstract
1. Introduction
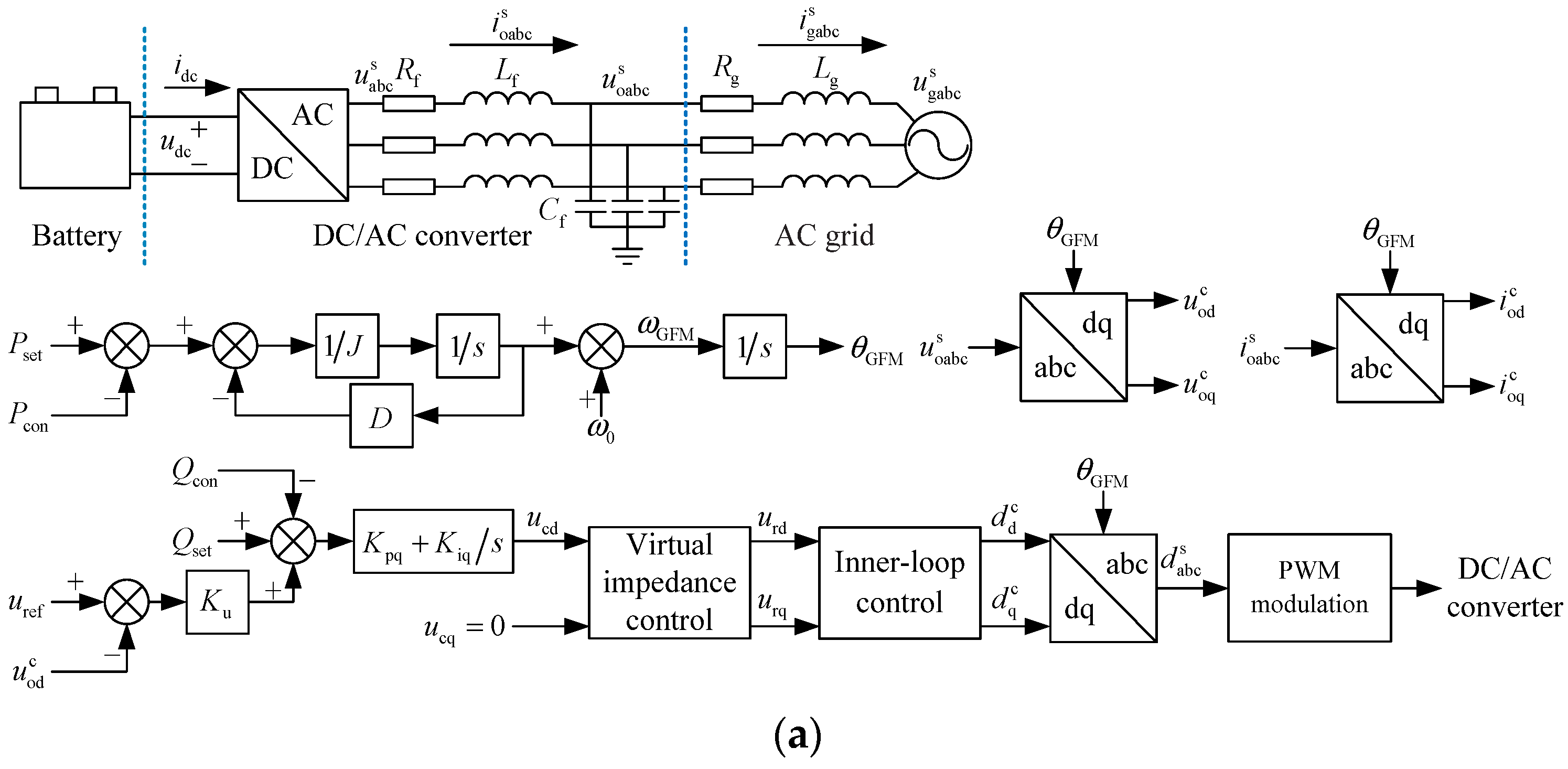
2. A Glimpse of the GFM Energy Storage Grid-Connected System
3. Low-Frequency Oscillation Stability Analysis of the GFM Energy Storage Grid-Connected System
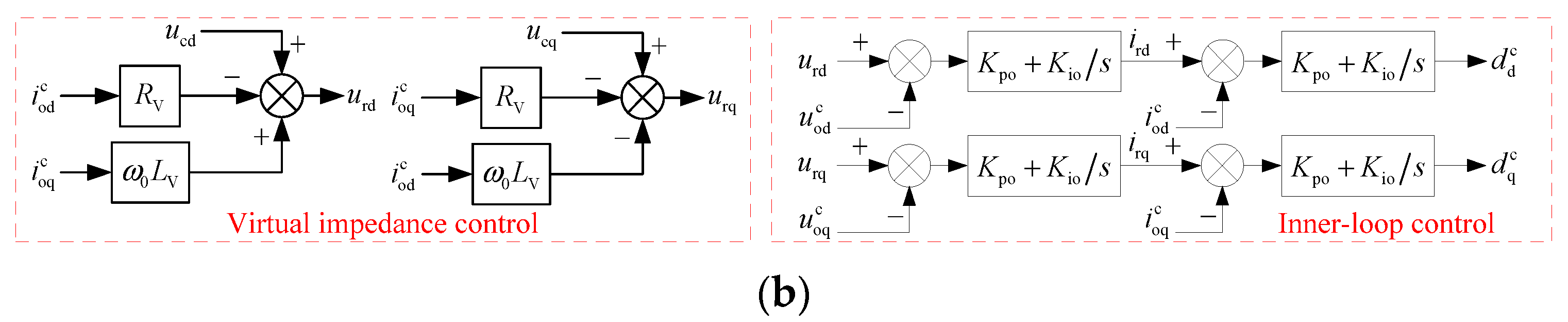
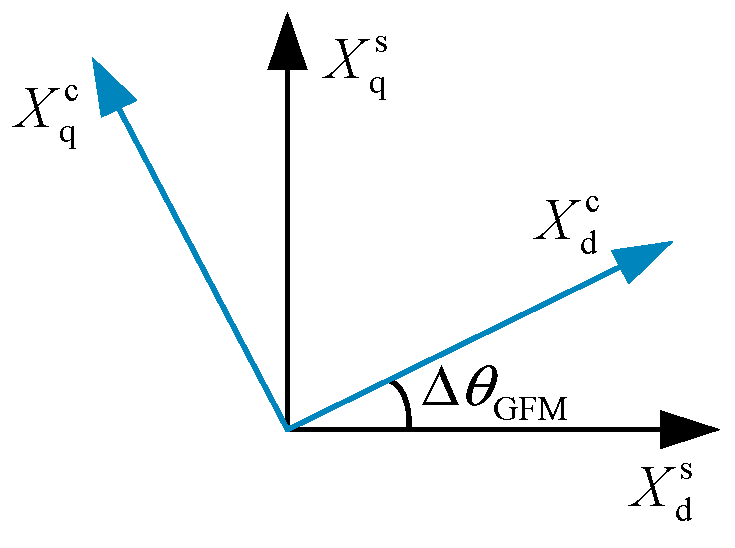
3.1. State-Space Small-Signal Mathematical Modeling of the GFM Energy Storage Grid-Connected System
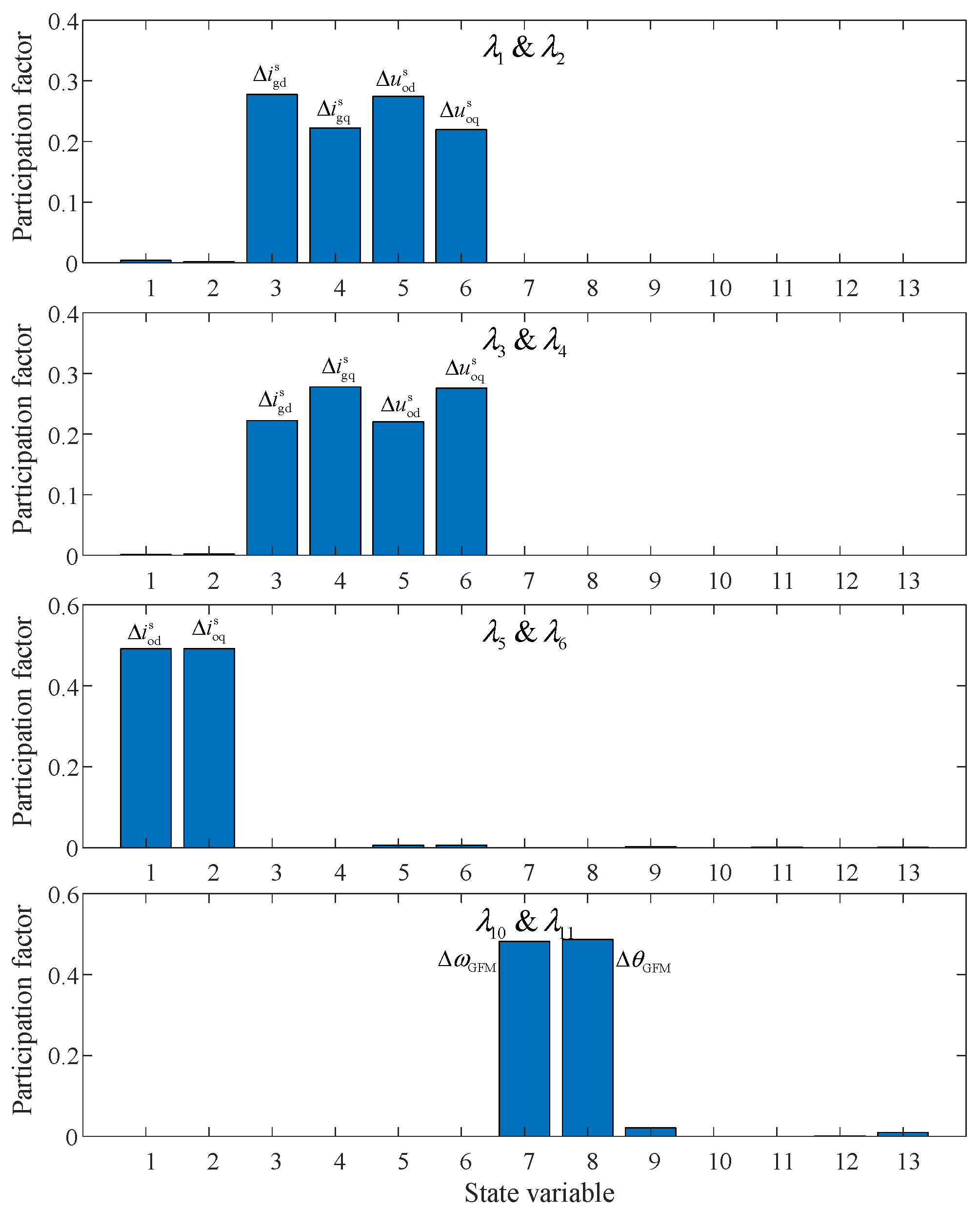
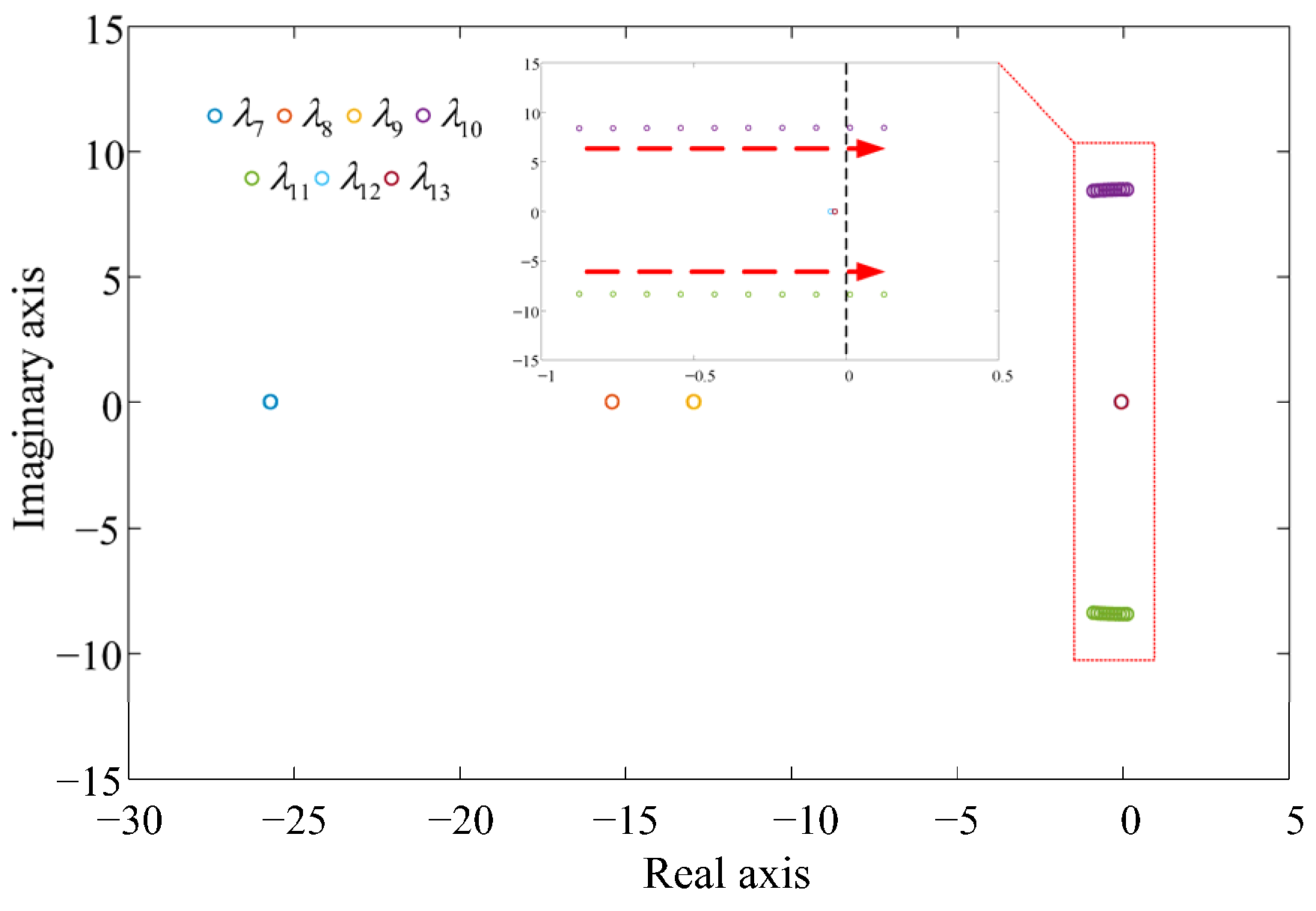
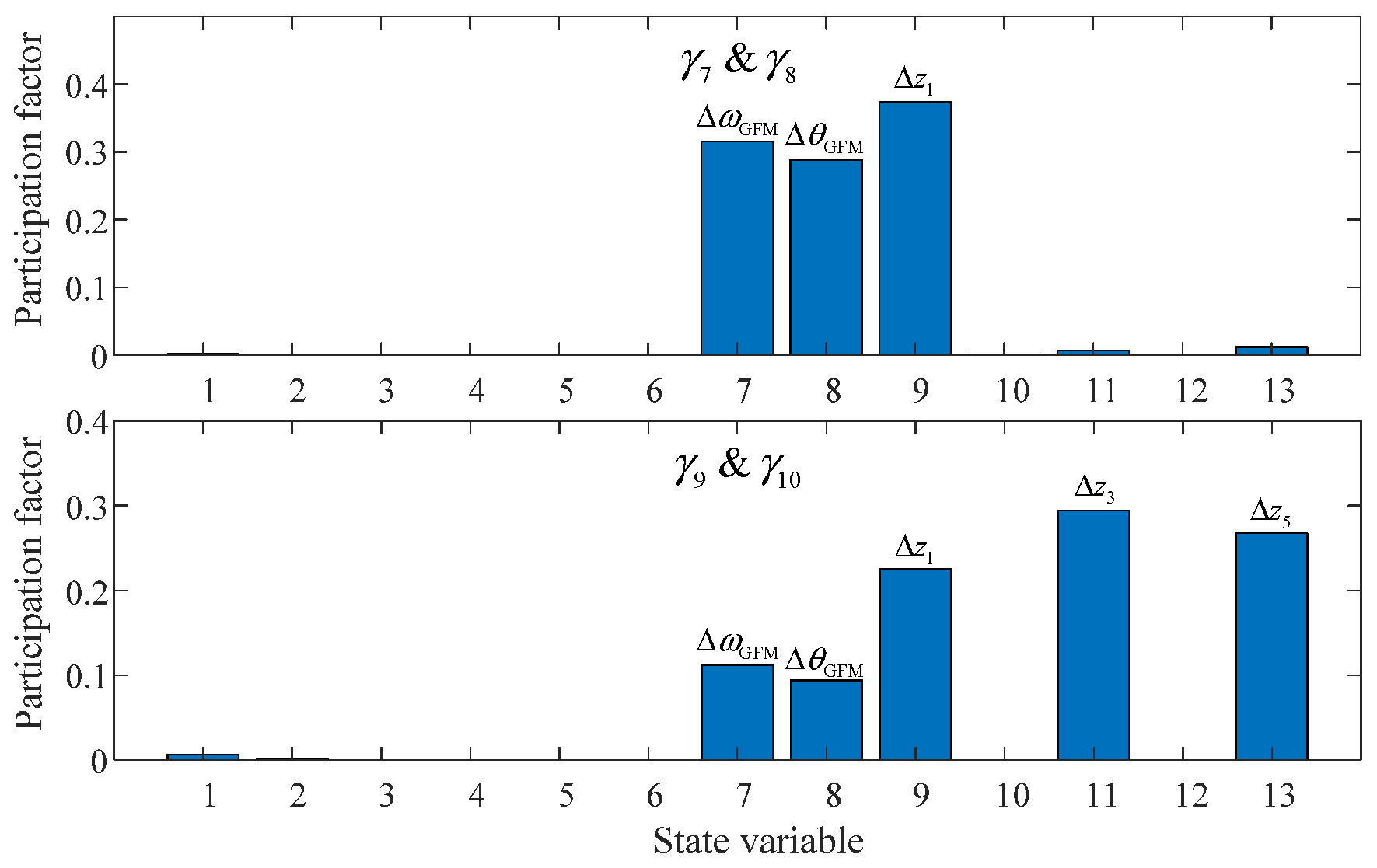
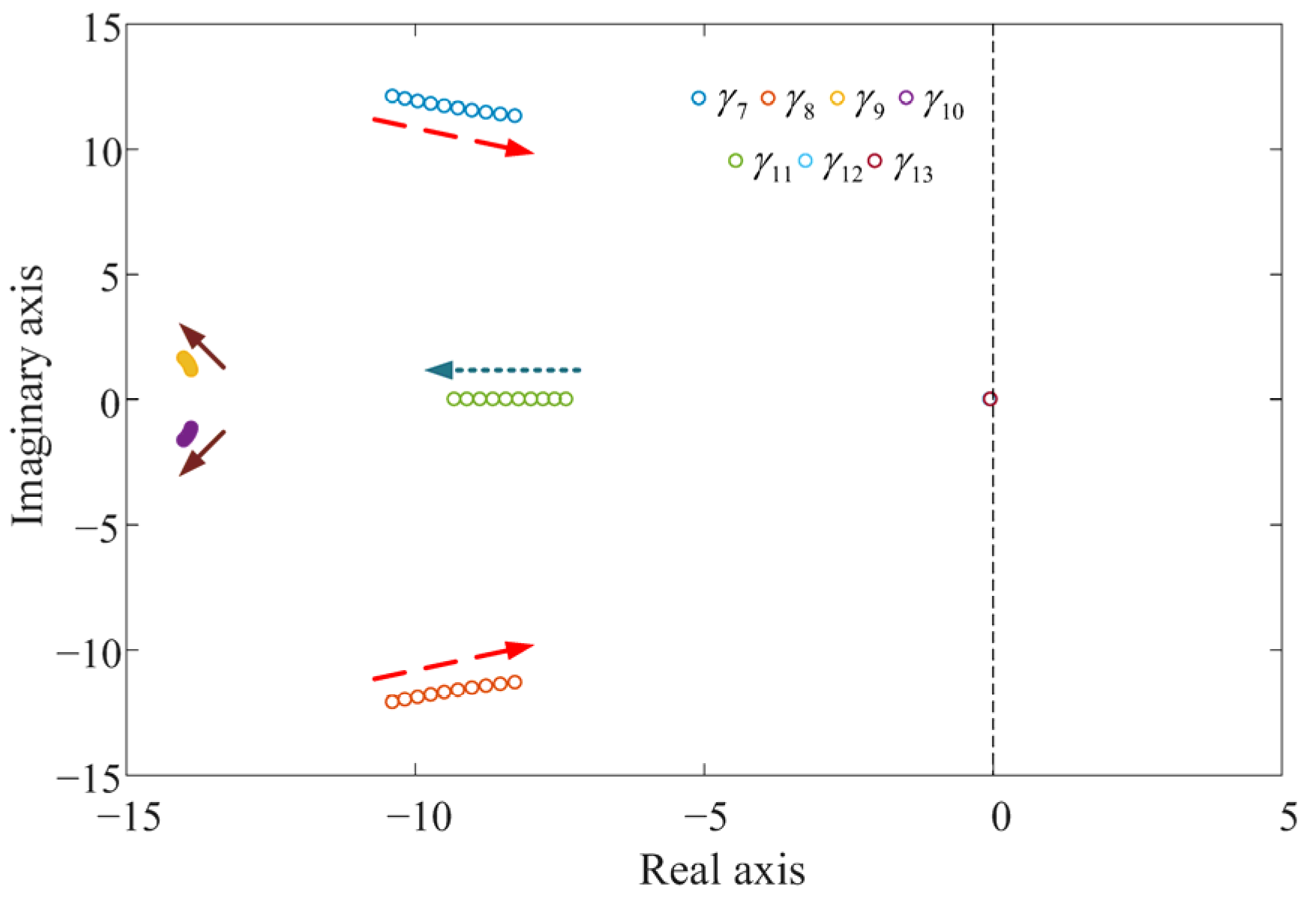
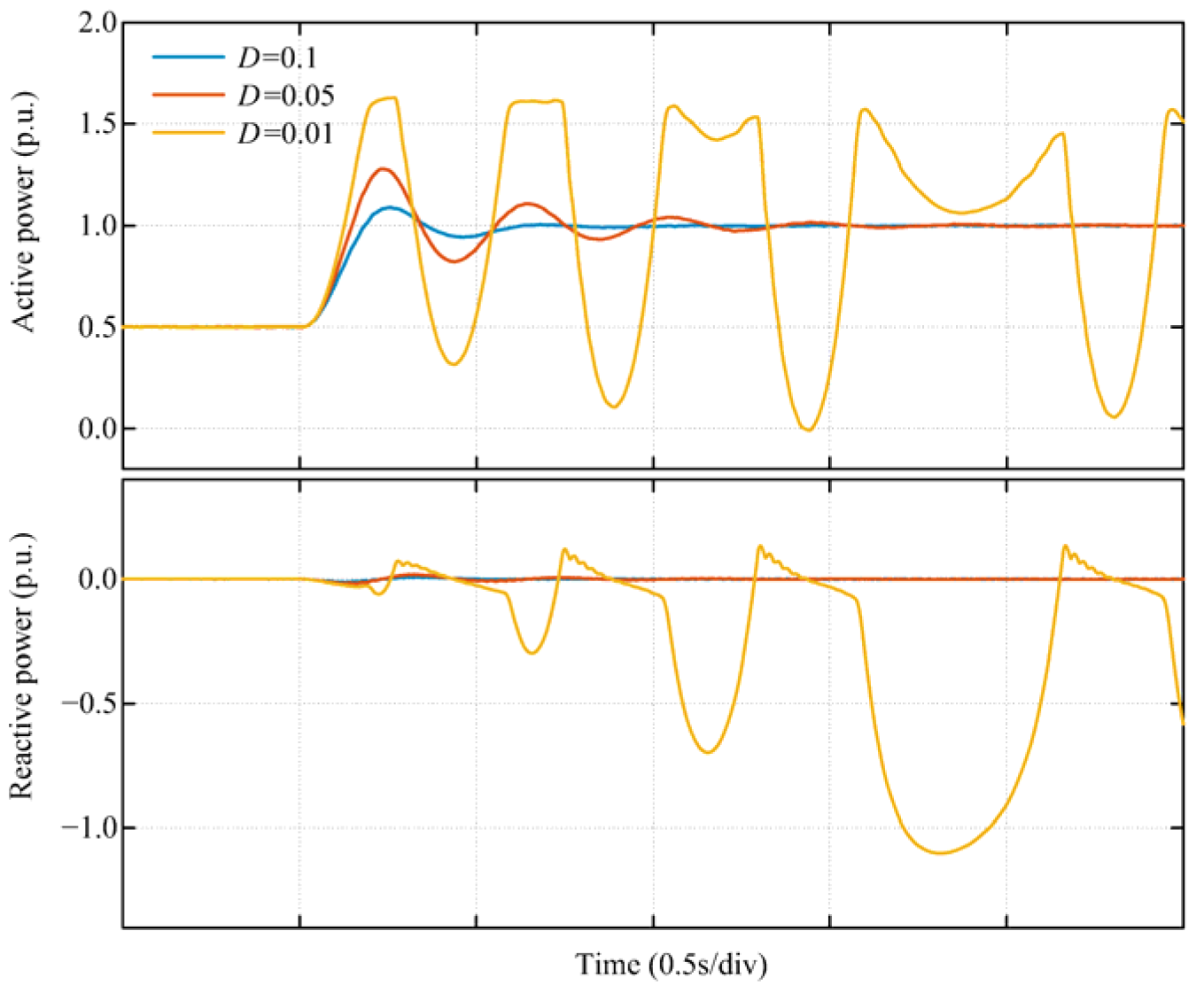
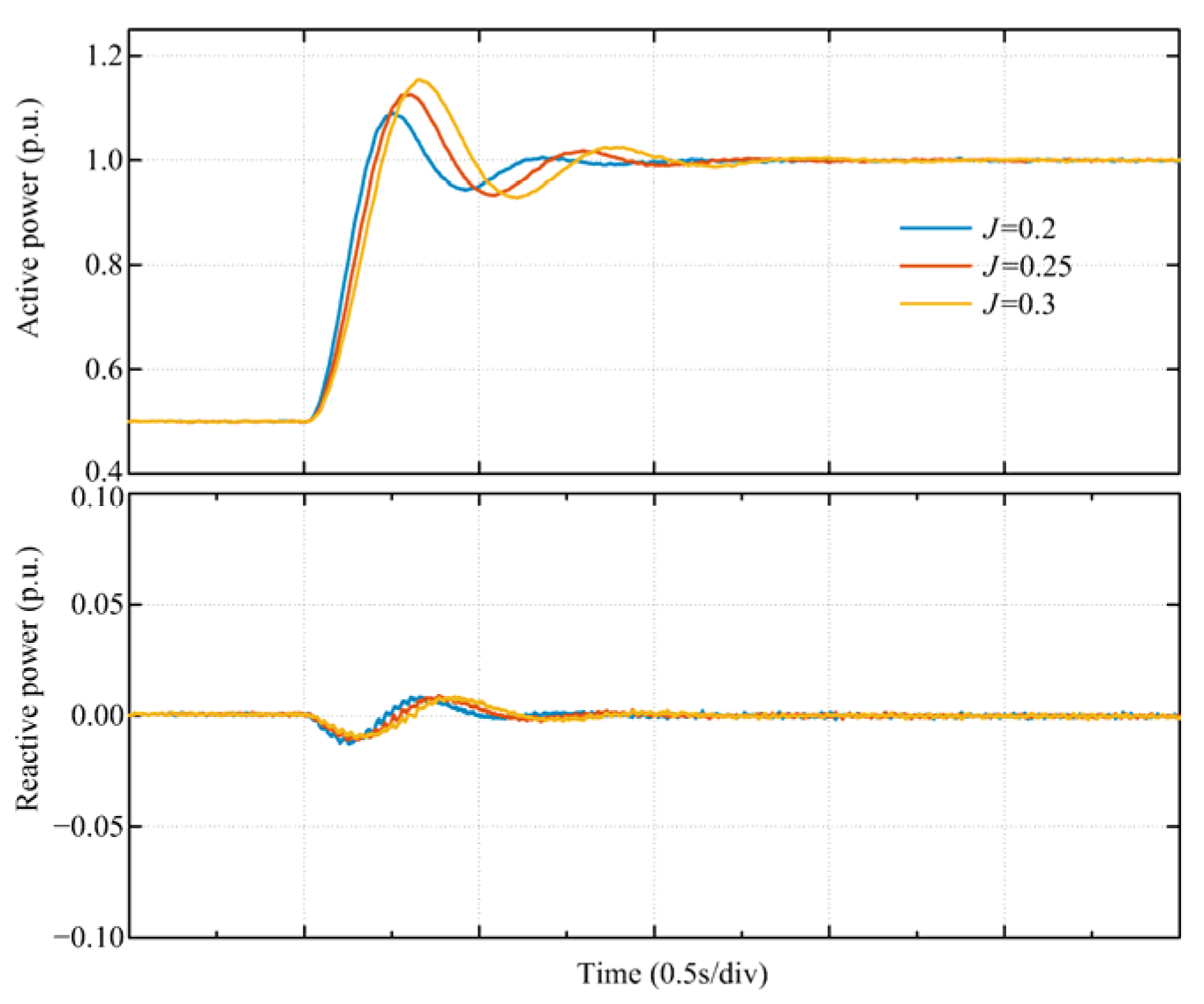
3.2. Mode Analysis of the GFM Energy Storage Grid-Connected System
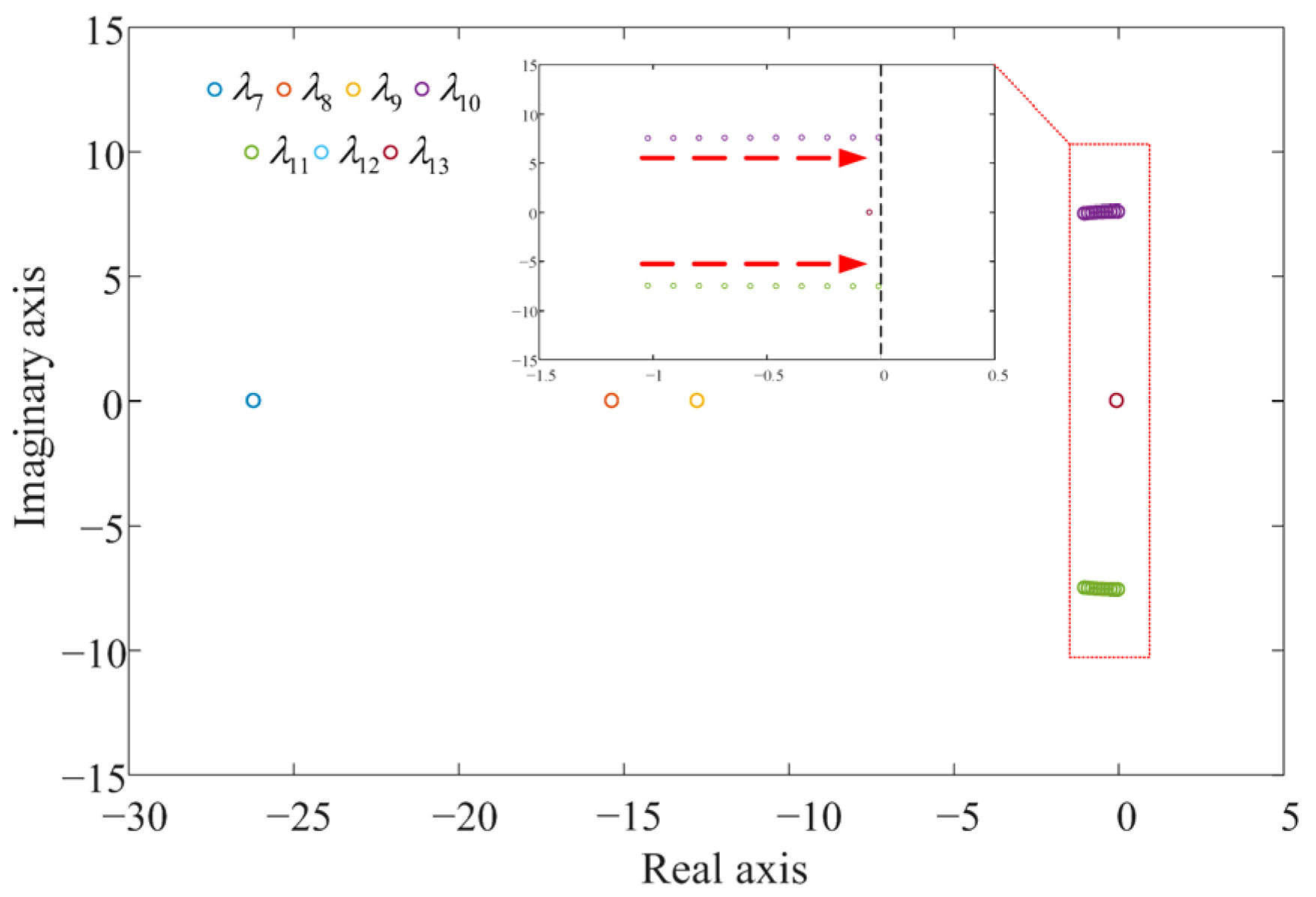
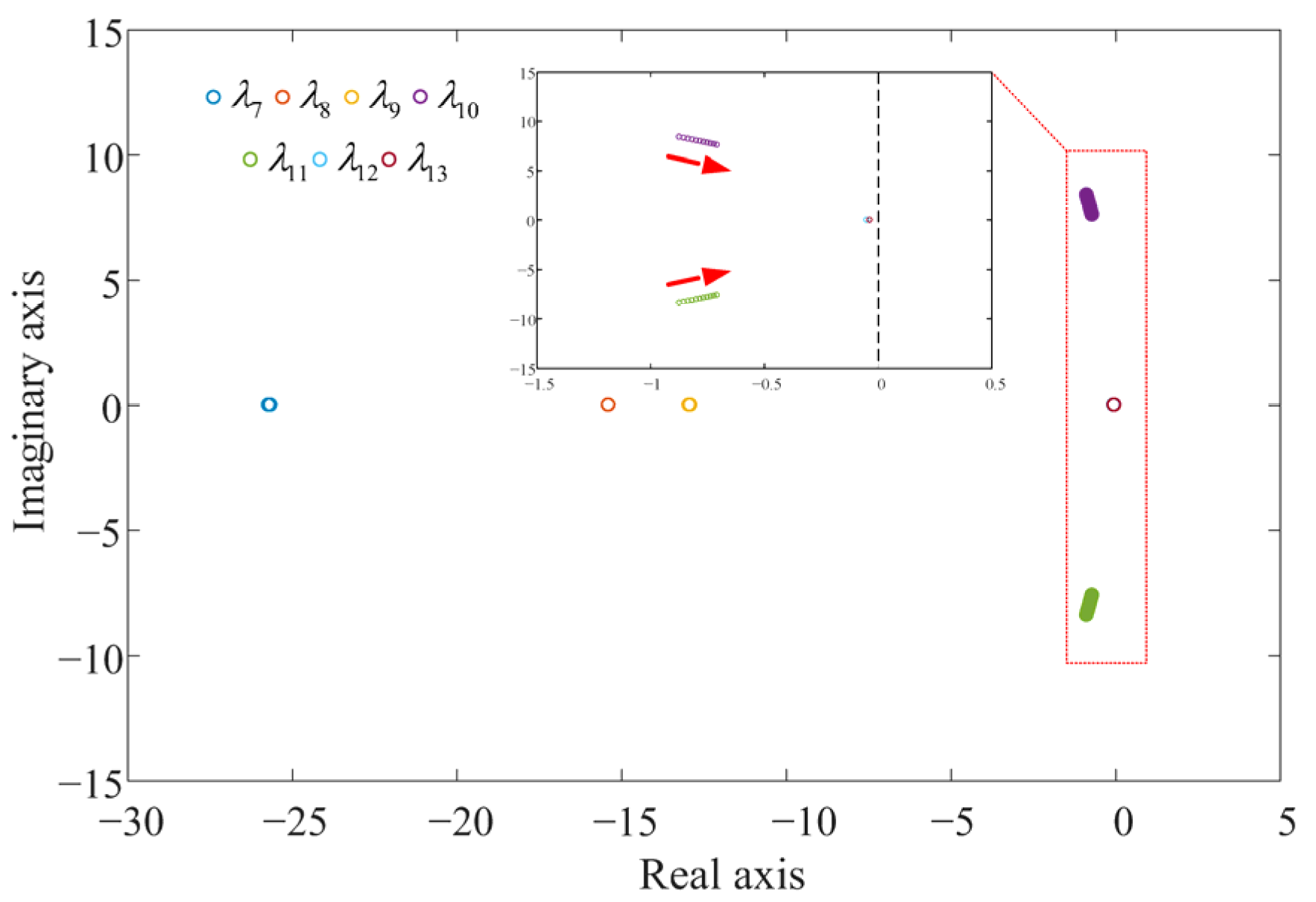
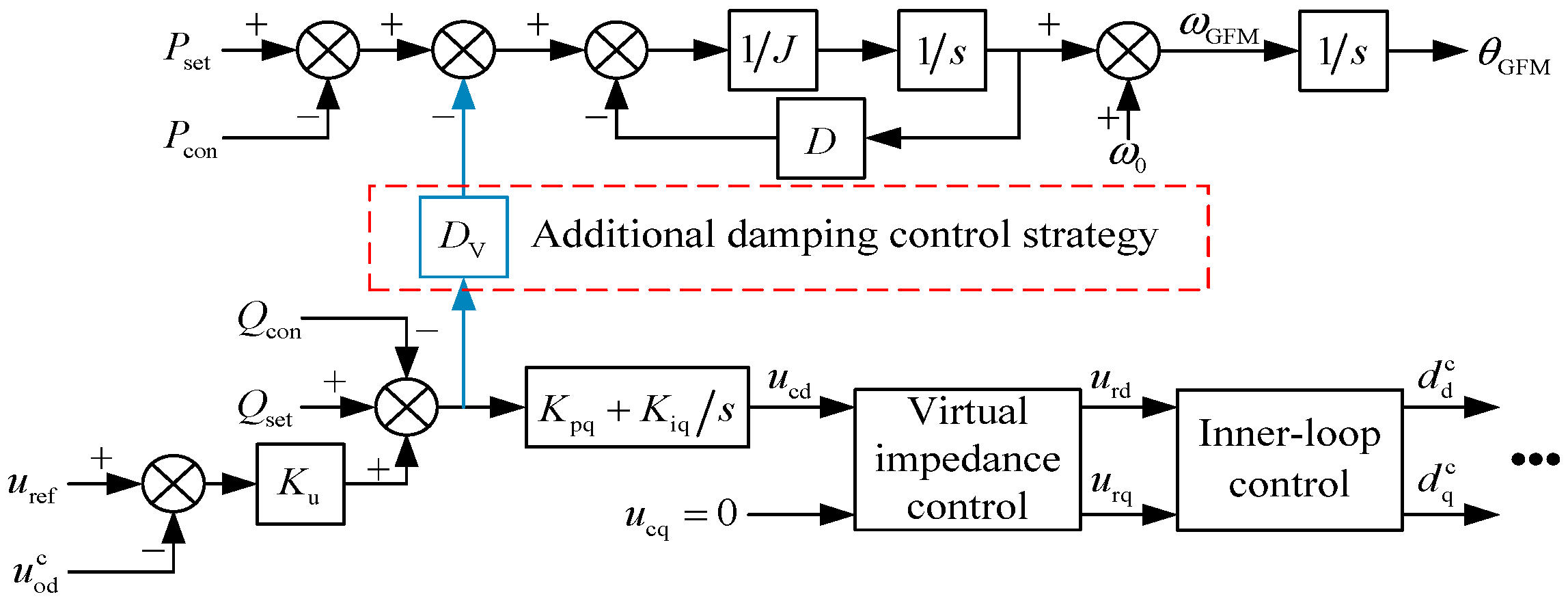
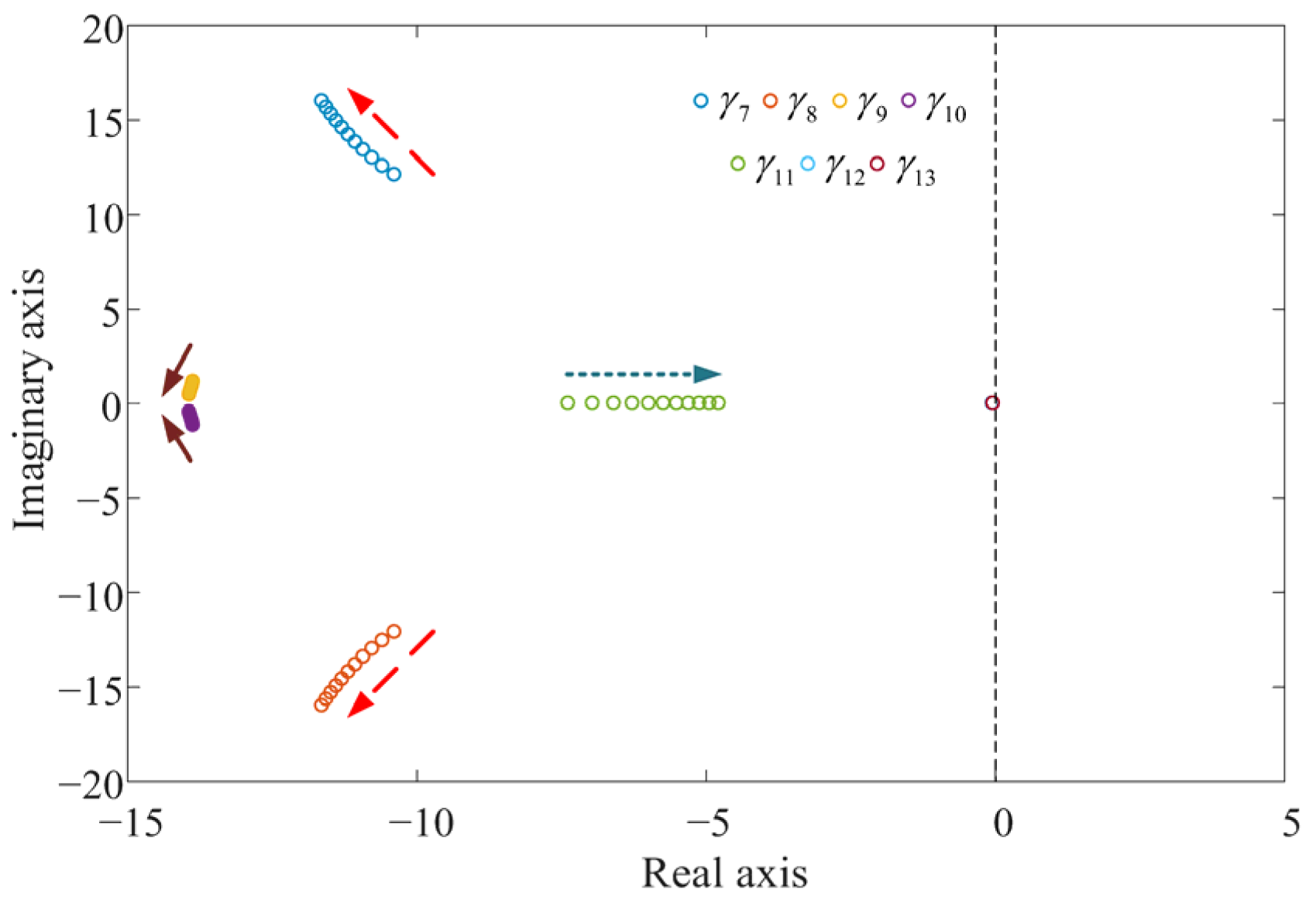
4. Additional Damping Control Strategy for the GFM Energy Storage
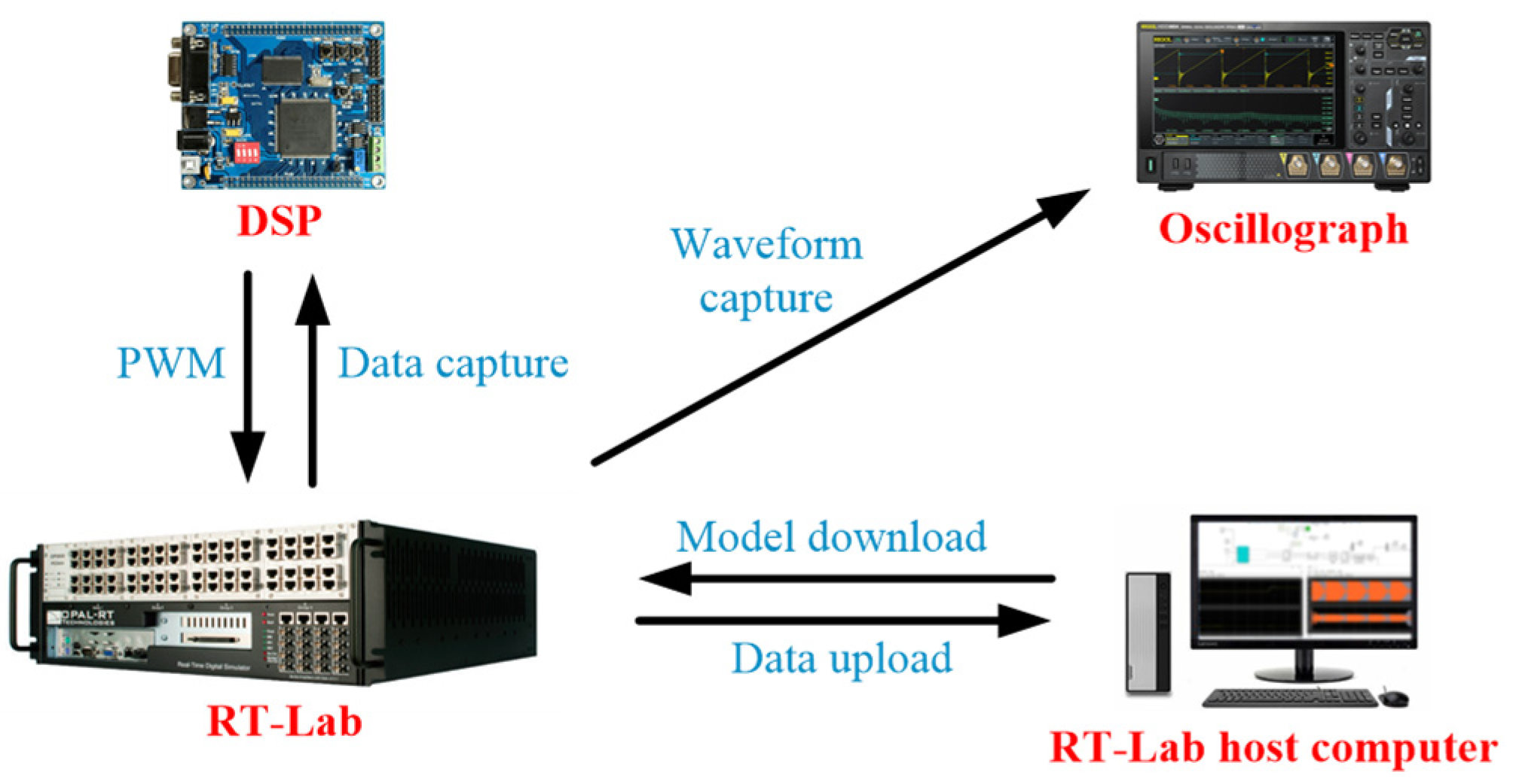
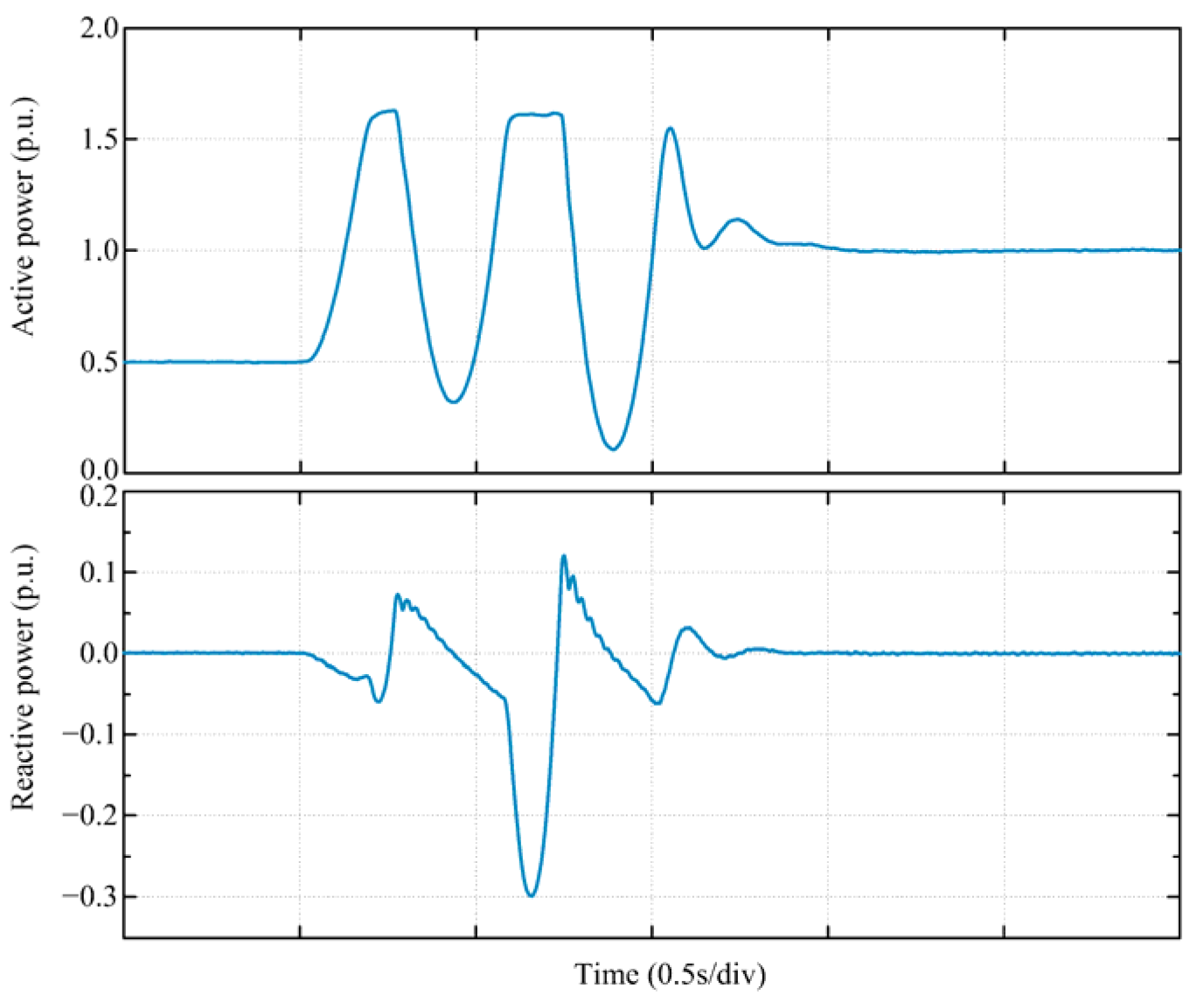
5. Semi-Physical Experiment Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

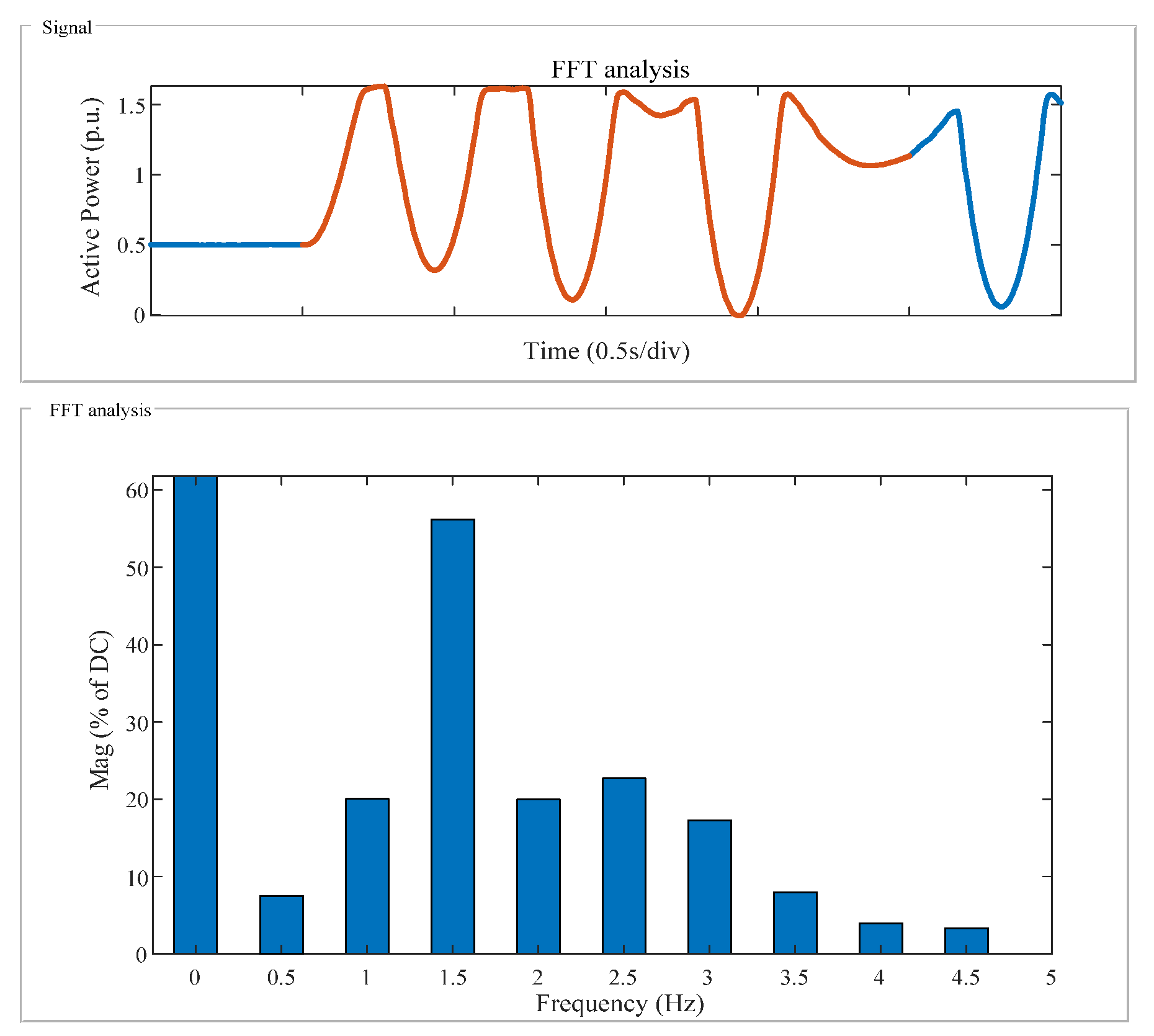
Appendix C
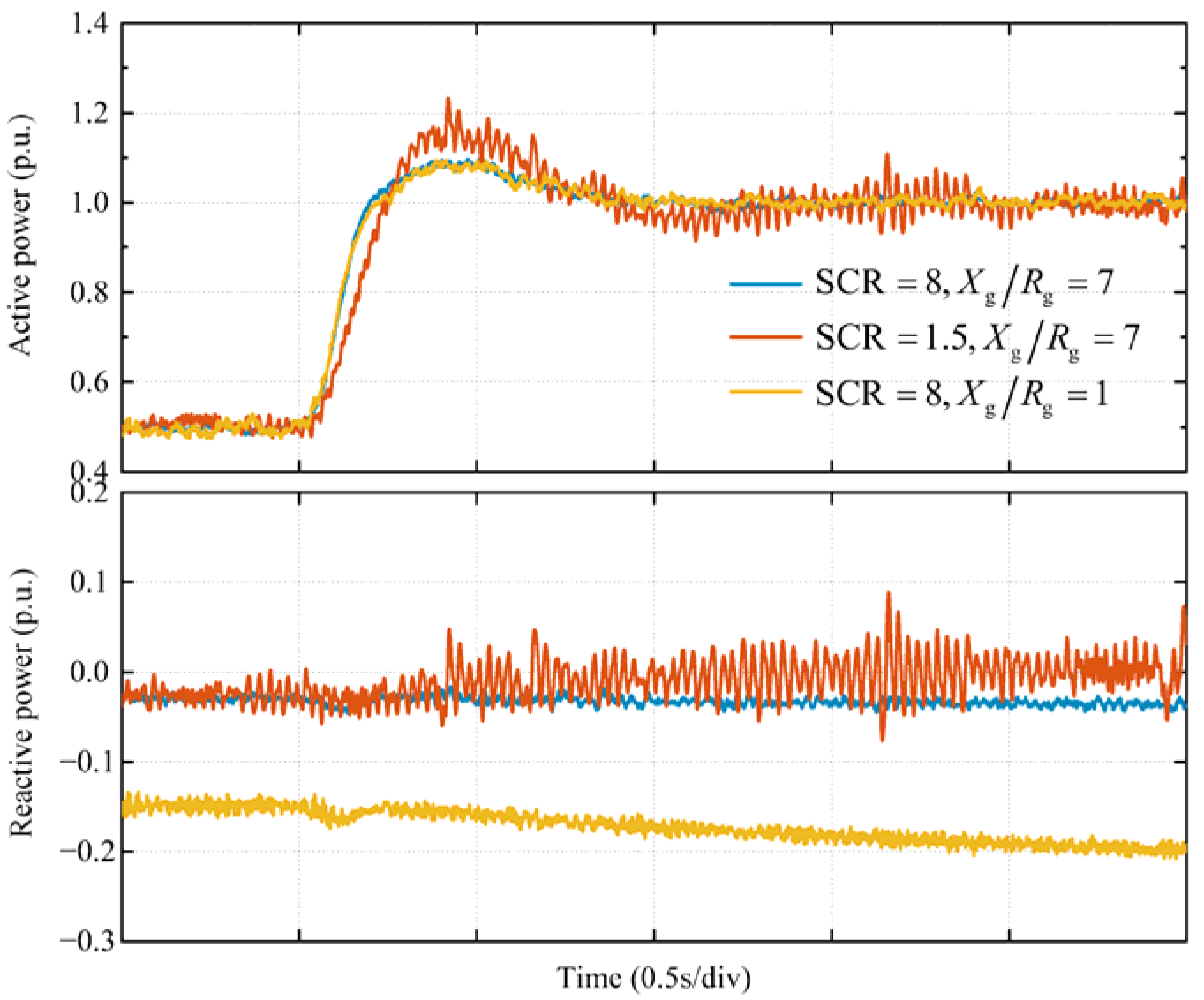
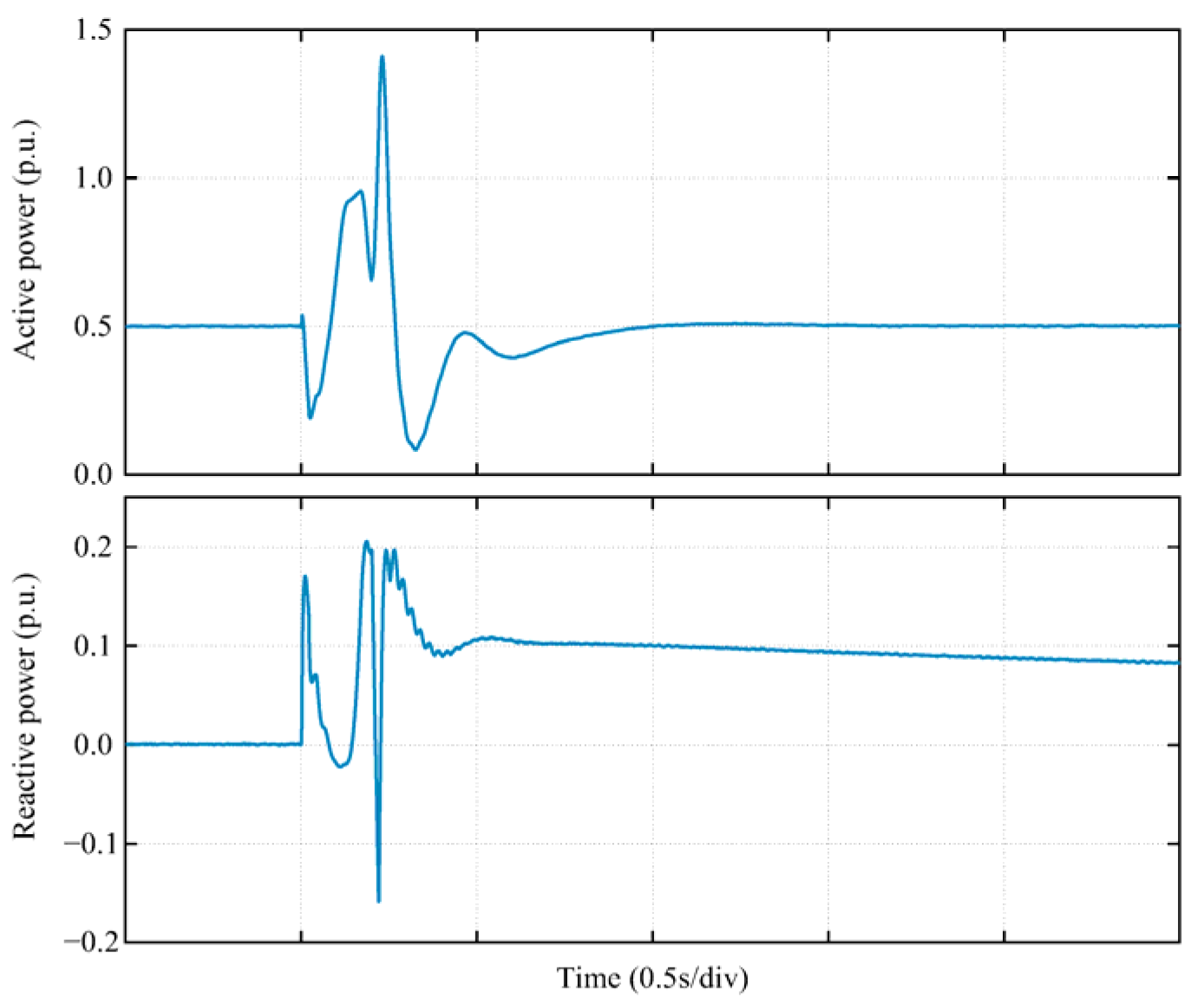
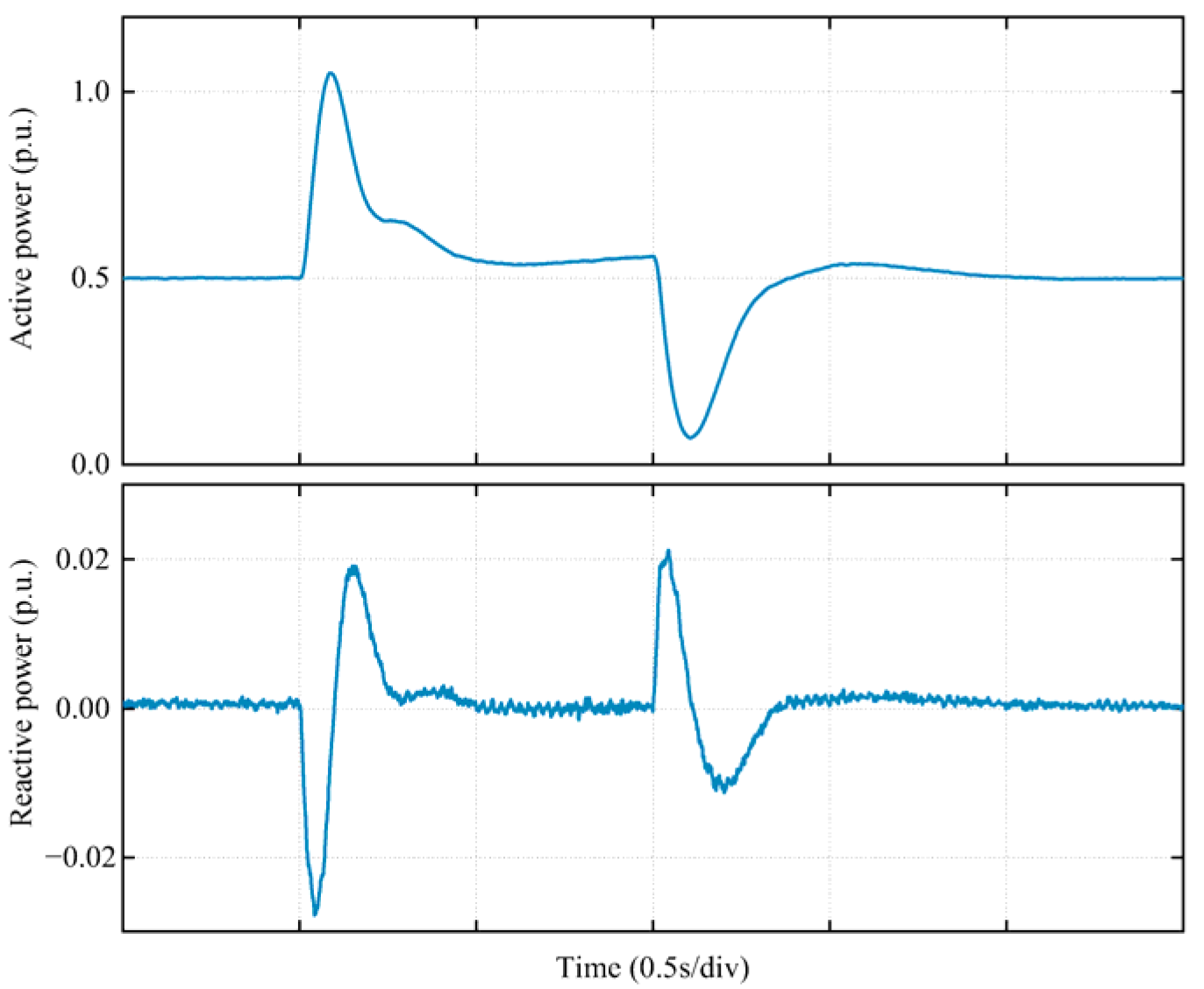
References
- Mohammed, N.; Udawatte, H.; Zhou, W.; Hill, D.; Bahrani, B. Grid-Forming Inverters: A comparative study of different control strategies in frequency and time domains. IEEE Open J. Ind. Electron. Soc. 2024, 5, 185–214. [Google Scholar] [CrossRef]
- Mastoi, M.; Zhuang, S.; Haris, M.; Hassan, M.; Ali, A. Large-scale wind power grid integration challenges and their solution: A detailed review. Environ. Sci. Pollut. Res. 2023, 30, 103424–103462. [Google Scholar] [CrossRef] [PubMed]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation damping of a distributed generator using a virtual synchronous generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Alawasa, K.; Mohamed, Y.; Xu, W. Active Mitigation of Subsynchronous Interactions Between PWM Voltage-Source Converters and Power Networks. IEEE Trans. Power Electron. 2014, 29, 121–134. [Google Scholar] [CrossRef]
- Zhou, J.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Liu, F.; Xin, K.; Liu, Y.; Blaabjerg, F. Symmetrical PLL for SISO Impedance Modeling and Enhanced Stability in Weak Grids. IEEE Trans. Power Electron. 2020, 35, 1473–1483. [Google Scholar] [CrossRef]
- Bahrani, B. Power-Synchronized Grid-Following Inverter Without a Phase-Locked Loop. IEEE Access 2021, 9, 112163–112176. [Google Scholar] [CrossRef]
- Mohammed, N.; Ravanji, M.; Zhou, W.; Bahrani, B. Enhanced Frequency Control for Power-Synchronized PLL-Less Grid-Following Inverters. IEEE Open J. Ind. Electron. Soc. 2023, 4, 189–204. [Google Scholar] [CrossRef]
- Ndreko, M.; Rüberg, S.; Winter, W. Grid forming control scheme for power systems with up to 100% power electronic interfaced generation: A case study on Great Britain test system. IET Renew. Power Gener. 2020, 14, 1268–1281. [Google Scholar] [CrossRef]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauss, P.; Welck, F. Overview on grid-forming inverter control methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Si, W.; Fang, J. Transient stability improvement of grid-forming converters through voltage amplitude regulation and reactive power injection. IEEE Trans. Power Electron. 2023, 38, 12116–12125. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, G.; Chen, Q.; Qiu, P.; Zhou, J.; Yang, R.; Zhang, J. Stability analysis and stabilization control of a grid-forming VSC-HVDC system. Front. Energy Res. 2024, 12, 1437287. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Schneider, K.; Lasseter, R.; Nandanoori, S.; Tuffner, F.; Kundu, S. A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Lu, M.; Dhople, S.; Johnson, B. Benchmarking nonlinear oscillators for grid-forming inverter control. IEEE Trans. Power Electron. 2022, 37, 10250–10266. [Google Scholar] [CrossRef]
- Poolla, B.; Gross, D.; Dörfler, F. Placement and implementation of grid-forming and grid-following virtual inertia and fast frequency response. IEEE Trans. Power Syst. 2019, 34, 3035–3046. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, Y.; Luo, B.; Cheng, P.; Blaabjerg, F. Analysis and suppression strategy of synchronous frequency resonance for grid-connected converters with power-synchronous control method. IEEE Trans. Power Electron. 2023, 38, 6945–6955. [Google Scholar] [CrossRef]
- Rathnayake, D.; Razzaghi, R.; Bahrani, B. Generalized virtual synchronous generator control design for renewable power systems. IEEE Trans. Sustain. Energy 2022, 13, 1021–1036. [Google Scholar] [CrossRef]
- Mohammed, N.; Ravanji, M.; Zhou, W.; Bahrani, B. Online grid impedance estimation-based adaptive control of virtual synchronous generators considering strong and weak grid conditions. IEEE Trans. Sustain. Energy 2023, 14, 673–687. [Google Scholar] [CrossRef]
- Beck, H.; Hesse, R. Virtual synchronous machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Visscher, K.; Haan, S. Virtual synchronous machines (VSG’S) for frequency stabilization in future grids with a significant share of decentralized generation. In Proceedings of the CIRED Seminar 2008: Smartgrids for Distribution, Frankfurt, Germany, 23–24 June 2008; pp. 1–4. [Google Scholar]
- Zhang, H.; Zhou, Y.; He, W.; Hu, J.; Huang, W.; Li, W.; Zhai, S. Mechanism Analysis of low-frequency oscillation caused by VSG from the perspective of vector motion. Processes 2023, 12, 2303. [Google Scholar] [CrossRef]
- Ruan, J.; Shi, Z.; Yu, M.; Wang, S. Simplified damping analysis and suppression method for low-frequency oscillation introduced by virtual synchronous generator. J. Power Electron. 2021, 21, 1600–1610. [Google Scholar] [CrossRef]
- Shi, Y.; Fang, C.; Chen, L.; Mao, M.; Chen, Z. Inertia parameter selection method for HVDC converter station based on VSG control. J. Electr. Eng. Technol. 2022, 17, 1019–1030. [Google Scholar]
- Lu, S.; Wang, T.; Liang, Y.; Cheng, S.; Cai, Y.; Wang, H.; Yang, J.; Sui, Y.; Yang, L. Low-frequency oscillation analysis of grid-connected VSG system considering multi-parameter coupling. Comput. Model. Eng. Sci. 2023, 135, 2373–2386. [Google Scholar] [CrossRef]
- Hu, S.; Meng, K.; Wu, Z. A parameter-adaptive method for primary frequency regulation of grid-forming direct-drive wind turbines. Sensors 2024, 24, 6651. [Google Scholar] [CrossRef] [PubMed]
- Xiong, K.; Hu, W.; Zhang, G.; Chen, Z. Deep reinforcement learning based parameter self-tuning control strategy for VSG. Energy Rep. 2022, 8, 219–226. [Google Scholar] [CrossRef]
- Xu, Q.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Artificial intelligence-based control design for reliable virtual synchronous generators. IEEE Trans. Power Electron. 2021, 36, 9453–9464. [Google Scholar] [CrossRef]
- Xiong, X.; Li, X.; Luo, B.; Huang, M.; Zhao, C.; Blaabjerg, F. An additional damping torque method for low-frequency stability enhancement of virtual synchronous generators. IEEE Trans. Power Electron. 2024, 39, 15858–15869. [Google Scholar] [CrossRef]
- Wang, H.; Hao, Y.; He, H.; Dong, H.; Lu, S.; Zhang, G.; Yang, J.; Chen, Z. Influence mechanism and virtual power system stabiliser method of virtual synchronous generator for low-frequency oscillation of power system. IET Energy Syst. Integr. 2023, 6, 104–116. [Google Scholar] [CrossRef]
- Yang, M.; Wu, X.; Yu, D.; Loveth, M.; Yu, S. An optimized power-angle and excitation dual loop virtual power system stabilizer for enhanced MMC-VSG control and low-frequency oscillation suppression. Energies 2024, 6, 4711. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Fixed-parameter damping methods of virtual synchronous generator control using state feedback. IEEE Access 2024, 7, 99177–99190. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Blaabjerg, F. An improved synchronization stability method of virtual synchronous generators based on frequency feedforward on reactive power control loop. IEEE Trans. Power Electron. 2021, 36, 9136–9148. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Mijatovic, N.; Dragicevic, T. Frequency stability assessment of grid-forming VSG in framework of MPME with feedforward decoupling control strategy. IEEE Trans. Ind. Electron. 2022, 69, 6903–6913. [Google Scholar] [CrossRef]
- Zhou, W.; Mohammed, N.; Bahrani, B. Comprehensive Modeling, Analysis, and Comparison of State-Space and Admittance Models of PLL-Based Grid-Following Inverters Considering Different Outer Control Modes. IEEE Access 2022, 10, 30109–30146. [Google Scholar] [CrossRef]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-Based WTs for Small-Signal Stability Analysis in DVC Timescale in Power Electronized Power Systems. IEEE Trans.Energy Conver. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Xu, L.; Fan, L.; Miao, Z. DC impedance-model-based resonance analysis of a VSC-HVDC system. IEEE Trans. Power Deliv. 2015, 30, 1221–1230. [Google Scholar] [CrossRef]
- Yu, G.; Xu, J.; Wu, G.; Ren, W. Reactive power decoupling control strategy for the grid-forming photovoltaic DC/AC converter. Electr. Power Syst. Res. 2024, 236, 110962. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance modeling and analysis of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-Link voltage control timescale. IEEE Trans. Power Syst. 2017, 32, 3981–3991. [Google Scholar] [CrossRef]
- Yu, G.; Xu, J.; Yan, Z.; Ren, W. An optimized grid-forming control strategy for the flexible interconnection system in distribution transformer areas. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 1311–1323. [Google Scholar] [CrossRef]
- Yu, G.; Xu, J.; Wu, G.; Zhang, Z.; Zhao, D. Improved virtual synchronous generator control strategy for the flexible interconnection system in distribution transformer areas. Electr. Power Syst. Res. 2023, 214, 108877. [Google Scholar] [CrossRef]
| GFM Control Name | Characteristics | Limitations |
|---|---|---|
| droop control | droop characteristics | no inertial response |
| VOC | spontaneous synchronization | harmonic problem |
| VSG control | droop characteristics and inertia response | low-frequency oscillation |
| GCVSG control | on-grid and off-grid mode stability | grid impedance |
| AVSG control | grid adaptability | grid impedance |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| ) | 250 | PWM frequency (kHz) | 15 |
| power grid voltage () | 380 | ||
| DC voltage () | 750 | J | 0.2 |
| ) | 50 | D | 0.1 |
| ) | 16 | Rv/Lv | 1.6 × 10−3/0.41× 10−3 |
| ) | 0.5 | Kpq/Kiq | 3/100 |
| ) | 39.79 | Kpo/Kio | 3/15 |
| ) | 0.41 | Kpi/Kii | 1/15 |
| ) | 1.6 | Ku | 10 |
| Eigenvalues | Oscillation Frequency () | Damping Ratio | |
|---|---|---|---|
| −16,304.05 ± 353,505.05i | 56,262.1 | 0.05 | |
| −14,844.13 ± 351,706.65i | 55,975.9 | 0.04 | |
| −1796.50 ± 5598.15i | 891.0 | 0.31 | |
| −25.71 | |||
| −15.39 | |||
| −12.94 | |||
| −0.87 ± 8.40i | 1.3 | 0.10 | |
| −0.05 | |||
| −0.04 |
| Eigenvalues | Oscillation Frequency () | Damping Ratio | |
|---|---|---|---|
| −16,304.05 ± 353,505.05i | 56,262.1 | 0.05 | |
| −14,844.13 ± 351,706.65i | 55,975.9 | 0.04 | |
| −1796.46 ± 5598.11i | 891.0 | 0.31 | |
| −10.39 ± 12.10i | 1.9 | 0.65 | |
| −13.87 ± 1.16i | 0.2 | 1.00 | |
| −7.38 | |||
| −0.05 | |||
| −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, C.; Xu, J.; Lin, X.; Yu, G.; Chen, W. An Additional Damping Control Strategy for Grid-Forming Energy Storage to Address Low-Frequency Oscillation. Energies 2025, 18, 3971. https://doi.org/10.3390/en18153971
Tian C, Xu J, Lin X, Yu G, Chen W. An Additional Damping Control Strategy for Grid-Forming Energy Storage to Address Low-Frequency Oscillation. Energies. 2025; 18(15):3971. https://doi.org/10.3390/en18153971
Chicago/Turabian StyleTian, Chi, Jianyuan Xu, Xin Lin, Gaole Yu, and Weidong Chen. 2025. "An Additional Damping Control Strategy for Grid-Forming Energy Storage to Address Low-Frequency Oscillation" Energies 18, no. 15: 3971. https://doi.org/10.3390/en18153971
APA StyleTian, C., Xu, J., Lin, X., Yu, G., & Chen, W. (2025). An Additional Damping Control Strategy for Grid-Forming Energy Storage to Address Low-Frequency Oscillation. Energies, 18(15), 3971. https://doi.org/10.3390/en18153971





