Isobaric Vapor-Liquid Equilibrium of Biomass-Derived Ethyl Levulinate and Ethanol at 40.0, 60.0 and 80.0 kPa
Abstract
1. Introduction
2. Experimental and/or Computational Methods
2.1. Chemicals
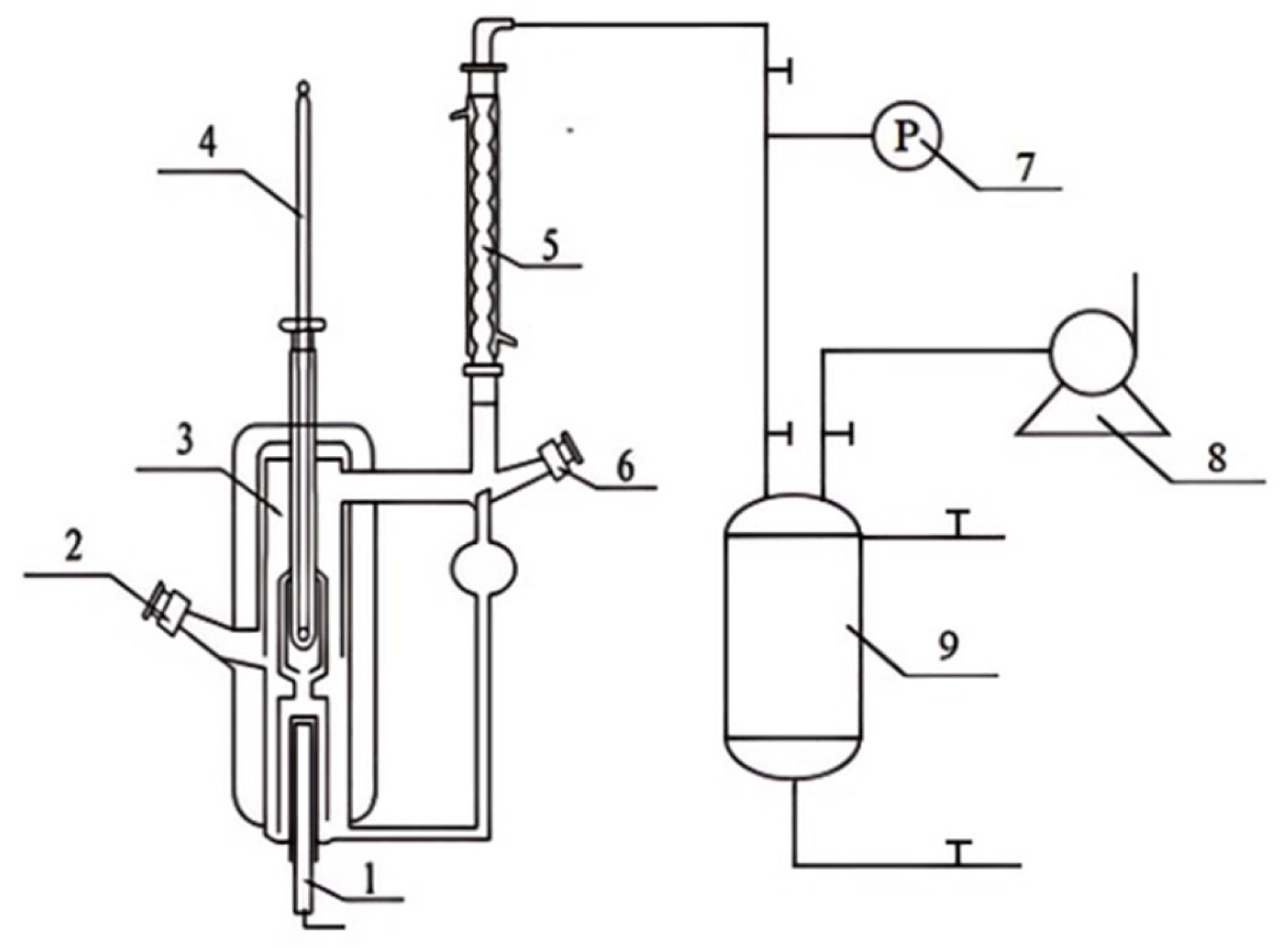
2.2. Apparatus and Procedure
2.3. Analysis
3. Results and Discussion
3.1. Vapor-Liquid Equilibrium Data
3.2. Thermodynamic Consistency Tests
3.3. Data Correlation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghosh, M.K.; Howard, M.S.; Zhang, Y.; Djebbi, K.; Capriolo, G.; Farooq, A.; Curran, H.J.; Dooley, S. The combustion kinetics of the lignocellulosic biofuel, ethyl levulinate. Combust. Flame 2018, 193, 157–169. [Google Scholar] [CrossRef]
- Api, A.M.; Belsito, D.; Botelho, D.; Bruze, M.; Burton, G.A., Jr.; Buschmann, J.; Dagli, M.L.; Date, M.; Dekant, W.; Deodhar, C.; et al. RIFM fragrance ingredient safety assessment, ethyl levulinate, CAS Registry Number 539-88-8. Food Chem. Toxicol. 2019, 127 (Suppl. 1), S48–S54. [Google Scholar] [CrossRef] [PubMed]
- Unlu, D.; Boz, N.; Ilgen, O.; Hilmioglu, N. Improvement of fuel properties of biodiesel with bioadditive ethyl levulinate. Open Chem. 2018, 16, 647–652. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Y.; Quan, Y. Preparation of Ethyl Levulinate by Sulfonating Active Carbon Catalytic Furfuryl Alcohol Alcoholysis Used as Plasticizer, Involves Dissolving Activated Carbon Powder in Deionized Water, Adding Concentrated Sulfuric Acid, and Placing Furfuryl Alcohol, Sulfonated Activated Carbon Catalyst, and Ethanol. CN118307401-A, 9 April 2024. [Google Scholar]
- Muzzio, M.; Yu, C.; Lin, H.; Yom, T.; Boga, D.A.; Xi, Z.; Li, N.; Yin, Z.; Li, J.; Dunn, J.A.; et al. Reductive amination of ethyl levulinate to pyrrolidones over AuPd nanoparticles at ambient hydrogen pressure. Green Chem. 2019, 21, 1895–1899. [Google Scholar] [CrossRef]
- Gomes, G.R.; Breitkreitz, M.C.; Pastre, J.C. Ash influence on the ethyl levulinate production from sugarcane molasses mediated by taurine hydrogen sulfate. Acs Sustain. Chem. Eng. 2021, 9, 13438–13449. [Google Scholar] [CrossRef]
- Hamryszak, L.; Grzesik, M. Levulinic esters. Production, application and kinetic studies. Przem. Chem. 2017, 96, 327–331. [Google Scholar]
- Khalid, M.; Mesa, M.G.; Scapens, D.; Osatiashtiani, A. Advances in sustainable γ-Valerolactone (GVL) production via catalytic transfer hydrogenation of levulinic acid and its esters. Acs Sustain. Chem. Eng. 2024, 12, 16494–16517. [Google Scholar] [CrossRef]
- Bhonsle, A.K.; Faujdar, E.; Rawat, N.; Singh, R.K.; Singh, J.; Trivedi, J.; Atray, N. Synthesis and characterization of novel ethyl levulinate coupled N-phenyl-p-phenylenediamine multifunctional additive: Oxidation stability and lubricity improver in biodiesel. Energy Sources Part A-Recovery Util. Environ. Eff. 2022, 44, 6236–6248. [Google Scholar] [CrossRef]
- Pasha, N.; Lingaiah, N.; Shiva, R. Zirconium exchanged phosphotungstic acid catalysts for esterification of levulinic acid to ethyl levulinate. Catal. Lett. 2019, 149, 2500–2507. [Google Scholar] [CrossRef]
- Li, M.; Wei, J.; Yan, G.; Liu, H.; Tang, X.; Sun, Y.; Zeng, X.; Lei, T.; Lin, L. Cascade conversion of furfural to fuel bioadditive ethyl levulinate over bifunctional zirconium-based catalysts. Renew. Energy 2020, 147, 916–923. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, B.; Zhang, W. Research progress in preparation of ethyl levulinate from cellulose. Mod. Chem. Ind. 2024, 44, 44–49, 54. [Google Scholar]
- Huang, Z.; Yuan, H. Research advances on preparation of ethyl levulinate through alcoholysis of biomass and its derivatives. Mod. Chem. Ind. 2021, 41, 42–46. [Google Scholar]
- Resk, A.J.; Peereboom, L.; Kolah, A.K.; Miller, D.J.; Lira, C.T. Phase equilibria in systems with levulinic acid and ethyl levulinate. J. Chem. Eng. Data 2014, 59, 1062–1068. [Google Scholar] [CrossRef]
- Wang, X.; Zhuang, X.; Yun, S.; Chen, J.; Jiang, D. Measurement and correlation of vapor-liquid equilibrium for a cyclohexene-cyclohexanol binary system at 101.3 kPa. Chin. J. Chem. Eng. 2011, 19, 484–488. [Google Scholar] [CrossRef]
- Yang, C.; Sun, Y.; Qin, Z.; Feng, Y.; Zhang, P.; Feng, X. Isobaric vapor-liquid equilibrium for four binary systems of ethane-1,2-diol, butane-1,4-diol, 2-(2-Hydroxyethoxy)ethan-1-ol, and 2- 2-(2-Hydroxyethoxy)ethoxy ethanol at 10.0 kPa, 20.0 kPa, and 40.0 kPa. J. Chem. Eng. Data 2014, 59, 1273–1280. [Google Scholar] [CrossRef]
- Mi, X.; Yang, C.; Sun, F.; Li, B. Vapor-liquid equilibrium for the binary of propylene glycol methyl ether acetate plus ethyl lactate and propylene glycol methyl ether plus ethyl lactate at 101.3 and 20.0 kPa. J. Chem. Eng. Data 2021, 66, 146–153. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, D.; Zhou, Y.; Shi, P.; Gao, J.; Wang, Y. Isobaric vapor-liquid phase equilibrium measurements, correlation, and prediction for separation of the mixtures of cyclohexanone and alcohols. J. Chem. Eng. Data 2018, 63, 2038–2045. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Pan, X.; Yang, J.; Cui, P.; Zhang, F.; Gao, J. Isobaric vapor-liquid equilibrium of a ternary system of ethyl acetate plus propyl acetate plus dimethyl sulfoxide and binary systems of ethyl acetate plus dimethyl sulfoxide and propyl acetate plus dimethyl sulfoxide at 101.3 kPa. J. Chem. Thermodyn. 2019, 135, 116–123. [Google Scholar] [CrossRef]
- De La Calle-Arroyo, C.; Lopez-Fidalgo, J.; Rodriguez-Aragon, L.J. Optimal designs for Antoine Equation. Chemom. Intell. Lab. Syst. 2021, 214, 104334. [Google Scholar] [CrossRef]
- Kumar, R.V.; Rao, M.A.; Rao, M.V.; Prasad, D.H.L. Activity coefficient and excess Gibbs free energy of allyl alcohol with tetrachloroethylene. Phys. Chem. Liq. 1997, 35, 121–126. [Google Scholar] [CrossRef]
- Wisniak, J.; Ortega, J.; Fernández, L. A fresh look at the thermodynamic consistency of vapour-liquid equilibria data. J. Chem. Thermodyn. 2017, 105, 385–395. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Thermodynamics of nonelectrolyte solutions-X-Y-T relations in a binary system. Ind. Eng. Chem. 1948, 40, 341–345. [Google Scholar] [CrossRef]
- Fredenslund, A.; Gmehling, J.; Rasmussen, P. Vapor-Liquid Equilibria Using Unifac, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1977; pp. 198–226. [Google Scholar]
- Vanness, H.C. Thermodynamics in the treatment of vapor-liquid-equilibriu (VLE) data. Pure Appl. Chem. 1995, 67, 859–872. [Google Scholar] [CrossRef]
- Pazuki, G.R.; Taghikhani, V.; Vossoughi, M. Correlation and prediction the activity coefficients and solubility of amino acids and simple peptide in aqueous solution using the modified local composition model. Fluid Phase Equilibria 2007, 255, 160–166. [Google Scholar] [CrossRef]
- Winter, B.; Winter, C.; Esper, T.; Schilling, J.; Bardow, A. SPT-NRTL: A physics-guided machine learning model to predict thermodynamically consistent activity coefficients. Fluid Phase Equilibria 2023, 568, 113731. [Google Scholar] [CrossRef]
- Bakhshi, H.; Mobalegholeslam, P. A modification of UNIQUAC model for electrolyte solutions based on the local composition concept. J. Solut. Chem. 2020, 49, 1485–1496. [Google Scholar] [CrossRef]
- Marcilla, A.; Olaya, M.M.; Reyes-Labarta, J.A. The unavoidable necessity of considering temperature dependence of the liquid Gibbs energy of mixing for certain VLE data correlations. Fluid Phase Equilibria 2018, 473, 17–31. [Google Scholar] [CrossRef]










| Chemicals | Formula | CAS Number | Mass Fraction | Source | Analysis Method | Tb (K)/101.3 kPa | |
|---|---|---|---|---|---|---|---|
| exp. | lit. | ||||||
| ethanol | C2H6O | 64-17-5 | 0.998 | Sinopharm Chemical Reagent Co., Ltd. | GC a | 351.52 | 351.44 [15] |
| cyclohexanone | C6H10O | 108-94-1 | 0.995 | Meryer Technologies Co., Ltd. | GC a | 428.73 | 428.80 [15] |
| ethyl levulinate | C7H12O3 | 539-88-8 | 0.99 | Meryer Technologies Co., Ltd. | GC a | 478.88 | 478.95 b |
| T(K) | x1 | y1 | γ1 | γ2 | ln(γ1/γ2) | gE | gM,V | gM,L |
|---|---|---|---|---|---|---|---|---|
| 40.0 kPa | ||||||||
| 329.58 | 0.0000 | 0.0000 | 0.9998 | 0.0000 | –0.0002 | |||
| 331.23 | 0.0748 | 0.0006 | 1.2477 | 1.0019 | 0.2194 | 0.0183 | –0.0773 | –0.2476 |
| 333.04 | 0.1551 | 0.0013 | 1.1653 | 1.0106 | 0.1424 | 0.0326 | –0.1600 | –0.3988 |
| 335.51 | 0.2586 | 0.0024 | 1.1096 | 1.0312 | 0.0733 | 0.0497 | –0.2709 | –0.5219 |
| 339.01 | 0.3742 | 0.0041 | 1.0625 | 1.0477 | 0.0140 | 0.0518 | –0.4241 | –0.6093 |
| 343.59 | 0.4983 | 0.0069 | 1.0286 | 1.0743 | –0.0435 | 0.0500 | –0.6185 | –0.6431 |
| 349.78 | 0.6177 | 0.0119 | 1.0114 | 1.0906 | –0.0754 | 0.0402 | –0.8700 | –0.6251 |
| 355.72 | 0.7041 | 0.0186 | 1.0073 | 1.1099 | –0.0970 | 0.0360 | –1.0992 | –0.5714 |
| 362.54 | 0.7757 | 0.0291 | 1.0061 | 1.1223 | –0.1093 | 0.0306 | –1.3465 | –0.5017 |
| 372.50 | 0.8476 | 0.0516 | 1.0036 | 1.1338 | –0.1220 | 0.0222 | –1.6734 | –0.4047 |
| 381.70 | 0.8921 | 0.0828 | 1.0026 | 1.1397 | –0.1282 | 0.0164 | –1.9315 | –0.3257 |
| 396.17 | 0.9371 | 0.1612 | 1.0019 | 1.1421 | –0.1310 | 0.0101 | –2.2190 | –0.2247 |
| 411.69 | 0.9664 | 0.3043 | 1.0015 | 1.1427 | –0.1319 | 0.0059 | –2.2778 | –0.1411 |
| 426.94 | 0.9848 | 0.5336 | 1.0012 | 1.1407 | –0.1304 | 0.0032 | –1.8987 | –0.0756 |
| 435.46 | 0.9924 | 0.7136 | 1.0006 | 1.1396 | –0.1301 | 0.0016 | –1.3651 | –0.0430 |
| 441.11 | 0.9967 | 0.8583 | 1.0002 | 1.1383 | –0.1293 | 0.0006 | –0.7940 | –0.0215 |
| 445.93 | 1.0000 | 1.0000 | 0.9999 | 0.0000 | –0.0001 | |||
| 60.0 kPa | ||||||||
| 338.72 | 0.0000 | 0.0000 | 0.9999 | 0.0000 | –0.0001 | |||
| 340.57 | 0.0811 | 0.0008 | 1.3091 | 1.0048 | 0.2646 | 0.0262 | –0.0815 | –0.2552 |
| 343.27 | 0.1914 | 0.0020 | 1.1859 | 1.0182 | 0.1525 | 0.0472 | –0.1970 | –0.4410 |
| 346.72 | 0.3145 | 0.0037 | 1.0979 | 1.0404 | 0.0538 | 0.0565 | –0.3407 | –0.5662 |
| 351.86 | 0.4613 | 0.0069 | 1.0516 | 1.0747 | –0.0217 | 0.0620 | –0.5478 | –0.6282 |
| 358.36 | 0.5945 | 0.0122 | 1.0223 | 1.1062 | –0.0789 | 0.0540 | –0.7980 | –0.6211 |
| 367.72 | 0.7229 | 0.0234 | 1.0070 | 1.1377 | –0.1220 | 0.0408 | –1.1348 | –0.5494 |
| 378.77 | 0.8174 | 0.0444 | 1.0043 | 1.1583 | –0.1427 | 0.0303 | –1.4933 | –0.4450 |
| 388.92 | 0.8733 | 0.0740 | 1.0019 | 1.1695 | –0.1547 | 0.0215 | –1.7779 | –0.3586 |
| 399.39 | 0.9126 | 0.1191 | 1.0010 | 1.1780 | –0.1628 | 0.0152 | –2.0134 | –0.2812 |
| 414.73 | 0.9498 | 0.2229 | 1.0009 | 1.1812 | –0.1656 | 0.0092 | –2.2068 | –0.1899 |
| 422.70 | 0.9633 | 0.3005 | 1.0008 | 1.1823 | –0.1667 | 0.0069 | –2.2057 | –0.1504 |
| 433.86 | 0.9779 | 0.4449 | 1.0005 | 1.1836 | –0.1681 | 0.0042 | –2.0323 | –0.1018 |
| 440.59 | 0.9849 | 0.5563 | 1.0003 | 1.1825 | –0.1673 | 0.0028 | –1.7944 | –0.0755 |
| 447.21 | 0.9908 | 0.6871 | 1.0002 | 1.1784 | –0.1640 | 0.0017 | –1.4219 | –0.0506 |
| 453.74 | 0.9959 | 0.8396 | 1.0000 | 1.1753 | –0.1615 | 0.0007 | –0.8592 | –0.0259 |
| 459.64 | 1.0000 | 1.0000 | 0.9999 | 0.0000 | –0.0001 | |||
| 80.0 kPa | ||||||||
| 345.58 | 0.0000 | 0.0000 | 0.9999 | 0.0000 | –0.0001 | |||
| 347.63 | 0.0875 | 0.0010 | 1.3515 | 1.0071 | 0.2941 | 0.0328 | –0.0866 | –0.2639 |
| 349.88 | 0.1766 | 0.0021 | 1.2417 | 1.0187 | 0.1980 | 0.0535 | –0.1786 | –0.4127 |
| 352.52 | 0.2728 | 0.0035 | 1.1605 | 1.0379 | 0.1117 | 0.0677 | –0.2844 | –0.5184 |
| 355.84 | 0.3791 | 0.0055 | 1.0994 | 1.0671 | 0.0298 | 0.0762 | –0.4142 | –0.5874 |
| 359.61 | 0.4798 | 0.0081 | 1.0512 | 1.1018 | –0.0470 | 0.0744 | –0.5577 | –0.6179 |
| 365.70 | 0.5976 | 0.0134 | 1.0271 | 1.1339 | –0.0989 | 0.0665 | –0.7806 | –0.6074 |
| 374.62 | 0.7167 | 0.0243 | 1.0119 | 1.1675 | –0.1430 | 0.0524 | –1.0873 | –0.5437 |
| 385.34 | 0.8101 | 0.0444 | 1.0084 | 1.2010 | –0.1748 | 0.0416 | –1.4215 | –0.4445 |
| 398.15 | 0.8784 | 0.0821 | 1.0047 | 1.2197 | –0.1939 | 0.0283 | –1.7620 | –0.3418 |
| 409.39 | 0.9168 | 0.1325 | 1.0021 | 1.2252 | –0.2010 | 0.0188 | –1.9921 | –0.2677 |
| 424.44 | 0.9509 | 0.2364 | 1.0010 | 1.2309 | –0.2067 | 0.0112 | –2.1545 | –0.1847 |
| 436.06 | 0.9687 | 0.3551 | 1.0006 | 1.2286 | –0.2053 | 0.0070 | –2.1123 | –0.1323 |
| 448.49 | 0.9828 | 0.5315 | 1.0003 | 1.2231 | –0.2011 | 0.0038 | –1.8181 | –0.0831 |
| 458.78 | 0.9919 | 0.7261 | 1.0002 | 1.2172 | –0.1964 | 0.0018 | –1.2710 | –0.0452 |
| 466.02 | 0.9973 | 0.8947 | 1.0002 | 1.2099 | –0.1903 | 0.0007 | –0.6050 | –0.0180 |
| 470.00 | 1.0000 | 1.0000 | 1.0001 | 0.0000 | 0.0001 | |||
| Components | ) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ethanol | 66.3962 | −7122.3 | 0 | 0 | −7.1424 | 2.8853 × 10−6 | 2 | 159.05 | 514.00 |
| ethyl levulinate | 68.4222 | −9228.7 | 0 | 0 | −7.2248 | 4.4062 × 10−18 | 6 | 240.40 | 666.10 |
| T (K) | ΔT (K) | x1 | y1 | γ1 | γ2 | gE | Δln(γ1/γ2) |
|---|---|---|---|---|---|---|---|
| 40.0 kPa | |||||||
| 329.58 | 0.00 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | ||
| 331.19 | 0.04 | 0.0748 | 0.0006 | 1.2636 | 1.0036 | 0.0208 | −0.0110 |
| 332.99 | 0.05 | 0.1551 | 0.0013 | 1.1755 | 1.0128 | 0.0358 | −0.0065 |
| 335.56 | −0.05 | 0.2586 | 0.0024 | 1.1055 | 1.0287 | 0.0469 | 0.0013 |
| 338.99 | 0.02 | 0.3742 | 0.0041 | 1.0597 | 1.0487 | 0.0514 | 0.0036 |
| 343.66 | −0.07 | 0.4982 | 0.0069 | 1.0314 | 1.0707 | 0.0497 | −0.0061 |
| 349.75 | 0.03 | 0.6177 | 0.0119 | 1.0156 | 1.0919 | 0.0432 | −0.0030 |
| 355.77 | −0.05 | 0.7040 | 0.0187 | 1.0087 | 1.1071 | 0.0362 | −0.0039 |
| 362.59 | −0.05 | 0.7757 | 0.0291 | 1.0048 | 1.1198 | 0.0291 | −0.0009 |
| 372.53 | −0.03 | 0.8476 | 0.0516 | 1.0022 | 1.1323 | 0.0208 | 0.0001 |
| 381.71 | −0.01 | 0.8921 | 0.0827 | 1.0011 | 1.1395 | 0.0151 | 0.0013 |
| 396.12 | 0.05 | 0.9371 | 0.1606 | 1.0004 | 1.1451 | 0.0089 | 0.0041 |
| 411.66 | 0.03 | 0.9664 | 0.3035 | 1.0002 | 1.1453 | 0.0047 | 0.0036 |
| 426.95 | −0.01 | 0.9848 | 0.5332 | 1.0001 | 1.1414 | 0.0021 | 0.0017 |
| 435.49 | −0.03 | 0.9924 | 0.7139 | 1.0001 | 1.1378 | 0.0010 | −0.0011 |
| 441.13 | −0.02 | 0.9967 | 0.8587 | 1.0000 | 1.1350 | 0.0005 | −0.0027 |
| 445.93 | 0.00 | 1.0000 | 1.0000 | 1.0001 | 0.0000 | ||
| 60.0 kPa | |||||||
| 338.72 | 0.00 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | ||
| 340.58 | −0.01 | 0.0811 | 0.0008 | 1.3103 | 1.0043 | 0.0258 | −0.0014 |
| 343.25 | 0.02 | 0.1914 | 0.0020 | 1.1872 | 1.0193 | 0.0483 | 0.0000 |
| 346.66 | 0.06 | 0.3145 | 0.0037 | 1.1069 | 1.0429 | 0.0607 | −0.0058 |
| 351.85 | 0.01 | 0.4613 | 0.0069 | 1.0527 | 1.0752 | 0.0628 | −0.0006 |
| 358.36 | 0.00 | 0.5945 | 0.0122 | 1.0254 | 1.1061 | 0.0558 | −0.0031 |
| 367.75 | −0.03 | 0.7229 | 0.0235 | 1.0105 | 1.1361 | 0.0429 | −0.0048 |
| 378.78 | −0.01 | 0.8174 | 0.0444 | 1.0043 | 1.1579 | 0.0303 | −0.0003 |
| 388.91 | 0.01 | 0.8733 | 0.0740 | 1.0020 | 1.1700 | 0.0217 | 0.0003 |
| 399.40 | −0.01 | 0.9126 | 0.1191 | 1.0010 | 1.1776 | 0.0152 | −0.0003 |
| 414.71 | 0.02 | 0.9498 | 0.2226 | 1.0003 | 1.1825 | 0.0087 | 0.0017 |
| 422.69 | 0.01 | 0.9633 | 0.3002 | 1.0002 | 1.1831 | 0.0064 | 0.0013 |
| 433.88 | −0.02 | 0.9779 | 0.4451 | 1.0001 | 1.1823 | 0.0038 | −0.0007 |
| 440.61 | −0.02 | 0.9849 | 0.5566 | 1.0001 | 1.1811 | 0.0026 | −0.0009 |
| 447.20 | 0.01 | 0.9908 | 0.6869 | 1.0001 | 1.1794 | 0.0016 | 0.0010 |
| 453.73 | 0.01 | 0.9959 | 0.8393 | 1.0000 | 1.1774 | 0.0007 | 0.0018 |
| 459.64 | 0.00 | 1.0000 | 1.0000 | 1.0001 | 0.0000 | ||
| 80.0 kPa | |||||||
| 345.58 | 0.00 | 0.0000 | 0.0000 | 1.0001 | 0.0000 | ||
| 347.66 | 0.02 | 0.0875 | 0.0010 | 1.3726 | 1.0059 | 0.0331 | −0.0167 |
| 349.84 | −0.04 | 0.1766 | 0.0021 | 1.2461 | 1.0203 | 0.0554 | −0.0020 |
| 352.44 | −0.08 | 0.2728 | 0.0035 | 1.1591 | 1.0413 | 0.0697 | 0.0044 |
| 355.81 | −0.03 | 0.3791 | 0.0055 | 1.0979 | 1.0685 | 0.0765 | 0.0027 |
| 359.72 | 0.11 | 0.4796 | 0.0082 | 1.0603 | 1.0964 | 0.0759 | −0.0136 |
| 365.75 | 0.05 | 0.5974 | 0.0135 | 1.0320 | 1.1310 | 0.0684 | −0.0072 |
| 374.61 | −0.01 | 0.7167 | 0.0243 | 1.0146 | 1.1679 | 0.0543 | −0.0022 |
| 385.41 | 0.07 | 0.8101 | 0.0445 | 1.0063 | 1.1977 | 0.0394 | −0.0007 |
| 398.18 | 0.03 | 0.8784 | 0.0820 | 1.0026 | 1.2185 | 0.0263 | 0.0012 |
| 409.34 | −0.05 | 0.9168 | 0.1321 | 1.0012 | 1.2281 | 0.0182 | 0.0032 |
| 424.42 | −0.02 | 0.9509 | 0.2361 | 1.0005 | 1.2320 | 0.0107 | 0.0014 |
| 436.05 | −0.01 | 0.9687 | 0.3548 | 1.0002 | 1.2296 | 0.0067 | 0.0012 |
| 448.49 | 0.00 | 0.9828 | 0.5314 | 1.0001 | 1.2231 | 0.0036 | 0.0002 |
| 458.80 | 0.02 | 0.9919 | 0.7264 | 1.0000 | 1.2153 | 0.0016 | −0.0014 |
| 466.03 | 0.01 | 0.9973 | 0.8948 | 1.0000 | 1.2086 | 0.0005 | −0.0009 |
| 470.00 | 0.00 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | ||
| Wilson |
|---|
| NRTL |
| UNIQUAC |
| Model | α | RMSDs | AADs | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T(K) | y1 | T(K) | y1 | ||||||
| 40.0 kPa | |||||||||
| Wilson | 1.214 | −0.614 | −712.28 | 360.39 | − | 0.04 | 0.0003 | 0.03 | 0.0002 |
| NRTL | 0.914 | −1.581 | −544.98 | 928.90 | 0.3 | 0.04 | 0.0003 | 0.03 | 0.0002 |
| UNIQUAC | −1.665 | 1.186 | 456.12 | −373.90 | − | 0.04 | 0.0003 | 0.03 | 0.0002 |
| 60.0 kPa | |||||||||
| Wilson | 0.819 | −0.419 | −567.91 | 274.83 | − | 0.02 | 0.0002 | 0.02 | 0.0001 |
| NRTL | 0.672 | −1.155 | −445.86 | 778.85 | 0.3 | 0.02 | 0.0002 | 0.01 | 0.0001 |
| UNIQUAC | −1.479 | 1.025 | 380.68 | −314.53 | − | 0.02 | 0.0002 | 0.02 | 0.0001 |
| 80.0 kPa | |||||||||
| Wilson | 1.650 | −0.962 | −886.16 | 463.07 | − | 0.04 | 0.0002 | 0.03 | 0.0001 |
| NRTL | 1.307 | −2.070 | −673.95 | 1136.03 | 0.3 | 0.04 | 0.0002 | 0.03 | 0.0001 |
| UNIQUAC | −2.095 | 1.454 | 602.82 | −475.74 | − | 0.05 | 0.0002 | 0.04 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bo, W.; Zhang, X.; Zhang, Q.; Chen, L.; Liu, J.; Ma, L.; Ma, S. Isobaric Vapor-Liquid Equilibrium of Biomass-Derived Ethyl Levulinate and Ethanol at 40.0, 60.0 and 80.0 kPa. Energies 2025, 18, 3939. https://doi.org/10.3390/en18153939
Bo W, Zhang X, Zhang Q, Chen L, Liu J, Ma L, Ma S. Isobaric Vapor-Liquid Equilibrium of Biomass-Derived Ethyl Levulinate and Ethanol at 40.0, 60.0 and 80.0 kPa. Energies. 2025; 18(15):3939. https://doi.org/10.3390/en18153939
Chicago/Turabian StyleBo, Wenteng, Xinghua Zhang, Qi Zhang, Lungang Chen, Jianguo Liu, Longlong Ma, and Shengyong Ma. 2025. "Isobaric Vapor-Liquid Equilibrium of Biomass-Derived Ethyl Levulinate and Ethanol at 40.0, 60.0 and 80.0 kPa" Energies 18, no. 15: 3939. https://doi.org/10.3390/en18153939
APA StyleBo, W., Zhang, X., Zhang, Q., Chen, L., Liu, J., Ma, L., & Ma, S. (2025). Isobaric Vapor-Liquid Equilibrium of Biomass-Derived Ethyl Levulinate and Ethanol at 40.0, 60.0 and 80.0 kPa. Energies, 18(15), 3939. https://doi.org/10.3390/en18153939








