Integration Strategies for Large-Scale Renewable Interconnections with Grid Forming and Grid Following Inverters, Capacitor Banks, and Harmonic Filters

Abstract

The transition towards a power system characterized by a reduced presence of synchronous generators (SGs) and an increased reliance on inverter-based resources (IBRs), including wind, solar photovoltaics (PV), and battery storage, presents new operational challenges, particularly when these sources exceed 50–60% of the system’s demand. While current grid-following (GFL) IBRs, which are equipped with fast and rigid control systems, continue to dominate the inverter landscape, there has been a notable surge in research focused on grid-forming (GFM) inverters in recent years. This study conducts a comparative analysis of the practicality and control methodologies of GFM inverters relative to traditional GFL inverters from a system planning perspective. A comprehensive framework aimed at assisting system developers and consulting engineers in the grid-integration of wide-scale renewable energy sources (RESs), incorporating strategies for the deployment of inverters, capacitor banks, and harmonic filters, is proposed in this paper. The discussion includes an examination of the reactive power capabilities of the plant’s inverters and the provision of additional reactive power to ensure compliance with grid interconnection standards. Furthermore, the paper outlines a practical approach to assess the necessity for enhanced filtering measures to mitigate potential resonant conditions and achieve harmonic compliance at the installation site. The objective of this work is to offer useful guidelines and insights for the effective addition of RES into contemporary power systems.

1. Introduction

In recent times, there has been a considerable shift in the research landscape related to IBRs, mainly due to the growing integration of renewable energy sources (RESs) into the power grid. Power electronic inverters are the primary means through which IBRs, including technologies such as solar photovoltaics and wind turbines, interface with the grid. These IBRs can be categorized into GFL and GFM types, each serving distinct roles in maintaining grid stability and reliability [1,2]. As the penetration of IBRs grows, traditional power grid dynamics, historically dominated by synchronous generators, are undergoing substantial changes. This shift necessitates a reevaluation of system stability concepts, particularly in terms of swing angle, frequency, and voltage stability, as the dynamics associated with IBRs differ markedly from those of conventional generators (synchronous machines). Furthermore, the transition to a grid with high IBR penetration raises critical challenges, including reduced short-circuit strength and increased susceptibility to small-disturbance stability issues, which are exacerbated by the fast-acting nature of inverter controls [3]. Consequently, ongoing research is focused on obtaining robust models and control strategies to enhance the integration of IBRs while ensuring the resilience and stability of modern power systems [4]. As consulting engineers for large electrical utilities, the authors have summarized their experiences with the integration of large-scale renewable interconnections with GFM and GFL inverters, capacitor banks with integrated harmonic filters, while meeting the system operator’s interconnection requirements. The authors have used a high-fidelity network model of the Texas regional grid for their simulation studies; however, the results can be extended for other electrical grids without losing any generality.

The grid-integration of large-scale renewable plants, particularly those utilizing inverters for power conversion, presents significant challenges in ensuring reactive power compliance at the point of interconnection (POI). A critical aspect of this challenge is the inverter’s reactive power (PQ) capability curve, which defines the limits of reactive power that can be injected or taken up by the IBR under varying operational conditions. The existing research highlights a notable gap in comprehensive studies addressing the effective management of reactive power in these systems. The limited reactive power capabilities of inverters, as highlighted by the authors in [5,6], necessitate optimal allocation strategies to maximize the reactive power transfer capability across multiple inverters in large-scale photovoltaic systems. This is particularly important given that the reactive power requirements can fluctuate significantly due to the intermittent character of renewable sources [7]. The ability to control reactive power output directly from power plants could enhance compliance with grid requirements, and to this effect, the authors have attempted to highlight the importance of IBR capability curves in the analysis of reactive power compensation analysis.

The development of detailed technical specifications for both GFM and GFL inverters is essential for system operators tasked with selecting the appropriate inverter technology to meet the growing challenges of the electric grid. As the integration of RES increases, the performance and intrinsic characteristics of inverters become critical in maintaining grid stability and reliability. GFM inverters, which can promptly regulate voltage and frequency, are identified as essential components for future IBR-dominated power systems, providing functionalities traditionally associated with synchronous generators [8,9]. In contrast, GFL inverters primarily follow the existing grid conditions, making them suitable for established systems but potentially less effective in scenarios with high renewable penetration [10,11].

The distinct operational capabilities of GFMs and GFLs inverters necessitate comprehensive specifications that outline their control methodologies, reactive power support, and fault recovery strategies. For instance, GFM inverters can offer enhanced stability and inertia emulation, which are crucial in weak grid situations, while GFL IBRs are more adept at integrating with existing grid structures [12,13]. Detailed specifications can assist operators in understanding how each inverter type contributes to grid dynamics, including their roles in voltage support and frequency [14]. As the grid transitions towards a higher penetration of IBRs, the need for hybrid inverter solutions that combine the strengths of both GFM and GFL technologies is becoming increasingly apparent. Hybrid systems of this kind can deliver rapid voltage and frequency assistance while satisfying active power needs [15]. Therefore, producing detailed inverter specifications, as outlined in this manuscript, will empower system operators to make informed procurement decisions, ensuring that the selected inverters align with the specific needs and challenges of their electric grid environments.

A crucial auxiliary consideration must be made while integrating IBRs in renewable rich grids so as to ensure the dominant harmonic signature of the grid is largely unaltered. The existing literature on high-pass harmonic filter design for IBR applications is notably limited, creating a gap in practical guidance for engineers and system operators. While various studies have explored harmonic mitigation techniques, there is a lack of comprehensive resources specifically addressing the design and implementation of high-pass filters tailored for industrial applications [16,17]. Now that the mechanics underlying the challenges of large renewable interconnections have been understood, the solutions presented in this manuscript address each of these systemic barriers. These solutions form the main motivation of this paper, and are documented below as follows:

• Highlighting the nuances of a carefully planned reactive power study to ensure the inverter reactive power capability along with the main power transformers are adequately sized from an MVAr standpoint.
• Providing a well-balanced set of specification requirements that could be readily used by system developers and utilities for inverter procurement, thereby helping them avoid potential technical omissions or misalignment on inverter specifications.
• Leveraging high-pass harmonic filter design for IBR applications by providing easily replicable examples for these grid filters. In addition, capacitor banks serving as an integral component of harmonic filter solutions are demonstrated to enhance the effectiveness of high-pass filters. They not only provide reactive power compensation but also help in tuning the filter to mitigate specific harmonic frequencies [18,19]. By strategically integrating capacitor banks with high-pass filters, system operators can improve voltage profiles, reduce power losses, and minimize the risk of resonance, thereby ensuring compliance with power quality standards.

The manuscript is structured to systematically explore practical and scalable grid integration strategies, and is divided as follows:

Section 2 examines the importance of a well-crafted reactive power study to meet interconnection compliance for large-scale renewable interconnection. Ambient temperate-based derating of large power transformers can affect its capability to meet both real power requirements at the point of interconnection along with providing adequate reactive power for voltage support, and solutions to such scenarios have been discussed.

Section 3 and Section 4 provide analytical treatment of GFM versus GFL inverters and their control mechanism, along with a framework to specify such inverters while taking into consideration monitoring, control, and other capabilities.

Section 5 addresses the harmonic compliance aspect of large renewable interconnection projects and provides a decision tree to help navigate through IEEE harmonic distortion limits between standards IEEE 519 and IEEE 2800. For a cost-efficiency standpoint, a unique solution is provided that uses the stages of a capacitor bank with a primary function to provide reactive power to be used as a harmonic filter to meet IEEE harmonic compliance.

Section 6 concludes the paper by integrating these insights into a cohesive roadmap to minimize the roadblock and duration of large renewable interconnection projects and to enhance the economic efficiency of power system operations with a high proportion of renewable resources.

2. Reactive Power Capability and Interconnection Requirements

The US Federal Energy Regulatory Commission (FERC) Order 827 issued in 2016 establishes critical reactive power requirements for IBRs, particularly focusing on wind and solar energy sources. As per the directive, generators are required to keep the power factor +0.95 lead to −0.95 lag at the POI [20]. The rationale behind this requirement is to ensure that these RES can contribute effectively to voltage stability and overall grid reliability, especially as their penetration into the energy mix increases.

The grid-integration of RES poses unique challenges, particularly concerning reactive power management. Traditional synchronous generators inherently provide reactive power support due to their mechanical inertia, which is not the case for many renewable sources that rely on power electronics for grid connection [21]. As a result, FERC Order 827 emphasizes the need for wind and solar plants to be equipped with advanced power electronics capable of delivering reactive power on demand, thereby enhancing grid stability. This capability is crucial, as the intermittent nature of renewable generation can lead to fluctuations in voltage levels, necessitating a responsive reactive power supply to maintain system integrity. When conducting a reactive power study for the integration of PV, solar, or the battery energy storage system (BESS), it is essential to consider the relevant reactive power requirements of the system operator. As an example, ERCOT’s nodal protocol on reactive power requirements is based on FERC Order 827 and in the ERCOT jurisdiction, the power factor range required is between 0.95 lagging/leading at maximum power output, and it must be provided at the POI with the transmission system for any voltage setpoint between 0.95 and 1.05 p.u.

While performing the necessary reactive power study as part of the larger interconnection study might appear relatively straightforward, complexities do exist, which are imperative to docket, such as the ones noted in the subsequent section. These complexities along with the necessary background information are noted as follows:

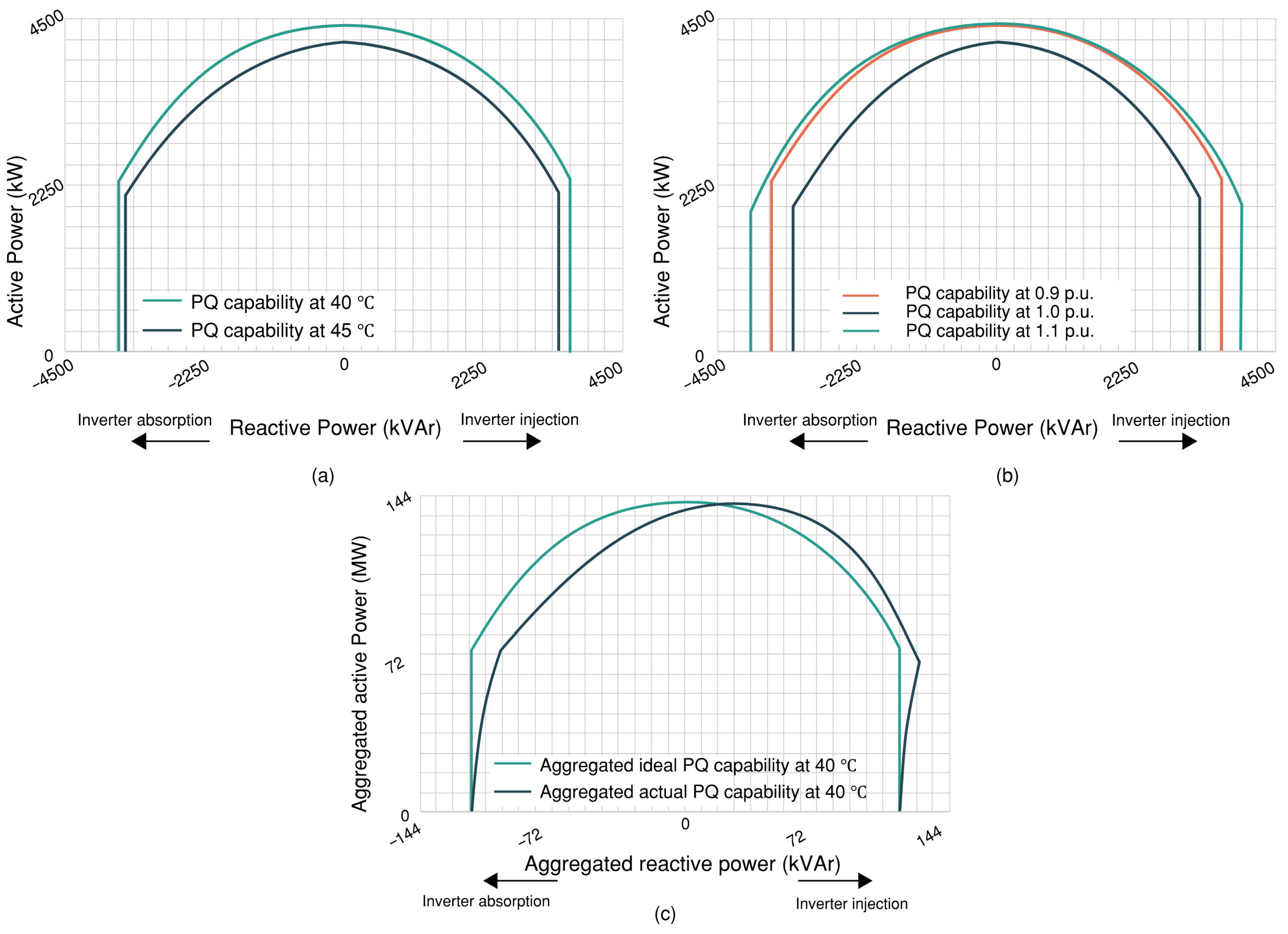
• Confirming with the inverter manufacturer about the selection of the correct active power/reactive power (PQ) capability curves, such that it reflects the accurate capability of the IBRs based on site-specific ambient temperature conditions and interconnection voltage (in p.u.).

For instance, for a utility class OEM inverter, the default inverter PQ capability curve provided by the manufacturer might be rated for an ambient temperature of 40 °C (104 °F). However, for applications where ambient temperatures are likely to reach 45 °C (113 °F) or higher, one has to explicitly ask the OEM for the PQ curve corresponding to the higher ambient temperature rating, so as to warrant that the project is still able to meet the system operator’s reactive power requirement at the POI with the budgeted number of inverters. Figure 1a shows the PQ capability curve of the OEM inverter at different ambient temperature ratings with a 1.0 terminal voltage rating, while the effect of varying the terminal voltage on the PQ capability curve for a fixed ambient temperature can be observed in Figure 1b. Readers are to note the wide variable nature of the inverter PQ curve, and as such, the PQ curve consistent with the interconnection terminal voltage cases and site ambient temperatures must be considered while conducting a reactive power study.

2.

Ensuring that the main generator step-up transformer (GSU) is not overloaded in terms of its kVA rating while the reactive power obligation at the POI is maintained for all dispatch levels.

Although at first glance, it might appear obvious that the violation of the kVA rating of the main power transformer might be a very low probability scenario, there are times where one witnessed a kVA violation with the execution of the reactive power study. Generally, the situation arises at renewable collector stations where the main power transformer(s) are usually specified and procured by a developer significantly ahead of the project (given the procurement lead times of such large power transformers). The developer usually wants to ensure that both kW rating (which drives the developer’s revenue stream and is not usually negotiable) and the kVAr rating of the plant (reactive power requirement at the POI, usually a mandatory requirement driven by the system operator) are within adequate bounds. Under bounds to meet the dual obligation of kW and kVAr, one might witness that the GSU behind the POI might be overloaded. Under scenarios where there might be a kVA violation for the main power transformer, it is imperative to determine the duration and degree by which the kVA rating of the main power transformer is being exceeded. Working closely with the transformer vendor, a determination can be made whether the duration and degree by which the kVA rating of the main power transformer is being exceeded contributes to the loss of life of the main power transformer. Usually in scenarios where the duration of the kVA overload is a few hours at every peak season of the year, the degradation and loss of life does not usually exceed the usual lifespan of the main power transformer. Under these scenarios, two solutions exist: the main power transformer is usually re-nameplated with a higher kVA rating by the vendor if loss of life is not an issue, or the developer is required to decrease the guaranteed MW output at the POI, if the temporary overload is deemed to affect the GSU’s lifespan.

In a scenario illustrated in

Table 1. Reactive power analysis of a 130 MW solar farm demonstrating power factor compliance as per ERCOT interconnection requirements but with temporary overload of GSU.

Temp for Inverter PQ Curve	Gross MW at GSU Terminal/Net MW at POI 1	Gross MVAr at GSU Terminal/Net MVAr at POI 2	Power Factor at POI/ Additional MVAr Needed 3	Corrected Power Factor and Additional MVAr	MVA at GSU Input Terminal 4	GSU Overload Status
40 °C	Gross—139.48 MW (with 32 inverters providing 4359 kW each)/Net—130.5 MW at POI	Gross—26.9 MVAr (with 32 inverters providing 840 kVAr)/Net—19 MVAr at POI	0.98/Yes	0.95/19.7 MVAr needed	142 MVA	GSU overloaded by 7 MVA. Remark—GSU may be re-nameplated if vendor confirms no loss of life for the GSU.
45 °C	Gross—152.5 MW (with 35 inverters providing 4359 kW each)/Net—138.3 MW at POI	Gross—29.4 MVAr (with 35 inverters providing 840 kVAr)/Net—21 MVAr at POI	0.98/Yes	0.95/24 MVAr needed	154.5 MVA	GSU overloaded, by 19.5 MVA. Remark—Set contractual obligation at POI needs to be decreased as GSU is significantly overloaded.

¹ Set contractual obligation for this study is for the plant is to provide 130 MW at POI. ² MVAr loss is mainly through capacitive charging of inverter feeder cables given the length they span through the site. ³ As outlined in Order 827, the FERC commission anticipates that non-synchronous generators can fulfill the dynamic reactive power obligation by employing a mix of the IBR’s inherent dynamic reactive power capacity, along with dynamic and static reactive power devices to recompense. ⁴ GSU ratings (ONAN/ONAF1/ONAF2) are 115/130/135 MVA.

, one may hypothesize that a developer is providing 32 inverters as part of a pre-contract obligation at a site where the ambient operating temperature is 40 °C (and hence one may follow the PQ curve from Figure 1a, and requires that 130 MW of the maximum output power be available at the POI. A well-modeled reactive power study (capturing all the inverter PQ curves, medium voltage feeder cable losses, GSU losses) revealed that that for the 32 units of inverters to provide 130 MW of maximum output power at the POI, 139.8 MW of power has to be provided on the input side of the main GSU. The inverter PQ capability curve from Figure 1a reveals that the inverters shall produce a corresponding gross 26.9 MVAr on the input side of the main GSU, which equates to 19 MVAr at the POI. However, additional MVAr (which could be in the form of static VARs such as the capacitor bank, and shall be discussed in greater details) may be needed at the collector station behind the POI to correct the power factor to 0.95 (lead or lag). Moreover, with a gross 139.48 MW and 26.9 MVAr inverter output, the plant’s GSU with a maximum rating of 135 MVA shall be overloaded by 7 MVA, and a possible remedy, such as re-nameplating the GSU, as noted in the preceding paragraph, may be needed.

One may draw a similar conclusion when the ambient operating temperature is 45 °C, as can be seen from the second row of Table 1, with the GSU now being overloaded by 19.5 MVA beyond its maximum capacity, requiring the resetting of the contractual obligation of MWs at POI.

3.

Accounting for the main power transformer’s (MPT’s) and inverter step up transformer’s (SUT’s) no load losses, unless those losses are factored in within the PQ curves being provided by the inverter manufacturers.

As a recommended practice, if the inverter’s step-up transformer is part of the inverter skid, it is best for one to ask the inverter manufacturer to provide the PQ curve at the higher voltage side of the inverter SUT, thus allowing the vendor-provided PQ curve to have the no load losses factored in by default.

4.

Accounting for any station auxiliary loads/seasonal operation and maintenance loads/storage building load.

5.

The need to account for the low voltage and medium voltage feeder cable impedance. As such, with large solar fields typically with a footprint of 500 acres or more, the collector system impedance is sufficient to skew the aggregate PQ curve of the inverters. Such an aggregated PQ curve, with an aggregation of 32 inverters, is shown in Figure 1c.

To sum up, it is imperative that accurate inverter PQ capability curves are used for the reactive compensation study. Furthermore, often given the vast geographic footprint of this renewable plant, it is imperative to summarize the value of power losses on the low voltage (PV module or wind turbine to inverter) and medium voltage cable runs (inverter to GSU located in the collector station).

3. GFM Versus GFL Inverters and Their Controls

Before presenting a detailed theoretical treatment of this subject, it is imperative to form a practical analogy of GFM versus GFL IBRs. One may picture a tranquil meadow where a pack of sheep grazes under the guidance of a few shepherd dogs. The sheep, akin to GFL inverters, respond instinctively to external cues—the calls of the shepherd and the subtle movements of their companions. Similarly, GFL inverters rely on synchronization elements, such as phase-locked loops, to align with the “rhythm” of the grid, represented by its frequency and voltage characteristics. This allows the GFL inverters to operate in harmony, adjusting their outputs much like sheep naturally fall into coordinated movement within the flock.

Yet, as sheep struggle when the shepherd’s guidance grows unclear or the terrain becomes unpredictable, GFL inverters face challenges in low-strength grid conditions. In these scenarios, where the grid’s signals become faint or erratic, GFL inverters can falter, much like sheep losing direction. This instability can ripple through the system, impacting overall grid performance.

Amid the flock, the shepherd dogs represent GFM inverters. Unlike the reactive sheep, the dogs take a proactive role, setting the pace and maintaining order. GFM inverters create their own voltage and frequency references, much like the shepherd dogs ensure the flock stays together even without clear guidance from the shepherd. When the grid’s “shepherd” weakens, GFM inverters step up (assuming in an electrical world that they are well placed), providing stability and direction. They maintain order and adapt to changes, much like skilled shepherd dogs that continue to guide the flock in challenging conditions. Their ability to operate independently ensures that the system remains reliable, even when external cues falter.

Imagine multiple shepherd dogs coordinating to manage a large flock. They communicate and adjust their movements to maintain harmony, reflecting the interplay between multiple GFM inverters working together. This collaboration requires precise tuning and synchronization, just as the dogs must align their efforts to ensure the flock’s cohesion. The synergy between the sheep (GFL inverters) and shepherd dogs (GFM inverters) highlights the balance required in modern power systems. Like a well-managed flock, the grid benefits from the complementary roles of followers and leaders, ensuring stability and reliability. This analogy underscores the importance of refining these technologies to adapt to evolving challenges, much like shepherds continually hone their skills to guide their flocks effectively.

GFM IBRs have become a pivotal resource for power grids around the world, as they provide fundamental capabilities that facilitate the grid-integration of RES and improve grid stability for applications such as PV, wind, and BESS. The ability of these inverters to establish grid voltage and frequency independently enhances system flexibility by allowing grids to form. GFM inverters possess inherent voltage–source characteristics, no longer solely relying on external voltage for operation. Their controllable damping and output impedance provide robust grid support, accommodating the integration of new energy sources and enabling connection to external grids. Compared to grid-following inverters, GFM inverters can respond instantaneously to system changes, adjusting voltage magnitude and frequency, supplying fault current, and contributing to system inertia. This makes them essential for ensuring grid strength, particularly in systems with high penetration of IBRs. Specifically, GFM inverters can provide the following key capabilities:

1. Black start: GFM inverters can independently set grid voltage and frequency, allowing them to form and energize the grid without relying on external voltage sources. This makes them essential for restoring power after a blackout.

A general limitation of GFM inverters, which is an area of active research [22], is that of black starting isolated microgrids with a significant percentage of motors or transformers. The inrush current for starting induction motors or transformers might drive the GFM IBRs to their maximum current limit (usually set at 1.2 p.u.). To consider inadvertent tripping of the GFM, prior consideration of the load characteristic of the microgrid where the GFM is likely to operate is essential, and protective relay settings must be adjusted accordingly.

2. Voltage response: The ability of GFMs to manage both positive and negative sequence voltages allow for effective voltage balancing, significantly reducing negative-sequence voltage impacts, thus ensuring reliable operation during disturbances. Moreover, GFMs are designed to withstand voltage dips and short-circuit conditions, employing advanced control strategies that limit the current to prevent damage to sensitive components.

3. Frequency response: GFM inverters can adjust the frequency of the system, contributing to system inertia and suppressing frequency fluctuations, which is crucial for maintaining grid stability. These capabilities are achieved through various control methods, such as droop control, voltage–frequency (V-f) control, and virtual synchronous generator (VSG) control. The selection and implementation of these control strategies are important for ensuring the reliable and effective performance of GFM inverters in modern power systems.

4. Inertia provision: One of the primary advantages of GFMs is their ability to provide virtual inertia, which allows them to respond to frequency changes similarly to synchronous generators. This capability is of the essence in preserving frequency stability in systems with high IBR penetration, which correlates to a lack in traditional system inertia. By implementing control algorithms that mimic the inertial response of synchronous machines, GFMs can contribute to a more stable grid environment, effectively decreasing the risk of load shedding events during disturbances.

While utilities or developers plan on integrating GFMs, it must be noted that every grid topology is different and reactions to disturbance conditions vary, but it is recommended for system operators to carry at least 15–30% GFM IBRs in the system, with grids having high penetration (75% and above) of IBRs due to their various strengths discussed above. As one may observe in Figure 2a,b, PSS^®E scenario analysis of voltage and frequency of an approximated ERCOT grid reveals that with GFM contributing to at least 15% of the total IBRs composition, the small system stability of the system can be ensured. Small signal stability is validated by the introduction of a three phase to ground fault at 3 s. Over several simulations, it was noted that the best location to install a GFM is in the weakest links of the grid (low short circuit ratio), so as to strengthen the GFM capability.

PSS^®E scenario analysis of frequency response for both GFL and GFM inverters were carried out at various short circuit ratios with an SCR 1.0 representing a weak power grid, an SCR of 3.0 representing a power grid of moderate strength, and an electrically strong grid with an SCR of 10.0, in order to understand their respective behaviors. At 1 s into the simulation, a load step was applied to both inverter systems; it was observed (Figure 3a,b) that a GFL under a weak grid scenario, as represented by an SCR of 1.0, loses stability, but is able to ride through the load step changes with improvements in the grid strength (SCR 3.0 and 10.0). GFM inverters, on the other hand, are able to ride through weak grid conditions without loss of synchronization, although the frequency dip and recovery conditions may last for 60–100 cycles. Another interesting aspect of small signal stability analysis that was investigated was the relative behavior of GFL and GFM inverters for weak (SCR 2.0) and strong grid (SCR 5.0) conditions under varying X/R ratios (inductive vs. resistive grids), ranging from 1.0 to 20.0, by observing the system’s dominant Eigen values. Real time grid conditions could exist where the grid is inherently weak (SCR of 2.0) yet predominantly inductive in nature (X/R ratio of 20 or higher). As may be seen in Figure 3c, when the SCR is 2.0 and the X/R ratio is increased and nears the upper threshold for this simulation (20.0 in this case), stability is lost for the GFL inverter setup, with the dominant Eigen values starting to move to the right-hand side of the real axis. However, as the SCR is increased to 5.0, the dominant Eigen values for the GFL inverter tend to move towards the right-hand side but remains in the negative side of the real axis, retaining the stability of the system. For the GFM inverters, under both SCRs of 2.0 and 5.0 conditions, stability is maintained up to an X/R ratio of 20.0.

Overall, it is important to avoid broadly categorizing the grid-following (GFL) control as inherently inferior and the grid-forming (GFM) control as universally superior. With appropriate tuning, GFL inverters can achieve performance levels comparable to GFM inverters under a wide range of operating scenarios. In certain grid conditions, the deployment of GFM inverters may not be necessary. Rigorous evaluation using time-domain simulations, electromagnetic transient (EMT) studies, and small-signal stability analysis is essential to determine whether GFM capability is justified for a given large-scale renewable integration project.

As to the definition of the short circuit ratio (SCR), it is a simple metric to determine the relative strength of a grid and is identified as the ratio of the short circuit capacity at the connecting bus where the IBR is located to the MW rating of the IBR (Equation (1)).

$${SCR}_{bus}={\displaystyle \frac{{MVA}_{SC BUS}}{{MW}_{rating IBR}}}$$

(1)

The SCR metric by itself is adequate for a single IBR connection, as it does not consider the impact of other nearby IBRs. For multiple IBRs connected electrically close to each other, the SCR metric tends to give very optimistic results. Therefore, other methods as the ones proposed in [23] to estimate the grid strength with multiple IBRs, such as the weighted short circuit ratio (WSCR) and equivalent circuit-based short circuit ratio (ESCR), are encouraged to be considered.

The weighted short circuit ratio (WSCR), as shown in Equation (2), calculates the SCR of the weighted average short circuits of the IBRs, where ${\mathrm{M}\mathrm{V}\mathrm{A}}_{\mathrm{S}\mathrm{C} \mathrm{B}\mathrm{U}\mathrm{S}\mathrm{i}}$ is the short circuit MVA at bus i and ${\mathrm{M}\mathrm{W}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{I}\mathrm{B}\mathrm{R}\mathrm{i}}$ is the MW rating of the ith IBR.

$$\mathrm{W}\mathrm{S}\mathrm{C}\mathrm{R}={\displaystyle \frac{{\sum }_{i=1}^N{MVA}_{SC BUS i}\times {MW}_{rating IBR} i }{{\sum }_{i=1}^N{MW}_{rating IBR i}}}\times {\displaystyle \frac{1}{{\sum }_{i=1}^N{MW}_{rating IBR i}}}$$

(2)

As of 2024, nearly all grid-connected inverters in the ERCOT grid are controlled with a GFL controller. However, since 2018, there has been some promising progress in grid-scale GFM, with some major commercial implementations in the US and globally, as documented in

Table 2. Commercial GFM projects under consideration or deployment as of 2025.

Operator, Location, and GFM Technology	Status and OEM	Size (MW)	Timeline
Zenobē Energy–Scotland (GFM BESS)	Under development, SMA (OEM)	Blackhillock 1–200 MW Blackhillock 2–100 MW Kilmarnock 1–200 MW Kilmarnock 2–100 MW Eccles—400 MW	2024–2026
Vattenfall—Denmark/Germany (GFM offshore wind via STATCOM)	Deployed, Hitachi Energy (OEM)	Kriegers Flak—605 MW	2018
AEMO—Australia (GFM BESS)	Deployed, Tesla (OEM)	Riverina and Darlington Point—150 MW	2023
AEMO—Australia (GFM BESS)	Under development, Power Electronics (OEM)	Liddell Battery Park—500 MW	2025
Pacific Gas & Electric—Oregon, US (GFM Hybrid of wind, solar, battery)	Under development, OEM unknown	Wheatridge Renewable Energy Facility—380 MW	2026
NESO—Great Britain (GFM BESS)	Under development, Sungrow (OEM)	Hams Hall—350 MW	2026
Eversource—New York, US (GFM offshore wind via STATCOM)	Deployed, OEM unknown	South Fork Wind—75 MW	2024
HECO—Hawaii, US (GFM BESS)	Deployed, Tesla (OEM)	Kapolei Energy Storage—185 MW	2023
HECO—Hawaii, US (GFM PV + BESS)	Deployed, OEM unknown	Waiawa Phase 2 Solar—60 MW	2024
Kauai Island Utility Cooperative—Hawaii, US (GFM BESS)	Deployed, Tesla (OEM)	Project #1–13 MW	2018

.

4. Technical Specification Details for Grid Inverters and Medium Voltage Step-Up Transformer

Well-documented technical specifications for grid inverters are essential for procurement purposes due to the high cost of the equipment and long lead times. This ensures that the procurement process is efficient, and the equipment meets the specific requirements of the project. Developers in the renewable energy field and engineering/procurement/consulting (EPC) firms can benefit from having a robust set of standards defining the needs and specifications for project-specific grid inverters. The key requirements for utility-scale PV inverters and medium voltage step-up transformers (which is often part of the inverter enclosure) can be summarized as follows:

• General specifications: These general specifications are fundamental in selecting a grid-scale inverter and highlight the underlying inverter technology and the control modes of the inverter, the power factor requirement that the inverter needs to satisfy, along with the kVA rating of the inverter.
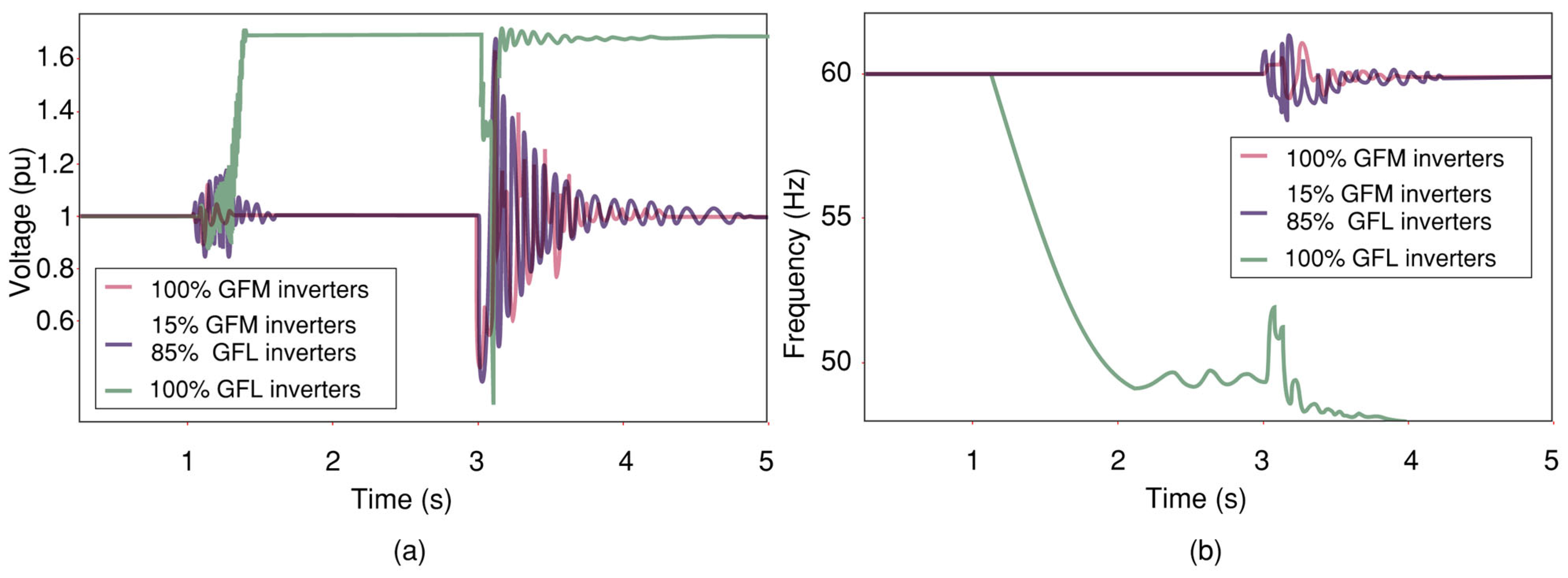
  • Inverter control technology: Unlike the GFL mode of control that functions as current sources, which require a phase-locked loop (PLL) and a current–control–loop, and cannot operate without an externally regulated voltage, the GFM mode of operation does not necessitate a PLL. GFMs can regulate their own instantaneous terminal voltages, with a behavior which may be approximated like a voltage source.
    Utility-scale renewable projects implementing GFM controllers must give due consideration to the IBR’s control system when the parallel operation of multiple GFM inverters is in question. The prevalent parallel operation control strategies (droop control, virtual synchronous generator control, etc.), each with their relevant strength and weakness, are documented in the following section. It is imperative for grid operators and system planners to note that the difference between GFLs and GFMs lies within its control strategy and not in the inverters’ hardware, and as such, the control systems for GFLs can be usually switched to its GFM counterpart mode. However, the transition needs to be seamless, as abrupt changes in the references of both inner control loops and outer control loops, such as the power or voltage loop, may lead to unacceptable deviation in voltages and currents or even compromising safe operations. An excellent reference on the seamless switching between the GFL and GFM control modes may be found here [24]. As of 2025, the GFM controls that are commercially available are the following:
    • Droop control [25,26]
      Advantage—Matured technology with well-documented references on proper tuning of the control parameters. Easy to automate load sharing among a collection of generators.
      Disadvantage—Lack of inertia support capability.
    • Virtual synchronous generator control [27]
      Advantage—Superior inertia support and hence superior dynamic response.
      Disadvantage—Prone to oscillations requiring precise parameter tuning.
      Note—Compensated generalized VSG (CGVSG)-based GFMI and adaptive VSG (AVSG)-based GFMI [28,29,30] are solutions addressing the deficiencies identified in VSG (under scenarios where robust operation cannot be guaranteed under different grid conditions), ensuring the stable operation of GFMIs in both weak and strong grid connections. Both the CGVSG and AVSG are primarily designed to accurately follow power reference signals while delivering the intended dynamic response. This is accomplished by taking into consideration grid parameters during the design phase. The CGVSG employs a lead–lag compensator to guarantee a predefined RoCoF limit and minimized overshoots. In contrast, the VSG structure is adopted by the AVSG; however, its parameters are adaptively tuned based on the real-time estimation of grid impedance. This adaptive approach ensures robust performance across various grid scenarios while adhering to predefined settling time and damping.
    • Virtual oscillation control [31]
      Advantage—Fast response and robust synchronizing capability. Can support island mode of microgrids.
      Disadvantage—Evolving and relatively complex control algorithm. Can pro duce third harmonic voltage output.
    • Matching control [32]
      Advantage—Fast response and the most robust synchronizing capability among all comparable GFM controls.
      Disadvantage—Evolving and relatively complex control algorithm.
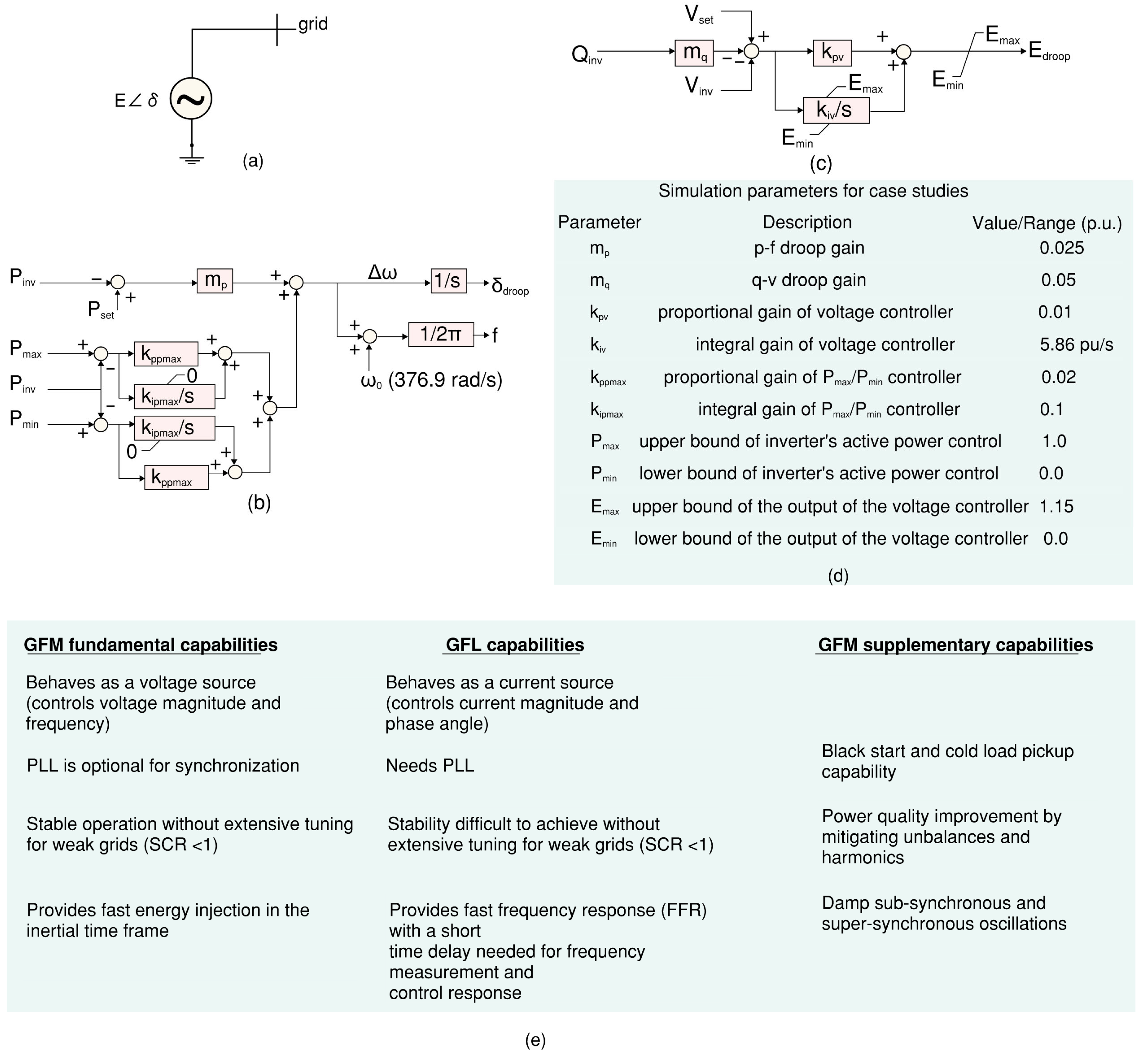
    In order to further enhance the collaborative control capability based on inverter resources in complex energy networks, it is possible to consider introducing a cooperative game method to model and coordinate the conflicts of interest between inverter sites, renewable energy, and local load agents under the constraints of shared grid resources, thereby improving the coordination and fairness of system operation [33]. Overall, GFM responds to changes in the grid’s load and generation to keep the synthesized frequency as close as possible to the set nominal value. These controls are robust enough to withstand grid disturbances such as transients, faults, and unexpected load swings, by adapting the internal control parameters to avert system instability. The GFM model used in this study takes advantage of p-f and q-v droop control, with its generic model and control system schematics shown in Figure 4a–c, with Figure 4d docketing the inverter and controller parameters. The outputs of the control system, E_droop and δ_droop, are used to establish the IBR internal voltage E∠δ_E. Some of the main differentiations between the GFM and GFL control are summarized in Figure 4e.
    Figure 4. Control schematic and simulation parameter for a GFM controller with droop control. (a) Simplistic representation of GFM inverter control. (b,c) P-f and q-v droop control [34]. (d) Simulation control parameter used for the case studies in this manuscript. Note: The p-f droop control guarantees synchronization of phase angles across numerous GFM IBRs, while the q-v droop loop alleviates significant circulation of reactive power between the same group of IBRs. (e) GFM and GFL major difference comparison.

    Figure 4. Control schematic and simulation parameter for a GFM controller with droop control. (a) Simplistic representation of GFM inverter control. (b,c) P-f and q-v droop control [34]. (d) Simulation control parameter used for the case studies in this manuscript. Note: The p-f droop control guarantees synchronization of phase angles across numerous GFM IBRs, while the q-v droop loop alleviates significant circulation of reactive power between the same group of IBRs. (e) GFM and GFL major difference comparison.
  • Minimum power rating (kVA) and altitude and temperature derating factor.
  • Interconnection power factor requirements.
  • Specification of operation mode such as wake up, sleep mode, synchronization, and disconnect.
  • Night-time reactive power availability, also known as the “Q at night” feature.
    Night-time reactive power capability, often referred to as “Q at night”, is an emerging area of interest in the operation of grid-scale inverters. This “Q at night” capability allows inverters to offer reactive power support to a grid even in the absence of solar irradiance, thereby enhancing grid stability and power quality.
  • Availability of vendor provided inverter Norton harmonic model. As such, the inverter Norton harmonic model is an important datapoint in additional harmonic filter design as the harmonic model helps one in evaluating the shift of the resonant point of the system as more inverters are added into the system.
  • Availability of vendor provided inverter PQ curves specifying the ambient temperature, and inverter terminal voltage.
• Monitoring and control capabilities: These monitoring and control capabilities are deemed secondary capabilities and are largely driven by the owner utility/ developer rather than the regional transmission operator. The specifications that fall in this category are the following:
  • Lag-free monitoring of PV system parameters such as voltage, current, power, and energy generation.
  • Remote monitoring and control of PV inverters through a centralized SCADA system.
  • Capability to implement advanced control strategies such as model predictive or back-stepping sliding control.
  • Connectivity to SCADA system via Modbus, Ethernet TCP, or fiber.
• Data management and analytics: The data management and analytics capabilities are mainly driven by the utility and the regional transmission operator control center needs, and these requirements can be broadly summarized as follows:
  • Compatibility for efficient data storage and retrieval mechanisms for historical data logging and analysis.
  • Ability for integration with cloud-based platforms or edge computing devices for data processing and analytics.
  • Ability to adopt lightweight communication protocols and IoT-based technologies to reduce data transmission overhead.
• Grid integration and support functions: The grid integration and support functions are driven by the regional transmission operator, and the obligation it sets on the developer or the interconnecting utility.
  • Ability to provide secondary services, such as frequency support and oscillation damping, reactive power control, and active power curtailment.
  • Compliance with grid code requirements and distribution network operator (DNO) guidelines.
  • Mitigation of power quality concerns, such as harmonics and resonance, through appropriate in-built filter design. Standards such as IEEE 519, UL 1741, and FCC part 15B might apply in connection to utility scale inverter’s harmonic contents and electromagnetic interference limits.
• Reliability and resilience: These requirements usually get cascaded from the project planning stage depending on the projected lifecycle of the project.
  • Must be able to perform an average of 50,000–75,000 charging, discharging cycles.
  • Robust and fault-tolerant system design to ensure reliable operation and minimize downtime.
  • Redundancy and failover mechanisms for critical components.
  • Cybersecurity measures (such as network segmentation, secure communication protocols like TLS/SSL) to protect the SCADA system from cyber threats.
  • Mean time to repair: 2–4 h per power module.
  • Mean time to failure: 10–15 years for 1 inverter power module.
• Protection features: The protection features and functionalities are specified by the protection engineering team to ensure the inverter is compatible with the overall and specific protection schemes in place. For instance, anti-islanding protection is a common feature for grid inverters whereas ground fault monitoring can be performed at the collector station without the need for such monitoring capability in the inverter itself.
  • Ground fault monitoring through ground-fault detector interrupter (GFDI).
  • Anti-islanding protection, which can be passive, active, or a combination of both. This protection allows detecting island situations and lead to the disconnection of the inverter [35] (thereby preventing it from feeding electricity back into the grid and potentially endangering utility workers who may be repairing lines).
  • Flexible frequency protection settings to allow for under/over frequency.
  • Grid support including frequency and voltage ride-through and recovery capabilities (within the framework of IEEE 1547 or similar standards), reactive power control, ramp rate, and rapid fault current injection at the POI in case of balanced faults.
  • Active heating capability at night where the inverter regulates its internal ambient temperature to prevent condensation, thereby helping with increasing longevity of the internal power electronic devices and controllers.
• Medium voltage step-up transformer parameters: The integration of medium voltage step-up transformer with the inverter, although optional, is preferred by utilities and developers as it streamlines the design of the foundation and overall conduit routing. The specifications for such MV transformers are the following:
  • Oil type, cooling type, and allowable transformer configuration, such as integrated dry-type transformer.
  • Guaranteed No Load Losses (NLLs) and guaranteed Load Losses (LLs) defined at a certain maximum ambient temperature.
  • Harmonic K Factors and indication of compliance to IEEE C57.110 standard. Note that the higher the K-Factor, the greater the overheating caused by the harmonics.
  • Tap changer specification capable of operating at a certain percentage above or below nominal voltage at full rating.

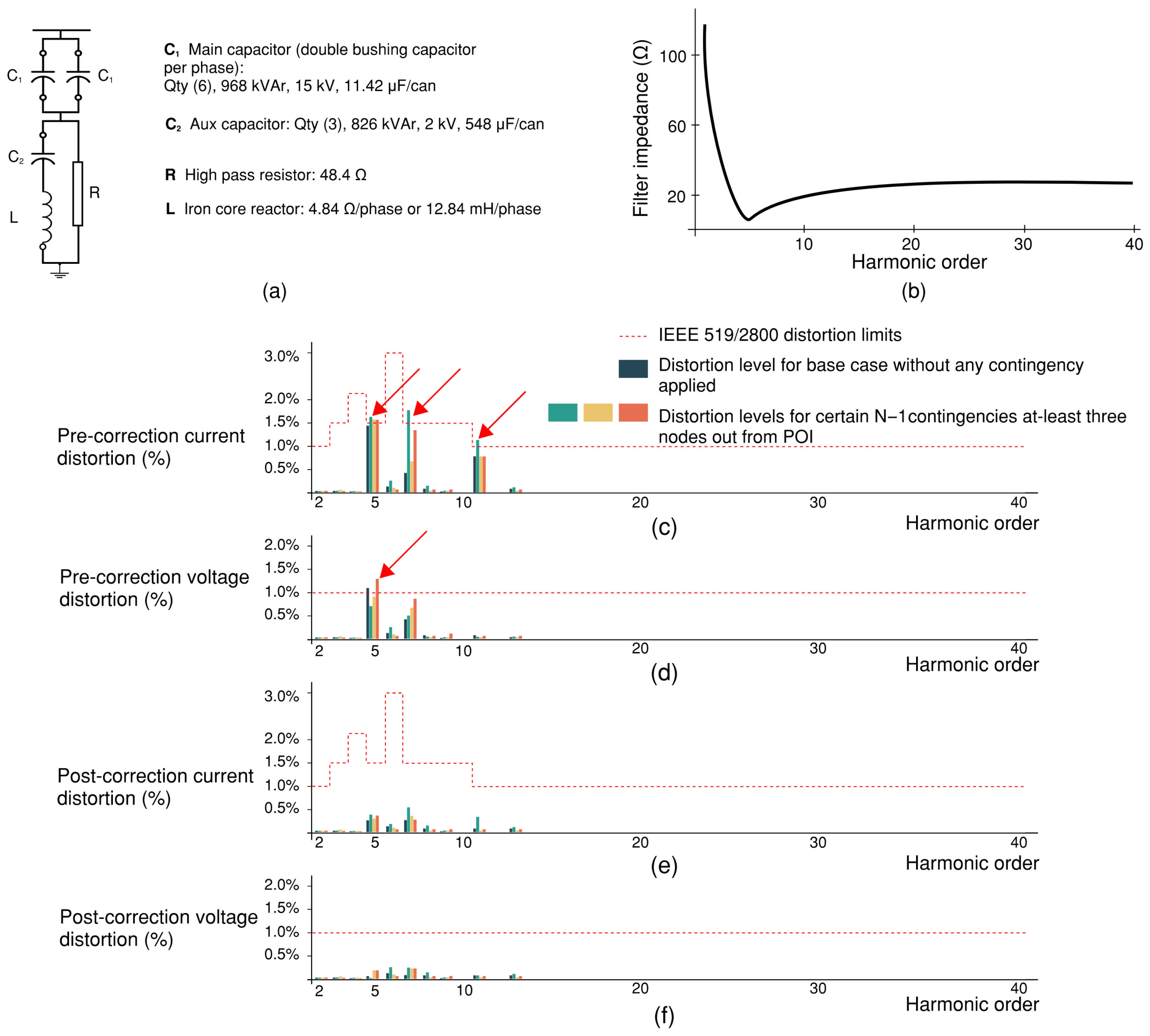
5. The Role of High-Pass Harmonic Filters for Utility-Scale Applications and the Filter Design Process

Now that the framework on the reactive power study and inverter specifications is understood, the focus is now shifted harmonic filters. Filters play a critical role in maintaining power quality and ensuring the smooth operation of electrical systems, with the following section describing the process and providing a guide in selecting the pertinent IEEE standard for designing the high-pass harmonic filters crucial in utility-scale applications.

5.1. High-Pass Harmonic Filters for Utility-Scale Applications

To comply with IEEE standards, notably IEEE 519 and IEEE 2800, integrating high-pass harmonic filters in utility-scale PV and wind farms has become more critical. These standards provide guidelines for harmonic distortion levels that must be maintained to ensure system reliability and power quality.

The effectiveness of high-pass filters in addressing specific harmonic frequencies has been documented in various contexts. Khalfalla et al. in [36] explored grid impedance estimation and noted that high-pass filtering effectively isolates harmonic components, allowing for better management of total harmonic distortion. In the literature, [37] further investigated the characteristics of high-frequency harmonics in traction networks and proposed high-pass filters as a viable solution to mitigate these distortions in power systems. This aligns with the findings from [38] indicating that damped high-pass filters could outperform traditional passive schemes in terms of harmonic resonance management, despite potential power losses.

In the domain of utility-scale filtering, the notch filter and high-pass filter, prevalent among which are 2nd high pass, 3rd high pass, and C-type high pass (also called C-hi type) filters, are commonly used. These filters are employed to attenuate pulse-width modulation-based high-frequency harmonics. It is interesting to note that by inserting a low-pass filter in between the power converter and the electric grid, the harmonic components from the PWM switching are prevented from affecting the power grid. However, the working of the low-pass filter can be influenced by changes in the grid inductance. If the grid inductance increases significantly, the response of the automatic current regulator (ACR) can deteriorate. To address this issue, some studies have proposed the use of high-pass filters in the grid-connected current feedback loop to create a parallel virtual impedance with the grid inductance, which can help mitigate the resonant point and improve the grid’s adaptability to weak system conditions [39]. Additionally, the C-hi pass filter can be used in combination with other filtering techniques, such as notch filters and derivative controllers, to further improve the robustness [40] of the grid-tied inverter to grid impedance variations. Although academic research in the field of utility-scale filter design exists, the design methodology and results are usually specific to a certain grid topology and are usually difficult to replicate. In an attempt to provide a generalized design that may be replicated by both academic and industrial professionals, a simplified treatment of the C-type high-pass and notch filter design, along with characteristic impedance behavior and harmonic attenuation performance, is presented in Section 5.1.1 and Section 5.1.2 of this article.

5.1.1. C-Type High Pass Filter Design for Harmonic Mitigation—Methodology and Observation

Methodology: A C-type high-pass filter shall be designed and tuned at the 5th harmonic for a renewable farm with a 6-pulse inverter load, with input parameters and design steps outlined in

Table 3. Example calculation workflow for designing a C-type high-pass filter for distribution level grid application.

Input parameters
kVsystem (line to line voltage rating, typically low voltage side of POI GSU)	13.2 kV
kVAreff (reactive power rating of filter stage)	1500 kVAr
htune (filter tuning point, assuming system frequency is 60 Hz) Note: For a three phase six pulse inverter, 5th harmonic is the first dominant odd harmonic	5 harmonic or (5 × 60) 300 Hz
Resistor and iron-core reactor design
$$\begin{gathered} {\mathrm{I}}_{\mathrm{rated}} \mathrm{at} 60 \mathrm{Hz} \\ where I_{rated at 60 Hz}={\displaystyle \frac{{kVAr}_{eff}}{{kV}_{system}}}\times {\displaystyle \frac{1}{\sqrt{3}}} \mathrm{A} \end{gathered}$$	65.6 A
$$\begin{gathered} {\mathrm{X}}_{\mathrm{eff}} (\mathrm{effective} \mathrm{reactance} \mathrm{of} \mathrm{filter} \mathrm{bank}) \\ where X_{eff}={\displaystyle \frac{{kV}_{system}^2}{{kVAr}_{eff}}}\times {\displaystyle \frac{1}{1000}}\mathsf{\Omega } \end{gathered}$$	116.16 Ω/phase
$$\begin{gathered} {\mathrm{X}}_{\mathrm{L}} (\mathrm{iron} \mathrm{core} \mathrm{filter} \mathrm{reactor}) \\ where X_L={\displaystyle \frac{X_{eff}}{h^2-1}}\mathsf{\Omega }/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e} \end{gathered}$$	$4.84 \mathsf{\Omega }/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}$ or 12.84 mH/phase
$$\begin{gathered} \mathrm{R} (\mathrm{Ohmic} \mathrm{rating} \mathrm{of} \mathrm{resistor}/\mathrm{phase}) \\ R=X_L\times Damping factor\times h_{tune}(\mathsf{\Omega }/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}) \end{gathered}$$	48.4 Ω (assuming a conservative value of 2.0 for damping factor)
Main and auxiliary capacitor design
kVmain cap rating	15 kV
$$\begin{gathered} {\mathrm{kVAr}}_{\mathrm{main}} \mathrm{cap} (\mathrm{reactive} \mathrm{power} \mathrm{rating} \mathrm{of} \mathrm{main} \mathrm{capacitor}) \\ where {kVAr}_{main cap}={\displaystyle \frac{{{(kV}_{main cap rating})}^2\times 1000}{X_{eff}}}\mathrm{k}\mathrm{V}\mathrm{A}\mathrm{r}/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e} \end{gathered}$$	1937 kVAr
${kVAr}_{main cap can}$ assuming double bushing capacitor per phase	968 kVAr
kVaux cap rating	2 kV
$$\begin{gathered} {\mathrm{kVAr}}_{\mathrm{aux} \mathrm{cap}} (\mathrm{reactive} \mathrm{power} \mathrm{rating} \mathrm{of} \mathrm{aux} \mathrm{capacitor}) \\ where {kVAr}_{aux cap}={\displaystyle \frac{{{(kV}_{aux cap rating})}^2\times 1000}{X_L}}\mathrm{k}\mathrm{V}\mathrm{A}\mathrm{r}/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e} \end{gathered}$$	826 kVAr
${kVAr}_{aux cap can}$ assuming single bushing capacitor per phase	826 kVAr

. As such, the C-type high-pass filter is appropriate for applications where low-tuning frequency is necessary. Specifications for the filter’s main and auxiliary capacitor, high-pass resistor, and iron core reactor are computed.

Observation: The default renewable plant was unable to meet harmonic compliance for individual harmonic levels, as evident from Figure 5c,d. An aggressively damped C-type high-pass filter, with its component one line shown in Figure 5a and characteristic impedance plotted in Figure 5b, sharply attenuates the 5th harmonic and reasonable attenuates higher order harmonics, to the point that both current and voltage distortions fall within acceptable IEEE limits, as can be seen in Figure 5e,f.

5.1.2. Notch Filter Design for Harmonic Mitigation—Methodology and Observation

Methodology: A notch filter shall be designed and tuned at the 5th harmonic for a renewable farm with a 6-pulse inverter load, with input parameters and design steps outlined in

Table 4. Example calculation workflow for designing a notch filter for distribution level grid application.

Input parameters
kVsystem (line to line voltage rating, typically low voltage side of POI GSU)	13.2 kV
kVAreff (reactive power rating of filter stage)	1500 kVAr
htune (filter tuning point, assuming system frequency is 60 Hz) Note: For a three phase six pulse inverter 5th harmonic is the first dominant odd harmonic	5 harmonic or (5 × 60) 300 Hz
Iron-core reactor and fuse design
$$\begin{gathered} {\mathrm{I}}_{\mathrm{rated}} \mathrm{at} 60 \mathrm{Hz} \\ where I_{rated at 60 Hz}={\displaystyle \frac{{kVAr}_{eff}}{{kV}_{system}}}\times {\displaystyle \frac{1}{\sqrt{3}}} \mathrm{A} \end{gathered}$$	65.6 A
$$\begin{gathered} {\mathrm{I}}_{\mathrm{fuse}} \mathrm{rating} \\ where I_{fuse rating}=\left({\displaystyle \frac{I_{rated at 60 Hz}}{Number of capacitor per phase(assume 2)}}\right)\times 1.75A \end{gathered}$$	57.4 A
$$\begin{gathered} \mathrm{Xeff} (\mathrm{effective} \mathrm{reactance} \mathrm{of} \mathrm{filter} \mathrm{bank}) \\ where X_{eff}={\displaystyle \frac{{kV}_{system}^2}{{kVAr}_{eff}}}\times {\displaystyle \frac{1}{1000}}\mathsf{\Omega } \end{gathered}$$	116.16 Ω/phase
$$\begin{gathered} \mathrm{XL} (\mathrm{iron} \mathrm{core} \mathrm{filter} \mathrm{reactor}) \\ where X_L={\displaystyle \frac{X_{eff}}{h^2-1}}\mathsf{\Omega }/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e} \end{gathered}$$	$4.84 \mathsf{\Omega }/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}$ or 12.84 mH/phase
Main capacitor design
kVmain cap rating	15 kV
$$\begin{gathered} {\mathrm{kVAr}}_{\mathrm{main}}\mathrm{cap} (\mathrm{reactive} \mathrm{power} \mathrm{rating} \mathrm{of} \mathrm{main} \mathrm{capacitor}) \\ where {kVAr}_{main cap}={\displaystyle \frac{{{(kV}_{main cap rating})}^2\times 1000}{X_{eff}\times \frac{h^2}{h^2-1}}}\mathrm{k}\mathrm{V}\mathrm{A}\mathrm{r}/\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e} \end{gathered}$$	1860 kVAr
${kVAr}_{main cap can}$ assuming double bushing capacitor per phase	930 kVAr

. Specifications for the main capacitor, capacitor fuse, and iron core reactor are computed.

Observation: The default renewable plant was unable to meet harmonic compliance for individual harmonic levels, as one may note in Figure 6c,d. A tuned notch filter, with its component one line shown in Figure 6a damps the 5th harmonic. Overall, post-corrected current and voltage distortions, as shown in Figure 6e,f, fall within acceptable IEEE limits. An inherit limitation of the notch filter lies in its inability to aggressively attenuate harmonics outside of its tuning frequency. As one may observe in Figure 6b, the notch filter blocks the 5th harmonic signature, but the filter’s impedance increases for higher order harmonics, which could be problematic. Although for this case under study, for a 6-pulse inverter with distinct 5th, 7th, 11th, and 13th harmonics, the notch filter was able to bring down all the individual harmonic levels to below IEEE acceptable limits, there may be cases where higher order non-compliant harmonics, if present, may remain unattenuated. A C-type high-pass filter, although costlier (and bulkier) than a notch filter, might be the best solution under such scenario.

To conclusively determine whether a notch filter is adequate for a given plant or an aggressive damping C-type high-pass filter is needed, a frequency scan simulation should be performed. These frequency scan simulations involve injecting frequency from the fundamental frequency up to a high order harmonic (usually 50th) with impedance characteristic of the system capture as a function of changing frequency. Change is the resonant frequency which should be noted as more inverters are brought online, and a holistic assessment should be made on the damping impacts of the different filter types.

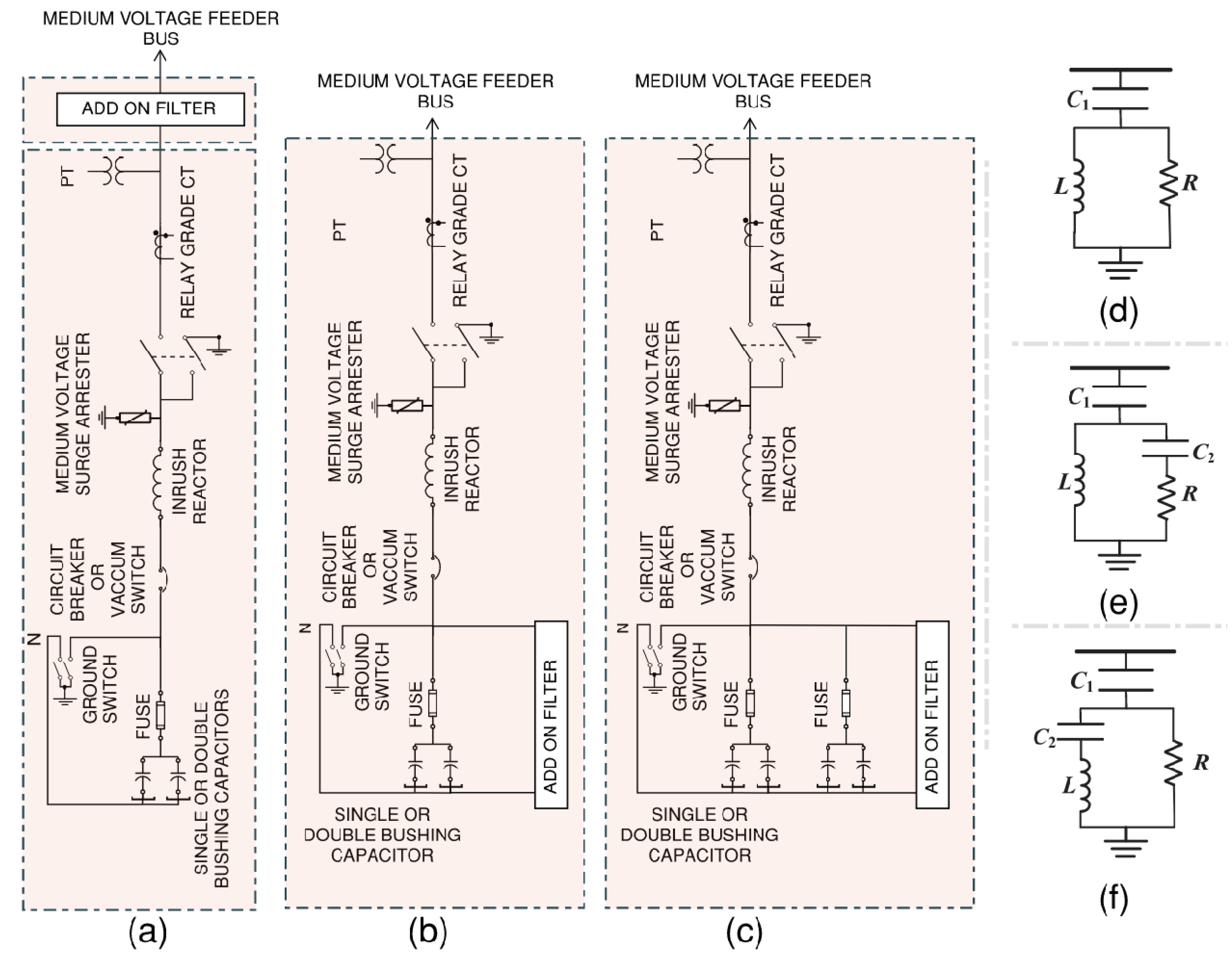
5.2. The Filter Design Process and Leveraging the Presence of a Capacitor Bank for Cost Efficiency

The filter design process for utility-scale application is usually an iterative process that involves dozens of simulations to determine problematic resonant points depending on the number of inverters being online, charging capacitance of online feeder cables, and N − 1 contingencies that are up to two to three nodes out (in most cases, given the meshed nature of the grid, contingencies beyond the third node out barely impact the harmonic resonant point). A simplified illustration of this filter design process has been made in Figure 7. If harmonic non-compliance or near non-compliance cases are observed for the individual harmonic level or as a total harmonic distortion, the mitigation of the problem through a notch or high-pass filter is necessary. For plants where additional reactive power support through capacitor banks is required, there could be potential cost savings in having a multi-stage capacitor bank with the capacitance from one of the stages serving as the main capacitor for a harmonic filter. An illustration is provided of doubling up one of the capacitor bank stages as a harmonic filter in a multistage capacitor bank, as one may see in Figure 8b,c. In other situations, as illustrated in Figure 8a where harmonic is not presently an issue, provision can be kept where a modular filter bank may be added later on, if changes to the grid topology are anticipated, generating harmonic signatures that require mitigation. In addition to the analytical treatment on the C-type and notch filter design discussed in the previous section, Figure 8d–f shows some of the commonly used filter topology for capacitor bank-integrated harmonic filter applications.

The optimization of capacitor bank size and placement is essential for maximizing the benefits of reactive power compensation, and voltage stabilization is an area worth documenting. At the medium voltage level (13.2 kV through 69 kV), system designers should consider larger step size. The following guideline might be useful in this regard:

• Vacuum interrupters are typically available in 200 A increments ranging from 200 to 600 A, without any smaller or intermediate ratings. A vacuum switch with a 200 A rating can switch up to 4 MVAr at 13.8 kV. Consequently, to maximize the switch rating, which significantly impacts the cost of the bank, it is advisable to consider a larger step size.
• The kVA ratings for short circuits at medium voltage levels are considerably higher than those of low-voltage systems. As a result, the voltage rise that occurs when capacitor banks are used is significantly reduced, allowing for the use of larger stage sizes.
• The leading power factor is typically not subject to charges by most utilities. Consequently, when power factor penalties are the primary concern, it is more cost effective to use larger stages.
• The equipment ampacity rating at medium voltage levels is relatively low, and copper bus bars are commonly used for most connections. Hence, the interconnection of components at this voltage level is somewhat unrelated to the size of the stage.

A scenario-based comparative listing of price for a common metal-enclosed capacitor bank and filter units for the US market in 2025 is provided in

Table 5. Scenario-based approximate indicative unit cost for common capacitor bank and harmonic filter units with filters tuned to 5th harmonic.

Metal-Clad Enclosed Capacitor Bank	V < 15 kV	15 kV < V < 34.5 kV
Single stage without filter with future filter provision	$11,650 (1 MVAr) $60,000 (5 MVAr) $300,000 (25 MVAr) $645,000 (50 MVAr)	$14,925 (1 MVAr) $75,000 (5 MVAr) $375,000 (25 MVAr) $856,000 (50 MVAr)
Two stages with integrated notch filter tuned	$13,000 (1 MVAr) $70,000 (5 MVAr) $320,000 (25 MVAr) $650,000 (50 MVAr)	$16,500 (1 MVAr) $82,000 (5 MVAr) $410,000 (25 MVAr) $900,000 (50 MVAr)
Three stages with integrated notch filter tuned	$18,650 (1 MVAr) $90,250 (5 MVAr) $456,000 (25 MVAr) $930,000 (50 MVAr)	$19,000 (1 MVAr $95,000 (5 MVAr) $475,000 (25 MVAr) $995,000 (50 MVAr)
Four stages with integrated notch filter tuned	$20,000 (1 MVAr) $100,000 (5 MVAr) $535,000 (25 MVAr) $1,100,000 (50 MVAr)	$23,000 (1 MVAr) $120,000 (5 MVAr) $600,000 (25 MVAr) $1,200,000 (50 MVAr)
Two stages with integrated C-type high-pass harmonic filter	$15,050 (1 MVAr) $80,450 (5 MVAr) $350,250 (25 MVAr) $795,000 (50 MVAr)	$18,000 (1 MVAr) $85,500 (5 MVAr) $470,000 (25 MVAr) $1,050,000 (50 MVAr)
Three stages with integrated C-type high-pass harmonic filter	$19,090 (1 MVAr) $100,450 (5 MVAr) $512,000 (25 MVAr) $1,220,000 (50 MVAr)	$20,950 (1 MVAr) $110,000 (5 MVAr) $625,000 (25 MVAr) $1,300,000 (50 MVAr)
Four stages with integrated C-type high-pass harmonic filter	$22,000 (1 MVAr) $101,000 (5 MVAr) $495,500 (25 MVAr) $1,250,000 (50 MVAr)	$24,000 (1 MVAr) $110,250 (5 MVAr) $625,000 (25 MVAr) $1,455,000 (50 MVAr)

. From Table 5, it is fair to conclude that installations without a pre-integrated harmonic filter and with a larger capacitor bank stage size are relatively cheaper. However, installing a harmonic filter post startup could have its challenges with the need for outages, and hence, lost opportunity costs. Also, for system operators which penalize for leading power factor, a higher stage size might be warranted, which might drive the overall cost of the reactive power compensation solution.

6. Summary and Future Scope of Work

The increasing prominence of wind, solar, and other IBRs within the power system is indicative of a rapidly transforming energy landscape. For system operators, developers, and consulting engineers, the successful planning and integration of these renewable energy plants necessitate a comprehensive understanding of market interconnection protocols, particularly regarding power factor requirements at the POI. The choice of reactive power compensation equipment emerges as a critical determinant in establishing the requisite number of solar farm inverters to ensure compliance with the standards set forth by system reliability operators. Notably, the generation capability curves, traditionally associated with synchronous generating stations, have demonstrated to be invaluable tools for the design and analysis of reactive power generation in solar farms.

Globally, the proliferation of IBRs is compelling these systems to enhance their operational capabilities to maintain stability and reliability. GFM inverters are increasingly recognized as viable solutions to various integration challenges, although GFL inverters will continue to constitute a significant portion of the IBR landscape. Consequently, a thorough understanding of the technologies and specifications associated with both inverter control methodologies is essential for stakeholders in the renewable energy sector. In addition to ensuring adequate reactive power compensation and judicious inverter selection, it is imperative for industry stakeholders to demonstrate harmonic compliance at the POI. In this context, high-pass filters, particularly C-type high-pass filters, have shown considerable efficacy. Furthermore, should the integration of a metal enclosed or air insulated capacitor bank be necessary for reactive power compensation at the renewable collector station, a strategic approach may involve utilizing a portion of the capacitance from the capacitor bank in the construction of the harmonic filter, thereby optimizing costs while enhancing system performance.

In summary, as the energy sector continues to evolve, a nuanced understanding of these technical considerations will be paramount in facilitating the seamless integration of RES, ultimately contributing to a more resilient and sustainable power system. To enable the seamless integration of large inverter-based resource (IBR) farms in alignment with grid reliability and long-term decarbonization goals, the following areas warrant focused attention from policymakers, utilities, and system developers:

• Standardized guidelines for reactive power support: There is a need for clearer, more actionable guidance on leveraging the reactive power capabilities of IBRs, particularly at the point of common coupling (PCC). Such guidelines would help harmonize planning and operational practices across jurisdictions and promote voltage stability in high-penetration scenarios.
• Enhanced IBR modeling frameworks: Current modeling approaches often fall short in capturing the nuanced steady-state and dynamic behaviors of IBRs. Developing models that reflect real-world control interactions, system-level feedback, and grid-forming or grid-following configurations is critical for accurate stability assessments and grid code compliance.
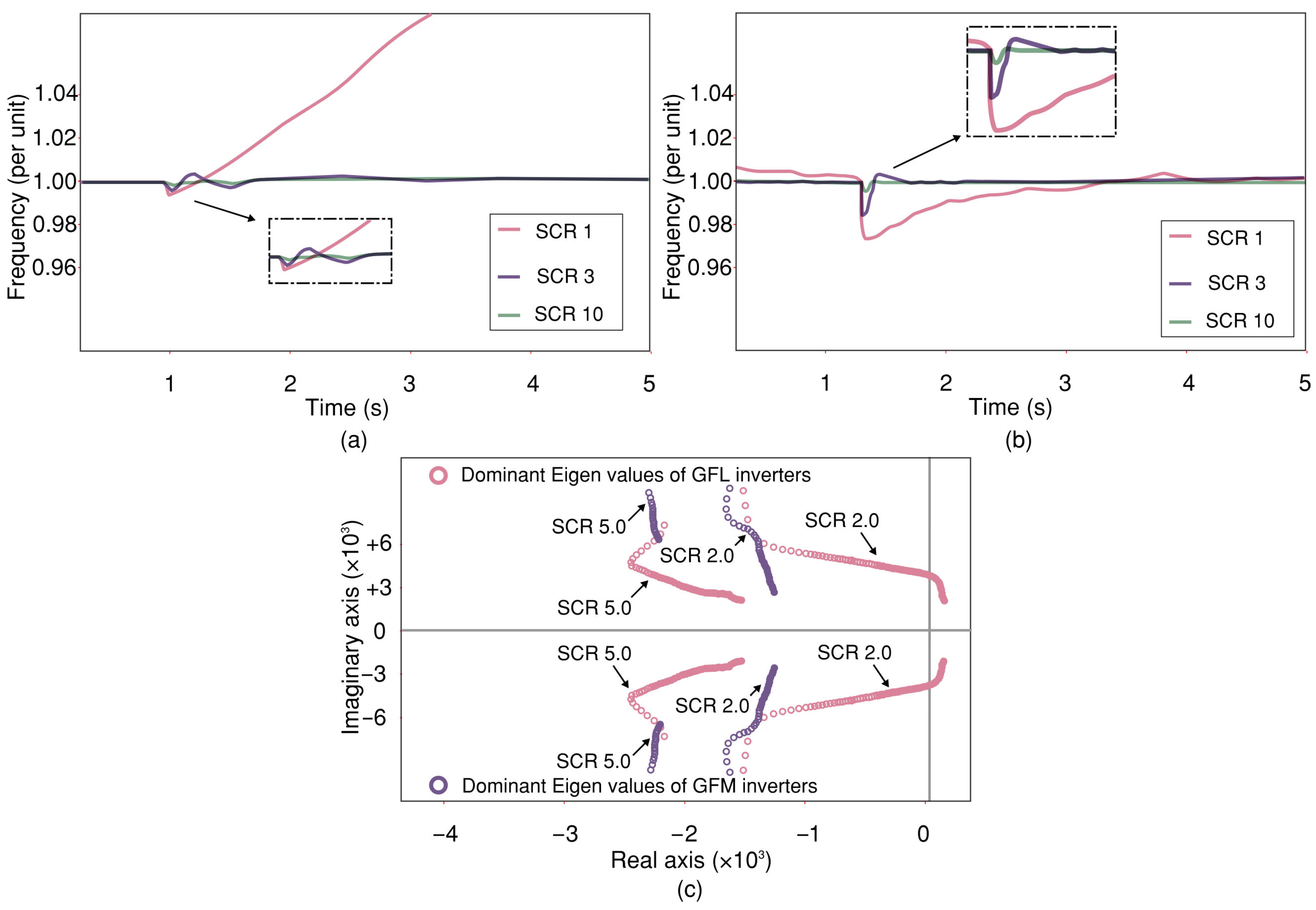
• Nuanced understanding of GFM vs. GFL: The prevailing perception that grid-following (GFL) inverters are inherently less suitable for weak grids compared to grid-forming (GFM) inverters oversimplifies the technological landscape. Future work should focus on advanced tuning methodologies and adaptive control strategies for GFL inverters, particularly under low short-circuit ratio (SCR) conditions, to unlock their full potential in weak-grid applications.