Performance Evaluation Model of Overhead Transmission Line Anti-Icing Strategies Considering Time Evolution

Abstract

Icing disasters can significantly reduce the reliability of overhead transmission lines, while limited budgets of power grid enterprises constrain the scale of investment. To improve investment efficiency, it is essential to balance the reliability and economic performance of anti-icing strategies. Most existing studies on the performance evaluation of anti-icing strategies for transmission lines focus primarily on reliability, neglecting their economic implications. To address this gap, this paper proposes a time-evolution-based performance evaluation model for overhead transmission line anti-icing strategies. First, a lifetime distribution function of transmission lines during the icing period is constructed based on the Nelson–Aalen method and metal deformation theory. Subsequently, a quantitative risk model for iced transmission lines is developed, incorporating the failure rate, value of lost load, and amount of lost load, providing a monetary-based indicator for icing risk. Finally, a performance evaluation method for anti-icing strategies is developed based on the risk quantification model. Implementation cost is treated as risk control expenditure, and strategy performance is assessed by integrating it with residual risk cost to identify the optimal strategy through composite cost analysis. The proposed model enables a comprehensive assessment of anti-icing strategy performance, improving the accuracy of strategy selection and achieving a dynamic balance between implementation cost and transmission line reliability. The case study results demonstrate that the proposed method effectively reduces the risk of failure in overhead transmission lines under ice disasters while lowering anti-icing costs. Compared with two existing strategy selection approaches, the strategy based on this method achieved 46.11% and 32.56% lower composite cost, and 60.26% and 48.41% lower residual risk cost, respectively.

1. Introduction

Overhead transmission lines are critical components in power systems for long-distance and high-capacity electricity transmission. Their failures can result in large-scale blackouts, making the reliability of overhead transmission lines crucial for the secure and stable operation of the power grid [1]. In recent years, the increasing frequency of extreme weather events has posed serious threats to the safe and reliable power supply of urban grids [2]. Among these events, icing disasters have had a particularly severe impact on transmission line reliability. Furthermore, the geographical extent of freezing rain zones has been gradually expanding northward, enlarging the area affected by ice disasters [3]. During icy weather conditions, overhead lines experience icing and galloping, which can lead to tower collapses, conductor breakages, and increased occurrences of regional power outages, resulting in significant economic losses [4]. Consequently, power grid enterprises are placing greater emphasis on the scientific and effective implementation of anti-icing and disaster mitigation measures.

The icing risk of overhead transmission lines primarily manifests as faults occurring when the lines operate under icing conditions. Morgan et al. conducted research on the galloping amplitude of overhead transmission lines affected by icing and analyzed line fault mechanisms under different galloping amplitudes, providing a theoretical basis for determining the inter-phase spacing of transmission lines [5]. However, early studies often used full-scale transmission lines as test objects, resulting in prohibitively high costs for building experimental platforms. The expansion of the scale of power grids has led to a rapid increase in testing costs, making cost control for testing essential. In recent years, Huang et al. and Xie et al. have adopted scaled-down transmission line models to simulate galloping and icing behaviors of full-size lines, effectively addressing the cost limitations of full-scale experiments [6,7,8]. These approaches offer cost-effective experimental schemes for determining the span design of overhead transmission lines. With the development of computer technology, numerical simulation methods have been widely applied. Xiao et al. developed a probabilistic failure assessment framework for transmission towers under combined ice and wind loads, using numerical analysis to evaluate line reliability [9]. These studies have thoroughly investigated the failure mechanisms of overhead transmission lines under icing conditions and proposed various simplified calculation formulas. Recently, machine learning techniques have also been introduced in this field due to their lower computational cost and higher predictive accuracy [10]. For instance, Sun et al. proposed an improved extreme learning machine for icing thickness prediction based on the bat optimization algorithm [11], while Wang et al. introduced a novel extreme learning machine model to predict damage to overhead lines caused by icing [12]. However, due to the temporal discreteness, short duration, and limited availability of characteristic data during icing periods, machine learning methods—often reliant on large datasets—lack applicability for accurately predicting icing-related failure rates at this stage. Therefore, this paper employs an empirical approach based on the Nelson–Aalen estimator and metal deformation theory to calculate the failure rate of transmission lines during icing periods and subsequently derive the lifetime distribution function for overhead lines under icing conditions.

Risk assessment of overhead transmission lines typically involves the use of specific indicators to quantify the severity of risk, with each indicator tailored to suit particular research contexts. Yi W et al., in their study of discharging and mechanical failure risks associated with the de-icing of iced transmission lines, employed gap breakdown voltage and impact factor as risk indicators for icing and analyzed how various mitigation measures reduced icing-related risks [13]. Lu J et al. proposed a spatiotemporal resilience evaluation framework for power systems to enhance recovery capability during ice disasters and used this framework to assess the risk imposed by ice disasters on power grids [14]. Fan R et al. investigated the impact of various natural disasters on transmission line reliability by evaluating potential risks based on disaster occurrence probabilities and severity [15]. In addition, some studies focused on the internal condition of equipment and adopted indicators such as the health index to characterize the line’s resilience to risk [16,17]. These studies have adopted different risk evaluation metrics tailored to their respective problems and, based on the assessment results, proposed corresponding risk mitigation strategies for transmission lines. However, these indicators fundamentally quantify line reliability and fail to realize a monetary quantification of icing-related risks. When it comes to comprehensively evaluating both the economic efficiency and reliability of anti-icing strategies, these approaches often fail to provide intuitive and actionable evaluation outcomes. Without effective integration of economic and reliability metrics, risk assessments of transmission lines cannot meaningfully guide the optimization of anti-icing strategies. To address this issue, this paper incorporates the value of lost load (VoLL) theory based on the failure rate of overhead transmission lines during the icing period and quantifies the icing risk as risk cost.

Overhead transmission lines are long-term operational assets, meaning that any investments in these systems inherently have temporal continuity. Therefore, time evolution must be explicitly considered [18,19]. The sum of the residual risk cost of anti-icing strategies considering time evolution and the implementation cost considering the time value of money is defined as the composite cost. Composite cost is used as the performance evaluation metric for anti-icing strategies. Accordingly, a performance evaluation model for overhead transmission line anti-icing strategies is proposed.

This model not only enables a scientific and intuitive assessment of strategy performance but also allows for comparative evaluation among different anti-icing strategies, thereby serving as a rational basis for strategy selection. To achieve strategy optimization, it is necessary to adopt appropriate optimization algorithms in a targeted manner [20]. In different scenarios, employing distinct optimization algorithms can efficiently and effectively address practical problems [21,22]. To address the frequent icing issue in distribution lines, Zhang L et al. proposed a multi-period de-icing strategy optimization method for power distribution networks. The model was solved using an elitist-preservation genetic algorithm, and the effectiveness of the optimized model was demonstrated [23]. To enhance power transmission grid resilience against ice disasters, NIU T et al. proposed a comprehensive resilience assessment metric and developed a two-stage robust resilience enhancement planning model [24]. This model was subsequently applied to optimize investment decisions. However, the aforementioned studies failed to effectively integrate economic and reliability metrics. To address this gap in anti-icing strategy optimization, this paper proposes a comprehensive approach that simultaneously considers both economic and reliability indicators, implemented through a heuristic algorithm.

The literature review is summarized in

Table 1. Literature review.

Number	Method	Advantage	Disadvantage	Consideration
[5]	Test	Theoretical basis for determining the inter-phase spacing of transmission lines	High costs for building experimental platforms	Cost control
[6,7,8]	Test	Scaled-down transmission line model	Lacks adaptability to ice-induced failure mechanisms	Enhance the targeted response to ice disaster risk
[9]	Numerical analysis	Propose various simplified calculation formulas
[10,11,12]	Machine learning	Lower computational cost and higher predictive accuracy
[13,14,15,16,17]	Reliability Assessment	Quantify line reliability	Fail to realize a monetary quantification of icing-related risks	Balance cost-reliability trade-offs in system planning
[19,20,21,22]	Optimization method	Optimization algorithm	Differs from the scenario considered in this study	Tailor the approach to the specific scenarios studied in this work

. Here, the third and fourth columns summarize the strengths and weaknesses of the existing literature, while reflections on addressing these limitations in this articles are presented in the fifth column.

The main contributions of this paper are summarized as follows:

• A method for deriving the lifetime distribution function of transmission lines during the icing period is proposed, based on the Nelson–Aalen estimation method and metal deformation theory.
• A quantitative risk model for overhead transmission lines under icing conditions is developed, integrating failure rate during the icing period, VoLL, and power outage energy loss, thereby providing a monetized risk indicator for icing events.
• Based on the proposed risk quantification model, a performance evaluation method for anti-icing strategies is introduced. In this method, the implementation cost of a strategy is treated as risk control cost, and the sum of risk control cost and residual risk cost is defined as the composite cost, which serves as a comprehensive metric for evaluating and selecting the optimal anti-icing strategy.

The rest of this paper is organized as follows: Section 2 introduces the method for deriving the transmission line lifetime distribution function during the icing period based on the Nelson–Aalen estimator and metal deformation theory. Section 3 presents the risk quantification model for icing on transmission lines. Section 4 proposes the anti-icing strategy performance evaluation method based on the risk model. Section 5 conducts a case study using actual provincial power grid and climatic data to verify the feasibility of the proposed method. Finally, Section 6 concludes the paper.

2. Estimation Method for the Lifetime Distribution Function of Transmission Lines During the Icing Period

The failure of transmission lines under icing conditions is primarily influenced by ice–wind loads, and their failure rate evolves with the progression of the icing process. The lifetime evolution behavior, therefore, differs significantly from that of conventional random failure patterns.

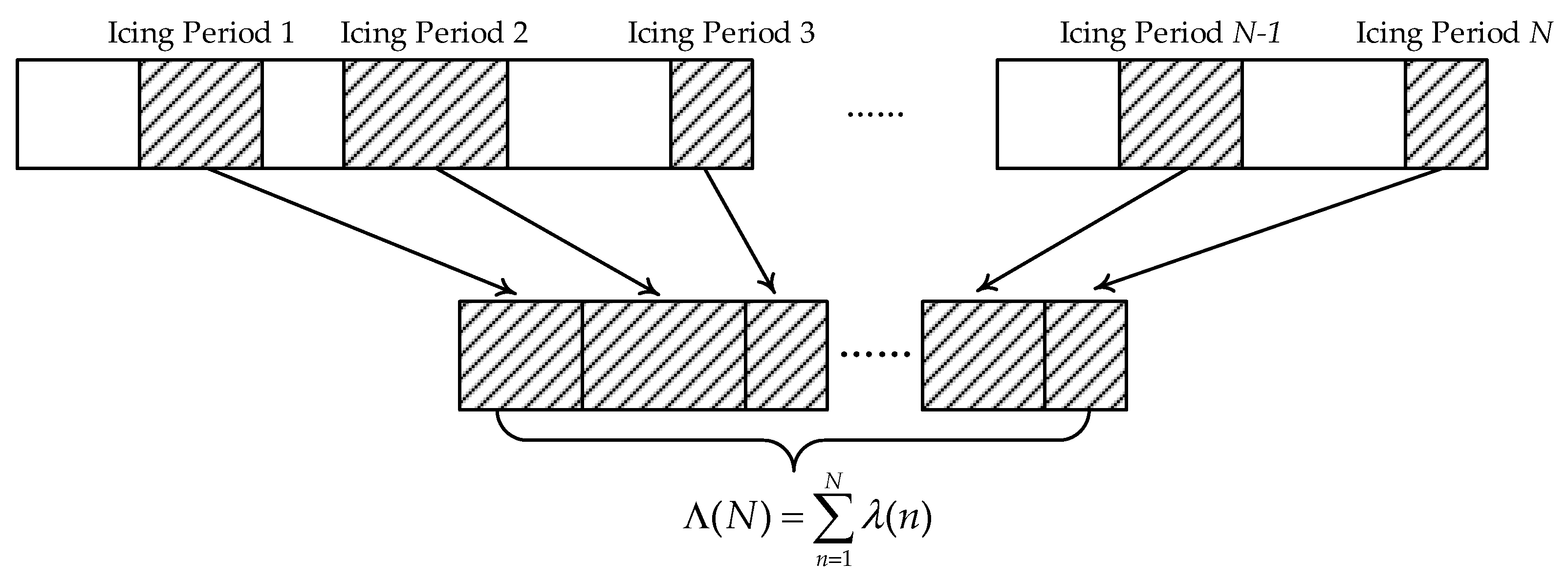
The Nelson–Aalen estimation method is a classical non-parametric approach for survival probability analysis, as illustrated in Figure 1. It mainly consists of the following three steps:

First, define the instantaneous hazard function λ(t), the cumulative hazard function Λ(T), and the lifetime distribution function F(T). These three functions are interrelated and satisfy the following relationship:

$$\begin{array}{l}\Lambda (T)={\displaystyle {\int }_0^T\lambda (t)dt}\\ F(T)=1-e^{-\Lambda (T)}\end{array},$$

(1)

Next, a time discretization is applied to the above functions, yielding the discrete instantaneous hazard λ(n), the discrete cumulative hazard Λ(N), and the discrete lifetime distribution function F(N). These three discrete forms maintain the following relationship:

$$\begin{array}{l}\Lambda (N)={\displaystyle \sum _{n=1}^N\lambda (n)}\\ F(N)=1-e^{-\Lambda (N)}\end{array},$$

(2)

Finally, the cumulative hazard function is estimated based on the observed event frequencies within the sample.

This study draws on the framework of hazard function and lifetime distribution function definitions and discretization as established in the Nelson–Aalen estimation method. In the context of icing-induced failures, the ice–wind load exerted on transmission line structures is primarily characterized by periodic icing periods, making the number of icing periods n a natural discrete time scale for describing the risk accumulation process, as illustrated in Figure 2. However, considering the short duration of a single icing period, the limited number of transmission lines within the same icing zone, and the sparse occurrence of observed failures in historical data, the empirical failure rates fail to adequately represent the true statistical characteristics of line failure during icing periods. Moreover, the failure mechanisms of transmission lines under icing conditions exhibit distinct material-dependent physical behavior. Therefore, this study does not adopt traditional non-parametric methods that estimate probability purely based on observed frequency. Instead, based on metal deformation theory, we constructed an empirical formula to calculate the hazard function values at each discrete time step, thereby providing a more reasonable representation of the accumulated damage process of conductors under ice load.

During the icing period n, the ice–wind load ${\mathit{l}}_{\mathrm{IW}}^n$ acting on a transmission line is represented as a vector composed of ice load $l_{\mathrm{I}}^n$ and wind load $l_{\mathrm{W}}^n$. The ice load results from the gravitational force of the accreted ice on the line and is always directed vertically downward. The wind load is caused by the wind acting on the line and is oriented horizontally. The relationship between the failure rate λ of transmission lines and the ice–wind load, as calculated using an empirical formula, is shown in Figure 3.

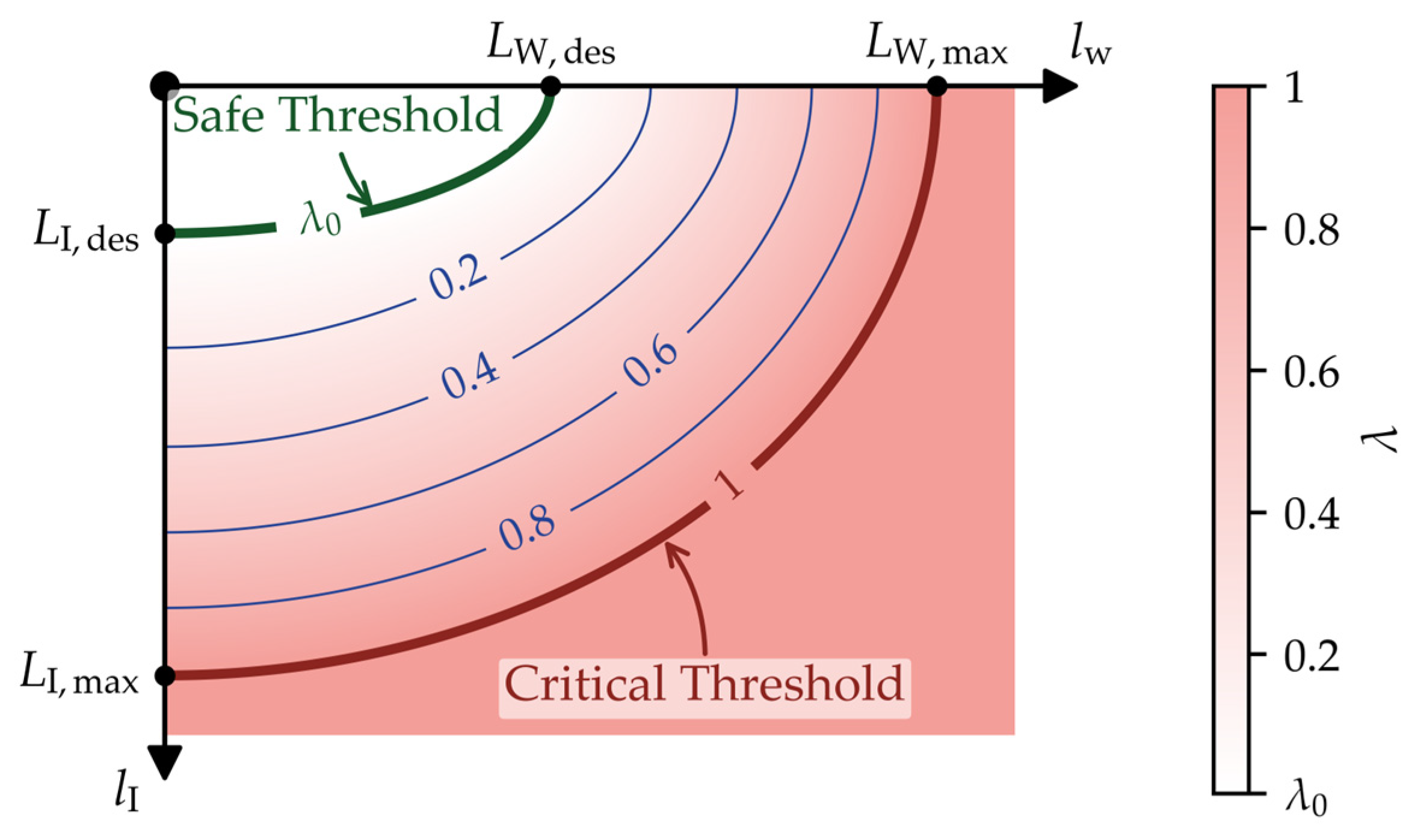
In Figure 3, the vertical axis and horizontal axis represent the ice load and wind load, respectively. Here, $L_{\mathrm{I},\mathrm{des}}$ and $L_{\mathrm{I},\max }$ denote the safe threshold and critical threshold of ice load that the overhead transmission line can withstand; $L_{\mathrm{W},\mathrm{des}}$ and $L_{\mathrm{W},\max }$ are the corresponding thresholds for wind load. The green curve in the figure represents the safe boundary of the ice–wind load, defined as an ellipse determined by $L_{\mathrm{I},\mathrm{des}}$ and $L_{\mathrm{W},\mathrm{des}}$. When the ice–wind load vector falls within this ellipse, the failure rate of the line remains at a relatively low level, denoted by λ_0. The red curve denotes the limit boundary, also an ellipse, determined by $L_{\mathrm{I},\max }$ and $L_{\mathrm{W},\max }$; if the ice–wind load falls outside this ellipse, the line is considered to fail with certainty [25]. The thin blue lines in the figure are iso-failure-rate curves, while the red background gradient indicates the magnitude of the failure rate, with darker shades representing higher failure rates.

Let the ice–wind load of the transmission line during icing period n be denoted as ${\mathit{l}}_{\mathrm{IW}}^n$, the safe threshold of ice–wind load as ${\mathit{L}}_{\mathrm{IW},\mathrm{des}}=(L_{\mathrm{W},\mathrm{des}},L_{\mathrm{I},\mathrm{des}})$, the critical threshold as ${\mathit{L}}_{\mathrm{IW},\max }=(L_{\mathrm{W},\max },L_{\mathrm{I},\max })$, and the failure rate as $\lambda ({\mathit{l}}_{\mathrm{IW}}^n,{\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\mathit{L}}_{\mathrm{IW},\max })$. Then, the icing-induced operational failure rate $\lambda (n)=\lambda ({\mathit{l}}_{\mathrm{IW}}^n,{\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\mathit{L}}_{\mathrm{IW},\max })$ can be expressed as follows:

$$\lambda ({\mathit{l}}_{\mathrm{IW}}^n,{\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\mathit{L}}_{\mathrm{IW},\max })=\left\{\begin{array}{ll}{\lambda }_0,\hfill & l_{\mathrm{IW}}^n\le L_{\mathrm{des}}({\theta }^n)\hfill \\ e^{[{\displaystyle \frac{(l_{\mathrm{IW}}^n-L_{\mathrm{des}}({\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\theta }^n))}{L_{\max }({\mathit{L}}_{\mathrm{IW},\max },{\theta }^n)-L_{\mathrm{des}}({\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\theta }^n)}}\ln (2-{\lambda }_0)]}-1+{\lambda }_0,\hfill & L_{\mathrm{des}}({\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\theta }^n)<l_{\mathrm{IW}}^n\le L_{\max }({\mathit{L}}_{\mathrm{IW},\max },{\theta }^n)\hfill \\ 1,\hfill & L_{\max }({\mathit{L}}_{\mathrm{IW},\max },{\theta }^n)<l_{\mathrm{IW}}^n\hfill \end{array}\right.$$

(3)

where $l_{\mathrm{IW}}^n$ and ${\theta }^n$ represent the magnitude and angle of the ice–wind load ${\mathit{l}}_{\mathrm{IW}}^n$, respectively, as illustrated in Figure 4. $L_{\mathrm{des}}({\mathit{L}}_{\mathrm{IW},\mathrm{des}},{\theta }^n)$ and $L_{\mathrm{des}}({\mathit{L}}_{\mathrm{IW},\max },{\theta }^n)$ denote the safe threshold and critical threshold of the transmission line under the load angle ${\theta }^n$, respectively.

The calculation method for the magnitude and angle of the ice–wind load on the transmission line is as follows:

$$\begin{array}{l}{l}_{\mathrm{IW}}^n=\left|{\mathit{l}}_{\mathrm{IW}}^n\right|=\sqrt{{\left(l_{\mathrm{I}}^n\right)}^2+{\left(l_{\mathrm{W}}^n\right)}^2}\\ {\theta }^n=\arctan {\displaystyle \frac{l_{\mathrm{W}}^n}{l_{\mathrm{I}}^n}}\end{array}$$

(4)

The design of overhead transmission lines must simultaneously comply with both wind load and ice load design standards. The Code for Design of 110 kV to 750 kV Overhead Transmission Lines (GB 50545-2010) in China specifies design standards for ice loads and wind loads on overhead transmission lines separately but does not provide design criteria for combined ice–wind load conditions. Since ice load and wind load act in perpendicular directions, the resulting combined load lies at an angle between the horizontal and vertical when both loads are applied simultaneously. Due to the direction-dependent load-bearing capacity of transmission lines, their safe thresholds and critical thresholds vary with different load directions [26]. At a given angle ${\theta }^n$, the thresholds can be expressed as follows:

$$L_{\mathrm{IW},\mathrm{des}}({\theta }^n)={\displaystyle \frac{L_{\mathrm{I},\mathrm{des}}{L}_{\mathrm{W},\mathrm{des}}}{\sqrt{{(L_{\mathrm{I},\mathrm{des}}\sin {\theta }^n)}^2+{(L_{\mathrm{W},\mathrm{des}}\cos {\theta }^n)}^2}}}$$

(5)

$$L_{\mathrm{IW},\max }({\theta }^n)={\displaystyle \frac{L_{\mathrm{I},\max }{L}_{\mathrm{W},\max }}{\sqrt{{(L_{\mathrm{I},\max }\sin {\theta }^n)}^2+{(L_{\mathrm{W},\max }\cos {\theta }^n)}^2}}}$$

(6)

During the icing period, the ice load and wind load on transmission lines are determined by the ice thickness d and the wind speed v [27]:

$$\left\{\begin{array}{c}{l}_{\mathrm{I}}(d)=9.8\times {10}^{-3}{\rho }_{\mathrm{I}}\pi d(D+d)\\ l_{\mathrm{W}}(d,v)=0.613a\beta (D+2d)v^2\times {10}^{-3}\end{array}\right.$$

(7)

where ${\rho }_{\mathrm{I}}$ denotes the density of the ice, with a value of 0.9 g/cm³ according to GB 50545-2010 in China (other regions may adopt localized standards); D is the diameter of the conductor. a represents the wind speed non-uniformity coefficient, with its value given as follows:

$$a=\left\{\begin{array}{cc}1& v\le 20 \mathrm{m}/\mathrm{s}\\ 0.85& 20 \mathrm{m}/\mathrm{s}<v\le 30 \mathrm{m}/\mathrm{s}\\ 0.75& 30 \mathrm{m}/\mathrm{s}<v\le 35 \mathrm{m}/\mathrm{s}\\ 0.7& v>35 \mathrm{m}/\mathrm{s}\end{array}\right.$$

(8)

β is the shape coefficient of wind load, with its value given as follows:

$$\beta =\left\{\begin{array}{cc}1.2& D\le 17 \mathrm{m}\mathrm{m}\\ 1.1& D>17 \mathrm{m}\mathrm{m}\end{array}\right.$$

(9)

According to [28], when only the effect of icing is considered, the transmission line is unlikely to experience a fault or outage if the ice thickness d is below the design ice thickness d_des. However, if d reaches 5d_des, the line is very likely to experience conductor breakage and result in a fault-induced outage. Similarly, if the wind speed v is below the design wind speed v_des, the line is not expected to fail. However, if v reaches 2v_des, the probability of conductor breakage and fault-induced outage becomes very high.

Therefore, by substituting d_des and v_des into Equation (7), the design value of ice load L_I,des and the design value of wind load L_W,des can be obtained as follows:

$$\left\{\begin{array}{c}{L}_{\mathrm{I},\mathrm{des}}=l_{\mathrm{I}}(d_{\mathrm{des}})\\ L_{\mathrm{W},\mathrm{des}}=l_{\mathrm{W}}(d_{\mathrm{des}},v_{\mathrm{des}})\end{array}\right.$$

(10)

Similarly, by substituting 5d_des and 2v_des into Equation (7), the critical value of ice load L_I,max and the critical value of wind load L_W,max can be obtained as follows:

$$\left\{\begin{array}{c}{L}_{\mathrm{I},\max }=l_{\mathrm{I}}(5d_{\mathrm{des}})\\ L_{\mathrm{W},\max }=l_{\mathrm{W}}(5d_{\mathrm{des}},2v_{\mathrm{des}})\end{array}\right.$$

(11)

3. Quantitative Risk Model for Icing of Overhead Transmission Lines

The purpose of evaluating the icing risk of overhead transmission lines is to formulate appropriate anti-icing strategies based on the severity of the risk. In previous studies, the severity of icing risk was often represented by indicators such as the health index or risk levels. Although these methods can quantify the effectiveness of anti-icing strategies after implementation, their outputs are non-monetary, making it impossible to directly compare them with the implementation costs of the strategies. As a result, it becomes difficult to conduct a comprehensive performance evaluation, which may lead to a significant mismatch between the cost and the effectiveness of anti-icing strategies. To address this issue, this paper proposes a quantitative risk model for overhead transmission lines under icing conditions, which is based on three core components during the icing period: the failure rate, the VoLL, and the amount of lost load.

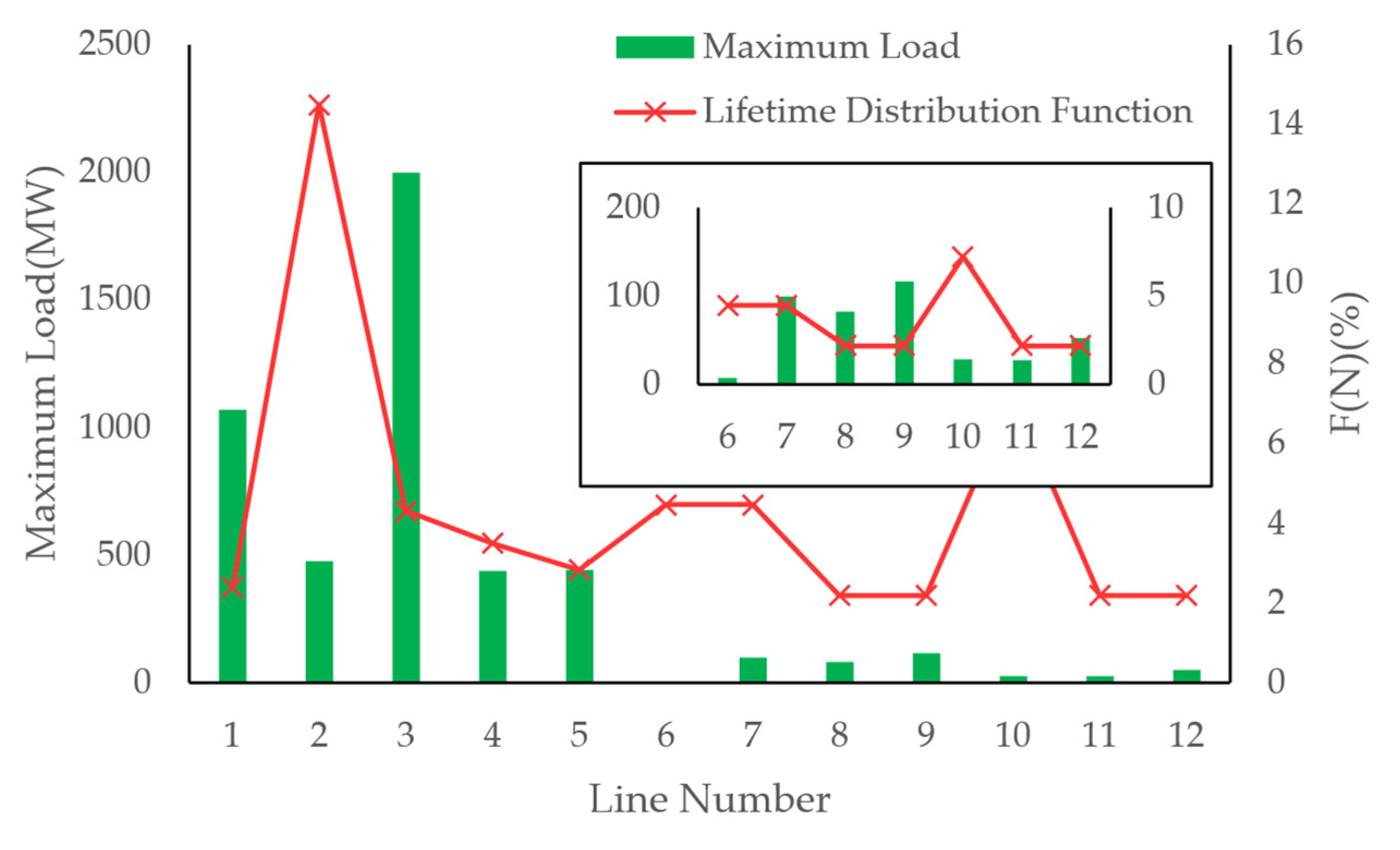
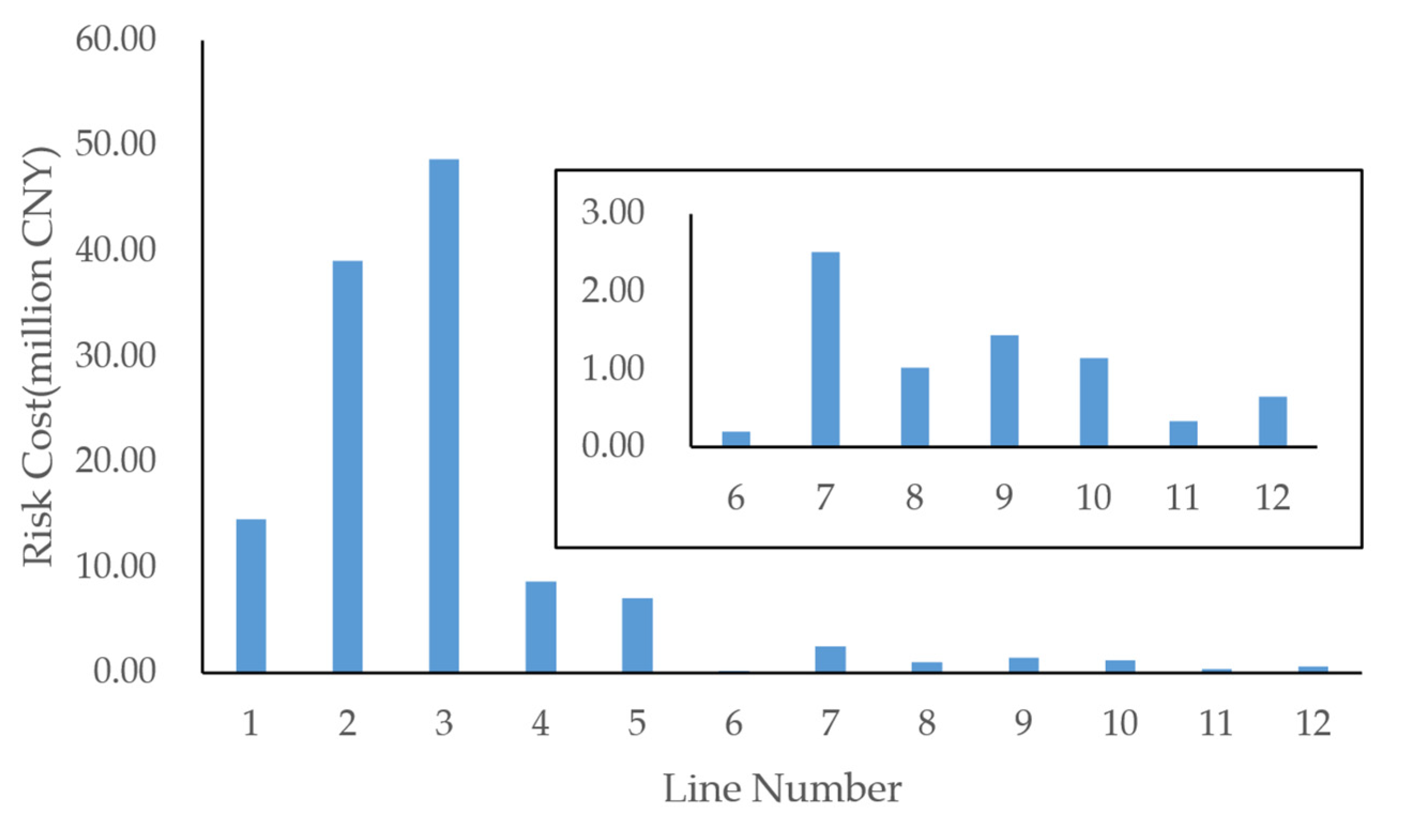
The risk quantification model is illustrated in Figure 5, where the model output is the icing risk cost RI of the overhead transmission line, defined as

$$RI=F(N)\times V_{\mathrm{L}}\times W_{\mathrm{out}}$$

(12)

where F represents the lifetime distribution function of the overhead transmission line under icing conditions, which can be calculated based on the failure rate λ described in Section 1; V_L denotes the VoLL due to fault-induced outages; and W_out is the amount of lost load.

The VoLL V_L for transmission lines is an indicator used to measure the economic loss caused by power supply interruption, reflecting the economic value per unit of electricity. In this study, the production function method is adopted to calculate the value of lost load.

The production function method, also known as the macroeconomic approach, views electricity as a production factor equivalent to capital and labor from a macroeconomic perspective, linking it directly to economic output. Power interruptions result in interruption losses. When viewed from an opportunity cost perspective, it can be represented by the output that electricity would have generated under normal supply conditions.

Since the primary contributors to economic output and electricity consumption are the industrial and service sectors, while households and public institutions contribute relatively little, this study focuses on the lost load cost associated with industrial and commercial electricity users.

The value of lost load V_L, representing the unit economic loss per kilowatt-hour of electricity not supplied in the industrial and service sectors, is calculated using the following formula [29]:

$$V_{\mathrm{L}}={\displaystyle \frac{\mathrm{GVA}}{\mathrm{ELC}}}$$

(13)

where GVA represents the total value added of the observed region, which is equivalent to the regional GDP; ELC denotes the electricity consumption of the observed region.

The amount of lost load W_out is obtained by multiplying the power loss P_L resulting from a transmission line failure by the outage duration t_out, as follows:

$$W_{\mathrm{out}}=P_{\mathrm{L}}\times t_{\mathrm{out}}$$

(14)

Among all types of transmission line failures, conductor breakage results in the greatest power loss. To enhance the reliability of the transmission line, more severe failure scenarios should be considered. Therefore, this study adopted the power loss caused by conductor breakage as the value of P_L. In the most critical conductor breakage scenarios, the power originally carried by the failed line cannot be rerouted through other lines, meaning the lost power equals the maximum transmission capacity P_l of the line. To ensure maximum reliability, the amount of lost load W_out is, therefore, determined according to Equation (15).

$$W_{\mathrm{out}}=P_l\times t_{\mathrm{out}}$$

(15)

The outage duration t_out refers to the time interval from the occurrence of a conductor breakage in an overhead transmission line to the completion of repair and restoration of power supply. Since icing-prone microtopographic and microclimatic areas are often located far from residential zones, line maintenance is typically hindered by poor accessibility and transportation difficulties. As a result, the repair duration tends to be relatively long. According to maintenance data surveys, the typical repair time ranges from 24 to 48 h. In this study, the average value of 36 h was adopted.

In summary, the icing risk cost RI of overhead transmission lines can be calculated using Equation (12).

4. Performance Evaluation of Transmission Line Anti-Icing Strategies Based on a Time Evolution Model

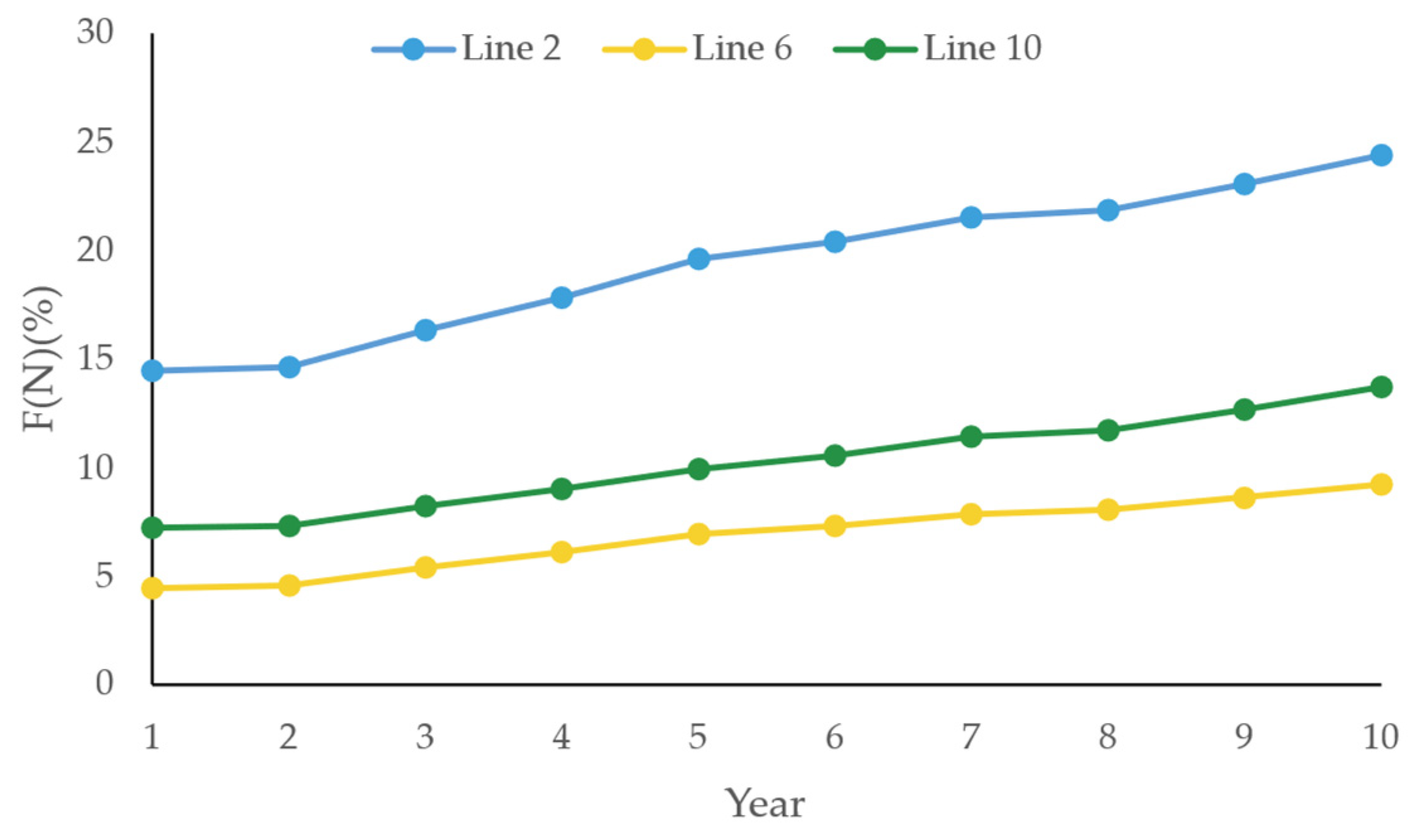
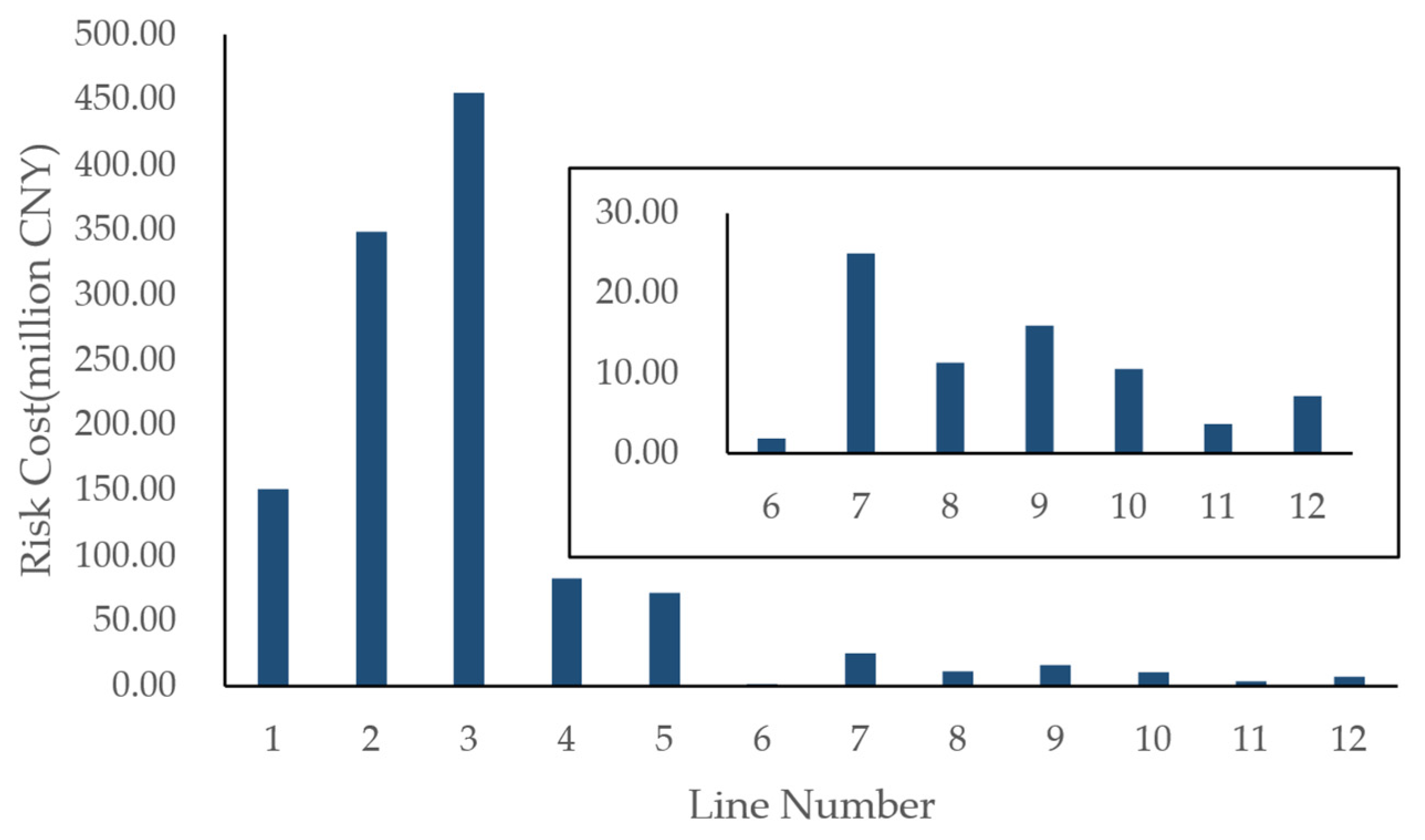
Anti-icing strategies for transmission lines are composed of a combination of anti-icing schemes applied across multiple lines. These schemes often differ significantly in terms of both investment cost and the sustainability of their effectiveness in mitigating the icing risk of overhead transmission lines. Therefore, evaluating the performance of anti-icing strategies solely based on their effectiveness in the year of implementation lacks scientific rigor. To address this limitation, this paper proposes a performance evaluation method for anti-icing strategies based on a time evolution model, which accounts for the dynamic risk control effect over multiple icing periods.

Let set S represent the candidate set of anti-icing schemes for a single transmission line, defined as S = {s₁, s₂,…, s_y,…, s_Y}. Define a vector k = (k₁, k₂,…, k_m,…, k_M) to represent a combination of anti-icing schemes across all lines, i.e., an anti-icing strategy. Here, M denotes the total number of transmission lines, and k_m denotes the anti-icing scheme selected for line m, with k_m ∈ S. For example, k_m = s_y indicates that line m adopts the anti-icing scheme s_y.

To comprehensively evaluate the performance of an anti-icing strategy by considering both the residual risk cost and the investment cost of transmission lines, the composite cost with time evolution for a given anti-icing strategy k is defined as E(k).

$$E(\mathit{k})={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{T=1}^{T_{\max }}\left(C_m(k_m,T)+R{I}_m(k_m,T)\right)}}$$

(16)

where T_max denotes the evaluation period for the anti-icing strategy’s performance. Its value can be determined based on the maximum effective duration among all anti-icing schemes within the strategy, the least common multiple of their durations, the lifetime of the transmission line, or the enterprise planning horizon. C_m(k_m, T) represents the present value of the investment cost in year T for line m when adopting anti-icing scheme k_m; RI_m(k_m, T) denotes the present value of the residual risk cost in year T for line m under scheme k_m. The residual risk cost refers to the quantified risk cost that remains over time even after an anti-icing scheme has been implemented.

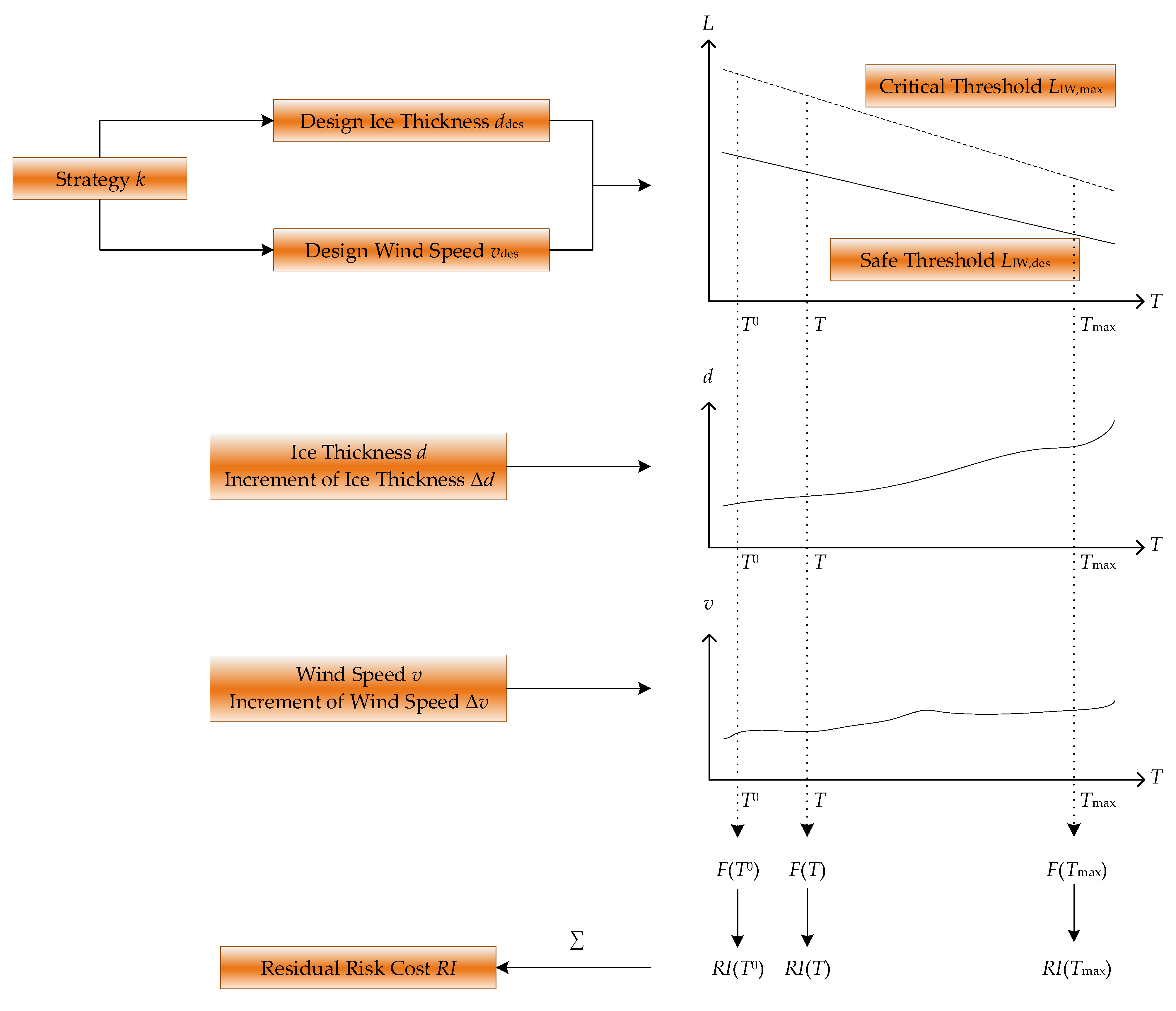
The calculation process of RI_m is illustrated in Figure 6.

The performance evaluation results consist of two components: C_m and RI_m, whose calculation methods are as follows:

$$C_m(k_m,T)={\displaystyle \frac{c_m(k_m,T)}{{(1+r)}^T}}$$

(17)

where c_m(k_m, T) is the investment cost in year T for line m when adopting the anti-icing scheme k_m, and r is the discount rate. Capital exhibits time value—a given amount of money today is worth more than the same nominal amount in the future. Therefore, the investment cost in year T cannot be directly compared to present-day costs. To enable temporal comparison, this study applies a discount rate r to convert future values to present values.

$$R{I}_m(k_m,T)={\displaystyle \frac{F_m(k_m,T,N)\times V_{\mathrm{L},m}\times W_{\mathrm{out},m}}{{(1+r)}^T}}$$

(18)

where F_m(k_m, T, N) is the lifetime distribution function of line m in year T, given that N icing periods occur after implementing anti-icing scheme k_m; V_L,m is the VoLL for line m; W_out,m is the amount of lost load for line m.

The investment cost of an anti-icing strategy is a key parameter for evaluating its economic performance. However, existing evaluation methods based on risk levels, health indices, and similar indicators cannot directly integrate the investment cost with the effectiveness metrics of anti-icing strategies. The method proposed in this paper addresses this issue by incorporating the impact of time evolution on the residual risk of transmission lines, as shown in Equation (18). It also accounts for the time value of money, converting future cash flows into their present values, which enables direct mathematical integration of the residual risk and the investment cost, as shown in Equation (16). As a result, the proposed method enables an objective and effective evaluation of the composite performance of anti-icing strategies.

In Equation (18),

$$F_m(k_m,T,N)=1-e^{-{\Lambda }_m(k_m,T,N)}$$

(19)

where Λ_m(k_m, T, N) is the cumulative hazard function of line m in year T, given that N icing periods occur after the implementation of anti-icing scheme k_m.

$${\Lambda }_m(k_m,T,N)={\displaystyle \sum _{n=1}^N{\lambda }_m^{T,n}}$$

(20)

where ${\lambda }_m^{T,n}$ denotes the failure rate of line m during the n-th icing period in year T, after the implementation of anti-icing scheme k_m. It is calculated based on Equation (3), using the line’s ice–wind load ${\mathit{l}}_{\mathrm{IW},m}^{T,n}$ during that icing period, the corresponding safe threshold ${\mathit{L}}_{\mathrm{IW},\mathrm{des},m}^{T,n}$, and the critical threshold ${\mathit{L}}_{\mathrm{IW},\max ,m}^{T,n}$ of the ice–wind load.

The ice–wind load ${\mathit{l}}_{\mathrm{IW},m}^{T,n}$ of a transmission line is calculated by substituting the maximum ice thickness d_m(T, n) and the maximum wind speed v_m(T, n) of line m during the icing period n in year T into Equation (7). The ice thickness and wind speed in year T directly influence the lifetime distribution function, thereby affecting the risk cost. To mitigate this risk cost, it becomes necessary to select an anti-icing scheme with enhanced ice-resistant capabilities. Therefore, the time evolution model must account for future variations in ice thickness and wind speed. Due to inter-annual variability in climatic conditions, the characteristics of icing differ across years and exhibit a certain degree of randomness [30]. Therefore, this study adopted a time evolution-based meteorological simulation method, in which the ice thickness and maximum wind speed in future years are modeled as the sum of the previous year’s values and a random variable with specific distribution characteristics, as shown in the following equation:

$$d_m=d_m^0+{\displaystyle \sum _{t=1}^T(\Delta d\sim {\Gamma }_d(t))}$$

(21)

$$v_m=v_m^0+{\displaystyle \sum _{t=1}^T(\Delta v\sim {\Gamma }_v(t))}$$

(22)

where $d_m^0$ and $v_m^0$ represent the maximum ice thickness and maximum wind speed during the icing period on line m during the implementation year of the anti-icing strategy; $\Delta d$ and $\Delta v$ denote the annual increment of maximum ice thickness and maximum wind speed, respectively, following stochastic distributions ${\Gamma }_d(t)$ and ${\Gamma }_v(t)$. The stochastic distributions should be derived from historical data of the study region.

This approach captures the uncertainty in meteorological conditions as they evolve over time.

After commissioning, overhead transmission lines undergo degradation due to wind and rain erosion, leading to a gradual reduction in load-bearing capacity over time [31]. The safe threshold ${\mathit{L}}_{\mathrm{IW},\mathrm{des},m}(k_m,T)$ and critical threshold ${\mathit{L}}_{\mathrm{IW},\max ,m}(k_m,T)$ of the ice–wind load borne by line m in year T after implementing anti-icing scheme k_m are influenced by both the anti-icing scheme itself and time evolution. The calculation method is as follows:

$${\mathit{L}}_{\mathrm{IW},\mathrm{des},m}(k_m,T)={\mathit{L}}_{\mathrm{IW},\mathrm{des},m}^0(k_m)-{\displaystyle \sum _{t=1}^T\Delta {\mathit{L}}_{\mathrm{IW},\mathrm{des},m}(k_m,t)}$$

(23)

$${\mathit{L}}_{\mathrm{IW},\max ,m}(k_m,T)={\mathit{L}}_{\mathrm{IW},\max ,m}^0(k_m)-{\displaystyle \sum _{t=1}^T\Delta {\mathit{L}}_{\mathrm{IW},\max ,m}(k_m,t)}$$

(24)

where ${\mathit{L}}_{\mathrm{IW},\mathrm{des},m}^0(k_m)$ and ${\mathit{L}}_{\mathrm{IW},\max ,m}^0(k_m)$ represent the initial safe threshold and initial critical threshold of the ice–wind load for line m in the year of implementing anti-icing scheme k_m, respectively; $\Delta {\mathit{L}}_{\mathrm{IW},\mathrm{des},m}(k_m,t)$ and $\Delta {\mathit{L}}_{\mathrm{IW},\max ,m}(k_m,t)$ denote the degradation of the safe threshold and critical threshold of the ice–wind load for line m in year t after the implementation of scheme k_m, respectively. In the time evolution model of this study, the degradation of line load-bearing capacity is primarily characterized by an annual decline in both the safety threshold and the critical threshold. To capture this behavior, we assumed a 1% yearly reduction in both thresholds.

The optimization of anti-icing strategies by power grid enterprises should be based on the performance evaluation results of those strategies. However, due to the limited annual investment budget for anti-icing measures on transmission lines and the need to ensure that the residual risk remains within acceptable reliability thresholds, it is important to avoid an imbalance between economic efficiency and system reliability. To address this, the anti-icing strategy optimization model proposed in this paper, based on performance evaluation, is formulated as follows:

$$\begin{array}{c}\underset{\mathit{k}}{\min }E(\mathit{k})\hfill \\ s.t.\hfill \\ \left\{\begin{array}{l}{\displaystyle \sum _{m=1}^M{c}_m(k_m,T)}\le c_{th}(T),T=1,2,\dots ,T_{\max }\\ F_m(k_m,T,N)\le F_{m,th}(T,N),m=1,2,\dots ,M;T=1,2,\dots ,T_{\max }\end{array}\right.\hfill \end{array}$$

(25)

where cth(T) denotes the investment cost threshold for anti-icing measures set by the power grid enterprise in year T; F_m,th(T, N) represents the reliability requirement specified by the enterprise for line m during N icing periods in year T.

The ice-resistant strategy optimization model (25) is a linear integer programming problem and constitutes an NP-hard problem, which could be solved by solvers like Gurobi or CPLEX. However, for optimization problems involving multiple lines, the solving difficulty may be significant.

On the other hand, it is noted that in the optimization model, the cost terms and lifetime distribution constraints are decoupled for different lines. The strategies for each line are only coupled through the total implementation cost. Therefore, heuristic methods can be employed to solve the ice-resistant strategy optimization model. First, the optimal solution is found without considering the implementation cost constraint, and then adjustments are made based on a greedy algorithm to obtain the optimal solution that satisfies the constraints.

The structural framework of the optimization model is illustrated in Figure 7. The pseudocode of the model-solving algorithm is shown in Algorithm 1. The algorithm consists of four steps. In Step 1, the implementation cost, residual risk cost, and lifetime distribution function are calculated for all strategies of all lines. In Step 2, feasible strategies for all lines are filtered based on lifetime distribution constraints. In Step 3, based on the feasible strategies from Step 2, the strategy with the lowest total cost is selected for each line. Finally, if the total implementation cost constraint is violated, Step 4 iteratively adjusts the ice-resistant strategies of the lines. Using the greedy algorithm, each adjustment selects the strategy with the lowest unit adjustment cost until the total implementation cost constraint is satisfied.

This model-solving algorithm leverages the near-decoupling characteristic of ice-resistant strategies across different lines, enabling faster determination of ice-resistant strategies. Additionally, methods like strategy adjustment backtracking can be incorporated to avoid local optima.

The anti-icing strategy optimization in this study constitutes an NP-hard linear integer programming problem. Although mathematically formulated as a linear integer programming model, the computational complexity is reduced due to the independence of strategies across different transmission lines. Consequently, a heuristic algorithm was employed for solution derivation, as shown in Algorithm 1.

Algorithm 1: Heuristic Algorithm for Ice-Prevention Strategy Selection under Budget Constraints
1:	Initiation. Let M be the number of transmission lines. Let S be the candidate set of anti-icing schemes for a single transmission line. Let T be the evaluation period for the anti-icing strategy’s performance.
Step 1: Calculate cost for all anti-icing schemes of all lines
2:	For each line m∈{1, 2, …, M}:
3:	For each scheme km∈S:
4:	For each time T∈{1, 2, …, Tmax}:
5:	Calculate the implementation cost Cm(km, T), the lifetime distribution function                F(N) and the residual risk cost RIm(km, T) through (17) and (18), respectively.
6:	endfor
7:	endfor
8:	endfor
Step 2: Feasible scheme reduction
9:	For each line m∈{1, 2, …, M}:
10	Define the feasible scheme set of line m:
11:	Sm←{sy|sy∈S and Fm(km, T, N) ≤ Fm, th(T, N), T ∈ {1, 2, …, Tmax}}
12:	If Sm= ∅:
13:	Terminate with infeasibility.
14:	endif
15:	endfor
Step 3: Initial strategy selection
16:	For each line m∈{1, 2, …, M}:
17:	Select the optimal scheme:
18:	km←$\underset{k_i\in S_m}{\arg \min }{\displaystyle \sum _{T=1}^{T_{\max }}{c}_m(k_i,T)+F_m(k_m,T,N)}$
19:	endfor
20:	Define current strategy:
21:	k←{km|m∈{1, 2, …, M}}
Step 4: Iterative strategy adjust
22:	Check implementation cost constraint:
23:	If ${\displaystyle \sum _{m=1}^M{c}_m(k_m,T)}\le c_{th}(T),T=1,2,\dots ,T_{\max }$:
24:	Terminate and return current strategy k
25:	endif
26:	Define the violate constraints year set as TVC
27:	TVC←{T|year T of violation of the implementation cost constraint}
28:	For each line m ∈ {1, 2, …, M}:
29:	For each feasible scheme sy ∈ Sm-{km}:
30
31:	Calculate Δcm(km, sy), the difference of the total implementation cost in the           years in TVC between scheme km and scheme sy
32:	Calculate ΔEm(km, sy), the difference of the total composite cost in the years           in TVC between scheme km and scheme sy
33:	Define unit adjustment cost of line m and scheme sy:
34:	ρm(km, sy)←|ΔEm(km, sy)/Δcm(km, sy)|
35:	endfor
36:	endfor
37:	While True
38	If ΔEm(km, sy) > 0 for all lines and schemes
39:	Terminate with infeasibility.
40:	endif
41:	Find the line m and scheme sy with the highest ρm(km, sy) and a negativeΔcm(km, sy)
42:	km←sy
43:	Update the violate constraints year set TVC
44:	If TVC = ∅:
45:	Terminate and return current strategy k
46:	endif
47:	Update unit adjustment cost for line m
48:	endwhile

5. Case Study

5.1. Quantification of Icing Risk Cost for Overhead Transmission Lines

To verify the effectiveness of the icing risk quantification model for transmission lines proposed in Section 3, this subsection presents a case study based on actual transmission line data and icing period meteorological data. Transmission lines located in a province of China, where severe icing conditions were observed, were selected as the case for analysis. The region experienced four icing periods between December 2023 and February 2024. The basic parameters of the line are listed in

Table 2. Basic parameters of the transmission line.

Line Number	Voltage Level (kV)	Age (year)	ddes (mm)	vdes (m/s)	Maximum Load (MW)
1	1000	14	10	30	1070.66
2	500	3	15	30	478.01
3	500	0	10	30	1997.85
4	500	14	15	30	437.70
5	500	14	15	30	442.42
6	220	3	15	25	7.61
7	220	4	15	25	99.59
8	220	15	10	25	82.63
9	220	15	10	25	115.99
10	110	4	10	25	28.20
11	110	14	10	25	26.93
12	110	7	10	25	52.08

.

First, Line 2 was selected as a case to calculate the failure rate and icing risk during the icing periods. The icing data and meteorological conditions for Line 2 during the four icing periods are presented in

Table 3. Icing and meteorological data for line 2.

Icing Period	d (mm)	v (m/s)
1	30	7.9
2	19	7.9
3	4	7.9
4	5.1	10.7

.

By substituting d_des and v_des from Table 2, as well as the meteorological data from Table 3, into Equations (3) through (11), and taking λ₀ = 0.004 [32], the failure rates of Line 2 during the four icing periods were calculated as 11.82%, 3.03%, 0.4%, and 0.4%, respectively. Using Equation (2), the lifetime distribution function value of Line 2 under the combined effect of four icing periods (N = 4) was calculated to be 14.49%. According to the latest data from the 2023 China Statistical Yearbook and using Equation (13), the VoLL in the region was determined to be 15.697 CNY/kWh. By substituting the above data into Equation (12), the icing risk cost of Line 2 during the period from December 2023 to February 2024 was calculated to be CNY 39.13 million. The lifetime distribution function values and maximum loads of all lines under four icing periods (N = 4) are shown in Figure 8.

Furthermore, the icing risk for all 12 transmission lines listed in Table 1 during the four icing periods from December 2023 to February 2024 was calculated. The results are presented in Figure 9.

As shown in Figure 9, the icing risk costs of Line 2 and Line 3 are significantly higher than those of the other lines, but for different reasons. For Line 2, certain sections pass through areas with severe icing conditions, resulting in a much higher lifetime distribution function value compared to other lines, which in turn leads to a higher icing risk cost. Although Line 3 has a moderate lifetime distribution function value, its maximum load is significantly higher than that of the other lines, contributing to its elevated risk cost.

Line 1 is an ultra-high voltage transmission line. While it also has a relatively high maximum load, it was built to the highest design standards, giving it the strongest anti-icing capability. Furthermore, it does not pass through areas of severe icing, resulting in a much lower lifetime distribution function value and a significantly lower risk cost than Line 2. Line 6 has the lowest icing risk cost. This is because the line does not pass through severely iced regions, and its load is relatively low, meaning that even in the event of an outage, the amount of lost load remains minimal.

5.2. Performance Evaluation of Anti-Icing Strategies for Overhead Transmission Lines

In this subsection, the anti-icing strategy performance evaluation method proposed in Section 4 is validated using actual transmission line data from the power grid. The selection of anti-icing strategies requires comprehensive consideration of potential icing events that may occur over a future period. Since climatic conditions tend to evolve over time, this study assumed that the meteorological data for the upcoming year can be simulated by adding a normally distributed random disturbance to the previous year’s data, thereby capturing the time evolution characteristics of the climate. A Monte Carlo method was used to generate icing scenarios for the next ten years. According to [33], the number of freezing rain days in recent years has shown an upward trend in a certain province north of the Qinling–Huaihe Line. South of the line is China’s primary freezing rain concentration zone, where freezing rain days have generally decreased in recent years. However, north of the line, freezing rain days show an overall increasing trend. Therefore, when analyzing temporal trends across different regions, geographical characteristics must be considered. In this paper, the mean of the normally distributed random variable was set as a small positive value slightly greater than zero.

In Equation (23), the variable was set to 1% of the safe threshold of the ice–wind load that the overhead transmission line can withstand. In Equation(24), ∆L_max(k_m, T) was set to 1% of the critical threshold of the ice–wind load. According to relevant regulations [34], the discount rate r used in Equations (17) and (18) was set to 8%. As an illustration, Figure 10 shows the year-by-year lifetime distribution function values under the time evolution model for Line 2, Line 6, and Line 10. Given the similar trends across multiple curves, plotting all data would result in excessive visual clutter. Therefore, representative curves were selected for display.

Under the time evolution model, the icing risk costs of overhead transmission lines in the icing-prone areas of a certain province over the next 10 years were calculated. The results are presented in Figure 11.

Next, based on the proposed method, the performances of three types of anti-icing schemes—reconstruction, reform, and maintenance—were quantitatively evaluated for each transmission line over the next ten years.

• In the reconstruction scheme, the original transmission line is replaced by a new line built to higher design standards or equipped with advanced anti-icing conductors. This scheme can significantly increase the ice–wind load thresholds, thereby substantially reducing the probability of failure due to excessive ice thickness. However, the investment cost of the reconstruction scheme is the highest among the three.
• In the reform scheme, reinforcing equipment is installed at weak points along the original transmission line. This scheme raises the design ice thickness and wind speed limits, thereby moderately enhancing the anti-icing capability and reducing the failure probability, though to a lesser extent than the reconstruction scheme. The cost of the reform scheme is lower than that of reconstruction.
• In the maintenance scheme, de-icing or ice-melting operations are conducted only after icing occurs. This scheme does not improve the inherent anti-icing capability of the line, but it can partially limit ice thickness during icing periods and thus reduce icing-related failure risk to some degree. It also has the lowest investment cost among the three.

The sample average costs of the three schemes are presented in

Table 4. Implementation costs of different anti-icing schemes for transmission lines of various voltage levels.

Voltage Level (kV)	Cost of Reconstruction (Million CNY/Time)	Cost of Reform (Million CNY/Time)	Cost of Maintenance (Million CNY/Year)
110	8	2	0.15
220	10	2.5	0.225
500	20	5	0.45
1000	40	10	0.6

.

In Equation (25), the economic constraint c_th and the reliability constraint F_m,th are determined based on the operation and maintenance requirements of the power grid company in a certain province, as shown in

Table 5. Economic and risk reliability constraints.

Voltage Level (kV)	cth (T) (Million CNY)	Fm,th (T,N)
110	10	4%
220	25	3.5%
500	50	3%
1000	100	2%

.

In the table, cth(T) represents the total implementation cost of the scheme over a 10-year period, and F_m,th(T,N) denotes the icing failure rate threshold, which must not be exceeded in any year during the 10 years following scheme implementation. If either the economic constraint or the reliability constraint is not satisfied, a scheme with a lower cost or lower icing failure rate is selected, and the constraints are re-evaluated accordingly.

Based on real-life data, this study defined the improvement in the anti-icing capability of overhead transmission lines after the implementation of the reconstruction and reform schemes. For the reconstruction scheme, the design ice thickness of the transmission line increased by 5–15 mm, with the specific value depending on the voltage level of the line. For the reform scheme, the equivalent design ice thickness increased by 10%. After the implementation of each of the three schemes (reconstruction, reform, and maintenance), the parameters related to the icing risk cost improved to varying degrees. By substituting the updated parameters into Equation (12), the residual icing risk cost of the transmission line under each scheme can be calculated. Based on the time evolution model, Figure 12 presents the cumulative residual icing risk costs of overhead transmission lines over a 10-year period after the implementation of each scheme.

As shown in Figure 12, the reconstruction scheme was the most effective approach for reducing risk cost, but it also incurred the highest implementation cost. The reform scheme achieved moderate reductions in risk cost and had lower implementation costs than reconstruction, but higher than maintenance. To comprehensively analyze the reliability and economic benefits of the three schemes, this study evaluated the 10-year performance of each scheme for every transmission line based on the time evolution model. For each line, the sum of the residual risk cost and implementation cost under each scheme, i.e., the composite cost, was calculated. The results are presented in Figure 13.

By comparing Figure 12 and Figure 13, it was observed that although Line 9 has the lowest residual risk cost under the reconstruction scheme, the high implementation cost of reconstruction results in a higher composite cost compared to the reform scheme. Therefore, the optimal anti-icing scheme for Line 9 is the reform scheme. According to Equation (25), the optimal anti-icing strategy for each line is the scheme that yields the lowest composite cost while satisfying both the economic and reliability constraints. The optimal anti-icing scheme and corresponding cost values for each transmission line are summarized in

Table 6. Selected anti-icing schemes for each transmission line and their corresponding costs.

Line Number	Anti-icing Scheme	Implementation Cost (Million CNY)	Residual Risk Cost (Million CNY)	Composite Cost (Million CNY)
1	Reconstruction	44.35	69.6	113.95
2	Reconstruction	33.26	105.3	138.56
3	Reconstruction	33.26	129.87	163.13
4	Reconstruction	33.26	37.67	70.93
5	Reconstruction	33.26	32.53	65.79
6	Maintenance	1.63	1.91	3.54
7	Maintenance	1.63	25.05	26.68
8	Maintenance	1.63	11.34	12.97
9	Reform	4.13	13.23	17.36
10	Maintenance	1.09	10.58	11.67
11	Maintenance	1.09	3.70	4.79
12	Maintenance	1.09	7.15	8.24

.

To further validate the superiority of the anti-icing scheme performance evaluation and selection method proposed in this study, a comparative analysis was conducted against two existing approaches: (1) the anti-icing scheme selection method based on the Weibull distribution of transmission line failure rates [35], and (2) the anti-icing scheme selection method based on transmission line condition assessment [36].

In the method described in [35], the anti-icing scheme for a transmission line was determined based on the relationship between the service age of the line (as shown in Table 1) and the Weibull distribution curve. Specifically, the maintenance scheme was applied during the steady period of the Weibull curve, the reform scheme was applied in the first 50% of the wear-out phase, and the reconstruction scheme was applied in the latter 50% of the wear-out phase. In [36], a health index was defined for each line, and the anti-icing scheme was selected based on the value of this index. When the health index fell within [80, 100], the maintenance scheme was adopted; when it fell within [50, 80), the reform scheme was selected; and when the health index was below 50, the reconstruction scheme was implemented.

The optimal anti-icing schemes for each transmission line obtained using the proposed method were compared with those derived from existing methods, as shown in Figure 14. The optimal anti-icing strategy determined by the proposed method is referred to as Strategy 1, while those derived from the methods in [35,36] are referred to as Strategy 2 and Strategy 3, respectively.

In Figure 12, the sum of the residual risk cost and the implementation cost under each strategy represents the composite cost of the selected anti-icing scheme for each transmission line.

For Strategy 1, the implementation costs of the anti-icing schemes for Lines 1 to 5 are significantly higher than those under Strategy 2. However, the composite costs for these lines under Strategy 1 are notably lower than those under Strategy 2. This is because the Weibull curve-based method used in Strategy 2 considers only the failure rate increase due to service age, while ignoring the additional failure risks caused by icing disasters. Increased ice accretion will elevate transmission line failure rates, a critical factor that must be accounted for. In the case of Lines 8, 11, and 12, although the residual risk costs under Strategy 1 are higher than the implementation costs under Strategy 2, the overall composite costs under Strategy 1 are still lower. Due to lower baseline costs, this strategy maintains the lowest composite cost even with rising ice risk expenses, outperforming all alternatives in cost-effectiveness. This is because the anti-icing schemes selected in Strategy 1 incur lower implementation costs.

These results demonstrate that the proposed method (Strategy 1) offers a more comprehensive evaluation by simultaneously accounting for both risk and economic costs, thus providing a more balanced anti-icing strategy compared to the method in [35]. Similarly, the composite costs of the anti-icing schemes selected in Strategy 1 are also lower than those in Strategy 3, indicating the superiority of the proposed method. Detailed comparisons with Strategy 3 have been omitted for brevity.

In summary, the composite cost of the proposed strategy (Strategy 1) is 46.11% lower than that of Strategy 2, and 32.56% lower than that of Strategy 3. The residual risk cost is also reduced by 60.26% and 48.41%, respectively. Therefore, the proposed method can more effectively balance reliability and economic efficiency in transmission line operation, consequently providing a more optimal anti-icing scheme for overhead transmission lines.

6. Conclusions

This paper proposes a time-evolution-based performance evaluation model for overhead transmission line anti-icing strategies, considering both reliability and economic performance. The model was employed to enhance ice mitigation strategies in operational transmission networks.

First, a transmission line icing failure rate model was established based on the Nelson–Aalen method and metal deformation theory. Combined with the VoLL and line load data, this model enables the quantification of icing risk costs under icing conditions, providing a monetized risk indicator.

Then, by taking into account risk control costs, implementation costs, and time effects, a method was proposed to compute the composite cost for evaluating the performance of anti-icing strategies. With minimization of the composite cost as the optimization objective, and subject to reliability and economic constraints, the proposed algorithm aimed to ensure both secure and stable power grid operation and cost control.

Finally, based on real-life power grid and meteorological data from a province in China, a case study was conducted to validate the effectiveness of the proposed risk quantification indicator and composite cost metric. The comparative analysis shows that the anti-icing strategy selection method proposed in this paper can effectively reduce the operational risks of overhead transmission lines under icing conditions while also controlling strategy implementation costs more efficiently than existing methods.

The proposed algorithm provides a scientific basis for power grid enterprises to develop anti-icing and disaster mitigation strategies and offers valuable guidance for risk control engineering and cost management in power transmission systems.

Future research should comprehensively account for heterogeneous ice accretion patterns and incorporate extreme weather events. The actual distribution of freezing rain and wind speed may involve nonlinear dynamics or extreme events, for which current research has not yet established clear patterns. Therefore, future work should prioritize this unresolved challenge. Additionally, investigating interdependencies among transmission lines in power grids presents another critical direction.