Key Factors, Degradation Mechanisms, and Optimization Strategies for SCO2 Heat Transfer in Microchannels: A Review
Abstract
1. Introduction
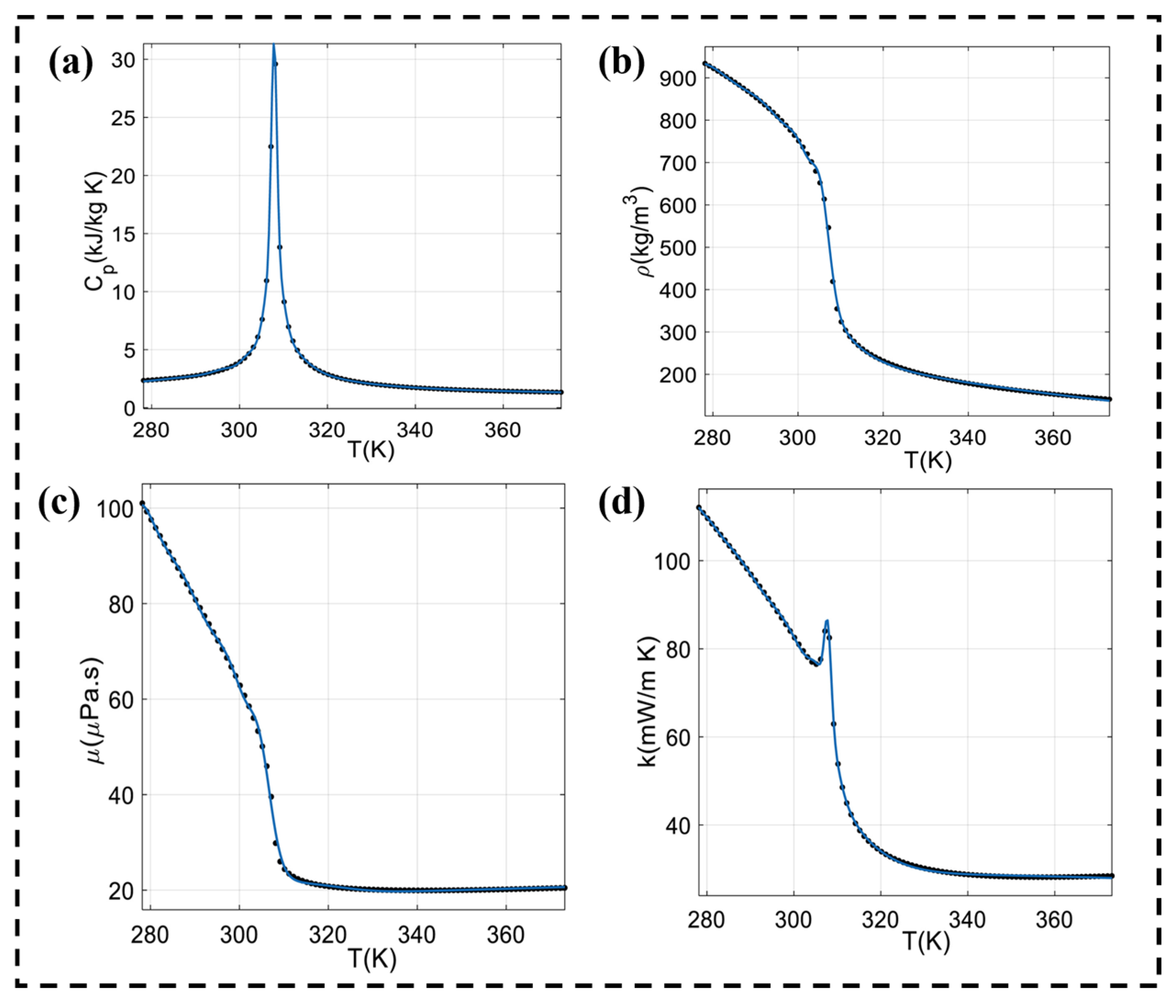
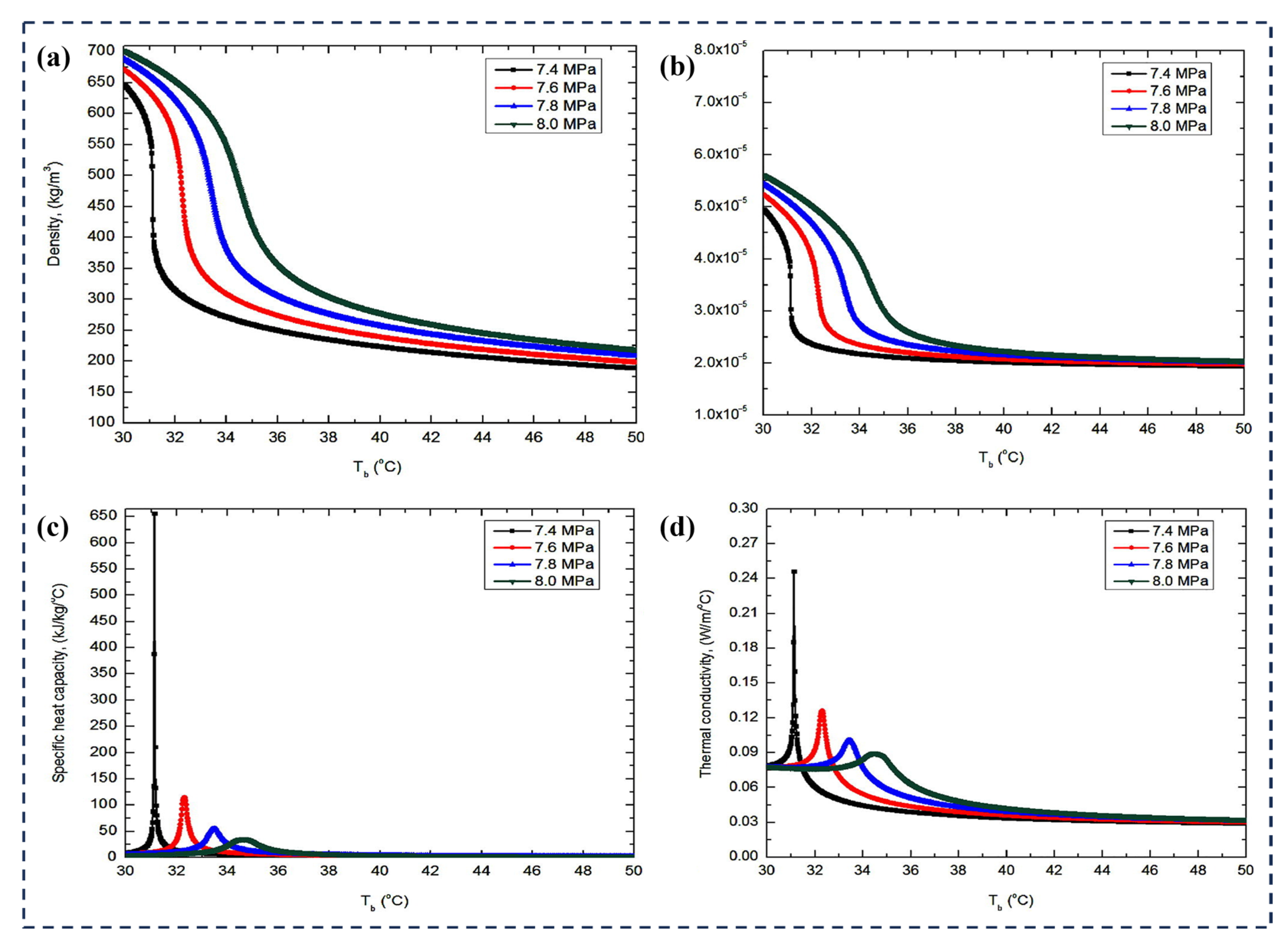
2. Thermodynamic Properties of Supercritical Carbon Dioxide
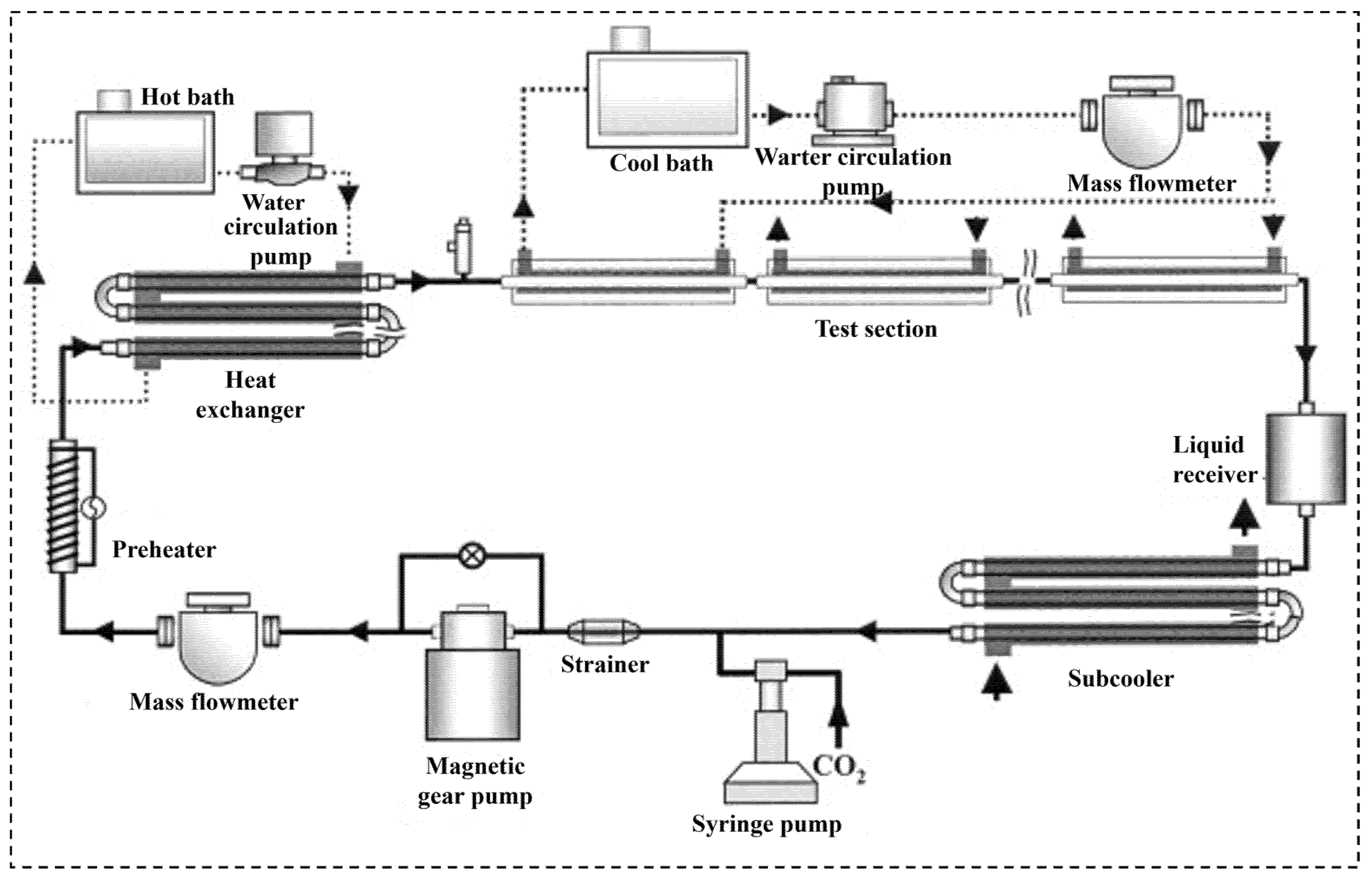
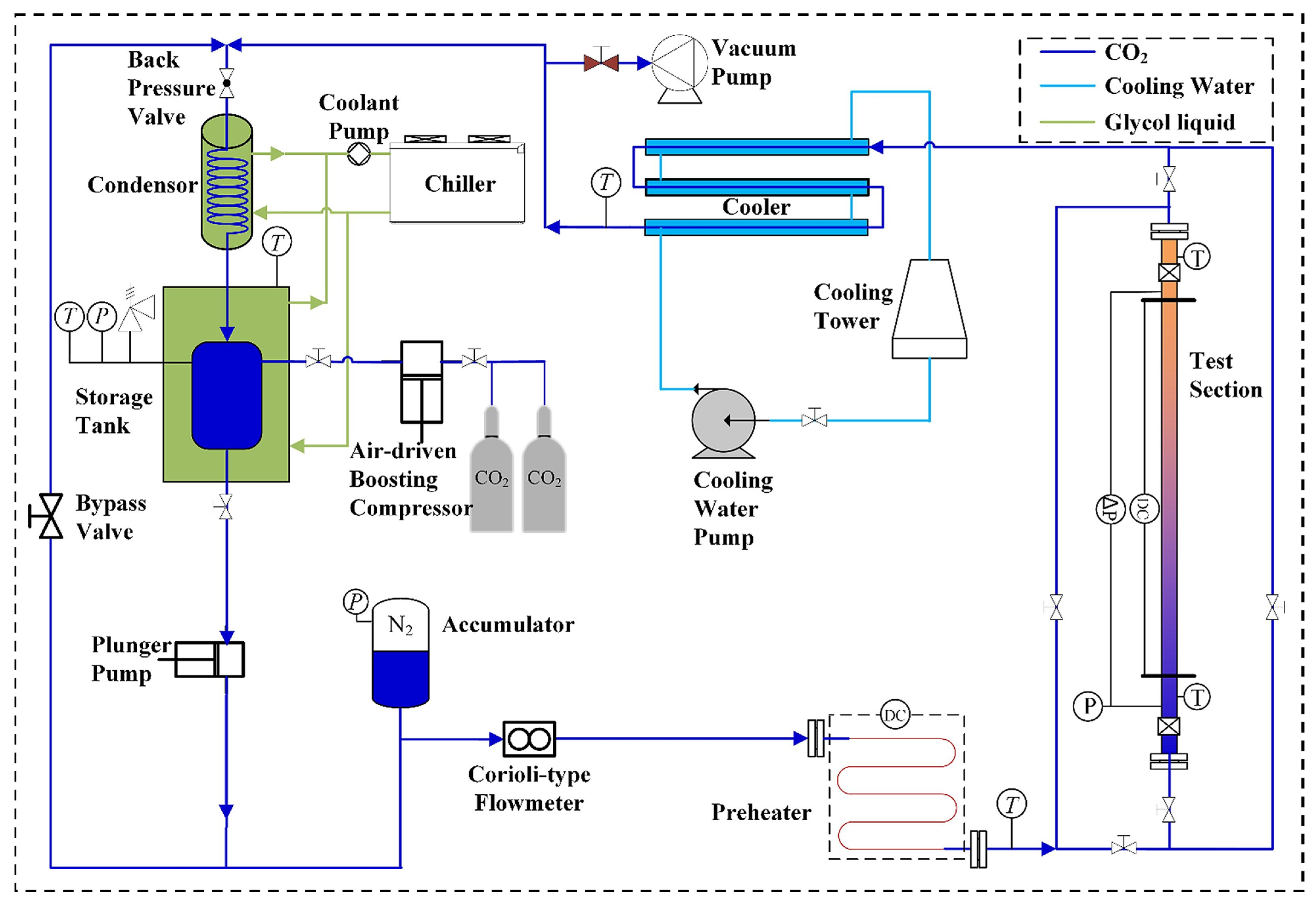
3. Experiments on SCO2 Heat Transfer in Microchannels
3.1. Horizontal Microchannels
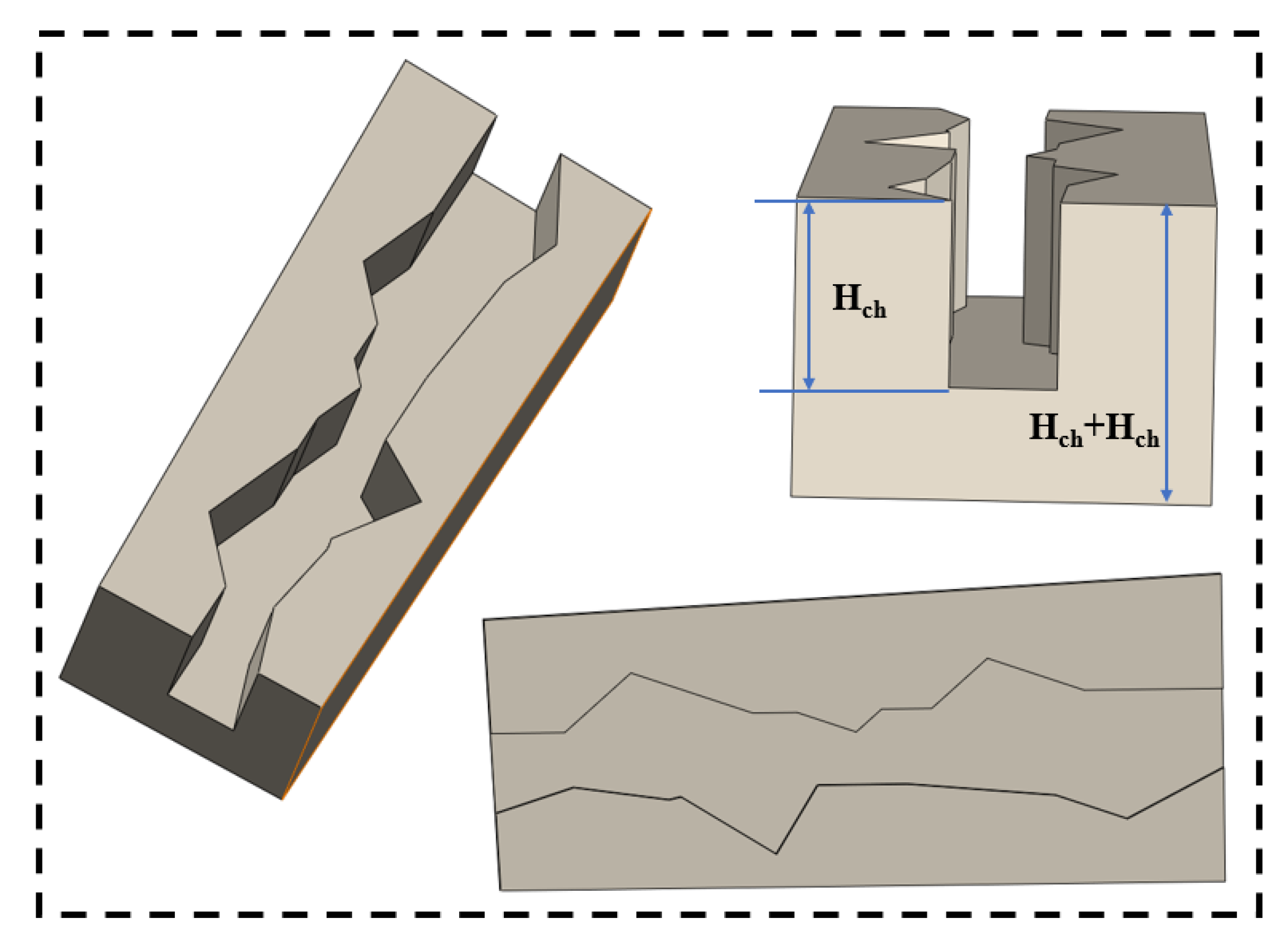
3.1.1. Section Size and Structure
3.1.2. Pressure Drop
3.1.3. Heat Transfer
3.2. Vertical Microchannels
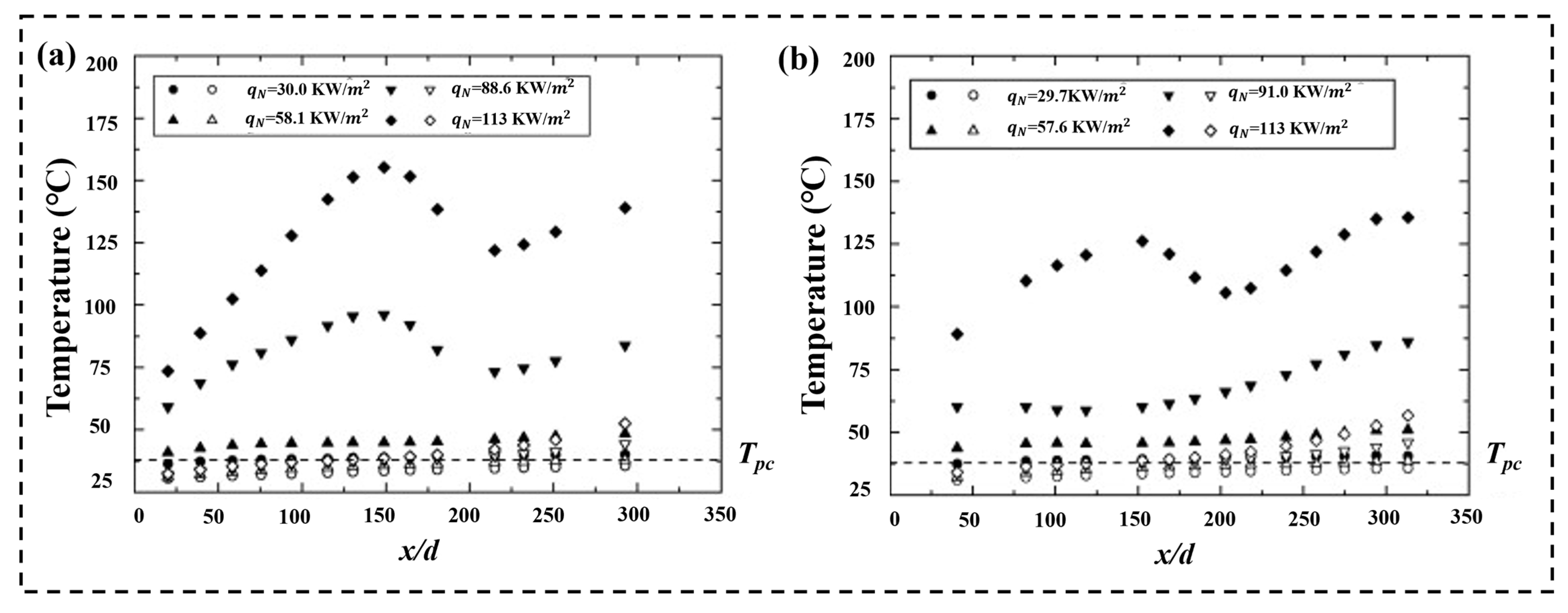
3.2.1. Heat Flux Effects
3.2.2. Buoyancy Role
4. SCO2 Heat Transfer Efficiency in Microchannels
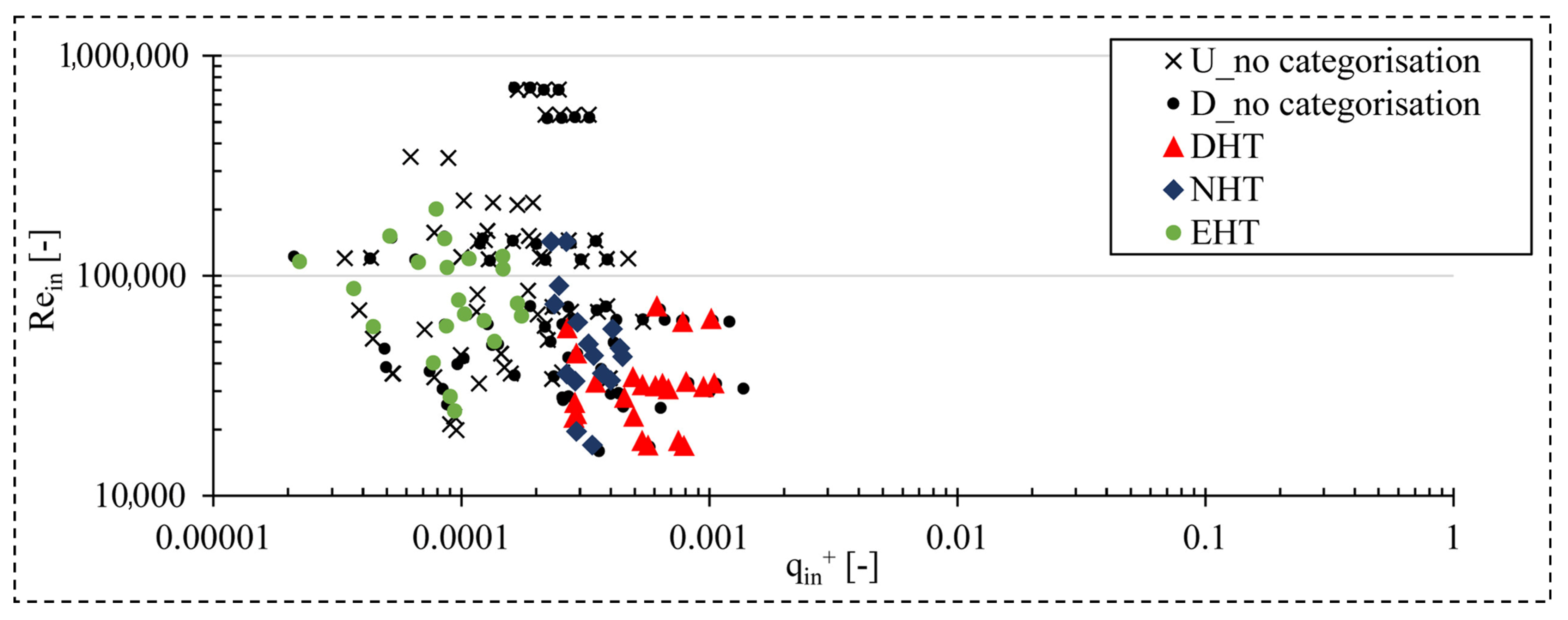
4.1. Heat Transfer Efficiency Evaluation Methods
4.2. Key Factors Affecting the Heat Transfer Efficiency of SCO2
4.3. Heat Transfer Efficiency Optimization Strategies
5. Heat Transfer Deterioration (HTD) in Microchannels
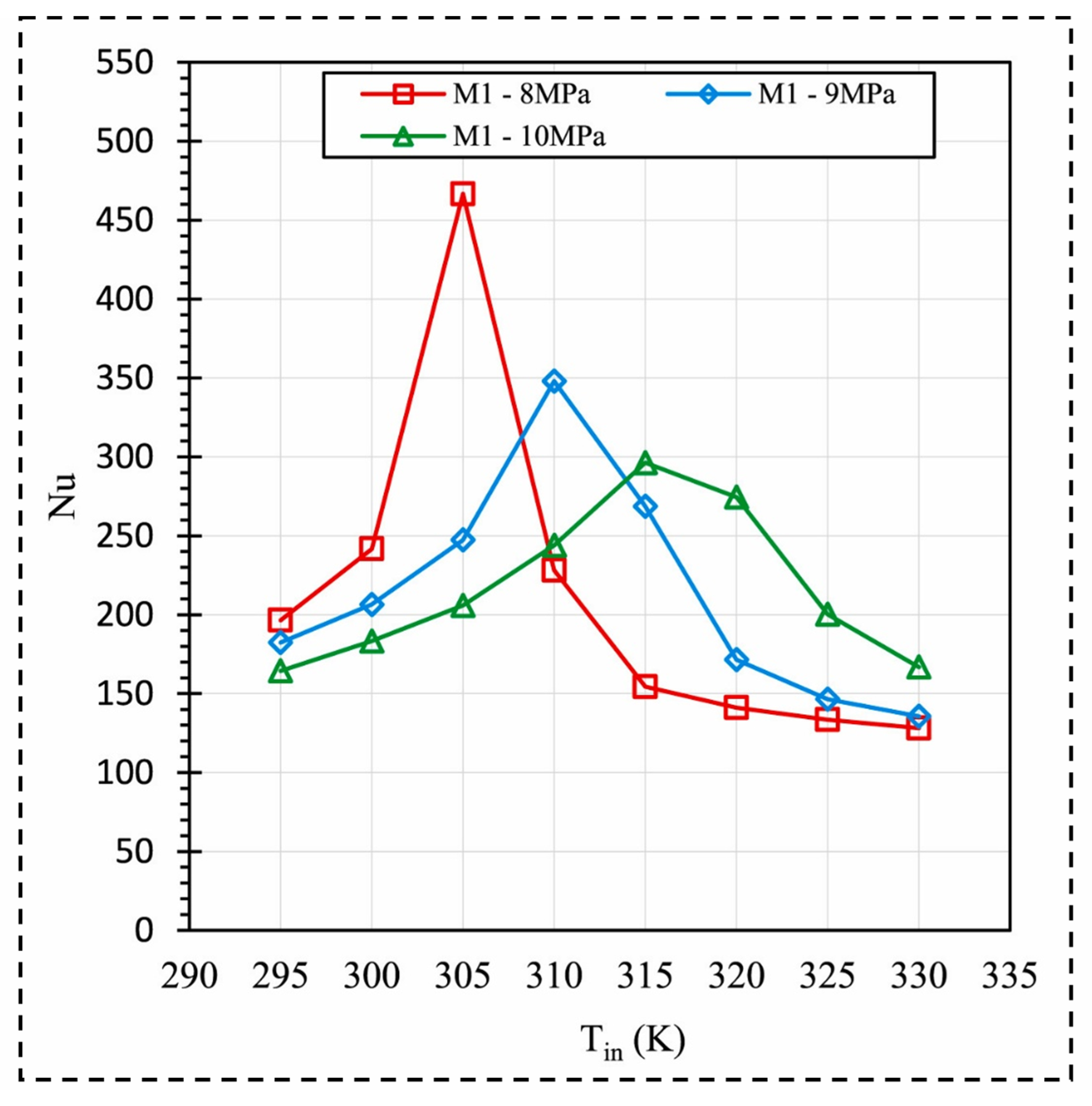
5.1. Mechanisms of HTD in Microchannels
5.2. Factors Influencing HTD
5.3. Mitigation Strategies
5.4. Research Gaps and Future Directions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Greek symbols | |
| Density, kg m−3 | |
| Dynamic viscosity, Pa s | |
| Thermal conductivity, mW mK−1 | |
| Specific heat capacity, kJ kg−1K−1 | |
| Pressure drop, Pa | |
| Darcy friction factor, - | |
| Mass flux, kg m−2 s−1 | |
| Length, m | |
| Inner tube diameter, m | |
| Nusselt number | |
| Convective heat transfer coefficient, W m−2 K−1 | |
| Hydraulic diameter, m | |
| Thermal conductivity, W m−1 K−1 | |
| Heat transfer rate, W | |
| Heat transfer area, m2 | |
| Log-mean temperature difference, K | |
| Average fluid velocity, m s−1 | |
| Reynolds number | |
| Heat flux, W m−2 | |
| Inlet temperature, °C | |
| Acronyms | |
| SCO2 | Supercritical carbon dioxide |
| CO2 | Carbon dioxide |
| HTD | Heat transfer deterioration |
| SH2O | Supercritical water |
| NHT | Normal heat transfer |
| EHT | Enhanced heat transfer |
| CFD | Computational fluid dynamics |
| Nu | Nusselt number |
| CHC | Chang–Hsieh–Chen model |
| SST | Menter model |
| V2F | Behnia–Pareix–Durbin model |
| AKN | Abe–Kondoh–Nagano model |
| Yang–Shih | YS model |
| Abid | AB model |
| MCHS | Microchannel heat sink |
| TVGs | Transverse vortex generators |
| HTC | Heat transfer coefficient |
References
- Maio, D.V.D.; Boccitto, A.; Caruso, G. Supercritical Carbon Dioxide Applications for Energy Conversion Systems. Energy Procedia 2015, 82, 819–824. [Google Scholar] [CrossRef][Green Version]
- Jiang, K.; Shi, J.; Zhao, Q.; Jin, H. Research progress of industrial application based on two-phase flow system of supercritical carbon dioxide and particles. Powder Technol. 2022, 407, 117621. [Google Scholar] [CrossRef]
- Li, Z.; Shi, M.; Shao, Y.; Zhong, W. Supercritical CO2 cycles for nuclear-powered marine propulsion: Preliminary conceptual design and off-design performance assessment. J. Therm. Sci. 2024, 33, 328–347. [Google Scholar] [CrossRef]
- Li, M.; Wang, G.; Xu, J.; Ni, J.; Sun, E. Life cycle assessment analysis and comparison of 1000 MW S-CO2 coal fired power plant and 1000 MW USC water-steam coal-fired power plant. J. Therm. Sci. 2020, 31, 463–484. [Google Scholar] [CrossRef]
- Xia, L.; Li, X.; Song, J.; Ren, X.; Gu, C. Design and analysis of S-CO 2 cycle and radial turbine for SOFC vehicle waste-heat recovery. J. Therm. Sci. 2019, 28, 559–570. [Google Scholar] [CrossRef]
- Uusitalo, A.; Ameli, A.; Turunen-Saaresti, T. Thermodynamic and turbomachinery design analysis of supercritical Brayton cycles for exhaust gas heat recovery. Energy 2019, 167, 60–79. [Google Scholar] [CrossRef]
- Saeed, M.; Berrouk, A.S.; AlShehhi, M.S.; AlWahedi, Y.F. Numerical investigation of the thermohydraulic characteristics of microchannel heat sinks using supercritical CO2 as a coolant. J. Supercrit. Fluids 2021, 176, 105306. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, L.; Wang, X.; Sun, R.; Yuan, P.; Tian, H.; Shu, G. Heat transfer characteristics of supercritical CO2 in horizontal rectangular microchannels. Appl. Therm. Eng. 2023, 220, 119727. [Google Scholar] [CrossRef]
- Xu, X.; Teng, L.; Ran, W.; Wang, Y.; Liu, C. A review of heat transfer deterioration mechanisms and mitigation strategies of supercritical CO2 heat transfer. Int. J. Heat Fluid Flow 2024, 109, 109534. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Liu, C.; Liu, X.; Dang, C. Experimental investigation on the heat transfer characteristics of supercritical CO2 at various mass flow rates in heated vertical-flow tube. Appl. Therm. Eng. 2019, 157, 113687. [Google Scholar] [CrossRef]
- Li, Z.; Tang, G.; Wu, Y.; Zhai, Y.; Xu, J.; Wang, H.; Lu, J. Improved gas heaters for supercritical CO2 Rankine cycles: Considerations on forced and mixed convection heat transfer enhancement. Appl. Energy 2016, 178, 126–141. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Cheng, J.; Li, X.; Cai, W.; Li, Z.; Li, F. A state-of-the-art overview on the developing trend of heat transfer enhancement by single-phase flow at micro scale. Int. J. Heat Mass Transf. 2019, 143, 118476. [Google Scholar] [CrossRef]
- Kruizenga, A.; Li, H.; Anderson, M.; Corradini, M. Supercritical carbon dioxide heat transfer in horizontal semicircular channels. J. Heat Transf. 2012, 134, 081802. [Google Scholar] [CrossRef]
- Pettersen, J.; Rieberer, R.; Munkejord, S.T. Heat transfer and pressure drop for flow of supercritical and subcritical CO2 in microchannel tubes. Nor. Univ. Sci. Technol./SINTEF Energy Res. TR A 2000, 5127, 2000. [Google Scholar]
- Wang, L.; Pan, Y.C.; Lee, J.D.; Fu, B.-R.; Pan, C. Convective heat transfer characteristics of supercritical carbon dioxide in vertical miniature tubes of a uniform heating experimental system. Int. J. Heat Mass Transf. 2021, 167, 120833. [Google Scholar] [CrossRef]
- Jackson, J.; WB, H. Influences of buoyancy on heat transfer to fluids flowing in vertical tubes under turbulent conditions. Inst. Mech. Eng. Conf. Publ. 1979, 2, 613–640. [Google Scholar]
- Habib, M.; Mobarak, A.; Sallak, M.; Abdel Hadi, E.; Affify, R. Experimental investigation of heat transfer and flow over baffles of different heights. J. Heat Transf. 1994, 116, 363–368. [Google Scholar] [CrossRef]
- Singh, R.; Akbarzadeh, A.; Mochizuki, M. Sintered porous heat sink for cooling of high-powered microprocessors for server applications. Int. J. Heat Mass Transf. 2009, 52, 2289–2299. [Google Scholar] [CrossRef]
- Liaw, K.L.; Kurnia, J.C.; Sasmito, A.P. Enhancing supercritical carbon dioxide heat transfer in helical tube heat exchangers with twisted tape inserts: A computational investigation. Int. J. Heat Mass Transf. 2024, 227, 125598. [Google Scholar] [CrossRef]
- Thielens, V.; Demeyer, F.; De Paepe, W. Performance comparison of sCO2 and steam cycles for waste heat recovery based on annual semi-transient modeling under complex industrial constraints. Case Stud. Therm. Eng. 2024, 60, 104691. [Google Scholar] [CrossRef]
- Niu, X.; Gu, Y.; Fan, J.; Yue, G.; Si, H.; Hong, W. Heat transfer characterization of SCO2 in non-uniformly heated rectangular cooling tubes under large mass flow and heat flux conditions. Case Stud. Therm. Eng. 2024, 61, 105150. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, H.; Zhuge, W.; Cai, R.; Yang, M.; Chen, H.; Qian, Y.; Zhang, Y. Flow loss mechanism in a supercritical carbon dioxide centrifugal compressor at low flow rate conditions. J. Therm. Sci. 2024, 33, 114–125. [Google Scholar] [CrossRef]
- Yamamoto, S.; Furusawa, T.; Matsuzawa, R. Numerical simulation of supercritical carbon dioxide flows across critical point. Int. J. Heat Mass Transf. 2011, 54, 774–782. [Google Scholar] [CrossRef]
- Cheng, L.; Xu, J.; Cao, W.; Zhou, K.; Liu, G. Supercritical carbon dioxide heat transfer in horizontal tube based on the Froude number analysis. Energy 2024, 294, 130980. [Google Scholar] [CrossRef]
- Kantharaj, B.; Garvey, S.; Pimm, A. Thermodynamic analysis of a hybrid energy storage system based on compressed air and liquid air. Sustain. Energy Technol. Assess. 2015, 11, 159–164. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z. Heat exchangers for cooling supercritical carbon dioxide and heat transfer enhancement: A review and assessment. Energy Rep. 2021, 7, 4085–4105. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Wang, F.; Ning, X.; Chuanbao, Z.; Zhang, J.; Zhang, C. Factor analysis and mechanism disclosure of supercritical CO2 filtration behavior in tight shale reservoirs. Environ. Sci. Pollut. Res. 2022, 29, 17682–17694. [Google Scholar] [CrossRef] [PubMed]
- Amooey, A.A. A simple correlation to predict thermal conductivity of supercritical carbon dioxide. J. Supercrit. Fluids 2014, 86, 1–3. [Google Scholar] [CrossRef]
- Rao, N.T.; Oumer, A.N.; Jamaludin, U.K. State-of-the-art on flow and heat transfer characteristics of supercritical CO2 in various channels. J. Supercrit. Fluids 2016, 116, 132–147. [Google Scholar] [CrossRef]
- Huang, D.; Wu, Z.; Sunden, B.; Li, W. A brief review on convection heat transfer of fluids at supercritical pressures in tubes and the recent progress. Appl. Energy 2016, 162, 494–505. [Google Scholar] [CrossRef]
- Hendricks, R.C. Correlation of Hydrogen Heat Transfer in Boiling and Supercritical Pressure States. Ars J. 1962, 32, 244–252. [Google Scholar] [CrossRef]
- Zhang, G.; Weng, T.; Xie, R.; Lu, G.; Zhou, L.; Zhao, D.; Hong, G.; Zhang, Y. Experimental study of supercritical carbon dioxide heat transfer deterioration in a vertical tube under high heat flux. Ann. Nucl. Energy 2024, 203, 110522. [Google Scholar] [CrossRef]
- Liu, M.; Liu, S.; Huang, Y.; Zheng, R.; Yuan, H.; Wang, J.; Gong, H.; Wang, Y.; Huang, S. Pool heat transfer studies of near-critical and supercritical carbon dioxide. Int. J. Heat Mass Transf. 2024, 229, 125669. [Google Scholar] [CrossRef]
- Kim, H.; Kim, H.Y.; Song, J.H.; Bae, Y.Y. Heat transfer to supercritical pressure carbon dioxide flowing upward through tubes and a narrow annulus passage. Prog. Nucl. Energy 2008, 50, 518–525. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Lu, J.; Zhang, D.; Zhang, H. Heat transfer to supercritical water in circular tubes with circumferentially non-uniform heating. Appl. Therm. Eng. 2014, 70, 190–200. [Google Scholar] [CrossRef]
- Duffey, R.B.; Pioro, I.L. Experimental heat transfer of supercritical carbon dioxide flowing inside channels (survey). Nucl. Eng. Des. 2005, 235, 913–924. [Google Scholar] [CrossRef]
- Liao, S.M.; Zhao, T.S. An experimental investigation of convection heat transfer to supercritical carbon dioxide in miniature tubes. Int. J. Heat Mass Transf. 2002, 45, 5025–5034. [Google Scholar] [CrossRef]
- Manda, U.; Mazumdar, S.; Peles, Y. Effects of cross-sectional shape on flow and heat transfer of the laminar flow of supercritical carbon dioxide inside horizontal microchannels. Int. J. Therm. Sci. 2024, 201, 108992. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, H.; Yang, J.; Qu, J. Numerical study on fluid flow and heat transfer characteristics of supercritical CO2 in horizontal tube under various non-uniform heating conditions. Int. J. Heat Mass Transf. 2025, 236, 126399. [Google Scholar] [CrossRef]
- Wang, L.; Pan, Y.C.; Der Lee, J.; Wang, Y.; Fu, B.-R.; Pan, C. Experimental investigation in the local heat transfer of supercritical carbon dioxide in the uniformly heated horizontal miniature tubes. Int. J. Heat Mass Transf. 2020, 159, 120136. [Google Scholar] [CrossRef]
- Yoon, S.H.; Kim, J.H.; Hwang, Y.W.; Kim, M.S.; Min, K.; Kim, Y. Heat transfer and pressure drop characteristics during the in-tube cooling process of carbon dioxide in the supercritical region. Int. J. Refrig. 2003, 26, 857–864. [Google Scholar] [CrossRef]
- Cheng, L.; Xu, J.; Wang, Q.; Dong, X. The influence of tube diameter parameters on the flow resistance and heat transfer characteristics of supercritical CO2 in horizontal tubes. Appl. Therm. Eng. 2024, 241, 122361. [Google Scholar] [CrossRef]
- Yan, C.; Shi, J.; Zhang, S.; Zhang, X.; Chen, Q. Investigation on heat transfer of supercritical CO2/Xe mixture crossing pseudo-critical temperature cooled in a horizontal circular tube. Appl. Therm. Eng. 2024, 257, 124245. [Google Scholar] [CrossRef]
- Manda, U.; Parahovnik, A.; Mazumdar, S.; Peles, Y. Heat transfer characteristics of turbulent flow of supercritical carbon dioxide (sCO2) in a short-heated microchannel. Int. J. Therm. Sci. 2023, 192, 108389. [Google Scholar] [CrossRef]
- Derby, M.; Lee, H.J.; Peles, Y.; Jensen, M.K. Condensation heat transfer in square, triangular, and semi-circular mini-channels. Int. J. Heat Mass Transf. 2012, 55, 187–197. [Google Scholar] [CrossRef]
- Wang, H.S.; Rose, J.W. A theory of film condensation in horizontal noncircular section microchannels. J. Heat Transf. 2005, 127, 1096–1105. [Google Scholar] [CrossRef]
- Liu, Z.-B.; He, Y.-L.; Yang, Y.-F.; Fei, J.-Y. Experimental study on heat transfer and pressure drop of supercritical CO2 cooled in a large tube. Appl. Therm. Eng. 2014, 70, 307–315. [Google Scholar] [CrossRef]
- Son, C.-H.; Park, S.-J. An experimental study on heat transfer and pressure drop characteristics of carbon dioxide during gas cooling process in a horizontal tube. Int. J. Refrig. 2006, 29, 539–546. [Google Scholar] [CrossRef]
- Yun, R.; Hwang, Y.; Radermacher, R. Convective gas cooling heat transfer and pressure drop characteristics of supercritical CO2/oil mixture in a minichannel tube. Int. J. Heat Mass Transf. 2007, 50, 4796–4804. [Google Scholar] [CrossRef]
- Wang, L.; Pan, Y.C.; Lee, J.D.; Wang, Y.; Fu, B.R.; Pan, C. Experimental investigation in the pressure drop characteristics of supercritical carbon dioxide in the uniformly heated horizontal miniature tubes. J. Supercrit. Fluids 2020, 162, 104839. [Google Scholar] [CrossRef]
- Manda, U.; Mazumdar, S.; Peles, Y. Effects of buoyancy in a laminar flow of supercritical carbon dioxide in a horizontal microchannel at different gravities. Int. Commun. Heat Mass Transf. 2024, 150, 107195. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S.; Shao, Y.; Zhong, W. Experimental study on convective heat transfer characteristics of supercritical carbon dioxide in a vertical tube with low mass flux. Appl. Therm. Eng. 2023, 230, 120798. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Zhang, Y.; Zhao, C.-R.; Shi, R.-F. Convection heat transfer of CO2 at supercritical pressures in a vertical mini tube at relatively low reynolds numbers. Exp. Therm. Fluid Sci. 2008, 32, 1628–1637. [Google Scholar] [CrossRef]
- Xu, R.-N.; Luo, F.; Jiang, P.-X. Buoyancy effects on turbulent heat transfer of supercritical CO2 in a vertical mini-tube based on continuous wall temperature measurements. Int. J. Heat Mass Transf. 2017, 110, 576–586. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, X.; Chen, Y.; Luo, X. Flow and heat transfer instability of supercritical carbon dioxide in a vertical heated tube. J. Therm. Sci. 2023, 32, 1477–1486. [Google Scholar] [CrossRef]
- Theologou, K.; Mertz, R.; Starflinger, J. Experimental investigation of the heat transfer characteristics of CO2 at supercritical pressures flowing in heated vertical pipes. Int. J. Heat Mass Transf. 2025, 236, 126367. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Zhao, C.-R.; Shi, R.-F.; Chen, Y.; Ambrosini, W. Experimental and numerical study of convection heat transfer of CO2 at super-critical pressures during cooling in small vertical tube. Int. J. Heat Mass Transf. 2009, 52, 4748–4756. [Google Scholar] [CrossRef]
- Van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- McEligot, D.; Coon, C.; Perkins, H. Relaminarization in tubes. Int. J. Heat Mass Transf. 1970, 13, 431–433. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, D.; Chen, Z.; Gao, X.; Ren, F.; Han, W. Performance analysis and evaluation of a supercritical CO2 Rankine cycle coupled with an absorption refrigeration cycle. J. Therm. Sci. 2020, 29, 1036–1052. [Google Scholar] [CrossRef]
- Guo, J. Design analysis of supercritical carbon dioxide recuperator. Appl. Energy 2016, 164, 21–27. [Google Scholar] [CrossRef]
- Hung, T.-C.; Huang, Y.-X.; Yan, W.-M. Thermal performance analysis of porous-microchannel heat sinks with different configuration designs. Int. J. Heat Mass Transf. 2013, 66, 235–243. [Google Scholar] [CrossRef]
- Xue, C.A.O.; Abed, A.M.; Singh, P.K.; Formanova, S.; Elmasry, Y.; Mahariq, I. Numerical study on thermal and hydraulic performance of supercritical CO2 flowing in a microchannel heat sink with porous substrates. Case Stud. Therm. Eng. 2024, 61, 105028. [Google Scholar] [CrossRef]
- Huang, H.; Zhai, Y.; Li, Z.; Wang, H. Thermo-hydraulic characteristics and structural optimization of supercritical CO2-cooled microchannel heat sink. Int. Commun. Heat Mass Transf. 2024, 154, 107438. [Google Scholar] [CrossRef]
- Zhai, Y.; Li, Z.; Wang, H.; Xu, J. Analysis of field synergy principle and the relationship between secondary flow and heat transfer in double-layered microchannels with cavities and ribs. Int. J. Heat Mass Transf. 2016, 101, 190–197. [Google Scholar] [CrossRef]
- Ghahremannezhad, A.; Vafai, K. Thermal and hydraulic performance enhancement of microchannel heat sinks utilizing porous substrates. Int. J. Heat Mass Transf. 2018, 122, 1313–1326. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Hwang, C.-Z. Calculation of turbulent flow and heat transfer in a porous-baffled channel. Int. J. Heat Mass Transf. 2003, 46, 771–780. [Google Scholar] [CrossRef]
- Sohankar, A. Heat transfer augmentation in a rectangular channel with a vee-shaped vortex generator. Int. J. Heat Fluid Flow 2007, 28, 306–317. [Google Scholar] [CrossRef]
- Valencia, A. Heat transfer enhancement due to self-sustained oscillating transverse vortices in channels with periodically mounted rectangular bars. Int. J. Heat Mass Transf. 1999, 42, 2053–2062. [Google Scholar] [CrossRef]
- Moosavi, R.; Banihashemi, M.; Lin, C.-X.; Abel Chuang, P.-Y. Combined effects of a microchannel with porous media and transverse vortex generators (TVG) on convective heat transfer performance. Int. J. Therm. Sci. 2021, 166, 106961. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Jiang, Q.; Li, Y.; Liu, Q.; Xu, J. A new structure of cooling wall tube for supercritical CO2 coal-fired power plants. J. Therm. Sci. 2023, 32, 1239–1250. [Google Scholar] [CrossRef]
- Eze, C.; Khan, S.A.; Ting Lau, K.; Ahmad, S.; Chen, L.; Wei, W.; Zhao, J. Numerical study on the heat transfer deterioration and its mitigations for supercritical CO2 flowing in a horizontal miniature tube. Ann. Nucl. Energy 2021, 151, 107982. [Google Scholar] [CrossRef]
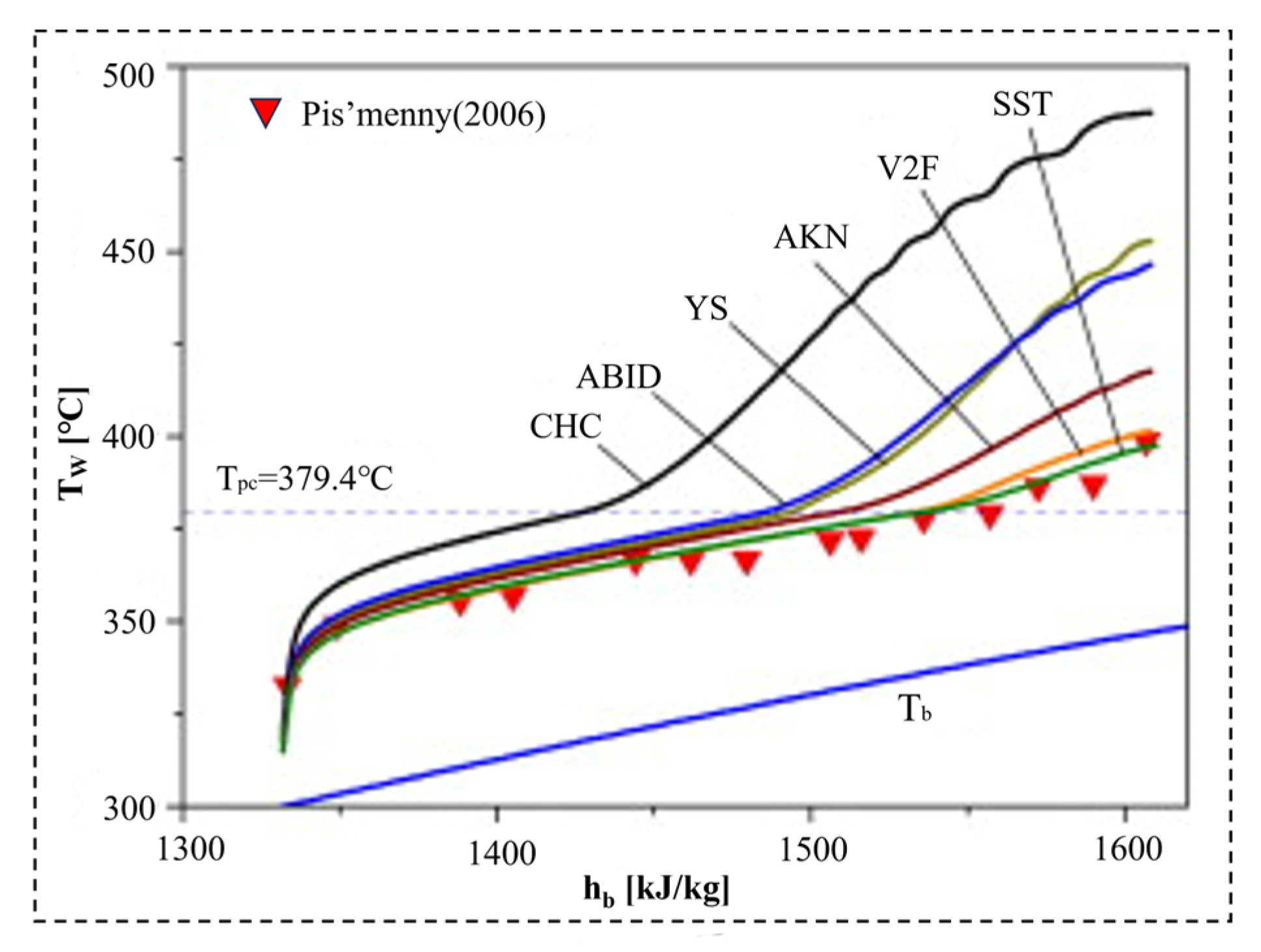
- He, S.; Kim, W.S.; Bae, J.H. Assessment of performance of turbulence models in predicting supercritical pressure heat transfer in a vertical tube. Int. J. Heat Mass Transf. 2008, 51, 4659–4675. [Google Scholar] [CrossRef]
- Wen, Q.L.; Gu, H.Y. Numerical simulation of heat transfer deterioration phenomenon in supercritical water through vertical tube. Ann. Nucl. Energy 2010, 37, 1272–1280. [Google Scholar] [CrossRef]
- Chang, K.-C.; Hsieh, W.; Chen, C. A modified low-Reynolds-number turbulence model applicable to recirculating flow in pipe expansion. J. Fluids Eng. 1995, 117, 417–423. [Google Scholar] [CrossRef]
- Abid, R. Evaluation of two-equation turbulence models for predicting transitional flows. Int. J. Eng. Sci. 1993, 31, 831–840. [Google Scholar] [CrossRef]
- Yang, Z.; Shih, T. A new time scale based k-epsilon model for near wall turbulence. AIAA J. 1993, 31, 1191–1198. [Google Scholar] [CrossRef]
- Abe, K.; Kondoh, T.; Nagano, Y. A new turbulence model for predicting fluid flow and heat transfer in separating and reattaching flows—I. Flow field calculations. Int. J. Heat Mass Transf. 1994, 37, 139–151. [Google Scholar] [CrossRef]
- Behnia, M.; Parneix, S.; Durbin, P.A. Prediction of heat transfer in an axisymmetric turbulent jet impinging on a flat plate. Int. J. Heat Mass Transf. 1998, 41, 1845–1855. [Google Scholar] [CrossRef]
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Kurganov, V.A.; Kaptilnyi, A.G. Flow structure and turbulent transport of a supercritical pressure fluid in a vertical heated tube under the conditions of mixed convection. Experimental data. Int. J. Heat Mass Transf. 1993, 36, 3383–3392. [Google Scholar] [CrossRef]
- Petukhov, B. Heat transfer in a single-phase medium at near-critical state parameters(Heat transfer in single phase medium at near critical state parameters). Teplofiz. Vysok. Temp. 1968, 6, 732–745. [Google Scholar]
- Song, J.H.; Kim, H.Y.; Kim, H.; Bae, Y.Y. Heat transfer characteristics of a supercritical fluid flow in a vertical pipe. J. Supercrit. Fluids 2008, 44, 164–171. [Google Scholar] [CrossRef]
- Zahlan, H.; Groeneveld, D.; Tavoularis, S. Measurements of convective heat transfer to vertical upward flows of CO2 in circular tubes at near-critical and supercritical pressures. Nucl. Eng. Des. 2015, 289, 92–107. [Google Scholar] [CrossRef]
- Zhao, C.-R.; Zhang, Z.; Jiang, P.-X.; Xu, R.-N.; Bo, H.-L. Influence of channel scale on the convective heat transfer of CO2 at supercritical pressure in vertical tubes. Int. J. Heat Mass Transf. 2018, 126, 201–210. [Google Scholar] [CrossRef]
- Oh, H.-K.; Son, C.-H. New correlation to predict the heat transfer coefficient in-tube cooling of supercritical CO2 in horizontal macro-tubes. Exp. Therm. Fluid Sci. 2010, 34, 1230–1241. [Google Scholar] [CrossRef]
- Kline, N.; Feuerstein, F.; Tavoularis, S. Onset of heat transfer deterioration in vertical pipe flows of CO2 at supercritical pressures. Int. J. Heat Mass Transf. 2018, 118, 1056–1068. [Google Scholar] [CrossRef]
- Bae, Y.-Y.; Kim, H.-Y.; Kang, D.-J. Forced and mixed convection heat transfer to supercritical CO2 vertically flowing in a uniformly-heated circular tube. Exp. Therm. Fluid Sci. 2010, 34, 1295–1308. [Google Scholar] [CrossRef]
- Luo, X.; Yang, Z.-N.; Zhang, J.; Chen, W.; Chyu, M. Effect of guide vane on pressure loss and heat transfer characteristics of supercritical CO2 in u-shaped channel. J. Therm. Sci. 2022, 31, 701–711. [Google Scholar] [CrossRef]
- Du, X.; Zhu, X.; Yu, X.; Wu, F.; Qiu, Q. Heat transfer deterioration and visualized flow state of supercritical CO2 in a vertical non-circular channel. Nucl. Eng. Des. 2022, 386, 111574. [Google Scholar] [CrossRef]
- He, S.; Jiang, P.-X.; Xu, Y.-J.; Shi, R.-F.; Kim, W.S.; Jackson, J.D. A computational study of convection heat transfer to CO2 at supercritical pressures in a vertical mini tube. Int. J. Therm. Sci. 2005, 44, 521–530. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Yan, C.; Wu, W.; Gao, E. Numerical Investigation on Characteristics of Supercritical CO2 Heat Transfer in Vertical Circular Tubes with Circumferentially Half-Side Heating. J. Therm. Sci. 2024, 33, 1744–1756. [Google Scholar] [CrossRef]


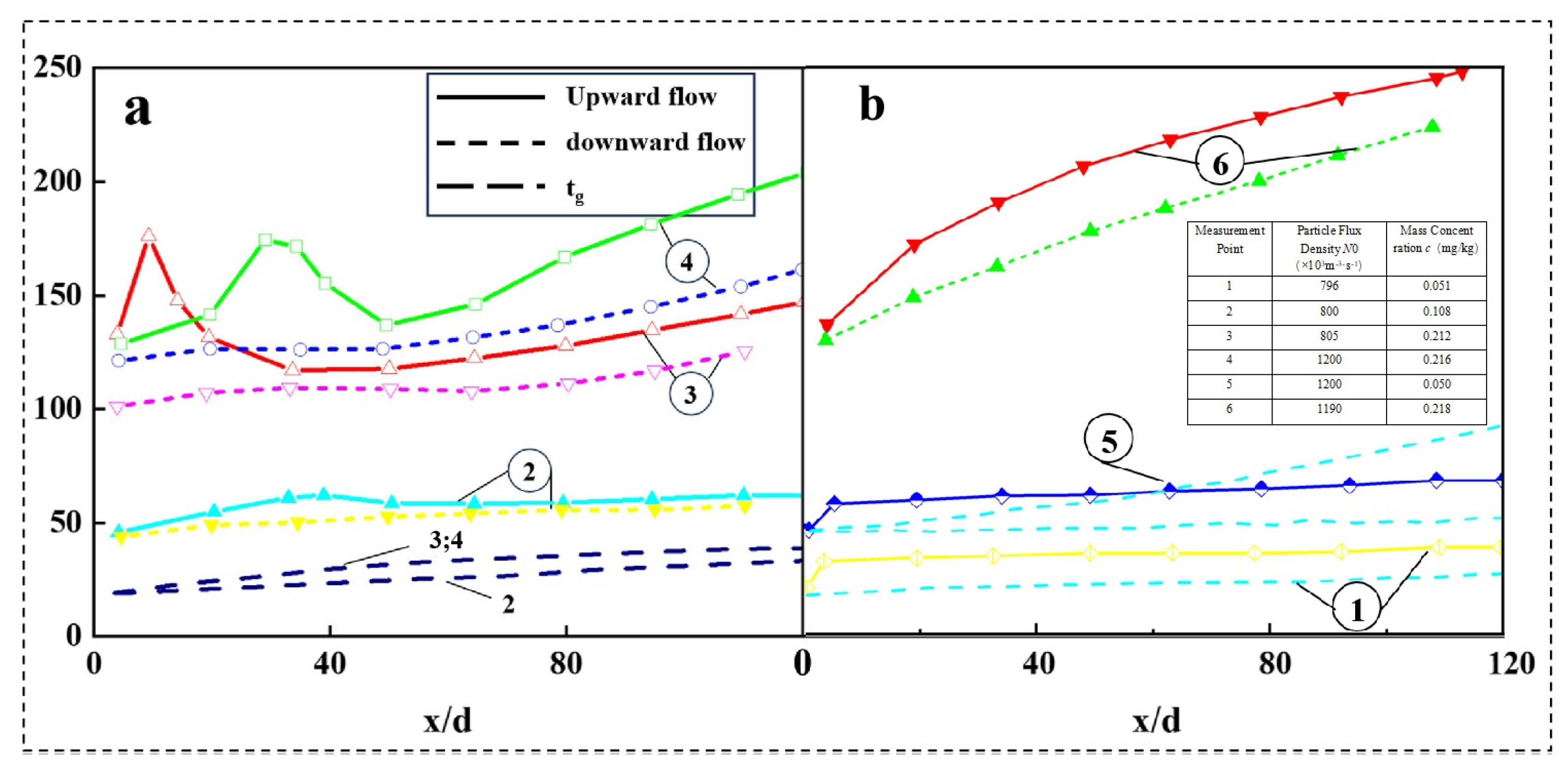
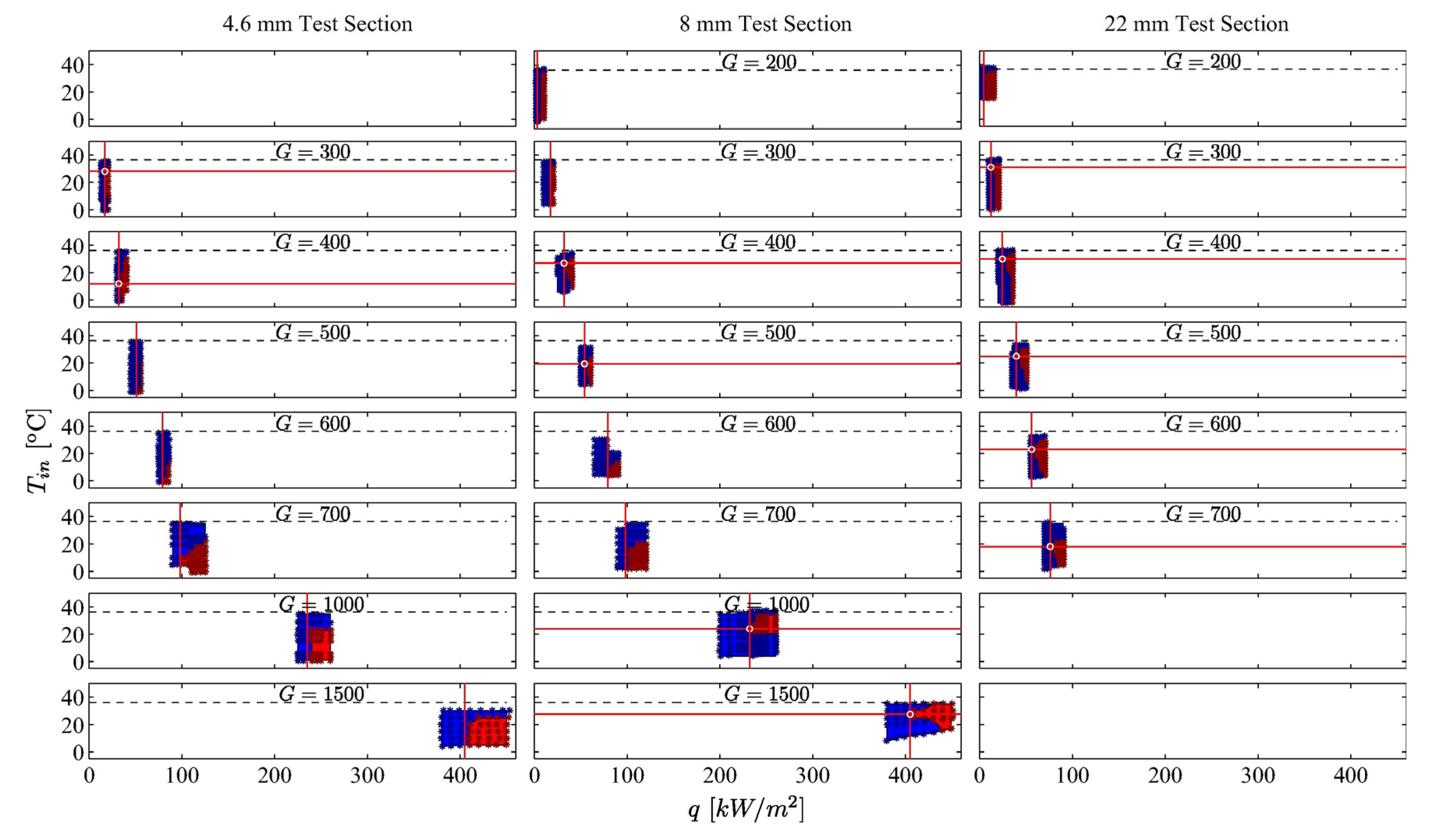
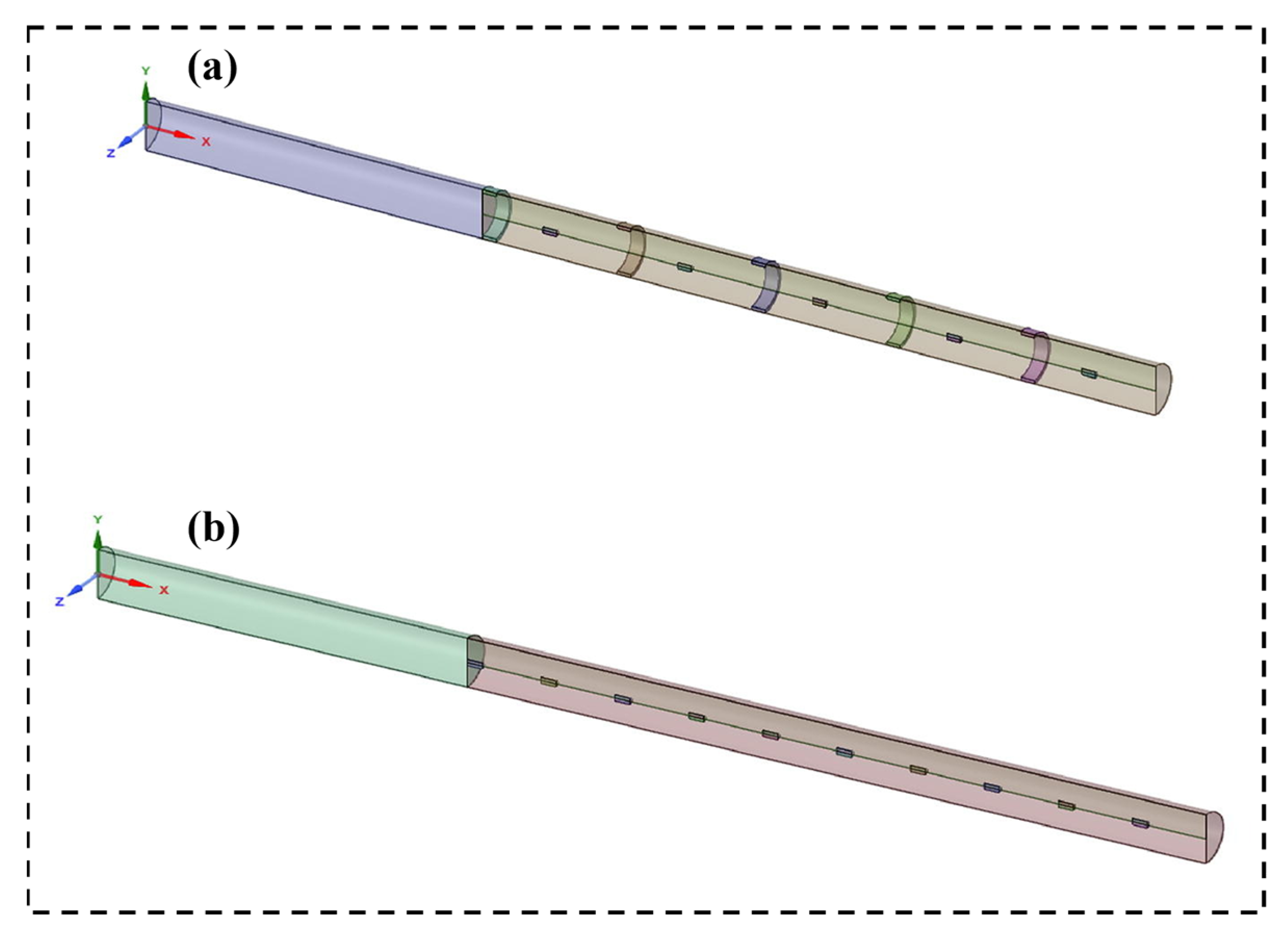

| Reference | Inner Diameter (mm) | Mass Flux (kg∙m−2∙s−1) | Inlet Pressure (MPa) | Heat Flux (kW∙m−2) | Inlet Temperature (K) | Total Length (mm) | Heated Length (mm) |
|---|---|---|---|---|---|---|---|
| Manda et al. [38] | 0.1 | 1.0 × 10−6–4.7 × 10−6 | 8, 9, and 10 | \ | 295 | 27 | 25 |
| Yang et al. [39] | 10 | 300 | 8 | 20–60 | 300–320 | 2000 | 1000 |
| Wang et al. [40] | 1.0, 0.75, and 0.5 | 848.8 | 7.66–9.00 | 124.8–130.8 | 304.1, and 303.9 | 200 | 170 |
| Yoon et al. [41] | 7.73 | 239–1337, and 225 | 7.5–8.8 | 20 | 323–353 | 500 | 250 |
| Chen et al. [42] | 8, 10, and 12 | 509.23–1267.34 | 7.57–20.32 | 91.91–410.43 | 300 | 2800 | 2000 |
| Yan et al. [43] | 8 | 280 | 8.3 | −50 | 295–355 | 3080 | 2600 |
| Manda et al. [44] | 0.69 | 1170 | 7.84 | 20.18, 29.69, 34.84, 43.4 and 48.88 | 295.65 | 14.08 | 5.84 |
| Reference | Inner Diameter (mm) | Mass Flux (kg∙m−2∙s−1) | Inlet Pressure (MPa) | Heat Flux (kW∙m−2) | Inlet Temperature (K) | Flow Direction |
|---|---|---|---|---|---|---|
| Wang et al. [15] | 0.5, 0.75, and 1.0 | 58.1, 78.2, and 98.2 | 7.66–9.00 | 21.7–168.4, 32.7-225.3, and 42.3–353.7 | 303.8–304.0, 303.8–304.0 and 303.9–304.0 | upward and downward |
| Li et al. [52] | 10 | 100–350 | 7.4–10 | 10–130 | 323–548 | upward and downward |
| Jiang et al. [53] | 0.27 | 0.12 | 8.6 | 30–113 | 303 | upward and downward |
| Xu et al. [54] | 0.953 | 255–685 | 7.6–9.5 | 12–63 | 293–296.5 | upward and downward |
| Liao et al. [37] | 0.70, 1.40, and 2.16 | 0.02–0.2 | 7.4–12 | 1 × 104–2 × 105 | 293–383 | horizontal, upward |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Liu, R.; Xiong, X.; Li, X.; Yin, A.; Han, R.; Zhang, J.; Liu, Z.; Zhi, K. Key Factors, Degradation Mechanisms, and Optimization Strategies for SCO2 Heat Transfer in Microchannels: A Review. Energies 2025, 18, 3864. https://doi.org/10.3390/en18143864
Guo L, Liu R, Xiong X, Li X, Yin A, Han R, Zhang J, Liu Z, Zhi K. Key Factors, Degradation Mechanisms, and Optimization Strategies for SCO2 Heat Transfer in Microchannels: A Review. Energies. 2025; 18(14):3864. https://doi.org/10.3390/en18143864
Chicago/Turabian StyleGuo, Lianghui, Ran Liu, Xiaoqin Xiong, Xinzhe Li, Aoxiang Yin, Runyao Han, Jiahao Zhang, Zhuoqian Liu, and Keke Zhi. 2025. "Key Factors, Degradation Mechanisms, and Optimization Strategies for SCO2 Heat Transfer in Microchannels: A Review" Energies 18, no. 14: 3864. https://doi.org/10.3390/en18143864
APA StyleGuo, L., Liu, R., Xiong, X., Li, X., Yin, A., Han, R., Zhang, J., Liu, Z., & Zhi, K. (2025). Key Factors, Degradation Mechanisms, and Optimization Strategies for SCO2 Heat Transfer in Microchannels: A Review. Energies, 18(14), 3864. https://doi.org/10.3390/en18143864






