Open-Switch Fault Diagnosis for Grid-Tied HANPC Converters Using Generalized Voltage Residuals Model and Current Polarity in Flexible Distribution Networks
Abstract
1. Introduction
2. Characteristics Analysis of HANPC Converter in Faulty Conditions
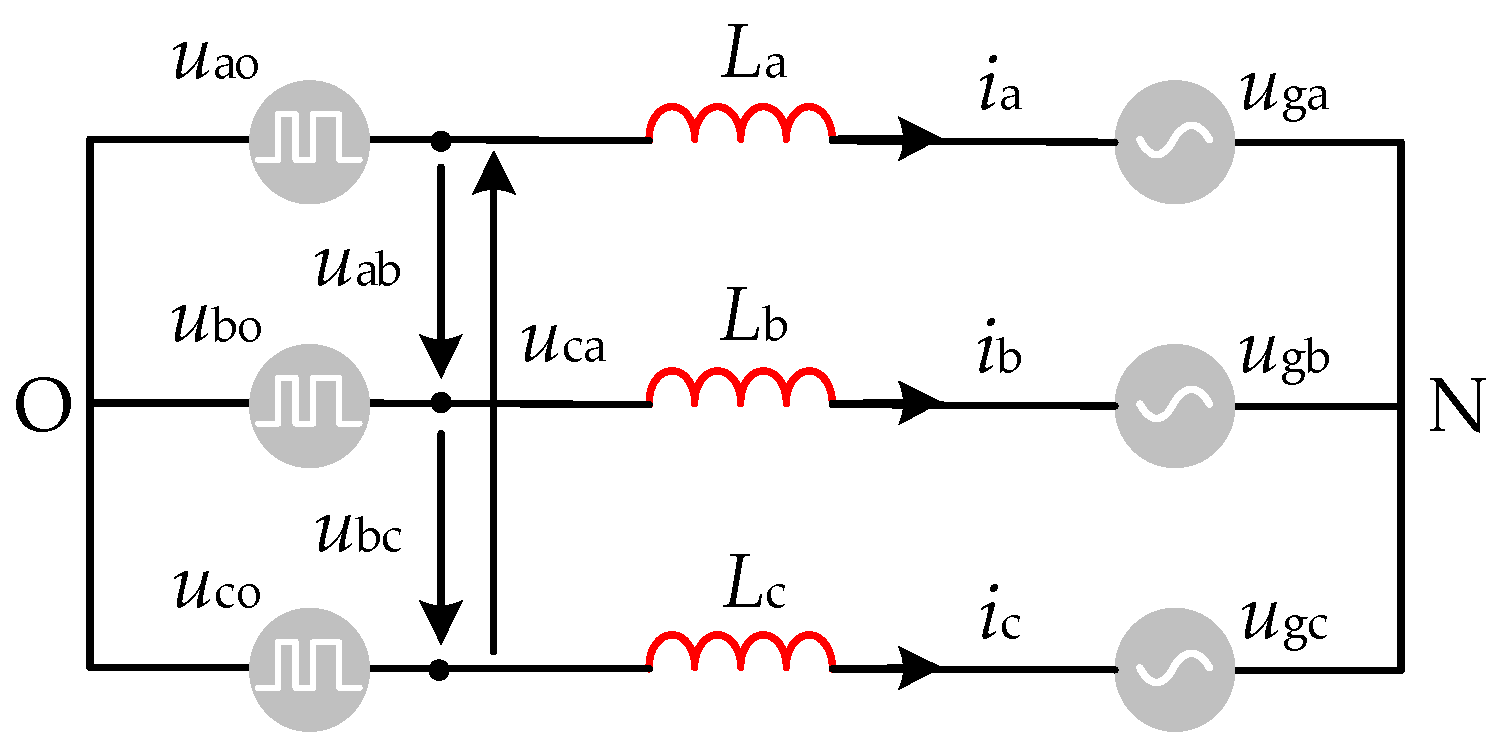
2.1. Modulation Description for HANPC
2.2. Effect of the Fault on Operation Mode of the Converter
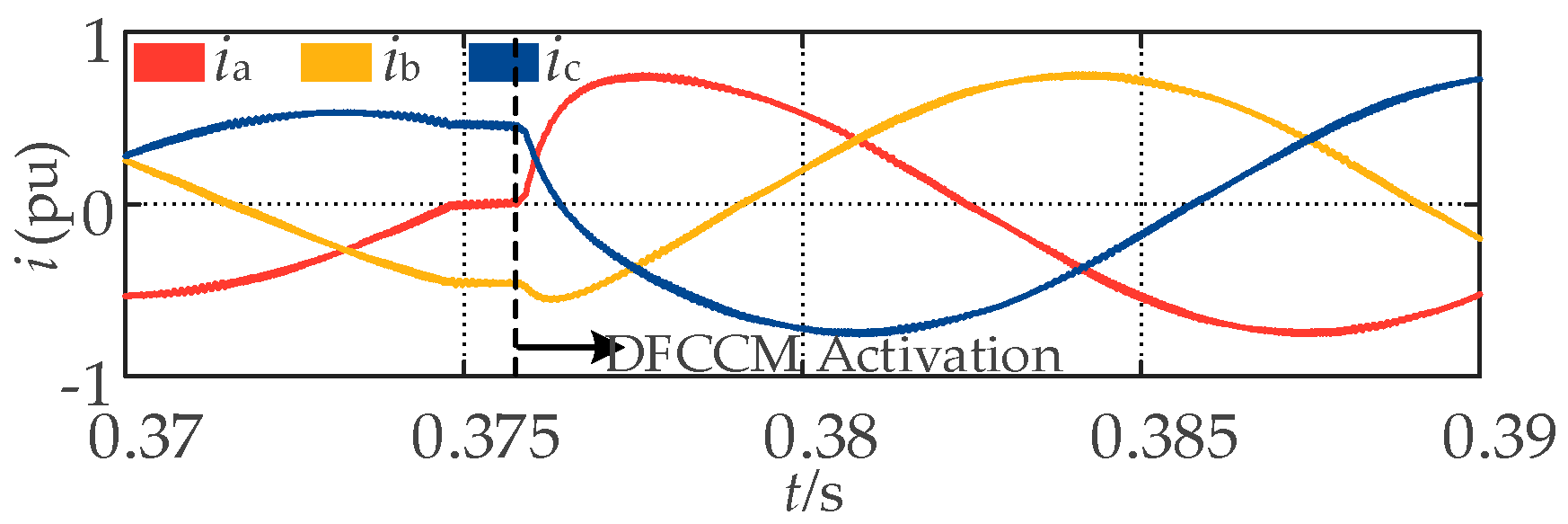
2.3. Behavior of Varying Electrical Quantities
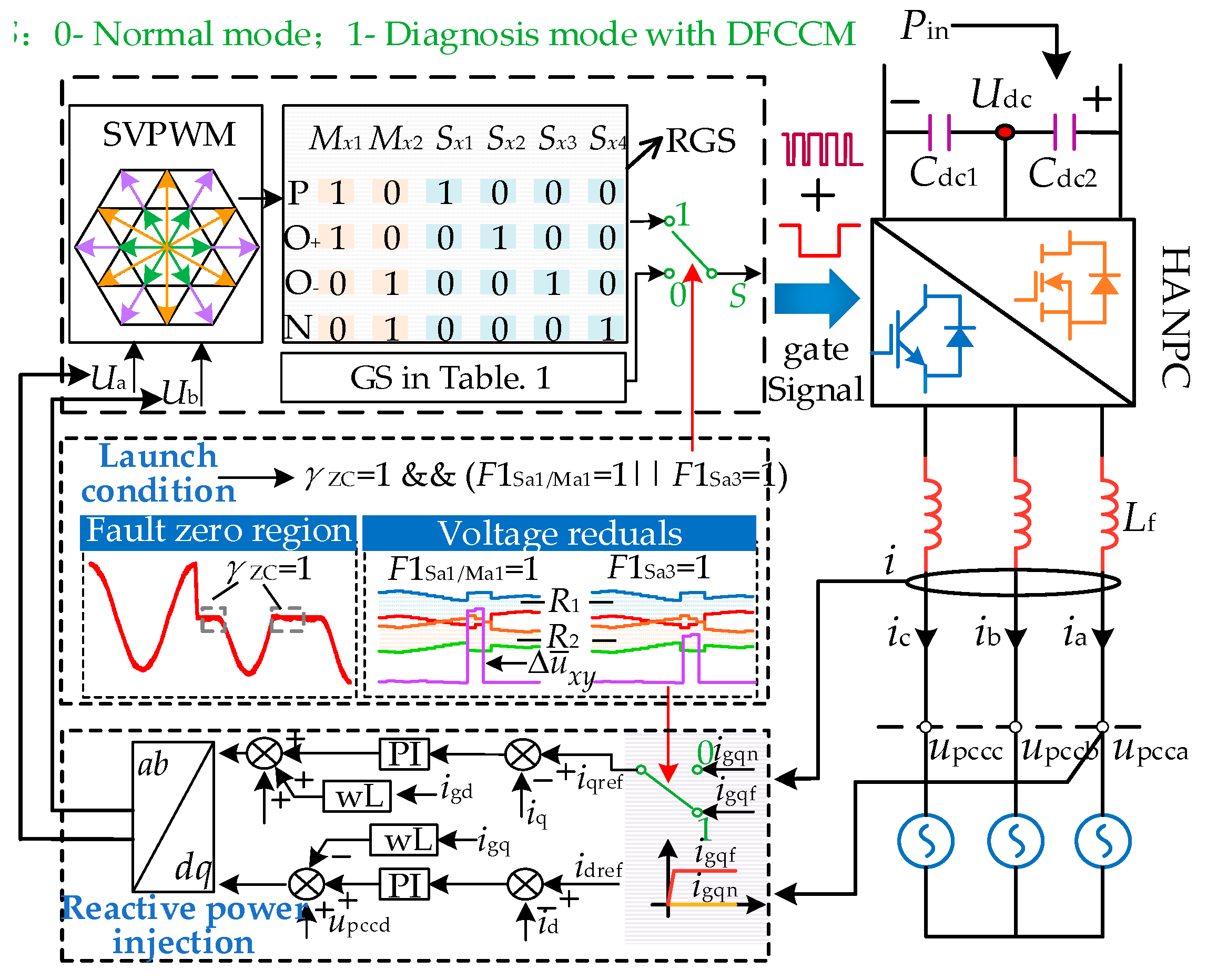
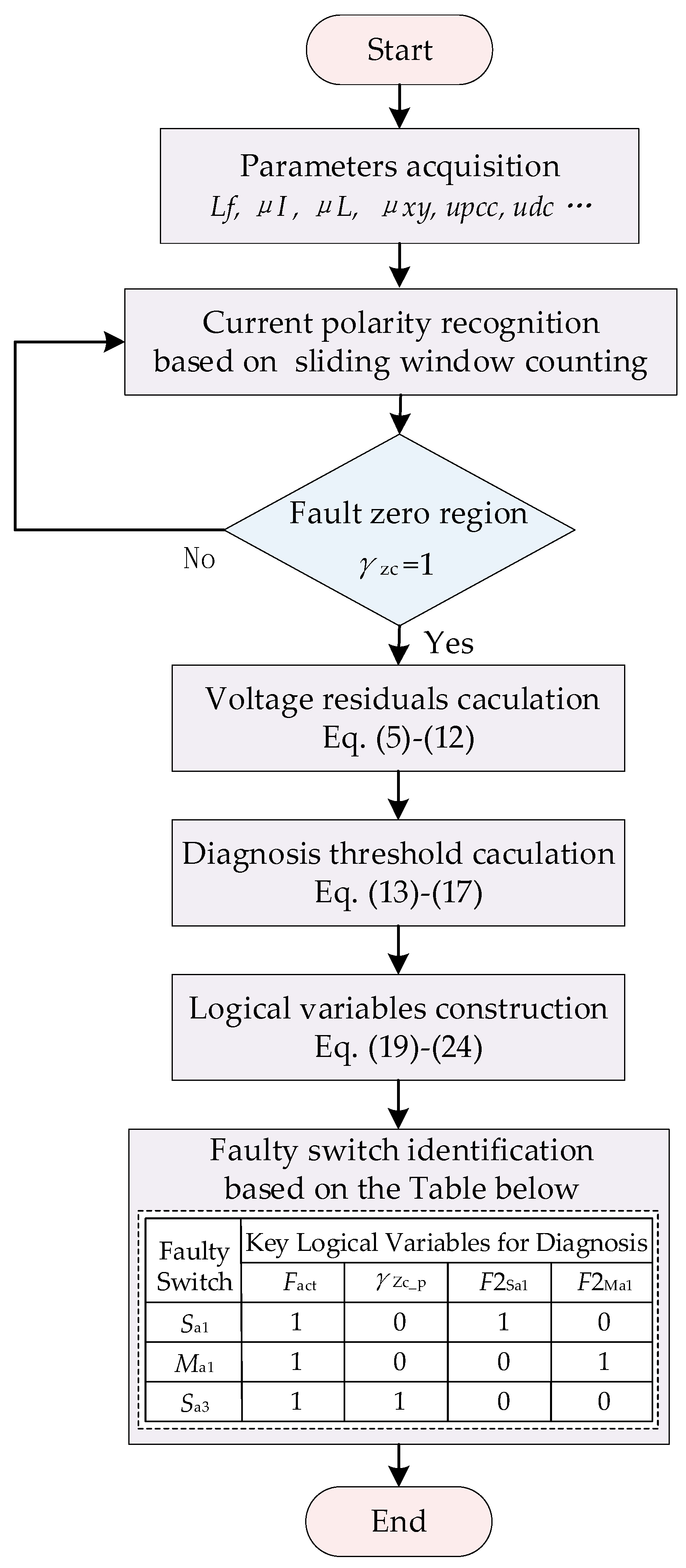
3. The Proposed Fault Diagnosis Method
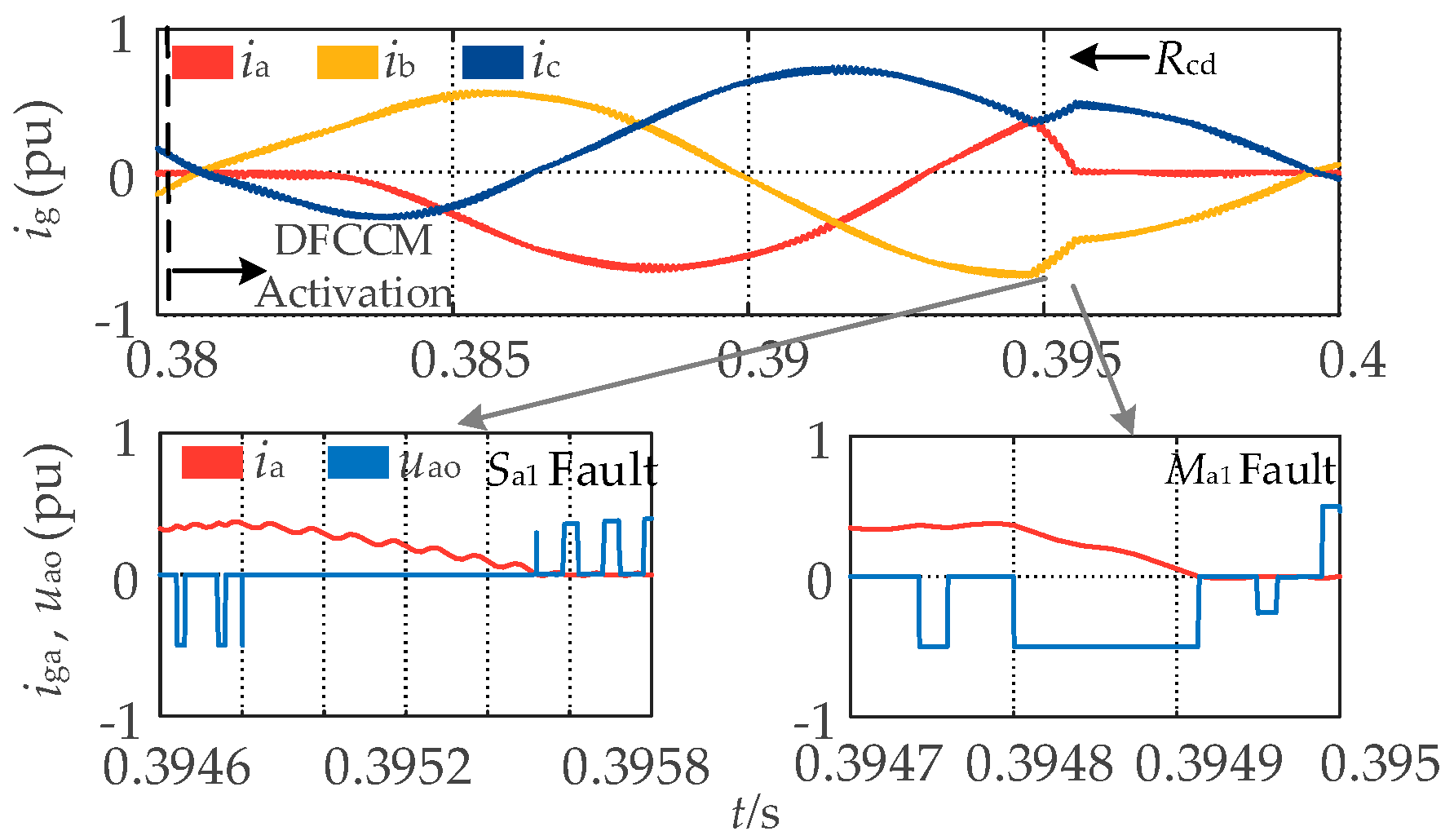
3.1. Behavior of Varying Electrical Quantities with DFCCM
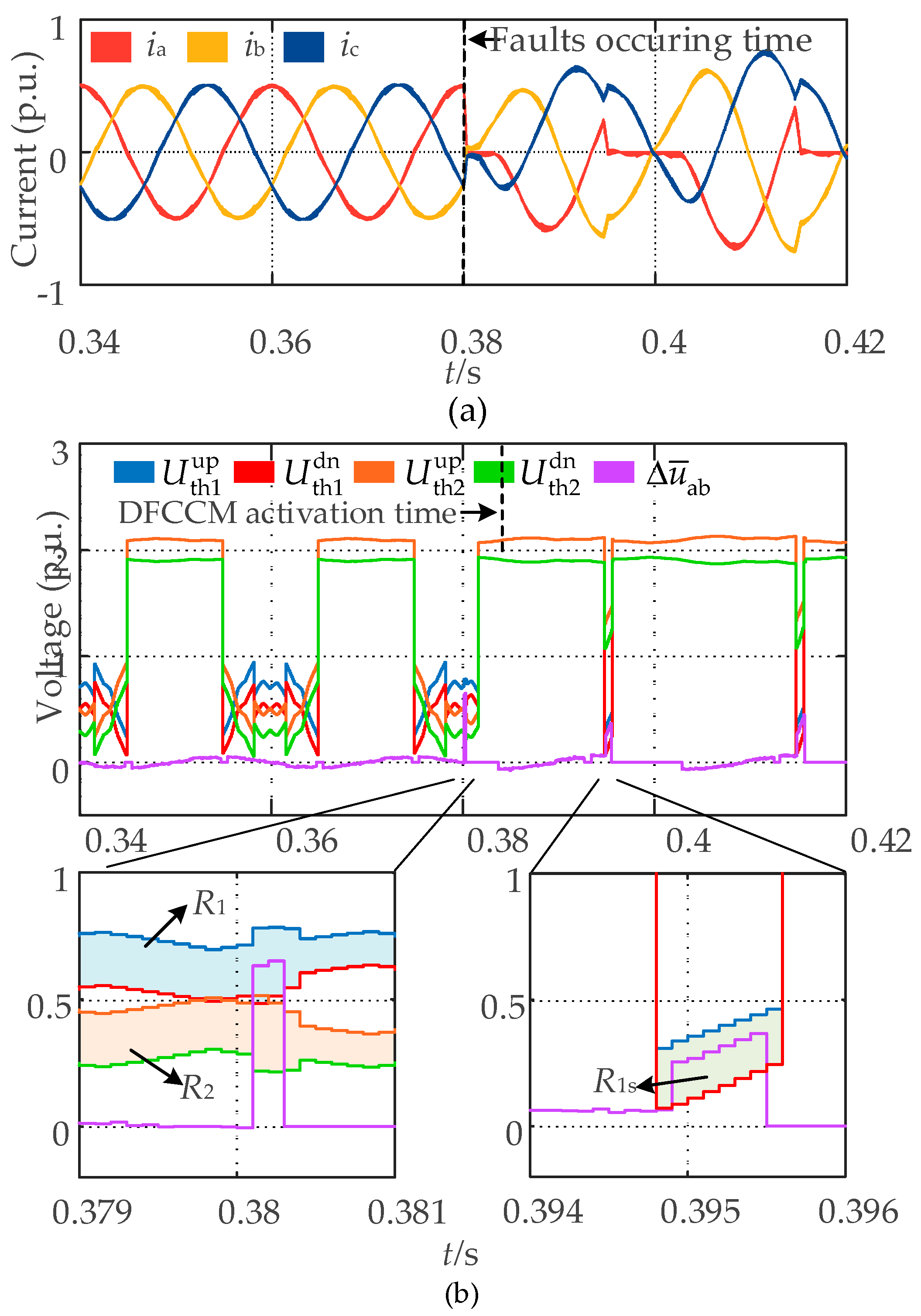
3.2. Generalized Voltage Residuals Model Based on the Variation of Pulse Equivalent Area
- (1)
- The variation in pulse equivalent area before and after the switch OC fault
- (2)
- Generalized voltage residuals model
3.3. Current Polarity Recognition
3.4. Threshold Selection
- (1)
- Adaptive voltage threshold
- (2)
- Zero current threshold
- (3)
- Counting threshold and the length of the sliding window
3.5. Fault Location Criterion
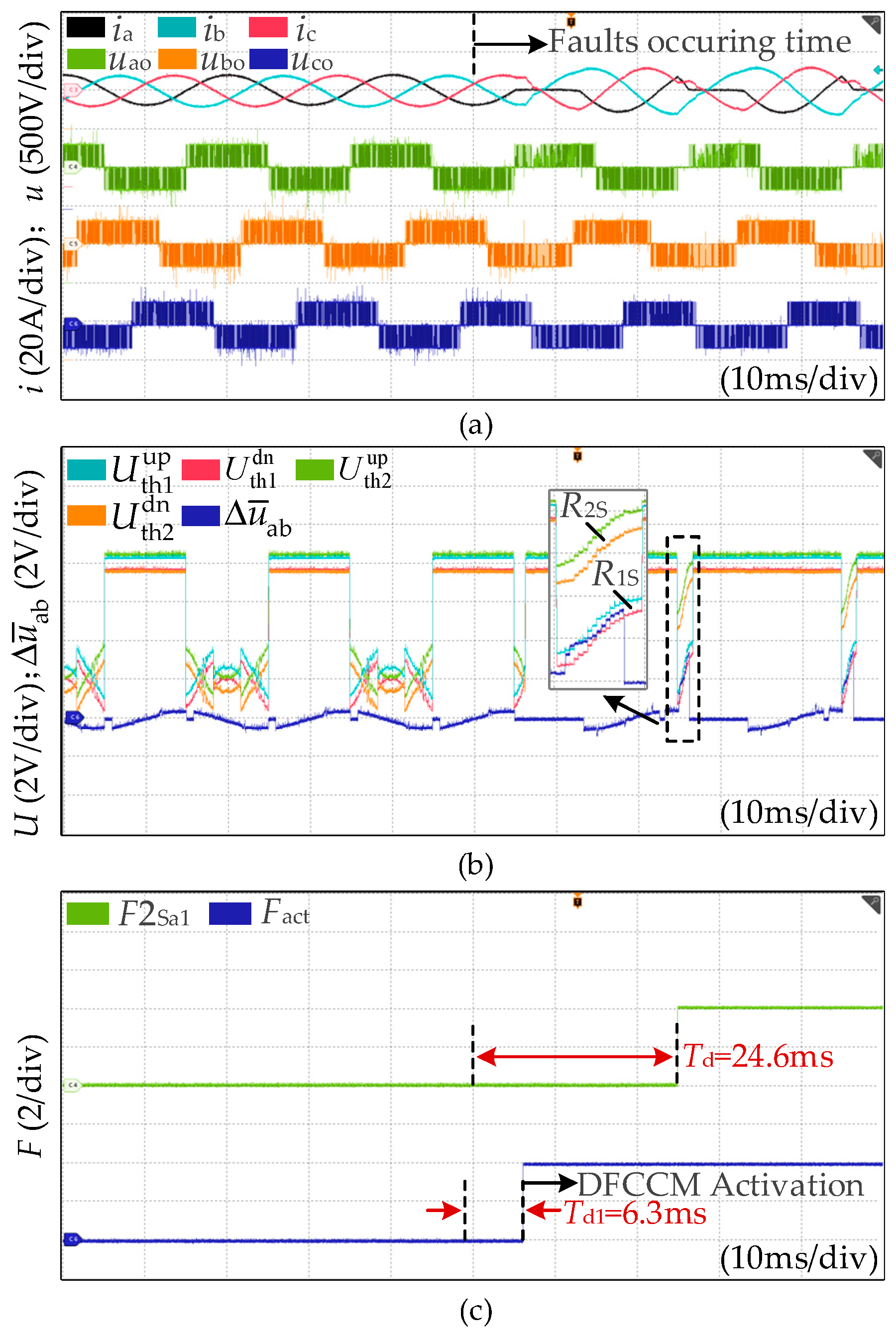
4. Experimental Results
4.1. Effectiveness Verification of Proposed Method
- (1)
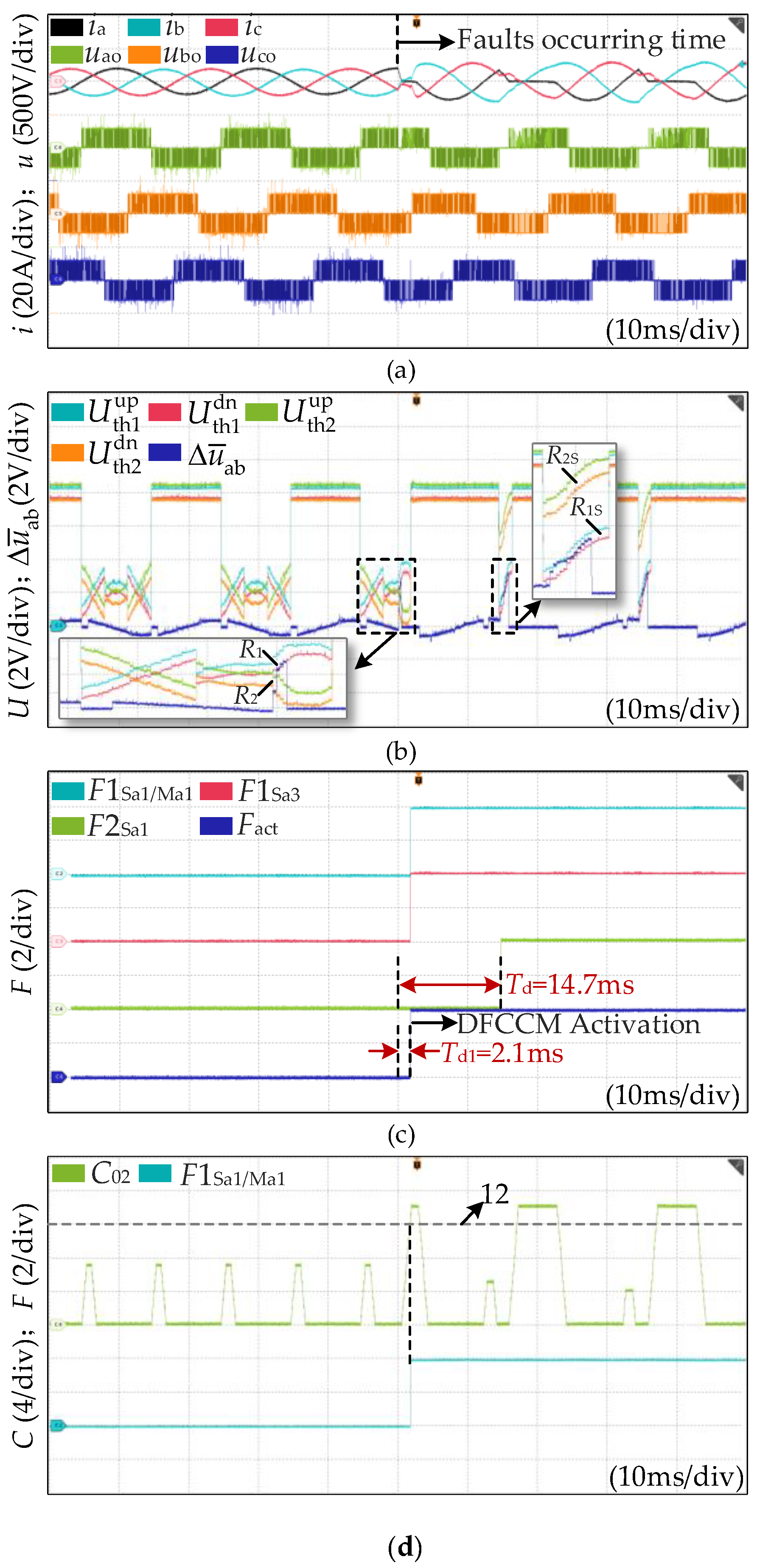
- Case 1: The OC fault occurs at Sa1 when ia > 0.
- (2)
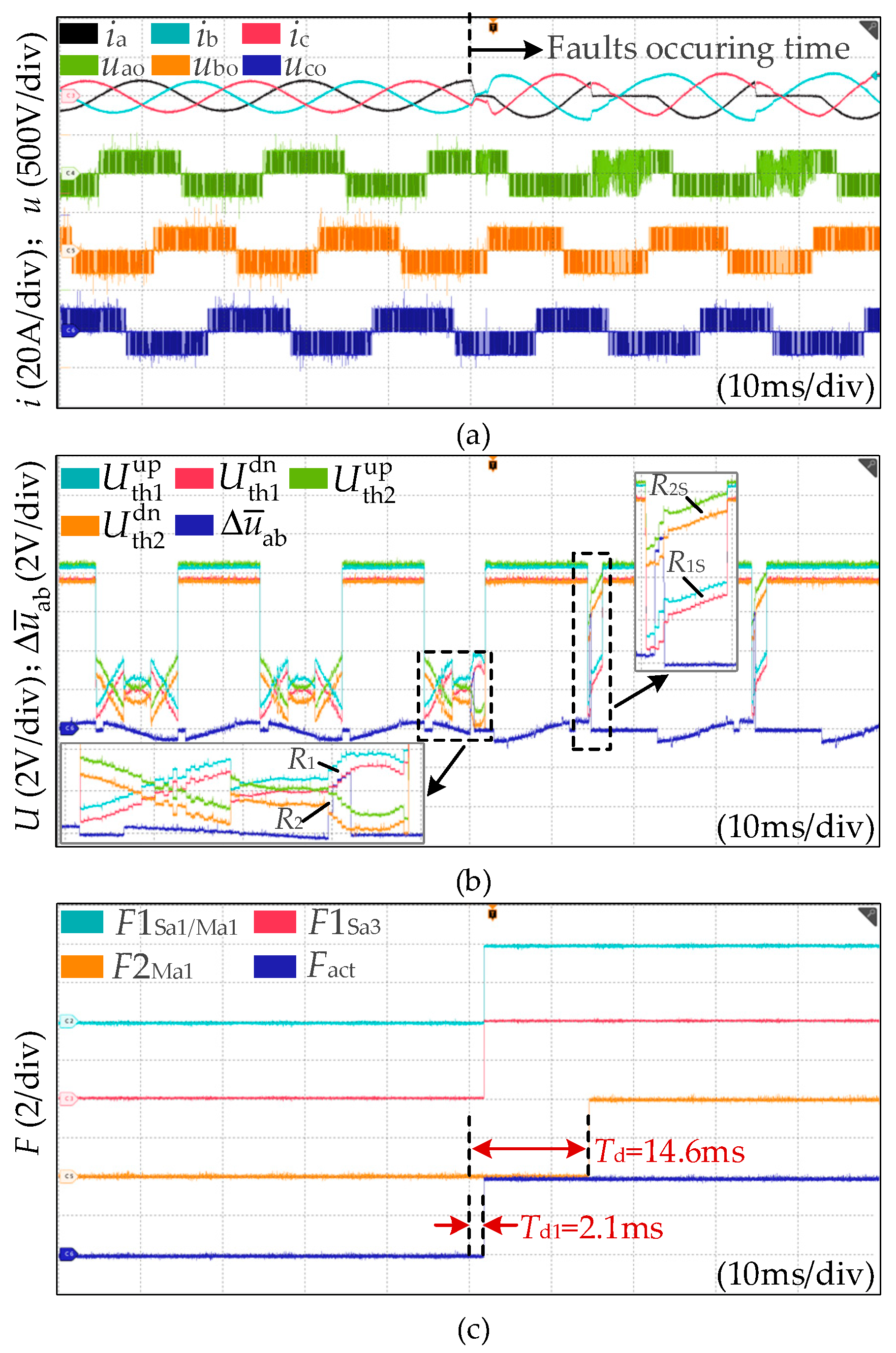
- Case 2: The OC fault occurs at Ma1 when ia > 0.
- (3)
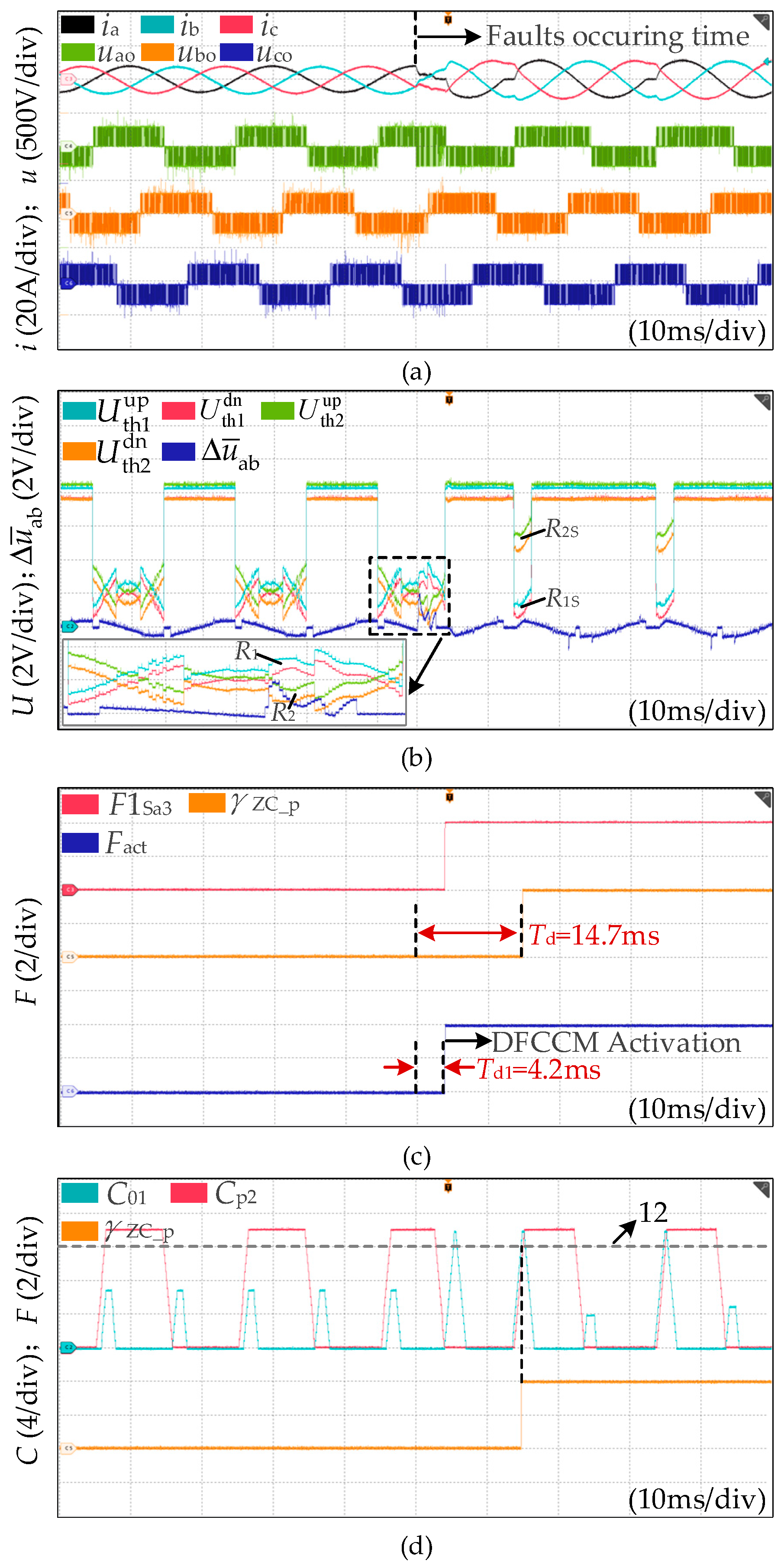
- Case 3: The OC fault occurs at Sa3 when ia > 0.
- (4)
- Case 4: The OC fault occurs at Sa1 when ia < 0.
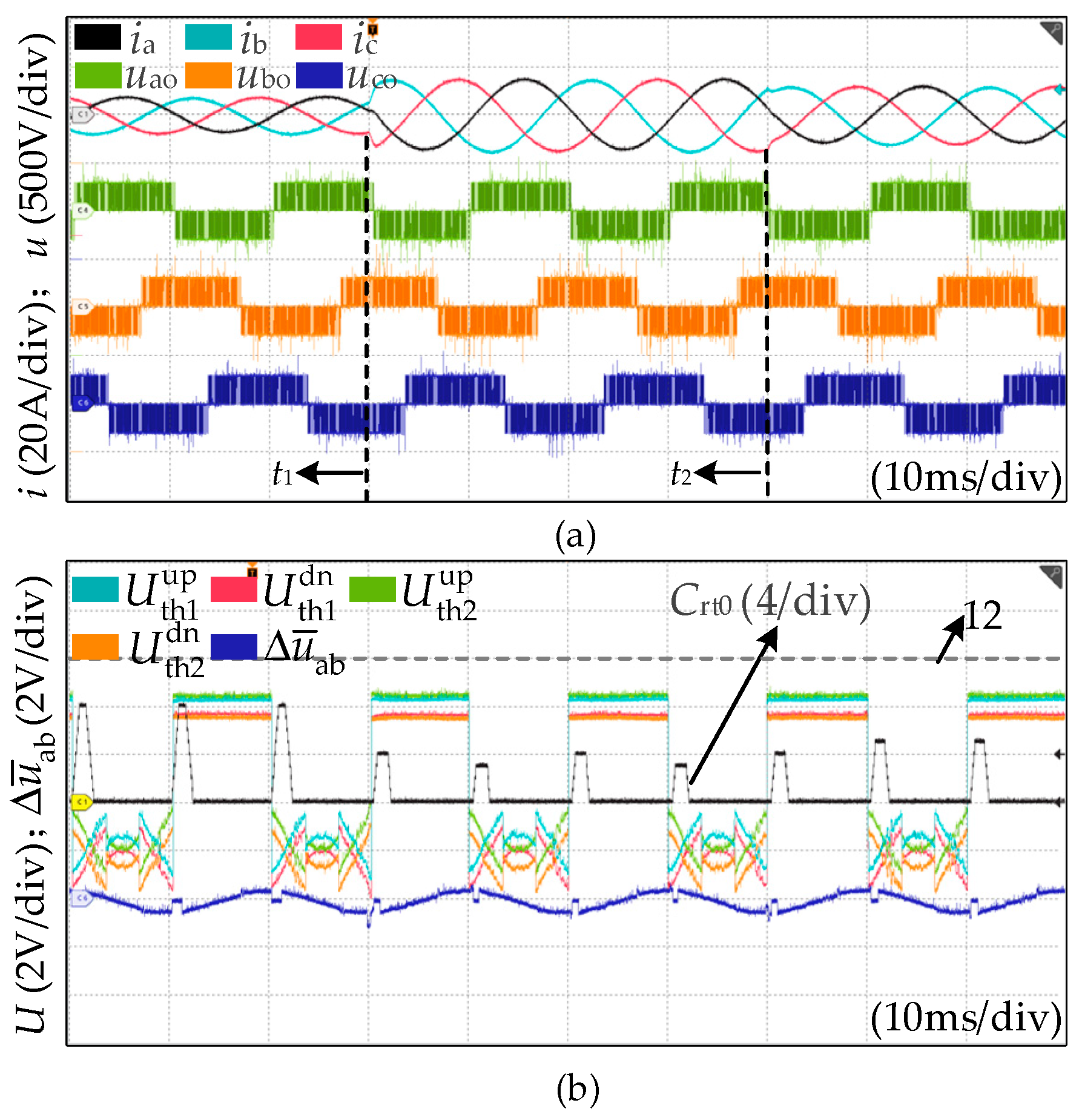
4.2. Robustness Verification of Proposed Method
- (1)
- Case 5: Operation conditions of power variation
- (2)
- Case 6: Operation conditions of voltage fluctuation
4.3. Comparison with Existing Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, R.; Lan, C.; Dong, Z.; Yang, G. An Active Power Dynamic Oscillation Damping Method for the Grid-Forming Virtual Synchronous Generator Based on Energy Reshaping Mechanism. Energies 2023, 16, 7723. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Che, L.; Xu, Z.; Xiao, F. A comprehensive control strategy for F-SOP considering three-phase imbalance and economic operation in ISLDN. IEEE Trans. Sustain. Energy 2025, 16, 149–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Zhang, L. Hybrid ANPC Grid-Tied Inverter Design with Passivity-Based Sliding Mode Control Strategy. Energies 2024, 17, 3655. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Kim, S.-M.; Lee, K.-B. Improving DC-link capacitor lifetime for three-level photovoltaic hybrid active NPC inverters in full modulation index range. IEEE Trans. Power Electron. 2021, 36, 5250–5261. [Google Scholar] [CrossRef]
- Hakami, S.S.; Halabi, L.M.; Lee, K.-B. Dual-carrier-based PWM method for DC-link capacitor lifetime extension in three-level hybrid ANPC Inverters. IEEE Trans. Ind. Electron. 2023, 70, 3303–3314. [Google Scholar] [CrossRef]
- Guo, Q.; Li, G.; Lin, J. A domain generalization network exploiting causal representations and non-causal representations for three-phase converter fault diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 2509713. [Google Scholar] [CrossRef]
- Xiang, C.; Ouyang, Z.; Zhang, X.; Lu, H.H.C.; Cheng, S. An improved predictive current control of eight switch three-level post-fault inverter with common mode voltage reduction. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 3861–3872. [Google Scholar] [CrossRef]
- Xu, S.; Xu, X.; Du, H.; Wang, H.; Chai, Y.; Zheng, W.; Xhen, H. Comprehensive diagnosis strategy for power switch, grid-side current sensor, DC-link voltage sensor faults in single-phase three-level rectifiers. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 3343–3356. [Google Scholar] [CrossRef]
- Fan, C.; Xiahou, K.; Wang, L.; Wu, Q.H. Hybrid fault diagnosis of multiple open-circuit faults for cascaded H-bridge multilevel converter based on perturbation estimation convolution network. IEEE Trans. Instrum. Meas. 2024, 73, 3508812. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Z.; Li, Z.; Wang, J.; Zhang, Y.; Liu, S. A simple and effective open-circuit-fault diagnosis method for grid-tied power converters-A new technique based on tellegen’s theorem. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2203–2213. [Google Scholar] [CrossRef]
- Xu, S.; Sun, Z.; Yao, C.; Liu, K.; Ma, G. Open-switch fault-tolerant operation of T-type active neutral-point-clamped converter using level-shifted PWM. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2598–2602. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y. A simple open-circuit fault diagnosis method for grid-tied T-type three-level inverters with various power factors based on instantaneous current distortion. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1071–1085. [Google Scholar] [CrossRef]
- Kwon, B.H.; Kim, S.-H.; Kim, S.-M.; Lee, K.-B. Fault diagnosis of open-switch failure in a grid-connected three-level Si/SiC hybrid ANPC inverter. Electronics 2020, 9, 399. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, S.-M.; Park, S.; Lee, K.-B. Switch open-fault detection for a three-phase hybrid active neutral-point-clamped rectifier. Electronics 2020, 9, 1437. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, J. Open-circuit fault diagnosis method for grid-connected bidirectional T-type converter based on geometrical similarity measurement. IEEE Trans. Power Electron. 2022, 37, 15571–15582. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Z.; Li, Z.; Chen, H.; Zhou, D. A unified open-circuit-fault diagnosis method for three-level neutral-point-clamped power converters. IEEE Trans. Power Electron. 2023, 38, 3834–3846. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W.; Wang, H.; Zheng, W.; Wang, J.; Chai, Y. A simultaneous diagnosis method for power switch and current sensor faults in grid-connected three-level NPC inverters. IEEE Trans. Power Electron. 2023, 38, 1104–1118. [Google Scholar] [CrossRef]
- Li, G.; Xu, S.; Sun, Z.; Yao, C.; Ren, G.; Ma, G. Open-circuit fault diagnosis for three-level ANPC inverter based on predictive current vector residual. IEEE Trans. Ind. Appl. 2023, 59, 6837–6851. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, J.; Luo, H.; Liu, Y. Real-time open-circuit fault diagnosis method for T-type rectifiers based on median current analysis. IEEE Trans. Power Electron. 2023, 38, 8956–8965. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, R.; Hu, B. Single-switch open-circuit diagnosis method based on average voltage vector for three-level T-type inverter. IEEE Trans. Power Electron. 2021, 36, 911–921. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S. Real-time IGBT open-circuit fault diagnosis in three-level neutral-point-clamped voltage-source rectifiers based on instant voltage error. IEEE Trans. Ind. Electron. 2015, 62, 1669–1678. [Google Scholar] [CrossRef]
- Chen, M.; He, Y. Multiple open-circuit fault diagnosis method in NPC rectifiers using fault injection strategy. IEEE Trans. Power Electron. 2022, 37, 8554–8571. [Google Scholar] [CrossRef]
- Wang, B.; Li, Z.; Bai, Z.; Krein, P.T.; Ma, H. A voltage vector residual estimation method based on current path tracking for T-type inverter open-circuit fault diagnosis. IEEE Trans. Power Electron. 2021, 36, 13460–13477. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y. A hypothesis method for T-type three-level inverters open-circuit fault diagnosis based on output phase voltage model. IEEE Trans. Power Electron. 2022, 37, 9718–9732. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y.; Chen, J. A robust open-circuit fault diagnosis method for three-level T-type inverters based on phase voltage vector residual under modulation mode switching. IEEE Trans. Power Electron. 2023, 38, 5309–5322. [Google Scholar] [CrossRef]
- Chen, M.; He, Y. Open-circuit fault diagnosis in NPC rectifiers using reference voltage deviation and incorporating fault-tolerant control. IEEE Trans. Power Electron. 2024, 39, 1514–1526. [Google Scholar] [CrossRef]
- Kim, S.-H.; Yoo, D.-Y.; An, S.-W.; Park, Y.-S.; Lee, J.-W.; Lee, K.-B. Fault detection method using a convolution neural network for hybrid active neutral-point clamped inverters. IEEE Access 2020, 8, 140632–140642. [Google Scholar] [CrossRef]
- Selvakumar, P.; Muthukumaran, G. An intelligent technique for fault detection and localization of three-level ANPC inverter with NP connection for electric vehicles. Adv. Eng. Softw. 2023, 176, 103354. [Google Scholar] [CrossRef]
- Yuan, W.; Li, Z.; He, Y.; Cheng, R.; Lu, L.; Ruan, Y. Open-circuit fault diagnosis of NPC inverter based on improved 1-D CNN network. IEEE Trans. Instrum. Meas. 2022, 71, 3510711. [Google Scholar] [CrossRef]
- Shen, H.; Tang, X.; Luo, Y.; Xie, F.; Shi, Z. Online open-circuit fault diagnosis for neutral point clamped inverter based on an improved convolutional neural network and sample amplification method under varying operating conditions. IEEE Trans. Instrum. Meas. 2024, 73, 3512612. [Google Scholar] [CrossRef]
- Yao, C.; Xu, S.; Ren, G.; Wu, S.; Li, G.; Sun, Z. Online open-circuit fault diagnosis for ANPC inverters using edge-based lightweight two-dimensional CNN. IEEE Trans. Power Electron. 2024, 39, 3979–3984. [Google Scholar] [CrossRef]
- Ma, G.; Yao, C.; Xu, S.; Ren, G.; Sun, Z.; Wu, S. Real-time diagnosis of multiple open-circuit faults in ANPC inverters based on lightweight deployment of edge 2D-CNN. IEEE Trans. Ind. Electron. 2025, 4, 1–12. [Google Scholar]
- Peng, X.; Xiao, F.; Tu, C.; Wang, L. A fault-tolerant control for hybrid active neutral-point-clamped converters with shared redundant unit under multiswitch open-circuit fault. IEEE Trans. Ind. Electron. 2025, 72, 8550–8560. [Google Scholar] [CrossRef]
- Li, Z.; Wang, B.; Ren, Y.; Wang, J.; Bai, Z.; Ma, H. L- and LCL-filtered grid-tied single-phase inverter transistor open-circuit fault diagnosis based on post-fault reconfiguration algorithms. IEEE Trans. Power Electron. 2019, 34, 10180–10192. [Google Scholar] [CrossRef]
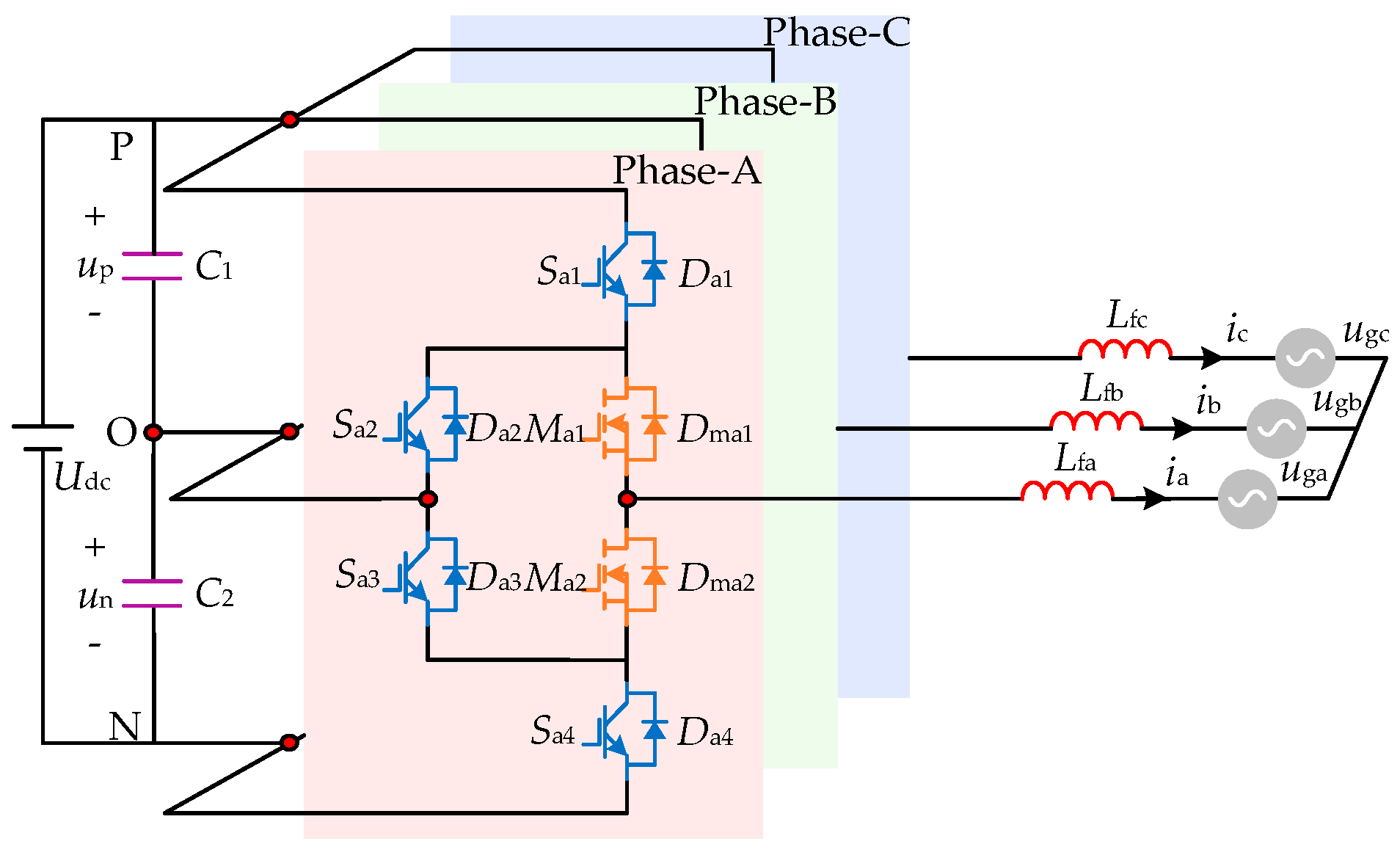
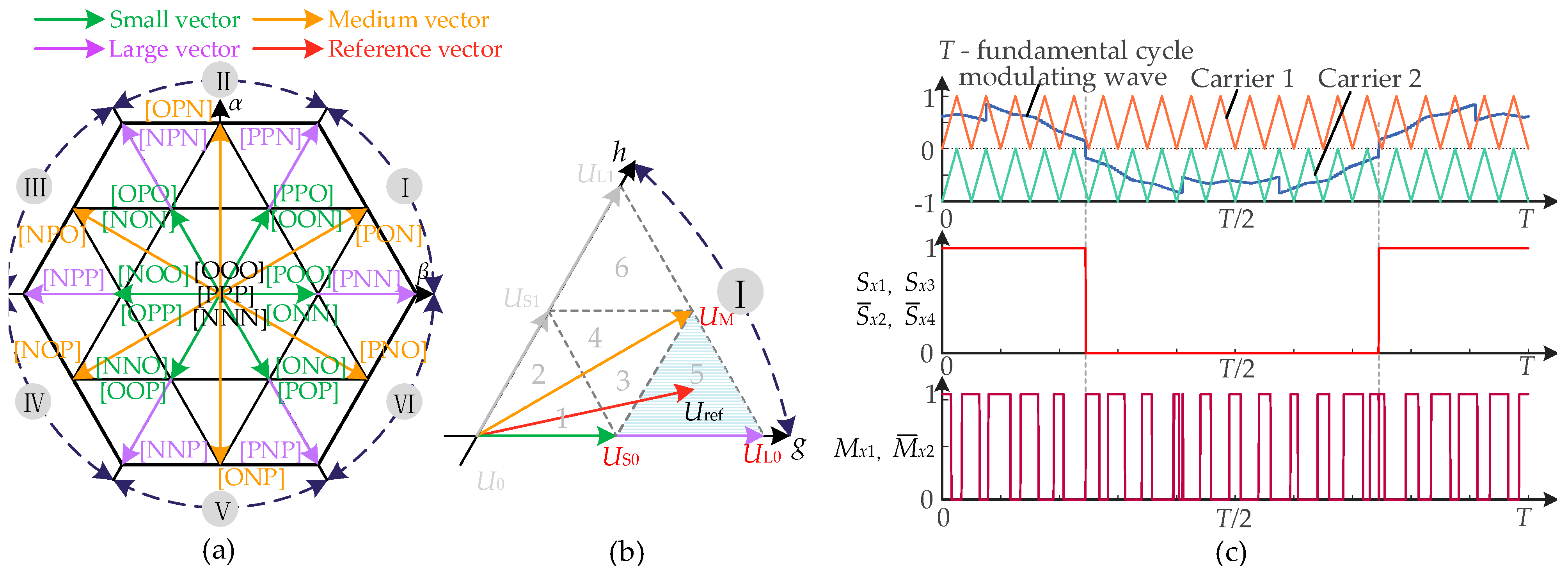
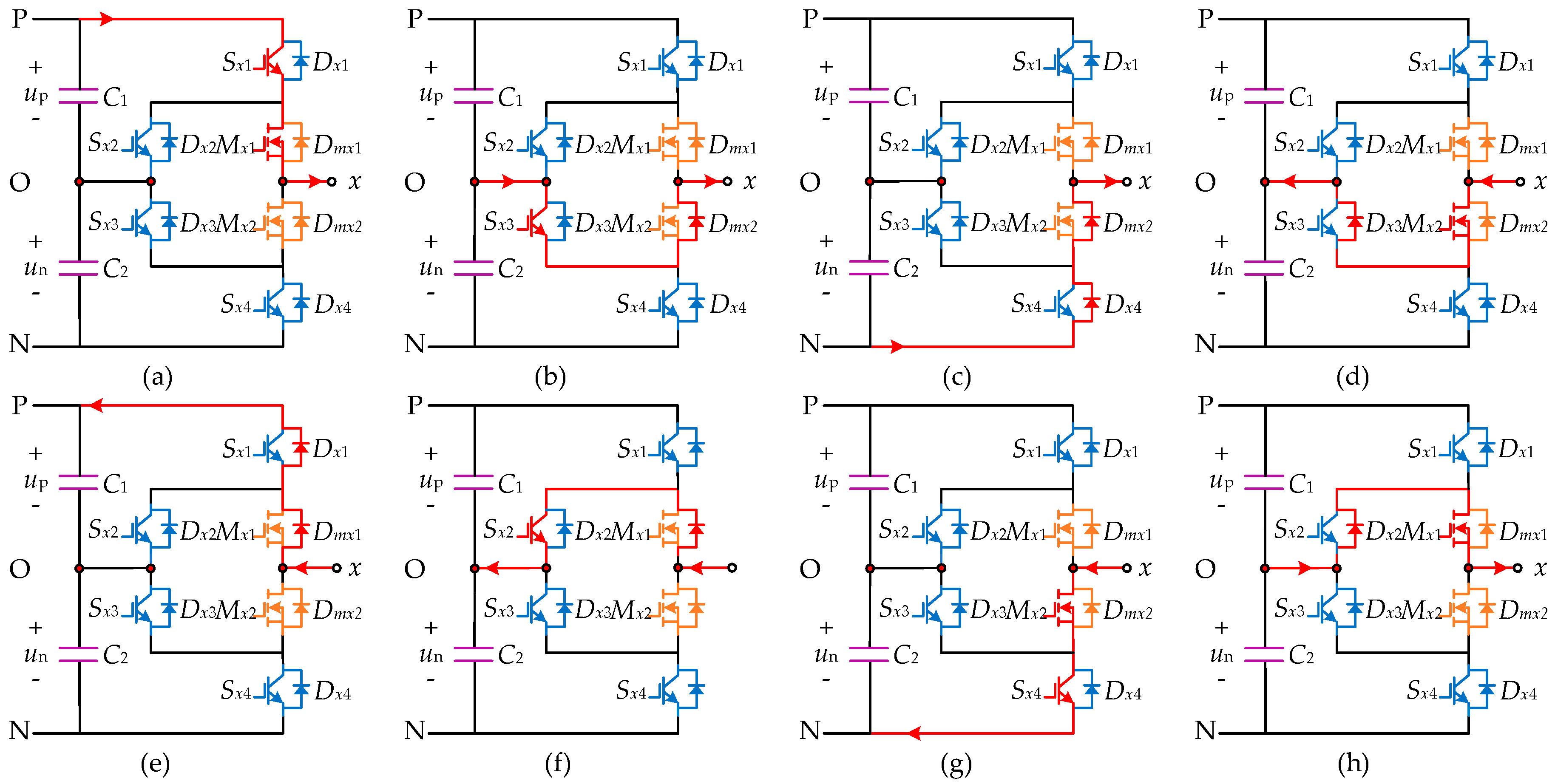






| Switching State | Gate Sequence | Output Voltage Level | |||||
|---|---|---|---|---|---|---|---|
| Mx1 | Mx2 | Sx1 | Sx2 | Sx3 | Sx4 | ||
| [P] | 1 | 0 | 1 | 0 | 1 | 0 | Udc/2 |
| [O−] | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| [O+] | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| [N] | 0 | 1 | 0 | 1 | 0 | 1 | −Udc/2 |
| Parameters | Symbol | Value |
|---|---|---|
| DC input voltage | Udc | 600 V |
| DC-link capacitor | C1, C2 | 1020 μF |
| AC filter inductor | L | 6 mH |
| AC grid phase-voltage | Ux | 150 V |
| Rated power | Prated | 10 kW |
| Grid frequency | fg | 50 Hz |
| Switching frequency | fs | 10 kHz |
| Switching dead time | Tdead | 2 μs |
| Case No | Fault Type | Td1 | Td | Identification Correctness |
|---|---|---|---|---|
| 1 | OC at Sa1, ia > 0 | 2.1 ms | 14.7 ms | Yes |
| 2 | OC at Ma1, ia > 0 | 2.1 ms | 14.6 ms | Yes |
| 3 | OC at Sa3, ia > 0 | 4.2 ms | 14.7 ms | Yes |
| 4 | OC at Sa1, ia < 0 | 6.3 ms | 24. 6 ms | Yes |
| Method | DT | CB (FLOPs) | DTT | Robustness | |
|---|---|---|---|---|---|
| OPF | GVF | ||||
| [13] | <30 ms | <400 | Fixed (Δ) | NO | NO |
| [14] | <15 ms | <400 | Fixed (Δ) | NO | NO |
| [18] | <20 ms | <500 | Fixed (Δ) | Yes | NO |
| [27] | <10 ms | >25,000 | Fixed (Δ) | NO | NO |
| [28] | <20 ms | >25,000 | Fixed (Δ) | NO | NO |
| [31] | <29.56 ms | >10,000 | Fixed (Δ) | NO | NO |
| [32] | <54 ms | >10,000 | Fixed (Δ) | NO | NO |
| Proposed | <25 ms | <350 | Adaptive (▲) | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Xiao, F.; Li, M.; Chen, Y.; Gao, Y.; Zhao, R.; Lu, J. Open-Switch Fault Diagnosis for Grid-Tied HANPC Converters Using Generalized Voltage Residuals Model and Current Polarity in Flexible Distribution Networks. Energies 2025, 18, 3855. https://doi.org/10.3390/en18143855
Peng X, Xiao F, Li M, Chen Y, Gao Y, Zhao R, Lu J. Open-Switch Fault Diagnosis for Grid-Tied HANPC Converters Using Generalized Voltage Residuals Model and Current Polarity in Flexible Distribution Networks. Energies. 2025; 18(14):3855. https://doi.org/10.3390/en18143855
Chicago/Turabian StylePeng, Xing, Fan Xiao, Ming Li, Yizhe Chen, Yifan Gao, Ruifeng Zhao, and Jiangang Lu. 2025. "Open-Switch Fault Diagnosis for Grid-Tied HANPC Converters Using Generalized Voltage Residuals Model and Current Polarity in Flexible Distribution Networks" Energies 18, no. 14: 3855. https://doi.org/10.3390/en18143855
APA StylePeng, X., Xiao, F., Li, M., Chen, Y., Gao, Y., Zhao, R., & Lu, J. (2025). Open-Switch Fault Diagnosis for Grid-Tied HANPC Converters Using Generalized Voltage Residuals Model and Current Polarity in Flexible Distribution Networks. Energies, 18(14), 3855. https://doi.org/10.3390/en18143855






