Improvement of Positive and Negative Feedback Power Hardware-in-the-Loop Interfaces Using Smith Predictor
Abstract
1. Introduction
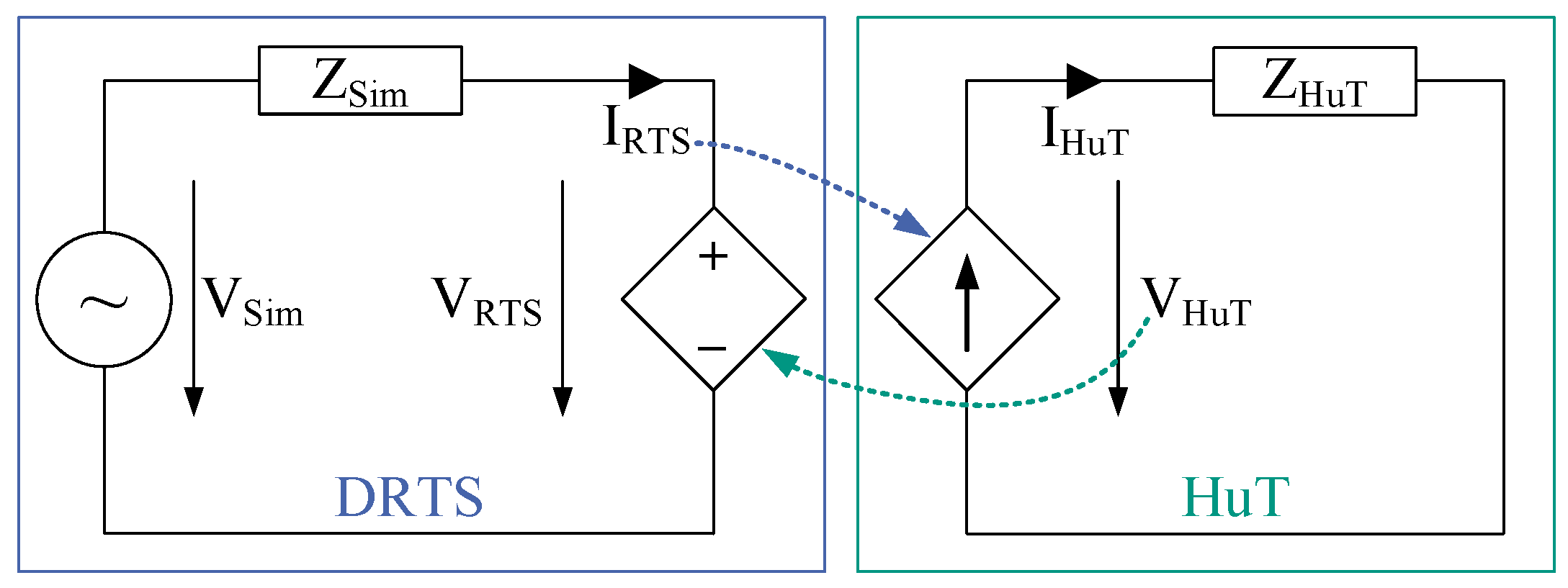
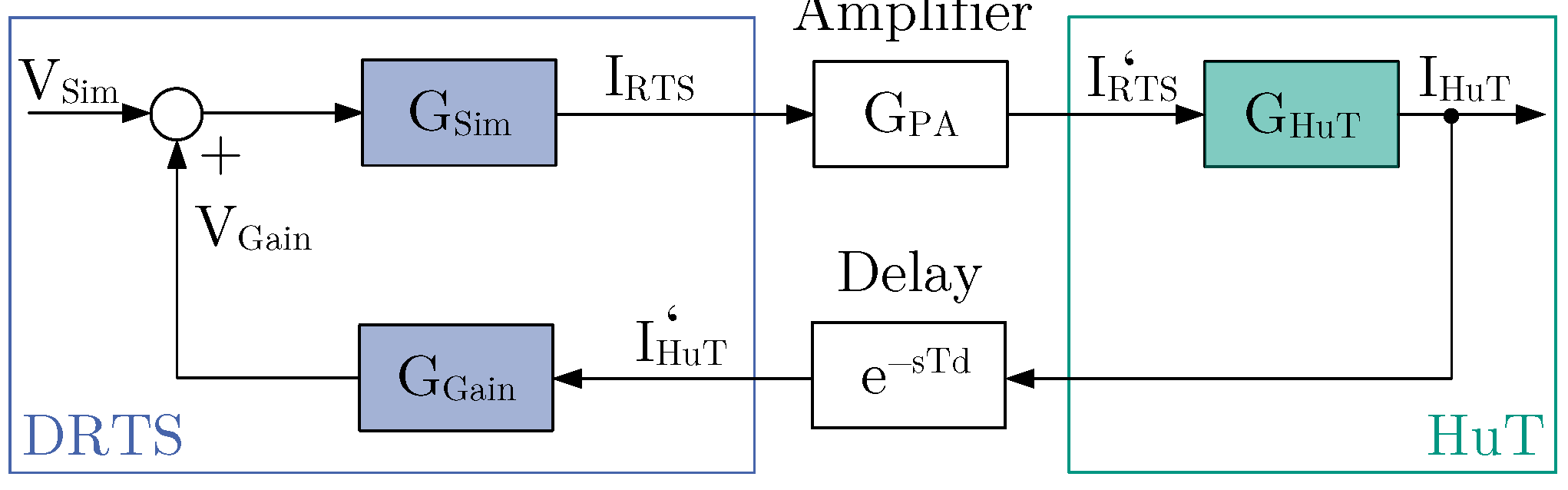
2. Interface Algorithms
2.1. Ideal Transformer Method
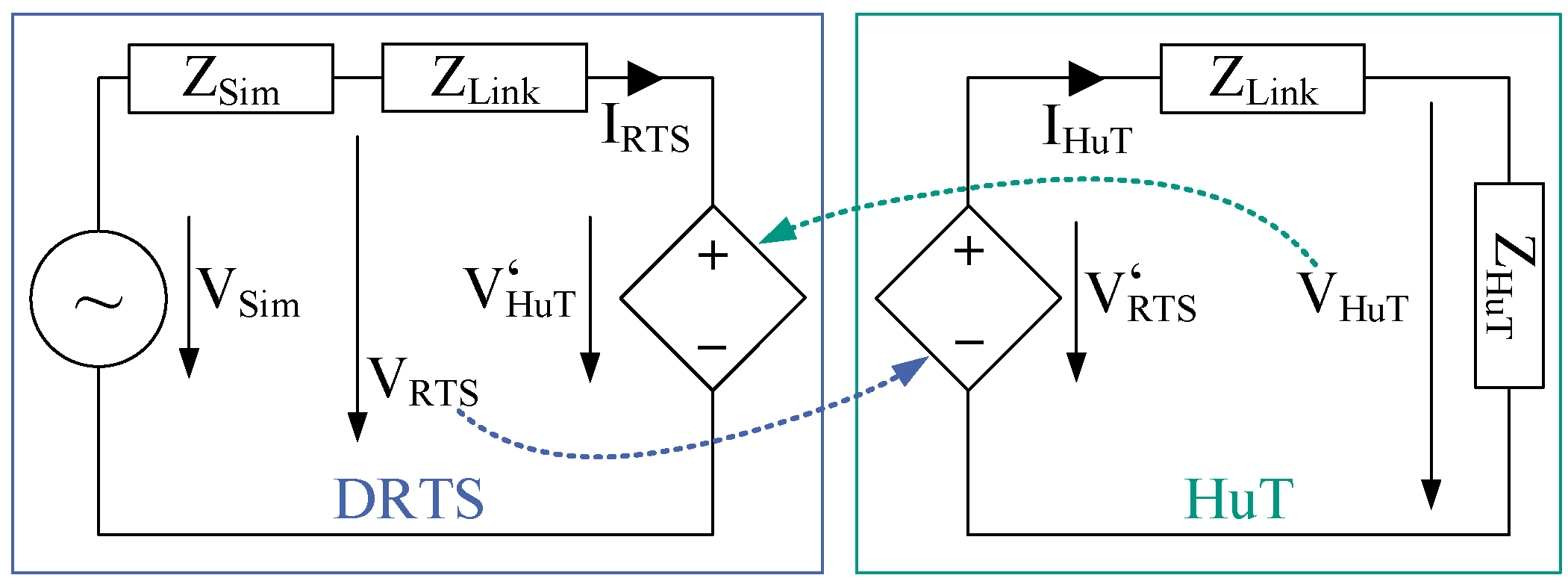
2.1.1. Voltage-Type ITM
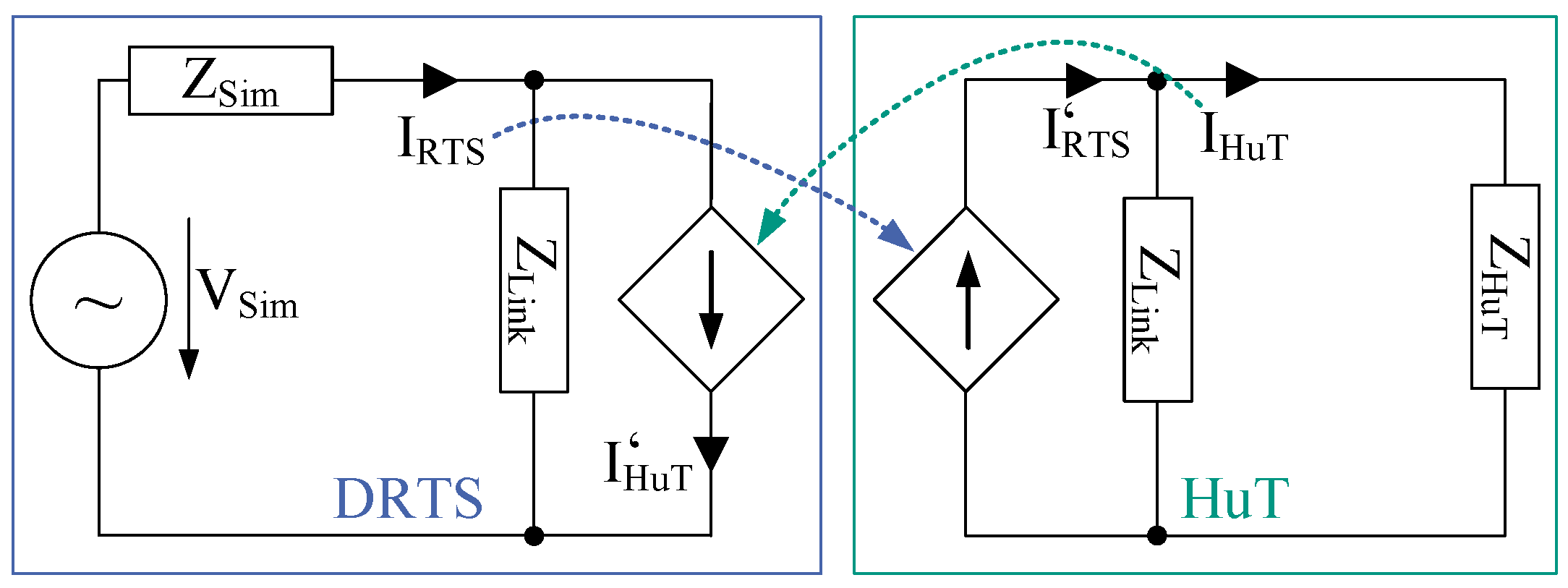
2.1.2. Current-Type ITM
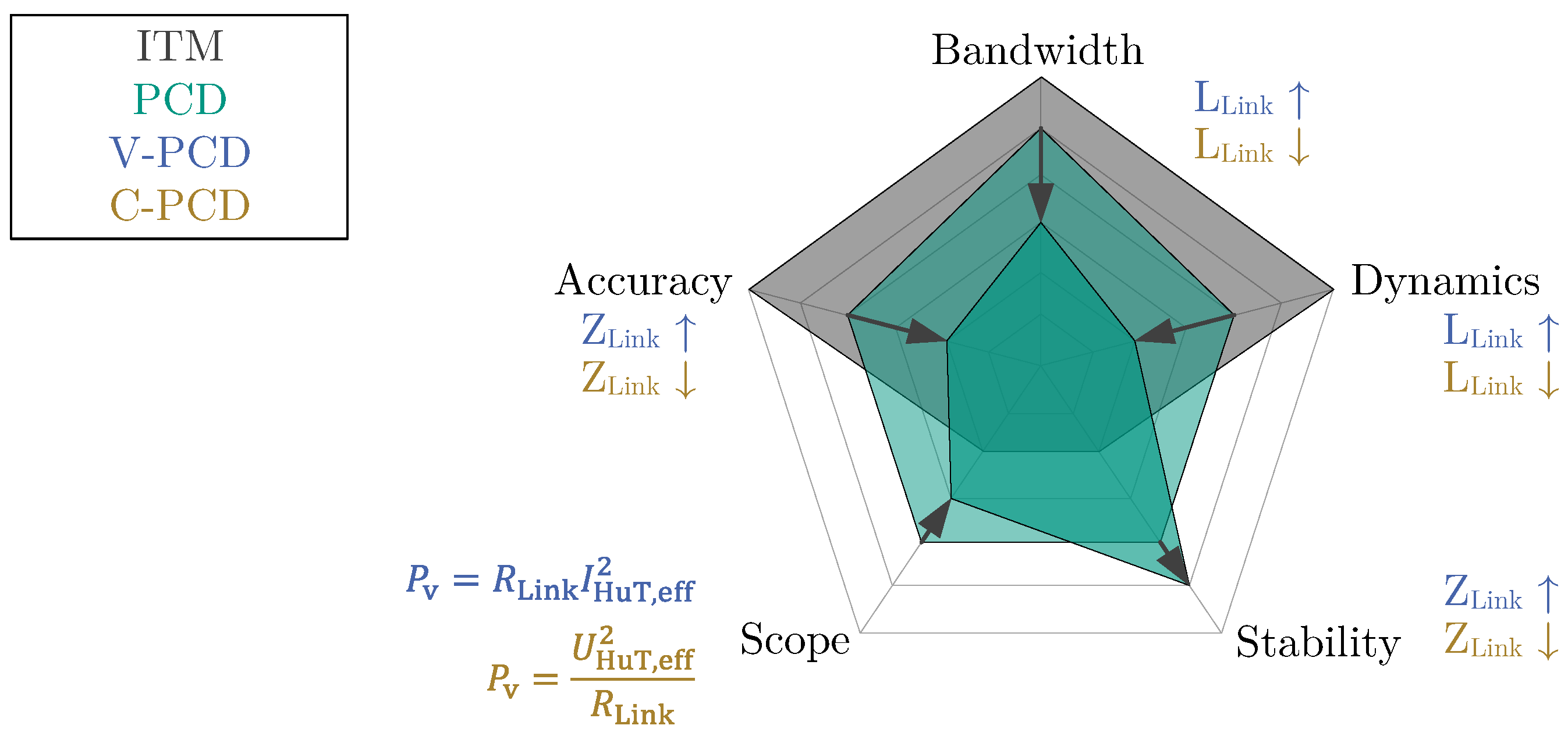
2.2. Partial Circuit Duplication
2.2.1. Voltage-Type PCD
2.2.2. Current-Type PCD
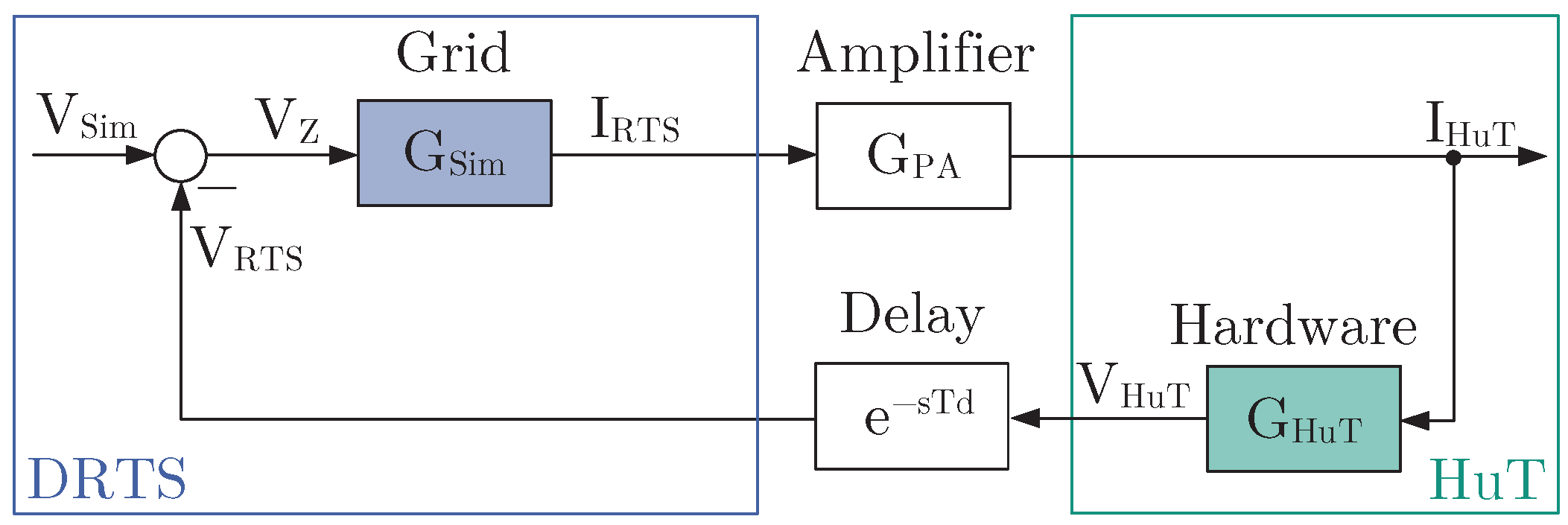
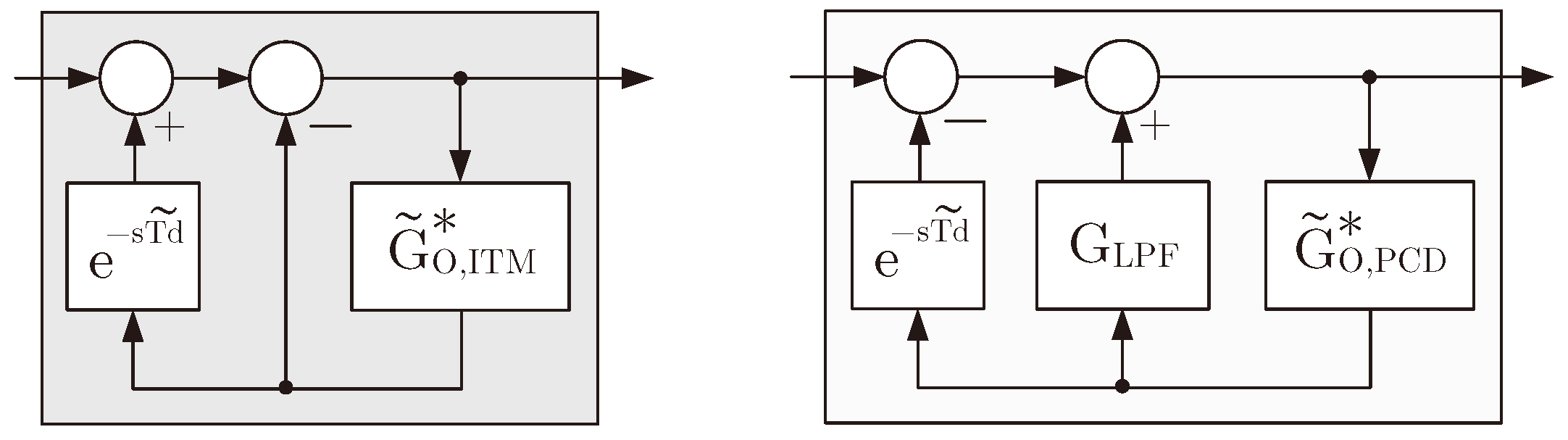
3. Smith Predictor
3.1. Compensated Voltage-Type ITM
3.2. Compensated Current-Type ITM
3.3. Compensated Voltage-Type PCD
3.4. Compensated Current-Type PCD
4. Simulation Results
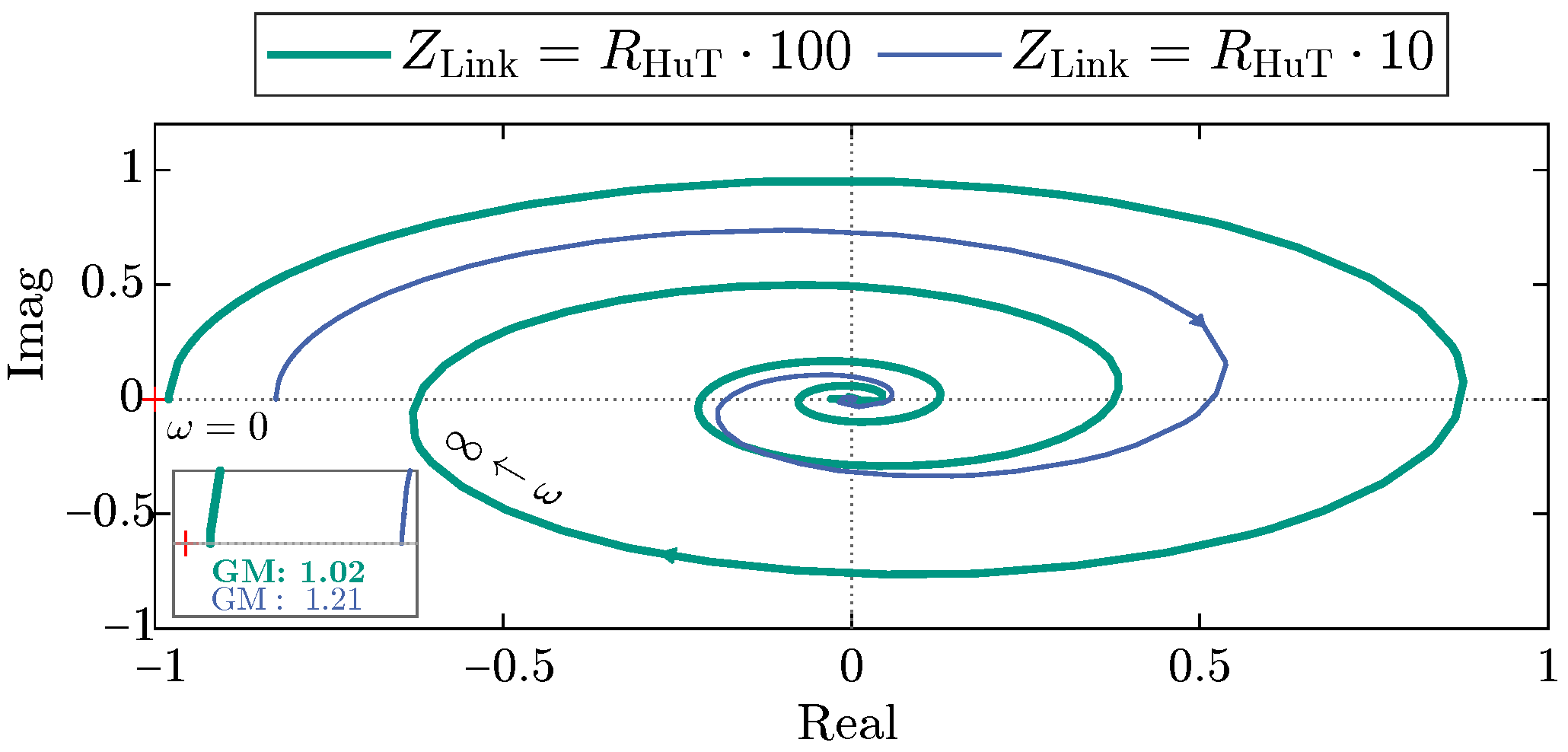
4.1. Negative Feedback: ITM
4.2. Positive Feedback: PCD
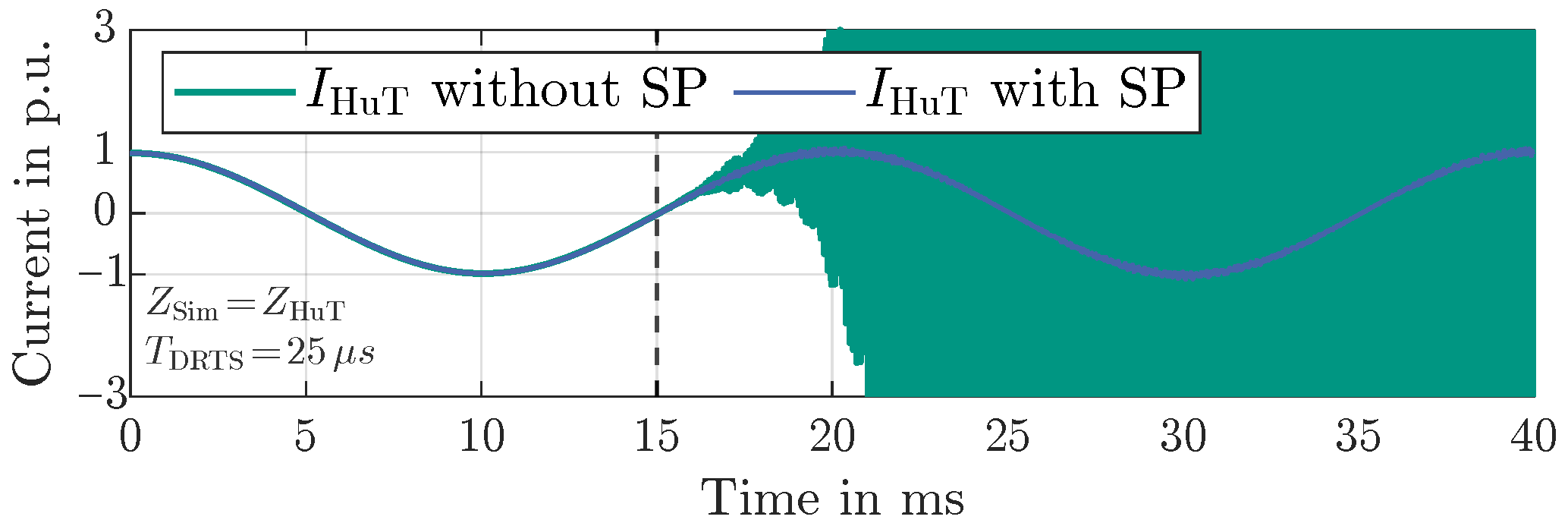
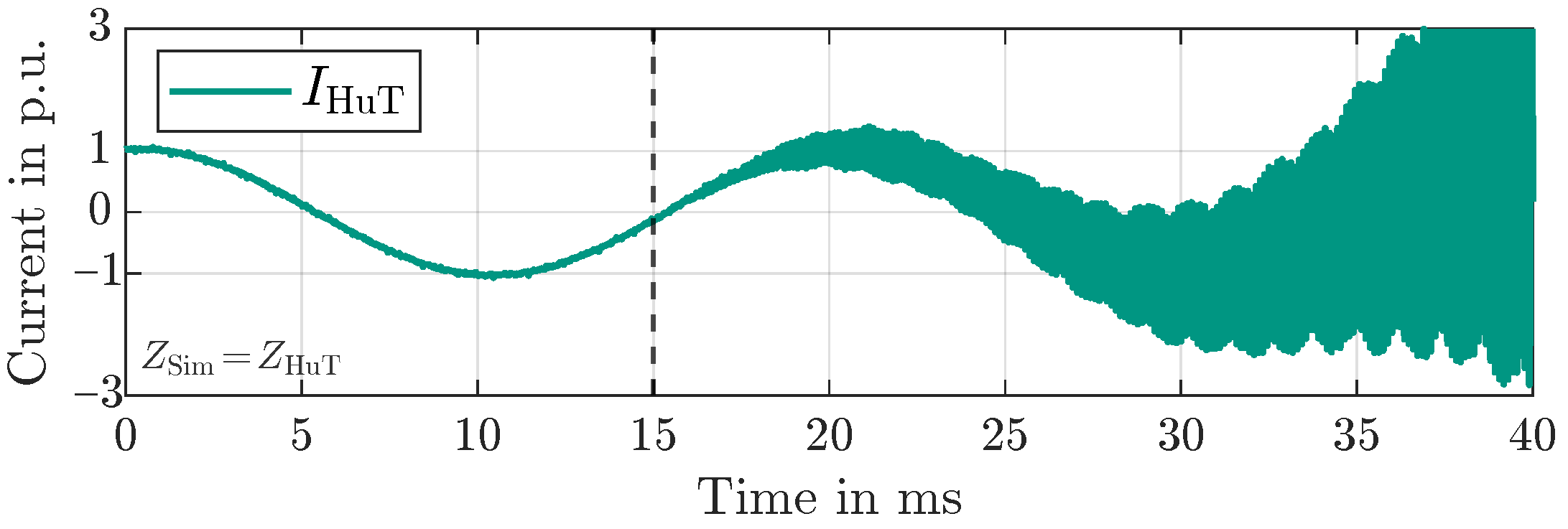
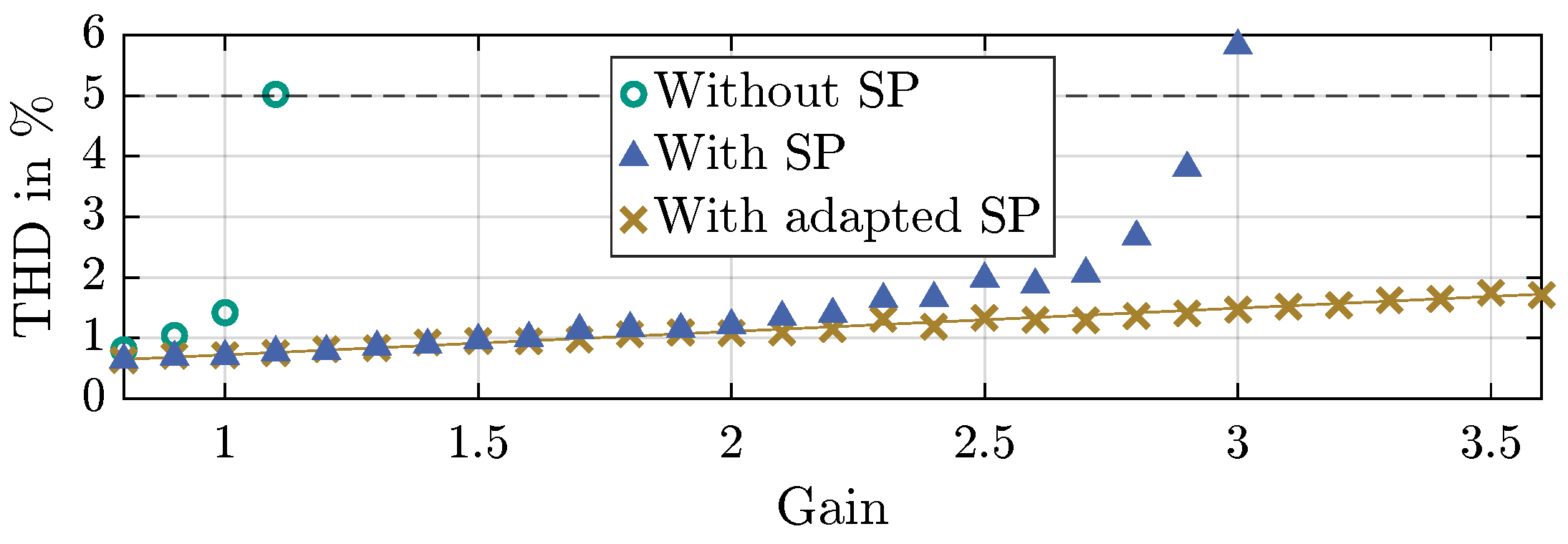
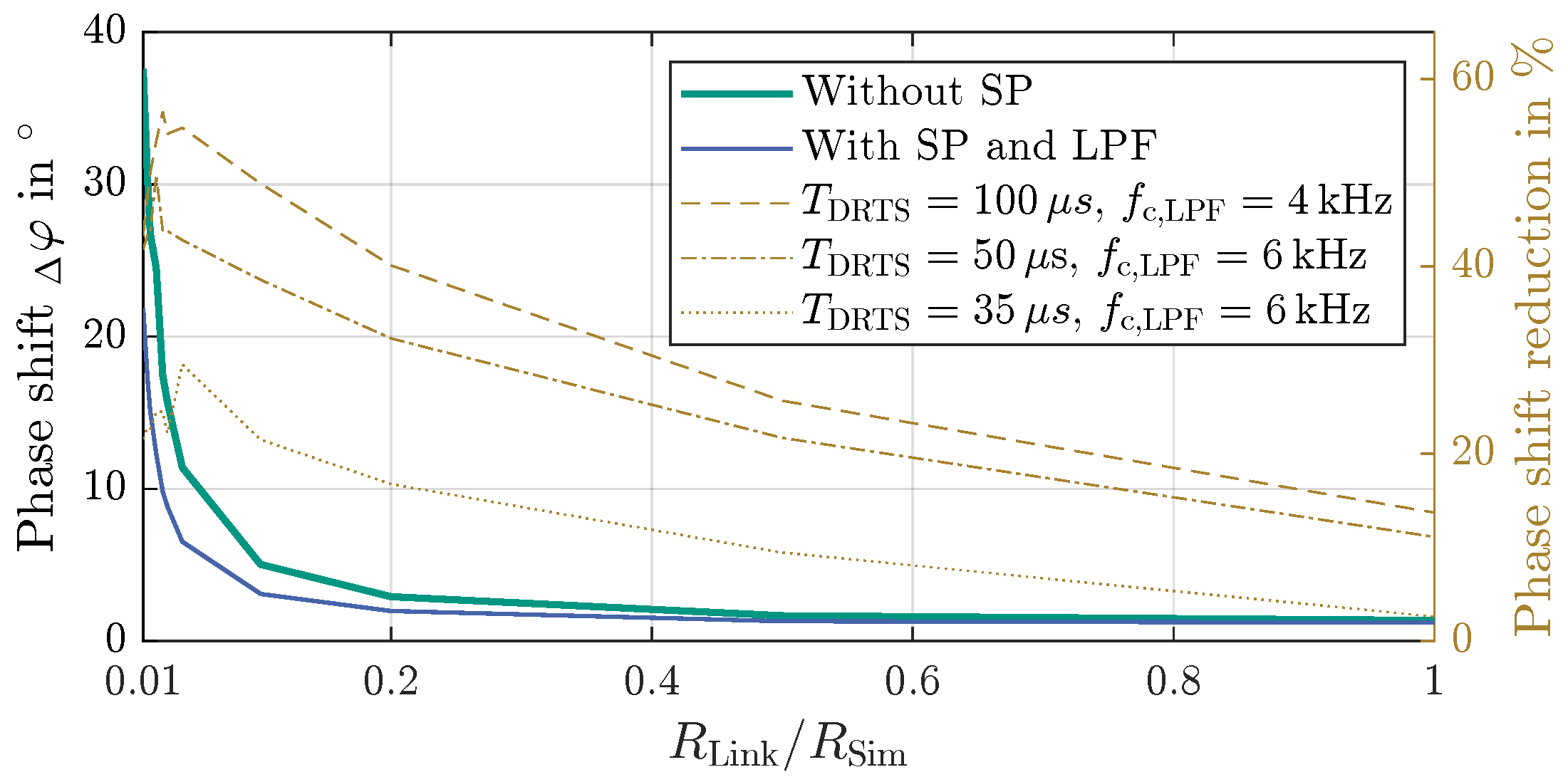
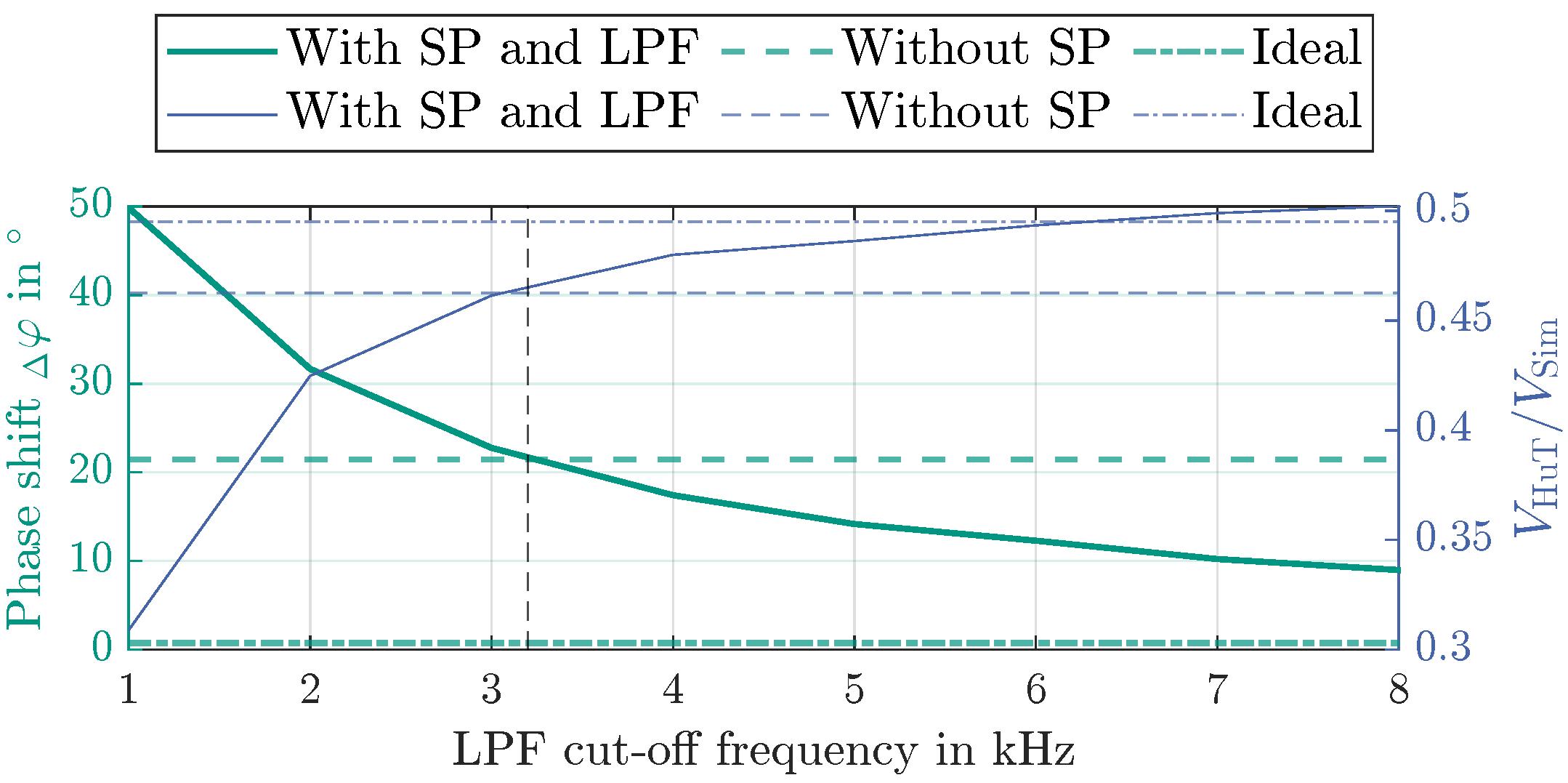
5. Experimental Results
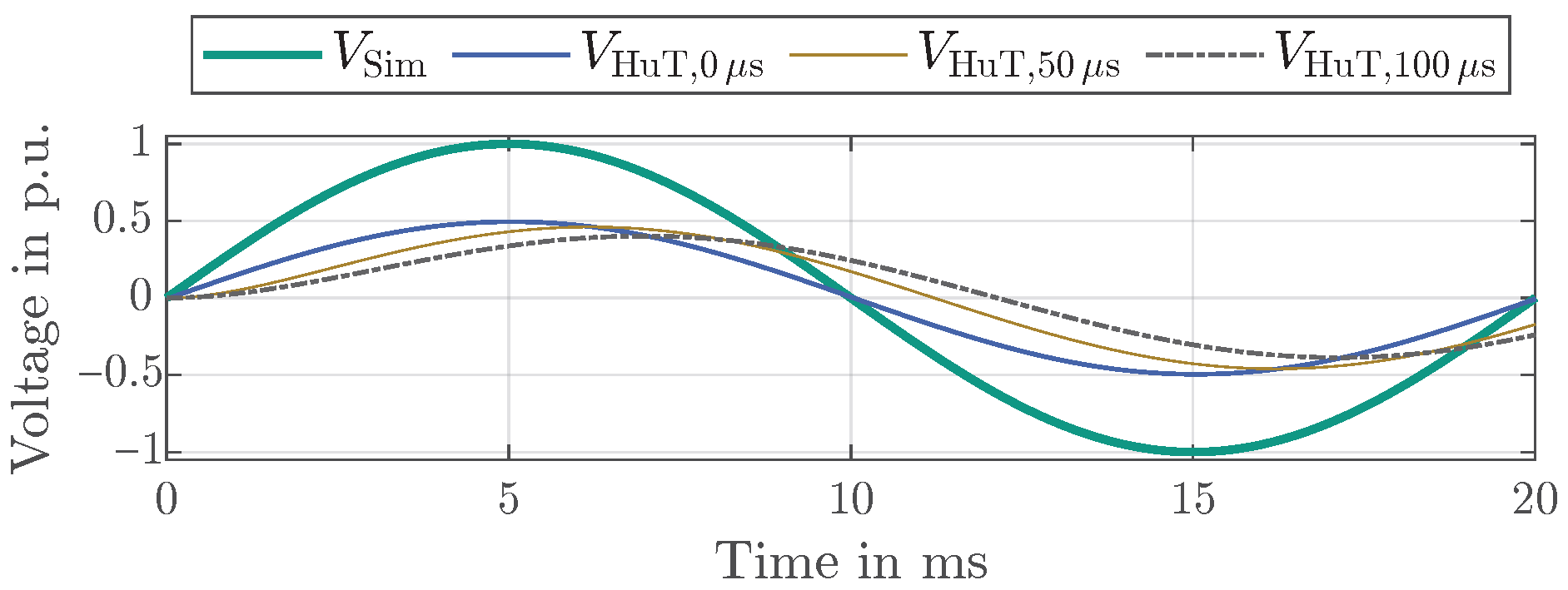
5.1. Negative Feedback: ITM
5.2. Positive Feedback: PCD
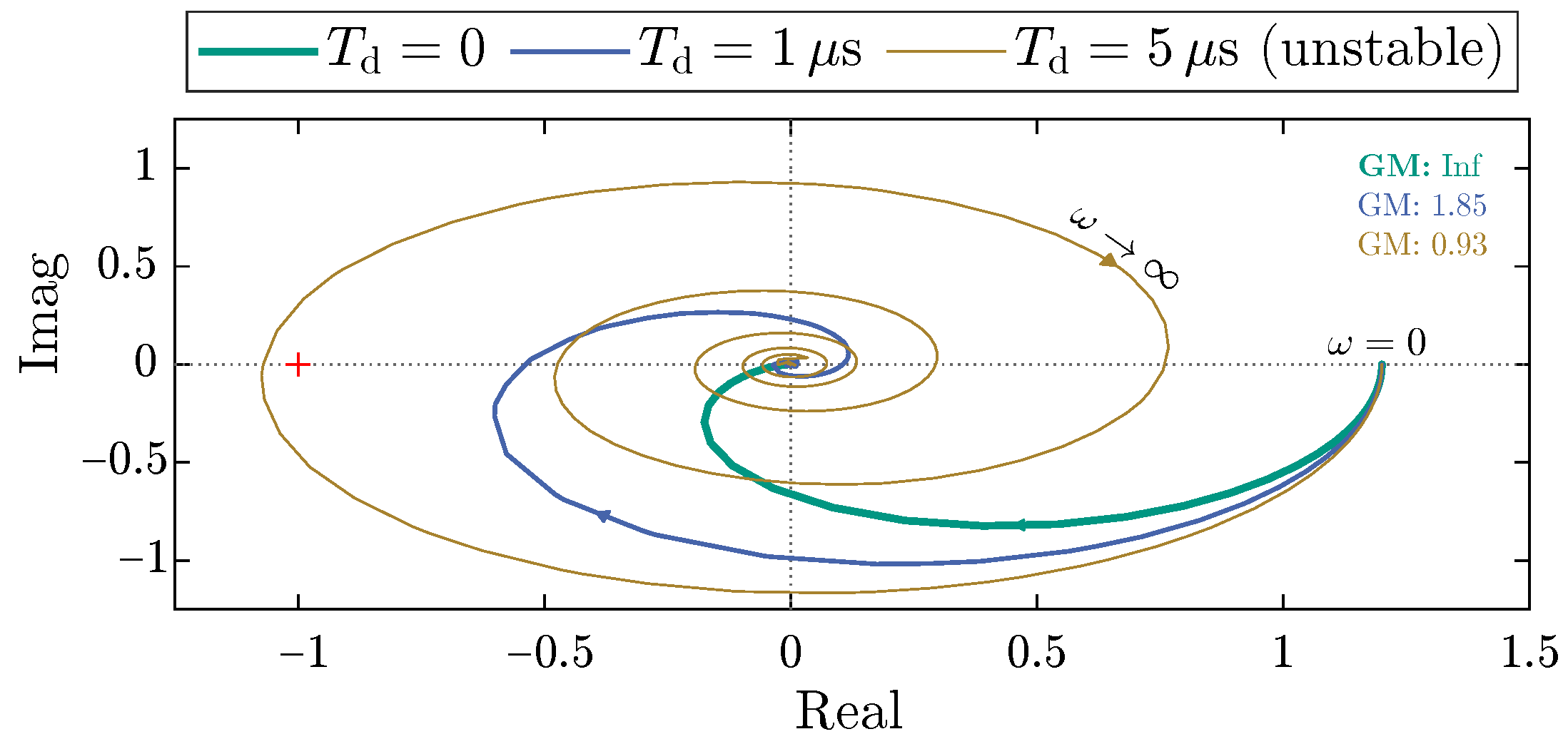
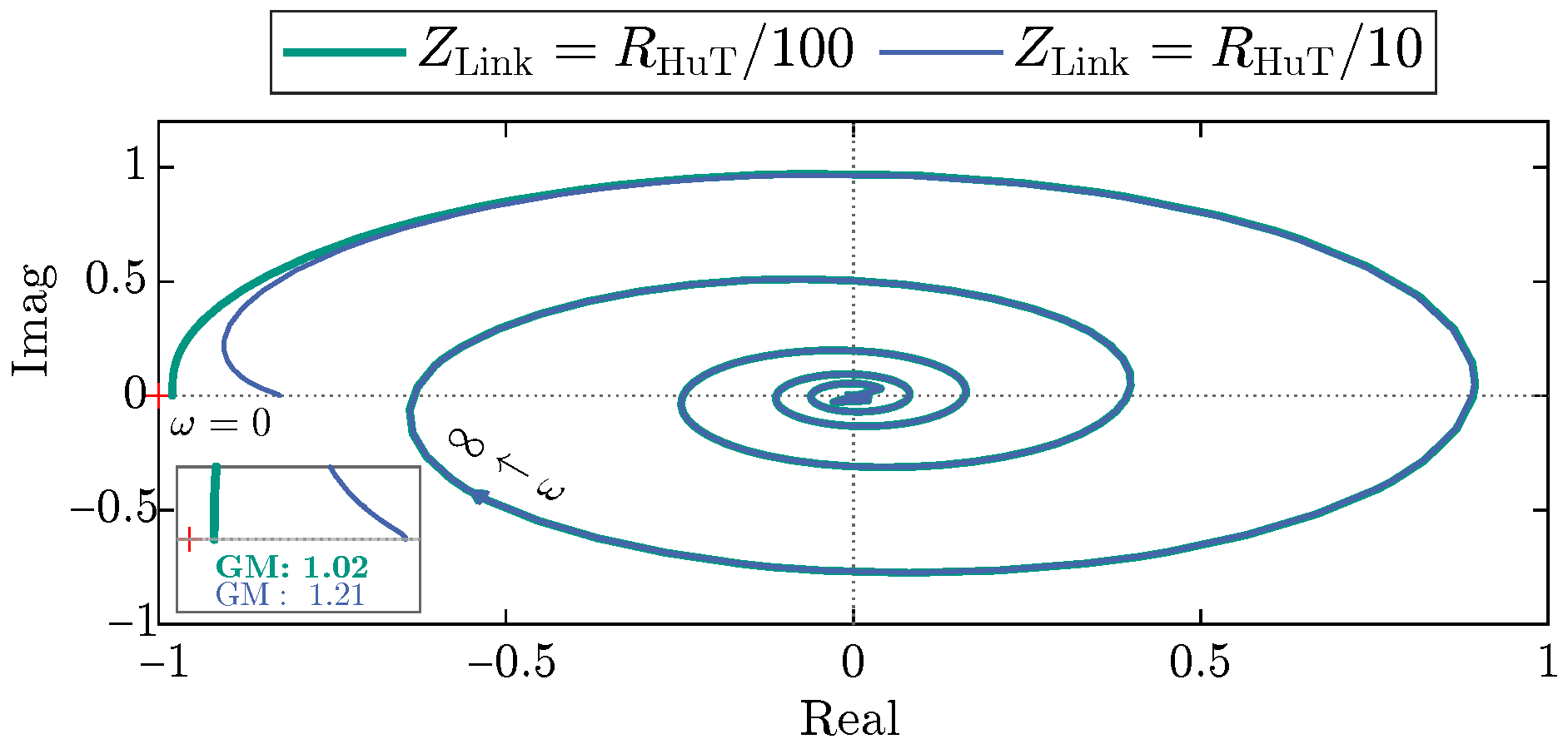
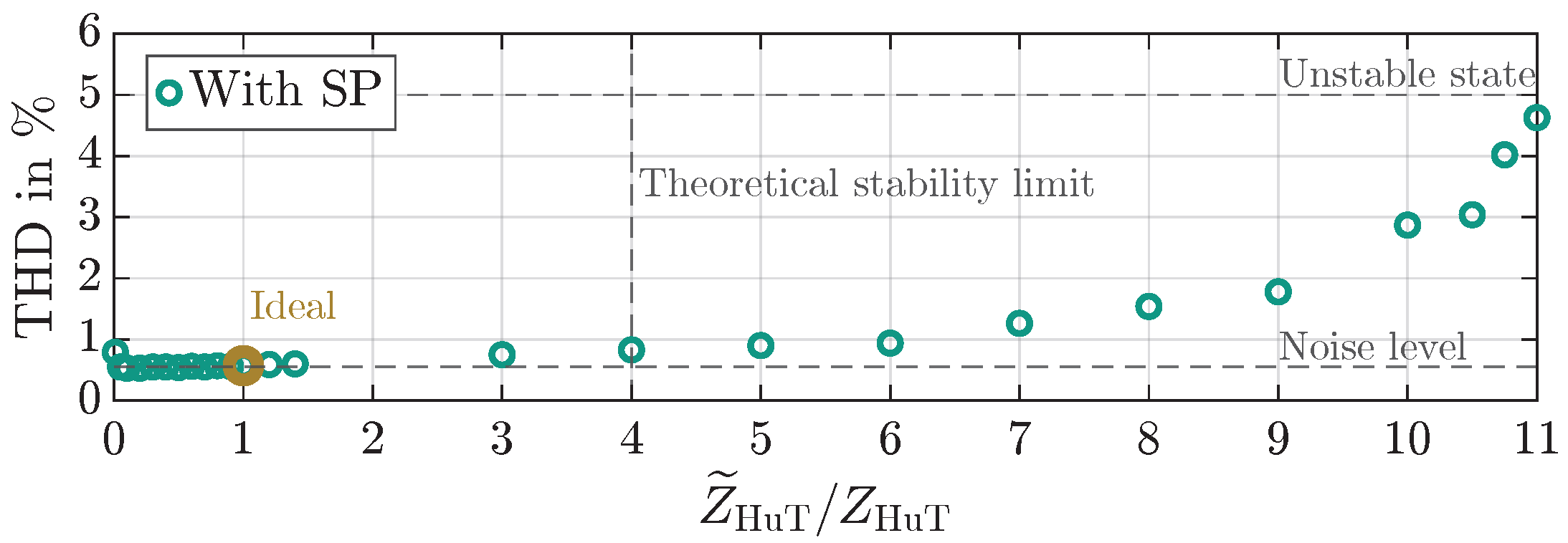
5.3. Influence of SP Model Deviation
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| C- | current-type |
| DRTS | digital real-time simulator |
| EMT | electromagnetic transient |
| GM | gain margin |
| HuT | hardware under test |
| IA | interface algorithm |
| ITM | ideal transformer method |
| LPF | low-pass filter |
| OL | optical link |
| PA | power amplifier |
| PCD | partial circuit duplication |
| PHIL | power hardware-in-the-loop |
| SP | Smith predictor |
| TLM | transmission line model |
| V- | voltage-type |
References
- Chang, H.; Vanfretti, L. A power hardware-in-the-loop smart inverter testing facility. In Proceedings of the 2024 9th International Conference on Smart and Sustainable Technologies (SpliTech), Bol and Split, Croatia, 25–28 June 2024; pp. 1–6. [Google Scholar]
- Pokharel, M.; Ho, C.N.M. Stability analysis of power hardware-in-the-loop architecture with solar inverter. IEEE Trans. Ind. Electron. 2021, 68, 4309–4319. [Google Scholar] [CrossRef]
- Langston, J.; Schoder, K.; Steurer, M.; Faruque, O.; Hauer, J.; Bogdan, F.; Bravo, R.; Mather, B.; Katiraei, F. Power hardware-in-the-loop testing of a 500 kW photovoltaic array inverter. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4797–4802. [Google Scholar]
- Kim, J.-G.; Kim, S.-K.; Park, M.; Yu, I.-K. Hardware-in-the-loop simulation for superconducting DC power transmission system. IEEE Trans. Appl. Supercond. 2015, 25, 5402404. [Google Scholar] [CrossRef]
- Watanabe, K.; Langston, J.; Hauer, J.; Coleman, M.; Stanovich, M.; Izumida, Y.; Steurer, M. Power hardware-in-the-loop simulation to verify protection coordination for DC microgrid. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 2646–2653. [Google Scholar]
- Gómez-Luna, E.; Candelo-Becerra, J.E.; Vasquez, J.C. A new digital twins-based overcurrent protection scheme for distributed energy resources integrated distribution networks. Energies 2023, 16, 5545. [Google Scholar] [CrossRef]
- Karrari, S.; Noe, M.; Geisbuesch, J. High-speed flywheel energy storage system (FESS) for voltage and frequency support in low voltage distribution networks. In Proceedings of the 2018 IEEE 3rd International Conference on Intelligent Energy and Power Systems (IEPS), Kharkiv, Ukraine, 10–14 September 2018; pp. 176–182. [Google Scholar]
- Debouza, M.; Al-Durra, A.; El-Fouly, T.H.M.; Zeineldin, H.H. Establishing realistic testbeds for DC microgrids studies validation: Needs and challenges. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–8. [Google Scholar]
- Singh, S.K.; Padhy, B.P.; Chakrabarti, S.; Singh, S.N.; Kolwalkar, A.; Kelapure, S.M. Development of dynamic test cases in OPAL-RT real-time power system simulator. In Proceedings of the 2014 Eighteenth National Power Systems Conference (NPSC), Guwahati, India, 18–20 December 2014; pp. 1–6. [Google Scholar]
- Braun, L.; Kist, S.; Eser, D.; Suriyah, M.; Leibfried, T. Stability improvement of a dynamic low-voltage power hardware-in-the-loop environment. In Proceedings of the Conference Sustainable Energy Supply Energy Storage Systems (NEIS), Hamburg, Germany, 16–17 September 2024. [Google Scholar]
- Ihrens, J.; Möws, S.; Wilkening, L.; Kern, T.A.; Becker, C. The impact of time delays for power hardware-in-the-loop investigations. Energies 2021, 14, 3154. [Google Scholar] [CrossRef]
- Lauss, G.F.; Faruque, M.O.; Schoder, K.; Dufour, C.; Viehweider, A.; Langston, J. Characteristics and design of power hardware-in-the-loop simulations for electrical power systems. IEEE Trans. Ind. Electron. 2016, 63, 406–417. [Google Scholar] [CrossRef]
- Braun, L.; Lutz, L.G.; Suriyah, M.; Leibfried, T. Establishing a PLC-based power hardware-in-the-loop setup for power grid applications. In Proceedings of the 2024 9th IEEE Workshop on the Electronic Grid (eGRID), Santa Fe, NM, USA, 19–21 November 2024; pp. 1–5. [Google Scholar]
- Lu, B.; Wu, X.; Figueroa, H.; Monti, A. A low-cost real-time hardware-in-the-loop testing approach of power electronics controls. IEEE Trans. Ind. Electron. 2007, 54, 919–931. [Google Scholar] [CrossRef]
- Resch, S.; Friedrich, J.; Wagner, T.; Mehlmann, G.; Luther, M. Stability analysis of power hardware-in-the-loop simulations for grid applications. Electronics 2022, 11, 7. [Google Scholar] [CrossRef]
- Ashrafidehkordi, F.; Kottonau, D.; Carne, G.D. Multi-rate discrete domain modeling of power hardware-in-the-loop setups. IEEE Open Power Electron. 2023, 4, 539–548. [Google Scholar] [CrossRef]
- Li, F.; Huang, Y.; Wu, F.; Zhang, X.; Zhao, W. Power-hardware-in-the-loop stability analysis of inverter. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Hong, M.; Horie, S.; Miura, Y.; Ise, T.; Dufour, C. A method to stabilize a power hardware-in-the-loop simulation of inductor coupled systems. In Proceedings of the International Conference on Power System Transients (IPST), Kyoto, Japan, 2–6 June 2009; pp. 1–7. [Google Scholar]
- Braun, L.; Kist, S.; Suriyah, M.; Leibfried, T. Stability analysis and real-time optimization of a power hardware-in-the-loop setup. In Proceedings of the 2024 59th International Universities Power Engineering Conference (UPEC), Cardiff, UK, 2–6 September 2024. [Google Scholar]
- Wang, J.; Lundstrom, B.; Mendoza, I.; Pratt, A. Systematic characterization of power hardware-in-the-loop evaluation platform stability. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1068–1075. [Google Scholar]
- Ren, W.; Steurer, M.; Baldwin, T.L. Improve the stability and the accuracy of power hardware-in-the-loop simulation by selecting appropriate interface algorithms. In Proceedings of the 2007 IEEE/IAS Industrial & Commercial Power Systems Technical Conference, Edmonton, AB, Canada, 6–11 May 2007; pp. 1–7. [Google Scholar]
- Lauss, G.; Lehfuß, F.; Viehweider, A.; Strasser, T. Power hardware-in-the-loop simulation with feedback current filtering for electric systems. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 3725–3730. [Google Scholar]
- Dmitriev-Zdorov, V.B. Generalized coupling as a way to improve the convergence in relaxation-based solvers. In Proceedings of the EURO-DAC ’96. European Design Automation Conference with EURO-VHDL ’96 and Exhibition, Geneva, Switzerland, 16–20 September 1996; pp. 15–20. [Google Scholar]
- Edrington, C.S.; Steurer, M.; Langston, J.; El-Mezyani, T.; Schoder, K. Role of power hardware in the loop in modeling and simulation for experimentation in power and energy systems. Proc. IEEE 2015, 103, 2401–2409. [Google Scholar] [CrossRef]
- Brandl, R. Operational range of several interface algorithms for different power hardware-in-the-loop setups. Energies 2017, 10, 1946. [Google Scholar] [CrossRef]
- Loku, F.; Osterkamp, L.; Düllmann, P.; Klein, C.; Maimer, M.; Bergwinkl, T. Utilization of the Impedance-based Stability Criterion for Stability Assessment of PHiL Interface Algorithms. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–7. [Google Scholar]
- Benedetto, G.; Mazza, A.; Pons, E.; Bompard, E. Key Stability Issues in a Power Hardware-In-the-Loop Experiment: Let’s Make it Converge. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar]
- Schwendemann, R.; Stefanski, L.; Hiller, M. Comparison of different interface algorithms for a highly dynamic grid emulator based on a series hybrid converter. In Proceedings of the 2022 IEEE 23rd Workshop on Control and Modeling for Power Electronics (COMPEL), Tel Aviv, Israel, 20–23 June 2022; pp. 1–8. [Google Scholar]
- Feng, Z.; Peña-Alzola, R.; Syed, M.H.; Norman, P.J.; Burt, G.M. Adaptive Smith predictor for enhanced stability of power hardware-in-the-loop setups. IEEE Trans. Ind. Electron. 2023, 70, 10204–10214. [Google Scholar] [CrossRef]
- Pokharel, M.; Ho, C.N.M. Development of interface model and design of compensator to overcome delay response in a PHIL setup for evaluating a grid-connected power electronic DUT. IEEE Trans. Ind. Appl. 2022, 58, 4109–4121. [Google Scholar] [CrossRef]
- Braun, L.; Suriyah, M.; Leibfried, T. Online Impedance Identification and Transfer Function Modeling in PHIL Applications. In Proceedings of the 2025 IEEE International Conference on Environment and Electrical Engineering and 2025 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Chania, Greece, 15–18 July 2025. [Google Scholar]









| in µs | V-ITM/C-ITM | V-ITM/C-ITM with SP | V-PCD | V-PCD with SP ∗ | C-PCD | C-PCD with SP ∗ |
|---|---|---|---|---|---|---|
| 5 | 1.1199 | 2.9692 | 1.0404 | 1.0404 | 1.0404 | 1.0404 |
| 50 | 1.0018 | 2.9994 | 1.0105 | 1.0404 | 1.0521 | 1.0404 |
| 70 | 1.0009 | 2.9997 | 1.0095 | 1.0404 | 1.0465 | 1.0404 |
| 100 | 1.0005 | 2.9999 | 1.0106 | 1.0404 | 1.0435 | 1.0404 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braun, L.; Mader, J.; Suriyah, M.; Leibfried, T. Improvement of Positive and Negative Feedback Power Hardware-in-the-Loop Interfaces Using Smith Predictor. Energies 2025, 18, 3773. https://doi.org/10.3390/en18143773
Braun L, Mader J, Suriyah M, Leibfried T. Improvement of Positive and Negative Feedback Power Hardware-in-the-Loop Interfaces Using Smith Predictor. Energies. 2025; 18(14):3773. https://doi.org/10.3390/en18143773
Chicago/Turabian StyleBraun, Lucas, Jonathan Mader, Michael Suriyah, and Thomas Leibfried. 2025. "Improvement of Positive and Negative Feedback Power Hardware-in-the-Loop Interfaces Using Smith Predictor" Energies 18, no. 14: 3773. https://doi.org/10.3390/en18143773
APA StyleBraun, L., Mader, J., Suriyah, M., & Leibfried, T. (2025). Improvement of Positive and Negative Feedback Power Hardware-in-the-Loop Interfaces Using Smith Predictor. Energies, 18(14), 3773. https://doi.org/10.3390/en18143773







