Hybrid NARX Neural Network with Model-Based Feedback for Predictive Torsional Torque Estimation in Electric Drive with Elastic Connection

Abstract

This paper proposes a hybrid methodology for one-step-ahead torsional torque estimation in an electric drive with an elastic connection. The approach integrates Nonlinear Autoregressive Neural Networks with Exogenous Inputs (NARX NNs) and model-based feedback. The NARX model uses real-time and historical motor speed and torque signals as inputs while leveraging physics-derived torsional torque as a feedback input to refine estimation accuracy and robustness. While model-based methods provide insight into system dynamics, they lack predictive capability—an essential feature for proactive control. Conversely, standalone NARX NNs often suffer from error accumulation and overfitting. The proposed hybrid architecture synergises the adaptive learning of NARX NNs with the fidelity of physics-based feedback, enabling proactive vibration damping. The method was implemented and evaluated on a two-mass drive system using an IP controller and additional torsional torque feedback. Results demonstrate high accuracy and reliability in one-step-ahead torsional torque estimation, enabling effective proactive vibration damping. MATLAB 2024a/Simulink and dSPACE 1103 were used for simulation and hardware-in-the-loop testing.

1. Introduction

Present industrial systems, including emerging electromobility solutions, heavily rely on mechanical transmission systems, which are significant in many fields, such as manufacturing, renewable energy and electric vehicle drivetrains. An example of such a system is the two-mass drive. This drive operates based on a mechanical transmission, where the first mass (the motor) is coupled to the second mass (the load) via a flexible shaft.

In electric vehicles (EVs) and other electromobility applications, where compact, lightweight, and high-efficiency drivetrain designs are paramount, managing the dynamic interaction between motor and load becomes increasingly important. The productivity of such a system depends on the transition time of torque transfer via the shaft. This transition time can be minimised by optimising the control strategy, particularly by increasing the controller gains to improve overall system responsiveness and productivity. However, this improvement comes at the cost of mechanical vibrations, which are inherently excited by shaft flexibility, resonance characteristics, and the dynamic interaction among mechanical components.

These vibrations adversely affect overall system performance by diminishing product quality and accelerating the wear and tear of mechanical components. In extreme cases, they may lead to system failure or reduced passenger comfort (in electromobility applications) due to noticeable vibrations. As a result, recent research has focused heavily on dampening these vibrations to ensure smoother operation and to enhance the productivity of transmission lines [1,2,3,4,5,6,7,8,9,10,11].

In the literature, effective vibration damping is frequently associated with the need for a detailed understanding of the system model or accurate knowledge of plant parameters, particularly the torsional (disturbance) torque. However, directly measuring or estimating this torsional torque is inherently challenging. Various observers, estimators, and filtering techniques have been proposed to address this issue. Nevertheless, achieving robust, accurate, and predictive estimation of the mechanical state variables of the system remains a significant challenge—especially in systems characterised by high nonlinearity, uncertainty, and external disturbances, as commonly seen in applications such as electric vehicles (EVs) with frequent load changes, regenerative braking, and road-induced disturbances.

This issue is even more pronounced in torsional vibration damping, which often relies on additional feedback from torsional torque [2,5,8,12,13,14,15,16,17,18,19,20]. Therefore, developing a robust, accurate, and predictive approach to torsional torque estimation is both essential and challenging, particularly in dual-mass drive systems with flexible coupling, where parameter uncertainties, nonlinearity, and external disturbances must be considered.

Consequently, both industrial experts and academic researchers have investigated various estimation methodologies, which are broadly categorised into four groups in this paper: traditional estimators, filtering techniques, advanced estimators, and intelligent estimators.

The first group includes traditional estimators and observers, with full-state estimators, such as the Luenberger Observer. These observers have been widely employed in dual-mass drive control and vibration damping, particularly in classical studies such as [20,21,22,23,24], which focus on state estimation under the assumption of unchangeable system parameters. These studies highlight the simplicity, computational efficiency, and convergence of full-state observers. However, due to their model-based nature, these methods are inherently sensitive to model uncertainty and parameter variations. This sensitivity results in parameter tuning for each new condition, which is time-consuming and challenging, especially for electric drives with fast dynamics. Furthermore, these types of estimators cannot anticipate future dynamic system behaviour, which is very important for proactive control and vibration damping.

The second group comprises filtering techniques, notably the Kalman Filter (KF), its nonlinear extension, the Extended Kalman Filter (EKF), and the Unscented Kalman Filter (UKF). These methods have been applied to estimate torsional (disturbance) in dual-mass drive systems, as demonstrated in studies such as [25,26,27,28]. These studies show that KF, EKF, and UKF can address nonlinearity by linearising around the current estimate. However, these methods require accurate models and noise assumptions. When model parameters and noise differ from the assumed values, estimation accuracy degrades. As a result, these estimators require expertise in tuning and modelling. Another drawback is their computational intensity, which makes them less suitable for electromobility systems with fast dynamics and tight real-time constraints.

The third group involves advanced estimators, including the Sliding Mode Observer (SMO) and the Disturbance Observer (DOB). In [29,30,31], the SMO is highlighted for using a discontinuous control law to drive the estimation error to zero in finite time, leveraging system nonlinearity to enhance robustness. In a dual-mass drive system, the SMO shows high robustness in high-precision control, as noted in [30]. However, the SMO has limitations. One issue is potential chattering, which increases wear on the physical system. Although higher-order sliding modes can reduce this, they add complexity. Another drawback is that the SMO is reactive, not predictive. It estimates the current states but does not anticipate future behaviour, making it unsuitable for proactive control and vibration-damping applications. Additionally, the SMO is not inherently robust to load parameter changes; its robustness depends on accurate model parameters and well-defined bounds for sliding surface design. Inaccuracies can degrade its effectiveness. Designing the sliding surface, gains, and reaching conditions also requires careful tuning, which can be time-consuming and non-intuitive.

The effectiveness of the DOB in estimating torque disturbance in dual-mass drive systems is demonstrated in [14,15,17,32,33,34,35,36,37]. The DOB estimates disturbances acting on the system, which are then compensated in the control law. When applied to a two-mass drive, the DOB is inherently robust to load parameter changes. Its design relies only on the motor-side parameters, which are most of the time unchanged. The drawback of this observer is that it includes a filter to avoid noise amplification caused by the motor dynamic equation, which involves the first derivative of the motor speed. This filter introduces an estimation delay. Such a delayed response is undesirable, as it leads to estimating and damping torsional oscillations only after they have developed in the system. This observer is also limited in situations where a step-ahead torsional or disturbance torque estimation is important for a proactive response.

Finally, this paper discusses an intelligent estimator, which includes Neural Networks (NNs) and Fuzzy Logic (FL). NN-based state estimators for two-mass drives have been investigated in [38,39,40,41,42,43]. These estimators are well-suited for highly nonlinear systems where accurate modelling is difficult. NNs can adapt to unmodelled nonlinearities in two-mass drive systems and offer predictive capabilities, which are important for anticipating the system’s future dynamic behaviour. This is especially relevant in electromobility, where predictive torque and vibration control can enhance transportation quality, efficiency, and system safety. However, NNs require a large dataset and are computationally intensive. They also face the challenge of balancing model complexity with the risk of overfitting. This trade-off often results in either a computationally intensive model that generalises well or a simpler model that compromises generalisation accuracy.

In [41], FL was applied to estimate mechanical state variables in a two-mass drive. FL is suitable for systems with vague or imprecise data, as it handles uncertainty without requiring a precise mathematical model. However, its performance depends heavily on the accuracy of the rule base and often requires extensive fine-tuning to optimise effectiveness. It is common practice to use NNs to optimise the FL rule base, but this approach inherits the previously discussed drawbacks of NNs.

This paper proposes the application of the Nonlinear Autoregressive model with Exogenous inputs (NARX), implemented using Neural Networks (NNs) with model-based or physics-driven feedback, for one-step-ahead estimation of torsional torque in a two-mass drive. The NARX model operates in open-loop mode, using motor speed (present and past values) and motor torque (present and past values) as input. To improve estimation accuracy during implementation, model-based feedback is incorporated as feedback input. This model-based feedback is derived from the motor’s dynamic equation, which is independent of load parameter changes. However, the direct use of the first derivative of the motor speed in the dynamic equation of the motor amplifies noise. To address this, the derivative term is transformed into an integration-based approach using an Integral-based Disturbance OBserver (IDOB). The IDOB enhances robustness by filtering out high-frequency noise while preserving the dynamics of the system. In general, the proposed method contributes the following nobility to the existing approach:

• Proactive Prediction: Unlike model-based estimators or observers such as SMO, DOB, Luenberger Observer, and other state observers, the proposed method estimates torsional torque one step ahead. This enables anticipatory control, which reactive observers cannot provide. Anticipatory control is crucial for proactive vibration damping, as it helps to reduce torsional oscillations before they fully develop. This improves the efficiency of the drive and prevents the drive from wear and tear caused by vibration. This capability is essential in applications such as electromobility, where proactive vibration damping can extend drivetrain life, reduce noise, and improve passenger comfort.
• Inherent Robustness: The design of both the NARX NN and the model-based feedback is independent of the load-side parameters, such as the load inertia and shaft stiffness. As a result, the proposed method is inherently robust to changes in these parameters. This eliminates extensive tuning, critical design adjustments, and the optimisation process, all of which contribute to numerical complexity and make real-time implementation more difficult.
• Modest Complexity for Implementation: The incorporation of model-based feedback helps the NARX NN to generalise effectively with a simple network structure. Specifically, the proposed method achieves efficient results using just five neurons and one hidden layer. Since the model-based feedback involves only simple mathematical calculations, the proposed method is suitable for real-time implementation.
• The proposed method is compared with different types of neural network estimators and shows superiority in terms of generalisation under parameter changes and network simplicity.

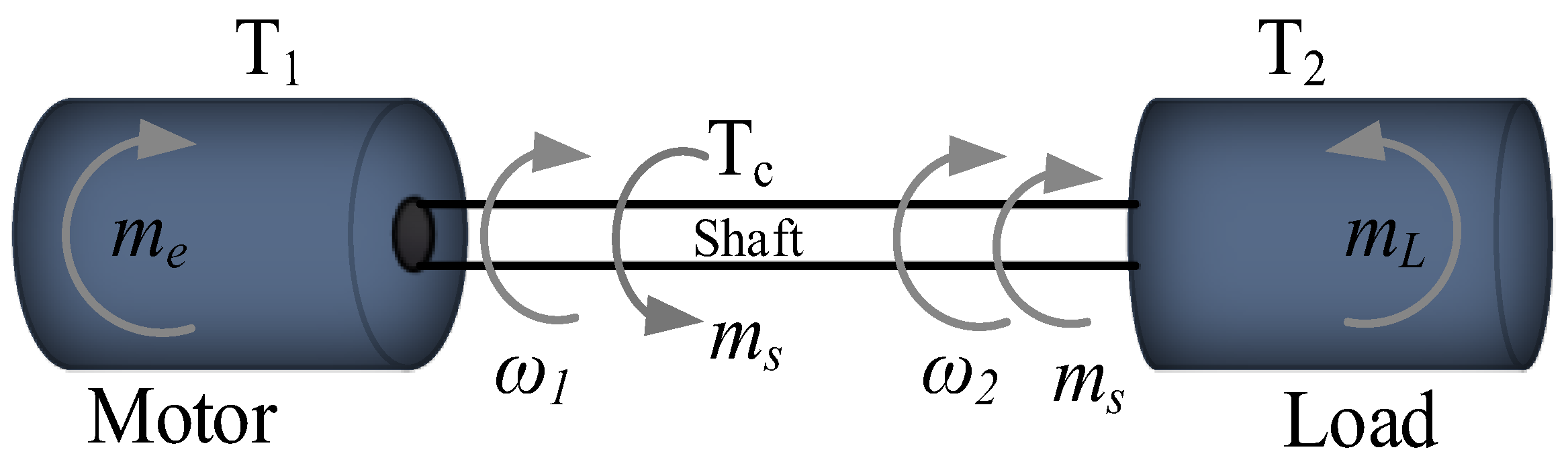
2. Mathematical Modelling of the Considered Dual-Mass Drive

This paper focuses on a two-mass drive, which is composed of a DC motor (driver), a load, and a flexible shaft that connects the driver and the load. The modelling of such a system is analysed using approaches that balance accuracy with computational complexity. Various models, such as field models, wave models, differential equation-based models, and inertial-free models, are discussed in the literature. As noted in [5], the inertial-free model is one of the most widely used methods for modelling two-mass drives and is adopted in this study. Accordingly, the state equation of the considered system is discussed below.

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\omega }_1\left(t\right)\\ {\omega }_2\left(t\right)\\ m_s\left(t\right)\end{array}\right]=\left[\begin{array}{ccc}0& 0& {\displaystyle \frac{-1}{T_1}}\\ 0& 0& {\displaystyle \frac{1}{T_2}}\\ {\displaystyle \frac{1}{T_c}}& {\displaystyle \frac{-1}{T_c}}& 0\end{array}\right]\left[\begin{array}{c}{\omega }_1\left(t\right)\\ {\omega }_2\left(t\right)\\ m_s\left(t\right)\end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{1}{T_1}}\\ 0\\ 0\end{array}\right]\left[m_e\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{-1}{T_2}}\\ 0\end{array}\right]\left[m_L\right]$$

(1)

where ω₁ and ω₂ are the speeds of the motor and load, respectively, m_e, m_s, and m_L are the motor, shaft, and load torques; T₁, T_2, and T_c are the mechanical time constants of the motor, load, and shaft, respectively.

A schematic diagram of the considered dual-mass system is presented in Figure 1.

The analysed system is characterised by the following parameters: T₁ = 203 ms, T₂ = 285 ms, and T_c = 2.6 ms. In this study, the nonlinear torsional torque is treated as a disturbance. The motor torque (m_e) is used as the system’s input control, while the motor speed (ω₁) is considered the system output. This setup ensures that the results are applicable to a wide range of electric motors with high-performance torque capabilities. Nonlinear effects (e.g., backlash, mechanical hysteresis, friction) are neglected for simulation purposes.

3. NARX NN

A NARX NN is a specialised Recurrent Neural Network (RNN) designed to model nonlinear dynamic systems. It predicts the current output as a function of the past outputs and previous external inputs, as indicated in Equation (2). This structure can be extended to predict future outputs by incorporating present output and input values, along with their respective delayed versions, as indicated in Equation (3).

$$y\left(k\right)=f \left(y\right(k-1), y(k-2),\dots ,y(k-d_y), u(k-1),\dots ,u(k-d_u\left)\right)$$

(2)

$$y(k+1)=f \left(y\right(k),y(k-1), y(k-2),\dots ,y(k-d_y), u(k), u(k-1),\dots ,u(k-d_u\left)\right)$$

(3)

where y(k) and y(k + 1) represent the system output at discrete time steps k and k + 1, respectively. The function f(·) is a nonlinear mapping function approximated by NARX NN. u(k) is the input vector at a discrete time step k, and $d_u$ and $d_y$ are the memory lengths for input and output (feedback), respectively, with $d_u\ge 1$ and $d_y\ge 1$.

In recent years, the application of NARX NN for nonlinear dynamic system estimation has gained significant attention. Several studies have demonstrated the effectiveness of NARX NNs in modelling complex dynamic systems and performing accurate nonlinear estimation. For instance, in [44], a NARX NN was used to estimate the actual harmonic contribution of nonlinear loads into microgrid power systems. The study highlights the reliability and accuracy of the NARX-based approach in capturing nonlinear behaviours within such a system. Similarly, in [45], a NARX NN was employed for a model predictive voltage controller for a boost converter. Additional studies have explored its application in areas such as fault detection, classification, monitoring, diagnosis, and speed estimation [46,47,48]. In [49], a NARX NN was used for online parameter tuning of an intelligent PID system.

In these studies, NARX NNs have been discussed in two main configurations: open-loop (series-parallel) and closed-loop (parallel). In the open-loop structure, the network uses actual output values from previous time steps as feedback during both training and practical implementation. In contrast, the closed-loop structure feeds the network’s own predicted output back into the model as delayed feedback. It has been demonstrated that the open-loop configuration is more stable and accurate where the actual output measurement or reliable calculations are available for feedback.

This paper focuses on the application of NARX NNs in two-mass drive systems, specifically for estimating mechanical state variables such as torsional or disturbance torque. Accurate predictive estimation in this context is vital for improving product quality, proactive vibration damping, and ensuring mechanical stability. The key features of NARX NNs that make them well-suited for this application are described below:

-

Dynamic Memory Structure: NARX NNs use delay buffers to capture time-lagged dependencies, making them suitable for two-mass drives, where rapid interaction between variables such as speed, torque, and load raises the complexity of the system.

-

Nonlinear Modelling Capability: Unlike linear models, NARX NNs can approximate complex nonlinear relationships, enabling more reliable estimation under parameter variations and external disturbances.

-

Training Efficiency: In an open-loop configuration, NARX NNs benefit from actual feedback during training. This reduces error propagation and promotes more stable and robust learning.

-

Flexibility: NARX NNs are robust and adaptable to diverse system architectures and operating conditions, making them effective for parameter estimation, control optimisation, and fault diagnosis of electric drives.

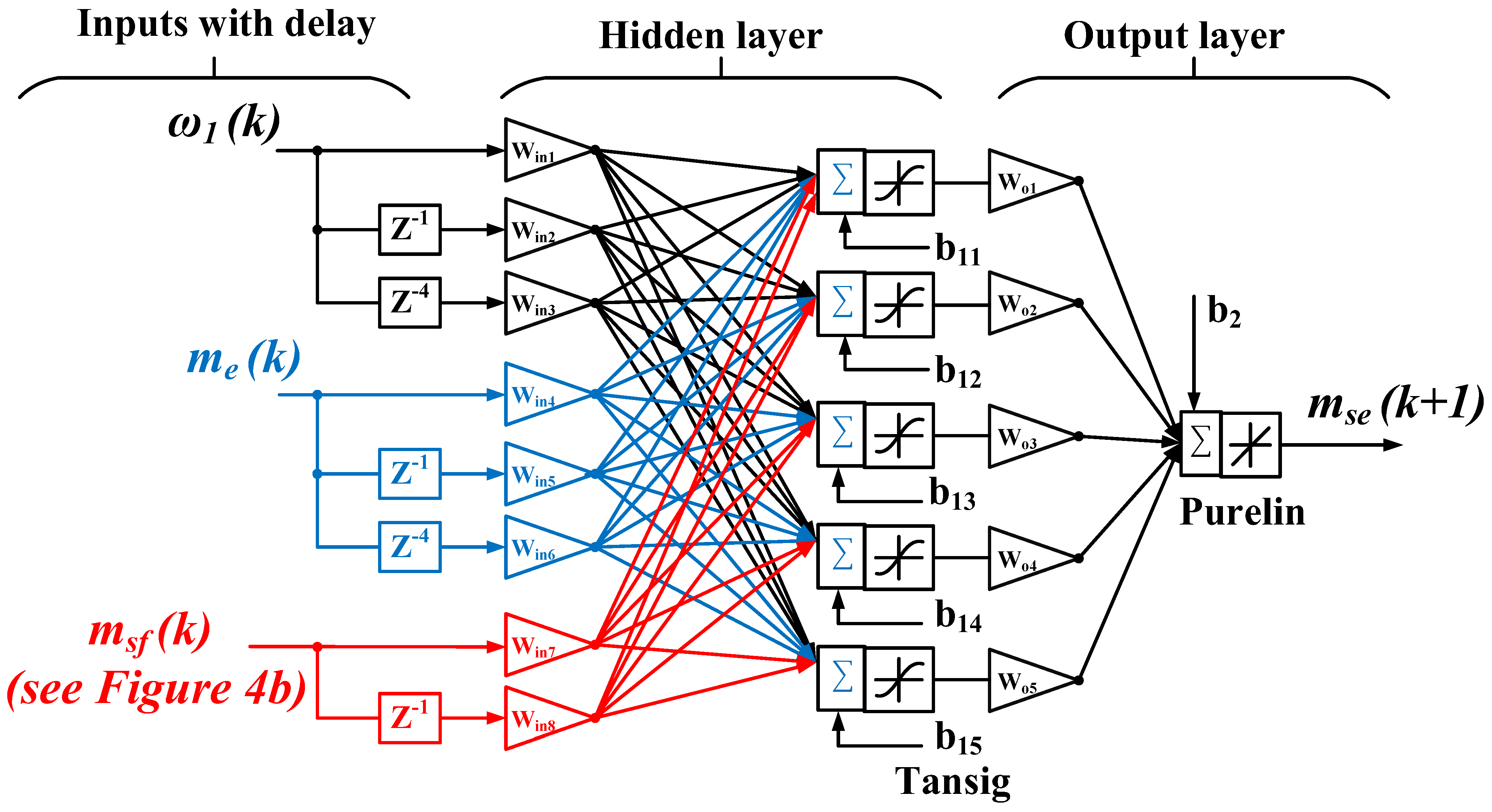
4. Modelling of Hybrid NARX NN with Model-Based Feedback

In this paper, a NARX NN is developed to estimate one-step-ahead torsional torque in a two-mass drive. The network takes the motor torque (m_e) and motor speed (ω₁) along with their corresponding time delays as inputs. A model-based calculated torsional torque (m_sf) is used as a feedback reference during real-time implementation. Diverse training data are generated through simulations conducted in MATLAB/Simulink, using a calculation period of 5 × 10⁻⁴ s (same as in the experiment). The waveforms of the training signals are indicated in Figure 2.

The estimated torsional torque for the given training signals is depicted in Figure 3. As illustrated in Figure 3b, despite the highly chaotic and nonlinear nature of torsional torque, the trained NARX NN achieves an estimation error of approximately 2%. This demonstrates the strong estimation capability of the trained NARX NN and its effectiveness in accurately capturing the system dynamics with minimal error.

The NARX NN configuration incorporates current and previous values of state variables (ω₁, m_e), and feedback (m_sf). The network consists of five neurons in a single hidden layer and one output neuron.. Numerous tests were carried out to determine the optimal number of layers, neurons, and feedback delays, ensuring a balance between model simplicity, predictive accuracy, and generalisation capability.

The model-based feedback is derived from the dynamic equation of the first mass (the driving motor), expressed as follows:

$$m_{sf}=m_e-{\dot{\omega }}_1·T_1$$

(4)

This formulation ensures that the model-based feedback signal depends solely on motor-side parameters, which are typically constant. As a result, the feedback becomes inherently robust against variations in load-side parameters—an essential property for improving estimation accuracy and generalisation capability.

However, calculating the model-based torsional torque involves the first derivative of the motor speed, which tends to amplify high-frequency measurement noise. To mitigate this issue, in many studies, the direct-derivative-based method is replaced by Filtered Derivative Disturbance Observer (FDDOB), as shown in Figure 4a. Although the FDDOB is a widely applicable approach [14,15,17], it poses a challenge in selecting an appropriate filter time constant. This time constant is essential for achieving a suitable trade-off between phase lag and noise amplification.

To address this limitation, an alternative approach is proposed in [5], where the derivative part is replaced with an integrator. This leads to the development of an Integral Disturbance Observer (IDOB), shown in Figure 4b.

For the FDDOB, the filter time constant (tf) is set to 0.01 s, determined through experimental investigation.

According to [5], the characteristic equation of the IDOB shown in Figure 4b is defined as follows:

$$p\left(s\right)=s^3+s^2{\displaystyle \frac{L_1}{T_1}}-s{\displaystyle \frac{L_2}{T_1}}-{\displaystyle \frac{L_3}{T_1}}$$

(5)

By equating this characteristic equation with a standard third-order polynomial design, the observer’s correction factors can be determined as follows:

$${\mathrm{L}}_1={\mathrm{T}}_1\left(2\mathrm{a}\mathrm{p}+\mathrm{p}\right)$$

(6)

$${\mathrm{L}}_2=-{\mathrm{T}}_1\left(2\mathrm{a}{\mathrm{p}}^2+{\mathrm{p}}^2\right)$$

(7)

$${\mathrm{L}}_3=-{\mathrm{T}}_1{\mathrm{p}}^3$$

(8)

Substituting Equations (6)–(8) into Equation (5) results in the desired polynomial for the IDOB, given by:

$$p\left(s\right)=\left(s^2+2aps+p^2\right)\left(s+p\right)$$

(9)

Since the IDOB is defined by a third-order polynomial, it is expected to have three poles and no zeros. For each positive value of a and p, the observer has one real pole at negative p (−p) and two complex conjugate poles with real part at negative ap (−ap) and imaginary parts at $\pm \sqrt{p^2-{\left(ap\right)}^2}$. As shown in Figure 5, all poles lie in the left half-plane, which confirms the stability of the observer for any positive values of a and p. However, selecting appropriate values of a and p is crucial. After performing several simulation tests, the IDOB exhibited optimal performance when a = 1 and p was within the range 60 ≤ p ≤ 120 s⁻¹. To balance the trade-off between fast dynamic response and sensitivity to noise, the value p = 90 s⁻¹ was selected.

After configuring the parameters for both the FDDOB and IDOB, comparative tests were conducted to identify the most effective model-based torsional torque calculation method for use as feedback in the practical implementation of the NARX NN. The evaluation focused on assessing the accuracy and robustness of each method under both noise-free and noisy conditions. The resulting waveforms from FDDOB and IDOB, with and without Gaussian noise, are shown in Figure 6. Based on the results presented in Figure 6a,b, the following conclusions can be drawn:

The FDDOB introduces a noticeable phase lag due to the filtering time constant. Additionally, it shows significant sensitivity to noise. While noise can be reduced by increasing the filtering time constant (tf), this also increases phase lag. Conversely, reducing tf to minimise phase lag leads to greater noise amplification. This inherent trade-off between minimal phase lag and noise sensitivity limits the effectiveness of FDDOB, particularly in applications, such as the proposed method, where high feedback accuracy is essential.

In contrast, the IDOB shows a negligible phase lag and low sensitivity to noise. These properties make it a more favourable and reliable choice for providing model-based feedback in the NARX NN-based one-step-ahead torsional torque estimation framework.

For numerical comparison, the loss function Mean Absolute Error (MAE) is calculated according to Equation (10):

$$MAE={\displaystyle \frac{1}{N}}\sum _{n=1}^{\mathrm{N}}\left|m_{{sf}_{act}}\left(n\right)-m_{{sf}_{IDOB/FDDOB}}\left(n\right)\right|$$

(10)

where n denotes the number of samples.

The obtained results are summarised in

Table 1. MAE comparison of IDOB and FDDOB.

Model-Based Torsional Torque Calculation	MAE
	Without Noise	With Noise
IDOB	0.0145	0.0192
FDDOB	0.0375	0.0474

. As can be seen from Table 1, the MAE for the FDDOB is around 2.59 times higher than that of the IDOB under noise-free conditions. With Gaussian noise, the FDDOB’s MAE remains significantly higher, by a factor of around 2.46, compared to the IDOB. These results clearly show the superior performance of IDOB in terms of estimation accuracy. Furthermore, the MAE values for IDOB are notably low, confirming its stability and applicability for the proposed task.

Following the selection of the optimal feedback model, the architecture of the NARX NN is shown in Figure 7, and it is summarised as follows:

• Input Layer: The exogenous inputs consist of motor speed (ω₁) and motor torque (m_e) at discrete time steps k, k−1, and k−4. Additionally, the model-based feedback signal (m_sf) is included at steps k and k−1. This delay selection was determined empirically through simulation studies. The complete input vector is defined in Equation (11):

  $${X\left(k\right)=\left[{\omega }_1\left(k\right),{\omega }_1\left(k-1\right),{\omega }_1\left(k-4\right),m_e\left(k\right),m_e\left(k-1\right),m_e\left(k-4\right),m_{sf}\left(k\right),m_{sf}\left(k-1\right)\right]}^T$$

  (11)
• Hidden Layer: The hidden layer consists of five neurons, each employing a hyperbolic tangent activation function. The output of the jth neuron is expressed as follows:

  $$h_j\left(k\right)=tanh \left(\sum _i^m{w_{ji}}^{\left(1\right)}{x}_i\left(k\right)+{b_j}^{\left(1\right)} \right)$$

  (12)

  where m is the number of inputs = 1, 2, …, 8, j is a number of neurons = 1, 2, …, 5, w_ji ⁽¹⁾ are input-to-hidden weights, and b_j ⁽¹⁾ are biases.
• Output Layer: The output layer comprises one neuron with a linear activation function, which is applied to estimate one-step-ahead torsional torque m_se (k + 1). The corresponding equation is presented in Equation (13):

  $$m_{se}\left(k+1\right)= \sum _{j=1}^5{w_j}^{\left(2\right)}{h}_j\left(k\right)+b^{\left(2\right)}$$

  (13)

  where j = 1, 2, …, 5 corresponds to the number of hidden neurons, w_j⁽²⁾ are hidden-to-output weights, and b⁽²⁾ is output bias.
• Loss function with Regularisation: To protect against overfitting and achieve good generalisation, the loss function combines Mean Squared Error (MSE) and L2 regularisation. This is indicated in Equation (14):

  $$\begin{array}{c}L={\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N}{\left[m_s\left(k+1\right)-m_{se}\left(k+1\right)\right]}^2\\ +{\displaystyle \frac{\lambda }{2}}\left({{\displaystyle \sum _{i,j}}{w_{ji}}^{\left(1\right)}}^2+{{\displaystyle \sum _j}{w_j}^{\left(2\right)}}^2+{{\displaystyle \sum _j}{b_j}^{\left(1\right)}}^2+{{\mathrm{b}}^{\left(2\right)}}^2\right)\end{array}$$

  (14)

  where m_s (k + 1) and m_se (k + 1) are the actual and estimated torsional torques at step time k + 1, respectively, N is the number of training samples, and λ is the regularisation hyperparameter, optimised via Bayesian regularisation with the value of 0.001.

5. Results

5.1. Testing of NARX NN Estimator

5.1.1. Testing in an Open-Loop Structure/Offline Testing

After training the NARX NN, testing is a critical step to evaluate the model’s generalisation capability to new and unseen data, its robustness to variations in input signals, and its resistance against parameter variation in the drive system. Accordingly, the proposed NARX NN was tested for new signals, as shown in Figure 8. In Figure 9, the estimated signals and their corresponding error transients are shown. During the offline test phase, the actual torsional torque—readily available from the simulation—was used as the reference feedback signal. In contrast, during real-time deployment, the model-based torsional torque, calculated using the structure shown in Figure 4b, was used as feedback for the NARX NN.

The NARX NN was tested for a new dataset under a variation in the load time constant. The numerical analysis results are presented in

Table 2. MAE and RMSE corresponding to Figure 9 under variation in the load time constant.

	T2N	2*T2N	3*T2N	0.5*T2N
RMSE	0.0098	0.0150	0.0180	0.0070
MAE	0.0050	0.0083	0.0105	0.0034

, based on the equation provided in Equation (15).

$$MAE={\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle \sum _{\mathrm{i}}^{\mathrm{N}}}\left|{\mathrm{X}}_{\mathrm{i}}-{\widehat{X}}_{\mathrm{i}}\right|, RMSE=\sqrt{{\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle \sum _{\mathrm{i}}^{\mathrm{N}}}{\left(X_{\mathrm{i}}-{\widehat{X}}_{\mathrm{i}}\right)}^2}$$

(15)

The minimal prediction error shown in Figure 9 was further confirmed by the numerical results presented in Table 2. In particular, the MAEs increased only by 0.0033, 0.0055, and 0.0016 when the load time constant was varied to twice, three times, and half of the nominal value, respectively. Similarly, the RMSEs increased by 0.0055, 0.0082, and 0.0028 for the same variation. These changes are relatively minor, indicating that the proposed NARX NN shows robustness against variations in load parameters.

5.1.2. Testing of NARX NN in a Closed-Loop Structure

To evaluate the proposed estimator in a closed-loop structure, a two-mass drive system with an IP controller and additional feedback from the estimated torsional torque, as depicted in Figure 10, was used.

The proposed control structure was composed of a two-mass drive, IP controller, model-based feedback (m_sf), which is shown in Figure 4b, additional feedback with gain k₁, and an NARX NN-based torsional torque estimator. In this paper, the pole placement method was used to model the transfer function of the control system with additional feedback from torsional torque, as shown in Equation (16).

$$G_{{\omega }_2}\left(s\right)={\displaystyle \frac{{\omega }_2\left(s\right)}{{\omega }_r\left(s\right)}}={\displaystyle \frac{G_r\left(s\right)\left(s^2{T}_2{T}_c+1\right)}{s^3{T}_2{T}_c{T}_1+s^2{T}_2{T}_c{G}_r\left(s\right)+s\left(T_1+T_2\left(1+k_1\right)\right)+G_r\left(s\right)}}$$

(16)

The transmittance of the IP controller and the characteristic equation of the whole system with the proposed control structure are given below.

$$G_r\left(s\right)=k_{\mathrm{p}}+k_{\mathrm{i}}{\displaystyle \frac{1}{s}}$$

(17)

where k_i and k_p are the controller gains.

$$p\left(s\right)=s^4+s^3{\displaystyle \frac{T_2{T}_c{k}_{\mathrm{p}}}{T_1{T}_2{T}_c}}+s^2{\displaystyle \frac{T_2{T}_c{k}_{\mathrm{i}}+T_1+T_2+T_2{k}_1}{T_1{T}_2{T}_c}}+s{\displaystyle \frac{k_{\mathrm{p}}}{T_1{T}_2{T}_c}}+{\displaystyle \frac{k_{\mathrm{i}}}{T_1{T}_2{T}_c}}$$

(18)

The coefficients of the IP controller and the feedback gain are calculated as follows:

$$k_p=4\xi {\omega }^3{T}_1{T}_2{T}_c$$

(19)

$$k_i={\omega }^4{T}_1{T}_2{T}_c$$

(20)

$$k_1=\left(2{\omega }^2+4{\xi }^2{\omega }^2\right)T_1{T}_c-{\omega }^4{T}_1{T}_2{T}_c^2-{\displaystyle \raisebox{1ex}{$T_1$}\!\left/ \!\raisebox{-1ex}{$T_2$}\right.}-1$$

(21)

To further evaluate the performance of the proposed NARX NN in a more practical approach, it was integrated into a closed-loop control system in the presence of noise. For the presented two-mass drive system with an IP controller and additional feedback from torsional torque, the prediction capabilities of the NARX NN were tested under the influence of Gaussian noise. The closed-loop transient responses are presented in Figure 11 and Figure 12. Gaussian noise was added to the motor speed signal to represent measurement noise, which is common in real-world applications. As shown in Figure 11a, the presence of the Gaussian noise is visible in the motor speed transient response, and its impact is also reflected in the electromagnetic or motor torque, as presented in Figure 11b. However, there are no visible noises or oscillations in the load speed (Figure 11a), which shows the effectiveness of the proposed control structure.

The actual and estimated torsional torques, along with the corresponding estimation error under variation in the load time constant, are depicted in Figure 12. From the illustrated waveforms, it can be concluded that the NARX NN can predict the torsional torque at a time step k + 1 with minimal noise and no significant degradation in performance as the load time constant varies. This observation is supported by the numerical analysis shown in

Table 3. MAE and RMSE corresponding to Figure 12 under variation in the load time constant.

	T2N	2*T2N	3*T2N	0.5*T2N
RMSE	0.0194	0.0154	0.0167	0.0070
MAE	0.0129	0.0116	0.0129	0.0175

.

The estimation error shown in Figure 12 is further confirmed by the numerical results in Table 3. The MAE decreases by only 0.0013 for twice the nominal value of the load time constant, remains unchanged for three times the nominal value, and increases slightly by 0.0046 when the nominal value is reduced by half. Similarly, the RMSE increases by 0.004, 0.0027, and 0.012 for the same variation. These changes are relatively minor, highlighting the strong robustness of the NARX NN against variations in load parameters.

Furthermore, the NARX NN was tested under impulse noise to evaluate its robustness. Two noise levels were considered: (i) low to moderate impulse noise levels (±2% to 5%) and (ii) high-level impulse noise (±7% to 10%). The corresponding results are depicted in Figure 13. As demonstrated in Figure 13a, the NARX NN shows good tolerance to low and moderate impulse disturbances. However, as shown in Figure 13b, it appears sensitive to higher impulse levels. Despite this, the network consistently recovers quickly to its original trajectory after each disturbance, which indicates good generalisation capability of the model. Overall, despite the impulse disturbances, the NARX maintains trajectory stability and returns to accurate tracking.

5.2. Experimental Verification

The simulation results were confirmed through laboratory experiments using a test bench designed for dual-mass systems research. The stand comprised two separately excited DC machines—Komel (Katowice, Poland) PZBb22b driving motor and Komel Poland PZBb22b generator dissipating the generated power to a braking resistor, which serves as the load. The motor has a rated power of 500 W, a rated armature circuit voltage of 220 V, a rated armature circuit current of 3.15 A, and a rated excitation circuit current of 0.254 A. The generator has a rated power of 400 W, a rated armature circuit voltage of 230 V, a rated armature circuit current of 1.74 A, and a rated excitation circuit current of 0.42 A. Both machines have a nominal speed of 1450 rpm. The initial time constants implied directly from the moment of inertia are 0.203 s for the motor and 0.285 s for the generator. The test bench allows for changing the time constant of the loading machine—this was achieved by attaching steel discs of varying thicknesses and weights on the load side. The machines are coupled via an elastic, steel shaft, with a length of 600 mm and a diameter of 5 mm, which has a time constant of 0.0013 s.

The driving motor is powered by an H-bridge power converter and each machine is excited using a diode rectifier. An incremental encoder generating 36,000 pulses per revolution is connected to each machine. The encoder mounted to the driving motor is integrated into the control system, whereas the encoder on the load machine is employed exclusively for data collection to evaluate the performance of the system estimation. The LEM transducer is used to measure the current. The dSPACE 1103 rapid prototyping board, designed for real-time operation, was used for experiments. It is based on a PowerPC processor and a Texas Instruments TMS320F240 DSP microcontroller. The PC software used for defining reference signals, changing controller parameters, taking measurements, and visualising them in real time was dSPACE Control Desk 3.7.3. Embedded software code was generated by a Coder application, directly from the MATLAB Simulink model. The PWM for the H-bridge works at 7 kHz. The sampling of speed and DC drive current was set to 2 kHz.

A schematic diagram of the experimental setup, along with its parameters, is presented in Figure 14.

The experimental test was performed at a reference speed of 0.2 p.u. under varying load time constants. The load time constant was varied using an additional disc on the load side. The nominal load time constant was 0.285 s. In addition, the NARX NN was also tested twice at the nominal load time constant (0.57 s) and three times at the nominal load time constant (0.855 s). The resulting waveforms are shown in Figure 15, and the numerical calculation of the MAE and RMSE is presented in

Table 4. MAE and RMSE corresponding to Figure 15 under variation in the load time constant.

	T2N	2 T2N	3 T2N
RMSE	0.0061	0.0063	0.0070
MAE	0.0047	0.0047	0.0057

.

The prediction errors and variation in the errors under variation in load time constant are notably minimal, indicating strong accuracy and generalisation capability of the trained NARX NN. Specifically, the MAE shows no change when the nominal load time constant is doubled and increases only by 0.001 when tripled. Similarly, the RMSE increases by 0.0002 and 0.0009 for the same variation in the load time constant. These values are smaller compared to the results in Table 3. This discrepancy is caused by the presence of measurement noise in the actual signals, in contrast to the simulation setup, where the noise was introduced only in the estimation process and the actual signals were noise-free. Nevertheless, the simulation results are confirmed to be correct by the experiment. The transient responses of the load and motor speeds, as well as the electromagnetic torque for the proposed method, are depicted in Figure 16, further validating the accuracy and effectiveness of the proposed approach.

The NARX NN was also tested under varying load conditions to assess its adaptability. The results are shown in Figure 17a, and the corresponding estimation performance with error bars is depicted in Figure 17b. As observed in Figure 17a, the NARX NN performs accurately and effectively across different load conditions, although it exhibits minor sensitivity to sudden spikes. These anomalies are likely caused by backlash and friction effects, which are consistent with the networks’ previously noted response to impulse disturbances.

To further evaluate the reliability of the NARX NN, a 95% confidence interval (CI) was calculated for each estimation, based on the standard deviation of the residuals. Error bars and shaded regions are used in Figure 17b to visualise the associated uncertainty.

Performance metrics, including the root mean square error (RMSE) and mean absolute error (MAE), were used to quantify estimation accuracy and generate the confidence interval. The results are summarised as follows:

• RMSE: 0.0081 (95% CI: 0.0076–0.0086)
• MAE: 0.0049 (95% CI: 0.0048–0.0049)

These findings confirm the statistical robustness and estimation reliability of the proposed approach.

The proposed method is also compared with different neural network estimators developed in previous studies [42,43]. These referenced works were conducted by different researchers using the same dual-mass drive system with the same parameters as considered in this paper. The comparison focuses on generalisation capability and model complexity, as summarised in

Table 5. Comparison of different neural network estimators based on generalisation capability.

Neural Network Estimator Type	MAE for			Error Increasing (+) or Decreasing (−) Factor Compared to Nominal Value
	Nominal Value of Load Time Constant (T2N)	Twice the Nominal Value of Load Time Constant (2*T2N)	Three Times the Nominal Value of Load Time Constant (3*T2N)	Twice the Nominal Value (2*T2N)	Three Times the Nominal Value (3*T2N)
LSTM [42]	2.05%	N/A	9.09%	N/A	+7.04%
CNN [42]	2.02%	N/A	9.10%	N/A	+7.08%
Parallel neural network, [42]	2.07%	N/A	8.36%	N/A	+6.29%
Feed forward NN optimised by Levenberg–Marquardt training and genetic algorithm [43]	1.00%	2.54%	N/A	1.54%	N/A
Proposed method (NARX NN + model-based feedback)	0.47%	0.47%	0.57%	0%	0.1%

and

Table 6. Comparison of different neural network estimators based on complexity.

Neural Network Estimator Type	Number of Inputs	Number of Hidden Layers	Total Number of Hidden/Output Layer Neurons	Hidden/Output Layer Activation Function Type	Filter Application
LSTM [1]	2	4	85	sigmoid and tanh/linear	Yes
CNN [1]	2	3	96	sigmoid, and tanh/linear	Yes
Parallel neural network [1]	2	7	117	ReLU, sigmoid, and tanh/linear	Yes
Feed forward NN optimised by Levenberg–Marquardt training and genetic algorithm [2]	6	2	12	tanh/linear	Yes, with a 5 ms filter time constant
Proposed method (NARX NN + model-based feedback)	5	1	6 neurons, and an additional 3 integration, 3 summation, and 3 multiplication operations from the model-based feedback.	tanh/linear	No

, respectively.

The result clearly shows the superiority of the proposed method in both generalisation capability and computational simplicity, which is important for real-time implementation.

6. Conclusions and Future Work

In this paper, a NARX NN with model-based feedback is proposed for one-step-ahead estimation of torsional torque in a two-mass drive system. Estimating torsional torque in advance enables the control system to counteract or damp potential vibrations before they fully develop, thereby protecting the drive from mechanical damage, reducing wear and tear, and improving both product quality and operational stability.

The key findings and contribution of this work are summarised as follows:

-

A NARX NN was trained using motor speed and torque as input signals, with the torsional torque as the target output. During offline simulations, the actual torsional torque (available from the simulation) was used as feedback to train, test, and validate the network. In real-time implementation, the NARX NN operates in an open-loop structure, where a model-based torsional torque is used as feedback instead of the network’s estimation.

-

For strong estimation accuracy and generalisation, the model-based feedback must be robust to measurement noise and parameter variation. To ensure this, a comparative study was conducted between the widely used filtered derivative disturbance observer (FDDOB) and the newly developed integral-based disturbance observer (IDOB). The IDOB demonstrated superior performance and was therefore selected for the proposed approach.

-

The proposed IDOB design is independent of the load parameters, which makes it inherently robust to load parameter changes. This eliminates the need for intensive tuning and parameter adjustment, which is a major drawback in state observers such as Luenberger Observers.

-

Although other model-based estimation methods like SMO, KF, EKF, and UKF could also be considered, the IDOB has a simpler design while maintaining robustness to load parameter changes without requiring additional tuning and complex setups.

-

Given these advantages, the IDOB was used to compute the torsional torque as feedback input to the open-loop NARX NN, forming a hybrid estimator for one-step-ahead torsional torque estimation. The NARX NN uses present and historical values of the motor speed, motor torque, and the calculated torsional torque to perform the estimation.

-

The proposed estimator was tested on a two-mass drive system with an IP controller and additional feedback from the estimated torsional torque. Both simulation and experimental results confirm the proposed estimator’s accuracy, robustness to noise, and adaptability to parameter variation, leading to effective vibration damping and smooth system operation.

-

The generalisation capability and computational efficiency of the proposed method were compared with several existing neural network estimators, including Long Short-Term Memory (LSTM) networks, Convolutional Neural Networks (CNNs), parallel neural networks, and feedforward neural networks trained using the Levenberg–Marquardt algorithm and genetic algorithms. The proposed method showed superior performance in terms of both generalisation and simplicity.

Future works will focus on the following:

-

Enhancing training by experimenting with different activation functions, optimisation algorithms, and noise injections, and performing a more in-depth analysis of the estimator’s performance under variation in disturbance types and levels.

-

Improving damping performance by incorporating additional feedback from the torsional torque derivative. This will increase the quality and reliability of the proposed method for practical implementation.