Abstract
This study presents an innovative methodology to optimize the operation of distribution transformers through the estimation of hourly load curves, aimed at minimizing technical losses due to oversizing, particularly in systems lacking advanced metering infrastructure. The proposed approach combines clustering techniques, K-Means with DTW, to identify representative daily consumption patterns and a supervised model based on LightGBM to estimate hourly load curves for unmetered transformers, using customer characteristics as input. These estimated curves are integrated into a process that calculates technical losses, both no-load and load losses, for different transformer sizes, selecting the optimal rating that minimizes losses without compromising demand. Empirical validation showed accuracy levels of 95.6%, 95.29%, and 98.14% at an individual transformer, feeder, and a complete electrical system with 16,864 transformers, respectively. The application of the methodology to a real distribution system revealed a potential annual energy savings of 3004 MWh, equivalent to an estimated economic reduction of 150,238 USD.
1. Introduction
1.1. Context
Distribution utilities face the challenge of improving operational efficiency, reducing technical losses, and optimizing infrastructure investment. Growing energy demand and global sustainability commitments have driven the need for power system overhaul. Distribution transformers, because of their strategic role in the electricity supply chain, represent one of the main elements on which to apply energy and economic optimization []. Recent studies on the carbon footprint of transformers show that efficient resizing could contribute significantly to the decarbonization objectives of the electricity sector [,]. The United for Efficiency (U4E) initiative estimates that proper management of this equipment could avoid the emission of up to 450 million tons of CO2 by 2040 [].
In this context, methodologies are required to enable optimal selection and sizing of distribution transformers, aiming to minimize energy losses and enhance operational efficiency. Recent studies have expanded the traditional focus on electrical design to include real-world operating conditions, such as the presence of harmonic currents, energy efficiency standards, and the regulatory and economic implications throughout the transformer’s life cycle [,,]. Additionally, works such as [,] propose strategies to reduce losses by analyzing transformer behavior under varying load conditions.
However, a major limitation in many developing countries is the lack of advanced metering infrastructure, which restricts access to detailed hourly load data and complicates accurate transformer sizing. Therefore, it becomes essential to develop a comprehensive methodology capable of evaluating the current operational status of distribution transformers, estimating their actual load profiles, and guiding optimal sizing decisions minimizing technical losses and operational costs, while improving the efficiency and reliability of power distribution systems.
1.2. Related Works
The need for efficient strategies to reduce losses in electrical systems has been widely documented in the technical literature. In [], the waste of electrical energy associated with the use of inefficient appliances and inadequate consumption habits is analyzed. On the other hand, Ref. [] studies the sensitivity of losses considering the transformer equivalent model and the impact of different load levels, which reaffirms the importance of efficient transformer management to guarantee the quality and continuity of service, minimize technical losses, and optimize the use of resources in infrastructure planning.
Given the limited availability of advanced metering infrastructure in many distribution networks, indirect methodologies are required for load profile estimation. In this context, data clustering, such as the K-Means algorithm with dynamic distance (DTW), has proven effective in generating representative load curves []; a technique based on artificial neural networks (ANN) for estimating transformer loading from incomplete records is proposed in []. Complementarily, Ref. [] presents a machine learning model to predict the load in buildings considering thermal and operational variables.
A particularly relevant contribution is the work of [], who emphasize that transformer-level load clustering improves planning decisions by characterizing transformer aging and supporting Demand Side Management (DSM). This methodology reduces information complexity for utilities and identifies opportunities for flexibility and efficiency at the low voltage level. Likewise, Ref. [] proposes a clustering approach based on wavelet transform and big data processing with Spark, allowing efficient handling of high-dimensional load data and supporting the implementation of demand response strategies in industrial contexts.
On the other hand, predictive models based on machine learning algorithms were used to estimate with high accuracy the hourly load curves corresponding to each transformer. For example, Ref. [] applies LightGBM to predict bus power consumption, highlighting its accuracy and low computational cost. In line with these efforts, Ref. [] demonstrate that load clustering not only improves transformer sizing but also minimizes the Total Owning Cost (TOC), reinforcing the importance of accurate consumption pattern recognition in transformer investment decisions.
Several studies have evidenced that optimization algorithms, such as exhaustive search [] or optimized loadability models like [], can significantly improve transformer sizing, reducing both load and no-load losses [,,]. This strategy not only increases the operational performance of the system but also contributes to minimizing the cumulative environmental impact by considering the entire transformer life cycle [,,]. As demonstrated by [], integrating genetic algorithms in transformer sizing allows simultaneous optimization of number, location, and capacity of transformers, achieving significant reductions in losses and investment costs.
Energy and economic optimization of transformers has been approached from different perspectives. In [], for example, a prototype transformer with hybrid core was designed and fabricated to reduce magnetic losses. In [], a comparative study between long term memory (LSTM) and transformer architectures was carried out to improve their sizing and prevent failures by accurately determining the rated power to be installed. Likewise, Refs. [,] analyzed methods to determine adequate loss capitalization values, essential for decision making in equipment resizing. In Ref. [] IEC 60076-7 standard is applied to estimate the temperature limits of distribution transformers and to identify the optimal transformer capacity for a distribution substation, based on the critical thresholds and constraints defined by the standard.
From a technical perspective, Ref. [] introduces a tool for calculating losses caused by harmonic currents, a phenomenon increasingly common in modern urban networks. In the same line, Ref. [] presents an improved algorithm to calculate losses in power transformers due to harmonics. In parallel, Ref. [] demonstrates the use of clustering for segmenting feeders with similar energy loss patterns, facilitating a representative sampling of distribution networks and enabling targeted efficiency measures even in the absence of detailed measurements.
Regarding energy efficiency, Refs. [,] propose an approach based on the carbon footprint, demonstrating that an adequate selection and operation of the transformer can generate a positive environmental impact.
Pooling methods have also evolved. For example, Ref. [] analyzes the efficiency of clustering techniques for grouping primary feeders with similar energy loss patterns. In the field of predictive models and artificial intelligence, Ref. [] proposes the Sparrow Search Algorithm optimized BP network (SSA-BP) algorithm to predict losses in unbalanced networks, while Ref. [] demonstrates how intelligent monitoring can improve the efficiency of electrical control in low-voltage networks, reducing both technical losses and energy theft.
Several papers such as [,,,] document the application of mathematical models and metaheuristic techniques for the economic sizing of transformers.
In this context, it is necessary to establish a methodology for sizing distribution transformers in locations where smart metering is unavailable. This work presents a comprehensive methodology for optimizing the operation and sizing of distribution transformers, with the goal of minimizing the technical losses associated with these devices. The proposed approach is based on the estimation of hourly load curves using historical records and the characteristics of connected users.
The methodology is structured into three main stages. In the first stage, unsupervised clustering techniques are applied specifically, the K-Means algorithm combined with the Dynamic Time Warping (DTW) distance, on historical load data from a sample of distribution transformers, to identify representative load curves that capture distinct demand behavior patterns.
In the second stage, a supervised model based on LightGBM is trained to assign these representative curves to the remaining transformers in the system. The model uses input features such as the type and number of connected users to estimate the individual hourly load curve for each transformer.
Finally, an optimization process is implemented to evaluate the no-load and load losses of transformers under different rated capacities. This process uses loss parameters defined in the NTE INEN 2114 [] and NTE INEN 2115 [] technical standards as reference. The optimal transformer capacity is the one that minimizes total losses while ensuring that the projected demand is met with a safety margin to accommodate future load growth.
The proposed methodology enables more accurate planning decisions, reduces energy losses in transformers, and quantifies the economic benefits associated with more efficient sizing. It is a replicable tool designed for contexts with limited availability of operational data. This paper is organized as follows: Section 2 describes the materials and methods; Section 3 presents the results through technical analysis and discussion; and Section 4 presents the conclusions and future work.
2. Materials and Methods
To address the distribution transformer power optimization problem, a systematic methodology, illustrated in Figure 1, was developed and applied to the operating data of Empresa Eléctrica Ambato Regional Centro Norte S.A., EEASA, located in Ambato of Ecuador.
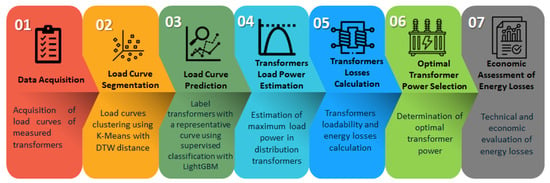
Figure 1.
Methodological framework for optimizing transformer operation using load estimation with K-Means clustering.
2.1. Data Acquisition
This work uses load records of 208 distribution transformers collected and processed in []. The load measurements have a time stamp every 10 min for a continuous period of seven days. Variables considered include apparent power in kVA, georeferenced location of transformers, and the number of customers by user type—residential, commercial, industrial, street lighting, and others.
In addition, extra data provided by EEASA was used, such as monthly consumption of consumers, public lighting and traffic lights, as well as transformer ratings and georeferencing connected to the electric system of this distribution company. As of March 2025, EEASA had a total of 311,546 customers, of which 86.5% belonged to the residential segment, followed by 9.8% commercial, 1.9% industrial, and 1.7% corresponding to other categories, as shown in Figure 2a. These proportions are consistent with the sample of transformers selected, as illustrated in Figure 2b, which represents the distribution of customers connected to the 208 transformers analyzed. In this sample, 89.1% of the customers are residential, 8.1% commercial, 1.8% industrial, and 1.0% belong to other categories.
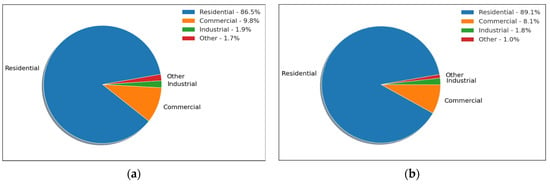
Figure 2.
Distribution of customers by tariff: (a) distribution of total customers in EEASA; (b) distribution of customers in sampled transformers.
2.2. Load Curve Segmentation
From the transformer measurement records, representative load curves were identified for the distribution transformers. These curves allow characterization of the typical load behavior under real operating conditions and, consequently, to estimate more accurately the maximum demand. To perform this segmentation, the methodology proposed in [] was applied, which combines the K-Means algorithm with the Dynamic Time Warping (DTW) metric. This combination has proved to be effective for time series clustering, as it captures similarities in curve shapes even when temporal shifts are present.
In the referenced comparative study, the authors evaluated this technique against other methods such as K-Shape and DBSCAN, concluding that the combination of K-Means with DTW provides superior segmentation. Specifically, they reported a cross-correlation similarity index of 0.9552 and a temporal consistency index of 0.9642, supporting the robustness and accuracy of this methodology for load profile classification.
2.3. Load Curve Prediction
Once the representative load curves were segmented, a supervised classification model was trained to predict which curve each transformer corresponds to. This prediction allows extension of the load behavior estimation even to transformers that do not have historical records.
For this purpose, the Light Gradient Boosting Machine (LightGBM) algorithm, selected for its high accuracy and computational efficiency, was used. This algorithm classifies transformers within previously defined clusters, using as input the available variables detailed in Table 1. LightGBM is based on decision tree techniques and builds models as ensembles using the gradient boosting approach. This method iteratively optimizes a loss function by fitting models through gradient minimization, which allows the efficient capture of complex nonlinear relationships.

Table 1.
Variables used for transformer load curve estimation with LightGBM.
The selection of LightGBM is supported by comparative studies in the energy domain, such as the one presented in [], where various algorithms including Linear Regression, Random Forest, and Support Vector Machines were evaluated. In this study, LightGBM achieved the highest prediction accuracy, with a coefficient of determination R2 of 0.995, a mean absolute percentage error (MAPE) of 3.92%, and a root mean squared error (RMSE) of 1.398 kWh on an independent test set. These results support LightGBM’s capability and reliability for energy consumption prediction tasks.
2.4. Estimation of Maximum Load Power in Distribution Transformers
Using the projected daily load curve and the recorded monthly energy consumption of the loads connected to each transformer, the maximum operating power of each unit is estimated with Equation (1). This formula establishes a relationship between the monthly energy consumed by the users connected to a transformer and the corresponding normalized daily load curve. The monthly electricity consumption data were obtained from EEASA’s Commercial System, while the consumption associated with public lighting and traffic signals was integrated using the georeferenced ArcGIS database.
In Equation (1) Pmax is the estimated maximum load power of the transformer; KWℎconnected_load is the monthly energy consumption of the customers connected to the transformer, including public lighting and traffic lights; Δt is the time interval between each point on the normalized load curve (10 min = 1/6 h); t is the number of days in the analyzed month; and ∑Pi is the sum of the instantaneous values of the normalized daily load curve assigned to the transformer.
This approach enables the estimation of peak demand by scaling the normalized load curve to align with the total measured energy consumption, providing a realistic approximation of the transformer’s maximum operating power.
The resulting load power estimates make it possible to identify oversized or underutilized transformers, supporting more accurate technical planning. This information is essential for reducing technical losses, optimizing existing infrastructure, and enhancing the operational efficiency of the distribution system.
2.5. Transformer Losses Calculation
2.5.1. Technical Losses in Distribution Transformers
Transformer losses consist of core losses, also known as no-load losses, which are constant and independent of the load, and are primarily caused by hysteresis and eddy currents in the transformer core and copper losses, also referred to as load losses, which vary with the square of the current flowing through the windings.
Manufacturers typically provide no-load and load loss values at the rated power of the transformer. In this study, the maximum allowable losses were used, calculated according to Equations (2)–(9), as specified in the Ecuadorian Technical Standards: NTE INEN 2114:2004 [] for single-phase transformers and NTE INEN 2115:2004 [] for three-phase transformers.
Single-phase transformers between 3 and 167 kVA.
Three-phase transformers from 15 kVA up to 150 kVA
Three-phase transformers greater than 150 kVA up to 800 kVA
Three-phase transformers greater than 800 kVA up to 2000 kVA
In Equations (2)–(9) PFe are the no-load losses, PCu are the load losses, and Sn is the rated power of the transformer.
Figure 3 illustrates the evolution of allowable losses as a function of the rated transformer power. Figure 3a depicts the no-load losses, which constitute a continuous source of energy losses and are particularly significant in oversized transformers. Conversely, Figure 3b shows the load losses, which increase substantially with transformer power since they depend on the square of the current flowing through the windings. This behavior underscores the importance of selecting the appropriate transformer rated capacity to minimize technical losses and optimize the performance of the electrical distribution system. It is worth noting that, in the case of two-phase transformers, the losses are assumed to be of the same magnitude as those of three-phase transformers, since the Ecuadorian technical standards do not specify maximum allowable loss values for two-phase trans-former configurations.
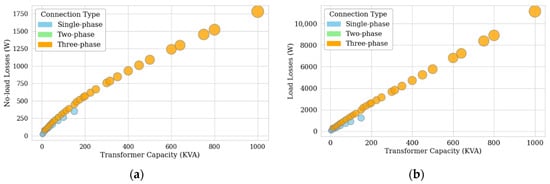
Figure 3.
Power losses in distribution transformers classified by the number of phases [W]: (a) no-load losses; (b) load losses at rated power.
The total losses for a given load level are calculated by Equation (10), which considers the transformer load rating:
In Equation (10) ΔPTotal are the total losses in the transformer, PFe are the no-load losses, and PCu are the load losses at rated power; C is the load rating of the transformer.
The load rating C is defined as the ratio of the actual load power to the rated power of the transformer. Substituting this definition into Equation (10), the total losses can be expressed as follows:
In Equation (11) ΔPTotal are the total losses in the transformer, PFe are the no-load losses, and PCu are the load losses at rated power; SL is the load power of the transformer and Sn is the rated power of the transformer.
This quadratic dependence of copper losses on load current arises from the physical principle that resistive losses vary with the square of the current (I2R). The values of PFe and PCu are determined in accordance with the maximum permissible limits specified in the Ecuadorian Technical Standards, NTE INEN 2114:2004 and NTE INEN 2115:2004, for single-phase and three-phase distribution transformers, respectively
Figure 4 presents the behavior of the losses under different load levels. For this purpose, Equation (11) was applied to different transformer power ratings, considering load levels of 25%, 50%, 75%, and 100%. Since the no-load losses remain constant, depending mainly on the core design and the applied voltage, it is observed that the increase in total losses is directly related to the increase in load.
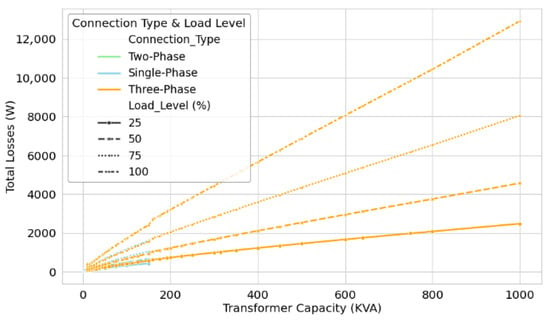
Figure 4.
Sensitivity of total losses in distribution transformers as a function of the load percentage.
2.5.2. Transformer No-Load Loss Energy
The annual no-load energy losses of transformers are calculated using Equation (12), which results from multiplying the no-load losses by the time t = 8760 h per year:
In Equation (12) ELoss_Fe represents the transformer no-load loss energy in kWh, PFe are the transformer no-load losses in kW, and t is the time in hours.
2.5.3. Transformer Load Loss Energy
The annual energy losses associated with transformer load losses are estimated using Equation (13). This calculation is based on the daily load curve, which is divided into 144 intervals representing 10 min periods. At each time step i, the load index Ci is computed in per unit and multiplied by the transformer’s rated load losses PCu, provided by the manufacturer in kW.
Assuming that load losses vary with the square of the load index, the instantaneous loss at each interval is evaluated as PCu⋅Ci2. These losses are then integrated over the day by summing across all intervals and multiplying by the time step duration Δt (10 min = 1/6 h) to obtain the daily load energy loss. Finally, this daily value is scaled to an annual estimate by multiplying by 365 days:
In Equation (13), ELoss_Cu represents the annual energy losses with load, expressed in kWh; PCu refers to the load losses of the transformers in kW, as specified by the manufacturer; Ci is the load index at each instant of time i from the load curve; Δt = 1/6 is the time interval in hours, each 10 min; 144 is the number of intervals per day.
2.5.4. Total Annual Energy Losses
The total annual energy losses are obtained by summing the no-load and load losses, as expressed in Equation (14):
In Equation (14) ELoss_Tot represents the total annual energy losses, ELoss_Fe is the no-load energy loss in kWh, ELoss_Cu is the annual load energy loss in kWh.
2.6. Selection of the Optimal Transformer
The selection of the optimal transformer is based on minimizing the total technical energy losses, which include both no-load losses (PFe) and load losses (PCu), considering a projected maximum load that incorporates an additional 40% margin to account for future demand growth.
As illustrated in Figure 5, the process begins with the identification of the transformer’s actual kVA rating, the projected peak load, and a list of standardized kVA ratings that comply with the technical loss limits established by the Ecuadorian Technical Standards, NTE INEN 2114:2004 (for single-phase) and NTE INEN 2115:2004 (for three-phase) distribution transformers. These standardized ratings form the pool of candidates for the optimization.
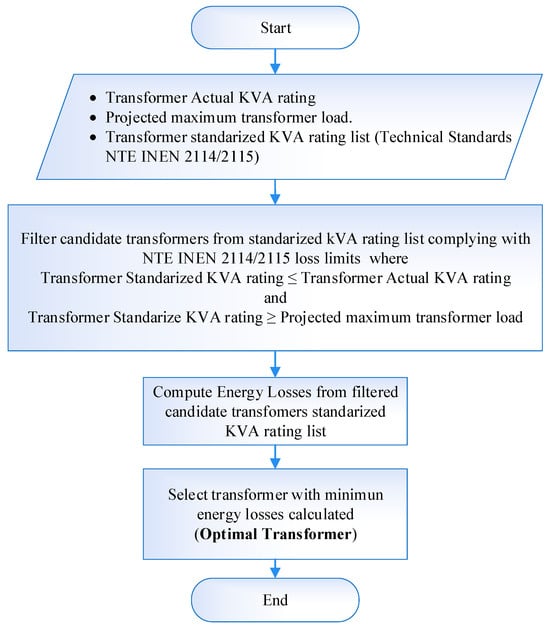
Figure 5.
Process for transformer optimization.
Candidate transformers are filtered from this list based on two criteria: (i) the standardized kVA rating must be less than or equal to the transformer’s actual kVA rating, and (ii) it must be greater than or equal to the projected peak load.
For each filtered candidate, total energy losses are computed using Equation (14), which integrates the instantaneous power losses calculated with Equation (11) at each point in the estimated daily load curve for each transformer. The transformer with the lowest total energy losses is selected as the optimal one, ensuring both compliance with technical standards and efficient operational performance.
2.7. Economic Assessment of Energy Losses
To quantify the economic savings resulting from transformer power optimization, a comparative analysis is conducted between current energy losses and those that would occur with transformers of optimal capacity. This comparison enables the estimation of potential energy and economic savings on an annual basis. For this purpose, Equation (15) is used, which calculates the annual cost associated with energy losses by multiplying the annual energy lost obtained from Equation (14) by the unit cost of electrical energy. The energy cost considered corresponds to the tariff set by the regulatory authority of the electricity sector in Ecuador, which is 0.05 USD per kWh. This value includes both generation and transmission costs. The application of this methodology allows for the evaluation of the economic impact of loss reduction, thereby supporting decision making aimed at improving operational efficiency and sustainability.
In Equation (15) CostLosses $ are the cost of energy losses, ELoss_Tot are the total energy losses in transformers, Cost_energy is the cost of energy per kWh.
3. Results and Discussion
3.1. Characteristic Load Curves
Based on the load curves recorded during the day of highest demand for the 208 transformers sampled, the average value at each hourly instant was calculated to determine the load behavior, resulting in the curve shown in Figure 6. This curve shows a characteristic pattern of the residential sector, with a progressive increase in demand starting in the early morning, stabilizing during the afternoon, and a pronounced peak between 19:00 and 21:00 h, corresponding to the time of greatest domestic activity. It is worth mentioning that, although the average profile reflects a clear predominance of residential behavior since most of the transformers are associated with this type of load, the result is actually a superposition of individual curves that also include transformers with commercial, industrial, and mixed customers.
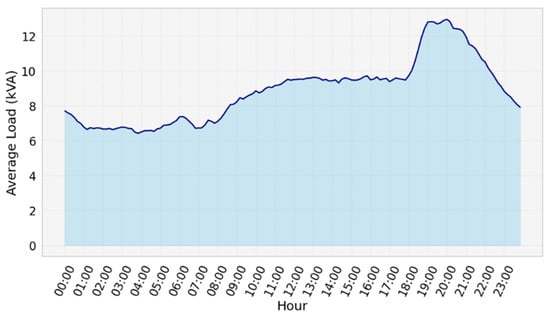
Figure 6.
Average daily load curve of the 208 sampled distribution transformers, expressed in kVA.
By applying the K-Means clustering in combination with Dynamic Time Warping (DTW), representative patterns of load behavior were identified based on the hourly records of a sample of distribution transformers. Using the elbow method to determine the optimal number of clusters, eight characteristic load curves were established and are presented in Figure 7. These curves capture distinct consumption profiles and serve as the basis for assigning typical load curves to the remaining system transformers.
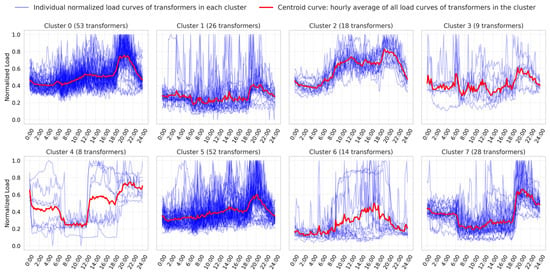
Figure 7.
Characteristic daily load curves obtained using K-Means clustering with DTW metric.
Each subgraph in Figure 7 corresponds to a cluster grouping of transformers with similar consumption patterns. The individual load curves within each cluster, shown in blue, were normalized to facilitate visual comparison. The centroidal curve, shown in red, represents the average hourly profile of the cluster and characterizes the typical behavior of the group.
A variety of load patterns were identified, reflecting the diversity of electricity usage within the distribution network. Clusters 0, 1, and 5 exhibit increasing demand toward the end of the day, with peaks between 18:00 and 22:00, characteristic of residential usage with heightened evening activity. On the other hand, clusters 2 and 4 display higher daytime loads, indicative of commercial, institutional, or administrative consumption, with secondary peaks after 18:00, likely associated with residential use and public lighting. Cluster 6 shows a unique daytime load increase between 14:00 and 18:00, followed by a sharp decline, suggesting industrial or manufacturing operations with defined work shifts. In contrast, cluster 3 presents a more distributed load, potentially corresponding to a mixed-use consumption profile.
Table 2 shows the number and percentage of transformers assigned to each cluster. This quantification highlights the relative prevalence of each characteristic load pattern within the sample, supporting the representativeness of the identified clusters.

Table 2.
Distribution of transformers per cluster and percentage representation.
The hourly load centroids obtained through clustering were expressed in normalized units relative to their maximum daily value, as shown in Figure 8. This normalization allows for the comparison of load consumption patterns regardless of absolute magnitude, thereby facilitating the identification and classification of typical profiles. These normalized representative profiles are subsequently used to estimate the load power and daily energy consumption of unmetered transformers by assigning each transformer to the most similar characteristic pattern.
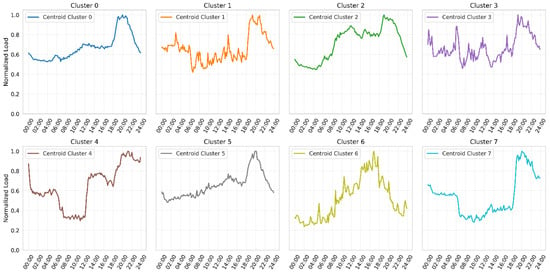
Figure 8.
Normalized hourly load curves for distribution transformers.
3.2. Transformer Load Curve Prediction
The normalized hourly load curves obtained through K-Means clustering combined with Dynamic Time Warping (DTW) were used to estimate the loadability of unmetered distribution transformers. The assignment of a representative load curve to each transformer was based on the number and type of customers connected to the equipment.
To automate this assignment process, the LightGBM classification algorithm was employed. For this purpose, the model was trained using the cluster labels corresponding to the previously identified characteristic curves as the target variable. The dataset was split into 90% for training and 10% for validation. The objective was to develop a predictive model capable of estimating the most appropriate load curve for each transformer based on the independent variables listed in Table 1. The performance of the LightGBM model was optimized using the hyperparameters detailed in Table 3.

Table 3.
Parameters in the LightGBM algorithm.
To determine the optimal hyperparameter configuration, a grid search was performed in combination with 5-fold cross validation. The parameters evaluated included n_estimators, learning_rate, and num_leaves, using classification accuracy as the evaluation metric. The best-performing combination, shown in Table 3, was then used to train the final model applied to the test set.
3.3. Transformer Peak Load Determination and Metodology Validation
Using the normalized load curve assigned to each transformer, the maximum load power of each unit was estimated by applying Equation (1), which relates the energy consumption of connected customers along with public lighting and traffic light loads obtained from the commercial system to the transformer’s load profile.
To validate the accuracy of this methodology, the load curve classification performed using the LightGBM algorithm, transformer No. 1615 (rated at 112.5 kVA) was selected as a test case. This transformer was not included in the model training process, and the actual load measurements were recorded between 4 April and 9 April 2025. The methodology estimated a maximum load power of 30.98 kW, while the measured peak demand yielded an average value of 32.41 kW at 20:00, corresponding to an accuracy of 95.6%.
Figure 9 presents a comparison between the estimated load curve assigned via LightGBM and corresponding to Cluster 0 and the actual measured curve, averaged over the observation period. The high degree of similarity between the curves confirms the validity and robustness of the proposed approach for peak load estimation in unmetered distribution transformers.
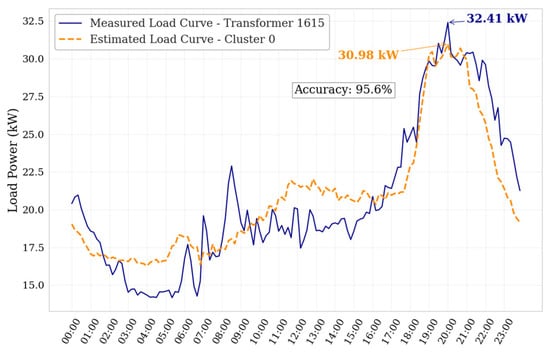
Figure 9.
Comparison of actual and projected load curve for transformer 1615 (112.5 kVA).
3.3.1. Evaluation on a Complete Feeder
The proposed methodology was applied to a total of 634 distribution transformers connected to the 13.8 kV primary feeder identified as 0100140T05, operated by EEASA. To validate the load estimation, the results were compared with actual power measurements recorded at the feeder on the peak demand day, which occurred on 22 April 2025. On that date, the recorded coincident demand was 1972.14 kW at 19:00, while the projected demand, obtained by aggregating the estimated load curves of the transformers, reached 1879.21 kW, resulting in an accuracy of 95.29%.
Figure 10 presents a comparison between the measured and estimated load curves for the entire feeder. As shown, both curves closely match during peak demand hours, 18:00 to 24:00, where the model accurately replicates the actual behavior. However, a slight underestimation is observed over the rest of the day. This deviation may be associated with the use of standardized load profiles, which do not fully capture time-dependent consumption patterns such as those found in schools, offices, or industrial facilities that operate primarily during daytime hours.
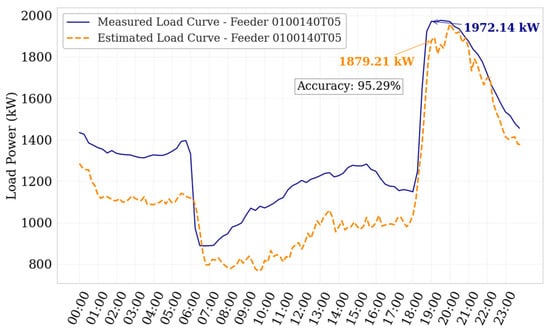
Figure 10.
Comparison between actual and estimated load curve at feeder level (Feeder 0100140T05 with 634 transformers).
Despite this partial deviation, the overall shape of the estimated curve remains very similar to the actual curve, reinforcing the model’s ability to accurately represent the aggregate demand dynamics at the feeder level. These results confirm the robustness of the methodology even in mid-scale applications and support its usefulness as a practical tool for energy planning and transformer sizing optimization in distribution networks lacking advanced metering infrastructure.
3.3.2. Generalization, Evaluation on a Complete Electrical System
To assess the applicability and generalization capability of the proposed methodology, it was applied to a complete electrical system comprising a total of 16,864 distribution transformers with customers registered at the low-voltage level.
Using this methodology, the overall system load curve was generated, as shown in Figure 11. This figure illustrates the disaggregation of the total load curve into its components, where each component represents the aggregated contribution of transformers belonging to a specific cluster.
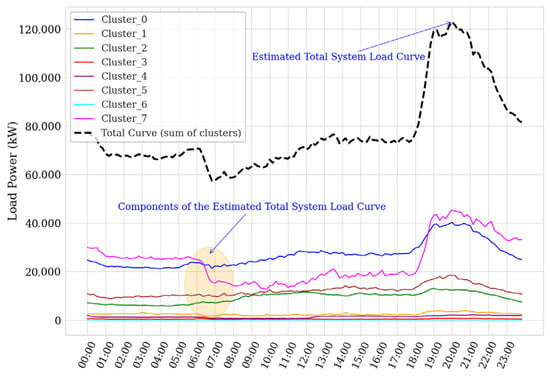
Figure 11.
Disaggregation of the estimated system load curve with 16,864 transformers.
These clusters were identified through K-Means clustering, and each characteristic load curve labeled as Cluster 0, Cluster 1, Cluster 2, and so forth corresponds to the typical load pattern of all transformers assigned to that cluster. Therefore, the total load curve is the weighted sum of these representative curves, reflecting the diversity of consumption patterns within the system.
Figure 12 presents a comparison between the actual measured system load curve and the projected load curve. The estimated coincident demand obtained through this approach was 118.99 MW, yielding an accuracy of 98.14% compared to the actual demand of 121.25 MW recorded on 22 April 2025, at 19:00. It is important to note that this demand corresponds only to transformers serving customers metered at low voltage, excluding those associated with medium-voltage private customers. This limitation is due to the methodology relying on energy consumption data from loads connected to the distribution transformers.
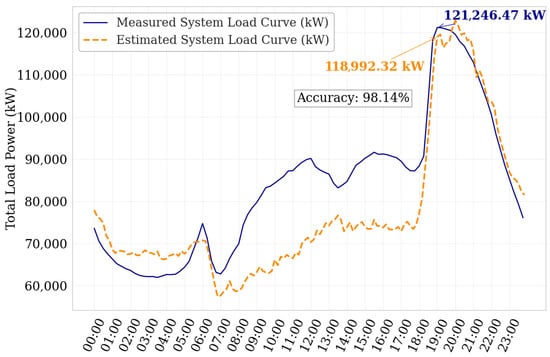
Figure 12.
Comparison between the actual and estimated load curve of the total electrical system with 16,864 transformers.
This level of accuracy demonstrates the model’s effectiveness in capturing the overall system behavior. Although the methodology performs with high precision during peak demand hours from 18:00 to 23:00, where the estimated and measured load curves align closely, a slight underestimation is observed between 07:00 and 18:00. This deviation may be attributed to the use of standardized daily load profiles and aggregated consumption patterns for residential, commercial, and industrial users, which may not fully reflect specific variations in demand behavior during medium load periods. Some transformers may supply loads with intermittent or time dependent usage patterns such as schools, offices, or industrial facilities that are active primarily during this time window, thus affecting the shape of the actual measured load curve. Nevertheless, the system level accuracy remains high, confirming the robustness and practical applicability of the proposed methodology for large scale applications.
Overall, the results obtained at the three validation levels—individual transformer, feeder, and complete system—demonstrate the robustness, scalability, and practical applicability of the proposed methodology. The accuracy achieved at each level shows slight variations attributable to the aggregation effect and the diversity of consumption patterns present at each scale. At the transformer level, the model is more sensitive to the specific load characteristics of each user, so small discrepancies in the estimated profiles have a proportionally greater impact. In contrast, at aggregated levels such as the feeder or the complete system, these variations tend to offset each other, increasing overall accuracy due to the averaging effect. Nonetheless, patterns of underestimation were identified during medium demand periods, associated with the use of standardized profiles that do not capture specific hourly consumption behaviors in sufficient detail. This analysis highlights both the overall effectiveness of the model and the identified opportunities for improvement, proposing as future work the incorporation of additional variables and advanced techniques to enhance the granularity and adaptability of the approach for more complex and dynamic systems.
3.4. Determination of Optimal Transformer Power
Once the methodology for estimating the load curves and transformer demand was validated, the optimal power rating selection process described in Figure 5 was applied to the 16,864 distribution transformers owned by EEASA. As a result, a total reduction of 274.34 MW in installed capacity was achieved, representing a 32.27% decrease compared to the current installed capacity of 405.05 MW. Additionally, 7476 transformers—corresponding to 44.3% of the total—were identified as being oversized relative to the actual demand. Therefore, it is recommended that these units be resized in order to reduce energy losses and enhance the operational efficiency of the distribution system.
Figure 13 shows the comparison of the probability distribution of transformer nominal power ratings in the current state and after the application of the optimization model. The blue curve represents the actual power currently installed, while the orange curve corresponds to the optimal selected power, determined by minimizing technical losses. It can be observed that the current distribution has its maximum around 11 kVA, while the optimized curve shifts the peak towards 5 kVA, suggesting that a significant number of transformers are in these actual and optimized power ranges.
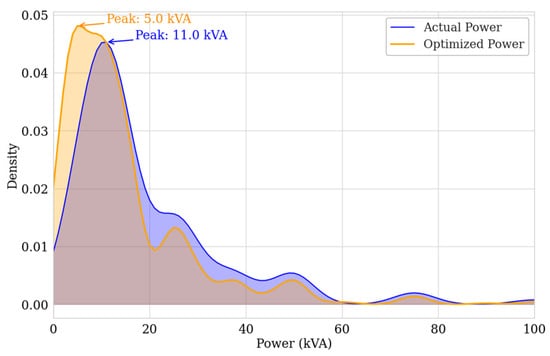
Figure 13.
Kernel Density Estimation (KDE) of the probability distribution of installed power vs. optimal power for distribution transformers.
Figure 14 presents a boxplot diagram summarizing the distribution of the differences between the installed power and the selected optimal power. The median power reduction is 7 kVA, indicating that at least 50% of the optimized transformers are oversized by this amount or more. Additionally, 75% of the transformers exhibit a derating of 15 kVA or less, while the minimum observed derating, represented by the lower whisker limit, is 2 kVA. This behavior indicates that most transformers exhibit moderate oversizing, making it feasible to optimize their capacity without compromising service quality. Furthermore, the significant number of cases with capacity reductions between 2 and 15 kVA highlights the importance of implementing sizing criteria that are aligned with actual and projected future demand.
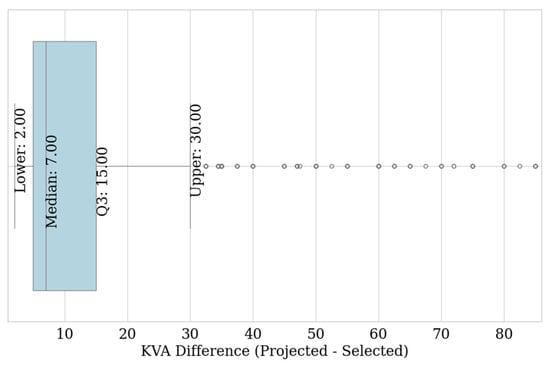
Figure 14.
Boxplot of power reduction in distribution transformers.
3.5. Evaluation of No-Load and Load Losses in Distribution Transformers
3.5.1. Results of the Evaluation of No-Load Losses in Distribution Transformers
Figure 15 shows a boxplot illustrating how no-load losses vary between the three-phase, two-phase, and single-phase transformers installed in EEASA’s distribution networks, applying Equations (2), (4), (6), and (8). Average losses close to 0.25 kW are observed in the three-phase transformers, with losses that can exceed 1.75 kW in the larger capacity transformers. On the other hand, the single-phase transformers present the lowest losses, with an average of 0.06 kW and a maximum of 0.35 kW.
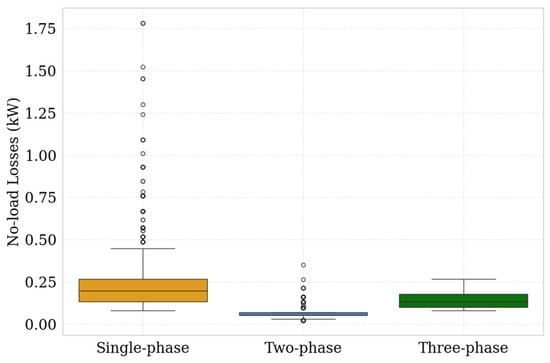
Figure 15.
Distribution of no-load losses in distribution transformers at different power ratings, classified by the number of phases (kW).
Figure 16a shows the distribution of no-load losses in terms of annual energy. Three-phase transformers generate no-load losses of about 2.21 MWh per year each, while single-phase transformers generate about 0.57 MWh per year each on average. However, due to the larger number of single-phase transformers installed, they contribute to the largest cumulative losses in the power system.
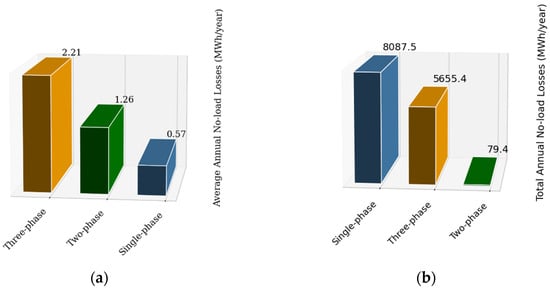
Figure 16.
Unloaded losses by transformer type: (a) average annual losses by transformer; (b) cumulative annual losses of all EEASA transformers.
Figure 16b shows that the annual accumulated no-load losses of all single-phase transformers reach 8087.5 MWh, while the losses of three-phase transformers total 5655.4 MWh and those of two-phase transformers amount to 79.4 MWh per year in the entire power system analyzed.
3.5.2. Results of the Evaluation of Load Losses in Distribution Transformers
Figure 17 presents an analysis of the current losses with load, generated by the 16,864 distribution transformers, considering their annual operation according to the load curves determined in this study. Figure 17a shows the average losses per transformer according to the type of connection, showing that three-phase transformers have the highest losses, with an average value of 0.51 MWh per year, followed by two-phase transformers 0.22 MWh per year and single-phase transformers 0.11 MWh per year. In contrast, Figure 17b shows the cumulative annual sum of load losses for each type of connection. In this case, single-phase transformers accumulate the highest total losses, reaching 1604.3 MWh per year, followed by three-phase transformers with 1299.5 MWh per year, while two-phase transformers present a marginal impact of only 13.8 MWh per year. This distribution is strongly influenced by the predominant number of single-phase transformers in the network, which highlights their significant contribution to total losses, despite their lower individual losses.
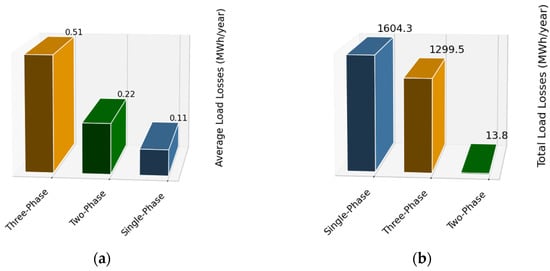
Figure 17.
Load losses by transformer type: (a) average annual losses by transformer; (b) cumulative annual losses of all EEASA transformers.
3.5.3. Evaluation of Total Energy Losses in Existing and Optimized Distribution Transformers
The energy losses estimated using Equation (14) are presented in Figure 18a, where the current annual losses without load and with load are broken down for the distribution transformers of the electric system analyzed. It is observed that single-phase transformers generate the highest total losses, reaching 9691.81 MWh per year, followed by three-phase transformers with 6954.84 MWh, while two-phase transformers present a marginal contribution of only 93.23 MWh per year.
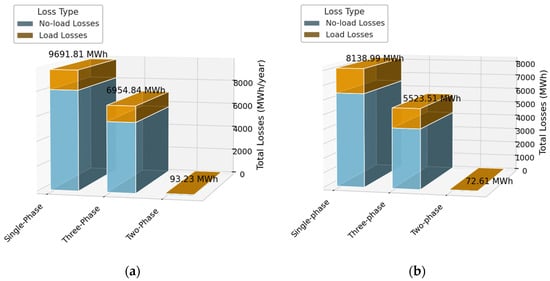
Figure 18.
Total energy losses by transformer type: (a) total annual energy losses in existing transformers; (b) total annual energy losses in optimized transformers.
In all cases, it should be noted that the largest proportion of losses corresponds to no-load losses, since these remain constant over time, as opposed to loaded losses, which depend directly on the load level. This condition is related to the system load curve Figure 12, which shows a predominantly residential profile, with consumption peaks at night and low utilization during the rest of the day. This indicates that many transformers operate at reduced load levels for much of the time, which reduces their contribution to load losses and accentuates the effect of no-load losses.
Figure 18b shows the estimated annual losses after transformer power rating optimization, revealing a significant reduction in total losses. In this scenario, single-phase transformer losses decrease to 8138.99 MWh per year, three-phase to 5523.51 MWh, and two-phase to 72.61 MWh per year. This improvement is evidence that the resizing of transformers based on the projected load allows for a substantial reduction in losses, especially no-load losses, which once again confirms the effectiveness of the proposed methodology to improve the energy efficiency of the distribution system.
Figure 19 shows the annual energy losses associated with existing transformers, which amount to 16,739 MWh. With the implementation of optimized transformers, these losses would be reduced to 13,735 MWh, which would represent an annual energy savings of 3004 MWh.
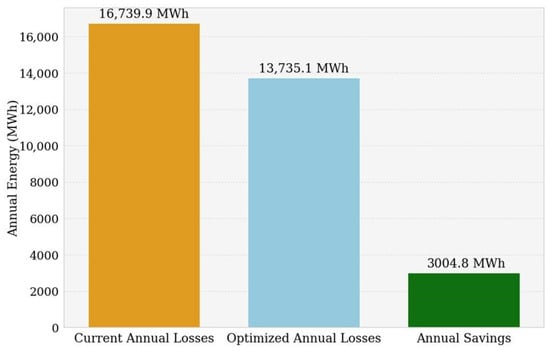
Figure 19.
Total losses and annual energy savings for the entire EEASA system.
3.6. Economic Evaluation of Energy Losses
The economic evaluation of energy losses was carried out using Equation (15), the cost of energy for generation and transmission, established at 0.05 USD/kWh for the electric company under analysis. Figure 20a presents a comparison between the annual cost associated with energy losses in the current scenario and the cost after applying the transformer power rating optimization, highlighting the resulting economic savings. The analysis shows that the total annual cost of losses in the current scenario amounts to 836,949.69 USD, while after applying the optimization model this value is reduced to 686,756.44 USD, generating an annual economic saving of 150,238.25 USD. This result demonstrates the impact that can be achieved through adequate capacity planning, improving technical efficiency, and reducing operating costs for the electric company.
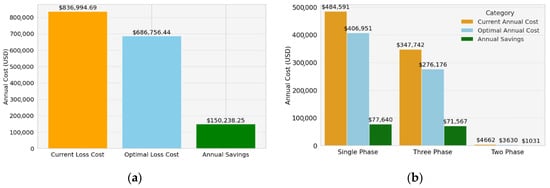
Figure 20.
Total cost losses for the entire electrical system: (a) total annual cost and savings; (b) total annual cost and savings, categorized by transformer type.
In addition, Figure 20b breaks down these results by type of transformer connection. Single-phase transformers represent the highest annual cost of losses in the current scenario with 484,591 USD, followed by three-phase transformers with 347,742 USD, and two-phase transformers with only 4662 USD. With the application of the optimization, these costs decrease to 406,951 USD for single-phase transformers, 276,176 USD for three-phase transformers, and 3630 USD for two-phase transformers, respectively. This translates into annual savings of 77,640 USD for single-phase transformers, 71,567 USD for three-phase transformers and 1031 USD for two-phase transformers. The breakdown identifies that, although single-phase transformers have lower unit losses, their large number in the network contributes predominantly to the total cost.
Sensitivity Analysis of Economic Savings to Energy Price Variations
Figure 21 illustrates the sensitivity analysis of economic savings generated by the transformer power optimization model, considering variations in the energy tariff between 0.04 and 0.08 USD/kWh. The analysis shows a clear positive correlation between electricity price and total annual savings. For example, at the base tariff of 0.05 USD/kWh representative of a fixed rate energy cost in Ecuador, savings reach approximately 150,238.71 USD per year. When the tariff increases to 0.08 USD/kWh, savings rise to 240,381.93 USD annually. Conversely, a reduction to 0.04 USD/kWh results in savings of 120,190.97 USD. These results demonstrate that the optimization method remains economically beneficial across a range of energy prices.
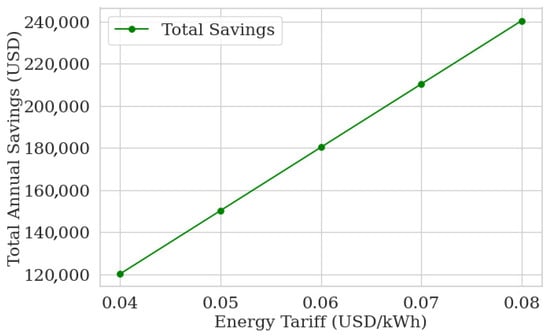
Figure 21.
Impact of electricity price changes on annual economic savings.
In some countries, such as Ecuador, energy tariffs are fixed and do not vary with hourly demand, unlike in other regions where variable pricing is common. The fixed tariff considered includes generation and transmission costs, although actual rates may vary depending on the country’s energy resource mix and market structure. The corresponding sensitivity analysis graph clearly visualizes these savings variations, highlighting the increasing economic benefit as the energy tariff rises.
4. Conclusions
The proposed methodology proves to be an effective tool for optimizing the operation of distribution transformers through the estimation of hourly load curves, based on clustering techniques, K-Means with Dynamic Time Warping, DTW, and supervised learning, LightGBM. It is specifically designed for power distribution networks lacking advanced metering infrastructure, enabling the characterization of transformer level demand based on customer attributes. These estimated profiles are then used to assess technical losses and to select transformer ratings that minimize energy losses. In this study, this strategy resulted in a significant reduction in losses, achieving annual energy savings of 3004 MWh and an estimated economic reduction of 150,238 USD.
The validation of the methodology for optimizing transformer operation showed high levels of accuracy when comparing the estimated and actual peak loads: 95.6% for an individual transformer, 95.29% for a feeder with 634 units, and 98.14% at the system level with 16,864 transformers. Furthermore, the estimated system-wide hourly load curve aggregated from the predicted profiles of each transformer closely replicated the actual system load curve, confirming the robustness, scalability, and practical applicability of the approach.
Although the model demonstrated high accuracy during peak demand hours (18:00 to 23:00), a slight underestimation was observed during mid-load periods (07:00 to 18:00), which was attributed to the use of standardized profiles that may not capture the specific temporal consumption behaviors of certain users, like schools, offices or public institutions. Moreover, the assumption that customer type, like residential, commercial, industrial, public lighting, and others, is a representative predictor of load profiles, while valid in many cases, may be increasingly challenged by the growing penetration of distributed energy resources, DER, photovoltaic systems, and electric vehicles (EVs), which introduce greater heterogeneity within each customer category. This highlights the need to incorporate greater granularity and additional variables to better reflect the diversity of modern consumption patterns.
For future research, it is recommended to integrate contextual variables such as ambient temperature, seasonality, and sociodemographic characteristics to enhance load curve estimation. Additionally, incorporating data on DER and EV adoption at the user level as well as exploring the application of probabilistic models to quantify demand uncertainty are encouraged. Ensemble learning techniques, such as stacking, that combine base models like LightGBM, neural networks, and Bayesian approaches could further strengthen the generalization and adaptability of the proposed model in more complex and dynamic distribution systems, overcoming the current limitations observed during periods of average load.
Author Contributions
Conceptualization, P.T.-B., K.L.-E. and J.V.-A.; methodology, P.T.-B., N.V. and K.L.-E.; software, P.T.-B.; validation, P.T.-B., K.L.-E. and J.V.-A.; formal analysis, P.T.-B., K.L.-E. and N.V.; investigation, P.T.-B., N.V. and K.L.-E.; resources, P.T.-B. and K.L.-E.; data curation, P.T.-B. and N.V.; writing—original draft preparation, P.T.-B. and N.V.; writing—review and editing, J.V.-A. and G.P.-N.; visualization, P.T.-B. and G.P.-N.; supervision, G.P.-N. and J.V.-A.; project administration, J.V.-A. and G.P.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to express their gratitude to Universidad Indoamerica for its support of this research through the “Tecnologias de la Industria 4.0 en Educacion, Salud, Empresa e Industria” project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Amoiralis, E.I.; Tsili, M.A.; Kladas, A.G. Economic evaluation of transformer selection in electrical power systems. In Proceedings of the 19th International Conference on Electrical Machines, ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Güldürek, M.; Esenboğa, B. Assessment of Corporate Carbon Footprint and Energy Analysis of Transformer Industry. Sustainability 2024, 16, 5800. [Google Scholar] [CrossRef]
- Piotrowski, T.; Markowska, D. Carbon Footprint of Power Transformers Evaluated Through Life Cycle Analysis. Energies 2025, 18, 1373. [Google Scholar] [CrossRef]
- Agha, A. Economic Evaluation of Transformer Selection in Distribution Systems. 2018. Available online: https://www.researchgate.net/publication/340133579 (accessed on 5 April 2025).
- León-Martínez, V.; Peñalvo-López, E.; Montañana-Romeu, J.; Andrada-Monrós, C.; Molina-Cañamero, L. Assessment of Load Losses Caused by Harmonic Currents in Distribution Transformers Using the Transformer Loss Calculator Software. Environments 2023, 10, 177. [Google Scholar] [CrossRef]
- Wijayapala, W.D.A.S.; Gamage, S.R.K.; Bandara, H.M.S.L.G. Determination of Capitalization Values for No Load Loss and Load Loss in Distribution Transformers. Eng. J. Inst. Eng. Sri Lanka 2016, 49, 11. [Google Scholar] [CrossRef]
- Al-Badi, A.H.; Elmoudi, A.; Metwally, I.; Al-Wahaibi, A.; Al-Ajmi, H.; Al Bulushi, M. Losses reduction in distribution transformers. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 16–18 March 2011; Available online: https://www.iaeng.org/publication/IMECS2011/IMECS2011_pp948-952.pdf (accessed on 15 June 2025).
- Wang, X.; Guo, Q.; Tu, C.; Li, J.; Xiao, F.; Wan, D. A two-stage optimal strategy for flexible interconnection distribution network considering the loss characteristic of key equipment. Int. J. Electr. Power Energy Syst. 2023, 152, 109232. [Google Scholar] [CrossRef]
- Cabral, T.W.; Fraidenraich, G.; Meloni, L.G.P.; Neto, F.B.; de Lima, E.R. Analysis of Variance Combined with Optimized Gradient Boosting Machines for Enhanced Load Recognition in Home Energy Management Systems. Sensors 2024, 24, 4965. [Google Scholar] [CrossRef] [PubMed]
- Torres-Bermeo, P.; López-Eugenio, K.; Varela-Aldás, J.; Del-Valle-Soto, C.; Palacios-Navarro, G. Sizing and Characterization of Load Curves of Distribution Transformers Using Clustering and Predictive Machine Learning Models. Energies 2025, 18, 1832. [Google Scholar] [CrossRef]
- Agudelo, L.; Velilla, E.; López, J.M. Load estimation of power transformers using an artificial neural network|Estimación de la carga de transformadores de potencia utilizando una red neuronal artificial. Inf. Tecnol. 2014, 25, 15–23. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, Y.; Liu, J.; Zhang, L.; Li, W.; Mohtaram, S. Machine Learning Approach to Predict Building Thermal Load Considering Feature Variable Dimensions: An Office Building Case Study. Buildings 2023, 13, 312. [Google Scholar] [CrossRef]
- Mulliez, E.; Sanz-Bobi, M.A.; Sanchez, Á.; Mazidi, P.; González, A.; Bachiller, R. Life characterization of power distribution transformers using clustering techniques. In Proceedings of the European Conference of the Prognostics and Health Management Society, Utrecht, The Netherlands, 3–6 July 2018; Volume 3, pp. 1–7. [Google Scholar]
- Yuan, S.; Zhang, X.; Geng, J.; Wan, D. Research on load curve clustering of distribution transformer based on wavelet transform and big data processing. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference, ITNEC 2017, Chengdu, China, 15–17 December 2017; pp. 348–351. [Google Scholar] [CrossRef]
- Zhao, J.; He, J.; Wang, J.; Liu, K. Energy Consumption Prediction for Electric Buses Based on Traction Modeling and LightGBM. World Electr. Veh. J. 2025, 16, 159. [Google Scholar] [CrossRef]
- Hajiaghapour-Moghimi, M.; Azimi-Hosseini, K.; Hajipour, E.; Vakilian, M. Residential Load Clustering Contribution to Accurate Distribution Transformer Sizing. In Proceedings of the 34th International Power System Conference, PSC 2019, Tehran, Iran, 9–11 December 2019; pp. 313–319. [Google Scholar] [CrossRef]
- Téllez, A.A.; Robayo, A.; Ortiz, L.; López, G.; Isaac, I.; González, J. Optimal sizing of distribution transformers using exhaustive search algorithm. In Proceedings of the 2019 Fise IEEE Cigre Conference Living the Energy Transition Fise Cigre 2019, Medellin, Colombia, 4–6 December 2019. [Google Scholar] [CrossRef]
- Agha, A.; Attar, H.; Luhach, A.K. Optimized Economic Loading of Distribution Transformers Using Minimum Energy Loss Computing. Math. Probl. Eng. 2021, 2021, 8081212. [Google Scholar] [CrossRef]
- Biçen, Y.; Aras, F.; Kirkici, H. Lifetime estimation and monitoring of power transformer considering annual load factors. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1360–1367. [Google Scholar] [CrossRef]
- Mendoza, J.E.; López, M.E.; Peña, H.E.; Labra, D.A. Low voltage distribution optimization: Site, quantity and size of distribution transformers. Electr. Power Syst. Res. 2012, 91, 52–60. [Google Scholar] [CrossRef]
- Li, Y.; Han, G.; Yue, S.; Wan, Z.; Yin, J. Structure design and magnetic-vibration characteristics analysis of hybrid core for high efficiency distribution transformer. AIP Adv. 2025, 15, 035041. [Google Scholar] [CrossRef]
- Schröder, K.; Farias, G.; Dormido-Canto, S.; Fabregas, E. Comparative Analysis of Deep Learning Methods for Fault Avoidance and Predicting Demand in Electrical Distribution. Energies 2024, 17, 2709. [Google Scholar] [CrossRef]
- Farahzad, K.; Shahbahrami, A.; Ashouri, M. Optimal Capacity Determination for Electrical Distribution Transformers Based On IEC 60076-7 And Practical Load Data. Int. J. Eng. Manuf. 2020, 10, 1. [Google Scholar] [CrossRef]
- Plienis, M.; Deveikis, T.; Jonaitis, A.; Gudžius, S.; Konstantinavičiūtė, I.; Putnaitė, D. Improved Methodology for Power Transformer Loss Evaluation: Algorithm Refinement and Resonance Risk Analysis. Energies 2023, 16, 7837. [Google Scholar] [CrossRef]
- Cartina, G.; Grigoras, G.; Bobric, E.C. Clustering techniques for energy losses evaluation in distribution networks. In Proceedings of the 2009 IEEE Bucharest PowerTech: Innovative Ideas Toward the Electrical Grid of the Future, Bucharest, Romania, 28 June–2 July 2009. [Google Scholar] [CrossRef]
- Grigoras, G.; Cartina, G.; Istrate, M.; Rotaru, F. The efficiency of the clustering techniques in the energy losses evaluation from distribution networks. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 133–141. [Google Scholar]
- Dai, Z.; Shi, K.; Zhu, Y.; Zhang, X.; Luo, Y. Intelligent Prediction of Transformer Loss for Low Voltage Recovery in Distribution Network with Unbalanced Load. Energies 2023, 16, 4432. [Google Scholar] [CrossRef]
- Alymov, I.; Averbukh, M. Monitoring Energy Flows for Efficient Electricity Control in Low-Voltage Smart Grids. Energies 2024, 17, 2123. [Google Scholar] [CrossRef]
- Schau, H.; Novitskiy, A. Economic transformer load estimation considering power quality. In Proceedings of the ICHQP 2008 13th International Conference on Harmonics and Quality of Power, Wollongong, NSW, Australia, 28 September–1 October 2008. [Google Scholar] [CrossRef]
- NTE INEN 2114:2004; Transformadores de Distribución Nuevos Monofásicos. Valores de Corriente Sin Carga, Pérdidas y Voltaje de Cortocircuito. Instituto Ecuatoriano de Normalización (INEN): Quito, Ecuador, 2004.
- NTE INEN 2115:2004; Transformadores de Distribución Nuevos Trifásicos. Valores de Corriente Sin Carga, Pérdidas y Voltaje de Cortocircuito. Instituto Ecuatoriano de Normalización (INEN): Quito, Ecuador, 2004.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).