Abstract
This paper presents an online efficiency optimization strategy for a six-phase induction generator (6PIG) operating in both healthy and faulty modes for micro-hydropower applications. The proposed method is based on an extended Loss Model Control (LMC) approach, in which the direct axis stator current Id is dynamically optimized in real time to minimize the total electrical losses. Unlike conventional LMC strategies, this method explicitly incorporates switching losses into the loss model, along with stator and rotor copper losses and iron losses. The optimization problem is solved using a numerical minimization routine, allowing the control system to adapt continuously to variations in torque requests. The proposed approach is validated under both healthy and faulty configurations of the 6PIG. It is implemented and tested through simulation in MATLAB/Simulink® and experimentally validated on a 24 kW squirrel cage six-phase induction generator (SC6PIG). The results are compared in terms of power losses, energy saving, and efficiency.
1. Introduction
Maximizing the energy efficiency of electric drives is a key objective in several fields, such as renewable energy applications, particularly in micro-hydropower systems, where the power availability is limited, typically in the range of 5–100 kW [1]; although this range is not universal, the speed is low, and the energy conversion has to be as effective as possible [2].
In such systems, induction generators, particularly conventional three-phase ones, are widely used due to their robustness and simplicity [3]. However, these machines are not fault-tolerant, which is a crucial requirement to ensure reliable and efficient operation.
When implemented in multiphase configurations such as six-phase generators, they offer superior fault-tolerance, maintaining operation even with the loss of up to three phases [4,5]. This capability is essential for autonomous operation in remote environments. They also provide more balanced power distribution, reduced torque pulsations, lower stator copper losses, and decreased rotor harmonic components, making them well-suited for energy generation in constrained environments.
Nevertheless, when a fault occurs, power oscillations appear, which require appropriate control strategies to attenuate and ensure stable operation [4].
In energy generation systems such as micro-hydropower, enhancing only the performance of the generator is not sufficient. Indeed, minimizing the losses in all the conversion chain components, including the converters, the generator, the mechanical transmissions, or the grid, is essential to improve overall system efficiency. While advances in materials and design have helped to reduce these losses, significant losses still occur in the converters and the generators, and both depend largely on the implemented control strategy [6].
One key challenge in improving energy conversion efficiency is minimizing total electrical losses, including stator and rotor copper, iron, and converter losses, particularly in inverter-fed drives. Furthermore, the converter losses become significant in inverter-powered drives operating at high frequencies. In this way, a comparative study [7] of switching losses in two-level and multilevel inverters highlights the necessity of optimizing these losses for high-frequency multiphase systems. Indeed, the converter losses are mainly of two types [8]: conduction losses when power devices (e.g., IGBT or MOSFET) conduct current, and switching losses, occurring during ON/OFF transitions due to the voltage–current overlap [9]. At high frequencies, the conduction losses become negligible, leaving switching losses as the dominant factor, especially with multiphase systems. The details of the mechanisms of conduction and switching losses in MOSFETs and their impact on the efficiency of power supplies are studied in [10].
While traditional control strategies, such as Indirect Rotor Field-Oriented Control, are commonly employed, they rely on fixed magnetizing current values and do not adapt to varying torque load or speed conditions [11]. This results in non-optimal efficiency, especially under partial load or variable speed operations [12], which are common in some systems like micro-hydropower contexts.
To address this, several approaches have been proposed in the literature. These methods are generally categorized into three types: model-based methods, search-based methods, or self-optimizing methods [13] and hybrid methods that combine elements of both [14]. Among the model-based approaches, Loss Model Control (LMC) [15] computes the optimal magnetizing current based on an analytical model of losses, such as copper and iron losses. It offers the advantage of fast response and good accuracy when the machine and the loss parameters are well identified. However, it can be sensitive to modeling errors and parameter uncertainties [15]. The Maximum Torque per Ampere (MTPA) strategy [16] minimizes the current magnitude for a given torque, which effectively reduces copper losses but ignores losses such as iron and switching, limiting its overall efficiency, particularly at low load torque.
In contrast, experimental search methods, such as Search Control (SC) [17] or Minimum Loss Search (MLS), do not require any knowledge of the machine or its losses, making them robust to uncertainties. However, their main drawback is the slow convergence, which makes them unsuitable for applications requiring fast dynamic response [18].
LMC has already been applied in electric vehicles and energy generation [15], considering only copper and iron losses. However, in multiphase applications that need additional converters and in constrained, lightly loaded environments where switching losses become significant, it becomes necessary to go further and explicitly include these losses in the optimization. This consideration forms the foundation of the contribution presented in this work.
In this way, this paper introduces an extended real-time Loss Model Control (LMC) strategy adapted for six-phase induction generators (6PIGs) operating in both healthy and faulty modes. The proposed models include a complete loss model explicitly accounting for switching losses of the converter often omitted in prior works in the conventional LMC.
In this paper, a 24 kW–230 V–125 rpm–12 poles pair 6PIG built in our laboratory, coupled to a gearmotor to simulate a wind turbine or microhydraulic turbine, is used to validate the proposed strategy. The high number of poles reduces the rated speed of the generator and simplifies or eliminates the gearbox, which is responsible for the mechanical faults and improves the robustness against electrical and mechanical faults.
Section 2 will provide a brief overview of the overall system architecture, while Section 3 will focus on the modeling and control of the generator for both healthy and faulty modes. The proposed control strategy is then studied in Section 4. Lastly, Section 5 will be dedicated to the results and discussions, followed by the conclusion in Section 6.
2. System Overview
Figure 1 shows the control of the whole system structure of the proposed control scheme in healthy and faulty operations. The following system consists of:
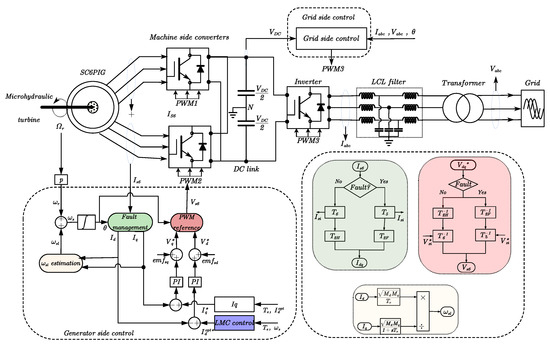
Figure 1.
Overall system.
- ▪
- A squirrel cage six-phase induction generator for power generation.
- ▪
- A back-to-back converter that links the generator and the grid and/or local load to extract and inject power. Two three-phase voltage source inverters (VSIs) are used to connect a six-phase generator, and the VSI used in the grid side is connected to the load and/or the grid through an LCL filter.
- ▪
- The control blocks of both the generator and the grid side.
This study focuses on the generator side by controlling both healthy and faulty operating modes based on the field-oriented control (FOC), while integrating the proposed extended LMC strategy.
The blocks related to fault management, slip speed estimation , and PWM reference generation are highlighted on the right-hand side using corresponding colors. Their operation is as follows: When the machine operates in a healthy mode, the and matrices from the fault management block (in green) are used to determine the currents in the rotating reference frame. To obtain the voltage references in this case, and matrices from the PWM reference block (in red) are applied. In the event of a fault (using a switch), such as one open phase (“a”) in this study, the corresponding system branch is automatically activated to adapt the control strategy accordingly.
The magnetizing current block (in pink) is derived using Equation (32) for conventional LMC and Equation (36) for the proposed extended LMC, while the quadrature current (in white) is derived using Equation (34).
All the proposed systems presented in this paper have been first modeled and simulated using MATLAB/simulink® software (R2024b).
3. Modeling and Control of a Six-Phase Induction Generator
3.1. Modeling
The squirrel cage six-phase induction generator (SC6PIG) is composed of a stator with six identical windings electrically shifted by 60° and a rotor of metal bars and a short-circuit ring. The stator windings are given in Figure 2. Then, it can be assimilated to a symmetrical structure with a single neutral. The machine model expressed in the natural (abcdef) reference frame is a simplified version of the internal equivalent circuit [19], where stator and rotor are represented by resistances, self- and mutual inductances.
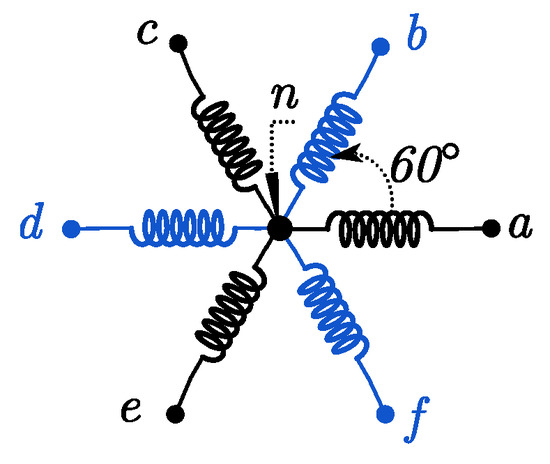
Figure 2.
Six-phase stator windings.
The voltage and flux equations are derived from Equation (1).
The electromagnetic torque expressed as a function of the stator and the rotor currents is given by Equation (2).
Based on it, the rotor speed is given in Equation (3) linking electrical and mechanical dynamics in the SC6PIG model.
3.2. Indirect Rotor Field Oriented Control
The Field-Oriented Control (FOC) allows separate control of the rotor flux and the electromagnetic torque to enhance generator performance. It operates using the rotating dq reference frame derived from the natural frame through a decoupling transformation noted given in Equation (4).
This transformation preserves power and depends on the number of active phases N (e.g., 6 in healthy mode and 5 in one missing phase case). This yields the αβzi frame, where components generate power. These zi components linked to 2 represent losses and are neglected in this work.
The vectors [α] and [β] are obtained by removing components related to any open stator phases from the reference vectors and . In healthy mode, these reference vectors are defined as in Equation (5) based on the stator phase angles . The reference angle is chosen to ensure the orthogonality between [α] and [β].
The stator and rotor voltages and flux equations can be expressed as follows:
Only the magnetizing inductances , and the stator inductances and are affected by the generator operating condition [4]. Indeed, then distinct operating scenarios are theoretically possible, including one healthy mode and nine faulty modes, depending on the combination of faulty phases. If more than three phases are lost, the machine can no longer operate, and the fault-tolerant control is no longer feasible. The corresponding inductance values for the two cases in this study, such as healthy (H) and one missing phase (F), are summarized in Table 1.

Table 1.
Inductance values in healthy and faulty modes.
In order to control the SC6PIG in healthy mode, the following transformation matrix is used to convert the previously derived equations into the synchronous rotating reference frame, where is the angle of the synchronous reference frame.
Following the application of the transformation matrix, the voltage equations for both stator and rotor can be reformulated in the synchronous reference frame as follows:
In this study, the IRFOC method is used to regulate the generator currents. Its main strategy includes maintaining the quadrature component of the rotor flux at zero while aligning the direct component with the rotor flux reference. This can be expressed as follows:
The required angle for the control scheme is obtained from the assumption in Equation (13).
In the case of a one-phase open fault, the decoupling matrix T5 is then applied, and the Park transformation matrix in faulty mode is adapted to reflect the faulty configuration.
To attenuate ripples in the dq stator currents, the T5 matrix is applied as described in the following equations, where current and inductance ratios are matched:
Assuming equal magnetizing inductance in both the αβ and dq frames under the same magnetomotive force conditions, the coefficients are derived from Equation (15):
Based on these parameters, the estimated electromagnetic torque and the electromagnetic power of the generator are given by:
4. Extended Loss Model Control
The aim of the LMC method consists in minimizing the total losses of the generator by dynamically adjusting the excitation current Id, according to the requested torque Te. Then, the proposed control will take into account switching losses in addition to generator power losses.
The total power losses in an induction generator and converter can be expressed as in Equation (18):
where , , , and represent the copper, core, mechanical, and switching losses, respectively, associated with the winding resistance, magnetic effects, and rotor motion.
For clarity, all variables and parameters used in the equations are summarized in the nomenclature provided in Appendix A.
In steady state, the stator and rotor copper losses are expressed as follows:
The core losses consist of eddy current losses and hysteresis losses and are given by:
where is the air-gap flux linkage, and and are the hysteresis and eddy current loss coefficients. The air-gap flux linkage can be expressed in terms of the current components as follows:
In the Indirect Rotor Flux Oriented Control strategy, the rotor current components in the rotating frame are expressed as in (22), and the air-gap flux linkage components are expressed as in Equation (23):
As a result, the core losses can be written as follows:
The mechanical losses are given as a function of the rotor speed , the dry friction torque , and the viscous friction coefficient :
In previous studies conducted on the same test bed [15], the switching losses of the used converter have been determined as follows:
where
Then, the full expression of the total power losses in steady state, including all components, can be written as follows (28):
This expression can also be reformulated as a function of the synchronous speed and the stator current components in the dq frame, as shown in Equation (29), since the mechanical losses are not electrically controllable through the IRFOC strategy and depend on the machine conditions [16].
4.1. Classical Loss Model Control
In the conventional LMC, only electrical power losses localized on the generator side are considered as follows:
where the coefficients and are defined as follows:
The optimal magnetizing current is then given by Equation (32). It is proportional to the quadrature current by the optimization factor, which depends on the angular speed .
4.2. Proposed LMC
By taking into account the switching losses of the converter, the global cost function of both the generator and converter is as follows:
The quadrature current obtained from the electromagnetic torque is then given by:
Using (34) to eliminate in (33), the optimizing losses function is as follows:
The cost function given in (35) is not easily solvable analytically as in the aforementioned classical LMC. Therefore, the proposed method will proceed with an online numerical solution using algorithms:
Table 2 summarizes the key differences between the three control strategies used in this study with respect to types of losses included in their optimization models and the nature of the optimization (static or dynamic). The proposed LMC extended strategy differs from conventional LMC by incorporating switching losses and performing dynamic current adjustment for real-time loss minimization.

Table 2.
Comparison of the considered loss model by control strategies and optimization type.
5. Results and Discussions
Equation (32) provides the expression of the optimal direct axis stator current obtained from the analytical minimization of the total loss function defined in Equation (30). The factor represents the optimal ratio between the magnetizing and the quadrature axis currents that reduces losses in classical LMC. It balances the components and of the losses given in Equation (31). Both of these components depend on the synchronous speed The factor enables dynamic adjustment of the excitation current to optimally distribute losses according to the operation speed. Figure 3 shows how the optimal factor evolves with in healthy and faulty modes.
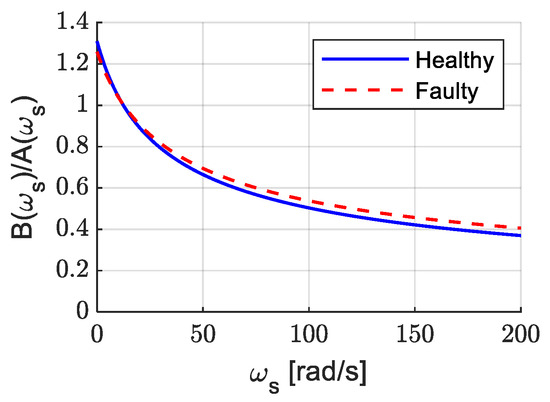
Figure 3.
The optimization factor in the classical method in both healthy and faulty modes.
The optimized direct axis current obtained using the extended LMC is shown in Figure 4. This figure includes the stator current obtained by the optimization method and compares it to the classical and the IFROC ones. The theoretical analysis confirms that LMC_Ext achieves an optimal compromise between Id and Iq to minimize losses. Unlike IRFOC control (red), which keeps Id constant and maximal, and LMC_Classic (blue), which overly reduces Id, the proposed LMC_Ext (black) intelligently adjusts Id with respect to torque. This avoids excessive growth in Iq and hence the stator current Is, leading to globally lower losses, especially at medium–high torque.
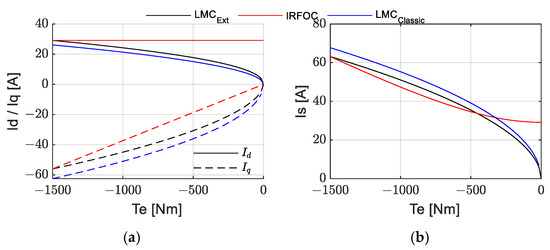
Figure 4.
The optimal current in both control methods: (a) dq currents and (b) stator currents.
The LMC_Ext (black) strategy achieves the lowest total losses thanks to an effective reduction in core losses and a well-balanced current distribution. The conventional LMC_Classic (blue) shows a better optimized core losses reduction, but this is not sufficient and optimal in the entire system. Under IRFOC control (red), copper losses are minimized, but core losses increase, making it non-optimal at low and medium load torque. The zoomed-in area (bottom-right) in Figure 5 highlights the increasing advantage of LMC_Ext and the non-optimal control of LMC_Classic at high torque.
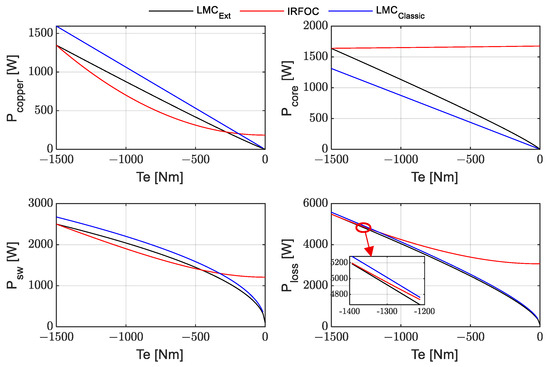
Figure 5.
Losses in different components.
This color convention (black for LMC_Ext, blue for LMC_Classic, and red for IRFOC) is maintained throughout all the figures below in this paper, as indicated in the legend of Figure 5.
As shown in Figure 6, LMC_Ext shows the highest energy saving (Figure 6a) at low load torque due to reduced core losses from minimizing the excitation current Id. This advantage decreases at high torque as all strategies tend to converge toward optimal behavior. The efficiency trend in (Figure 6b) confirms this since LMC_Ext remains slightly superior to LMC_classic due to a better ratio Id/Iq trade-off, while IRFOC control suffers from high core losses at low torque but improves at high torque load, as shown in the zoom area.
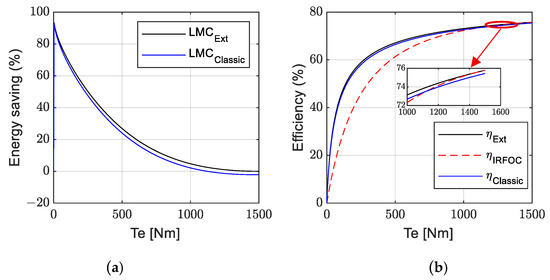
Figure 6.
(a) Energy saving and (b) efficiency comparison between LMC and IRFOC.
5.1. Simulation
The simulation results presented in this section were obtained using MATLAB/Simulink® software.
Figure 7 depicts the copper, core, switching, and total losses for different torque references (−200 N·m, −400 N·m, −600 N·m, −800 N·m, and −1000 N·m) with the three strategies (black curves for extended LMC, blue for classical LMC, red for IRFOC).
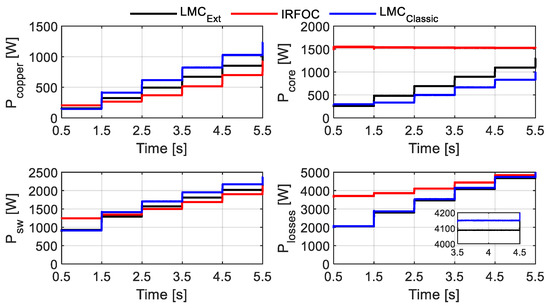
Figure 7.
Copper (Top-left), core (top-right), switching (bottom-left), and total (bottom-right) losses in healthy mode.
As illustrated in Figure 7, the proposed LMC_Ext strategy consistently reduces total losses compared to the conventional ones LMC_Classic and even more so relative to IRFOC. This improvement is mainly due to a significant reduction in core ore iron losses achieved through better control of the magnetizing current Id. Although LMC_Ext may show slightly higher copper losses than IRFOC, the overall balance between copper, core, and switching losses makes it globally more efficient.
Energy savings presented in Figure 8a are observed at large torque levels with particularly high gains at low and medium torque loads, resulting in a higher efficiency than both the LMC_Classic strategy and IRFOC control.
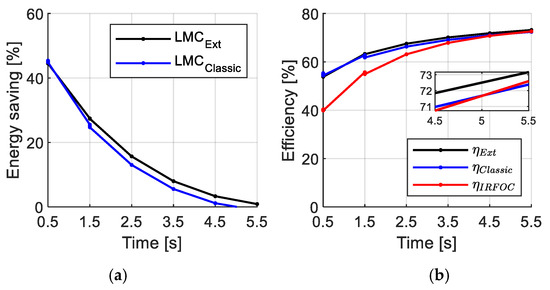
Figure 8.
(a) Energy saving and (b) efficiency in healthy mode.
It can be noticed that, at high torque, LMC_Classic tends to select a suboptimal Id/Iq compromise by reducing the magnetizing current Id too much, which increases Iq and rotor and core losses. In contrast, the IRFOC control, with a maximized Id, naturally approaches optimal performance in this range of values. As a result, LMC_Classic may become less effective, even showing negative energy gains in some cases.
Figure 9 shows the performance of the three control strategies under one missing phase operation. The LMC_Ext strategy (black bar) remains globally slightly efficient than LMC_Classic (blue bar) even under fault conditions. The difference in total power losses is especially significant at low torque load, for instance reaching 156 W at −100 N·m, which highlights the better adaptability of LMC_Ext in faulted mode. Although the gap narrows at higher torque levels, LMC_Ext maintains a slight advantage, confirming its robustness in faulty operation. Despite the low load torque request, losses become considerable in faulty mode, highlighting the importance of an adaptive control strategy such as LMC_Ext.
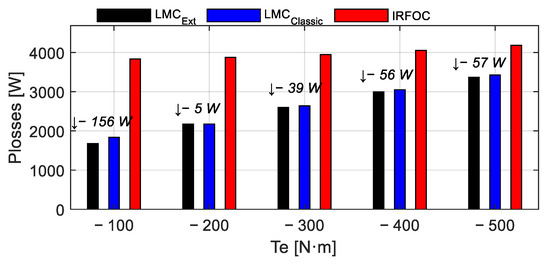
Figure 9.
Total power losses in the faulty mode.
Figure 10 shows that in faulty mode, the energy saving delivered by LMC_Ext remains significant across the entire torque range, although slightly lower than in healthy mode. Regarding efficiency, LMC_Ext has the best performance across the range. Overall, LMC_Ext proves to be the most robust and energy-efficient strategy even under fault conditions. In the faulty mode case, the requested torques are kept low because the phase currents increase significantly under fault conditions. This limitation is intentional, aiming to prevent excessive current stress on the remaining healthy phases.
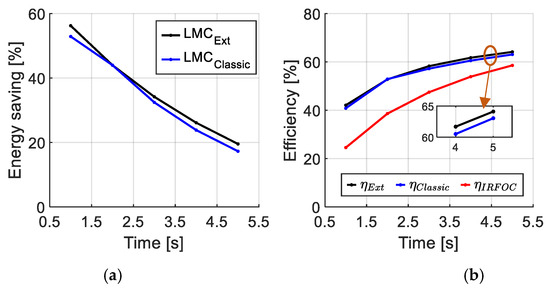
Figure 10.
(a) Energy saving and (b) efficiency in faulty mode.
Table 3 presents the efficiency results under both healthy and faulty modes for different torque values. The column in grey quantifies the improvement achieved by the proposed LMC-Ext strategy compared to both IRFOC and classical LMC strategies. The comparison highlights that the proposed LMC_Ext strategy provides a significant efficiency gain over IRFOC, especially under low and medium torque levels in both healthy and faulty modes. Although the gain over classical is more moderate, it remains notable and consistent, particularly at low load conditions where switching and core losses are more pronounced. This confirms the benefit of adjusting the excitation current while taking switching losses into account. The blue column represents the losses’ reduction (gain) achieved by the proposed LMC_Ext strategy compared to IRFOC and LMC_Classic. The results show that LMC_Ext consistently reduces total losses, particularly at low and medium torque levels and in faulty conditions, confirming its effectiveness for real-time energy optimization.

Table 3.
Simulation comparison of efficiency and loss reduction among control strategies (IRFOC, LMC_Classic, and LMC_Ext).
5.2. Experimentation
Figure 11 illustrates the test bench developed to replicate the behavior of a micro-hydraulic or a wind energy system. The setup includes a gearmotor composed of a 45 kW three-phase induction machine equipped with a gearbox. This system emulates the kinetic energy of flowing water in micro-hydropower or wind force in wind energy applications. The gearmotor is controlled by a LEROY SOMER® (Angoulême, France) variable speed drive using a V/f (Voltage/frequency) control strategy. This drive allows the generator to operate within a speed range of 0 to 133 rpm. The position is measured via an optical encoder with 4096 pulses per revolution. The gearmotor is coupled to a torque sensor with data acquisition performed using a MAGTROL system (Model 3411), Paris, France and also coupled to the squirrel cage six-phase induction generator (SC6PIG) rated at 24 kW–125 rpm–24 poles–230 V. Electrical power is extracted via two 3-phase back-to-back converters each with their dc link connected from the brand Triphase® (Holsbeek, Belgium), controlled in real time by an industrial PC from Triphase®, which runs the compiled control program from MATLAB/Simulink® software via the workstation. Measurements are carried out at a frequency of 8 kHz, enabling detailed current and power analysis through high-speed data acquisition using a National Instruments® DAQ system (Paris, France).

Figure 11.
Experimental test bench.
Figure 12 represents the experimental power losses under healthy operating conditions with the three control strategies and different references of torque in the same conditions as in simulation (Figure 7). The experimental results (Figure 12) are really close to the simulation ones (Figure 7) and validate the theoretical analysis. They also confirm the best performance of the LMC Ext strategy by minimizing total power losses. At the same torque Te = −200 N·m, losses in faulty mode (Figure 12 at 1.5–2.5 s) are significantly higher than in healthy mode (Figure 7, 0.5–1.5 s) due to current redistribution and added stress on remaining phases. Yet the proposed LMC_Ext strategy maintains the lowest losses in both modes, demonstrating both its efficiency and robustness under faulted conditions.
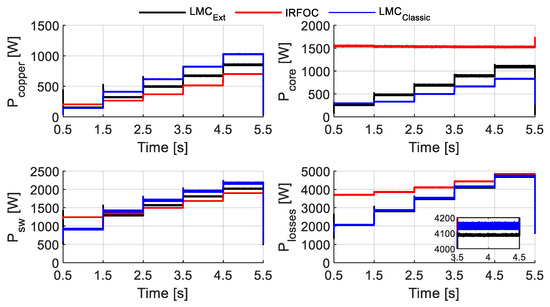
Figure 12.
Copper (top-left), core (top-right), switching (bottom-left), and total (bottom-right) losses in faulty mode.
In the zoom area of Figure 12, we can observe ripples of the order of a few tens of watts (±50), which are relatively minor and do not affect the overall trend or the validity of the experimental results. This behavior is expected and attributed to several practical factors, such as measurement noises, nonlinearities in the power components, and other imperfections.
Figure 13 depicts the energy efficiency under faulty conditions (one phase missing) with the three control strategies in the same torque conditions. This experimental test confirms the effectiveness of the proposed LMC_Ext control compared to the classical LMC and IRFOC under fault conditions.
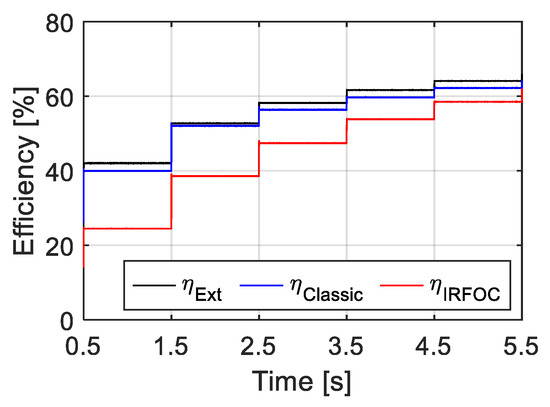
Figure 13.
Efficiency in a faulty condition.
Table 4 presents the experimental results that validate the effectiveness of the proposed control strategy. Compared to IRFOC, LMC_Ext shows clear efficiency improvements, particularly at low to medium load torque, even under faulty conditions. The gain compared to LMC_Classic is moderate but remains constant, demonstrating that the dynamic adaptation of the magnetizing current is beneficial in real hardware. Unlike the simulation, where the behavior is idealized, the experimental data confirm that LMC_Ext maintains its performance advantage despite real-world imperfections, reinforcing its practical applicability for energy-aware control in both healthy and faulty modes, with differences for some values.

Table 4.
Comparison of efficiency and loss reduction of IRFOC, LMC_Classic, and LMC_Ext experimental results.
The proposed control strategy offers a good compromise between core and switching losses by choosing an optimal magnetizing current value, effectively reducing total power losses. This approach also leads to lower stator current levels, resulting in reduced stress on a converter. As a consequence, it decreases the converter operating temperature, protecting the semiconductor components and contributing to a longer lifetime.
6. Conclusions
The proposed study demonstrated the effectiveness of an extended loss model control (LMC_Ext) strategy for improving the efficiency of a six-phase induction generator in both healthy and faulty operating conditions. By including switching losses in the optimization process and dynamically adjusting the magnetizing current Id, the proposed method achieves consistent reductions in total power losses.
Simulation and experimental results confirm that LMC_Ext consistently outperforms both the classical LMC and the IRFOC approaches, particularly at low and medium torque loads, where energy savings are most sensitive to excitation current tuning. In simulation, the gain over IRFOC is particularly significant, with notable improvements in both efficiency and energy savings. The experimental results confirm this trend, albeit with slightly higher margins. This difference can be attributed to practical imperfections, including measurement noises, system non-linearities, and inherent imperfections of components, which are not fully captured in the model.
Despite these non-idealities, the experimental validation confirms that LMC_Ext remains robust and beneficial. Its ability to maintain superior performance even under faulted conditions illustrates its real-time applicability and resilience. These findings highlight the importance of considering dynamic losses in control design and open perspectives for the application of this approach in higher power and more complex multiphase systems. However, finding the optimal point online requires additional computation, albeit manageable in real time.
Several future directions are envisioned to extend this work. First, a sensitivity analysis will be conducted on the key machine parameter (e.g., Rs, M, or Lr) to evaluate the robustness of the proposed strategy under model uncertainties. Further studies will also explore additional fault scenarios, such as inter-phase short circuits and voltage unbalance, to reinforce the fault-tolerant capabilities of the system. Moreover, a comparative analysis with other optimization strategies, including Minimum Loss Search (MLS), Maximum Torque Per Ampere (MTPA), and intelligent control approaches (e.g., fuzzy adaptive control), is currently under development. Finally, a broader system-level assessment will be pursued, considering turbine–generator interaction load variability and possible integration with energy storage to evaluate the global impact of the proposed control on micro-hydropower system efficiency.
Author Contributions
Conceptualization, M.O., A.Y. and F.B.; Methodology, M.O., A.Y. and F.B.; Software, M.O., A.Y. and F.B.; Validation, M.O., A.Y. and F.B.; Formal analysis, M.O., A.Y. and F.B.; Investigation, M.O., A.Y. and F.B.; Resources, M.O., A.Y. and F.B.; Data curation, M.O., A.Y. and F.B.; Writing—original draft, M.O., A.Y. and F.B.; Writing—review & editing, M.O., A.Y. and F.B.; Visualization, M.O., A.Y. and F.B.; Supervision, M.O., A.Y. and F.B.; Project administration, M.O., A.Y. and F.B.; Funding acquisition, M.O., A.Y. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the «Hauts de France» Region Council and Grand-Soissons Agglomeration.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| SC6PIG | Squirrel Cage 6-Phase Induction Generator |
| 6PIG | 6-Phase Induction Generator |
| LMC | Loss Model Control |
| MLS | Minimum Loss Search |
| IGBT | Isolated Gate Bipolar Transistor |
| MOSFET | Metal Oxide Semiconductor Field Effect Transistor |
| SC | Search Control |
| MTPA | Maximum Torque per Ampere |
| IRFOC | Indirect Rotor Field Oriented Control |
| LMC_Ext | LMC Extended (the proposed method) |
| LMC_Classic | Conventional LMC |
| PWM | Pulse Width Modulation |
| VSI | Voltage Source Inverter |
Appendix A

Table A1.
Rated parameters of the SC6PIG.
Table A1.
Rated parameters of the SC6PIG.
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 24 | kW |
| Rated torque | 2350 | Nm |
| Rated voltage | 230 | V |
| Rated speed | 125 | rpm |
| Rated current | 32.3 | A |
| Frequency | 25 | Hz |
| Number of pole pairs | 12 | - |
| Stator resistance Rs | 0.262 | Ჲ |
| Rotor resistance Rr | 0.64 | Ჲ |
| Stator inductance Ls | 0.0827 | H |
| Rotor inductance Lr | 0.0813 | H |
| Mutual inductance M | 0.0789 | H |
| Friction coefficient | 21.39 | Nm/rad/s |
| Inertia coefficient | 704 | kg |
| Eddy current coefficient | 0.0001 | m |
| Hysteresis coefficient | 2 | 2 |
| Dry torque coefficient | 4.5 | - |
| Viscous friction coefficient | 0.0001 | - |

Table A2.
Nomenclature of the variables and parameters used in the modeling and control strategy of the SC6PIG.
Table A2.
Nomenclature of the variables and parameters used in the modeling and control strategy of the SC6PIG.
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Stator resistance | Magnetizing flux, quadrature, and direct axis (Wb) | ||
| Rotor resistance | Rotor current, quadrature, and direct axis | ||
| , | Stator and rotor inductance | , | Stator current, quadrature, and direct axis |
| M | Mutual inductance | Hysteresis and Eddy current coefficient | |
| P | Number of pole pairs | Dry torque coefficient | |
| , | Synchronous angular and rotor speed | Friction coefficient | |
| Switching losses | Torque coefficient | ||
| Stator and rotor copper losses | Electromagnetic losses | ||
| Core losses | Mechanical losses | ||
| Optimized direct-axis stator current | |||
| Total electrical losses under the extended LMC strategy | Total electrical losses under the classical LMC strategy |
References
- Sikiru, A.O.; Abdulazeez; Yisah, Y.A.; Yusuf, Y.O.; Salawu, B.U.; Momoh, S.U. Micro Hydro-Electric Energy Generation-An Overview. Am. J. Eng. Res. 2017, 6, 5–12. Available online: https://www.researchgate.net/publication/356028778_Micro_Hydro-Electric_Energy_Generation-An_Overview (accessed on 4 July 2025).
- Windings Inc. The Role of Electric Motors in Renewable Energy Systems. Windings. Available online: https://www.windings.com/post/the-role-of-electric-motors-in-renewable-energy-systems/ (accessed on 25 May 2025).
- Smith, N.P.A. Induction generators for stand-alone micro-hydro systems. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; Volume 2, pp. 669–673. [Google Scholar] [CrossRef]
- Pantea, A.; Yazidi, A.; Betin, F.; Carriere, S.; Sivert, A.; Vacossin, B.; Henao, H.; Capolino, G.-A. Fault-Tolerant Control of a Low-Speed Six-Phase Induction Generator for Wind Turbines. IEEE Trans. Ind. Appl. 2019, 55, 426–436. [Google Scholar] [CrossRef]
- Levi, E.; Barrero, F.; Duran, M.J. Multiphase machines and drives—Revisited. IEEE Trans. Ind. Electron. 2016, 63, 429–432. [Google Scholar] [CrossRef]
- Nam, S.W.; Uddin, M.N. Model-Based Loss Minimization Control of an Induction Motor Drive. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 2367–2372. [Google Scholar] [CrossRef]
- Singh, J.; Raju, B.S.N. Switching Losses Analysis of Multi-Level Inverter FED 3-Φ Induction Motor Drive. 2017, Volume 4. Available online: https://troindia.in/journal/ijcesr/vol4iss4part2/27-34.pdf (accessed on 26 May 2025).
- Sadigh, A.K.; Dargahi, V.; Corzine, K.A. Analytical Determination of Conduction and Switching Power Losses in Flying-Capacitor-Based Active Neutral-Point-Clamped Multilevel Converter. IEEE Trans. Power Electron. 2016, 31, 5473–5494. [Google Scholar] [CrossRef]
- Measuring IGBT Conduction Loss to Maximize Efficiency. Available online: https://www.bourns.com/docs/technical-documents/technical-library/igbt/bourns_measuring_igbt_conduction_loss_to_maximize_efficiency_white_paper.pdf?sfvrsn=eb4853f6_12 (accessed on 11 June 2025).
- MOSFET Power Losses and How They Affect Power-Supply Efficiency. Available online: https://www.ti.com/lit/an/slyt664/slyt664.pdf?ts=1752310286755&ref_url=https%253A%252F%252Fwww.google.com.hk%252F (accessed on 25 May 2025).
- Borisevich, A.; Schullerus, G. Energy Efficient Control of an Induction Machine under Load Torque Step Change. arXiv 2014. [Google Scholar] [CrossRef]
- Attaianese, C.; Di Monaco, M.; Tomasso, G. Maximum Torque Per Watt (MTPW) field-oriented control of induction motor. Electr. Eng. 2021, 103, 2611–2623. [Google Scholar] [CrossRef]
- Kirschen, D.S.; Novotny, D.W.; Lipo, T.A. On-Line Efficiency Optimization of a Variable Frequency Induction Motor Drive. In Proceedings of the 1984 Annual Meeting Industry Applications Society, Chicago, IL, USA, 30 September–4 October 1984; pp. 488–493. Available online: https://ieeexplore.ieee.org/document/10120456 (accessed on 11 June 2025).
- Bazzi, A.M.; Krein, P.T. Review of Methods for Real-Time Loss Minimization in Induction Machines. IEEE Trans. Ind. Appl. 2010, 46, 2319–2328. [Google Scholar] [CrossRef]
- Pantea, A.; Sivert, A.; Yazidi, A.; Betin, F.; Carriere, S.; Capolino, G.A. Efficient Field Oriented Control with power losses optimisation of a six-phase induction generator for wind turbines. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1912–1917. [Google Scholar] [CrossRef]
- Hrkel, M.; Vittek, J.; Biel, Z. Maximum torque per ampere control strategy of induction motor with iron losses. In Proceedings of the 2012 ELEKTRO, Rajecke Teplice, Slovakia, 21–22 May 2012; pp. 185–190. [Google Scholar] [CrossRef]
- Sousa, G.C.D.; Bose, B.K.; Cleland, J.G. Fuzzy logic based on-line efficiency optimization control of an indirect vector controlled induction motor drive. In Proceedings of the IECON ’93—19th Annual Conference of IEEE Industrial Electronics, Maui, HI, USA, 15–19 November 1993; Volume 2, pp. 1168–1174. [Google Scholar] [CrossRef]
- Qu, Z.; Ranta, M.; Hinkkanen, M.; Luomi, J. Loss-Minimizing Flux Level Control of Induction Motor Drives. IEEE Trans. Ind. Appl. 2012, 48, 952–961. [Google Scholar] [CrossRef]
- Yazidi, A.; Pantea, A.; Betin, F.; Carriere, S.; Henao, H.; Capolino, G.-A. Six-phase induction machine model for simulation and control purposes. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 881–887. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).