Technical and Economic Analysis of a Newly Designed PV System Powering a University Building

Abstract

The use of renewable energy sources on university campuses is crucial for sustainable development, environmental protection by reducing greenhouse gas emissions, improving energy security, and public education. This study addresses technical and economic aspects of the newly designed photovoltaic system on the campus of the Bialystok University of Technology. The first part of the article presents the results of 9 years of research on an experimental photovoltaic system that is part of a hybrid wind and PV small system. The article proposes five variants of the arrangement of photovoltaic panels on the pergola. A new method was used to determine the energy efficiency of individual options selected for analysis. This method combines energy simulations using DesignBuilder software and regression analysis. The basic economic indicators NPV and IRR were applied to select the most appropriate arrangement of PV panels. In the recommended solution, the panels are arranged in three rows, oriented vertically, and tilted at 37°. The photovoltaic system, consisting of 438 modules, has a peak power of 210 kWp and is able to produce 166,392 kWh of electricity annually. The NPV is 679,506 EUR, and the IRR is over 38% within 30 years of operation.

1. Introduction

Energy consumption of university buildings is an important issue that is often the subject of scientific publications [1,2]. Choosing the right energy management method is a fundamental problem to be solved in times of high energy prices, climate change, and economic instability. A significant aspect of this topic is the widespread implementation of building management systems (BMS) and building information modelling (BIM) [3] combined with comprehensive monitoring of energy consumption [4,5]. This would reduce energy demand primarily through automatic regulation of heating/cooling temperature and changing lighting intensity depending on the occupancy of people [6]. Another problem related to energy management is the correct determination of the number of sensors and their arrangement. Equally important is the selection or development of appropriate algorithms adapted to the specifics of buildings performing various functions located on a campus [7,8]. The method of proper management of energy consumption in university buildings should include, in addition to technological aspects, minimising the impact on the environment.

The need to implement a sustainable development policy was primarily due to limited and shrinking conventional energy resources, as well as increasing climate change. Universities should set an example in the application of such strategies by meeting the energy needs of buildings with renewable energy sources (RES).

One of the more popular and effective solutions is the increasingly widespread development of technology for converting solar radiation into electricity and heat. Solar thermal collectors are more than twice as efficient under operating conditions as photovoltaic (PV) panels with the same absorber surface area. Despite this, the second type of device enjoys greater and still increasing popularity among investors. The main advantage of this fast-growing PV technology is its high versatility in the year-round use of electricity. The construction of systems based on solar energy conversion on university campuses is of particular importance. Such systems are a good advertisement for renewable energy sources among future engineering staff and additionally allow for the reduction in the operating costs of these educational facilities. It should be noted that the peak electricity demand of university buildings occurs during the day, i.e., during the period of the highest solar radiation. In addition, PV installations are often an excellent source of measurement results used for scientific and teaching purposes.

Therefore, the main reasons for using renewable energy sources at universities are low operating costs as well as improved energy security and price stability. The educational and social aspects should also not be forgotten. Universities should use their energy management as an example to promote sustainable development and educate both the local community and the academic community in this respect. An additional and equally important aspect of implementing RES is the environmental benefits associated with reducing pollution and protecting ecosystems.

It should be noted that a common barrier to the development of energy-saving technologies is the high initial costs. Therefore, in addition to the energy assessment of this type of project, a thorough financial analysis should be performed. An example of such an approach is the case study described in this article.

The selected and most representative examples of the use of photovoltaic systems on university campuses are characterised below.

Hasapis et al. [9] presented the assumptions and the most important stages of designing a PV system on the campus of the Technical University of Crete (TUC). It has been estimated using PVGIS that the daily horizontal surface irradiance within the campus area is over 5.20 kWh/m², and the annual average generation is 1900 kWh/m². The University’s electricity demand has been calculated at around 4000 MWh/year. The authors designed a PV system that will consist of eight separate systems made of 8206 multi-crystalline silicon photovoltaic modules. The installed capacity of the entire PV system will be 2.01 MWp, enabling the annual production of an average of 1899 MWh of electricity. The shortened economic analysis allowed for to estimation of the simple payback period of the investment at 4.2 years, while the levelized cost of electricity (LCOE) at 0.11 EUR/kWh.

Furukakoi et al. [10] developed a strategy for reducing electricity costs for Sanyo-Onoda City University. For this purpose, they performed a technical and economic analysis of a PV system integrated with an energy storage system. The PV installation consisted of 40 panels (16 kW of power and 88.5 m² of installation area each) and a battery storage with a capacity of 428 kWh. Implementing this project would allow the University to save approximately 15% on its electricity expenses.

The optimisation of the American University of Beirut (AUB) campus microgrid was carried out by Chedid et al. [11]. The power demand of the entire campus varies from 3 MW to 7.2 MW in winter and from 3 MW to 9.3 MW in summer. Using a heuristic genetic algorithm approach, it was found that the PV system rated power is 2400 kW, and the optimal battery energy storage system (BESS) capacity should be no less than 26,685 kWh. The proposed technological solution allowed for the reduction in the total cost of electricity (COE) from 0.137 USD/kWh to 0.088 USD/kWh in the first year of operation.

A method for determining the availability of PV installations on the roofs of university buildings based on simulation results and cartographic data was developed by Hurtado-Perez et al. [12]. The proposed methodology was applied at the Universitat Politécnica de Valencia, Vera-Campus, which has 88,913 m² of roofs suitable for the integration of a PV system. The location assumed in this article is characterised by high average annual solar radiation of 1735 kWh/m². The analysis included three PV systems with a capacity of 5439 kW, 3946 kW, and 2824 kW. For these cases, yearly production was estimated at 9171 MWh, 6653 MWh, and 4762 MWh, respectively.

The cooperation of the PV system together with the ground heat pump in terms of energy efficiency and economy was tested by Sim and Suh [13]. The optimisation analysis used heuristic solutions and a multi-criteria genetic algorithm, while energy simulations were performed in the DesignBuilder software environment. The case study was a 10-story residential building located on a university campus in Gyeongbuk Province (Korea). Comparison of the results obtained using the optimisation technique showed that a 19% efficient PV system with a power of 15 kW, together with a 40 kW ground source heat pump, is the most efficient solution for this reference building.

A 1.05 MW PV system at the University of Jaen (Spain) was the subject of an analysis carried out by Munoz-Rodriguez et al. [6]. The authors used a methodology for the detailed analysis of large rooftop PV systems, taking auto-consumption into account. The PV installation consists of five separate installations, including three located on the roofs of university buildings and two car park roofs. The results show that the PV system has good energy efficiency as the performance ratio exceeded 0.83 and the global capacity factor was 0.19.

A technical and economic analysis of PV systems placed on the roofs of university buildings in the Ouargla Province (Algeria) was performed by Mokhtar et al. [14]. The annual energy demand of the case study building was 1487.35 MWh. It was estimated that 60% of the roof area, which is 18,209 m², could be adapted to the installation of PV panels. Based on the results of calculations performed in the HOMER software environment, it was determined that a 1300 kW PV system can produce 2333.11 MWh per year. In the optimal variant, a low energy cost of 0.043 USD/kWh was achieved.

He et al. [15] studied the performance of the PV-BESS system in the university building located in Changsha University of Technology (China). DesignBuilder and TRNSYS software were used to perform energy simulations of 36 different variants of integrated PV systems with energy storage. The PV system consisted of 820 panels with an area of 1.944 m². The simulation results showed that the PV panels are able to generate 305654 kWh per year.

As part of the green campus initiative, one of the new teaching facilities of Kashiwa University of Tokyo (Japan) was designed a PV installation by Teah et al. [16]. The PV system consisted of panels with an area of approximately 100,000 m², which allowed for obtaining a peak power of 14,851 kWp. The size of the PV system was able to cover 31% of the electricity demand of the Kashiwa campus in the spring period. In summer, autumn, and winter, the self-sufficiency rates were lower and amounted to 0.26, 0.18, and 0.19, respectively. Assuming an interest rate of 1.7%, the LCOE value was obtained as 0.07 USD/kWh, while assuming a rate of return of 3.2%, this value was 0.09 USD/kWh.

The non-dominated sorting genetic algorithm II was applied by Huang et al. [17] to optimise the PV system. The research facility was located on the Ryukyu Senbaru University Campus (Japan), covering an area of 1186307 m². Three cases were considered, combining a PV installation, batteries, and an electrical grid: Case 1—Battery 68 kWh, 11,736 PV modules; Case 2—Battery 68 kWh, 11,736 PV modules, Grid 1270 kWh; and Case 3—Battery 591 kWh, 11,320 PV modules. Based on the results of the calculations, the loss of power supply probability (LPSP) was estimated to be 0.0472% in Case 2 and 0.0038% in Case 3. While the waste of energy was equal to 2.28 × 10⁴ kWh, 1.60 × 10⁶ kWh, and 1.36 × 10⁶ kWh, for Case 1, Case 2, and Case 3, respectively.

Ahmed et al. [18] used the PV*SOL computer programme to simulate the energy performance of a rooftop PV installation on the campus of NED University of Engineering and Technology (Pakistan). The total roof area of the academic buildings is 28,417 m², and the total roof area of all buildings on the campus is 68,768 m². It turned out that 59% of the roof area of the teaching building and 62% of the other buildings are suitable for installing a PV system. Based on the calculation results, it was found that a PV system, generating 5389.2 MWh/year, can be built on the university campus in Karachi. The highest energy production will be possible in April, 562.7 MWh, and the lowest, as could be expected, in December, and this value would be 306.2 MWh. The economic analysis allowed for the determination of the LCOE of the PV system equal to 0.05 USD/kWh, and the discounted payback period will be 11.17 years.

The installation of photovoltaic panels in Poland is also very popular due to subsidies from government funds. Selected research studies related to the optimisation of this type of system are presented below.

Marchwiński and Kurtz-Orecka [19] considered various methods of supplying heat to a nursery building in the climatic conditions of Warsaw (Poland). The analysis covered 24 configurations of ground and air heat pumps cooperating with photovoltaic installations of various power.

The impact of a photovoltaic system on reducing the energy demand of a large food processing plant located near Poznan (Poland) was studied by Dobrzycki et al. [20]. The authors developed their original concept of using a building-integrated photovoltaic installation.

Wciślik and Kotrys-Działak [21] analysed the profitability of a photovoltaic installation for a house in Suchowola (Poland), which is located in the geometrical centre of Europe. The cooperation of a heat pump with a photovoltaic installation in an off-grid system supplying energy to a renovated building was considered only as a specific case study.

Woroniak [22] analysed the operation of a photovoltaic installation located on the roof of a building with an office part and a kindergarten part in Bialystok (Poland). As a result of the analysis of measurement results, it turned out that the PV system can reduce carbon dioxide emissions by about half of the previous value.

The procedures for designing and optimising photovoltaic systems supported by GIS and CAD tools were proposed by Davybid et al. [23]. The roof of a building located on the campus of the Poznan University of Technology (Poland) was a case study for modelling different variants of PV panel layout. The calculation results showed that the considered surface allows for the annual electricity generation of about 100 MWh.

The energy efficiency of PV panels with a total power of about 8 kWp located on the roof of a teaching building in Krakow (Poland) was tested by Żołądek et al. [24]. Energy simulations using Polysun and TRNSYS software were used as the research method. The paper presents three alternative modelling approaches aimed at improving the performance of this small PV system.

To sum up the literature review, it can be stated that the issue of establishing PV systems in university campuses is very promising and has gained interest in many research and scientific works. The examples described above allow us to conclude that designing photovoltaic systems on university campuses requires an individual approach for several key reasons. The first is the diversity of the functions buildings perform. The differences depend on the age of the university buildings, their construction technology, size, orientation, and roof construction. The second parameter is the location of the university, which influences the intensity of solar radiation and outside temperature. As is widely known, local weather conditions have a decisive influence on the energy efficiency of PV panels. Unfortunately, none of the PV systems described above are characterised by similar climatic conditions to the case study considered in this article and cannot be compared. Universities also have different priorities and goals for using RES. These include sustainable development, energy security, reliability of energy supply, and reduction in operating costs. In some cases, RES systems are built for the development of scientific research or for educational purposes.

The main objective of this study is to determine an optimal arrangement of PV panels placed on a pergola near an academic building that partially shades it.

As a novelty, a new method combining energy simulations and analytical calculations was presented. A cost analysis based on basic investment evaluation indicators such as net present value (NPV) and internal rate of return (IRR) was included in this study. Another new element is the presentation of the results of 9 years of experimental tests of the efficiency of a PV system located a short distance from the newly designed generating system were summarised. An assessment of the potential for solar radiation conversion was also presented. The results of meteorological measurements being collected from 2015 on the campus of the Bialystok University of Technology were used for this purpose.

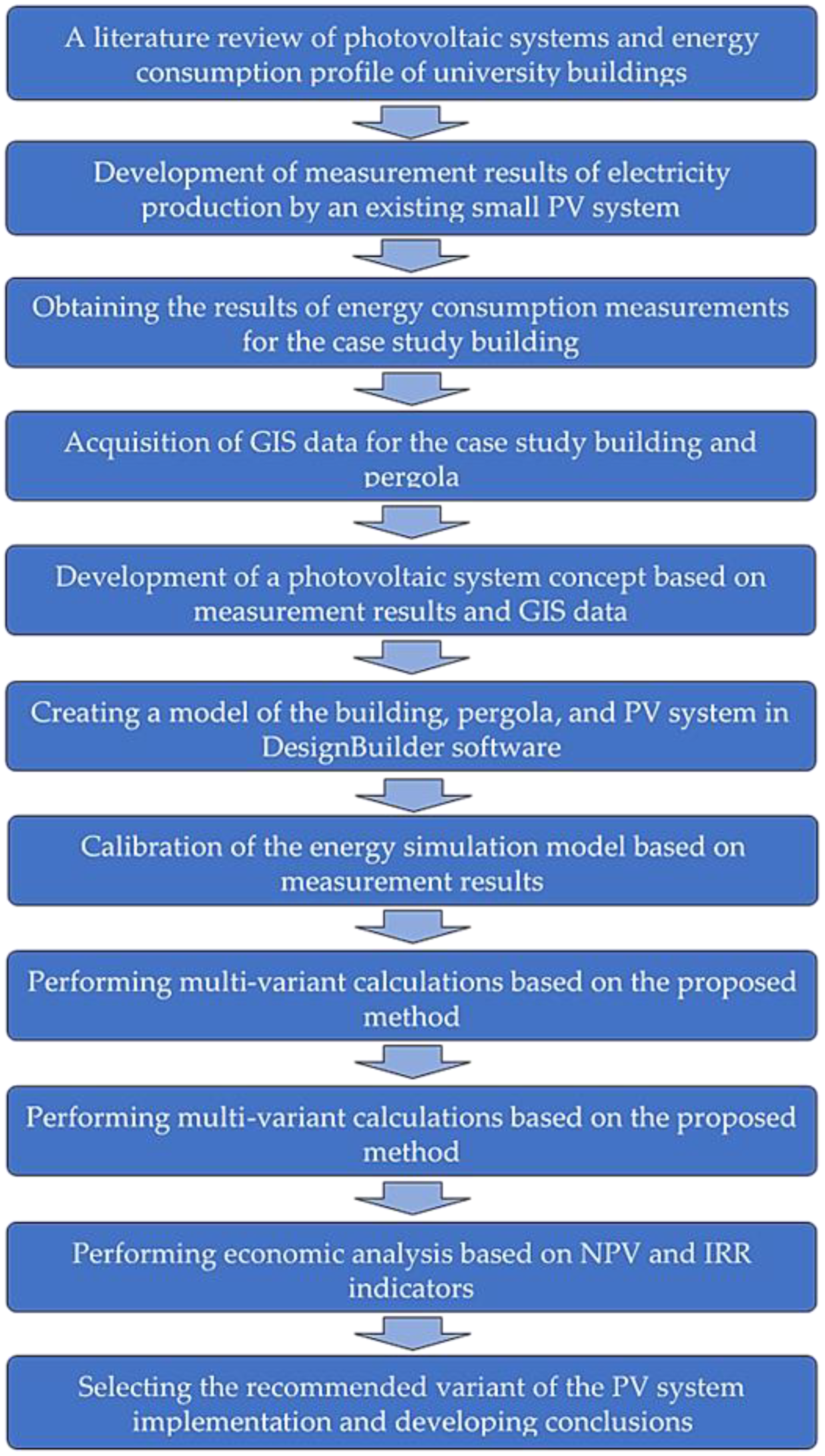
2. Materials and Methods

In order to carry out this study, real measurements and energy simulation results were used to determine the demand for electricity of the Faculty buildings and the energy production by the PV system. The economic analysis was based on the commonly accepted methodology, including the determination of basic financial indicators, which are the NPV and IRR. Figure 1 presents the subsequent steps of this analysis in a flowchart form.

2.1. Description of the Site Where the New PV System Can Be Located

The Faculty of Civil Engineering and Environmental Sciences (FCEES) of Bialystok University of Technology (BUT) consists of three teaching and research buildings: Building A (3-storey), Building B (1-storey), and the newest INNO-EKO-TECH Building (4-storey with a machine hall), all with basements (Figure 2). The WBiNoS building part A is planned to be the main recipient of electricity from the newly designed PV system. It has the following dimensions: a length of 118.0 m, a width of 19 m, and an average height of 13.6 m. Currently, the BUT campus is powered from the medium voltage (MV) distribution grid. The pergola on which the PV panels are planned to be installed is shown in the further part of the article in Figure 8B.

2.2. Energy Modelling Assumptions

Energy simulations of the FCEES Building A and the PV system were performed in DesignBuilder version 6.1.8.021. A monocrystalline PV module with an area of 2 m² was a single component from which the PV system would be built. The technical specification of such a module is shown in

Table 1. Basic PV module data.

Parameters	Parameter Value
Active area (m2)	2.0
Outside width [m]	1.9
Outside length [m]	1.1
Cells type	N-type monocrystalline
Rated power [W]	480
Module heat loss coefficient (W/(m2K))	30
Peak-power voltage [V]	35.38
Peak-power current [A]	13.57
Open circuit voltage [V]	42.71
Short circuit current [A]	14.31
Temperature coefficient of short circuit current (A/K)	0.0064
Temperature coefficient of open circuit voltage [V/K]	−0.105

Explanation of terms used in the table: Active area—this is the part of the panel where solar radiation is converted into electrical energy. Open circuit voltage—this is the maximum voltage produced by the photovoltaic panel when no electrical load is connected. Short circuit current—this is the value of the maximum current that flows in the PV panel in the event of a short circuit. Temperature coefficient of short circuit current—this is a coefficient that indicates how the temperature change affects the short-circuit current. Temperature coefficient of open circuit voltage—this is a coefficient that indicates how temperature affects the voltage value of the photovoltaic module.

.

The mathematical model called “Equivalent One Diode” [25] was used to determine the efficiency of PV modules in the DesignBuilder environment. It is called the “Five-Parameter PV Model” in the TRNSYS simulation environment. This approach allows for accurate modelling of PV module efficiency as it takes into account changes in temperature and solar radiation intensity. In order to calculate the temperature of the module cells, the “Decoupled” option was used, in which an energy balance is performed under nominal operating cell temperature (NOCT) conditions. The schematic configuration of the single PV panel used in the software model is shown in Figure 3. The inverter efficiency is assumed to be 95%.

In order to determine the energy yield of PV panels, a set of weather data representing the typical meteorological year (TMY) for Bialystok within one year (Bialystok 122950—IMGW) [26] was used.

To determine the optimal tilt angle of the PV modules, the online tool Photovoltaic Geographical Information System (PVGIS) version is used. Version 5.3 was used. It was developed by the Joint Research Centre Energy Efficiency and Renewables Unit of the European Commission. The system consists of three calculation modules:

• Photovoltaic performance [27]—used to determine solar radiation and performance of the PV system.
• Solar radiation [28]—used to calculate the value of solar radiation and the efficiency of PV panels.
• Typical meteorological year [29]—used to generate climate parameters in a typical meteorological year for a selected period.

2.3. Basic Assumptions of Financial Cost Analysis

The selection of the recommended PV system variant was based on the NPV indicator. NPV is a commonly used coefficient for assessing the profitability of an investment from a given financial perspective. A project under test is considered profitable when the NPV is positive. The value of this indicator was calculated, similar to the formula proposed in [18], using the following equation:

$$\begin{gathered} NPV=-IC+{{\displaystyle \sum }}_{i=1}^{i=T}CF\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}-{{\displaystyle \sum }}_{i=1}^{i=T}{C}_{O\&M}\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}- \\ {{\displaystyle \sum }}_{i=1}^{i=T}{C}_R\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}\left[\mathrm{EUR}/\mathrm{kWp}\right] \end{gathered}$$

(1)

where

• IC—initial capital cost of investment, including the cost of design, equipment, transportation, and installation of the system and infrastructure [EUR/kWp];
• CF—cost flows related to the annual cost reduction resulting from the use of energy from the PV system [EUR/kWp];
• C_O&M—annual cost resulting from the operation and maintenance of the entire system [EUR/kWp];
• C_R—annual cost resulting from the need to replace worn-out components of the PV system [EUR/kWp];
• T—life cycle period [year];
• r—discount rate [%].

Equation (1) consists of four terms: initial costs, financial flows, operating costs, and costs related to replacing worn-out system components. The last three terms are discounted annually based on the discount rate. The total initial cost was estimated based on preliminary calculations received from leading contractors and amounted to 447.3 EUR/kWp. It was assumed that the annual cost of operation and maintenance would be 5% [18] of the initial costs, that is, 22.4 EUR/kWp in the first year. When calculating the C_R value, it was determined that the inverters would be replaced after 15 years, and this cost will be 81.1 EUR/kWp. The number of converters depended on the system peak power in the individual variants, and the power of a single converter was approximately 50 kW.

The main assumption of the financial analysis was based on a rather optimistic scenario of the development of the financial situation, i.e., a discount rate of 3% and an annual increase in electricity costs of 2%. The discount rate is used to determine the time value of money. This parameter allows you to take into account the risk associated with future cash flows.

Due to the increasing technical progress in the construction of PV modules, it was assumed that the life span of a PV system is 30 years.

The IRR was used to determine the real rate of return from building and operating a PV system. This next economic indicator is calculated iteratively by finding the value at which the NPV is equal to 0:

$$\begin{gathered} -IC+{{\displaystyle \sum }}_{i=1}^{i=T}CF\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}-{{\displaystyle \sum }}_{i=1}^{i=T}{C}_{O\&M}\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}- \\ {{\displaystyle \sum }}_{i=1}^{i=T}{C}_R\left(i\right)·{\displaystyle \frac{1}{{\left(1+r/100\right)}^i}}=0. \end{gathered}$$

(2)

PV modules systematically lose their efficiency due to environmental impacts. Therefore, in the calculations related to determining the amount of energy produced from the PV system E_PV,i in the year i, a degradation rate dr [30] of 0.5%/year was used:

$$E_{PV,i}=E_{PV,0}{\left(1-{\displaystyle \frac{dr}{100}}\right)}^i\left[\mathrm{kWh}\right].$$

(3)

The dr indicator allows for taking into account the decrease in the output power of the PV panel over a year.

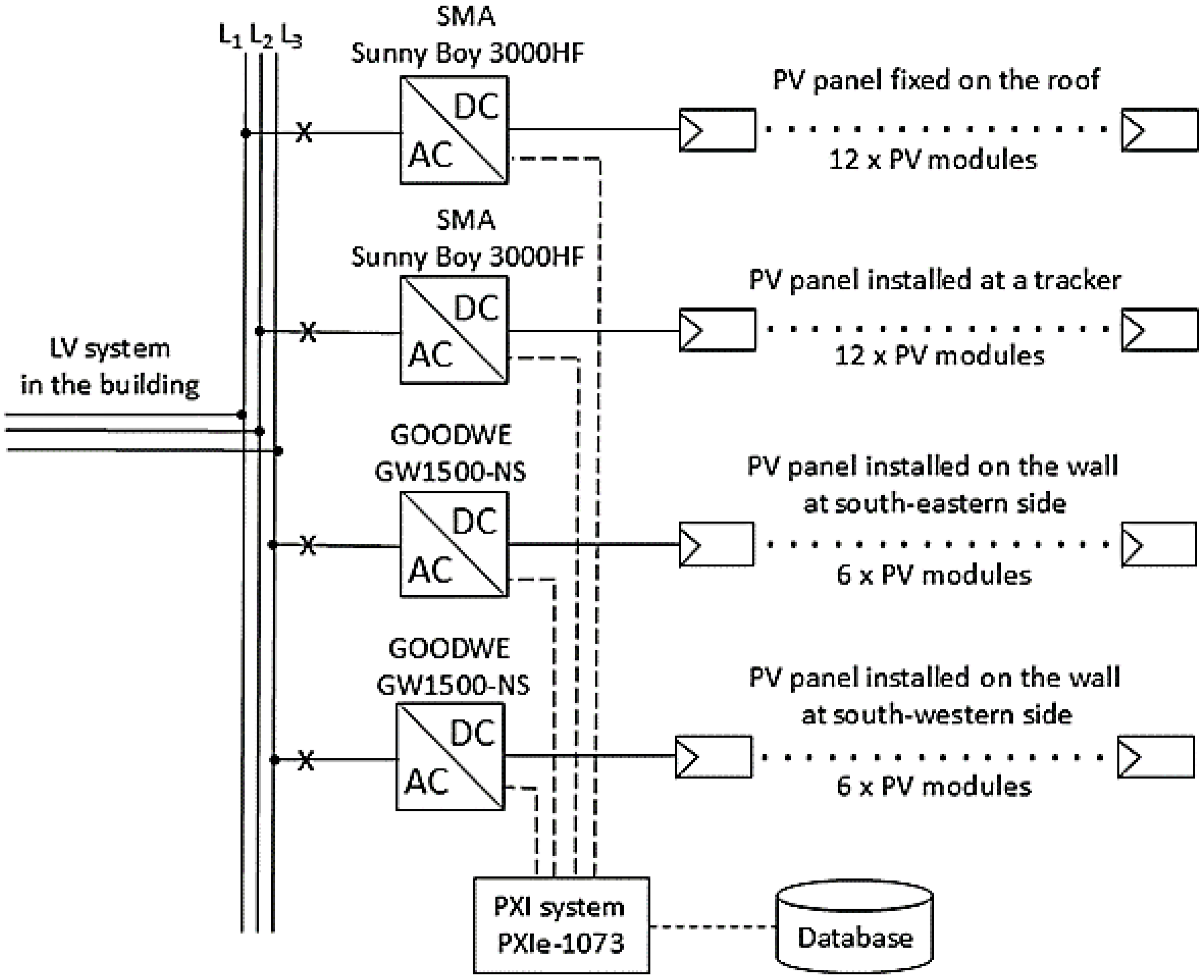
2.4. Characteristics of the Measurement System

A small PV system was installed at the Bialystok University of Technology as part of a hybrid wind and PV system to perform experimental research. It is located in the building situated in the middle of the campus (Figure 4). The system has been in operation from February 2015 till now. It consists of four units, i.e., two installed on the roof (first fixed mounted and the second at a tracker), and two assembled on the wall (first at the southeastern side, and second at the southwestern side). The capacity of each panel established on the roof is 3 kWp (each panel consists of 12 PV modules of 250 Wp of rated power). The capacity of each panel installed on the wall is 1.5 kWp (each panel consists of 6 PV modules). The fixed panel is arranged with two rows (one by one), and each row includes six modules. The module’s inclination angle is 38°. The panel assembled tracker is arranged with an array of 4 modules horizontally × 3 modules vertically. Each of the panels mounted on the wall is arranged with an array of 3 modules horizontally × 2 modules vertically. The technology of PV cells used in all modules is polycrystalline silicon.

Figure 5 presents the schematic of the internal electrical installation in the PV system. Each PV panel is interconnected to an individual on-grid inverter at the DC side. The one-phase AC side of the inverters is interconnected to a single bus of a three-phase busbar. The busbar is a component of the low-voltage (LV) system of the building. The different types of inverters are depicted in Figure 5. All the features (e.g., instant power and energy generated, to name a few) are being transferred online from inverters to the PXI system by National Instruments. The dataset of 1s resolution is stored in an external database and can be used for statistical analysis, data visualisation, and so on. Since the features are being gathered directly from the inverters, the measurement range is fully adapted to the technical specification of the inverters. The measurement accuracy is enough for operational control, to control the current to be fed into the low voltage, and for evaluation of energy generation. The measurement error of energy generated can be neglected since it is much smaller compared to the error (underestimation) of energy not served because of switching of the PV system for maintenance, hardware failures, faults, and so on.

3. Hybrid Method for Estimating PV System Performance

A new method for determining the amount of energy produced by a PV system, E_PV, has been proposed. It is based on a combination of numerical modelling and analytical calculations. Three basic steps must be completed to obtain the final result.

I.

In the first stage, the efficiency of PV modules should be calculated using dedicated energy simulation software. We do not model the entire PV system, but only perform calculations at selected and characteristic zones/places of the installation. The result of simulation calculations is the relationship between the amount of energy produced and the location of the panel or group of panels.

II.

Then, using the regression method, we develop a polynomial equation (preferably of the third degree) that analytically describes the calculation results (Equation (1)).

$$E_{PV}\left(x\right)={ax}^3+{bx}^2+cx+d\left[\mathrm{kWh}/\mathrm{m}\right],$$

(4)

where a, b, c, d—polynomial coefficients; x—distance [m].

III.

In the third and final step of this method, we calculate the amount of energy produced by the entire PV system. One way to obtain the final result could be to integrate the polynomial equation over the region under consideration.

$$E_{PV}={{\displaystyle \int }}_{x_1}^{x_2}\left({ax}^3+bx{bx}^2+cx+d\right)dx\left[\mathrm{kWh}\right].$$

(5)

$$E_{PV}\left(x_1\right)=0.2·a{x}_1^4+0.3333·b{x}_1^3+0.5·c{x}_1^2+dx.$$

(6)

$$E_{PV}\left(x_2\right)=0.2·a{x}_2^4+0.3333·b{x}_2^3+0.5·c{x}_2^2+dx.$$

(7)

$$E_{PV}=E_{PV}\left(x_2\right)-E_{PV}\left(x_1\right).$$

(8)

This approach constitutes a great simplification and time saving, for example, when performing energy simulations using DesignBuilder software. Each PV panel or thermal solar collector must be placed in the model in this computer programme.

The method is dedicated to rather large systems that are partially shaded by adjacent objects. It works best in cases where the mounting surfaces are long and narrow. Then it is easier to use regression analysis to determine electricity production as a function of panel position. The accuracy of this method depends primarily on the degree of detail in modelling the objects that are the source of shading. For large trees, it is recommended to factor the change in opacity into seasonal schedules.

It should also be noted that the same methodology can be used to model systems converting solar radiation into heat.

4. Results and Discussion

The choice of the PV system layout was determined by many factors, the most important of which included: system location, panel position (vertical or horizontal), distance between rows, orientation to the cardinal directions, the influence of shading, power demand, and its time-domain profile. In order to examine this issue in detail, a number of variants were selected and described below in this chapter.

4.1. Measurement Results of the Energy Output of the Existing PV System

The annual energy production of the PV system, installed on the campus of the Bialystok University of Technology, in the period of 2016–2024, is presented in

Table 2. Historical data on energy production from PV panels located on the BUT campus.

	Energy Generated [kWh] by:
Year	PV Panel Fixed on the Roof	PV Panel Installed on a Tracker	PV Panel Installed on the Wall at the Southeastern Side	PV Panel Installed on the Wall at the Southwestern Side
2016	2823	4072	1110	890
2017	2616	3744	998	871
2018	3184	4552	1209	996
2019	3235	4655	1219	1034
2020	3050	4340	1133	941
2021	2833	4156	1145	923
2022	3022	4370	1180	952
2023	2961	3508	1104	922
2024	2749	2951	1006	872
	Energy generated by PV panels [kWh] per 1 m2 of panel area within the period 2016–2024
2016–2024	1572	2125	1192	978
	Energy generated by PV panels [kWh] per 1 m2 of panel area per year
2016–2024	175	236	133	109

.

From the comparison of real measurements, it is concluded that the tracking system assures the highest electricity production per 1 m². Its energy efficiency is over 25% higher than panels positioned on the roof at an optimal slope to the south. However, this type of solution is characterised by very high investment and maintenance costs and problems related to the installation on the roof. Therefore, in this study, the solution of placing the PV system on the roof with a constant angle of inclination of the panels was chosen.

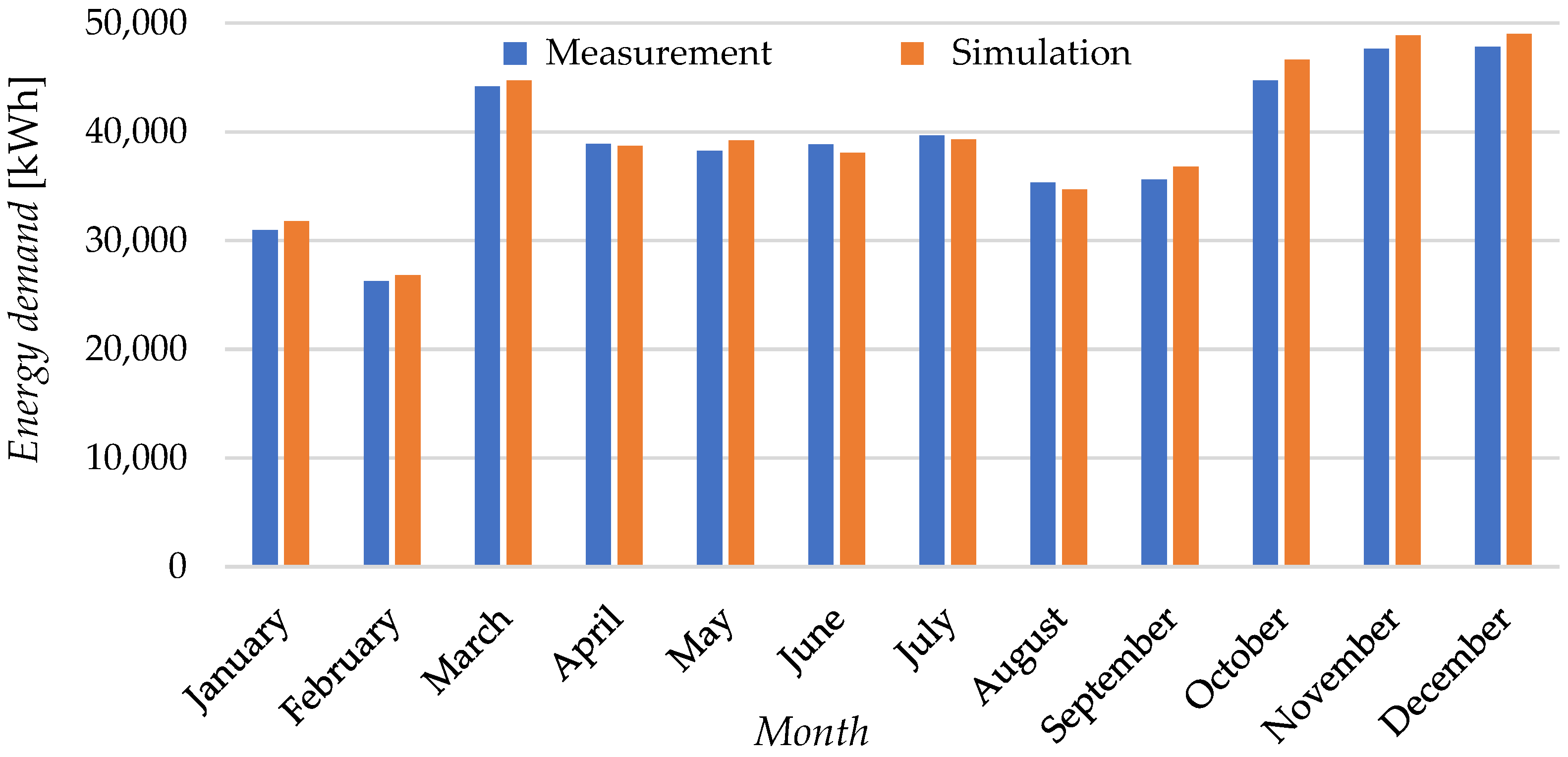
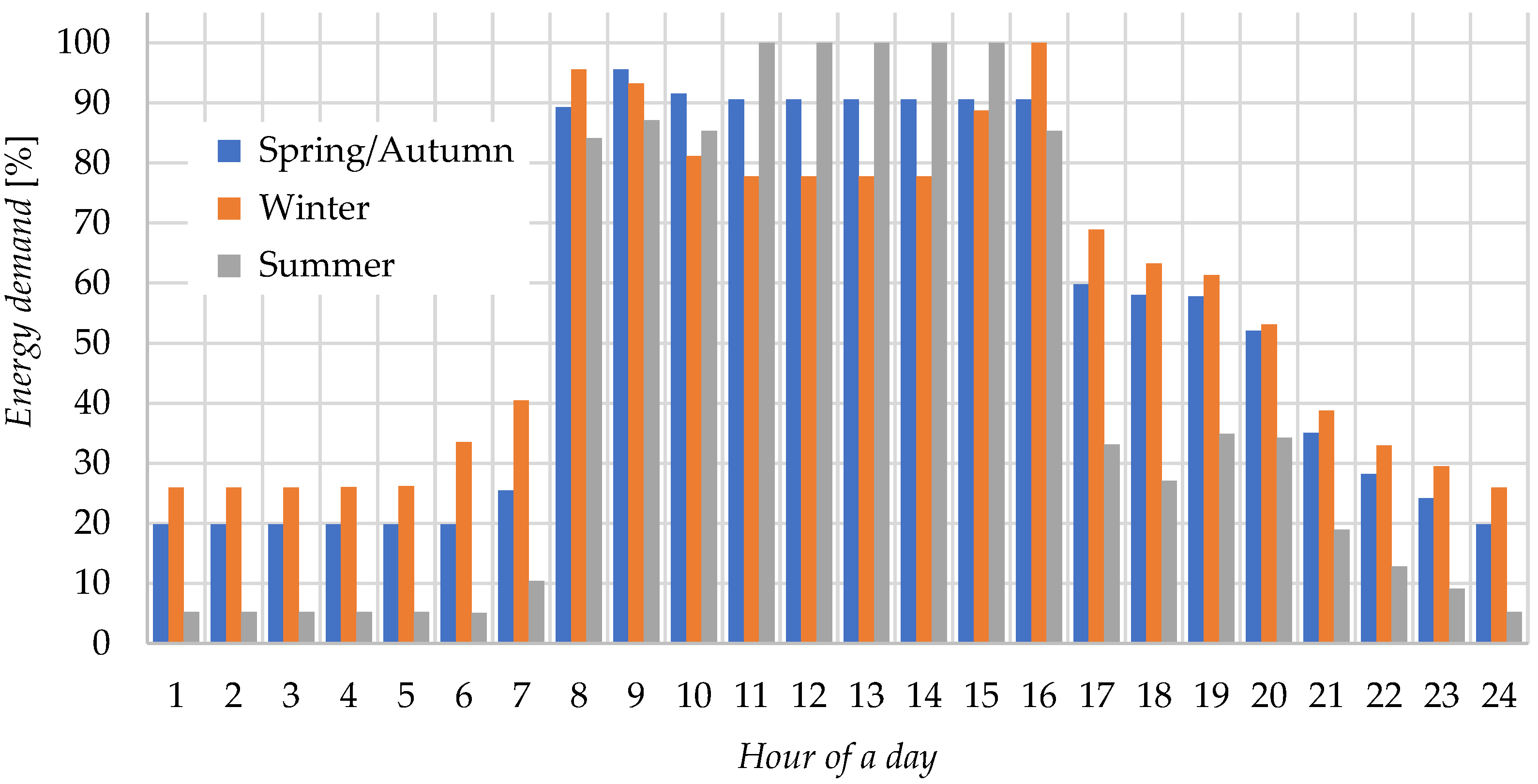
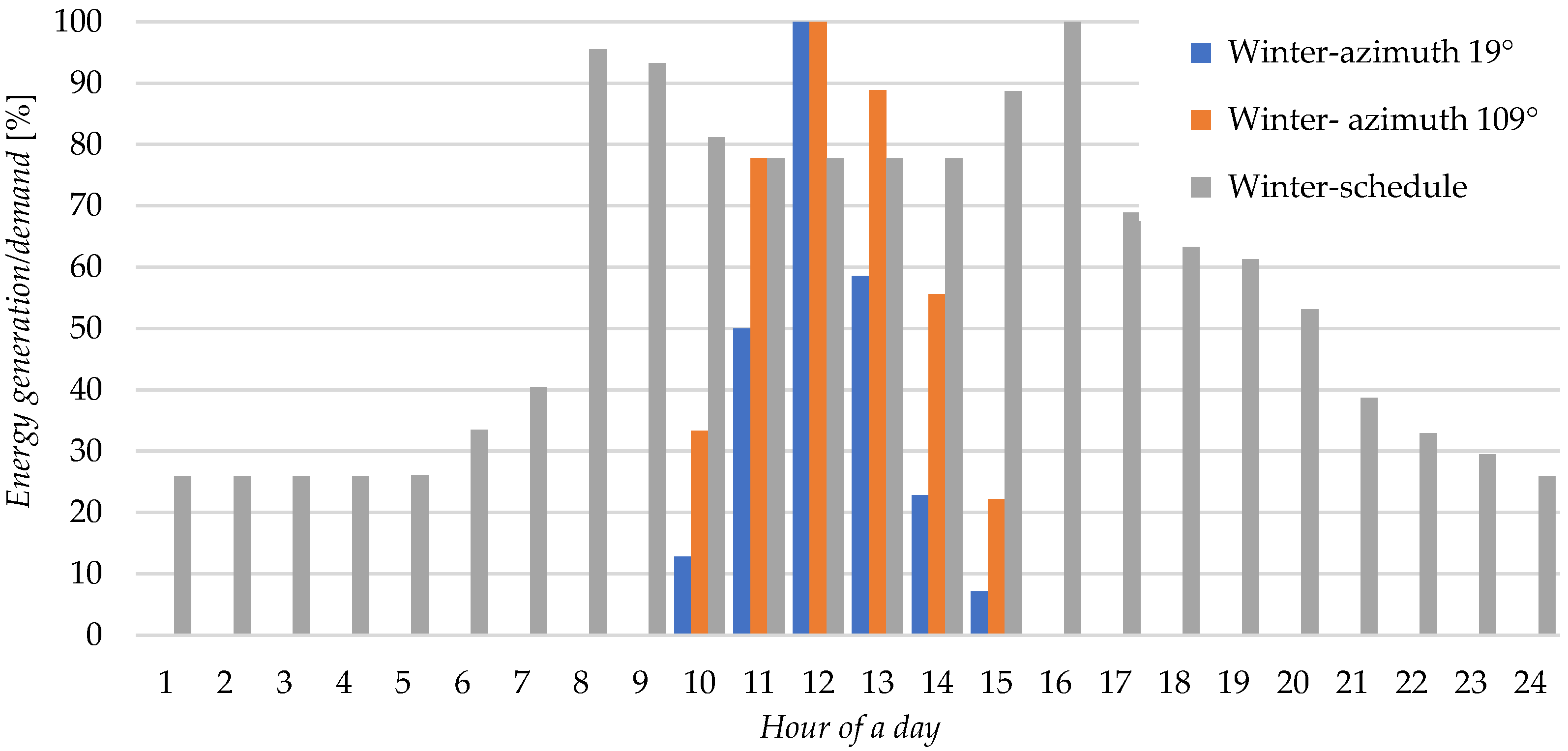
4.2. Determination of Energy Demand

Electricity consumption in 2024 was determined based on measurements gathered from meters installed at the point of common coupling at the MV side of the distribution grid and provided by the head of the BUT Power Department. The total energy demand was 468,200 kWh in 2024. These data, separated into monthly average values, were also used to accurately calibrate the model developed in DesignBuilder software. A comparison of the measured and energy simulation results is shown in Figure 6. A good agreement was achieved, as the mean error ranged from about 1% in July to 4.4% in October. The building model used daily profiles of energy demand, presented in Figure 7, were specially developed separately for each season. The university building under analysis is used for teaching, research, and student services. It should be noted that the profile of energy demand in such facilities is similar to the profile of obtaining energy from PV panels.

4.3. Assessment of Solar Radiation Energy Potential

Some meteorological features referring to the BUT campus site have been investigated. Detailed information on this project and measurement results from 2015 to 2023 can be found in the article [31].

The average of measured solar radiation falling on a flat surface after taking into account data from 2015 to 2024 was 1077.77 kWh/m², while the average annual temperature in the similar period was 9.7 °C. The same values for TMY are 1086.7 kWh/m² and 6.87 °C, respectively. The decisive factor influencing energy efficiency is the intensity of solar radiation. In this case, the difference is only 1%. Therefore, it can be expected that the results of energy simulations will also be characterised by a small discrepancy. There is a significant difference in the outside temperature, but its influence on the results of simulation calculations is much smaller.

4.4. Identification of Suitable Locations for PV System Installation

Figure 8A shows a part of the area occupied by the Faculty with a pergola (marked with a green dashed line) where the PV system is planned to be installed. As can be seen in the plan, the roofs of the buildings contain a large number of devices and ducts that are part of the mechanical ventilation system. Therefore, it would be inefficient to install a PV panel in this place. Another contraindication is thermal insulation made of mineral wool, which is placed on the roof and covered only with roofing felt. Therefore, the only reasonable solution is to use a pergola that has the following dimensions: length × width × height—415 × 5 × 3.3 m. Only part of the pergola roof will be useful for the setting up of the PV system due to shading from the relatively high building of the Faculty of Electrical Engineering. In addition, the investor will probably have to trim some trees located between the building and the pergola (Figure 8B).

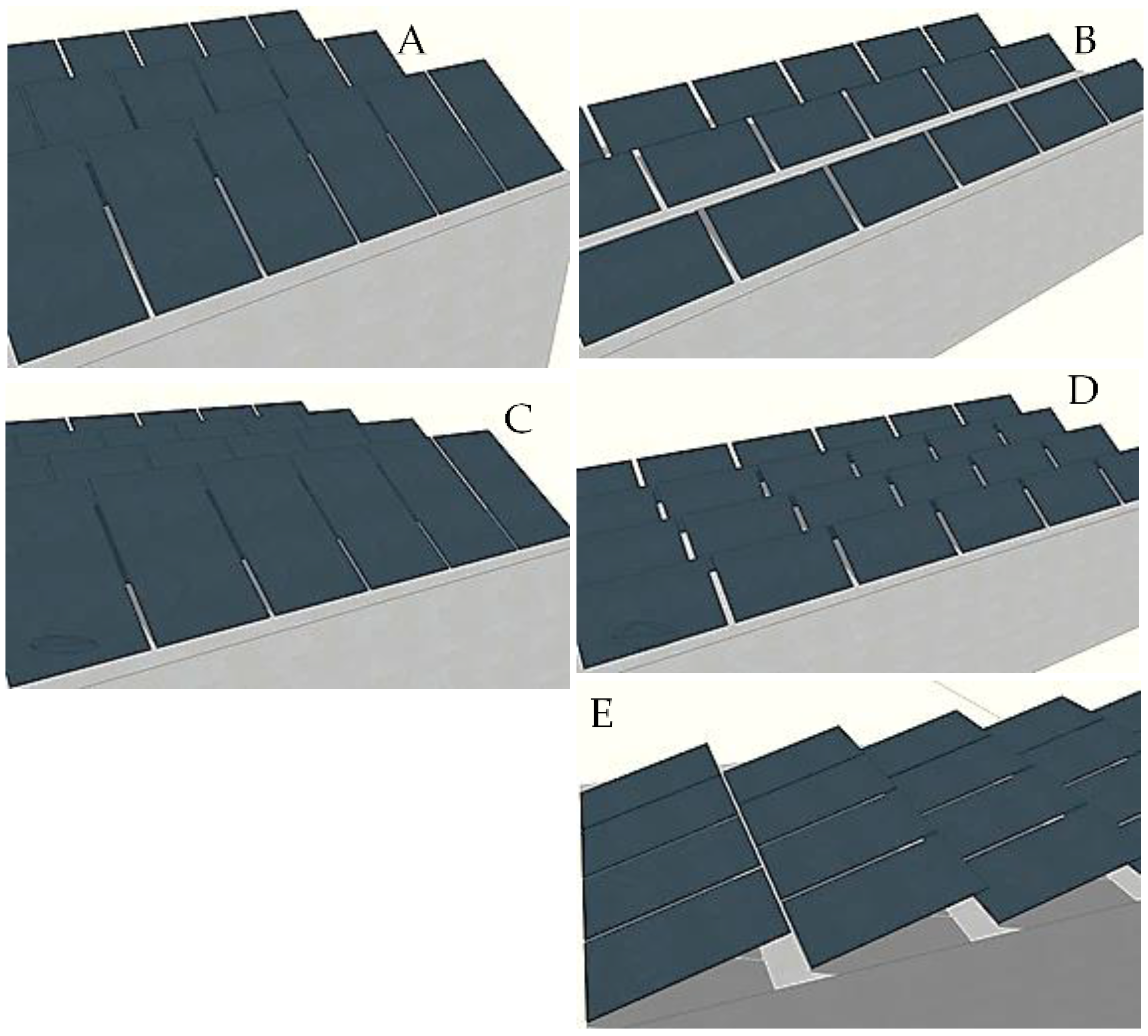
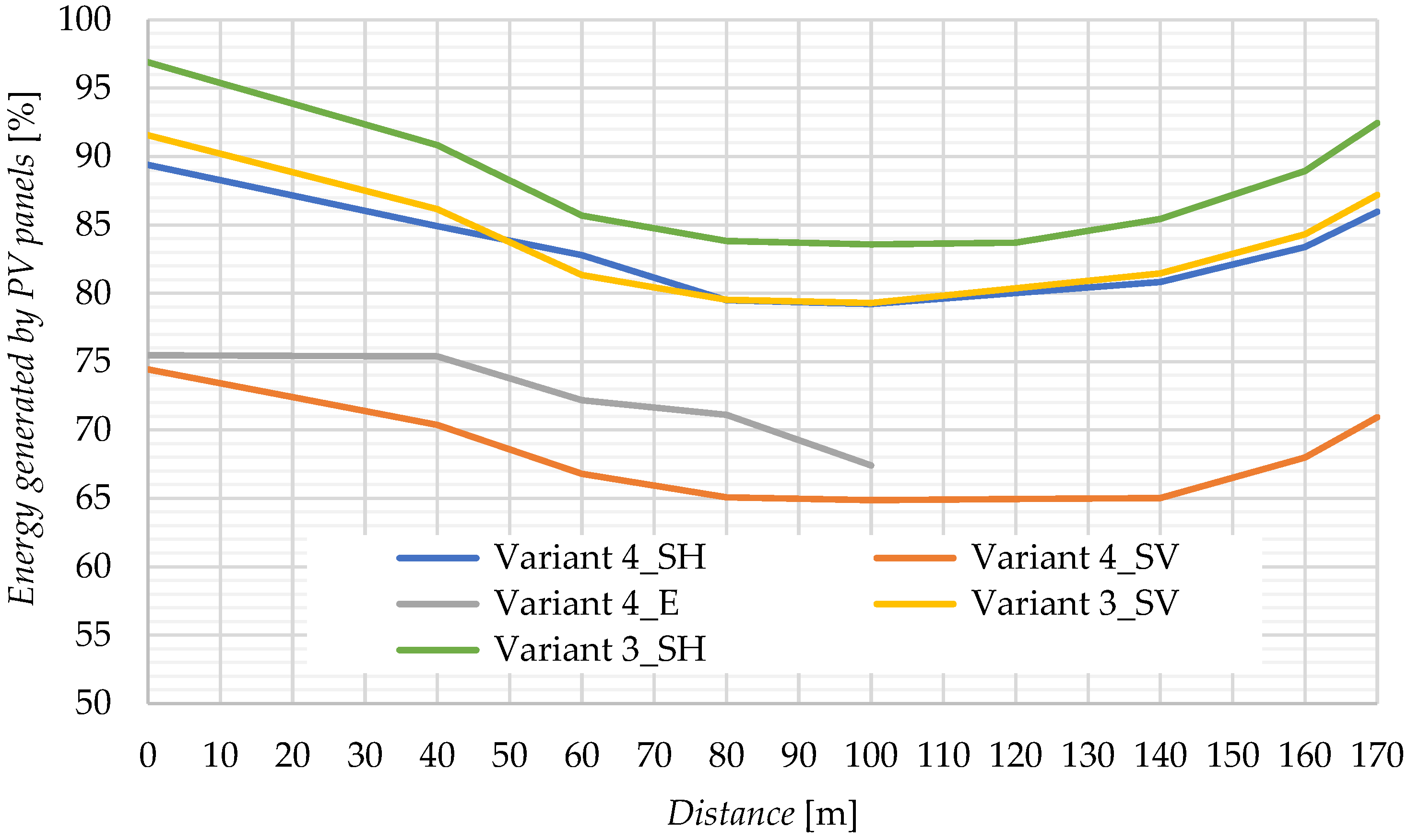
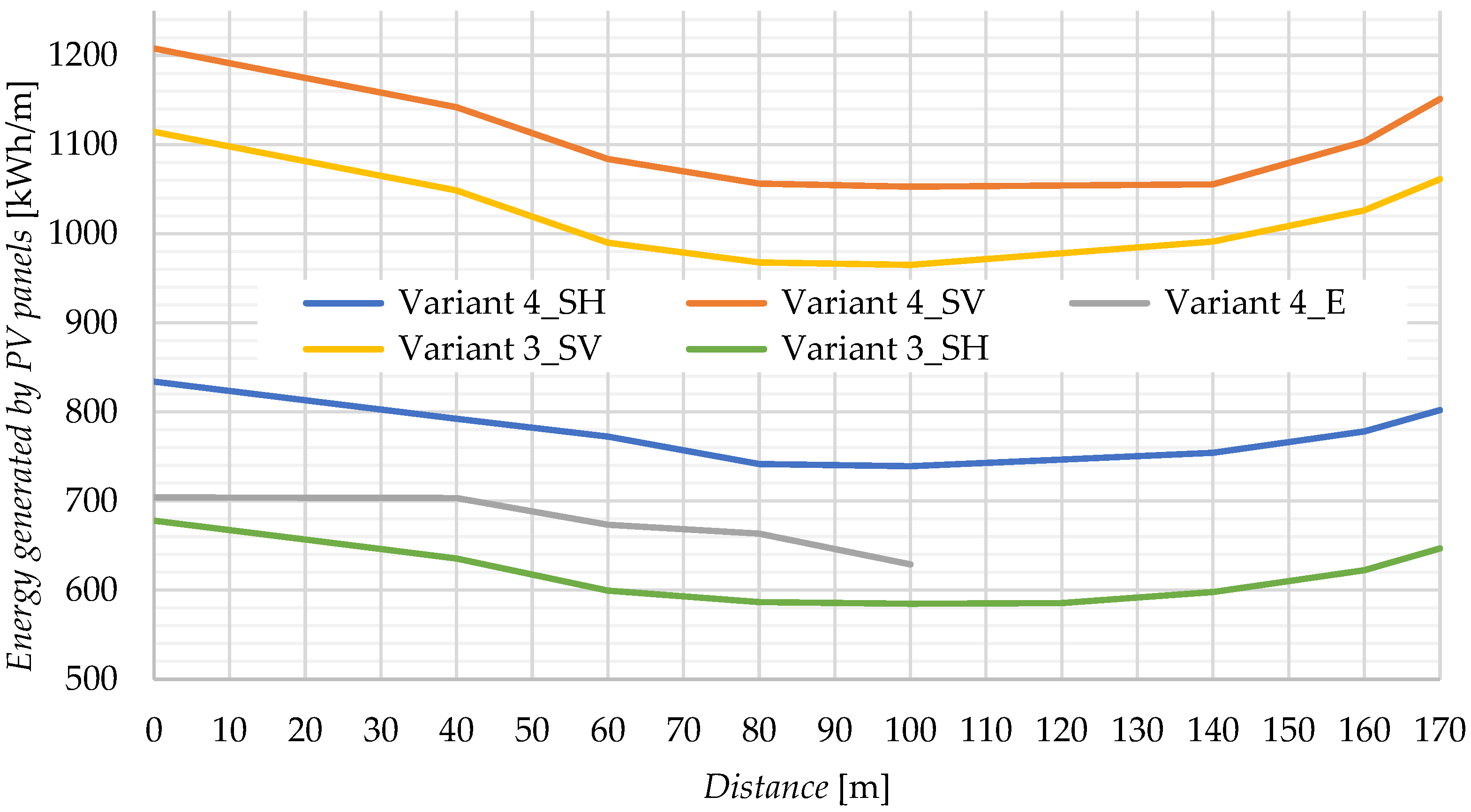
4.5. A PV System Arrangement

The optimal tilt angle of the PV panels was determined using online software PVGIS Photovoltaic performance [14], and for this location (53.119, 23.152), it is 37° for azimuth 19° (Southwest orientation) and 0° for an azimuth of 109° (Southeast orientation). For the latter orientation, an inclination angle of 15° was assumed due to the cleaning of the panels by rainfall and better protection against snow accumulation. For these slope values, different variants of module arrangement were developed.

The following PV panel arrangement methods were selected for the preliminary analysis:

• Variant 3_SV—three rows of panels along the pergola, vertical position, azimuth 19°, (Figure 9A).
• Variant 3_SH—three rows of panels along the pergola, horizontal position, azimuth 19° (Figure 9B).
• Variant 4_SV—four rows of panels along the pergola, vertical position, azimuth 19°, (Figure 9C).
• Variant 4_SH—four rows of panels along the pergola, horizontal position, azimuth 19° (Figure 9D).
• Variant 4_E—panels along the pergola, azimuth 109° (Figure 9E).

4.6. Assessment of Energy Efficiency of Individual Arrangement Variants

First, it was decided to investigate the influence of the orientation of the panels relative to the cardinal directions and the amount of energy produced over one day. For this purpose, three graphs were prepared (Figure 10, Figure 11 and Figure 12) comparing the relative value of the amount of energy produced and the hourly energy demand. The results shown in the graphs were calculated as the hourly current value divided by the maximum value and expressed as a percentage. Investigating the distribution of energy production and demand, it can be concluded that during the transitional periods of the year, energy production by panels oriented to the southeast (109°) starts about an hour earlier. However, the demand at this time is low. A similar shift also occurs during the summer. The production of energy begins from four in the morning. Also, at this time, the energy demand is minimal. During the winter, PV panels yield electricity for the same period of approximately 6 h regardless of orientation.

Table 3. The electricity demand coverage factor [%].

Time	Spring/Autumn		Summer		Winter
	Azimuth 19°	Azimuth 109°	Azimuth 19°	Azimuth 109°	Azimuth 19°	Azimuth 109°
4	0	0	0	19	0	0
5	0	0	>100	>100	0	0
6	0	0	>100	>100	0	0
7	0	4	>100	>100	0	0
8	9	4	86	29	0	0
9	13	5	97	30	0	0
10	29	9	>100	30	10	4
11	95	23	89	26	39	9
12	>100	28	71	21	79	11
13	>100	28	63	19	46	10
14	>100	23	54	16	18	6
15	99	15	43	13	5	2
16	65	8	37	12	0	0
17	22	6	65	22	0	0
18	0	0	41	15	0	0
19	0	0	5	0	0	0

presents a summary of the most important results shown in Figure 10, Figure 11 and Figure 12 in a more readable form. The percentage of the building’s electricity demand that can be covered by photovoltaic panels was determined depending on their orientation. The PV system set at azimuth 109° in the summer starts producing electricity an hour earlier, covering only 19% of the energy demand. However, in the transition period, it is only 4% of the demand. In the following hours, the efficiency of this system is significantly lower compared to the orientation of the panels with azimuth 19°. On this basis, it can be clearly stated that the east orientation of the PV panels has no practical application in terms of increasing the uniformity of electricity production. In the event of overproduction of electrical energy, marked as >100, it will be possible to have it be used by other Faculty buildings.

Figure 13 compares the annual amount of energy produced by PV panels in individual variants with the maximum amount of electricity that the panels can generate. It is visible that the most effective solution is to use horizontal installation of panels in three rows, i.e., Variant 3_SH. The highest reduction in energy production is achieved by Variant 4_SV, in which the panels are arranged vertically in four rows. Of course, this is influenced by the too small distance between the modules, which causes their mutual shading. Very similar characteristics are obtained in Variant 4_SH and Variant 3_SV. In the case of panels oriented to the southeast (Variant 4_E), calculations were made up to a distance of 100 m, as it is not planned that the entire pergola will be arranged in such a way. This arrangement was planned to evaluate the possibility of using a hybrid panel arrangement.

An important parameter, in addition to energy efficiency, is also the amount of energy E_PV(x) that can be obtained from the available roof surface. Figure 14 shows the amount of energy produced by the PV system converted per metre of pergola length. As you might expect, the more efficient variants are capable of converting less energy. Therefore, a dilemma arises whether the priority is to obtain the highest possible efficiency of PV panels or to maximise the energy produced from the limited roof area. Economic analysis should provide the answer to this question.

The basic parameter before performing the economic analysis was to determine the annual energy production E_PV for the cases analysed in this study. After examining the preliminary results of the energy simulation, Variant 4_E was not considered any further. This was due to the lower efficiency of the panels facing south-east (azimuth 109°) compared to the southwest orientation (azimuth 19°). The earlier start of electricity production by about an hour is an undisputed advantage of this variant. However, at this time, the building’s demand for energy is small.

To estimate the E_PV value, the method described in Section 3 was used. First, the equations describing the trend lines shown in Figure 11 were determined. The coefficients of the third-degree polynomial equations E_PV(x) and the R-squared (coefficient of determination) values are shown in

Table 4. Description of approximating functions, their fitness value, and electricity production.

Case Name	Polynomial Coefficients				R2 [-]	EPV
	a	b	c	d		[kWh]
Variant 3_SV	0.00006	0.0012	−2.2575	1119.8	0.9759	166,392
Variant 3_SH	0.00000011	−0.000067	−0.1622	340.215	0.9849	93,171
Variant 4_SV	0.0001	−0.0098	−1.7008	1209.9	0.9799	179,732
Variant 4_SH	0.00006	−0.0048	−1.0319	835.08	0.9833	127,255
Variant 4_E	0.00003	−0.0137	0.3393	703.99	0.9726	67,927

. The regression model fits the data very well because the statistical measure R-squared is close to 1. The amount of annual electricity production E_PV was calculated from equations Equation (6) ÷ Equation (8) and placed in the last column of Table 4.

The self-sufficiency rates defined by the ratio of total electricity production from the PV system to its total consumption for the individual variants have the following values: 0.36—Variant 3_SV, 0.2—Variant 3_SH, 0.38—Variant 4_SV, and 0.27—Variant 4_SH.

4.7. Economic Analysis of the Studied Cases

The calculation methodology used in the economic analysis was based on the equations presented in Section 2.4. The basic data for the cost analysis, presented in

Table 5. Basic input data for economic analysis.

Case Name	IC [EUR]	CF for 1 Year [EUR]	CO&M for 1 Year [EUR]	CR in 15th Year [EUR]	Peak Power [kWp]
Variant 3_SV	94,033	35,312	4702	13,645	210.24
Variant 3_SH	54,101	19,700	2705	5888	120.96
Variant 4_SV	125,377	36,952	6269	22,741	280.32
Variant 4_SH	72,135	26,995	3607	7850	161.28

, included: initial capital cost of investment, annual profits resulting from replacing electricity from the distribution grid with that from the PV system, annual cost of the operation and maintenance, and costs of replacing worn-out inverters after 15 years of operation. In addition, the power peak value was determined for the individual variants, which was used to estimate the costs mentioned above.

The NPV indicator does not take into account all factors that affect the risk of financial failure of the investment. However, in this case, the construction of a PV system should not be classified as a high-risk undertaking. Moreover, the results presented in

Table 6. Summary of economic analysis results.

Case Name	NPV [EUR]	IRR-3 Years [%]	IRR-5 Years [%]	IRR-10 Years [%]	IRR-30 Years [%]
Variant 3_SV	679,506	6.73	26.32	36.88	38.65
Variant 3_SH	378,679	5.06	24.81	35.62	37.51
Variant 4_SV	668,468	−5.49	15.22	27.70	30.40
Variant 4_SH	521,657	6.54	26.15	36.73	38.53

show that the NPV is very high in all variants, and this largely compensates for any possible risk factors of this investment. The main aspect that influenced such a good financial result is the relatively high price of electricity and taking into account its increase by 2% per year. Assuming a constant price of energy would cause a decrease in profitability by about 31% on average. The analysis also assumed that the investment would be financed from its own funds or non-refundable environmental protection subsidies.

The IRR values (Table 5) show the rate of return that the construction of the PV system will provide in selected periods of its duration. It can be seen that all the cases subjected to analysis are characterised by high attractiveness. Investment in renewable energy sources should be classified as moderate risk. In this case, the limit/expected value of IRR should be between 15% and 20%. Therefore, it can be stated that in the analysed cases, the value of future cash flows will exceed the initial investment costs after just 5 years.

To sum up the above considerations, the Variant 3_SV (three rows of panels along the pergola in vertical position) was selected as the recommended arrangement. The competitive case is Variant 4_SV, which has a similar NPV. The energy production using an additional row of panels is only 7% higher, while the initial investment outlays are 25% higher.

The positioning of the panels at an optimal angle causes them to be exposed to high wind forces on their surface. This creates a potentially increased risk of damage to the collectors and supporting structure. Several such incidents have been reported in our region following severe storms. Therefore, an additional series of calculations was performed for Variant 4_SH with a panel inclination angle of 15°.

As expected, not using the optimal inclination of the collectors resulted in a decrease in the amount of electricity produced by the PV system. However, this value was not significant and was equal to 6.8%. Compared to Variant 3_SV, this decrease was much higher and amounted to 29%.

The results of the economic analysis were also slightly worse. The NPV was 9% lower compared to Variant 4_SH and approximately 30% lower compared to the recommended panel configuration. Therefore, when choosing a safer arrangement option, one should take into account a decrease in the efficiency of the photovoltaic system and a longer payback period for this investment.

5. Summary and Conclusions

An individual approach to designing photovoltaic systems at universities enables the optimal utilisation of local resources, adaptation to specific needs and development goals, as well as ensuring the reliability and security of the energy supply system. This study focused on identifying the best configuration of PV panels for a newly designed PV system on the campus of Bialystok University of Technology. Energy efficiency and, foremost, basic economic indicators served as the selection criteria. The pergola near the Faculty of Civil Engineering and Environmental Sciences was chosen as the location for a small PV system. The PV panel setup concept was developed using the results of nine years of measurements of energy production by a PV system, part of a research hybrid wind and PV system. Five panel configurations, differing in the number of rows, horizontal and vertical orientation, as well as azimuth and tilt angle, were selected for detailed analysis. The optimal configuration was chosen based on calculations using a novel method proposed by the authors for modelling the operation and design of photovoltaic systems. The main achievements of this research are listed below:

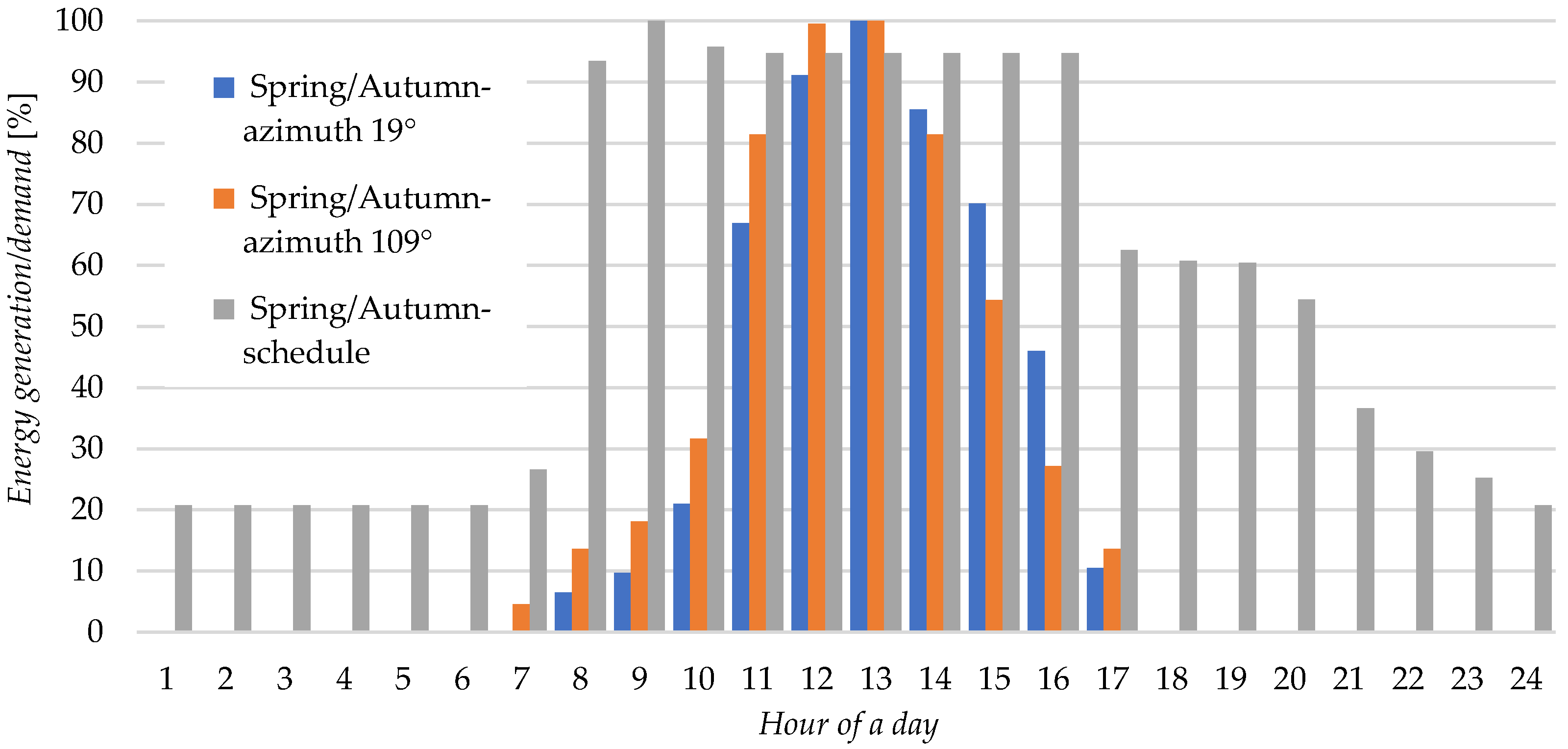
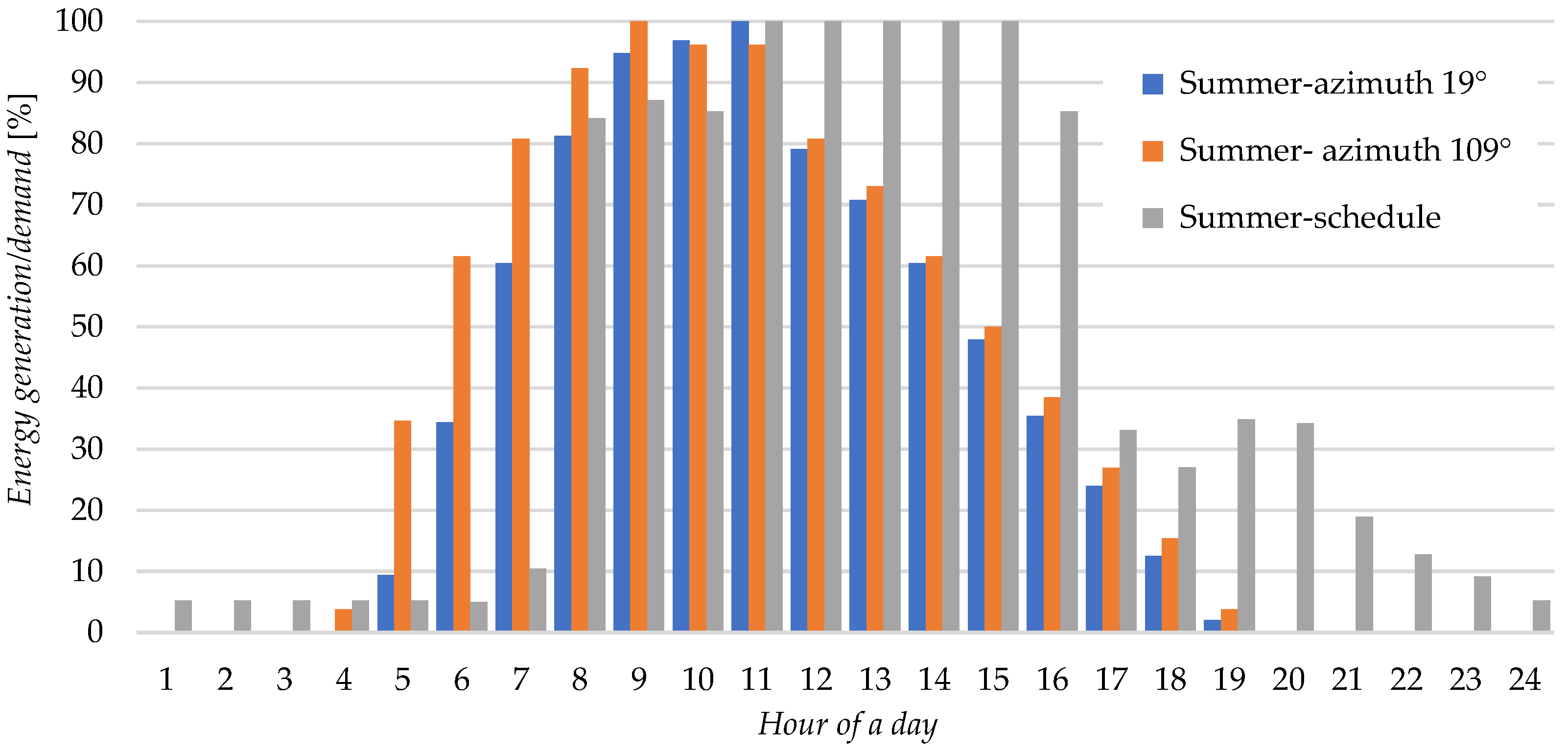
• In this article, we proposed, as a novelty item, a profile of hourly energy consumption for a typical university building in Poland, linking teaching, research, and administrative functions for students (Figure 10, Figure 11 and Figure 12). Such seasonal schedules can be implemented to create activity schedules for building models in an energy simulation software.
• Ten years of measurements of meteorological parameters on the BUT campus allowed to determination of the average value of solar radiation falling on a flat surface of 1078 kWh/m². It turned out that the same parameter for a typical meteorological year used for energy simulations was only 2% higher. Thanks to this, it can be expected that the results obtained from numerical modelling will be close to the values obtained in real operating conditions.
• This paper introduces a novel, hybrid approach for determining the amount of energy produced from the conversion of solar radiation into heat or electricity. It utilises energy simulation techniques to estimate energy output at specific, representative locations within the system. Subsequently, a regression method is employed, preferably using third-degree polynomials, to establish the relationship between the amount of electricity or heat generated and the position of the solar collector or set of collectors. The final step involves integrating these polynomial functions using Equations (6) and (7). The required value is then derived from the relationship given in Equation (8). This approach is especially advantageous when modelling large systems, as it requires modelling only a part of the solar conversion system.
• In order to determine the optimal configuration of photovoltaic panels, the authors used the method described above and a typical economic analysis. The PV panels that are arranged in three rows in a vertical orientation and tilted at an angle of 37° proved to be the recommended setup for the selected company installing this system. The power plant in this configuration consists of 438 modules with a total peak power of 210 kWp and can produce 166,392 kWh of energy. The NPV and IRR of this investment after 30 years of operation will be 679,506 EUR and over 38%, respectively. This proves the potentially high profitability of this project. The energy demand coverage in this variant is approximately 36%. Energy consumption profiles are similar to its production, so the PV system can operate in off-grid mode without the need for batteries. The initial cost of the selected investment is relatively low and amounts to 447 EUR/kWp.

Future work: The construction of a small PV system on the BUT campus is scheduled to be completed in the 4th quarter of 2025. The investment plan includes new grid analysers that enable remote monitoring of the PV system’s basic operating parameters. Therefore, it is planned to conduct year-long tests to determine the actual characteristics of this medium-sized PV system and compare the measurements with the results of energy simulations.