Marangoni Convection of Self-Rewetting Fluid Layers with a Deformable Interface in a Square Enclosure and Driven by Imposed Nonuniform Heat Energy Fluxes
Abstract
1. Introduction
2. Problem Formulation, Governing Equations, and the Surface Tension Relation for SRFs
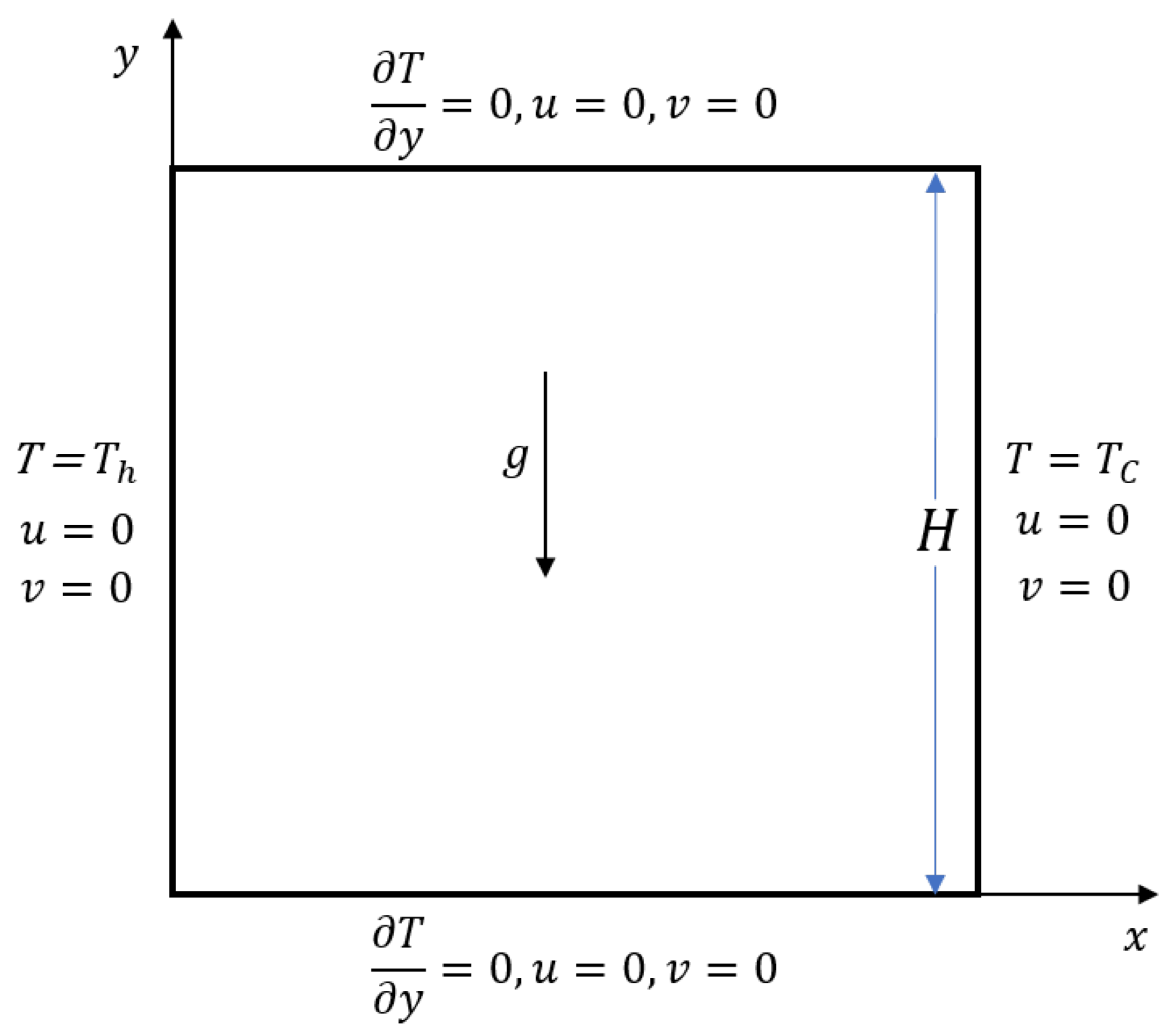
2.1. Problem Formulation
2.2. Bulk Fluid Motions and Energy Transport: Governing Equations
2.3. Surface Tension’s Interfacial Equation of State for Self-Rewetting Fluids
2.3.1. Dimensionless Surface Tension Sensitivity Coefficients
2.3.2. Nonuniform Heating Condition
3. Computational Modeling
4. Central-Moment LBM for Interfacial Capturing, Two-Fluid Flow, and Energy Transport
4.1. LBM for Interfacial Capturing
- Calculate the Pre-Collision Raw Moments: Obtain the raw moments from the distribution functions using the transformation ;
- Compute the Pre-Collision Central Moments: Convert the raw moments to central moments using the relation ;
- Apply the Collision Step: Relax the central moments () toward their equilibrium values () using the following relation:where the indices correspond to , and , and represents the relaxation parameter for a given moment order (). The relaxation parameters for first-order moments follow , which relates to the mobility coefficient () in Equation (8) as . Meanwhile, for moments of order , the relaxation parameters are typically set at 1.0, i.e., . The updated central moments are collected in as follows:
- Convert the post-collision central moments back to raw moments using the inverse transformation ();
- Obtain the post-collision distribution functions by transforming the following post-collision raw moments using the following inverse mapping: ;
- Perform the streaming step by updating the distribution functions according to the following rule: , where , ensuring the distribution is advected to neighboring lattice nodes;
- Update the order parameter () in the phase-field model to capture the interfacial dynamics using the following expression:
4.2. LBM for Two-Fluid Motion
- Compute the Pre-Collision Raw Moments: Obtain the raw moments from the distribution functions using the transformation ;
- Compute the Pre-Collision Central Moments: Transform the raw moments to central moments using ;
- Perform the Collision Step: Apply the relaxation process, ensuring that the central moments () approach their equilibrium values () while incorporating the following effects of the source terms (): To enable the independent specifications of the shear viscosity () and bulk viscosity (), the trace of the second-order moments, given by , must be treated separately from the remaining second-order moments. To achieve this, the diagonal components of the second-order moments are combined before the collision step as follows (see, for instance, [53,54]):As a result, and will evolve independently during the collision process. Following this, the post-collision central moments, incorporating both relaxation effects and force contributions, can be determined using the following expression:The parameter represents the relaxation time associated with the central moment (), where . The relaxation parameter () is linked to the bulk viscosity through the relation . Similarly, the relaxation parameters ( and ) are associated with the shear viscosity, given by , where . Typically, the speed of sound squared is set at . According to Equation (13), if the bulk fluid properties vary, the relaxation parameters ( and ) will also change locally across the interface. The remaining central-moment relaxation parameters are generally set at unity, i.e., , where .Furthermore, the combined post-collision central moments ( and ) are decomposed to their respective components, and , as follows:Finally, incorporating the segregation described above, the results obtained from Equation (24) are systematically organized into the vector , representing the post-collision central moments as follows:
- Convert the Post-Collision Central Moments to Raw Moments: Transform the post-collision central moments back to raw moments using the inverse moment transformation ();
- Reconstruct the Post-Collision Distribution Functions: Retrieve the post-collision distribution functions from the corresponding raw moments using the inverse mapping ();
- Perform the Streaming Step: Update the distribution functions by propagating them to neighboring lattice nodes according to , where ;
- Update the Pressure Field and Fluid Velocity Components: Compute the pressure field (p) and the velocity components () using the following expressions:
4.3. LBM for the Energy Equation
- Compute the Pre-Collision Raw Moments: Obtain the raw moments from the distribution functions using the following transformation: ;
- Compute the Pre-Collision Central Moments: Convert the raw moments to central moments using ;
- Perform the Collision Step: Relax the central moments () toward their equilibrium values () using the following relation:where , and , and represents the relaxation parameter corresponding to each central moment of order (). The relaxation parameters for the first-order moments, = = , are related to the thermal diffusivity, , through the following expression: . For higher-order central moments, the relaxation parameters are typically set at unity. The updated post-collision central moments obtained from Equation (29) are then assembled into the vector .
- Convert the Post-Collision Central Moments to Raw Moments: Transform the post-collision central moments back to raw moments using the following inverse moment transformation: ;
- Reconstruct the Post-Collision Distribution Functions: Retrieve the post-collision distribution functions from the corresponding raw moments using the following inverse mapping: ;
- Execute the Streaming Step: Update the distribution functions by propagating them to neighboring lattice nodes according to , where , ensuring the proper advection of the thermal information across the computational domain;
- Update the Temperature Field: The temperature field (T) is computed as follows:
5. Validation of the Numerical Method
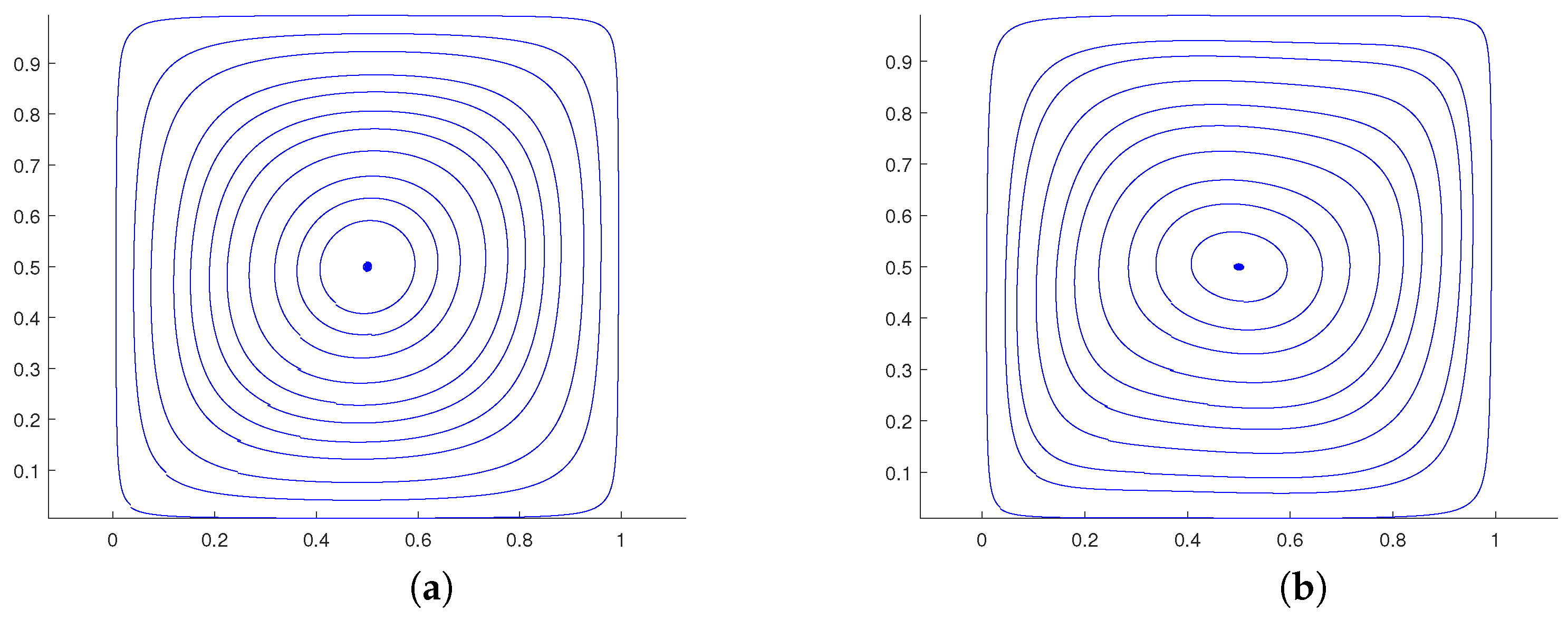
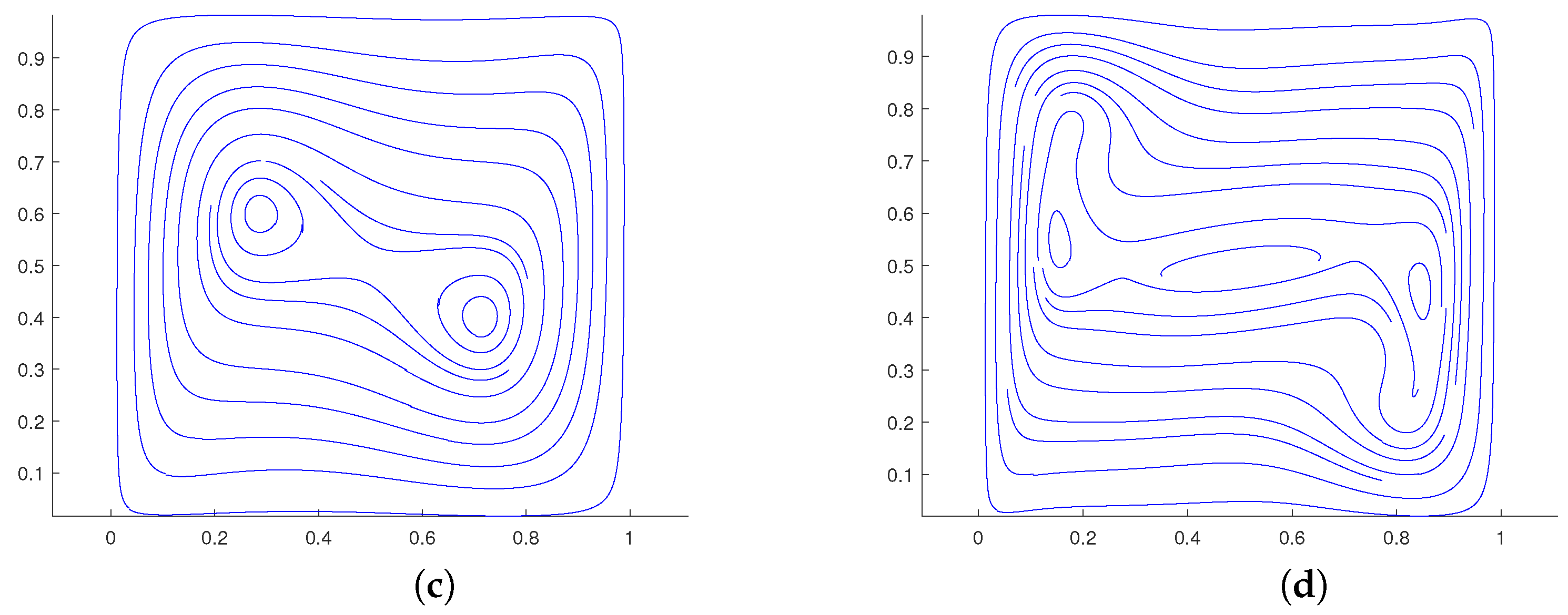
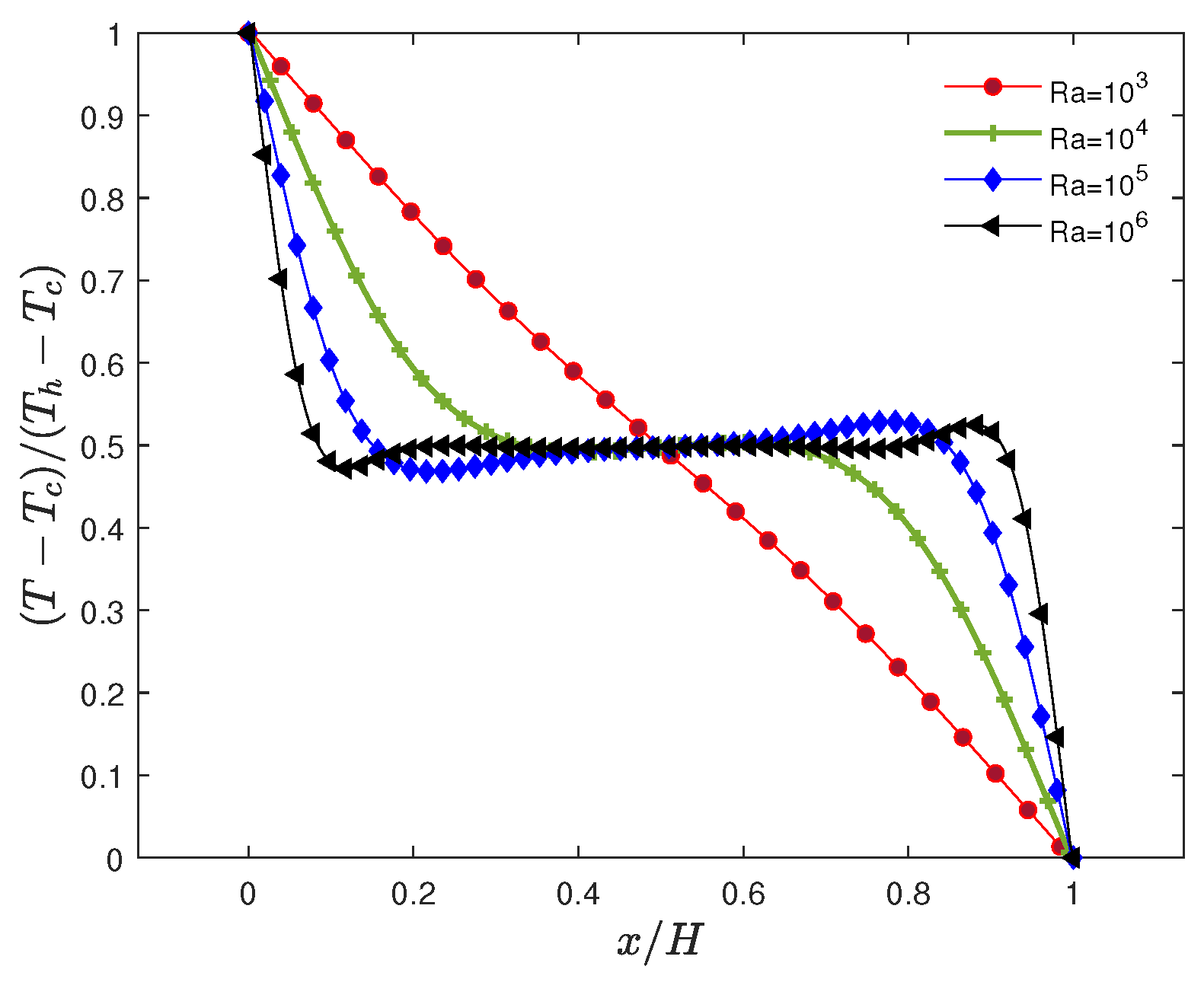
5.1. Natural Convection in a Square Cavity
5.2. Surface-Tension-Driven Thermocapillary Flow in Two Superimposed Self-Rewetting Fluid (SRF) Layers
Grid Independence Test
6. Simulation Results and Discussion
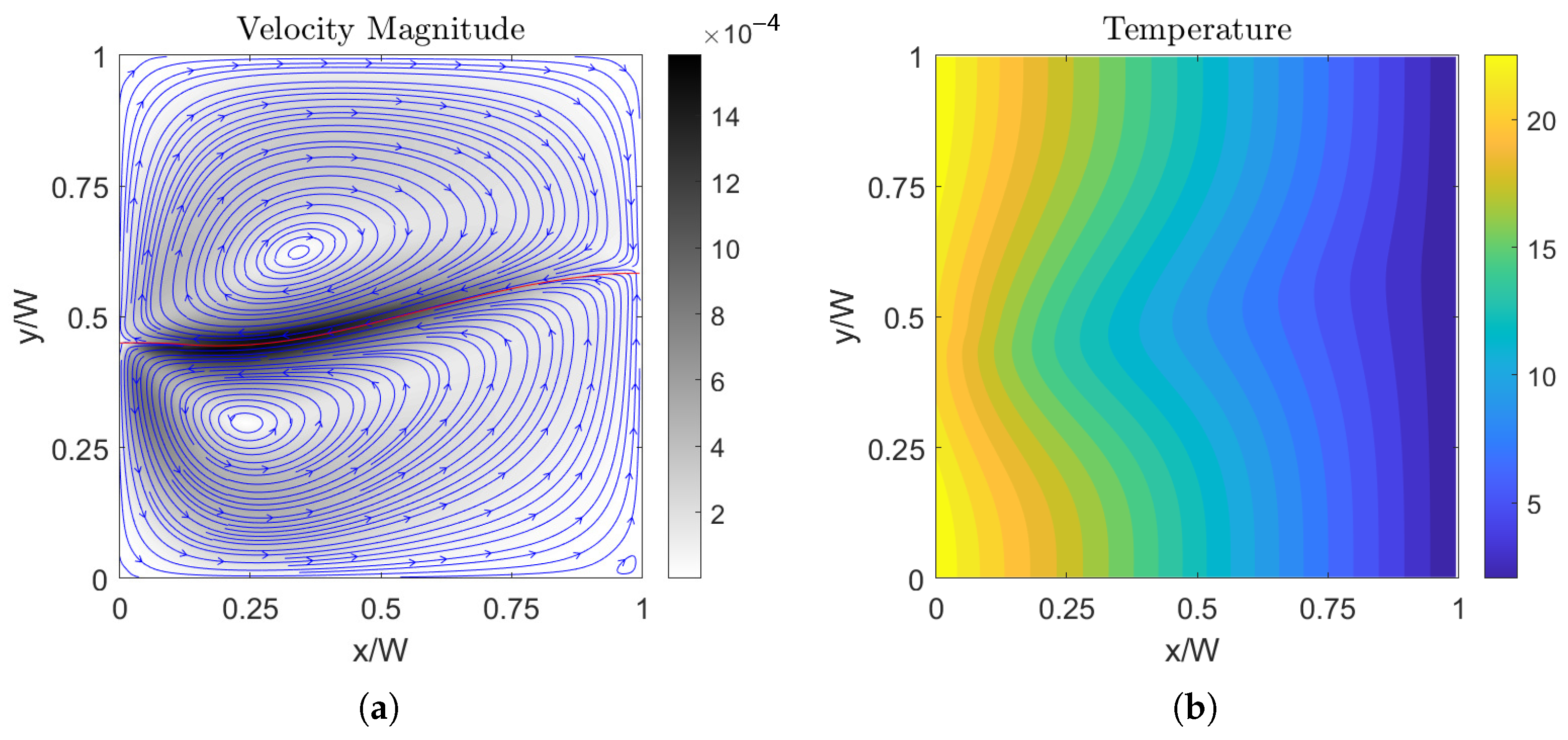
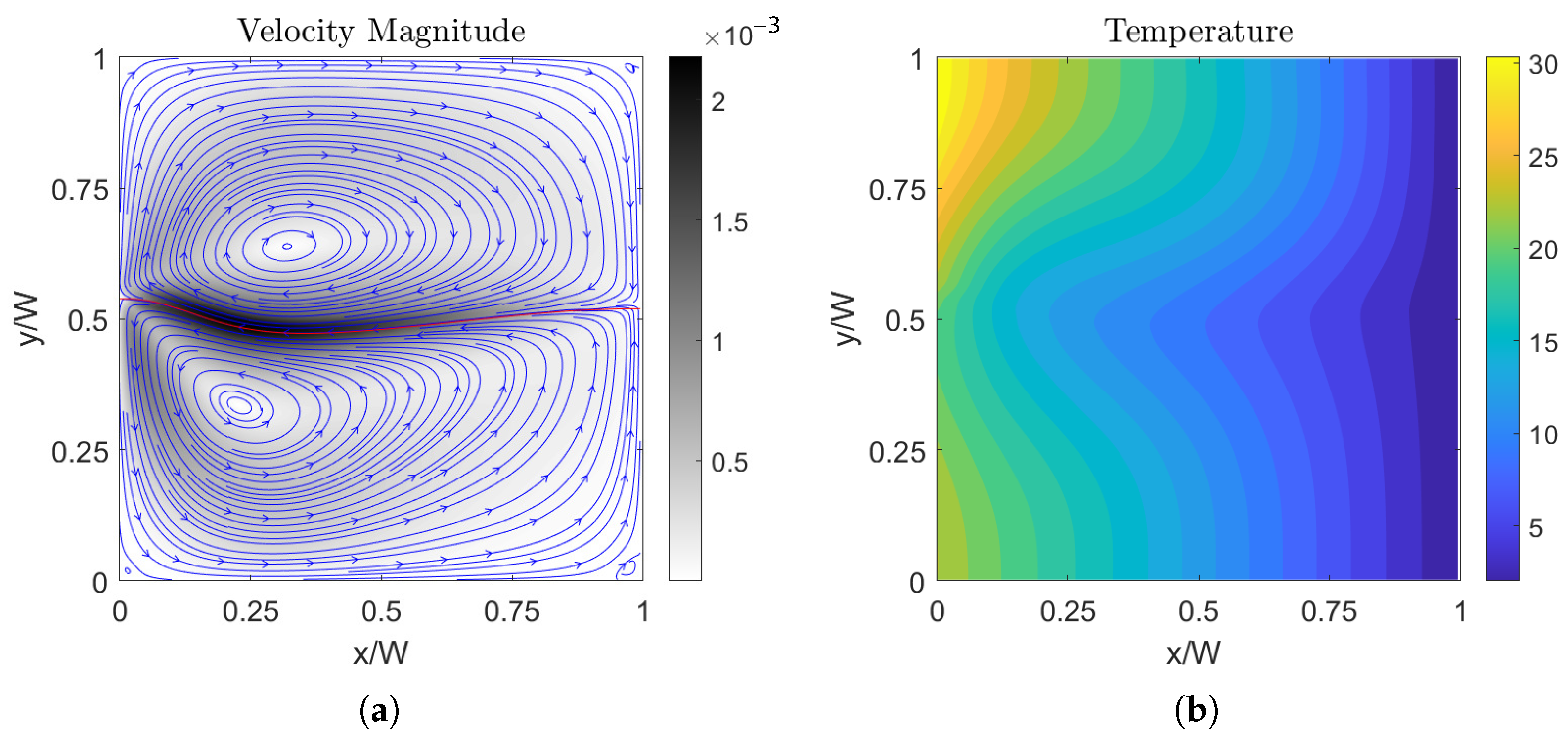
6.1. The Streamlines and Isotherms for the Two-Layer Flow of Normal Fluids (NFs)
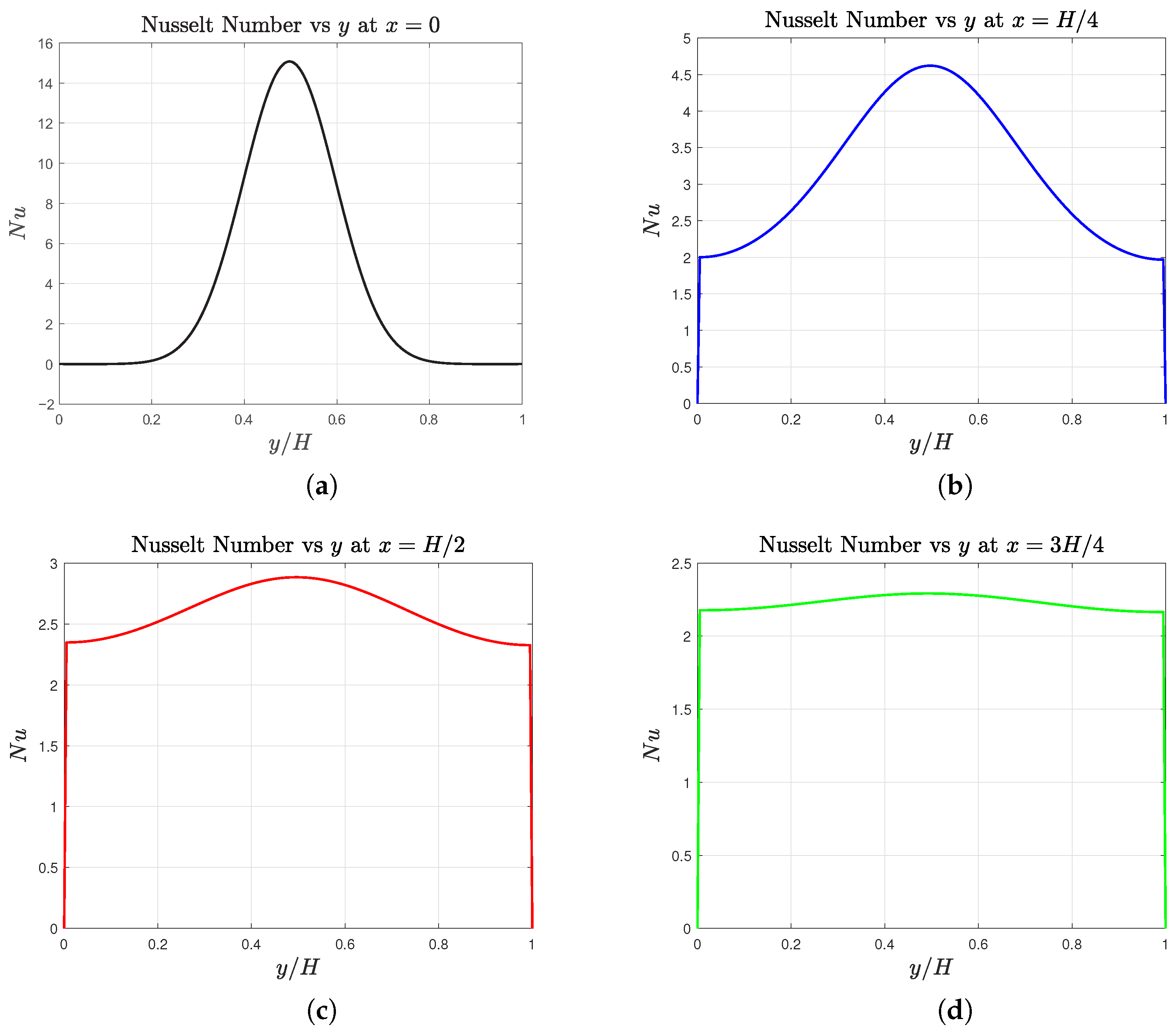
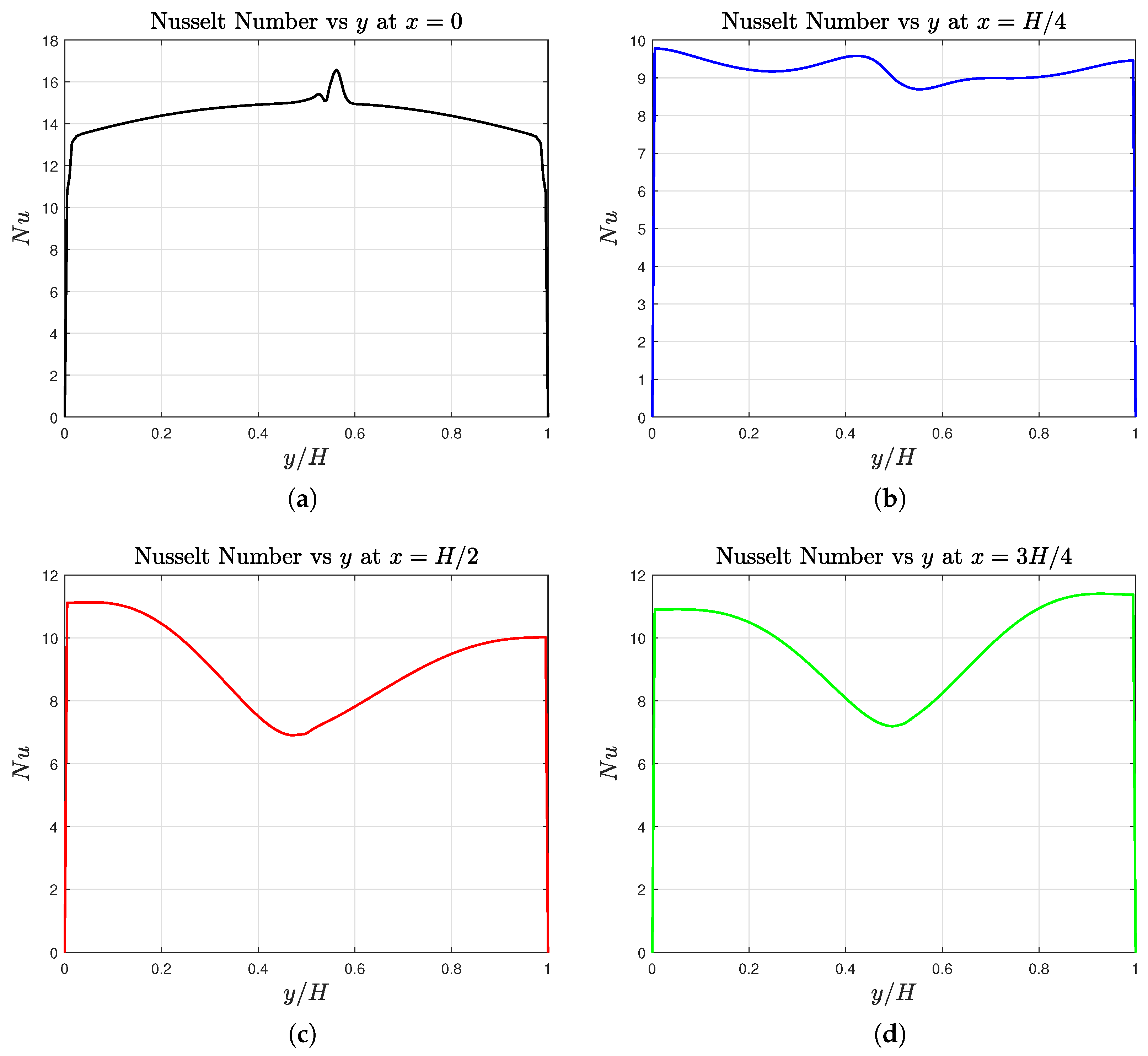
Heat Transfer Rate Characterization: Nusselt Numbers
6.2. The Streamlines and Isotherms for the Two-Layer Flow of Self-Rewetting Fluids (SRFs)
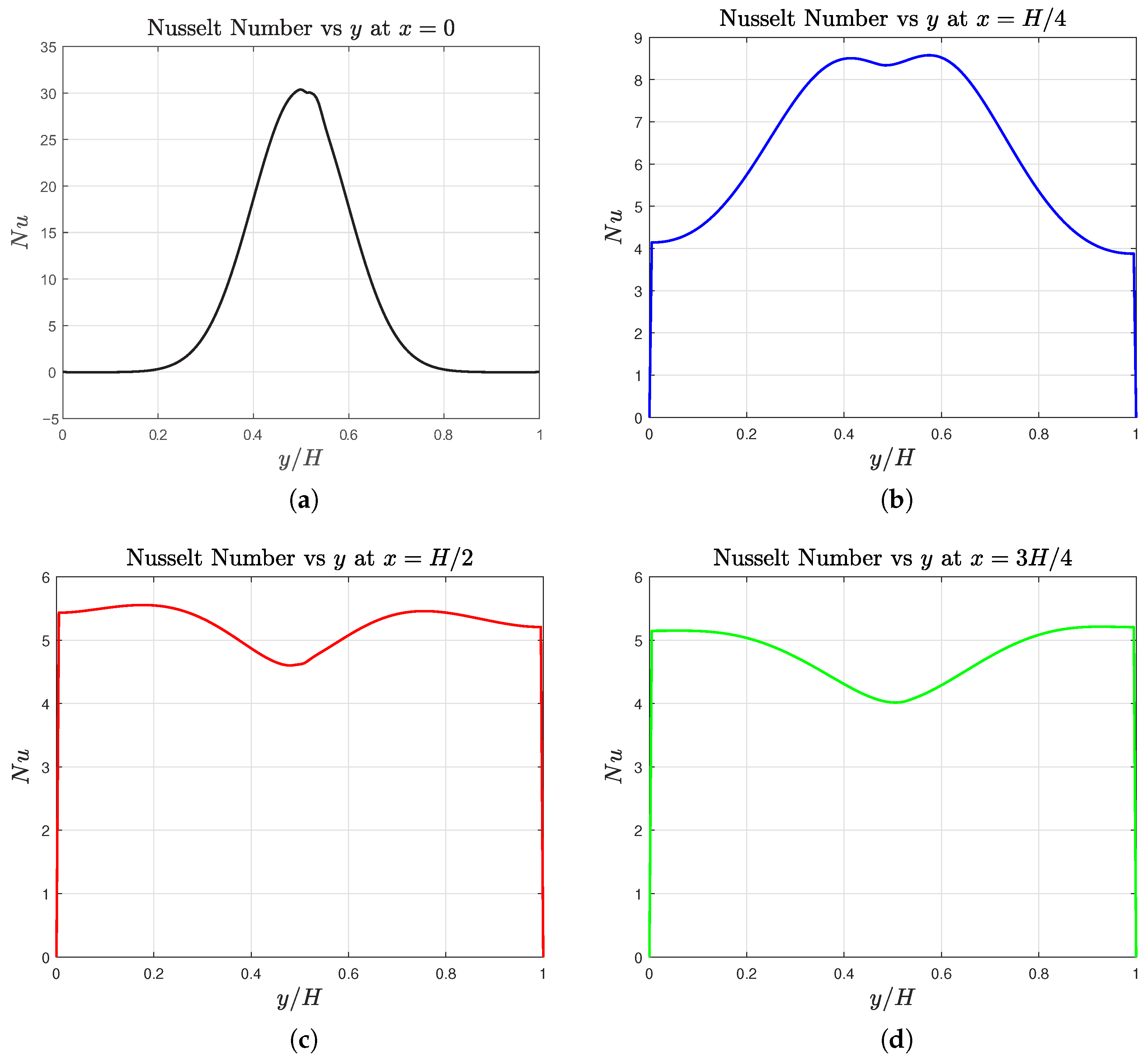
Heat Transfer Rate Characterization: Nusselt Numbers
6.3. Effect of the Dynamic Viscosity Ratio () on the Two-Layer Flow of SRFs for the Case of Distributed Heating
6.4. Effect of the Thermal Conductivity Ratio () on the Two-Layer Flow of SRFs for the Case of Distributed Heating
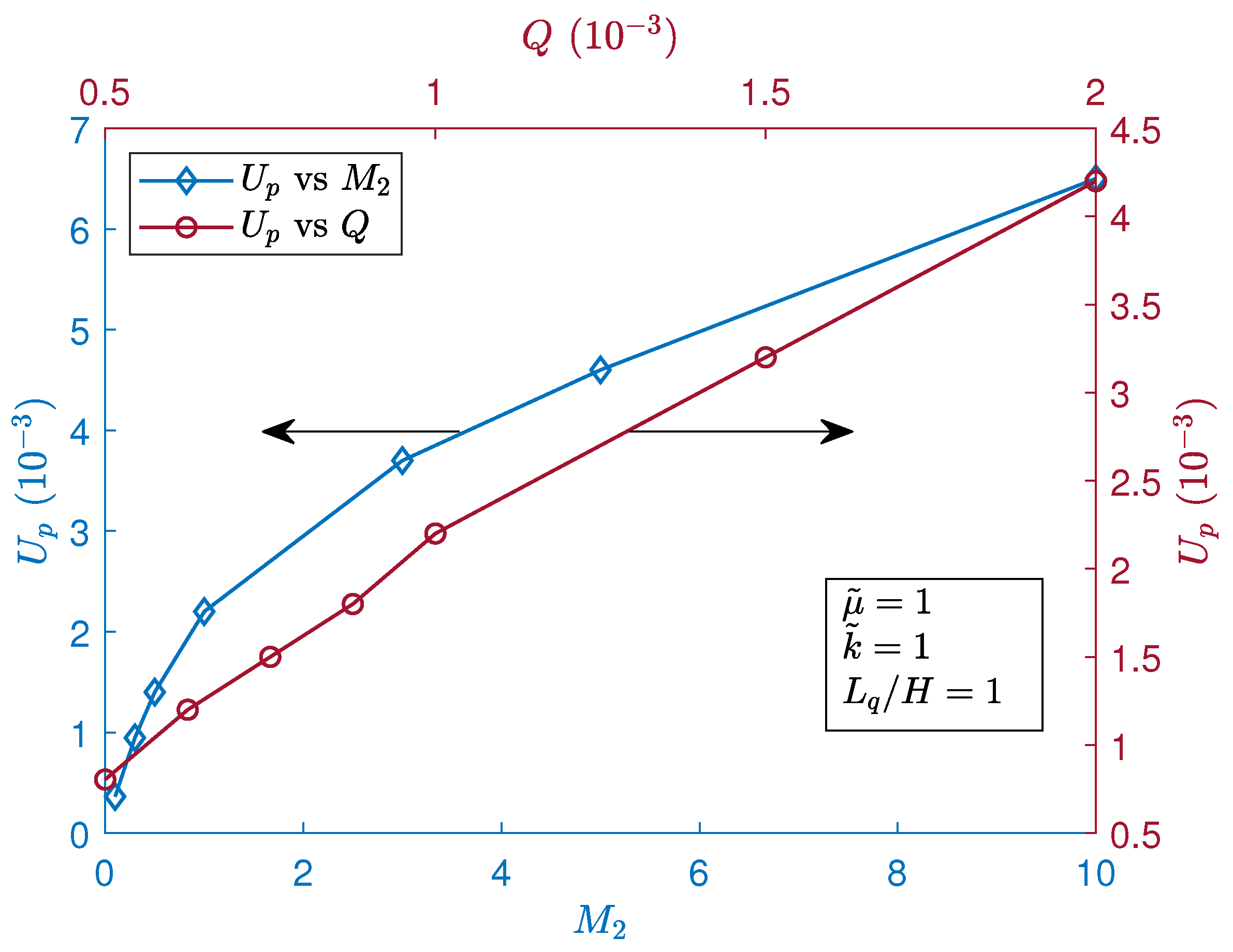
6.5. Effects of the Dimensionless Sensitivity Coefficients of the Surface Tension ( and ) and Dimensionless Heat Flux (Q) on the Magnitude of the Normalized Peak Interfacial Thermocapillary Velocity ()
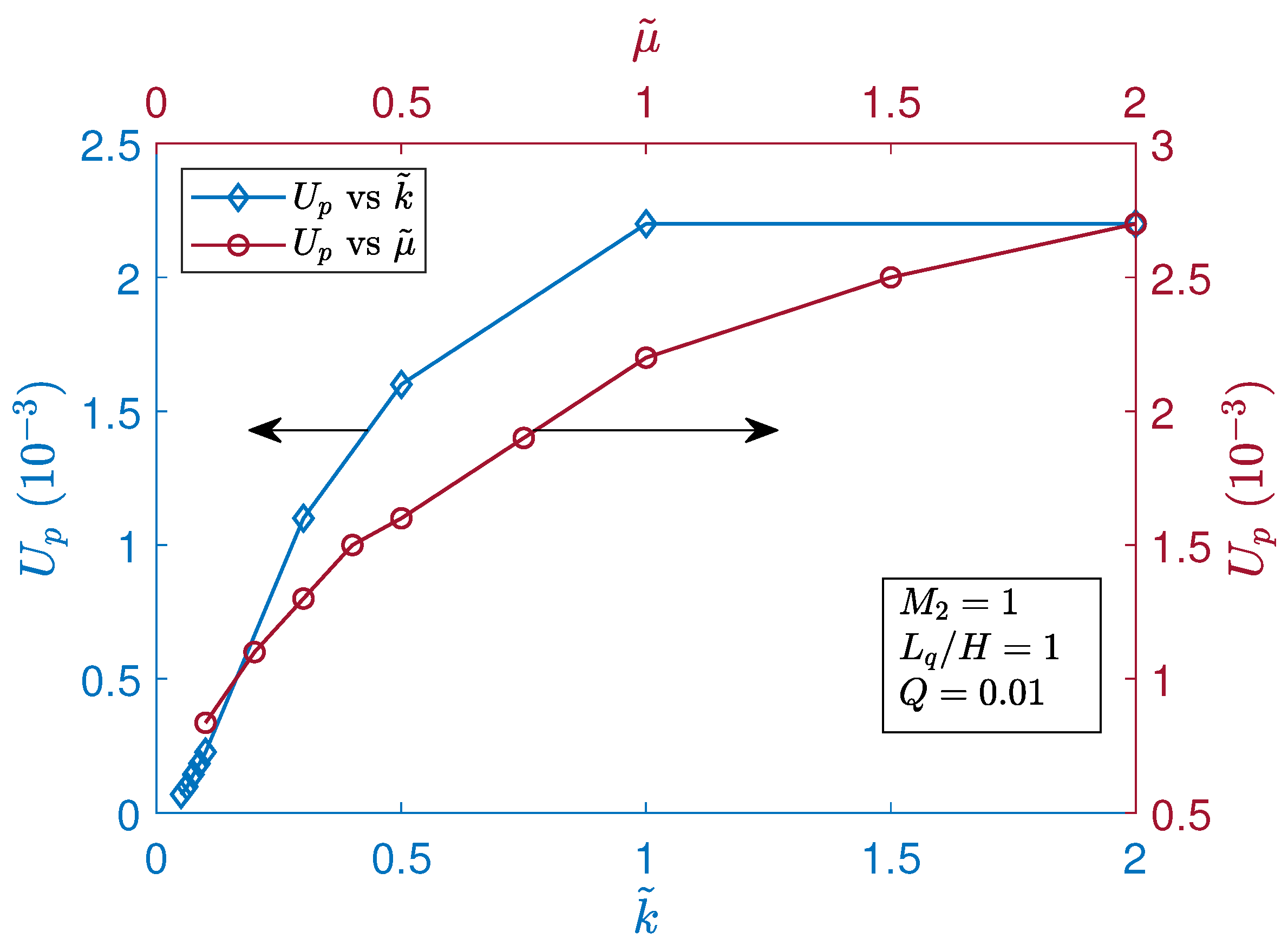
6.6. Effects of the Thermal Conductivity Ratio () and Dynamic Viscosity Ratio () on the Magnitude of the Normalized Peak Interfacial Thermocapillary Velocity () in SRFs
6.7. Effects of Localized Heating Versus Distributed Heating on the Magnitude of the Normalized Peak Interfacial Thermocapillary Velocity () in SRFs
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhong, Y.; Zhuo, Y.; Wang, Z.; Sha, Y. Marangoni convection induced by simultaneous mass and heat transfer during evaporation of n-heptane/ether binary liquid mixture. Int. J. Heat Mass Transf. 2017, 108, 812–821. [Google Scholar] [CrossRef]
- Ma, H.B.; Wilson, C.; Borgmeyer, B.; Park, K.; Yu, Q.; Choi, S.U.S.; Tirumala, M. Effect of nanofluid on the heat transport capability in an oscillating heat pipe. Appl. Phys. Lett. 2006, 88, 143116. [Google Scholar] [CrossRef]
- Sha, Y.; Li, Z.; Wang, Y.; Huang, J. The Marangoni convection induced by acetone desorption from the falling soap film. Heat Mass Transf. 2012, 48, 749–755. [Google Scholar] [CrossRef][Green Version]
- Toolan, D.T.; Pullan, N.; Harvey, M.J.; Topham, P.D.; Howse, J.R. In situ studies of phase separation and crystallization directed by Marangoni instabilities during spin-coating. Adv. Mater. 2013, 25, 7033–7037. [Google Scholar] [CrossRef]
- Barash, L.Y. Marangoni convection in an evaporating droplet: Analytical and numerical descriptions. Int. J. Heat Mass Transf. 2016, 102, 445–454. [Google Scholar] [CrossRef][Green Version]
- Young, N.O.; Goldstein, J.S.; Block, M.J. The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 1959, 6, 350–356. [Google Scholar] [CrossRef]
- Arbin, N.; Suhaimi, N.S.; Hashim, I. Simulation on double-diffusive Marangoni convection with the presence of entropy generation. Indian J. Sci. Technol. 2016, 9, 1–5. [Google Scholar] [CrossRef]
- Bobach, B.; Boman, R.; Celentano, D.; Terrapon, V.E.; Ponthot, J. Simulation of the Marangoni effect and phase change using the particle finite element method. Appl. Sci. 2021, 11, 11893. [Google Scholar] [CrossRef]
- Saidi, M.H.; Asadi, B.; Ahmadi, G. Computational simulation of Marangoni convection under microgravity condition. Sci. Iran. 2009, 16, 513–524. [Google Scholar]
- Mitchell, T.R.; Majidi, M.; Rahimian, M.H.; Leonardi, C.R. Computational modeling of three-dimensional thermocapillary flow of recalcitrant bubbles using a coupled lattice boltzmann-finite difference method. Phys. Fluids 2021, 33, 032108. [Google Scholar] [CrossRef]
- Holzer, M.; Mitchell, T.R.; Leonardi, C.R.; Rüde, U. Development of a central-moment phase-field lattice boltzmann model for thermocapillary flows: Droplet capture and computational performance. J. Comput. Phys. 2024, 518, 113337. [Google Scholar] [CrossRef]
- Elbousefi, B.; Schupbach, W.; Premnath, K.N.; Welch, S.W.J. Investigation of surfactant-laden bubble migration dynamics in self-rewetting fluids using lattice boltzmann method. Phys. Fluids 2024, 36, 112106. [Google Scholar] [CrossRef]
- Yan, H.; Wang, L.; Huang, J.; Yu, Y. Thermocapillary migration of a self-rewetting droplet on an inclined surface: A phase-field simulation. Appl. Therm. Eng. 2025, 263, 125345. [Google Scholar] [CrossRef]
- Elbousefi, B.; Schupbach, W.; Premnath, K.N.; Welch, S.W.J. Thermocapillary convection in superimposed layers of self-rewetting fluids: Analytical and lattice boltzmann computational study. Int. J. Heat Mass Transf. 2023, 208, 124049. [Google Scholar] [CrossRef]
- Majidi, M.; Haghani-Hassan-Abadi, R.; Rahimian, M. Single recalcitrant bubble simulation using a hybrid lattice boltzmann finite difference model. Int. J. Multiph. Flow 2020, 127, 103289. [Google Scholar] [CrossRef]
- Scherr, R.; Markl, M.; Körner, C. Volume of fluid based modeling of thermocapillary flow applied to a free surface lattice boltzmann method. J. Comput. Phys. 2023, 492, 112441. [Google Scholar] [CrossRef]
- Zhang, J.; Sekimoto, A.; Okano, Y.; Dost, S. Numerical simulation of thermal-solutal marangoni convection in a shallow rectangular cavity with mutually perpendicular temperature and concentration gradients. Phys. Fluids 2020, 32, 102108. [Google Scholar] [CrossRef]
- Cicek, K.; Baytas, A. A numerical study of combined natural and Marangoni convection in a square cavity. Transnav Int. J. Mar. Navig. Saf. Sea Transp. 2009, 3, 173–178. [Google Scholar]
- del Arco, E.C.; Extremet, G.P.; Sani, R.L. Thermocapillary convection in a two-layer fluid system with flat interface. Adv. Space Res. 1991, 11, 129–132. [Google Scholar] [CrossRef]
- Ciccotosto, B.E.; Brooks, C.S. Free surface motion of a liquid pool with isothermal sidewalls as a benchmark for Marangoni convection problems. Energies 2023, 16, 6824. [Google Scholar] [CrossRef]
- Ma, C.; Bothe, D. Direct numerical simulation of thermocapillary flow based on the volume of fluid method. Int. J. Multiph. Flow 2011, 37, 1045–1058. [Google Scholar] [CrossRef]
- Abir, F.M.; Barua, S.; Barua, S.; Saha, S. Numerical analysis of Marangoni effect on natural convection in two-layer fluid structure inside a two-dimensional rectangular cavity. Aip Conf. Proc. 2019, 2121, 030025. [Google Scholar]
- Zhou, X.; Chi, F.; Jiang, Y.; Chen, Q. Moderate Prandtl number nanofluid thermocapillary convection instability in rectangular cavity. Microgravity Sci. Technol. 2022, 34, 24. [Google Scholar] [CrossRef]
- Chen, C.; Feng, S.; Peng, H.; Peng, X.; Chaoyue, L.; Zhang, R. Thermocapillary convection flow and heat transfer characteristics of graphene nanoplatelet based nanofluid under microgravity. Microgravity Sci. Technol. 2021, 33, 40. [Google Scholar] [CrossRef]
- Chang, Q.; Alexander, J.I.D. Application of the lattice boltzmann method to two-phase rayleigh–benard convection with a deformable interface. J. Comput. Phys. 2006, 212, 473–489. [Google Scholar] [CrossRef]
- Kaba, S.; Cheddadi, A.; Achoubir, K.; Semma, A. Numerical simulation by a lattice Boltzmann method of fluid flow and heat transfer characteristics in a discreetly heated cavity containing water near its density maximum. Phys. Fluids 2022, 34, 093611. [Google Scholar] [CrossRef]
- Saleh, H.; Hashim, I. Buoyant Marangoni convection of nanofluids in square cavity. Appl. Math. Mech. 2015, 36, 1169–1184. [Google Scholar] [CrossRef]
- Mohamad, A.A.; Bennacer, R.; El-Ganaoui, M. Double dispersion, natural convection in an open end cavity simulation via lattice Boltzmann method. Int. J. Therm. Sci. 2010, 49, 1944–1953. [Google Scholar] [CrossRef]
- Xie, H.; Zeng, Z.; Zhang, L.; Lu, Y. Lattice Boltzmann simulation of the thermocapillary flow in an annular two liquid layers system with deformable interface. Int. Commun. Heat Mass Transf. 2015, 68, 78–84. [Google Scholar] [CrossRef]
- Vochten, R.; Petre, G. Study of the heat of reversible adsorption at the air-solution interface. ii. experimental determination of the heat of reversible adsorption of some alcohols. J. Colloid Interface Sci. 1973, 42, 320–327. [Google Scholar] [CrossRef]
- Petre, G.; Azouni, M.A. Experimental evidence for the minimum of surface tension with temperature at aqueous alcohol solution/air interfaces. J. Colloid Interface Sci. 1984, 98, 261–263. [Google Scholar] [CrossRef]
- Limbourg-Fontaine, M.C.; Pétré, G.; Legros, J.C. Thermocapillary movements under microgravity at a minimum of surface tension. Naturwissenschaften 1986, 73, 360–362. [Google Scholar] [CrossRef]
- Villers, D.; Platten, J.K. Temperature dependence of the interfacial tension between water and long-chain alcohols. J. Phys. Chem. 1988, 92, 4023–4024. [Google Scholar] [CrossRef]
- Abe, Y.; Iwasaki, A.; Tanaka, K. Microgravity experiments on phase change of self-rewetting fluids. Ann. N. Y. Acad. Sci. 2004, 1027, 269–285. [Google Scholar] [CrossRef]
- Abe, Y. Terrestrial and microgravity applications of self-rewetting fluids. Microgravity Sci. Technol. 2007, 19, 11–12. [Google Scholar] [CrossRef]
- Zaaroura, I.; Harmand, S.; Carlier, J.; Toubal, M.; Fasquelle, A.; Nongaillard, B. Thermal performance of self-rewetting gold nanofluids: Application to two-phase heat transfer devices. Int. J. Heat Mass Transf. 2021, 174, 121322. [Google Scholar] [CrossRef]
- Savino, R.; Cecere, A.; Paola, R.D. Surface tension-driven flow in wickless heat pipes with self-rewetting fluids. Int. J. Heat Fluid Flow 2009, 30, 380–388. [Google Scholar] [CrossRef]
- Savino, R.; Cecere, A.; Vaerenbergh, S.V.; Abe, Y.; Pizzirusso, G.; Tzevelecos, W.; Mojahed, M.; Galand, Q. Some experimental progresses in the study of self-rewetting fluids for the SELENE experiment to be carried in the thermal platform 1 hardware. Acta Astronaut. 2013, 89, 179–188. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, T.; Li, X.; Wang, S. Heat transfer enhancement of micro oscillating heat pipes with self-rewetting fluid. Int. J. Heat Mass Transf. 2014, 70, 496–503. [Google Scholar] [CrossRef]
- Wu, S.; Lee, T.; Lin, W.; Chen, Y. Study of self-rewetting fluid applied to loop heat pipe with PTFE wick. Appl. Therm. Eng. 2017, 119, 622–628. [Google Scholar] [CrossRef]
- Cecere, A.; Cristofaro, D.D.; Savino, R.; Ayel, V.; Sole-Agostinelli, T.; Marengo, M.; Romestant, C.; Bertin, Y. Experimental analysis of a flat plate pulsating heat pipe with self-rewetting fluids during a parabolic flight campaign. Acta Astronaut. 2018, 147, 454–461. [Google Scholar] [CrossRef]
- Zhu, M.; Huang, J.; Song, M.; Hu, Y. Thermal performance of a thin flat heat pipe with grooved porous structure. Appl. Therm. Eng. 2020, 173, 115215. [Google Scholar] [CrossRef]
- Abe, Y. Self-rewetting fluids: Beneficial aqueous solutions. Ann. N. Y. Acad. Sci. 2006, 1077, 650–667. [Google Scholar] [CrossRef]
- Chaurasiya, V.K.; Tripathi, R.; Singh, R. On the solutal and thermal Marangoni convection arising in the self-rewetting fluid flow under hydromagnetic consideration. Sci. Iran. 2024, 31, 1007–1019. [Google Scholar] [CrossRef]
- Hajabdollahi, F.; Premnath, K.N.; Welch, S.W.J. Central moment lattice Boltzmann method using a pressure-based formulation for multiphase flows at high density ratios and including effects of surface tension and Marangoni stresses. J. Comput. Phys. 2021, 425, 109893. [Google Scholar] [CrossRef]
- Chiu, P.; Lin, Y. A conservative phase field method for solving incompressible two-phase flows. J. Comput. Phys. 2011, 230, 185–204. [Google Scholar] [CrossRef]
- Sun, Y.; Beckermann, C. Sharp interface tracking using the phase-field equation. J. Comput. Phys. 2007, 220, 626–653. [Google Scholar] [CrossRef]
- Folch, R.; Casademunt, J.; Hernández-Machado, A.; Ramirez-Piscina, L. Phase-field model for Hele-Shaw flows with arbitrary viscosity contrast. i. theoretical approach. Phys. Rev. E 1999, 60, 1724. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Kumar, A. Isotropic finite-differences. J. Comput. Phys. 2004, 201, 109–118. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef] [PubMed]
- Premnath, K.N.; Banerjee, S. On the three-dimensional central moment lattice Boltzmann method. J. Stat. Phys. 2011, 143, 747–794. [Google Scholar] [CrossRef]
- Yahia, E.; Premnath, K.N. Central moment lattice Boltzmann method on a rectangular lattice. Phys. Fluids 2021, 33, 057110. [Google Scholar] [CrossRef]
- Geier, M.; Schönherr, M.; Pasquali, A.; Krafczyk, M. The cumulant lattice Boltzmann equation in three dimensions: Theory and validation. Comput. Math. Appl. 2015, 70, 507–547. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A lattice boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh–Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Elseid, F.M.; Welch, S.W.J.; Premnath, K.N. A cascaded lattice boltzmann model for thermal convective flows with local heat sources. Int. J. Heat Fluid Flow 2018, 70, 279–298. [Google Scholar] [CrossRef]
- de Vahl Davis, G. Natural convection of air in a square cavity: A bench mark numerical solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Hortmann, M.; Perić, M.; Scheuerer, G. Finite volume multigrid prediction of laminar natural convection: Bench-mark solutions. Int. J. Numer. Methods Fluids 1990, 11, 189–207. [Google Scholar] [CrossRef]



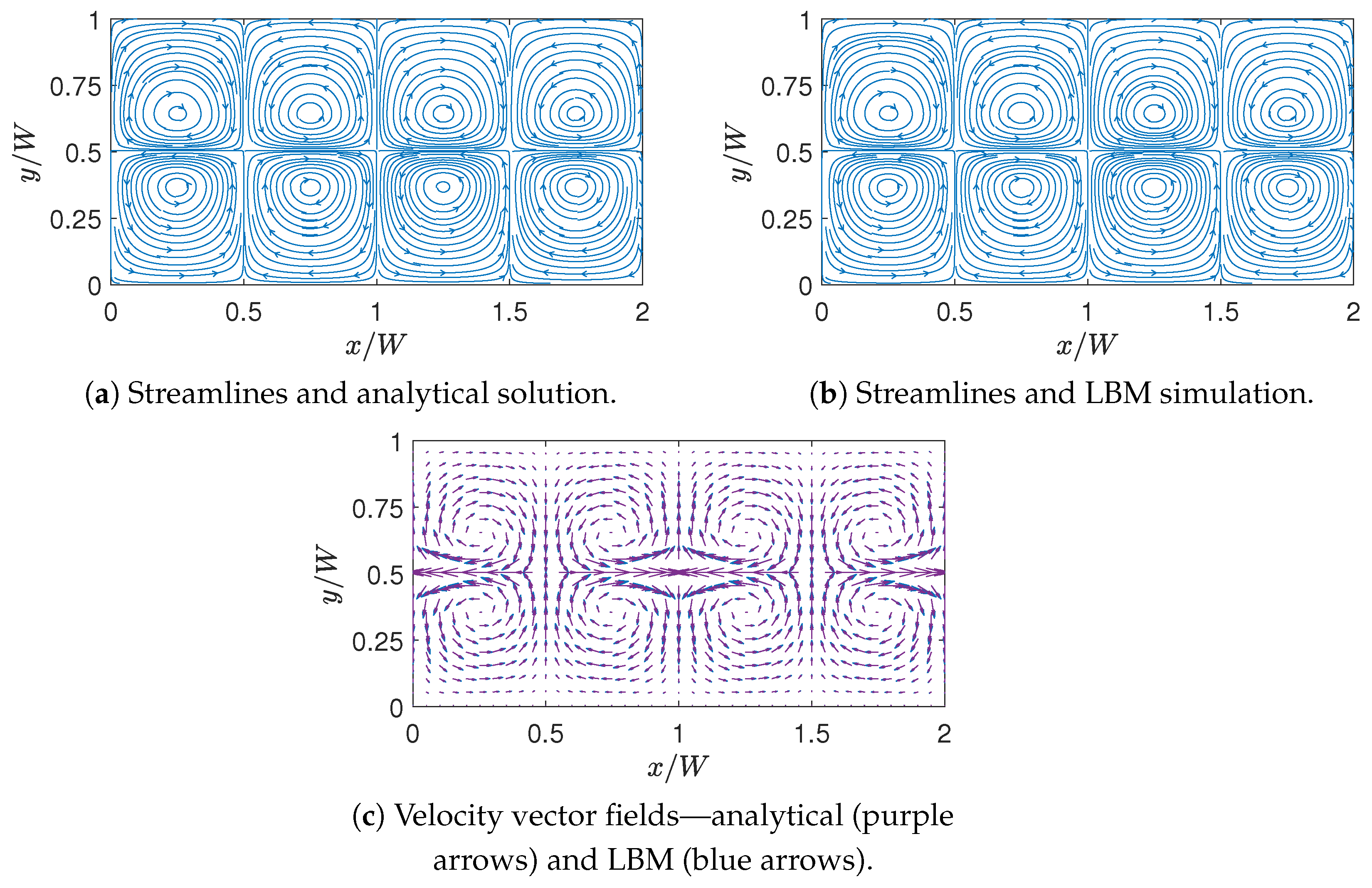
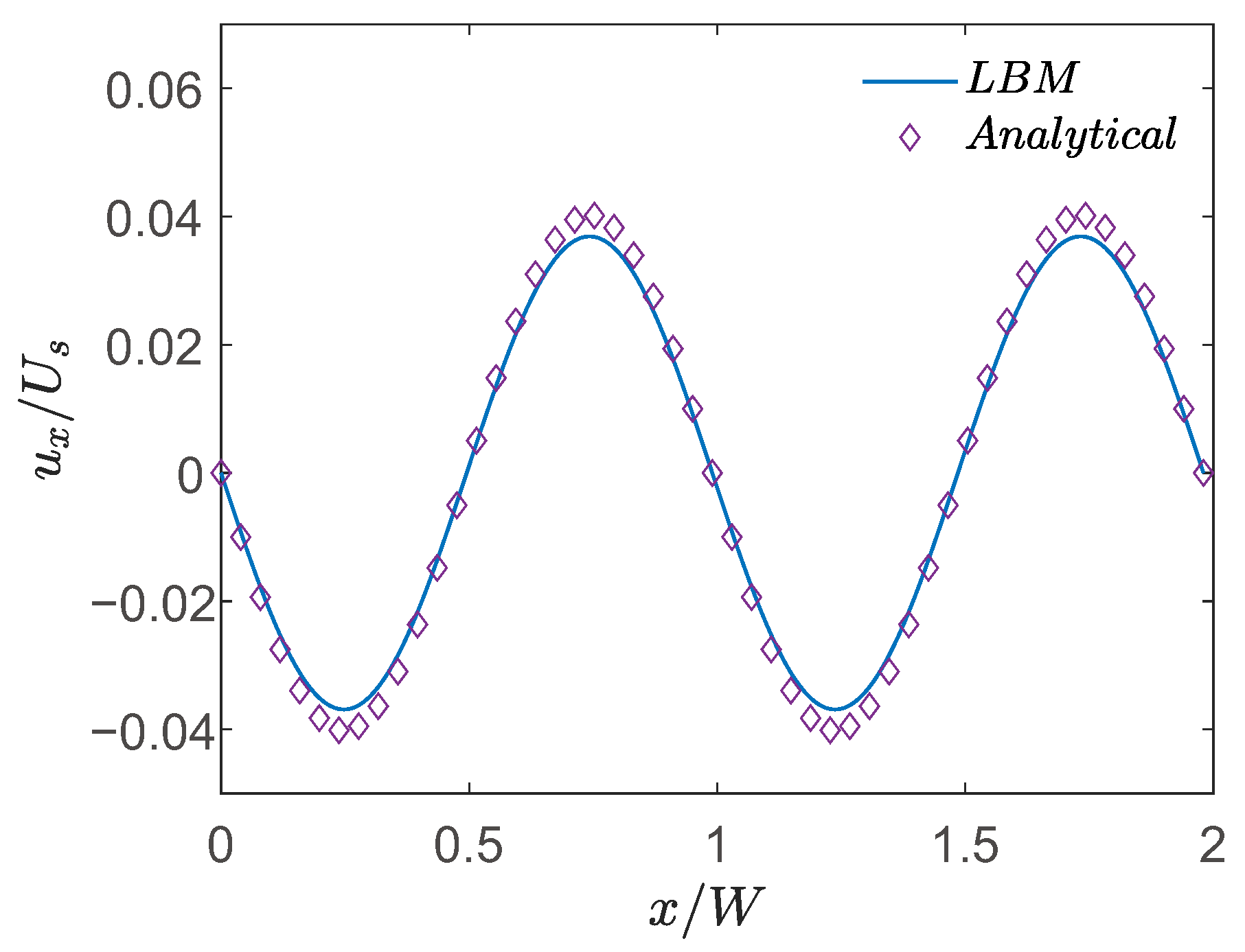









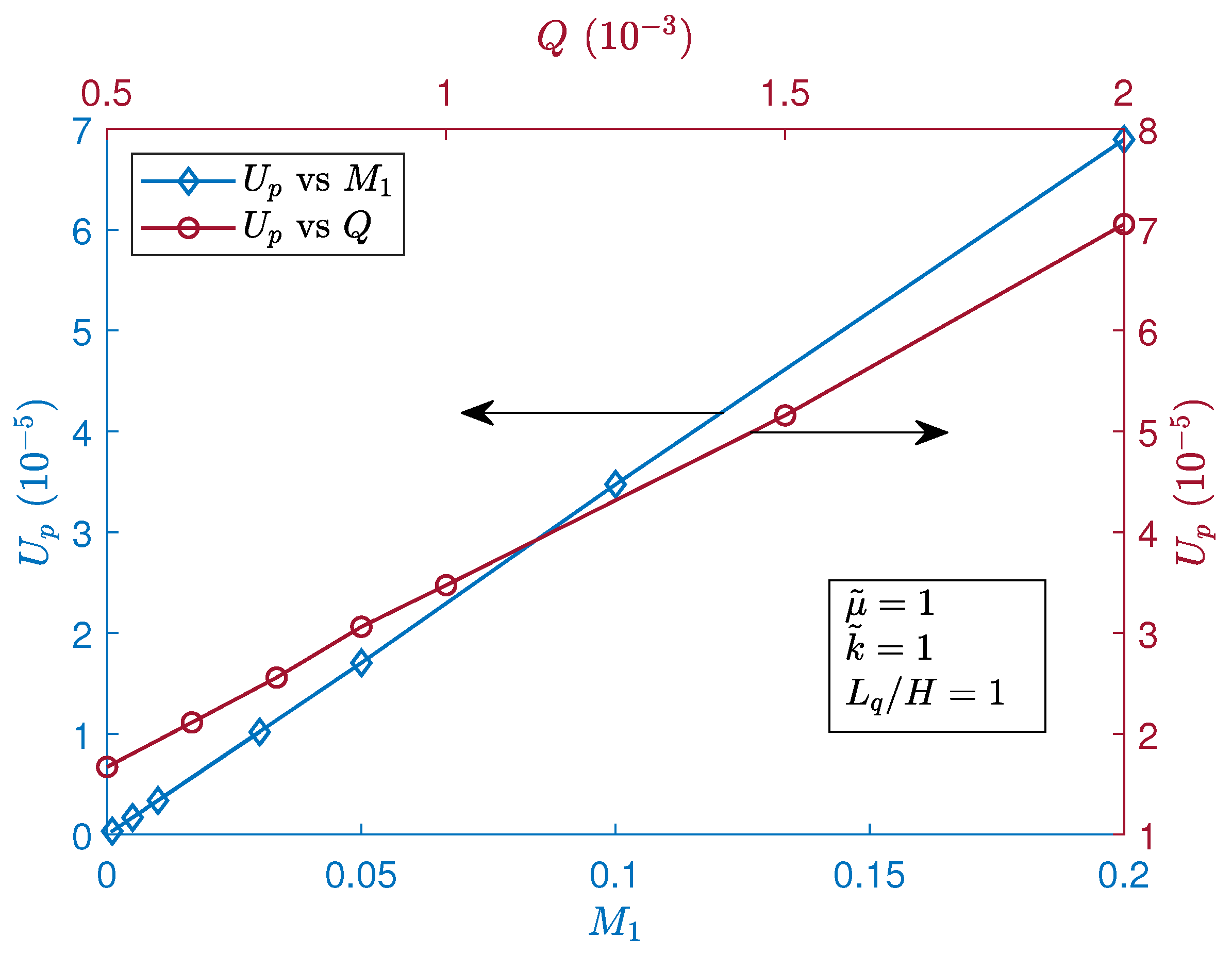

| LB Solver | Parameters and Constants |
|---|---|
| Interfacial tracking | |
| Two-fluid motion | |
| Energy transport | |
| Lattice parameters | |
| Ra | ||||||||
|---|---|---|---|---|---|---|---|---|
| Present | 3.5990 | 0.8110 | 3.6502 | 0.1811 | 1.1234 | 1.5123 | 0.91406 | |
| LBM [56] | 3.605 | 0.816 | 3.654 | 0.176 | 1.117 | NA | NA | |
| FDM [57] | 3.634 | 0.813 | 3.679 | 0.179 | 1.116 | NA | NA | |
| FVM [58] | NA | NA | NA | NA | NA | NA | NA | |
| Present | 16.1342 | 0.8220 | 19.5400 | 0.1204 | 2.2501 | 3.5492 | 0.8594 | |
| LBM [56] | 16.182 | 0.824 | 19.551 | 0.12 | 2.237 | NA | NA | |
| FDM [57] | 16.182 | 0.823 | 19.509 | 0.12 | 2.23 | NA | NA | |
| FVM [58] | 16.1759 | 0.8255 | 19.624 | 0.12 | 2.24475 | 3.5309 | 0.8531 | |
| Present | 34.8385 | 0.8549 | 68.4101 | 0.0667 | 4.5331 | 7.7728 | 0.9219 | |
| LBM [56] | 35.137 | 0.856 | 68.511 | 0.064 | 4.509 | NA | NA | |
| FDM [57] | 34.81 | 0.855 | 68.22 | 0.066 | 4.51 | NA | NA | |
| FVM [58] | 34.7398 | 0.8531 | 68.6465 | 0.0656 | 4.521 | 7.7201 | 0.9180 | |
| Present | 64.9520 | 0.8510 | 220.0331 | 0.0392 | 8.8440 | 17.6215 | 7 | |
| LBM [56] | 65.57 | 0.856 | 219.95 | 0.032 | 8.797 | NA | NA | |
| FDM [57] | 65.33 | 0.851 | 216.75 | 0.0387 | 8.798 | NA | NA | |
| FVM [58] | 64.8659 | 0.85312 | 219.861 | 0.0406 | 8.825 | 17.5360 | 0.9608 |
| Parameter | Ma | Pr | Ca | ||||
|---|---|---|---|---|---|---|---|
| Value | 10 | 10 | 0.1 | 0 | 1.0 | 0.5 | 0.5 |
| 1.0 | 1.0 | ||||||
| 2.0 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbousefi, B.; Schupbach, W.; Premnath, K.N. Marangoni Convection of Self-Rewetting Fluid Layers with a Deformable Interface in a Square Enclosure and Driven by Imposed Nonuniform Heat Energy Fluxes. Energies 2025, 18, 3563. https://doi.org/10.3390/en18133563
Elbousefi B, Schupbach W, Premnath KN. Marangoni Convection of Self-Rewetting Fluid Layers with a Deformable Interface in a Square Enclosure and Driven by Imposed Nonuniform Heat Energy Fluxes. Energies. 2025; 18(13):3563. https://doi.org/10.3390/en18133563
Chicago/Turabian StyleElbousefi, Bashir, William Schupbach, and Kannan N. Premnath. 2025. "Marangoni Convection of Self-Rewetting Fluid Layers with a Deformable Interface in a Square Enclosure and Driven by Imposed Nonuniform Heat Energy Fluxes" Energies 18, no. 13: 3563. https://doi.org/10.3390/en18133563
APA StyleElbousefi, B., Schupbach, W., & Premnath, K. N. (2025). Marangoni Convection of Self-Rewetting Fluid Layers with a Deformable Interface in a Square Enclosure and Driven by Imposed Nonuniform Heat Energy Fluxes. Energies, 18(13), 3563. https://doi.org/10.3390/en18133563








