Site Selection Evaluation of Pumped Storage Power Station Based on Multi-Energy Complementary Perspective: A Case Study in China
Abstract
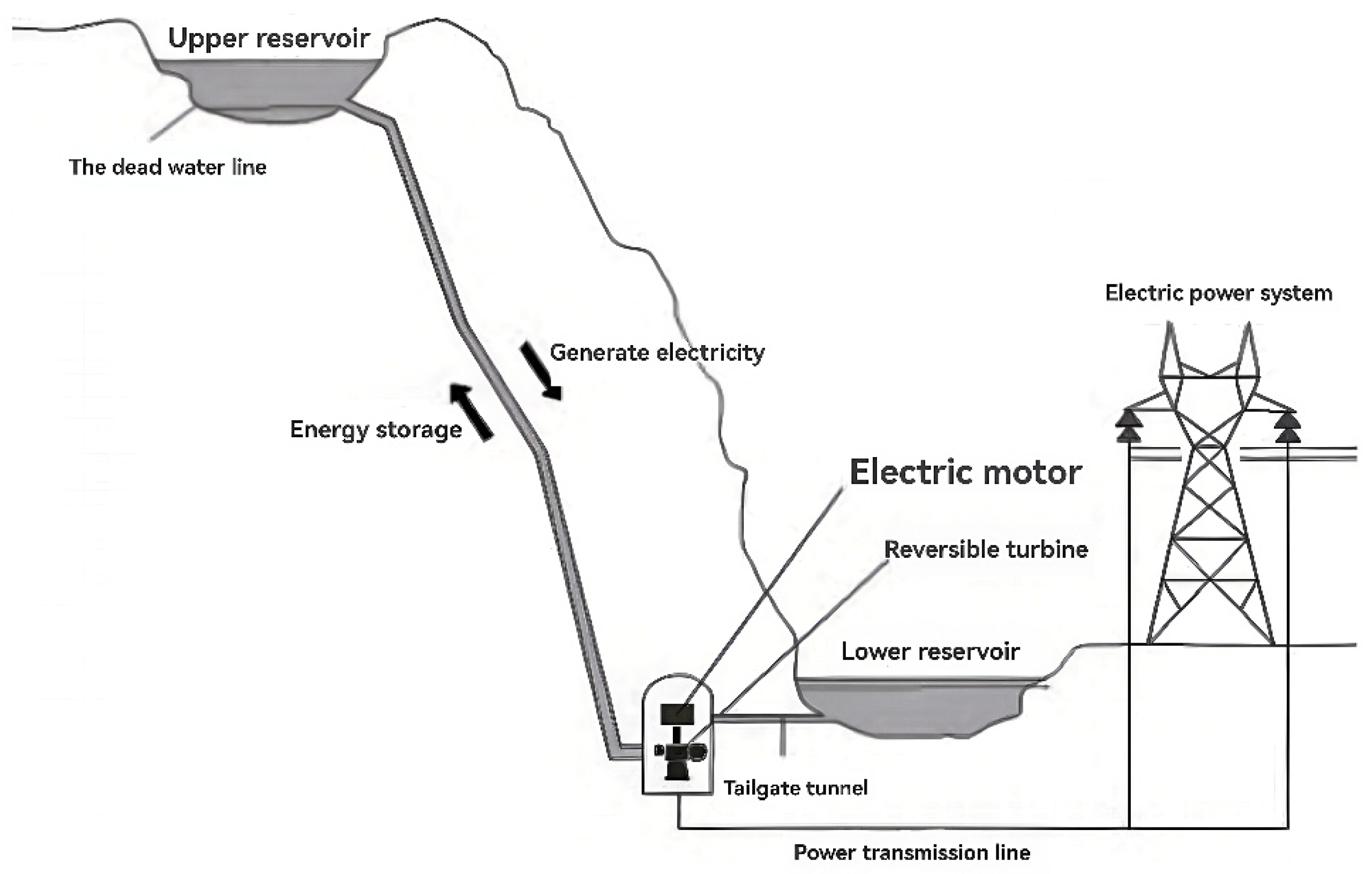
1. Introduction
2. Literature Review
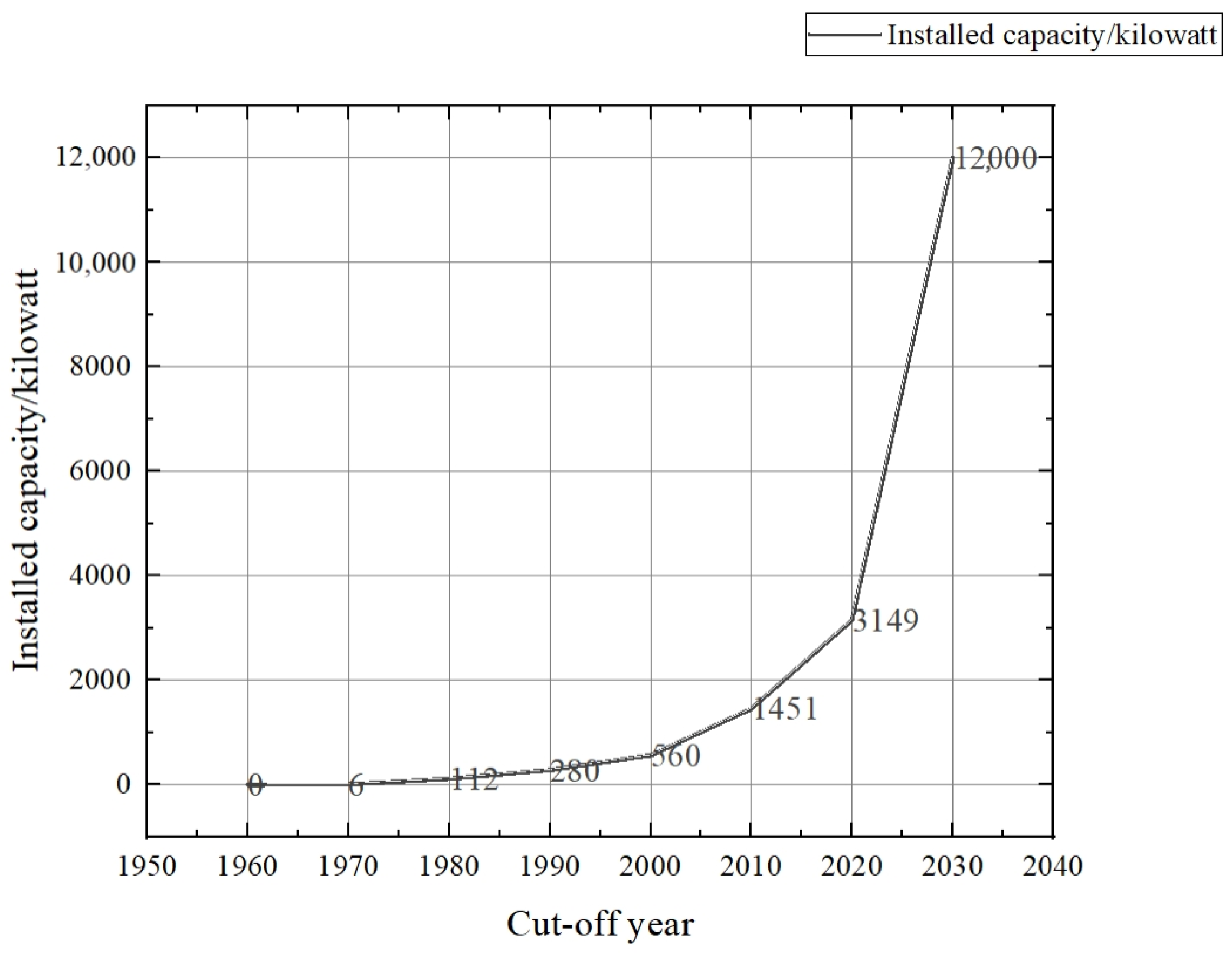
2.1. Development Status of PSPS Based on Multi-Energy Complementarity
2.2. PSPS Site Selection Research
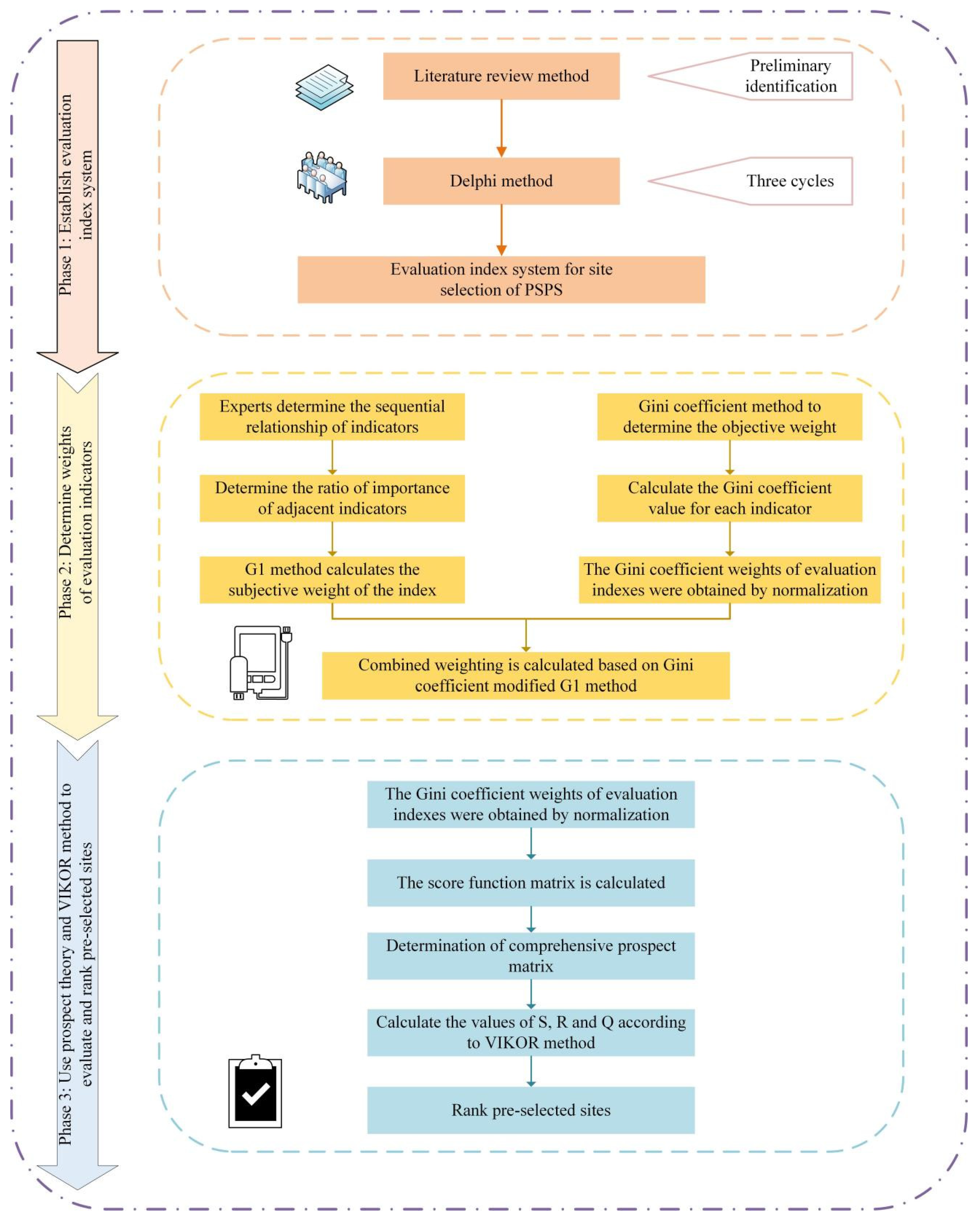
3. Establish the Evaluation Index System of Site Selection
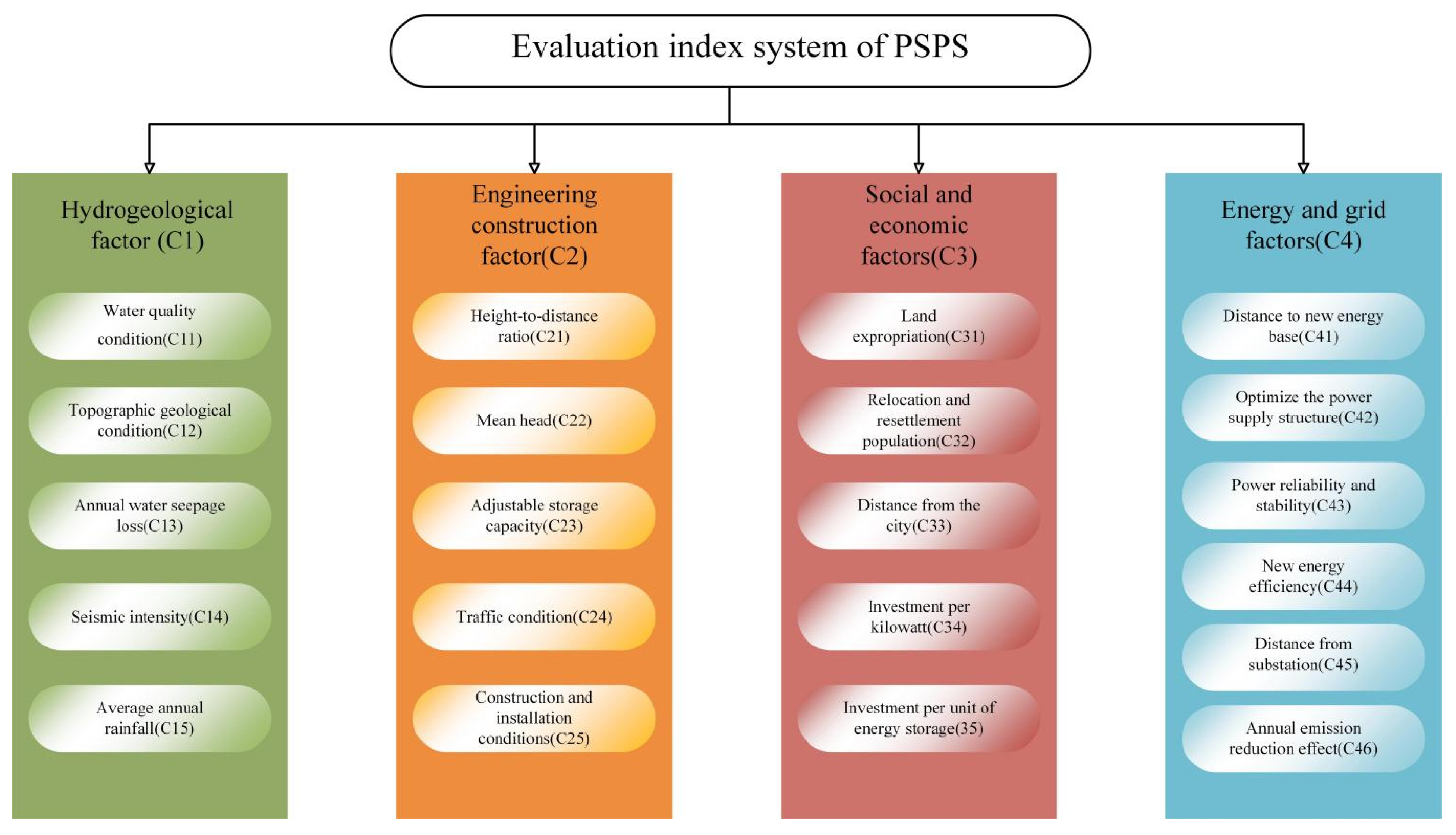
3.1. PSPS Site Selection Evaluation Index Summary
3.2. Index System Construction
4. Methodology
4.1. Calculate the Weights of Evaluation Indicators
4.1.1. Calculation of Subjective Weight by G1 Method
- (1)
- Indicator Sequencing
- (2)
- Adjacent indicator comparison
- (3)
- Subjective weight calculation using G1 method
4.1.2. Determination of Objective Weight by Gini Coefficient
4.1.3. Combinatorial Weighting Calculation Based on Modified Gini Coefficient G1 Method
- (1)
- The importance ranking of evaluation indicators is given by experts.
- (2)
- Calculate the importance ratio of adjacent indicators based on the weight of the Gini coefficient. Through Equations (6) and (7), the Gini coefficient weights of the evaluation indicators can be obtained, fully reflecting the data information of the indicators. Then, by comparing the Gini coefficient weights of the two adjacent indicators, the ratio of the importance degree of the adjacent indicators and is determined. Details are shown in Equation (8).
- (3)
- Determine the combined weights. Using the idea of the G1 method to calculate the combined weight, the combined weight of the last ranked mth indicator is
4.2. PSPS Site Selection Evaluation Model Calculation Steps
- (1)
- According to the comprehensive prospect matrix, the positive ideal solution and the negative ideal solution of each index are calculated:
- (2)
- Calculate the group benefit value and individual regret value of each evaluation object:
- (3)
- Determine the interest ratio Qi of each evaluation object:where , , , , is the maximum utility of the group, is the minimum regret of the individual, and represents the decision preference of the decision-maker.
- (4)
- Determine the ranking of alternatives and compromise:
5. Case Studies
5.1. The Gini Coefficient Modified G1 Method Was Applied to Assign Weights to Indicators
- (1)
- First, 10 experts were given a ranking according to their previous engineering experience; then, through organizing online discussion among experts, each expert explained his reasons for such ranking, and other experts put forward questions and opinions; finally, after three rounds of discussion, 10 experts jointly gave the final index ranking through continuous adjustment, as follows: .
- (2)
- The ratio of the importance of adjacent indicators based on the weight of the Gini coefficient was calculated by Equations (6) and (7) and included in column 2 of Table 5.
- (3)
- According to Equation (8), the combined weight is listed in column 3 of Table 5.
- (4)
- Inter-indicator Correlation Validation
5.2. The Prospective Theory and VIKOR Method Were Used to Evaluate and Sort the Pre-Selected Sites
6. Sensitivity Analysis and Comparative Analysis
6.1. Sensitivity Analysis
- (1)
- In the case application, coefficient selection affects the decision result. To balance benefits and regrets, = 0.5 is chosen as a compromise. However, experts have different preferences and will choose different compromise coefficients, resulting in changes in scheme ranking. Therefore, in this paper, with 0.1 step is taken for 11 times to obtain 11 groups of the comprehensive evaluation value (Table 11). The stability of the model is investigated through a sensitivity analysis.
- (2)
- In the case study section, we adopted the risk-neutral assumption for experts by setting = 0.5 as the baseline. To systematically evaluate the parameter’s influence, we conducted sensitivity tests with ranging across {0, 0.25, 0.5, 0.75, 1} at intervals of 0.25, covering both extreme and intermediate values. The test results are presented in Table 12. Key findings reveal the following: Lower values (minimization-oriented completion) elevate the ranking of Y3 (low-risk alternative). Higher values (maximization-oriented completion) favor Y5 (high-return alternative). Stability threshold: Ranking outcomes remain completely consistent when ∈ [0.4, 0.6], empirically validating the rationality of the default = 0.5 setting.
- (3)
- Sensitivity Analysis of Prospect Theory Parameters
6.2. Comparative Analysis
- (1)
- VIKOR method
- (2)
- GRA-TOPSIS method:
- (3)
- Prospect Theory-TOPSIS Method:
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Y1 | Y2 | Y3 | Y4 | Y5 | |
|---|---|---|---|---|---|
| Water quality condition | good | good | relatively good | relatively poor | medium |
| Topographic geological condition | relatively good | good | good | medium | relatively poor |
| Annual water seepage loss (/10,000 cubic meters) | 73 | 58 | 64 | 80 | 79 |
| Seismic intensity (/degree) | 6 | 4 | 3 | 4 | 5 |
| Average annual rainfall (/mm) | 2004.3 | 1978.7 | 1665.2 | 2108.9 | 1883.9 |
| Height-to-distance ratio | 6.0 | 4.1 | 7.3 | 5.6 | 4.5 |
| Mean head(/m) | 699.6 | 485 | 400.5 | 493 | 558.3 |
| Adjustable storage capacity (/10,000 cubic meters) | 735 | 785 | 1008 | 774.9 | 660 |
| Traffic condition | medium | relatively poor | relatively good | medium | relatively good |
| Construction and installation conditions | relatively good | good | good | relatively poor | relatively poor |
| Land expropriation (/hm2) | 344.03 | 372.64 | 40.04 | 339 | 326.44 |
| Relocation and resettlement population (/person) | 200 | 778 | 0 | 240 | 71 |
| Distance from the city (/km) | 153 | 180 | 175 | 128 | 81 |
| Investment per kilowatt (yuan/kw) | 5033 | 5229 | 3424 | 5713 | 5222 |
| Investment per unit of energy storage (yuan/kwh) | 706 | 741 | 231 | 935 | 733 |
| Distance to new energy base (/km) | 70 | 140 | 90 | 170 | 160 |
| Optimize the power supply structure | good | relatively good | medium | relatively poor | medium |
| Power reliability and stability | relatively good | good | relatively poor | medium | relatively good |
| New energy efficiency | good | medium | relatively good | relatively poor | relatively poor |
| Distance from substation (/km) | 36 | 17 | 77 | 41 | 36 |
| Annual emission reduction effect (ten thousand tons/year) | 122.6 | 23.1 | 47.1 | 90 | 39.5 |
Appendix B
| C11 | C12 | C13 | C14 | C15 | C21 | C22 | C23 | |
| C11 | 1.0000 | 0.7059 | 0.7449 | −0.2354 | −0.2182 | 0.0151 | 0.2877 | 0.1515 |
| C12 | 0.7059 | 1.0000 | 0.9050 | 0.4372 | −0.3488 | −0.3470 | −0.3392 | 0.7234 |
| C13 | 0.7449 | 0.9050 | 1.0000 | 0.4442 | −0.4068 | −0.0103 | −0.4035 | 0.5508 |
| C14 | −0.2354 | 0.4372 | 0.4442 | 1.0000 | −0.4857 | −0.3106 | −0.9885 | 0.7808 |
| C15 | −0.2182 | −0.3488 | −0.4068 | −0.4857 | 1.0000 | 0.5213 | 0.4935 | −0.6744 |
| C21 | 0.0151 | −0.3470 | −0.0103 | −0.3106 | 0.5213 | 1.0000 | 0.2084 | −0.7568 |
| C22 | 0.2877 | −0.3392 | −0.4035 | −0.9885 | 0.4935 | 0.2084 | 1.0000 | −0.6980 |
| C23 | 0.1515 | 0.7234 | 0.5508 | 0.7808 | −0.6744 | −0.7568 | −0.6980 | 1.0000 |
| C24 | −0.4125 | −0.4125 | −0.4431 | 0.1048 | −0.6386 | −0.5173 | −0.1443 | 0.2077 |
| C25 | 0.8344 | 0.9609 | 0.9365 | 0.3181 | −0.4778 | −0.2854 | −0.2411 | 0.6443 |
| C31 | 0.0185 | 0.4387 | 0.3036 | 0.653 | −0.8687 | −0.8263 | −0.6050 | 0.8998 |
| C32 | −0.4285 | −0.4091 | −0.5732 | −0.0319 | −0.4616 | −0.6652 | 0.0316 | 0.1949 |
| C33 | −0.7866 | −0.9566 | −0.9787 | −0.4118 | 0.4713 | 0.1927 | 0.3485 | −0.6422 |
| C34 | 0.3201 | 0.5650 | 0.4842 | 0.5048 | −0.9339 | −0.7396 | −0.4580 | 0.8456 |
| C35 | 0.4318 | 0.7480 | 0.6135 | 0.5306 | −0.8189 | −0.7584 | −0.4530 | 0.9145 |
| C41 | 0.0011 | −0.4666 | −0.3701 | −0.7488 | 0.8702 | 0.7518 | 0.7099 | −0.9186 |
| C42 | 0.9081 | 0.4036 | 0.4030 | −0.6154 | 0.0288 | 0.0863 | 0.6618 | −0.1771 |
| C43 | 0.4372 | −0.0673 | 0.1923 | −0.5385 | 0.5183 | 0.8799 | 0.4840 | −0.7093 |
| C44 | 0.7647 | 0.6176 | 0.3965 | −0.2691 | −0.2831 | −0.5583 | 0.3792 | 0.3693 |
| C45 | 0.2065 | −0.1960 | 0.0124 | −0.5183 | 0.7385 | 0.9057 | 0.4685 | −0.7795 |
| C46 | −0.0439 | −0.1613 | −0.5152 | −0.5837 | 0.4616 | −0.4011 | 0.6764 | −0.1844 |
| C24 | C25 | C31 | C32 | C33 | C34 | C35 | C41 | |
| C11 | −0.4125 | 0.8344 | 0.0185 | −0.4258 | −0.7866 | 0.3201 | 0.4318 | 0.0011 |
| C12 | −0.4125 | 0.9609 | 0.4387 | −0.4091 | −0.9566 | 0.5650 | 0.7480 | −0.4666 |
| C13 | −0.4431 | 0.9365 | 0.3036 | −0.5732 | −0.9787 | 0.4842 | 0.6135 | −0.3701 |
| C14 | 0.1048 | 0.3181 | 0.6530 | −0.0319 | −0.4118 | 0.5048 | 0.5306 | −0.7488 |
| C15 | −0.6386 | −0.4778 | −0.8687 | −0.4616 | 0.4713 | −0.9339 | −0.8189 | 0.8702 |
| C21 | −0.5173 | −0.2854 | −0.8263 | −0.6652 | 0.1927 | −0.7396 | −0.7584 | 0.7518 |
| C22 | −0.1443 | −0.2411 | −0.6050 | 0.0316 | 0.3485 | −0.4580 | −0.4530 | 0.7099 |
| C23 | 0.2077 | 0.6443 | 0.8998 | 0.1949 | −0.6422 | 0.8456 | 0.9145 | −0.9186 |
| C24 | 1.0000 | −0.3152 | 0.6043 | 0.9408 | 0.3589 | 0.5144 | 0.2953 | −0.5484 |
| C25 | −0.3152 | 1.0000 | 0.4390 | −0.3613 | −0.9872 | 0.6342 | 0.7722 | −0.4577 |
| C31 | 0.6043 | 0.4390 | 1.0000 | 0.5544 | −0.4155 | 0.9454 | 0.9019 | −0.9893 |
| C32 | 0.9408 | −0.3613 | 0.5544 | 1.0000 | 0.4435 | 0.4373 | 0.2658 | −0.4647 |
| C33 | 0.3589 | −0.9872 | −0.4155 | 0.4435 | 1.0000 | −0.5977 | −0.7331 | 0.4570 |
| C34 | 0.5144 | 0.6342 | 0.9454 | 0.4373 | −0.5977 | 1.0000 | 0.9640 | −0.9272 |
| C35 | 0.2953 | 0.7722 | 0.9019 | 0.2658 | −0.7331 | 0.9640 | 1.0000 | −0.8881 |
| C41 | −0.5484 | −0.4577 | −0.9893 | −0.4647 | 0.4570 | −0.9272 | −0.8881 | 1.0000 |
| C42 | −0.3669 | 0.5494 | −0.2336 | −0.3022 | −0.4630 | 0.0667 | 0.1532 | 0.2967 |
| C43 | −0.6814 | 0.0289 | −0.8336 | −0.7539 | −0.0672 | −0.6302 | −0.5811 | 0.7985 |
| C44 | −0.0458 | 0.6827 | 0.3273 | 0.1056 | −0.5579 | 0.5189 | 0.6237 | −0.2350 |
| C45 | −0.7444 | −0.1715 | −0.9449 | −0.7647 | 0.1239 | −0.8255 | −0.7563 | 0.9049 |
| C46 | −0.0070 | −0.2418 | −0.1806 | 0.3236 | 0.3734 | −0.2271 | −0.1474 | 0.3022 |
| C42 | C43 | C44 | C45 | C46 | ||||
| C11 | 0.9081 | 0.4372 | 0.7647 | 0.2065 | −0.0439 | |||
| C12 | 0.4036 | −0.0673 | 0.6176 | −0.1960 | −0.1613 | |||
| C13 | 0.4030 | 0.1923 | 0.3965 | 0.0124 | −0.5152 | |||
| C14 | −0.6154 | −0.5385 | −0.2691 | −0.5183 | −0.5837 | |||
| C15 | 0.0288 | 0.5183 | −0.2831 | 0.7385 | 0.4616 | |||
| C21 | 0.0863 | 0.8799 | −0.5583 | 0.9057 | −0.4011 | |||
| C22 | 0.6618 | 0.4840 | 0.3792 | 0.4685 | 0.6764 | |||
| C23 | −0.1771 | −0.7093 | 0.3693 | −0.7795 | −0.1844 | |||
| C24 | −0.3669 | −0.6814 | −0.0458 | −0.7444 | −0.0070 | |||
| C25 | 0.5494 | 0.0289 | 0.6827 | −0.1715 | −0.2418 | |||
| C31 | −0.2336 | −0.8336 | 0.3273 | −0.9449 | −0.1806 | |||
| C32 | −0.3022 | −0.7539 | 0.1056 | −0.7647 | 0.3236 | |||
| C33 | −0.4630 | −0.0672 | −0.5579 | 0.1239 | 0.3734 | |||
| C34 | 0.0667 | −0.6302 | 0.5189 | −0.8255 | −0.2271 | |||
| C35 | 0.1532 | −0.5811 | 0.6237 | −0.7563 | −0.1474 | |||
| C41 | 0.2967 | 0.7985 | −0.2350 | 0.9049 | 0.3022 | |||
| C42 | 1.0000 | 0.5385 | 0.7736 | 0.3482 | 0.2652 | |||
| C43 | 0.5385 | 1.0000 | −0.1009 | 0.9525 | −0.1728 | |||
| C44 | 0.7736 | −0.1009 | 1.0000 | −0.2677 | 0.4618 | |||
| C45 | 0.3482 | 0.9525 | −0.2677 | 1.0000 | −0.0564 | |||
| C46 | 0.2652 | −0.1728 | 0.4618 | −0.0564 | 1.0000 |
References
- Kai, Z.; Bo, C. Development and Application of “Multi-Energy Complementary” Technology. Technol. Ind. 2018, 18, 92–99. [Google Scholar]
- Ogbonnaya, C.; Turan, A.; Abeykoon, C. Energy and Exergy Efficiencies Enhancement Analysis of Integrated Photovoltaic-Based Energy Systems. J. Energy Storage 2019, 26, 101029. [Google Scholar] [CrossRef]
- El-Kady, M.F.; Ihns, M.; Li, M.; Hwang, J.Y.; Mousavi, M.F.; Chaney, L.; Lech, A.T.; Kaner, R.B. Engineering Three-Dimensional Hybrid Supercapacitors and Microsupercapacitors for High-Performance Integrated Energy Storage. Proc. Natl. Acad. Sci. USA 2015, 112, 4233–4238. [Google Scholar] [CrossRef]
- He, X. Study on Cooperative Optimal Dispatching and Benefit Balance of Clean Energy Based on Multi-Energy Complementarity. Ph.D. Thesis, North China Electric Power University (Beijing), Beijing, China, 2019. [Google Scholar]
- Song, Y.; Yan, Y.; Zhai, L.; Wu, B.; Yao, J.; He, H. Analysis of Geographical Elements and GIS Site Selection for the Construction of Pumped Storage Power Stations. Hydropower Gener. Yunnan 2022, 38, 131–134. [Google Scholar]
- Hall, C.R. 2023 Pumped Energy Storage Industry Data Statistics: The Global Pumped Energy Storage Compound Annual Growth Rate Will Exceed 15%. 2023. Available online: https://m.chinabgao.com/k/choushuichunen/68006.html (accessed on 20 May 2025).
- Ren, H.; Yu, B.; Wang, K.; Wang, L. Development and Prospect of Pumped Storage Power Station Under the Background of “Dual Carbon”. Inn. Mong. Power Technol. 2022, 40, 25–30. [Google Scholar] [CrossRef]
- Sun, P.; Chang, Y.; Jiang, Q.; Yi, C. Research of Simulation Analysis on Multi-energy Complementary Wind-PV-pumped Storage System Based on Different Types of Pumped Storage Units. In Proceedings of the 8th International Conference on Hydraulic and Civil Engineering—Deep Space Intelligent Development and Utilization Forum (ICHCE), Xi’an, China, 25–27 November 2022; pp. 1281–1286. [Google Scholar]
- Li, X.; Yang, W.; Zhao, Z.; Wang, R.; Yin, X. Advantage of Priority Regulation of Pumped Storage for Carbon-Emission-Oriented Co-Scheduling of Hybrid Energy System. J. Energy Storage 2023, 58, 106400. [Google Scholar] [CrossRef]
- Gao, R.; Wu, F.; Zou, Q.; Chen, J. Optimal Dispatching of Wind-PV-Mine Pumped Storage Power Station: A Case Study in Lingxin Coal Mine in Ningxia Province, China. Energy 2022, 243, 123061. [Google Scholar] [CrossRef]
- Wang, J.; Yin, X.; Liu, Y.; Cai, W. Optimal Design of Combined Operations of Wind Power-Pumped Storage-Hydrogen Energy Storage Based on Deep Learning. Electr. Power Syst. Res. 2023, 218, 109216. [Google Scholar] [CrossRef]
- Zhang, L.; Song, Z. Discussion on the Complementarity of Pumped Storage and Wind Power. Northwest Hydropower 2007, 79–81+87. [Google Scholar]
- Salimi, A.A.; Karimi, A.; Noorizadeh, Y. Simultaneous Operation of Wind and Pumped Storage Hydropower Plants in a Linearized Security-Constrained Unit Commitment Model For High Wind ENERGY penetration. J. Energy Storage 2019, 22, 318–330. [Google Scholar] [CrossRef]
- Ji, L.; Li, C.; Li, X.; Li, P.; Zhu, H.; Zhang, Z. Multi-Method Combination Site Selection of Pumped Storage Power Station Considering Power STRUCTURE optimization. Sustain. Energy Technol. Assess. 2022, 49, 101680. [Google Scholar] [CrossRef]
- Nzotcha, U.; Kenfack, J.; Blanche Manjia, M. Integrated MULTI-criteria Decision Making Methodology for Pumped Hydro-Energy Storage Plant Site Selection from a Sustainable Development Perspective with an Application. Renew. Sustain. Energy Rev. 2019, 112, 930–947. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, J.; Chang, F.; Gong, Z. Site Selection Evaluation of pumped Storage Power Station Based on Game Theory Combination. Hydroelectr. Power Gener. 2024, 1–6. [Google Scholar]
- Wu, Y.; Liu, L.; Gao, J.; Chu, H.; Xu, C. An Extended VIKOR-Based Approach for Pumped Hydro Energy Storage Plant Site Selection with Heterogeneous Information. Information 2017, 8, 106. [Google Scholar] [CrossRef]
- Zhao, H.; Lu, X. Principle of Site Selection for Pumped Storage Power Station. Northeast. Water Resour. Hydropower 2012, 30, 1–2+71. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Odigie, O.; Munda, J.L. A Multi-Criteria GIS Based Model for Wind Farm Site Selection Using Interval Type-2 Fuzzy Analytic Hierarchy Process: The Case Study of Nigeria. Appl. Energy 2018, 228, 1853–1869. [Google Scholar] [CrossRef]
- Caner, H.I.; Aydin, C.C. Shipyard Site Selection by Raster Calculation Method and AHP in GIS Environment, İskenderun, Turkey. Mar. Policy 2021, 127, 104439. [Google Scholar] [CrossRef]
- Geng, S.; Lin, L.; Zhang, L.; Liu, X.; Huang, Z. Site Selection Framework of Fishing Photovoltaic Hybrid Project Under Interval-Valued Intuitionistic Fuzzy Environment. J. Clean. Prod. 2020, 252, 119774. [Google Scholar] [CrossRef]
- Hosseini, S.; Sarder, M.D. Development of a Bayesian Network Model for Optimal Site Selection of Electric Vehicle Charging Station. Int. J. Electr. Power Energy Syst. 2019, 105, 110–122. [Google Scholar] [CrossRef]
- Tan, Q.; Wei, T.; Peng, W.; Yu, Z.; Wu, C. Comprehensive Evaluation Model of Wind Farm Site Selection Based on Ideal Matter Element and Grey Clustering. J. Clean. Prod. 2020, 272, 122658. [Google Scholar] [CrossRef]
- Yang, Z.; Chang, J. A multi-Attribute Decision-Making-Based Site Selection Assessment Algorithm for Garbage Disposal Plant Using Interval q-Rung Orthopair Fuzzy Power Muirhead Mean Operator. Environ. Res. 2021, 193, 110385. [Google Scholar] [CrossRef] [PubMed]
- Kotb, K.M.; Elkadeem, M.R.; Khalil, A.; Imam, S.M.; Hamada, M.A.; Sharshir, S.W.; Dán, A. A Fuzzy Decision-Making Model for Optimal Design of Solar, Wind, Diesel-Based RO Desalination Integrating Flow-Battery and Pumped-Hydro Storage: Case Study in Baltim, Egypt. Energy Convers. Manag. 2021, 235, 113962. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Haider, H.; Yousuf, I.; Shafiquzamman, M. Sustainable Development of Small-Sized Hydropower Plants: Multilevel Decision-Making from Site Selection to Optimal Design. Arab. J. Sci. Eng. 2020, 45, 4141–4159. [Google Scholar] [CrossRef]
- Rojanamon, P.; Chaisomphob, T.; Bureekul, T. Application of Geographical Information SYSTEM to site Selection of Small Run-of-River Hydropower Project by Considering Engineering/Economic/Environmental Criteria and Social Impact. Renew. Sustain. Energy Rev. 2009, 13, 2336–2348. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen Van, T.; Su, C.-C. The Study of a Multicriteria Decision Making Model for Wave Power Plant Location Selection in Vietnam. Processes 2019, 7, 650. [Google Scholar] [CrossRef]
- Shimray, B.A.; Singh, K.M.; Khelchandra, T.; Mehta, R.K. Ranking of Sites for Installation of Hydropower Plant Using MLP Neural Network Trained with GA: A MADM Approach. Comput. Intell. Neurosci. 2017, 2017, 4152140. [Google Scholar] [CrossRef]
- Ji, L.; Li, X.; Huang, W.; Dong, J.; Bai, M.; Li, C. Study on Site Selection Combination Evaluation of Pumped-Storage Power Station Based on Cycle Elimination-BASED on the Empirical Analysis of North China. J. Energy Storage 2022, 52, 104824. [Google Scholar] [CrossRef]
- Long, W. Study on Site Selection and Joint Operation Optimization of Pumped Storage Power Station and Wind Power. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2017. [Google Scholar]
- Guangdong Nuclear Engineering Survey Institute. Environmental Impact Assessment Report for Huizhou Huidong 220kV Baipenzhu (Duozhu) Power Transmission and Transformation Project (Public Draft); Guangdong Power Grid Corporation: Huizhou, China, 2019. Available online: http://www.huidong.gov.cn/hdzdly/hfsaq/201909/1dff204c97c24702ac8ecb278546ede9/files/672328da7f204635a1966cc132d64243.pdf (accessed on 20 May 2025).
- Chen, H.; Chen, T.; Qin, X.; Lu, K. Analysis of Site Selection Conditions for hybrid pumped storage power station. Hydropower Pumped Storage 2017, 3, 28–31+44. [Google Scholar]
- Zhang, L. Research on Dam Site Selection Model of Hydropower Station Based on Entropy-TOPSIS Method. Master’s Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar]
- Yuan, Y.; Wu, W.; Zhang, Y.; Zhao, Y.; Zhang, H. Optimization Evaluation of Pumped Storage Sites in Guangdong Province Based on AHP-entropy Weight Method and TOPSIS. Guangdong Water Resour. Hydropower 2023, 37–42. [Google Scholar]
- Ren, Y.; Hou, S.C. Study on Site Selection of Pumped Storage Power Station Based on Multi-Energy Complementarity. Hydropower Pumped Storage 2021, 7, 37–39. [Google Scholar]
- Wu, Y.; Zhang, T.; Xu, C.; Zhang, X.; Ke, Y.; Chu, H.; Xu, R. Location Selection of Seawater Pumped Hydro Storage Station in China based on multi-attribute decision making. Renew. Energy 2019, 139, 410–425. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, S.; Bu, Z.; Liu, X. Supplier Selection of Prefabricated Building Components Based on Prospect Theory. J. Civ. Eng. Manag. 2020, 37, 1–7+14. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, S.; Bu, Z.; Zhang, X. VIKOR Hesitant Fuzzy Multi-Attribute Decision Making Method Based on Prospect Theory. Pract. Underst. Math. 2020, 50, 124–136. [Google Scholar]
- Wang, X.; Guo, Y. Consistency Analysis of Judgement Matrix Based on G1 Method. Chin. Manag. Sci. 2006, 3, 65–70. [Google Scholar] [CrossRef]
- Li, G.; Cheng, Y.; Dong, L.; Wang, W. Research on Objective Weighting Method of Gini Coefficient. Manag. Rev. 2014, 26, 12–22. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in Prospect Theory: Cumulative Representation of Uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.; Wang, Y.; Zhu, K.; He, L. The evolution of CCS-EOR Technology Diffusion Involving Multi-Agent Participation Under Dual Carbon Targets: A System Dynamics and Prospect Theory Approach. Sustain. Futures 2025, 9, 100642. [Google Scholar] [CrossRef]
- Guangdong Provincial Department of Water Resources, Guangdong Provincial Hydrological Bureau. The Heavy Rain and Flood in Beijing in 2022, 1st ed.; China Water Resources and Hydropower: Beijing, China, 2022; p. 154. [Google Scholar]




| Factor | [19] | [20] | [21] | [22] | [23] | [24] | [25] | [26] | [27] | [28] | [29] | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Social | √ | √ | √ | √ | √ | √ | √ | √ | √ | 9 | ||
| Service | √ | 1 | ||||||||||
| Economic | √ | √ | √ | √ | √ | √ | √ | √ | √ | 9 | ||
| Resource | √ | √ | √ | √ | √ | √ | √ | √ | 8 | |||
| Environmental | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | 10 | |
| Technical | √ | √ | √ | √ | √ | 5 | ||||||
| Safety | √ | √ | √ | 2 | ||||||||
| Traffic | √ | √ | √ | 3 | ||||||||
| Support Condition | √ | 1 | ||||||||||
| Risk | √ | 1 | ||||||||||
| Climate | √ | 1 |
| No | Work Unit | Position | Research Focus | Relevance to PSPS Site Selection |
|---|---|---|---|---|
| 1 | North China Electric Power University | Professor | Power system planning, renewable energy integration | Provides theoretical support for hydrological/geological and grid compatibility indicators |
| 2 | Shandong University | Professor | Environmental engineering, social impact assessment of energy projects | Leads optimization of environmental and socio-economic indicators |
| 3 | Shandong Electric Power Survey and Design Institute | Senior engineer | Power engineering geological survey, topographic mapping | Validates technical aspects of hydrological/geological and construction indicators |
| 4 | Shandong Electric Power Survey and Design Institute | Senior engineer | Electrical design, grid connection solutions | Refines energy/grid factors |
| 5 | China Shandong Electric Power Construction Group | Project manager | Large-scale power infrastructure project management, construction risk assessment | Optimizes engineering/construction indicators and risk management |
| 6 | China 11th Water Conservancy and Hydropower Engineering Bureau | Project manager | Hydraulic engineering construction, geological adaptability analysis | Verifies practicality of hydrological/geological indicators |
| 7 | Institute of Water Conservancy and Hydropower Planning | Senior engineer | Regional water resource planning, ecological impact assessment | Supplements cross-cutting indicators |
| 8 | China Electric Power Planning and Design Institute | Senior engineer | Power system stability analysis, energy storage project planning | Strengthens energy/grid factors |
| 9 | China International Engineering Consulting Corporation | Professional consultant | Life-cycle assessment of energy projects, policy compliance | Ensures comprehensiveness of socio-economic factors |
| 10 | Hebei Electric Power Company of State Grid | Dispatching specialist | Grid operation/dispatch, grid-connected energy storage experience | Provides operational insights to optimize grid compatibility and dispatch flexibility |
| Evaluation Indicators | Indicator Description |
|---|---|
| Water quality condition | Evaluating the plant’s water source quality primarily hinges on the extent of water contamination and the level of dissolved oxygen present, crucial for the efficient functioning and upkeep of energy storage and power generation machinery [30]. |
| Topographic geological condition | When PSPS are located, the geological conditions need to be ideal, which affects construction, costs, and long-term operation. Site surveys to determine optimal geological conditions are essential [31]. |
| Annual water seepage loss | Annual water loss due to leakage within the factory area. |
| Seismic intensity | Reflect the intensity of earthquake impact on the surface and engineering buildings [14]. |
| Average annual rainfall | When PSPSs are built in arid areas, water is insufficient; when they are built in places with heavy rainfall, although the water source is stable, the flood control requirements are increased [32]. |
| Height-to-distance ratio | The height-to-distance ratio describes the ratio between the horizontal distance between the inlet/outlet of the upper reservoir and the inlet/outlet of the lower reservoir, and the average total head of the power station [33]. |
| Mean head | At present, generally, the economic head of PSPSs is 330–600 m, and the highest is not more than 700 m. A higher water head will increase the complexity and cost of equipment; a lower water head requires a larger flow rate, resulting in an increase in unit cost [18]. |
| Adjustable storage capacity | Adjustable storage capacity refers to the effective capacity of PSPSs that can store or release water by adjusting the amount of water in and out during operation [14]. |
| Traffic condition | The site is located with excellent transportation facilities, which helps lay a solid foundation for the construction of the power station. The evaluation parameters mainly include the weighted average distance (km) to highways/railways and the heavy-load vehicle passability index (1–5 scale) [34]. |
| Construction and installation conditions | The construction and installation conditions mainly refer to the construction site conditions (hydropower layout, plant layout), technical difficulty, and the difficulty of equipment installation. Quantification is usually based on terrain adaptability index (slope stability, excavation difficulty), equipment transport accessibility (road class, bridge capacity), and modular construction feasibility (%) [34]. |
| Land expropriation | The cost of acquiring land for the construction of PSPSs [30]. |
| Relocation and resettlement population | The number of people relocated due to the construction of PSPSs [35]. |
| Distance from the city | The distance from the site to the city [35]. |
| Investment per kilowatt | When constructing a power station facility, this is the investment cost required per kilowatt of installed capacity [35]. |
| Investment per unit of energy storage | The investment cost per unit of storage capacity required when constructing storage facilities [35]. |
| Distance to new energy base | Feasibility study on the complementary operation of PSPSs and a clean energy base [36]. |
| Optimize the power supply structure | The ability of PSPSs to improve the electricity supply structure. Quantified as the percentage reduction in fossil-fuel-based generation capacity displaced by PSPS-flexible renewable integration over a 5-year horizon [30]. |
| Power reliability and stability | This is usually measured by two sub-indicators: the System Average Interruption Frequency Index (SAIFI, occurrences/year) and the Voltage Deviation Rate (%) from nominal levels during peak loads [14]. |
| New energy efficiency | The ratio (%) of actual electricity output to maximum theoretical output when integrating renewable energy sources, calculated as . |
| Distance from substation | If there is a substation near the project site, it can reduce unnecessary power loss along the transmission line, and good power transmission conditions can greatly reduce the cost of embedded cables [34]. |
| Annual emission reduction effect | The power station can reduce pollutant emissions within a year by complementing clean energy [37]. |
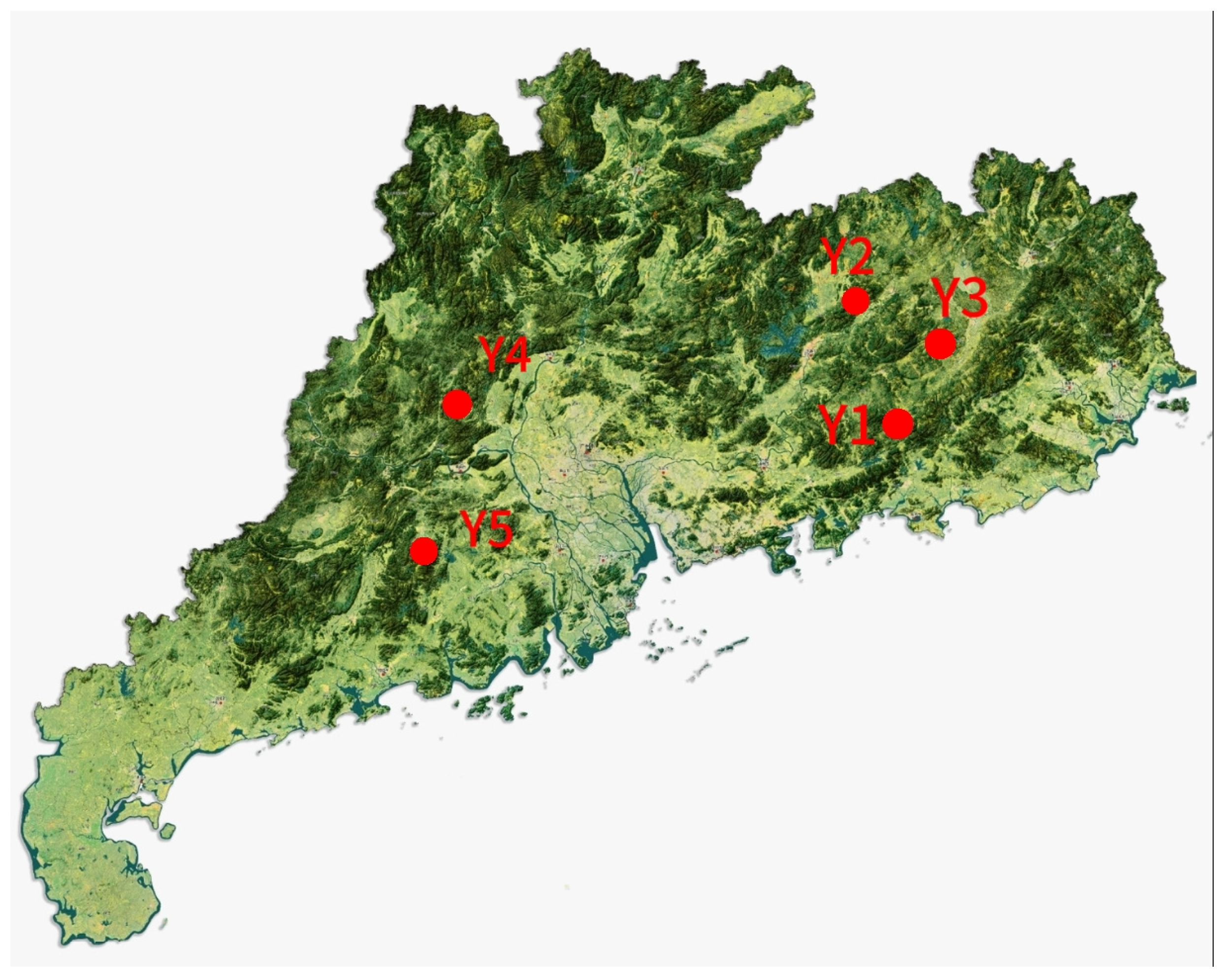
| Site Name | Location | Brief Introduction |
|---|---|---|
| Zhongdong | Huidong County, Huizhou City | The water source of Zhongdong PSPS in Huizhou is sufficient and the average water head is large, and the proximity to the new energy power station is conducive to the power transmission of the power station. |
| Centian | Dongyuan County, Heyuan City | Centian PSPS lower reservoir has a large drainage area and belongs to a large-scale PSPS. The area where the power station is located belongs to the coverage area of the Guangdong power grid, which can be continuously full for 7 h. |
| Meixu Phase II | Wuhua County, Meizhou City | The basin area of the lower reservoir of the second phase of Meixu Phase II PSPS is also very large, but the static investment is smaller than that of Centian Power Station, and the economic advantage is large. |
| Langjiang | Guangning County, Zhaoqing City | Langjiang PSPS is located in the Huanglian Mountain range, the terrain between the upper and lower reservoirs is different, and the rainfall is greater in the south. |
| Shuiyuan Mountain | Xinxing County, Yunfu City | The water supply of Shuiyuan Mountain PSPS is sufficient and the distance from the city is close, which is conducive to improving the transmission efficiency. However, the ecological red line is involved in the region, which is not advantageous in investment. |
| Evaluation Index | ||
|---|---|---|
| C11 | 2 | 0.0016 |
| C12 | 1.0552 | 0.1512 |
| C13 | 2 | 0.0190 |
| C14 | 1 | 0.0031 |
| C15 | 2 | 0.0031 |
| C21 | 1.9931 | 0.0758 |
| C22 | \ | 0.2154 |
| C23 | 1.3508 | 0.1519 |
| C24 | 1.5228 | 0.0125 |
| C25 | 1 | 0.0190 |
| C31 | 1 | 0.0031 |
| C32 | 1 | 0.0031 |
| C33 | 2 | 0.0062 |
| C34 | 2 | 0.0379 |
| C35 | 1 | 0.0379 |
| C41 | 1 | 0.0758 |
| C42 | 1 | 0.0012 |
| C43 | 1.3516 | 0.0012 |
| C44 | 1 | 0.0016 |
| C45 | 1 | 0.1595 |
| C46 | 1 | 0.0125 |
| Risk Probability | Option | C11 | C12 | C13 | C14 | C15 |
|---|---|---|---|---|---|---|
| P1 = 0.3 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 | ||||||
| P2 = 0.5 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 | ||||||
| P3 = 0.2 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 |
| Risk Probability | Option | C11 | C12 | C13 | C14 | C15 |
|---|---|---|---|---|---|---|
| P1 = 0.3 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 | ||||||
| P2 = 0.5 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 | ||||||
| P3 = 0.2 | Y1 | |||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 | ||||||
| Y5 |
| Status | Option | C11 | C12 | C13 | C14 | C15 |
|---|---|---|---|---|---|---|
| P1 | Y1 | 0.1944 | 0.0000 | 0.0000 | −0.6363 | 0.0000 |
| Y2 | 0.2426 | 0.1788 | 0.2828 | 0.0897 | 0.0897 | |
| Y3 | −0.0994 | 0.1788 | 0.2617 | 0.3168 | −0.7405 | |
| Y4 | −0.5887 | −0.2481 | −0.4097 | 0.0813 | −0.1829 | |
| Y5 | 0.0000 | −0.7799 | −0.4810 | −0.4373 | −0.2018 | |
| P2 | Y1 | 0.2138 | 0.0000 | 0.0000 | −0.7799 | 0.0897 |
| Y2 | 0.2358 | 0.1944 | 0.3466 | 0.0000 | 0.0813 | |
| Y3 | 0.0442 | 0.1318 | 0.1944 | 0.2426 | −0.3457 | |
| Y4 | −0.5093 | −0.2966 | −0.5459 | 0.0000 | 0.1788 | |
| Y5 | −0.1829 | −0.7127 | −0.4810 | −0.5459 | −0.0994 | |
| P3 | Y1 | 0.0000 | −0.1829 | 0.0813 | −0.2613 | −0.1829 |
| Y2 | 0.1318 | 0.1103 | 0.1318 | −0.1829 | −0.2613 | |
| Y3 | 0.1537 | 0.1821 | −0.2018 | 0.1537 | −0.1829 | |
| Y4 | −0.2481 | 0.0000 | 0.0897 | −0.1829 | 0.1537 | |
| Y5 | −0.2481 | −0.2966 | −0.1829 | 0.0442 | 0.0442 |
| Y1 | Y2 | Y3 | Y4 | Y5 | |
|---|---|---|---|---|---|
| C11 | 0.1944 | 0.2426 | −0.0994 | −0.5887 | 0.0000 |
| C12 | 0.0000 | 0.1788 | 0.1788 | −0.2481 | −0.7799 |
| C13 | 0.0000 | 0.2828 | 0.2617 | −0.4097 | −0.4810 |
| C14 | −0.6363 | 0.0897 | 0.3168 | 0.0813 | −0.4373 |
| C15 | 0.0000 | 0.0897 | −0.7405 | −0.1829 | −0.2018 |
| C21 | −0.4810 | 0.2138 | −0.6363 | 0.1318 | 0.0000 |
| C22 | 0.3168 | −0.2613 | −0.4024 | 0.0000 | 0.2617 |
| C23 | −0.6363 | 0.0813 | 0.1318 | 0.0000 | −0.7127 |
| C24 | −0.1829 | −0.5459 | 0.1162 | 0.0000 | 0.1788 |
| C25 | 0.0000 | 0.2138 | 0.0813 | −1.0046 | −0.8632 |
| C31 | −0.5459 | −0.6363 | 0.2987 | 0.0000 | 0.1788 |
| C32 | 0.0000 | −0.9273 | 0.2426 | −0.2966 | 0.1537 |
| C33 | 0.0000 | −0.8770 | −0.5842 | 0.1650 | 0.3168 |
| C34 | 0.2828 | −0.1829 | 0.4177 | −0.4810 | 0.0000 |
| C35 | 0.2596 | −0.2481 | 0.2828 | −0.3457 | −0.2481 |
| C41 | 0.1788 | 0.0000 | 0.0813 | −0.8632 | −0.6363 |
| C42 | 0.1318 | 0.0000 | 0.0897 | −0.6682 | −0.4024 |
| C43 | 0.1103 | 0.0000 | −0.6363 | −0.3714 | 0.0442 |
| C44 | 0.4546 | 0.0813 | 0.0813 | −0.1829 | −0.2481 |
| C45 | −0.1829 | 0.2264 | −0.4024 | 0.0000 | 0.0813 |
| C46 | 0.3836 | −0.4810 | 0.0000 | 0.1103 | −0.2481 |
| Y1 | Y2 | Y3 | Y4 | Y5 | |
|---|---|---|---|---|---|
| 0.3448 | 0.2644 | 0.5318 | 0.4857 | 0.5504 | |
| 0.1310 | 0.0929 | 0.2154 | 0.1319 | 0.1595 | |
| 0.2960 | 0.0000 | 0.9675 | 0.5462 | 0.7718 | |
| Rank | 2 | 1 | 5 | 3 | 4 |
| Q1 | Q2 | Q3 | Q4 | Q5 | Rank | |
|---|---|---|---|---|---|---|
| 0 | 0.3108 | 0.0000 | 1.0000 | 0.3185 | 0.5435 | 21453 |
| 0.1 | 0.3079 | 0.0000 | 0.9935 | 0.3640 | 0.5892 | 21453 |
| 0.2 | 0.3049 | 0.0000 | 0.9870 | 0.4096 | 0.6348 | 21453 |
| 0.3 | 0.3019 | 0.0000 | 0.9805 | 0.4551 | 0.6805 | 21453 |
| 0.4 | 0.2990 | 0.0000 | 0.9740 | 0.5006 | 0.7261 | 21453 |
| 0.5 | 0.2960 | 0.0000 | 0.9675 | 0.5462 | 0.7718 | 21453 |
| 0.6 | 0.2930 | 0.0000 | 0.9610 | 0.5917 | 0.8174 | 21453 |
| 0.7 | 0.2901 | 0.0000 | 0.9545 | 0.6373 | 0.8631 | 21453 |
| 0.8 | 0.2871 | 0.0000 | 0.9480 | 0.6828 | 0.9087 | 21453 |
| 0.9 | 0.2841 | 0.0000 | 0.9415 | 0.7284 | 0.9544 | 21435 |
| 1 | 0.2812 | 0.0000 | 0.9350 | 0.7739 | 1.0000 | 21435 |
| Rank | |
|---|---|
| 0 | Y2 > Y1 > Y4 > Y3 > Y5 |
| 0.25 | Y2 > Y1 > Y4 > Y3 > Y5 (When = 0.25, Y3/Y5 reverses.) |
| 0.5 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.75 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 1 | Y2 > Y1 > Y4 > Y5 > Y3 |
| Value | Y1 | Y2 | Y3 | Y4 | Y5 | Rank |
|---|---|---|---|---|---|---|
| 1.0 | 0.322 | 0.000 | 0.970 | 0.510 | 0.740 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 1.500 | 0.310 | 0.000 | 0.987 | 0.455 | 0.589 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 2.0 | 0.298 | 0.000 | 0.961 | 0.592 | 0.817 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 2.25 | 0.296 | 0.000 | 0.967 | 0.546 | 0.772 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 2.5 | 0.284 | 0.000 | 0.948 | 0.729 | 0.909 | Y2 > Y1 > Y4 > Y3 > Y5 |
| 3.0 | 0.281 | 0.000 | 0.935 | 0.774 | 0.974 | Y2 > Y1 > Y4 > Y3 > Y5 |
| Y1 | Y2 | Y3 | Y4 | Y5 | Rank | |
|---|---|---|---|---|---|---|
| 0.50 | 0.298 | 0.000 | 0.967 | 0.546 | 0.772 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.60 | 0.296 | 0.000 | 0.962 | 0.550 | 0.768 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.70 | 0.293 | 0.000 | 0.958 | 0.563 | 0.763 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.80 | 0.291 | 0.000 | 0.954 | 0.575 | 0.758 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.88 | 0.296 | 0.000 | 0.967 | 0.546 | 0.772 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.90 | 0.289 | 0.000 | 0.950 | 0.585 | 0.750 | Y2 > Y1 > Y4 > Y5 > Y3 |
| Y1 | Y2 | Y3 | Y4 | Y5 | Rank | |
| 0.50 | 0.296 | 0.000 | 0.967 | 0.546 | 0.772 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.60 | 0.294 | 0.000 | 0.969 | 0.541 | 0.776 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.70 | 0.291 | 0.000 | 0.965 | 0.538 | 0.781 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.80 | 0.289 | 0.000 | 0.963 | 0.535 | 0.786 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.88 | 0.296 | 0.000 | 0.967 | 0.546 | 0.772 | Y2 > Y1 > Y4 > Y5 > Y3 |
| 0.90 | 0.288 | 0.000 | 0.961 | 0.531 | 0.790 | Y2 > Y1 > Y4 > Y5 > Y3 |
| Y1 | Y2 | Y3 | Y4 | Y5 | |
|---|---|---|---|---|---|
| The method used in this article | 0.2960 | 0.0000 | 0.9675 | 0.5462 | 0.7718 |
| Rank | 2 | 1 | 5 | 3 | 4 |
| VIKOR method | 0.2393 | 0.0000 | 0.7143 | 0.6287 | 0.6904 |
| Rank | 2 | 1 | 5 | 3 | 4 |
| GRA-TOPSIS decision | 0.6097 | 0.6542 | 0.4763 | 0.5223 | 0.4917 |
| Rank | 2 | 1 | 5 | 3 | 4 |
| Prospect theory improves TOPSIS method | 0.5932 | 0.6310 | 0.4663 | 0.5271 | 0.5049 |
| Rank | 2 | 1 | 5 | 3 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Xu, Y. Site Selection Evaluation of Pumped Storage Power Station Based on Multi-Energy Complementary Perspective: A Case Study in China. Energies 2025, 18, 3549. https://doi.org/10.3390/en18133549
Zhao H, Xu Y. Site Selection Evaluation of Pumped Storage Power Station Based on Multi-Energy Complementary Perspective: A Case Study in China. Energies. 2025; 18(13):3549. https://doi.org/10.3390/en18133549
Chicago/Turabian StyleZhao, Hui, and Yanqi Xu. 2025. "Site Selection Evaluation of Pumped Storage Power Station Based on Multi-Energy Complementary Perspective: A Case Study in China" Energies 18, no. 13: 3549. https://doi.org/10.3390/en18133549
APA StyleZhao, H., & Xu, Y. (2025). Site Selection Evaluation of Pumped Storage Power Station Based on Multi-Energy Complementary Perspective: A Case Study in China. Energies, 18(13), 3549. https://doi.org/10.3390/en18133549






