Validation of PCHE-Type CO2–CO2 Recuperative Heat Exchanger Modeling Using Conductance Ratio Method
Abstract
1. Introduction

2. Methodology
- The experiments were performed using two different PCHEs (sCO2 recuperators), one with a zigzag configuration and one with s-shaped fins.
- By comparing the experimental results with the results from a conventional heat-exchanger model, three traditional and three zigzag PCHE specific heat-transfer correlations were reviewed.
- By comparing the experimental results with those of the conductance ratio method, different approaches to find the characteristic parameter, i.e., the conductance ratio, were evaluated.
- The versatility of this method was then tested by applying the best-suited heat-transfer correlation to the conductance ratio method.
2.1. Experimental Methodology
2.1.1. sCO2 Test Facility
2.1.2. sCO2 Recuperator
2.1.3. Experimental Campaign
- The mass flow is the same for both sides.
- The cold-side inlet temperature results from the liquid condition before the pump (condition 1 in Figure 3).
- The cold-side pressure is limited by the achievable pressure drop at the expansion valve, which is dependent on valve inlet conditions (condition 4 in Figure 3).
- The hot-side pressure is a function of the temperature of the low-pressure part (condition 7 in Figure 3) and was not varied considerably in this study. The limited range of hot-side pressure narrows the impact on the heat transfer.
2.1.4. Data Reduction
2.2. Conventional Heat-Exchanger Modeling
2.3. Conductance Ratio Method for Off-Design Calculation
- A reference case: Temperatures, pressures, and mass flow rates at the inlets and outlets of both sides of the heat exchanger.
- Option: Use supplier information (the design case of the heat exchanger);
- Option: Use operational data (pick a data set most likely to be representative for the off-design cases you want to calculate);
- Option: Define the conditions (which means designing a “virtual” heat exchanger).
- The characteristic parameter : The conductance ratio is a single value characteristic for the heat-transfer ratio between the hot and cold side.
- Option: Use from literature (Pick this option if you do not have the area available. Choose the ratio of a similar type heat exchanger).
- Option: Use supplier data. (Often, suppliers state the overall heat-transfer conductance of the hot and cold side and . With Equation (12), one derives the conductance ratio).
- Option: Use a different heat-exchanger model to calculate that uses the heat-exchange area and results in heat transfer on both sides for a reference case.
- Option: Use operational data sets. (Fit to the available data set of off-design cases via the conductance ratio method. Use this then to calculate more off-design cases).
- The calculation parameter—number of nodes : For discretization of the heat exchanger.
- Choose according to your requirements regarding accuracy and calculation time.
- Choose so that properties change not significantly between nodes.
2.4. Values for Comparison
3. Results and Discussion
3.1. Overall Results
3.2. Conventional Modeling for Zigzag PCHE
3.3. Conductance Ratio Method for Zigzag PCHE
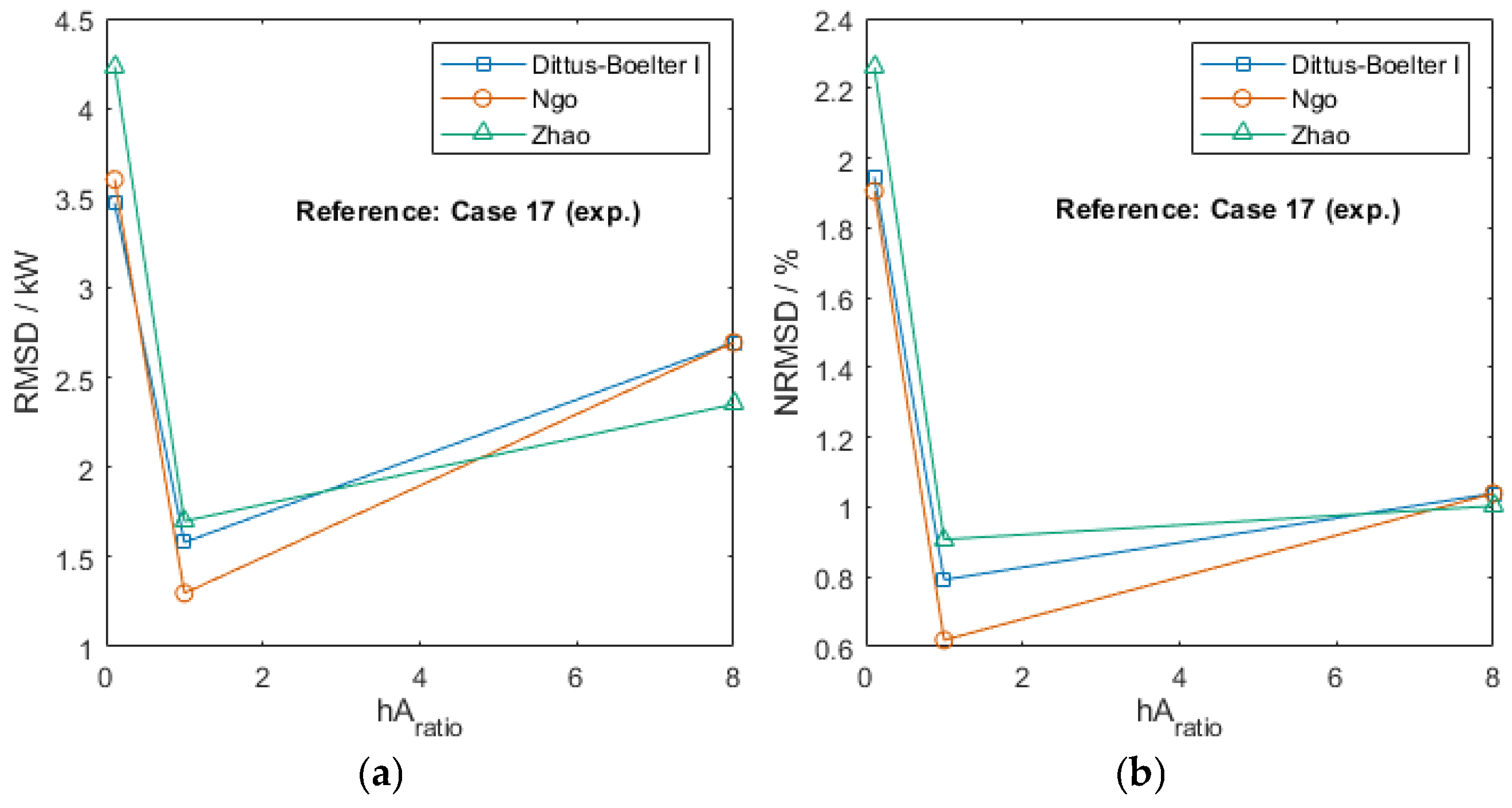
3.4. Conductance Ratio Method for S-Shaped Fin PCHE
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| NRMSD | Normalized Root-Mean-Square Deviation |
| PCHE | Printed-Circuit Heat Exchanger |
| RMSD | Root-Mean-Square Deviation |
| sCO2 | Supercritical Carbon Dioxide |
| area, m2 | |
| constants in general structure of heat-transfer power-law correlation, - | |
| specific heat at constant pressure, J/kgK | |
| specific heat averaged over the cross-section of the channel, J/kgK | |
| inner diameter, m | |
| hydraulic diameter, m | |
| modified hydraulic diameter, m | |
| friction factor, m | |
| enthalpy, J/kgK | |
| conductance ratio, - | |
| thermal conductance, W/K | |
| thermal conductivity, W/mK | |
| heated length, m | |
| linear pitch (of the mini channel), m | |
| exponents in general structure of heat-transfer power-law correlation, - | |
| mass flow, kg/s | |
| p | pressure, Pa |
| perimeter, m | |
| transferred heat, W | |
| thermal resistance, K/W | |
| temperature, K | |
| heat transfer conductance, W/K | |
| bend angle (of the mini channel), - | |
| difference operator, - | |
| dynamic viscosity, Pas | |
| density, kg/m3 |
| Nu | Nusselt number, - |
| Pr | Prandtl number, - |
| Re | Reynolds number, - |
| x | indicating position where properties are evaluated, e.g., bulk |
| b | bulk |
| C | cold (side of the heat exchanger) |
| f | film |
| H | hot (side of the heat exchanger) |
| i | inner |
| in | inlet |
| m | mean value in a section between calculation nodes |
| off | off-design |
| out | outlet |
| pc | pseudocritical |
| ref | reference (case) |
| T, t | indicating which temperatures are used in correlations |
| w | wall |
Appendix A. Reference Case Parameters for Input to Conductance Ratio Method
| Parameter | Zigzag Channel PCHE Design case | Zigzag Channel PCHE Case 33 | S-Shaped Fin PCHE Case 17 |
|---|---|---|---|
| /kg/s | 0.6 | 0.55 | 0.6 |
| /°C | 621.7 | 386.3 | 578.5 |
| /°C | 143.0 | 67.5 | 75.9 |
| /°C | 25.9 | 13.4 | 19.6 |
| /°C | 358.0 | 160.1 | 363.2 |
| /bar | 65.0 | 62.5 | 61.7 |
| /bar | 64.0 | 61.4 | 61.1 |
| /bar | 215.0 | 90.6 | 146.6 |
| /bar | 214.8 | 90.3 | 146.1 |
Appendix B. Results for Recalculated Data Sets
| Recalculated Set: Conventional Model, Zigzag PCHE | RMSD/kW | NRMSD/% |
|---|---|---|
| Meshram VI | 58.5 | 32.9 |
| Meshram V | 143.6 | 75.0 |
| Dittus–Boelter I | 34.5 | 20.6 |
| Gnielinski | 42.1 | 24.5 |
| Kim | 80.5 | 38.9 |
| Saeed–Kim | 202.0 | 106.9 |
| Cheng | 173.5 | 96.8 |
| Recalculated Set: CR Method, S-Shaped Fin PCHE | RMSD/kW | NRMSD/% |
|---|---|---|
| Dittus–Boelter I, hAratio = 1/9 | 3.5 | 1.9 |
| Dittus–Boelter I, hAratio = 1 | 1.6 | 0.8 |
| Dittus–Boelter I, hAratio = 8 | 2.7 | 1.0 |
| Ngo, hAratio = 1/9 | 3.6 | 1.9 |
| Ngo, hAratio = 1 | 1.3 | 0.6 |
| Ngo, hAratio = 8 | 2.7 | 1.0 |
| Zhao, hAratio = 1/9 | 4.2 | 2.3 |
| Zhao, hAratio = 1 | 1.7 | 0.9 |
| Zhao, hAratio = 8 | 2.4 | 1.0 |
| Recalculated Set: CR Method, Zigzag PCHE, Case 33 | RMSD/kW | NRMSD/% |
|---|---|---|
| Dittus–Boelter I, hAratio = 1/9 | 7.1 | 5.0 |
| Dittus–Boelter I, hAratio = 0.875 | 8.2 | 4.8 |
| Dittus–Boelter I, hAratio = 1.1 | 8.4 | 4.7 |
| Dittus–Boelter I, hAratio = 8 | 9.5 | 4.3 |
| Meshram V, hAratio = 1/9 | 7.1 | 4.6 |
| Meshram V, hAratio = 0.875 | 9.8 | 5.0 |
| Meshram V, hAratio = 1.1 | 10.1 | 5.0 |
| Meshram V, hAratio = 8 | 11.6 | 4.8 |
| Kim, hAratio = 1/9 | 7.2 | 5.4 |
| Kim, hAratio = 0.875 | 7.2 | 5.2 |
| Kim, hAratio = 1.1 | 7.2 | 5.2 |
| Kim, hAratio = 8 | 7.3 | 4.9 |
| Saeed–Kim, hAratio = 1/9 | 7.5 | 4.4 |
| Saeed–Kim, hAratio = 0.875 | 11.5 | 5.2 |
| Saeed–Kim, hAratio = 1.1 | 11.9 | 5.2 |
| Saeed–Kim, hAratio = 8 | 13.7 | 5.2 |
| Cheng, hAratio = 1/9 | 7.3 | 5.4 |
| Cheng, hAratio = 0.875 | 7.1 | 5.0 |
| Cheng, hAratio = 1.1 | 7.1 | 4.9 |
| Cheng, hAratio = 8 | 7.2 | 4.5 |
| Recalculated Set: CR Method, Zigzag PCHE, Design Case | RMSD/kW | NRMSD/% |
|---|---|---|
| Dittus–Boelter I, hAratio = 1/9 | 9.8 | 6.5 |
| Dittus–Boelter I, hAratio = 0.875 | 5.8 | 3.7 |
| Dittus–Boelter I, hAratio = 1.1 | 5.4 | 3.3 |
| Dittus–Boelter I, hAratio = 8 | 6.0 | 3.1 |
| Meshram V, hAratio = 1/9 | 7.3 | 4.8 |
| Meshram V, hAratio = 0.5 | 5.0 | 3.1 |
| Meshram V, hAratio = 0.875 | 4.9 | 2.7 |
| Meshram V, hAratio = 1.1 | 5.2 | 2.7 |
| Meshram V, hAratio = 2 | 6.6 | 3.4 |
| Meshram V, hAratio = 4 | 8.3 | 4.4 |
| Meshram V, hAratio = 6 | 9.1 | 4.9 |
| Meshram V, hAratio = 8 | 9.6 | 5.2 |
| Kim, hAratio = 1/9 | 11.6 | 7.8 |
| Kim, hAratio = 0.875 | 9.2 | 6.3 |
| Kim, hAratio = 1.1 | 8.8 | 6.0 |
| Kim, hAratio = 8 | 6.7 | 4.6 |
| Saeed–Kim, hAratio = 1/9 | 6.5 | 4.0 |
| Saeed–Kim, hAratio = 0.875 | 5.7 | 2.9 |
| Saeed–Kim, hAratio = 1.1 | 6.4 | 3.3 |
| Saeed–Kim, hAratio = 8 | 12.5 | 7.1 |
| Cheng, hAratio = 1/9 | 11.9 | 7.9 |
| Cheng, hAratio = 0.875 | 9.3 | 6.2 |
| Cheng, hAratio = 1.1 | 8.9 | 5.9 |
| Cheng, hAratio = 8 | 6.6 | 4.1 |
References
- Crespi, F.; Gavagnin, G.; Sánchez, D.; Martínez, G.S. Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy 2017, 195, 152–183. [Google Scholar] [CrossRef]
- Huang, C.; Cai, W.; Wang, Y.; Liu, Y.; Li, Q.; Li, B. Review on the characteristics of flow and heat transfer in printed circuit heat exchangers. Appl. Therm. Eng. 2019, 153, 190–205. [Google Scholar] [CrossRef]
- Chai, L.; Tassou, S.A. A review of printed circuit heat exchangers for helium and supercritical CO2 Brayton cycles. Therm. Sci. Eng. Prog. 2020, 18, 100543. [Google Scholar] [CrossRef]
- Crespi, F.; Sánchez, D.; Hoopes, K.; Choi, B.; Kuek, N. The Conductance Ratio Method for Off-Design Heat Exchanger Modeling and its Impact on an sCO2 Recompression Cycle. In Volume 9: Oil and Gas Applications; Supercritical CO2 Power Cycles; Wind Energy; American Society of Mechanical Engineers: Charlotte, NC, USA, 2017. [Google Scholar] [CrossRef]
- Kwon, J.S.; Bae, S.J.; Heo, J.Y.; Lee, J.I. Development of accelerated PCHE off-design performance model for optimizing power system operation strategies in S-CO2 Brayton cycle. Appl. Therm. Eng. 2019, 159, 113845. [Google Scholar] [CrossRef]
- Neises, T. Steady-state off-design modeling of the supercritical carbon dioxide recompression cycle for concentrating solar power applications with two-tank sensible-heat storage. Sol. Energy 2020, 212, 19–33. [Google Scholar] [CrossRef]
- Alfani, D.; Binotti, M.; Macchi, E.; Silva, P.; Astolfi, M. sCO2 power plants for waste heat recovery: Design optimization and part-load operation strategies. Appl. Therm. Eng. 2021, 195, 117013. [Google Scholar] [CrossRef]
- Xie, L.; Zhuang, D.; Li, Z.; Ding, G. Technical Characteristics and Development Trend of Printed Circuit Heat Exchanger Applied in Floating Liquefied Natural Gas. Front. Energy Res. 2022, 10, 885607. [Google Scholar] [CrossRef]
- Cabeza, L.F.; De Gracia, A.; Fernández, A.I.; Farid, M.M. Supercritical CO2 as heat transfer fluid: A review. Appl. Therm. Eng. 2017, 125, 799–810. [Google Scholar] [CrossRef]
- Duffey, R.B.; Pioro, I.L. Experimental heat transfer of supercritical carbon dioxide flowing inside channels (survey). Nucl. Eng. Des. 2005, 235, 913–924. [Google Scholar] [CrossRef]
- Ehsan, M.M.; Guan, Z.; Klimenko, A.Y. A comprehensive review on heat transfer and pressure drop characteristics and correlations with supercritical CO2 under heating and cooling applications. Renew. Sustain. Energy Rev. 2018, 92, 658–675. [Google Scholar] [CrossRef]
- Pioro, I.L.; Khartabil, H.F.; Duffey, R.B. Heat transfer to supercritical fluids flowing in channels—Empirical correlations (survey). Nucl. Eng. Des. 2004, 230, 69–91. [Google Scholar] [CrossRef]
- Lienhard, J.H.I.; Lienhard, J.H.V. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2020. [Google Scholar]
- McAdams, W.H. Heat Transmission; McGraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1942. [Google Scholar]
- Kruizenga, A.; Anderson, M.; Fatima, R.; Corradini, M.; Towne, A.; Ranjan, D. Heat Transfer of Supercritical Carbon Dioxide in Printed Circuit Heat Exchanger Geometries. J. Therm. Sci. Eng. Appl. 2011, 3, 031002. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Univ. Calif. Publ. Eng. 1930, 2, 443–461. [Google Scholar] [CrossRef]
- Winterton, R.H.S. Where did the Dittus and Boelter equation come from? Int. J. Heat Mass Transf. 1998, 41, 809–810. [Google Scholar] [CrossRef]
- Gnielinski, V. G1: Heat Transfer in Pipe Flow. In VDI Heat Atlas, 2nd ed.; VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin, Germany; London, UK, 2010. [Google Scholar]
- Gnielinski, V. Neue Gleichungen für den Wärme- und den Stoffiübergang in turbulent durchströmten Rohren und Kanälen. Forsch. Ing.-Wes. 1975, 41, 1. [Google Scholar] [CrossRef]
- Ma, Y.; Xie, G.; Hooman, K. Review of printed circuit heat exchangers and its applications in solar thermal energy. Renew. Sustain. Energy Rev. 2022, 155, 111933. [Google Scholar] [CrossRef]
- Li, Q.; Zhan, Q.; Yu, S.; Sun, J.; Cai, W. Study on thermal-hydraulic performance of printed circuit heat exchangers with supercritical methane based on machine learning methods. Energy 2023, 282, 128711. [Google Scholar] [CrossRef]
- Kim, S.G.; Lee, Y.; Ahn, Y.; Lee, J.I. CFD aided approach to design printed circuit heat exchangers for supercritical CO2 Brayton cycle application. Ann. Nucl. Energy 2016, 92, 175–185. [Google Scholar] [CrossRef]
- Meshram, A.; Jaiswal, A.K.; Khivsara, S.D.; Ortega, J.D.; Ho, C.; Bapat, R.; Dutta, P. Modeling and analysis of a printed circuit heat exchanger for supercritical CO2 power cycle applications. Appl. Therm. Eng. 2016, 109, 861–870. [Google Scholar] [CrossRef]
- Hoopes, K.; Sánchez, D.; Crespi, F. A new method for modelling off-design performance of sCO2 heat exchangers without specifying detailed geometry. In Proceedings of the 5th International Symposium—Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016. [Google Scholar]
- Illyés, V.; Thanheiser, S.; Schwarzmayr, P.; David, P.-L.; Guerif, X.; Werner, A.; Haider, M. sCO2 test facility at TU Wien: Design, operation and results. In Proceedings of the 5th European sCO2 Conference for Energy Systems, Prague, Czech Republic, 14–16 March 2023; p. 22. [Google Scholar] [CrossRef]
- Drosg, M. Dealing with Uncertainties: A Guide to Error Analysis; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Baik, S.; Kim, S.G.; Lee, J.; Lee, J.I. Study on CO2—Water printed circuit heat exchanger performance operating under various CO2 phases for S-CO2 power cycle application. Appl. Therm. Eng. 2017, 113, 1536–1546. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Thermal-hydraulic analysis of sinusoidal fin-based printed circuit heat exchangers for supercritical CO2 Brayton cycle. Energy Convers. Manag. 2019, 193, 124–139. [Google Scholar] [CrossRef]
- Cheng, K.; Zhou, J.; Huai, X.; Guo, J. Experimental exergy analysis of a printed circuit heat exchanger for supercritical carbon dioxide Brayton cycles. Appl. Therm. Eng. 2021, 192, 116882. [Google Scholar] [CrossRef]
- Ngo, T.L.; Kato, Y.; Nikitin, K.; Ishizuka, T. Heat transfer and pressure drop correlations of microchannel heat exchangers with S-shaped and zigzag fins for carbon dioxide cycles. Exp. Therm. Fluid Sci. 2007, 32, 560–570. [Google Scholar] [CrossRef]
- Zhao, J.-W.; Zhao, R.; Nian, Y.-L.; Cheng, W.-L. Experimental study of supercritical CO2 in a vertical adaptive flow path heat exchanger. Appl. Therm. Eng. 2021, 188, 116597. [Google Scholar] [CrossRef]
- Arriba, P.R.-D.; Crespi, F. Assessment of part-load operation strategies of supercritical power cycles using carbon dioxide mixtures in CSP plants, including air-cooled condenser optimisation. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Volume 12: Supercritical CO2, Boston, MA, USA, 26–30 June 2023. [Google Scholar]

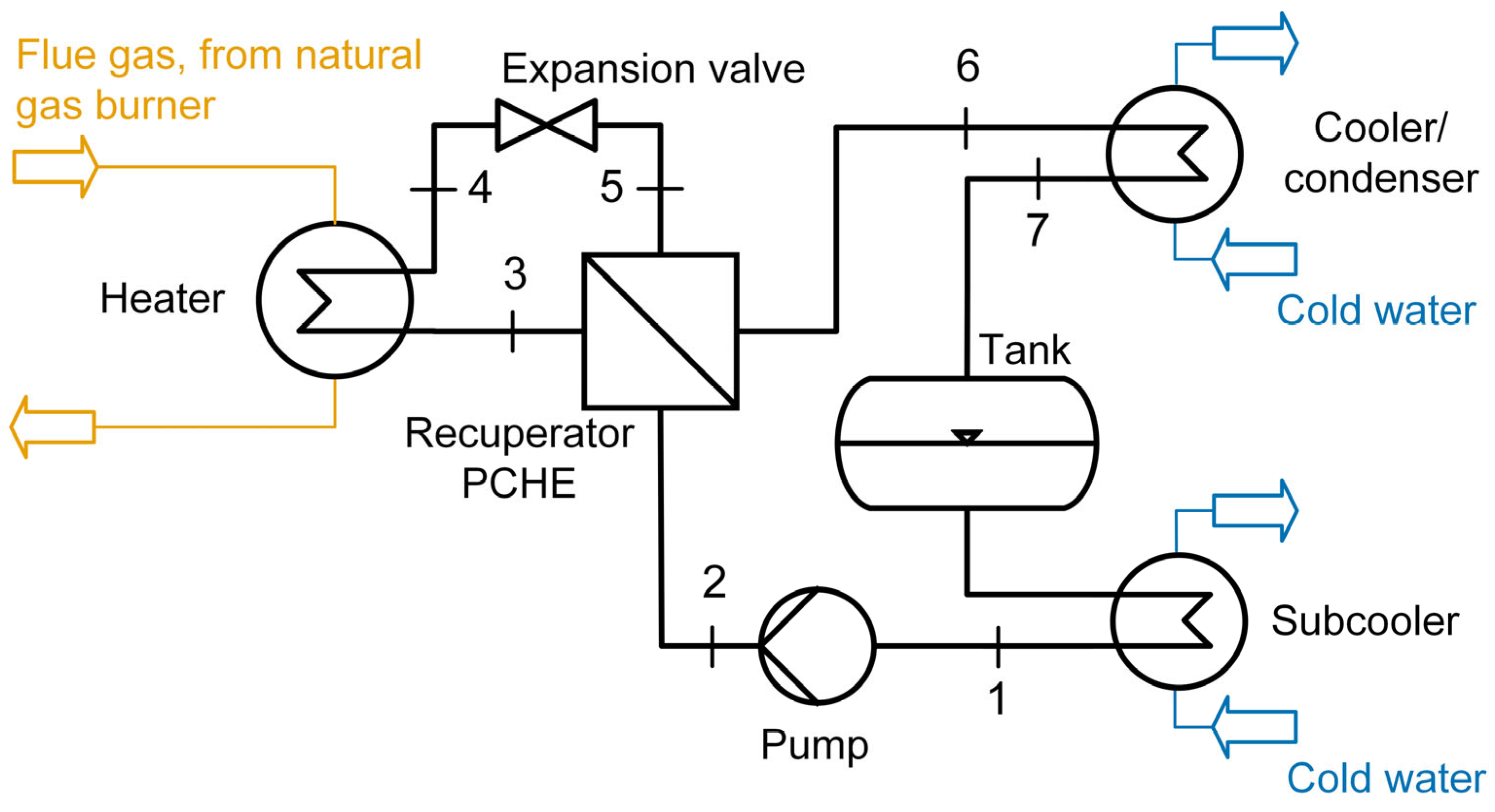

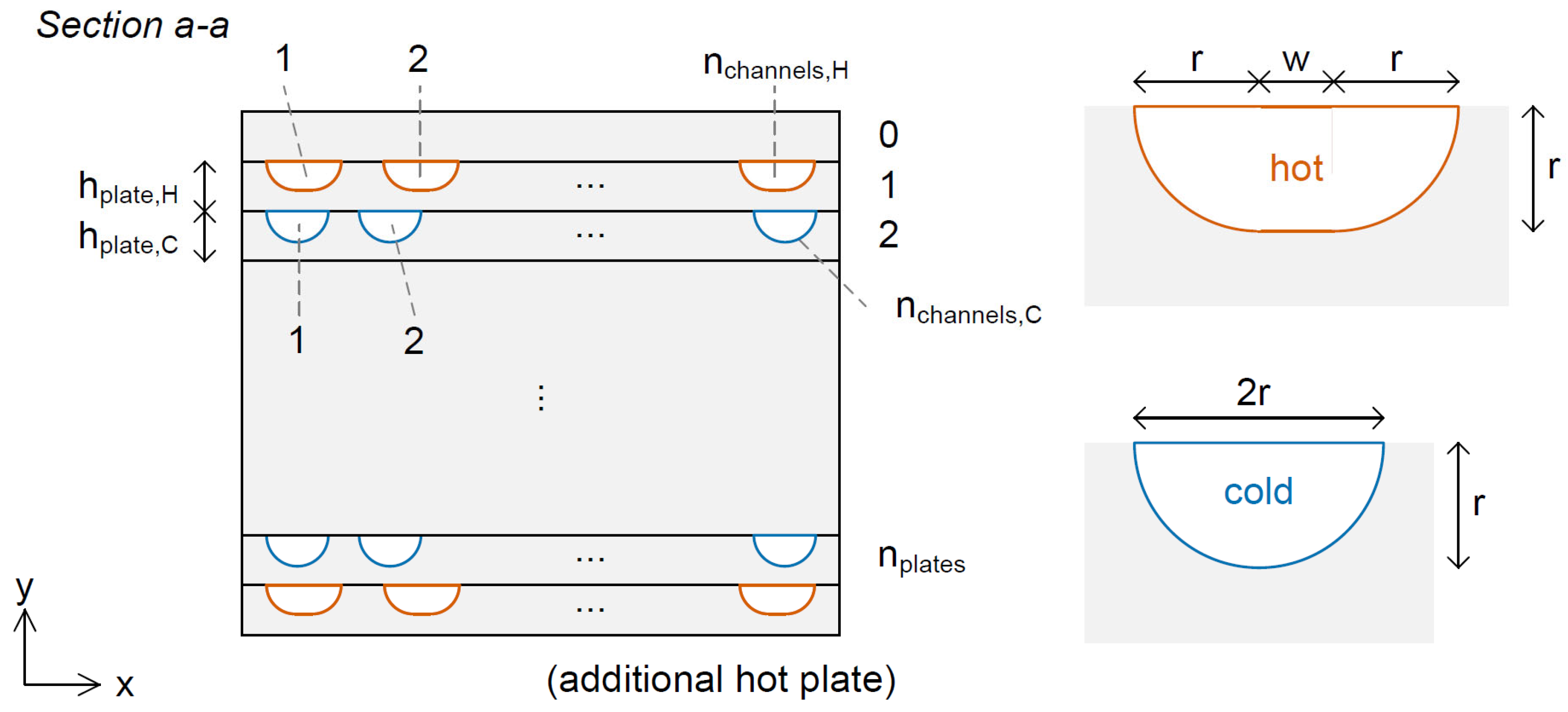


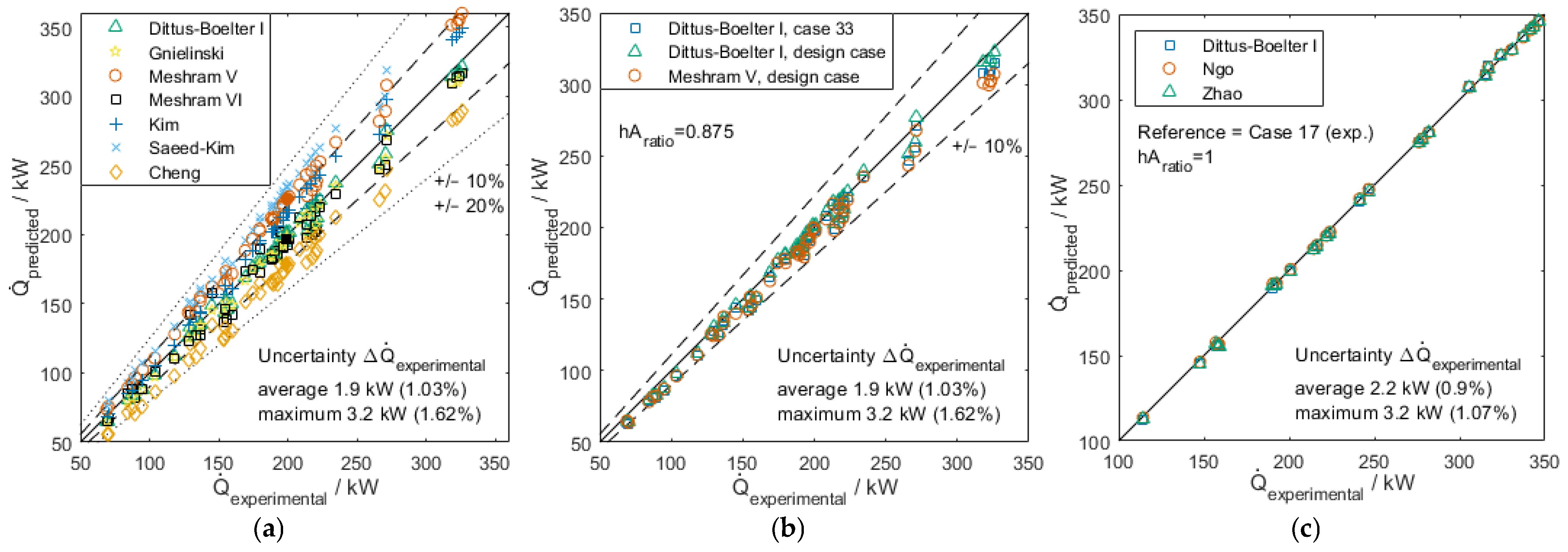

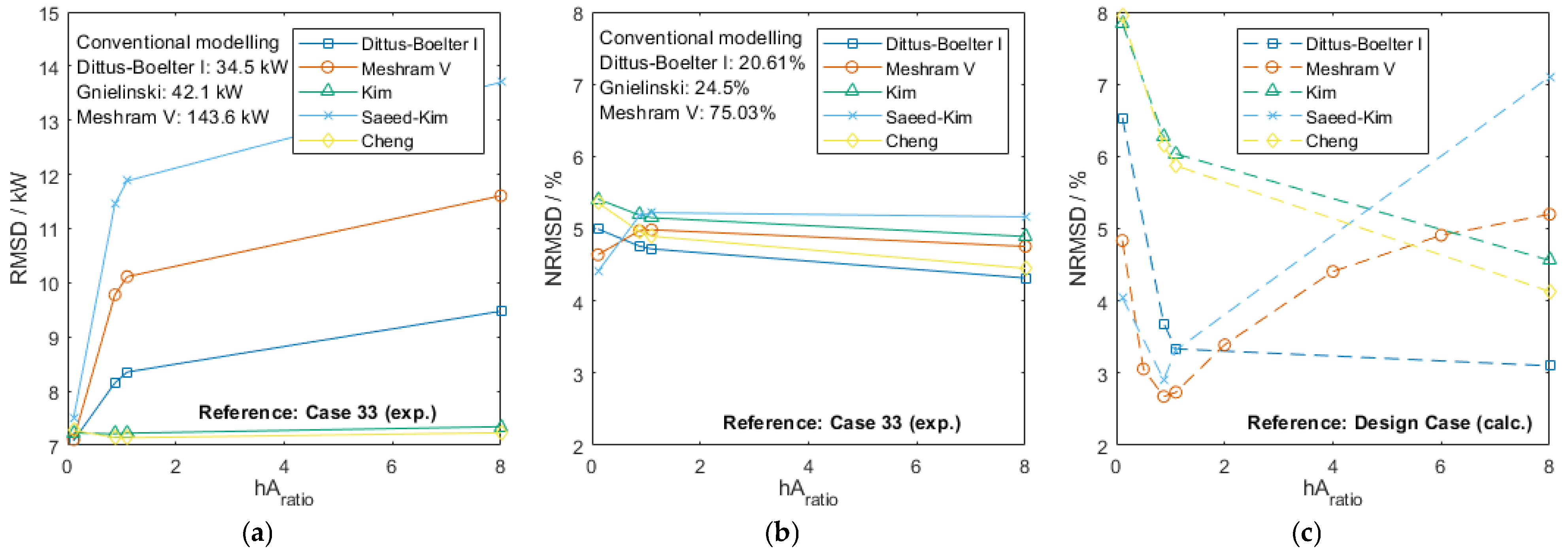

| Type and Location (See Figure 3) | Type |
|---|---|
| FI at 2 | Coriolis sensor from Endress & Hauser, Reinach, Switzerland |
| TI at 2 | Temperature measurement from Coriolis sensor from Endress & Hauser; accuracy ±0.5 ± 0.005 T (°C) |
| TI at 5 | Thermocouple (TE) from TCDirect, Mönchengladbach, Germany, Type J, tolerance class 2 according to DIN EN 60 584-2, with converter to 4–20 mA signal |
| TI at 3, 6 | Resistance thermometer (PT100) from TCDirect; Pt100, 4-wire, class A |
| PI at 2, 3, 5, 6 | Pressure transmitter from ICCP Messtechnik, Wien, Austria, PCE-28 |
| Location | Range Zigzag Channel PCHE | Range S-Shaped Fin PCHE |
|---|---|---|
| (at pos. 2) | 0.26–0.6 kg/s | 0.4–0.6 kg/s |
| (at pos. 5) | 161.9–576.9 °C | 254.1–576.9 °C |
| (at pos. 2) | 11.2–19.6 °C | 12.4–19.6 °C |
| (at pos. 5) | 57.6–65.2 bar | 59.6–61.7 bar |
| (at pos. 2) | 75.1–147.8 bar | 79.4–147.8 bar |
| Number of recorded data points | 53 | 28 |
| ID | Reference | Formulas | Additional Remarks | Channels | Applicability |
|---|---|---|---|---|---|
| I | “Dittus and Boelter” as introduced by McAdams [14] | Evaluated at bulk temperature ; often used (only) for heating (cold side) | Single-phase HT, heating, cooling; non-fluid specific, non-geometry-specific | ||
| II | “Dittus and Boelter” for cooling | Evaluated at bulk temperature ; often used for cooling (hot side) in combination with (I) | Cooling; non-fluid specific, non-geometry-specific | ||
| III | “Dittus and Boelter” for PCHE | Hot side:
Cold side: | Adapted for the conductance ratio method for CO2-CO2 PCHE by Crespi [4] | Mini-channels (geometry not disclosed) | |
| IV | Gnielinski [18] | Evaluated at bulk temperature ; friction factor from Konakov | Smooth, circular macrotube (in-tube) | Single-phase HT, turbulent, 2300 < Re < 106, 0.6 < Pr < 105; non-fluid specific, non-geometry-specific | |
| V | Meshram [23] | Hot side (470 K < Tb < 630 K): Hot side (580 K < Tb < 730 K): Cold side (400 K < Tb < 520 K): Cold side (500 K < Tb < 640 K): | For zigzag-channel PCHEs; developed for CO2-CO2; in this paper: in overlapping temperature ranges (580–630 K; 500–520 K): mean value of both correlations | Semicircular zigzag minichannels D = 2 mm, α = 110°, Lp = 10 mm | Hot: 470 < Tb < 730 K, 5000 < Re < 32,000 Cold: 500 < Tb < 640 K, 5000 < Re < 32,000 |
| VI | Meshram [23] | Hot side: Cold side: | For zigzag-channel PCHEs; developed for CO2-CO2 | Semicircular zigzag minichannels D = 2 mm, 110° < α < 120°, 8 < Lp < 10 mm | Hot: 470 < Tb < 630 K, 5000 < Re < 32,000 Cold: 400 < Tb < 520 K, 5000 < Re < 32,000 |
| VII | Kim [22] | Hot side: Cold side: | For zigzag-channel PCHEs; developed for CO2-CO2 | Semicircular zigzag minichannels; D = 1.9 mm Hot: α = 115°, Lp = 9 mm Cold: α = 100°, Lp = 7.24 mm | 0.7 < Pr < 1 Hot: 2300 < Re < 58,000 Cold: 2300 < Re < 55,000 |
| VIII | Saeed and Kim [28] | For zigzag-channel PCHEs; developed for CO2-CO2 | Semicircular zigzag minichannels; α = 100° | 0.7 < Pr < 1.2 3000 < Re <60,000 | |
| IX | Cheng [29] | Hot side: Cold side: | For zigzag-channel PCHEs; developed for CO2-CO2 | Semicircular zigzag minichannels; α = 115°, D/Lp = 6 | 0.765 < Pr < 0.784 3000 < Re <60,000 |
| X | Ngo [30] | Hot and cold side: | For s-shaped fin-channel PCHEs | Staggered, s-shaped fin minichannels; same geometry for both sides (see Table 1 [30] for specific values) | 3500 < Re < 23,000 0.75 < Pr < 2.2 |
| XI | Zhao [31] | Hot side: Cold side: | For s-shaped fin-channel PCHEs | Intended to be used to calculate overall heat-transfer coefficient; staggered, s-shaped fin minichannels (see Table 1 [31] for specific geometry); cold upward flow, hot downward flow | Hot: 2700 < Re < 7000, 0.9593 < Pr < 1.1184 Cold: 1000 < Re < 2700, 1.6816 < Pr < 1.9917 |
| Input | Zigzag Channel PCHE | S-Shaped Fin PCHE |
|---|---|---|
| Reference case |
|
|
| ||
| Only for Meshram V and reference design case; additionally: {0.5, 2, 4, 6} | ||
| HT correlation | Dittus–Boelter I, Gnielinski, Meshram V, Meshram VI, Kim, Saeed-Kim, Cheng | Dittus–Boelter I, Ngo, Zhao |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Illyés, V.C.; Crespi, F.; Guerif, X.; Werner, A. Validation of PCHE-Type CO2–CO2 Recuperative Heat Exchanger Modeling Using Conductance Ratio Method. Energies 2025, 18, 3547. https://doi.org/10.3390/en18133547
Illyés VC, Crespi F, Guerif X, Werner A. Validation of PCHE-Type CO2–CO2 Recuperative Heat Exchanger Modeling Using Conductance Ratio Method. Energies. 2025; 18(13):3547. https://doi.org/10.3390/en18133547
Chicago/Turabian StyleIllyés, Viktoria Carmen, Francesco Crespi, Xavier Guerif, and Andreas Werner. 2025. "Validation of PCHE-Type CO2–CO2 Recuperative Heat Exchanger Modeling Using Conductance Ratio Method" Energies 18, no. 13: 3547. https://doi.org/10.3390/en18133547
APA StyleIllyés, V. C., Crespi, F., Guerif, X., & Werner, A. (2025). Validation of PCHE-Type CO2–CO2 Recuperative Heat Exchanger Modeling Using Conductance Ratio Method. Energies, 18(13), 3547. https://doi.org/10.3390/en18133547








