Recent Advancements in Understanding Hot Carrier Dynamics in Perovskite Solar Cells
Abstract
1. Introduction
2. Unique Properties of Metal Halide Perovskite
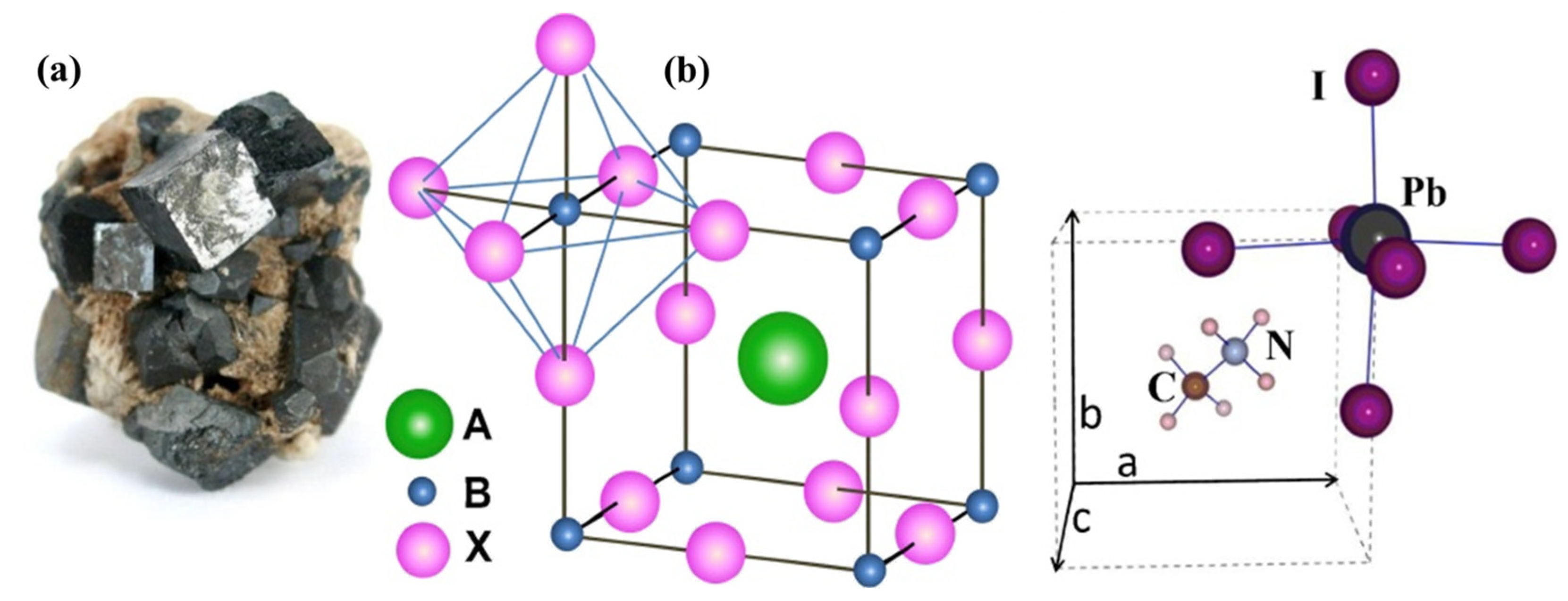
2.1. Perovskite Crystal Structure
2.2. Perovskite Electronic Structure
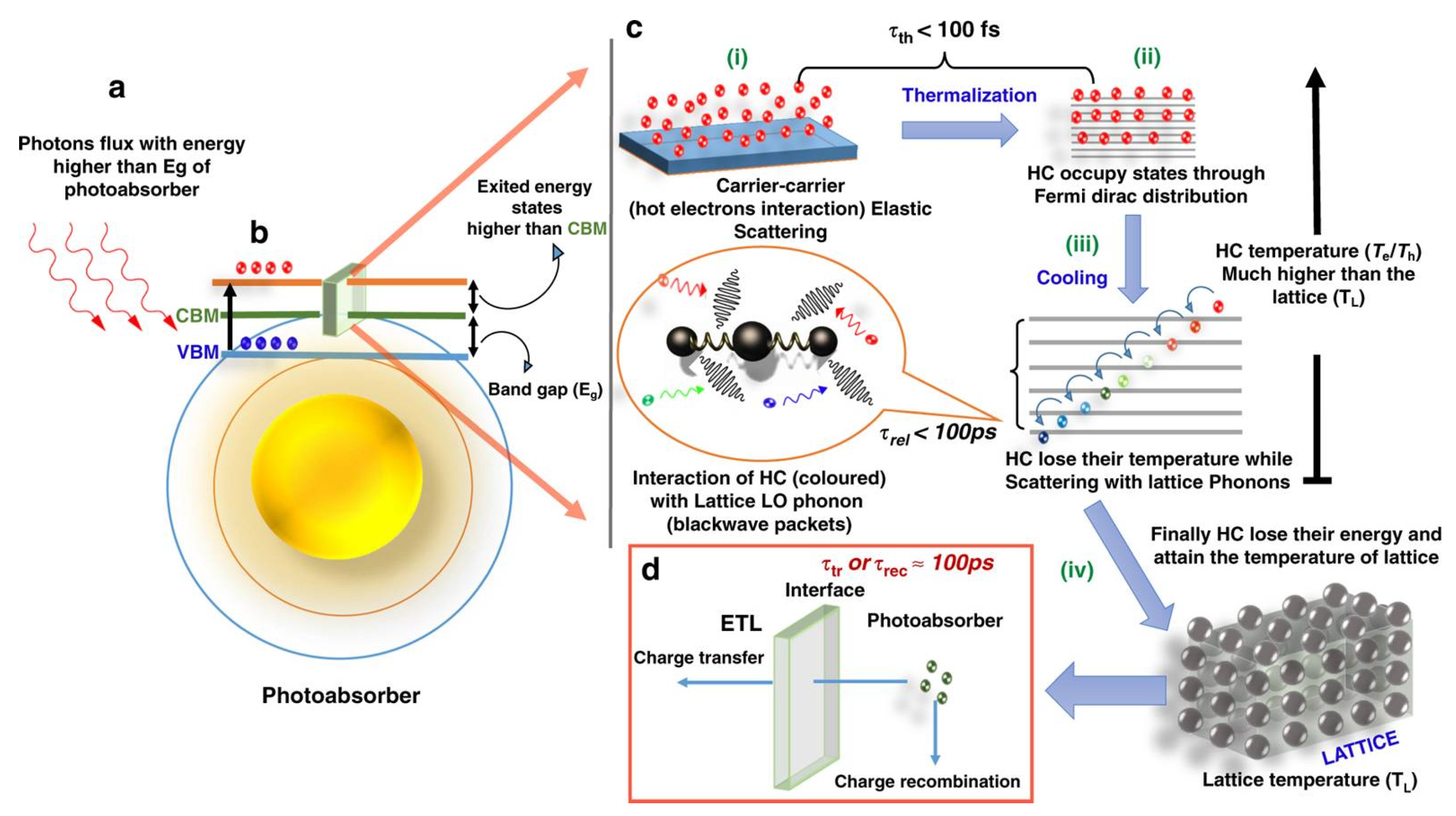
2.3. Carrier Excitation
2.4. Exciton Binding Energy of Perovskite
2.5. Phonon Coupling in Perovskite
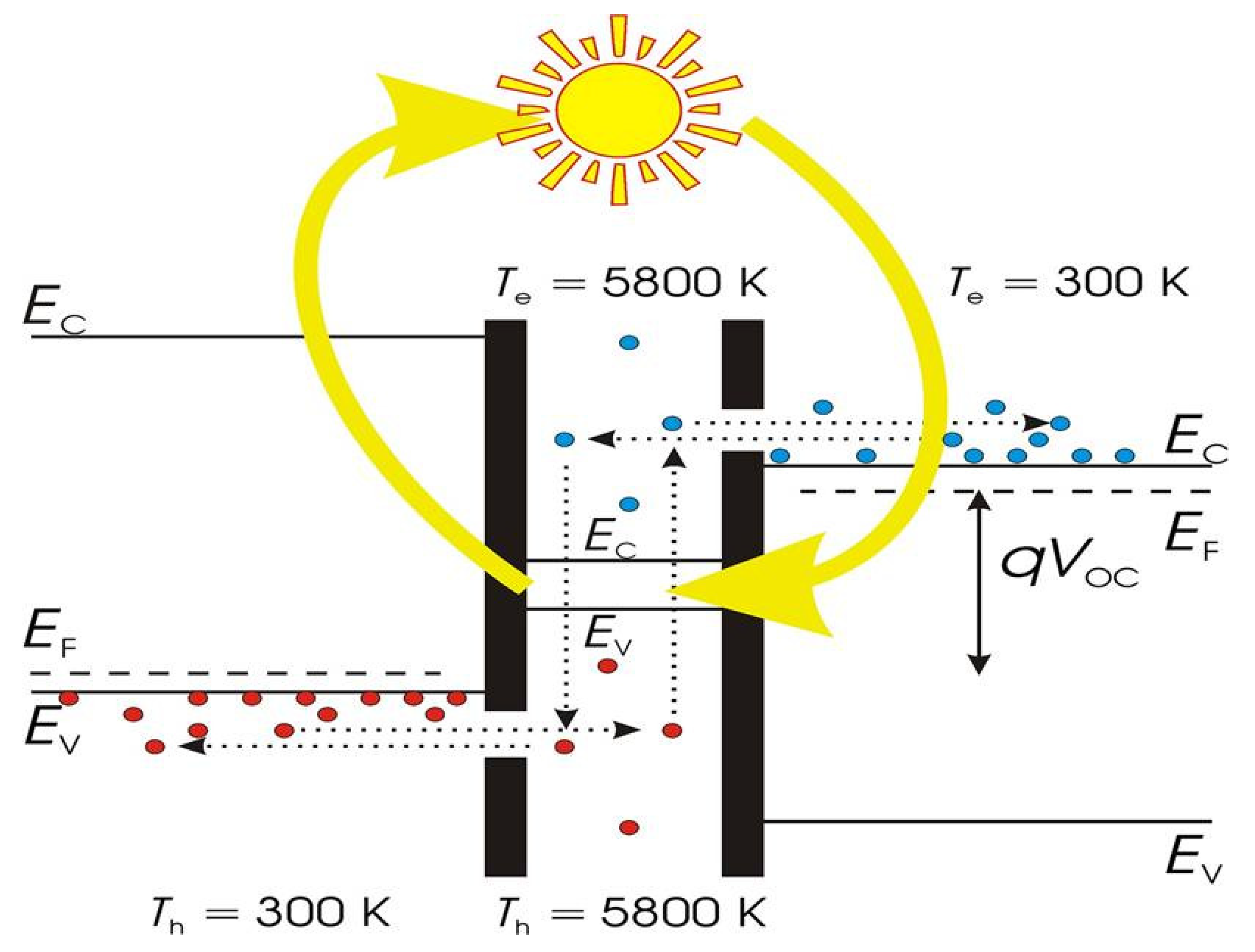
3. Fundamental of HC Dynamics in Semiconductor
3.1. Carrier Dynamics in Perovskite
3.2. The Concept of Relaxation
3.3. The Hot Hole and Hot Electron Thermalization
3.4. Auger Heating Effect
3.5. Bottleneck Effect
3.6. Defect Management
3.7. Critical Analysis of Hot Carrier Dynamics
4. Experimental Techniques for Studying HC
4.1. Transient Absorption Spectroscopy (TAS)
4.2. Time-Resolved Photoluminescence (TRPL)
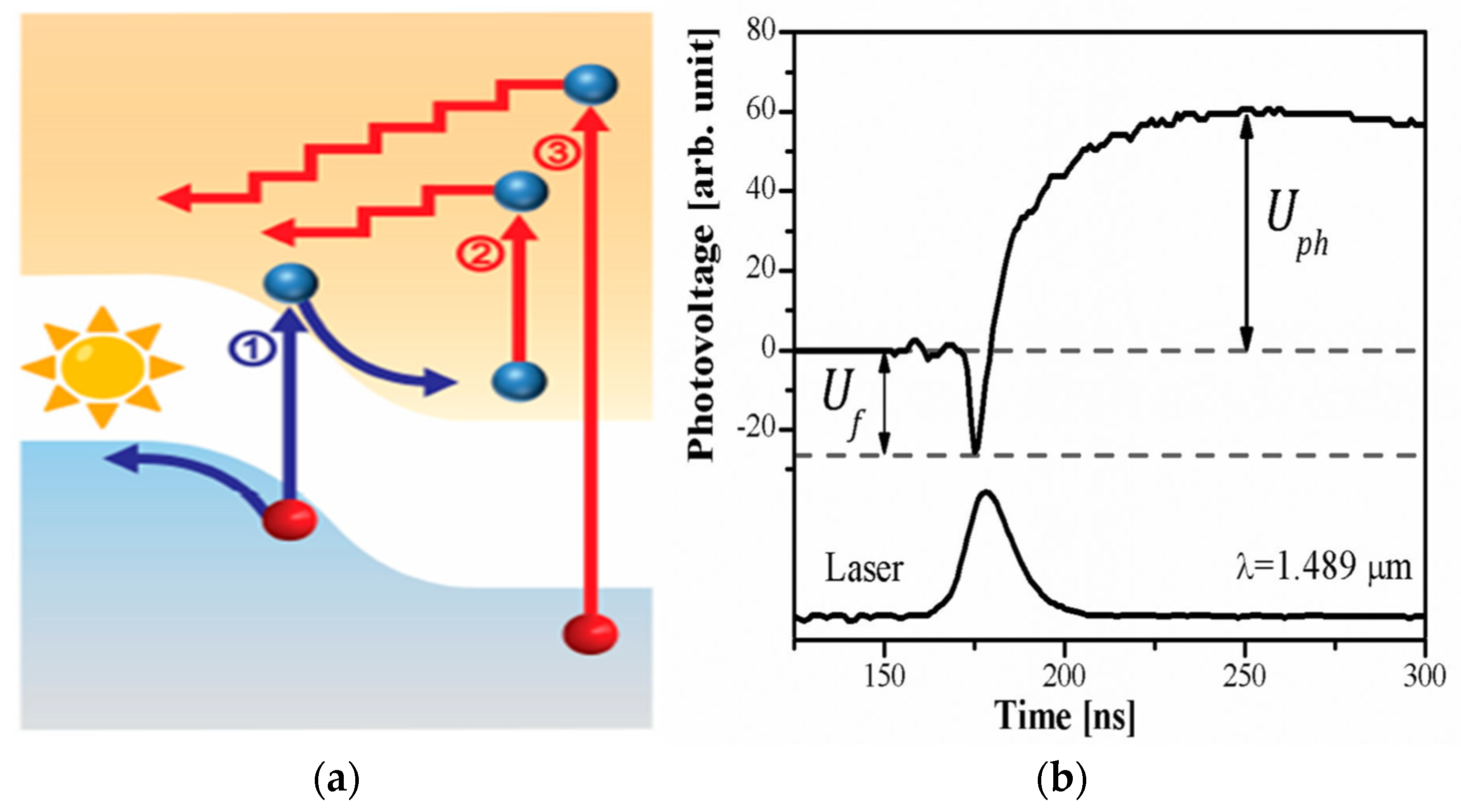
4.3. Transient Photovoltage Measurements
4.4. Device Integration Challenges
5. Conclusions and Outlook
Funding
Conflicts of Interest
References
- Ahmed, I.; Shi, L.; Pasanen, H.; Vivo, P.; Maity, P.; Hatamvand, M.; Zhan, Y. There is plenty of room at the top: Generation of hot charge carriers and their applications in perovskite and other semiconductor-based optoelectronic devices. Light Sci. Appl. 2021, 10, 174. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Kong, L.; Wang, L.; Wang, S.; Chen, W.; Mao, R.; Turyanska, L.; Jia, G.; Yang, X. Core/shell metal halide perovskite nanocrystals for optoelectronic applications. Adv. Funct. Mater. 2021, 31, 2100438. [Google Scholar] [CrossRef]
- Wang, R.; Mujahid, M.; Duan, Y.; Wang, Z.K.; Xue, J.; Yang, Y. A review of perovskites solar cell stability. Adv. Funct. Mater. 2019, 29, 1808843. [Google Scholar] [CrossRef]
- Zuo, C.; Bolink, H.J.; Han, H.; Huang, J.; Cahen, D.; Ding, L. Advances in perovskite solar cells. Adv. Sci. 2016, 3, 1500324. [Google Scholar] [CrossRef]
- Park, N.-G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Katz, E.A. Perovskite: Name Puzzle and German-Russian Odyssey of Discovery. Helv. Chim. Acta 2020, 103, e2000061. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Isikgor, F.H.; Zhumagali, S.T.; Merino, L.V.; De Bastiani, M.; McCulloch, I.; De Wolf, S. Molecular engineering of contact interfaces for high-performance perovskite solar cells. Nat. Rev. Mater. 2023, 8, 89–108. [Google Scholar] [CrossRef]
- Aloysius, D.; Mondal, A.; Gupta, S.; Edri, E.; Mukhopadhyay, S. Effect of formamidinium (FA) ions on mixed ‘A’-site based bromide perovskite (APbBr3) thin films. New J. Chem. 2022, 46, 22229–22236. [Google Scholar] [CrossRef]
- Dastgeer, G.; Nisar, S.; Zulfiqar, M.W.; Eom, J.; Imran, M.; Akbar, K. A review on recent progress and challenges in high-efficiency perovskite solar cells. Nano Energy 2024, 132, 110401. [Google Scholar] [CrossRef]
- Johnsson, M.; Lemmens, P. Perovskites and thin films-crystallography and chemistry. J. Phys. Condens. Matter 2008, 20, 264001. [Google Scholar] [CrossRef]
- Rini, M.; Tobey, R.A.; Dean, N.; Itatani, J.; Tomioka, Y.; Tokura, Y.; Schoenlein, R.W.; Cavalleri, A. Control of the electronic phase of a manganite by mode-selective vibrational excitation. Nature 2007, 449, 72–74. [Google Scholar] [CrossRef]
- Li, C.; Lu, X.; Ding, W.; Feng, L.; Gao, Y.; Guo, Z. Formability of ABX 3 (X = F, Cl, Br, I) halide perovskites. Acta Crystallogr. Sect. B Struct. Sci. 2008, 64, 702–707. [Google Scholar] [CrossRef]
- Mujahid, M.; Chen, C.; Zhang, J.; Li, C.; Duan, Y. Recent advances in semitransparent perovskite solar cells. InfoMat 2021, 3, 101–124. [Google Scholar] [CrossRef]
- Correa-Baena, J.-P.; Saliba, M.; Buonassisi, T.; Grätzel, M.; Abate, A.; Tress, W.; Hagfeldt, A. Promises and challenges of perovskite solar cells. Science 2017, 358, 739–744. [Google Scholar] [CrossRef]
- Duan, L.; Uddin, A. Defects and stability of perovskite solar cells: A critical analysis. Mater. Chem. Front. 2022, 6, 400–417. [Google Scholar] [CrossRef]
- Holzhey, P.; Saliba, M. A full overview of international standards assessing the long-term stability of perovskite solar cells. J. Mater. Chem. A 2018, 6, 21794–21808. [Google Scholar] [CrossRef]
- Kahandal, S.S.; Tupke, R.S.; Bobade, D.S.; Kim, H.; Piao, G.; Sankapal, B.R.; Said, Z.; Pagar, B.P.; Pawar, A.C.; Kim, J.M. Perovskite Solar Cells: Fundamental Aspects, Stability Challenges, and Future Prospects. Prog. Solid State Chem. 2024, 74, 100463. [Google Scholar] [CrossRef]
- Yang, M.; Wang, H.; Cai, W.; Zang, Z. Mixed-Halide Inorganic Perovskite Solar Cells: Opportunities and Challenges. Adv. Opt. Mater. 2023, 11, 2301052. [Google Scholar] [CrossRef]
- Chi, W.; Banerjee, S.K. Achieving resistance against moisture and oxygen for perovskite solar cells with high efficiency and stability. Chem. Mater. 2021, 33, 4269–4303. [Google Scholar] [CrossRef]
- Xiong, J.; Qi, Y.; Zhang, Q.; Box, D.; Williams, K.; Tatum, J.; Das, P.; Pradhan, N.R.; Dai, Q. Enhanced moisture and water resistance in inverted perovskite solar cells by poly (3-hexylthiophene). ACS Appl. Energy Mater. 2021, 4, 1815–1823. [Google Scholar] [CrossRef]
- Srivastava, A.; Shirage, P.M. Overcoming Intrinsic and Extrinsic Challenges in Perovskite Solar Cells: A Pathway Toward Advancement. In Perovskite Solar Cells: Fundamental Approaches and Materials Processing for Sustainable Future; Springer: Berlin/Heidelberg, Germany, 2024; pp. 55–89. [Google Scholar]
- Nazir, G.; Lee, S.Y.; Lee, J.H.; Rehman, A.; Lee, J.K.; Seok, S.I.; Park, S.J. Stabilization of perovskite solar cells: Recent developments and future perspectives. Adv. Mater. 2022, 34, 2204380. [Google Scholar] [CrossRef]
- Guo, Q.; Duan, J.; Zhang, J.; Zhang, Q.; Duan, Y.; Yang, X.; He, B.; Zhao, Y.; Tang, Q. Universal dynamic liquid interface for healing perovskite solar cells. Adv. Mater. 2022, 34, 2202301. [Google Scholar] [CrossRef]
- Xu, B.; Sheibani, E.; Liu, P.; Zhang, J.; Tian, H.; Vlachopoulos, N.; Boschloo, G.; Kloo, L.; Hagfeldt, A.; Sun, L. Carbazole-based hole-transport materials for efficient solid-state dye-sensitized solar cells and perovskite solar cells. Adv. Mater. 2014, 26, 6629–6634. [Google Scholar] [CrossRef]
- Niu, T.; Chao, L.; Gao, W.; Ran, C.; Song, L.; Chen, Y.; Fu, L.; Huang, W. Ionic liquids-enabled efficient and stable perovskite photovoltaics: Progress and challenges. ACS Energy Lett. 2021, 6, 1453–1479. [Google Scholar] [CrossRef]
- Yang, Y.; Ostrowski, D.P.; France, R.M.; Zhu, K.; van de Lagemaat, J.; Luther, J.M.; Beard, M.C. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 2016, 10, 53–59. [Google Scholar] [CrossRef]
- Shi, J.; Li, Y.; Li, Y.; Li, D.; Luo, Y.; Wu, H.; Meng, Q. From Ultrafast to Ultraslow: Charge-Carrier Dynamics of Perovskite Solar Cells. Joule 2018, 2, 879–901. [Google Scholar] [CrossRef]
- Yuan, Y.; Huang, J. Ion migration in organometal trihalide perovskite and its impact on photovoltaic efficiency and stability. Acc. Chem. Res. 2016, 49, 286–293. [Google Scholar] [CrossRef]
- Gong, S.; Qu, G.; Qiao, Y.; Wen, Y.; Huang, Y.; Cai, S.; Zhang, L.; Jiang, K.; Liu, S.; Lin, M. A hot carrier perovskite solar cell with efficiency exceeding 27% enabled by ultrafast hot hole transfer with phthalocyanine derivatives. Energy Environ. Sci. 2024, 17, 5080–5090. [Google Scholar] [CrossRef]
- Nozik, A.J.; Miller, J. Introduction to Solar Photon Conversion; ACS Publications: Washington, DC, USA, 2010; Volume 110, pp. 6443–6445. [Google Scholar]
- Jones, S.C.; Braunlich, P.; Casper, R.T.; Shen, X.-A.; Kelly, P. Recent progress on laser-induced modifications and intrinsic bulk damage of wide-gap optical materials. Opt. Eng. 1989, 28, 1039–1068. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, S.; Song, H. Photon management to reduce energy loss in perovskite solar cells. Chem. Soc. Rev. 2021, 50, 7250–7329. [Google Scholar] [CrossRef]
- Alharbi, F.H.; Kais, S. Theoretical limits of photovoltaics efficiency and possible improvements by intuitive approaches learned from photosynthesis and quantum coherence. Renew. Sustain. Energy Rev. 2015, 43, 1073–1089. [Google Scholar] [CrossRef]
- Wang, B.; Iocozzia, J.; Zhang, M.; Ye, M.; Yan, S.; Jin, H.; Wang, S.; Zou, Z.; Lin, Z. The charge carrier dynamics, efficiency and stability of two-dimensional material-based perovskite solar cells. Chem. Soc. Rev. 2019, 48, 4854–4891. [Google Scholar] [CrossRef]
- Qin, P.; Kast, H.; Nazeeruddin, M.K.; Zakeeruddin, S.M.; Mishra, A.; Bäuerle, P.; Grätzel, M. Low band gap S, N-heteroacene-based oligothiophenes as hole-transporting and light absorbing materials for efficient perovskite-based solar cells. Energy Environ. Sci. 2014, 7, 2981–2985. [Google Scholar] [CrossRef]
- Fu, H. Review of lead-free halide perovskites as light-absorbers for photovoltaic applications: From materials to solar cells. Sol. Energy Mater. Sol. Cells 2019, 193, 107–132. [Google Scholar] [CrossRef]
- Kahmann, S.; Loi, M.A. Hot carrier solar cells and the potential of perovskites for breaking the Shockley–Queisser limit. J. Mater. Chem. C 2019, 7, 2471–2486. [Google Scholar] [CrossRef]
- Wang, Z.; Song, Z.; Yan, Y.; Liu, S.; Yang, D. Perovskite—A perfect top cell for tandem devices to break the S–Q limit. Adv. Sci. 2019, 6, 1801704. [Google Scholar] [CrossRef]
- Sharma, V.; Aharon, S.; Gdor, I.; Yang, C.; Etgar, L.; Ruhman, S. New insights into exciton binding and relaxation from high time resolution ultrafast spectroscopy of CH3NH3PbI3 and CH3NH3PbBr3 films. J. Mater. Chem. A 2016, 4, 3546–3553. [Google Scholar] [CrossRef]
- Ghosh, T.; Aharon, S.; Etgar, L.; Ruhman, S. Free Carrier Emergence and Onset of Electron–Phonon Coupling in Methylammonium Lead Halide Perovskite Films. J. Am. Chem. Soc. 2017, 139, 18262–18270. [Google Scholar] [CrossRef]
- Collavini, S.; Völker, S.F.; Delgado, J.L. Understanding the Outstanding Power Conversion Efficiency of Perovskite-Based Solar Cells. Angew. Chem. Int. Ed. Engl. 2015, 54, 9757–9759. [Google Scholar] [CrossRef]
- Viswanath, A.K.; Lee, J.I.; Kim, D.; Lee, C.; Leem, J. Exciton-phonon interactions, exciton binding energy, and their importance in the realization of room-temperature semiconductor lasers based on GaN. Phys. Rev. B 1998, 58, 16333. [Google Scholar] [CrossRef]
- Sze, S.M.; Li, Y.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: New York, NY, USA, 2021. [Google Scholar]
- Colinge, J.-P.; Colinge, C.A. Physics of Semiconductor Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Shi, J.; Xu, X.; Zhang, H.; Luo, Y.; Li, D.; Meng, Q. Intrinsic slow charge response in the perovskite solar cells: Electron and ion transport. Appl. Phys. Lett. 2015, 107, 163901. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Armaroli, G. Optoelectronic Investigation of Defects in Hybrid Metal Halide Perovskites. Ph.D. Thesis, Università di Bologna, Bologna, Spain, 2023. [Google Scholar]
- Wright, A. Electronic Processes in Metal Halide Perovskites. Ph.D. Thesis, University of Oxford, Oxford, UK, 2018. [Google Scholar]
- Peng, J.; Chen, Y.; Zheng, K.; Pullerits, T.; Liang, Z. Insights into charge carrier dynamics in organo-metal halide perovskites: From neat films to solar cells. Chem. Soc. Rev. 2017, 46, 5714–5729. [Google Scholar] [CrossRef]
- Saba, M.; Cadelano, M.; Marongiu, D.; Chen, F.; Sarritzu, V.; Sestu, N.; Figus, C.; Aresti, M.; Piras, R.; Geddo Lehmann, A.; et al. Correlated electron–hole plasma in organometal perovskites. Nat. Commun. 2014, 5, 5049. [Google Scholar] [CrossRef]
- Goldschmidt, V. The laws of crystal chemistry. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- KAUFFMAN, G.B. Victor Moritz Goldschmidt (1888–1947): A tribute to the founder of modern geochemistry on the fiftieth anniversary of his death. Chem. Educ. 1997, 2, 1–26. [Google Scholar] [CrossRef]
- Viswanathan, B.; Suryakumar, V.; Venugopal, B.; Roshna, S.; Hariprasad, N. (Eds.) Perovskite Materials an Introduction; National Centre for Catalysis Research Department of Chemistry Indian Institute of Technology Madras: Chennai, India, 2019. [Google Scholar]
- Rhodes, C.J. Perovskites and their potential use in solar energy applications. Sci. Prog. 2014, 97, 279–287. [Google Scholar] [CrossRef]
- Lin, T.-C.; Qi, X. Cation Valences and Multiferroic Properties of EuTiO3 Co-Doped with Ba and Transition Metals of Co/Ni. Materials 2022, 15, 6652. [Google Scholar] [CrossRef]
- Kim, K.; Kim, H.; Park, J. Bandgap modulation of Cs2AgInX6 (X = Cl and Br) double perovskite nano-and microcrystals via Cu2+ doping. ACS Omega 2021, 6, 26952–26958. [Google Scholar] [CrossRef]
- Lim, E.L.; Hagfeldt, A.; Bi, D. Toward highly efficient and stable Sn2+ and mixed Pb2+/Sn2+ based halide perovskite solar cells through device engineering. Energy Environ. Sci. 2021, 14, 3256–3300. [Google Scholar] [CrossRef]
- Mitzi, D.B. Templating and structural engineering in organic–inorganic perovskites. J. Chem. Soc. Dalton Trans. 2001, 1–12. [Google Scholar] [CrossRef]
- Nikl, M.; Mihokova, E.; Nitsch, K. Photoluminescence & decay kinetics of Cs4PbCl6 single crystals. Solid State Commun. 1992, 84, 1089–1092. [Google Scholar]
- Tidrow, S.C. Mapping comparison of Goldschmidt’s tolerance factor with Perovskite structural conditions. Ferroelectrics 2014, 470, 13–27. [Google Scholar] [CrossRef]
- Megaw, H.D. Crystal structure of double oxides of the perovskite type. Proc. Phys. Soc. 1946, 58, 133. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Kanatzidis, M.G. The Renaissance of Halide Perovskites and Their Evolution as Emerging Semiconductors. Acc. Chem. Res. 2015, 48, 2791–2802. [Google Scholar] [CrossRef]
- Sun, Q.; Yin, W.-J. Thermodynamic stability trend of cubic perovskites. J. Am. Chem. Soc. 2017, 139, 14905–14908. [Google Scholar] [CrossRef]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing Optoelectronic Properties of Metal Halide Perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef]
- Ungersboeck, E.; Dhar, S.; Karlowatz, G.; Sverdlov, V.; Kosina, H.; Selberherr, S. The Effect of General Strain on the Band Structure and Electron Mobility of Silicon. IEEE Trans. Electron Devices 2007, 54, 2183–2190. [Google Scholar] [CrossRef]
- Duan, J.; Li, J.; Divitini, G.; Cortecchia, D.; Yuan, F.; You, J.; Liu, S.; Petrozza, A.; Wu, Z.; Xi, J. 2D Hybrid Perovskites: From Static and Dynamic Structures to Potential Applications. Adv. Mater. 2024, 36, 2403455. [Google Scholar] [CrossRef]
- Liang, Y.; Huang, X.; Huang, Y.; Wang, X.; Li, F.; Wang, Y.; Tian, F.; Liu, B.; Shen, Z.X.; Cui, T. New metallic ordered phase of perovskite CsPbI3 under pressure. Adv. Sci. 2019, 6, 1900399. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Almutlaq, J.; Sarmah, S.; Dursun, I.; Zhumekenov, A.A.; Begum, R.; Pan, J.; Cho, N.; Mohammed, O.F.; Bakr, O.M. Pure Cs4PbBr6: Highly luminescent zero-dimensional perovskite solids. ACS Energy Lett. 2016, 1, 840–845. [Google Scholar] [CrossRef]
- Giorgi, G.; Fujisawa, J.-I.; Segawa, H.; Yamashita, K. Small photocarrier effective masses featuring ambipolar transport in methylammonium lead iodide perovskite: A density functional analysis. J. Phys. Chem. Lett. 2013, 4, 4213–4216. [Google Scholar] [CrossRef]
- Lehner, A.J.; Fabini, D.H.; Evans, H.A.; Hébert, C.-A.; Smock, S.R.; Hu, J.; Wang, H.; Zwanziger, J.W.; Chabinyc, M.L.; Seshadri, R. Crystal and electronic structures of complex bismuth iodides A 3Bi2I9 (A = K, Rb, Cs) related to perovskite: Aiding the rational design of photovoltaics. Chem. Mater. 2015, 27, 7137–7148. [Google Scholar] [CrossRef]
- Umari, P.; Mosconi, E.; De Angelis, F. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 Perovskites for Solar Cell Applications. Sci. Rep. 2014, 4, 4467. [Google Scholar] [CrossRef]
- Wei, S.-H.; Zunger, A. Electronic and structural anomalies in lead chalcogenides. Phys. Rev. B 1997, 55, 13605. [Google Scholar] [CrossRef]
- Lang, L.; Yang, J.-H.; Liu, H.-R.; Xiang, H.; Gong, X. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. A 2014, 378, 290–293. [Google Scholar] [CrossRef]
- Tan, L.; Wang, W.; Li, Q.; Luo, Z.; Zou, C.; Tang, M.; Zhang, L.; He, J.; Quan, Z. Colloidal syntheses of zero-dimensional Cs4SnX6 (X = Br, I) nanocrystals with high emission efficiencies. Chem. Commun. 2020, 56, 387–390. [Google Scholar] [CrossRef]
- Wu, Y.; Han, D.; Chakoumakos, B.C.; Shi, H.; Chen, S.; Du, M.-H.; Greeley, I.; Loyd, M.; Rutstrom, D.J.; Stand, L. Zero-dimensional Cs4EuX6 (X = Br, I) all-inorganic perovskite single crystals for gamma-ray spectroscopy. J. Mater. Chem. C 2018, 6, 6647–6655. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Frazer, L.; Clark, D.J.; Kim, Y.S.; Rhim, S.H.; Freeman, A.J.; Ketterson, J.B.; Jang, J.I.; Kanatzidis, M.G. Hybrid Germanium Iodide Perovskite Semiconductors: Active Lone Pairs, Structural Distortions, Direct and Indirect Energy Gaps, and Strong Nonlinear Optical Properties. J. Am. Chem. Soc. 2015, 137, 6804–6819. [Google Scholar] [CrossRef]
- Brivio, F.; Butler, K.T.; Walsh, A.; van Schilfgaarde, M. Relativistic quasiparticle self-consistent electronic structure of hybrid halide perovskite photovoltaic absorbers. Phys. Rev. B 2014, 89, 155204. [Google Scholar] [CrossRef]
- Motta, C.; El-Mellouhi, F.; Kais, S.; Tabet, N.; Alharbi, F.; Sanvito, S. Revealing the role of organic cations in hybrid halide perovskite CH3NH3PbI3. Nat. Commun. 2015, 6, 7026. [Google Scholar] [CrossRef]
- Nathan, V.; Guenther, A.H.; Mitra, S.S. Review of multiphoton absorption in crystalline solids. J. Opt. Soc. Am. B 1985, 2, 294–316. [Google Scholar] [CrossRef]
- Fu, J.; Ramesh, S.; Melvin Lim, J.W.; Sum, T.C. Carriers, Quasi-particles, and Collective Excitations in Halide Perovskites. Chem. Rev. 2023, 123, 8154–8231. [Google Scholar] [CrossRef]
- Colbeau-Justin, C.; Valenzuela, M. Time-resolved microwave conductivity (TRMC) a useful characterization tool for charge carrier transfer in photocatalysis: A short review. Rev. Mex. Fís. 2013, 59, 191–200. [Google Scholar]
- Hutter, E.M.; Eperon, G.E.; Stranks, S.D.; Savenije, T.J. Charge Carriers in Planar and Meso-Structured Organic–Inorganic Perovskites: Mobilities, Lifetimes, and Concentrations of Trap States. J. Phys. Chem. Lett. 2015, 6, 3082–3090. [Google Scholar] [CrossRef]
- Pasanen, H. Discovering Perovskite Photophysics with Transient Reflectance Spectroscopy. Ph.D. Thesis, Tampere University, Tampere, Finland, 2021. [Google Scholar]
- Savenije, T.J.; Ponseca, C.S., Jr.; Kunneman, L.; Abdellah, M.; Zheng, K.; Tian, Y.; Zhu, Q.; Canton, S.E.; Scheblykin, I.G.; Pullerits, T. Thermally activated exciton dissociation and recombination control the carrier dynamics in organometal halide perovskite. J. Phys. Chem. Lett. 2014, 5, 2189–2194. [Google Scholar] [CrossRef]
- Ponseca, C.S., Jr.; Savenije, T.J.; Abdellah, M.; Zheng, K.; Yartsev, A.; Pascher, T.R.; Harlang, T.; Chabera, P.; Pullerits, T.; Stepanov, A. Organometal halide perovskite solar cell materials rationalized: Ultrafast charge generation, high and microsecond-long balanced mobilities, and slow recombination. J. Am. Chem. Soc. 2014, 136, 5189–5192. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.-H.; Lee, J.H.; Hong, K.-H. The role of intrinsic defects in methylammonium lead iodide perovskite. J. Phys. Chem. Lett. 2014, 5, 1312–1317. [Google Scholar] [CrossRef]
- Leijtens, T.; Stranks, S.D.; Eperon, G.E.; Lindblad, R.; Johansson, E.M.; McPherson, I.J.; Rensmo, H.; Ball, J.M.; Lee, M.M.; Snaith, H.J. Electronic properties of meso-superstructured and planar organometal halide perovskite films: Charge trapping, photodoping, and carrier mobility. ACS Nano 2014, 8, 7147–7155. [Google Scholar] [CrossRef]
- Yu, P. Fundamentals of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Leppert, L. Excitons in metal-halide perovskites from first-principles many-body perturbation theory. J. Chem. Phys. 2024, 160, 050902. [Google Scholar] [CrossRef]
- Baranowski, M.; Plochocka, P. Excitons in Metal-Halide Perovskites. Adv. Energy Mater. 2020, 10, 1903659. [Google Scholar] [CrossRef]
- Menéndez-Proupin, E.; Palacios, P.; Wahnón, P.; Conesa, J. Self-consistent relativistic band structure of the CH3NH3PbI3 perovskite. Phys. Rev. B 2014, 90, 045207. [Google Scholar] [CrossRef]
- Even, J.; Pedesseau, L.; Katan, C. Analysis of multivalley and multibandgap absorption and enhancement of free carriers related to exciton screening in hybrid perovskites. J. Phys. Chem. C 2014, 118, 11566–11572. [Google Scholar] [CrossRef]
- Yamada, Y.; Nakamura, T.; Endo, M.; Wakamiya, A.; Kanemitsu, Y. Photoelectronic Responses in Solution-Processed Perovskite CH3NH3PbI3 Solar Cells Studied by Photoluminescence and Photoabsorption Spectroscopy. IEEE J. Photovolt. 2014, 5, 401–405. [Google Scholar] [CrossRef]
- Lin, Q.; Armin, A.; Nagiri, R.C.R.; Burn, P.L.; Meredith, P. Electro-optics of perovskite solar cells. Nat. Photonics 2015, 9, 106–112. [Google Scholar] [CrossRef]
- Fang, H.H.; Raissa, R.; Abdu-Aguye, M.; Adjokatse, S.; Blake, G.R.; Even, J.; Loi, M.A. Photophysics of organic–inorganic hybrid lead iodide perovskite single crystals. Adv. Funct. Mater. 2015, 25, 2378–2385. [Google Scholar] [CrossRef]
- Gong, J.; Yang, M.; Ma, X.; Schaller, R.D.; Liu, G.; Kong, L.; Yang, Y.; Beard, M.C.; Lesslie, M.; Dai, Y.; et al. Electron–Rotor Interaction in Organic–Inorganic Lead Iodide Perovskites Discovered by Isotope Effects. J. Phys. Chem. Lett. 2016, 7, 2879–2887. [Google Scholar] [CrossRef]
- Galkowski, K.; Mitioglu, A.; Miyata, A.; Plochocka, P.; Portugall, O.; Eperon, G.E.; Wang, J.T.-W.; Stergiopoulos, T.; Stranks, S.D.; Snaith, H.J. Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors. Energy Environ. Sci. 2016, 9, 962–970. [Google Scholar] [CrossRef]
- Miyata, A.; Mitioglu, A.; Plochocka, P.; Portugall, O.; Wang, J.T.-W.; Stranks, S.D.; Snaith, H.J.; Nicholas, R.J. Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites. Nat. Phys. 2015, 11, 582–587. [Google Scholar] [CrossRef]
- Elliott, R. Intensity of optical absorption by excitons. Phys. Rev. 1957, 108, 1384. [Google Scholar] [CrossRef]
- Davies, C.L.; Filip, M.R.; Patel, J.B.; Crothers, T.W.; Verdi, C.; Wright, A.D.; Milot, R.L.; Giustino, F.; Johnston, M.B.; Herz, L.M. Bimolecular recombination in methylammonium lead triiodide perovskite is an inverse absorption process. Nat. Commun. 2018, 9, 293. [Google Scholar] [CrossRef]
- Zhang, Y.; Saidaminov, M.I.; Dursun, I.; Yang, H.; Murali, B.; Alarousu, E.; Yengel, E.; Alshankiti, B.A.; Bakr, O.M.; Mohammed, O.F. Zero-dimensional Cs4PbBr6 perovskite nanocrystals. J. Phys. Chem. Lett. 2017, 8, 961–965. [Google Scholar] [CrossRef]
- Zhou, C.; Tian, Y.; Khabou, O.; Worku, M.; Zhou, Y.; Hurley, J.; Lin, H.; Ma, B. Manganese-doped one-dimensional organic lead bromide perovskites with bright white emissions. ACS Appl. Mater. Interfaces 2017, 9, 40446–40451. [Google Scholar] [CrossRef]
- Jun, T.; Sim, K.; Iimura, S.; Sasase, M.; Kamioka, H.; Kim, J.; Hosono, H. Lead-free highly efficient blue-emitting Cs3Cu2I5 with 0D electronic structure. Adv. Mater. 2018, 30, 1804547. [Google Scholar] [CrossRef]
- Pal, J.; Bhunia, A.; Chakraborty, S.; Manna, S.; Das, S.; Dewan, A.; Datta, S.; Nag, A. Synthesis and optical properties of colloidal M3Bi2I9 (M = Cs, Rb) perovskite nanocrystals. J. Phys. Chem. C 2018, 122, 10643–10649. [Google Scholar] [CrossRef]
- Wehrenfennig, C.; Liu, M.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Homogeneous emission line broadening in the organo lead halide perovskite CH3NH3PbI3–xClx. J. Phys. Chem. Lett. 2014, 5, 1300–1306. [Google Scholar] [CrossRef]
- Zhu, H.; Miyata, K.; Fu, Y.; Wang, J.; Joshi, P.P.; Niesner, D.; Williams, K.W.; Jin, S.; Zhu, X.-Y. Screening in crystalline liquids protects energetic carriers in hybrid perovskites. Science 2016, 353, 1409–1413. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Z.; Nan, P.; Xiong, F.; Lin, S.; Zhang, X.; Chen, Y.; Chen, L.; Ge, B.; Pei, Y. Lattice strain advances thermoelectrics. Joule 2019, 3, 1276–1288. [Google Scholar] [CrossRef]
- Mayers, M.Z.; Tan, L.Z.; Egger, D.A.; Rappe, A.M.; Reichman, D.R. How lattice and charge fluctuations control carrier dynamics in halide perovskites. Nano Lett. 2018, 18, 8041–8046. [Google Scholar] [CrossRef]
- Menahem, M.; Dai, Z.; Aharon, S.; Sharma, R.; Asher, M.; Diskin-Posner, Y.; Korobko, R.; Rappe, A.M.; Yaffe, O. Strongly anharmonic octahedral tilting in two-dimensional hybrid halide perovskites. ACS Nano 2021, 15, 10153–10162. [Google Scholar] [CrossRef]
- Quarti, C.; Grancini, G.; Mosconi, E.; Bruno, P.; Ball, J.M.; Lee, M.M.; Snaith, H.J.; Petrozza, A.; De Angelis, F. The Raman spectrum of the CH3NH3PbI3 hybrid perovskite: Interplay of theory and experiment. J. Phys. Chem. Lett. 2013, 5, 279–284. [Google Scholar] [CrossRef]
- Pérez-Osorio, M.A.; Milot, R.L.; Filip, M.R.; Patel, J.B.; Herz, L.M.; Johnston, M.B.; Giustino, F. Vibrational properties of the organic–inorganic halide perovskite CH3NH3PbI3 from theory and experiment: Factor group analysis, first-principles calculations, and low-temperature infrared spectra. J. Phys. Chem. C 2015, 119, 25703–25718. [Google Scholar] [CrossRef]
- Yaffe, O.; Guo, Y.; Tan, L.Z.; Egger, D.A.; Hull, T.; Stoumpos, C.C.; Zheng, F.; Heinz, T.F.; Kronik, L.; Kanatzidis, M.G. Local polar fluctuations in lead halide perovskite crystals. Phys. Rev. Lett. 2017, 118, 136001. [Google Scholar] [CrossRef]
- Calistru, D.M.; Mihut, L.; Lefrant, S.; Baltog, I. Identification of the symmetry of phonon modes in CsPbCl3 in phase IV by Raman and resonance-Raman scattering. J. Appl. Phys. 1997, 82, 5391–5395. [Google Scholar] [CrossRef]
- Hirotsu, S.; Suzuki, T. Elastic constants and thermal expansion of CsPbCl3. J. Phys. Soc. Jpn. 1978, 44, 1604–1611. [Google Scholar] [CrossRef]
- Phuong, L.Q.; Nakaike, Y.; Wakamiya, A.; Kanemitsu, Y. Free excitons and exciton–phonon coupling in CH3NH3PbI3 single crystals revealed by photocurrent and photoluminescence measurements at low temperatures. J. Phys. Chem. Lett. 2016, 7, 4905–4910. [Google Scholar] [CrossRef]
- Diab, H.; Trippé-Allard, G.; Lédée, F.; Jemli, K.; Vilar, C.; Bouchez, G.; Jacques, V.L.; Tejeda, A.; Even, J.; Lauret, J.-S. Narrow linewidth excitonic emission in organic–inorganic lead iodide perovskite single crystals. J. Phys. Chem. Lett. 2016, 7, 5093–5100. [Google Scholar] [CrossRef]
- Guo, Z.; Wu, X.; Zhu, T.; Zhu, X.; Huang, L. Electron–phonon scattering in atomically thin 2D perovskites. ACS Nano 2016, 10, 9992–9998. [Google Scholar] [CrossRef]
- Ni, L.; Huynh, U.; Cheminal, A.; Thomas, T.H.; Shivanna, R.; Hinrichsen, T.F.; Ahmad, S.; Sadhanala, A.; Rao, A. Real-time observation of exciton–phonon coupling dynamics in self-assembled hybrid perovskite quantum wells. ACS Nano 2017, 11, 10834–10843. [Google Scholar] [CrossRef]
- Thirumal, K.; Chong, W.K.; Xie, W.; Ganguly, R.; Muduli, S.K.; Sherburne, M.; Asta, M.; Mhaisalkar, S.; Sum, T.C.; Soo, H.S. Morphology-independent stable white-light emission from self-assembled two-dimensional perovskites driven by strong exciton–phonon coupling to the organic framework. Chem. Mater. 2017, 29, 3947–3953. [Google Scholar] [CrossRef]
- Dohner, E.R.; Jaffe, A.; Bradshaw, L.R.; Karunadasa, H.I. Intrinsic white-light emission from layered hybrid perovskites. J. Am. Chem. Soc. 2014, 136, 13154–13157. [Google Scholar] [CrossRef]
- Klimov, V.I. Mechanisms for photogeneration and recombination of multiexcitons in semiconductor nanocrystals: Implications for lasing and solar energy conversion. J. Phys. Chem. B 2006, 110, 16827–16845. [Google Scholar] [CrossRef]
- Luo, J.-W.; Franceschetti, A.; Zunger, A. Carrier multiplication in semiconductor nanocrystals: Theoretical screening of candidate materials based on band-structure effects. Nano Lett. 2008, 8, 3174–3181. [Google Scholar] [CrossRef]
- Kirk, A.P.; Fischetti, M.V. Fundamental limitations of hot-carrier solar cells. Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 86, 165206. [Google Scholar] [CrossRef]
- Konovalov, I.; Emelianov, V. Hot carrier solar cell as thermoelectric device. Energy Sci. Eng. 2017, 5, 113–122. [Google Scholar] [CrossRef]
- Ross, R.T.; Nozik, A.J. Efficiency of hot-carrier solar energy converters. J. Appl. Phys. 1982, 53, 3813–3818. [Google Scholar] [CrossRef]
- Clady, R.; Tayebjee, M.J.Y.; Aliberti, P.; König, D.; Ekins-Daukes, N.J.; Conibeer, G.J.; Schmidt, T.W.; Green, M.A. Interplay between the hot phonon effect and intervalley scattering on the cooling rate of hot carriers in GaAs and InP. Prog. Photovolt. Res. Appl. 2012, 20, 82–92. [Google Scholar] [CrossRef]
- Konovalov, I.; Emelianov, V.; Linke, R. Hot carrier solar cell with semi infinite energy filtering. Sol. Energy 2015, 111, 1–9. [Google Scholar] [CrossRef]
- Dimmock, J.A.; Day, S.; Kauer, M.; Smith, K.; Heffernan, J. Demonstration of a hot-carrier photovoltaic cell. Prog. Photovolt. Res. Appl. 2014, 22, 151–160. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Adams, M.J. Radiative and Auger processes in semiconductors. J. Lumin. 1973, 7, 3–34. [Google Scholar] [CrossRef]
- Kaniyankandy, S. Evidence of auger heating in hot carrier cooling of CsPbBr3 nanocrystals. Colloids Surf. A Physicochem. Eng. Asp. 2022, 635, 128025. [Google Scholar] [CrossRef]
- van de Ven, L.J.M.; Tekelenburg, E.K.; Pitaro, M.; Pinna, J.; Loi, M.A. Cation Influence on Hot-Carrier Relaxation in Tin Triiodide Perovskite Thin Films. ACS Energy Lett. 2024, 9, 992–999. [Google Scholar] [CrossRef]
- Wörle, M.; Holleitner, A.W.; Kienberger, R.; Iglev, H. Ultrafast hot-carrier relaxation in silicon monitored by phase-resolved transient absorption spectroscopy. Phys. Rev. B 2021, 104, L041201. [Google Scholar] [CrossRef]
- Green, M.A. Third Generation Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fu, J.; Xu, Q.; Han, G.; Wu, B.; Huan, C.H.A.; Leek, M.L.; Sum, T.C. Hot carrier cooling mechanisms in halide perovskites. Nat. Commun. 2017, 8, 1300. [Google Scholar] [CrossRef]
- Ašmontas, S.; Gradauskas, J.; Sužiedėlis, A.; Šilėnas, A.; Širmulis, E.; Vaičikauskas, V.; Vaičiūnas, V.; Žalys, O.; Fedorenko, L.; Bulat, L. Photovoltage formation across GaAs p–n junction under illumination of intense laser radiation. Opt. Quantum Electron. 2016, 48, 448. [Google Scholar] [CrossRef]
- Ašmontas, S.; Gradauskas, J.; Sužiedėlis, A.; Šilėnas, A.; Širmulis, E.; Švedas, V.; Vaičikauskas, V.; Žalys, O. Hot carrier impact on photovoltage formation in solar cells. Appl. Phys. Lett. 2018, 113, 071103. [Google Scholar] [CrossRef]
- Ašmontas, S.; Masalskyi, O.; Zharchenko, I.; Sužiedėlis, A.; Gradauskas, J. Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction. Inorganics 2024, 12, 174. [Google Scholar] [CrossRef]
- Ašmontas, S.; Gradauskas, J.; Sužiedélis, A.; Šilénas, A.; Širmulis, E.; Švedas, V.; Vaičikauskas, V.; Vaičiūnas, V.; Žalys, O.Ž.; Kostylyov, V. Photovoltage formation across Si pn junction exposed to laser radiation. Mater. Sci.-Pol. 2018, 36, 337–340. [Google Scholar] [CrossRef]
- Asmontas, S.P.; Gradauskas, J.; Seliuta, D.; Sirmulis, E. Nonresonant Laser-Matter Interaction (NLMI-10). In Photoelectrical Properties of Nonuniform Semiconductor Under Infrared Laser Radiation; SPIE: Bellingham, DC, USA, 2001; pp. 18–27. [Google Scholar]
- McCluskey, M.D.; Haller, E.E. Dopants and Defects in Semiconductors; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lutz, J.; Schlangenotto, H.; Scheuermann, U.; De Doncker, R. Semiconductor Power Devices: Physics, Characteristics, Reliability; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2. [Google Scholar]
- Euvrard, J.; Yan, Y.; Mitzi, D.B. Electrical doping in halide perovskites. Nat. Rev. Mater. 2021, 6, 531–549. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Bakr, O.M.; Sun, H.-T. Metal-doped lead halide perovskites: Synthesis, properties, and optoelectronic applications. Chem. Mater. 2018, 30, 6589–6613. [Google Scholar] [CrossRef]
- Chen, R.; Chen, L.; Liang, Z. Strategic doping in metal halide perovskites for thermoelectrics. Adv. Funct. Mater. 2023, 33, 2303774. [Google Scholar] [CrossRef]
- Deschler, F.; Price, M.; Pathak, S.; Klintberg, L.E.; Jarausch, D.-D.; Higler, R.; Hüttner, S.; Leijtens, T.; Stranks, S.D.; Snaith, H.J. High photoluminescence efficiency and optically pumped lasing in solution-processed mixed halide perovskite semiconductors. J. Phys. Chem. Lett. 2014, 5, 1421–1426. [Google Scholar] [CrossRef]
- Stranks, S.D.; Burlakov, V.M.; Leijtens, T.; Ball, J.M.; Goriely, A.; Snaith, H.J. Recombination kinetics in organic-inorganic perovskites: Excitons, free charge, and subgap states. Phys. Rev. Appl. 2014, 2, 034007. [Google Scholar] [CrossRef]
- Yamada, Y.; Nakamura, T.; Endo, M.; Wakamiya, A.; Kanemitsu, Y. Photocarrier recombination dynamics in perovskite CH3NH3PbI3 for solar cell applications. J. Am. Chem. Soc. 2014, 136, 11610–11613. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, J.; Parida, M.R.; Ahmed, G.H.; Pan, J.; Bakr, O.M.; Brédas, J.-L.; Mohammed, O.F. Direct-indirect nature of the bandgap in lead-free perovskite nanocrystals. J. Phys. Chem. Lett. 2017, 8, 3173–3177. [Google Scholar] [CrossRef]
- Filip, M.R.; Hillman, S.; Haghighirad, A.A.; Snaith, H.J.; Giustino, F. Band gaps of the lead-free halide double perovskites Cs2BiAgCl6 and Cs2BiAgBr6 from theory and experiment. J. Phys. Chem. Lett. 2016, 7, 2579–2585. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Hong, F.; Mao, X.; Zheng, K.; Yang, S.; Li, Y.; Pullerits, T.; Deng, W.; Han, K. Lead-free, air-stable all-inorganic cesium bismuth halide perovskite nanocrystals. Angew. Chem. Int. Ed. 2017, 56, 12471–12475. [Google Scholar] [CrossRef]
- Yang, B.; Hong, F.; Chen, J.; Tang, Y.; Yang, L.; Sang, Y.; Xia, X.; Guo, J.; He, H.; Yang, S. Colloidal synthesis and charge-carrier dynamics of Cs2AgSb1−yBiyX6 (X: Br, Cl; 0 ≤ y ≤ 1) double perovskite nanocrystals. Angew. Chem. 2019, 131, 2300–2305. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Yang, S.; Hong, F.; Sun, L.; Han, P.; Pullerits, T.; Deng, W.; Han, K. Lead-free silver-bismuth halide double perovskite nanocrystals. Angew. Chem. 2018, 130, 5457–5461. [Google Scholar] [CrossRef]
- Slavney, A.H.; Hu, T.; Lindenberg, A.M.; Karunadasa, H.I. A bismuth-halide double perovskite with long carrier recombination lifetime for photovoltaic applications. J. Am. Chem. Soc. 2016, 138, 2138–2141. [Google Scholar] [CrossRef]
- Volonakis, G.; Haghighirad, A.A.; Milot, R.L.; Sio, W.H.; Filip, M.R.; Wenger, B.; Johnston, M.B.; Herz, L.M.; Snaith, H.J.; Giustino, F. Cs2InAgCl6: A new lead-free halide double perovskite with direct band gap. J. Phys. Chem. Lett. 2017, 8, 772–778. [Google Scholar] [CrossRef]
- Meng, W.; Wang, X.; Xiao, Z.; Wang, J.; Mitzi, D.B.; Yan, Y. Parity-forbidden transitions and their impact on the optical absorption properties of lead-free metal halide perovskites and double perovskites. J. Phys. Chem. Lett. 2017, 8, 2999–3007. [Google Scholar] [CrossRef]
- Chang, Z.; Cao, X. Doping Induced Bandgap Narrowing and Indirect-to-Direct Bandgap Transition in Cs2pt1-Xpdxbr6 Double Perovskite. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4760400 (accessed on 15 January 2025).
- Boriskina, S.V.; Chen, G. Exceeding the solar cell Shockley–Queisser limit via thermal up-conversion of low-energy photons. Opt. Commun. 2014, 314, 71–78. [Google Scholar] [CrossRef]
- Gruber, M.; Wagner, J.; Klein, K.; Hörmann, U.; Opitz, A.; Stutzmann, M.; Brütting, W. Thermodynamic efficiency limit of molecular donor-acceptor solar cells and its application to diindenoperylene/C60-based planar heterojunction devices. Adv. Energy Mater. 2012, 2, 1100–1108. [Google Scholar] [CrossRef]
- Price, M.B.; Butkus, J.; Jellicoe, T.C.; Sadhanala, A.; Briane, A.; Halpert, J.E.; Broch, K.; Hodgkiss, J.M.; Friend, R.H.; Deschler, F. Hot-carrier cooling and photoinduced refractive index changes in organic–inorganic lead halide perovskites. Nat. Commun. 2015, 6, 8420. [Google Scholar] [CrossRef]
- Richter, J.M.; Branchi, F.; Valduga de Almeida Camargo, F.; Zhao, B.; Friend, R.H.; Cerullo, G.; Deschler, F. Ultrafast carrier thermalization in lead iodide perovskite probed with two-dimensional electronic spectroscopy. Nat. Commun. 2017, 8, 376. [Google Scholar] [CrossRef]
- Guo, Z.; Wan, Y.; Yang, M.; Snaider, J.; Zhu, K.; Huang, L. Long-range hot-carrier transport in hybrid perovskites visualized by ultrafast microscopy. Science 2017, 356, 59–62. [Google Scholar] [CrossRef]
- Kawai, H.; Giorgi, G.; Marini, A.; Yamashita, K. The Mechanism of Slow Hot-Hole Cooling in Lead-Iodide Perovskite: First-Principles Calculation on Carrier Lifetime from Electron–Phonon Interaction. Nano Lett. 2015, 15, 3103–3108. [Google Scholar] [CrossRef]
- Yang, J.; Wen, X.; Xia, H.; Sheng, R.; Ma, Q.; Kim, J.; Tapping, P.; Harada, T.; Kee, T.W.; Huang, F.; et al. Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Commun. 2017, 8, 14120. [Google Scholar] [CrossRef]
- Sheng, X.; Chen, G.; Wang, C.; Wang, W.; Hui, J.; Zhang, Q.; Yu, K.; Wei, W.; Yi, M.; Zhang, M. Polarized optoelectronics of CsPbX3 (X = Cl, Br, I) perovskite nanoplates with tunable size and thickness. Adv. Funct. Mater. 2018, 28, 1800283. [Google Scholar] [CrossRef]
- Herz, L.M. Charge-carrier dynamics in organic-inorganic metal halide perovskites. Annu. Rev. Phys. Chem. 2016, 67, 65–89. [Google Scholar] [CrossRef]
- Wehrenfennig, C.; Eperon, G.E.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. High charge carrier mobilities and lifetimes in organolead trihalide perovskites. Adv. Mater. 2013, 26, 1584. [Google Scholar] [CrossRef]
- Johnston, M.B.; Herz, L.M. Hybrid perovskites for photovoltaics: Charge-carrier recombination, diffusion, and radiative efficiencies. Acc. Chem. Res. 2016, 49, 146–154. [Google Scholar] [CrossRef]
- Othonos, A. Probing ultrafast carrier and phonon dynamics in semiconductors. J. Appl. Phys. 1998, 83, 1789–1830. [Google Scholar] [CrossRef]
- Burda, C.; Link, S.; Mohamed, M.; El-Sayed, M. The relaxation pathways of CdSe nanoparticles monitored with femtosecond time-resolution from the visible to the IR: Assignment of the transient features by carrier quenching. J. Phys. Chem. B 2001, 105, 12286–12292. [Google Scholar] [CrossRef]
- Marjit, K.; Das, A.; Ghosh, D.; Patra, A. Providing a Review of Hot Carrier (HC) Relaxation Dynamics and Strategies of HC Extraction in Perovskites Nanocrystals. ChemNanoMat 2024, 10, e202300629. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Conibeer, G.; König, D.; Green, M.; Guillemoles, J. Slowing of carrier cooling in hot carrier solar cells. Thin Solid Film. 2008, 516, 6948–6953. [Google Scholar] [CrossRef]
- Wen, Y.-C.; Chen, C.-Y.; Shen, C.-H.; Gwo, S.; Sun, C.-K. Ultrafast carrier thermalization in InN. Appl. Phys. Lett. 2006, 89, 232114. [Google Scholar] [CrossRef]
- Hirst, L.C.; Lumb, M.P.; Hoheisel, R.; Bailey, C.G.; Philipps, S.P.; Bett, A.W.; Walters, R.J. Spectral sensitivity of hot carrier solar cells. Sol. Energy Mater. Sol. Cells 2014, 120, 610–615. [Google Scholar] [CrossRef]
- Le Bris, A.; Guillemoles, J.-F. Hot carrier solar cells: Achievable efficiency accounting for heat losses in the absorber and through contacts. Appl. Phys. Lett. 2010, 97, 113506. [Google Scholar] [CrossRef]
- Le Bris, A.; Lombez, L.; Laribi, S.; Boissier, G.; Christol, P.; Guillemoles, J.F. Thermalisation rate study of GaSb-based heterostructures by continuous wave photoluminescence and their potential as hot carrier solar cell absorbers. Energy Environ. Sci. 2012, 5, 6225–6232. [Google Scholar] [CrossRef]
- Fraas, L.M.; Partain, L.D. Solar Cells and Their Applications; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Esipov, S.; Levinson, Y. The temperature and energy distribution of photoexcited hot electrons. Adv. Phys. 1987, 36, 331–383. [Google Scholar] [CrossRef]
- Nozik, A.J. Spectroscopy and hot electron relaxation dynamics in semiconductor quantum wells and quantum dots. Annu. Rev. Phys. Chem. 2001, 52, 193–231. [Google Scholar] [CrossRef]
- Li, M.; Fu, J.; Xu, Q.; Sum, T.C. Slow hot-carrier cooling in halide perovskites: Prospects for hot-carrier solar cells. Adv. Mater. 2019, 31, 1802486. [Google Scholar] [CrossRef]
- Tsai, C.Y. The effects of intraband and interband carrier-carrier scattering on hot-carrier solar cells: A theoretical study of spectral hole burning, electron-hole energy transfer, Auger recombination, and impact ionization generation. Prog. Photovolt. Res. Appl. 2019, 27, 433–452. [Google Scholar] [CrossRef]
- Takeda, Y.; Motohiro, T.; König, D.; Aliberti, P.; Feng, Y.; Shrestha, S.; Conibeer, G. Practical Factors Lowering Conversion Efficiency of Hot Carrier Solar Cells. Appl. Phys. Express 2010, 3, 104301. [Google Scholar] [CrossRef]
- Madjet, M.E.-A.; Akimov, A.V.; El-Mellouhi, F.; Berdiyorov, G.R.; Ashhab, S.; Tabet, N.; Kais, S. Enhancing the carrier thermalization time in organometallic perovskites by halide mixing. Phys. Chem. Chem. Phys. 2016, 18, 5219–5231. [Google Scholar] [CrossRef]
- Takeda, Y.; Ito, T.; Motohiro, T.; König, D.; Shrestha, S.; Conibeer, G. Hot carrier solar cells operating under practical conditions. J. Appl. Phys. 2009, 105, 074905. [Google Scholar] [CrossRef]
- Gibelli, F.; Lombez, L.; Guillemoles, J.-F. 4-Hot-Carrier Solar Cells: Modeling Carrier Transport. In Advanced Micro- and Nanomaterials for Photovoltaics; Ginley, D., Fix, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 53–92. [Google Scholar]
- Zhang, P.; Zhu, G.; Shi, Y.; Wang, Y.; Zhang, J.; Du, L.; Ding, D. Ultrafast interfacial charge transfer of cesium lead halide perovskite films CsPbX3 (X = Cl, Br, I) with different halogen mixing. J. Phys. Chem. C 2018, 122, 27148–27155. [Google Scholar] [CrossRef]
- Wei, Q.; Yin, J.; Bakr, O.M.; Wang, Z.; Wang, C.; Mohammed, O.F.; Li, M.; Xing, G. Effect of Zinc-doping on the Reduction of the Hot-carrier Cooling Rate in Halide Perovskites. Angew. Chem. Int. Ed. 2021, 60, 10957–10963. [Google Scholar] [CrossRef]
- Chen, J.; Messing, M.E.; Zheng, K.; Pullerits, T. Cation-Dependent Hot Carrier Cooling in Halide Perovskite Nanocrystals. J. Am. Chem. Soc. 2019, 141, 3532–3540. [Google Scholar] [CrossRef]
- Gao, W.; Chen, C.; Ran, C.; Zheng, H.; Dong, H.; Xia, Y.; Chen, Y.; Huang, W. A-site cation engineering of metal halide perovskites: Version 3.0 of efficient tin-based lead-free perovskite solar cells. Adv. Funct. Mater. 2020, 30, 2000794. [Google Scholar] [CrossRef]
- Madjet, M.E.; Berdiyorov, G.R.; El-Mellouhi, F.; Alharbi, F.H.; Akimov, A.V.; Kais, S. Cation Effect on Hot Carrier Cooling in Halide Perovskite Materials. J. Phys. Chem. Lett. 2017, 8, 4439–4445. [Google Scholar] [CrossRef]
- Talbert, E.M.; Zarick, H.F.; Boulesbaa, A.; Soetan, N.; Puretzky, A.A.; Geohegan, D.B.; Bardhan, R. Bromine substitution improves excited-state dynamics in mesoporous mixed halide perovskite films. Nanoscale 2017, 9, 12005–12013. [Google Scholar] [CrossRef]
- Wu, J.-R.; Thakur, D.; Chiang, S.-E.; Chandel, A.; Wang, J.-S.; Chiu, K.-C.; Chang, S.H. The Way to Pursue Truly High-Performance Perovskite Solar Cells. Nanomaterials 2019, 9, 1269. [Google Scholar] [CrossRef]
- Hedley, G.J.; Quarti, C.; Harwell, J.; Prezhdo, O.V.; Beljonne, D.; Samuel, I.D. Hot-hole cooling controls the initial ultrafast relaxation in methylammonium lead iodide perovskite. Sci. Rep. 2018, 8, 8115. [Google Scholar] [CrossRef]
- Shen, Q.; Ripolles, T.S.; Even, J.; Zhang, Y.; Ding, C.; Liu, F.; Izuishi, T.; Nakazawa, N.; Toyoda, T.; Ogomi, Y. Ultrafast selective extraction of hot holes from cesium lead iodide perovskite films. J. Energy Chem. 2018, 27, 1170–1174. [Google Scholar] [CrossRef]
- Dursun, I.; Maity, P.; Yin, J.; Turedi, B.; Zhumekenov, A.A.; Lee, K.J.; Mohammed, O.F.; Bakr, O.M. Why are hot holes easier to extract than hot electrons from methylammonium lead iodide perovskite? Adv. Energy Mater. 2019, 9, 1900084. [Google Scholar] [CrossRef]
- Lim, S.S.; Giovanni, D.; Zhang, Q.; Solanki, A.; Jamaludin, N.F.; Lim, J.W.M.; Mathews, N.; Mhaisalkar, S.; Pshenichnikov, M.S.; Sum, T.C. Hot carrier extraction in CH3NH3PbI3 unveiled by pump-push-probe spectroscopy. Sci. Adv. 2019, 5, eaax3620. [Google Scholar] [CrossRef]
- Zhou, Z.; He, J.; Frauenheim, T.; Prezhdo, O.V.; Wang, J. Control of hot carrier cooling in lead halide perovskites by point defects. J. Am. Chem. Soc. 2022, 144, 18126–18134. [Google Scholar] [CrossRef]
- Li, M.; Bhaumik, S.; Goh, T.W.; Kumar, M.S.; Yantara, N.; Grätzel, M.; Mhaisalkar, S.; Mathews, N.; Sum, T.C. Slow cooling and highly efficient extraction of hot carriers in colloidal perovskite nanocrystals. Nat. Commun. 2017, 8, 14350. [Google Scholar] [CrossRef]
- Acharjee, D.; Mahato, A.B.; Das, A.; Ghosh, S. Electron Transfer from an Optically Pumped Polyhedral Perovskite Nanocrystal to Pristine Fullerene. J. Phys. Chem. C 2023, 127, 19643–19650. [Google Scholar] [CrossRef]
- Ghosh, D.; Marjit, K.; Ghosh, G.; Ghosh, S.; Patra, A. Charge transfer dynamics of two-dimensional ruddlesden popper perovskite in the presence of short-chain aromatic thiol ligands. J. Phys. Chem. C 2022, 126, 14590–14597. [Google Scholar] [CrossRef]
- Ghosh, G.; Marjit, K.; Ghosh, S.; Ghosh, D.; Patra, A. Evidence of Hot Charge Carrier Transfer in Hybrid CsPbBr3/Functionalized Graphene. ChemNanoMat 2022, 8, e202200172. [Google Scholar] [CrossRef]
- Ghosh, G.; Marjit, K.; Ghosh, S.; Ghosh, A.; Ahammed, R.; De Sarkar, A.; Patra, A. Hot hole cooling and transfer dynamics from lead halide perovskite nanocrystals using porphyrin molecules. J. Phys. Chem. C 2021, 125, 5859–5869. [Google Scholar] [CrossRef]
- Hardouin Duparc, O. Pierre Auger–Lise Meitner: Comparative contributions to the Auger effect. Int. J. Mater. Res. 2009, 100, 1162–1166. [Google Scholar] [CrossRef]
- Hofmann, S. Auger electron spectroscopy. In Comprehensive Analytical Chemistry; Elsevier: Amsterdam, The Netherlands, 1979; Volume 9, pp. 89–172. [Google Scholar]
- Diroll, B.T.; Schaller, R.D. Intraband cooling in all-inorganic and hybrid organic–inorganic perovskite nanocrystals. Adv. Funct. Mater. 2019, 29, 1901725. [Google Scholar] [CrossRef]
- Achermann, M.; Bartko, A.P.; Hollingsworth, J.A.; Klimov, V.I. The effect of Auger heating on intraband carrier relaxation in semiconductor quantum rods. Nat. Phys. 2006, 2, 557–561. [Google Scholar] [CrossRef]
- Delerue, C.; Lannoo, M.; Allan, G.; Martin, E.; Mihalcescu, I.; Vial, J.-C.; Romestain, R.; Muller, F.; Bsiesy, A. Auger and Coulomb charging effects in semiconductor nanocrystallites. Phys. Rev. Lett. 1995, 75, 2228. [Google Scholar] [CrossRef]
- Downer, M.; Shank, C. Ultrafast heating of silicon on sapphire by femtosecond optical pulses. Phys. Rev. Lett. 1986, 56, 761. [Google Scholar] [CrossRef]
- Haug, A. Auger recombination in direct-gap semiconductors: Band-structure effects. J. Phys. C Solid State Phys. 1983, 16, 4159. [Google Scholar] [CrossRef]
- Ghosh, G.; Marjit, K.; Ghosh, S.; Patra, A. Hot Carrier Cooling and Biexciton Dynamics of Anisotropic-Shaped CsPbBr3 Perovskite Nanocrystals. J. Phys. Chem. C 2023, 127, 8670–8679. [Google Scholar] [CrossRef]
- Papagiorgis, P.; Protesescu, L.; Kovalenko, M.V.; Othonos, A.; Itskos, G. Long-Lived Hot Carriers in Formamidinium Lead Iodide Nanocrystals. J. Phys. Chem. C 2017, 121, 12434–12440. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, X.; Liu, S.; Zhang, B.; Lin, K.; Zhang, J.; Conibeer, G. A review on thermalization mechanisms and prospect absorber materials for the hot carrier solar cells. Sol. Energy Mater. Sol. Cells 2021, 225, 111073. [Google Scholar] [CrossRef]
- Choi, C.; Kwon, Y.; Krasinski, J.; Park, G.; Setlur, G.; Song, J.; Chang, Y. Ultrafast carrier dynamics in a highly excited GaN epilayer. Phys. Rev. B 2001, 63, 115315. [Google Scholar] [CrossRef]
- Nie, Z.; Gao, X.; Ren, Y.; Xia, S.; Wang, Y.; Shi, Y.; Zhao, J.; Wang, Y. Harnessing hot phonon bottleneck in metal halide perovskite nanocrystals via interfacial electron–phonon coupling. Nano Lett. 2020, 20, 4610–4617. [Google Scholar] [CrossRef]
- Zhang, Y.; Conibeer, G.; Liu, S.; Zhang, J.; Guillemoles, J.F. Review of the mechanisms for the phonon bottleneck effect in III–V semiconductors and their application for efficient hot carrier solar cells. Prog. Photovolt. Res. Appl. 2022, 30, 581–596. [Google Scholar] [CrossRef]
- Faber, T.; Filipovic, L.; Koster, L. The Hot Phonon Bottleneck Effect in Metal Halide Perovskites. J. Phys. Chem. Lett. 2024, 15, 12601–12607. [Google Scholar] [CrossRef]
- Klemens, P. Anharmonic decay of optical phonons. Phys. Rev. 1966, 148, 845. [Google Scholar] [CrossRef]
- Pomeroy, J.; Kuball, M.; Lu, H.; Schaff, W.; Wang, X.; Yoshikawa, A. Phonon lifetimes and phonon decay in InN. Appl. Phys. Lett. 2005, 86, 223501. [Google Scholar] [CrossRef]
- Inoshita, T.; Sakaki, H. Electron-phonon interaction and the so-called phonon bottleneck effect in semiconductor quantum dots. Phys. B Condens. Matter 1996, 227, 373–377. [Google Scholar] [CrossRef]
- Sugawara, M.; Mukai, K.; Shoji, H. Effect of phonon bottleneck on quantum-dot laser performance. Appl. Phys. Lett. 1997, 71, 2791–2793. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, L.; Zhang, B.; Wang, P.; Xu, C. Quantitative study on the mechanisms underlying the phonon bottleneck effect in InN/InGaN multiple quantum wells. Appl. Phys. Lett. 2020, 116, 103104. [Google Scholar] [CrossRef]
- Prabhu, S.; Vengurlekar, A.; Roy, S.; Shah, J. Nonequilibrium dynamics of hot carriers and hot phonons in CdSe and GaAs. Phys. Rev. B 1995, 51, 14233. [Google Scholar] [CrossRef]
- Prabhu, S.; Vengurlekar, A. Hot-carrier energy-loss rates in alloy semiconductors. Phys. Rev. B 1996, 53, 7815. [Google Scholar] [CrossRef]
- Conibeer, G.; Zhang, Y.; Bremner, S.P.; Shrestha, S. Towards an understanding of hot carrier cooling mechanisms in multiple quantum wells. Jpn. J. Appl. Phys. 2017, 56, 091201. [Google Scholar] [CrossRef]
- Prezhdo, O.V. Multiple excitons and the electron–phonon bottleneck in semiconductor quantum dots: An ab initio perspective. Chem. Phys. Lett. 2008, 460, 1–9. [Google Scholar] [CrossRef]
- Wright, A.D.; Verdi, C.; Milot, R.L.; Eperon, G.E.; Pérez-Osorio, M.A.; Snaith, H.J.; Giustino, F.; Johnston, M.B.; Herz, L.M. Electron–phonon coupling in hybrid lead halide perovskites. Nat. Commun. 2016, 7, 11755. [Google Scholar] [CrossRef]
- Siekmann, J.; Ravishankar, S.; Kirchartz, T. Apparent defect densities in halide perovskite thin films and single crystals. ACS Energy Lett. 2021, 6, 3244–3251. [Google Scholar] [CrossRef]
- Jamal, M.; Shahahmadi, S.; Wadi, M.A.A.; Chelvanathan, P.; Asim, N.; Misran, H.; Hossain, M.; Amin, N.; Sopian, K.; Akhtaruzzaman, M. Effect of defect density and energy level mismatch on the performance of perovskite solar cells by numerical simulation. Optik 2019, 182, 1204–1210. [Google Scholar] [CrossRef]
- Lian, Z.; Yan, Q.; Gao, T.; Ding, J.; Lv, Q.; Ning, C.; Li, Q.; Sun, J.-l. Perovskite CH3NH3PbI3 (Cl) single crystals: Rapid solution growth, unparalleled crystalline quality, and low trap density toward 108 cm−3. J. Am. Chem. Soc. 2016, 138, 9409–9412. [Google Scholar] [CrossRef]
- Pathak, C.; Pandey, S.K. Design, performance, and defect density analysis of efficient eco-friendly perovskite solar cell. IEEE Trans. Electron Devices 2020, 67, 2837–2843. [Google Scholar]
- Fang, T.-T. Elements of Structures and Defects of Crystalline Materials; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Bera, S.; Saha, A.; Mondal, S.; Biswas, A.; Mallick, S.; Chatterjee, R.; Roy, S. Review of defect engineering in perovskites for photovoltaic application. Mater. Adv. 2022, 3, 5234–5247. [Google Scholar] [CrossRef]
- Hassan, A.; Wang, Z.; Ahn, Y.H.; Azam, M.; Khan, A.A.; Farooq, U.; Zubair, M.; Cao, Y. Recent defect passivation drifts and role of additive engineering in perovskite photovoltaics. Nano Energy 2022, 101, 107579. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; Qi, W.; Zhou, X.; Li, J.; Cheng, J.; Zhao, Y.; Li, Y.; Zhang, X. Passivation of defects in perovskite solar cell: From a chemistry point of view. Nano Energy 2020, 77, 105237. [Google Scholar] [CrossRef]
- Ball, J.M.; Petrozza, A. Defects in perovskite-halides and their effects in solar cells. Nat. Energy 2016, 1, 16149. [Google Scholar] [CrossRef]
- Warby, J.; Zu, F.; Zeiske, S.; Gutierrez-Partida, E.; Frohloff, L.; Kahmann, S.; Frohna, K.; Mosconi, E.; Radicchi, E.; Lang, F. Understanding performance limiting interfacial recombination in pin perovskite solar cells. Adv. Energy Mater. 2022, 12, 2103567. [Google Scholar] [CrossRef]
- Jin, H.; Debroye, E.; Keshavarz, M.; Scheblykin, I.G.; Roeffaers, M.B.; Hofkens, J.; Steele, J.A. It’s a trap! On the nature of localised states and charge trapping in lead halide perovskites. Mater. Horiz. 2020, 7, 397–410. [Google Scholar] [CrossRef]
- Min, J.; Choi, Y.; Kim, D.; Park, T. Beyond Imperfections: Exploring Defects for Breakthroughs in Perovskite Solar Cell Research. Adv. Energy Mater. 2024, 14, 2302659. [Google Scholar] [CrossRef]
- Khan, M.T.; Almohammedi, A.; Kazim, S.; Ahmad, S. Charge carrier dynamics in perovskite solar cells. In Perovskite Solar Cells: Materials, Processes, and Devices; Wiley-VCH GmbH: Weinheim, Germany, 2021; pp. 389–429. [Google Scholar]
- Yin, W.-J.; Shi, T.; Yan, Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014, 26, 4653–4658. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, Y.; He, J.; Frauenheim, T.; Prezhdo, O.V. Enhancing Extraction and Suppressing Cooling of Hot Electrons in Lead Halide Perovskites by Dipolar Surface Passivation. J. Am. Chem. Soc. 2024, 146, 29905–29912. [Google Scholar] [CrossRef]
- Ye, J.; Mondal, N.; Carwithen, B.P.; Zhang, Y.; Dai, L.; Fan, X.-B.; Mao, J.; Cui, Z.; Ghosh, P.; Otero-Martínez, C.; et al. Extending the defect tolerance of halide perovskite nanocrystals to hot carrier cooling dynamics. Nat. Commun. 2024, 15, 8120. [Google Scholar] [CrossRef]
- Hopper, T.R.; Gorodetsky, A.; Frost, J.M.; Müller, C.; Lovrincic, R.; Bakulin, A.A. Ultrafast Intraband Spectroscopy of Hot-Carrier Cooling in Lead-Halide Perovskites. ACS Energy Lett. 2018, 3, 2199–2205. [Google Scholar] [CrossRef]
- Ghosh, D.; Perez, C.M.; Prezhdo, O.; Nie, W.; Tretiak, S.; Neukirch, A.J. Impact of composition engineering on charge carrier cooling in hybrid perovskites: Computational insights. J. Mater. Chem. C 2022, 10, 9563–9572. [Google Scholar] [CrossRef]
- Kovalenko, M.V.; Protesescu, L.; Bodnarchuk, M.I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 2017, 358, 745–750. [Google Scholar] [CrossRef]
- Wieghold, S.; Sullivan, C.M.; Nienhaus, L. Turning Up the Heat: Ultrafast Hot Carrier Extraction in FAPbBr(3). ACS Cent. Sci. 2024, 10, 10–12. [Google Scholar] [CrossRef]
- Nadinov, I.; Almasabi, K.; Gutiérrez-Arzaluz, L.; Thomas, S.; Hasanov, B.E.; Bakr, O.M.; Alshareef, H.N.; Mohammed, O.F. Real-Time Tracking of Hot Carrier Injection at the Interface of FAPbBr3 Perovskite Using Femtosecond Mid-IR Spectroscopy. ACS Cent. Sci. 2024, 10, 43–53. [Google Scholar] [CrossRef]
- Gélvez-Rueda, M.C.; Renaud, N.; Grozema, F.C. Temperature Dependent Charge Carrier Dynamics in Formamidinium Lead Iodide Perovskite. J. Phys. Chem. C 2017, 121, 23392–23397. [Google Scholar] [CrossRef]
- Lin, W.; Canton, S.E.; Zheng, K.; Pullerits, T. Carrier Cooling in Lead Halide Perovskites: A Perspective on Hot Carrier Solar Cells. ACS Energy Lett. 2024, 9, 298–307. [Google Scholar] [CrossRef]
- Bernardi, M.; Vigil-Fowler, D.; Ong, C.S.; Neaton, J.B.; Louie, S.G. Ab initio study of hot electrons in GaAs. Proc. Natl. Acad. Sci. USA 2015, 112, 5291–5296. [Google Scholar] [CrossRef]
- Rosenwaks, Y.; Hanna, M.C.; Levi, D.H.; Szmyd, D.M.; Ahrenkiel, R.K.; Nozik, A.J. Hot-carrier cooling in GaAs: Quantum wells versus bulk. Phys. Rev. B 1993, 48, 14675–14678. [Google Scholar] [CrossRef]
- Zhang, C.; Fan, Y.; Huang, X.; Zhang, K.H.L.; Beard, M.C.; Yang, Y. Hot-carrier transfer at photocatalytic silicon/platinum interfaces. J. Chem. Phys. 2020, 152, 144705. [Google Scholar] [CrossRef]
- Yan, W.; Long, L.; Zang, Y.; Yang, G.; Liang, G. Direct observation of significant hot carrier cooling suppression in a two-dimensional silicon phononic crystal. NPG Asia Mater. 2022, 14, 51. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, C.; Chen, L.; Qin, Z.; Huang, X.; Wang, X.; Xiao, M. Ultrafast dynamics of photoexcited carriers in perovskite semiconductor nanocrystals. Nanophotonics 2021, 10, 1943–1965. [Google Scholar] [CrossRef]
- Minda, I.; Horn, J.; Ahmed, E.; Schlettwein, D.; Schwoerer, H. Ultrafast charge dynamics in mixed cation–mixed halide perovskite thin films. ChemPhysChem 2018, 19, 3010–3017. [Google Scholar] [CrossRef]
- Valverde-Chávez, D.A.; Ponseca, C.S.; Stoumpos, C.C.; Yartsev, A.; Kanatzidis, M.G.; Sundström, V.; Cooke, D.G. Intrinsic femtosecond charge generation dynamics in single crystal CH3NH3PbI3. Energy Environ. Sci. 2015, 8, 3700–3707. [Google Scholar] [CrossRef]
- Piatkowski, P.; Cohen, B.; Ponseca, C.S., Jr.; Salado, M.; Kazim, S.; Ahmad, S.; Sundstrom, V.; Douhal, A. Unraveling charge carriers generation, diffusion, and recombination in formamidinium lead triiodide perovskite polycrystalline thin film. J. Phys. Chem. Lett. 2016, 7, 204–210. [Google Scholar] [CrossRef]
- Piatkowski, P.; Cohen, B.; Ramos, F.J.; Di Nunzio, M.; Nazeeruddin, M.K.; Grätzel, M.; Ahmad, S.; Douhal, A. Direct monitoring of ultrafast electron and hole dynamics in perovskite solar cells. Phys. Chem. Chem. Phys. 2015, 17, 14674–14684. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Y.; Fang, Y.; Jiang, Y.; Dai, Z.; Miao, J. Recent Advances in the A-Site Cation Engineering of Lead Halide Perovskites. Adv. Opt. Mater. 2024, 12, 2401367. [Google Scholar] [CrossRef]
- Vasa, P.; Ropers, C.; Pomraenke, R.; Lienau, C. Ultra-fast nano-optics. Laser Photonics Rev. 2009, 3, 483–507. [Google Scholar] [CrossRef]
- Shah, J. Ultrafast Spectroscopy of Semiconductors and Semiconductor Nanostructures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 115. [Google Scholar]
- Kovalenko, S.A.; Schanz, R.; Hennig, H.; Ernsting, N.P. Cooling dynamics of an optically excited molecular probe in solution from femtosecond broadband transient absorption spectroscopy. J. Chem. Phys. 2001, 115, 3256–3273. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Li, C.; Wang, A.; Deng, X.; Wang, S.; Yuan, Y.; Ding, L.; Hao, F. Insights into Ultrafast Carrier Dynamics in Perovskite Thin Films and Solar Cells. ACS Photonics 2020, 7, 1893–1907. [Google Scholar] [CrossRef]
- Ruckebusch, C.; Sliwa, M.; Pernot, P.; de Juan, A.; Tauler, R. Comprehensive data analysis of femtosecond transient absorption spectra: A review. J. Photochem. Photobiol. C Photochem. Rev. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Pydzińska, K.; Karolczak, J.; Kosta, I.; Tena-Zaera, R.; Todinova, A.; Idígoras, J.; Anta, J.A.; Ziółek, M. Determination of Interfacial Charge-Transfer Rate Constants in Perovskite Solar Cells. ChemSusChem 2016, 9, 1647–1659. [Google Scholar] [CrossRef]
- Cao, Y.; Feng, J.; Wang, M.; Yan, N.; Lou, J.; Feng, X.; Xiao, F.; Liu, Y.; Qi, D.; Yuan, Y.; et al. Interface Modification by Ammonium Sulfamate for High-Efficiency and Stable Perovskite Solar Cells. Adv. Energy Mater. 2023, 13, 2302103. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, T.; Zhang, C.; Liu, X.; Wang, J.; Lin, J.; Chen, X. Unveiling Charge Carrier Recombination, Extraction, and Hot-Carrier Dynamics in Indium Incorporated Highly Efficient and Stable Perovskite Solar Cells. Adv. Sci. 2022, 9, 2103491. [Google Scholar] [CrossRef]
- Berera, R.; van Grondelle, R.; Kennis, J.T.M. Ultrafast transient absorption spectroscopy: Principles and application to photosynthetic systems. Photosynth. Res. 2009, 101, 105–118. [Google Scholar] [CrossRef]
- Sum, T.C.; Mathews, N.; Xing, G.; Lim, S.S.; Chong, W.K.; Giovanni, D.; Dewi, H.A. Spectral features and charge dynamics of lead halide perovskites: Origins and interpretations. Acc. Chem. Res. 2016, 49, 294–302. [Google Scholar] [CrossRef]
- Chen, K.; Barker, A.J.; Morgan, F.L.; Halpert, J.E.; Hodgkiss, J.M. Effect of carrier thermalization dynamics on light emission and amplification in organometal halide perovskites. J. Phys. Chem. Lett. 2015, 6, 153–158. [Google Scholar] [CrossRef]
- Motti, S.G.; Meggiolaro, D.; Martani, S.; Sorrentino, R.; Barker, A.J.; De Angelis, F.; Petrozza, A. Defect activity in lead halide perovskites. Adv. Mater. 2019, 31, 1901183. [Google Scholar] [CrossRef]
- Norrish, R.G.W.; Porter, G. Chemical reactions produced by very high light intensities. Nature 1949, 164, 658. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Halas, N.J.; Nordlander, P. Plasmon-induced hot carrier science and technology. Nat. Nanotechnol. 2015, 10, 25–34. [Google Scholar] [CrossRef]
- Brown, A.M.; Sundararaman, R.; Narang, P.; Schwartzberg, A.M.; Goddard, W.A., III; Atwater, H.A. Experimental and ab initio ultrafast carrier dynamics in plasmonic nanoparticles. Phys. Rev. Lett. 2017, 118, 087401. [Google Scholar] [CrossRef]
- Hayes, G.; Samuel, I.; Phillips, R. Exciton dynamics in electroluminescent polymers studied by femtosecond time-resolved photoluminescence spectroscopy. Phys. Rev. B 1995, 52, R11569. [Google Scholar] [CrossRef]
- Tauc, J. Time-resolved spectroscopy of electronic relaxation processes. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 1984; Volume 21, pp. 299–327. [Google Scholar]
- Chen, X.; Kamat, P.V.; Janáky, C.; Samu, G.F. Charge transfer kinetics in halide perovskites: On the constraints of time-resolved spectroscopy measurements. ACS Energy Lett. 2024, 9, 3187–3203. [Google Scholar] [CrossRef]
- Narra, S.; Chung, C.-C.; Diau, E.W.-G.; Shigeto, S. Simultaneous Observation of an Intraband Transition and Distinct Transient Species in the Infrared Region for Perovskite Solar Cells. J. Phys. Chem. Lett. 2016, 7, 2450–2455. [Google Scholar] [CrossRef]
- Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- Blancon, J.-C.; Nie, W.; Neukirch, A.J.; Gupta, G.; Tretiak, S.; Cognet, L.; Mohite, A.D.; Crochet, J.J. The Effects of Electronic Impurities and Electron–Hole Recombination Dynamics on Large-Grain Organic–Inorganic Perovskite Photovoltaic Efficiencies. Adv. Funct. Mater. 2016, 26, 4283–4292. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, Z.; Lou, H.; Lin, C.; Chen, Z.; Li, J.; He, H.; Ye, Z. Achieving long carrier lifetime and high optical gain in all-inorganic CsPbBr3 perovskite films via top and bottom surface modification. Phys. Chem. Chem. Phys. 2019, 21, 21996–22001. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X.; Jiang, Q.; Wang, P.; Yin, Z.; Zhang, X.; Tan, H.; Yang, Y.; Wei, M.; Sutherland, B.R.; et al. Ultra-bright and highly efficient inorganic based perovskite light-emitting diodes. Nat. Commun. 2017, 8, 15640. [Google Scholar] [CrossRef]
- Pazos-Outón, L.M.; Szumilo, M.; Lamboll, R.; Richter, J.M.; Crespo-Quesada, M.; Abdi-Jalebi, M.; Beeson, H.J.; Vrućinić, M.; Alsari, M.; Snaith, H.J.; et al. Photon recycling in lead iodide perovskite solar cells. Science 2016, 351, 1430–1433. [Google Scholar] [CrossRef]
- Ashmontas, S.; Gradauskas, I.; Naudjyus, K.; Shirmulis, E. Photoresponse of InSb-based pn structures during illumination by a CO2 laser. Semiconductors 1994, 28, 1089–1091. [Google Scholar]
- Mujahid, M.; Čerškus, A.; Gradauskas, J.; Grigucevičienė, A.; Giraitis, R.; Leinartas, K.; Lučun, A.; Petrauskas, K.; Selskis, A.; Sužiedėlis, A.; et al. Unveiling the Influence of Hot Carriers on Photovoltage Formation in Perovskite Solar Cells. Materials 2025, 18, 85. [Google Scholar] [CrossRef]
- Hidayat, R.; Nurunnizar, A.A.; Fariz, A.; Herman; Rosa, E.S.; Shobih; Oizumi, T.; Fujii, A.; Ozaki, M. Revealing the charge carrier kinetics in perovskite solar cells affected by mesoscopic structures and defect states from simple transient photovoltage measurements. Sci. Rep. 2020, 10, 19197. [Google Scholar] [CrossRef]
- Ratner, M. The Physics of Solar Cells; Third Generation Photovoltaics: Advanced Solar Energy Conversion. Phys. Today 2004, 57, 71–72. [Google Scholar] [CrossRef]
- König, D.; Casalenuovo, K.; Takeda, Y.; Conibeer, G.; Guillemoles, J.F.; Patterson, R.; Huang, L.M.; Green, M.A. Hot carrier solar cells: Principles, materials and design. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 2862–2866. [Google Scholar] [CrossRef]
- Sherkar, T.S.; Momblona, C.; Gil-Escrig, L.; Avila, J.; Sessolo, M.; Bolink, H.J.; Koster, L.J.A. Recombination in perovskite solar cells: Significance of grain boundaries, interface traps, and defect ions. ACS Energy Lett. 2017, 2, 1214–1222. [Google Scholar] [CrossRef]
- Yang, S.; Fu, W.; Zhang, Z.; Chen, H.; Li, C.-Z. Recent advances in perovskite solar cells: Efficiency, stability and lead-free perovskite. J. Mater. Chem. A 2017, 5, 11462–11482. [Google Scholar] [CrossRef]
- Kamarudin, M.A.; Hayase, S. Passivation of Hybrid/Inorganic Perovskite Solar Cells. In Perovskite Solar Cells; Wiley-VCH: Weinheim, Germany, 2021; pp. 91–111. [Google Scholar]
- Ašmontas, S.; Gradauskas, J.; Grigucevičienė, A.; Leinartas, K.; Lučun, A.; Mujahid, M.; Petrauskas, K.; Selskis, A.; Sužiedėlis, A.; Šilėnas, A. Triple-cation perovskite/silicon tandem solar cell. Ukr. J. Phys. Opt. 2022, 23, 193. [Google Scholar] [CrossRef]
- Ašmontas, S.; Mujahid, M. Recent progress in perovskite tandem solar cells. Nanomaterials 2023, 13, 1886. [Google Scholar] [CrossRef]


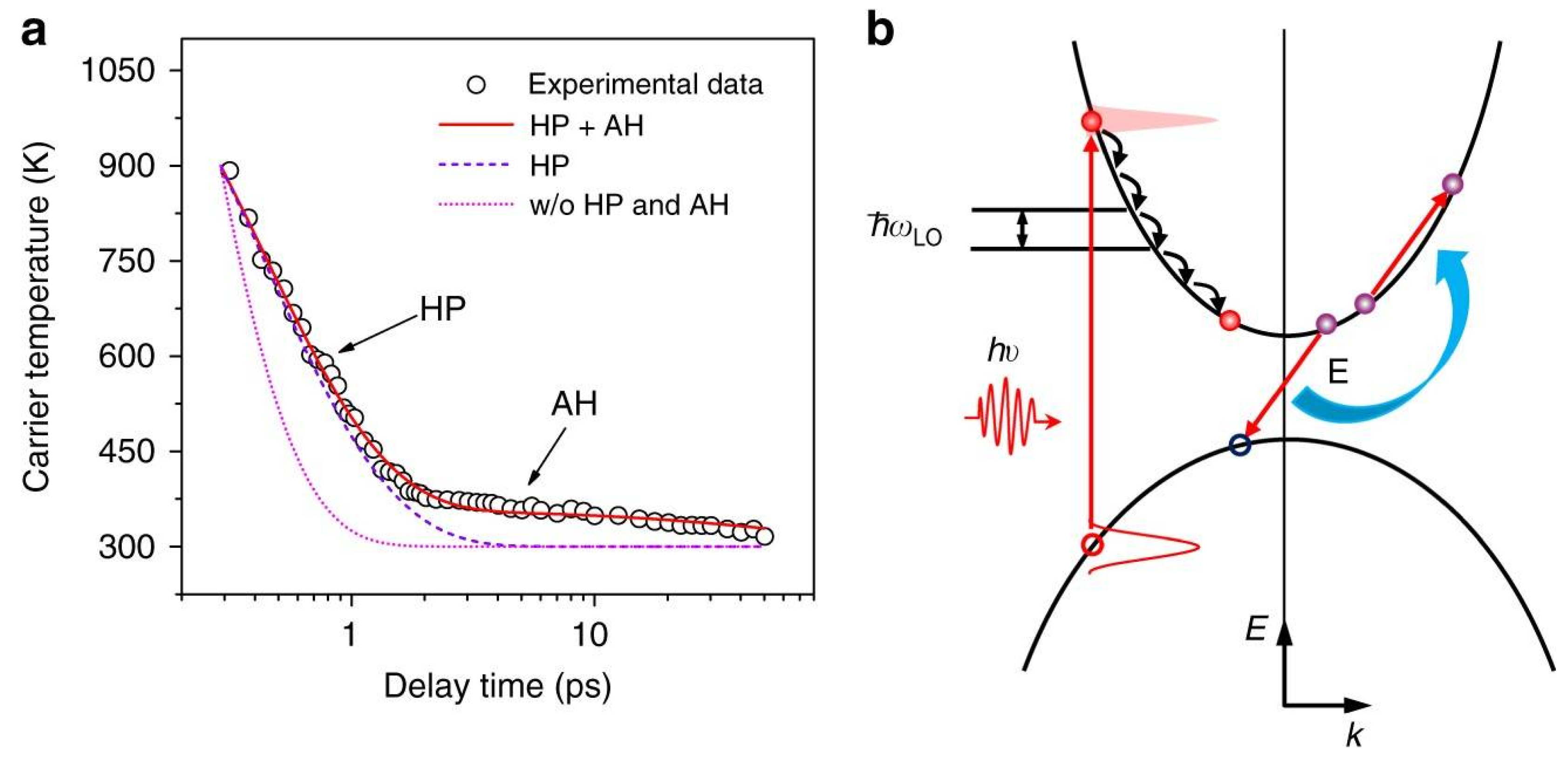

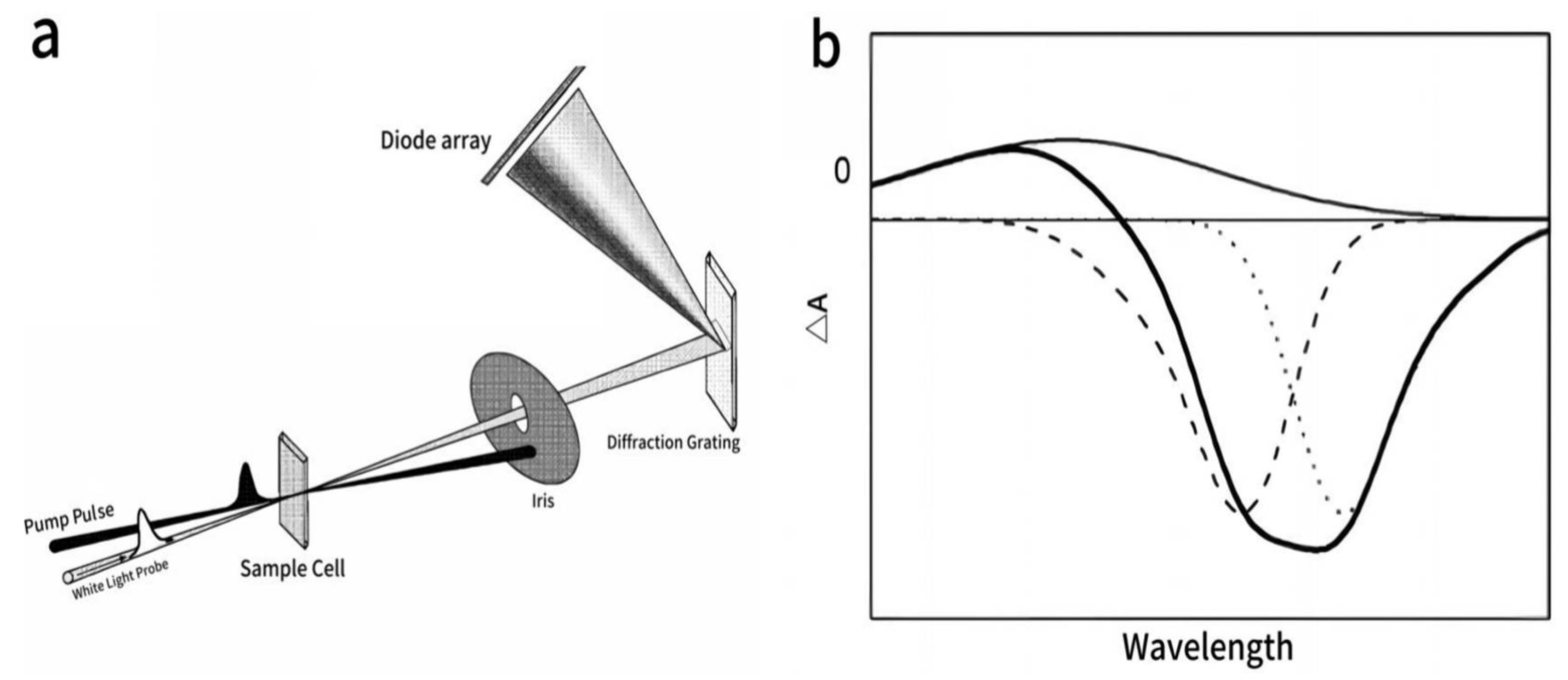
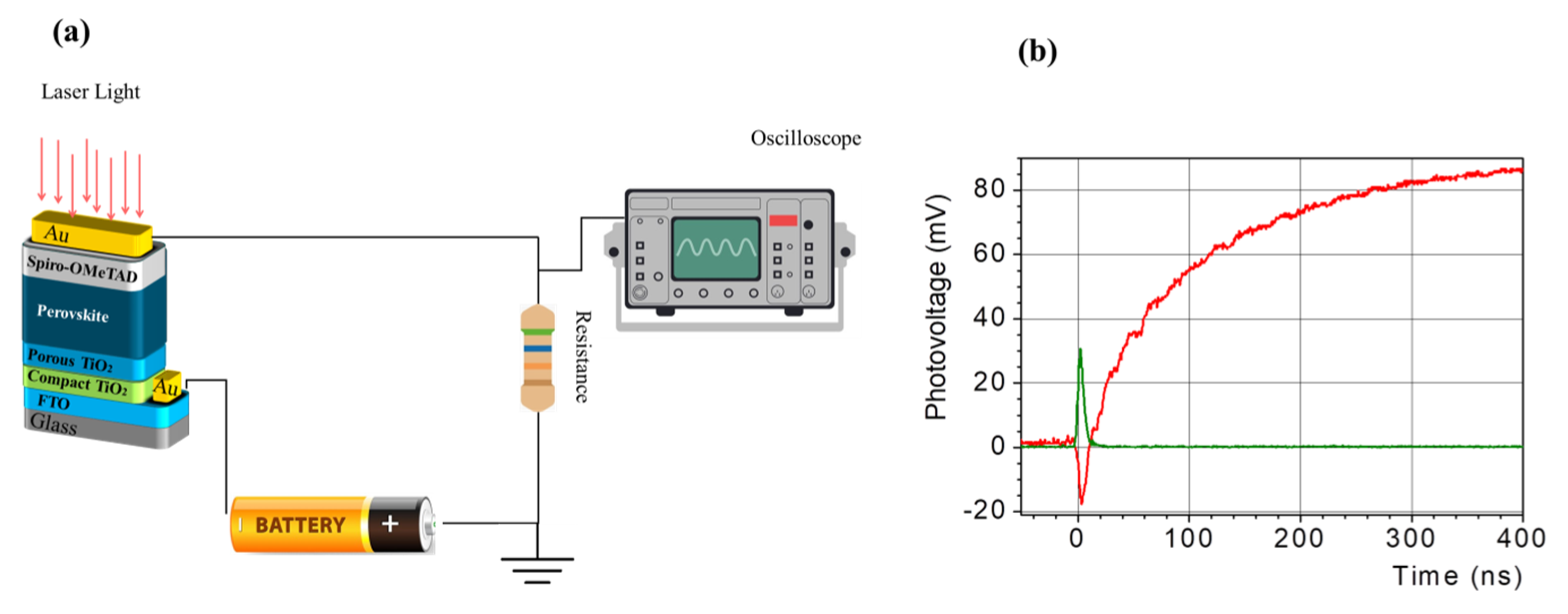
| Material | Cooling Time (to Near-Band-Edge Temperature) | Finding | Ref |
|---|---|---|---|
| MAPbI3 | ≈60 ps (high fluence, up to 600 K) | Nearly two orders of magnitude slower than GaAs; lifetime reaches ≈ 60 ps at elevated carrier density | [135] |
| CsPbBr3 | 0.8 ps (moderate density) to 17 ps (high density) | Bottleneck yields 0.8 ps at ∼2 × 1018 cm−3, stretching to ∼17 ps above 1018 cm−3 | [131] |
| GaAs | ≈0.6 ps | Inferred from perovskite–GaAs comparison: perovskite is ~100× slower (MAPbI3 ∼60 ps vs. GaAs ∼0.6 ps) | [1] |
| Si | ≈0.15 ps (150 fs) | Thermalization via electron-phonon scattering in Si occurs in ~150 fs | [133] |
| Material | τcool (ps) | Conditions | Ref |
|---|---|---|---|
| Perovskites | 0.2–1 ps | FA/Cs/MA lead halides (varies with composition) | [250] |
| GaAs (bulk) | ~1.4 ps | Overall cooling to CBM via Γ-valley | [251] |
| GaAs (QWs, n > 1018 cm−3) | tens–hundreds ps | Hot-phonon bottleneck at high density | [252] |
| Si (bulk) | ~0.35 ± 0.08 ps | Probe-wavelength TAS | [253] |
| Si (2D phononic) | 10–16 ps | Phononic crystal suppression | [254] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mujahid, M.; Gradauskas, J.; Sužiedėlis, A.; Širmulis, E.; Ašmontas, S. Recent Advancements in Understanding Hot Carrier Dynamics in Perovskite Solar Cells. Energies 2025, 18, 3543. https://doi.org/10.3390/en18133543
Mujahid M, Gradauskas J, Sužiedėlis A, Širmulis E, Ašmontas S. Recent Advancements in Understanding Hot Carrier Dynamics in Perovskite Solar Cells. Energies. 2025; 18(13):3543. https://doi.org/10.3390/en18133543
Chicago/Turabian StyleMujahid, Muhammad, Jonas Gradauskas, Algirdas Sužiedėlis, Edmundas Širmulis, and Steponas Ašmontas. 2025. "Recent Advancements in Understanding Hot Carrier Dynamics in Perovskite Solar Cells" Energies 18, no. 13: 3543. https://doi.org/10.3390/en18133543
APA StyleMujahid, M., Gradauskas, J., Sužiedėlis, A., Širmulis, E., & Ašmontas, S. (2025). Recent Advancements in Understanding Hot Carrier Dynamics in Perovskite Solar Cells. Energies, 18(13), 3543. https://doi.org/10.3390/en18133543







