Flat vs. Curved: Machine Learning Classification of Flexible PV Panel Geometries
Abstract
1. Introduction
2. Background
3. Experimental Setup
- is the maximum power point in [W];
- is the surface area of the photovoltaic panel in [m2];
- is the solar irradiance in [W/m2].
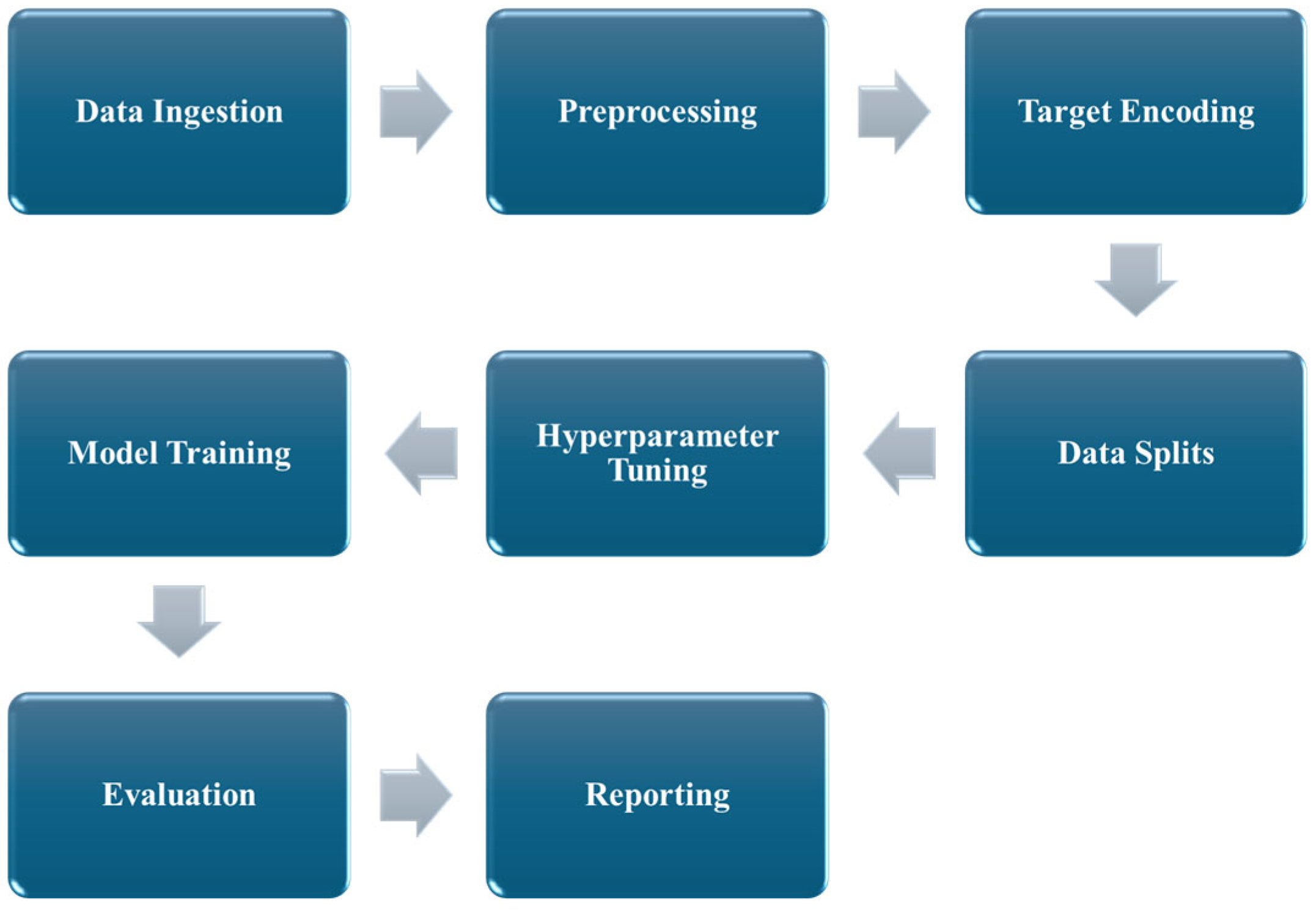
4. Deployed Machine Learning Methods
4.1. Data Description
4.2. Machine Learning Models
4.2.1. Random Forest
4.2.2. Extreme Gradient Boosting
4.2.3. Kolmogorov–Arnold Network
4.2.4. Multi-Layer Perceptron
4.2.5. Cross-Validation and Hyperparameter Tuning Strategies
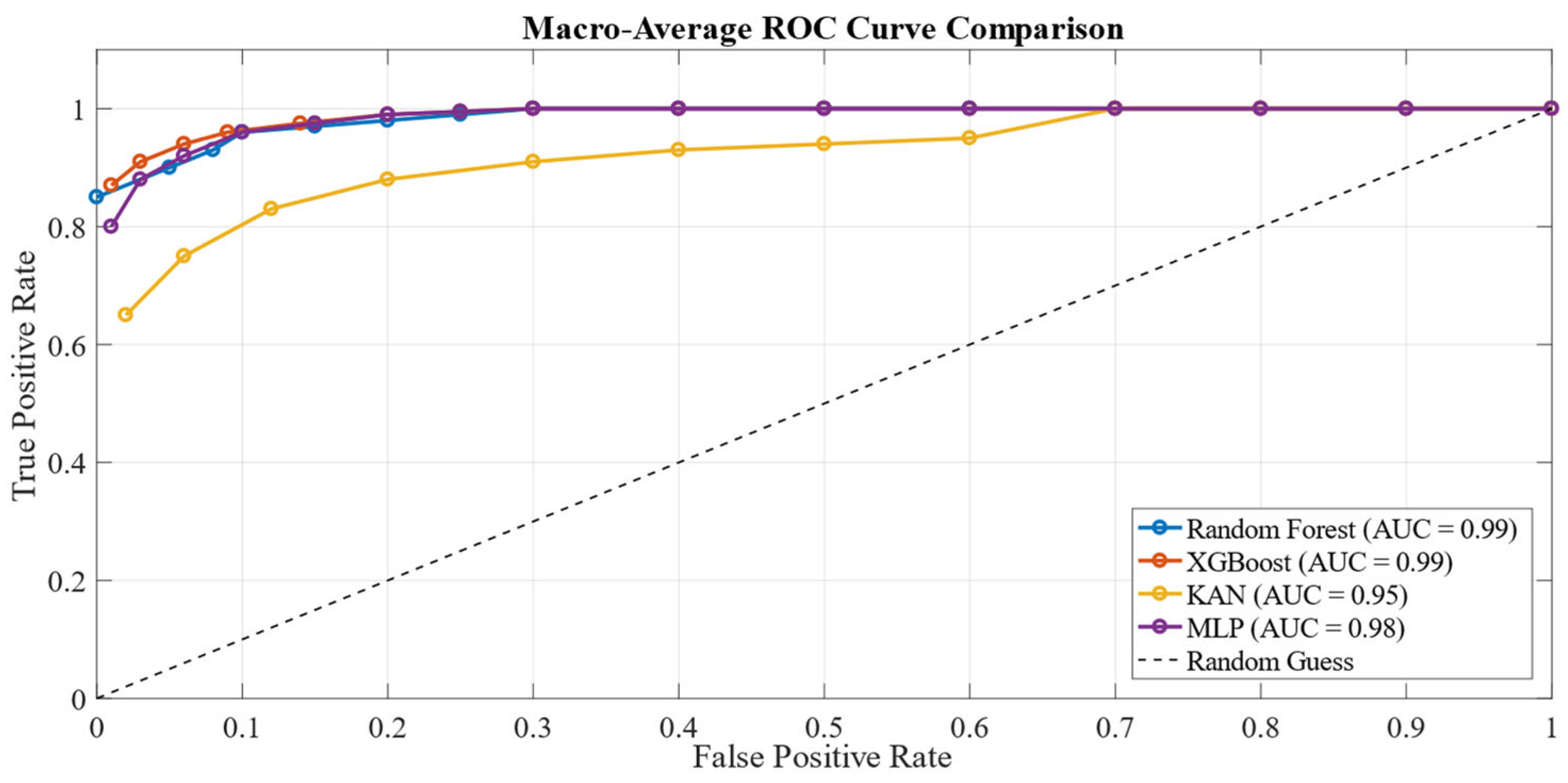
5. Results
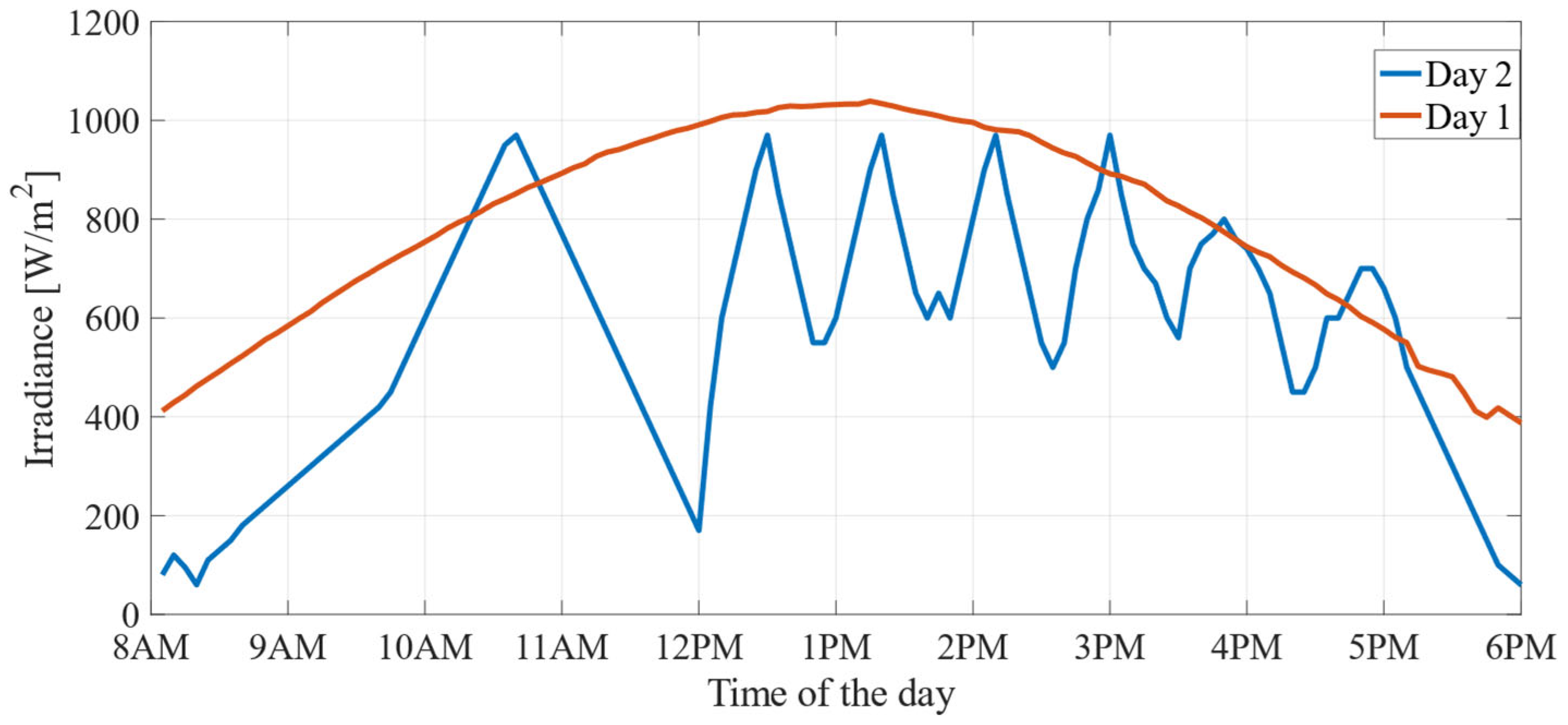
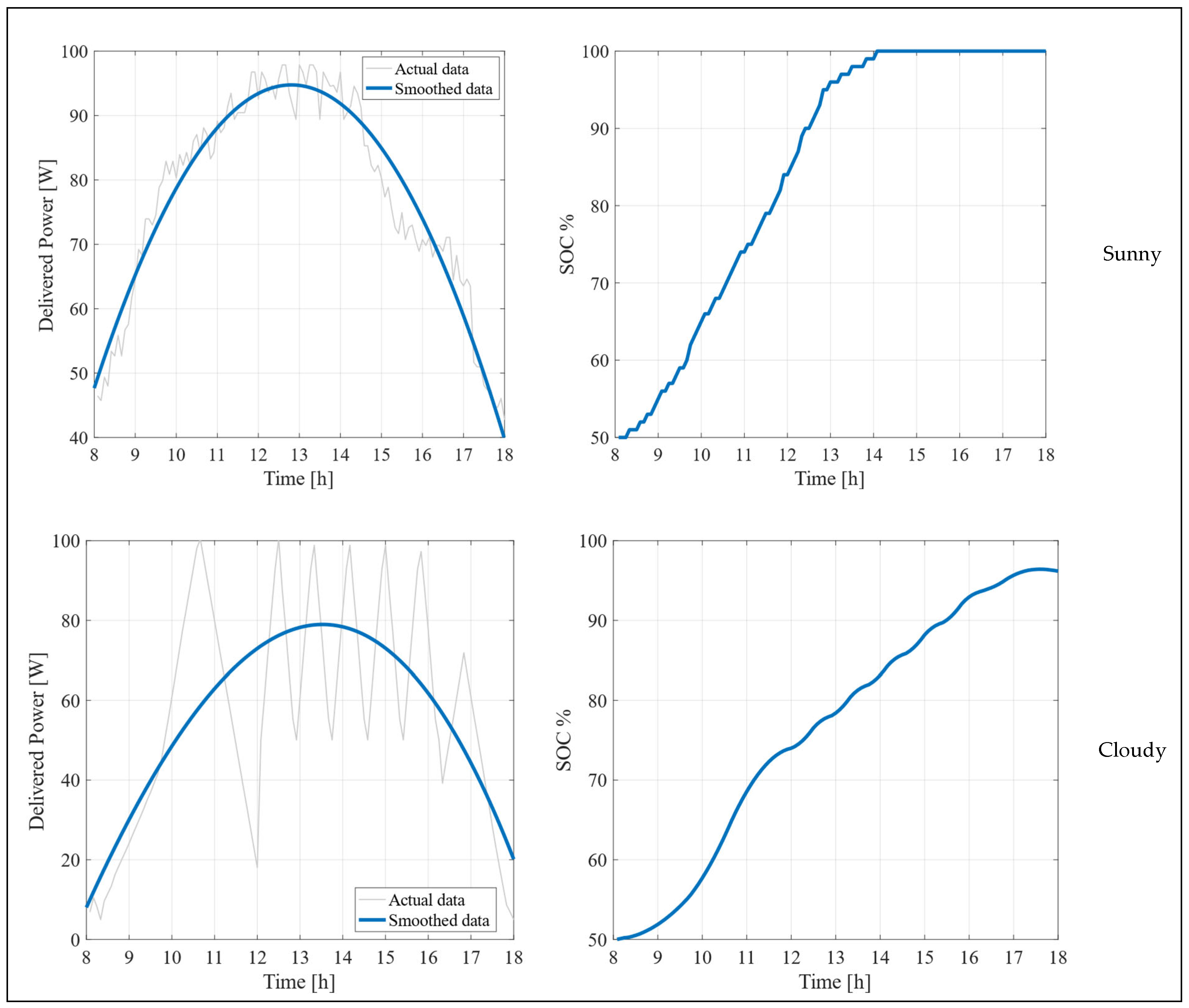
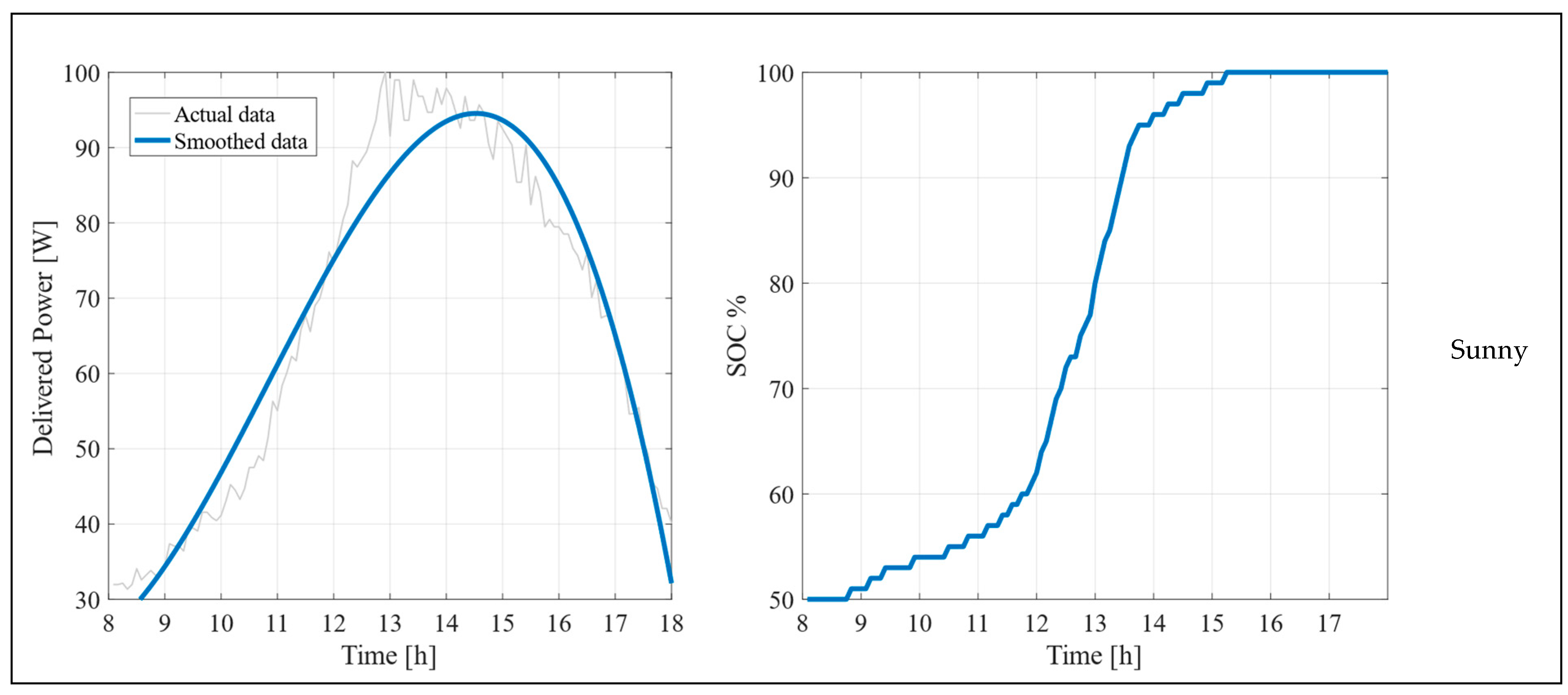
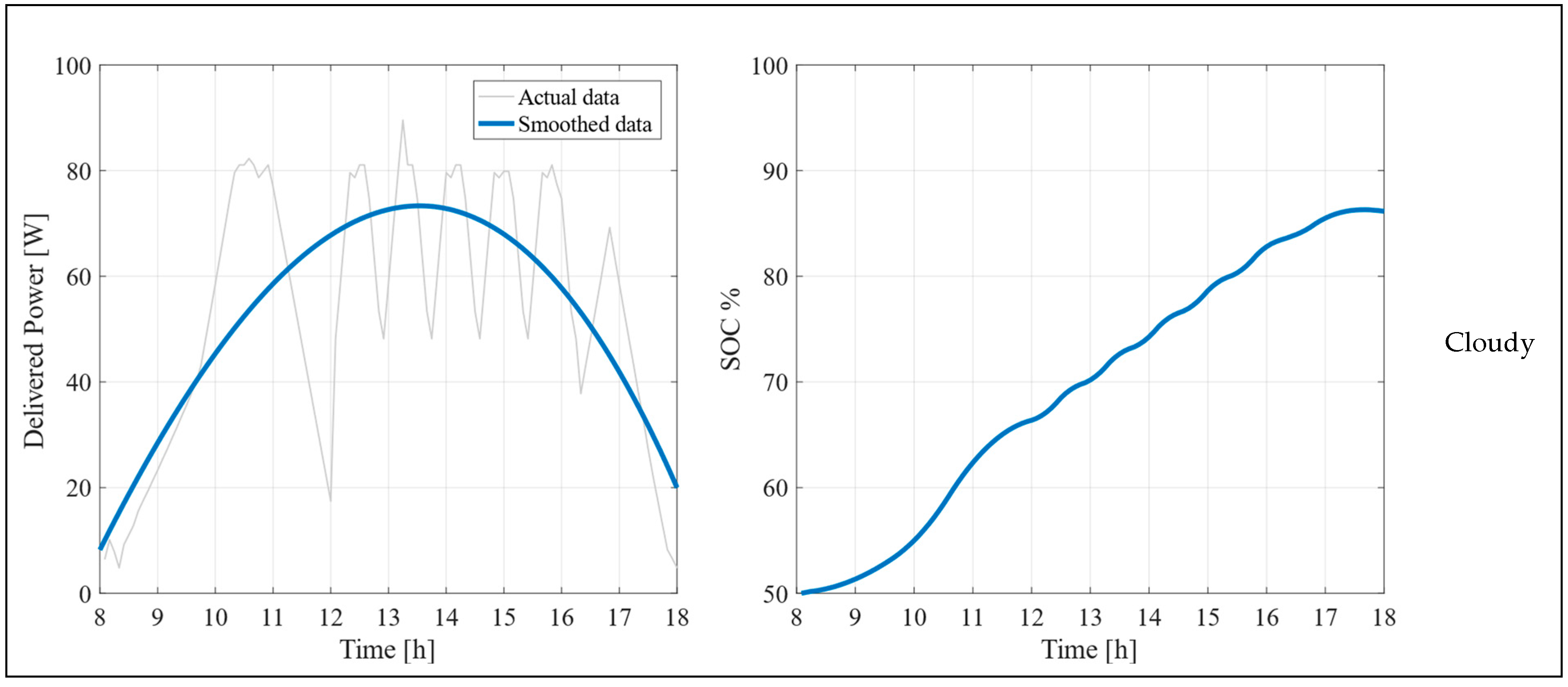
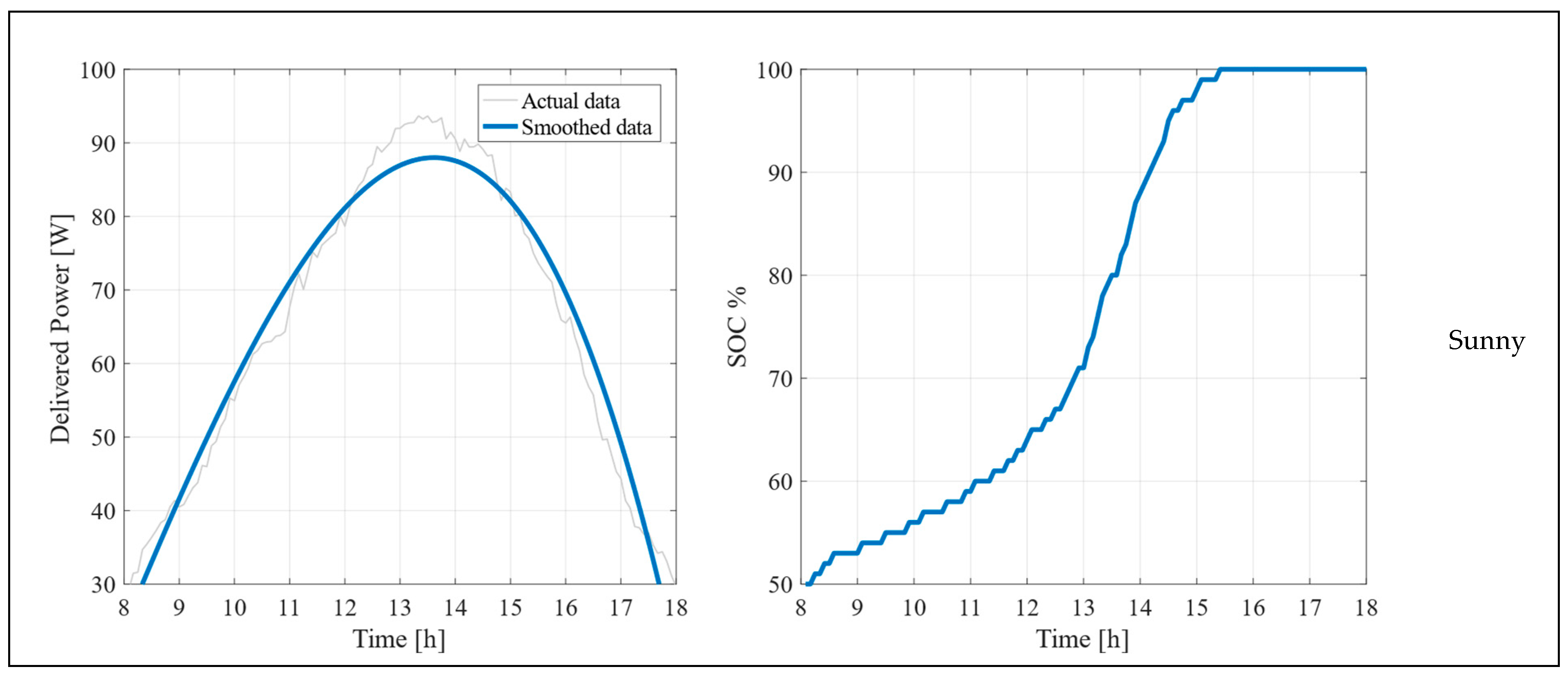
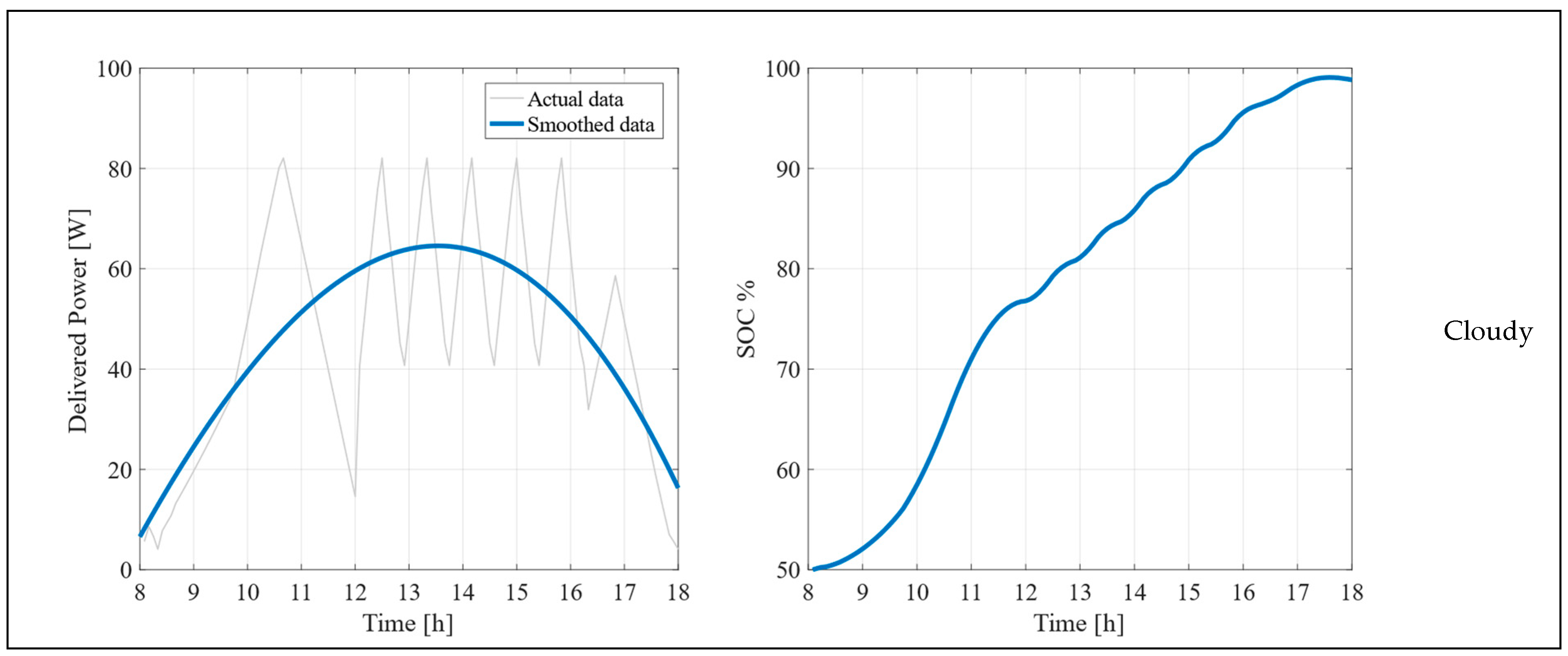
5.1. Experimental Results
5.2. ML Models Results
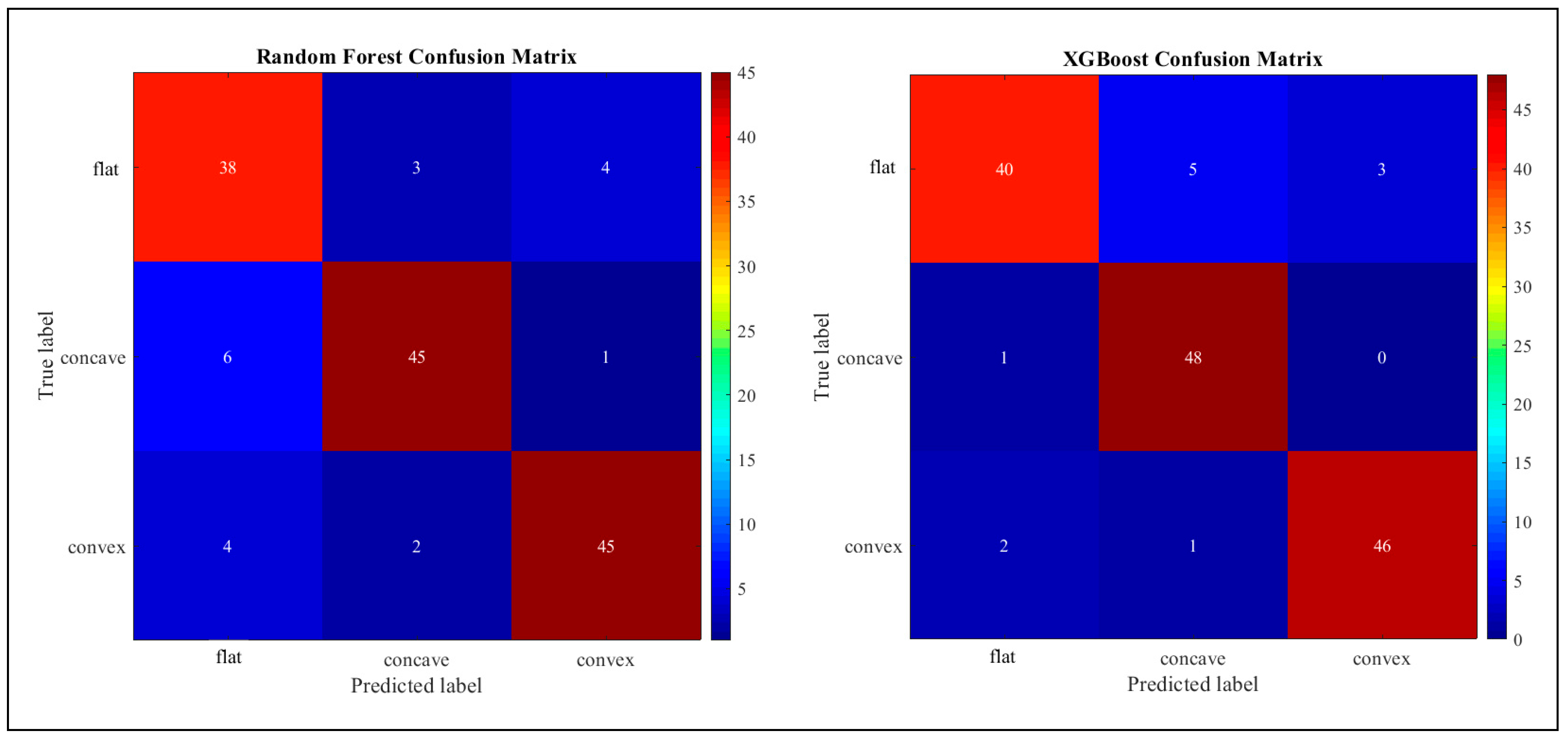
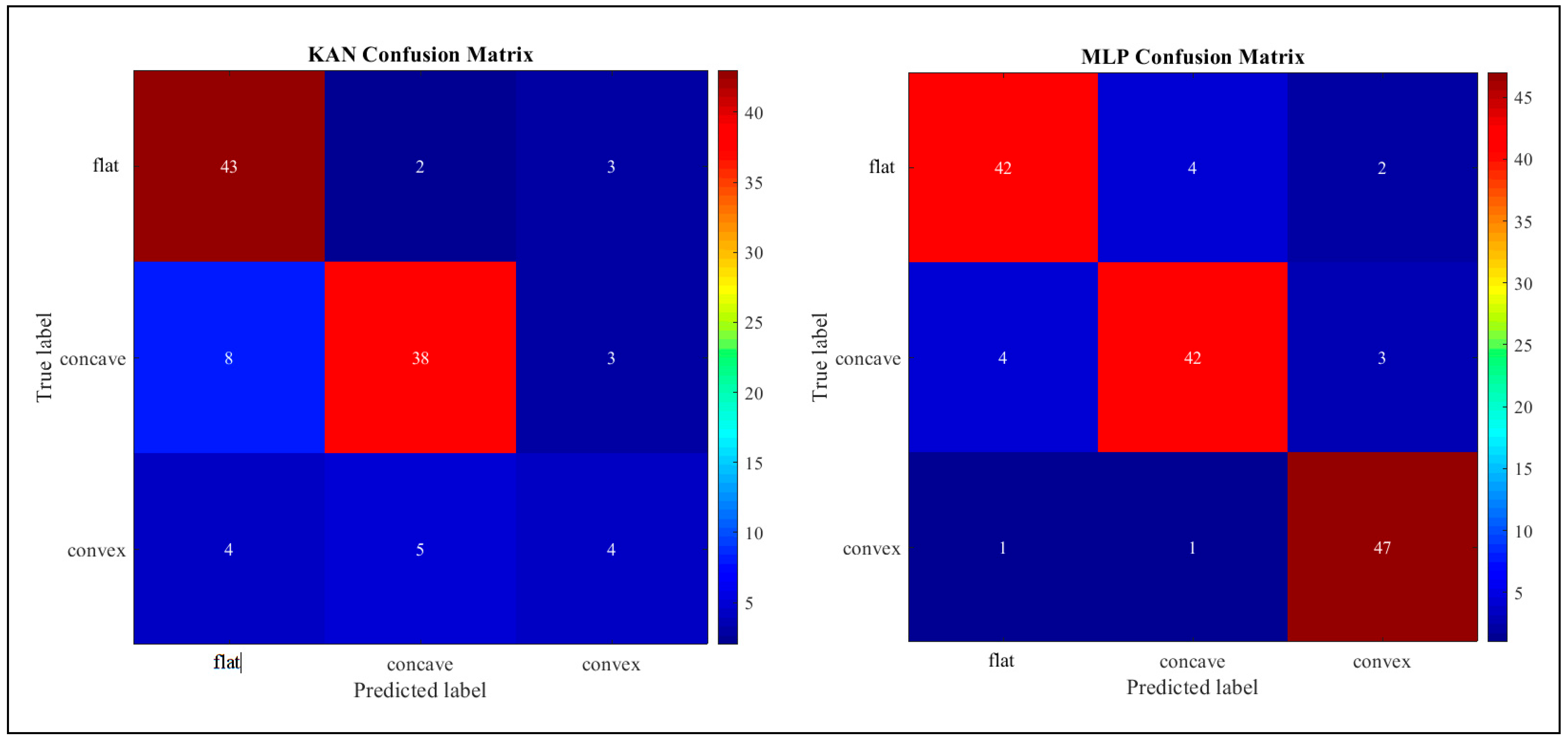
5.2.1. Confusion Matrix Insights
- The Random Forest (RF) classifier shows accurate results distinguishing between concave and convex PV modules with a recall of 90% but does not perform well with the flat module configuration, achieving 88% precision and 79% recall. This suggests that RF’s splitting criteria are more suitable with unique geometries.
- XGBoost achieved the best performance among all ML models, with 93% precision with the flat module and 98% recall with the unique module geometries.
- The Kolmogorov–Arnold Network (KAN) achieved a high recall of 90% with the flat PV module but a precision of only 78%, showing the false identification of curved modules’ instances. The KAN’s recall with the concave PV module was only 78%, showing some difficulty in identifying unique module geometries.
- The Multi-Layer Perceptron (MLP) showed 96% recall with the convex PV module and mediocre precision and recall with the other setups. Figure 8 illustrates the confusion matrices of all four deployed models.
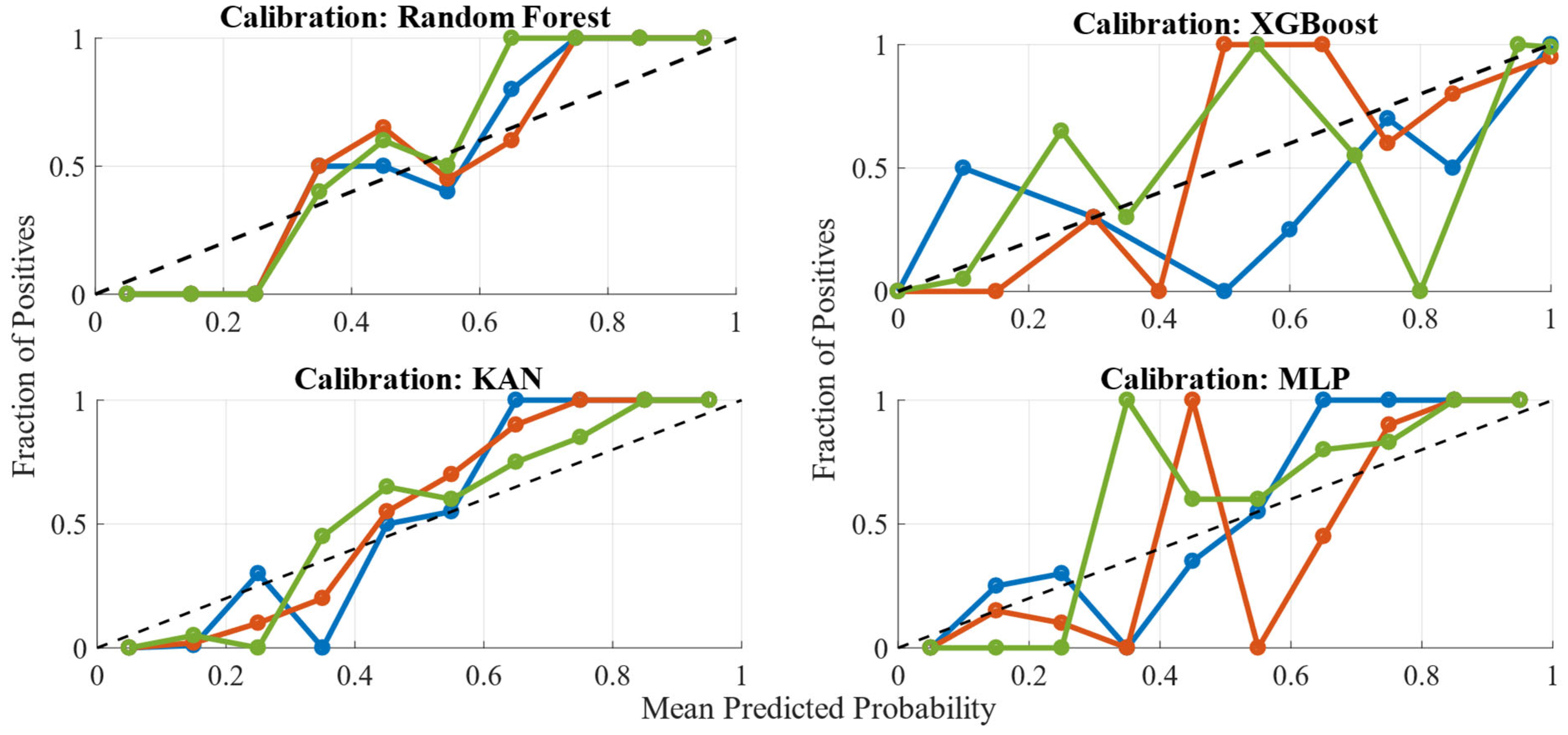
5.2.2. Calibration Analysis Across Models
5.2.3. Shapley Additive Explanations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| G | Solar Irradiance (W/m2) |
| IEA | International Energy Agency |
| Isc | Short Circuit Current |
| KAN | Kolmogorov–Arnold Network |
| LSTM | Long Short-Term Memory |
| MLP | Multi-Layer Perceptron |
| ML | Machine Learning |
| PV | Photovoltaic |
| RF | Random Forest |
| RNN | Recurrent Neural Network |
| ROC–AUC | Receiver operating characteristics–Area under the curve |
| SHAP | Shapley Additive Explanations |
| SOC | State of Charge |
| SVM | Support Vector Machine |
| V | Voltage (Volts) |
| Voc | Open Circuit Voltage |
| W | Watt/Power |
| XGBoost | Extreme Gradient Boosting |
References
- Renewables-2024. Available online: https://www.iea.org/reports/renewables-2024 (accessed on 20 March 2025).
- IEA Report. 2025. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 20 March 2025).
- Vodapally, S.N.; Ali, M.H. A Comprehensive Review of Solar Photovoltaic (PV) Technologies, Architecture, and Its Applications to Improved Efficiency. Energies 2023, 16, 319. [Google Scholar] [CrossRef]
- Chung, J.; Kim, S.-W.; Li, Y.; Mariam, T.; Wang, X.; Rajakaruna, M.; Saeed, M.M.; Abudulimu, A.; Shin, S.S.; Guye, K.N.; et al. Engineering Perovskite Precursor Inks for Scalable Production of High-Efficiency Perovskite Photovoltaic Modules. Adv. Energy Mater. 2023, 13, 2300595. [Google Scholar] [CrossRef]
- Manasrah, A.; Masoud, M.; Jaradat, Y.; Bevilacqua, P. Investigation of a Real-Time Dynamic Model for a PV Cooling System. Energies 2022, 15, 1836. [Google Scholar] [CrossRef]
- Nezamisavojbolaghi, M.; Davodian, E.; Bouich, A.; Tlemçani, M.; Mesbahi, O.; Janeiro, F.M. The Impact of Dust Deposition on PV Panels’ Efficiency and Mitigation Solutions: Review Article. Energies 2023, 16, 8022. [Google Scholar] [CrossRef]
- Manasrah, A.; Masoud, M.; Jaradat, Y.; Alia, M.; Almanasra, S.; Suwais, K. Shading Anomaly Detection Framework for Bi-Facial Photovoltaic Modules. Energy Sources Part Recovery Util. Environ. Eff. 2023, 45, 12955–12972. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zhang, X.; Yang, D.; Ma, D.; Ramakrishna, S.; Yuan, W.; Ye, T. Flexible Photovoltaic Micro-Power System Enabled with a Customized MPPT. Appl. Energy 2024, 367, 123425. [Google Scholar] [CrossRef]
- Fukuda, K.; Sun, L.; Du, B.; Takakuwa, M.; Wang, J.; Someya, T.; Marsal, L.F.; Zhou, Y.; Chen, Y.; Chen, H.; et al. A Bending Test Protocol for Characterizing the Mechanical Performance of Flexible Photovoltaics. Nat. Energy 2024, 9, 1335–1343. [Google Scholar] [CrossRef]
- Chen, Z.; Song, W.; Yu, K.; Ge, J.; Zhang, J.; Xie, L.; Peng, R.; Ge, Z. Small-Molecular Donor Guest Achieves Rigid 18.5% and Flexible 15.9% Efficiency Organic Photovoltaic via Fine-Tuning Microstructure Morphology. Joule 2021, 5, 2395–2407. [Google Scholar] [CrossRef]
- Tian, X.; Wang, J.; Ji, J.; Xia, T. Comparative Performance Analysis of the Flexible Flat/Curved PV Modules with Changing Inclination Angles. Energy Convers. Manag. 2022, 274, 116472. [Google Scholar] [CrossRef]
- Manasrah, A.; Al Zyoud, A.; Abdelhafez, E. Effect of Color and Nano Film Filters on the Performance of Solar Photovoltaic Module. Energy Sources Part Recovery Util. Environ. Eff. 2021, 43, 705–715. [Google Scholar] [CrossRef]
- Rollo, A.; Settino, J.; Bevilacqua, P.; Ferraro, V. Influence of Different Photovoltaic Cooling Strategies on Its Average Monthly Performance. In Proceedings of the 2023 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Milano, Italy, 29–31 May 2023; pp. 162–167. [Google Scholar]
- Fatima, K.; Faiz Minai, A.; Malik, H.; García Márquez, F.P. Experimental Analysis of Dust Composition Impact on Photovoltaic Panel Performance: A Case Study. Sol. Energy 2024, 267, 112206. [Google Scholar] [CrossRef]
- Oufettoul, H.; Lamdihine, N.; Motahhir, S.; Lamrini, N.; Abdelmoula, I.A.; Aniba, G. Comparative Performance Analysis of PV Module Positions in a Solar PV Array Under Partial Shading Conditions. IEEE Access 2023, 11, 12176–12194. [Google Scholar] [CrossRef]
- Nicoletti, F.; Cucumo, M.A.; Ferraro, V.; Kaliakatsos, D.; Gigliotti, A. A Thermal Model to Estimate PV Electrical Power and Temperature Profile along Panel Thickness. Energies 2022, 15, 7577. [Google Scholar] [CrossRef]
- Alcañiz, A.; Grzebyk, D.; Ziar, H.; Isabella, O. Trends and Gaps in Photovoltaic Power Forecasting with Machine Learning. Energy Rep. 2023, 9, 447–471. [Google Scholar] [CrossRef]
- Al-Qawabah, S.M.; Abu Shaban, N.; Al Aboushi, A.; Al-Salaymeh, A.; Alma’aitah, A.; Abdelhafez, E. Prediction of the Output of the Tri-Generation Concentrated Solar Power System Based on Artificial Neural Network. In Proceedings of the 2024 6th Global Power, Energy and Communication Conference (GPECOM), Budapest, Hungry, 4 June 2024; pp. 345–349. [Google Scholar] [CrossRef]
- Nicoletti, F.; Bevilacqua, P. Hourly Photovoltaic Production Prediction Using Numerical Weather Data and Neural Networks for Solar Energy Decision Support. Energies 2024, 17, 466. [Google Scholar] [CrossRef]
- Output Power Prediction of a Photovoltaic Module Through Artificial Neural Network|IEEE Journals & Magazine|IEEE Xplore. Available online: https://ieeexplore.ieee.org/abstract/document/9926050 (accessed on 29 March 2025).
- Alabdeli, H.; Rafi, S.; IG, N.; Rao, D.D.; Nagendar, Y. Photovoltaic Power Forecasting Using Support Vector Machine and Adaptive Learning Factor Ant Colony Optimization. In Proceedings of the 2024 Third International Conference on Distributed Computing and Electrical Circuits and Electronics (ICDCECE), Ballari, India, 26–27 April 2024; pp. 1–5. [Google Scholar]
- Amiri, A.F.; Oudira, H.; Chouder, A.; Kichou, S. Faults Detection and Diagnosis of PV Systems Based on Machine Learning Approach Using Random Forest Classifier. Energy Convers. Manag. 2024, 301, 118076. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Almohaimeed, Z.M.; Muhammad, M.A.; Khairuddin, A.S.M.; Akram, R.; Hussain, M.M. An Hour-Ahead PV Power Forecasting Method Based on an RNN-LSTM Model for Three Different PV Plants. Energies 2022, 15, 2243. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, X.; Li, G.; Gu, P.; Huang, J.; Yang, B. XGBoost–SFS and Double Nested Stacking Ensemble Model for Photovoltaic Power Forecasting under Variable Weather Conditions. Sustainability 2023, 15, 13146. [Google Scholar] [CrossRef]
- Manasrah, A.; Masoud, M.; Jaradat, Y.; Jannoud, I. Advancements in Bifacial Photovoltaics: A Review of Machine Learning Techniques for Enhanced Performance. Eurasia Proc. Sci. Technol. Eng. Math. 2024, 27, 239–245. [Google Scholar] [CrossRef]
- Yunqiao, L.; Yan, F. An Innovative Power Prediction Method for Bifacial PV Modules. Electr. Eng. 2023, 105, 2151–2159. [Google Scholar] [CrossRef]
- Ghenai, C.; Ahmad, F.F.; Rejeb, O.; Bettayeb, M. Artificial Neural Networks for Power Output Forecasting from Bifacial Solar PV System with Enhanced Building Roof Surface Albedo. J. Build. Eng. 2022, 56, 104799. [Google Scholar] [CrossRef]
- Kumar, B.S.; Kunar, B.M.; Murthy, C.S. Performance Evaluation and Machine Learning Analysis of 3 kW Grid-Connected Bifacial Solar Photovoltaic Systems. J. Inst. Eng. India Ser. B 2025. [Google Scholar] [CrossRef]
- Mubarak, H.; Abdellatif, A.; Ahmad, S.; Hammoudeh, A.; Mekhilef, S.; Mokhlis, H. Prediction of Solar Photovoltaic Energy Output Based on Thin-Film Technology Utilizing Various Machine Learning Techniques. In Proceedings of the 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT), New Delhi, India, 23–25 September 2022; pp. 1–6. [Google Scholar]
- Graditi, G.; Ferlito, S.; Adinolfi, G.; Tina, G.M.; Ventura, C. Energy Yield Estimation of Thin-Film Photovoltaic Plants by Using Physical Approach and Artificial Neural Networks. Sol. Energy 2016, 130, 232–243. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, J.-M.; Hong, S. A Multi-Layer Perceptron Based Deep Learning Model to Quantify the Energy Potentials of a Thin Film a-Si PV System. Energy Rep. 2020, 6, 1331–1336. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Ali, R.; Usama, M.; Muhammad, M.A.; Khairuddin, A.S.M. A Hybrid Deep Learning Method for an Hour Ahead Power Output Forecasting of Three Different Photovoltaic Systems. Appl. Energy 2022, 307, 118185. [Google Scholar] [CrossRef]
- Kurz, D.; Morawska, L.; Piechota, R.; Trzmiel, G. Analysis of the Impact of a Flexible Photovoltaic Tile Shape on Its Performance. E3S Web Conf. 2018, 44, 00085. [Google Scholar] [CrossRef]
- Bednar, N.; Caviasca, A.; Sevela, P.; Severino, N.; Adamovic, N. Modelling of Flexible Thin-Film Modules for Building and Product Integrated Photovoltaics. Sol. Energy Mater. Sol. Cells 2018, 181, 38–45. [Google Scholar] [CrossRef]
- Du, D.; Qiao, F.; Guo, Y.; Wang, F.; Wang, L.; Gao, C.; Zhang, D.; Liang, J.; Xu, Z.; Shen, W.; et al. Photovoltaic Performance of Flexible Perovskite Solar Cells under Bending State. Sol. Energy 2022, 245, 146–152. [Google Scholar] [CrossRef]
- Dong, Q.; Chen, M.; Liu, Y.; Eickemeyer, F.T.; Zhao, W.; Dai, Z.; Yin, Y.; Jiang, C.; Feng, J.; Jin, S.; et al. Flexible Perovskite Solar Cells with Simultaneously Improved Efficiency, Operational Stability, and Mechanical Reliability. Joule 2021, 5, 1587–1601. [Google Scholar] [CrossRef]
- Kumar, D.D.S.; Agrawal, D.M.; Kasulla, M.S.; Kumar, D.A. A Textbook on Fundamentals of Renewable Energy and Green Technology; Academic Guru Publishing House: Bhopal, India, 2024; ISBN 978-81-973048-4-2. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]



| Power | 100 [W] |
| Rated Voltage | 18 [V] |
| Rated Current | 5.5 [Amp] |
| Voc | 21.6 [V] |
| Isc | 6.5 [Amp] |
| Dimensions | 1030 × 520 × 2 mm |
| ML Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| RF | 0.919 ± 0.016 | 0.921 ± 0.015 | 0.920 ± 0.016 | 0.919 ± 0.016 |
| XGBoost | 0.949 ± 0.014 | 0.950 ± 0.014 | 0.949 ± 0.014 | 0.949 ± 0.014 |
| KAN | 0.853 ± 0.022 | 0.860 ± 0.020 | 0.853 ± 0.022 | 0.852 ± 0.021 |
| MLP 2 | 0.922 ± 0.020 | 0.924 ± 0.019 | 0.922 ± 0.021 | 0.922 ± 0.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manasrah, A.; Jaradat, Y.; Masoud, M.; Alia, M.; Suwais, K.; Bevilacqua, P. Flat vs. Curved: Machine Learning Classification of Flexible PV Panel Geometries. Energies 2025, 18, 3529. https://doi.org/10.3390/en18133529
Manasrah A, Jaradat Y, Masoud M, Alia M, Suwais K, Bevilacqua P. Flat vs. Curved: Machine Learning Classification of Flexible PV Panel Geometries. Energies. 2025; 18(13):3529. https://doi.org/10.3390/en18133529
Chicago/Turabian StyleManasrah, Ahmad, Yousef Jaradat, Mohammad Masoud, Mohammad Alia, Khaled Suwais, and Piero Bevilacqua. 2025. "Flat vs. Curved: Machine Learning Classification of Flexible PV Panel Geometries" Energies 18, no. 13: 3529. https://doi.org/10.3390/en18133529
APA StyleManasrah, A., Jaradat, Y., Masoud, M., Alia, M., Suwais, K., & Bevilacqua, P. (2025). Flat vs. Curved: Machine Learning Classification of Flexible PV Panel Geometries. Energies, 18(13), 3529. https://doi.org/10.3390/en18133529








