Predicting the Evolution of Capacity Degradation Histograms of Rechargeable Batteries Under Dynamic Loads via Latent Gaussian Processes
Abstract
1. Introduction
1.1. Literature Review
1.2. Article Organization
2. Methodology
2.1. Framework of Methodology
2.2. Battery Capacity Histogram Definition
2.3. Principal Component Analysis
2.4. Gaussian Processes
2.5. Evaluation Metrics
3. Results
3.1. Datasets
3.2. Predictive Performance
3.3. Comparison with Conventional Baselines
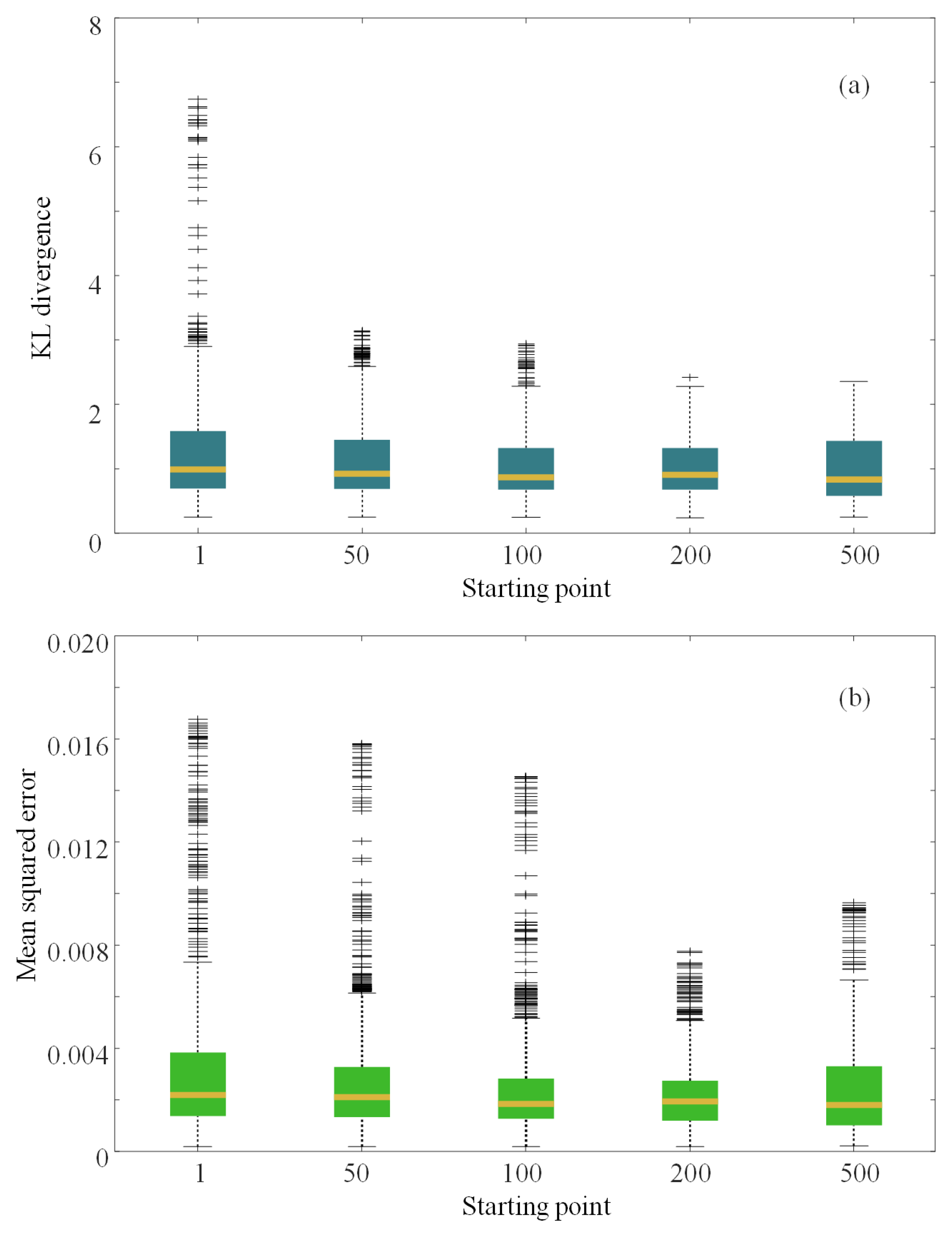
3.4. Performance with Different Starting Points
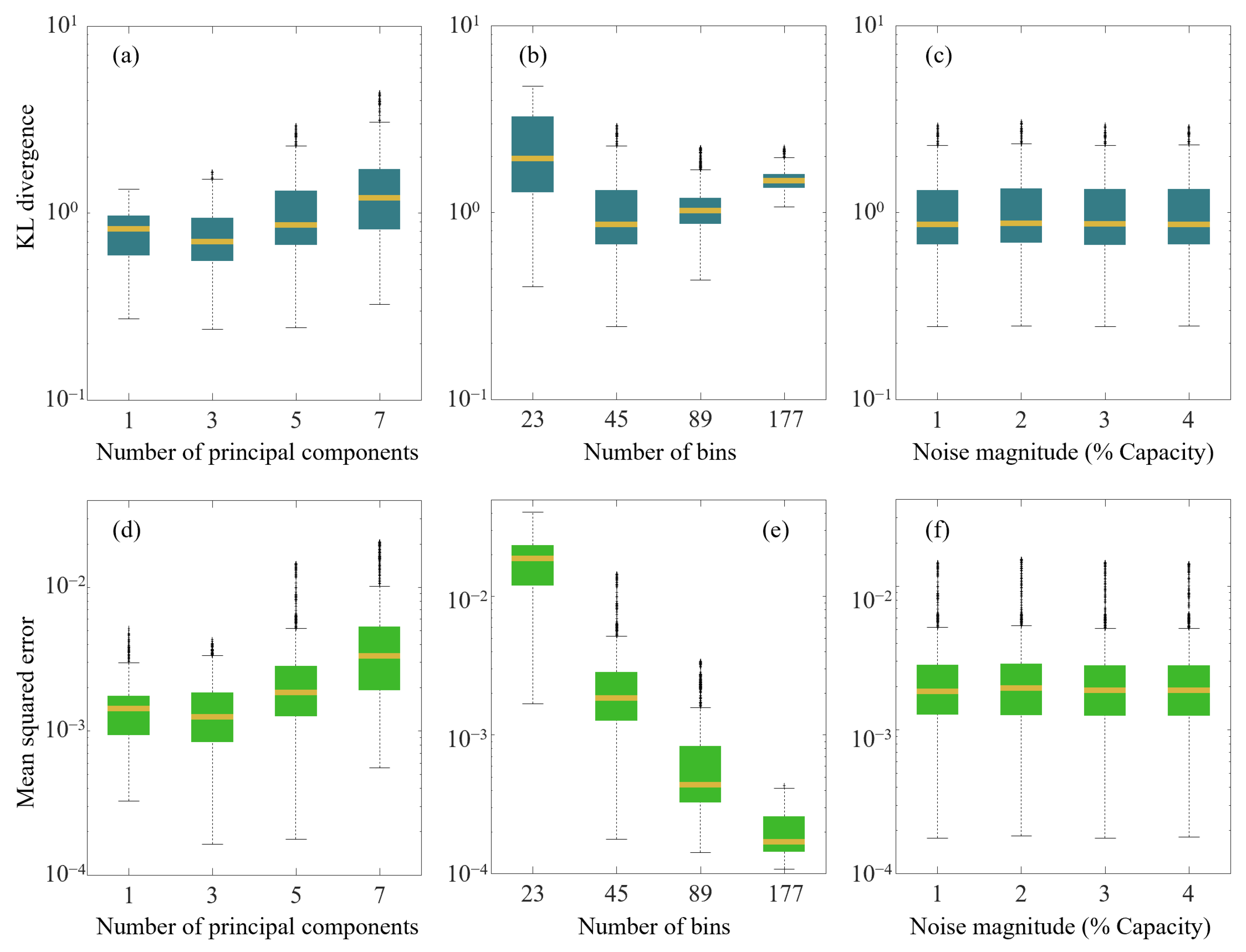
3.5. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adhikari, N.; Bhandari, R.; Joshi, P. Thermal analysis of lithium-ion battery of electric vehicle using different cooling medium. Appl. Energy 2024, 360, 122781. [Google Scholar] [CrossRef]
- Balasundar, C.; Sundarabalan, C.K.; Santhanam, S.N.; Sharma, J.; Guerrero, J.M. Mixed Step Size Normalized Least Mean Fourth Algorithm of DSTATCOM Integrated Electric Vehicle Charging Station. IEEE Trans. Ind. Inform. 2023, 19, 7583–7591. [Google Scholar] [CrossRef]
- Kuzovchikov, S.M.; Zefirov, V.V.; Neudachina, V.S.; Zakharchenko, T.K.; Zybkovets, A.L.; Nikiforov, A.A.; Gusak, D.I.; Reveguk, A.; Kondratenko, M.S.; Yashina, L.V.; et al. Electrolyte refilling as a way to recover capacity of aged lithium-ion batteries. J. Power Sources 2024, 601, 234257. [Google Scholar] [CrossRef]
- Teliz, E.; López-Vázquez, C.; Díaz, V. Degradation study for 18650 NMC batteries at low temperature. Electrochim. Acta 2024, 475, 143540. [Google Scholar] [CrossRef]
- You, H.; Wang, X.; Zhu, J.; Jiang, B.; Han, G.; Wei, X.; Dai, H. Investigation of lithium-ion battery nonlinear degradation by experiments and model-based simulation. Energy Storage Mater. 2024, 65, 103083. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Garg, A.; Gao, L. Enhancing real-time degradation prediction of lithium-ion battery: A digital twin framework with CNN-LSTM-attention model. Energy 2024, 286, 129681. [Google Scholar] [CrossRef]
- Oh, S.; Jeon, A.-R.; Lim, G.; Cho, M.K.; Chae, K.H.; Sohn, S.S.; Lee, M.; Jung, S.-K.; Hong, J. Fast discharging mitigates cathode-electrolyte interface degradation of LiNi0.6Mn0.2Co0.2O2 in rechargeable lithium batteries. Energy Storage Mater. 2024, 65, 103169. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.S.; Hussain, A.; Md Saad, M.H. Jellyfish optimized recurrent neural network for state of health estimation of lithium-ion batteries. Expert Syst. Appl. 2024, 238, 121904. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; Wang, J.; He, H.; Peng, S.; Pecht, M. Lithium-Ion Battery Health Prognosis Based on a Real Battery Management System Used in Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 4110–4121. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Liu, D.; Xie, W.; Liao, H.; Peng, Y. An Integrated Probabilistic Approach to Lithium-Ion Battery Remaining Useful Life Estimation. IEEE Trans. Instrum. Meas. 2015, 64, 660–670. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M. Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model. Microelectron. Reliab. 2016, 65, 265–273. [Google Scholar] [CrossRef]
- He, W.; Li, Z.; Liu, T.; Liu, Z.; Guo, X.; Du, J.; Li, X.; Sun, P.; Ming, W. Research progress and application of deep learning in remaining useful life, state of health and battery thermal management of lithium batteries. J. Energy Storage 2023, 70, 107868. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.; Ge, T.; Yu, H.; Wang, L.; Ma, N. A lead-acid battery’s remaining useful life prediction by using electrochemical model in the Particle Filtering framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, T.; Xia, Q.; Zhang, K.; Tian, J.; Hu, D.; Yang, D.; Sun, B.; Feng, Q.; Qian, C. A data and physical model joint driven method for lithium-ion battery remaining useful life prediction under complex dynamic conditions. J. Energy Storage 2024, 79, 110065. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.S.; Van Mierlo, J.; Berecibar, M. Towards machine-learning driven prognostics and health management of Li-ion batteries. A comprehensive review. Renew. Sustain. Energy Rev. 2024, 192, 114224. [Google Scholar] [CrossRef]
- Alsuwian, T.; Ansari, S.; Zainuri, M.A.A.M.; Ayob, A.; Hussain, A.; Lipu, M.H.; Alhawari, A.R.; Almawgani, A.; Almasabi, S.; Hindi, A.T. A review of expert hybrid and co-estimation techniques for SOH and RUL estimation in battery management system with electric vehicle application. Expert Syst. Appl. 2024, 246, 123123. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, P.; Lu, J.; Xiong, R.; Cai, Z. A transferable long-term lithium-ion battery aging trajectory prediction model considering internal resistance and capacity regeneration phenomenon. Appl. Energy 2024, 360, 122825. [Google Scholar] [CrossRef]
- Zhao, H.; Meng, J.; Peng, Q. Early perception of Lithium-ion battery degradation trajectory with graphical features and deep learning. Appl. Energy 2025, 381, 125214. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Wu, X.; Fu, L.; Gao, X.; Xie, X.; Ouyang, Q. Battery pack capacity prediction using deep learning and data compression technique: A method for real-world vehicles. J. Energy Chem. 2025, 106, 553–564. [Google Scholar] [CrossRef]
- Du, J.; Zhang, C.; Li, S.; Zhang, L.; Zhang, W. Two-stage prediction method for capacity aging trajectories of lithium-ion batteries based on Siamese-convolutional neural network. Energy 2024, 295, 130947. [Google Scholar] [CrossRef]
- Zafar, M.H.; Mansoor, M.; Houran, M.A.; Khan, N.M.; Khan, K.; Moosavi, S.K.R.; Sanfilippo, F. Hybrid deep learning model for efficient state of charge estimation of Li-ion batteries in electric vehicles. Energy 2023, 282, 128317. [Google Scholar] [CrossRef]
- Xiang, Y.; Fan, W.; Zhu, J.; Wei, X.; Dai, H. Semi-supervised deep learning for lithium-ion battery state-of-health estimation using dynamic discharge profiles. Cell Rep. Phys. Sci. 2024, 5, 101763. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.S.; Daigle, M. Adaptation of an electrochemistry-based Li-ion battery model to account for deterioration observed under randomized use. In PHM 2014—Proceedings of the Annual Conference of the Prognostics and Health Management Society 2014; Prognostics and Health Management Society: New York, NY, USA, 2014; pp. 502–510. [Google Scholar]
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Hsu, C.-W.; Tsou, N.-T.; Sun, F.; Li, J. Battery degradation prediction against uncertain future conditions with recurrent neural network enabled deep learning. Energy Storage Mater. 2022, 50, 139–151. [Google Scholar] [CrossRef]
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Sun, F. Deep learning to predict battery voltage behavior after uncertain cycling-induced degradation. J. Power Sources 2023, 581, 233473. [Google Scholar] [CrossRef]
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Sun, F. Deep learning to estimate lithium-ion battery state of health without additional degradation experiments. Nat. Commun. 2023, 14, 2760. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2022, 122, 10899–10969. [Google Scholar] [CrossRef]
- Nobre, J.; Neves, R.F. Combining Principal Component Analysis, Discrete Wavelet Transform and XGBoost to trade in the financial markets. Expert Syst. Appl. 2019, 125, 181–194. [Google Scholar] [CrossRef]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef] [PubMed]
- Valverde, J.M.; Tohka, J. Region-wise loss for biomedical image segmentation. Pattern Recognit. 2023, 136, 109208. [Google Scholar] [CrossRef]
- Van Erven, T.; Harrëmos, P. Rényi divergence and kullback-leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation. arXiv 2015, arXiv:1506.02157. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Li, X.; Lu, J. Predicting the Evolution of Capacity Degradation Histograms of Rechargeable Batteries Under Dynamic Loads via Latent Gaussian Processes. Energies 2025, 18, 3503. https://doi.org/10.3390/en18133503
Wang D, Li X, Lu J. Predicting the Evolution of Capacity Degradation Histograms of Rechargeable Batteries Under Dynamic Loads via Latent Gaussian Processes. Energies. 2025; 18(13):3503. https://doi.org/10.3390/en18133503
Chicago/Turabian StyleWang, Daocan, Xinggang Li, and Jiahuan Lu. 2025. "Predicting the Evolution of Capacity Degradation Histograms of Rechargeable Batteries Under Dynamic Loads via Latent Gaussian Processes" Energies 18, no. 13: 3503. https://doi.org/10.3390/en18133503
APA StyleWang, D., Li, X., & Lu, J. (2025). Predicting the Evolution of Capacity Degradation Histograms of Rechargeable Batteries Under Dynamic Loads via Latent Gaussian Processes. Energies, 18(13), 3503. https://doi.org/10.3390/en18133503






