An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties
Abstract
1. Introduction
- The research addresses the computational inefficiency of running optimal power flow (OPF) multiple times by proposing an ML-based approach to predict optimal setpoints of voltage-regulating devices under different loading conditions. The approach reduces the need for repeatedly solving OPF problems, enhancing real-time operational efficiency.
- The proposed coordinated control scheme involving PV smart inverters, DSTATCOM, and OLTC enables effective voltage regulation and power flow management by leveraging the combined capabilities of multiple devices in the power system.
- The centralized AC optimal power flow (CACCOPF) adopted in this research ensures that the control strategy accounts for nonlinear power system dynamics, improving the accuracy and robustness of the coordination.
- The use of ML models as local controllers to determine the best operational points of PV smart inverters, DSTATCOM, and OLTC allows a scalable and communication-efficient control mechanism, enabling faster decision making.
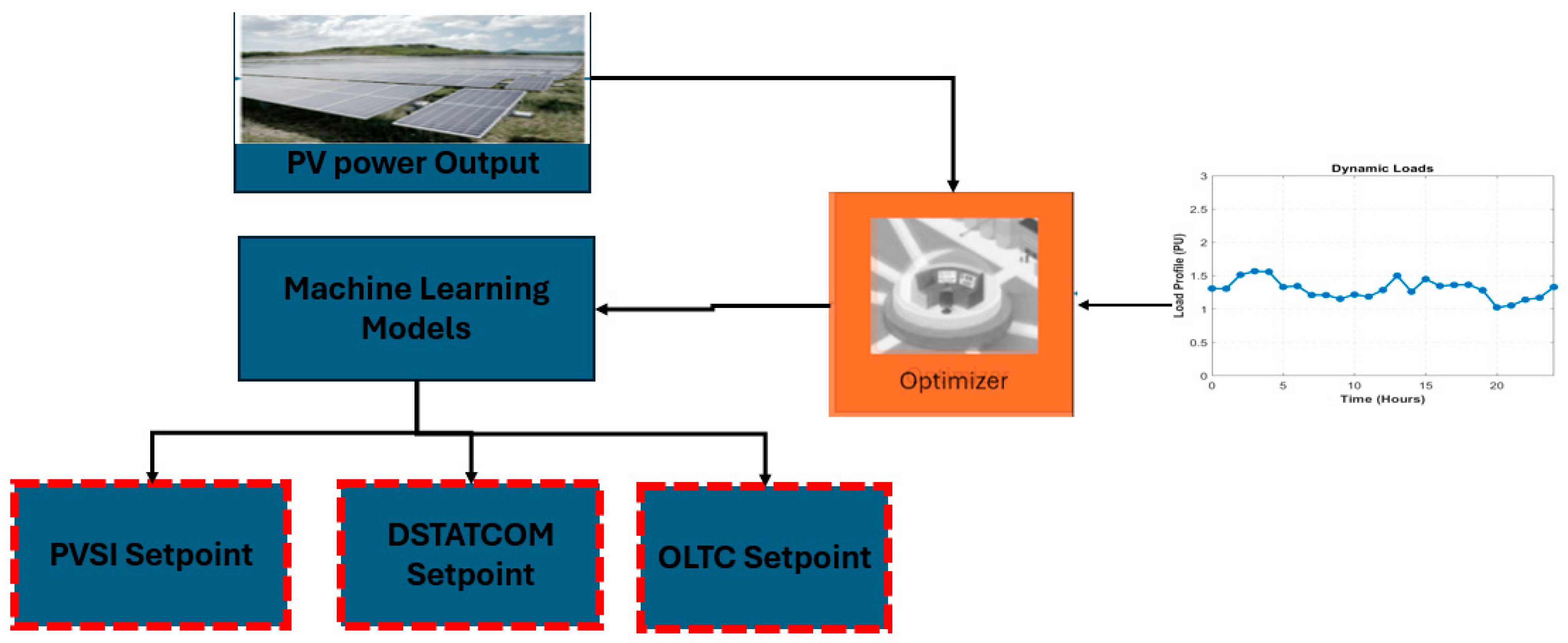
2. Proposed Framework
3. Mathematical Modeling
3.1. Nonlinear Centralized AC OPF (CACOPF)
3.2. OLTC Model
3.3. Smart Inverter Model
3.4. Distribution Static Synchronous Compensator (DSTATCOM) Model
4. Objective Function and Constraints
4.1. Objective Function
4.2. Constraints
4.2.1. Voltage Constraint
4.2.2. Thermal Capacity Constraint
4.2.3. Tap Position of OLTC Constraints
4.2.4. Smart Inverter (SI) Constraints
4.2.5. Power Flow Constraints
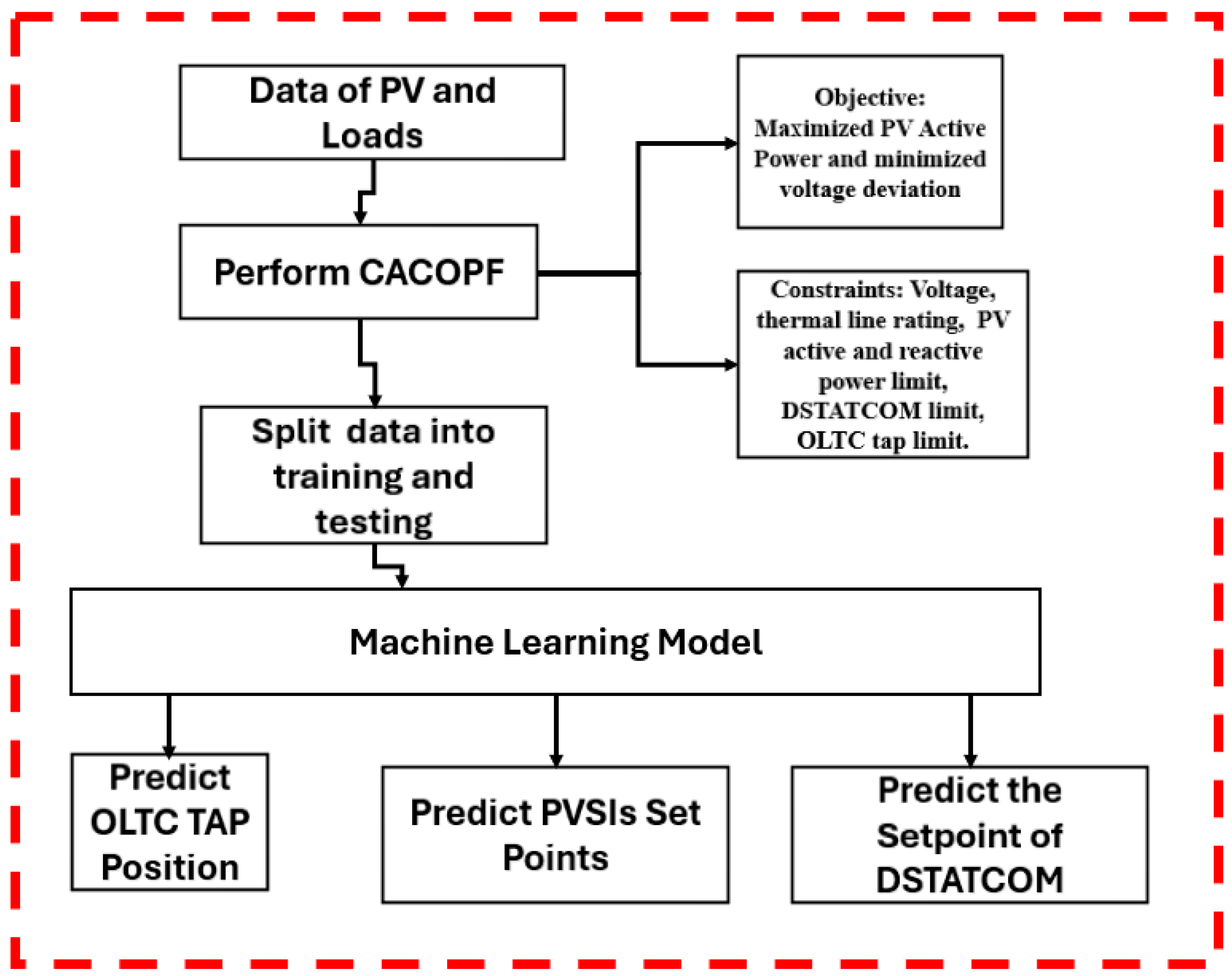
5. Machine Learning Approaches in Predicting the Optimal Setpoints of PVSIs and Voltage Regulating Devices
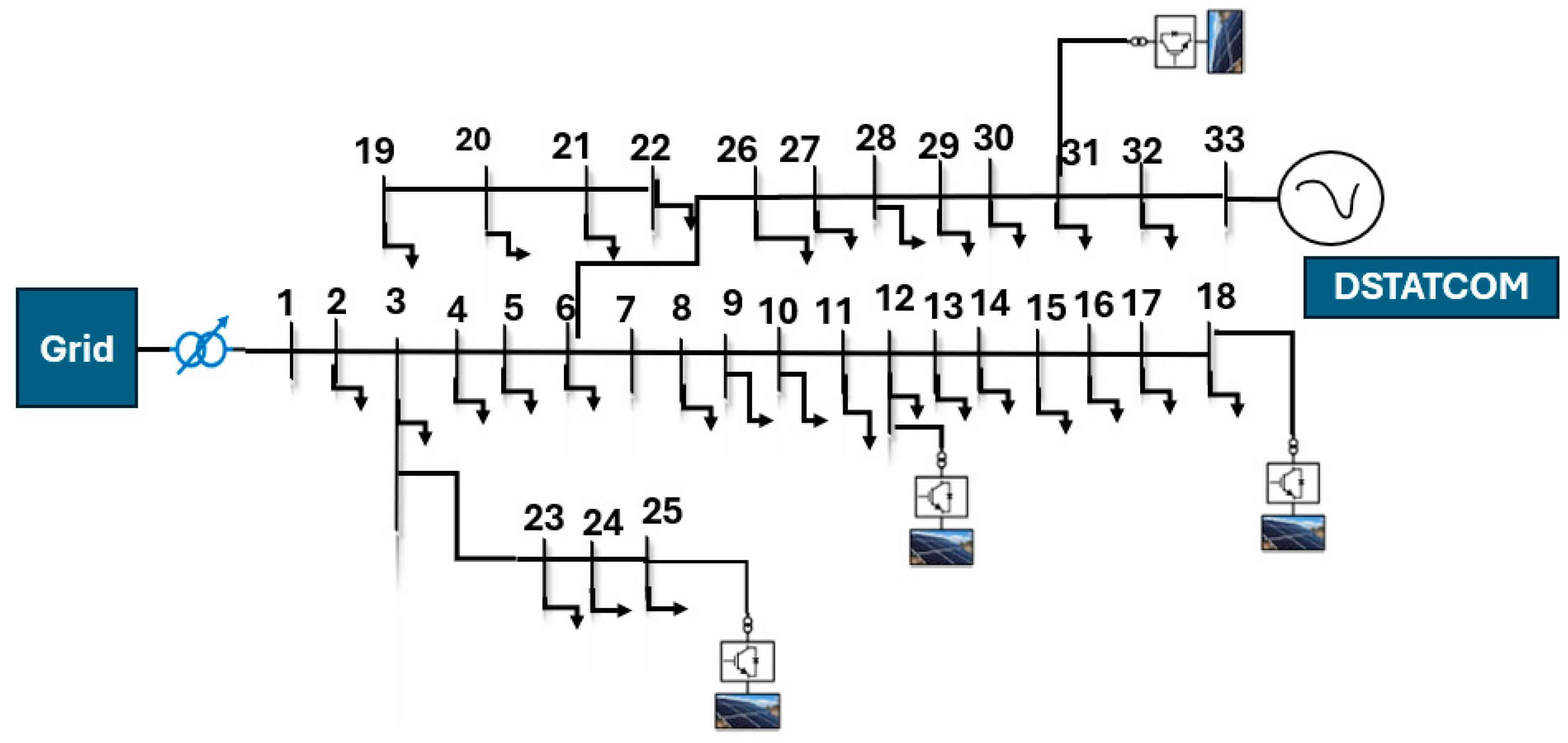
6. Simulation Setup
7. Results and Analysis
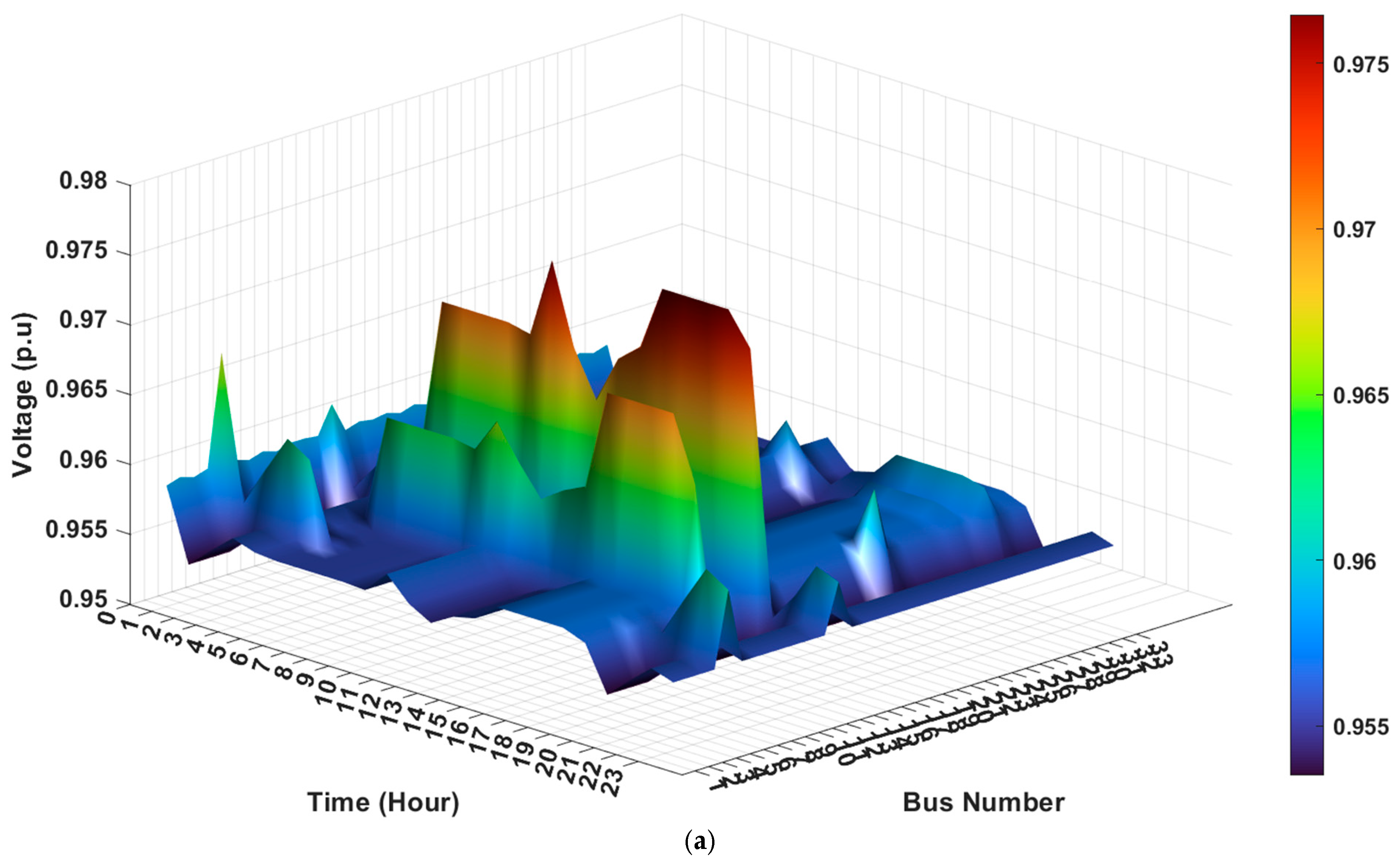
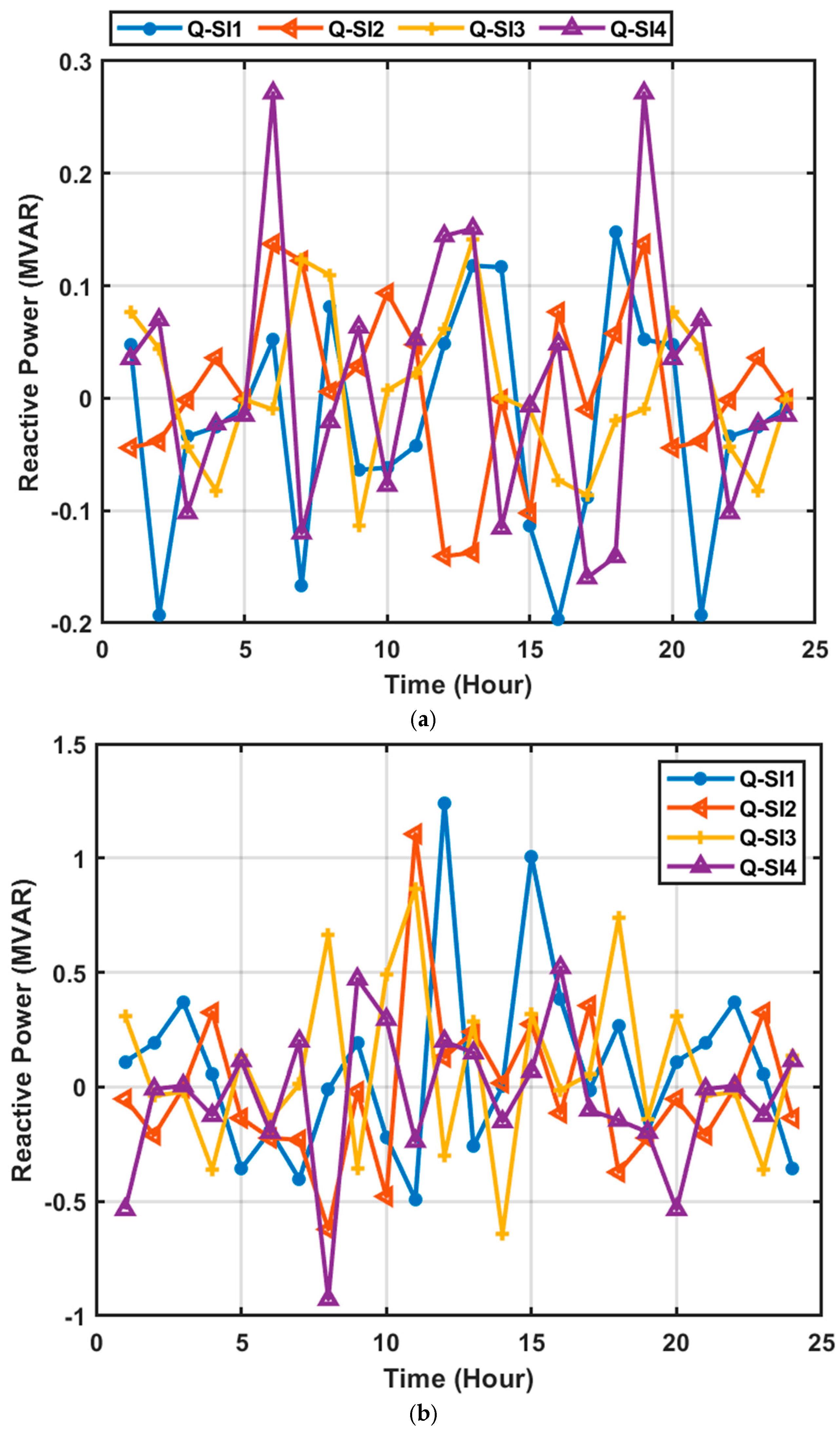
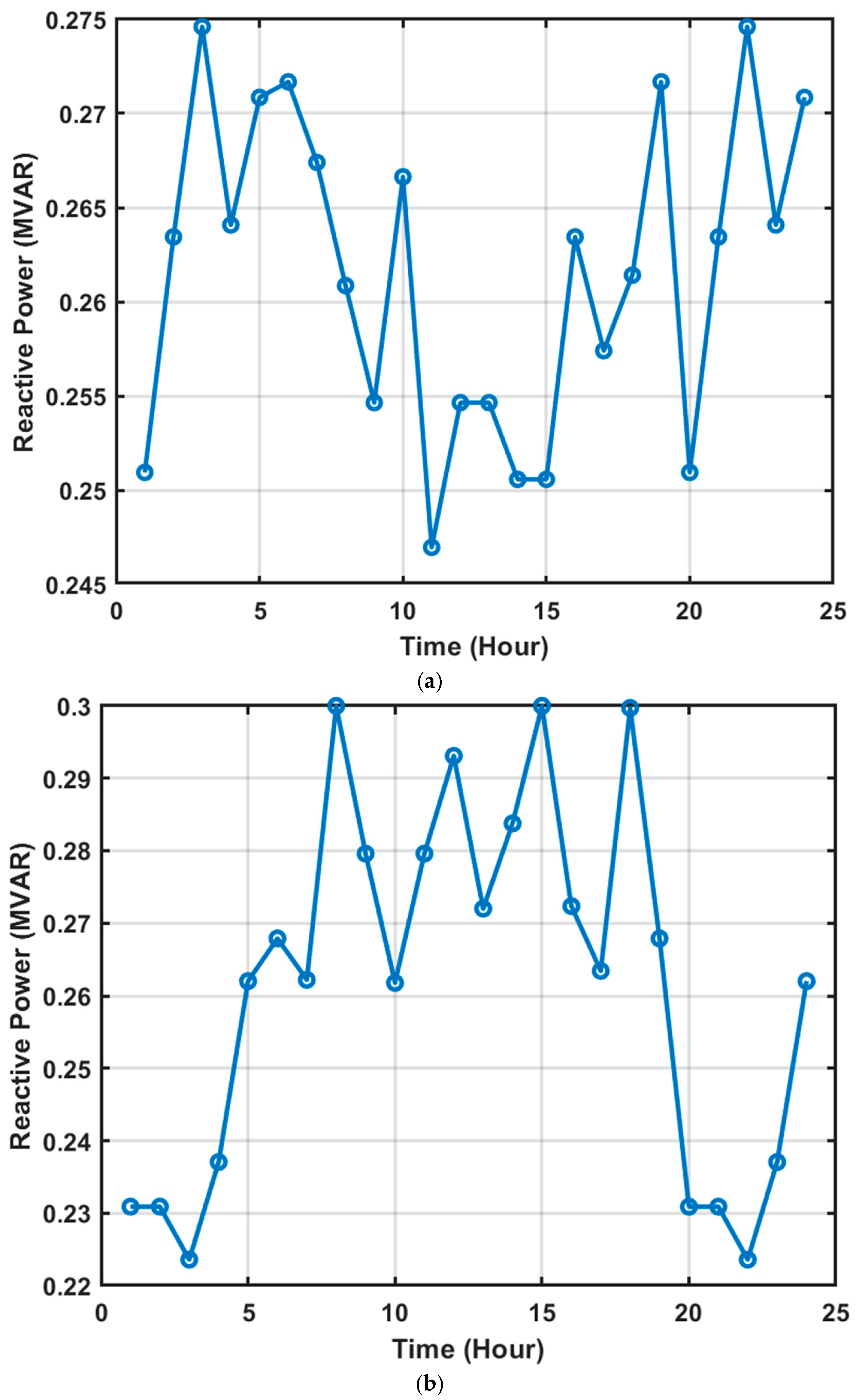
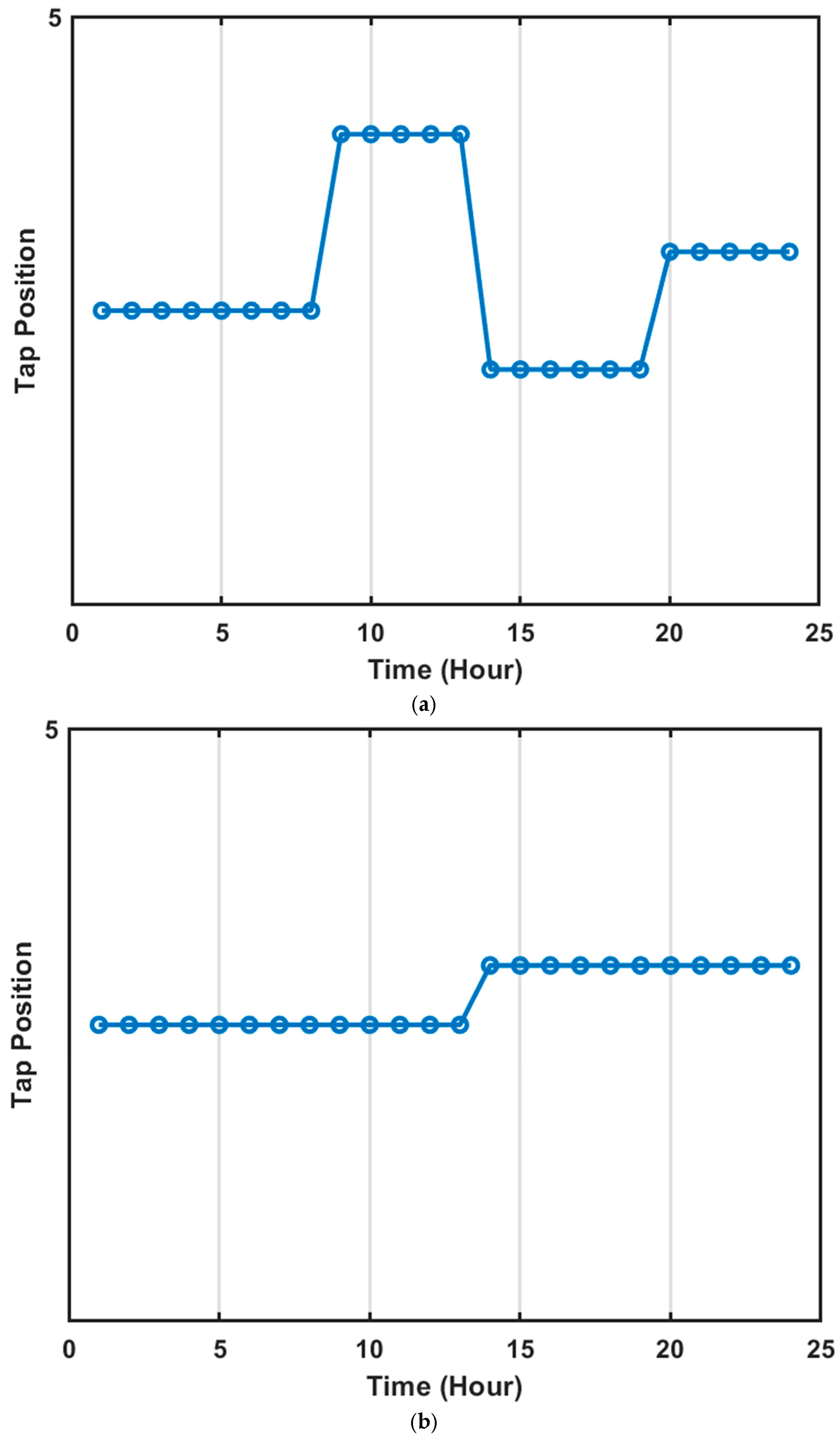
7.1. Daily Voltage Profile and Optimal Setpoint of OLTC, PVSI, and DSTATCOM Network
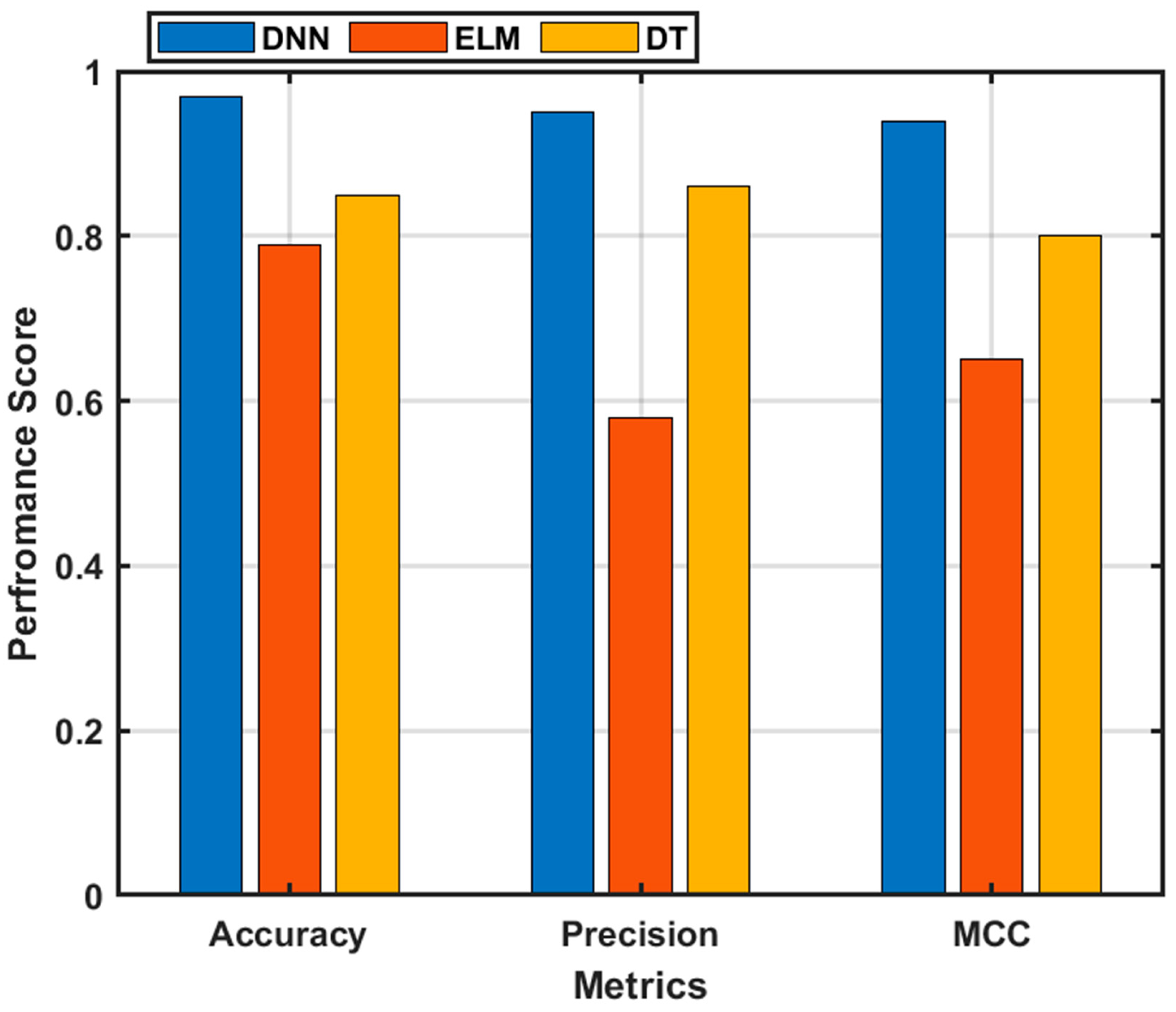
7.2. Machine Learning Prediction Results
7.2.1. Smart Inverter Reactive Power Prediction
7.2.2. OLTC Taps Position Classification Performance
7.2.3. DSTATCOM Reactive Power Prediction Performance
7.3. Testing of the DNN-Based Controller
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hossain, T.; Hossen, Z.; Badal, F.R.; Islam, R.; Hasan, M.; Ali, F.; Tasneem, Z. Next generation power inverter for grid resilience: Technology review. Helicon 2024, 10, 2–40. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, T.B.; Siddiqui, M.; Khalid, M.; Asif, M. Distributed energy systems: A review of classification, technologies, applications, and policies. Energy Strategy Rev. 2023, 48, 101096. [Google Scholar] [CrossRef]
- Djalab, A.; Djalab, Z.; El Amomum, A.; Tina, G.M.; Motahhir, S.; Laouid, A.A. A comprehensive review of floating photovoltaic systems: Tech advances, marine environmental influences on offshore PV systems, and economic feasibility analysis. Sol. Energy 2024, 277, 112711. [Google Scholar] [CrossRef]
- Saxena, V.; Manna, S.; Rajput, S.K.; Kumar, P.; Sharma, B.; Alsharif, M.H.; Kim, M.K. Navigating the complexities of distributed generation: Integration, challenges, and solutions. Energy Rep. 2024, 12, 3302–3322. [Google Scholar] [CrossRef]
- Twaisan, K.; Barışçı, N. Integrated distributed energy resources (DER) and microgrids: Modeling and optimization of DERs. Electronics 2022, 11, 2816. [Google Scholar] [CrossRef]
- Ahmad, T.; Madonski, R.; Zhang, D.; Huang, C.; Mujeeb, A. Data-driven probabilistic machine learning in sustainable smart energy/smart energy systems: Key developments, challenges, and future research opportunities in the context of smart grid paradigm. Renew. Sustain. Energy Rev. 2022, 160, 112128. [Google Scholar] [CrossRef]
- Iweh, C.D.; Gyamfi, S.; Tanyi, E.; Effah-Donyina, E. Distributed generation and renewable energy integration into the grid: Prerequisites, push factors, practical options, issues and merits. Energies 2021, 14, 5375. [Google Scholar] [CrossRef]
- Jose, J.; Kowli, A. Optimal augmentation of distribution networks for improved reliability. IEEE Syst. J. 2022, 16, 1965–1973. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Wu, L. Coordinated optimal network reconfiguration and voltage regulator/DER control for unbalanced distribution systems. IEEE Trans. Smart Grid 2019, 10, 2912–2922. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S.; Ge, L.; Wu, L. Distributed generation hosting capacity evaluation for distribution systems considering the robust optimal operation of OLTC and SVC. IEEE Trans. Sustain. Energy 2016, 7, 1111–1123. [Google Scholar] [CrossRef]
- Escalera, A.; Prodanovi, M.; Castronuovo, E.D.; RoldanPerez, J. Contribution of active management technologies to the reliability of power distribution networks. Appl. Energy 2020, 267, 114919. [Google Scholar] [CrossRef]
- IEEE Standard 1547-2018 (Revision of IEEE Standard 1547-2003); IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018.
- Wick, S.; Gonzalez, C.; Driesen, J. Combined central and local active and reactive power control of PV inverters. IEEE Trans. Sustain. Energy 2014, 5, 776–784. [Google Scholar]
- Li, P.; Zhang, C.; Wu, Z.; Xu, Y.; Hu, M.; Dong, Z. Distributed adaptive robust Voltage/VAR control with network partition in active distribution networks. IEEE Trans. Smart Grid 2020, 11, 2245–2256. [Google Scholar] [CrossRef]
- Ren, H.; Jha, R.R.; Dubey, A.; Schulz, N.N. Extremum-seeking adaptive-droop for model-free and localized Volt-VAR optimization. IEEE Trans. Power Syst. 2022, 37, 179–190. [Google Scholar] [CrossRef]
- Ali, A.; Mahmoud, K.; Lehtonen, M. Maximizing hosting capacity of uncertain photovoltaics by coordinated management of OLTC, Var sources and stochastic EVs. Int. J. Elect. Power Energy Syst. 2021, 127, 106627. [Google Scholar] [CrossRef]
- Guo, Y.; Baker, K.; Dall’Anese, E.; Hu, Z.; Summers, T.H. Data-based distributionally robust stochastic optimal power flow—Part II: Case studies. IEEE Trans. Power Syst. 2019, 34, 1493–1503. [Google Scholar] [CrossRef]
- Karagiannopoulos, S.; Aristidou, P.; Hug, G. Data-driven local control design for active distribution grids using off-line optimal power flow and machine learning techniques. IEEE Trans. Smart Grid 2019, 10, 6461–6471. [Google Scholar] [CrossRef]
- Jalali, M.; Kekatos, V.; Gatsis, N.; Deka, D. Designing reactive power control rules for smart inverters using support vector machines. IEEE Trans. Smart Grid 2020, 11, 1759–1770. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J.; Tao, Y.; Ma, Y.; Zhao, J. A multi-mode data-driven Volt/Var control strategy with conservation voltage reduction in active distribution networks. IEEE Trans. Sustain. Energy 2022, 13, 1073–1085. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, L.; Meng, G.; Zhang, F.; Liu, W. Research on multi-objective reactive power optimization of power grid with high proportion of new energy. IEEE Access 2022, 10, 116443–116452. [Google Scholar]
- Ai, M.; Du, Z.; Pan, Z.; Li, G. The optimization of reactive power for distribution network with PV generation based on NSGA-III. CPSS Trans. Power Electron. Appl. 2021, 6, 193–200. [Google Scholar] [CrossRef]
- Li, C.; Lu, Q.; He, H.; Zhao, J.; Jiang, Y.; Xu, B.; Yan, Y.; Bian, J.; Du, W. Reactive power optimization of active distribution networks based on simulated annealing algorithm. In Proceedings of the 2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023; pp. 1022–1026. [Google Scholar]
- Ilyushin, P.; Volnyi, V.; Suslov, K.; Filippov, S. State-of-the-art literature review of power flow control methods for low-voltage AC and AC-DC microgrids. Energies 2023, 16, 3153. [Google Scholar] [CrossRef]
- Rehman, N.; Mufti, M.U.D.; Gupta, N. Power flow analysis in a distribution system penetrated with renewable energy sources: A review. Int. J. Ambient Energy 2024, 45, 2305701. [Google Scholar] [CrossRef]
- Nair, A.S.; Abhyankar, S.; Peles, S.; Ranganathan, P. Computational and numerical analysis of AC optimal power flow formulations on large-scale power grids. Electr. Power Syst. Res. 2022, 202, 107594. [Google Scholar] [CrossRef]
- Tshivhase, N.; Hasan, A.N.; Shongwe, T. Proposed Fuzzy Logic System for Voltage Regulation and Power Factor Improvement in Power Systems with High Infiltration of Distributed Generation. Energies 2020, 13, 4241. [Google Scholar] [CrossRef]
- Makanju, T.D.; Shongwe, T.; Famoriji, O.J. Machine Learning Approaches for Power System Parameters Prediction: A Systematic Review. IEEE Access 2024, 12, 66646–66679. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Luque, A.; Carrasco, A.; Martín, A.; de las Hera, A. The impact of class imbalance in classification performance metrics based on the binary confusion matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]
- Makanju, T.D.; Famoriji, O.J.; Hasan, A.N.; Shongwe, T. Machine learning approaches for identifying and predicting voltage conditions in power system networks using network topology behavior input formulation. Sci. Afr. 2024, 26, e02493. [Google Scholar] [CrossRef]

| Scenarios | Maximum Active Power (MW) | Average Voltage Deviation (PU) |
|---|---|---|
| 1 | 130.239 | 0.0425 |
| 2 | 131.4998 | 0.0340 |
| PVSI | ELM | DNN | DT | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| Q1 | 0.106 | 0.0870 | 0.0543 | 0.0455 | 0.0933 | 0.0914 |
| Q2 | 0.0985 | 0.0830 | 0.0683 | 0.0457 | 0.0898 | 0.0832 |
| Q3 | 0.0789 | 0.0970 | 0.0675 | 0.0551 | 0.0668 | 0.0543 |
| Q4 | 0.1024 | 0.2305 | 0.0435 | 0.0572 | 0.0932 | 0.0891 |
| ELM | DNN | DT | |||
|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE |
| 0.786 | 0.907 | 0.0267 | 0.0229 | 0.034 | 0.0498 |
| Techniques | Average Voltage Deviation (PU) | Simulation Time (Seconds) |
|---|---|---|
| Optimizer | 0.0392 | 108.45 |
| DNN Controller | 0.0413 | 2.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makanju, T.D.; Hasan, A.N.; Famoriji, O.J.; Shongwe, T. An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties. Energies 2025, 18, 3481. https://doi.org/10.3390/en18133481
Makanju TD, Hasan AN, Famoriji OJ, Shongwe T. An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties. Energies. 2025; 18(13):3481. https://doi.org/10.3390/en18133481
Chicago/Turabian StyleMakanju, Tolulope David, Ali N. Hasan, Oluwole John Famoriji, and Thokozani Shongwe. 2025. "An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties" Energies 18, no. 13: 3481. https://doi.org/10.3390/en18133481
APA StyleMakanju, T. D., Hasan, A. N., Famoriji, O. J., & Shongwe, T. (2025). An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties. Energies, 18(13), 3481. https://doi.org/10.3390/en18133481






