Model-Data Hybrid-Driven Real-Time Optimal Power Flow: A Physics-Informed Reinforcement Learning Approach
Abstract
1. Introduction
- (1)
- Distributed renewable energy sources exhibit pronounced stochastic, intermittent, and fluctuating characteristics, leading to a continuous increase in operational uncertainty in the new power system. This results in frequent node voltage fluctuations and flicker and rapidly shifting power flow [2], which constrain the space for safe and stable operation in the new power system, thereby endangering its overall stability.
- (2)
- The increasing integration of controllable power electronic equipment and higher interruptible load access ratios has made the operation and dispatch of the modern power system more flexible, thereby heightening the complexity of power system optimization [3].
- (1)
- As a supervised learning paradigm, DL relies on high-quality, large-scale labeled datasets for support, and the trained models are typically limited to addressing the specific system represented by the training dataset. This makes DL poorly suited to adapting to the rapidly evolving operational conditions and structures of modern power systems.
- (2)
- Power system dispatch optimization is a multi-timestep decision-making process constrained by unit ramp-rate limits. DL methods struggle to produce accurate multi-timestep decision trajectories when solving dispatch strategies, rendering them impractical for direct application and significantly limiting their generalizability.
- (1)
- After the mathematical model of the RT-OPF problem is systematically formulated, a Markov decision process (MDP) model is developed based on this optimization problem, incorporating unit ramping constraints. Safety and economic efficiency are modeled as reward functions to support the agent’s training process, enabling the acquisition of gradient information that combines safety and economic performance.
- (2)
- Based on power flow sensitivity, the influence relationship between agent actions and system states is established, serving as the prior model knowledge essential for guiding the agent. Then, building on the PINN method, the PI-actor network is introduced after an action constraint violation degree index, incorporating safety gradient information, and utilized as a regularization term for model knowledge. This actor network leverages the action–system state loop for backpropagation to derive gradients of safety information, thereby providing critical model guidance during the network update process.
- (3)
- An RT-OPF solution framework based on a model–data hybrid-driven PIRL approach is established. Compared to classical data-driven methods, the proposed approach builds upon the PPO algorithm by embedding a PI-actor network, leveraging both model knowledge and data-driven techniques to compute safety-economic gradient information for training the agent. The proposed method demonstrates significant advantages in terms of safety and economic performance in RT-OPF. Furthermore, the integration of black-box models with white-box knowledge substantially enhances the trustworthiness of the actor network.
2. Preliminaries
2.1. RT-OPF Problem Description
2.1.1. Objective Function
2.1.2. Constraints
- (a)
- Node power balance constraints:where represents the unit reactive power output and and indicate the active power and reactive power consumption in the node and represent the conductance and susceptance between the and nodes. The set of nodes in the system is denoted by .
- (b)
- Node voltage security constraints:where and indicate the lower and upper limits of the node’s voltage, while represents the node’s voltage.
- (c)
- Unit generation constraints:where the active and reactive power output limit of the unit are denoted by , , , and , respectively.
- (d)
- Ramp rate limits:where and denote the generation ramp-up limit and ramp-down limit of the unit.
2.2. MDP Modeling of RT-OPF Problem
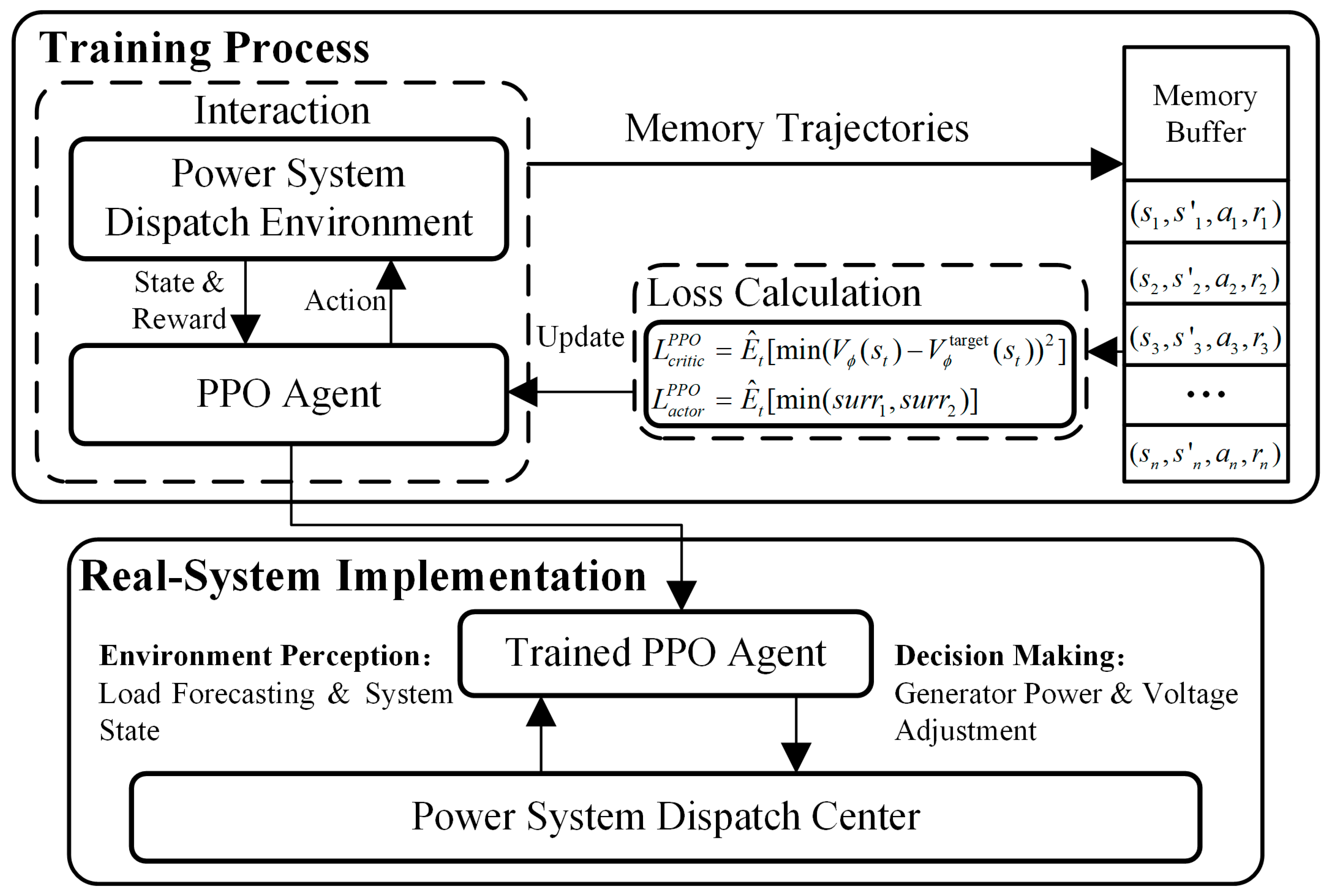
3. Proposed Algorithm
3.1. Baseline PPO Algorithm
3.2. Proposed PIRL Algorithm
- (1)
- Direct Guidance and Efficiency: The framework formulates a model-driven regularization term from a power flow sensitivity-based feedback loop. This term provides direct, physics-based guidance to the agent’s learning process at every step, which significantly accelerates training and reduces overall computational costs.
- (2)
- Enhanced Robustness and Stability: The model-driven and data-driven components are decoupled. This architecture prevents the deterministic physics-based guidance from being destabilized by the stochastic nature of the data-driven exploration, resulting in a more robust and stable training phase with less sensitivity to hyperparameters.
- (3)
- Modularity and Extensibility: The decoupled design is inherently modular. The physics-informed component can be adapted or replaced to suit different physical systems or constraints without requiring a complete redesign of the core DRL agent. This simplifies deployment and enhances the algorithm’s extensibility.
| Algorithm 1 PIRL training process |
| Initial PIRL agent, memory buffer |
| for in episode |
| Initial power system simulator environment |
| Reset memory buffer |
| for time in 24 × 2 |
| for in step times |
| Agent’s actor network selects action based on state |
| Environment returns the reward and the next state |
| Memory buffer records |
| Break if power flow not converges |
| end for |
| end for |
| for in epochs |
| extract total experiences samples from Memory Buffer |
| utilizing experiences samples to calculate loss by: |
| backpropagate loss value to compute the network gradients based on loss value, update PIRL agent network by: |
| end for |
| end for |
| return PIRL model |
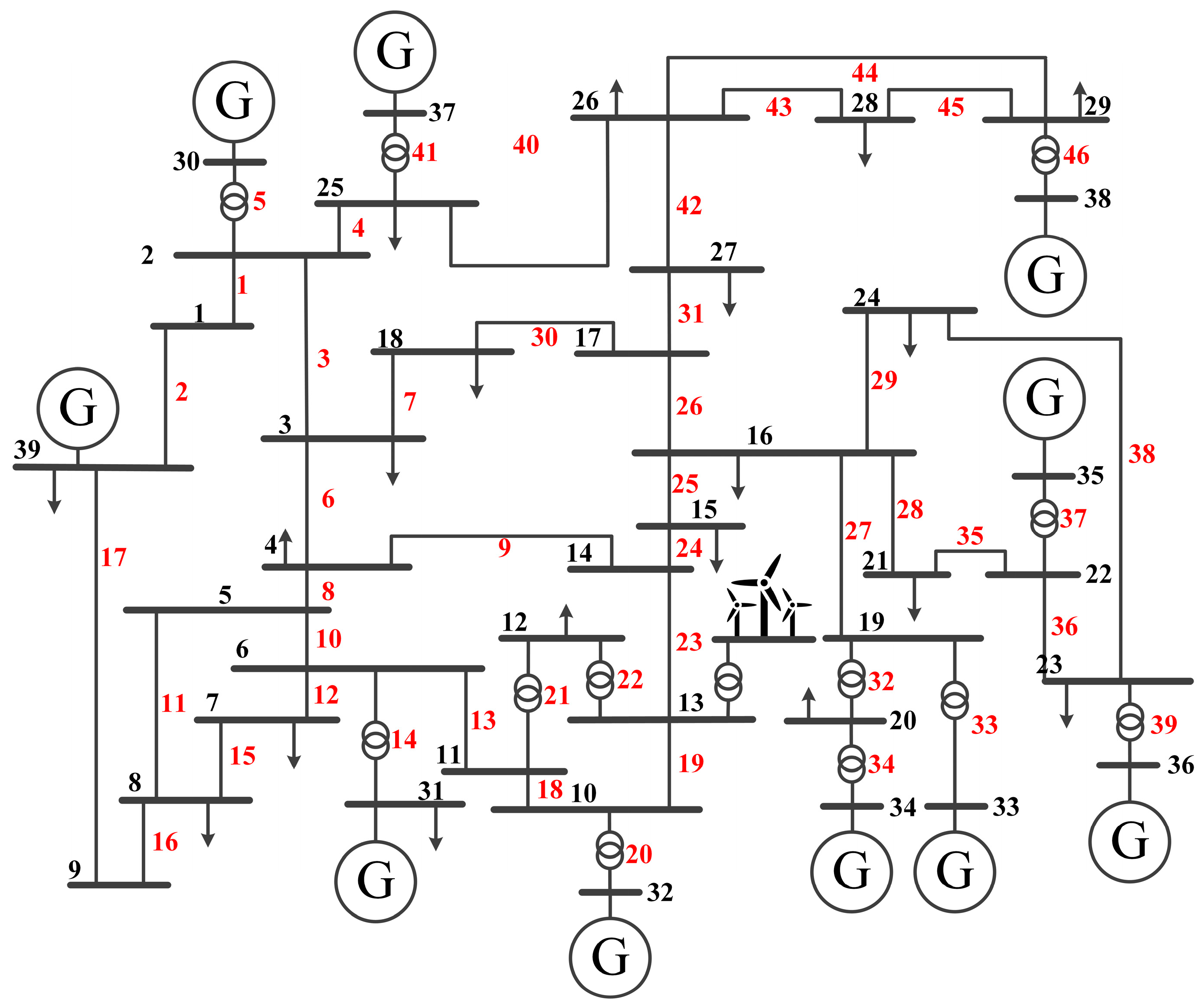
4. Case Study
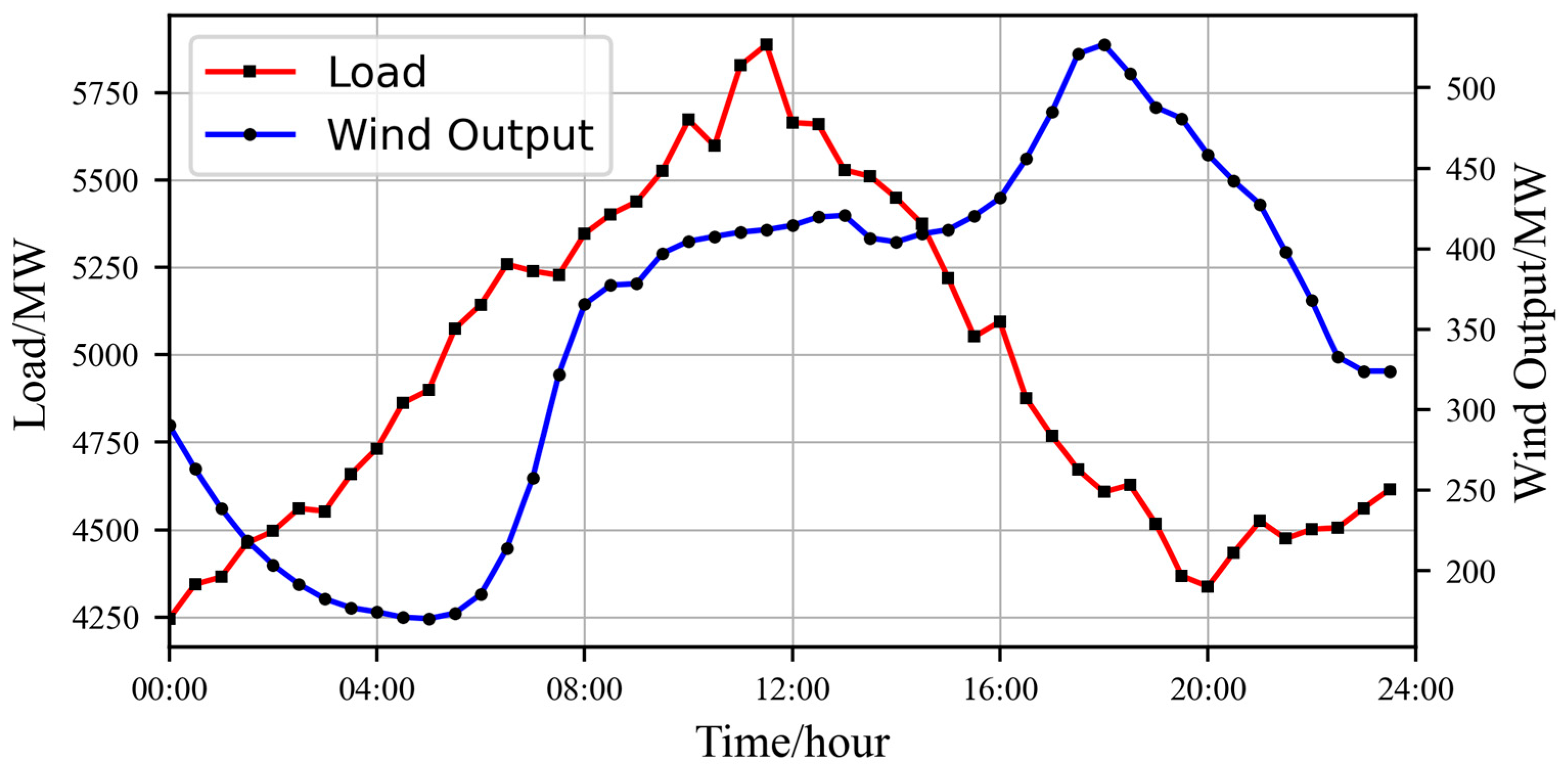
4.1. Algorithm and Environment Settings
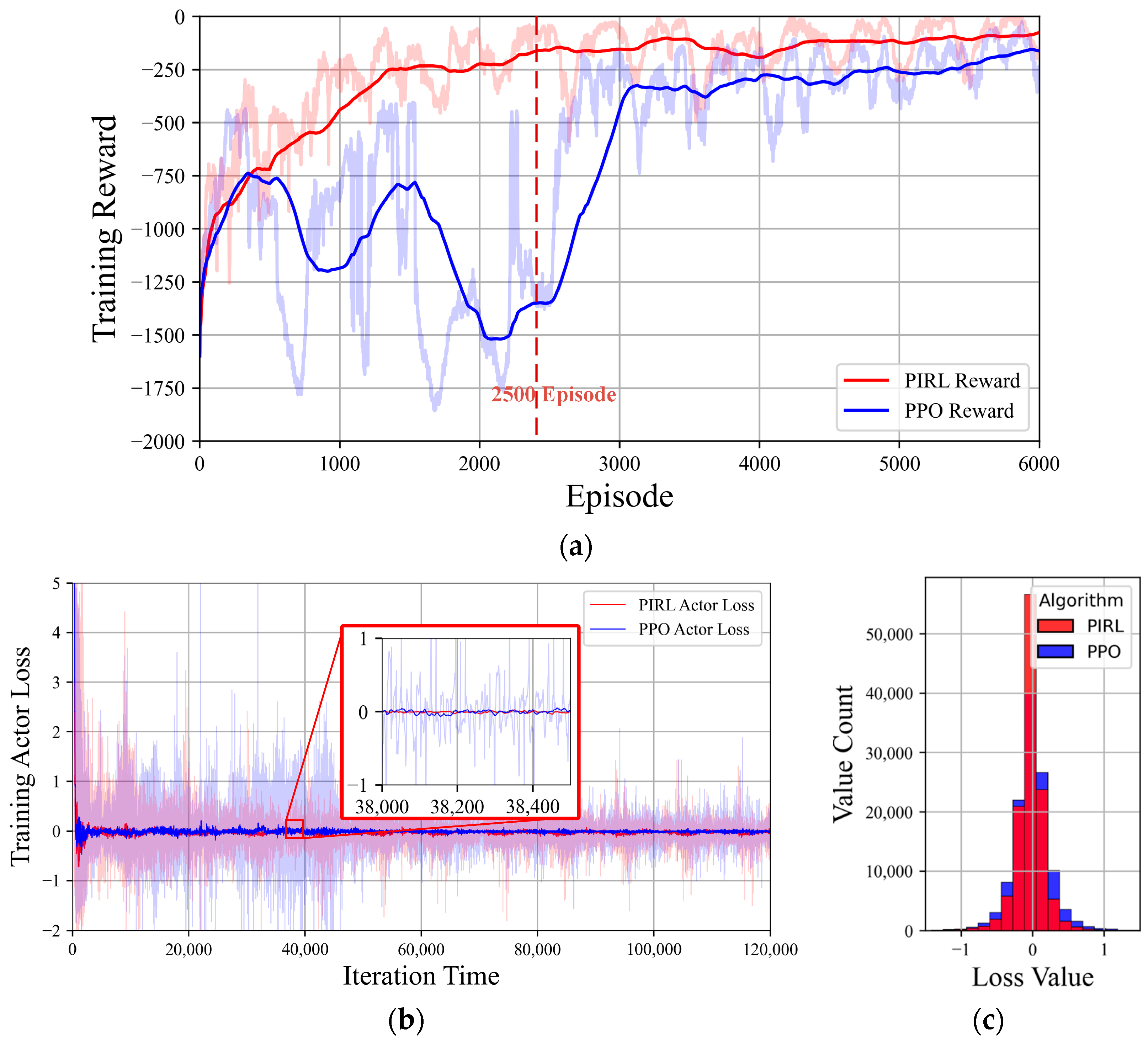
4.2. Comparison in the Training Process
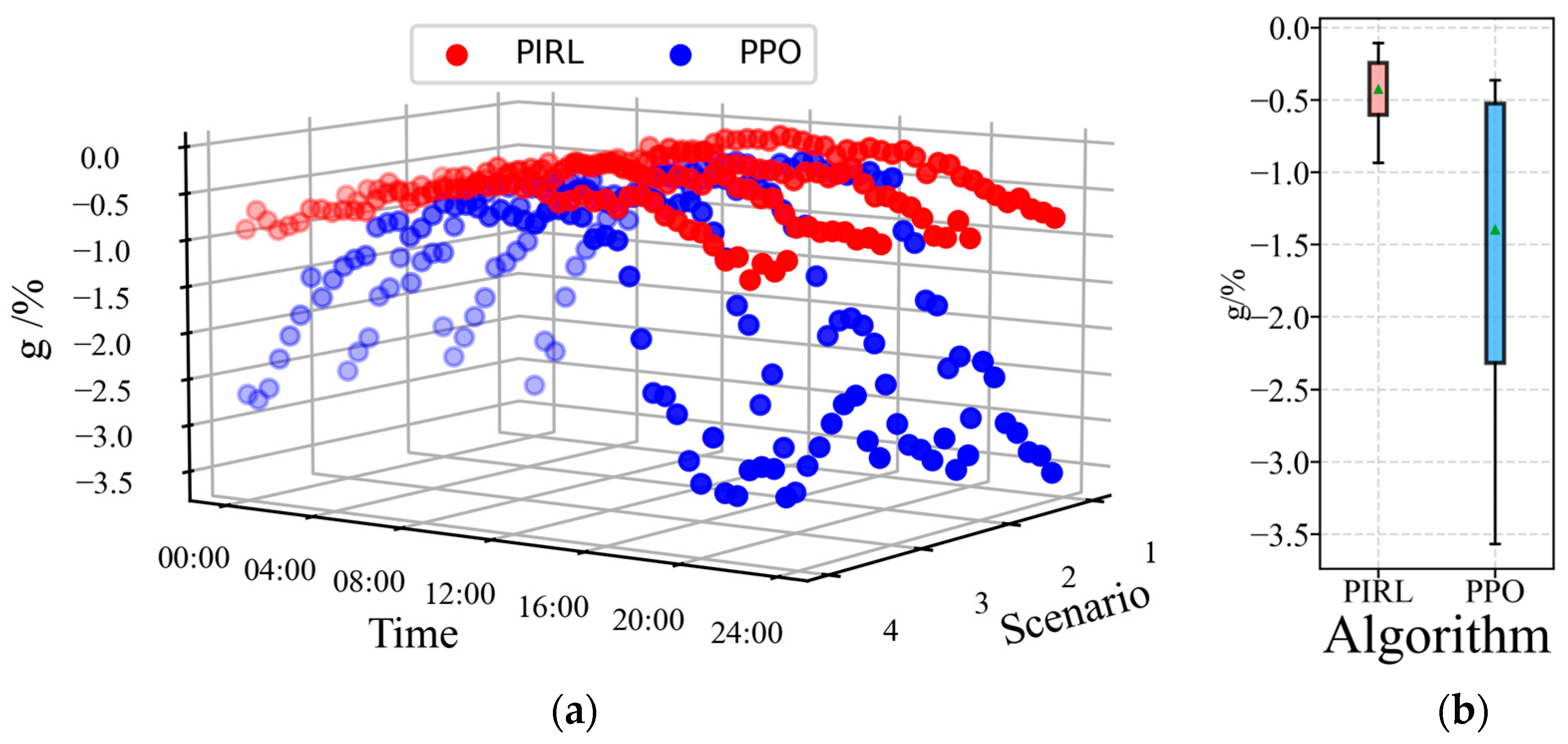
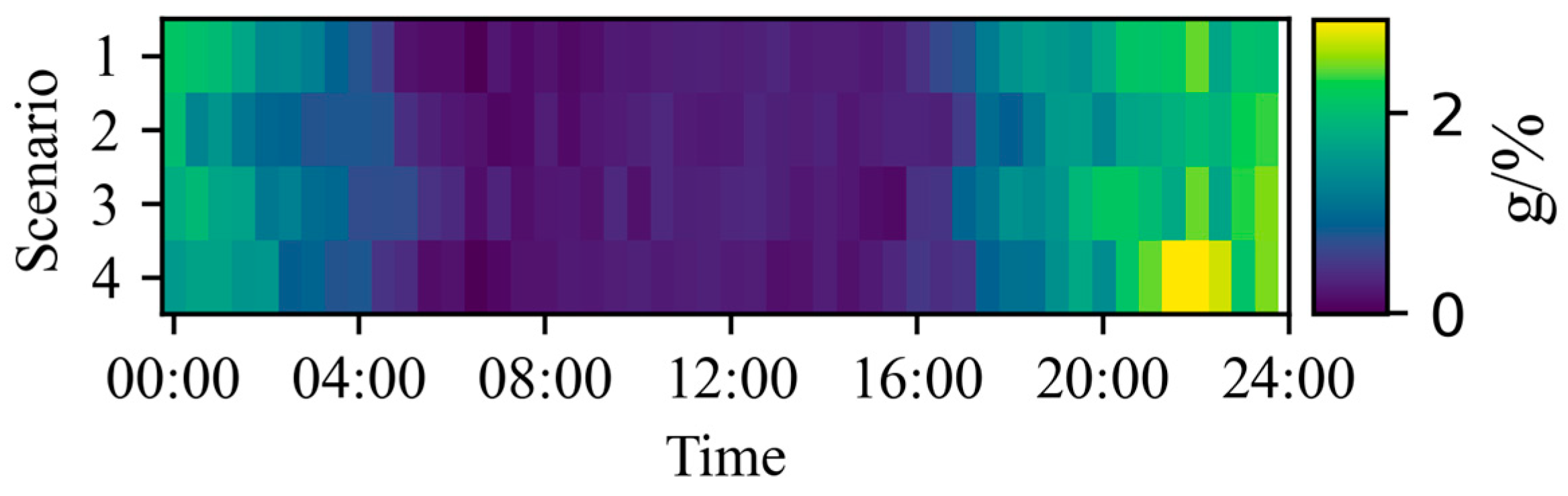
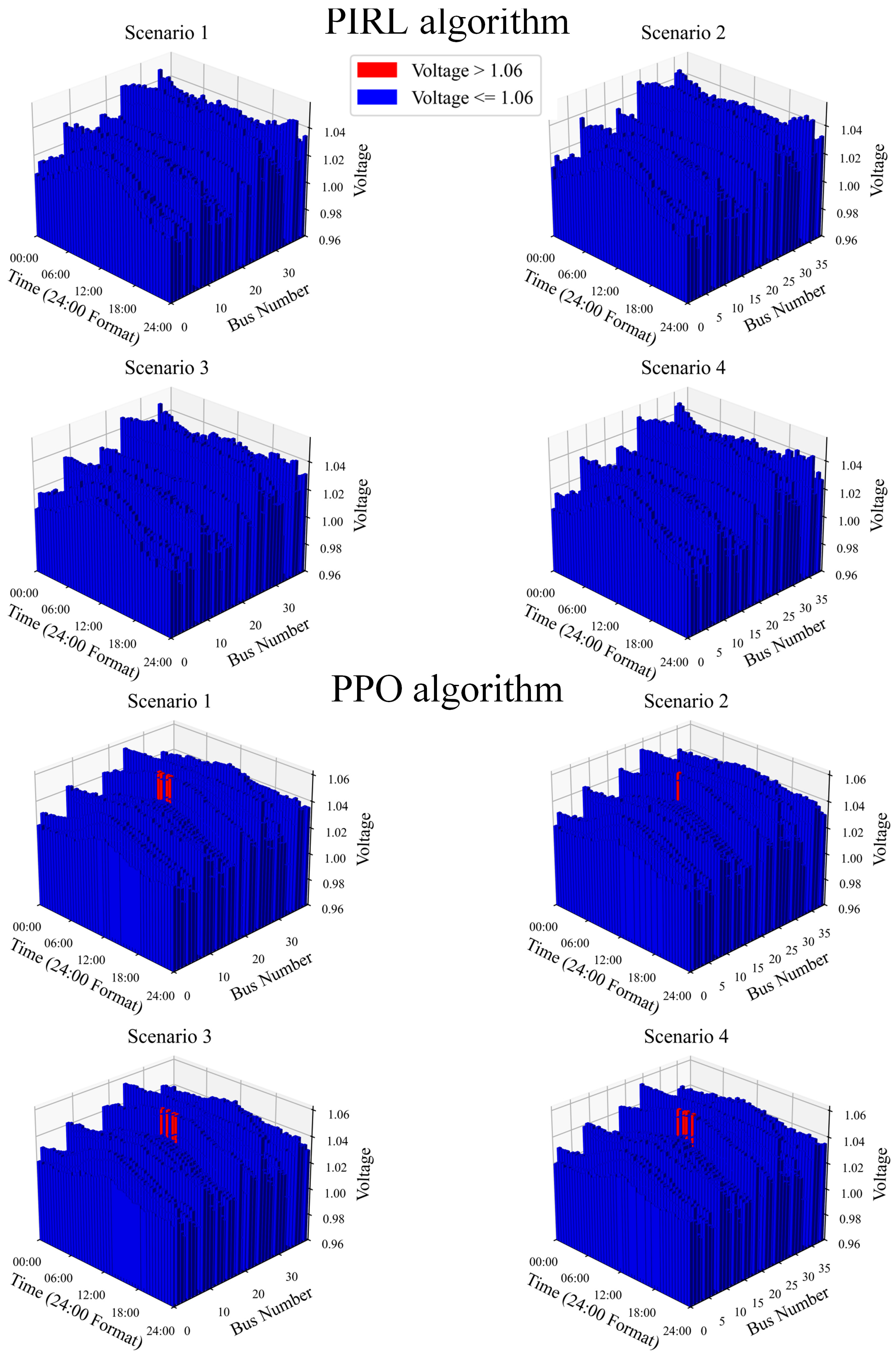
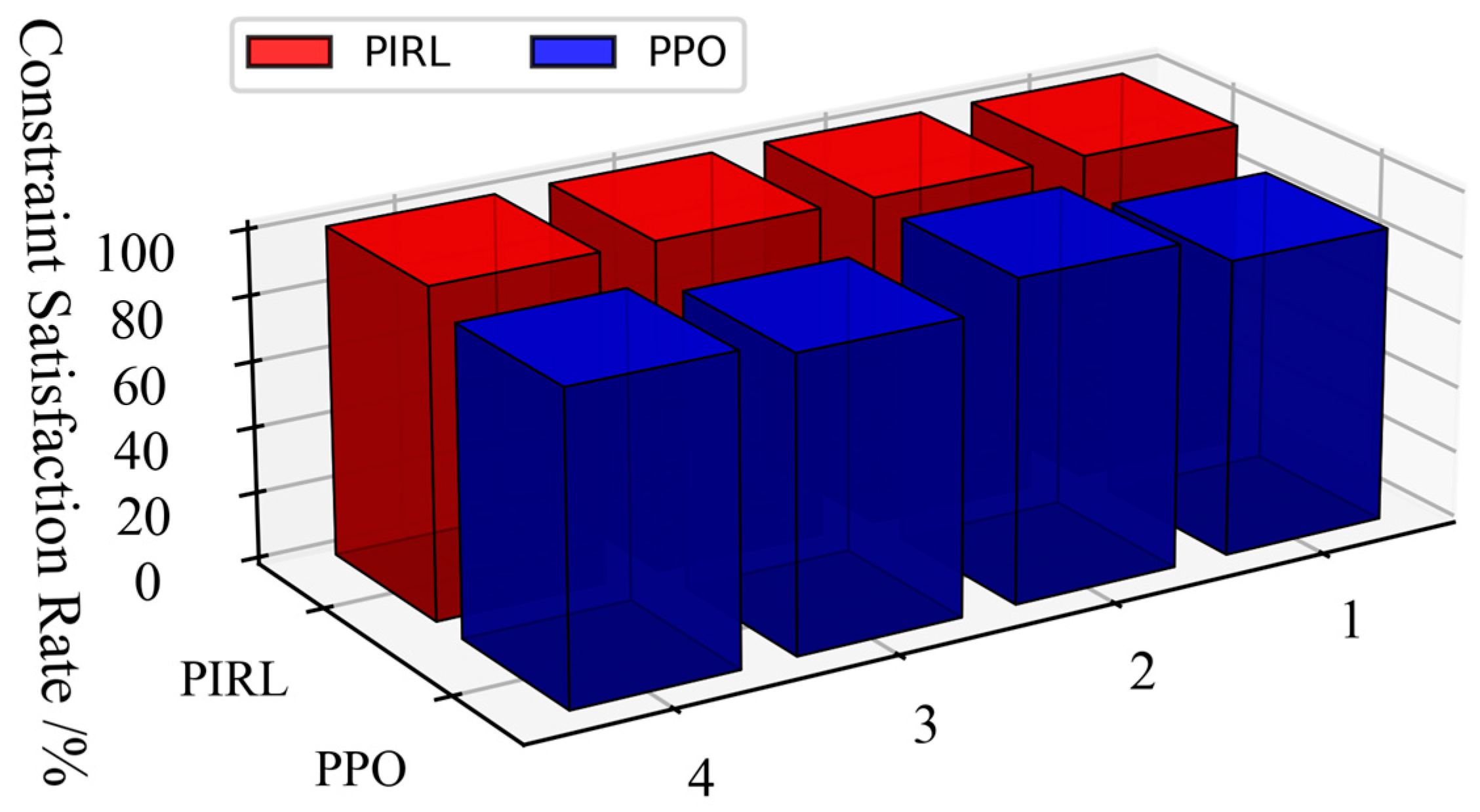
4.3. Comparison of Optimality and Security
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Han, Y.; Liu, Y.; Zalhaf, Y.L.; Zhao, E.; Mahmoud, K. Multi-Timescale Modeling and Dynamic Stability Analysis for Sustainable Microgrids: State-of-the-Art and Perspectives. Prot. Control Mod. Power Syst. 2024, 9, 1–35. [Google Scholar] [CrossRef]
- Brinkel, N.B.G.; Gerritsma, M.K.; Alskaif, T.A.; Lampropoulos, I.; Voorden, A.M.V.; Fidder, H.A.; Sark, W.G.J.H.M.V. Impact of rapid PV fluctuations on power quality in the low-voltage grid and mitigation strategies using electric vehicles. Int. J. Electr. Power Energy Syst. 2020, 118, 105741. [Google Scholar] [CrossRef]
- Zhao, S.; Shao, C.; Ding, J.; Hu, B.; Xie, K.; Yu, X. Unreliability Tracing of Power Systems for Identifying the Most Critical Risk Factors Considering Mixed Uncertainties in Wind Power Output. Prot. Control Mod. Power Syst. 2024, 9, 96–111. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, U.; Choudhary, N.K.; Singh, N. Advancements in Protection Coordination of Microgrids: A Comprehensive Review of Protection Challenges and Mitigation Schemes for Grid Stability. Prot. Control Mod. Power Syst. 2024, 9, 156–183. [Google Scholar] [CrossRef]
- Xiao, J.; Zhou, Y.; She, B.; Bao, Z. A General Simplification and Acceleration Method for Distribution System Optimization Problems. Prot. Control Mod. Power Syst. 2025, 10, 148–167. [Google Scholar] [CrossRef]
- Milano, F. Continuous Newton’s Method for Power Flow Analysis. IEEE Trans. Power Syst. 2009, 24, 50–57. [Google Scholar] [CrossRef]
- Ponnambalam, K.; Quintana, V.H.; Vannelli, A. A fast algorithm for power system optimization problems using an interior point method. IEEE Trans. Power Syst. 1992, 7, 892–899. [Google Scholar] [CrossRef]
- Narimani, M.R.; Molzahn, D.K.; Davis, K.R.; Crow, M.L. Tightening QC Relaxations of AC Optimal Power Flow through Improved Linear Convex Envelopes. IEEE Trans. Power Syst. 2025, 40, 1465–1480. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, C.; Wu, W.; Wang, B.; Wang, G.; Liu, H. A Nested Decomposition Method for the AC Optimal Power Flow of Hierarchical Electrical Power Grids. IEEE Trans. Power Syst. 2024, 38, 2594–2609. [Google Scholar] [CrossRef]
- Chowdhury, M.M.-U.-T.; Biswas, B.D.; Kamalasadan, S. Second-Order Cone Programming (SOCP) Model for Three Phase Optimal Power Flow (OPF) in Active Distribution Networks. IEEE Trans. Smart Grid. 2023, 14, 3732–3743. [Google Scholar] [CrossRef]
- Huang, Y.; Ju, Y.; Ma, K.; Short, M.; Chen, T.; Zhang, R.; Lin, Y. Three-phase optimal power flow for networked microgrids based on semidefinite programming convex relaxation. Appl. Energy 2022, 305, 117771. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wang, L.; Gu, Q. Multi-objective optimal power flow with stochastic wind and solar power. Appl. Soft Comput. 2022, 114, 108045. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, H.D.; Duong, M.Q. Optimal power flow solutions for power system considering electric market and renewable energy. Appl. Sci. 2023, 13, 3330. [Google Scholar] [CrossRef]
- Ehsan, A.; Joorabian, M. An improved cuckoo search algorithm for power economic load dispatch. Int. Trans. Electr. Energy Syst. 2015, 25, 958–975. [Google Scholar]
- Yin, X.; Lei, M. Jointly improving energy efficiency and smoothing power oscillations of integrated offshore wind and photovoltaic power: A deep reinforcement learning approach. Prot. Control Mod. Power Syst. 2023, 8, 1–11. [Google Scholar] [CrossRef]
- Fang, G.; Xu, Z.; Yin, L. Bayesian deep neural networks for spatio-temporal probabilistic optimal power flow with multi-source renewable energy. Appl. Energy 2004, 353, 122106. [Google Scholar]
- Zhen, F.; Zhang, W.; Liu, W. Multi-agent deep reinforcement learning-based distributed optimal generation control of DC microgrids. IEEE Trans. Smart Grid 2023, 14, 3337–3351. [Google Scholar]
- Zhang, K.; Zhang, J.; Xu, P.; Gao, T.; Gao, W. A multi-hierarchical interpretable method for DRL-based dispatching control in power systems. Int. J. Electr. Power Energy Syst. 2023, 152, 109240. [Google Scholar] [CrossRef]
- Rahul, N.; Chatzivasileiadis, S. Physics-informed neural networks for ac optimal power flow. Electr. Power Syst. Res. 2022, 212, 108412. [Google Scholar]
- Nellikkath, R.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Minimising Worst-Case Violations in DC Optimal Power Flow. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; pp. 419–424. [Google Scholar]
- Lakshminarayana, S.; Sthapit, S.; Maple, C. Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability 2022, 14, 2051. [Google Scholar] [CrossRef]
- Stiasny, J.; Misyris, G.S.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Non-linear System Identification for Power System Dynamics. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar]
- Zeng, Y.; Xiao, Z.; Liu, Q.; Liang, G.; Rodriguez, E.; Zou, G. Physics-informed deep transfer reinforcement learning method for the input-series output-parallel dual active bridge-based auxiliary power modules in electrical aircraft. IEEE Trans. Transp. Electrif. 2025, 11, 6629–6639. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, M.; Gao, S.; Wu, Z.G.; Guan, X. Physics-Informed Reinforcement Learning for Real-Time Optimal Power Flow with Renewable Energy Resources. IEEE Trans. Sustain. Energy 2025, 16, 216–226. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, Y. Physics informed deep reinforcement learning for aircraft conflict resolution. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8288–8301. [Google Scholar] [CrossRef]
- Biswas, A.; Acquarone, M.; Wang, H.; Miretti, F.; Misul, D.A.; Emadi, A. Safe reinforcement learning for energy management of electrified vehicle with novel physics-informed exploration strategy. IEEE Trans. Transp. Electrif. 2024, 10, 9814–9828. [Google Scholar] [CrossRef]
- Wu, P.; Chen, C.; Lai, D.; Zhong, J.; Bie, Z. Real-time optimal power flow method via safe deep reinforcement learning based on primal-dual and prior knowledge guidance. IEEE Trans. Power Syst. 2024, 40, 597–611. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. The Reinforcement Learning Problem. In Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 1998; pp. 51–85. [Google Scholar]
- Sayed, A.R.; Wang, C.; Anis, H.I.; Bi, T. Feasibility constrained online calculation for real-time optimal power flow: A convex constrained deep reinforcement learning approach. IEEE Trans. Power Syst. 2022, 38, 5215–5227. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Xu, X.; Wu, Q.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep Reinforcement Learning Based Approach for Optimal Power Flow of Distribution Networks Embedded with Renewable Energy and Storage Devices. J. Mod. Power Syst. Clean Energy 2021, 9, 1101–1110. [Google Scholar] [CrossRef]
- Li, H.; He, H. Learning to Operate Distribution Networks with Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 1860–1872. [Google Scholar] [CrossRef]
- Yi, Z.; Wang, X.; Yang, C.; Yang, C.; Niu, M.; Yin, W. Real-time sequential security-constrained optimal power flow: A hybrid knowledge-data-driven reinforcement learning approach. IEEE Trans. Power Syst. 2023, 39, 1664–1680. [Google Scholar] [CrossRef]


| Parameter | Meaning | Value |
|---|---|---|
| Algorithm | ||
| Discount Coefficient | 0.95 | |
| Priority Discount Coefficient | 0.9 | |
| Physics-Guided Weighting Coefficient | 1.0 | |
| Episodes | 6 × 103 | |
| Step Times | 1 × 102 | |
| Actor-Network Learning Rate | 4 × 10−6 | |
| Critic-Network Learning Rate | 1.3 × 10−5 | |
| Environment | ||
| Cost Penalty Coefficient | −1 × 104 | |
| Violating Penalty Coefficient | −0.4 | |
| Non-convergence Penalty Coefficient | −600 | |
| Scenario | Constraint Satisfaction Rate/% | Optimality Gap Metric (Mean)/% | Computation Time/ms | ||||
|---|---|---|---|---|---|---|---|
| PIRL | PPO | PIRL | PPO | PIRL | PPO | IPS | |
| 1 | 100 | 89.6 | −0.41 | −1.34 | 8 | 8 | 426 |
| 2 | 100 | 97.9 | −0.36 | −1.18 | / | / | / |
| 3 | 100 | 89.6 | −0.41 | −1.35 | / | / | / |
| 4 | 100 | 89.6 | −0.39 | −1.30 | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ma, X.; Yu, Y.; Yang, D.; Lin, Z.; Zhou, C.; Xu, H.; Li, Z. Model-Data Hybrid-Driven Real-Time Optimal Power Flow: A Physics-Informed Reinforcement Learning Approach. Energies 2025, 18, 3483. https://doi.org/10.3390/en18133483
Zhang X, Ma X, Yu Y, Yang D, Lin Z, Zhou C, Xu H, Li Z. Model-Data Hybrid-Driven Real-Time Optimal Power Flow: A Physics-Informed Reinforcement Learning Approach. Energies. 2025; 18(13):3483. https://doi.org/10.3390/en18133483
Chicago/Turabian StyleZhang, Ximing, Xiyuan Ma, Yun Yu, Duotong Yang, Zhida Lin, Changcheng Zhou, Huan Xu, and Zhuohuan Li. 2025. "Model-Data Hybrid-Driven Real-Time Optimal Power Flow: A Physics-Informed Reinforcement Learning Approach" Energies 18, no. 13: 3483. https://doi.org/10.3390/en18133483
APA StyleZhang, X., Ma, X., Yu, Y., Yang, D., Lin, Z., Zhou, C., Xu, H., & Li, Z. (2025). Model-Data Hybrid-Driven Real-Time Optimal Power Flow: A Physics-Informed Reinforcement Learning Approach. Energies, 18(13), 3483. https://doi.org/10.3390/en18133483





