Novel Hybrid Islanding Detection Technique Based on Digital Lock-In Amplifier †
Abstract
1. Introduction
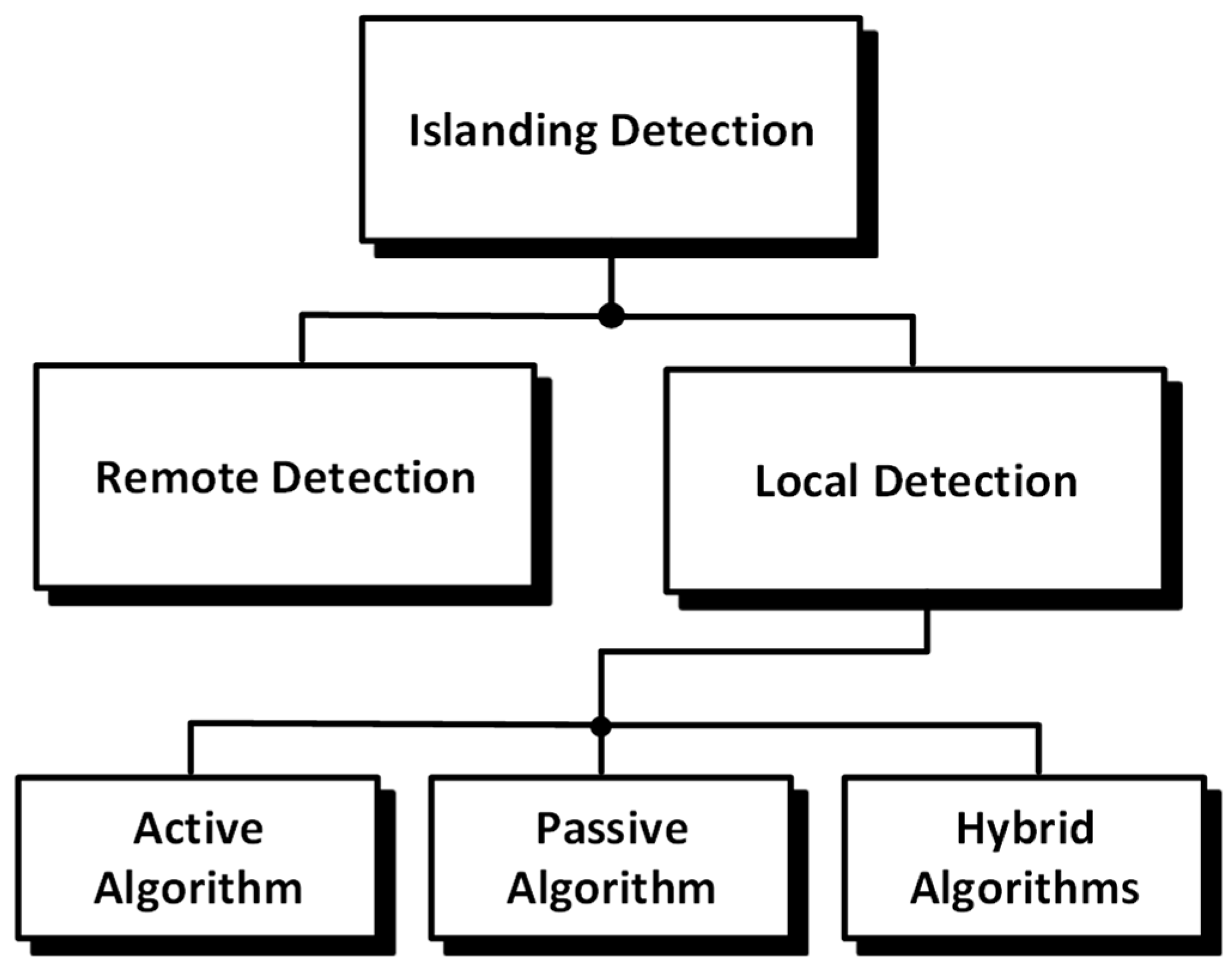
2. Islanding Detection Methods Review
3. Harmonic Distribution in the Grid
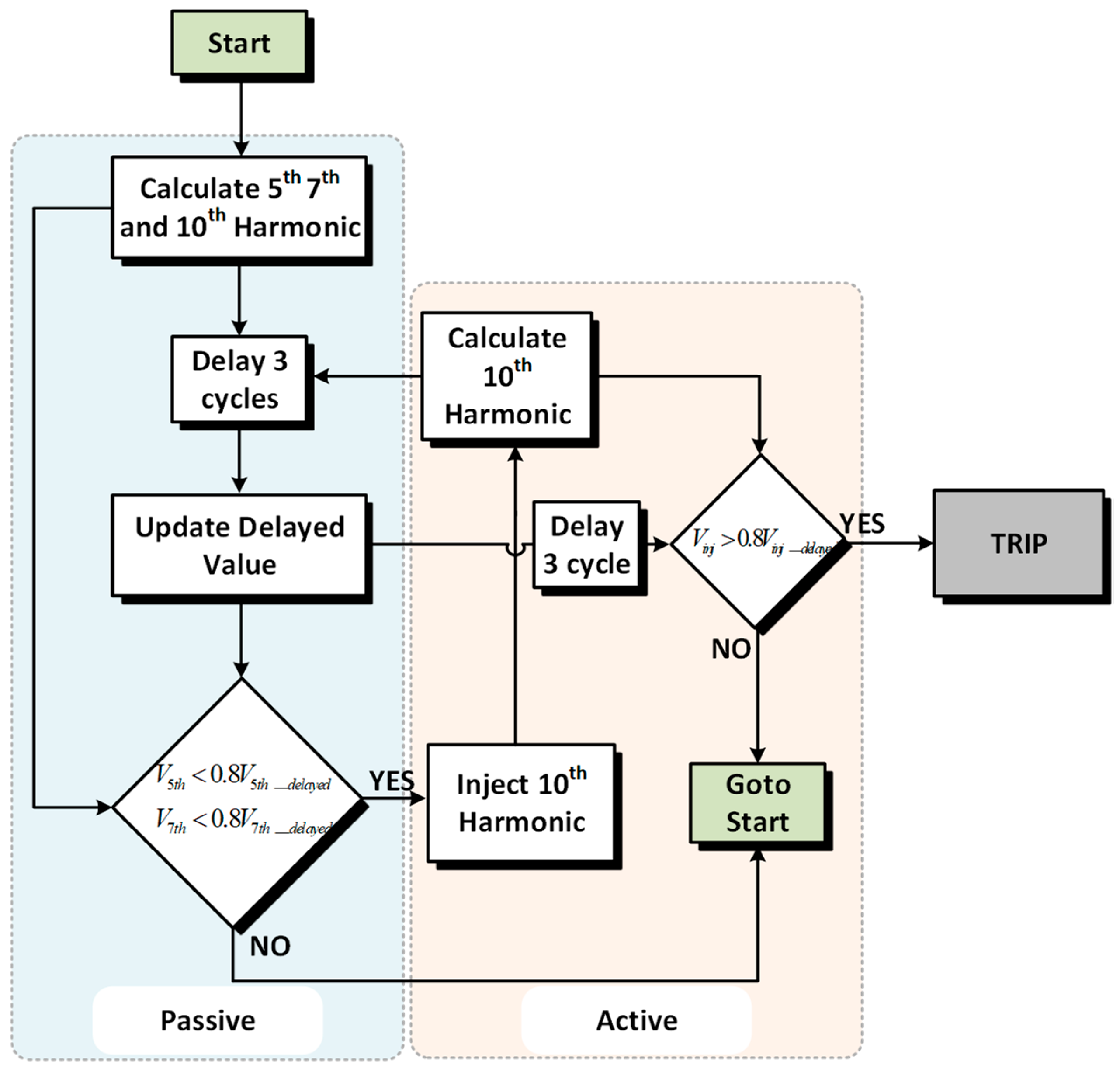
4. Proposed Digital Lock-In Amplifier Anti-Islanding Detection
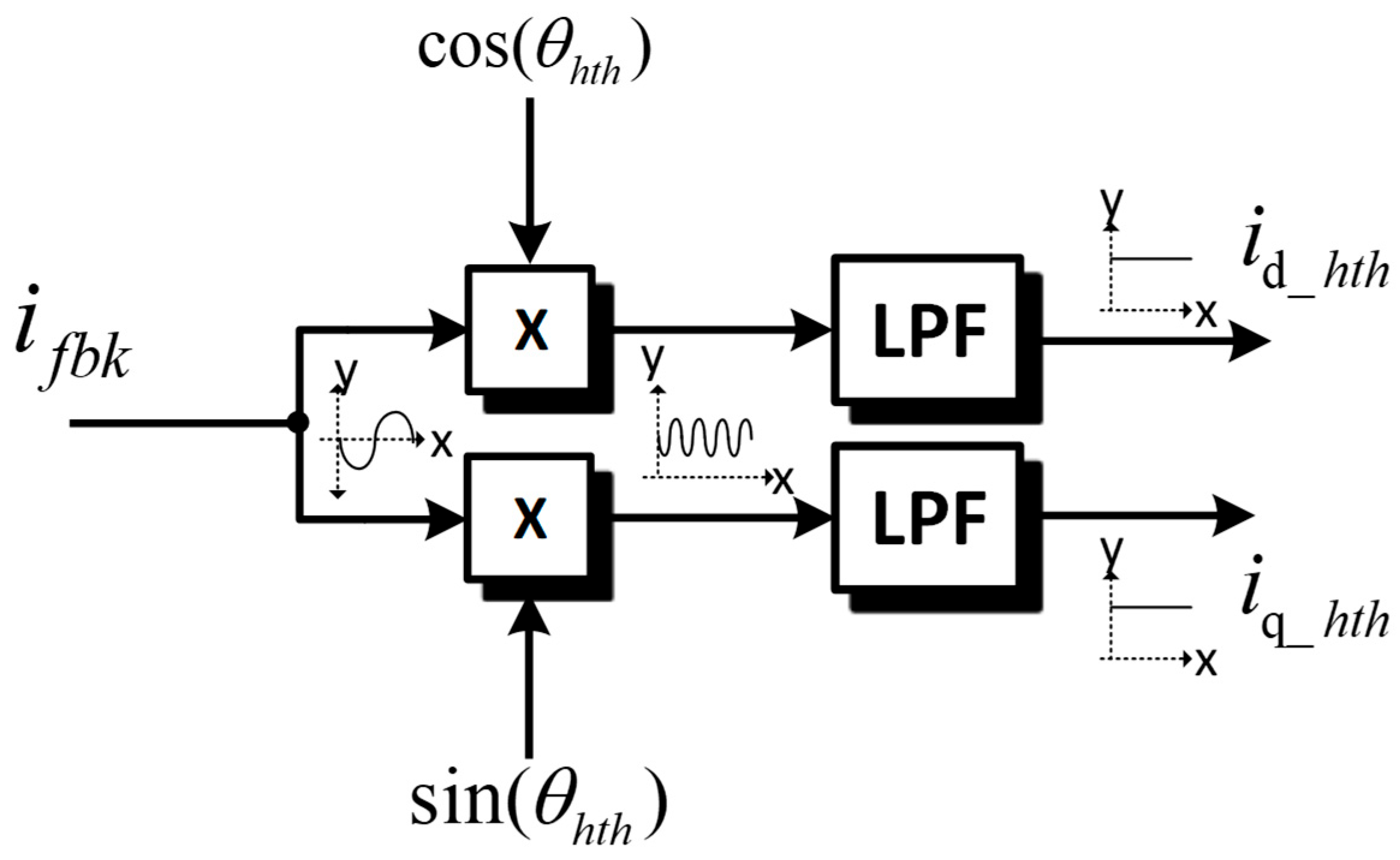
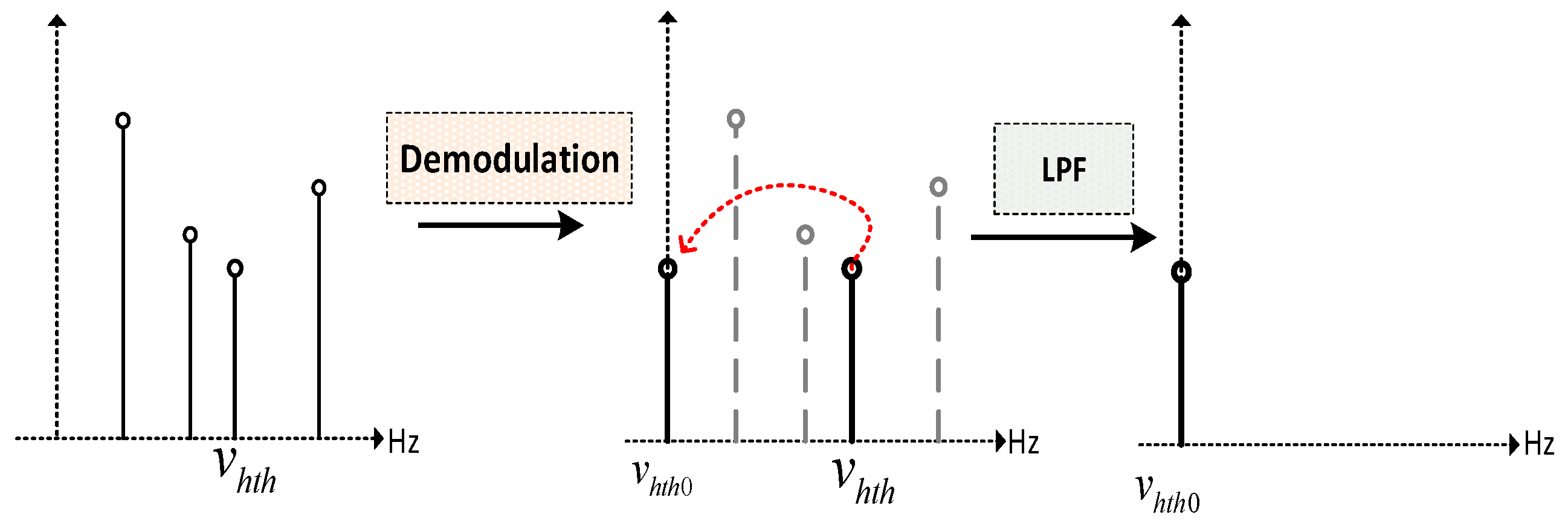
4.1. Digital Lock-In Working Principle
4.2. Passive Detection
4.3. Active Detection
4.4. LPF Filter Design
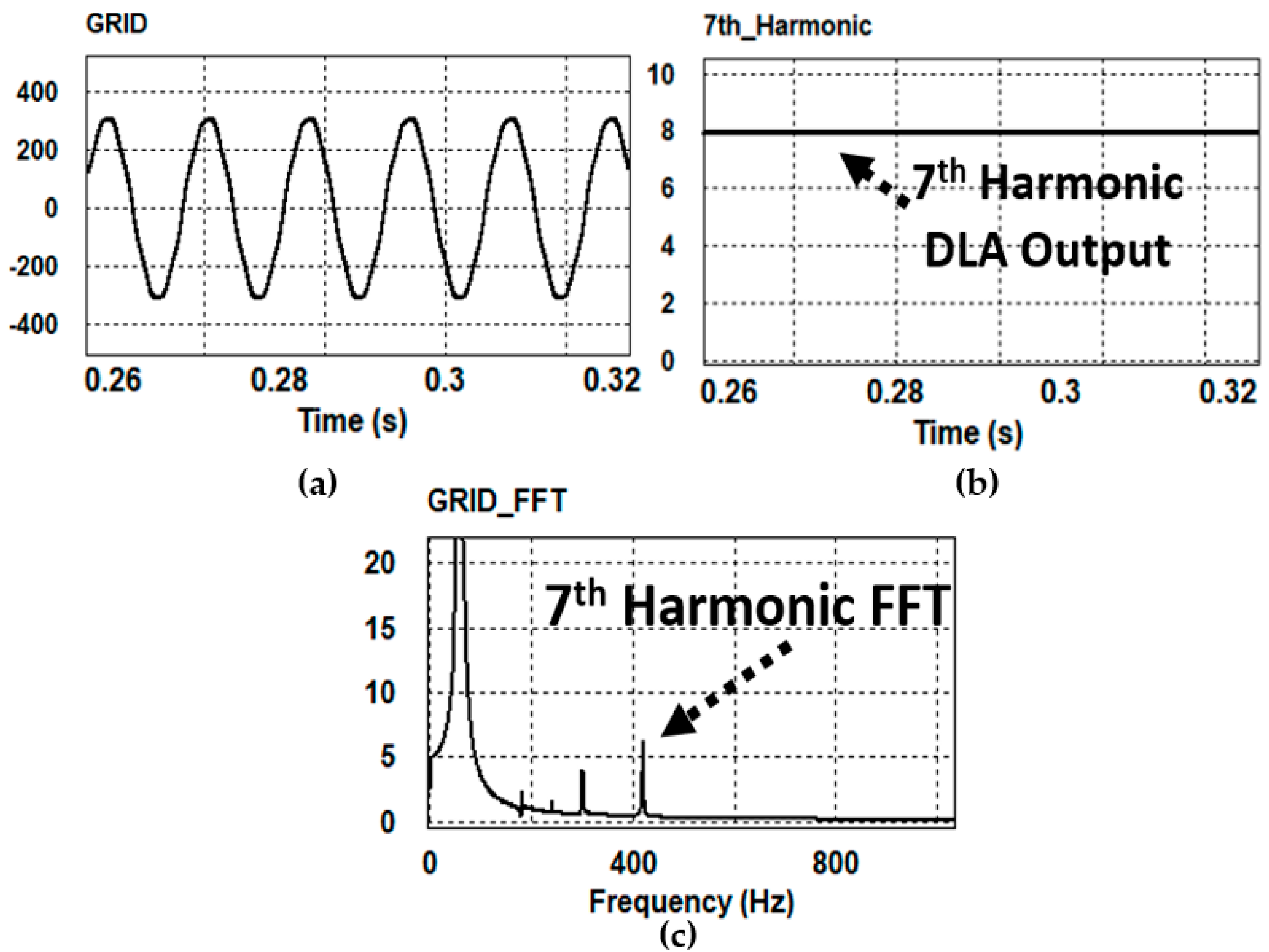
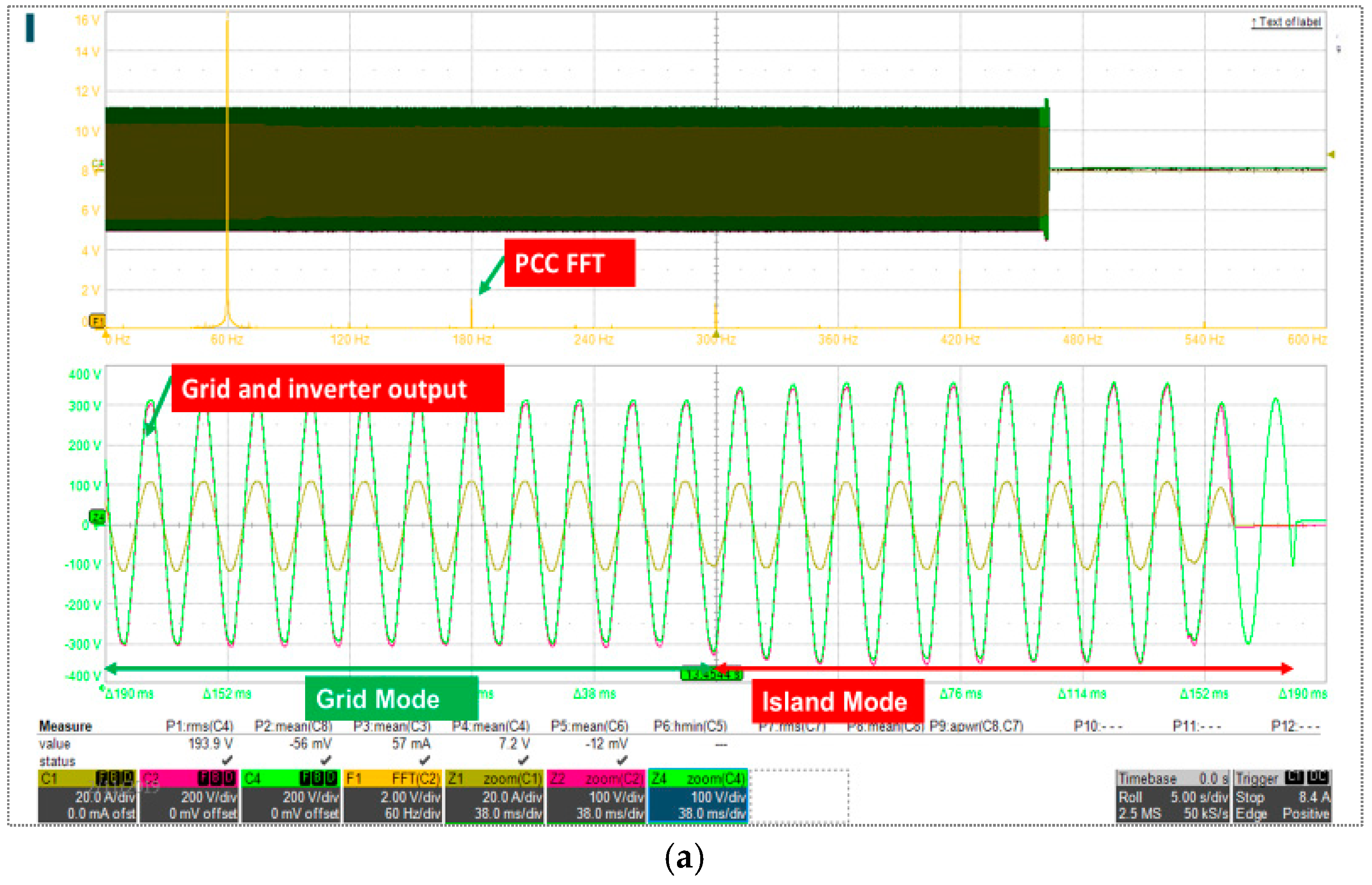
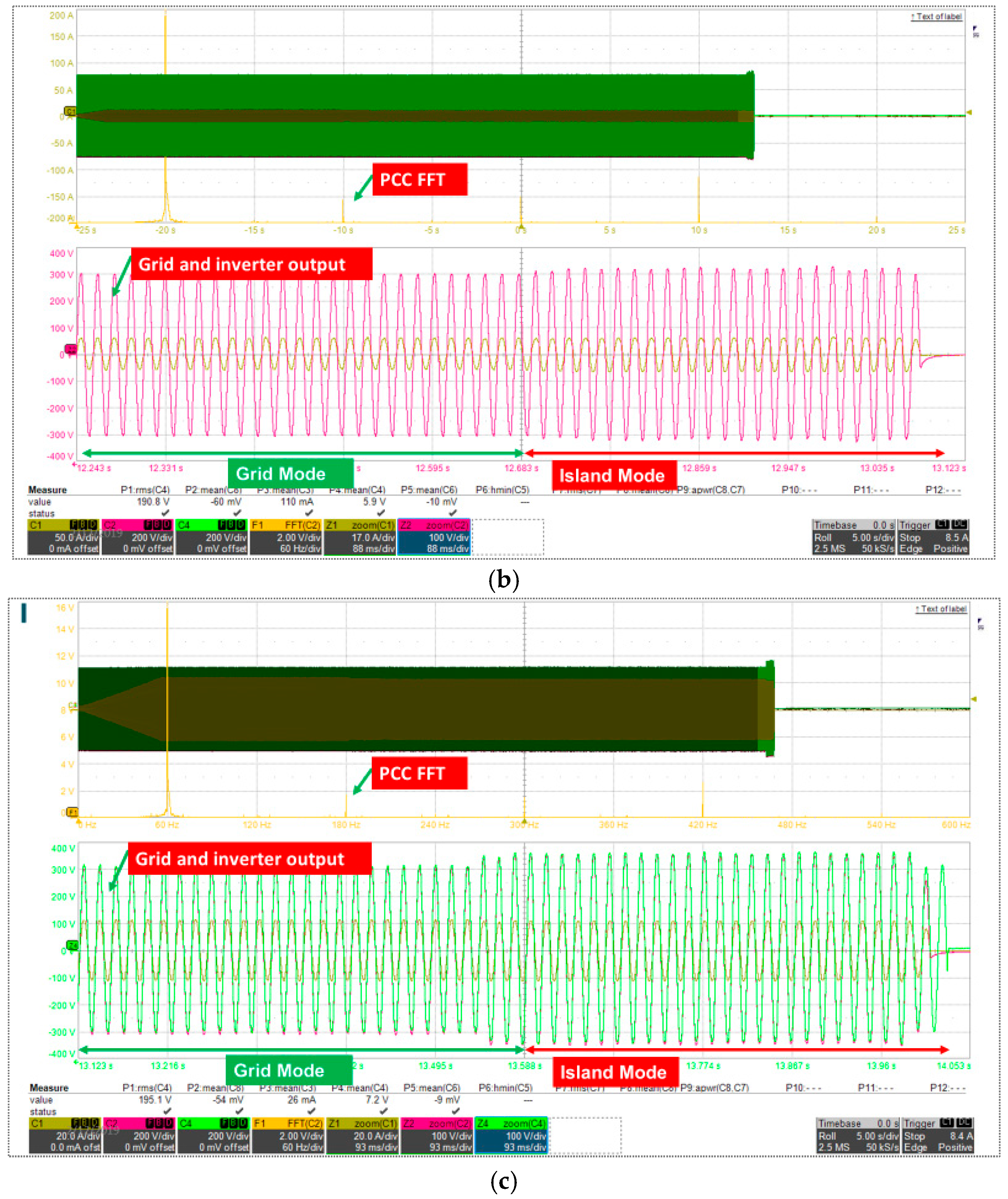
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ropp, M.E.; Aaker, K.; Haigh, J.; Sabbah, N. Using Power Line Carrier Communications to Prevent Islanding. In Proceedings of the 28th IEEE Photovoltaic Specialist Conference, Anchorage, AK, USA, 15–22 September 2000; pp. 1675–1678. [Google Scholar]
- Ashraf, M.N.; Choi, W. A Novel Hybrid Islanding Detection Method Using Digital Lock-In Amplifier. In Proceedings of the KIPE Conference; The Korean Institute of Power Electronics: Seoul, Republic of Korea, 2019; pp. 77–79. [Google Scholar]
- Balaguer-Álvarez, I.; Ortiz-Rivera, E. Survey of distributed generation islanding detection methods. IEEE Latin Am. Trans. 2010, 8, 565–570. [Google Scholar] [CrossRef]
- Chowdhury, S.; Chowdhury, S.; Crossley, P. Islanding protection of active distribution networks with renewable distributed generators: A comprehensive survey. Electr. Power Syst. Res. 2009, 79, 984–992. [Google Scholar] [CrossRef]
- Mango, F.D.; Liserre, M.; Aquila, A.D.; Pigazo, A. Overview of anti-islanding algorithms for PV systems. Part I: Passive methods. In Proceedings of the 12th International Conference Power Electron. Motion Control EPE-PEMC, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1878–1883. [Google Scholar]
- Zeineldin, H.H.; El-Saadany, E.F.; Salama, M.M.A. Islanding detection of inverter-based distributed generation. Proc. Inst. Elect. Eng.-Gener. Transm. Distrib. 2006, 153, 644–652. [Google Scholar] [CrossRef]
- Ye, Z.; Kolwalkar, A.; Zhang, Y.; Du, P.; Walling, R. Evaluation of anti-islanding schemes based on non-detection zone concept. IEEE Trans. Power Electron. 2004, 19, 1171–1176. [Google Scholar] [CrossRef]
- Freitas, W.; Xu, W.; Affonso, C.M.; Huang, Z. Comparative analysis between ROCOF and vector surge relays for distributed generation applications. IEEE Trans. Power Deliv. 2005, 20, 1315–1324. [Google Scholar] [CrossRef]
- Redfern, M.A.; Usta, O.; Fielding, G. Protection against loss of utility grid supply for a dispersed storage and generation unit. IEEE Trans. Power Deliv. 1993, 8, 948–954. [Google Scholar] [CrossRef]
- Yin, J.; Chang, L.; Diduch, C. A new adaptive logic phase shift algorithm for anti-islanding protections in inverter-based DG systems. In Proceedings of the Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 2482–2486. [Google Scholar]
- O’Kane, P.; Fox, B. Loss of mains detection for embedded generation by system impedance monitoring. In Proceedings of the Sixth International Conference on Developments in Power System Protection, Nottingham, UK, 25–27 March 1997; pp. 95–98. [Google Scholar]
- Ebadollah, K.; Javad, S. Islanding detection method for photovoltaic distributed generation based on voltage drifting. IET Gener. Transm. Distrib. 2013, 7, 584–592. [Google Scholar]
- Jang, S.; Kim, K. An islanding detection method for distributed generation using voltage unbalance and total harmonic distortion of current. IEEE Trans. Power Deliv. 2004, 19, 745–752. [Google Scholar] [CrossRef]
- Lidula, N.; Perera, N.; Rajapakse, A. Investigation of a fast islanding detection methodology using transient signals. In Proceedings of the IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar]
- Sun, R.; Wu, Z.; Centeno, V. Power system islanding detection and identification using topology approach and decision tree. In Proceedings of the IEEE Power Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Abdolrasol, M.; Mekhilef, S. Hybrid anti-islanding algorithm for utility interconnection of distributed generation. In Proceedings of the International Conference for Technical Postgraduates, Kuala Lumpur, Malaysia, 14–15 December 2009; pp. 1–5. [Google Scholar]
- Karegar, H.; Shatace, A. Islanding detection of wind farms by THD. In Proceedings of the 3rd International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2793–2797. [Google Scholar]
- Gaing, Z.-L. Wavelet-based neural network for power disturbance recognition and classification. IEEE Trans. Power Del. 2004, 19, 1560–1568. [Google Scholar] [CrossRef]
- El-Arroudi, K.; Joós, G. Data mining approach to threshold settings of islanding relays in distributed generation. IEEE Trans. Power Syst. 2007, 22, 1112–1119. [Google Scholar] [CrossRef]
- El-Arroudi, K.; Joós, G.; Kamwa, I.; McGillis, D.T. Intelligent-based approach to islanding detection in distributed generation. IEEE Trans. Power Del. 2007, 22, 828–835. [Google Scholar] [CrossRef]
- Najy, W.K.A.; Zeineldin, H.H.; Alaboudy, A.H.K.; Woon, W.L. A Bayesian passive islanding detection method for inverter-based distributed generation using ESPRIT. IEEE Trans. Power Del. 2011, 26, 2687–2696. [Google Scholar] [CrossRef]
- Liu, F.; Kang, Y.; Zhang, Y.; Duan, S.; Lin, X. Improved SMS islanding detection method for grid-connected converters. IET Renew. Power Gener. 2010, 4, 36–42. [Google Scholar] [CrossRef]
- Zeineldin, H.H.; Conti, S. Sandia frequency shift parameter selection for multi-inverter systems to eliminate non-detection zone. IET Renew. Power Gener. 2011, 5, 175–183. [Google Scholar] [CrossRef]
- Stevens, J.W., III; Bonn, R.H.; Ginn, J.W.; Gonzalez, S.; Kern, G. Development and Testing of an Approach to Anti-Islanding in Utility Interconnected Photovoltaic Systems; Sandia National Laboratories Report SAND2000-1939; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2000. [Google Scholar]
- Chiang, W.-J.; Jou, H.-L.; Wu, J.-C. Active islanding detection method for inverter-based distribution generation power system. Int. J. Electr. Power Energy Syst. 2012, 42, 158–166. [Google Scholar] [CrossRef]
- Jou, H.-L.; Chiang, W.-J.; Wu, J.-C. Virtual inductor-based islanding detection method for grid-connected power inverter of distributed power generation system. IET Renew. Power Gener. 2007, 1, 175–181. [Google Scholar] [CrossRef]
- Velasco, D.; Trujillo, C.; Garcera, G.; Figueres, E. An active anti-islanding method based on phase-PLL perturbation. IEEE Trans. Power Electron. 2011, 26, 1056–1066. [Google Scholar] [CrossRef]
- Pourbabak, H.; Kazemi, A. A new technique for islanding detection using voltage phase angle of inverter-based DGs. Int. J. Electr. Power Energy Syst. 2014, 57, 198–205. [Google Scholar] [CrossRef]
- Huili, S.; Lopes, L.A.C.; Zhixiang, L. Analysis and comparison of islanding detection methods using a new load parameter space. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society (IECON), Busan, Republic of Korea, 2–6 November 2004; Volume 2, pp. 1172–1177. [Google Scholar]
- Ye, Z.; Li, L.; Garces, L.; Wang, C.; Zhang, R.; Dame, M.; Walling, R.; Miller, N. A new family of active anti-islanding schemes based on DQ implementation for grid-connected inverters. In Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 235–241. [Google Scholar]
- Hunter, I. Power quality issues—A distribution company perspective. Power Eng. J. 2001, 15, 75–80. [Google Scholar] [CrossRef]
- Hanif, M.; Street, K.; Gaughan, K. A discussion of anti-islanding protection schemes incorporated in inverter-based DG. In Proceedings of the Environment and Electrical Engineering (EEEIC), Rome, Italy, 8–11 May 2011; pp. 1–5. [Google Scholar]
- Hernandez-Gonzalez, G.; Iravani, R. Current injection for active islanding detection of electronically-interfaced distributed resources. IEEE Trans. Power Deliv. 2006, 21, 1698–1705. [Google Scholar] [CrossRef]
- Karimi, H.; Yazdani, A.; Iravani, R. Negative-sequence current injection for fast islanding detection of a distributed resource unit. IEEE Trans. Power Electron. 2008, 23, 298–307. [Google Scholar] [CrossRef]
- Byeong-Heon, K.; Seung-Ki, S.; Chun-Ho, L. Anti-islanding detection method using Negative Sequence Voltage. In Proceedings of the International Conference Power Electronics and Motion Control, Harbin, China, 2–5 June 2012; pp. 604–608. [Google Scholar]
- Reigosa, D.; Briz, F.; Blanco, C.; García, P.; Guerrero, J.M. Active islanding detection for multiple parallel-connected inverter-based distributed generators using high-frequency signal injection. IEEE Trans. Power Electron. 2014, 29, 1192–1199. [Google Scholar] [CrossRef]
- Cobben, J.F.G.; Kling, W.L.; Myrzik, J.M.A. Power quality aspects of a future micro grid. In Proceedings of the International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005; p. 5. [Google Scholar]
- Bhattacharyya, S.; Cobben, J.F.G.; Kling, W. Harmonic current pollution in a low voltage network. In Proceedings of the IEEE Power Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Lauwers, P.; Pirenne, C.; Sommereyns, P.; Vancoetsem, W.; De Jaeger, E.; De Witte, M. Power quality monitoring in Belgian distribution networks. In Proceedings of the 18th International Conference and Exhibition on Electricity Distribution, Turin, Italy, 6–9 June 2005; pp. 1–6. [Google Scholar]
- Emanuel, A.; Orr, J.; Cyganski, D.; Gulachenski, E.M. A survey of harmonic voltages and currents at distribution substations. IEEE Trans. Power Del. 1991, 6, 1883–1890. [Google Scholar] [CrossRef]
- Emanuel, A.; Orr, J.; Cyganski, D.; Gulachenski, E.M. A survey of harmonic voltages and currents at the customer’s bus. IEEE Trans. Power Del. 1993, 8, 411–421. [Google Scholar] [CrossRef]
- Nejdawi, I.; Emanuel, A.; Pileggi, D.; Corridori, M.J.; Archambeault, R.D. Harmonics trend in NE USA: A preliminary survey. IEEE Trans. Power Del. 1999, 14, 1488–1494. [Google Scholar] [CrossRef]
- Lidula, N.W.A.; Rajapakse, A.D. A pattern recognition approach for detecting power islands using transient signals—Part I: Design and implementation. IEEE Trans. Power Del. 2010, 25, 3070–3077. [Google Scholar] [CrossRef]
- Khamis, A.; Shareef, H.; Mohamed, A.; Bizkevelci, E. Islanding detection in a distributed generation integrated power system using phase space technique and probabilistic neural network. Neurocomputing 2015, 148, 587–599. [Google Scholar] [CrossRef]
- Khamis, A.; Shareef, H.; Mohamed, A. Islanding detection and load shedding scheme for radial distribution systems integrated with dispersed generations. IET Gener. Transm. Distrib. 2015, 9, 2261–2275. [Google Scholar] [CrossRef]




| Parameters | Values | |
|---|---|---|
| Grid voltage | Vg | 220 Vrms |
| Rated Power | Po | 5 kW |
| Grid frequency | fg | 60 Hz |
| Switching/Sampling frequency | fsw | 10 kHz |
| Dead time | td | 0.5 µs |
| Inverter side inductor | Li | 1.4 mH |
| Grid side inductor | Lg | 1.2 mH |
| Inductor resistances | Ri + Rg | 0.15 Ω |
| Damping resistor | Rd | 3.0 ohm |
| Filter capacitor | Cf | 6.0 µF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, M.N.; Akram, A.S.; Choi, W. Novel Hybrid Islanding Detection Technique Based on Digital Lock-In Amplifier. Energies 2025, 18, 3449. https://doi.org/10.3390/en18133449
Ashraf MN, Akram AS, Choi W. Novel Hybrid Islanding Detection Technique Based on Digital Lock-In Amplifier. Energies. 2025; 18(13):3449. https://doi.org/10.3390/en18133449
Chicago/Turabian StyleAshraf, Muhammad Noman, Abdul Shakoor Akram, and Woojin Choi. 2025. "Novel Hybrid Islanding Detection Technique Based on Digital Lock-In Amplifier" Energies 18, no. 13: 3449. https://doi.org/10.3390/en18133449
APA StyleAshraf, M. N., Akram, A. S., & Choi, W. (2025). Novel Hybrid Islanding Detection Technique Based on Digital Lock-In Amplifier. Energies, 18(13), 3449. https://doi.org/10.3390/en18133449







