Impact of Blade Ice Coverage on Wind Turbine Power Generation Efficiency: A Combined CFD and Wind Tunnel Study
Abstract
1. Introduction
2. Theory Related to Wind Turbine Airfoil Ice Coverage
2.1. Aerodynamic Theory of Airfoils
2.2. Blade Element Momentum Theory
2.3. Similarity Theory
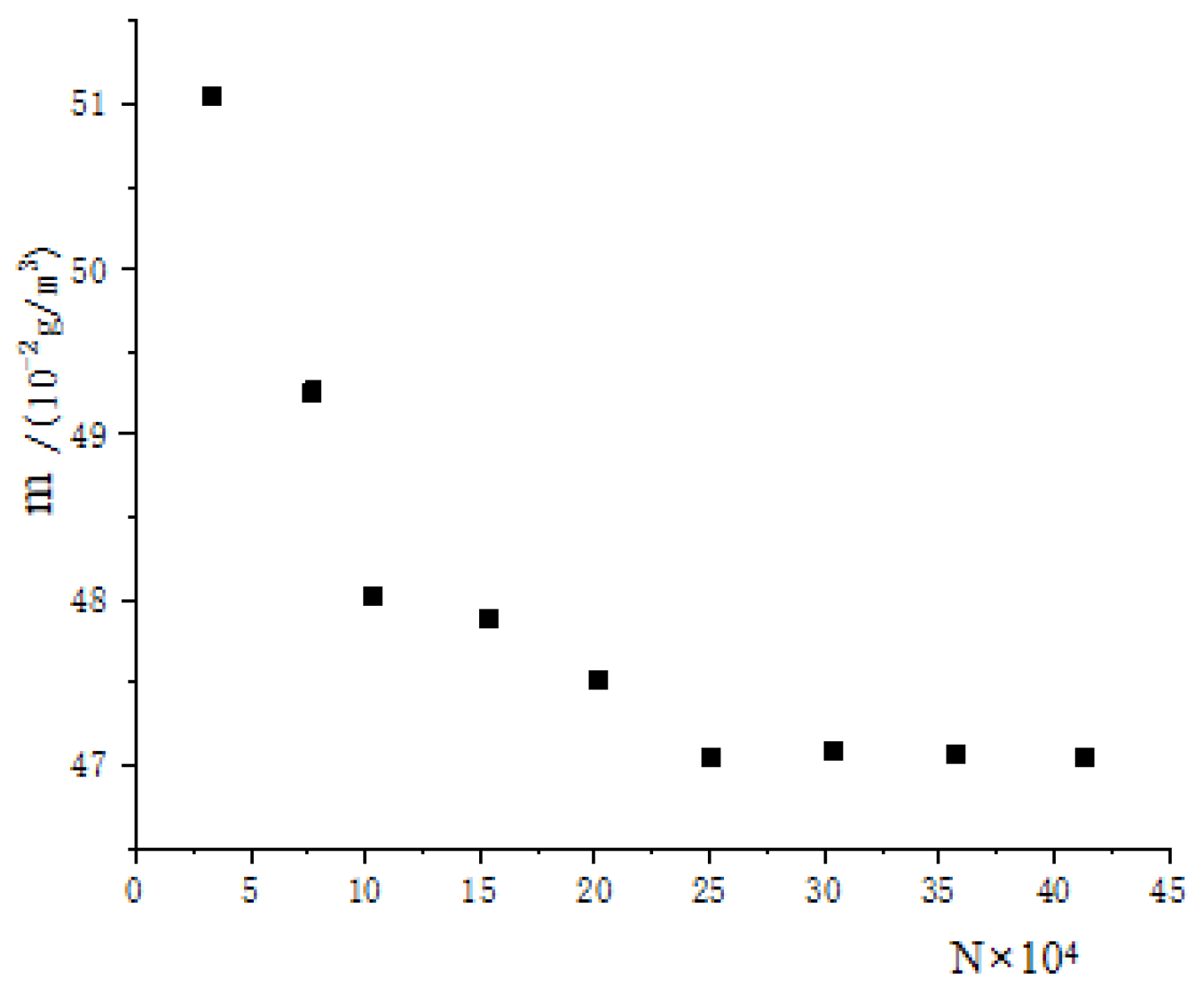
3. Numerical Simulation of Wind Turbine Blade Surface Ice Coverage
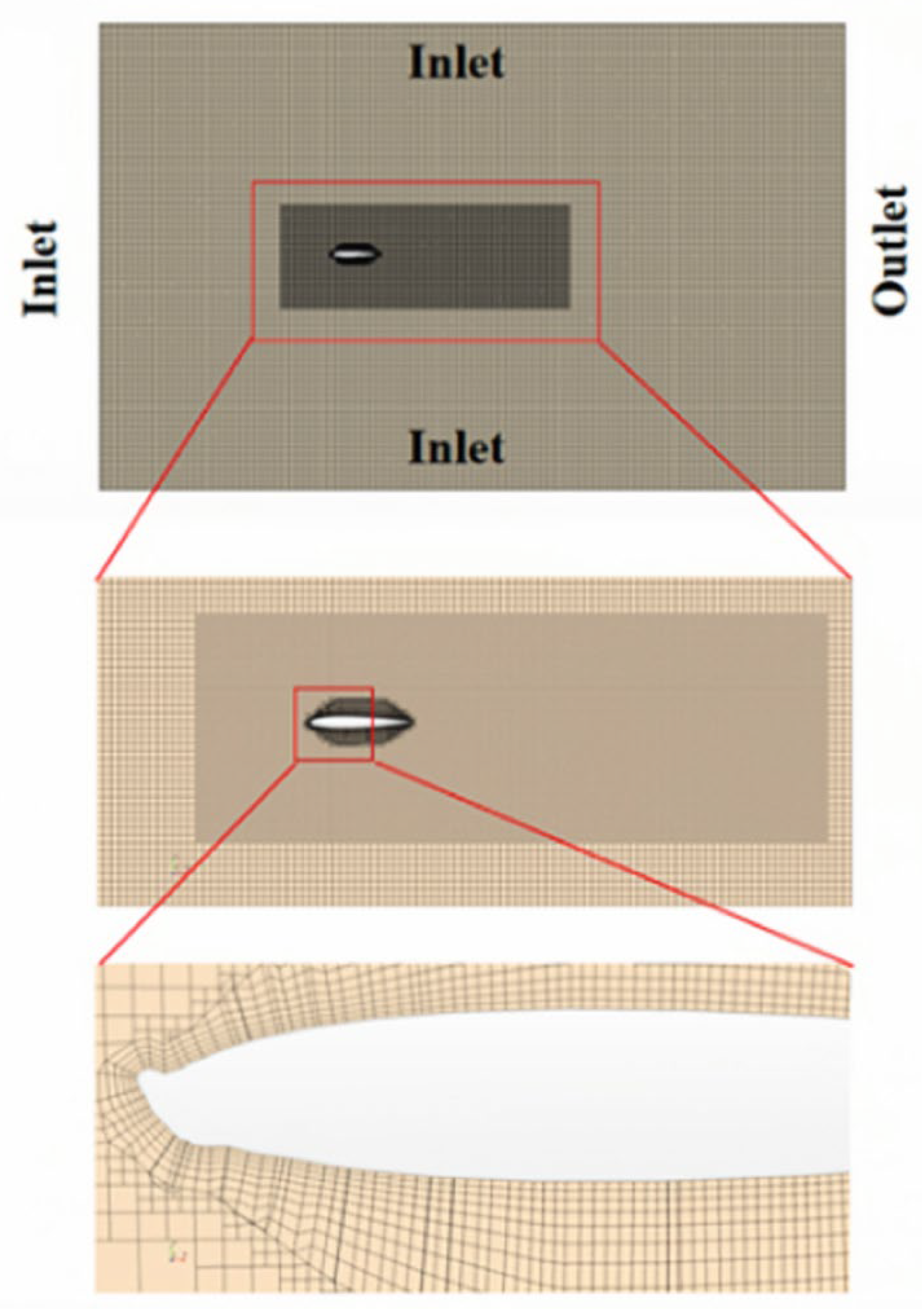
3.1. NACA0012 Airfoil Boundary Conditions and Meshing
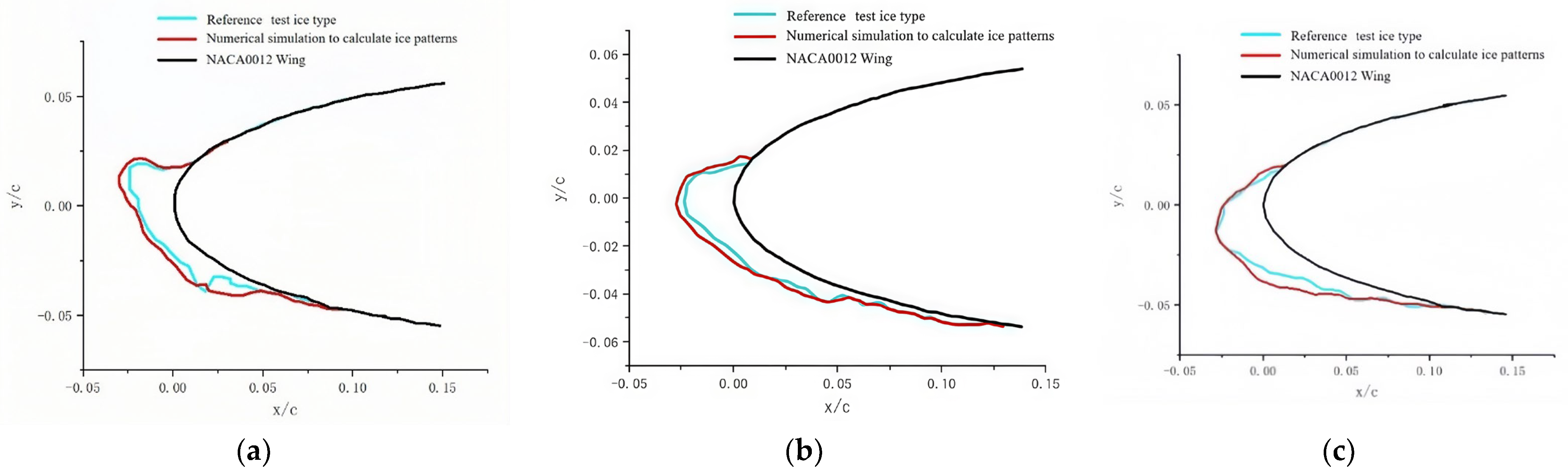
3.2. NACA0012 Wing Ice Cover Simulation Validation Study
4. Experimental Methodology for Aerodynamic Performance Assessment
4.1. Experimental Equipment
- 1.
- Test section (1500 × 1000 × 800 mm) with optically transparent walls for flow visualization (Evonik, Germany).
- 2.
- Force measurement: 6-axis transducer (ATI Gamma SI-130-10) with pitch control mechanism (±30°, 0.1° resolution).
- 3.
- PIV system: Dual-cavity Nd: YAG laser (532 nm) (ATI Gamma SI-130-10) and 4MP CCD camera (LaVision Imager Pro X) synchronized via programmable timing unit (LaVision GmbH, Göttingen, Germany).
- 4.
- Data acquisition: NI PXIe-1071 chassis (10 kHz sampling) (National Instruments (NI), Austin, TA, USA).
4.2. Experimental Model
4.3. Design of Experimental Conditions
5. Aerodynamic Performance Analysis Based on Numerical Simulation
Numerical Methods
6. Effect of Icing on Wind Turbine Output Power
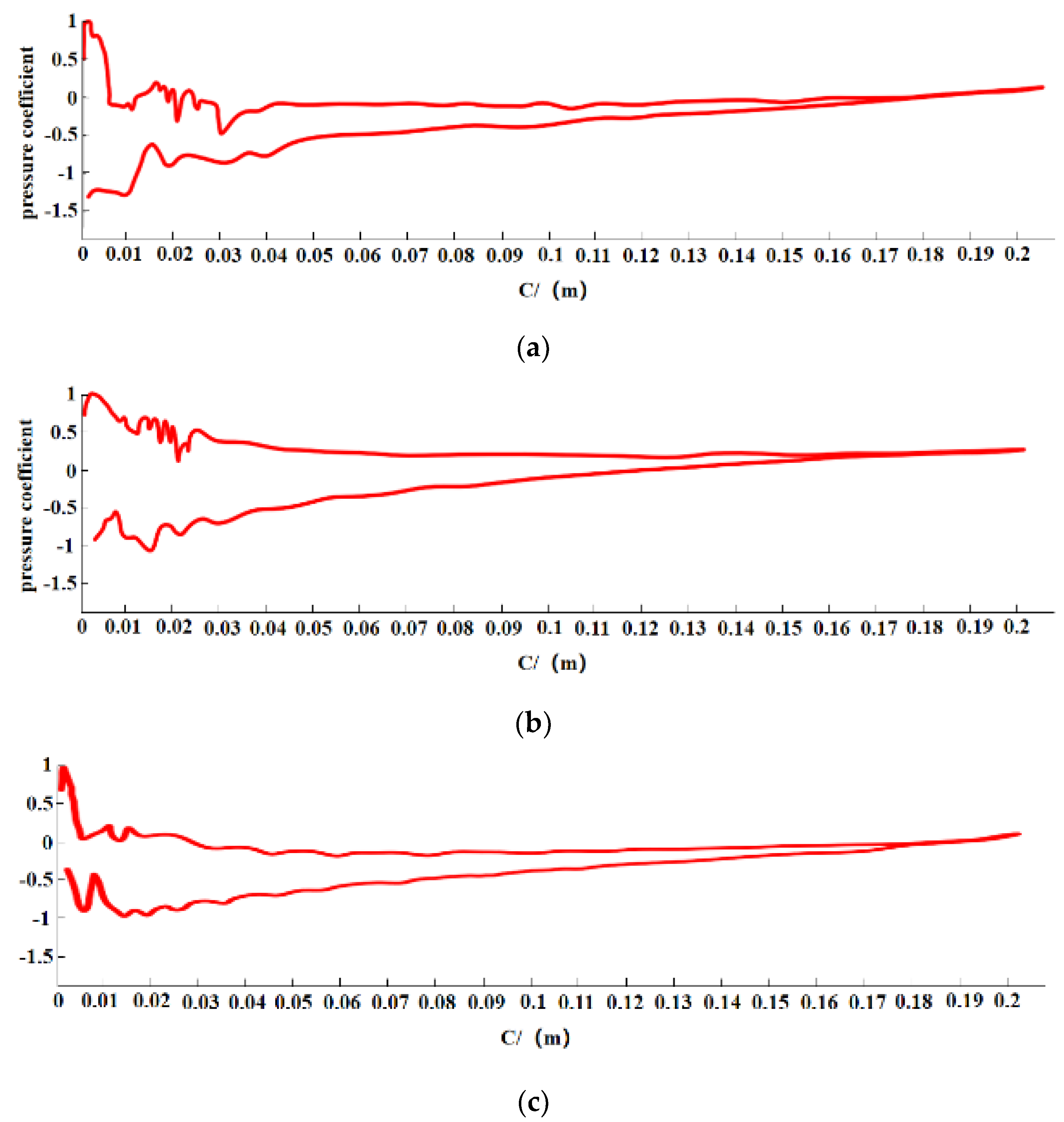
6.1. Effect of Airfoil Ice Cover on Airfoil Surface Pressure Coefficients
6.2. Effect of Airfoil Ice Cover on Airfoil Flow Field
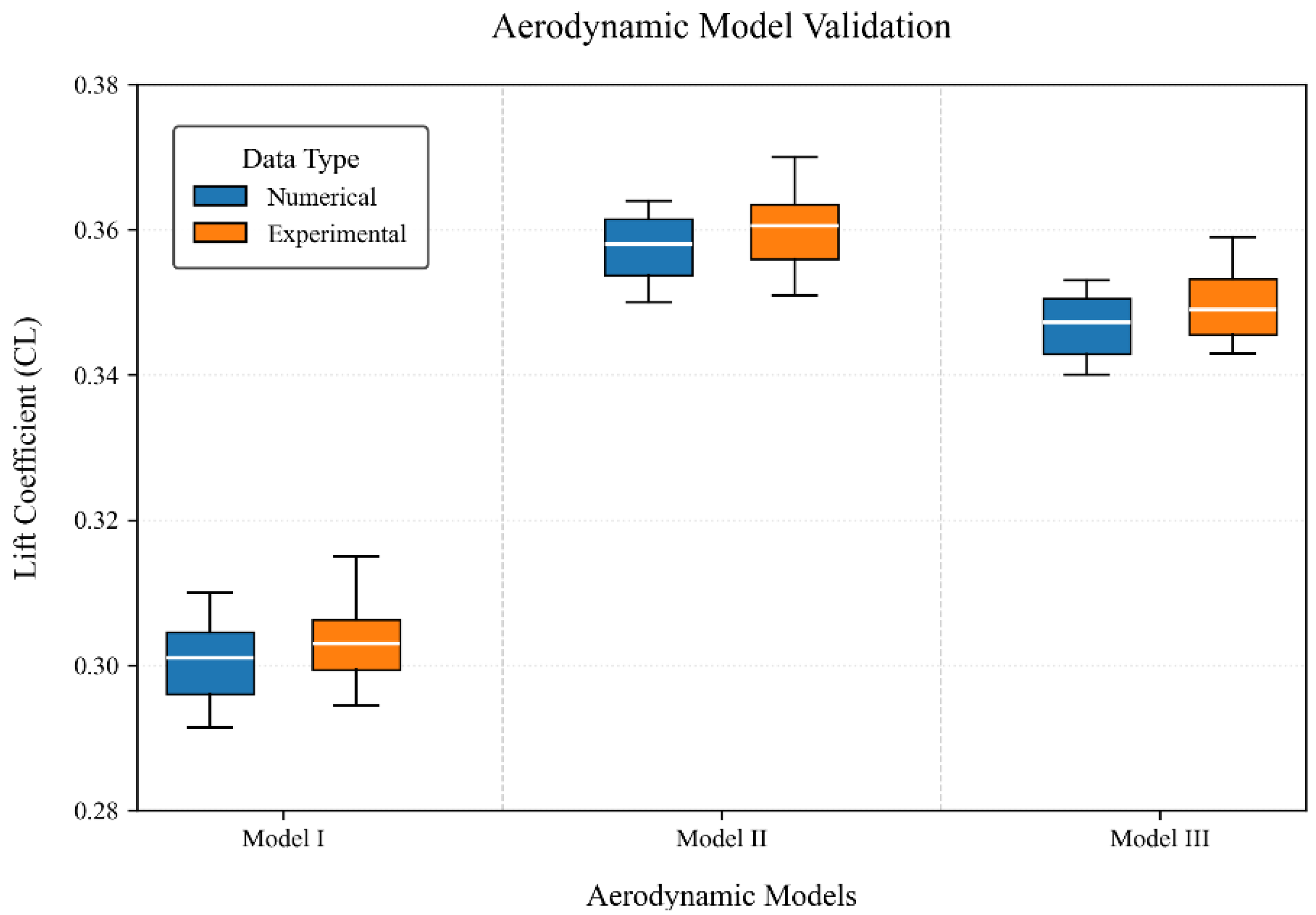
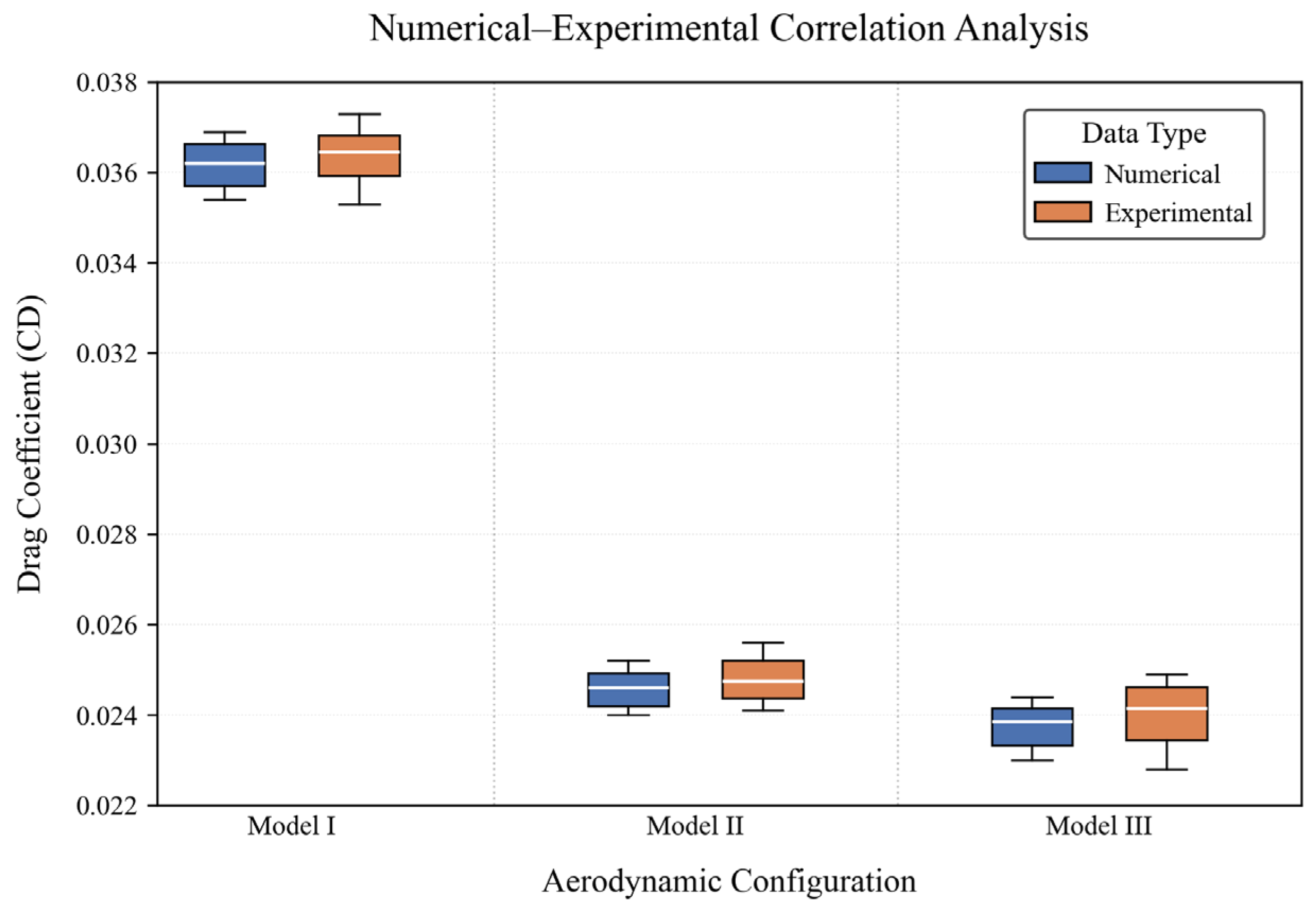
6.3. Effect of Wing Ice Cover on Wing Lift Coefficient of Resistance
6.4. Effect of Wing Ice Cover on Wind Energy Utilization Factor of Wind Turbines
7. Conclusions
- (1)
- Different types of ice cover have varying effects on airfoil aerodynamic performance, with the most significant impact occurring when ice is attached to the airfoil’s leading edge: at an incoming flow velocity of 10 m/s, glaze ice causes a 34.9% reduction in the airfoil’s lift coefficient and a 97.2% increase in the drag coefficient, accompanied by the most obvious and severe irregular fluctuations in the pressure coefficient at the leading edge due to its angular structure; mixed ice leads to a 33.6% lift coefficient decrease and a 22.7% drag coefficient increase, with moderate pressure coefficient agitation; rime ice results in a 24.1% lift coefficient reduction and a 27.2% drag coefficient increase, with relatively mild pressure coefficient fluctuations. The degree of pressure coefficient irregularity at the leading edge directly correlates with the geometric irregularity of the ice, highlighting that glaze ice with sharp protrusions has the most detrimental effect on aerodynamic performance.
- (2)
- Icing on the airfoil leading edge alters the airflow separation point by modifying the surface geometry, making it easier for airflow to separate from the airfoil surface. This shift in the separation point induces irregular pressure distributions across the airfoil, disrupting its aerodynamic characteristics. The velocity maximum occurs at the ice-covered leading edge—particularly at angular protrusions formed by ice—while separation vortices develop at the trailing edge. Both flow separation and vortex generation diminish lift production by disrupting coherent flow attachment and the pressure differential across the airfoil.
- (3)
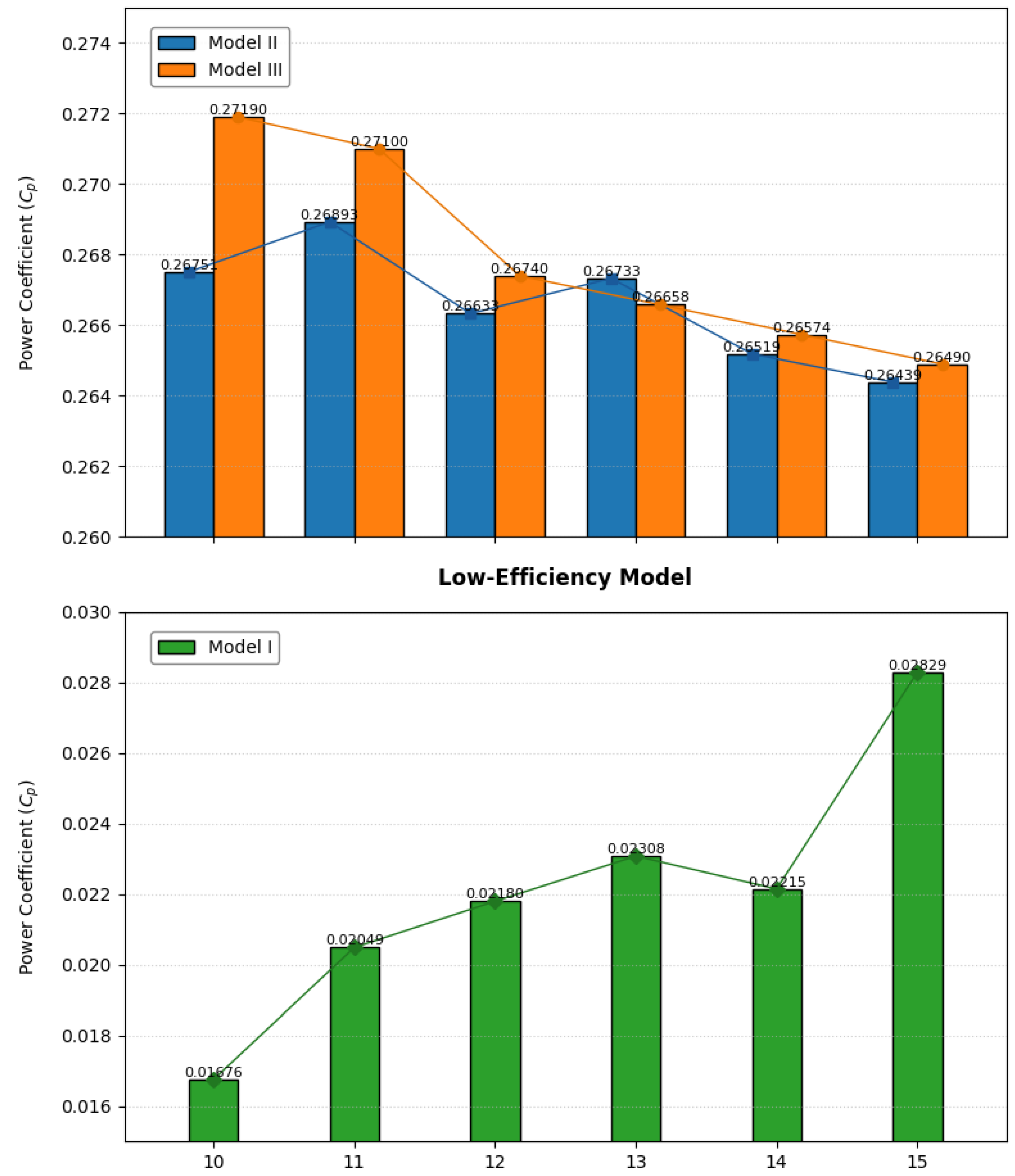
- Through an analysis of the wind energy utilization coefficient (Cp) values of three ice-covered airfoils, it was found that under identical environmental conditions, the Cp values were significantly lower for airfoils with glaze ice attached to the leading edge compared to those with rime ice or mixed ice. Specifically, in the wind speed range of 10–15 m/s, the Cp values for airfoils with rime ice and mixed ice on the leading edge were more consistent, stabilizing between 0.26 and 0.28. Notably, the average Cp of airfoils with mixed ice on the leading edge increased by 91.71% compared to those with glaze ice, while the average Cp of airfoils with rime ice increased by 91.74% compared to those with glaze ice. These results highlight the critical impact of ice morphology on the wind energy capture efficiency, with rime and mixed ice demonstrating superior aerodynamic performance over glaze ice in cold-flow environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, C.; Dinh, M.-C.; Sung, H.-J.; Kim, K.-H.; Choi, J.-H.; Graber, L.; Yu, I.-K.; Park, M. Design, Implementation, and Evaluation of an Output Prediction Model of the 10 MW Floating Offshore Wind Turbine for a Digital Twin. Energies 2022, 15, 6329. [Google Scholar] [CrossRef]
- Clarke, L.; Wei, Y.-M.; De La Vega Navarro, A.; Garg, A.; Hahmann, A.N.; Khennas, S.; Azevedo, I.M.L.; Löschel, A.; Singh, A.K.; Steg, L.; et al. Chapter 6: Energy systems. In Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC, Ed.; Cambridge University Press: Cambridge, UK, 2022; pp. 613–746. [Google Scholar]
- Gao, L.Y.; Hu, H. Wind turbine icing characteristics and icing-induced power losses to utility-scale wind turbines. Proc. Natl. Acad. Sci. USA 2021, 118, e2111461118. [Google Scholar] [CrossRef] [PubMed]
- Wallenius, T.; Lehtomäki, V. Overview of cold climate wind energy: Challenges, solutions, and future needs. Wiley Interdiscip. Rev. Energy Environ. 2015, 5, 128–135. [Google Scholar] [CrossRef]
- Villalpando, F.; Reggio, M.; Ilinca, A. Prediction of ice accretion and anti-icing heating power on wind turbine blades using standard commercial software. Energy 2016, 114, 1041–1052. [Google Scholar] [CrossRef]
- Manatbayev, R.; Baizhuma, Z.; Bolegenova, S.; Georgiev, A. Numerical simulations on static Vertical Axis Wind Turbine blade icing. Renewable Energy 2021, 170, 997–1007. [Google Scholar] [CrossRef]
- Son, C.; Kim, T. Development of an icing simulation code for rotating wind turbines. J. Wind. Eng. Ind. Aerodyn. 2020, 203, 104239. [Google Scholar] [CrossRef]
- Cao, H.; Bai, X.; Ma, X.; Yin, Q.; Yang, X.-Y. Numerical simulation of icing on NREL 5-MW reference offshore wind turbine blades under different icing conditions. China Ocean. Eng. 2022, 36, 767–780. [Google Scholar] [CrossRef]
- Kreutz, M.; Ait Alla, A.; Lütjen, M.; Ohlendorf, J.-H.; Freitag, M.; Thoben, K.-D.; Zimnol, F.; Greulich, A. Ice prediction for wind turbine rotor blades with time series data and a deep learning approach. Cold Reg. Sci. Technol. 2023, 206, 103741. [Google Scholar] [CrossRef]
- Ye, F.; Ezzat, A.A. Icing detection and prediction for wind turbines using multivariate sensor data and machine learning. Renew. Energy 2024, 231, 120879. [Google Scholar] [CrossRef]
- Cheng, T.; Tao, T.; Bai, X.; Liu, Y. A CNN-Attention-GRU-based model for ice accretion prediction on wind turbine blades. J. Renew. Sustain. Energy 2023, 15, 033301. [Google Scholar]
- Zhang, T.; Lian, Y.; Xu, Z.; Li, Y. Effects of Wind Speed and Heat Flux on De-icing Characteristics of Wind Turbine Blade Airfoil Surface. Coatings 2024, 14, 852. [Google Scholar] [CrossRef]
- Fahed, M.; Martini, F.; Ibrahim, H.; Rizk, P.; Ilinca, A. Quasi-3D modeling for ice accretion prediction on wind turbine blades. Wind. Energy Sci. 2022, 8, 123–134. [Google Scholar]
- Bazilevs, Y.; Hsu, M.-C.; Akkerman, I.; Wright, S.; Takizawa, K.; Henicke, B.; Spielman, T.; Tezduyar, T.E. 3D simulation of wind turbine rotors at full scale. Part I: Geometry modeling and aerodynamics. Int. J. Numer. Methods Fluids 2010, 65, 207–235. [Google Scholar] [CrossRef]
- Srinath, D.N.; Mittal, S. Optimal aerodynamic design of airfoils in unsteady viscous flows. Comput. Methods Appl. Mech. Eng. 2010, 199, 1976–1991. [Google Scholar] [CrossRef]
- Lagdani, O.; Tarfaoui, M.; Nachtane, M.; Trihi, M.; Laaouidi, H. A numerical investigation of the effects of ice accretion on the aerodynamic and structural behavior of offshore wind turbine blade. Wind. Eng. 2020, 45, 1433–1446. [Google Scholar] [CrossRef]
- Askan, A.; Tangöz, S.; Konar, M. An investigation of aerodynamic behaviours and aerodynamic performance of a model wing formed from different profiles. Aeronaut. J. 2023, 127, 676–697. [Google Scholar] [CrossRef]
- Chen, P.W.; Bai, C.J.; Wang, W.C. Experimental and numerical studies of low aspect ratio wing at critical Reynolds number. Eur. J. Mech. B-Fluids 2016, 59, 161–168. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Blasco, P.; Palacios, J.; Schmitz, S. Effect of icing roughness on wind turbine power production. Wind Energy 2017, 20, 601–617. [Google Scholar] [CrossRef]
- Davis, N.N.; Pinson, P.; Hahmann, A.N.; Clausen, N.; Žagar, M. Identifying and characterizing the impact of turbine icing on wind farm power generation. Wind Energy 2016, 19, 1503–1518. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Kehtarnavaz, N.; Rotea, M.; Dasari, T. Prediction of Icing on Wind Turbines Based on SCADA Data via Temporal Convolutional Network. Energies 2024, 17, 2175. [Google Scholar] [CrossRef]
- Scher, S.; Molinder, J. Machine learning-based prediction of icing-related wind power production loss. IEEE Access 2019, 7, 129421–129429. [Google Scholar] [CrossRef]
- Kreutz, M.; Ait-Alla, A.; Varasteh, K.; Oelker, S.; Greulich, A.; Freitag, M.; Thoben, K.-D. Machine learning-based icing prediction on wind turbines. Procedia CIRP 2019, 81, 423–428. [Google Scholar] [CrossRef]
- Chuang, Z.; Yi, H.; Chang, X.; Liu, H.; Zhang, H.; Xia, L. Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. J. Mar. Sci. Eng. 2023, 11, 1125. [Google Scholar] [CrossRef]
- Abbasi, S.; Mahmoodi, A.; Joodaki, A. A Numerical Study on Effects of Ice Formation on Vertical-axis Wind Turbine Performance and Flow Field at Optimal Tip Speed Ratio. J. Appl. Fluid Mech. 2024, 17, 1896–1911. [Google Scholar]
- Kollar, L.E.; Mishra, R. Inverse design of wind turbine blade sections for operation under icing conditions. Energy Convers. Manag. 2019, 180, 844–858. [Google Scholar] [CrossRef]
- ISO 12494; Atmospheric Icing of Structures. International Organization for Standardization: Geneva, Switzerland, 2001.
- IEC 61400-12-1; Wind Turbines—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Woebbeking, M.; Argyriadis, K. New guidelines for the certification of offshore wind turbines. In Proceedings of the International Ocean and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Cai, X.; Wang, H.; Wang, Y.; Xu, B.; Zheng, Y.; Zhang, L. (Eds.) Wind Power Generation Engineering Technology Series: Wind Turbine Blades, 2nd ed.; China Water & Power Press: Beijing, China, 2022. [Google Scholar]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill: New York, NY, USA, 2016. [Google Scholar]
- Jacobs, E.N.; Ward, K.E.; Pinkerton, R.M. NACA Report No. 460: Characteristics of 78 Related Airfoil Sections; NACA: Washington, DC, USA, 1933. [Google Scholar]





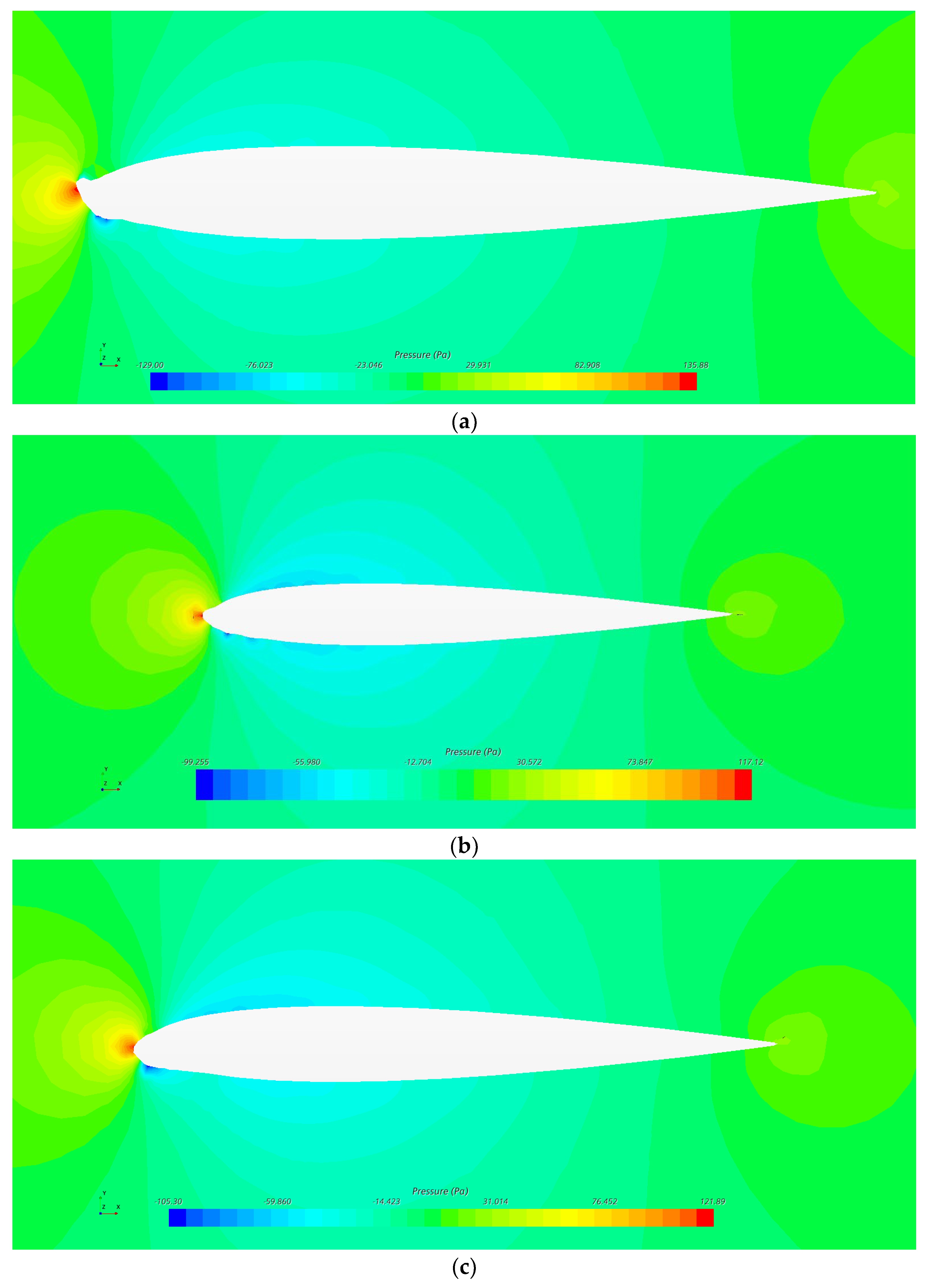
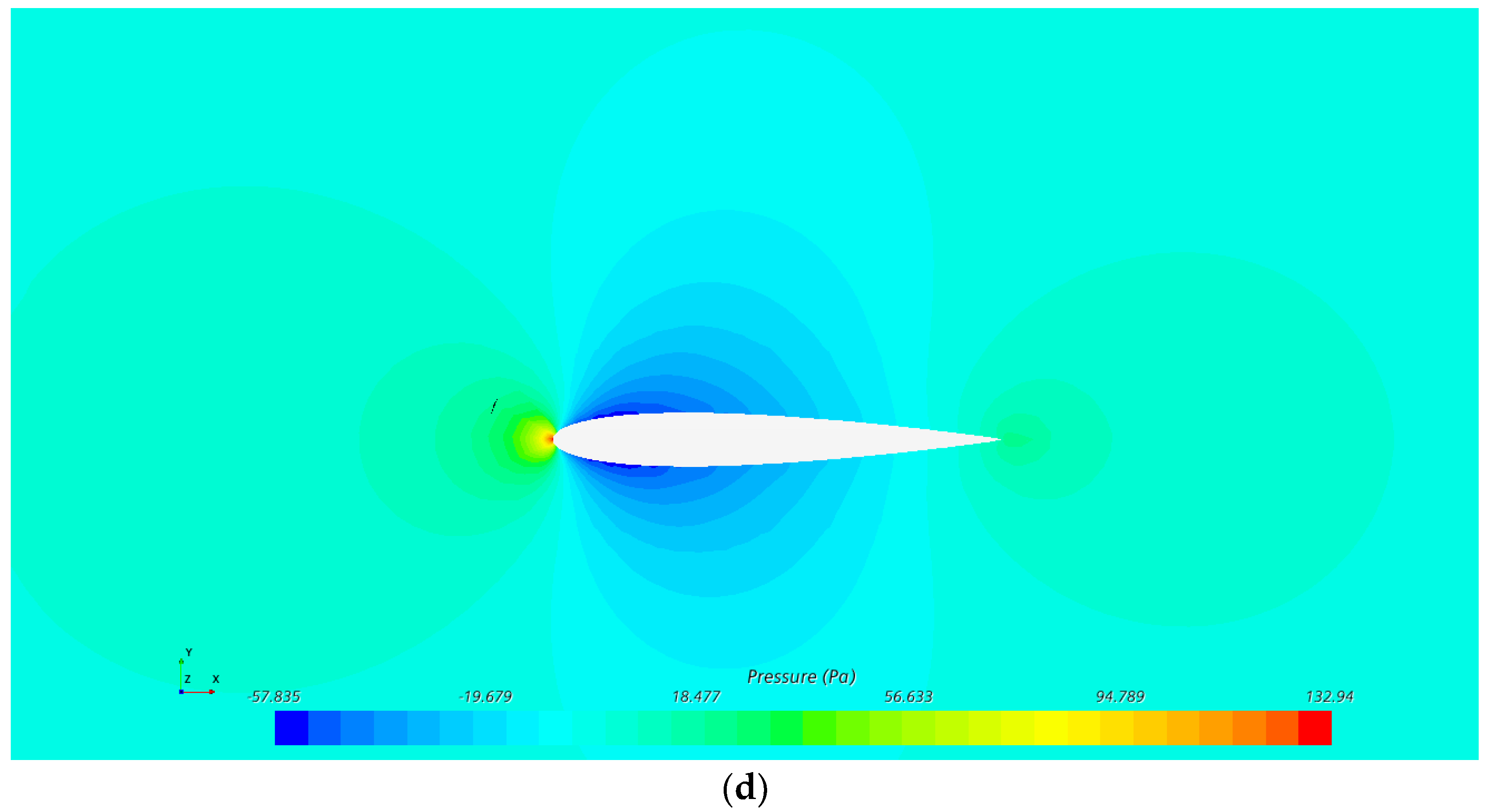
| Temperature (°C) | Angle of Attack (°) | Incoming Flow Rate (m/s) | LWC (g/m3) | MVD (μm) | Icing Time (s) | |
|---|---|---|---|---|---|---|
| Model I | −5.56 | 4 | 67 | 1 | 20 | 360 |
| Model II | −11.11 | 4 | 67 | 1 | 20 | 360 |
| Model III | −26.11 | 4 | 67 | 1 | 20 | 360 |
| 1 | 2 | 3 | |
|---|---|---|---|
| Maximum ice thickness tested/mm | 12.828 | 12.620 | 15.197 |
| Numerical maximum ice thickness/mm | 13.852 | 13.618 | 14.439 |
| Relative standard deviation | 7.98% | 7.91% | 4.99% |
| Model | Temperature (°C) | Incoming Flow Rate (m·s−1) | Kinematic Viscosity (m2·s−1) | Simulated Wind Speed (m·s−1) |
|---|---|---|---|---|
| Model I | −5.56 | 67 | 1.53 × 10−5 | 209.05 |
| Model II | −11.11 | 67 | 1.648 × 10−5 | 194.08 |
| Model III | −26.11 | 67 | 1.832 × 10−5 | 174.6 |
| Experimental Condition Design | |
|---|---|
| Temperature | 16.4 °C |
| Atmospheric air density | 1.22 Kg·m−3 |
| Kinematic viscosity of air | 1.79 × 10−5 |
| Air velocity | 10 m·s−1, 11 m·s−1, 12 m·s−1, 13 m·s−1, 14 m·s−1, 15 m·s−1 |
| Flow field uniformity | ≤1.0% |
| Stability of the flow field | ≤0.5% |
| Turbulence | ≤1.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Wang, J.; Wen, H.; Liu, C.; Liu, Y.; Zhang, D. Impact of Blade Ice Coverage on Wind Turbine Power Generation Efficiency: A Combined CFD and Wind Tunnel Study. Energies 2025, 18, 3448. https://doi.org/10.3390/en18133448
Ji Y, Wang J, Wen H, Liu C, Liu Y, Zhang D. Impact of Blade Ice Coverage on Wind Turbine Power Generation Efficiency: A Combined CFD and Wind Tunnel Study. Energies. 2025; 18(13):3448. https://doi.org/10.3390/en18133448
Chicago/Turabian StyleJi, Yang, Jinxiao Wang, Haiming Wen, Chenyang Liu, Yang Liu, and Dayong Zhang. 2025. "Impact of Blade Ice Coverage on Wind Turbine Power Generation Efficiency: A Combined CFD and Wind Tunnel Study" Energies 18, no. 13: 3448. https://doi.org/10.3390/en18133448
APA StyleJi, Y., Wang, J., Wen, H., Liu, C., Liu, Y., & Zhang, D. (2025). Impact of Blade Ice Coverage on Wind Turbine Power Generation Efficiency: A Combined CFD and Wind Tunnel Study. Energies, 18(13), 3448. https://doi.org/10.3390/en18133448





