Neural ODE-Based Dynamic Modeling and Predictive Control for Power Regulation in Distribution Networks
Abstract
1. Introduction
1.1. The Background and Motivation
1.2. The Literature Review
1.2.1. Distribution Network Modeling
1.2.2. Distribution Network Control
1.3. Gap Identification and Contributions
- The application and validation of NODEs for accurately modeling the aggregate dynamic power response of a complex DN using only the measurements available at the PCC, effectively capturing its continuous-time behavior;
- The development and formulation of a computationally efficient MPC framework for DN active power control, based on local linearization of the trained NODE model, resulting in a standard Quadratic Programming (QP) problem;
- Demonstration of the computational feasibility of the proposed linearized NODE-MPC approach through the typical QP solve times, enabling its potential use in real-time control loops;
- Comprehensive validation of the entire framework through an offline analysis and online co-simulation involving a detailed DN simulator (CloudPSS) and an external Python-based controller, demonstrating the model’s accuracy, control effectiveness, and practical applicability in scenarios like CVR and supply–demand balancing.
1.4. The Paper Outline
2. Problem Formulation
2.1. System Description
- : The magnitude of the RMS voltage (line-to-line);
- : The voltage angle;
- : The total active power flowing into the DN;
- : The total reactive power flowing into the DN.
2.2. Assumptions and Constraints
- The aggregate dynamic relationship between and can be adequately captured using a low-dimensional continuous-time dynamic model (specifically, a NODE) using only PCC measurements.
- Sufficient measurement data is available from the PCC (either via simulation or real-world measurements) to train the NODE model.
- The internal network topology and the parameters of its constituent components are considered stable over the operational timescale of the controller (seconds to minutes). This implies that the aggregate dynamic behavior captured by the NODE model remains consistent during a control session. The data-driven model can adapt to slower, long-term changes (occurring over hours or days) through periodic retraining.
- The primary control objective is regulating the active power by manipulating the voltage magnitude . The voltage angle is included as an input to the NODE model during training to capture its full dynamic influence. However, for the MPC design, it is treated as a measured disturbance that is assumed to be constant over the short prediction horizon. This simplification is justified because for active power control at the PCC of a distribution network connected to a relatively stiff upstream grid, the P-V sensitivity is typically much more significant than the P- sensitivity. This approach allows the controller to focus on the dominant P-V relationship, which is most relevant to CVR applications, while still accounting for the current operating angle in its predictions, thus reducing the complexity of the optimization problem without a significant loss of accuracy.
- The control action (voltage setpoint ) determined by the MPC can be implemented at the PCC within one control time step .
2.3. Mathematical Formulation
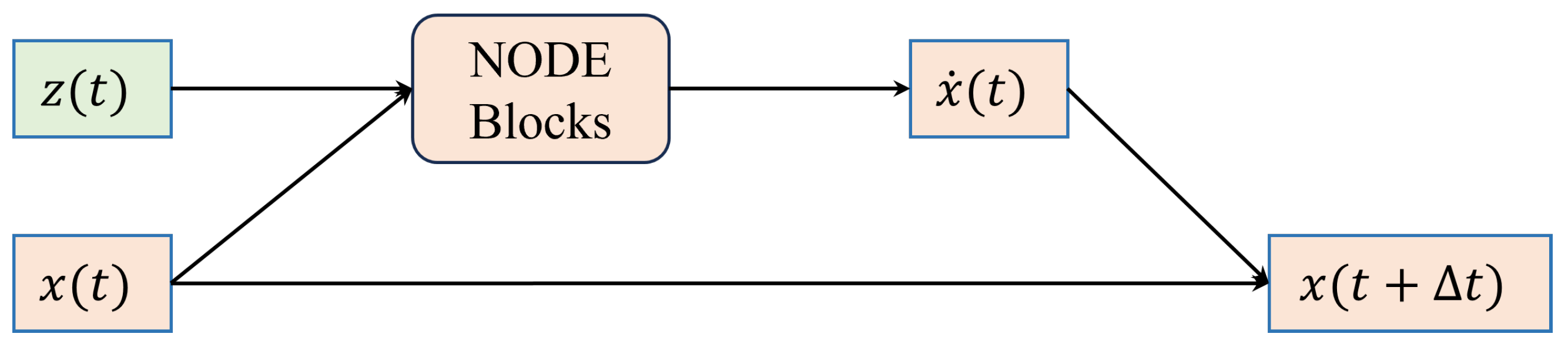
2.3.1. The NODE Modeling Problem
2.3.2. The MPC Problem (Initial Formulation)
3. The Proposed Methodology: NODE Modeling and Linearized MPC
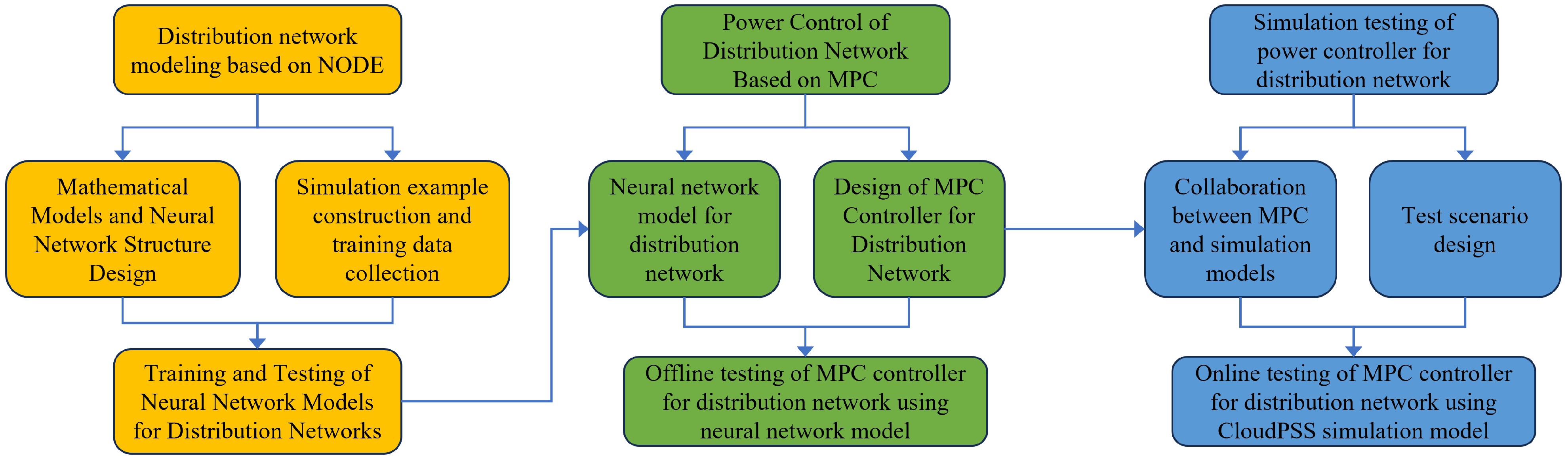
3.1. The Overall Framework
- Offline NODE model training: A NODE model is trained using historical or simulated data from the target DN to capture its aggregate dynamic behavior at the PCC.
- Online linearized NODE-based MPC: The trained NODE model is used within an MPC framework. To overcome the computational challenges, the NODE model’s relevant dynamics are linearized locally at each control step, allowing the MPC optimization to be formulated and solved efficiently as a QP problem.
3.2. Part 1—NODE-Based Dynamic Distribution Network Modeling
3.3. Part 2—Linearized NODE-Based Model Predictive Control
3.3.1. The Linearization Technique
3.3.2. QP Formulation
3.3.3. QP Solution
3.4. The Implementation Workflow
| Algorithm 1 Online linearized NODE-based MPC algorithm |
|
4. Simulation Setup and Case Studies
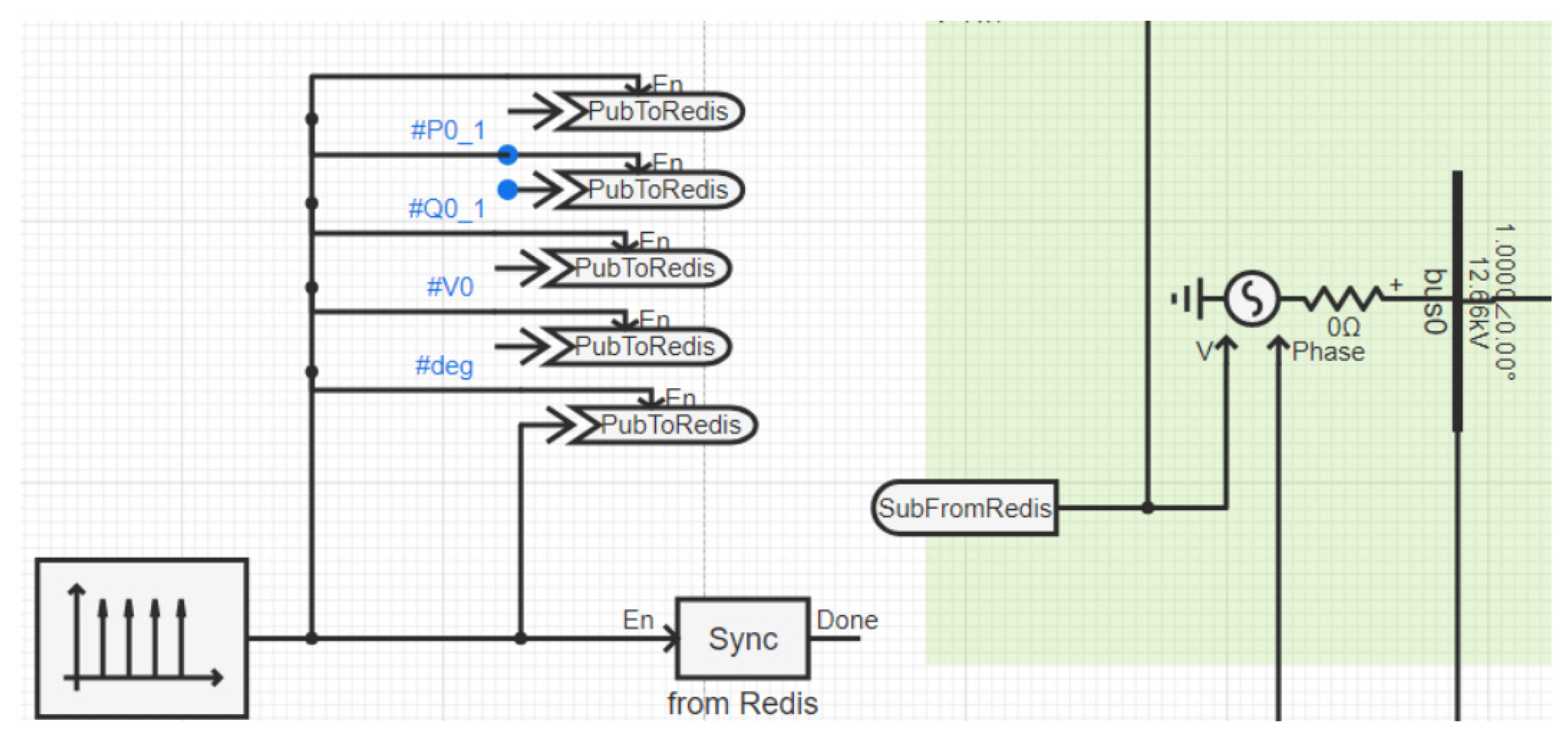
4.1. The Simulation Environment
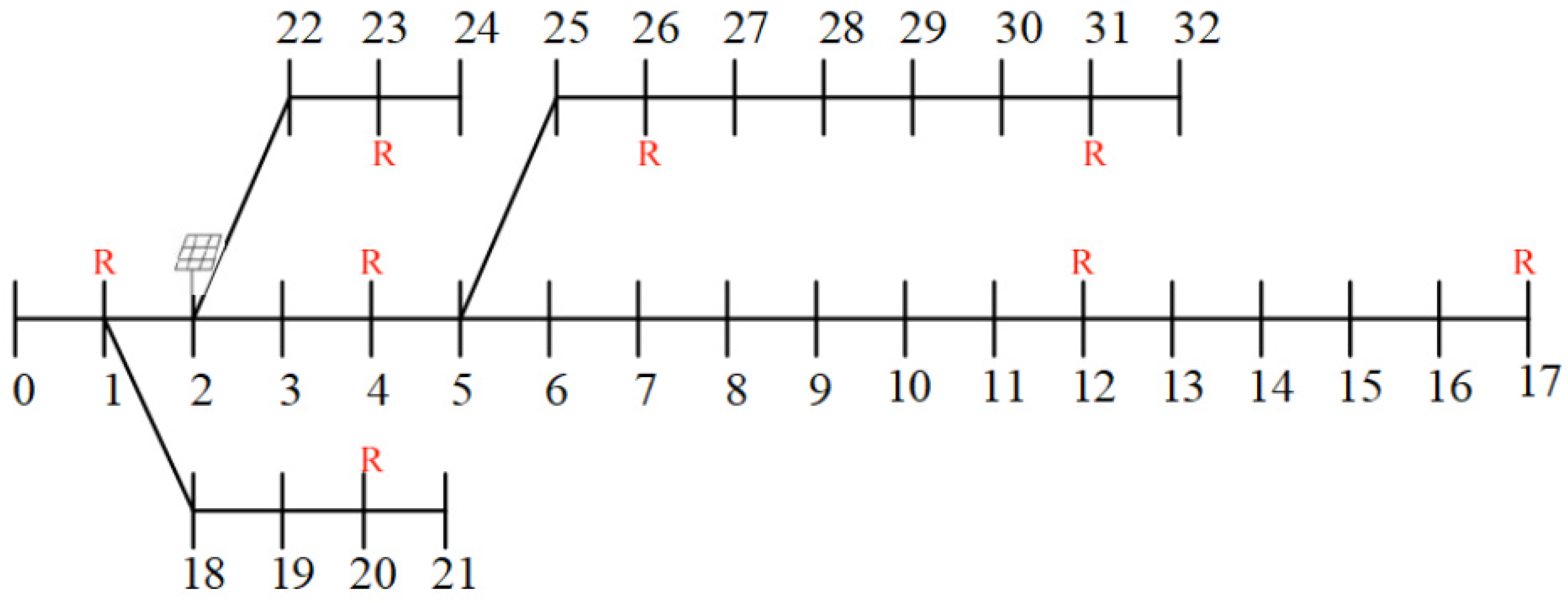
4.2. The Benchmark Distribution Network
- A PV microgrid with a capacity of 0.178 MVA was connected to Node 2.
- Static constant-impedance loads (R = ) were added at Nodes 1, 4, 12, 17, 20, 23, 26, and 31, in addition to the original constant-power loads.
- The network is supplied from Node 0 through a step-down transformer (at a 1.2:1 ratio from primary to secondary) connected to a controllable voltage source representing the PCC at the secondary side. The nominal secondary voltage is 12.66 kV line to line.
4.3. Data Generation and Training Scenarios
- A single disturbance: The voltage undergoes a step change at a specific time during the simulation. Multiple simulations were run with varying initial voltages and step change magnitudes (an initial voltage randomized between and , a step change to to of the initial value). Data segments of a 1 s length around the step change were collected. This yielded 995 data segments for training/testing.
- A continuous disturbance: The voltage is continuously varied by combining low-frequency large perturbations (random values between kV and kV, updated at Hz) and high-frequency small fluctuations (random values between kV and kV, filtered and updated at 10 Hz) fed into the controlled voltage source. Longer simulations (53 s each) were run, and the data ( at the PCC) was segmented into 2.5 s intervals. A total of 50 such simulations were run with the base voltage randomized between and , yielding 1000 segments of 2.5 s data.
4.4. The MPC Test Scenarios and Metrics
4.4.1. Offline Tests (Using the Trained NODE Model as a Plant)
- Reference tracking: Step changes and varying reference signals ;
- Constraint handling: Scenarios where the control action hits the (0.9 pu) or (1.1 pu) limits;
- Parameter sensitivity: The impact of varying the weights and control interval .
4.4.2. Online Co-Simulation Tests (Using CloudPSS as the Plant)
- Basic tracking: Step changes in ;
- Complex tracking: Following more dynamic trajectories;
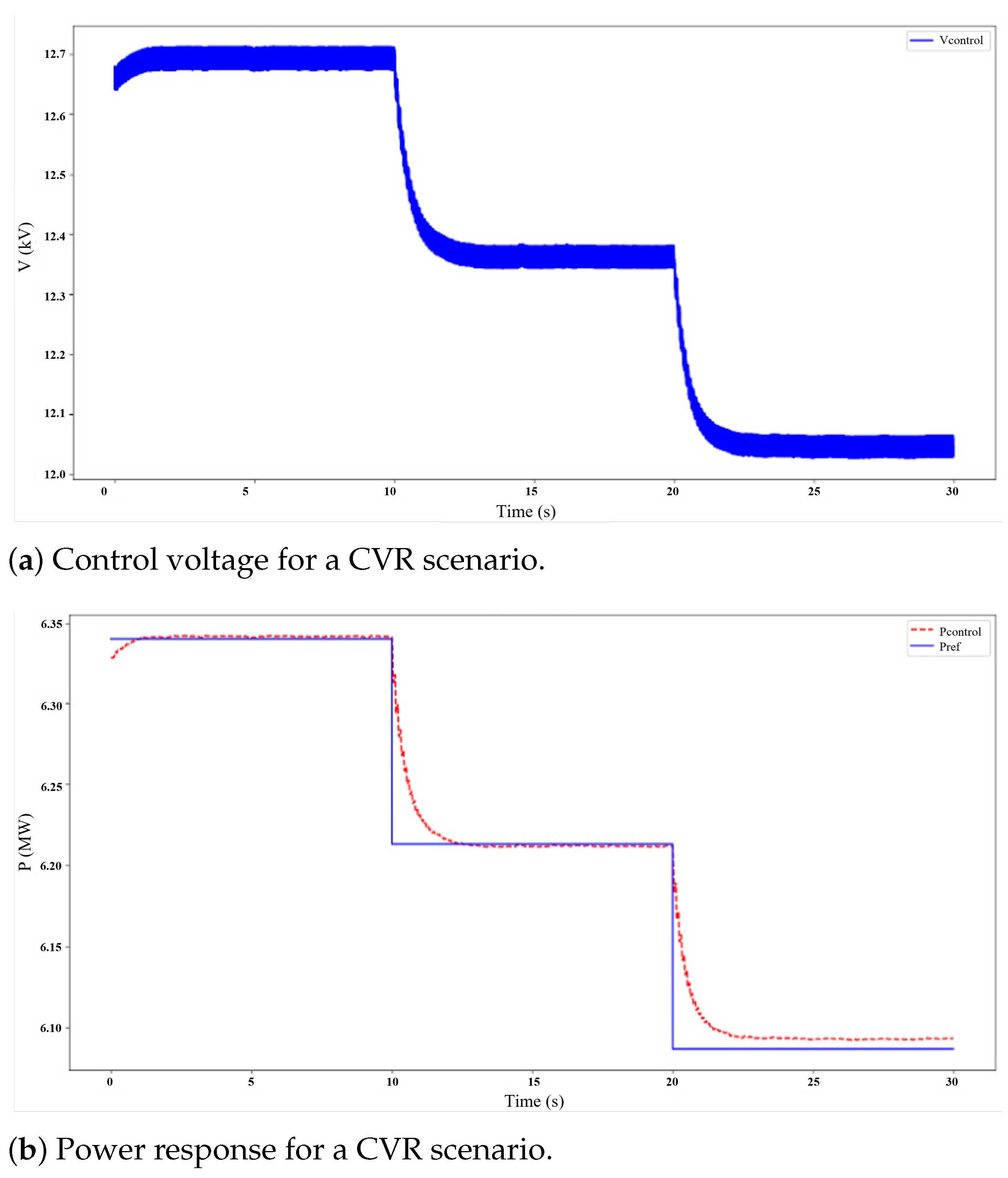
- CVR scenario: Applying a stepped reduction profile to (e.g., from 100% to 98%, then 96% of the nominal power) to simulate a CVR objective;
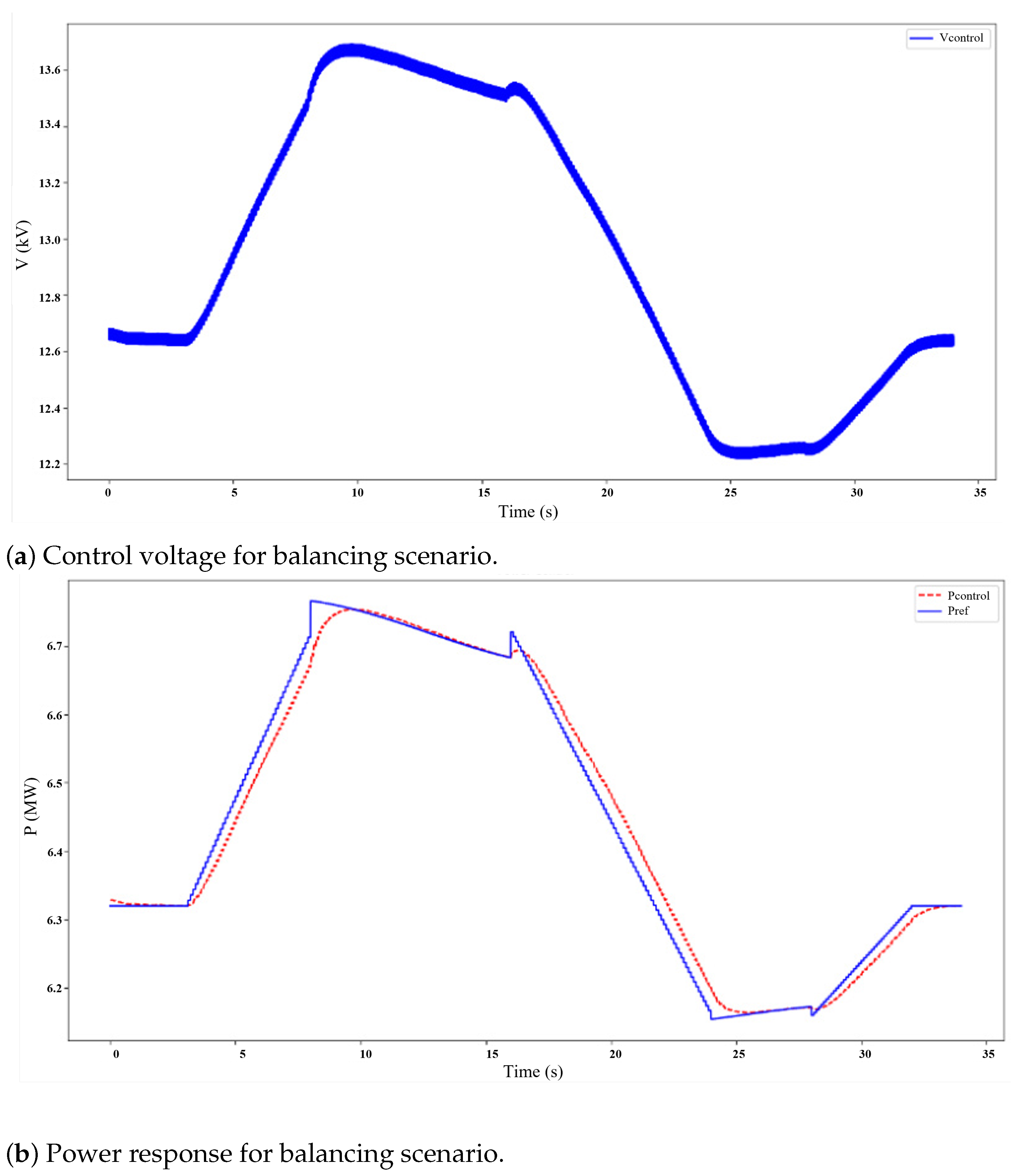
- Supply–demand balancing: Tracking a fluctuating profile potentially representing available renewable generation.
4.4.3. Performance Metrics
- The NODE model’s accuracy: the mean squared error (MSE), Mean Absolute Error (MAE), and Relative Error (RE) between the NODE model’s predicted power () and the simulated power from CloudPSS.
- The MPC controller’s performance: The Root Mean Squared Error (RMSE) between the actual DN power and the reference , the adherence to the voltage constraints (), and the computational time required to solve the QP problem at each control step.
5. Results and Discussion
5.1. NODE Model Validation
5.2. MPC Performance—Offline Analysis
- Reference tracking: The controller effectively steered the system power towards the desired reference .
- Constraint handling: When demanded voltages beyond the limits (), the controller saturated the voltage at the boundary, respecting the constraints.
- Parameter tuning: Adjusting the weights and allowed the tracking accuracy to be traded off against the voltage deviation. Prioritizing tracking () led to a faster power response, while prioritizing voltage stability () resulted in smoother voltage profiles but potentially slower or less exact tracking.
- Control intervals: Reducing the control interval generally led to a faster response but could introduce undesirable voltage spikes or instability if too small. A value of s provided a good balance between responsiveness and smooth control action.
- Computational efficiency: The linearization successfully converted the complex optimization into a QP problem. The QP solve time using CVXOPT was typically less than 0.1 s on the standard computing hardware for a prediction horizon of 9 steps, well within the typical control interval of 0.1 s, confirming the feasibility for real-time implementation.
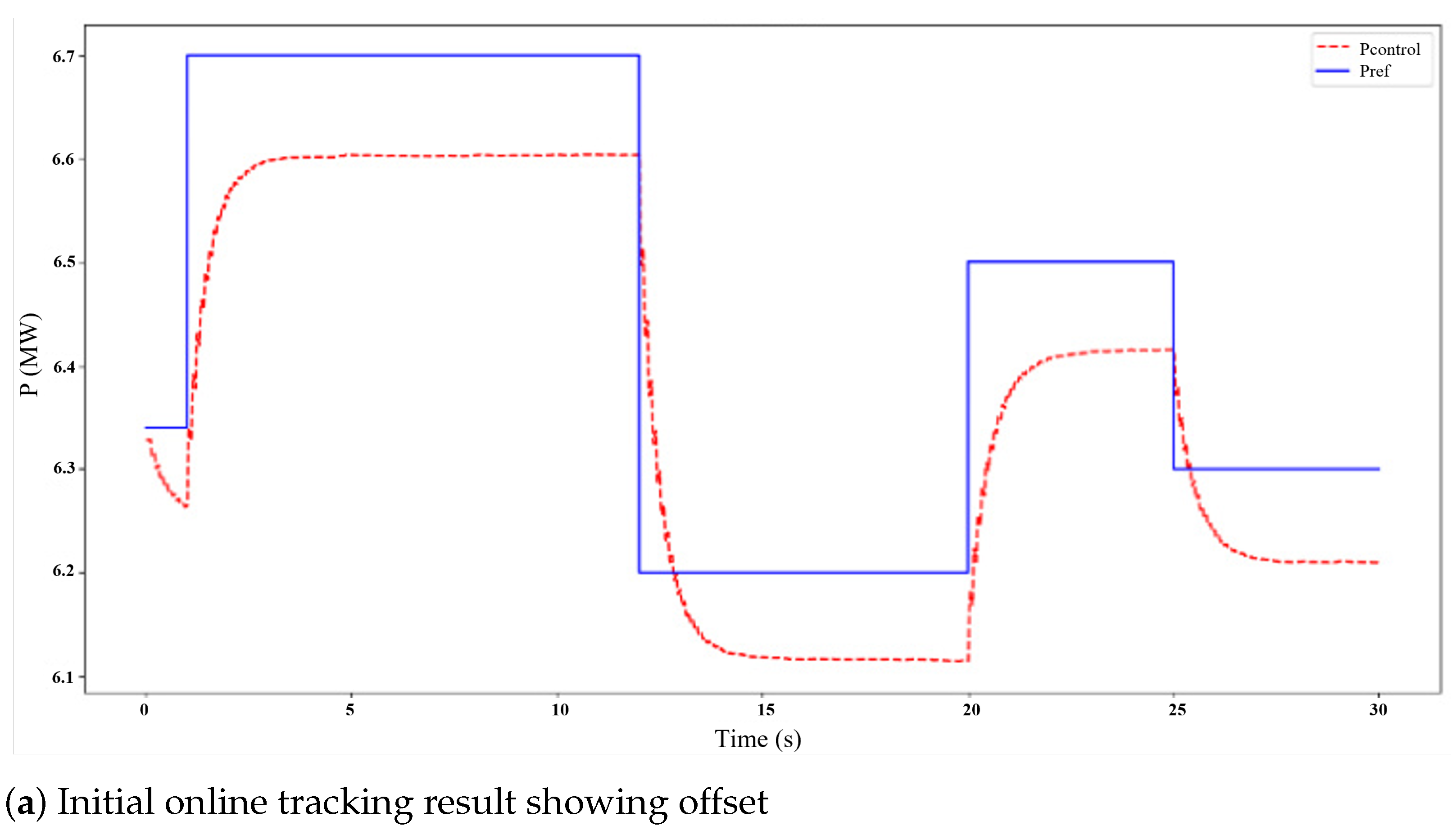
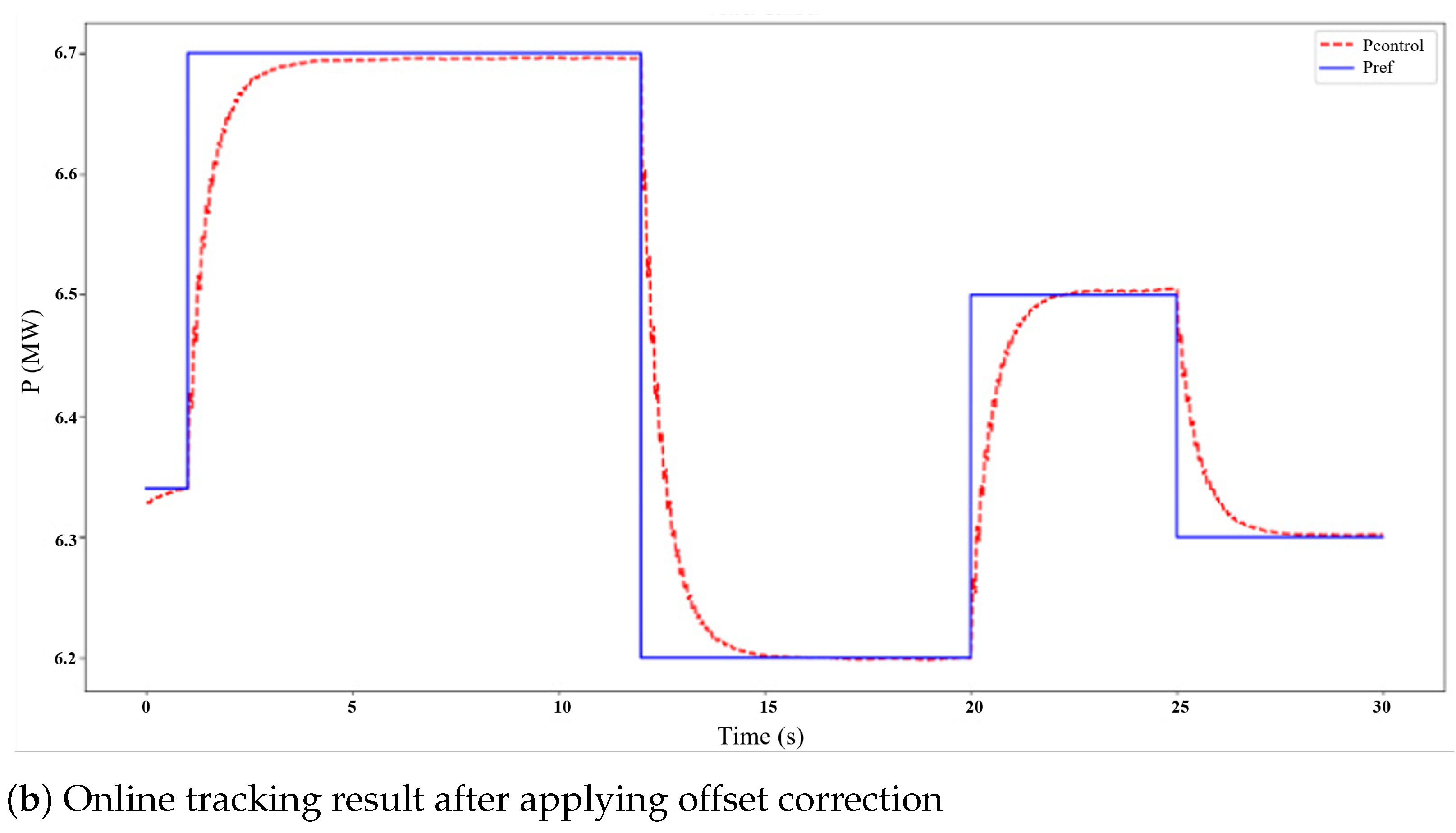
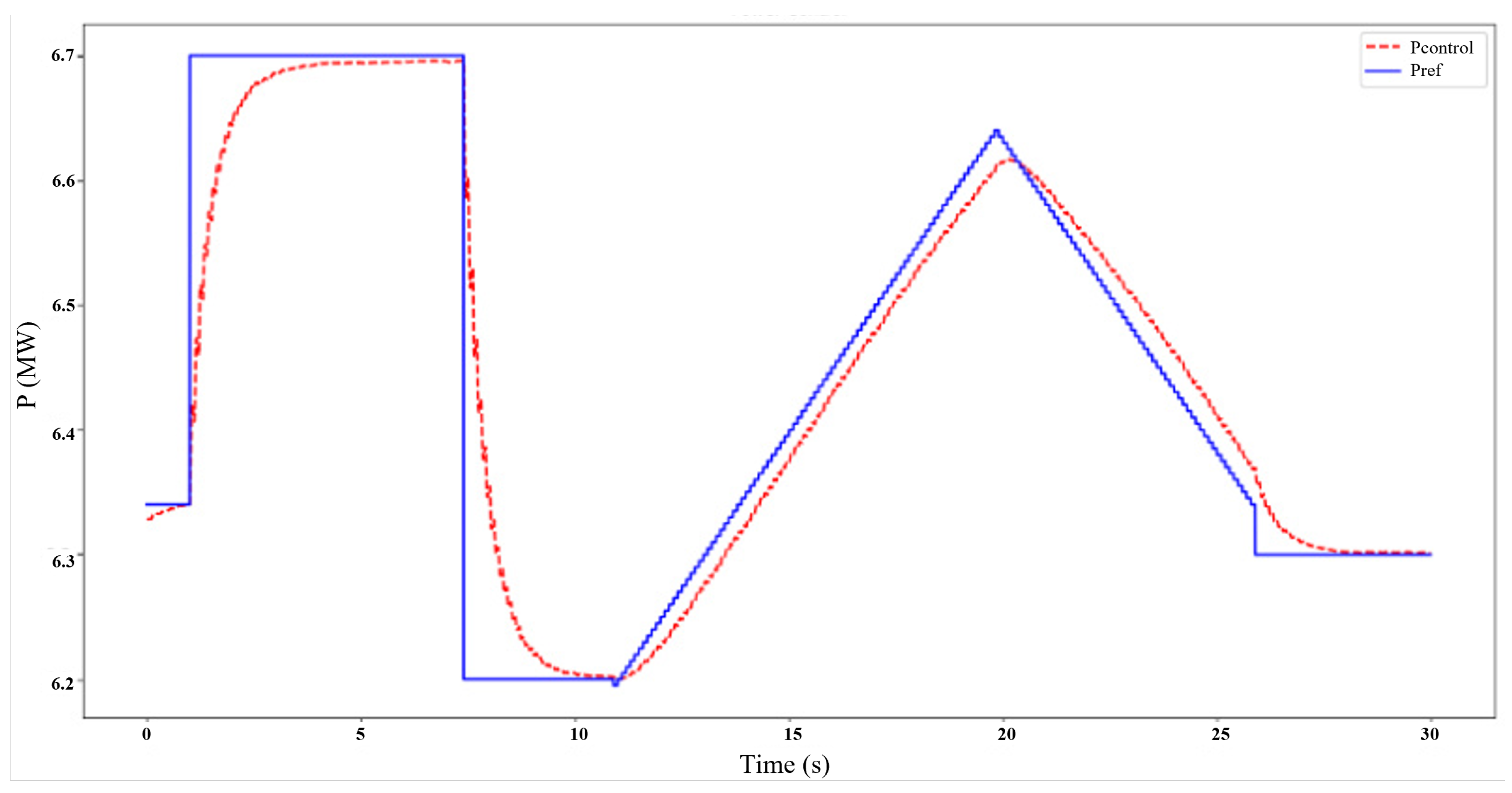
5.3. MPC Performance—Online Co-Simulation Validation
5.4. Application Scenario Demonstrations
5.4.1. Conservation Voltage Reduction (CVR)
5.4.2. Supply–Demand Balancing
5.5. Discussion
6. Conclusions
- Extending the control objectives from aggregating the power regulation and voltage constraint adherence based on PCC measurements to multi-objective optimization to include economic costs, internal loss reductions, and explicit renewable energy dispatching, which would necessitate greater internal network observability or advanced state estimation techniques.
- Developing adaptive mechanisms to handle model mismatches and time-varying network conditions, such as online NODE parameter updates or adaptive linearization schemes. Exploring the use of higher-order approximations or piecewise linear models within the MPC framework could enhance the control accuracy for highly dynamic or widely varying operating conditions, while carefully managing the computational efficiency.
- Investigating the inclusion of the reactive power and voltage angle control within the MPC framework could broaden its applicability.
- Exploring extending the NODE model to Neural Stochastic Differential Equations (Neural SDEs) to explicitly quantify the forecast uncertainty to enhance the framework’s robustness against inherent system stochasticity and measurement noise. This would enable the development of robust or stochastic MPC strategies that could maintain reliable control under uncertain conditions.
- Assessing the scalability and robustness of the approach for significantly larger, more complex distribution systems. Further quantitative comparisons with other state-of-the-art data-driven modeling and control techniques would provide valuable context.
- Testing and validating the framework in real-world scenarios, explicitly addressing the implications of the communication latency, measurement loss, sensor errors, and voltage control devices’ limits. This would involve investigating robust state estimation techniques and delay compensation strategies within the MPC framework.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| t | A continuous-time variable |
| k | A discrete-time index for control steps |
| A discretization time step for the MPC control interval | |
| The active power consumed by the DN at the PCC (continuous, discrete) [MW] | |
| The reactive power consumed by the DN at the PCC (continuous, discrete) [MVar] | |
| The voltage magnitude (RMS, line to line) at the PCC (continuous, discrete) [kV] | |
| The voltage angle at the PCC (continuous, discrete) [rad or deg] | |
| The state vector of the DN model, | |
| The input vector to the DN model, | |
| A neural network function parameterizing the ODE, with the parameters | |
| The state vector predicted by the model (continuous, discrete) | |
| The predicted active power at step , based on the info at step k | |
| The training dataset | |
| The loss function for model training | |
| The control input at discrete time k, | |
| The planned voltage at step decided at step k | |
| The prediction horizon (number of steps) | |
| The control horizon (number of steps) (in this work, ) | |
| The sequence of control inputs at step k, | |
| The reference active power target at time step k | |
| The vector of reference active power targets over the prediction horizon | |
| The MPC cost function at time step k | |
| Weighting factors in the cost function | |
| The nominal voltage magnitude [kV] | |
| The minimum and maximum allowable voltage magnitudes [kV] | |
| NODE | Neural Ordinary Differential Equation |
| MPC | Model Predictive Control |
| DN | Distribution network |
| PCC | Point of common coupling |
| DER | Distributed energy resource |
| PV | Photovoltaic |
| CVR | Conservation Voltage Reduction |
| QP | Quadratic Programming |
| MLP | Multi-Layer Perceptron |
| MSE | Mean squared error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| RE | Relative error |
| AD | Automatic Differentiation |
| ANN | Artificial Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| ZIP | Constant-impedance, constant-current, constant-power model |
| IM | Induction motor |
References
- National Energy Administration. Notice on Issuing the Measures for the Supervision of Fair and Open Grid Access. 2021. Available online: https://www.gov.cn/gongbao/content/2022/content_5667313.htm (accessed on 3 December 2024).
- National Energy Administration. Transcript of the Press Conference for the First Quarter of 2023. 2023. Available online: http://www.nea.gov.cn/2023-02/13/c_1310697149.htm (accessed on 5 December 2024).
- Diaz-Aguiló, M.; Sandraz, J.; Macwan, R.; De Leon, F.; Czarkowski, D.; Comack, C.; Wang, D. Field-validated load model for the analysis of CVR in distribution secondary networks: Energy conservation. IEEE Trans. Power Del. 2013, 28, 2428–2436. [Google Scholar] [CrossRef]
- Zhang, Q.; Dehghanpour, K.; Wang, Z. Distributed CVR in unbalanced distribution systems with PV penetration. IEEE Trans. Smart Grid 2019, 10, 5308–5319. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Wang, J.; Chen, C. Load modeling—A review. IEEE Trans. Smart Grid 2018, 9, 5986–5999. [Google Scholar] [CrossRef]
- Bokhari, A.; Alkan, A.; Dogan, R.; Diaz-Aguiló, M.; De Leon, F.; Czarkowski, D.; Zabar, Z.; Birenbaum, L.; Noel, A.; Uosef, R.E. Experimental determination of the ZIP coefficients for modern residential, commercial, and industrial loads. IEEE Trans. Power Del. 2014, 29, 1372–1381. [Google Scholar] [CrossRef]
- Samadi, A.; Soder, L.; Shayesteh, E.; Hooshmand, R.A. Static equivalent of distribution grids with high penetration of PV systems. IEEE Trans. Smart Grid 2015, 6, 1763–1774. [Google Scholar] [CrossRef]
- Zali, S.M.; Milanović, J.V. Generic model of active distribution network for large power system stability studies. IEEE Trans. Power Syst. 2013, 28, 3126–3133. [Google Scholar] [CrossRef]
- Choi, B.-K.; Li, D.C.H.; Li, Y. Development of composite load models of power systems using on-line measurement data. J. Electr. Eng. Technol. 2006, 1, 161–169. [Google Scholar] [CrossRef][Green Version]
- Milanović, J.V.; Zali, S.M. Validation of equivalent dynamic model of active distribution network cell. IEEE Trans. Power Syst. 2013, 28, 2101–2110. [Google Scholar] [CrossRef]
- Ma, R.; Ma, J.; Hill, D.J. Composite load modeling via measurement approach. IEEE Trans. Power Syst. 2006, 21, 663–672. [Google Scholar]
- Ma, J.; Ma, R.; Hill, D.J. Load modeling by finding support vectors of load data from field measurements. IEEE Trans. Power Syst. 2006, 21, 726–735. [Google Scholar]
- Wang, X.; Wang, Y.; Shi, D.; Wang, J.; Wang, Z. Two-stage WECC composite load modeling: A double deep Q-learning networks approach. IEEE Trans. Smart Grid 2020, 11, 4331–4344. [Google Scholar] [CrossRef]
- Cai, C.; Liu, H.; Tao, Y.; Zhang, J.; Song, W. Microgrid equivalent modeling based on long short-term memory neural network. IEEE Access 2020, 8, 23120–23133. [Google Scholar] [CrossRef]
- Ji, Y.; Buechler, E.; Rajagopal, R. Data-driven load modeling and forecasting of residential appliances. IEEE Trans. Smart Grid 2020, 11, 2652–2661. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Badr, M.A.L.; Younes, A.H. Dynamic load modeling of an Egyptian primary distribution system using neural networks. Int. J. Electr. Power Energy Syst. 2007, 29, 637–649. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I.; Sowa, P. Artificial neural network-based dynamic equivalents for distribution systems containing active sources. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 681–688. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I. Identification of dynamic equivalents for distribution power networks using recurrent ANNs. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 348–353. [Google Scholar]
- Denecke, J.; Erlich, I. Dynamic equivalents of active distribution networks. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Stankovic, A.M.; Saric, A.T.; Milosevic, M. Identification of nonparametric dynamic power system equivalents with artificial neural networks. IEEE Trans. Power Syst. 2003, 18, 1478–1486. [Google Scholar] [CrossRef]
- Saviozzi, M.; Massucco, S.; Silvestro, F. Implementation of advanced functionalities for Distribution Management Systems: Load forecasting and modeling through Artificial Neural Networks ensembles. Electr. Power Syst. Res. 2019, 167, 230–239. [Google Scholar] [CrossRef]
- He, R.-M.; Germond, A.J. Comparison of dynamic load modeling using neural network and traditional method. In Proceedings of the Second International Forum on Applications of Neural Networks to Power Systems, Kobe, Japan, 19–22 April 1993; pp. 253–258. [Google Scholar]
- Visconti, I.F.; Lima, D.A.; Costa, J.M.C.d.S.; Sobrinho, N.R.d.B.C. Measurement-based load modeling using transfer functions for dynamic simulations. IEEE Trans. Power Syst. 2014, 29, 111–120. [Google Scholar] [CrossRef]
- Ospina, L.D.P.; Salazar, V.U.; Ospina, D.P. Dynamic equivalents of nonlinear active distribution networks based on Hammerstein-Wiener models: An application for long-term power system phenomena. IEEE Trans. Power Syst. 2022, 37, 3799–3809. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Kidger, P. On neural differential equations. arXiv 2022, arXiv:2202.02435. [Google Scholar]
- Lee, K.; Parish, E.J. Parameterized neural ordinary differential equations: Applications to computational physics problems. Proc. R. Soc. A 2021, 477, 20210162. [Google Scholar] [CrossRef]
- Lei, D.; Wu, K.; Zhang, L.; Li, W.; Liu, Q. Neural ordinary differential grey model and its applications. Expert Syst. Appl. 2021, 177, 114923. [Google Scholar] [CrossRef]
- Xiao, T.; Chen, Y.; Huang, S.; Zhang, R.; Wang, Z.; Sun, Y. Feasibility study of neural ODE and DAE modules for power system dynamic component modeling. IEEE Trans. Power Syst. 2023, 38, 1267–1279. [Google Scholar] [CrossRef]
- Preiss, R.F.; Warnock, V.J. Impact of voltage reduction on energy and demand. IEEE Trans. Power App. Syst. 1978, PAS-97, 1665–1671. [Google Scholar] [CrossRef]
- Scalley, B.R.; Kasten, D.G. The effects of distribution voltage reduction on power and energy consumption. IEEE Trans. Educ. 1981, 24, 210–216. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Review on implementation and assessment of conservation voltage reduction. IEEE Trans. Power Syst. 2014, 29, 1306–1315. [Google Scholar] [CrossRef]
- Singh, R.; Tuffner, F.; Fuller, J.; Chassin, D.; Kumar, N.P. Effects of distributed energy resources on conservation voltage reduction (CVR). In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Efheij, H.; Albagul, A.; Ammar Albraiki, N. Comparison of Model Predictive Control and PID Controller in Real Time Process Control System. In Proceedings of the 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; pp. 64–69. [Google Scholar]
- Abdallaoui, S.; Kribèche, A.; Aglzim, E.H. Comparative study of MPC and PID controllers in autonomous vehicle application. In Advances in Automation, Mechanical and Design Engineering; Laribi, M.A., Carbone, G., Jiang, Z., Eds.; Springer: Cham, Switzerland, 2023; Volume 121, pp. 100–110. [Google Scholar]
- Akpan, V.A.; Hassapis, G.D. Nonlinear model identification and adaptive model predictive control using neural networks. ISA Trans. 2011, 50, 177–194. [Google Scholar] [CrossRef]
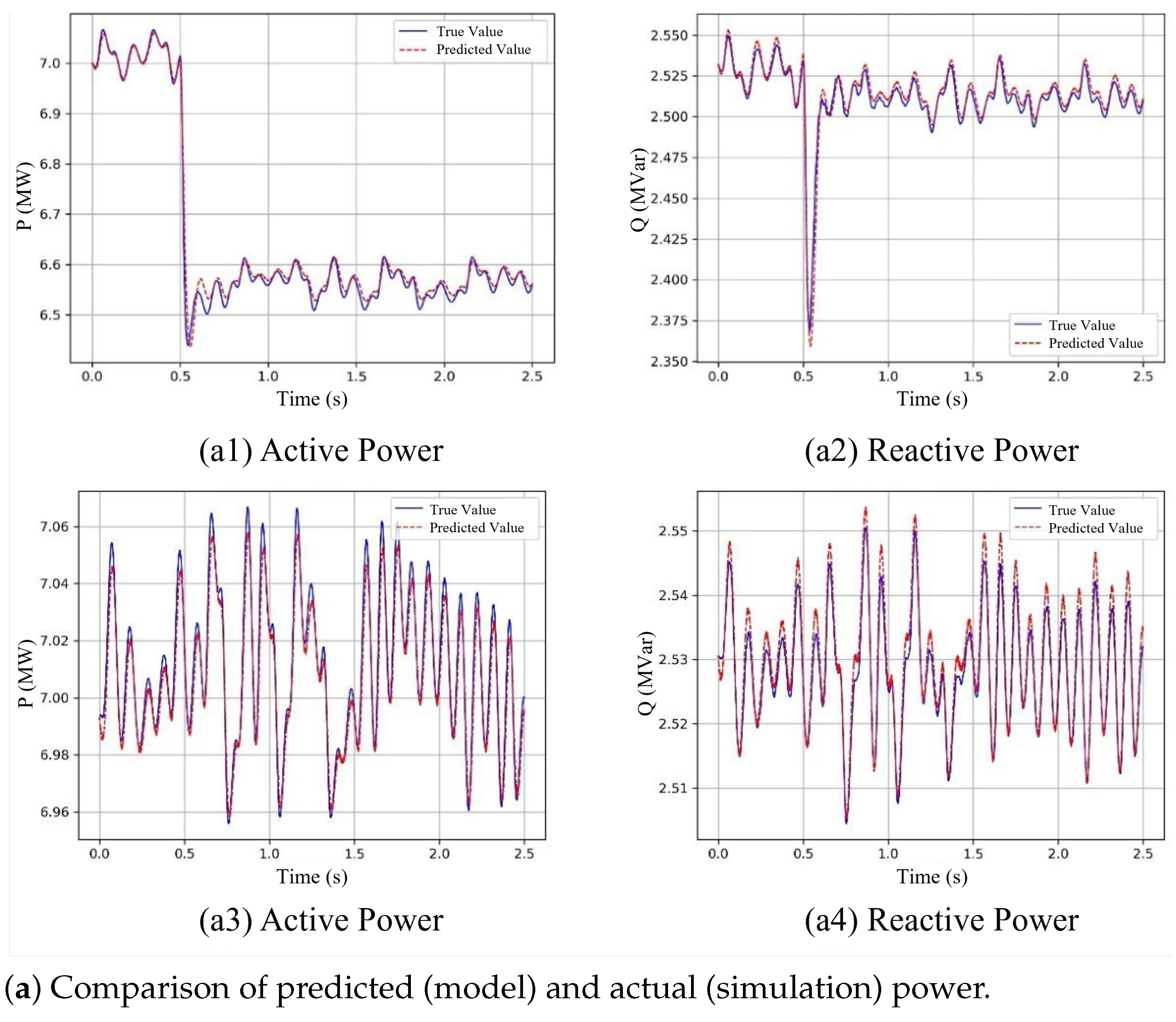
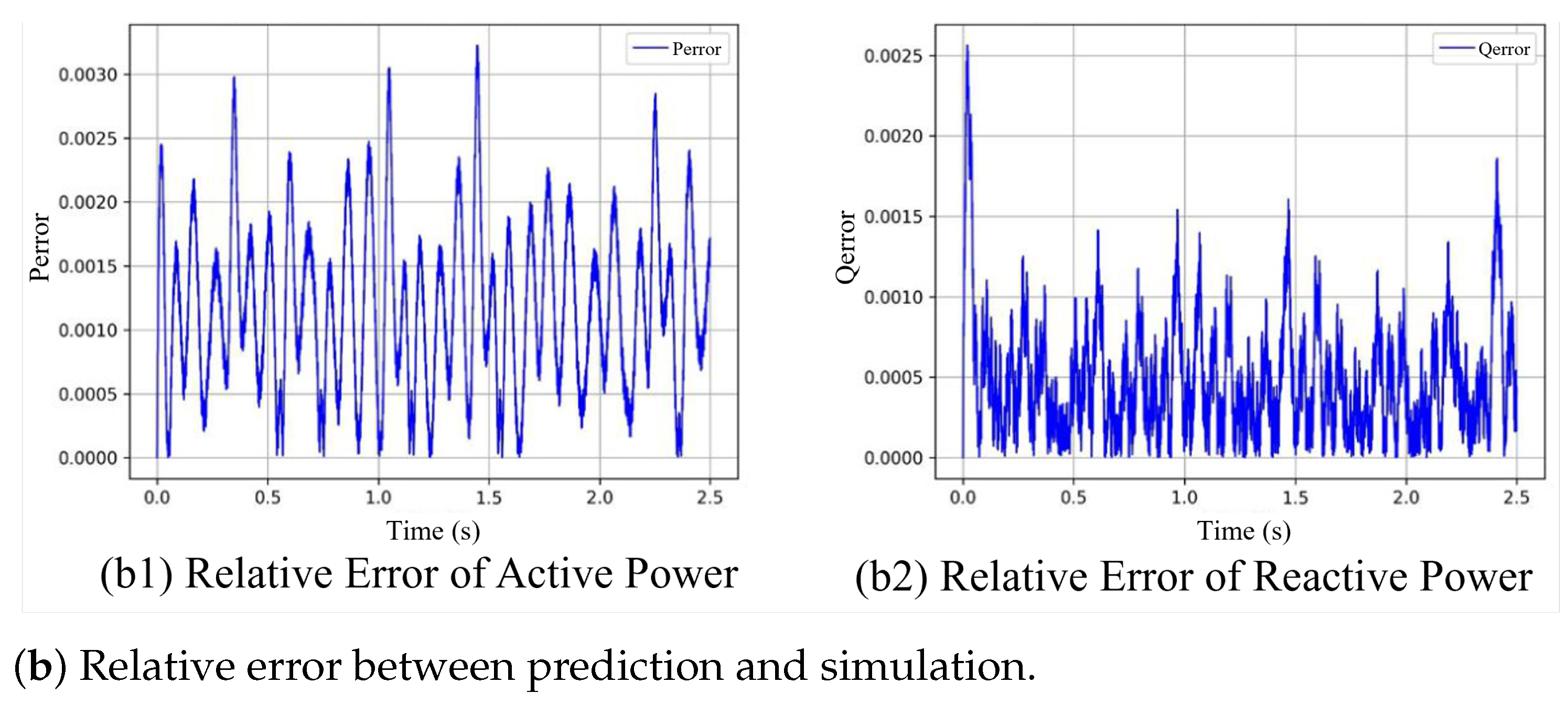
| Metric | Active Power (P) | Reactive Power (Q) |
|---|---|---|
| Max Relative Error | <0.35% | <0.30% |
| Normalized MSE | ||
| Final Training Loss (MSE) | ||
| Metric | Value |
|---|---|
| Steady-State Error (Corrected) | <0.005 MW |
| Voltage Constraint Adherence | Maintained within [0.9, 1.1] pu |
| Typical QP Computation Time per Step | <0.1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, L.; Xi, J.; Hu, H.; Xiong, L.; Lu, G.; Xiao, T. Neural ODE-Based Dynamic Modeling and Predictive Control for Power Regulation in Distribution Networks. Energies 2025, 18, 3419. https://doi.org/10.3390/en18133419
Wen L, Xi J, Hu H, Xiong L, Lu G, Xiao T. Neural ODE-Based Dynamic Modeling and Predictive Control for Power Regulation in Distribution Networks. Energies. 2025; 18(13):3419. https://doi.org/10.3390/en18133419
Chicago/Turabian StyleWen, Libin, Jinji Xi, Hong Hu, Li Xiong, Guangling Lu, and Tannan Xiao. 2025. "Neural ODE-Based Dynamic Modeling and Predictive Control for Power Regulation in Distribution Networks" Energies 18, no. 13: 3419. https://doi.org/10.3390/en18133419
APA StyleWen, L., Xi, J., Hu, H., Xiong, L., Lu, G., & Xiao, T. (2025). Neural ODE-Based Dynamic Modeling and Predictive Control for Power Regulation in Distribution Networks. Energies, 18(13), 3419. https://doi.org/10.3390/en18133419






