Optimised Neural Network Model for Wind Turbine DFIG Converter Fault Diagnosis
Abstract
1. Introduction
1.1. Research Gap and Motivation
1.2. Research Contribution and Future Work
- Development of a high-fidelity Simulink model for fault injection in GSCs of DFIG wind turbines.
- Designing a CNN-LSTM-based time-series classification model tailored for multivariate current signals.
- Performance benchmarking against other neural architectures with accuracy and confusion matrix evaluations.
2. Article Reviews
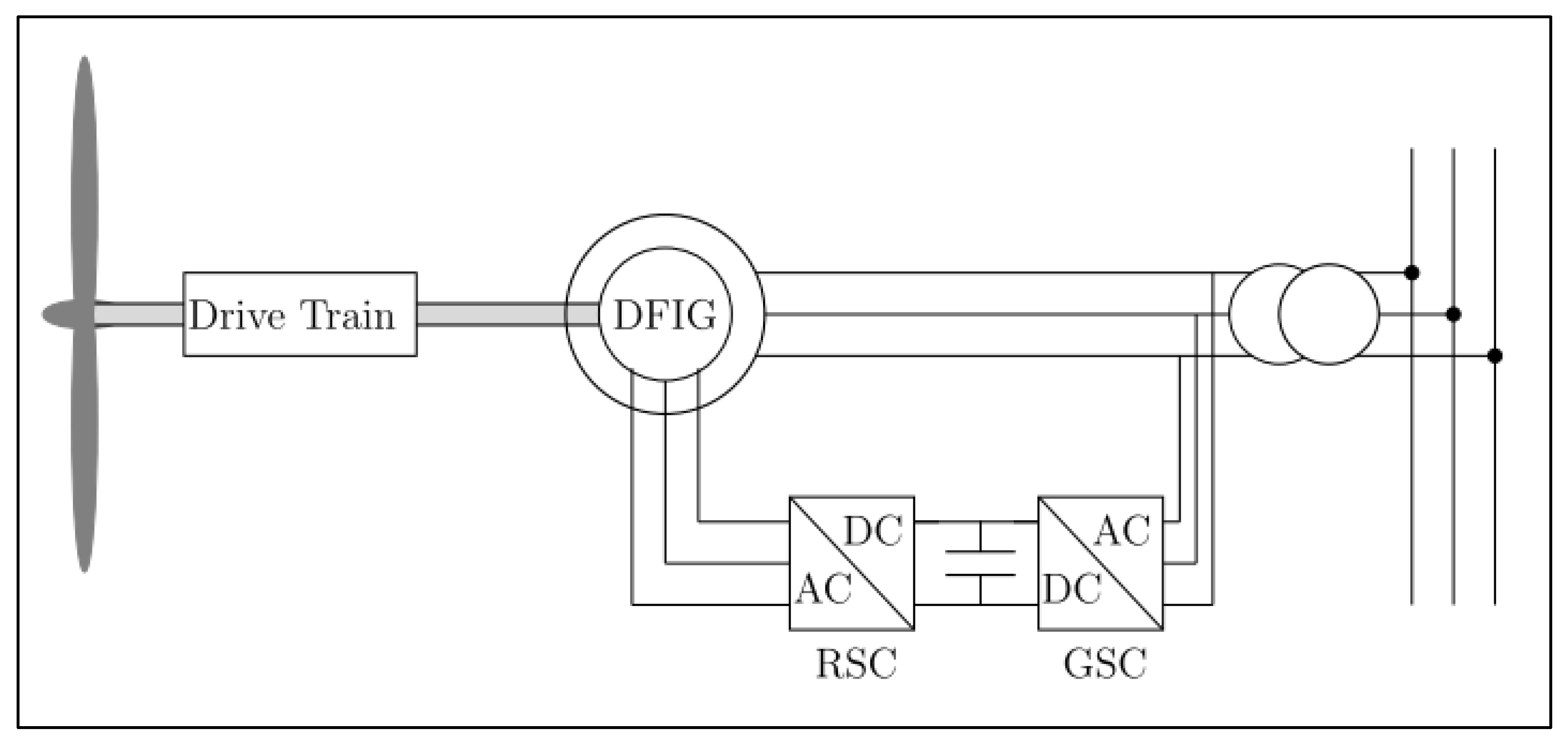
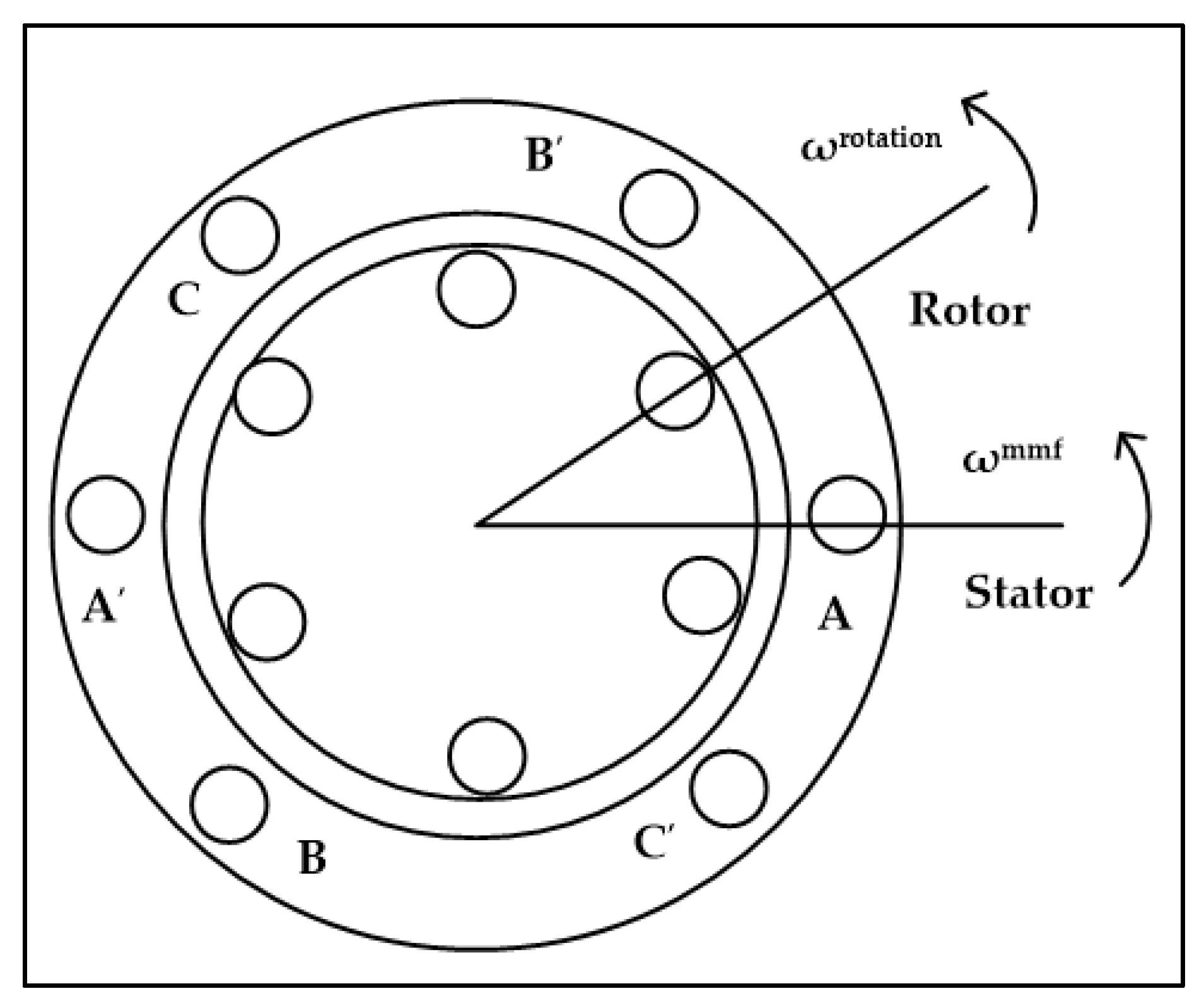
3. Modelling and Controlling of DFIG
3.1. Power Control
3.2. DFIG Rotor Side Control
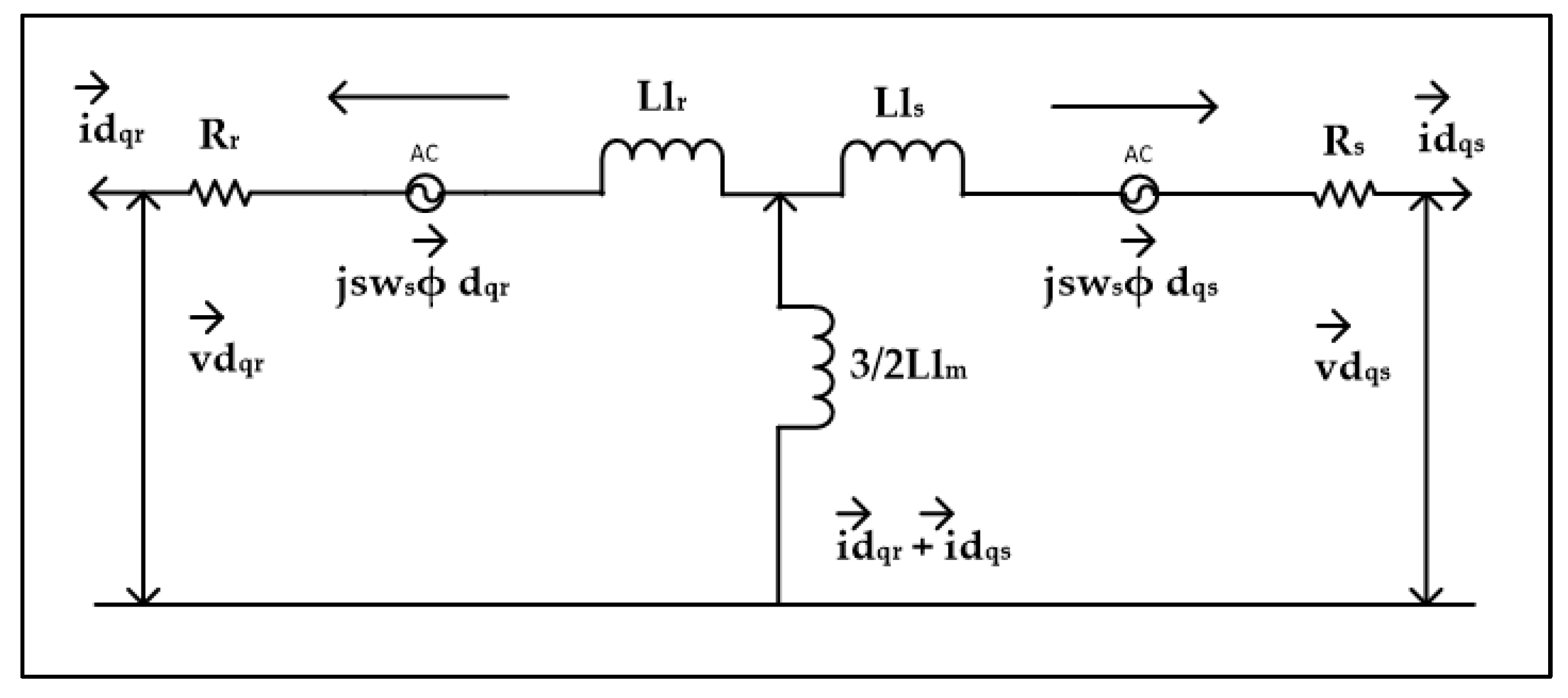
3.3. DFIG Grid Side Control
3.4. Modeling IGBTs Fault in GSC
4. Methodology
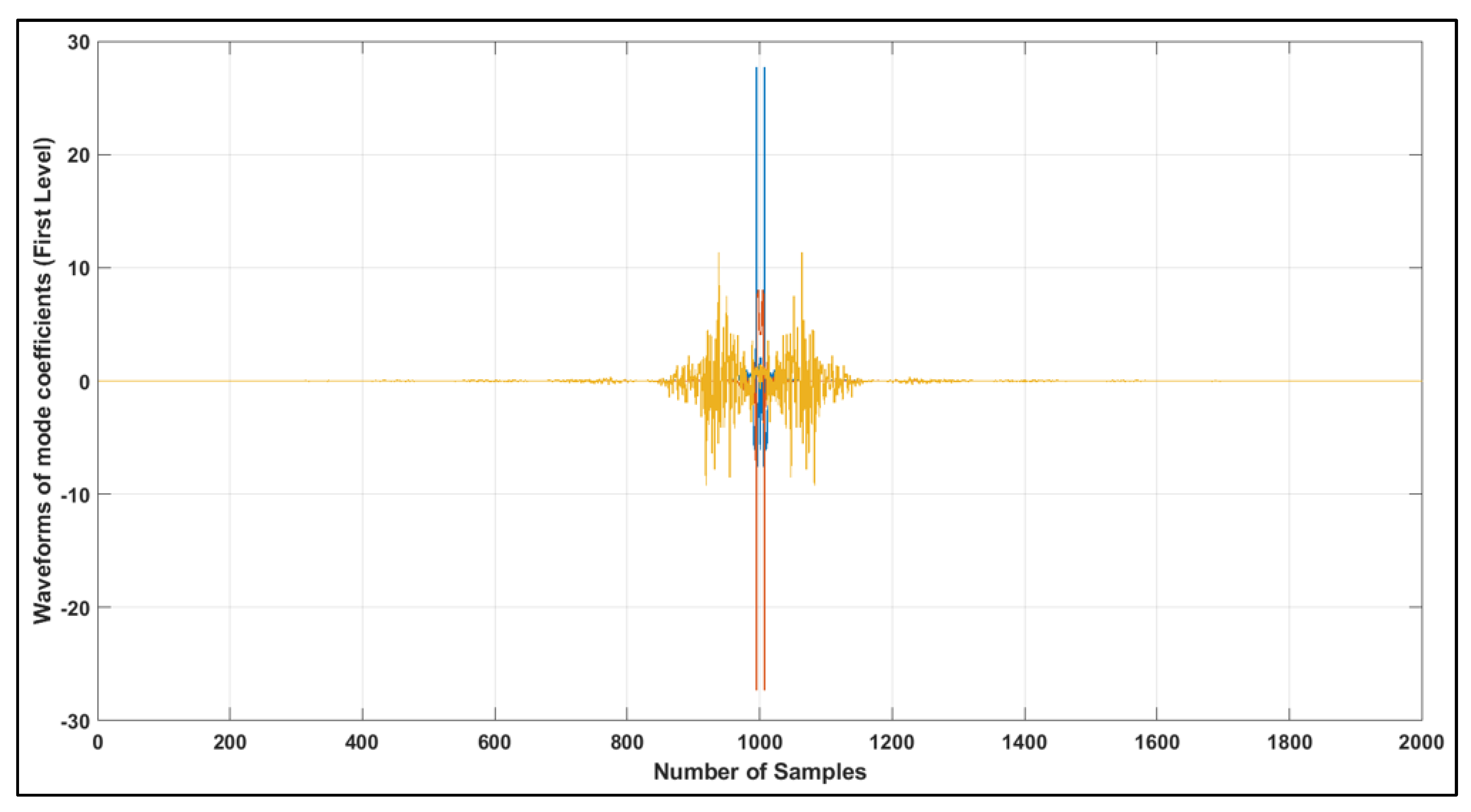
4.1. Variational Mode Decomposition (VMD)
Implications of LCL Filter on Feature Extraction
4.2. Data Normalisation and Augmentation
4.3. Deep Learning Models
4.3.1. CNN-LSTM Hybrid Model
4.3.2. CNN Only Model
4.4. Classification and Evaluation
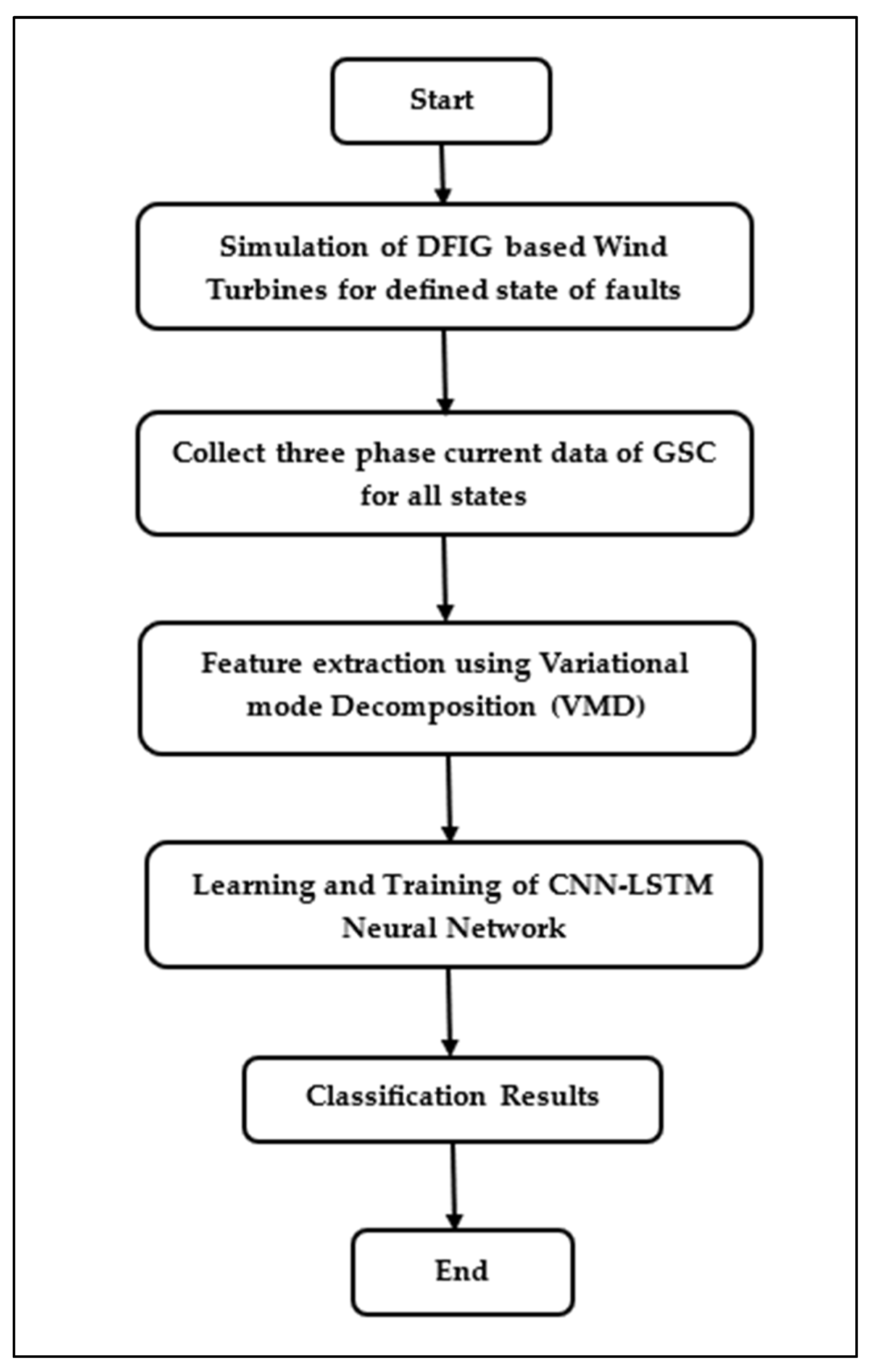
4.4.1. Simulation of DFIG-Based Wind Turbine for Specified Fault Conditions
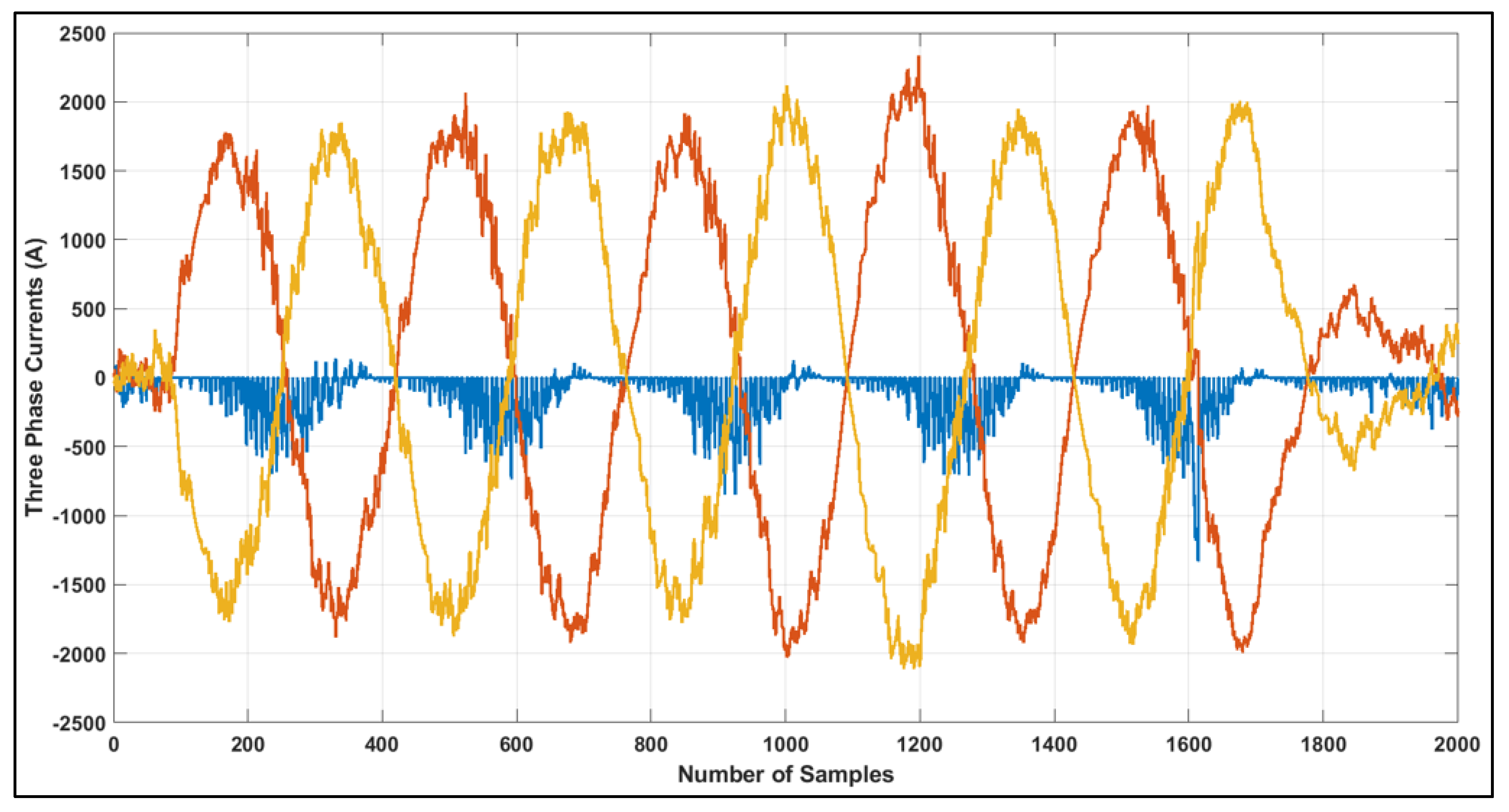
4.4.2. Collection of Three-Phase Current Data from GSC
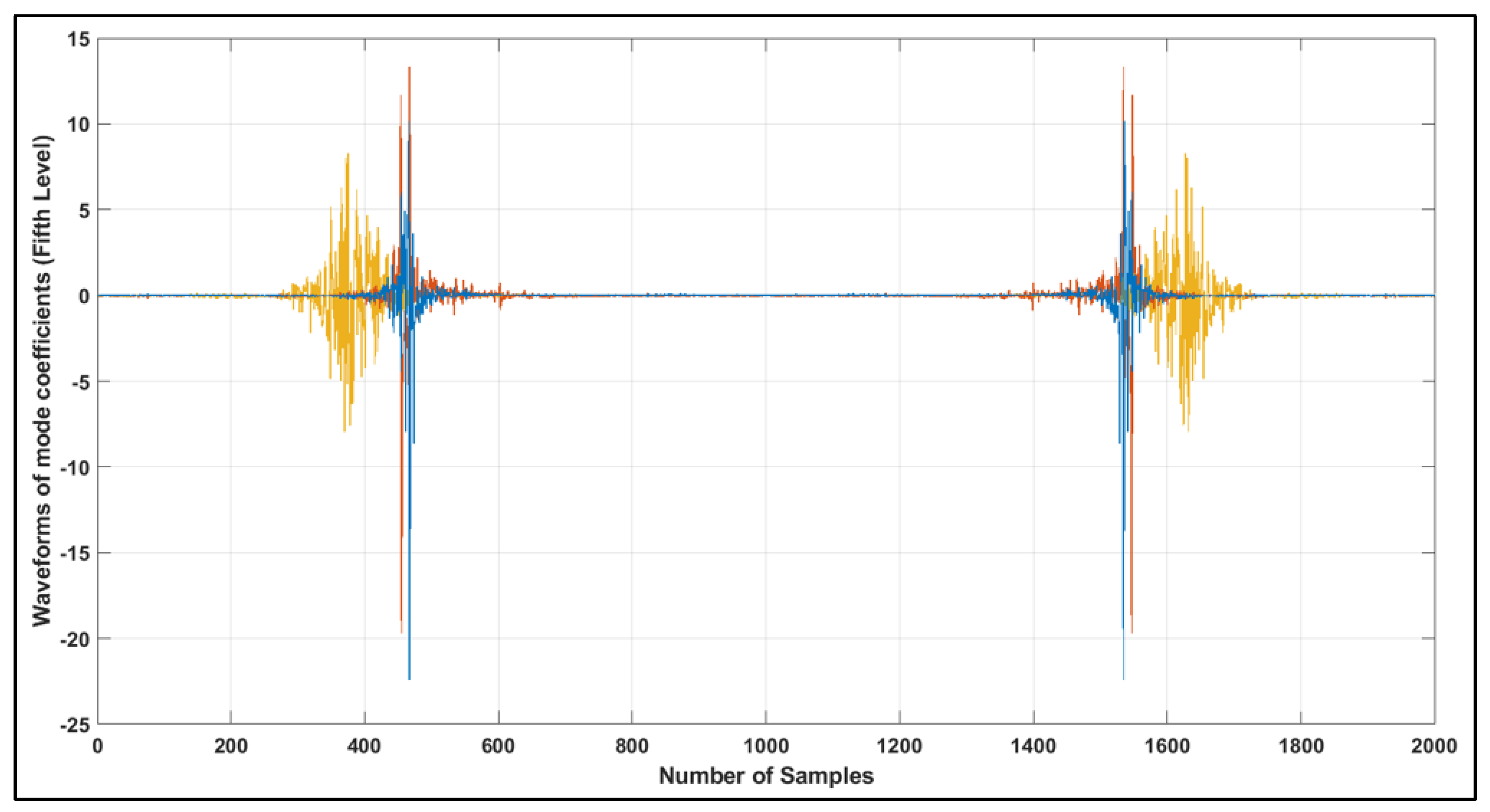
4.4.3. Feature Extraction by Variational Mode Decomposition (VMD)
4.4.4. Training of CNN-LSTM Neural Network
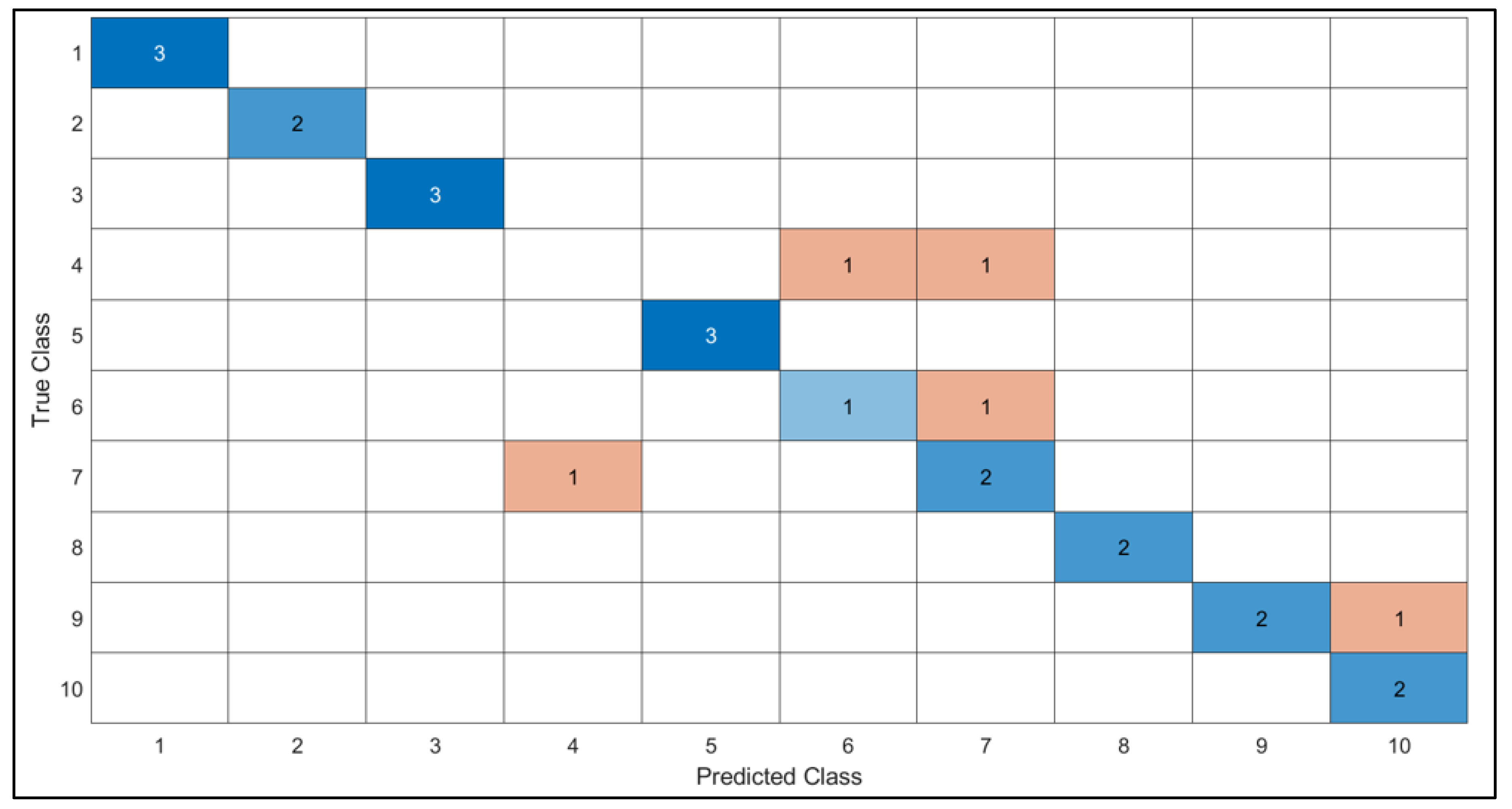
4.4.5. Classification Outcomes
4.4.6. End
5. Simulation Results
5.1. Signal Exchange and Fault Simulation
5.2. Neural Network Training
5.3. Accuracy Comparison
6. Discussion and Comparison
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ukoba, K.; Kunene, T.J.; Harmse, P.; Lukong, V.T.; Jen, T.C. The Role of Renewable Energy Sources and Industry 4.0 Focus for Africa: A Review. Appl. Sci. 2023, 13, 1074. [Google Scholar] [CrossRef]
- Selenko, E.; Bankins, S.; Shoss, M.; Warburton, J.; Restubog, S.L.D. Artificial Intelligence and the Future of Work: A Functional-Identity Perspective. Curr. Dir. Psychol. Sci. 2022, 31, 272–279. [Google Scholar] [CrossRef]
- Pandey, V.; Sircar, A.; Bist, N.; Solanki, K.; Yadav, K. Accelerating the renewable energy sector through Industry 4.0: Optimization opportunities in the digital revolution. Int. J. Innov. Stud. 2023, 7, 171–188. [Google Scholar] [CrossRef]
- Gupta, R.; Chaturvedi, K.T. Adaptive Energy Management of Big Data Analytics in Smart Grids. Energies 2023, 16, 6016. [Google Scholar] [CrossRef]
- Sabev, E.; Trifonov, R.; Pavlova, G.; Rainova, K. Cybersecurity Analysis of Wind Farm SCADA Systems. In Proceedings of the 2021 International Conference on Information Technologies (InfoTech), Varna, Bulgaria, 16–17 September 2021. [Google Scholar]
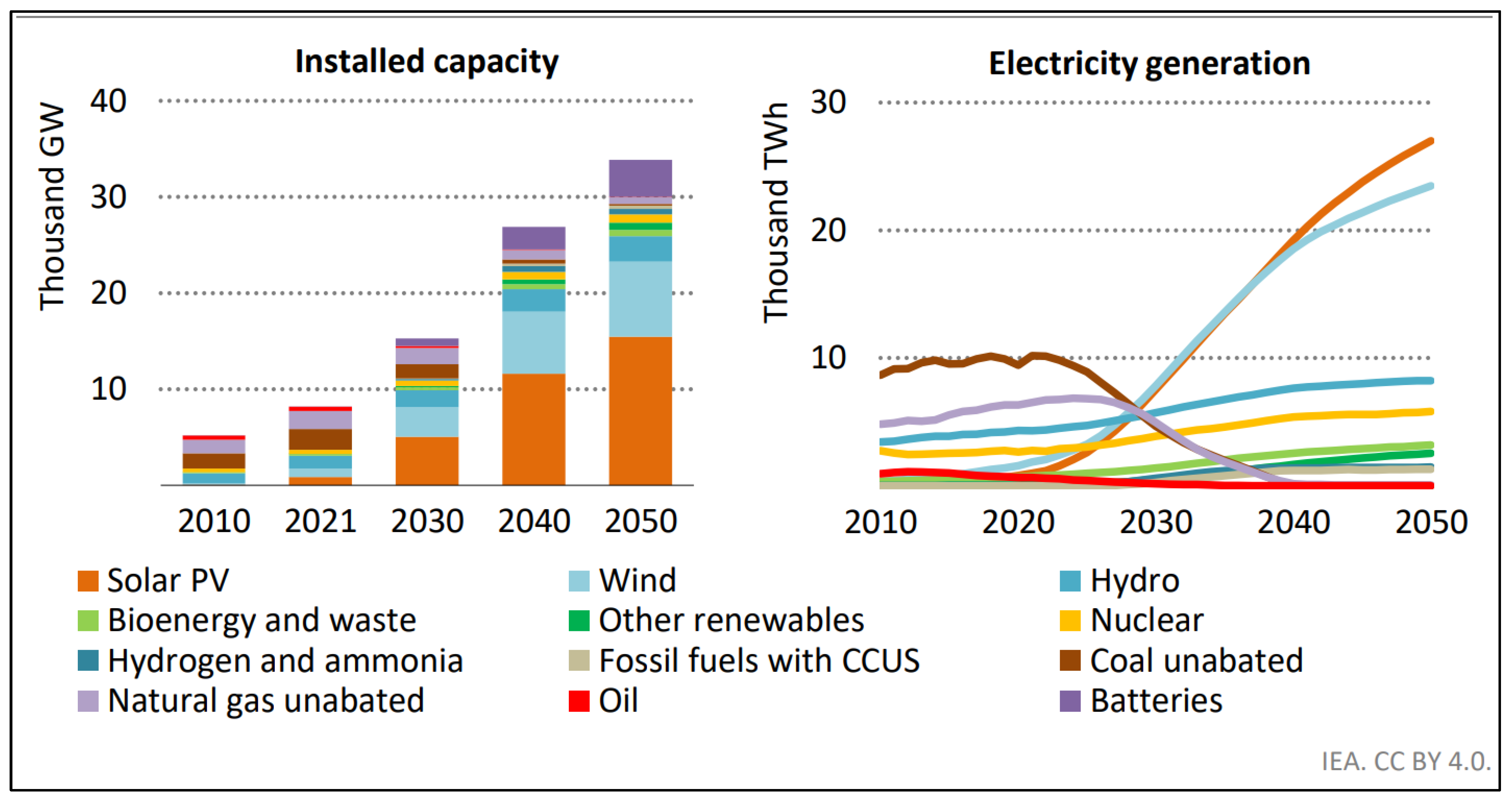
- International Energy Agency. International Energy Agency (IEA) World Energy Outlook. 2022. Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 8 November 2024).
- Ullah, T.; Sobczak, K.; Liśkiewicz, G.; Khan, A. Two-Dimensional URANS Numerical Investigation of Critical Parameters on a Pitch Oscillating VAWT Airfoil under Dynamic Stall. Energies 2022, 15, 5625. [Google Scholar] [CrossRef]
- Yousef, L.A.; Yousef, H.; Rocha-Meneses, L. Artificial Intelligence for Management of Variable Renewable Energy Systems: A Review of Current Status and Future Directions. Energies 2023, 16, 8057. [Google Scholar] [CrossRef]
- Chojaa, H.; Derouich, A.; Zamzoum, O.; Mahfoud, S.; Taoussi, M.; Albalawi, H.; Benbouhenni, H.; Mosaad, M.I. A Novel DPC Approach for DFIG-Based Variable Speed Wind Power Systems Using DSpace. IEEE Access 2023, 11, 9493–9510. [Google Scholar] [CrossRef]
- Hamid, C.; Derouich, A.; Taoussi, M.; Zamzoum, O.; Hanafi, A. An improved performance variable speed wind turbine driving a doubly fed induction generator using sliding mode strategy. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Ntuli, K.; Kabeya, M.; Sharma, G. A Comparative Study of Wind Energy Conversion System incorporating the Doubly Fed Induction Generator and the Permanent Magnet Synchronous Generator. Int. Conf. Intell. Innov. Comput. Appl. 2022, 2022, 238–244. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. Improved rotor flux and torque control based on the third-order sliding mode scheme applied to the asynchronous generator for the single-rotor wind turbine. Mathematics 2021, 9, 2297. [Google Scholar] [CrossRef]
- Chongjarearn, Y. Stator-Voltage Vector Control of a Doubly-Fed Induction Generator Stator-Voltage Vector Control of a Doubly-Fed Induction Generator. In Proceedings of the 34th Electrical Engineering Conference (EECON-34), Eveleigh, Australia, 12–13 November 2014; Volume 1, pp. 4–8. [Google Scholar]
- Agrawal, A.K.; Munshi, B.; Kayal, S. Study of Wind Turbine Driven Dfig Using Ac/Dc/Ac Converter. Bachelor’s Thesis, National Institute of Technology Rourkela, Rourkela, India, 2009. [Google Scholar]
- Madhav, G.V.; Obulesu, Y.P. A new hybrid artificial neural network based control of doubly fed induction generator. Int. J. Electr. Comput. Eng. 2015, 5, 379–390. [Google Scholar] [CrossRef]
- Demidova, G.; Rassolkin, A.; Vaimann, T.; Kallaste, A.; Zakis, J.; Suzdalenko, A. An Overview of Fuzzy Logic Approaches for Fault Diagnosis in Energy Conversion Devices. In Proceedings of the 2021 28th International Workshop on Electric Drives: Improving Reliability of Electric Drives (IWED), Moscow, Russia, 27–29 January 2021. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F. Toward reliable power electronics: Challenges, design tools, and opportunities. IEEE Ind. Electron. Mag. 2013, 7, 17–26. [Google Scholar] [CrossRef]
- Zhu, C.; Li, Y. Reliability Analysis of Wind Turbines. In Stability Control and Reliable Performance of Wind Turbines; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef]
- ĆUK, S.; Middlebrook, R.D. Advances in Switched-Mode Power Conversion Part I. IEEE Trans. Ind. Electron. 1983, IE-30, 10–19. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An overview of artificial intelligence applications for power electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- De Nazareth Ferreira, V.; Cupertino, A.F.; Pereira, H.A.; Rocha, A.V.; Seleme, S.I.; De Jesus Cardoso Filho, B. Design and Selection of High Reliability Converters for Mission Critical Industrial Applications: A Rolling Mill Case Study. IEEE Trans. Ind. Appl. 2018, 54, 4938–4947. [Google Scholar] [CrossRef]
- Burgos, R.; Chen, G.; Wang, F.; Boroyevich, D.; Odendaal, W.G.; Van Wyk, J.D. Reliability-oriented design of three-phase power converters for aircraft applications. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1249–1263. [Google Scholar] [CrossRef]
- Bugaieva, L.; Beznosyk, O. Prediction of Electricity Generation by Wind Farms Based on Intelligent Methods: State of the Art and Examples. Energy Eng. Control Syst. 2022, 8, 104–109. [Google Scholar] [CrossRef]
- Lee, M.; He, G. An empirical analysis of applications of artificial intelligence algorithms in wind power technology innovation during 1980–2017. J. Clean. Prod. 2021, 297, 126536. [Google Scholar] [CrossRef]
- Reznik, A.; Simoes, M.G.; Al-Durra, A.; Muyeen, S.M. LCL Filter design and performance analysis for grid-interconnected systems. IEEE Trans. Ind. Appl. 2014, 50, 1225–1232. [Google Scholar] [CrossRef]
- Thaler, J.M.; Schweizer, M.; Blattmann, R.; Kolar, J.W.; Ecklebe, A. Optimal design of lcl harmonic filters for three-phase pfc rectifiers. IEEE Trans. Power Electron. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Sera, D.; Blaabjerg, F. Lifetime Evaluation of Grid-Connected PV Inverters Considering Panel Degradation Rates and Installation Sites. IEEE Trans. Power Electron. 2018, 33, 1125–1236. [Google Scholar] [CrossRef]
- Naderi, S.B.; Davari, P.; Zhou, D.; Negnevitsky, M.; Blaabjerg, F. A review on fault current limiting devices to enhance the fault ride-through capability of the doubly-fed induction generator basedwind turbine. Appl. Sci. 2018, 8, 2059. [Google Scholar] [CrossRef]
- Behara, R.K.; Saha, A.K. Artificial Intelligence Control System Applied in Smart Grid Integrated Doubly Fed Induction Generator-Based Wind Turbine: A Review. Energies 2022, 15, 6488. [Google Scholar] [CrossRef]
- Behara, R.K.; Saha, A.K. Artificial Intelligence Methodologies in Smart Grid-Integrated Doubly Fed Induction Generator Design Optimization and Reliability Assessment: A Review. Energies 2022, 15, 7164. [Google Scholar] [CrossRef]
- Behara, R.K.; Saha, A.K. Neural Network Predictive Control for Improved Reliability of Grid-Tied DFIG-Based Wind Energy System under the Three-Phase Fault Condition. Energies 2023, 16, 4881. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; Choice Reviews Online; John Wiley & Sons: Hoboken, NJ, USA, 1990; Volume 27, pp. 27–6393. [Google Scholar] [CrossRef]
- de Oliveira, I.R.; Tofoli, F.L.; Mendes, V.F. Influence of low-voltage ride-through control techniques on the thermal behavior of power converters applied to wind energy conversion systems based on the doubly-fed induction generator. Electr. Power Syst. Res. 2025, 239, 111272. [Google Scholar] [CrossRef]
- Abbas, M.; Chafouk, H.; Ardjoun, S.A.E.M. Fault Diagnosis in Wind Turbine Current Sensors: Detecting Single and Multiple Faults with the Extended Kalman Filter Bank Approach. Sensors 2024, 24, 728. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Wu, X.; Yang, Z. A review of recent advances in wind turbine condition monitoring and fault diagnosis. In Proceedings of the 2009 IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009. [Google Scholar] [CrossRef]
- Elshenawy, L.; Gafar, A.; Awad, H.; Abouomar, M.S. Fault detection of wind turbine system based on data-driven methods: A comparative study. Neural Comput. Appl. 2024, 36, 1–18. [Google Scholar] [CrossRef]
- Alrifaey, M.; Lim, W.H.; Ang, C.K.; Natarajan, E.; Solihin, M.I.; Juhari, M.R.M.; Tiang, S.S. Hybrid Deep Learning Model for Fault Detection and Classification of Grid-Connected Photovoltaic System. IEEE Access 2022, 10, 13852–13869. [Google Scholar] [CrossRef]
- Helbing, G.; Ritter, M. Deep Learning for fault detection in wind turbines. Renew. Sustain. Energy Rev. 2018, 98, 189–198. [Google Scholar] [CrossRef]
- Raju, S.K.; Periyasamy, M.; Alhussan, A.A.; Kannan, S. Machine learning boosts wind turbine efficiency with smart failure detection and strategic placement. Sci. Rep. 2025, 15, 1485. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Zhang, Q.; Xie, Y.; Zhang, J.; Ke, J. Research on Wind Turbine Fault Detection Based on CNN-LSTM. Energies 2024, 17, 4497. [Google Scholar] [CrossRef]
- Moshtaghi, P.; Hajialigol, N.; Rafiei, B. A comprehensive review of artificial intelligence applications in wind energy power generation. Sustain. Futur. 2025, 9, 100638. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, M.; Zhou, Z. Enhanced Control Strategies for Improving Low Fault Ride-Through Capability of Grid-Connected Doubly Fed Induction Wind Turbines. Energies 2025, 18, 767. [Google Scholar] [CrossRef]
- Talani, R.A.; Kaloi, G.S.; Ali, A.; Bijarani, M.A.; Abbas, G.; Hatatah, M.; Mercorelli, P.; Touti, E. Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator. Machines 2025, 13, 110. [Google Scholar] [CrossRef]
- Dayo, S.A.; Memon, A.; Memon, Z.A.; Jumani, T.A.; Abbas, G.; Othmen, S.; Yousef, A.; Wijaya, A.A. A new approach for improving dynamic fault ride through capability of gridctied based wind turbines. Sci. Rep. 2025, 15, 6144. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N.; Yessef, M.; Elbarbary, Z.M.S.; Colak, I.; Alammar, M.M.; Bossoufi, B. Enhancing the power quality of dual rotor wind turbines using improved fuzzy space vector modulation and super twisting sliding techniques. Sci. Rep. 2025, 15, 7290. [Google Scholar] [CrossRef]
- Stallon, D.; Zaid, I.E.; Vidal, Y. Two-Stage Fault Detection and Control Approach for DFIG-Based Wind Energy Conversion System. Proc. Int. Conf. Inform. Control. Autom. Robot. 2024, 1, 209–216. [Google Scholar] [CrossRef]
- Megahed, T.F.; Morgan, E.F.; Timo, P.N.; Saeed, M. Neural network predictive control for fault detection and identification in DFIG with SMES for low voltage ride-through requirements. Ain Shams Eng. J. 2024, 15, 102775. [Google Scholar] [CrossRef]
- Lopez, A.R.; Rumbo-Morales, J.Y.; Ortiz-Torres, G.; Valdez-Resendiz, J.E.; Vazquez, G.; Rosas-Caro, J.C. Fault-Tolerant Control Implemented for Sustainable Active and Reactive Regulation of a Wind Energy Generation System. Sustainability 2024, 16, 10875. [Google Scholar] [CrossRef]
- Wang, Y. Enhancing Transient Stability of DFIG-Based Wind Turbine Systems Using Deep Learning-Controlled Resistance-Based Fault Current Limiters. Adv. Eng. Intell. Syst. 2024, 3, 10–22. [Google Scholar]
- Liang, J.; Zhang, K. A Robust Fault Diagnosis Scheme for Converter in Wind Turbine Systems. Electron. 2023, 12, 1597. [Google Scholar] [CrossRef]
- Yahiaoui, M.A.; Kinnaert, M.; Gyselinck, J. Robust Diagnosis of Multiple Open-Circuit Faults in DFIG Wind Turbines in Both Sub- and Super-Synchronous Operating Modes. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1054–1067. [Google Scholar] [CrossRef]
- Zhang, S.; Robinson, E.; Basu, M. Wind Turbine Predictive Fault Diagnostics Based on a Novel Long Short-Term Memory Model. Algorithms 2023, 16, 546. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, P.; Zhang, W.; Wang, M. CNN-LSTM-Attention with PSO optimization for temperature and fault prediction in meat grinder motors. Discov. Appl. Sci. 2025, 7, 438. [Google Scholar] [CrossRef]
- Guo, K.; Lu, Z.; Liu, P.; Mo, Z. Fault Diagnosis Method for Sub-Module Open-Circuit Faults in Photovoltaic DC Collection Systems Based on CNN-LSTM. Electron. 2025, 14, 1205. [Google Scholar] [CrossRef]
- Assia, H.; Boulouiha, H.M.; Chicaiza, W.D.; Escaño, J.M.; Kacimi, A.; Martínez-Ramos, J.L.; Denai, M. Wind Turbine Active Fault Tolerant Control Based on Backstepping Active Disturbance Rejection Control and a Neurofuzzy Detector. Energies 2023, 16, 5455. [Google Scholar] [CrossRef]
- Fekih, A.; Habibi, H.; Simani, S. Fault Diagnosis and Fault Tolerant Control of Wind Turbines: An Overview. Energies 2022, 15, 7186. [Google Scholar] [CrossRef]
- Kamarzarrin, M.; Refan, M.H.; Amiri, P.; Dameshghi, A. Fault Diagnosis of Wind Turbine Double-Fed Induction Generator Based on Multi-Level Fusion and Measurement of Back-to-Back Converter Current Signal. Iran. J. Electr. Electron. Eng. 2022, 18, 1. [Google Scholar] [CrossRef]
- Ng, E.Y.K.; Lim, J.T. Machine Learning on Fault Diagnosis in Wind Turbines. Fluids 2022, 7, 371. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, K.; Al-Durra, A.; Zhou, D. A novel fault diagnostic method in power converters for wind power generation system. Appl. Energy 2020, 266, 114851. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Sun, Z.; Dong, Y.; Dong, W. Open-circuit fault diagnosis ofwind power converter using variational mode decomposition, trend feature analysis and deep belief network. Appl. Sci. 2020, 10, 2146. [Google Scholar] [CrossRef]
- Fournier, J. Modeling, Control and Experimental Validation of a DFIG-Based Wind Turbine Test Bench. Master’s Thesis, Universitat Politecnica de Catalunya, Barcelona, Spain, 2013. Available online: http://upcommons.upc.edu//handle/2099.1/18983 (accessed on 12 January 2025).
- Hamon, C.; Elkington, K.; Ghandhari, M. Doubly-fed induction generator modeling and control in DigSilent PowerFactory. In Proceedings of the 2010 International Conference on Power System Technology—(POWERCON 2010), Hangzhou, China, 24–28 October 2010. [Google Scholar] [CrossRef]
- Badreldien, M.; Usama, R.; El-wakeel, A.; Abdelaziz, A.Y. Modeling, Analysis and Control of Doubly Fed Induction Generators for Wind Turbines. In Proceedings of the International Conference on Electrical Engineering, Bangalore, India, 25–26 October 2014; pp. 1–18. [Google Scholar] [CrossRef]
- Mazari, S. Control Design and Analysis of Doubly-Fed Induction Generator in Wind Power Application. Master’s Thesis, The University of Alabama, Tuscaloosa, AL, USA, 2009. [Google Scholar]
- Junyent-ferré, A.; Gomis-bellmunt, O.; Sumper, A.; Sala, M. Simulation Modelling Practice and Theory Modeling and control of the doubly fed induction generator wind turbine. Elsevier 2010, 18, 1365–1381. [Google Scholar] [CrossRef]
- Arnaltes, S.; Rodriguez-Amenedo, J.L.; Montilla-Djesus, M.E. Control of Variable Speed Wind Turbines with Doubly Fed Asynchronous Generators for Stand-Alone Applications. Energies 2018, 26, 26. [Google Scholar] [CrossRef]
- Hamane, B.; Doumbia, M.L.; Bouhamida, A.M.; Benghanem, M. Direct active and reactive power control of DFIG based WECS using PI and sliding mode controllers. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2050–2055. [Google Scholar] [CrossRef]
- Alhato, M.M.; Bouallègue, S. Direct Power Control Optimization for Doubly Fed Induction Generator Based Wind Turbine Systems. Math. Comput. Appl. 2019, 24, 77. [Google Scholar] [CrossRef]
- Fei, H.; Zhang, C.; Xu, S.; Zhang, J.; Wu, L. Variational Mode Decomposition Guided by Time-Frequency Domain Difference Information. In International Conference on the Efficiency and Performance Engineering Network; Springer Nature: Cham, Switzerland, 2024; pp. 81–94. [Google Scholar]
- Hu, P.; Tong, J.; Wang, J.; Yang, Y.; De Oliveira Turci, L. A hybrid model based on CNN and Bi-LSTM for urban water demand prediction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1088–1094. [Google Scholar] [CrossRef]
- Bharti, O.P.; Saket, R.K.; Nagar, S.K. Controller design of DFIG based wind turbine by using evolutionary soft computation technique 2017. Eng. Technol. Appl. Sci. Res. 2017, 7, 1732–1736. [Google Scholar] [CrossRef]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Reference-Frame Theory. In Analysis of Electric Machinery and Drive Systems; IEEE: Piscataway, NJ, USA, 2013; pp. 86–120. [Google Scholar] [CrossRef]
- Fletcher, J.; Yang, J. Introduction to the doubly fed induction generator for wind power applications. In Paths to Sustainable Energy; IntechOpen: Rijeka, Croatia, 2010. [Google Scholar] [CrossRef]
- Didactic, S.F. Electricity and New Energy Principles of Doubly-Fed Induction Generators (DFIG). 2011. Available online: www.festo-didactic.com (accessed on 20 April 2025).
- Xiao, C.; Liu, Z.; Zhang, T.; Zhang, X. Deep Learning Method for Fault Detection of Wind Turbine Converter. Appl. Sci. 2021, 11, 1280. [Google Scholar] [CrossRef]





| Reference | Method and Model | Objective | Key Result/Contribution |
|---|---|---|---|
| [10] | DFIG converter topology | Explain DFIG structure and roles of RSC and GSC | Operational framework of converters |
| [11,29,33] | Review and thermal stress analysis | Identify GSC vulnerabilities | High temp > 150 °C leads to IGBT failure |
| [34,35,36,37] | Traditional signal thresholding | Fault detection | Limited adaptability under wind variations |
| [38,39,40,41] | CNN-LSTM | Real-time non-linear pattern detection | High accuracy fault classification |
| [42] | Crowbar-based WSE-MPPT and FRT | Enhance FRT under symmetrical faults | Stable recovery under faults |
| [43] | Stator current rotor voltage comp. | Improve LVRT performance | Reduced rotor overcurrent |
| [44] | Fuzzy logic and SSOA | Optimise PI and enhance response | Reduced active/reactive power overshoot |
| [43] | ICA-CC + EMCABN + MSEOA | Intelligent fault classification | 98% accuracy, grid stability |
| [45] | NNPC + SMES | LVRT and transient oscillation reduction | Improved detection and voltage stability |
| [46] | State feedback + SMC | FTC with PI observer | Improved power regulation |
| [47] | RNN + LSTM + FCL | Deep learning FCL for stability | Superior transient stability |
| [48] | EEMD + IMF + PE | Data-driven voltage fault diagnosis | 98.3% accuracy under noise |
| [49] | Chi-square current-based | Detect IGBT open-circuit faults | Precise diagnostics, 21 fault types |
| [50] | T2V-LSTM | SCADA-based fault prediction | 84.97% accuracy up to 210 min ahead |
| [51] | NNPC + BADRC + ANFIS | Fault-tolerant grid control | 95.1% actuator fault accuracy |
| [52] | EMD + LS-WSVM + GA | ITSC detection | 98.27% accuracy |
| [53,54] | SCADA + ML (kNN, ANN, XGBoost) | Gearbox/power failure prediction | Early fault detection |
| [55] | EMD + noise reduction | Noise-resilient fault classification | 99.57% accuracy |
| [56] | VMD + trend feature + DBN | IGBT open fault classification | Superior DBN-based detection |
| State Types | T1 | T2 | T3 | T4 | T5 | T6 |
|---|---|---|---|---|---|---|
| State 1 (Normal operation) | 1 | 1 | 1 | 1 | 1 | 1 |
| State 2 (Single open-circuit) | 0 | 1 | 1 | 1 | 1 | 1 |
| State 3 (Single open-circuit) | 1 | 0 | 1 | 1 | 1 | 1 |
| State 4 (Single open-circuit) | 1 | 1 | 0 | 1 | 1 | 1 |
| State 5 (Single open-circuit) | 1 | 1 | 1 | 0 | 1 | 1 |
| State 6 (Single open-circuit) | 1 | 1 | 1 | 1 | 0 | 1 |
| State 7 (Single open-circuit) | 1 | 1 | 1 | 1 | 1 | 0 |
| State 8 (Double open-circuit in phase a) | 0 | 1 | 1 | 0 | 1 | 1 |
| State 9 (Double open-circuit in phase b) | 1 | 1 | 0 | 1 | 1 | 0 |
| State 10 (Double open-circuit in the phase c) | 1 | 0 | 1 | 1 | 0 | 1 |
| Statistics | Value |
|---|---|
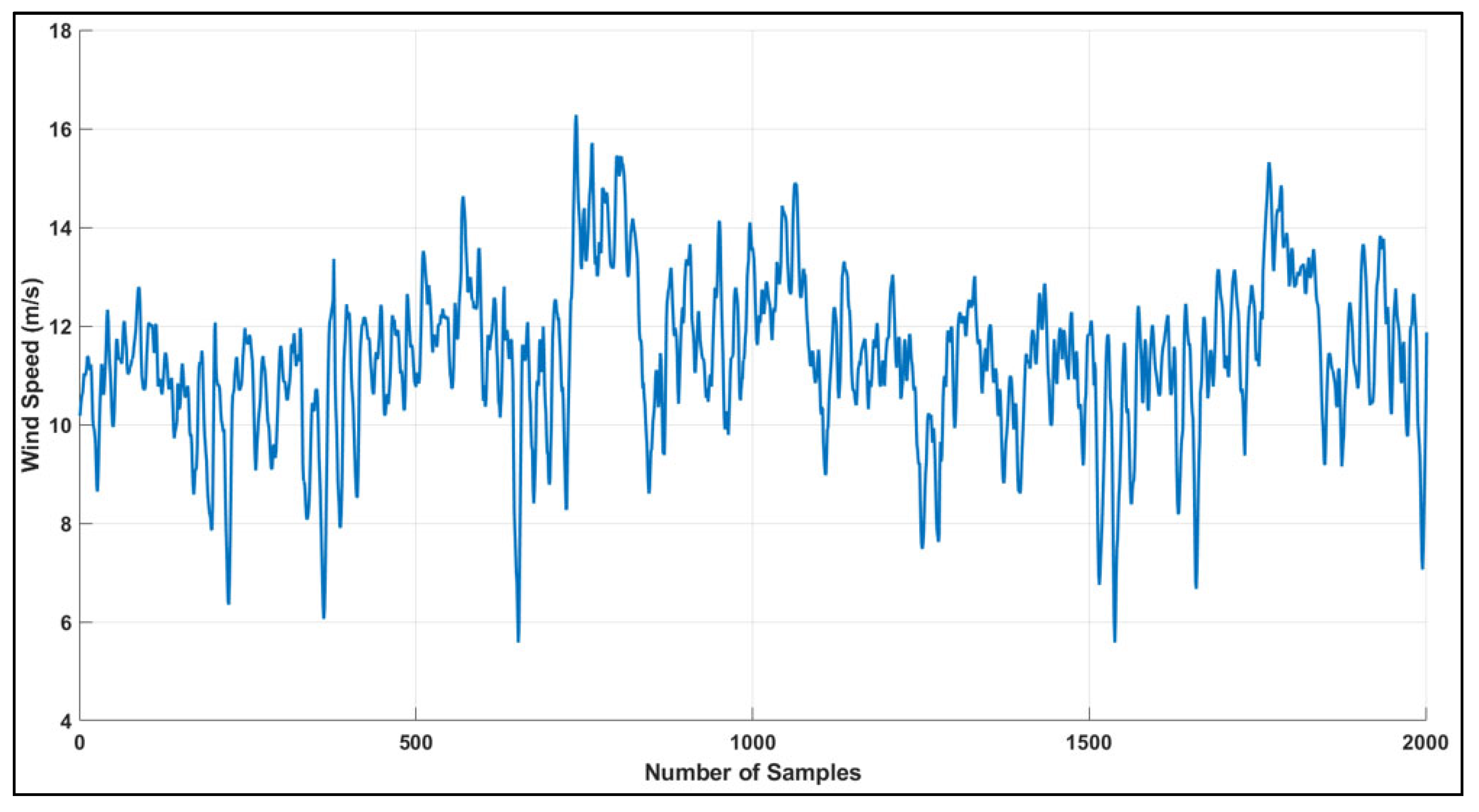
| Mean wind speed | 8.0 m/s |
| Standard deviation | 2.0 m/s |
| Minimum wind speed | 2.5 m/s |
| Maximum wind speed | 15–18 m/s |
| Typical range (68%) | 6.0–10.0 m/s |
| Distribution type | Positively skewed, non-normal |
| Sampling interval | Daily to hourly |
| Model | Accuracy (%) | Recall (%) | F1 (%) | Precision (%) |
|---|---|---|---|---|
| CNN-LSTM | 88 | 90 | 85.71 | 84 |
| LSTM | 86 | 87 | 83.50 | 80 |
| CNN | 84 | 83 | 82.33 | 73.17 |
| MLP | 81 | 79 | 77.80 | 76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behara, R.K.; Saha, A.K. Optimised Neural Network Model for Wind Turbine DFIG Converter Fault Diagnosis. Energies 2025, 18, 3409. https://doi.org/10.3390/en18133409
Behara RK, Saha AK. Optimised Neural Network Model for Wind Turbine DFIG Converter Fault Diagnosis. Energies. 2025; 18(13):3409. https://doi.org/10.3390/en18133409
Chicago/Turabian StyleBehara, Ramesh Kumar, and Akshay Kumar Saha. 2025. "Optimised Neural Network Model for Wind Turbine DFIG Converter Fault Diagnosis" Energies 18, no. 13: 3409. https://doi.org/10.3390/en18133409
APA StyleBehara, R. K., & Saha, A. K. (2025). Optimised Neural Network Model for Wind Turbine DFIG Converter Fault Diagnosis. Energies, 18(13), 3409. https://doi.org/10.3390/en18133409






