Abstract
In this contribution, a model order reduction (MOR) strategy for systems characterized by Warburg-type impedance behavior, frequently encountered in electrochemical applications, is addressed. In particular, the interest is focused on the time-domain approach for deriving low-order models of such a system, in contrast to the current approaches based on the frequency domain. By exploiting the peculiar structure of positive real (PR) systems, a characteristic value technique relying on the Riccati Equation Balancing strategy is introduced to approximate such models with reduced complexity. The characteristic values of the system are used to define suitable reduced-order models. A numerical case study is presented to validate the effectiveness of the proposed method. The model is also compared against experimental data from the literature, confirming its capability to capture dominant Warburg behavior. Performance indices are computed to quantitatively assess the approximation accuracy across different model orders. The results are critically compared with those obtained using conventional MOR techniques, allowing a thorough assessment of accuracy, stability, and implementation feasibility.
1. Introduction
A wide interest has been given today to new devices related to energy saving. This is also due to the increasing need to conceive systems that include both electronic devices and power sources, such as batteries, supercapacitors, and fuel cells [1,2].
The effort in considering the power supply together with other electronic equipment, with the goal of achieving integrated packaging, further increases interest in modeling each part of the system accurately, in order to obtain appropriate complete models in the framework of systems of systems [3]. Therefore, more components are taken into account. Indeed, in this class of devices, the complexity of the engineering system strongly emerges, especially when considering the integration of these devices into real-world consumer applications with sustainable performance. This study focuses on the reduced-order modeling of transmissive Warburg diffusion impedance.
Despite the significant efforts recently reported in the literature, essentially based on the frequency domain and often related to Electrochemical Spectroscopy studies [4], several reasons lead us to consider MOR techniques in the time domain, from a system engineering perspective. In fact, recent studies have highlighted key limitations of frequency-domain approaches when modeling Warburg-type impedance. For instance, they often rely on an artificial separation between diffusion and interfacial impedance, which can result in incorrect physical interpretations and parameter estimation [5]. Moreover, frequency-domain techniques typically assume stationarity and linearity, assumptions that are frequently violated during realistic battery operations, such as under varying loads or during battery aging [6]. From a practical perspective, frequency-based models are also less compatible with real-time simulation and embedded applications compared to their time-domain counterparts [7]. Moreover, the model reduction technique proposed in this work is based on the computation of characteristic values, which are intrinsically defined in the time domain through state-space realizations. Therefore, the adoption of a time-domain formulation is not only advantageous, but also necessary for the implementation of our method.
The recent literature highlights the importance of analyzing these systems across different contexts, requiring models that can be seamlessly integrated into broader engineering frameworks. Some recent studies have emphasized the need for accurate modeling of power sources, particularly in relation to thermal effects and real-time estimation capabilities. In fact, in [8], a comprehensive review on the thermal safety of lithium-ion batteries has been conducted, focusing on failure mechanisms, early warning strategies, and modeling approaches aimed at improving fault diagnosis and fire prevention. The behavior of batteries operating in a wide temperature range has been further investigated in [9], where a reduced-order electrochemical model was proposed and experimentally validated under various dynamic conditions, demonstrating accuracy and robustness from from to .
In other works, various model order reduction (MOR) strategies have been explored to improve the efficiency of time-domain simulations for complex electrochemical systems. For instance, authors in [10] applied Proper Orthogonal Decomposition (POD) to derive reduced-order models of lithium-ion batteries for vehicle applications, achieving accurate State-Of-Charge predictions with significantly lower computational effort. In [11], the authors proposed a Padé-based reduction approach combined with a transmission-line circuit model structure, enabling real-time simulation of electrochemical dynamics with high fidelity. In parallel, authors in [12] addressed the reduction of fractional-order electrochemical models, used in batteries, fuel cells, and supercapacitors, by approximating them with equivalent low-order integer systems, thus facilitating their integration into time–frequency analysis frameworks. These contributions reflect the ongoing development of MOR strategies aimed at enabling fast and accurate simulation of electrochemical systems in the time domain.
The aspect of online behavior characterization strongly motivates the efforts to adapt reduced-order models in the time domain, as discussed in [13], where the use of physics-based models in battery management systems is shown to require model order reduction to ensure feasibility in real-time applications. The reliability of lithium-ion batteries requires state-of-health estimation based on accurate low-order models, as demonstrated in [14], where a 2-RC equivalent-circuit model with degradation and temperature dependency achieves real-time SoH estimation with low computational cost.
The adoption of such models in intelligent connected vehicles for new energy applications, where power devices are central to system operation [15], further motivates the evaluation of reliable reduced-order models in the time domain, with the aim of integrating them into networks that also include nonlinear electronic components. Moreover, simulation platforms such as SPICE and Simulink [16] require additional new simulation blocks in order to perform accurate global simulations, while avoiding numerical issues.
The increasing demand for sustainable, scalable energy storage solutions is driving the development of advanced lithium-ion and sodium-ion batteries. Comparative studies emphasize their differing characteristics in terms of cost, supply chain, and energy density, underlining the need for accurate impedance-based modeling to guide technology choices and system design [17].
In the recent literature, great efforts have been made to obtain reduced-order models of Warburg diffusion devices in order to directly obtain equivalent devices. Therefore, model reduction approaches have been developed by considering the same representation area, aiming to obtain an approximated device by using classical electrical network techniques based on ladder and Foster structures. The proposed strategy is essentially based on a high-order approximation of the transcendental Warburg diffusion impedance, which is then reduced by means of the PR balancing technique. This allows deriving a lower-order model that guarantees both an upper bound on the approximation error and a physically reliable representation. Indeed, a subsequent Cauer–Foster representation of the obtained reduced-order model can be proposed, as supported by classical circuit theory.
It is worth noting that alternative data-driven approaches, including machine learning and heuristic optimization methods, have been widely adopted to fit experimental EIS data [18]. These methods are often tailored to match Nyquist or Bode plots. However, they typically do not yield a dynamic model in state-space form, nor do they ensure structural properties such as passivity or physical realizability. In contrast, our approach aims to derive reduced-order models that preserve such properties and are suitable for simulation and control applications.
The theoretical basis for using ladder and Foster structures to approximate electrochemical impedance can be traced back to transmission line models derived from the Nernst–Planck and Poisson equations, as discussed in classical works on fixed-component equivalent circuits [19]. Recent analytical developments of the Blocked-Diffusion Warburg Impedance have extended the modeling to incorporate frequency dispersion effects, leading to transfer functions capable of representing both straight-line and constant-phase behavior in the Nyquist domain [20]. These formulations have also been implemented in Simulink environments for the simulation of impedance and output voltage responses of lithium-ion batteries. An earlier contribution addressed similar transfer function modeling for time-domain voltage prediction based on silicon nanowire and NiMH battery measurements [21].
Reduced-order models are particularly relevant in the context of battery monitoring, where mid-frequency impedance responses can be used for fast estimation of capacity degradation [22]. In other approaches, State Of Charge (SoC) tracking has been performed by combining Randles-type equivalent circuits fitted to Electrochemical Impedance Spectroscopy (EIS) data with machine learning techniques, as demonstrated in [23]. The use of electrical equivalent-circuit models remains a standard practice in simulating the dynamic behavior of electrochemical systems. A recent comparative study on commercial 18650 lithium-ion cells demonstrated how different equivalent models, based on impedance spectroscopy, affect simulation accuracy and design trade-offs [24]. In a broader context, deviations from the ideal Warburg response have been analyzed in supercapacitor electrodes, where low-frequency diffusion dynamics and the transition from capacitive to diffusive behavior were investigated using reflexive impedance models and physically grounded circuit representations [1]. For a theoretical and practical overview of EIS and its application in electrochemical characterization, see [25]. The diagnostic capabilities of impedance models are further enhanced by the use of pseudocapacitance-derived indicators, which offer rapid assessment of device health in batteries and supercapacitors. Novel diagrammatic tools based on these concepts have been proposed for real-time monitoring and failure diagnosis, especially in the context of lifetime testing under varying charge/discharge conditions [26].
In this contribution, starting from the previous considerations, a class of reduced-order models is proposed, in accordance with the peculiarities of Warburg diffusion devices, which are characterized as PR Systems [27]. Therefore, from a rational transfer function of a high-order system, which is just an approximation of the transcendental Warburg impedance, a Riccati-based Balanced Representation is proposed. The characteristic values of the system are then considered as a measure of each state variable, allowing for the identification of only a few significant state variables and enabling the derivation of reduced-order models in the time domain.
The paper is organized as follows. In Section 2, the transmissive Warburg diffusion is discussed, and the classical model is introduced. Section 3 presents a general overview of MOR strategies, including the approach adopted in this work. Section 4 provides the details of the MOR technique based on the Riccati Equation balancing strategy. The results of the various reduced-order models are reported in Section 5. The discussion refers to models operating at low frequencies. Conclusive remarks are given in the final section, where future research perspectives are also proposed. Appendix A includes the MATLAB R2024b code used to implement the proposed approach.
2. Warburg Impedance Models (WIMs)
2.1. Background and Models
The main features of the WIMs pertain to mixed ionic–electronic conductors operating under specific conditions [4]. These phenomena arise in electrochemical cells where an ionic species is electroactive at both electrodes, a behavior closely resembling that of ion-exchange membrane systems, as found in supercapacitors, fuel cells, and rechargeable-battery components. WIMs are typically defined by their operating frequency range.
One commonly cited model is the Transmissive Finite-Length Diffusion Warburg (TFLW) [1], whose impedance function is given by
The impedance of finite-length diffusion with a reflective boundary, termed the Blocked-Diffusion Warburg Impedance (BDWI), is given by the following function:
Respectively, in (1) and (2), the following definitions hold: is the characteristic diffusion resistance for the diffusion process , and is the diffusion time constant.
There are specific relationships between the electrical parameters and the chemical parameters governing the electrochemical diffusion process, as described by the Nernst–Planck equation. For example, if we consider an electrochemical system of length L, with D as the diffusion coefficient, the time constant is .
The behavior of the element must be characterized over the full frequency range; in particular, low-frequency dynamics have attracted considerable interest in recent literature [1,2,20] in various processes:
- Cell membranes [25];
- Forster-Cyanidin systems [21];
- Solid oxide fuel cells [26];
- Li-ion batteries [8,9,24].
The model expressed in Equation (2) indeed expresses an ideal capacitive effect at the electrode-blocking interface in the low-frequency impedance [1].
Frequency-domain studies for this class of components have been widely conducted using the EIS technique. In many experimental datasets, it appears that both the models expressed in (1) and (2) are insufficient to match the data [2,4].
Therefore, a generalized Warburg model applicable to both (1) and (2) has been introduced. It involves adding a further parameter in the previous equations by considering instead of , with .
The physical motivation is to account for non-uniform diffusion along multiple paths within the system. This leads to models of noninteger order. This issue was also noted in [28,29], who referred to the process as an S-transfer characterization by dissipation in a “Minkowski sausage” at the electrode–electrolyte interface, resulting in higher fractality and, therefore, a dynamical noninteger-order system.
Under these considerations, although several low-order equivalent circuits have been proposed to approximate both Equations (1) and (2), the need for a general strategy to characterize the appropriate circuit order for the system has become evident.
In particular, the approximation techniques must account for the peculiarities of the original system. Furthermore, the infinite pole–zero maps of the system must be accurately evaluated to provide the necessary information for reduced-order modeling techniques.
In this discussion, we focus on the model in (1), which can also be generalized to the model in (2). The approximation strategies presented here will be used to obtain finite-order models for noninteger-order integrators and differentiators, which are of primary importance in the analysis of Generalized Transmissive Finite-Length Warburg (GTFLW) and Generalized Blocked-Diffusion Warburg Impedance (GBDWI) systems [2]. The objective is to optimize performance in the low-frequency regime.
2.2. Adopted Model
Let us consider the bipole in Figure 1.
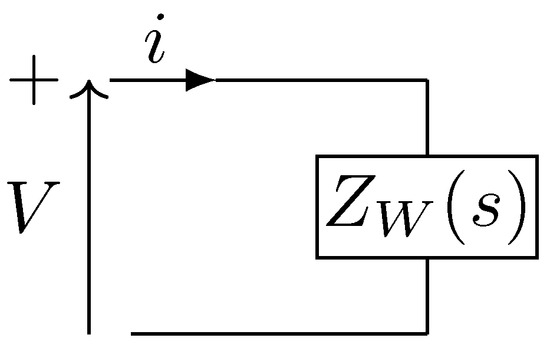
Figure 1.
Bipole representation with input voltage V and impedance .
Where is given by expression (1). It is given by a transcendental transfer function with an infinite number of poles and zeros that can be rewritten as
Approximation of Weierstrass Product Expansion
Let us consider expression (3), where both the zeros and the poles can be derived by obtaining, respectively, the infinite roots of the numerator and of the denominator; the zeros are given by
while the poles are
therefore, it is
where the subscript norm denotes the normalized form of the Warburg impedance transfer function.
Let us now introduce the scaled Laplace variable
which leads to the normalized transfer function
with zeros
and poles
then, truncating the infinite product to a finite number of terms, a reduced-order model of the normalized transfer function is obtained as
where the constant K is defined as
Theorem 1.
The finite dimensional system (11) is PR and Negative Imaginary.
Proof of Theorem 1.
Let us consider the zeros in (9) and the poles in (10). Zeros and poles are interlaced, which means that
This is proved by noting that the following chain of inequalities holds for every n:
The interleaving property assures that the system is PR and each residual is positive. System (11) is also called a relaxation system. □
Remark 1.
A system with positive residuals and distinct poles is Imaginary Negative. This means that the imaginary parts of result in .
The adopted strategy aims to achieve optimal low-frequency performance and to ensure that the reduced-order model is a PR relaxation system. In this case, the Negative Imaginary property will also be maintained. In the next section, the adopted strategy, based on PR System concepts, will be presented.
2.3. Mittag-Leffler Model
The Warburg impedance is widely used to describe the frequency-dependent behavior of electrochemical systems in which diffusion processes are dominant. A classical analytical representation of this impedance is given by an infinite series expansion involving characteristic relaxation times. Among the several formulations proposed in the literature, the Mittag-Leffler model stands out for its compact representation and analytical tractability.
Let us consider the Mittag-Leffler series model of the Warburg impedance, expressed as follows:
where and are the characteristic resistance and time constant, respectively. Notably, the poles of the system lie on the negative real axis and follow the pattern of the Weierstrass expansion used in the formulation of Mittag-Leffler functions, as introduced in (10).
This formulation allows one to model the diffusion-related impedance as a sum of first-order terms, each associated with a different mode of the system. Such a structure is particularly advantageous when considering MOR strategies, since it facilitates the identification of dominant dynamics and enables truncation with minimal loss of accuracy.
In the following section, we shall exploit this structure to derive a reduced-order approximation of the Warburg impedance that preserves the essential features of the original model while drastically reducing the computational burden.
The adoption of the Mittag-Leffler model is further motivated by its favorable structural and numerical properties. Unlike alternative formulations based on direct Foster expansions or Padé approximations, the Mittag-Leffler representation provides a compact sum of first-order dynamics with real and negative poles, each of which can be directly interpreted in terms of relaxation processes. This structure is inherently compatible with PR System theory and is particularly suited for the application of Riccati-based MOR techniques. In addition, the Mittag-Leffler model supports physically meaningful realizations through RC ladder networks, making it not only analytically tractable but also suitable for implementation and interpretation. These features make the Mittag-Leffler model clearly preferable over other representations, which may fail to preserve essential system properties such as positive realness, passivity, or relaxation structure.
3. Model Order Reduction Strategy
Let us consider the Mittag-Leffler series model of the Warburg impedance, expressed in (14). A graphical block diagram representation of this model is provided in Figure 2. The structure highlights the scalar gain , followed by a parallel connection of rational terms corresponding to different orders n. Each term is associated with a dynamic block of the form , whose outputs are then summed to produce the impedance response .
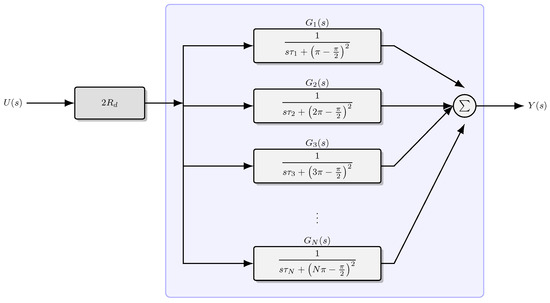
Figure 2.
Block diagram representation of the Mittag-Leffler impedance model in Equation (14), where denotes the n-th elementary diffusive term and is a common gain factor.
The proposed MOR technique is based on a different approach compared to those commonly reported in the literature. Typically, MOR methods refer to the block diagram in scheme 1 (Figure 3), where a suitable reduced-order model of is obtained by selecting a limited number of elements from the series, thereby obtaining . In contrast, the proposed approach, illustrated in scheme 2 (Figure 4), considers a large number N of terms and then applies a strategy to approximate the model . In particular, taking into account the property of , a method based on the Riccati Balanced technique is adopted to obtain, as the MOR, a transfer function . The selection of the order of the reduced model r can be guided by an error analysis derived from truncation-based balanced methods.
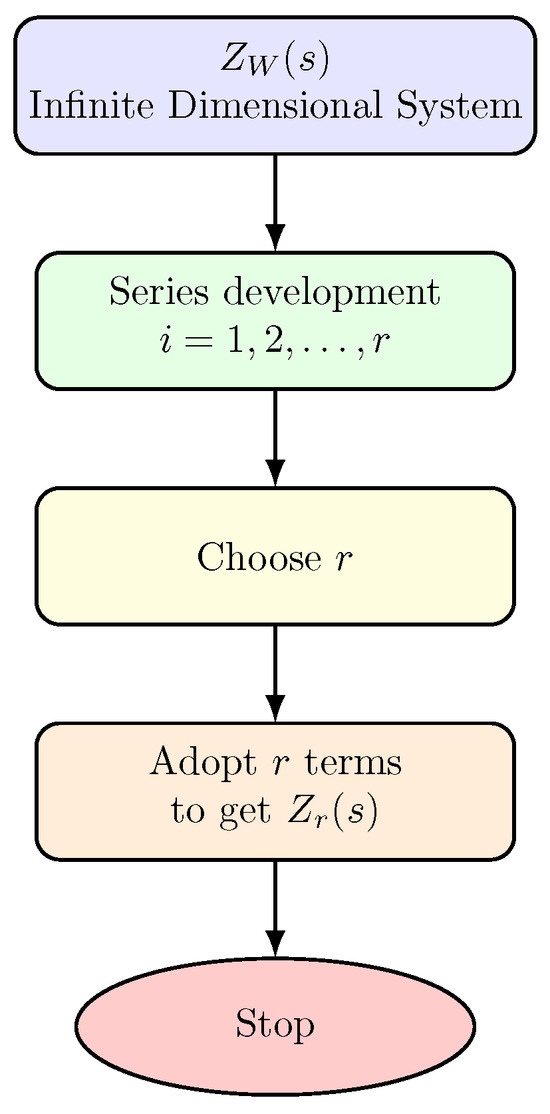
Figure 3.
Block scheme 1: classical MOR approach applied directly to the Warburg model.
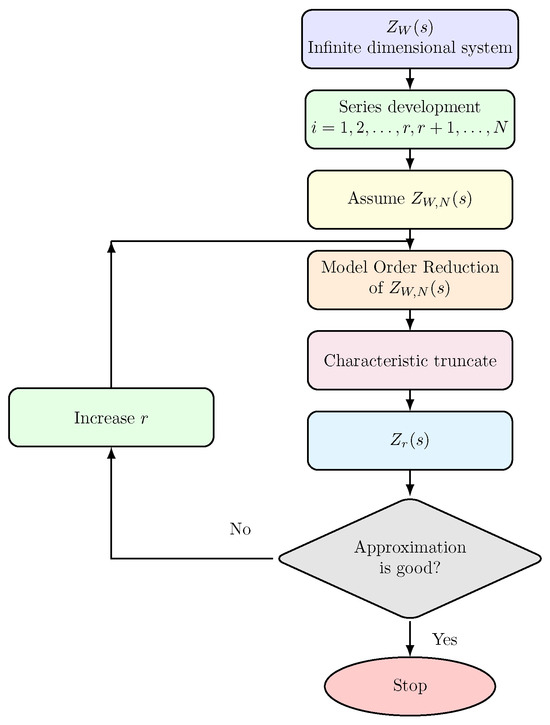
Figure 4.
Block scheme 2: proposed approach using balanced reduction of the approximated model.
In particular, it is possible to determine the reduced order r by imposing a bound on the approximation error between the original (transcendental) model and its truncated representation. A suitable metric for this purpose is the -norm of the error system, which, for the Mittag-Leffler formulation, can be estimated by the following expression:
This formula quantifies the deviation between the infinite series and its truncated counterpart. For instance, choosing yields an error bound of approximately . Therefore, given a desired maximum error threshold, it is possible to compute the minimum value of N that satisfies the inequality .
Importantly, this selection criterion does not depend on the specific parameters of the physical system under consideration, but is instead systemic and intrinsic to the mathematical structure of the Mittag-Leffler expansion. It is remarked that the same procedure can also be applied to the Weierstrass representation.
In the following section, we describe how a further reduction of the system order can be achieved using the PR balanced truncation technique based on Riccati equations. Subsequently, in Section 5, we will show how the order of this second-stage reduction can also be selected based on analogous error bound considerations.
4. PR System Based on Riccati Equation Balanced Technique
Starting from the transfer function expressed in relation (11), a minimal-form state-space realization can be obtained by taking terms [30]. This yields a system of order , represented by the realization matrix
Accordingly, the associated transfer function is given by
Being the system PR, the two Riccati equations from the PR Lemma,
and
admit stabilizing, Positive Definite solutions, denoted respectively by and .
Remark 2.
The Riccati Equation Balanced Representation of the PR System (16) given as
has the property that the two Riccati Equations (18) and (19) in the representation (20) admit diagonal, Positive Definite solutions:
where are the so-called characteristic values of (16), which are non-negative invariants of the system [30].
The diagonal terms are ordered in descending order. Each characteristic value of the system reflects how much each state variable in (20) contributes to passivity (positive realness). That is, if the following holds:
matrices can be partitioned as follows:
with .
This means that instead of , a reduced-order model transfer function can be adopted to represent the system as follows:
This transfer function is guaranteed to have the structural properties of the original one, which means that it is a Relaxation Negative Imaginary PR transfer function.
The state-space representation of the reduced-order system is given by
In this way, a direct truncation procedure is adopted. It means neglecting the contribution of the subsystem
Therefore, the state variable is completely neglected. Moreover, let us consider the complete equations of the Balanced Representation (23)
Let us assume (not ), it is therefore obtained from (27b)
Including this one in the (27a) and in (27c) results in
From them, the reduced-order model is derived:
which leads to the reduced-order transfer function
Remark 3.
The error bound between the full-order and reduced-order systems in terms of the norm is represented by the following expression:
where the error number quantifies the approximation of the reduced-order PR System, as the sum of the discarded PR characteristic values.
The peculiarity of this approach is that the characteristic values are preserved. Moreover, it exactly matches the steady-state response of the original system, thereby ensuring optimal low-frequency performance [31]. Our next results are based on model (31).
5. Reduced-Order Models Results
Before discussing the results, the following remarks are due. The obtained models are normalized both in amplitude and in time referring to the impedance model of expression (8) and to the normalized frequency given in (7).
The strongly recommended reduced-order technique is that of Section 4 that will guarantee the structural property of the system regarding both the passivity and the imaginary negative behavior.
Let us consider the norm error bound expressed in the following relation:
Assuming we evaluate the approximation error between the truncated and N-order systems, we define
The bound of interest is guaranteed to satisfy
if and only if the following conditions hold:
These conditions are satisfied due to the structural properties of , which ensure passivity and boundedness in the frequency domain.
In order to select the appropriate reduced order r for the final PR-balanced model, a quantitative criterion is adopted based on the decay profile of the characteristic values derived from the balanced realization. Specifically, the reduction error is estimated through the expression
where d denotes the feedthrough term of the system, which, in the SISO case considered, reduces to a scalar quantity.
Figure 5 illustrates how the approximation error, quantified by the upper bound , varies as a function of the reduced model order r. The plot clearly shows that the contribution of discarded characteristic values becomes negligible for , due to the rapid decay of the sequence. This highlights that meaningful approximations can be achieved with only a few dominant components, supporting the selection of low-order models in subsequent analyses.
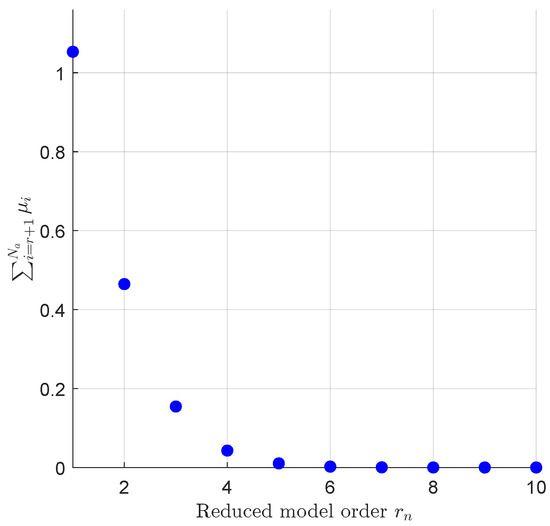
Figure 5.
Evaluation of the model reduction error as a function of the reduced model order r.
Note that this plot refers to the normalized case with . Consequently, if a certain value of the normalized error is observed in the graph, the actual bound on the error, computed as , is guaranteed to be satisfied for any , due to the inverse proportionality of the bound with respect to d.
By inspecting the graph, the most significant reduced orders are identified as and . These two values represent a good compromise between model complexity and approximation quality, and have therefore been selected for the comparative analyses presented in the following sections.
This procedure ensures a principled and transparent selection of the final model order, balancing approximation accuracy and complexity, while preserving the structural properties guaranteed by the PR-balanced technique described in Section 4.
In the following Figure 6, the 3D Nyquist plot is reported, showing the frequency behavior of the transcendental model, the model with , and the reduced-order models with and .
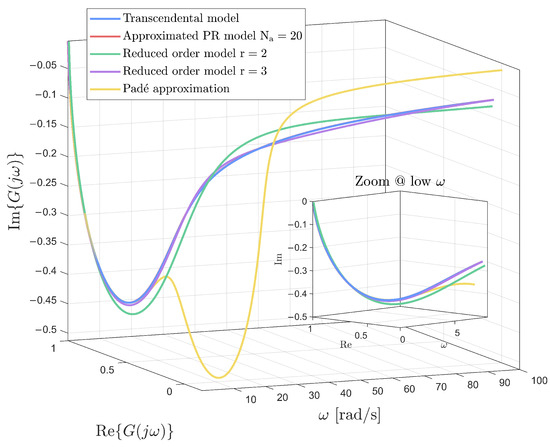
Figure 6.
Three-dimensional Nyquist plot of the transcendental model, PR-based approximations, and Padé model.
The yellow line, in the same plot, represents the frequency response of the third-order Padé-approximated model with transfer function
The 3D Nyquist plot provides an effective visual tool to qualitatively assess the behavior of the reduced-order models, especially in the low-frequency region where Warburg-type dynamics are most relevant. This graphical approach supports the consistency of the approximation and complements the quantitative performance indicators discussed in the manuscript. In particular, the trajectories of the second- and third-order reduced models are displayed, as they represent a good compromise between complexity and fidelity. While higher-order models may further reduce the approximation error, their Nyquist trajectories largely overlap with those of lower-order models, making them less informative in this context. For this reason, the second-order and third-order models are selected for illustration, in line with the broader objective of deriving compact, control-oriented representations where low-order realizations are often preferable [1].
The reduced-order models both match the original model at low frequencies, as indicated in the figure. The error bound with respect to the model of order is respectively given as
In Figure 7, a plot of the same type as the previous one is shown, this time representing the comparison with the open-loop unbalanced realization. In this case, the reduced-order models are not guaranteed to preserve the structural properties of the original system. By comparing the two Nyquist plots, it can be observed that the reduction obtained through the PR-based technique closely matches the full-order model in the low-frequency region (Figure 6), a behavior that is not maintained when using the open-loop reduction approach (Figure 7).
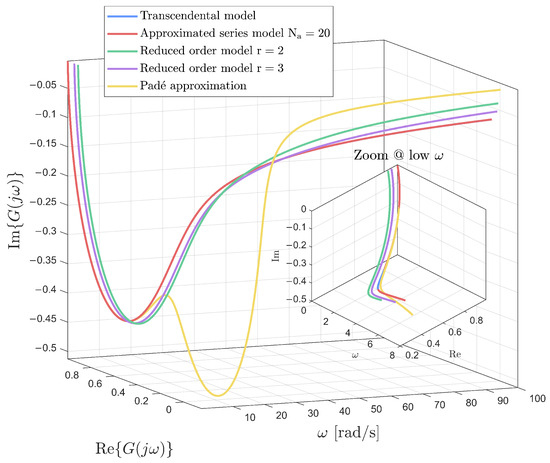
Figure 7.
Three-dimensional Nyquist plot of the transcendental model, series approximations, and Padé model.
Figure 6 and Figure 7 illustrate the Nyquist behavior of the considered reduced-order models in comparison with the non-rational benchmark. The Padé approximation (yellow) exhibits a significant deviation from the reference (light blue), especially in the low-frequency region, where the Warburg effect dominates. On the other hand, the PR-based reduced models of order 2 (green) and 3 (violet) better follow the characteristic shape of the benchmark curve, particularly in Figure 6, where the balanced realization preserves low-frequency dynamics more effectively.
Figure 8 compares the step responses of four models with different levels of approximation. The step response is particularly informative for analyzing low-frequency behavior and cumulative effects. The reference curve corresponds to the original non-rational model, whose time-domain response is obtained via numerical Laplace inversion using the Euler algorithm. A truncated series approximation with terms is included to represent the full-order rational model derived from modal decomposition. In addition, two reduced-order models with orders and are shown, both obtained through the PR Riccati-balanced realization and selected according to the characteristic value truncation criterion discussed previously.
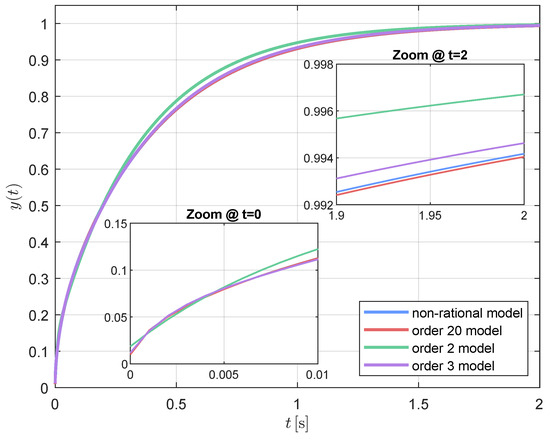
Figure 8.
Step response comparison for the transcendental model, model with order , and reduced-order PR models with and .
The models considered in our comparative analysis are summarized in Table 1. In addition to reporting structural information such as the number of poles and zeros, two performance indices have been computed for each model based on their step response. These are the Integral of Squared Error (ISE) and the Integral of Absolute Error (IAE), defined respectively as
where denotes the step response of the non-rational transcendental model (used as reference), and is the response of each approximated model.

Table 1.
Comparison of the considered models in terms of complexity, structure, and performance indices.
Table 1 summarizes the main characteristics of all the approximations in terms of implementation complexity, and integral performance indices (ISE and IAE). The third-order PR model achieves the best compromise between accuracy and complexity, clearly outperforming the series-truncated alternatives while maintaining a low computational burden.
In Figure 9, the norm of the error between the normalized transcendent model and the reduced-order models are shown. In particular, the blue curve represents the error obtained using the proposed balanced truncation approach, while the red curve shows the error resulting from direct truncation of the series. It is clearly shown that the proposed method yields a significantly lower error for each model order compared to the direct truncation strategy.
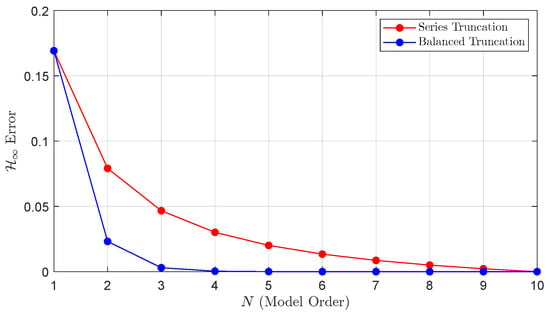
Figure 9.
Comparison of H∞ errors for reduced models.
For these reasons, the third-order model obtained via PR-based balanced truncation is selected as the most suitable approximation. Its transfer function is given from (32) as
It is a relaxation system with non-negative residues. The electrical circuit representation shown in Figure 10 provides an equivalent implementation of the third-order model previously analyzed. The circuit is constructed using a ladder network composed of resistors and capacitors arranged to reproduce the dynamical behavior of the reduced-order transfer function (41).
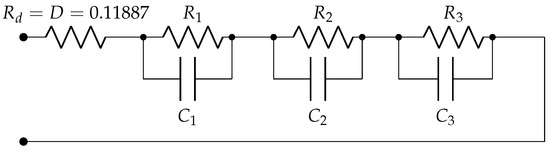
Figure 10.
Electrical circuit representation.
Each block results in
and also
The denormalized values of the electrical parameters are obtained as follows. For the resistors (in ohm),
and for the capacitors (in farad),
To support the practical applicability of the proposed reduced-order model, we performed a comparison with experimental data taken from the work in [32], where the impedance spectrum of lithium-ion diffusion in solid polymer electrolytes is reported after long-term storage. The selected data refer to the frequency range in which the relaxation dynamics are governed by a Warburg-type behavior, not yet influenced by fractal crystallization phenomena. In order to perform the comparison, the reduced model in Equation (41) has been denormalized in both amplitude and frequency by applying the scaling parameters and . The resulting Nyquist plot is shown in Figure 11, where the continuous line corresponds to the denormalized model response and the markers represent the experimental measurements. We also report in Table 2 the numerical values of the experimental data points used to generate the figure extracted from [32]. The fitting confirms that the third-order reduced model captures the dominant impedance behavior with a satisfactory degree of accuracy in the selected operating range.
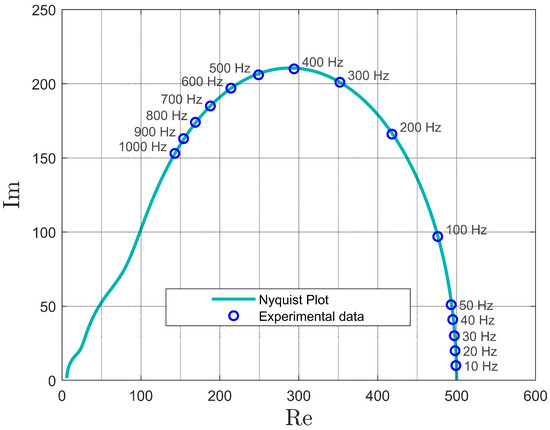
Figure 11.
Nyquist plot of the proposed reduced-order model and experimental data used for fitting validation.

Table 2.
Experimental impedance data used for the fitting shown in Figure 11.
6. Conclusions
In this contribution, the approximation of the Warburg diffusion device is discussed. In particular, the Transmissive Finite-Length Warburg (TFLW) model is considered. The technique adopted to obtain structurally consistent electrical models is based on the PR Riccati characteristic values.
The approach we have taken into account focuses on low-frequency approximation. The resulting models are compared with other reduced-order models obtained using classical techniques. To visualize the frequency behavior, the 3D Nyquist plot, commonly used in the field of Electrochemical Spectroscopy, is adopted.
The proposed technique is quite general and can be directly applied to more complex Warburg diffusion models, such as the Generalized TFLW (GTFLW) and the Generalized Bounded Diffusion Warburg Type (GBDWT), which involve fractional-order model approximations.
This paper represents a further step toward the development of low-order models for innovative devices in power and energy-saving applications, through a system control engineering approach that enhances the structural precision and reliability of the reduced-order models. Moreover, this study introduces a new perspective in device characterization, showing how complex diffusion-based impedance behaviors can be approximated by finite-dimensional models using system theory in the context of control and electrical network modeling. In particular, a different procedural approach to MOR is introduced, starting from the approximation of the transcendental transfer function. The reduced-order model is obtained in two steps: first, by combining a sufficient number of terms of the expansion, and then by selecting the reduced model based on the approximation error performance. The proposed approach allows for the derivation of a third-order linear time-invariant reduced model, which exhibits better performance compared to the one obtained through the classical procedure. This is demonstrated both through 3D Nyquist plots and by evaluating the quantitative norm of the error. A three-dimensional Nyquist plot was used to qualitatively assess the consistency of the reduced-order model with theoretical expectations. This visualization confirms the preservation of the low-frequency dynamics and the Mittag-Leffler structure. While already informative, the analysis could be complemented by advanced identification techniques to further consolidate the model validation. In this work, a further comparison with experimental data from the literature was conducted to validate the proposed reduced-order model and performance indices such as the ISE and the IAE were computed to provide a quantitative assessment of the approximation quality across different model orders. These metrics confirm the favorable trade-off offered by the third-order PR-based model. Finally, an electrical circuit representation based on the Foster ladder scheme is provided for the third-order reduced model.
Author Contributions
Conceptualization, L.F.; methodology, L.F. and G.G.; software MATLAB R2024b, G.G.; validation, L.F. and G.G.; formal analysis, L.F. and G.G.; investigation, L.F. and G.G.; resources, L.F.; data curation, G.G.; writing—original draft preparation, L.F. and G.G.; writing—review and editing, L.F. and G.G.; visualization, G.G.; supervision, L.F.; project administration, L.F. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Luigi Fortuna was employed by the company STLab s.r.l. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BDWI | Blocked-Diffusion Warburg Impedance |
| EIS | Electrochemical Impedance Spectroscopy |
| GBDWI | Generalized Blocked-Diffusion Warburg Impedance |
| GTFLW | Generalized Transmissive Finite-Length Warburg |
| ISE | Integral of Squared Error |
| IAE | Integral of Absolute Error |
| MOR | Model Order Reduction |
| NI | Negative Imaginary |
| PR | Positive Real |
| PRBT | Positive Real Balanced Truncation |
| RC | Resistor-Capacitor |
| SoC | State of Charge |
| SPICE | Simulation Program with Integrated Circuit Emphasis |
| TFLW | Transmissive Finite-Length Warburg |
| WIM | Warburg Impedance Model |
Appendix A. MATLAB Code for PR-MOR
This appendix reports the MATLAB code used to perform the MOR of a high-order system representing a rational approximation of the Warburg impedance. The system is defined by a set of real poles and zeros and is converted to state-space form. Then, a balanced realization tailored to passive systems is computed, and reduced models of order 2 and 3 are extracted. The code is organized in a main script, supported by two custom auxiliary functions: PBALR, which computes the PR balanced realization, and CAREPR, which solves the Riccati equations required in the PR balancing process. All functions are fully reported to ensure reproducibility.
Appendix A.1. Main Script
- % MODEL DEFINITION
- N = 20; % Order of the initial model
- D = 0.01; % Feedthrough term of the system
- % Define poles according to the Mittag-Leffler formulation
- for n = 1:N
- p(n) = −pi^2 ∗ (n − 1/2)^2;
- end
- % Construct state-space realization (diagonal A, constant B and C)
- A = diag (p);
- C = sqrt (2) ∗ ones (1, N);
- B = sqrt (2) ∗ ones (N, 1);
- % Perform Balanced Positive Real Riccati Realization
- [S1, Miu] = PBALR(A, B, C, D);
- [AB, BB, CB, D] = ssdata(S1);
- % Compute approximation error for reduced models of order 2 and 3
- E2 = sum(Miu (3:end));
- E3 = sum(Miu (4:end));
- % Reduced models
- S2 = modred (S1, 3:N, ’MatchDC’);
- S3 = modred (S1, 4:N, ’MatchDC’);
- [AB, BB, CB, D] = ssdata (S1);
- [A2, B2, C2, D] = ssdata (S2);
- [A3, B3, C3, D] = ssdata (S3);
- % Impulse responses
- SYS = ss (AB, BB, CB, D); [Y, t] = impulse (SYS);
- SYS2 = ss (A2, B2, C2, D); [Y2, t] = impulse (SYS2);
- SYS3 = ss (A3, B3, C3, D); [Y3, t] = impulse (SYS3);
Appendix A.2. Function PBALR
- function [SYS2, Miu] = PBALR (A, B, C, D)
- % Compute a PR balanced realization
- CC = C;
- n = size (A, 1);
- [PIGREEK,~] = CAREPR (A’, CC’, B’, D);
- [Uc, Sc2, Vc] = svd (PIGREEK);
- T1 = Vc ∗ sqrt (Sc2);
- Atilde = inv (T1)∗A∗T1;
- Btilde = inv (T1)∗B;
- Ctilde = CC∗T1;
- [Pcaretilde,~] = CAREPR (Atilde, Btilde, Ctilde, D);
- [Uo, S2o, Vo] = svd (Pcaretilde);
- T2 = Vo ∗ S2o^(−1/4);
- % Balanced PR Riccati system
- Abil = inv (T2)∗Atilde∗T2;
- Bbil = inv (T2)∗Btilde;
- Cbil = Ctilde∗T2;
- [Pcaretilde,~] = CAREPR (Abil, Bbil, Cbil, D);
- for ii = 1:n
- Miu(ii) = Pcaretilde (ii, ii);
- end
- SYS2 = ss (Abil, Bbil, Cbil, D);
- end
Appendix A.3. Function CAREPR
- function [P, PROVE] = CAREPR (A, B, C, D)
- % Riccati solver for passive systems
- P = 0;
- for e = 1:30
- K = (D+D’)^(−1)∗(C’ − P∗B);
- A1 = A − B∗K’;
- Q = −C’∗(D+D’)^(−1)∗C + ...
- P∗B∗(D+D’)^(−1)∗B’∗P’;
- P = lyap(A1’, −Q);
- end
- PROVE = P∗A + A’∗P + ...
- (C’ − P∗B)∗(D+D’)^(−1)∗(C’ − P∗B)’;
- end
References
- Moya, A. Low-frequency approximations to the finite-length Warburg diffusion impedance: The reflexive case. J. Energy Storage 2024, 97, 112911. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Greenwood, P. Analytical transfer function to simulate the dynamic response of the finite-length Warburg impedance in the time-domain. J. Energy Storage 2022, 55, 105529. [Google Scholar] [CrossRef]
- Nielsen, C.B.; Larsen, P.G.; Fitzgerald, J.; Woodcock, J.; Peleska, J. Systems of systems engineering: Basic concepts, model-based techniques, and research directions. ACM Comput. Surv. (CSUR) 2015, 48, 1–41. [Google Scholar] [CrossRef]
- Lasia, A. Electrochemical impedance spectroscopy and its applications. In Modern Aspects of Electrochemistry; Springer: Berlin/Heidelberg, Germany, 2002; pp. 143–248. [Google Scholar]
- Orazem, M.E.; Ulgut, B. On the Proper Use of a Warburg Impedance. J. Electrochem. Soc. 2024, 171, 040526. [Google Scholar] [CrossRef]
- Hallemans, N.; Howey, D.; Battistel, A.; Saniee, N.F.; Scarpioni, F.; Wouters, B.; La Mantia, F.; Hubin, A.; Widanage, W.D.; Lataire, J. Electrochemical impedance spectroscopy beyond linearity and stationarity—A critical review. Electrochim. Acta 2023, 466, 142939. [Google Scholar] [CrossRef]
- Ospina Agudelo, B.; Zamboni, W.; Monmasson, E. A Comparison of Time-Domain Implementation Methods for Fractional-Order Battery Impedance Models. Energies 2021, 14, 4415. [Google Scholar] [CrossRef]
- Liu, Z.; Han, K.; Zhang, Q.; Li, M. Thermal safety focus and early warning of lithium-ion batteries: A systematic review. J. Energy Storage 2025, 115, 115944. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, B.; Liu, Y.; Sun, Z.; Chen, S.; Guo, B.; Huang, J.; Chen, Y.; Fan, G.; Zhang, X. A reduced-order electrochemical battery model for wide temperature range based on Pareto multi-objective parameter identification method. J. Energy Storage 2024, 84, 110876. [Google Scholar] [CrossRef]
- Masoudi, R.; Taghavipour, A.; Azad, N.; McPhee, J. A Robust Model Order Reduction Scheme for Lithium-Ion Batteries in Control-Oriented Vehicle Models. J. Electrochem. Soc. 2024, 171, 053501. [Google Scholar] [CrossRef]
- Xie, Y.; Xu, J.; Chengwei, J.; Zhenyu, J.; Mei, X. A novel reduced-order electrochemical model of lithium-ion batteries with both high fidelity and real-time applicability. Energy 2024, 306, 132425. [Google Scholar] [CrossRef]
- Li, W.; Huang, Q.A.; Bai, Y.; Wang, J.; Wang, L.; Liu, Y.; Zhao, Y.; Li, X.; Zhang, J. Model reduction of fractional impedance spectra for time–frequency analysis of batteries, fuel cells, and supercapacitors. Carbon Energy 2023, 6. [Google Scholar] [CrossRef]
- Li, Y.; Karunathilake, D.; Vilathgamuwa, D.M.; Mishra, Y.; Farrell, T.W.; Choi, S.S.; Zou, C. Model Order Reduction Techniques for Physics-Based Lithium-Ion Battery Management: A Survey. IEEE Ind. Electron. Mag. 2022, 16, 36–51. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic Equivalent Circuit Model to Estimate State-of-Health of Lithium-Ion Batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
- Li, H.; Jia, H.; Xiao, P.; Jiang, H.; Chen, Y. Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles. Energies 2025, 18, 2144. [Google Scholar] [CrossRef]
- Guran, I.C.; Florescu, A.; Perişoară, L.A. SPICE model of a passive battery management system. IEEE Access 2024, 12, 4000–4014. [Google Scholar] [CrossRef]
- Nekahi, A.; Dorri, M.; Rezaei, M.; Bouguern, M.D.; Madikere Raghunatha Reddy, A.K.; Li, X.; Deng, S.; Zaghib, K. Comparative issues of metal-ion batteries toward sustainable energy storage: Lithium vs. sodium. Batteries 2024, 10, 279. [Google Scholar] [CrossRef]
- Huang, S.; Lin, N.; Wang, Z.; Zhang, Z.; Wen, S.; Zhao, Y.; Li, Q. A novel data-driven method for online parameter identification of an electrochemical model based on cuckoo search and particle swarm optimization algorithm. J. Power Sources 2024, 601, 234261. [Google Scholar] [CrossRef]
- Brumlev, T.R.; Buck, R.P. Transmission line equivalent circuit models for electrochemical impedances. J. Electroanal. Chem. Interfacial Electrochem. 1981, 126, 73–104. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Greenwood, P. Analytical transfer function for the blocked-diffusion warburg impedance with frequency dispersion. Simulation of the impedance spectrum and voltage response of a lithium-ion battery. Future Batter. 2025, 5, 100051. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Martínez-Zárate, I. Analytical transfer function for the simulation of the frequency-domain and time-domain responses of the blocked-diffusion Warburg impedance. J. Energy Storage 2023, 72, 108676. [Google Scholar] [CrossRef]
- Thomas, H.; Weatherspoon, M.H. Capacity and State-of-Health Prediction of Lithium-Ion Batteries Using Reduced Equivalent Circuit Models. Batteries 2025, 11, 162. [Google Scholar] [CrossRef]
- Buchicchio, E.; De Angelis, A.; Santoni, F.; Carbone, P.; Bianconi, F.; Smeraldi, F. Battery SOC estimation from EIS data based on machine learning and equivalent circuit model. Energy 2023, 283, 128461. [Google Scholar] [CrossRef]
- Estaller, J.; Kersten, A.; Kuder, M.; Thiringer, T.; Eckerle, R.; Weyh, T. Overview of battery impedance modeling including detailed state-of-the-art cylindrical 18650 lithium-ion battery cell comparisons. Energies 2022, 15, 3822. [Google Scholar] [CrossRef]
- Panchal, K.; Bhakar, K.; Sharma, K.S.; Kumar, D.; Prasad, S. Review on electrochemical impedance spectroscopy: A technique applied to hollow structured materials for supercapacitor and sensing applications. Appl. Spectrosc. Rev. 2025, 60, 30–55. [Google Scholar] [CrossRef]
- Kurzweil, P.; Scheuerpflug, W.; Schell, C.; Schottenbauer, J. Useful Quantities and Diagram Types for Diagnosis and Monitoring of Electrochemical Energy Converters Using Impedance Spectroscopy: State of the Art, Review and Outlook. Batteries 2024, 10, 177. [Google Scholar] [CrossRef]
- Anderson, B.D.; Vongpanitlerd, S. Network Analysis and Synthesis: A Modern Systems Theory Approach; Courier Corporation: Mumbai, India, 2013. [Google Scholar]
- Le Méhauté, A. Fractal Geometries Theory and Applications; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Arena, P. Nonlinear Noninteger Order Circuits and Systems: An Introduction; World Scientific: Singapore, 2000; Volume 38. [Google Scholar]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Fortuna, L.; Muscato, G.; Nunnari, G. Closed-loop balancing and singular perturbation: A new result. Electron. Lett. 1991, 27, 1193–1194. [Google Scholar] [CrossRef]
- Hamaide, T.; Guyot, J.; Mehaute, A.L.; Crepy, L.; Marcellin, G. Experimental analysis of the scaling properties of solid polymer electrolytes upon five years of storage: From fractal crystallization to carrier relaxation. J. Electrochem. Soc. 1989, 136, 3152. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).