Resilience Enhancement for Distribution Networks Under Typhoon-Induced Multi-Source Uncertainties

Abstract

The increasing prevalence of extreme weather events poses significant challenges to the stability of distribution networks (DNs). To enhance the resilience of DNs against such events, a typhoon-oriented resilience framework for DNs is proposed that incorporates multiple sources of typhoon uncertainty. First, component failure probability is modeled by tracking time-sequential variations in typhoon landfall parameters, trajectory, and intensity, thereby improving the quantitative estimation of typhoon impacts. Then, the integrated component failure probability and the importance factor of bus load under disaster are combined and hierarchical analysis is performed to achieve the vulnerability identification for DNs. Next, based on the vulnerability identification results, a resilience enhancement model for DNs is constructed through the strategy of coordinating line reinforcement and energy storage configuration, and the resilience optimization scheme that takes into account the system resilience enhancement effect and economy is obtained under the optimal investment cost. Finally, analysis and verification are conducted in the IEEE 33-bus system. The results indicate that the proposed method can reduce the load loss cost of the system by 5.112 million and 0.2459 million, respectively.

1. Introduction

Driven by climate change and human activities, extreme weather events have grown more frequent and severe, these trends undermine the stability and security of distribution networks (DNs) [1,2]. The impact of typhoon disasters on DNs is extremely prominent [3]. For instance, in 2015, Typhoon Rainbow made landfall in Zhanjiang, Guangdong Province, with strong wind and widespread rainfall having a significant impact on the local power grid, with a loss load of 724 MW, affecting 400,000 power users. Super typhoon Meranti made landfall in Xiamen, Fujian Province in 2016, as one of the strongest tropical cyclones in the world, Meranti brought unprecedented damage to Xiamen’s DNs [4]. Therefore, improving the resilience of DNs to extreme typhoon disasters is an important task to ensure the safe and stable operation of DNs.

To enhance the resilience of DNs, the effective modelling of disasters is required to quantify the impact on DNs, which in turn leads to targeted resilience measures. While prior research has largely focused on uncertainties in disaster-triggering factors, the variability inherent in typhoon trajectories and landfall characteristics remains underexplored [5,6]. The simplified model viewed the typhoon trajectory as a straight line, and the wind speed at different points in DNs could be quantified based on the typhoon trajectory and the radius of the maximum wind speed [7]. However, this simplified approach ignored the multiple uncertainties of disasters and failed to accurately quantify the impact of disaster. In addition, parameterized wind field models can be used to simulate changes in wind speed at various locations within typhoon wind fields, in order to quantify the intensity of disaster-triggering factors [8]. In [9], a multi-phase and multi-region distribution line fault state uncertainty set was constructed to portray the spatial and temporal characteristics of disaster evolution, as well as the fault uncertainty affecting the lines. The Extra Tree method was applied to predict time series of power outages after typhoon landfall in [8], and a typhoon secondary disaster situation assessment model was established based on disaster intensity and geographical environment [10]. However, the above methods did not consider the uncertainty of the disaster from multiple perspectives. The specified direction of travel, stochastic parameters and other simplified simulation methods will lead to significant deviation in the quantification of disaster-triggering factors, which in turn affects the simulation results for the failure probability of components.

Due to limited resilience resources and investment costs, it is difficult to allocate resilience resources to all elements within DNs. Therefore, vulnerability assessment can enable targeted resilience enhancement and improve the effectiveness and economics of resilience enhancement. Vulnerable line and bus assessment indicators could be defined based on power flow distribution and the operational status of the power grid, and comprehensive vulnerability evaluation can be carried out based on the principle of minimum discriminant information [11]. In [12], a new graph-theoretic approach was proposed to analyze whether faults create saturated cutsets in mesh power networks and thus identify the vulnerability. In [13], vulnerability metrics were defined based on the topology and operational state of DNs to assess the vulnerability of critical components under different distributed generation (DG) output scenarios. Most studies defined vulnerability assessment indicators from the perspective of grid operational status, but ignore the impact of component failure probability. Failure probability reflects the likelihood of system component failure under typhoon disasters and is the core element in the definition of vulnerability indicators.

To reduce the impact of extreme typhoon disasters, resilience-enhancing measures for DNs are essential. Line reinforcement [1], DG [14] and energy storage configuration [15] are effective measures to enhance resilience. A three-stage robust optimization model based on line reinforcement and the installation of distributed power generation strategies at potential fault points can improve the resilience of the distribution system [16]. In [17], a multi-type flexible resource cooperative scheduling method for power supply restoration in DNs was proposed, which realized the co-operation between maintenance teams and mobile energy storage under wind and flood compound disaster scenarios, and completed the transfer of important loads through topology reconfiguration. In addition, configuring mobile energy storage vehicles could form a dynamic microgrid to supply power to disaster-affected areas, thereby reducing load losses caused by power outages [18]. There are many lines in DNs, and it is both difficult and economically unfeasible to reinforce lines individually under a single line reinforcement strategy, and the number and capacity of energy storage configuration in the system are limited, so a single energy storage configuration strategy is ineffective for resilience enhancement.

Therefore, to improve the accuracy of disaster simulation and increase the resilience for DNs, a resilience enhancement method that considers the multiple uncertainties of typhoons is proposed. The key contributions of this paper are summarized as follows:

(1)

Based on the uncertainties of typhoon landing parameters, moving trajectory and disaster-triggering factors, the typhoon disaster simulation is realized and the component failure probability model is constructed to quantify the failure probability of each location in DNs. The proposed method can accurately quantify the impact of the disaster on DNs.

(2)

Novel vulnerability assessment indicators are defined by integrating component failure probability and load importance factors based on the hierarchical analysis, enabling an objective, hierarchical assessment of spatial vulnerability under typhoon impacts.

(3)

A resilience enhancement method coordinating line reinforcement and energy storage configuration is established to improve ability of DNs to withstand disasters. Compared with the non-resilience scheme and the single-resilience scheme, the method proposed in this paper greatly reduces the system’s lost load cost and safeguards the system’s power supply to a greater extent.

The rest of this paper is organized as follows: Section 2 introduces a dynamic modelling method for typhoons that considers multiple uncertainties. Section 3 establishes a resilience enhancement model based on vulnerability identification, which unites line reinforcement and energy storage configuration strategies. Calculus analysis and conclusions are presented in Section 4 and Section 5, respectively.

2. Dynamic Modelling of Typhoon Considering Multiple Uncertainties

The uncertainties of typhoons mainly arises from the landfall parameters, moving trajectory and intensity of disaster-triggering factors. Considering typhoon-induced multi-source uncertainty will improve the accuracy of disaster dynamics modelling. A typical typhoon landfall scenario can be extracted based on the uncertainty of the landfall parameters, which has local typhoon landfall characteristics.

2.1. Uncertainty in Landfall Parameters

The moving direction angle, moving speed and central air pressure difference at the moment of typhoon landfall together constitute a set of typhoon landfall parameters, which can be implemented to simulate the operation of the typhoon after landfall. The typhoon path is dominated by large-scale circulation, and the moving direction angle fluctuations can be regarded as the superposition of multiple random factors, which conforms to the central limit theorem and leads to a normal distribution. The central moving speed is affected by the product effect of multiple factors. For example, an increase in pressure gradient may exponentially accelerate typhoons, which conforms to the characteristics of a lognormal distribution where the product of multiple random variables is logarithmically normal. The pressure difference reflects the strength of a typhoon, and its maximum value is limited by ocean heat capacity, wind shear, etc., which conforms to the threshold effect of Weibull distribution. The process of typhoon intensification is similar to a “chain reaction”, and Weibull’s shape parameters can flexibly fit the different stages of typhoon development.

As shown in Equations (1)–(3), the corresponding parameters were simulated using normal distribution, lognormal distribution and Weibull distribution, respectively [19].

The moving direction angle at the moment of typhoon landfall $\theta (0)$ obeys the normal distribution with a probability density function:

$$f_1(\theta (0))={\displaystyle \frac{1}{\sqrt{2\pi }{\sigma }_{\theta }}}\exp \left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{(\theta (0)-{\mu }_{\theta })}^2}{{{\sigma }_{\theta }}^2}}\right)$$

(1)

where ${\mu }_{\theta }$ is the mean of $\theta (0)$ in the normal distribution. ${\sigma }_{\theta }$ is the standard deviation of the normal distribution.

The central moving speed at the moment of typhoon landfall $v(0)$ obeys the lognormal distribution with a probability density function:

$$f_2(v(0))={\displaystyle \frac{1}{v(0)\sqrt{2\pi }{\sigma }_{\ln v}}}\exp \left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{(\ln v(0)-{\mu }_{\ln v})}^2}{{{\sigma }_{\ln v}}^2}}\right)$$

(2)

where ${\mu }_{\ln v}$ is the mean of $v(0)$ in the lognormal distribution. ${\sigma }_{\ln v}$ is the standard deviation of the lognormal distribution.

The central air pressure difference at the moment of typhoon landfall $\Delta P(0)$ obeys the Weibull distribution with a probability density function:

$$f_3(\Delta P(0))={\displaystyle \frac{\kappa }{\chi }}{\left({\displaystyle \frac{\Delta P(0)}{\chi }}\right)}^{\kappa -1}\exp \left[-{\left({\displaystyle \frac{\Delta P(0)}{\chi }}\right)}^{\kappa }\right]$$

(3)

where $\chi$ is the scale parameter of the Weibull distribution. $\kappa$ is the shape parameter of the Weibull distribution.

Based on the probability density function of each typhoon landfall parameter, several sets of typhoon landfall parameters can be generated by Monte Carlo method [20]. Subsequently, K-means clustering based on the contour coefficient method is used to obtain typical typhoon landfall parameters [21].

2.2. Uncertainty in Typhoon Trajectory Modelling

Existing studies mostly regard the typhoon motion as a straight-line moving path, which has the problem of low accuracy and also affects the calculation accuracy of the subsequent typhoon disaster-triggering factors [22,23]. Therefore, this paper adopts the storm track model to achieve typhoon disaster path derivation, which can achieve real-time simulation of typhoon movement direction and movement speed, and better consider the uncertainty of the typhoon trajectory, so as to achieve accurate modelling of disasters [24].

Based on the storm track model, the change in the natural logarithmic value of the typhoon center’s speed of movement and the change in the angle of direction of movement for the next moment can be determined from the typhoon center’s position, speed of movement and angle of direction of movement at the historical moment, as shown in the following equation [24]:

$$\Delta \ln v(t+1)={\lambda }_1+{\lambda }_2\psi (t)+{\lambda }_3\lambda (t)+{\lambda }_{4}v(t)+{\lambda }_5\theta (t)$$

(4)

$$\Delta \theta (t+1)=k_1+k_2\psi (t)+k_3\lambda (t)+k_{4}v(t)+k_5\theta (t)+k_6\theta (t-1)$$

(5)

where ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_5,k_1,k_2,\dots ,k_6$ are the storm track model parameter. $\psi (t)$ and $\lambda (t)$ are the longitude and latitude of the typhoon center at time $t$, respectively. $v(t)$ is the moving speed of the typhoon center at time $t$. $\theta (t)$ and $\theta (t-1)$ are the moving direction angle of the typhoon center at time $t$ and time $t-1$, respectively.

Therefore, the speed and direction of movement of the typhoon center at time $t+1$ are calculated as follows:

$$v(t+1)=v(t)\exp [\Delta \ln v(t+1)]$$

(6)

$$\theta (t+1)=\theta (t)+\Delta \theta (t+1)$$

(7)

2.3. Uncertainty in the Intensity of Disaster-Triggering Factors

2.3.1. Typhoon Wind Field Simulation

In this paper, the Batts model is used to simulate the typhoon wind field [25]. Due to the different geographical locations of DNs components and the changing location of the typhoon wind field, the intensity of the disaster-triggering factor to which the components are subjected is time-varying. The wind speed disaster-triggering factor is calculated as shown in the following equation:

$$\left\{\begin{array}{c}{V}_{\mathrm{rin}}=V_{R_{\max }}{\displaystyle \frac{R}{R_{\max }}}, R\le R_{\max }\\ V_{rout}=V_{R_{\max }}{({\displaystyle \frac{R_{\max }}{R}})}^{\mathrm{x}}, R>R_{\max }\end{array}\right.$$

(8)

where $V_{\mathrm{rin}}$ and $V_{\mathrm{rout}}$ are the wind speed inside and outside the maximum wind radius, respectively. $R_{\max }$ is the maximum wind radius. $V_{R_{\max }}$ is the maximum wind speed; $R$ is the distance from the typhoon center to the component location. $x$ is the attenuation parameter.

The maximum wind radius and maximum wind speed are modelled as shown in the following equation:

$$\left\{\begin{array}{l}{R}_{\max }=e^{(-0.1239\Delta P^{0.6003}+5.1043)}\\ \Delta P(t)=\Delta P_0-0.675(1+\sin \beta )t\end{array}\right.$$

(9)

$$\left\{\begin{array}{l}{V}_{R_{\max }}=0.865V_{\mathrm{gx}}+0.5V_T\\ V_{\mathrm{gx}}=\mathrm{K}\sqrt{\Delta P}-R_{\max }{\mathrm{\omega }}_1\sin \phi \end{array}\right.$$

(10)

where $\Delta P(t)$ is the central air pressure difference at time $t$. $\Delta P_0$ is the central air pressure difference at the time of typhoon landfall. $\beta$ is the angle between the horizontal direction and the direction of typhoon travel. $V_{\mathrm{gx}}$ is the typhoon cyclone gradient wind speed. $V_T$ is the overall typhoon movement speed. K is the empirical coefficient, which is taken to be 6.72. ${\mathsf{\omega }}_1$ is the angular speed of Earth’s rotation, which is taken to be 0.004178°/s. $\phi$ is the geographical latitude.

2.3.2. Component Failure Probability Model

When a typhoon strikes, strong wind and heavy rain cause great strain on the lines and towers of DNs, causing failure events such as broken lines and collapsed or tilted towers [26]. Therefore, the failure probability of lines and towers caused by the disaster-triggering factors is considered.

(1)

Tower Failure Probability

Typhoon wind damage mainly affects towers, and its failure rate can be quantified by the bending moment $M_{\mathrm{g}}$ on the towers caused by the wind load ${\omega }_{\mathrm{d}}$ on the lines and ${\omega }_{\mathrm{g}}$ on the towers [26]:

$${\omega }_{\mathrm{d}}={\alpha }_{\mathrm{w}}{\mu }_{\mathrm{z}}{\mu }_{\mathrm{sc}}d{l}_{\mathrm{H}}{(\sin \psi )}^2{\displaystyle \frac{V_{\mathrm{in}}^2}{1600}}$$

(11)

$${\omega }_g={\xi }_{\mathrm{w}}{\mu }_{\mathrm{z}}{\mu }_{\mathrm{s}}B{\displaystyle \frac{V_{\mathrm{in}}^2}{1600}}$$

(12)

$$M_{\mathrm{g}}=(({\omega }_{\mathrm{d}}{h}_{\mathrm{g}}+2{\omega }_{\mathrm{d}}{h}_{\mathrm{x}}))(1+m_{\mathrm{g}})+({\omega }_{\mathrm{g}}{\displaystyle \frac{d_0+d_{\mathrm{x}}}{2}}{h}_{\mathrm{g}})({\displaystyle \frac{h_{\mathrm{g}}}{3}}{\displaystyle \frac{2d_0+d_{\mathrm{x}}}{d_0+d_{\mathrm{x}}}})(1+m_{\mathrm{g}})$$

(13)

where ${\alpha }_{\mathrm{w}}$ is the wind pressure inhomogeneity coefficient. ${\mu }_{\mathrm{z}}$ is the wind pressure height variation coefficient. ${\mu }_{\mathrm{sc}}$ is the line body shape coefficient. $d$ is the outer diameter of the line. $l_{\mathrm{H}}$ is the distance from the tower. $\psi$ is the angle between the line and the wind direction. ${\xi }_{\mathrm{w}}$ is the wind vibration coefficient. ${\mu }_{\mathrm{s}}$ is the wind load body shape coefficient. $B$ is the projected area of the tower. $h_{\mathrm{g}}$ is the height of the tower. $h_{\mathrm{x}}$ is the distance from the root of the pole to the cross-burden. $m_{\mathrm{g}}$ is the additional bending moment coefficient. $d_0$ and $d_x$ are the diameters at the top and at the root of the pole, respectively.

The tower flexural strength approximately follows a normal distribution with a failure probability:

$$P_{\mathrm{f}}=P\left\{(M_{\mathrm{A}}-M_{\mathrm{g}})<0\right\}={\displaystyle {\int }_0^{M_{\mathrm{g}}}\frac{1}{\sqrt{2\pi }{\delta }_A}{e}^{-\frac{1}{2}(\frac{M_A-{\mu }_A}{{\delta }_A})}}d{M}_A$$

(14)

where $M_{\mathrm{g}}$, ${\mu }_{\mathrm{A}}$ and ${\delta }_{\mathrm{A}}$ are the maximum bending moment, average bending strength and standard deviation that the tower can withstand, respectively.

(2)

Line Failure Probability

The impact of typhoon rainfall on DNs is mainly concentrated on the power lines. The horizontal pressure $G_{\mathrm{s}}$ and vertical pressure $G_{\mathrm{c}}$ due to raindrops on the lines are calculated as follows [26]:

$$\left\{\begin{array}{l}{G}_{\mathrm{s}}=102{\mathrm{\rho }}_{\mathrm{y}}{S}_{\mathrm{y}}{n}_{\mathrm{y}}{V}_{\mathrm{s}}^3{D}_{\mathrm{s}}^3\\ V_{\mathrm{s}}=\gamma V_{\mathrm{in}}\\ \gamma =\left\{\begin{array}{c}(0.2372H^{-0.5008}-0.0167){({\displaystyle \frac{D_{\mathrm{s}}}{3}})}^{0.8}{\displaystyle \frac{{\alpha }_{\mathrm{f}}}{0.12}}+1, H\le 150 \mathrm{m}\\ 1 , H>150 \mathrm{m}\end{array}\right.\\ n_y=8000\exp (-4.1I^{-0.21}{D}_{\mathrm{s}})\end{array}\right.$$

(15)

$$\left\{\begin{array}{l}{G}_{\mathrm{c}}=102{\mathrm{\rho }}_{\mathrm{y}}{S}_{\mathrm{y}}{n}_{\mathrm{y}}{V}_{\mathrm{c}}^3{D}_{\mathrm{s}}^3\\ V_{\mathrm{c}}=9.4(1-\exp (-0.557D_{\mathrm{s}}^{1.15}))\end{array}\right.$$

(16)

where ${\mathrm{\rho }}_{\mathrm{y}}$ is the rain density. $S_{\mathrm{y}}$ is the normalized curve integral value. $n_{\mathrm{y}}$ is the raindrop spectrum. $V_{\mathrm{s}}$ and $V_{\mathrm{c}}$ are the horizontal and vertical wind speed of the typhoon, respectively. $D_{\mathrm{s}}$ is the diameter of the raindrops. $\gamma$ is the velocity ratio. $H$ is the elevation of the line. ${\alpha }_{\mathrm{f}}$ is the correction coefficient. $I$ is the rainfall intensity.

Line failure probability is quantified by loading under the influence of rainfall:

$$\left\{\begin{array}{c}\overrightarrow{F_{\mathrm{r}1}}=\overrightarrow{F_{\mathrm{s}}}+\overrightarrow{F_{\mathrm{c}}}\\ \overrightarrow{F_{\mathrm{s}}}={\displaystyle {\int }_0^7{G}_{\mathrm{s}}\mathrm{\pi }\mathrm{d}{\mathrm{l}}_{\mathrm{H}}d{D}_{\mathrm{s}}}\\ \overrightarrow{F_{\mathrm{c}}}={\displaystyle {\int }_0^7{G}_{\mathrm{c}}\mathrm{\pi }\mathrm{d}{\mathrm{l}}_{\mathrm{H}}d{D}_{\mathrm{s}}}\end{array}\right.$$

(17)

where ${\overrightarrow{F}}_{\mathrm{s}}$, $\overrightarrow{F_{\mathrm{c}}}$ and $\overrightarrow{F_{\mathrm{r}1}}$ are the horizontal, vertical and total loads on the line from the rainstorm, respectively.

The line tensile strength approximately follows a normal distribution with a failure probability:

$$P_{\mathrm{y}}=P\left\{(F_{\mathrm{y}}-F_{\mathrm{r}1})<0\right\}={\displaystyle {\int }_0^{F_{\mathrm{r}1}}\frac{1}{\sqrt{2\mathrm{\pi }}{\delta }_{\mathrm{y}}}{e}^{-\frac{1}{2}(\frac{F_{\mathrm{y}}-Y_{\mathrm{y}}}{{\delta }_{\mathrm{y}}})}d{F}_{\mathrm{y}}}$$

(18)

where $P_{\mathrm{y}}$ is the line failure probability. $F_{\mathrm{y}}$ is the maximum elastic limit of the line. $Y_{\mathrm{y}}$ and ${\delta }_{\mathrm{Y}}$ are the mean and standard deviation of the maximum elastic limit of the line, respectively.

(3)

Integrated Failure Probability

Compared with the wind field, the scale of a single line of DNs is smaller, so the tower and line within the range of the bus can be regarded as a set of series components. Therefore, the integrated failure probability of DNs under combined wind and rain disasters is shown in the following equation [27]:

$$P_{\mathrm{total}}=1-(1-P_{\mathrm{f}})(1-P_{\mathrm{y}})$$

(19)

where $P_{\mathrm{total}}$ is the integrated failure probability.

3. Vulnerability-Based Resilience Enhancement

Based on the integrated failure probability and the importance factor of bus load, vulnerability identification is achieved, and targeted resilience enhancement is carried out for vulnerabilities. The model is demonstrated in Figure 1.

3.1. Vulnerability Identification

Vulnerable assessments can identify vulnerability in DNs, allowing resilience measures to be targeted in subsequent enhancement. This improves the effectiveness and economy of enhancement.

Based on the integrated failure probability and the importance factor of bus load under the influence of typhoon disaster, the integrated vulnerability index is defined as shown in the following equation:

$$C=k_1{P}_{\mathrm{total}}+k_{2}w$$

(20)

$$k_1+k_2=1$$

(21)

where $C$ is the integrated vulnerability indicator. $k_1$ and $k_2$ are the weighting factor. $w$ is the importance factor of the bus load.

This paper adopts the hierarchical analysis method to determine the weight of each indicator [28]. Firstly, based on the relative importance of each element to the upper level of decision-making, all the constituent elements of each level are compared two by two to form a judgement matrix. Then, the maximum eigenvalue solved according to the judgement matrix is checked for consistency. Finally, the vector of weights of each indicator is calculated. The steps are as follows:

(1)

Creating the judgement matrix

Set $m$ indicator be $x=\{x_1,x_2,x_3,\dots ,x_{\mathrm{m}}\}$. Adopt the 1–9 scale method shown in

Table 1. 1–9 scalar method.

$\mathbf{Scale} {\mathit{a}}_{\mathit{i}\mathit{j}}$	Hidden Meaning
1	Two elements are of equal importance
3	Element i is slightly more important than j
5	Element i is significantly more important than j
7	Element i is more strongly important than j
9	Element i is more extremely important than j
2, 4, 6, 8	The intermediate value of the above judgements
Inverse Number	$a_{ji}=1/a_{ij}$

to obtain the scoring information of each indicator according to the preset scale from the experts, compare the scores of each feature quantity in the indicator layer two by two, and construct the judgement matrix [28]:

$$\mathit{A}={\left[a_{ij}\right]}_{m\times m}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1\mathrm{m}}\\ a_{21}& a_{22}& \dots & a_{2\mathrm{m}}\\ \dots & \dots & \dots & \dots \\ a_{\mathrm{m}1}& a_{\mathrm{m}2}& \dots & a_{\mathrm{mm}}\end{array}\right]$$

(22)

(2)

Consistency check

The construction of judgement matrices using the hierarchical analysis method depends mainly on the personal experience of the decision maker, and different decision makers construct different judgement matrices, which ultimately leads to the arbitrariness of the results, so the results must be checked for consistency. The consistency indicator is shown in the following equation:

$$CI={\displaystyle \frac{{\lambda }_{\max }-m}{m-1}}$$

(23)

where $m$ and ${\lambda }_{\max }$ are the order and maximum eigenvalue of the judgement matrix, respectively.

The consistency ratio indicator is:

$$CR={\displaystyle \frac{CI}{RI}}$$

(24)

where $RI$ is the stochastic consistency indicator.

The smaller the calculated $CR$ is, the better the consistency of the judgement matrix. The feature vectors that pass the calibration are the weight vectors, otherwise the judgement matrix needs to be reconstructed.

(3)

Calculation of weights

Normalize each column element of the judgement matrix:

$$a_{ij}^{’}={\displaystyle \frac{a_{ij}}{{\displaystyle \sum _{i=1}^{\mathrm{n}}{a}_{ij}}}}(j=1,2,\dots ,\mathrm{n})$$

(25)

The judgement matrix is summed by rows to obtain the initial subjective weight ${\alpha }_i^{’}$:

$${\alpha }_i^{’}={\displaystyle \sum _{j=1}^{\mathrm{n}}{a}_{ij}^{’}}(i=1,2,\dots ,\mathrm{n})$$

(26)

Normalized again to obtain the final subjective weight matrix:

$$\alpha ={\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{\mathrm{n}}\right]}^{\mathrm{T}}$$

(27)

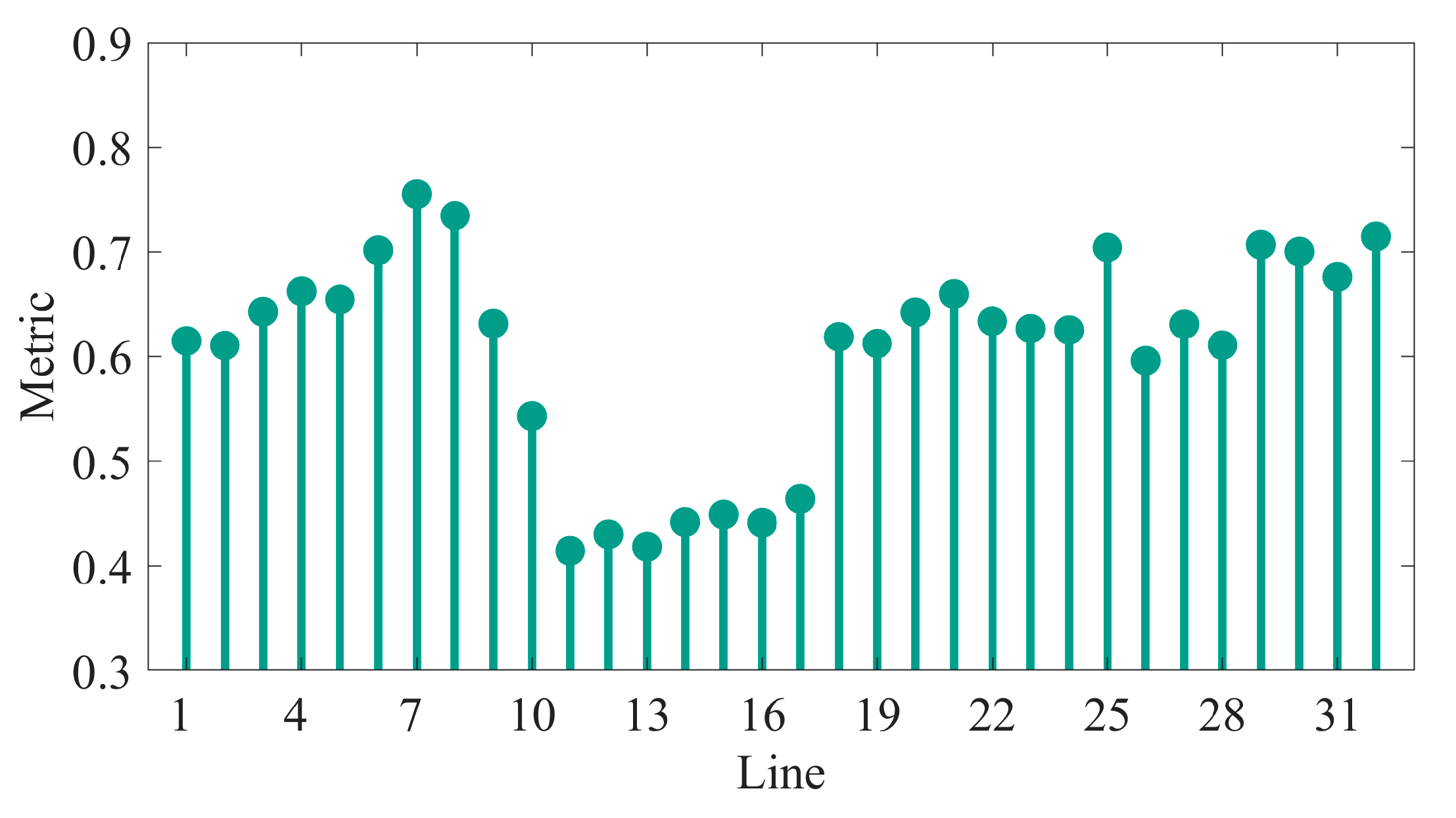
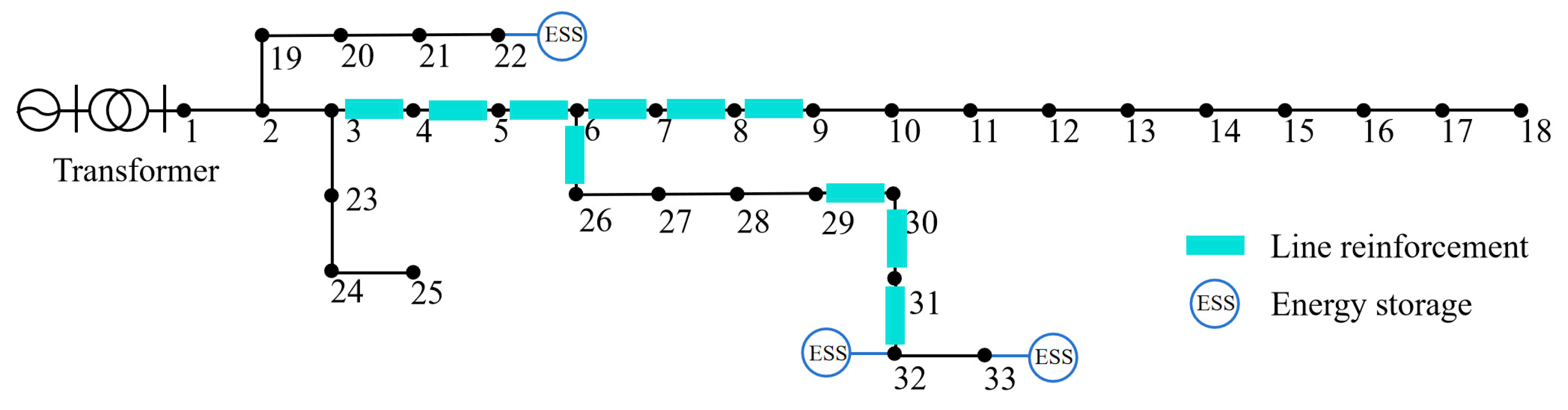
Compared with the quantification of a single indicator, the integrated vulnerability calculation method in this paper can more accurately identify the vulnerability of the system. When the integrated failure probability is large but the load importance is average, these lines are prone to be attacked and generate load loss when the typhoon passes through, so they should be analyzed for vulnerability. At the same time, for those links that have low failure probability but high load importance, although the probability of failure is low, once it occurs, it will cause great loss to the system, so it should be paid enough attention to it as well. After determining the calculation weights of each indicator, the integrated vulnerability indicator corresponding to each line can be calculated, and the higher the value of this indicator, the more likely it is to suffer load loss in a typhoon scenario. Therefore, the top 12 lines with high vulnerability indexes are selected as the vulnerability of DNs, for which line reinforcement and energy storage configuration measures are taken during the typhoon transit to reduce the load loss after the typhoon attack.

3.2. Resilience Index

In order to quantify the resilience of DNs under extreme typhoon weather, this paper takes the system lost load cost as the resilience indicator, as shown in the following equation [29]. The larger the value of lost load cost is, the worse the system resilience is, and the smaller the value is, the smaller the load loss of DNs under typhoon disaster is, i.e., the better the system resilience performance is.

$$R_{\mathrm{D}}=c_{\mathrm{s}}{\displaystyle \sum _{j\in \mathrm{B}}{w}_j{P}_j^{\mathrm{ls}}}$$

(28)

where $R_{\mathrm{D}}$ is the cost of lost load in DNs. $c_{\mathrm{s}}$ is the cost per unit of lost load. $w_j$ is the load weighting factor of bus $j$. $P_j^{\mathrm{ls}}$ is the amount of lost load at bus $j$.

3.3. Vulnerability-Based Resilience Enhancement Model

Line reinforcement improves the physical resilience of the system, and energy storage configuration enables emergency response in disasters [30]. Based on the two resilience enhancement strategies, the location and capacity of the reinforced lines and energy storage configuration are determined with the aim of maximizing the resilience enhancement of the system during the emergency response to the disaster at a limited investment cost. The optimal investment cost is determined by the resilience enhancement benefit index. The index quantifies the resilience enhancement effect under the unit investment cost, and takes into account the system resilience enhancement effect and economy, as shown in the following equation:

$$f={\displaystyle \frac{R_D}{C_L+C^{ESS}}}$$

(29)

where $R_D$ is the resilience enhancement effect. $C_L$ is the line reinforcement cost. $C^{ESS}$ is the energy storage cost.

Line reinforcement cost is [9]:

$$C_{\mathrm{L}}={\displaystyle \sum _{(i,j)\in \mathrm{L}}({\mathrm{c}}_{\mathrm{L}}{s}_{ij}{h}_{ij})}$$

(30)

where ${\mathrm{c}}_{\mathrm{L}}$ is the cost of line reinforcement per unit length. $s_{ij}$ is the length of line $ij$. $h_{ij}$ indicates whether line $ij$ is reinforced or not. $\mathrm{L}$ is the set of lines.

The cost of energy storage $C^{\mathrm{ESS}}$ consists of the cost of the storage equipment $C_{\mathrm{equipment}}^{\mathrm{ESS}}$, the cost of the storage site $C_{\mathrm{site}}^{\mathrm{ESS}}$, and the total O&M cost $C_{\mathrm{om}}^{\mathrm{ESS}}$ [9]:

$$\left\{\begin{array}{c}{C}_{\mathrm{equipment}}^{\mathrm{ESS}}={\displaystyle \sum _{j\in \mathrm{B}}({\mathrm{c}}_{\mathrm{p}}{P}_{\mathrm{inv},j}^{\mathrm{ESS}}+{\mathrm{c}}_{\mathrm{E}}{E}_{\mathrm{inv},j}^{\mathrm{ESS}})}\\ C_{\mathrm{site}}^{\mathrm{ESS}}={\displaystyle \sum _{j\in B}(c_j^{\mathrm{site}}{\sigma }_j)}\\ C_{\mathrm{om}}^{\mathrm{ESS}}={\displaystyle \frac{1}{{\mathrm{\beta }}^{\mathrm{ESS}}}}{\displaystyle \sum _{j\in \mathrm{B}}({\mathrm{c}}_{\mathrm{om}}{P}_{\mathrm{inv},j}^{\mathrm{ESS}})}\end{array}\right.$$

(31)

$$C^{\mathrm{ESS}}=C_{\mathrm{equipment}}^{\mathrm{ESS}}+C_{\mathrm{site}}^{\mathrm{ESS}}+C_{\mathrm{om}}^{\mathrm{ESS}}$$

(32)

where ${\mathrm{c}}_{\mathrm{p}}$ and ${\mathrm{c}}_{\mathrm{E}}$ are energy storage unit power and capacity cost coefficients, respectively. $C_j^{\mathrm{site}}$ is the energy storage site cost coefficient. ${\mathrm{c}}_{\mathrm{om}}$ is the energy storage annual O&M cost coefficient. ${\mathrm{\beta }}^{\mathrm{ESS}}$ is the energy storage capital recovery coefficient. $P_{\mathrm{inv},j}^{\mathrm{ESS}}$ and $E_{\mathrm{inv},j}^{\mathrm{ESS}}$ are the rated power and capacity of the energy storage installed at bus $j$, respectively. ${\sigma }_j$ is a 0–1 variable that indicates whether or not to install the energy storage at bus $j$, and takes 1 if it is installed, and vice versa. $\mathrm{B}$ is the set of buses.

The objective function is to minimize the cost of system loss of load, as demonstrated in the following equation, aiming to minimize the resilience metrics proposed in this paper, i.e., to maximize the system resilience performance, by adopting the resilience enhancement strategy using line reinforcement and energy storage configuration.

$$\left\{\begin{array}{l}\min R_D=\min c_s{\displaystyle \sum _{j\in B}{w}_j{P}_j^{ls}}\\ \mathrm{s}.\mathrm{t}. g_k\le 0 k=1,2,\dots n\\ h_r=0 r=1,2,\dots m\end{array}\right.$$

(33)

where $g_k$ and $h_r$ are the inequality constraints and equation constraints, respectively, specified as [9]:

(1)

Investment budget constraint

$$C_{\mathrm{L}}+C^{\mathrm{ESS}}\le B_{\mathrm{inv}}$$

(34)

(2)

Active and reactive power balance constraints

$$\left\{\begin{array}{c}{\displaystyle \sum _{s\in \mathrm{\delta }(j)}{P}_{js,t}-{\displaystyle \sum _{i\in \mathrm{\pi }(j)}{P}_{ij,t}=P_{j,t}^{\mathrm{g}}+P_{j,t}^{\mathrm{ESS}}-(P_{j,t}^{\mathrm{L}}-P_{j,t}^{\mathrm{ls}})}}\\ {\displaystyle \sum _{s\in \mathrm{\delta }(j)}{Q}_{js,t}-{\displaystyle \sum _{i\in \mathrm{\pi }(j)}{Q}_{ij,t}=Q_{j,t}^{\mathrm{g}}+Q_{j,t}^{\mathrm{ESS}}-(Q_{j,t}^{\mathrm{L}}-Q_{j,t}^{\mathrm{ls}})}}\end{array}\right.$$

(35)

where $i$, $j$ and $s$ are different buses. $\mathrm{\pi }\left(j\right)$ and $\mathrm{\delta }\left(j\right)$ are the set of parent and child buses of bus $j$, respectively. $P_{ij,t}$ and $Q_{ij,t}$ are the active and reactive power flowing on line $ij$ at time $t$, respectively. $P_{j,t}^{\mathrm{g}}$ and $Q_{j,t}^{\mathrm{g}}$ are the active and reactive power injected into DNs by the transformer at time $t$, respectively. $P_{j,t}^{\mathrm{ESS}}$ is the storage discharge power at bus $j$ at time $t$. $Q_{j,t}^{\mathrm{ESS}}$ is the reactive power output of the storage system at bus $j$ at time $t$, assuming that there is sufficient reactive power compensation capacity for the storage. $P_{j,t}^{\mathrm{L}}$ and $Q_{ij,t}$ are the active and reactive loads at bus $j$ at time $t$ in the normal case, respectively. $Q_{j,t}^{\mathrm{ls}}$ is the reactive power load lost at bus $j$ at time $t$.

(3)

Voltage relaxation constraints

$$\left\{\begin{array}{c}{V}_{i,t}-V_{j,t}\le \mathrm{M}(1-z_{ij,t})+{\displaystyle \frac{r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}}{V_0}}\\ V_{i,t}-V_{j,t}\ge -\mathrm{M}(1-z_{ij,t})+{\displaystyle \frac{r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}}{V_0}}\end{array}\right.$$

(36)

where $V_{j,t}$ is the voltage value at bus $j$ at time $t$. $V_0$ is the rated voltage value. $r_{ij}$ and $x_{ij}$ are the resistance and reactance values of line $ij$, respectively. $\mathrm{M}$ is a large constant. $z_{ij,t}$ is the state of line $ij$ at time $t$.

(4)

Line current constraints

$$\left\{\begin{array}{c}-z_{ij,t}{S}_{ij}^{\max }\le P_{ij,t}\le z_{ij,t}{S}_{ij}^{\max }\\ -z_{ij,t}{S}_{ij}^{\max }\le Q_{ij,t}\le z_{ij,t}{S}_{ij}^{\max }\\ -\sqrt{2}{z}_{ij,t}{S}_{ij}^{\max }\le P_{ij,t}+Q_{ij,t}\le \sqrt{2}{z}_{ij,t}{S}_{ij}^{\max }\\ -\sqrt{2}{z}_{ij,t}{S}_{ij}^{\max }\le P_{ij,t}-Q_{ij,t}\le \sqrt{2}{z}_{ij,t}{S}_{ij}^{\max }\end{array}\right.$$

(37)

where $S_{ij}^{\max }$ is the transmission capacity of line $ij$.

(5)

Loss load constraints

$$\left\{\begin{array}{c}0\le P_{j,t}^{\mathrm{ls}}\le P_{j,t}^{\mathrm{L}}\\ 0\le Q_{j,t}^{\mathrm{ls}}\le Q_{j,t}^{\mathrm{L}}\end{array}\right.$$

(38)

(6)

Bus power injection power constraints

$$\left\{\begin{array}{c}0\le P_{j,t}^{\mathrm{g}}\le P_{j,\max }^{\mathrm{g}}\\ 0\le Q_{j,t}^{\mathrm{g}}\le Q_{j,\max }^{\mathrm{g}}\end{array}\right.$$

(39)

where $P_{j,\max }^{\mathrm{g}}$ and $Q_{j,\max }^{\mathrm{g}}$ are the maximum active and reactive power injections from the power supply at bus $j$, respectively.

(7)

Bus voltage constraint

$$V_{j,\min }^2\le V_{j,t}^2\le V_{j,\max }^2$$

(40)

where $V_{j,\max }$ and $V_{j,\min }$ are the upper and lower voltage limits at bus $j$, respectively.

(8)

Buses are allowed to install energy storage ratings and capacity constraints

$$\left\{\begin{array}{c}0\le P_{\mathrm{inv},j}^{\mathrm{ESS}}\le {\sigma }_j{P}_{\mathrm{inv},j,\max }^{\mathrm{ESS}}\\ 0\le E_{\mathrm{inv},j}^{\mathrm{ESS}}\le {\sigma }_j{E}_{\mathrm{inv},j,\max }^{\mathrm{ESS}}\end{array}\right.$$

(41)

where $P_{\mathrm{inv},j,\max }^{\mathrm{ESS}}$ and $E_{\mathrm{inv},j,\max }^{\mathrm{ESS}}$ are the maximum rated power and capacity of the energy storage allowed to be installed at bus $j$, respectively.

(9)

Constraint on the amount of energy storage allowed to be installed in DNs

$${\displaystyle \sum _{j\in \mathrm{B}}{\sigma }_j\le N_{\mathrm{ESS}}}$$

(42)

where $N_{\mathrm{ESS}}$ is the maximum number of energy storage installations permitted for DNs.

(10)

Energy storage discharge power constraint

$$0\le P_{j,t}^{\mathrm{ESS}}\le P_{\mathrm{inv},j}^{\mathrm{ESS}}$$

(43)

(11)

Energy storage charge state constraint

$$S_{\min }^{\mathrm{SOC}}{E}_{\mathrm{inv},j}^{\mathrm{ESS}}\le E_{j,t}^{\mathrm{ESS}}\le S_{\max }^{\mathrm{SOC}}{E}_{\mathrm{inv},j}^{\mathrm{ESS}}$$

(44)

where $S_{\min }^{\mathrm{SOC}}$ and $S_{\max }^{\mathrm{SOC}}$ are the minimum and maximum charge state values of the stored energy, respectively. $E_{j,t}^{\mathrm{ESS}}$ is the residual power from energy storage at bus $j$ at time $t$.

(12)

Energy storage power balance constraint

$$E_{j,t+1}^{\mathrm{ESS}}=E_{j,t}^{\mathrm{ESS}}-{\displaystyle \frac{P_{j,t}^{\mathrm{ESS}}\Delta t}{{\eta }_{\mathrm{d}}}}$$

(45)

where ${\eta }_d$ is the discharge efficiency for energy storage.

(13)

Energy storage initial power state constraint

$$E_{j,t}^{\mathrm{ESS}}=S_{j,t}^{\mathrm{soc}}{E}_{\mathrm{inv},j}^{\mathrm{ESS}}$$

(46)

where $E_{j,t}^{\mathrm{ESS}}$ is the electricity value of energy storage at bus $j$ at time $t$.

4. Calculus Analysis

In order to verify the validity of the models and methods proposed in this paper, the Gurobi solver is invoked in MATLAB R2020b to solve the models and the IEEE 33-bus distribution system is used as an example to analyze and verify them.

4.1. Typhoon Disaster Modelling Results

4.1.1. Simulation Results of Typical Typhoon Landfall Parameters

In this paper, based on the typhoon data that made landfall in China in the past 20 years, the data simulation of the direction angle, the central moving speed and the central air pressure difference at the moment of typhoon landfall is carried out based on the normal distribution, the lognormal distribution and the Weibull distribution. Figure 2, Figure 3 and Figure 4 demonstrate the data fitting results for three typhoon landfall parameters, respectively. The fit probability density curves are plotted using actual typhoon data. As shown in the figures, the differences between the historical data fitting curves and the probability density function curves constructed in this paper are small, and the two curves exhibit a high degree of consistency in their overall trends. This indicates that the probability density function can characterize the relevant features of typhoon landfall, further validating the effectiveness of the typhoon landfall parameter probability density model adopted in this paper.

The relevant parameters of the probability density function shown in

Table 2. Parameters related to the probability density function.

Moving Direction Angle	Moving Speed	Central Air Pressure Difference
${\mu }_{\theta }$ = 0.9644	${\mu }_{\ln c}$ = 2.9066	$\chi$ = 46.7348
${\sigma }_{\theta }$ = 0.8623	${\sigma }_{\ln c}$ = 0.3269	$\kappa$ = 2.2759

are obtained. Based on the probability density function, several sets of typhoon landfall parameters are generated by Monte Carlo method. The optimal number of clusters for each scenario was obtained as 3 by the contour coefficient method, and finally the typical typhoon landfall parameters were obtained by K-means clustering. The data combinations with the highest probability of occurrence were selected as follows: the angle of direction at the moment of landfall is 0.905 rad, the moving speed is 14.179 km/h, and the central air pressure difference is 42.0123 pa.

4.1.2. Typhoon Trajectory and Disaster-Triggering Factors Simulation

Based on the typical typhoon landfall parameters, the storm track model is used to achieve the trajectory simulation with a time scale of one hour. As illustrated in Figure 5 below, the typhoon landfalls at the location of (150,10) and travels to the northwest direction. After the typhoon makes landfall, the wind circle should gradually become larger with the gradual decay of the intensity, but compared to the typhoon scale and the impact range, the scale of DNs is small, so the maximum wind radius after the typhoon makes landfall is regarded as a fixed value. For the convenience of demonstrating the typhoon trajectory, the figure illustrates a reduced wind circle, and the actual wind circle radius is greater than 50 km.

In order to simplify the model, existing research always used straight paths to simulate the motion trajectory of typhoons. But in reality, typhoons cannot travel in one direction. To verify the effectiveness of the dynamic path model used in this article, a comparative analysis is conducted in Figure 6. In Figure 6, path 1 is the simulation result of the typhoon path in this paper, path 2 is the movement path of Typhoon Maria after its landfall in 2018, and path 3 is a straight path. From path 2, it can be seen that during the actual movement of a typhoon, its direction of motion changes in real-time rather than being fixed and unchanging. Since the component failure probability model is established based on the relative position of components in the wind field, determining the center position of the typhoon at each moment is crucial for improving modeling accuracy. But the straight path ignores the spatiotemporal changes of typhoon motion, which will reduce the accuracy of disaster simulation and thus affect the formulation of subsequent resilience strategies. Therefore, dynamic simulation of typhoon paths is crucial for improving the accuracy of disaster modeling.

Based on the typhoon path simulation results and the geographical locations of each line, the wind speed of the components can be quantified using the Batts model. Taking the maximum wind speed as an example, Figure 7 shows the maximum wind speeds experienced by each line. Through comparative analysis, it can be seen that the intensity of disaster-causing factors varies significantly across different lines. This spatial variability is primarily related to the dynamic path of the typhoon and the relative position of the components within the wind field.

4.1.3. Component Failure Probability Simulation Results

With the evolution of the typhoon, for each component, the typhoon wind circle always goes from far to near and then slowly moves away, so the disaster intensity suffered by each component also illustrates a trend of increasing and then decreasing. Figure 8 demonstrates the time-varying failure probability of line 15 to line 23, with a trend of increasing and then decreasing fault probabilities. Extreme typhoon weather affects DNs not only by wind disaster, but also by heavy rain as a factor that cannot be ignored. For the wind and rain disaster, a single wind disaster and a single rainstorm disaster three cases of failure probability to start a comparative analysis, to line 18 as an example, as can be seen in Figure 9, the failure probability under wind and rain disaster has a significant difference than under a single disaster, that is, a single disaster is difficult to completely portray the impact of the typhoon on DNs.

4.2. Vulnerability Identification Results

Regarding vulnerability assessment, only the importance factor of bus load was considered in [9], and component failure probability was only considered in [26]. Accordingly, Figure 10 illustrates the calculation results of a single index, which may lead to an incomplete assessment of vulnerability. The importance factor of load bus is not only reflected in the impact on the stability of the system, but also in the impact on the economy, if it is ignored, it may lead to irrational allocation of resources, thus affecting the resilience improvement effect. Similarly, the line failure probability is also an important factor affecting the stability of the system, especially in extreme natural disasters, the vulnerability of the line for the stability of the system is particularly significant, if the line failure probability is ignored, it may not be able to take effective resilience enhancement measures in a timely manner, which in turn affects the system resilience performance. A component with a high failure probability connected to a non-critical load may actually have a much lower impact on system vulnerability than a component connected to a critical load. Conversely, even if the load is critical, if the component’s failure probability is extremely low, its actual vulnerability may be overestimated. Therefore, the two indicators should be considered comprehensively to identify vulnerabilities.

Based on Table 1, the importance of failure probability is three times that of load factor, so the judgement matrix can be obtained as $\left[\begin{array}{cc}3& 1\\ 1& {\displaystyle \frac{1}{3}}\end{array}\right]$. Then the consistency index $CI$ is calculated to be 0, so $CR$ = 0, which satisfies the condition of being less than 0.1. Furthermore, since the judgement matrix is a second-order matrix, there is no third-party element introducing logical conflicts, so the consistency of the judgement matrix is acceptable. Therefore, based on the hierarchical analysis, the indicator weighting ratio can be obtained by $k_1:k_2=0.65:0.35$. Figure 11 illustrates the calculation results of vulnerability index for each line. There are significant differences in vulnerability between different lines. The first 12 line numbers and the corresponding vulnerability index values are shown in

Table 3. Vulnerability indicators for the first 12 routes.

Line Number	Vulnerability Indicator	Line Number	Vulnerability Indicator
7	0.755	30	0.700
8	0.735	31	0.676
32	0.715	4	0.663
29	0.707	21	0.660
25	0.704	5	0.655
6	0.702	3	0.643

, so lines 7, 8, 32, 29, 25, 6, 30, 31, 4, 21, 5 and 3 are the vulnerability, and the subsequent resilience enhancement measures are taken for the 12 lines to reduce the load loss in the system.

4.3. Comparative Analysis of Resilience Enhancement Programmers

The resilience enhancement based on line reinforcement and energy storage configuration aims to maximize the system resilience to disasters within limited investment costs. The main references for the costs associated with line reinforcement and energy storage configuration are listed in [9]. In order to verify the effectiveness of the proposed method, the following three cases are set up for comparative analysis based on the resilience enhancement model for DNs proposed in this paper.

Case 1: no resilience enhancement measures.

Case 2: line reinforcement only.

Case 3: line reinforcement and energy storage configuration measures.

Figure 12 and Figure 13 demonstrate the enhancement results for Case 2 and Case 3, respectively. Case 2 only performs line reinforcement of vulnerable lines to achieve power supply stability and reliability. In this paper, under the typhoon scenario, Scenario 1 can achieve the reinforcement of vulnerability within the enhancement cost, but if the DN is severely affected, there are practical difficulties in reinforcing all the power supply path between the loads and higher-level power sources. Case 3 coordinates line reinforcement with energy storage configuration, reinforcing part of the line and using buses to allocate energy storage for the rest of the faulty lines to achieve load power supply, and this strategy can take into account the economy to a greater extent while ensuring system resilience enhancement under extreme typhoon disasters. The results of energy storage configuration for Case 3 are shown in

Table 4. Energy storage configuration results for Case 3.

Bus	Rated Power (kW)	Rated Capacity (kW·h)	Equipment Cost (USD 10,000)	Site Cost (USD 10,000)	O&M Cost (USD 10,000)	Investment Cost (USD 10,000)
22	77.35	2000.00	17.24	2.00	0.47	19.71
32	9.77	176.44	1.57	2.00	0.06	3.63
33	68.68	1889.40	16.21	2.00	0.41	18.62

. As can be seen from Table 4, energy storage configuration is carried out at buses 22, 32 and 33 in Case 3. The configured power, configured capacity, equipment cost, site cost, and O&M cost can all be found in Table 4.

Table 5. Case enhancement results.

	Loss Load Cost (USD 10,000)	Line Reinforcement Cost (USD 10,000)	Energy Storage Configuration Cost (USD 10,000)	Total Enhancement Cost (USD 10,000)
Case 1	550.33	—	—	—
Case 2	63.73	144.05	—	144.05
Case 3	39.14	108.04	41.96	150.00

shows the enhancement results for different cases, including the loss load cost, line reinforcement cost, energy storage configuration cost, and total enhancement cost under different resilience optimization cases. The cost of lost load in DNs is as high as 5.503 million when no resilience enhancement measures are taken. Comparing and analyzing the enhancement results of Case 2, Case 2 adopts a enhancement cost of 1.4405 million for line reinforcement, and its loss of load is reduced by 4.8660 million compared to the case when no measures are taken, and the system toughness is greatly improved. Comparing and analyzing the enhancement results of Case 2 and Case 3, the enhancement cost of Case 3 is higher than that of Case 2 by 0.0595 million, but its lost load cost is reduced by 0.2459 million compared with that of Case 2, i.e., it exchanges smaller enhancement cost for greater resilience enhancement effect, which embodies the effectiveness of the resilience enhancement strategy proposed in this paper.

The load loss at each bus in different cases is demonstrated in Figure 14, and the load loss at each moment is demonstrated in Figure 15. In this paper, three resilience enhancement strategies are proposed, and it can be seen by comparing the loss of load curves that the loss of load when no resilience measures are taken is extremely large, and the stability of the system power supply is poor. The significant decrease in system loss of load in Case 2 compared to Case 1 demonstrates that the proposed line reinforcement strategy can improve the physical strength of the system to resist disaster attack, which, in turn, safeguards the system power supply to a certain extent. Due to the limitation of investment cost, although the coordinated measures of line reinforcement and energy storage configuration in Case 3 cannot fully guarantee the power supply of the system, it can improve the physical strength of the components and provide emergency power support at the same time, which is optimal in reducing the load loss of the system, and verifies the validity of the method proposed in this paper.

5. Conclusions

To address DN vulnerability under extreme weather, a typhoon-specific resilience enhancement method is proposed that incorporates multiple sources of typhoon uncertainty. First, typhoon impacts are simulated and network vulnerabilities are identified. Then, an optimization model is established to maximize system resilience. The effectiveness of the method proposed in this paper is verified, and the following conclusions are drawn:

(1)

A disaster simulation method based on multiple uncertainties has been achieved. This solves the problem of poor accuracy in disaster simulation due to random parameters and linear trajectory in traditional methods, and improves the accuracy of the component failure probability model.

(2)

A method for identifying vulnerability in DNs is proposed. This takes into account the impact of disasters and the stability of the power supply, providing a basis for the subsequent development of anti-disaster measures and avoiding the waste of resources associated with the traditional method.

(3)

A resilience enhancement model based on line reinforcement and energy storage configuration is established. Compared to Case 1, the proposed method can reduce the system’s load loss by 5.112 million. And compared to Case 2, the proposed method reduces the load loss cost by up to 0.2459 million with a cost difference of 0.0595 million, which solves the problems of uneven resource allocation and poor economy of a single resilience enhancement strategy.

In this paper, only the pre-disaster resilience enhancement for typhoons is considered, and in the future, a variety of resilience resources can be combined for post-disaster scheduling to further improve the resilience of the distribution network under extreme typhoon disasters.