Assessment of Tunnel Explosion Mitigation Techniques for Fire Scenarios Involving Hydrogen Tank Rupture ^†

Abstract

This paper presents a review of explosion mitigation techniques for road tunnels, with a focus on scenarios involving high-pressure hydrogen tank rupture under fire conditions. Both passive and active strategies are considered—including structural configurations (e.g., tunnel branching, vent openings, right-angle bends) and protective systems (e.g., drop-down perforated plates, high-performance fibre-reinforced cementitious composite (HPFRCC) panels)—to reduce blast impact on tunnel occupants and structures. The review highlights that while measures such as blast walls or energy-absorbing barriers can significantly attenuate blast pressures, an integrated approach addressing both blast load reduction and structural resilience is essential. This paper outlines how coupled computational fluid dynamics–finite element method (CFD–FEM) simulations can evaluate these mitigation methods, and we discuss design considerations (e.g., optimising barrier placement and tunnel geometry) for enhanced safety. The findings provide guidance for designing safer hydrogen vehicle tunnels, and they identify gaps for future research, including the need for experimental validation of combined CFD–FEM models in hydrogen fire–explosion scenarios.

1. Introduction

A tunnel fire represents a critical risk for vehicles equipped with high-pressure hydrogen storage systems. If the thermally activated pressure release device (TPRD) fails to activate for the safe release of hydrogen stored in the tank, it could result in a blast wave and fireball, which pose significant dangers. Consequently, accurately predicting the explosion’s impact is essential to evaluate, prevent, and lessen the repercussions of such an explosion on both infrastructure and individuals.

To achieve structural safety against unexpected incidents, several independent safety protocols should be implemented, such as:

• Diminishing the likelihood of accidental events: Specifically, the risk of hydrogen tank explosions can be minimized by lowering both the frequency and intensity of vehicle accidents within the tunnel (for instance, through reduced speed limits, limiting the number of vehicles in the tunnel, enhancing lighting, expanding emergency lanes, and establishing rapid fire suppression systems).
• Mitigating the impact of the action (specifically the pressure wave resulting from the hydrogen tank explosion) through the implementation of measures designed to lessen the explosion’s intensity, along with the ensuing blast wave and fireball.
• Enhancing the resilience of the structure by improving the strength or dimensions of the individual components, or by augmenting the continuity of the structural system, thereby facilitating stress redistribution among various structural elements or sections. This first approach tends to be particularly effective in tunnels, which generally possess a high level of structural continuity (consider, for example, the load-bearing walls of a drilled tunnel or the monolithic precast concrete sections of a submerged tunnel).
• Minimising the potential for progressive collapse in the structure, ensuring that the failure of one component does not trigger the failure of nearby members or sections. In tunnel scenarios, a collapse of one portion should not result in the failure of adjacent portions. In the case of bridges, this necessitates the deliberate interruption of structural continuity at specified points throughout the tunnels.

The initial two measures focus on prevention and mitigation efforts. Consequently, their execution is vital as it also enhances safety for individuals.

The likelihood of a hydrogen explosion occurring, as previously described, is considered to be low; however, ongoing efforts to reduce this risk will enhance the safety and acceptance of hydrogen technologies. Regrettably, complete elimination of risk is impossible, but the primary objective is to continuously enhance safety by minimising the chances of accidents. Below are instances of accidents that possess a very low likelihood yet could lead to catastrophic outcomes. While such risks might be deemed acceptable, the implications in terms of loss of life and both direct and indirect expenses resulting from structural damage, necessary repairs, and infrastructure downtime are usually extremely high. In the context of crucial and strategic infrastructures like tunnels, preventing these interruptions is essential.

Consequently, mitigating the risk of progressive collapse necessitates intricate collapse analysis. This can be quite challenging, especially in tunnel scenarios, and while it may prevent catastrophic results, it does not fully negate the expenses related to downtime and repairs, which can also be considerable.

For instance, imagine a busy highway tunnel carrying mixed traffic including hydrogen-fuelled vehicles. In the event of a severe collision and fire involving a hydrogen car or bus, the onboard high-pressure tank could overheat and rupture if its TPRD fails [1]. Such a rupture would lead to a blast wave and fireball confined within the tunnel, potentially causing devastating overpressures. Historical fire incident data support the plausibility of this scenario—in Australian road tunnels [2], there were 78 fire incidents recorded from 1992 to 2016. A separate study [3] examined a dataset of 156 fire incidents over the years, with over half attributed to spontaneous vehicle ignition caused by factors such as engine malfunctions, tire issues, fuel leaks, electrical problems, etc. While not all fires lead to explosions, these statistics show that the risk of a hydrogen tank rupture in a tunnel fire is not merely theoretical. This paper, therefore, addresses an urgent safety question: If such an explosion occurs, how can the tunnel’s design and safety systems mitigate the consequences? The answer to this question were provided for a first time in our previous research [4].

2. Review of Modelling and Mitigation of Explosions

The investigation into the spread of blast waves within a complicated tunnel network [5] demonstrated that the succession of blast waves flowing from the test area into a neighbouring tunnel merges to create an even more intense wave, and that the dissipation of the wave through this standard tunnel configuration is surprisingly minimal. Research conducted by Fondaw (1993) [6] has highlighted the shock-absorbing properties of low-density foam. The ideal thickness of the foam is contingent upon the tunnel’s length and the extent of shock absorption needed. A blast was created using approximately 1.25 kg of C-4 explosive in a tunnel with a diameter of 2 m. The tunnel containing 10 cm of foam exhibited over a 50% decrease in peak overpressure when compared to the tunnel without foam. Further, tunnels with 20 cm and 30 cm of foam demonstrated even more significant reductions of 70% and 78%, respectively. In the bare tunnel, the overpressure surpasses the threshold for lung damage (82 kPa) throughout almost the entire tunnel length. However, with 10 cm of foam, the overpressure falls below this threshold at around 30 m, and with 20 cm of foam, it decreases below this level at approximately 25 m.

Hager and Naury (1996) [7] forecasted the pressure behaviour within a storage chamber, a secondary tunnel, and a primary tunnel in an underground storage facility; they evaluated how the length of the tunnel and boundary conditions impact peak blast pressures and the duration of these pressures, while also comparing observed and anticipated pressure time-histories, yielding the following findings:

• In straight tunnels, peak pressures decreased gradually along the tunnel’s length. A medium modelled by a cylinder embedded within the chamber and access tunnel measured 7.8 m in radius and 115 m in length along the tunnel walls, causing negligible alterations to the anticipated peak pressures.
• In a complex tunnel comprising various tunnels and chambers, the responding media diminished peak pressures by 10 to 30%.
• Peak pressures predicted by Autodyne were higher than the measured values by at least 100% in the near field, indicating the increase reached up to ten times the measured pressure at junctions, which could be attributed to reflected pressures at those junctions.

In the experiment conducted by Smith et al. (1998) [8], a scaled model test was carried out to observe the blast wave propagation through straight tunnels measuring 50 mm in width, 100 mm in height, and 500 mm in length, constructed from a 3 mm thick steel plate. They found that the roughness of the tunnel walls significantly influences the propagation of the blast wave. It was noted that introducing discrete roughness elements along the walls of a straight tunnel leads to greater reductions in blast impacts compared to a smooth tunnel. Attenuation generally improves with an increase in the height of the roughness elements. For uniformly spaced roughness, the quantity of elements correlates closely with the distances between them. In these scenarios, the height-to-spacing ratio plays a crucial role in influencing attenuation. They also referenced [9], which mentioned that a recognised form of passive attenuator is the inclusion of right-angled bends within a tunnel, which can lessen the overpressure by 6% for each bend.

The impact of a water wall on the creation and spread of blast waves resulting from nearby explosives has been studied through a numerical method [10]. It was demonstrated that a water-to-explosive weight ratio of 1–3 is effective for practical uses. This volume of water can diminish peak overpressure by approximately 30–60%.

Sklavounos and Rigas (2006) [11] conducted a parametric analysis of the attenuation effects produced by the side vents of a branched tunnel, where a blast wave forms and moves following an explosion. They observed that increasing the number or diameter of the vents results in greater attenuation of the explosion wave, thereby enhancing their protective function.

The Netherlands Organisation for Applied Scientific Research [12] executed finite element simulations to investigate the impact of high-rate loadings from a gas explosion and a BLEVE (Boiling Liquid Expanding Vapour Explosion) on wall and roof deformations. They analysed three existing tunnels: the Caland tunnel, which consists of two sections measuring 14.45 × 6.09 m each; the Drecht tunnel, made up of four two-lane sections measuring 10.35 × 4.8 m each; and the Leidsche Rijn tunnel, which includes two three-lane sections measuring 16.47 × 6.45 m each and two four-lane sections measuring 21.67 × 6.45 m each. The study incorporated realistic permanent and distributed loads on the walls and ceilings, as well as the material properties used in construction. They examined wall and ceiling deflections at explosion loads of 5.13, 6.5, and 4.35 bar for each tunnel, respectively. The loads were assumed to increase to a maximum value before decreasing exponentially, ultimately reducing to zero by t = 160 ms. They concluded that the Caland tunnel would not fail, cracking is anticipated in the Drecht tunnel, and failure might occur in the Leidsche Rijn tunnel. This report provides valuable information regarding the concrete and steel material properties as well as the design layouts of the tunnels.

A numerical simulation involving three-dimensional nonlinear dynamic finite element analysis for an explosion test inside a tunnel was performed in [13] and was validated against experimental data. A formula for attenuating the overpressure peak was derived under varying TNT mass equivalents. Comparisons between the formula’s predictions and experimental outcomes indicate that the overpressure peak can be estimated by the formula presented in this paper when the scaled distance ($L·m-1/3$) exceeds 1, where L represents the distance from the detonation point and m denotes the TNT mass.

Xu et al. (2019) [14] provided a comprehensive overview of the research on dispersion and explosion risks conducted as part of the HyTunnel project, along with other relevant studies, enhancing the understanding of the potential dangers linked to hydrogen vehicles in road tunnels. In their research, Pennetier et al. (2012) [15] analysed both numerically and experimentally the location of the transition zone within the tunnel, where, during wave propagation and subsequent multiple reflections against the tunnel’s walls, it behaves like a one-dimensional wave using a scaled model.

A study on blast wave mitigation using a particulate foam barrier was conducted in [16], which found that this type of foam can diminish the damage caused by actual blasts and make them safer. Subsequently, a numerical analysis [17] concerning the placement of baffles to reduce blast waves in tunnels showed that:

• The configuration of baffles can slow down the velocity of blast wave propagation, postpone the arrival time of the blast wave, and decrease the peak overpressure of the blast wave within the tunnel.
• When a single row of baffles is used along the tunnel, symmetrical baffles are recommended for better blast wave attenuation.
• For two or more rows of baffles arranged along the tunnel, alternate baffles are suggested as more effective at mitigating blast waves.
• The width of the baffles (b) and the spacing between them (c) significantly influence the attenuation of the blast wave; the overpressure attenuation ratio (a) increases with larger b and decreases with larger c, with recommendations for b to be greater than 0.5 and c to be less than 0.5.

De et al. (2013) [18] performed a numerical investigation into the effectiveness of both compressible protective barriers (constructed from polyurethane foam) and rigid barriers (made of concrete) in mitigating the effects of surface explosions, demonstrating that both types offer positive effects. Research by Mckenzie et al. (2014) [19] indicated that lightweight but sturdy drop-down perforated barriers, activated by a gravity motion sensor, could help alleviate the effects of blast waves. A forecasting analysis regarding overpressure in subway tunnels was conducted in [20], where a calculation model for blast effects in a tunnel was developed based on experimental data. This model’s applicability was validated through comparisons with numerical results and experimental data, revealing that factors such as tunnel geometry, charge placement, and distance from the explosion centre significantly impact blast effects. The cumulative overpressure from blasts in the subway tunnel was summarised, leading to a proposed formula. Studies [21,22] explored the implications of surface explosions above buried tunnels at different depths, investigating how much TNT can be detonated safely above tunnel surfaces, noting that the modelling techniques could also be applicable for internal explosions. A design methodology that utilises a simplified finite element (FE) model for underground tunnels subjected to internal explosions, and possibly preceded by fire incidents, was proposed by Colombo et al. [23]. The FE model underwent testing under static serviceability loads (like soil pressure); following this, dynamic analyses were performed to simulate the blast scenario in an 8.15 m diameter metro line tunnel. Various material properties were taken into account in the analysis, leading to the conclusion that segments made of conventional reinforced concrete, as well as a new configuration involving a layered precast tunnel segment using different fibre-reinforced cementitious composites, demonstrate superior performance under static loads, during fire incidents, and when subjected to internal explosions. Several in situ tests were executed in [24] in the far field to assess the blast mitigation effectiveness of a water-filled plastic wall, with results indicating that the water-filled plastic wall provides significant mitigation. Additionally, numerical simulations discussing the overpressure reduction in relation to the scaled height of the water wall and the scaled distance from the structure were analysed.

The performance of a full-scale porous glass fibre reinforced polymer (GFRP) barrier subjected to blast loads [25] demonstrated that a barrier made of GFRP pipe elements installed on precast concrete effectively disrupts the blast wave generated by an explosion, thereby diminishing the loads experienced by targets positioned behind the barrier. An explosive charge equivalent to 4 kg of TNT was utilised, with the distances separating the charge from the barrier set at 5 m, 3 m, and 0.5 m. The total impulse reduction factors recorded were 6% and 25%, while the pressure reduction observed was 11% and 36% in two tests conducted at distances of 5 m and 0.5 m, respectively. A study on the impact of blast waves on both open and closed cell foam barriers was carried out in [26] to evaluate the attenuation effects related to varying front face geometries of the foam barriers. Five distinct geometries were examined while maintaining a constant mass for the foam barrier. The front faces where the incident blast wave strikes were shaped into one, two, three, or four convergent forms, and the findings were compared to those of a foam block featuring a flat front face. Experimental results indicated there was no notable difference among the five geometries or between the two foam types. Zhao et al. 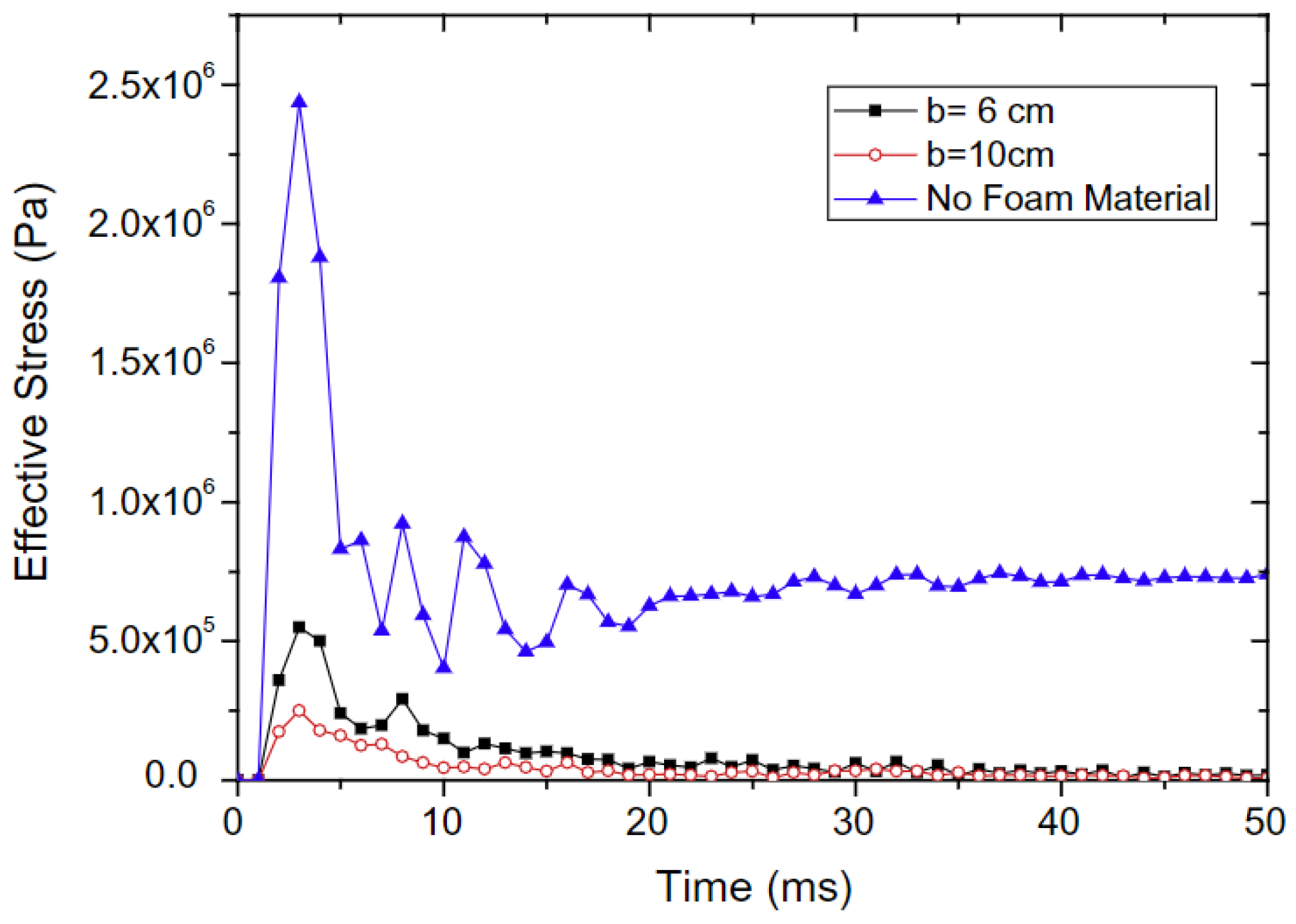(2015) [27] explored the blast mitigation effects of foamed cement-based sacrificial cladding in tunnel structures through both experimental and numerical analysis. They compared the effective stress experienced by the tunnel vault in three different configurations: one without cladding, one with a 6 cm thick foamed cement-based cladding, and another with a 10 cm thick foamed cement-based cladding. The effective stress peak values for the three structures, as illustrated in Figure 1, were found to be 2.49 MPa, 0.52 MPa, and 0.25 MPa, respectively.

In a research study [28], the authors discovered that wall roughness increases the maximum impulse near the blast source, challenging the common belief that rough walls mainly reduce the blast wave impulse compared to smooth walls.

The investigation into the blast attenuation by foam barriers was conducted both through experimental and numerical methods in [29]. Conventional shaving foam was utilised to create the foam barrier. The density of the samples was approximately ρ ≈ 100 kg/m³, equating to a liquid volume fraction of α = 0.1. They observed that the overall attenuation rate was significantly faster than the rate of blast decay in air. In the case of a single barrier, a pressure reduction ranging from 86% to 96.5% was recorded across various configurations. The primary mechanism contributing to the decrease of peak pressure of the blast wave travelling through foam is the “catching up” of the rarefaction wave with the wavefront, thus effectively decreasing its intensity. This phenomenon is also supported by the notably low sound speed in foam (around 40 m/s), allowing ample time for the rarefaction wave to converge with the wavefront over shorter distances.

A coupled fluid-structure-interaction analysis of an internal blast resulting from 44 kg of TNT in circular and square tunnels, each with a characteristic size of 5.5 m, examined its influence on underground tunnels in soil [30]. This paper identified several factors that impact the structural integrity of the tunnel. The presence of stiffer soil surrounding a buried tunnel mitigates structural damage. In tunnels with shallow burial depths (resulting in low confinement from the soil), the lining experiences significant strain, which could lead to structural harm. A circular tunnel is more susceptible to damage compared to a square tunnel of equal height and width as its diameter. The charge’s location is also crucial and greatly influences the outcome, with wall placement proving to be the least favourable compared to the centre location.

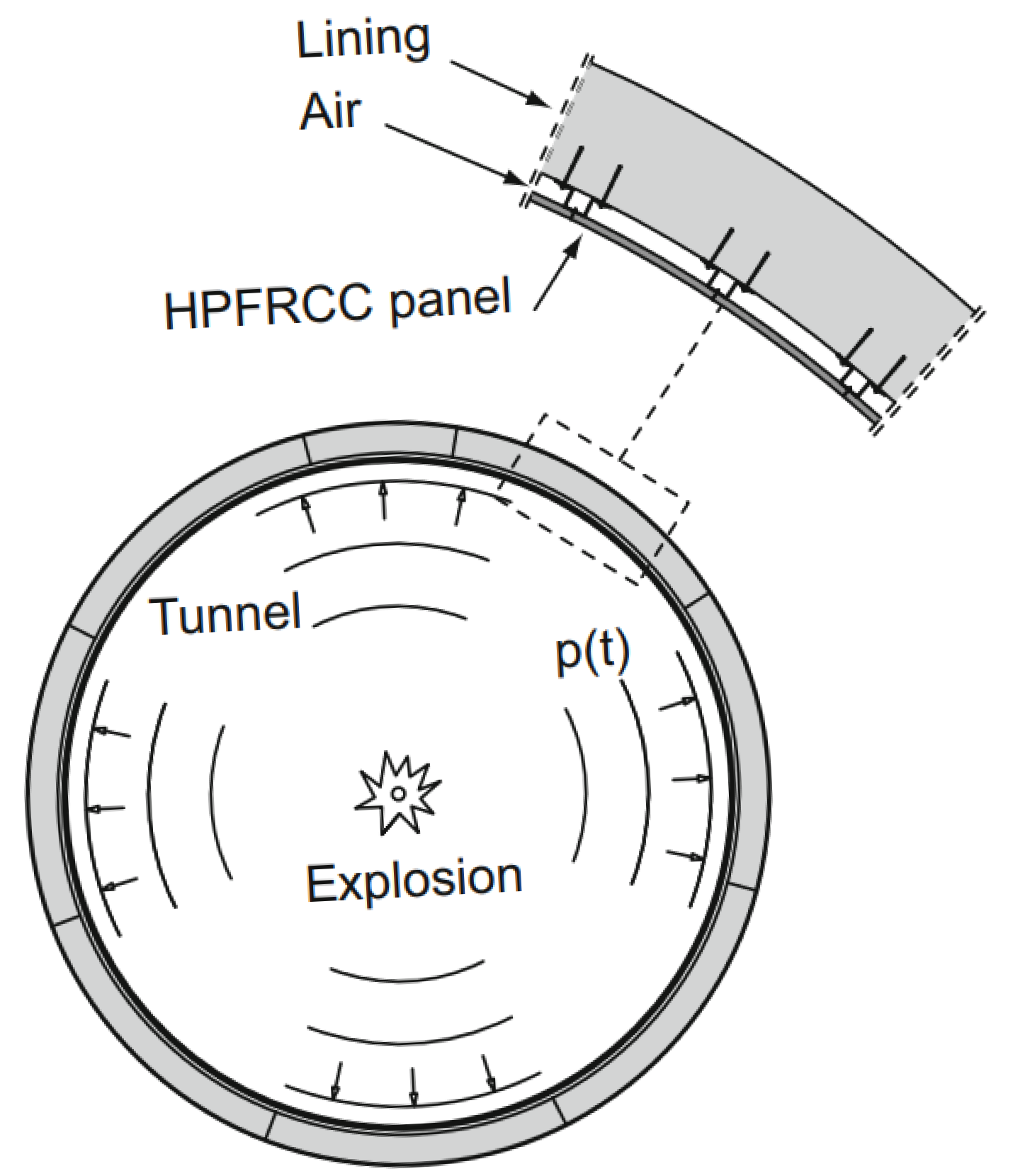
A subsequent study by Colombo et al. [31] details an experimental assessment of a critical scenario involving an internal tunnel explosion, specifically the response of HPFRCC panels applied to the internal surfaces of new or existing tunnels. These panels are designed as a protective measure for tunnels during blast incidents, and they also enhance tunnel performance in fire situations. In this context, there exists an air gap between the lining and the installed panels (Figure 2). The panels are relatively small (0.5–1 × 0.5–1 m) to facilitate easy handling and have a limited thickness (20 mm) for reasons of cost and space efficiency.

The findings indicated that tests conducted with a shock tube on concrete samples confirmed that thin HPFRCC panels could fail under blast pressures of 0.3 MPa, particularly with anchor spans of approximately 40 cm, if an air space is utilised to mitigate thermal impacts on the tunnel segment. It was noted that the failure of the panel results in a 50% reduction in the acceleration transmitted, signifying greater energy dissipation due to the formation of plastic strain and cracking in the panel.

Research by Kumar et al. (2017) [32] demonstrated numerical analyses regarding blast wave propagation through the shock tube and how the wave interacts with perforated plates. It was shown that the pressure of the blast wave decreases as it travels through the perforated plates, with pressure drops varying between 43.75% and 26%. Consequently, perforated plates can effectively be employed to attenuate blast waves. The theoretical effectiveness of blast mitigation using lightweight cladding was also evaluated in [33].

Small-scale experiments conducted in [34] aimed to investigate the mitigating effects of water contained in a bag within the tube to lessen the blast wave generated by an explosion. The blast pressure outside the tube was recorded and analysed. Results indicated that the peak overpressure was reduced by 33–45% with the water bag. It was concluded that the findings from this research could be widely applicable to explosions in confined spaces, such as underground magazines, subsurface storage, and tunnels, for the reduction of blast waves.

Experimental findings regarding the blast wave attenuation properties of aluminium foam sandwich panels exposed to blast loading in [35] illustrated that, while the wave attenuation rate on a mild steel structure is only 11.3%, the rate on the sandwich structure can surpass 90%. A recent case study by a team from China on the blast wave attenuation characteristics in a lengthy highway tunnel [36] involved modifying the decay equation presented in [37] and applying it to the Micangshan highway tunnel in China, demonstrating that the modified equation is more effective in describing the attenuation of blast waves within that tunnel compared to the original equation.

A recent CFD study outlined in [38,39] simulated the decay of a blast in a tunnel without any mitigation strategies and revealed that the majority of the energy from the blast is utilised for demolishing the vehicle instead of displacing it. Therefore, to reduce the strength of the blast wave in proximity due to the mechanical energy loss of compressed gas, further simulation of vehicle destruction following tank rupture is necessary and remains an area of ongoing investigation. The validation of the CFD fireball model in [39] was conducted against a standalone experiment, showing that the model’s predictions for both the size and shape of the fireball in tests and simulations were closely matched. An intriguing finding during tunnel simulations revealed a stationary combustion zone at the outset of the blast for about 9 ms, in contrast to scenarios in open air, where the fireball expands outward in all directions.

Recent research addressed the dynamic blast response of underground structures and advanced mitigation concepts. For example, [40] examined the effect of installing a protective blast barrier above a shallow tunnel using 3D numerical simulations. Their results showed that the presence of a properly designed barrier can significantly attenuate blast loads—peak pressures on the tunnel lining were reduced by up to ~80% in some configurations with a barrier, compared to an unprotected tunnel. This finding underscores the value of external protective systems in enhancing tunnel resilience against explosions.

Advanced simulation techniques have also been applied to assess structural blast response. In this study [41], authors used a high-fidelity finite element model (LS-DYNA) to evaluate how different TNT charge sizes would damage a concrete bridge deck. Their case study, while not a tunnel, illustrated that blast effects on structures are highly non-linear—for instance, a 1630 kg TNT explosion caused roughly double the damage length on the deck compared to 1000 kg of TNT. This highlights the importance of using non-linear dynamic analysis to capture structural response under extreme loads. In the context of tunnels, similar 3D FEM or coupled CFD–FEM approaches are being pursued to predict both the blast wave propagation and the structural deformation. Combined fluid-structure simulations (e.g., ALE methods in LS-DYNA or separate CFD + FEM coupling) enable a more accurate assessment of how mitigation measures perform under realistic hydrogen explosion scenarios.

In addition, recent hydrogen safety studies provide valuable insights specific to tunnel fires and explosions. An empirical correlation for blast wave decay in tunnels following hydrogen tank rupture was derived, based on similitude analysis [42]. It can serve as a benchmark to validate tunnel blast models. Another group of researchers [43] carried out CFD simulations of hydrogen release, dispersion, and combustion in a road tunnel with fuel cell vehicles, confirming that ventilation and tunnel geometry strongly influence hydrogen flame propagation. Moreover, in this study [44], the structural response of a hydrogen–air explosion in a tunnel-like geometry was investigated, finding that certain tunnel design parameters (e.g., cross-sectional shape and wall material) can significantly affect the blast impact on the structure. These recent contributions from the literature—particularly from the hydrogen safety domain—have been incorporated into our review to provide a more up-to-date and robust understanding of tunnel explosion phenomena and mitigation strategies.

3. Effect of Laybys on the Mitigation of the Blast Wave in a Tunnel

A study utilising CFD simulation has been conducted to evaluate how the presence of laybys impacts the mitigation of blast wave overpressure in a tunnel. ANSYS 2020 R2 Fluent served as the CFD engine, utilising a pressure-based solver alongside the PISO pressure-velocity algorithm. The numerical model incorporates large eddy simulation (LES) to address turbulence, employing the Smagorinsky–Lilly model for simulating sub-grid scale turbulence, and adopting the EDC for combustion with a one-step reaction. The governing equations stem from the filtered conservation equations for mass, momentum, and energy in their compressible forms. The tunnel walls and floor are treated as non-adiabatic to facilitate heat transfer from the combustion process, and no-slip wall conditions are applied. The external non-reflecting boundary is characterised as a pressure outlet set at zero gauge pressure. To improve the accuracy of the simulation for compressible flows, a second-order upwind discretisation scheme is employed for pressure, while convective terms also utilise a second-order upwind approach. Time advancement is executed using a first-order scheme. To preserve the mechanical energy of the compressed hydrogen, the volume of the simulated tank with “ideal gas” is adjusted downward compared to the actual tank volume. This adjustment is determined using the equation $V_{ideal}=V_{real}-mb$, where V is volume (m³), m denotes mass (kg), and b = 7.69 × 10⁻³ is the co-volume constant (m³/kg). The original time-step adaptation method is implemented to sustain a constant Courant–Friedrichs–Lewy (CFL) number of 0.2. All calculations involve 20 iterations for each time-step. In practice, each time-step is solved with an inner iteration loop until the solution meets a specified convergence tolerance. A cap of 20 iterations per time-step is based on preliminary tests for stability and accuracy; this was sufficient for the solver to converge the blast pressure at each time-step, while controlling computational cost. The CFD model is based on [39], and a complete validation and description can be found there.

The dimensions of the tunnel and laybys were derived from the Norwegian Road Tunnels standards [45]; the simulation involved a tunnel measuring 500 m in length and a hydrogen storage tank with a volume of 120 L at 700 Bar, positioned 50 m from the entrance of the double-lane tunnel, as illustrated in Figure 3.

The highest pressure peak was measured throughout the tunnel length for both the straight section and the laybys. As illustrated in Figure 4, the pressure graphs intersect within the straight section while decreasing in the laybys area, indicating virtually no influence on overpressure reduction upon exiting the laybys zone. This results in the conclusion that the expansion of the tunnel maintains the conservation of energy within the tunnel and does not serve as an effective mitigation strategy.

4. Structural Vulnerability to Hydrogen Tank Explosions

A rupture of a hydrogen tank within a tunnel can lead to significant structural damage because of the tunnel’s semi-open design. To diminish the risk of tunnels experiencing blasts, utilising passive mitigation techniques is a widely adopted approach. These passive mitigation strategies for tunnels focus on aspects such as their geometry, materials, and boundaries. The susceptibility of a tunnel may be lessened by altering the natural period and enhancing energy dissipation through these passive techniques. So far, modifying tunnel components, incorporating flexible supports, and employing high-performance materials represent three common passive mitigation strategies for tunnel structures [46].

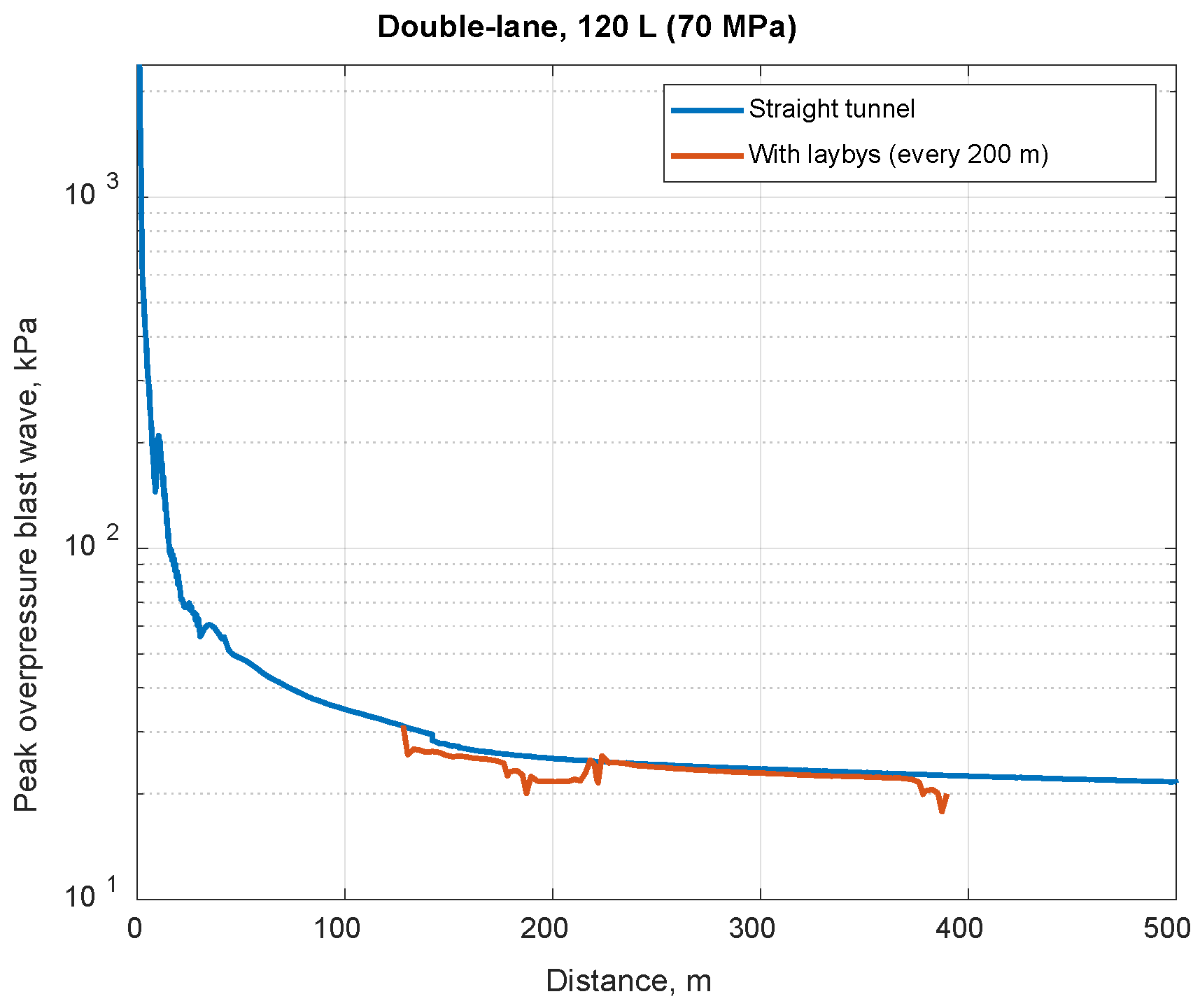
According to the HyTunnel project [47], the peak pressure generated by a blast wave from an unmitigated hydrogen tank explosion exceeds 100 kPa. For instance, one report [48] indicates an overpressure peak of 150 kPa on the ceiling slab of a tunnel with a cross-sectional area of 38 m², resulting from the explosion of a hydrogen tank with a capacity of 62.4 L, pressurised to 70.0 MPa, as can be seen from Figure 5. It is recognized that any combined CFD–FEM simulation of tunnel explosions must be validated against empirical evidence. To that end, we plan to validate our modelling approach in future work using available benchmark data. For instance, the blast–wave decay correlation developed by Molkov and Dery [42] for hydrogen tank ruptures in tunnels provides a quantitative target for our predictions of pressure attenuation along the tunnel. We will compare the simulated pressure–distance profiles to such correlations and adjust the model accordingly.

Another experimental study conducted by Park et al. (2022) [49] noted a maximum overpressure peak of 265 kPa, lasting 10 ms, during a detonation of a Type IV hydrogen tank measuring 870 mm × 363 mm filled with a pressure of 70.7 MPa in a cylindrical explosion test facility measuring 20 m in diameter and 15 m in height. The pressures mentioned are significantly greater than the load-bearing capacity of a tunnel ceiling slab that supports the ventilation system and is fabricated for typical conditions. This indicates that if this pressure were to be applied in a quasi-static manner, it could lead to the collapse of the slab. However, the length of time such overpressure occurs is very brief and likely much less than the natural vibration period of a long structural element, such as the previously mentioned concrete slab. For instance, in the first study cited, the overpressure dissipates in about 40 ms, while in the second study, it lasts for under 20 ms. In contrast, the natural vibration period of a simply supported slab that is 10 m long, with a minimum thickness of 350 mm and made of standard concrete reinforced with Ø 16 steel bars spaced at 150 mm, is approximately 10 ms.

Depending on how effective the mitigation strategies are, the peak pressure value can be considerably decreased. Although this reduction is crucial for ensuring the safety of individuals and limiting the safe distance for occupants, these strategies may not be as effective in alleviating structural repercussions, as the duration of the overpressure remains largely unchanged by these measures.

A more efficient structural solution would involve designing sacrificial stiffening components (like restraining rods) that would fail during an explosion, thereby increasing the natural vibration period of the tunnel slab or other vital elements. For example, a full-scale examination of tunnel segmental linings subjected to internal explosions was conducted by Yuetang Zhao [27], analysing the failure patterns and mechanical strength of the tunnel lining. According to these assessments, a proposed mitigation approach involved incorporating flexible damping cushions at the lining joints. This mitigation method allows for greater deformation of the tunnel structure and enhances energy dissipation within the tunnel.

Colombo (2016) [31] investigated the effect of high-performance materials on the blast resistance of tunnels. In this research, two materials were examined: HPFRCC and steel fibre-reinforced concrete (SFRC). The findings showed that single-layer specimens made with HPFRCC stored more energy compared to multi-layer specimens made with HPFRCC and SFRC under identical input energy conditions. Additionally, the multi-layer specimen exhibited a higher capacity to transfer energy to the soil and had a longer natural period. It is important to highlight that high-performance materials characterised by high stiffness and low mass can cause a higher natural frequency or longer natural period in structures. However, if the stiffness of the high-performance material is excessively high and the mass is too low, it could lead to a shorter natural period, which may not be suitable for some applications.

5. Limitations

The authors acknowledge several limitations of this study. First, this review is based on available literature and analytical reasoning, but it lacks new experimental data; as such, conclusions drawn (e.g., expected efficacy of certain mitigation measures) remain to be validated under real tunnel conditions. Second, our proposed CFD–FEM simulation framework for future study has not yet been benchmarked against experiments; validation will be required to ensure its accuracy. Additionally, the scope of literature covered, while extensive, is not exhaustive; due to limited published studies specifically on hydrogen tank blasts in tunnels, some mitigation concepts are extrapolated from conventional tunnel blast or fire research. Finally, we have made a few simplifying assumptions (e.g., treating the hydrogen tank rupture as an idealised worst-case explosion, assuming uniform tunnel geometry and neglecting traffic obstacles, and tunnel internal infrastructure) to focus on fundamental effects. These assumptions may limit the direct applicability of our quantitative insights to all scenarios. Despite these limitations, the authors believe the study provides a useful framework and identifies critical areas for further investigation.

6. Conclusions

In this study, we reviewed and assessed a range of explosion mitigation techniques applicable to road tunnels, with a particular focus on the emerging scenario of hydrogen fuel tank rupture during a fire. Our approach combined a comprehensive literature survey with engineering analysis to evaluate how various passive and active strategies can reduce blast effects in a tunnel environment.

Key findings indicate that an integrated safety design is crucial for tunnels intended for hydrogen vehicles. Passive design measures such as strategically placed branch tunnels, expansion chambers, or sharp curvature can help dissipate blast waves and lower peak overpressures. Active or add-on systems including ventilation shafts for venting explosions, drop-down perforated plates, and HPFRCC blast panels further contribute by either reducing the explosion’s intensity or shielding the tunnel structure and users. Notably, mitigating the consequences of a hydrogen tank blast requires both reducing the blast load (e.g., via venting or barriers that absorb energy) and enhancing the tunnel’s structural resistance (e.g., using high-performance materials or retrofitting weak points). A compilation of recent studies supports this dual approach: For instance, tailored blast barriers can cut down pressure transmitted to the structure by up to 80%, and advanced materials like HPFRCC can improve structural ductility under blast loading.

The outcomes of this review serve to guide tunnel safety engineering in the context of hydrogen energy. They suggest that current tunnel design standards may need updating to account for high-pressure tank explosion scenarios—for example, incorporating requirements for emergency venting or blast-resistant linings in tunnels with hydrogen transport. Importantly, our work brings hydrogen safety research (often conducted in laboratories or simulations) into the tunnel design area, bridging a gap between these fields.

Future work should focus on validating and extending these insights. We recommend detailed coupled CFD–FEM simulations of hydrogen tank rupture events in tunnels, validated against experiments or real incident data, to quantify the benefits of different mitigation measures (e.g., recent blast wave decay data for tunnel blasts [42] to account for the energy loss due to mechanical deformation of obstacles and vehicles). Field tests or large-scale experiments on promising techniques (such as drop-down plates or novel hydrogen tank technologies such as “TPRD-less” self-venting tanks that prevent explosions [1]) would also be invaluable. By addressing these research needs, the tunnel engineering community can develop optimised, multi-faceted safety strategies—ensuring that the advent of hydrogen vehicles does not compromise the safety of underground transportation infrastructure.