Interpretable Machine Learning for High-Accuracy Reservoir Temperature Prediction in Geothermal Energy Systems
Abstract
1. Introduction
2. Theory
2.1. Support Vector Regression (SVR)
2.2. Random Forest (RF)
2.3. Deep Neural Network (DNN)
2.4. Gaussian Process (GP)
2.5. Graph Neural Network (GNN)
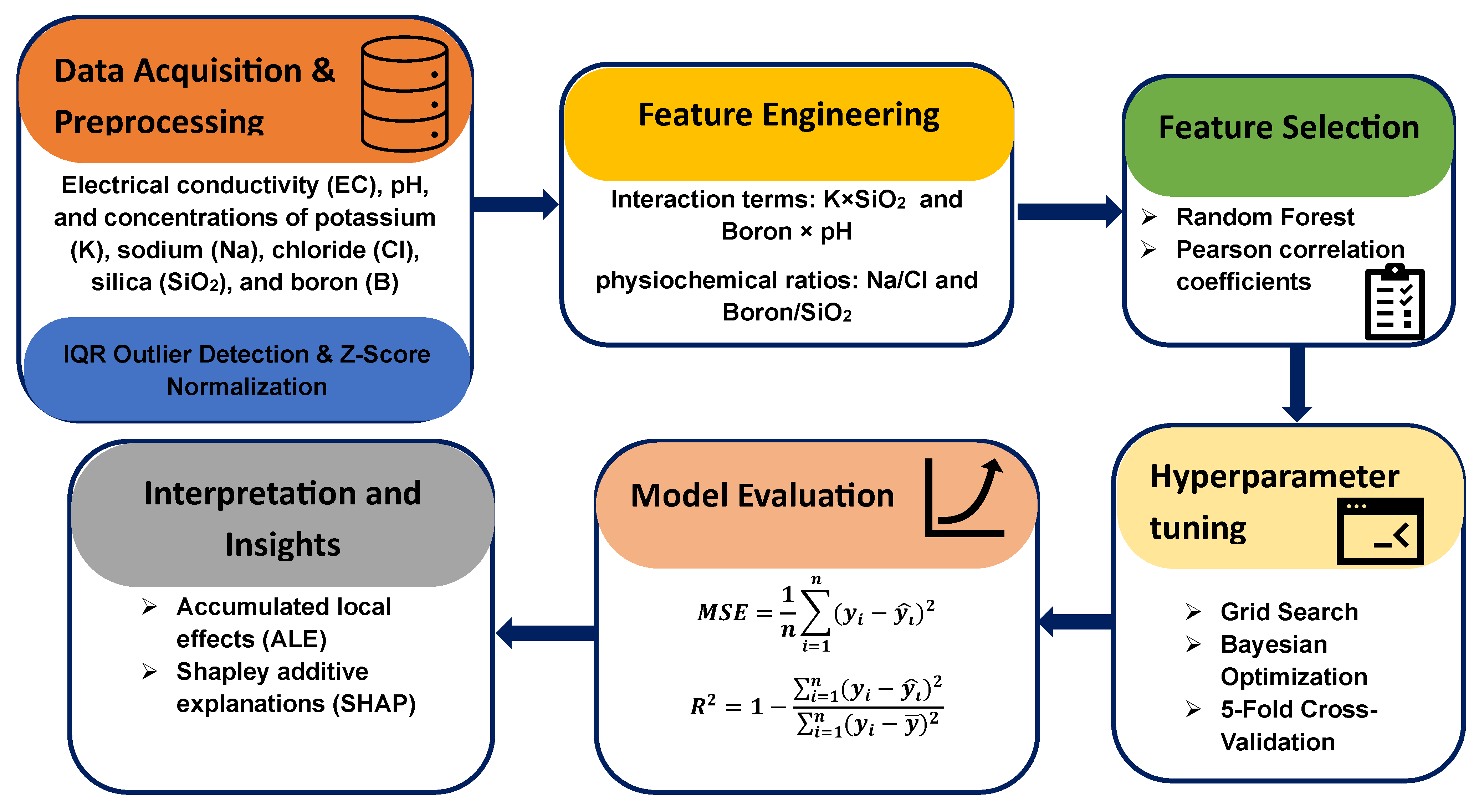
3. Methodology
4. Results and Discussion
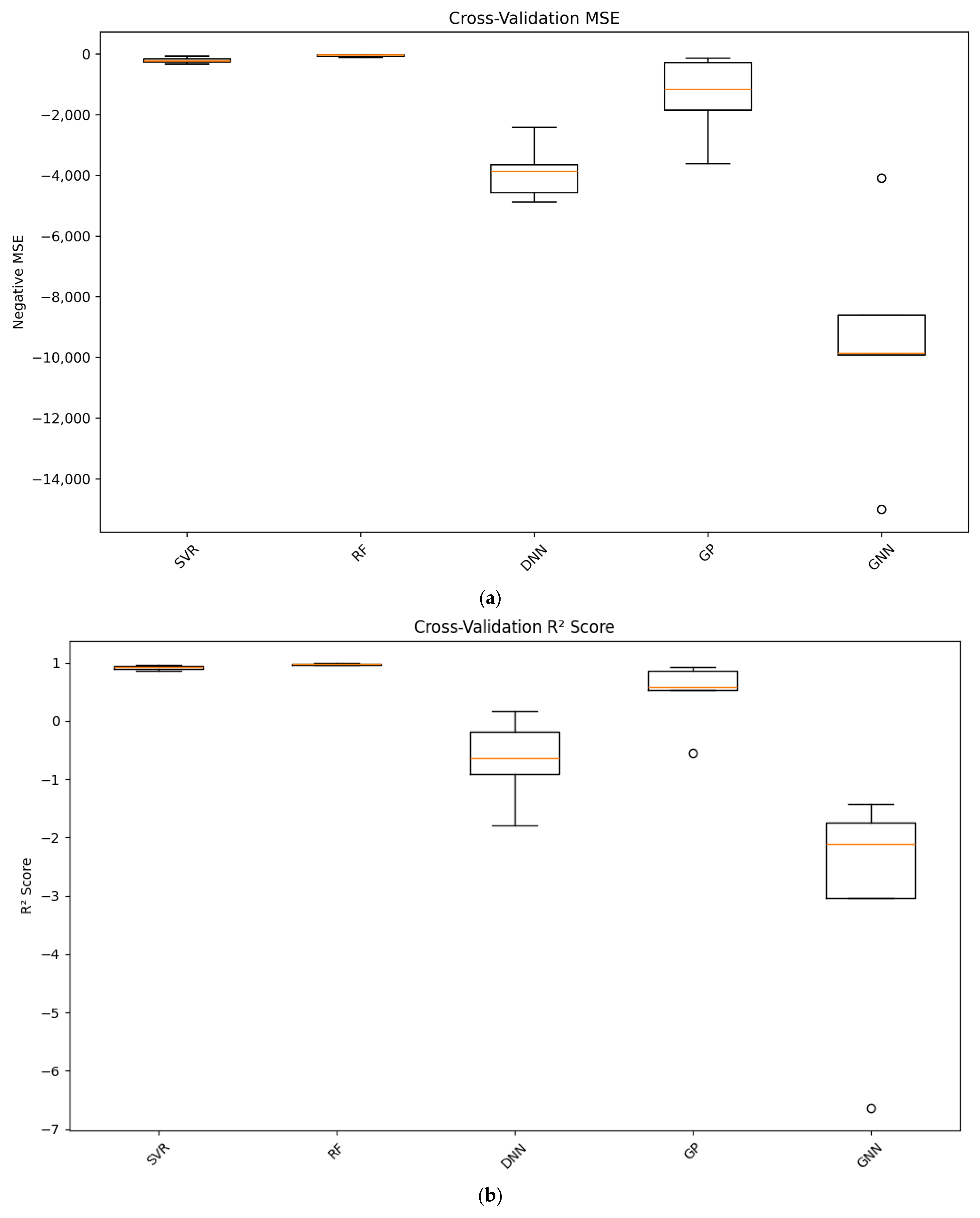
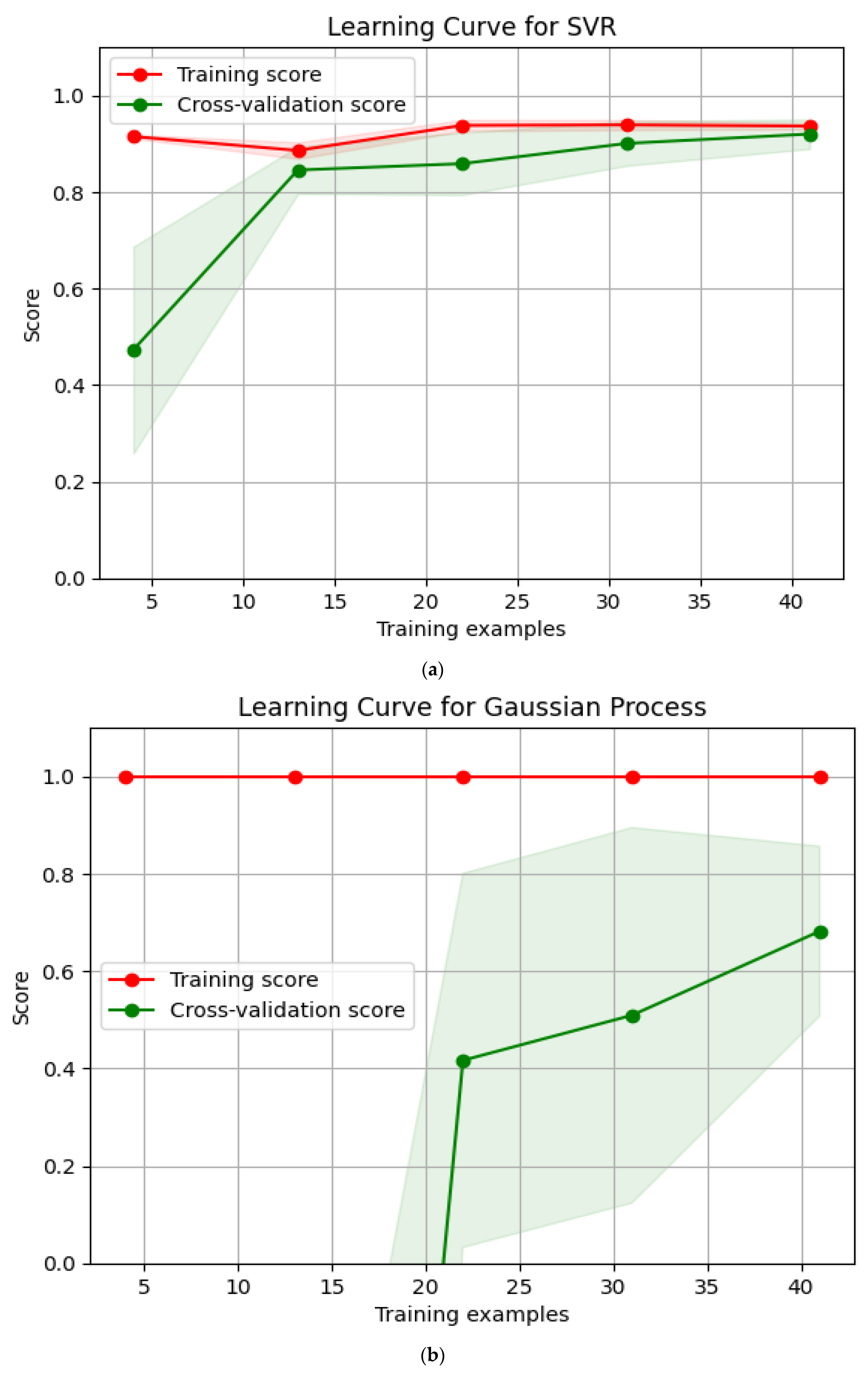
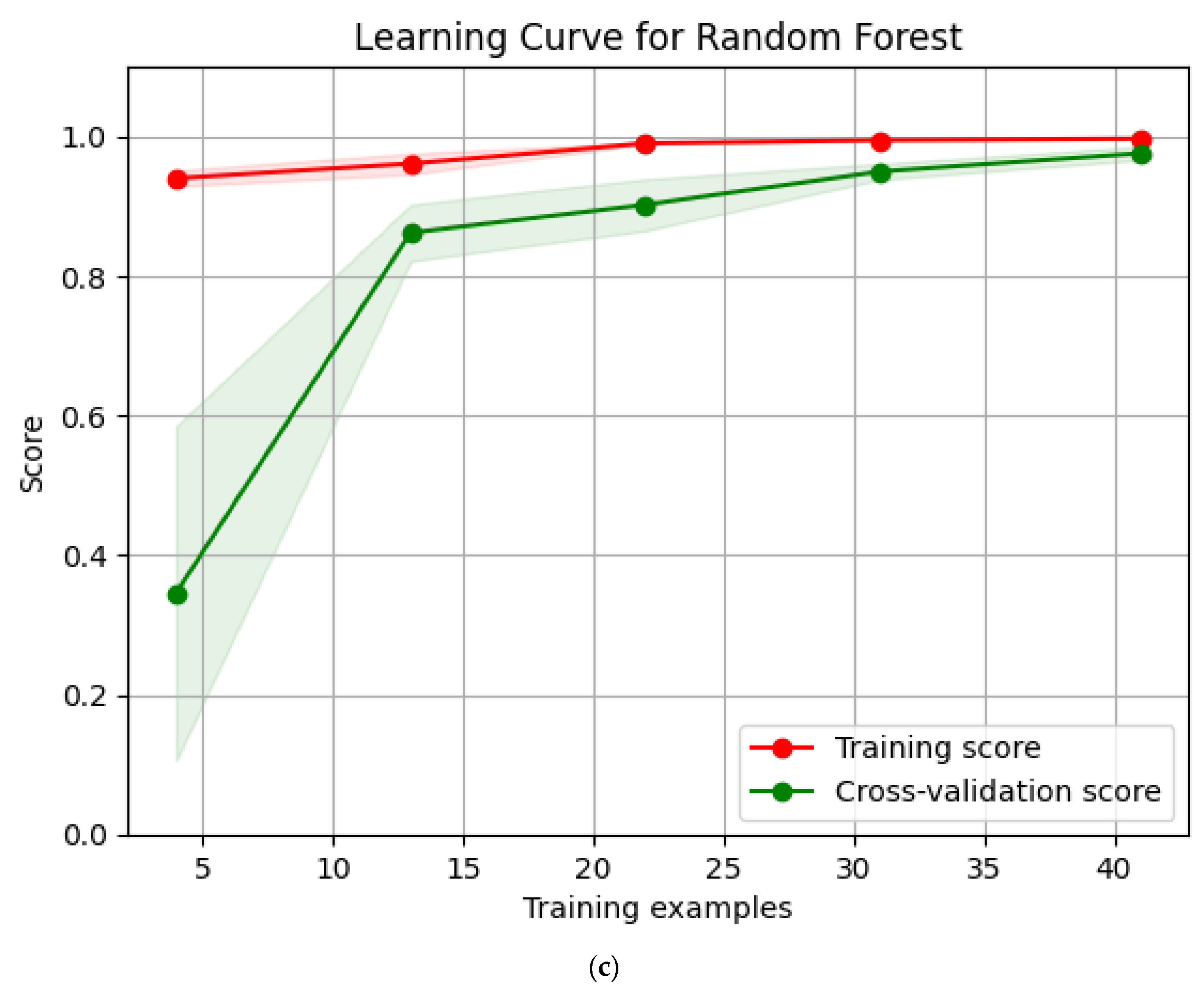
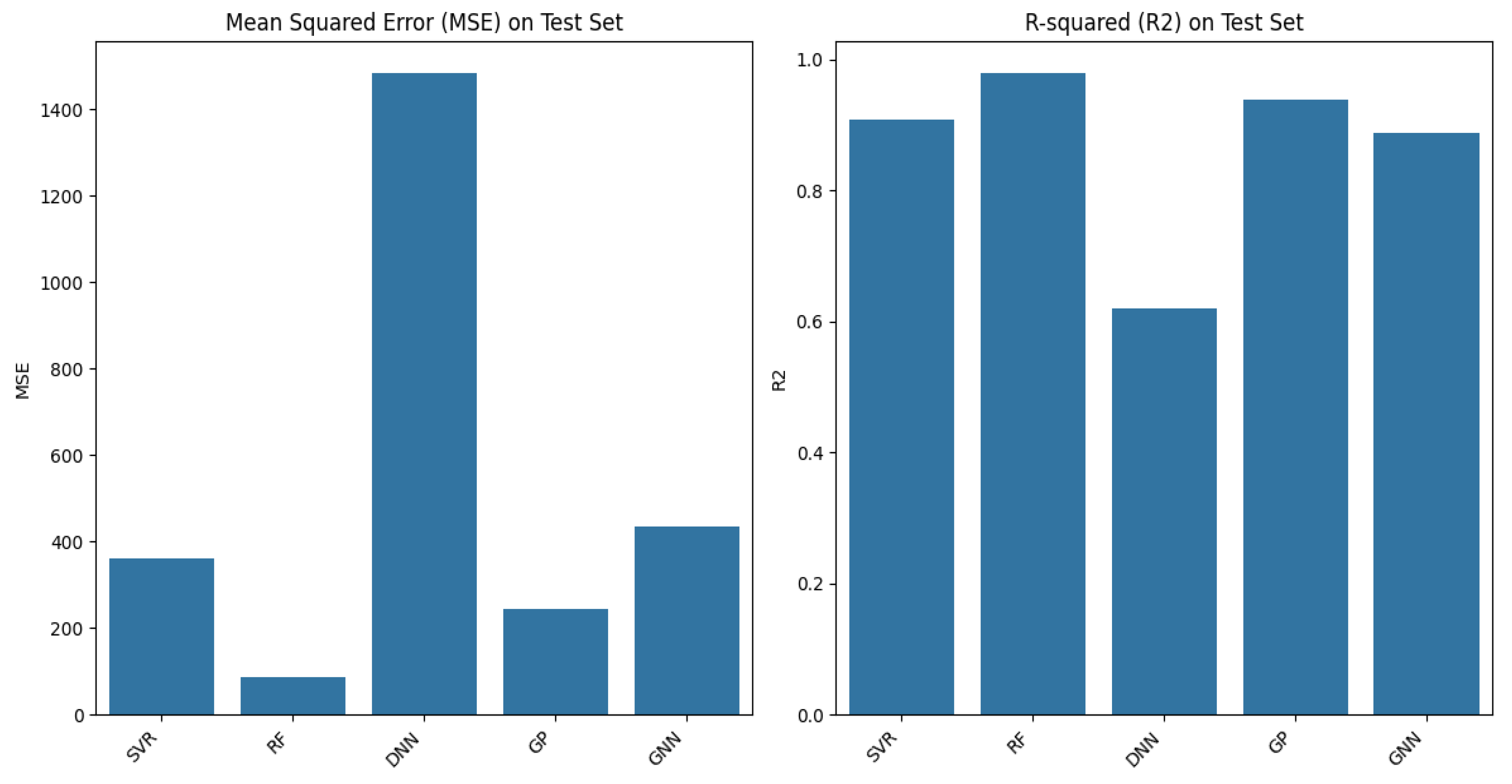
4.1. Comparison of Model Prediction Performance
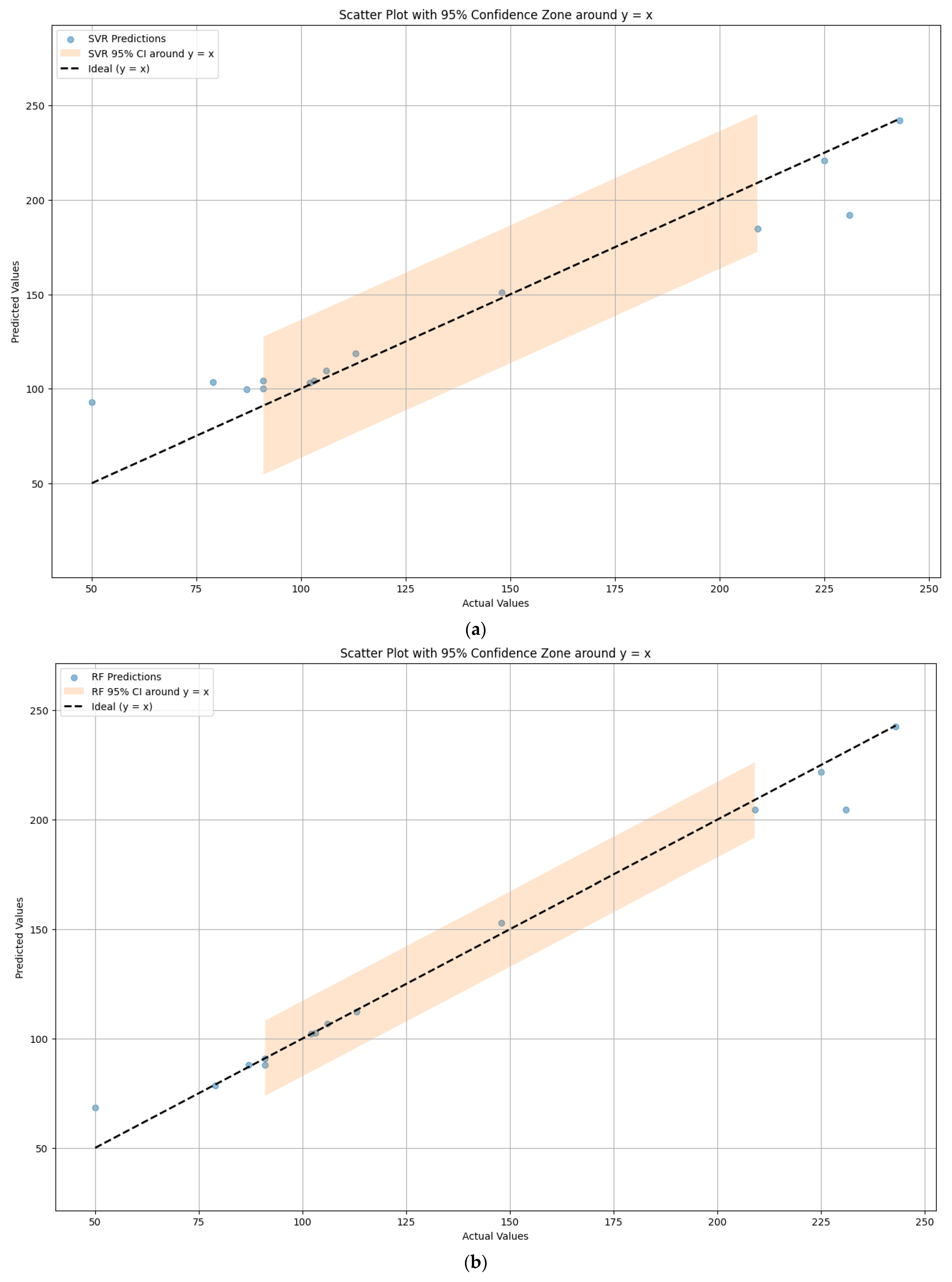
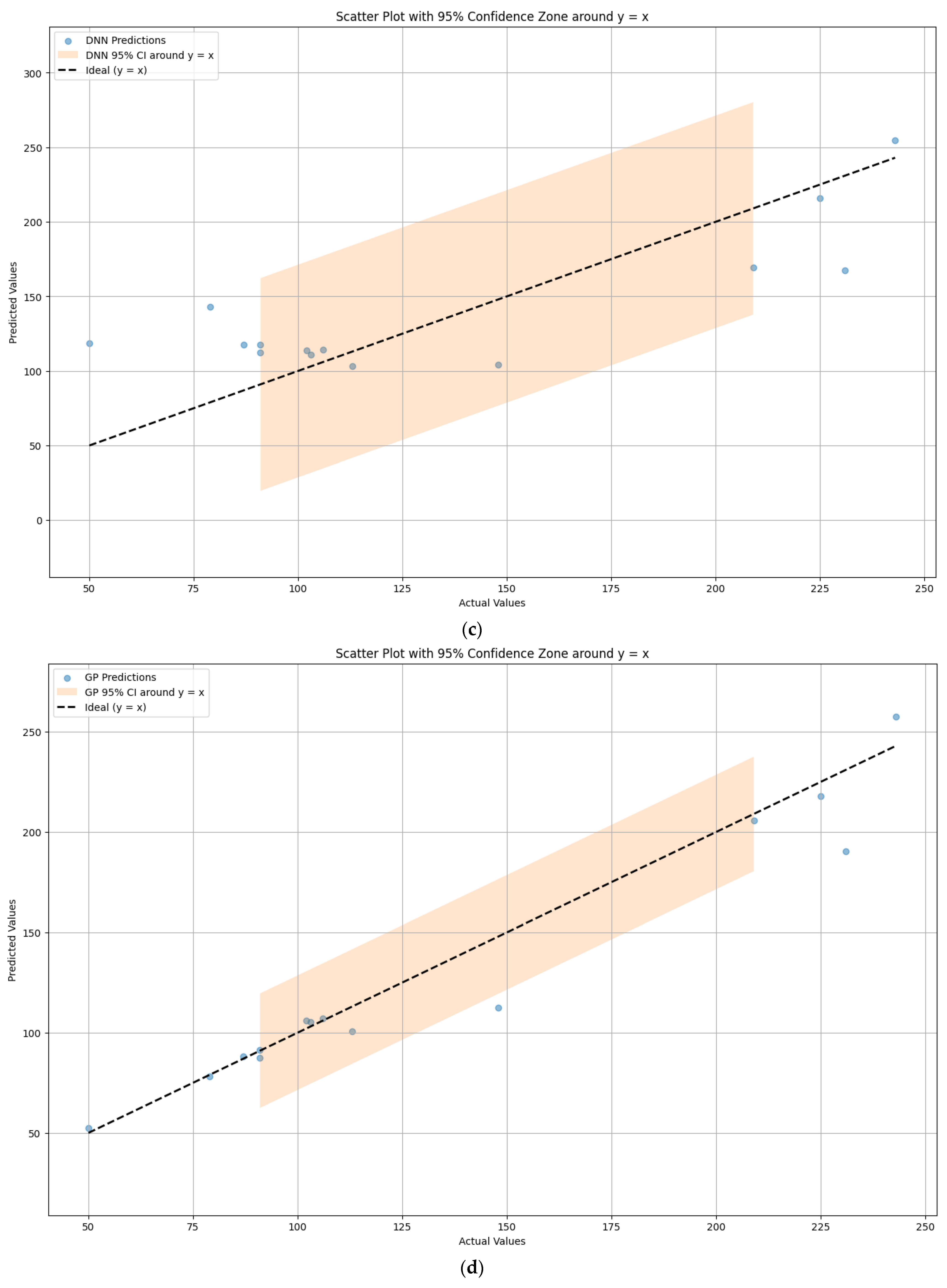
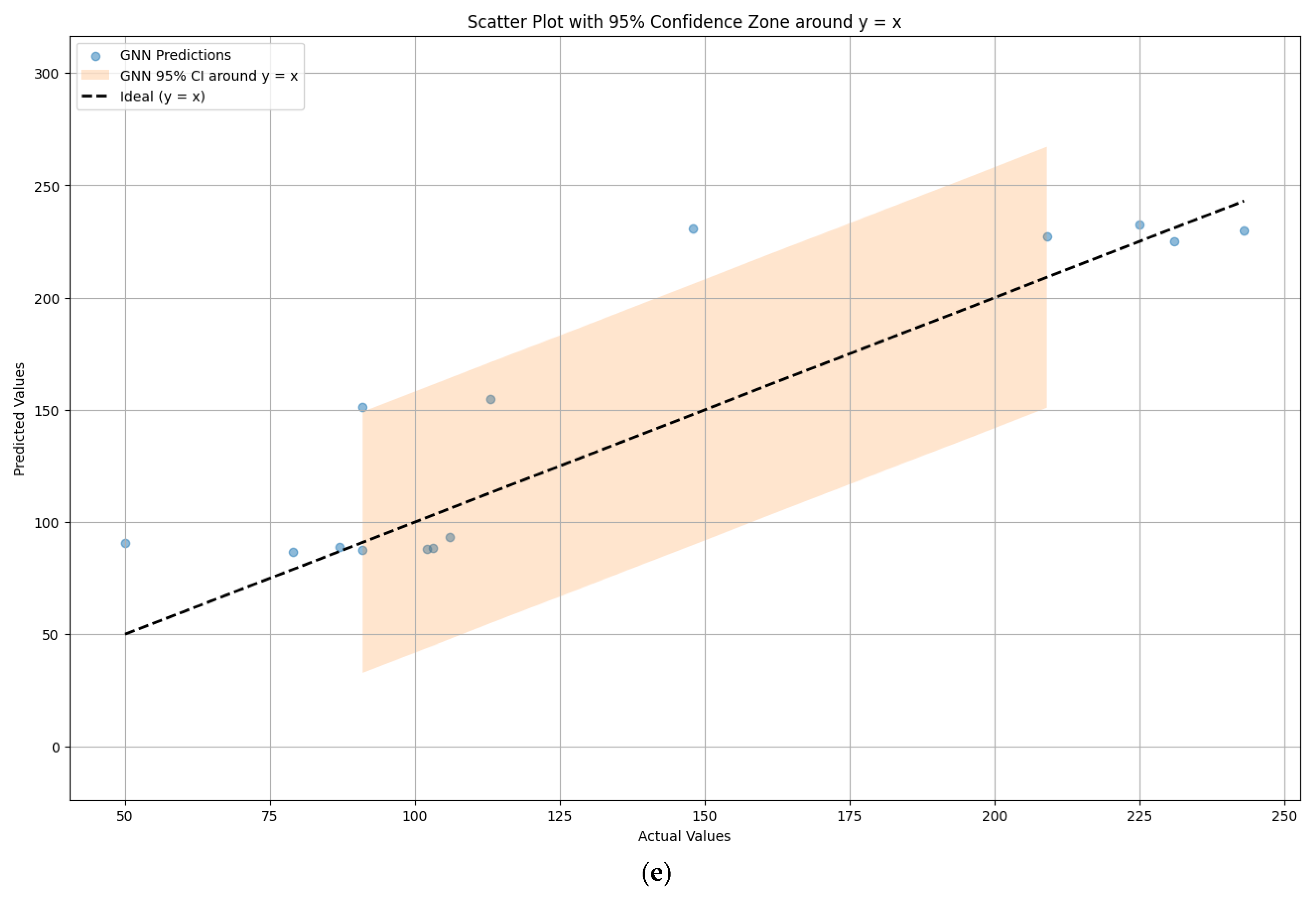
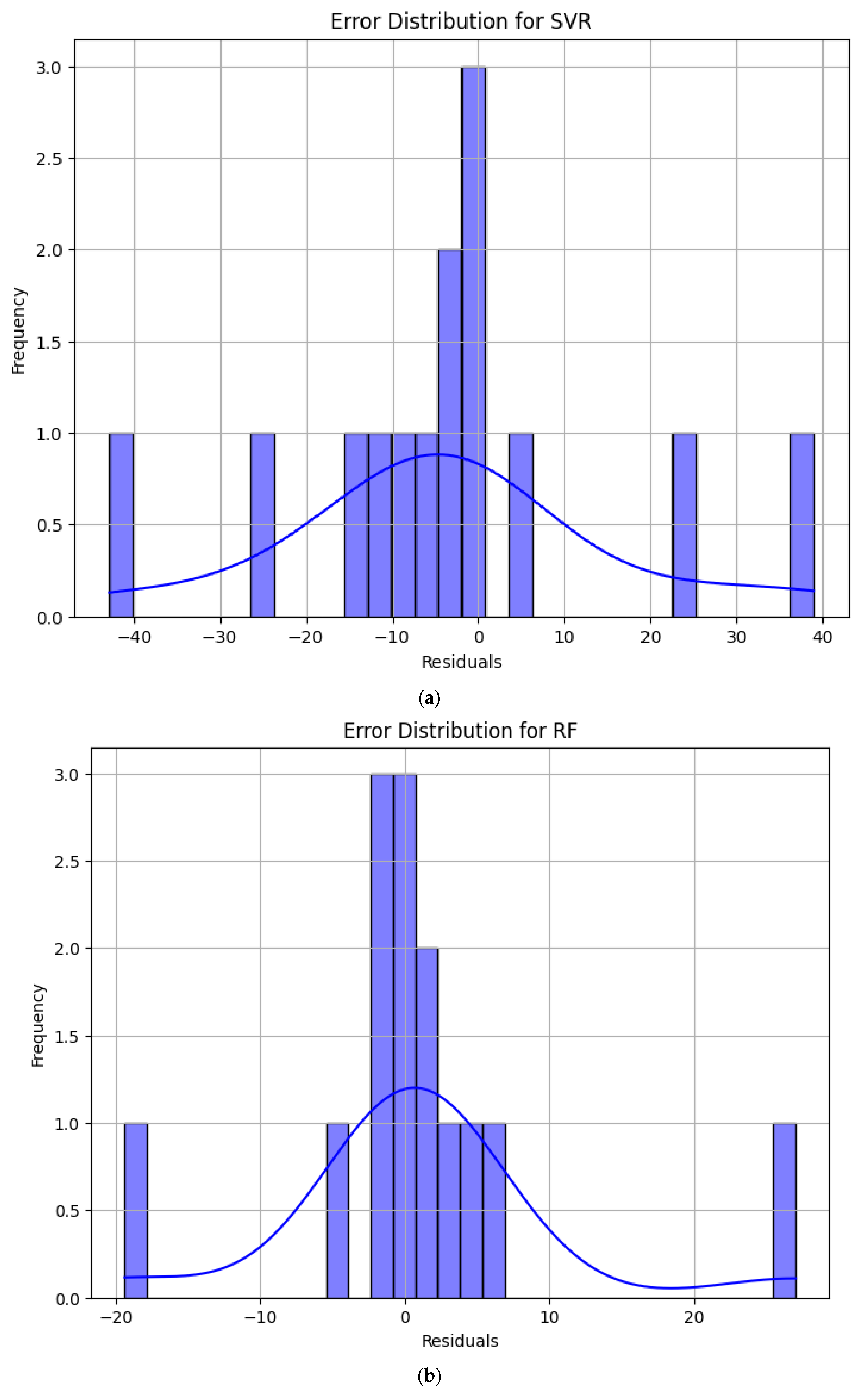
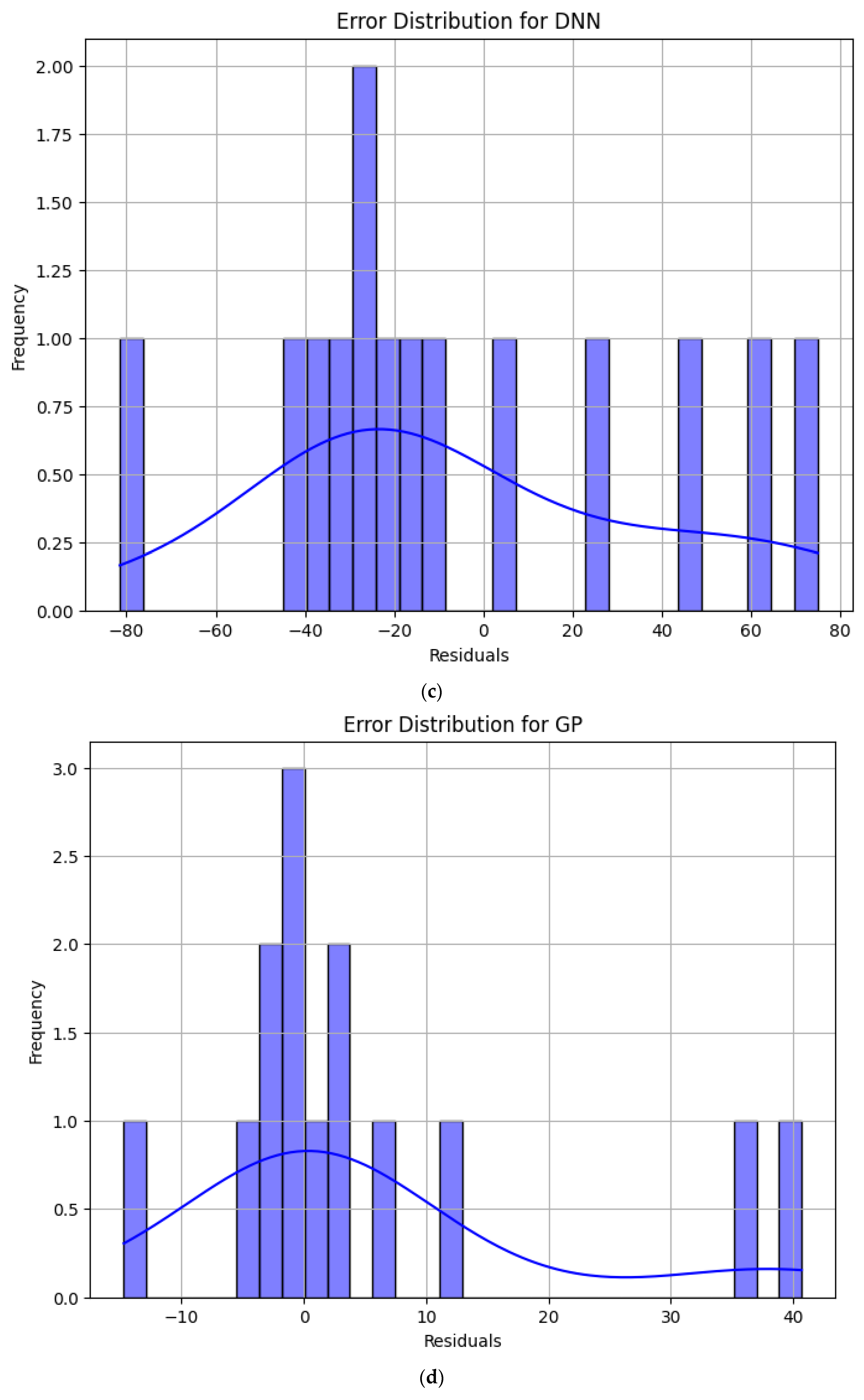
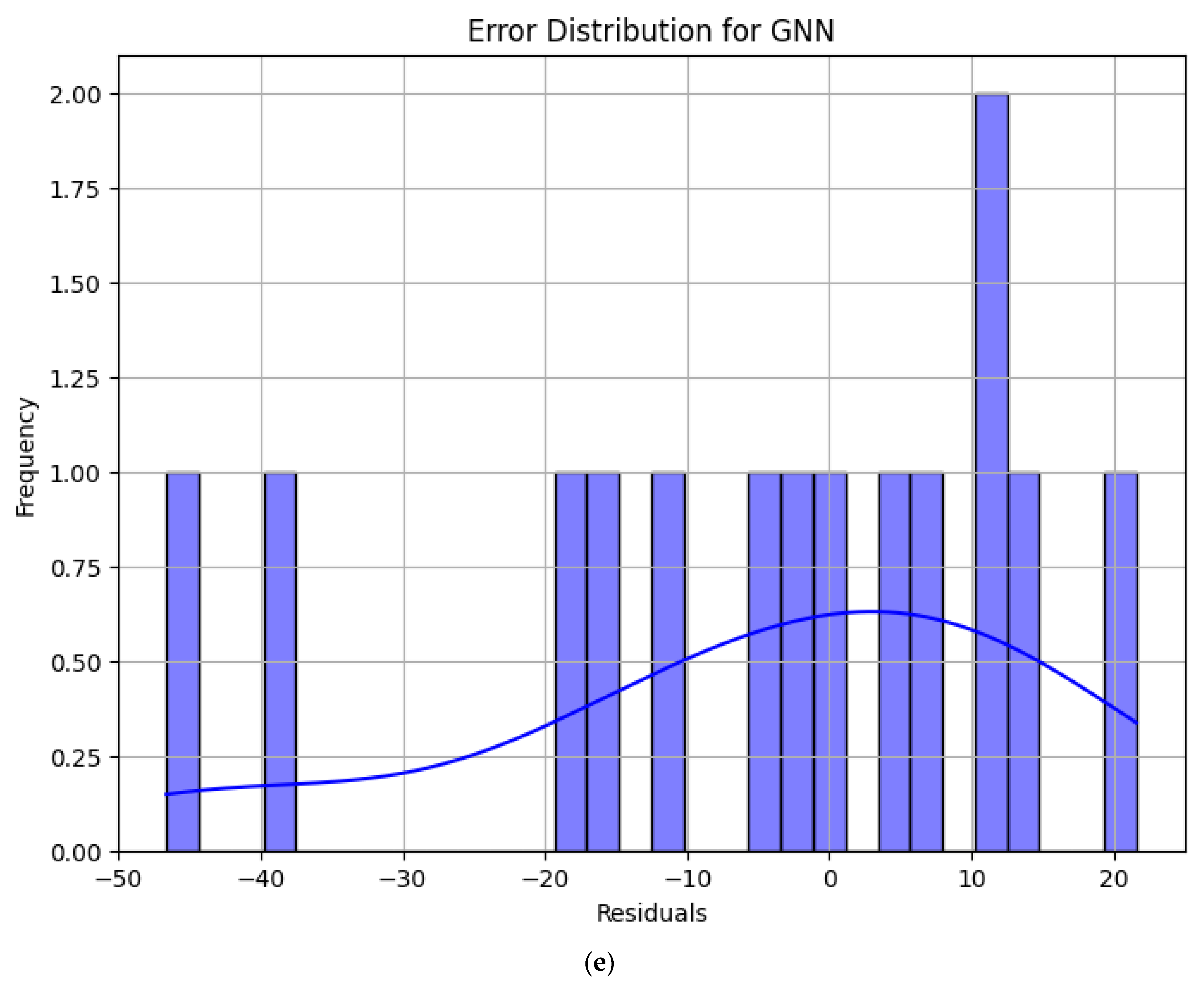
4.2. Error Analysis of Model Prediction Results
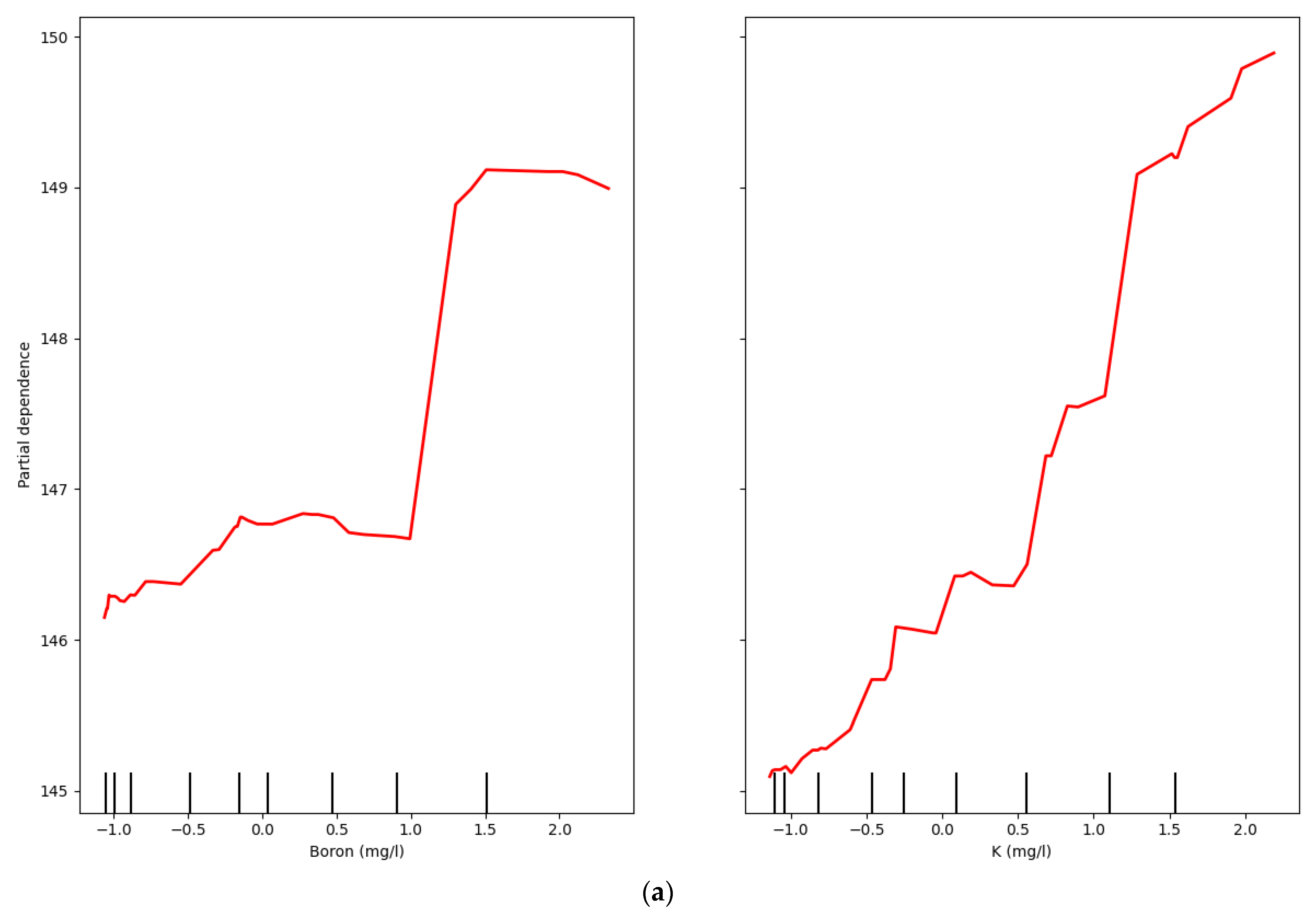
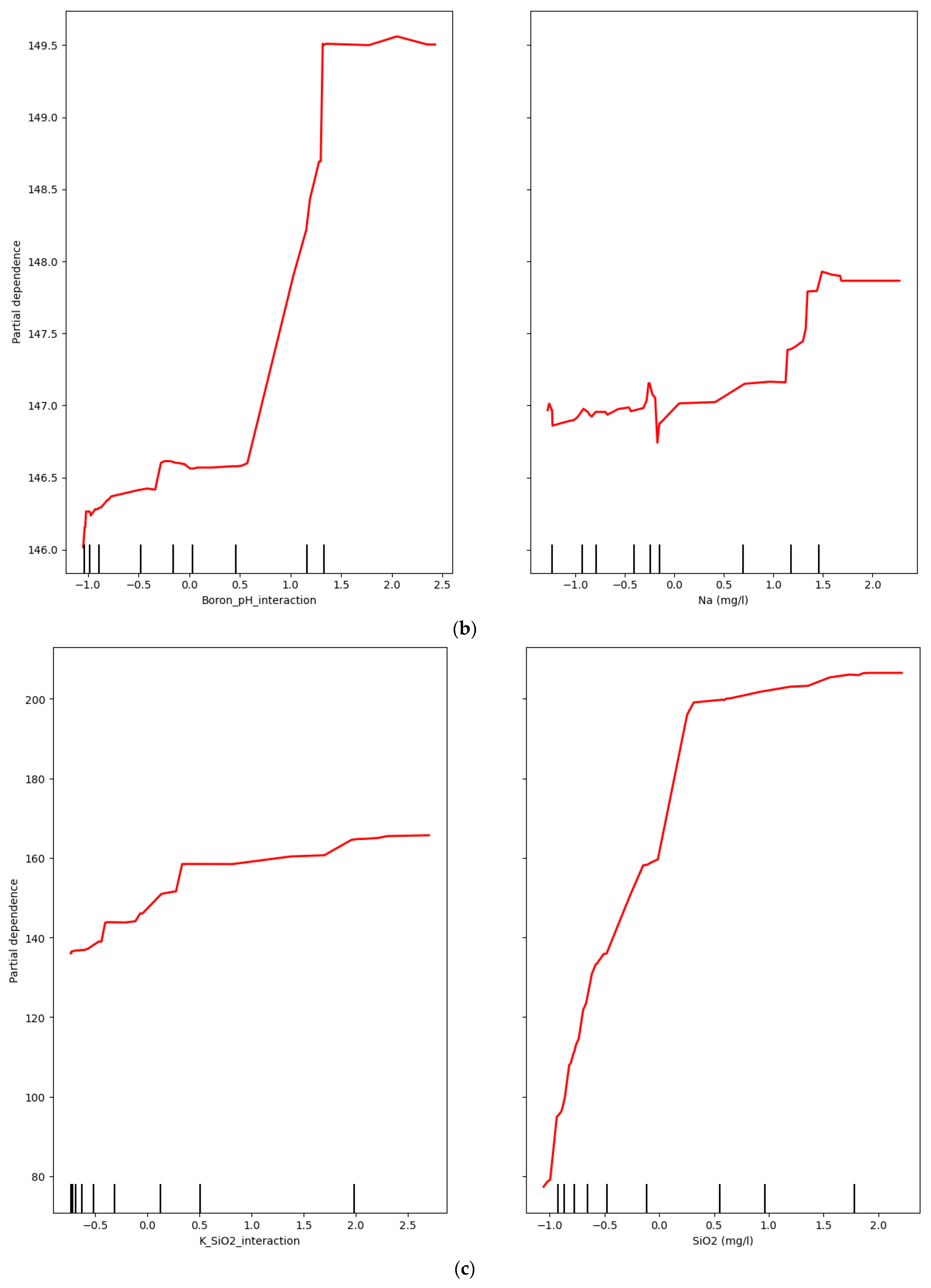
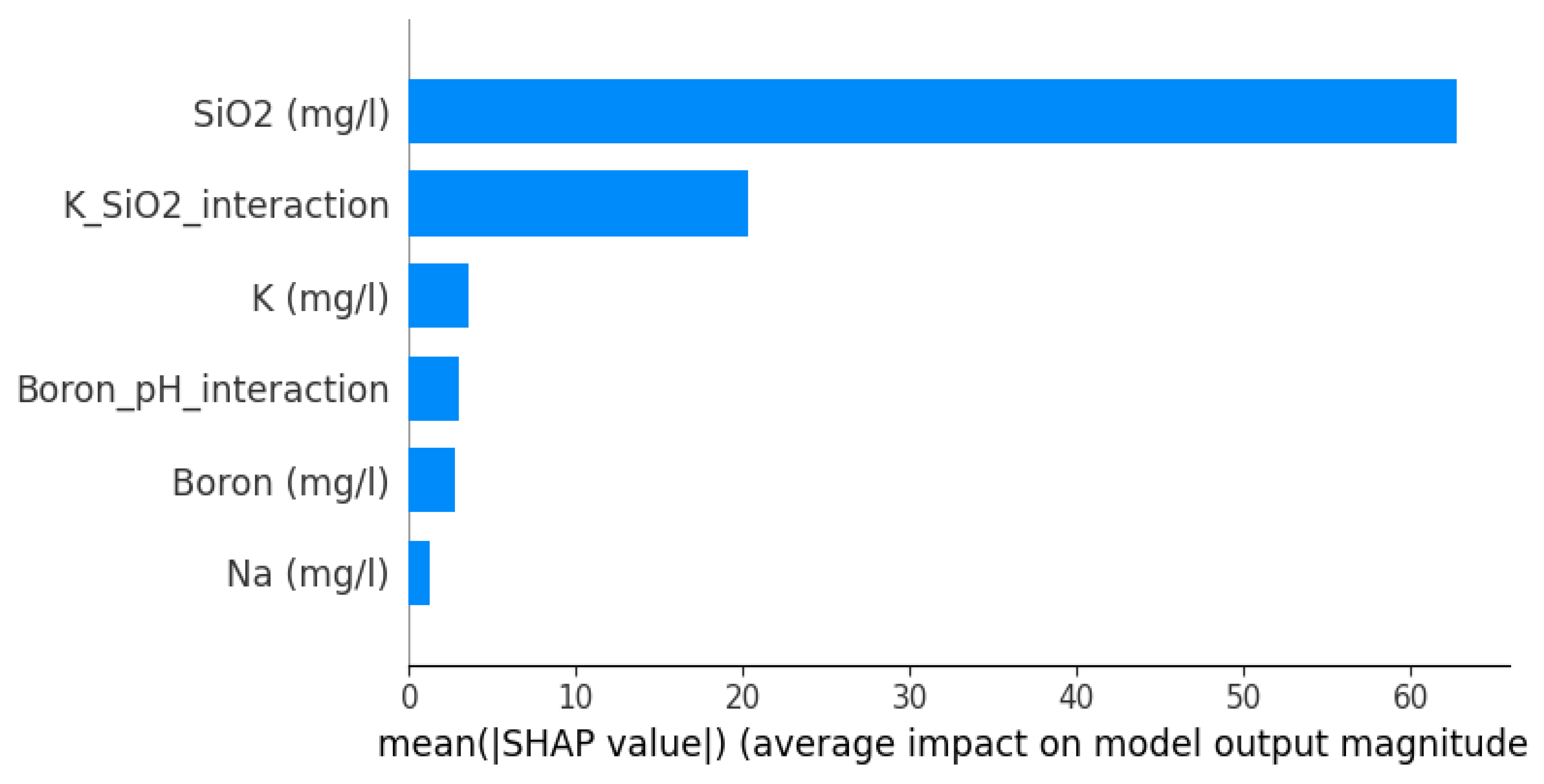
4.3. Analysis of Model Interpretability
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ALE | Accumulated local effects |
| ANNs | Artificial neural networks |
| BHT | Bottom-hole temperature |
| BPNN | Back propagation neural network |
| DNN | Deep neural networks |
| ELM | Extreme learning machine |
| GMDH | Group method of data handling |
| GNN | Graph neural networks |
| GCNs | Graph convolutional networks |
| GATs | Graph attention networks |
| GP | Gaussian process regression |
| GRNN | Generalized regression neural network |
| IQR | Interquartile range |
| MAE | Mean absolute error |
| ML | Machine learning |
| NGB | Natural gradient boosting |
| RF | Random forest |
| RMSE | Root mean square error |
| SFT | Static formation temperatures |
| SHAP | Shapley additive explanations |
| SVR | Support vector regression |
| Variables | |
| Prediction of the b-th tree | |
| Average of the predictions | |
| Noise variance | |
| a | Learnable attention vector |
| a(l−1) | Activation from the previous layer |
| b | Bias term |
| B | number of trees |
| b(l) | Bias vector for layer l |
| g(l) | Activation function |
| hi(l) | Feature vector of node i at layer l |
| K (X, X) | Kernel matrix |
| k(x,x′) | Covariance function |
| m(x) | Mean function |
| w | Weight vector |
| W(l) | Weight matrix |
| W(l) | Weight matrix for layer l |
| X | Raw feature value |
| αij | Attention coefficient |
| γ | Kernel coefficient |
| ΔImpurity (f, t) | Reduction in variance due to splitting on feature f at node t |
| μ | Mean of feature |
| ξi, ξi∗ | Slack variables |
| σ | Standard deviation of feature |
| ϕ(xi) | Mapping to a higher-dimensional feature space |
| Set of neighbors of node i |
References
- Younger, P.L. Geothermal Energy: Delivering on the Global Potential. Energies 2015, 8, 11737–11754. [Google Scholar]
- Anderson, A.; Rezaie, B. Geothermal technology: Trends and potential role in a sustainable future. Appl. Energy 2019, 248, 18–34. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, M.; Zhou, H.; Chen, L.; Wang, X. Performance evaluation of enhanced geothermal systems with intermittent thermal extraction for sustainable energy production. J. Clean. Prod. 2024, 434, 139954. [Google Scholar] [CrossRef]
- Izadi, G.; Freitag, H.-C. Resource assessment and management for different geothermal systems (hydrothermal, enhanced geothermal, and advanced geothermal systems). In Geothermal Energy Engineering; Elsevier: Amsterdam, The Netherlands, 2025; pp. 23–72. [Google Scholar]
- Wang, K.; Yuan, B.; Ji, G.; Wu, X. A comprehensive review of geothermal energy extraction and utilization in oilfields. J. Pet. Sci. Eng. 2018, 168, 465–477. [Google Scholar] [CrossRef]
- Song, G.; Shi, Y.; Xu, F.; Song, X.; Li, G.; Wang, G.; Lv, Z. The magnitudes of multi-physics effects on geothermal reservoir characteristics during the production of enhanced geothermal system. J. Clean. Prod. 2024, 434, 140070. [Google Scholar] [CrossRef]
- Sharmin, T.; Khan, N.R.; Akram, M.S.; Ehsan, M.M. A state-of-the-art review on geothermal energy extraction, utilization, and improvement strategies: Conventional, hybridized, and enhanced geothermal systems. Int. J. Thermofluids 2023, 18, 100323. [Google Scholar] [CrossRef]
- Muñoz, G.; Bauer, K.; Moeck, I.; Schulze, A.; Ritter, O. Exploring the Groß Schönebeck (Germany) geothermal site using a statistical joint interpretation of magnetotelluric and seismic tomography models. Geothermics 2010, 39, 35–45. [Google Scholar] [CrossRef]
- Spichak, V.; Manzella, A. Electromagnetic sounding of geothermal zones. J. Appl. Geophys. 2009, 68, 459–478. [Google Scholar] [CrossRef]
- Bundschuh, J.; Arriaga, M.S. Introduction to the Numerical Modeling of Groundwater and Geothermal Systems; CRC Press: London, UK, 2010; Volume 10, p. b10499. [Google Scholar]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Ranjbarzadeh, R.; Sappa, G. Numerical and Experimental Study of Fluid Flow and Heat Transfer in Porous Media: A Review Article. Energies 2025, 18, 976. [Google Scholar] [CrossRef]
- Huntington, K.W.; Lechler, A.R. Carbonate clumped isotope thermometry in continental tectonics. Tectonophysics 2015, 647, 1–20. [Google Scholar] [CrossRef]
- Guan, B.; Xia, J.; Liu, Y.; Zhang, H.; Zhou, C. Near-surface radial anisotropy tomography of geothermal reservoir using dense seismic nodal array. J. Phys. Conf. Ser. 2023, 2651, 012023. [Google Scholar] [CrossRef]
- Jia, X.; Lin, Y.; Ouyang, M.; Wang, X.; He, H. Numerical simulation of hydrothermal flow in the North China Plain: A case study of Henan Province. Geothermics 2024, 118, 102910. [Google Scholar] [CrossRef]
- Kadri, M.; Muztaza, N.M.; Nordin, M.N.M.; Zakaria, M.T.; Rosli, F.N.; Mohammed, M.A.; Zulaika, S. Integrated geophysical methods used to explore geothermal potential areas in Siogung-Ogung, North Sumatra, Indonesia. Bull. Geol. Soc. Malays. 2023, 76, 47–53. [Google Scholar] [CrossRef]
- Buster, G.; Siratovich, P.; Taverna, N.; Rossol, M.; Weers, J.; Blair, A.; Huggins, J.; Siega, C.; Mannington, W.; Urgel, A. A new modeling framework for geothermal operational optimization with machine learning (Gooml). Energies 2021, 14, 6852. [Google Scholar] [CrossRef]
- Khaled, M.S.; Wang, N.; Ashok, P.; van Oort, E.; Wisian, K. Real-time prediction of bottom-hole circulating temperature in geothermal wells using machine learning models. Geoenergy Sci. Eng. 2024, 238, 212891. [Google Scholar] [CrossRef]
- Otchere, D.A.; Latiff, A.H.A.; Taki, M.Y.; Dafyak, L.A. Machine-learning-based proxy modelling for geothermal field development optimisation. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2023; p. D021S027R004. [Google Scholar]
- Ahmadi, M. Advancing Geotechnical Evaluation of Wellbores: A Robust and Precise Model for Predicting Uniaxial Compressive Strength (UCS) of Rocks in Oil and Gas Wells. Appl. Sci. 2024, 14, 10441. [Google Scholar] [CrossRef]
- Ahmadi, M. Artificial Intelligence for a More Sustainable Oil and Gas Industry and the Energy Transition: Case Studies and Code Examples; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Dashtgoli, D.S.; Giustiniani, M.; Busetti, M.; Cherubini, C. Artificial intelligence applications for accurate geothermal temperature prediction in the lower Friulian Plain (north-eastern Italy). J. Clean. Prod. 2024, 460, 142452. [Google Scholar] [CrossRef]
- Bassam, A.; Santoyo, E.; Andaverde, J.; Hernández, J.; Espinoza-Ojeda, O.M. Estimation of static formation temperatures in geothermal wells by using an artificial neural network approach. Comput. Geosci. 2010, 36, 1191–1199. [Google Scholar] [CrossRef]
- Pérez-Zárate, D.; Santoyo, E.; Acevedo-Anicasio, A.; Díaz-González, L.; García-López, C. Evaluation of artificial neural networks for the prediction of deep reservoir temperatures using the gas-phase composition of geothermal fluids. Comput. Geosci. 2019, 129, 49–68. [Google Scholar] [CrossRef]
- Tut Haklidir, F.S.; Haklidir, M. Prediction of reservoir temperatures using hydrogeochemical data, Western Anatolia geothermal systems (Turkey): A machine learning approach. Nat. Resour. Res. 2020, 29, 2333–2346. [Google Scholar] [CrossRef]
- Haklıdır, F.S.T.; Haklıdır, M. The reservoir temperature prediction using hydrogeochemical indicators by machine learning: Western Anatolia (Turkey) case. In Proceedings of the World Geothermal Congress, Online, 26 April–1 May 2020; p. 1. [Google Scholar]
- Shahdi, A.; Lee, S.; Karpatne, A.; Nojabaei, B. Exploratory analysis of machine learning methods in predicting subsurface temperature and geothermal gradient of Northeastern United States. Geotherm. Energy 2021, 9, 18. [Google Scholar] [CrossRef]
- Altay, E.V.; Gurgenc, E.; Altay, O.; Dikici, A. Hybrid artificial neural network based on a metaheuristic optimization algorithm for the prediction of reservoir temperature using hydrogeochemical data of different geothermal areas in Anatolia (Turkey). Geothermics 2022, 104, 102476. [Google Scholar] [CrossRef]
- Ibrahim, B.; Konduah, J.O.; Ahenkorah, I. Predicting reservoir temperature of geothermal systems in Western Anatolia, Turkey: A focus on predictive performance and explainability of machine learning models. Geothermics 2023, 112, 102727. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Support vector regression. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 123–140. [Google Scholar]
- Deng, N.; Tian, Y.; Zhang, C. Support Vector Machines: Optimization Based Theory, Algorithms, and Extensions; CRC press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Basak, D.; Pal, S.; Patranabis, D.C. Support vector regression. Neural Inf. Process.-Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Clarke, S.M.; Griebsch, J.H.; Simpson, T.W. Analysis of support vector regression for approximation of complex engineering analyses. J. Mech. Des. 2005, 127, 1077–1087. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Ngu, J.C.Y.; Yeo, W.S.; Thien, T.F.; Nandong, J. A comprehensive overview of the applications of kernel functions and data-driven models in regression and classification tasks in the context of software sensors. Appl. Soft Comput. 2024, 164, 111975. [Google Scholar] [CrossRef]
- Zhang, L.; Suganthan, P.N. Random forests with ensemble of feature spaces. Pattern Recognit. 2014, 47, 3429–3437. [Google Scholar] [CrossRef]
- Reis, I.; Baron, D.; Shahaf, S. Probabilistic random forest: A machine learning algorithm for noisy data sets. Astron. J. 2018, 157, 16. [Google Scholar] [CrossRef]
- Kotsiantis, S. Combining bagging, boosting, rotation forest and random subspace methods. Artif. Intell. Rev. 2011, 35, 223–240. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Vieira, S.; Pinaya, W.H.L.; Garcia-Dias, R.; Mechelli, A. Deep neural networks. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 157–172. [Google Scholar]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Fundamentals of artificial neural networks and deep learning. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Berlin/Heidelberg, Germany, 2022; pp. 379–425. [Google Scholar]
- Kamalov, F.; Leung, H.H. Deep learning regularization in imbalanced data. In Proceedings of the 2020 International Conference on Communications, Computing, Cybersecurity, and Informatics (CCCI), Virtual, 3–5 November 2020; pp. 1–5. [Google Scholar]
- Mehdi, C.A.; Nour-Eddine, J.; Mohamed, E. Check for updates Regularization in CNN: A Mathematical Study for L1, L2 and Dropout Regularizers. In International Conference on Advanced Intelligent Systems for Sustainable Development: Volume 1-Advanced Intelligent Systems on Artificial Intelligence, Software, and Data Science; Springer: Berlin/Heidelberg, Germany, 2023; Volume 637, p. 442. [Google Scholar]
- Liu, H.; Ong, Y.-S.; Shen, X.; Cai, J. When Gaussian process meets big data: A review of scalable GPs. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4405–4423. [Google Scholar] [CrossRef] [PubMed]
- Khemani, B.; Patil, S.; Kotecha, K.; Tanwar, S. A review of graph neural networks: Concepts, architectures, techniques, challenges, datasets, applications, and future directions. J. Big Data 2024, 11, 18. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Haklidir, F.T.; Sengun, R.; Haizlip, J.R. The geochemistry of the deep reservoir wells in Kizildere (Denizli City) geothermal field (Turkey). Geochemistry 2015, 19, 25. [Google Scholar]
- Avşar, Ö.; Altuntaş, G. Hydrogeochemical evaluation of Umut geothermal field (SW Turkey). Environ. Earth Sci. 2017, 76, 582. [Google Scholar] [CrossRef]
- Tut Haklıdır, F. Geochemical Study of Thermal, Mineral and Ground Water in Bursa City and Surroundings. Ph.D. Thesis, Dokuz Eylul University, İzmir, Türkiye, 2007. [Google Scholar]
- Gökgöz, A. Geochemistry of the Kizildere-Tekkehamam-Buldan-Pamukkale Geothermal Fields, Turkey; United Nations University: Tokyo, Japan, 1998. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, M. Interpretable Machine Learning for High-Accuracy Reservoir Temperature Prediction in Geothermal Energy Systems. Energies 2025, 18, 3366. https://doi.org/10.3390/en18133366
Ahmadi M. Interpretable Machine Learning for High-Accuracy Reservoir Temperature Prediction in Geothermal Energy Systems. Energies. 2025; 18(13):3366. https://doi.org/10.3390/en18133366
Chicago/Turabian StyleAhmadi, Mohammadali. 2025. "Interpretable Machine Learning for High-Accuracy Reservoir Temperature Prediction in Geothermal Energy Systems" Energies 18, no. 13: 3366. https://doi.org/10.3390/en18133366
APA StyleAhmadi, M. (2025). Interpretable Machine Learning for High-Accuracy Reservoir Temperature Prediction in Geothermal Energy Systems. Energies, 18(13), 3366. https://doi.org/10.3390/en18133366






