Pulse Compression Probing for Active Islanding Detection †
Abstract
1. Introduction
1.1. Related Work
| Active Islanding Detection Method | Disturbance While Grid-Connected | Detection Time | Performance with Multiple Inverters | Test System Size | Microgrid-Compatible |
|---|---|---|---|---|---|
| Hybrid Sandia Frequency Shift [22] | Small Frequency Perturbation | Order of ms, Varies | Tested, but missed detection shown [11] | Single Node | No—Destabilizes |
| Impedance Angle Measurement [21] | Small Frequency Perturbation | Up to 1 s | Good Performance, Synchronization Needed | 4 Nodes | Yes |
| Negative Sequence Injection [18] | Constant 4% Negative Sequence Injection | 60 ms | Single Inverter Only | Single Node | Balanced Networks Only |
| d-q Reactive Power [19] | 5% Reactive Power Variation | 1.8 s | Not Tested | Single Node | Yes |
| d-q Real Power [10] | 1% Real Power Variation | 500 ms | Good Performance, GPS Coordination Needed | 5 Nodes | Yes |
| Harmonic Profile Injection [20] | < THD While Probing | 100–133 ms | Good Performance | 9 Nodes | No—Destabilizes |
| High-Frequency Impedance Estimation [11] | < THD While Probing | 200 ms | Tested, Degraded Performance | 3 Nodes | Yes |
| PCP (This Work) | < THD While Probing | 167–223 ms | Good Performance | 34 Nodes | Yes |
1.2. Contributions
- Our islanding detection scheme, like other active methods, handles the case of a balanced island.
- It allows simultaneous probing signal injection from multiple IBRs.
- It does not destabilize an island to detect it, making it microgrid-compatible.
- A logical implementation is developed for single H-bridge inverters, allowing direct injection from each IBR and eliminating any need for new physical devices.
- Detection is achieved without the need for any inter-IBR cooperation or communication infrastructure.
- As special devices and communication are not required, the implementation cost is low, and only a software update would be required to implement PCP on most inverters.
1.3. Paper Organization
2. Materials and Methods
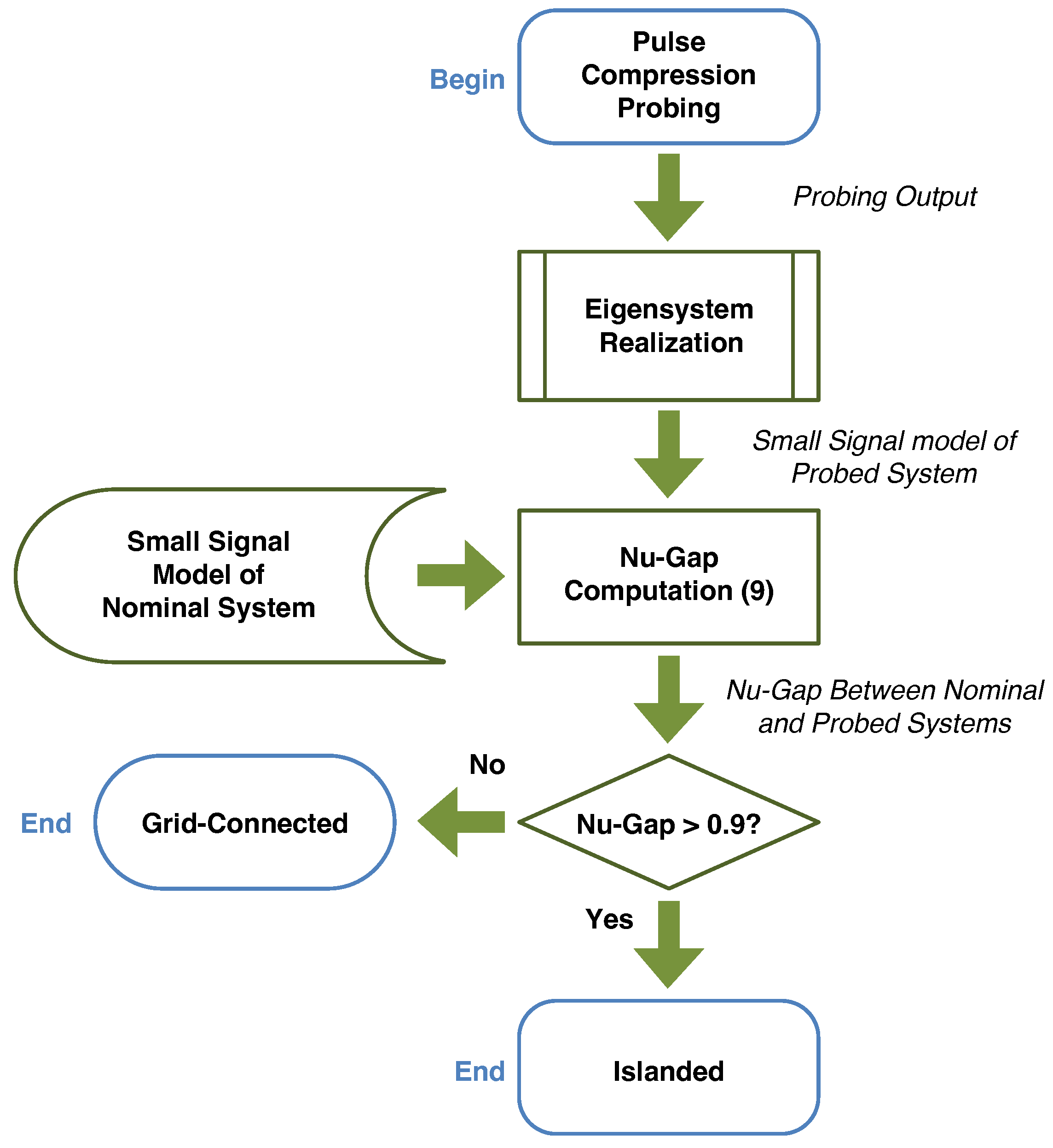
2.1. Nu-Gap-Based Detection
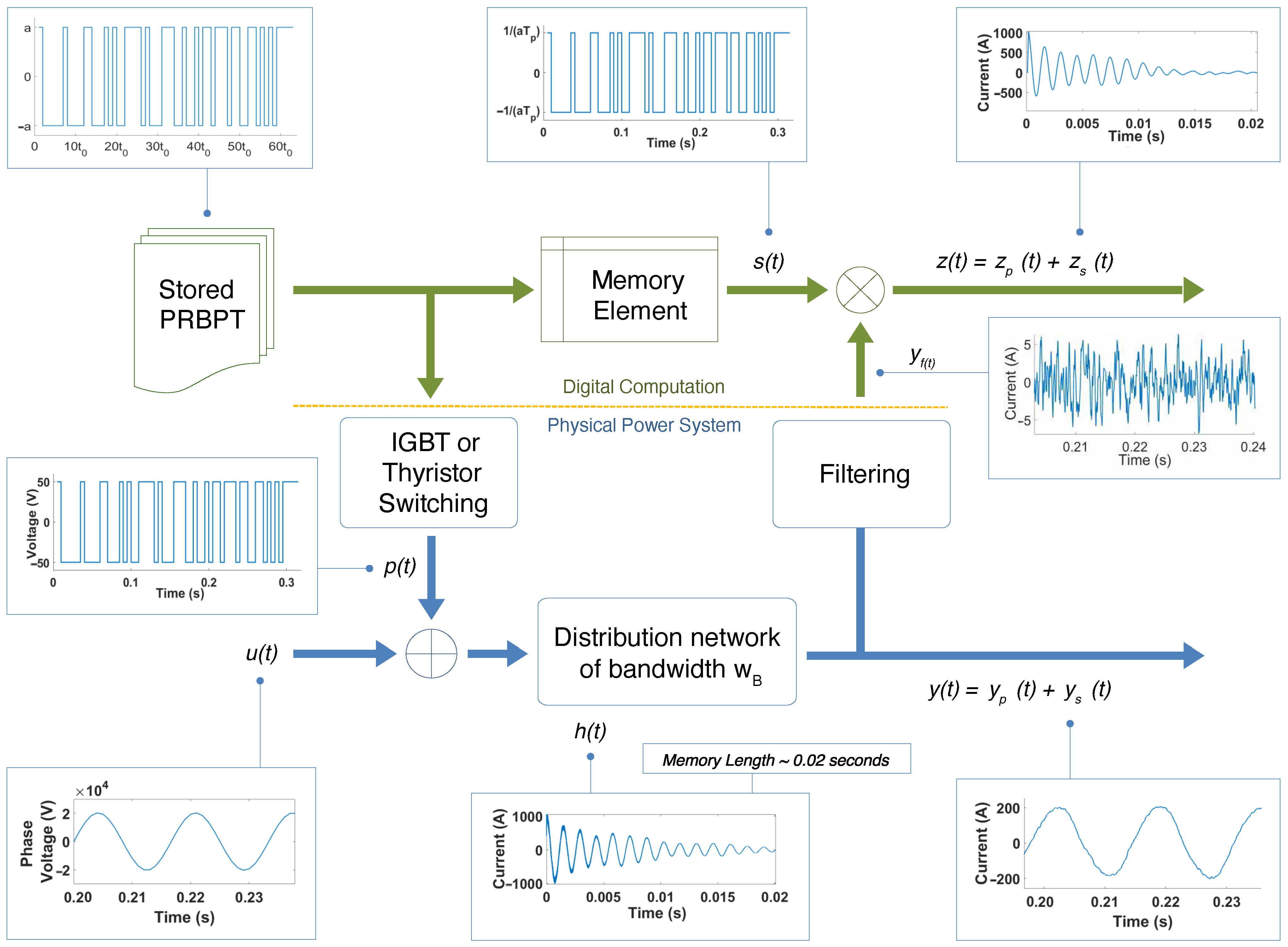
2.2. Overview of PCP
2.3. PCP Signal Design
3. Change Detection with PCP
3.1. Small Signal Representation of PCP Outputs
3.2. Measurement Noise and Harmonic Distortion
4. Islanding Detection Results with PCP
- grid-connected, defined as having an electrical connection to the transmission network, represented by bus 800;
- islanded, defined as being isolated from bus 800.
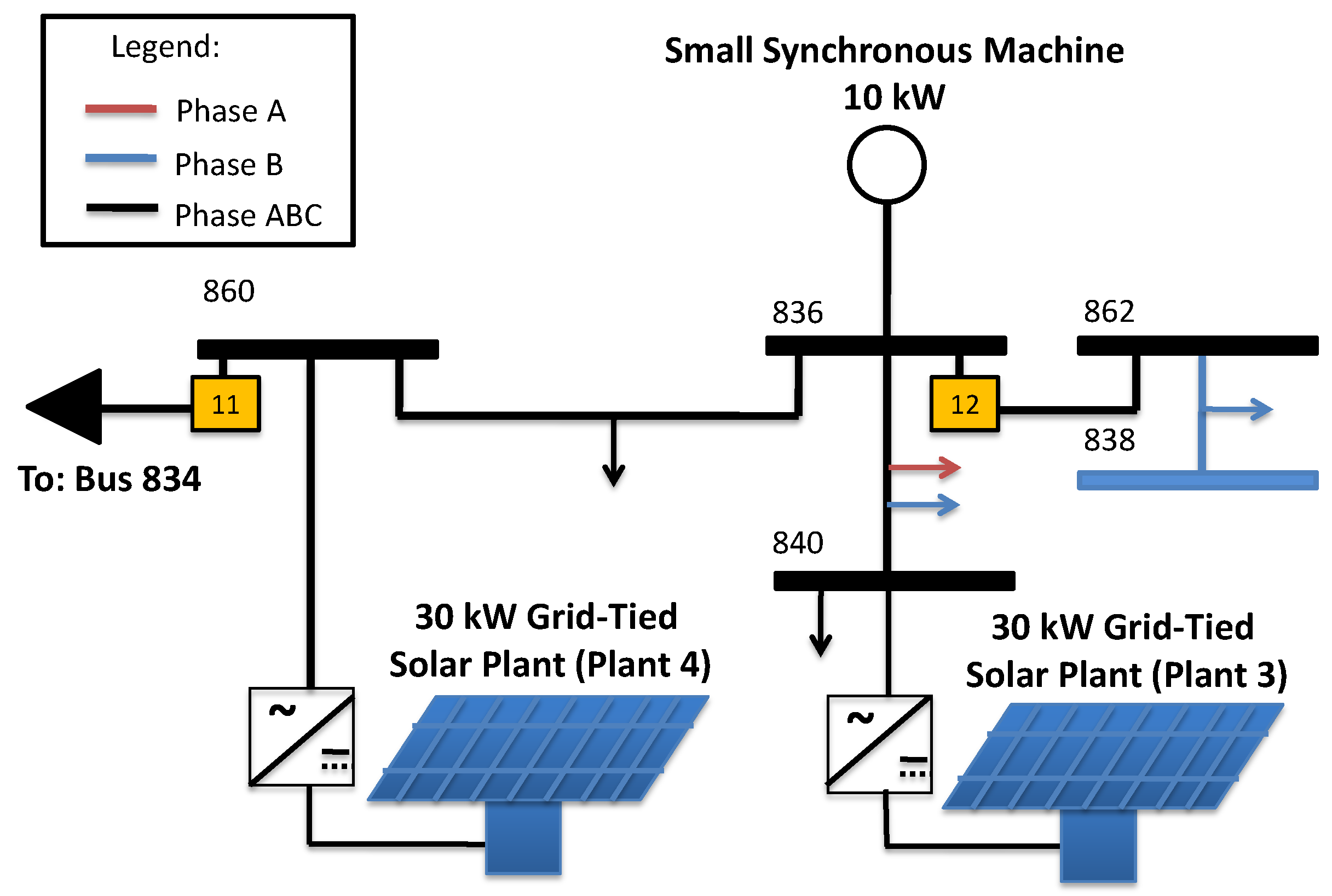
4.1. Problem Setup
4.2. PCP Signal and Injection Circuit Design
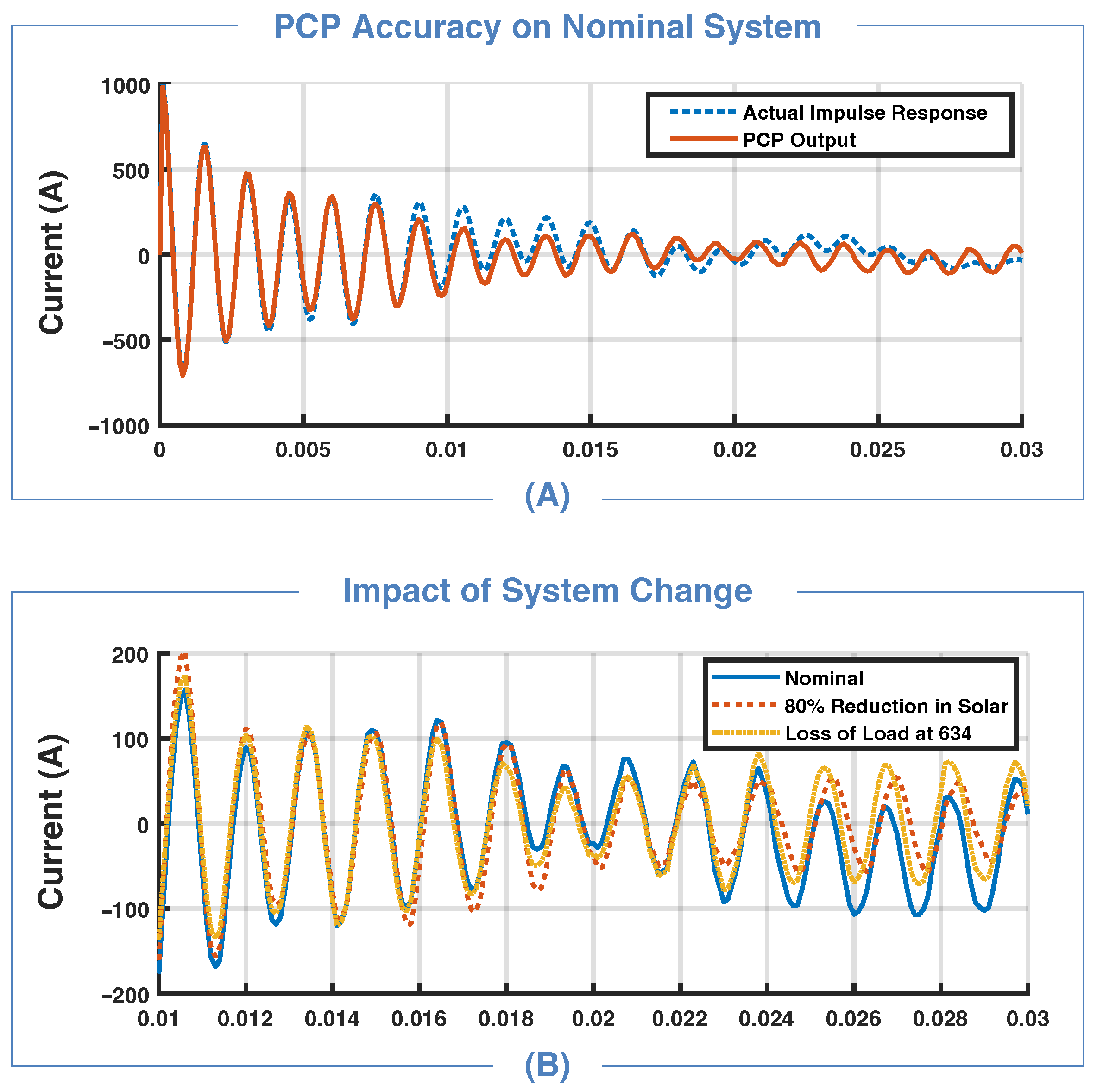
4.3. Nu-Gap-Based Detection Results on the 34-Bus System
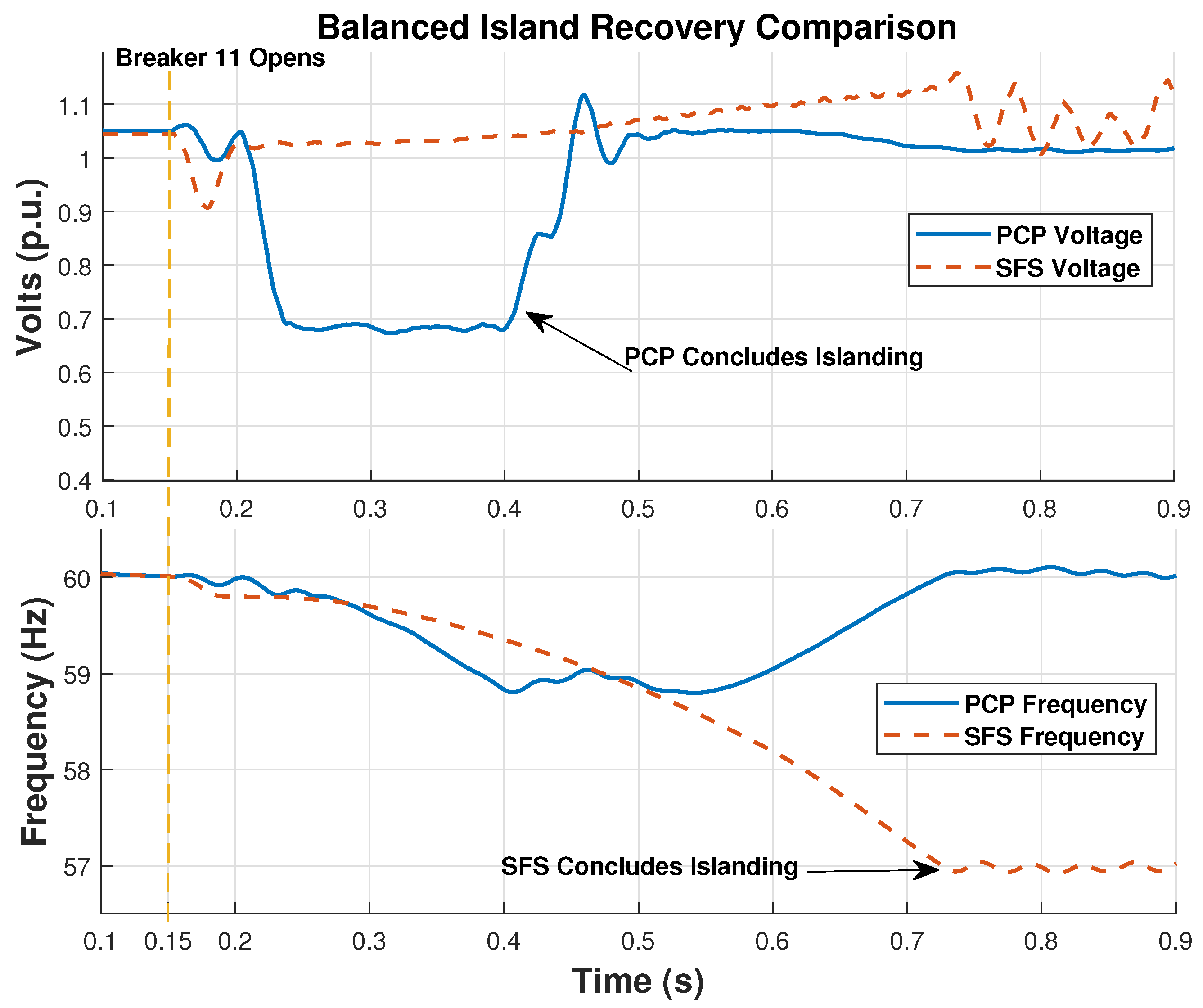
4.4. Case Study for an Island with Balanced Generation and Load
4.5. PCP Disturbance on the Balanced Case
4.6. Performance vs. Sandia Frequency Shift
- It works for most multiple inverter cases without needing a communication network. Methods like negative sequence injection [18] and d-q reactive power [19] are meant for a single inverter only. Impedance Angle Measurement [21] and d-q real power [10] require a communications infrastructure to handle multiple inverters.
- It requires no special hardware to implement, so we can test it on the same system as PCP, using the inverters themselves as signal injection points. Harmonic Profile Injection [20] requires a multi-level voltage source converter, so it cannot be applied to the single-stage inverters in this study. High-Frequency Impedance Estimation [11] requires a special injection device to be constructed and added to the network.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMT | electromagnetic transient |
| ERA | Eigensystem Realization Algorithm |
| GPS | global positioning system |
| IBR | inverter-based resource |
| IEEE | Institute of Electrical and Electronics Engineers |
| IGBT | Insulated-Gate Bipolar Transistor |
| PCP | Pulse Compression Probing |
| PRBPT | pseudo-random binary pulse train |
| PRBS | pseudo-random binary sequence |
| PWM | pulse width modulation |
| SFS | Sandia Frequency Shift |
| SNR | signal-to-noise ratio |
| THD | total harmonic distortion |
| Operators: | |
| ∗ | convolution |
| ⊗ | cross-correlation |
| Functions: | |
| Dirac delta function | |
| Hankel matrix of a discrete-time series | |
| point-wise nu-gap function, as seen in (1) | |
| root mean square | |
| Time Series: | |
| impulse response/pulse response | |
| rectangular pulse | |
| pseudo-random binary pulse train (probing signal) | |
| cyclic repetition of a probing signal | |
| pseudo-random binary sequence | |
| system nominal input | |
| system output | |
| filtered system output | |
| system output due to probing signal | |
| system output due to nominal inputs | |
| probing output | |
| probing output due to probing signal | |
| probing output due to nominal inputs | |
| Parameters: | |
| a | probing signal magnitude |
| m | number of samples for system realization |
| n | probing signal order |
| bit duration | |
| probing signal period | |
| positive DC source voltage | |
| negative DC source voltage | |
| Variables: | |
| nu-gap | |
| Phase A inverter current | |
| current in jth harmonic of 60 Hz | |
| k | index variable |
| M | memory length |
| system signal-to-noise ratio | |
| probing signal-to-noise ratio | |
| t | time |
| frequency | |
| system bandwidth | |
| Phase A inverter terminal voltage |
References
- Bekhradian, R.; Sanaye-Pasand, M. A Comprehensive Survey on Islanding Detection Methods of Synchronous Generator-Based Microgrids: Issues, Solutions and Future Works. IEEE Access 2022, 10, 76202–76219. [Google Scholar] [CrossRef]
- Independent System Operator New England. 2023 Regional System Plan; Technical Report; Independent System Operator New England: Holyoke, MA, USA, 2023. [Google Scholar]
- Resende, E.C.; Simoes, M.G.; Freitas, L.C.G. Anti-Islanding Techniques for Integration of Inverter-Based Distributed Energy Resources to the Electric Power System. IEEE Access 2024, 12, 17195–17230. [Google Scholar] [CrossRef]
- Vinnicombe, G. Frequency domain uncertainty and the graph topology. IEEE Trans. Automat. Contr. 1993, 38, 1371–1383. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mlakić, D.; Nikolovski, S.; Dragicević, T. Support Vector Machine-Based Islanding and Grid Fault Detection in Active Distribution Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2385–2403. [Google Scholar] [CrossRef]
- Matic-Cuka, B.; Kezunovic, M. Islanding Detection for Inverter-Based Distributed Generation Using Support Vector Machine Method. IEEE Trans. Smart Grid 2014, 5, 2676–2686. [Google Scholar] [CrossRef]
- Gomes, E.A.; Vieira, J.C.; Coury, D.V.; Delbem, A.C. Islanding detection of synchronous distributed generators using data mining complex correlations. IET Gener. Transm. Distrib. 2018, 12, 3935–3942. [Google Scholar] [CrossRef]
- Igbineweka, E.; Chowdhury, S. Application of Dual-Tree Complex Wavelet Transform in Islanding Detection for a Hybrid AC/DC Microgrid with Multiple Distributed Generators. Energies 2024, 17, 5133. [Google Scholar] [CrossRef]
- Salman, M. Application of Multiple Model Filters to Fault Diagnosis and Islanding Detection in Electric Grids. Ph.D. Thesis, State University of New York at Binghamton, Binghamton, NY, USA, 2020. [Google Scholar]
- Sivadas, D.; Vasudevan, K. An Active Islanding Detection Strategy with Zero Nondetection Zone for Operation in Single and Multiple Inverter Mode Using GPS Synchronized Pattern. IEEE Trans. Ind. Electron 2020, 67, 5554–5564. [Google Scholar] [CrossRef]
- Jia, K.; Wei, H.; Bi, T.; Thomas, D.W.P.; Sumner, M. An Islanding Detection Method for Multi-DG Systems Based on High-Frequency Impedance Estimation. IEEE Trans. Sustain. Energy 2017, 8, 74–83. [Google Scholar] [CrossRef]
- Bei, T.Z. Accurate active islanding detection method for grid-tied inverters in distributed generation. IET Renew. Power Gener. 2017, 11, 1633–1639. [Google Scholar] [CrossRef]
- Timbus, A.; Oudalov, A.; Ho, C.N. Islanding detection in smart grids. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3631–3637. [Google Scholar] [CrossRef]
- Bower, W.; Ropp, M. Evaluation of Islanding Detection Methods for Utility-Interactive Inverters in Photovoltaic Systems; Technical Report; Sandia National Laboratories: Livermore, CA, USA, 2002.
- Amini, H.; Mehrizi-Sani, A.; Noroozian, R. Passive Islanding Detection of Inverter-Based Resources in a Noisy Environment. Energies 2024, 17, 4405. [Google Scholar] [CrossRef]
- Li, M.; Chen, A.; Liu, P.; Ren, W.; Zheng, C. Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration. Energies 2024, 17, 877. [Google Scholar] [CrossRef]
- Ropp, M.; Begovic, M.; Rohatgi, A. Analysis and performance assessment of the active frequency drift method of islanding prevention. IEEE Trans. Energ. Convers. 1999, 14, 810–816. [Google Scholar] [CrossRef]
- Karimi, H.; Yazdani, A.; Iravani, R. Negative-Sequence Current Injection for Fast Islanding Detection of a Distributed Resource Unit. IEEE Trans. Power Electron. 2008, 23, 298–307. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, D.; He, N.; Ma, J.; Zhang, J.; Zhang, Y.; Shen, G.; Hu, C. A Novel RPV (Reactive-Power-Variation) Anti-islanding Method Based on Adapted Reactive Power Perturbation. IEEE Trans. Power Electron. 2013, 28, 4998–5012. [Google Scholar] [CrossRef]
- Dhar, S.; Dash, P.K. Harmonic Profile Injection-Based Hybrid Active Islanding Detection Technique for PV-VSC-Based Microgrid System. IEEE Trans. Sustain. Energy 2016, 7, 1473–1481. [Google Scholar] [CrossRef]
- Yang, F.; Lei, Y.; Chen, H.; Yang, Z.; Xu, H.; Chen, H.; Chen, Y. An Anti-Islanding Protection Method Based on Voltage-Synchronous Impedance Angle Measurements. Energies 2023, 16, 7139. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Vahedi, H.; Khazaeli, F.; Oraee, H. A Novel Hybrid Islanding Detection Method for Inverter-Based DGs Using SFS and ROCOF. IEEE Trans. Power Deliv. 2017, 32, 2162–2170. [Google Scholar] [CrossRef]
- Wu, N.E.; Huang, J. On-line impulse response extraction of a power transfer path using pulse compression probing. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 1346–1351. [Google Scholar] [CrossRef]
- Kersting, W. Radial distribution test feeders. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 908–912. [Google Scholar] [CrossRef]
- The MathWorks Inc. Specialized Power Systems Toolbox, R2024b; The MathWorks Inc.: Natick, MA, USA, 2024.
- Piaquadio, N.; Wu, N.E.; Sarailoo, M.; Huang, J. Pulse Compression Probing for Tracking Distribution Feeder Models. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting, PESGM, Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Piaquadio, N.; Wu, N.E.; Sarailoo, M. Active Islanding Detection Using Pulse Compression Probing. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting, PESGM, Seattle, DC, USA, 21–25 July 2024; pp. 1–5. [Google Scholar]
- Wu, N.E.; Ruschmann, M.C.; Huang, J.; Huang, K. Probing the NASA Generic Transport Aircraft in Real-Time for Health Monitoring. IEEE Trans. Control Syst. Technol. 2011, 19, 1288–1295. [Google Scholar] [CrossRef]
- Juang, J.; Pappa, R. An Eigensystem Realization Algorithm (ERA) for Modal Parameter Identification and Model Reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control, 1st ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Wu, N.E.; Wang, X. A pulse-compression method for process monitoring. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 3, pp. 2127–2130. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, X.; Wu, X.; Shi, C.; Zhang, J.; Zhang, Y. Performance Evaluation of High-Power SiC MOSFET Modules in Comparison to Si IGBT Modules. IEEE Trans. Power Electron. 2019, 34, 1181–1196. [Google Scholar] [CrossRef]
- Tartakovsky, A.; Nikiforov, I.; Basseville, M. Sequential Analysis: Hypothesis Testing and Changepoint Detection, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Giroux, P.; Sybille, G.; Osorio, C.; Chandrachood, S. Grid-Connected PV Array. MATLAB Central File Exchange. 2012. [Google Scholar]
- Chen, C.T. Linear System Theory and Design, 3rd ed.; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- IEEE Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2003.
- General Electric Grid Solutions. Protection Automation Application Guide; General Electric: Sesto San Giovanni, MI, Italy, 2016. [Google Scholar]
- Saadat, H. Power System Analysis; WCB/McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]







| Criteria | Magnitude | Order | Bit Duration |
|---|---|---|---|
| High | Small | - | - |
| High | Large | Large | - |
| Low Probing Latency | - | Small | Small |
| High Probing Resolution | - | - | Small |
| Low Switching Frequency | - | - | Large |
| Probing Parameter | Symbol | Value |
|---|---|---|
| Bit Duration | 100 μs | |
| PRBPT Order | n | 12 |
| PRBPT Magnitude | a | 10 Volts |
| Probing Period | 0.4095 s |
| 0.1% | 0.5% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 12 | 23.53 | 29.93 | 36.10 | 42.07 | 48.39 | n = 12 | 10.57 | 15.91 | 22.42 | 28.30 | 34.16 |
| n = 13 | 25.84 | 33.43 | 38.97 | 45.16 | 50.88 | n = 13 | 13.18 | 19.20 | 24.64 | 30.51 | 37.06 |
| n = 14 | 30.20 | 36.16 | 42.29 | 48.12 | 54.32 | n = 14 | 16.51 | 21.74 | 27.80 | 35.36 | 40.48 |
| Probing Parameter | Symbol | Value |
|---|---|---|
| Bit Duration (Plant 1) | 40 μs | |
| Bit Duration (Plant 2) | 48 μs | |
| Bit Duration (Plant 3) | 56 μs | |
| PRBPT Order | n | 12 |
| Inverter DC Voltage | a | 600 Volts |
| Open Switch | Plant 1 | Plant 2 | Plant 3 |
|---|---|---|---|
| 1 | 0.981 | 0.989 | 0.977 |
| 2 | 0.068 | 0.039 | 0.117 |
| 3 | 0.082 | 0.988 | 0.977 |
| 4 | 0.070 | 0.051 | 0.242 |
| 5 | 0.069 | 0.041 | 0.153 |
| 6 | 0.067 | 0.042 | 0.106 |
| 7 | 0.073 | 0.028 | 0.976 |
| 8 | 0.071 | 0.044 | 0.491 |
| 9 | 0.068 | 0.041 | 0.114 |
| 10 | 0.069 | 0.027 | 0.116 |
| 11 | 0.072 | 0.041 | 0.974 |
| 12 | 0.068 | 0.039 | 0.149 |
| Open Switch | Number of Replications | Replications Where Plant 1 Detects an Island | Replications Where Plant 2 Detects an Island | Replications Where Plant 3 Detects an Island |
|---|---|---|---|---|
| None | 18 | 0 | 0 | 0 |
| 1 | 22 | 22 | 22 | 22 |
| 2 | 25 | 0 | 0 | 0 |
| 3 | 26 | 0 | 26 | 26 |
| 4 | 25 | 0 | 0 | 0 |
| 5 | 21 | 0 | 0 | 0 |
| 6 | 16 | 0 | 0 | 0 |
| 7 | 31 | 0 | 0 | 31 |
| 8 | 20 | 0 | 0 | 0 |
| 9 | 16 | 0 | 0 | 0 |
| 10 | 37 | 0 | 0 | 37 |
| 11 | 24 | 0 | 0 | 0 |
| 12 | 19 | 0 | 0 | 0 |
| Open Switch | Plant 3 | Plant 4 |
|---|---|---|
| 11 | 0.966 | 0.994 |
| 12 | 0.008 | 0.046 |
| R/X Ratio | Plant 3 | Plant 4 | ||
|---|---|---|---|---|
| Open Switch: | 11 | 12 | 11 | 12 |
| 11.11 | 0.951 | 0.144 | 0.997 | 0.268 |
| 5.56 | 0.983 | 0.088 | 0.996 | 0.051 |
| 2.78 | 0.964 | 0.083 | 0.995 | 0.072 |
| 1.83 | 0.964 | 0.012 | 0.995 | 0.031 |
| 1.36 | 0.966 | 0.008 | 0.994 | 0.046 |
| 0.68 | 0.976 | 0.122 | 0.994 | 0.029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piaquadio, N.; Wu, N.E.; Sarailoo, M. Pulse Compression Probing for Active Islanding Detection. Energies 2025, 18, 3354. https://doi.org/10.3390/en18133354
Piaquadio N, Wu NE, Sarailoo M. Pulse Compression Probing for Active Islanding Detection. Energies. 2025; 18(13):3354. https://doi.org/10.3390/en18133354
Chicago/Turabian StylePiaquadio, Nicholas, N. Eva Wu, and Morteza Sarailoo. 2025. "Pulse Compression Probing for Active Islanding Detection" Energies 18, no. 13: 3354. https://doi.org/10.3390/en18133354
APA StylePiaquadio, N., Wu, N. E., & Sarailoo, M. (2025). Pulse Compression Probing for Active Islanding Detection. Energies, 18(13), 3354. https://doi.org/10.3390/en18133354






