Conjugate Heat Transfer Modelling in a Centrifugal Compressor for Automotive Applications
Abstract
1. Introduction
2. Reference Case
3. Numerical Model
3.1. Governing Equations
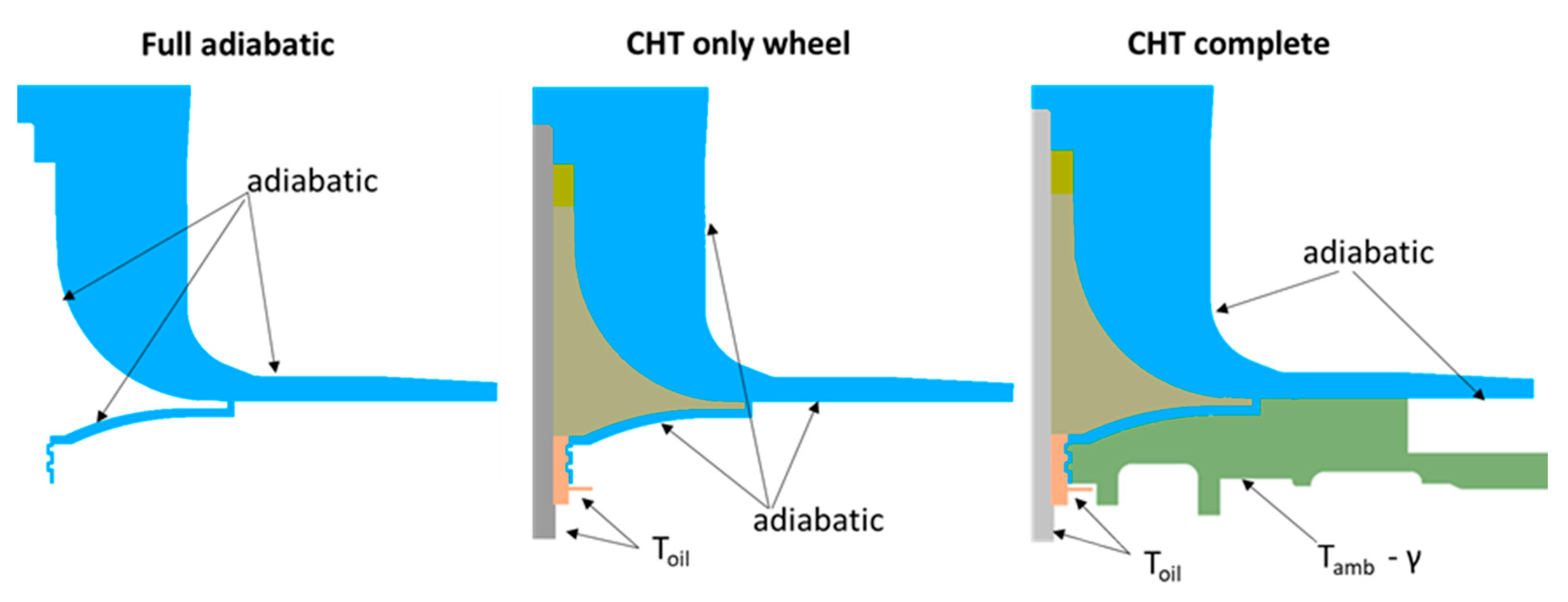
3.2. CFD Models
3.2.1. Full Adiabatic Model
3.2.2. CHT Only Wheel
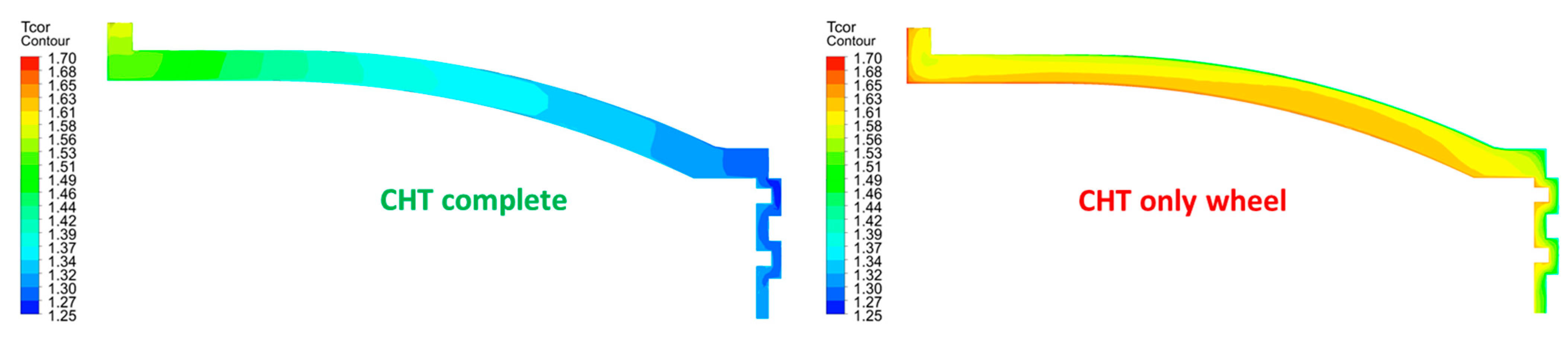
3.2.3. CHT Complete
4. Results
4.1. Comparison Among Full Adiabatic, CHT Only Wheel and CHT Complete Models
4.1.1. Global Performance
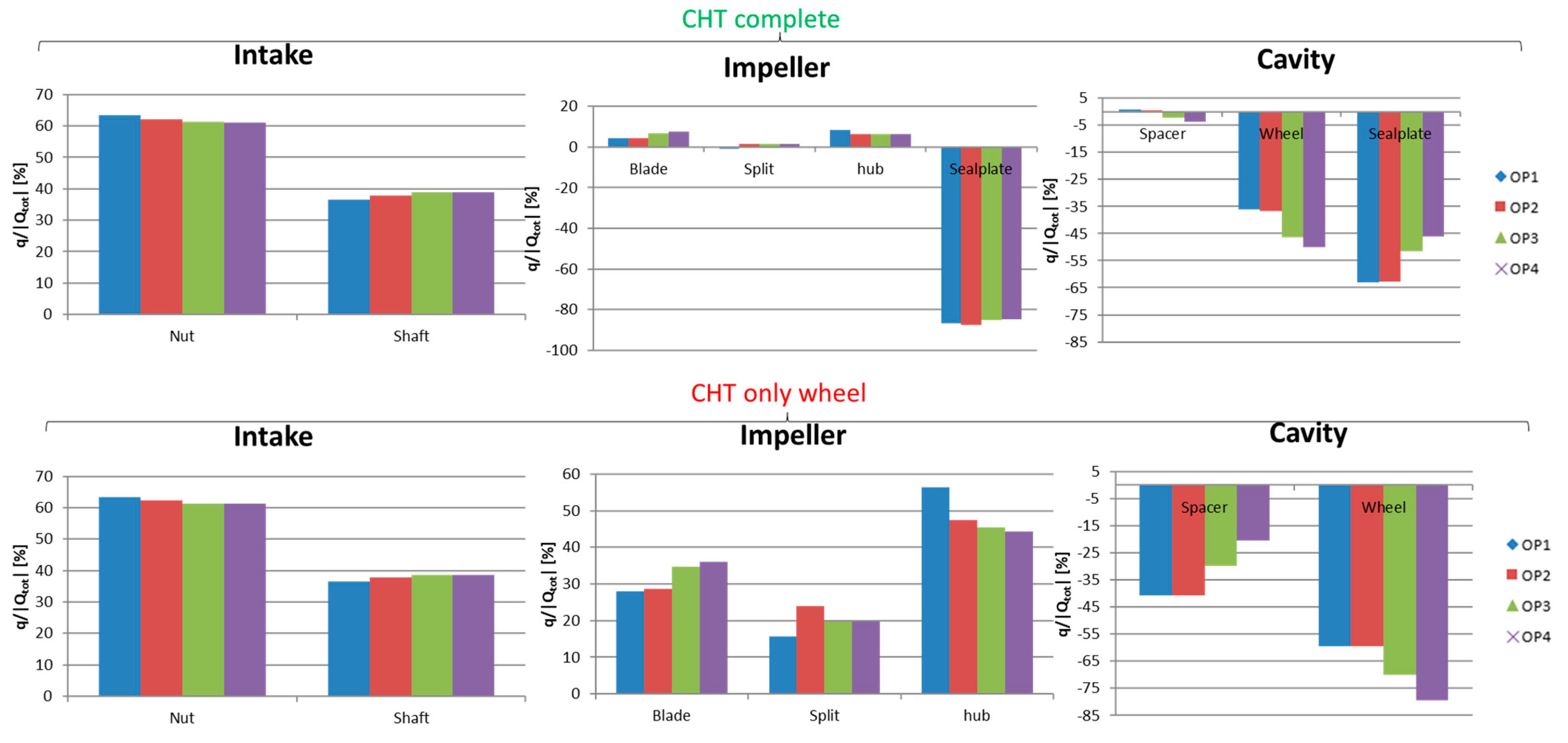
4.1.2. Back Cavity
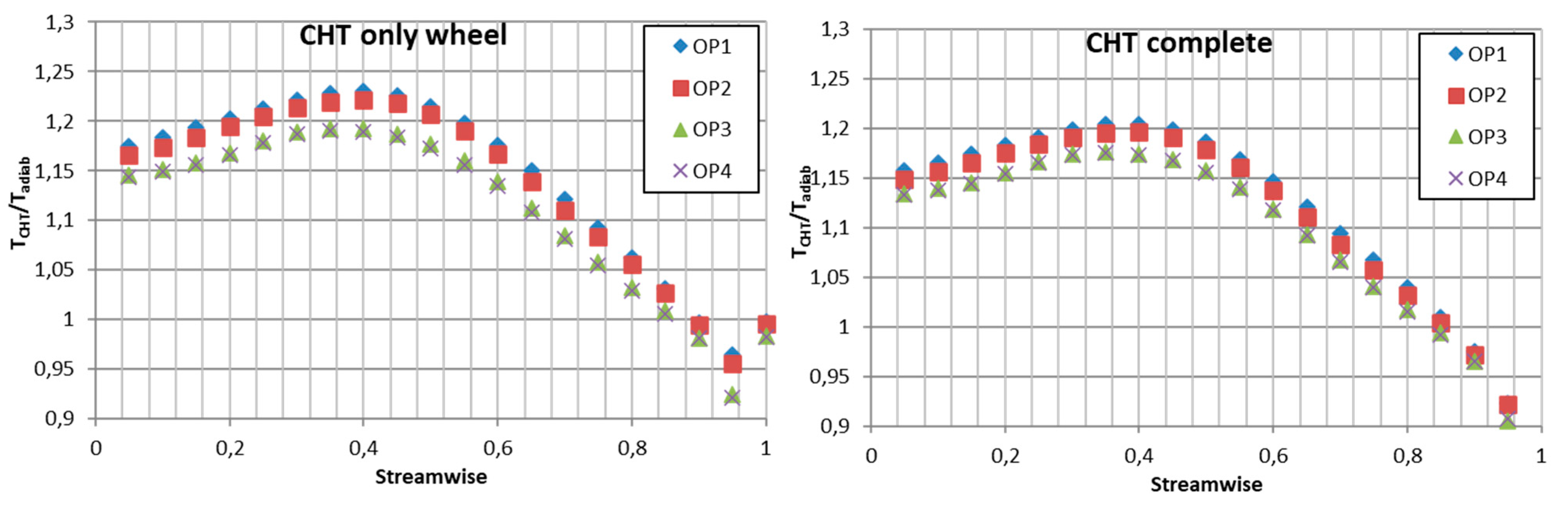
4.1.3. Thermal Analysis
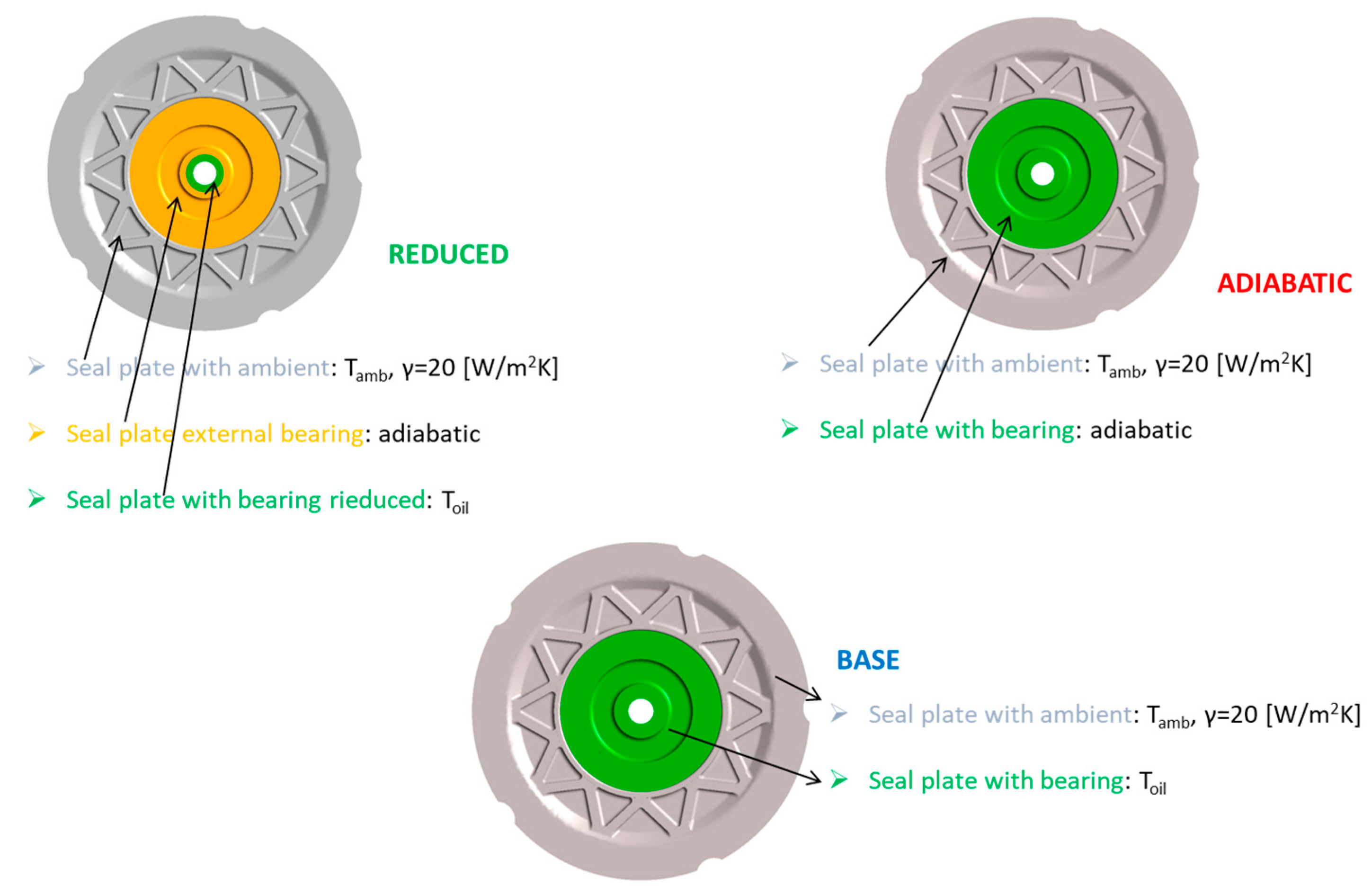
4.2. Effect of the Seal Plate Conditioning
4.2.1. Different Patches
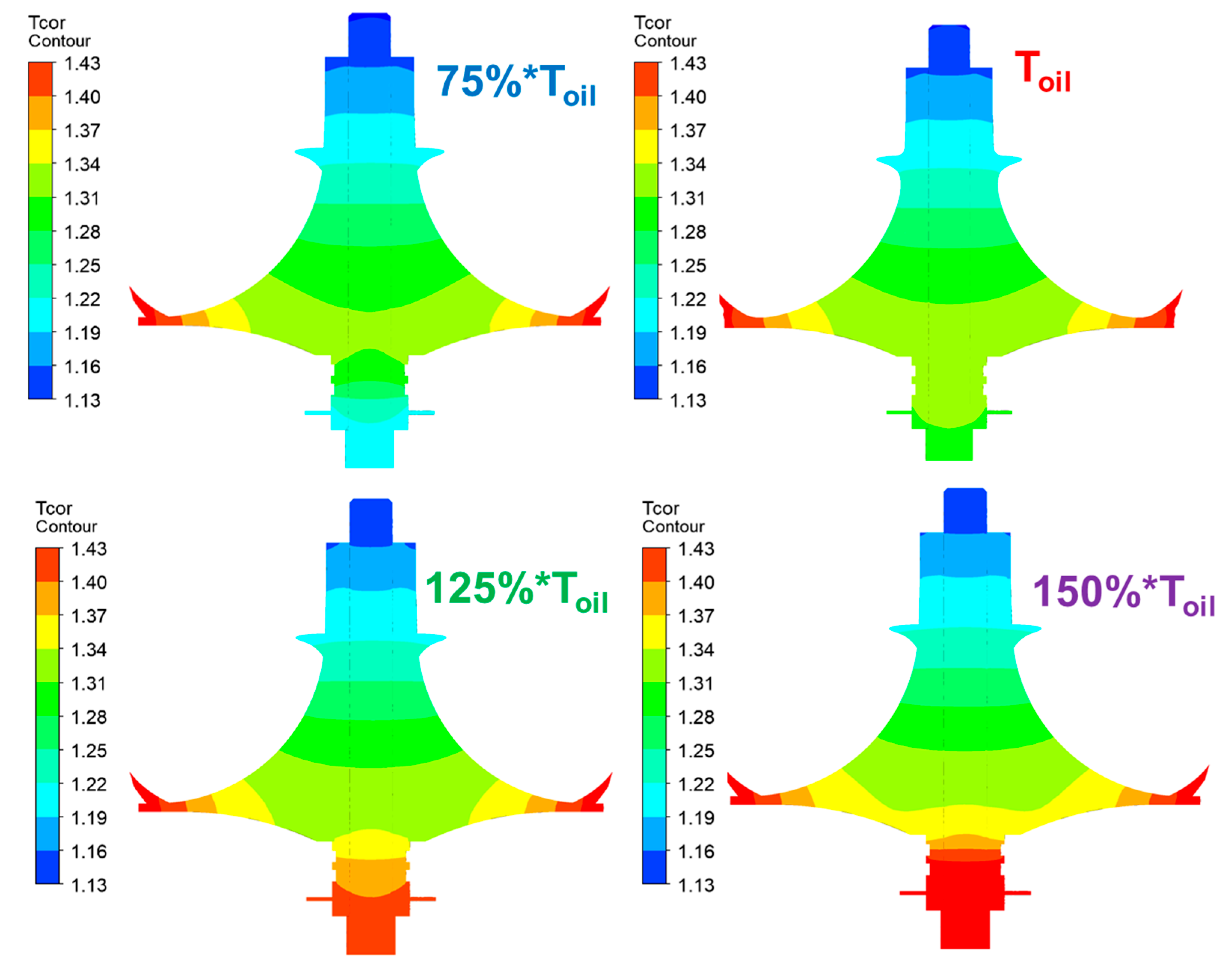
4.2.2. Different Oil Temperatures
4.3. Effect of the Heat Exchange of the Shroud
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| b | Span height |
| E | Thermal power |
| h | Enthalpy |
| k | Turbulent kinetic energy |
| K | Thermal conductivity |
| ṁ | Mass flow rate |
| MRF | Mass flow ratio |
| p | Static pressure |
| PR | Pressure ratio |
| q | Thermal flux |
| Q | Total thermal flux |
| R | Radius |
| t | Time |
| T | Temperature |
| u | Velocity |
| U | Thermal transmittance |
| Y+ | Non dimensional boundary layer distance from wall |
| Zb | Blades number |
| γ | Thermal convective coefficient |
| ε | Rate of dissipation of turbulent kinetic energy |
| η | Efficiency |
| μ | Viscosity |
| ρ | Density |
| τ | Tensor of tangential and normal stress |
| ω | Specific rate of dissipation |
| Subscripts | |
| 0 | Model inlet (adduction duct inlet) |
| 4 | Diffuser inlet |
| 5 | Diffuser outlet |
| amb | Ambient |
| cor | Corrected |
| ext | External |
| int | Internal |
| LE | Leading edge |
| t | total |
| TE | Trailing edge |
References
- European Commission Website. A European Green Deal—Striving to Be the First Climate-Neutral Continent. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal_en (accessed on 10 March 2025).
- Casey, M.A. Computational geometry for the blades and internal flow channels of centrifugal compressors. In Proceedings of the ASME 1982 International Gas Turbine Conference and Exhibit, London, UK, 18–22 April 1982; p. V001T01A062. [Google Scholar]
- Bonaiuti, D.; Arnone, A.; Ermini, M.; Baldassarre, L. Analysis and optimization of transonic centrifugal compressor impellers using the design of experiments technique. J. Turbomach. 2006, 128, 786–797. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.H.; Husain, A.; Kim, K.Y. Multi-objective optimization of a centrifugal compressor impeller through evolutionary algorithms. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 711–721. [Google Scholar] [CrossRef]
- Mojaddam, M.; Pullen, K.R. Optimization of a centrifugal compressor using the design of experiment technique. Appl. Sci. 2019, 9, 291. [Google Scholar] [CrossRef]
- Fisher, F.B. Application of Map Width Enhancement Devices to Turbocharger Compressor Stages. J. Engines 1988, 97, 1303–1310. [Google Scholar]
- Zheng, X.; Zhang, Y.; Yang, M.; Bamba, T.; Tamaki, H. Stability Improvement of High-Pressure-Ratio Turbocharger Centrifugal Compressor by Asymmetrical Flow Control—Part II: Nonaxisymmetrical Self-Recirculation Casing Treatment. J. Turbomach. 2002, 135, 021007. [Google Scholar] [CrossRef]
- Li, Z.; Han, G.; Lu, X.; Huang, E.; Zhao, S. Improving the operating range using a centrifugal compressor with a tandem impeller. Aerosp. Sci. Technol. 2020, 96, 105548. [Google Scholar] [CrossRef]
- Denton, J.D. Loss mechanisms in turbomachines. J. Turbomach. 1993, 115, 621–657. [Google Scholar] [CrossRef]
- Rautenberg, M.; Mobarak, A.; Malobabic, M. Influence of heat transfer between turbine and compressor on the performance of small turbochargers. In Tokyo International Gas Turbine Congress; Gas Turbine Society of Japan: Tokyo, Japan, 1983; Volume 2, pp. 567–574. [Google Scholar]
- Shaaban, S.; Seume, J. Impact of turbocharger nonadiabatic operation on engine volumetric efficiency and turbo lag. Int. J. Rotating 2012, 2012, 625453. [Google Scholar]
- Kim, H.R.; Kim, K.Y.; Jeong, J.; Song, S.J. An analysis of heat transfer effect on surge characteristics in turbo heat pumps. In Proceedings of the International Compressor Engineering Conference, Purdue, IN, USA, 12–15 July 2010; p. 1521. [Google Scholar]
- Chesse, P.; Chalet, D.; Tauzia, X. Impact of the heat transfer on the performance calculations of automotive turbocharger compressor. Oil Gas Sci. Technol. 2011, 66, 791–800. [Google Scholar] [CrossRef]
- Shaaban, S. Experimental Investigation and Extended Simulation of Turbocharger Non-Adiabatic Performance. Ph.D. Thesis, Universite de Hannover, Hanover, Germany, 2004. [Google Scholar]
- Serrano, J.R.; Olmeda, P.; Vidal, F. An experimental procedure to determine heat transfer properties of turbochargers. Meas. Sci. Technol. 2010, 21, 035109. [Google Scholar] [CrossRef]
- Jung, M.; Ford, R.G.; Glover, K.; Collings, N.; Christen, U.; Watts, M.J. Parameterization and transient validation of a variable geometry turbocharger for mean-value modeling at low and medium speed-load points. In Proceedings of the SAE Powertrain and Fluid Systems Conference, San Diego, CA, USA, 21–24 October 2002; p. 2002-01-2729. [Google Scholar]
- Aghaali, H. On-Engine Turbocharger Performance Considering Heat Transfer. Licentiate Thesis, Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
- Bohn, D.; Heuer, T.; Kusterer, K. Conjugate flow and heat transfer investigation of a turbo charger. J. Eng. Gas Turbines Power 2005, 127, 663–669. [Google Scholar] [CrossRef]
- Geller, M.; Kluck, N.; Magiera, R. Numerical computation of heat transfer coefficient for a radial compressor stage using CFD and comparison with analytical model computations. In Proceedings of the 24th CADFEM Users’ Meeting, Schwabenlandhalle Stuttgart/Fellbach, Germany, 25–27 October 2006. [Google Scholar]
- Cormerais, M.; Chesse, P.; Hetet, J. Turbocharger heat transfermodeling under steady and transient conditions. Int. J. Thermodyn. 2009, 12, 193–202. [Google Scholar]
- Baines, N.; Wygant, K.D.; Dris, A. The analysis of heat transfer in automotive turbochargers. J. Eng. Gas Turbines Power 2010, 132, 042301. [Google Scholar] [CrossRef]
- Moosania, S.M.; Zheng, X. Effect of internal heat leakage on the performance of a high pressure ratio centrifugal compressor. Appl. Therm. Eng. 2017, 111, 317–324. [Google Scholar] [CrossRef]
- Gu, L.; Zemp, A.; Abhari, R.S. Numerical study of the heat transfer effect on a centrifugal compressor performance. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2207–2220. [Google Scholar] [CrossRef]
- Cui, M.; Hohlweg, W. Numerical and experimental investigation of heat transfer in a low flow single stage centrifugal compressor. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; Volume 49729, p. V02DT42A030. [Google Scholar]
- Diefenthal, M.; Tadesse, H.; Rakut, C.; Wirsum, M.; Heuer, T. Experimental and numerical investigation of temperature fields in a radial turbine wheel. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 45585, p. V01BT24A015. [Google Scholar]
- Roclawski, H.; Oberste-Brandenburg, C.; Böhle, M. Conjugate Heat Transfer Analysis of a Centrifugal Compressor for Turbocharger Applications. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Romagnoli, A.; Martinez-Botas, R. Heat transfer analysis in a turbocharger turbine: An experimental and computational evaluation. Appl. Therm. Eng. 2012, 38, 58–77. [Google Scholar] [CrossRef]
- Cormerais, M.; Hetet, J.F.; Chesse, P.; Maiboom, A. Heat transfer analysis in a turbocharger compressor: Modeling and experiments. In Proceedings of the SAE 2006 World Congress & Exhibition, Detroit, MI, USA, 3–6 April 2006; p. SAE 2006-01-0023. [Google Scholar]
- Abdelhamid, S.; Berndt, R.; Grigoriadis, P.; Hagelstein, D.; Nickel, J.; Pucher, H.; Seume, J.R. Advanced presentation and extrapolation of turbocharger maps as a boundary condition of the engine process simulation. In Proceedings of the Stuttgart International Symposium on Motor Vehicles and Engines, Stuttgart, Germany, 2–3 July 2003. [Google Scholar]
- Chapman, K.S.; Nguru, R.; Shultz, J. Simplified Methodology to Correct Turbocharger Field Measurements for Heat Transfer and Other Effects; Final Report for Gas Research Institute; Gas Technology Institute: Des Plaines, IL, USA, 2002; p. GRI-02/0156. [Google Scholar]
- Bardelli, M.; Cravero, C.; Marini, M.; Marsano, D.; Milingi, O. Numerical Investigation of Impeller-Vaned Diffuser Interaction in a Centrifugal Compressor. Appl. Sci. 2019, 9, 1619. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Criteria for the Stability Limit Prediction of High-Speed Centrifugal Compressors with Vaneless Diffuser. Part I: Flow Structure Analysis. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Online, 21–25 September 2020; ASME: New York, NY, USA, 2020; p. GT2020-14579. [Google Scholar]
- Cravero, C.; Marsano, D. Criteria for the Stability Limit Prediction of High-Speed Centrifugal Compressors with Vaneless Diffuser. Part II: The development of Prediction Criteria. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Online, 21–25 September 2020; ASME: New York, NY, USA, 2020; p. GT2020-14589. [Google Scholar]
- Cravero, C.; Marsano, D. A comparison of strategies to extend the operating range of radial compressors for turbocharging. E3S Web Conf. 2023, 414, 02011. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D.; Sishtla, V.; Halbe, C.; Cousins, W.T. Numerical investigations of near surge operating conditions in a two-stage radial compressor with refrigerant gas. J. Eng. Gas Turbines Power 2024, 146, 021010. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Numerical prediction of tonal noise in centrifugal blowers. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; Volume 50985, p. V001T09A001. [Google Scholar]
- Carrattieri, L.; Cravero, C.; Marsano, D.; Valenti, E. The use of Approximate Entropy analysis for flow pattern identification in radial compressors to detect instable operating conditions. J. Phys. Conf. Ser. 2024, 2893, 012127. [Google Scholar] [CrossRef]
- Carrattieri, L.; Cravero, C.; Marsano, D.; Valenti, E.; Sishtla, V.; Halbe, C. The Development of Machine Learning Models for Radial Compressor Monitoring With Instability Detection. J. Turbomach. 2025, 147, 051004. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys CFX Theory Guide v.17; ANSYS Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Menter, F.; Kuntz, M.; Langstry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Smirnov, P.; Menter, F. Sensitization of the SST turbulence model to rotation and curvature by applying the Spalart-Shur correction term. J. Turbomach. 2009, 131, 041010. [Google Scholar] [CrossRef]
- Casey, M.V.; Fesich, T.M. The efficiency of turbocharger compressors with diabatic flows. J. Eng. Gas Turbines Power 2010, 132, 7. [Google Scholar] [CrossRef]
- Sirakov, B.; Casey, M. Evaluation of heat transfer effects on turbocharger performance. J. Turbomach. 2013, 135, 2. [Google Scholar] [CrossRef]
- Zheng, X.; Jin, L.; Du, T.; Gan, B.; Liu, F.; Qian, H. Effect of temperature on the strength of a centrifugal compressor impeller for a turbocharger. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 896–904. [Google Scholar] [CrossRef]
- Gibson, L.; Spence, S.; Kim, S.I.; Schwitzke, M.; Starke, A. A numerical investigation of a turbocharger compressor back-disk cavity at widely varying operating conditions. In Proceedings of the International Turbocharging Seminar, London, UK, 16–17 May 2018; Volume 2018, p. 11. [Google Scholar]
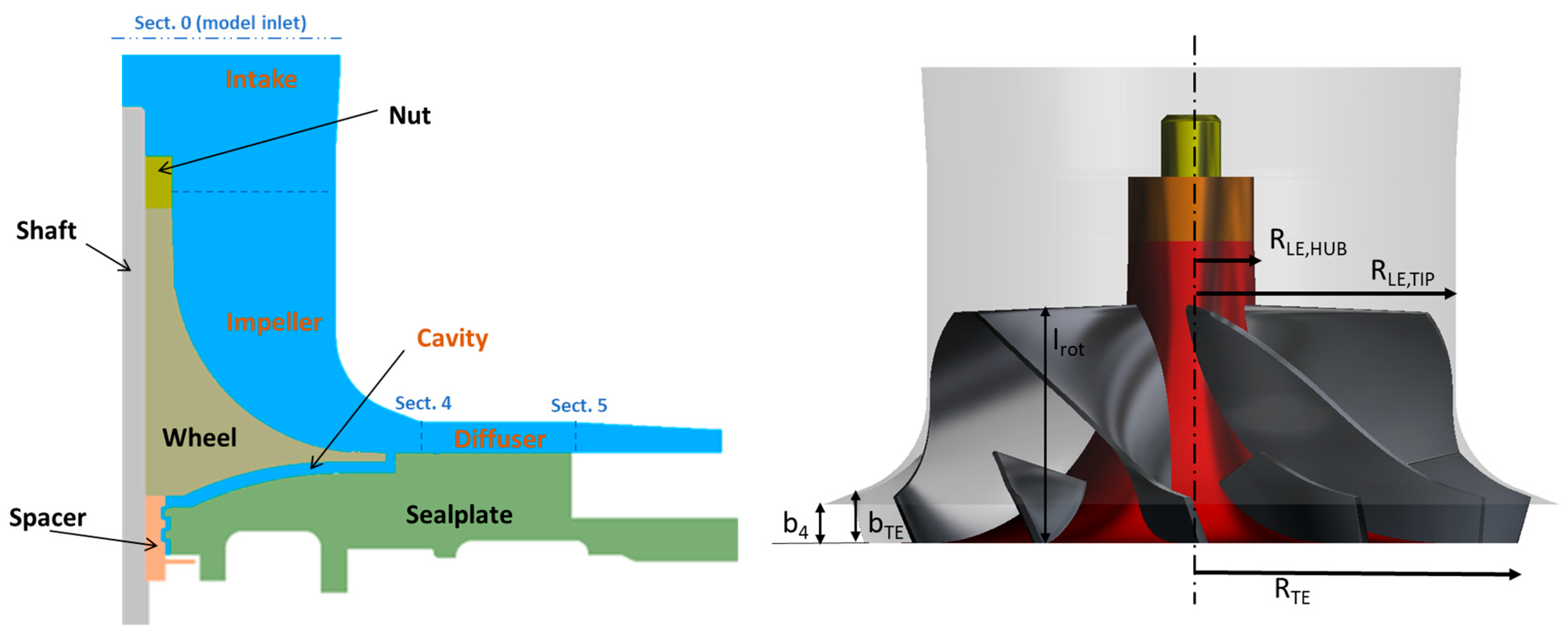
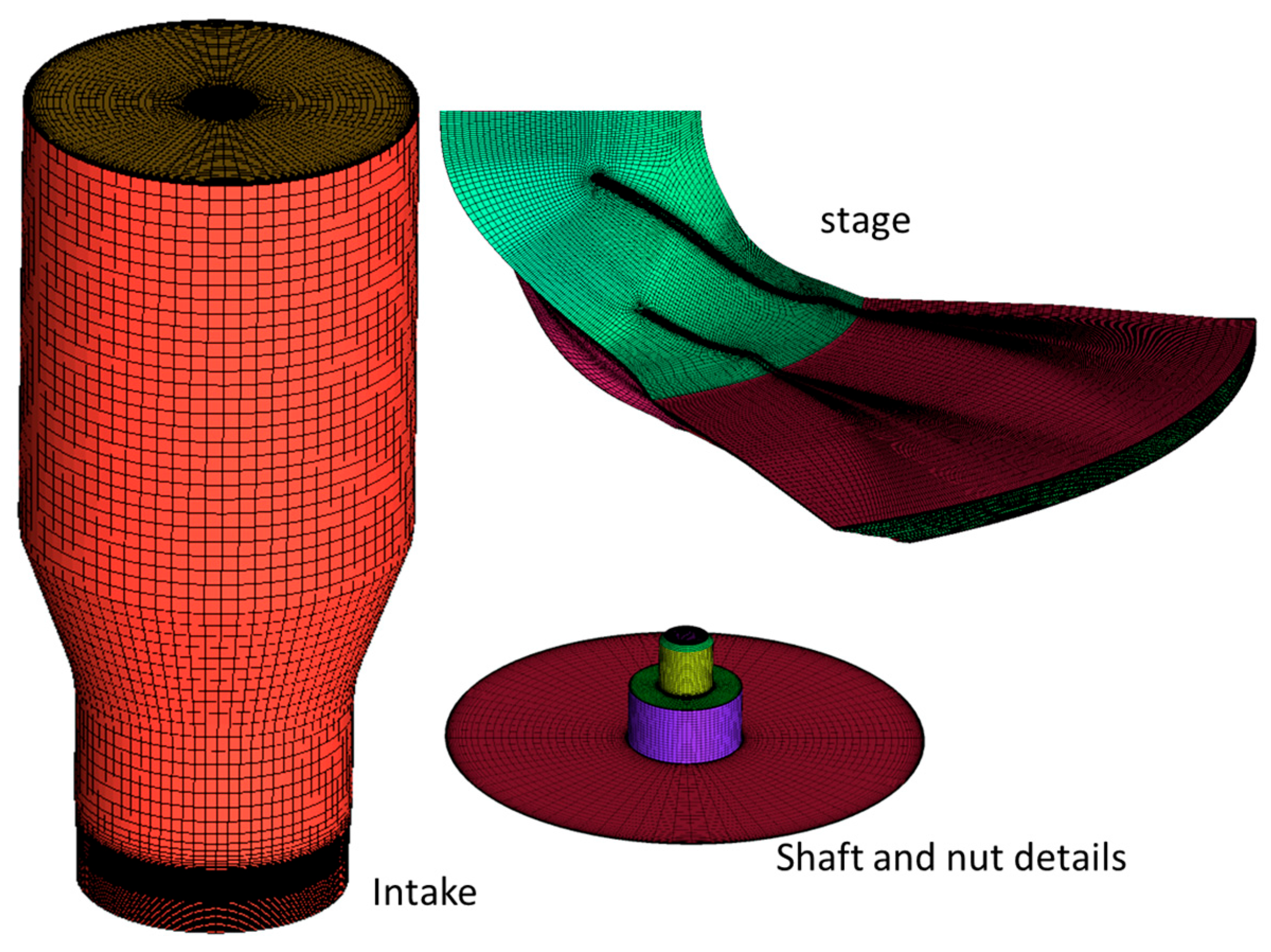
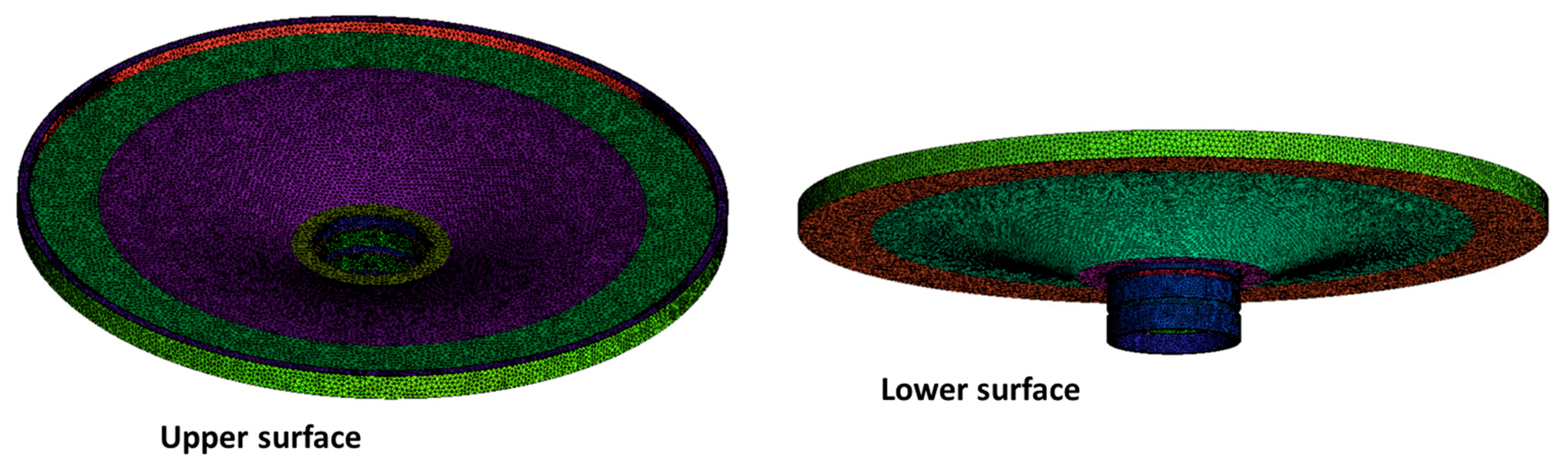
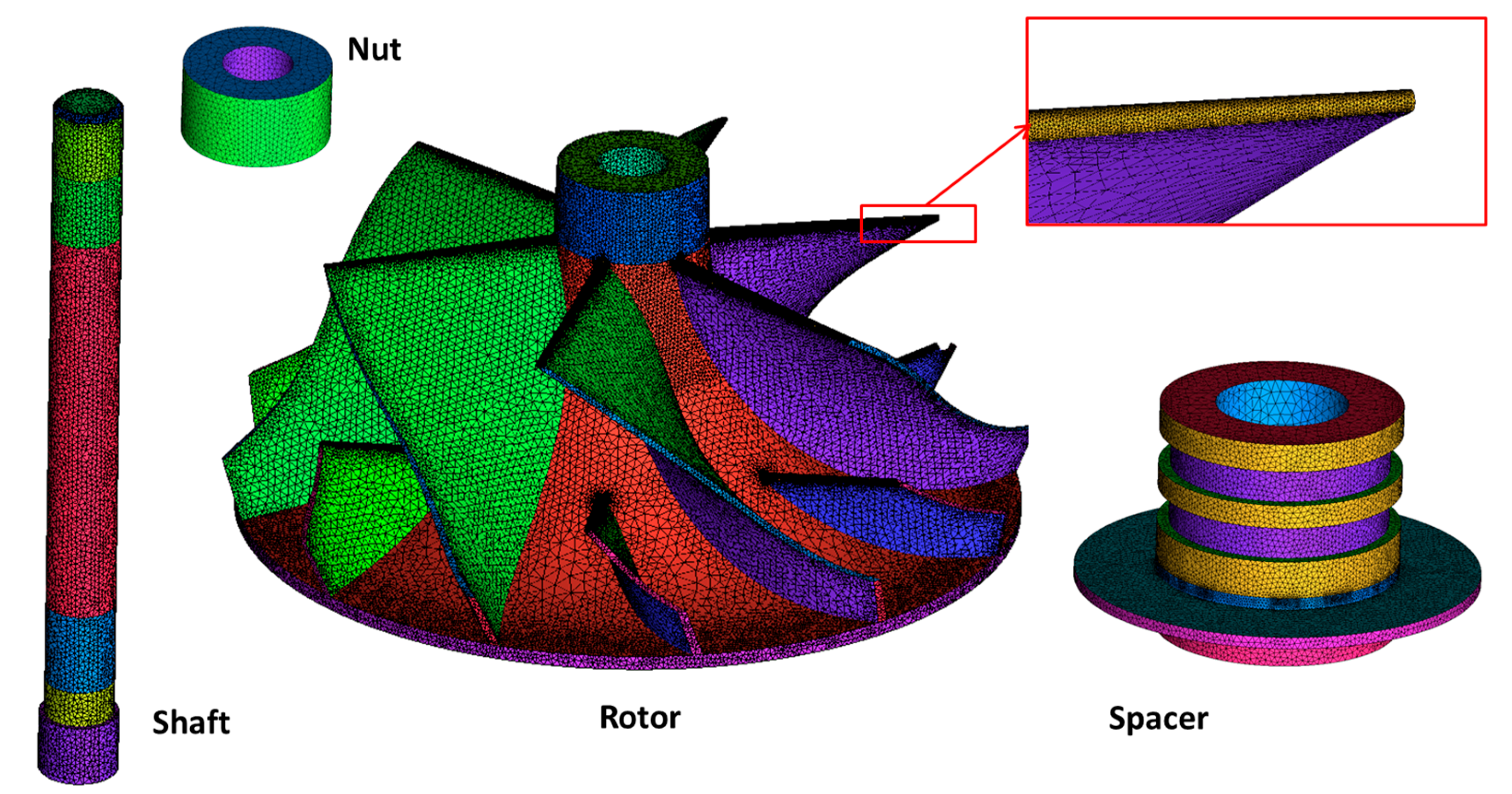

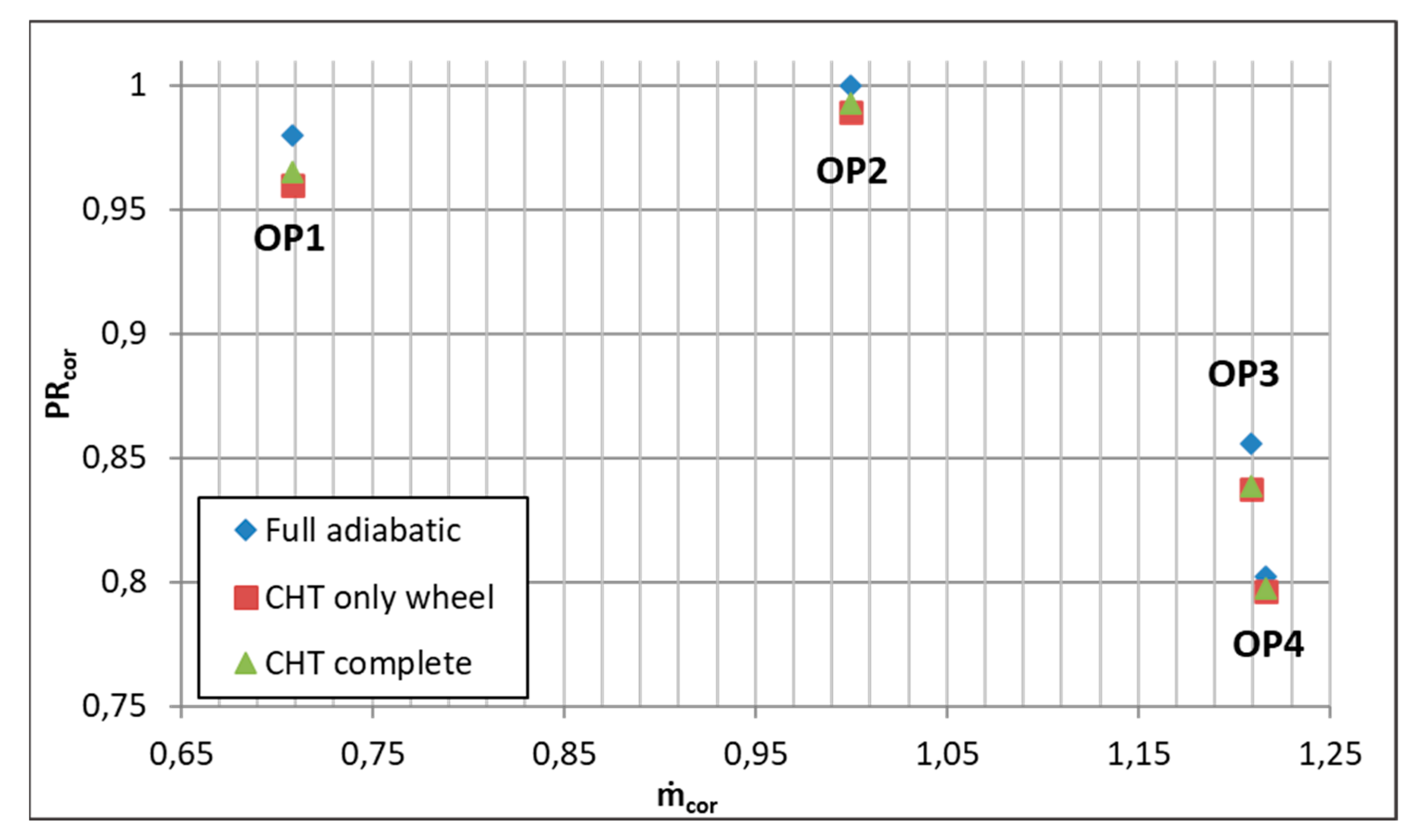
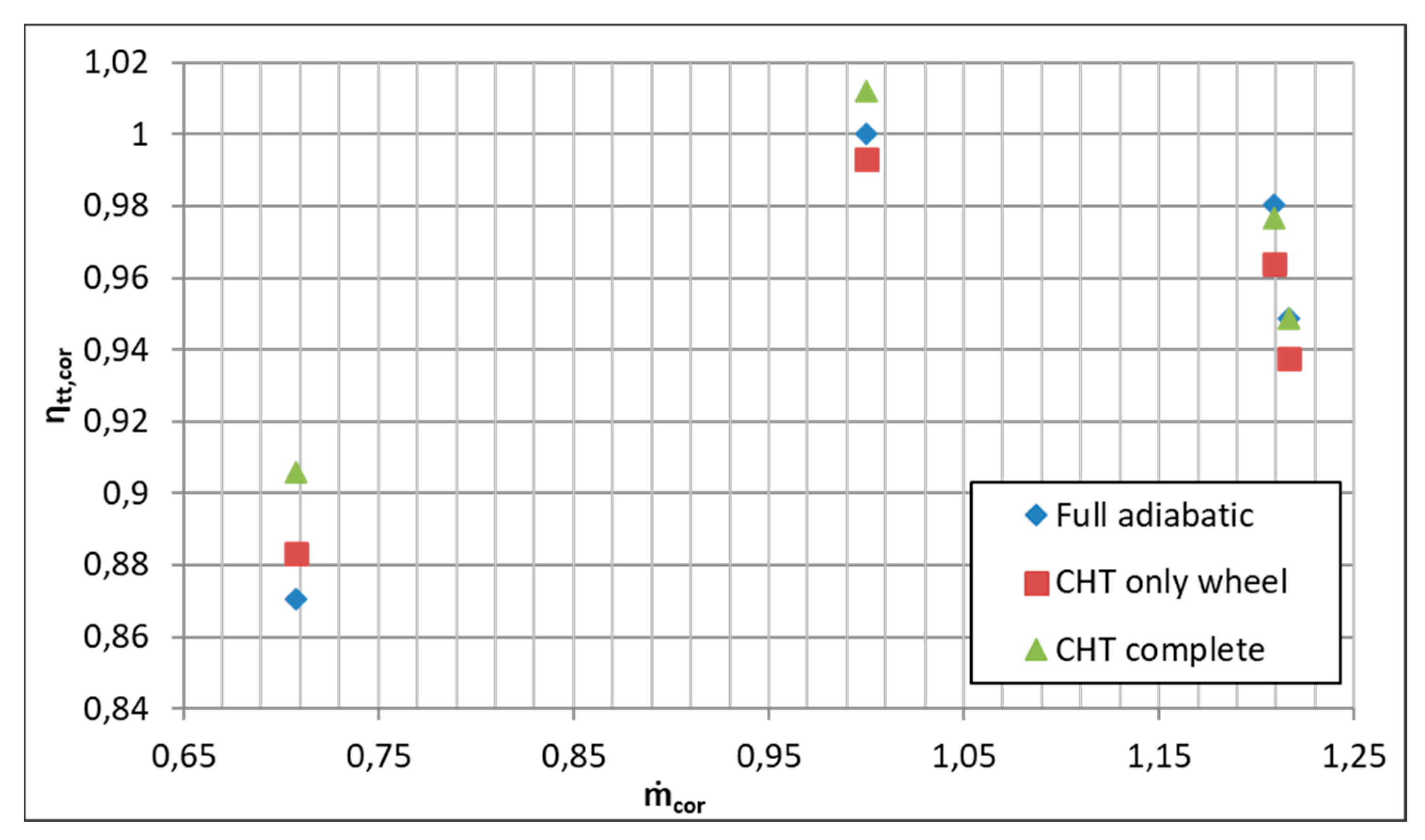

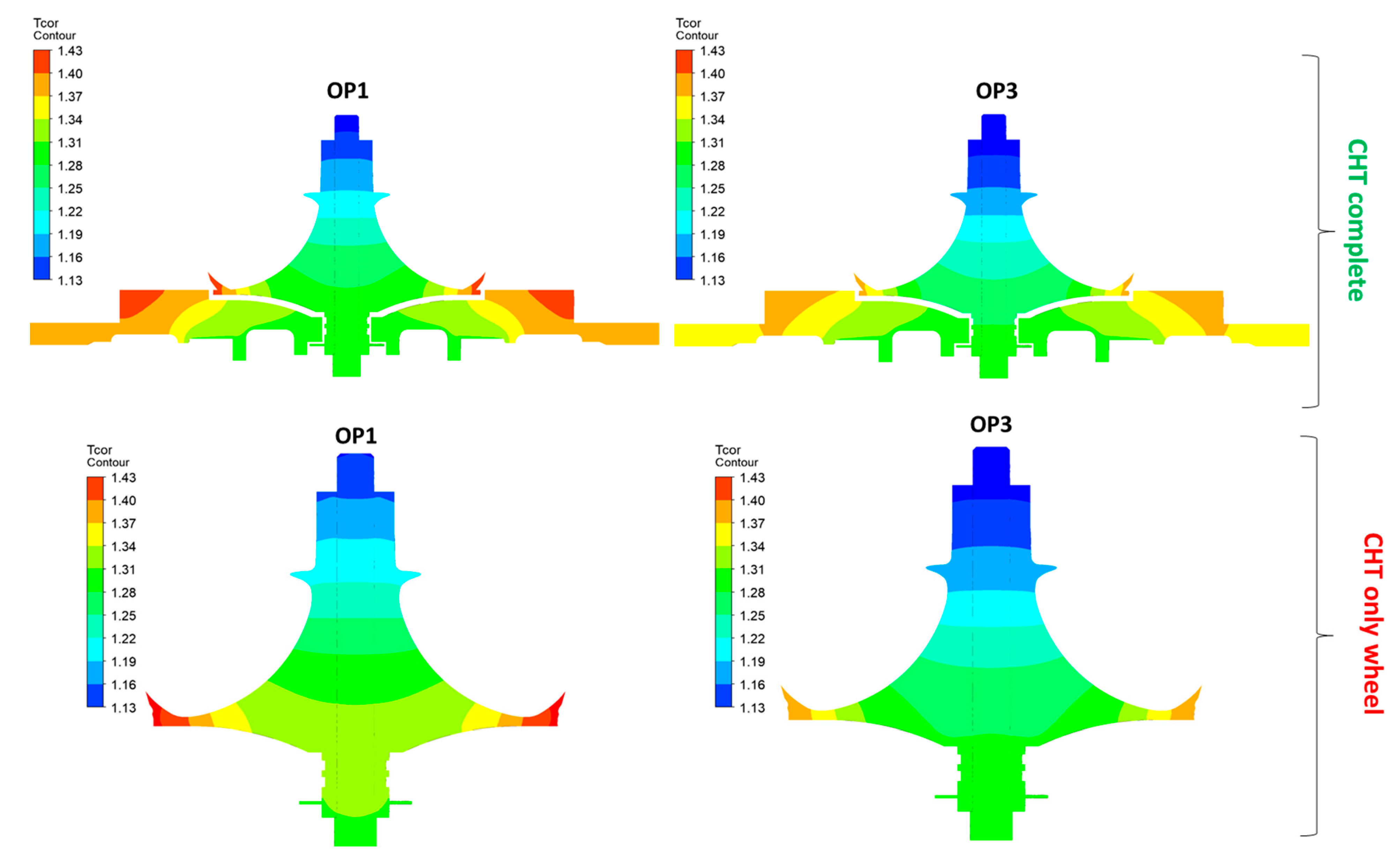


| Geometric Parameter | Value |
|---|---|
| Impeller blade number: Zb | 6 main + 6 splitter blades |
| Span at diffuser inlet: b4/R4 | 0.0706 |
| Radius at rotor leading edge hub: RLE,hub/R4 | 0.1755 |
| Radius at rotor leading edge tip: RLE,tip/R4 | 0.7166 |
| Radius at diffuser outlet: R5/R4 | 1.5323 |
| Mesh | Cell Number (Mcells) | PRcor | MRF [%] |
|---|---|---|---|
| M1 | 0.8 | 0.977 | 0.49 |
| M2 | 1.2 | 0.980 | 0.45 |
| M3 | 1.6 | 0.980 | 0.45 |
| Case | OP1 PR; η | OP2 PR; η | OP3 PR; η | OP4 PR;η |
|---|---|---|---|---|
| CHT only wheel | −2.04%; 1.50% | −1.05%; −0.68% | −2.14%; −1.70% | −0.72%; −1.19% |
| CHT complete | −1.55%; 4.11% | −0.71%; 1.22% | −1.98%; −0.39% | −0.60%; −0.1% |
| OP1 PR; η | OP2 PR; η | OP3 PR; η | OP4 PR; η |
|---|---|---|---|
| 2.17%; 1.07% | 1.83%; 0.14% | 2.02%; 0.3% | 0.98%; 0.86% |
| E [W] Impeller | E [W] Cavity | E [W] Diffuser | E [W] Oil | E [W] Ambient |
|---|---|---|---|---|
| 126.6 | 236.6 | 786.4 | −1117.4 | −32.2 |
| Case | OP1 PR; η | OP2 PR; η | OP3 PR; η | OP4 PR; η |
|---|---|---|---|---|
| Adiabatic | −0.35%; −2.37% | −0.29%; −2.0% | −0.19%; −1.39% | −0.07%; −1.23% |
| Reduced | −0.25%; −1.79% | −0.21%; −1.51% | −0.18%; −1.04% | −0.05%; −0.86% |
| Case | OP1 PR; η | OP2 PR; η | OP3 PR; η | OP4 PR; η |
|---|---|---|---|---|
| 75%*Toil | 0.02%; 0.02% | 0.01%; 0.01% | 0.06%; 0.02% | 0.01%; 0.04% |
| 125%*Toil | −0.01%; −0.04% | −0.01%; −0.04% | −0.13%; −0.19% | −0.01%; −0.01% |
| 150%*Toil | −0.04%; −0.09% | −0.04%; −0.06% | −0.22%; −0.22% | −0.02%; −0.03% |
| OP1 PR; η | OP2 PR; η | OP3 PR; η | OP4 PR; η |
|---|---|---|---|
| 0.05%; 0.08% | 0.02%; 0.06% | −0.11%; −0.02% | −0.01%; 0.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cravero, C.; Hoffer, P.-A.; Marsano, D.; Mattiello, D.; Mosciaro, L. Conjugate Heat Transfer Modelling in a Centrifugal Compressor for Automotive Applications. Energies 2025, 18, 3348. https://doi.org/10.3390/en18133348
Cravero C, Hoffer P-A, Marsano D, Mattiello D, Mosciaro L. Conjugate Heat Transfer Modelling in a Centrifugal Compressor for Automotive Applications. Energies. 2025; 18(13):3348. https://doi.org/10.3390/en18133348
Chicago/Turabian StyleCravero, Carlo, Pierre-Alain Hoffer, Davide Marsano, Daniele Mattiello, and Luigi Mosciaro. 2025. "Conjugate Heat Transfer Modelling in a Centrifugal Compressor for Automotive Applications" Energies 18, no. 13: 3348. https://doi.org/10.3390/en18133348
APA StyleCravero, C., Hoffer, P.-A., Marsano, D., Mattiello, D., & Mosciaro, L. (2025). Conjugate Heat Transfer Modelling in a Centrifugal Compressor for Automotive Applications. Energies, 18(13), 3348. https://doi.org/10.3390/en18133348








