Adaptive Damping PTO Control of Wave Energy Converter for Irregular Waves Supported by Wavelet Transformation
Abstract
1. Introduction
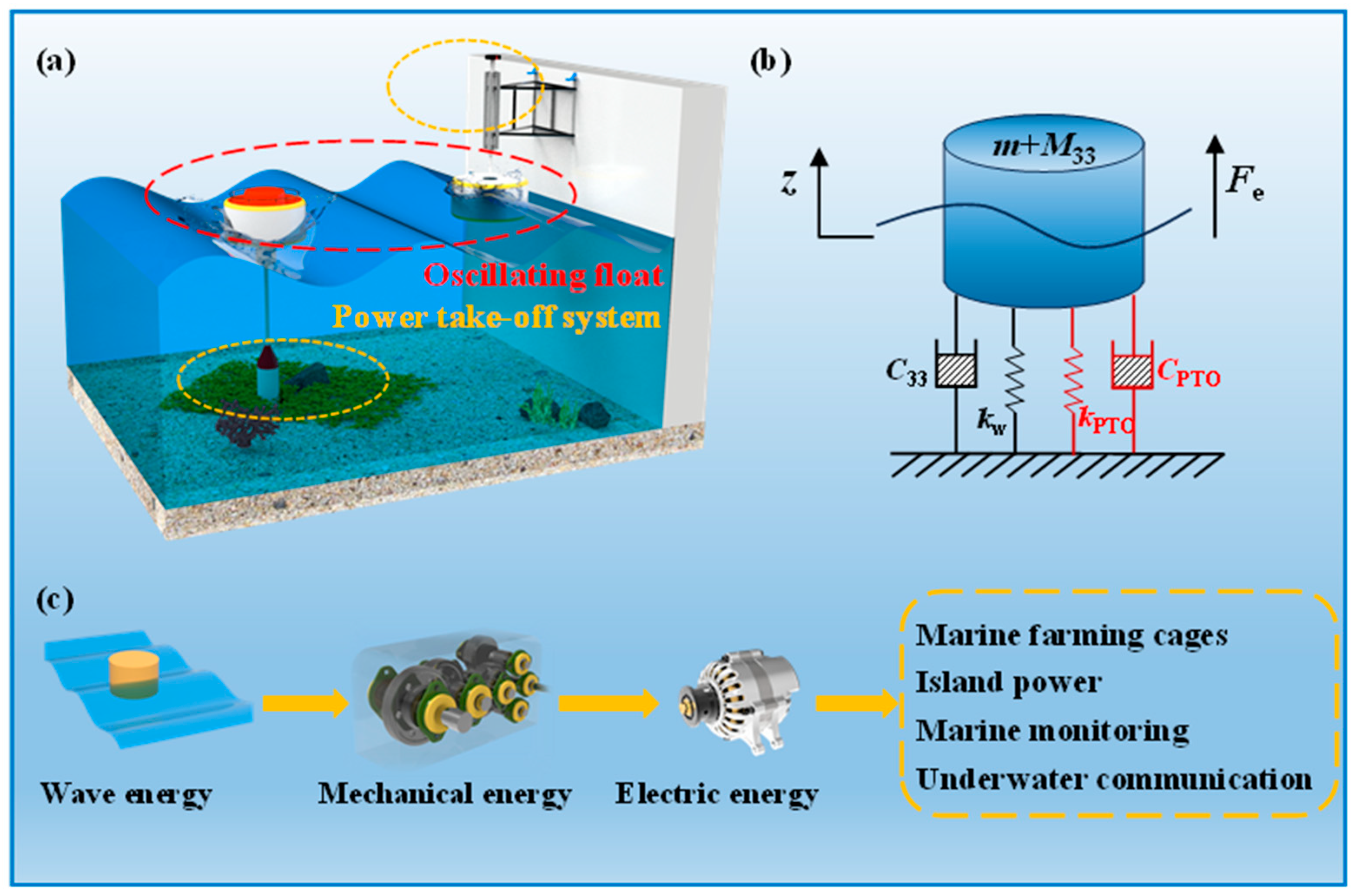
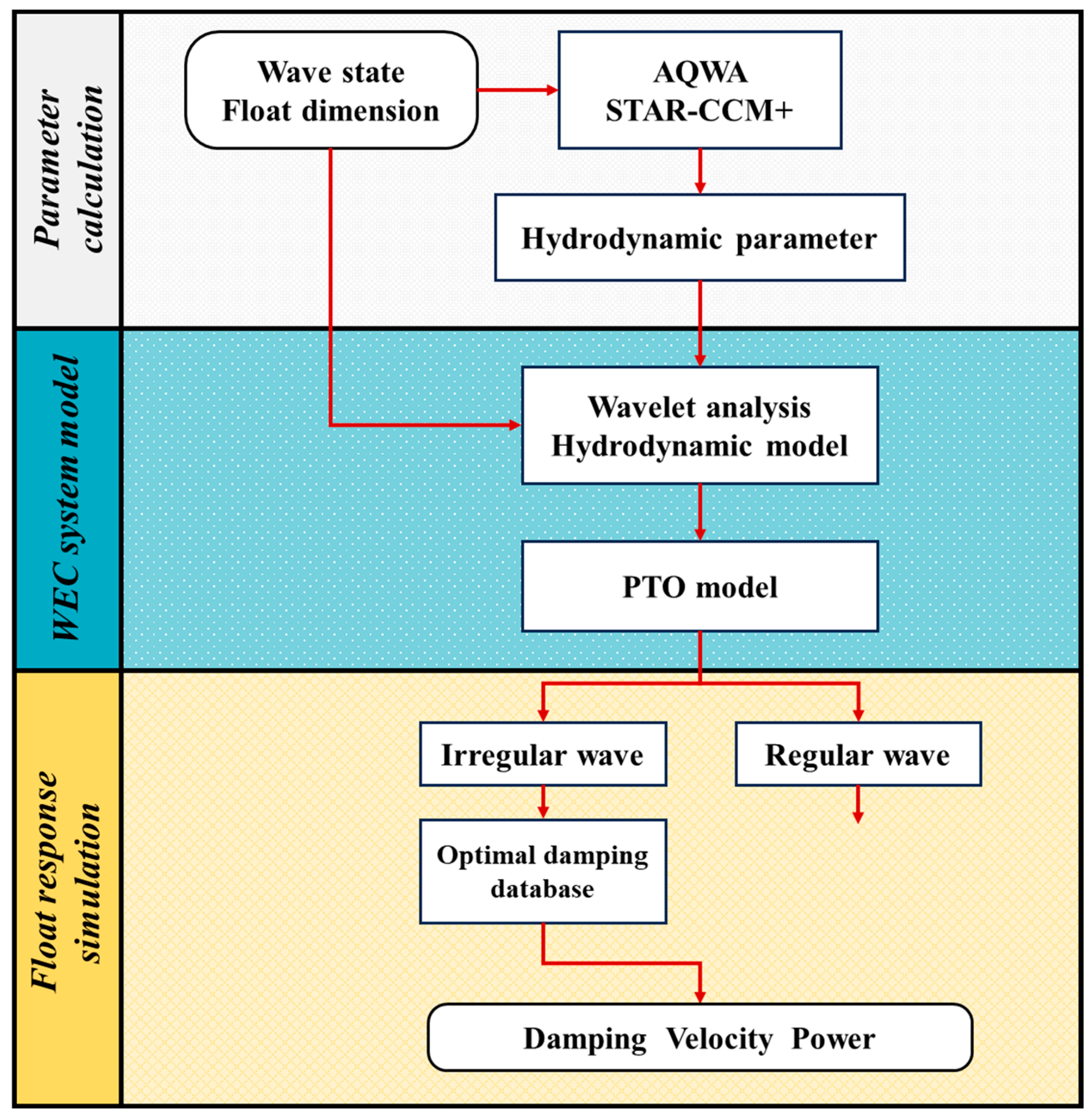
2. Modeling the Adaptive Damping PTO System
2.1. Mathematical Model of the WEC
2.2. Establishing the Optimal Damping Database in Regular Waves
2.3. Irregular Wave Frequency Extraction Based on the Wavelet Transform
3. Validation of the Optimal Damping Database and Wavelet Transform
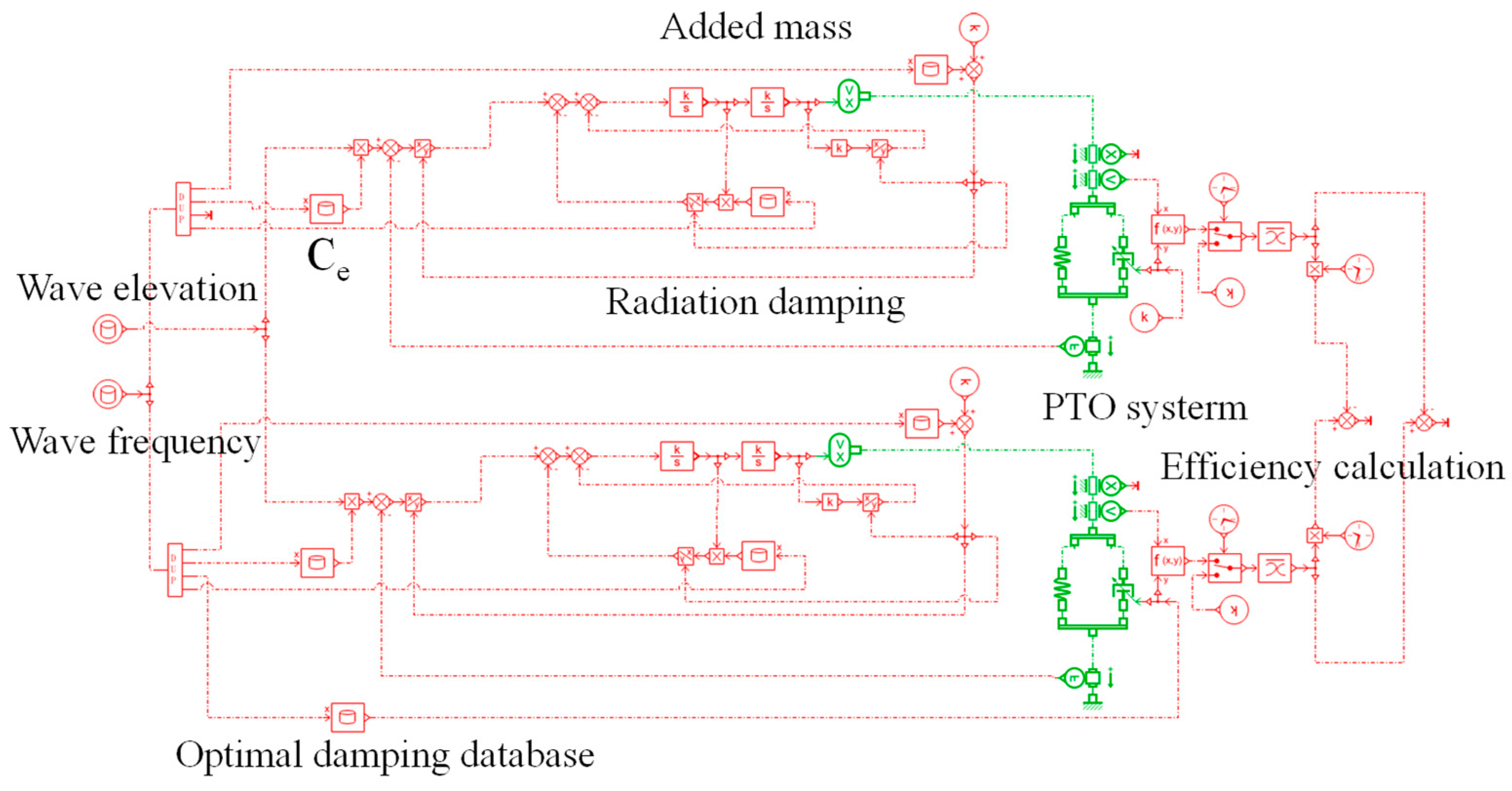
3.1. Co-Simulation to Verify the PTO Optimal Damping Database
3.2. Verification of Wavelet Transform
4. Results of Different Waves Efficiency with the Wavelet Transform
4.1. Calculation of Combined Waves
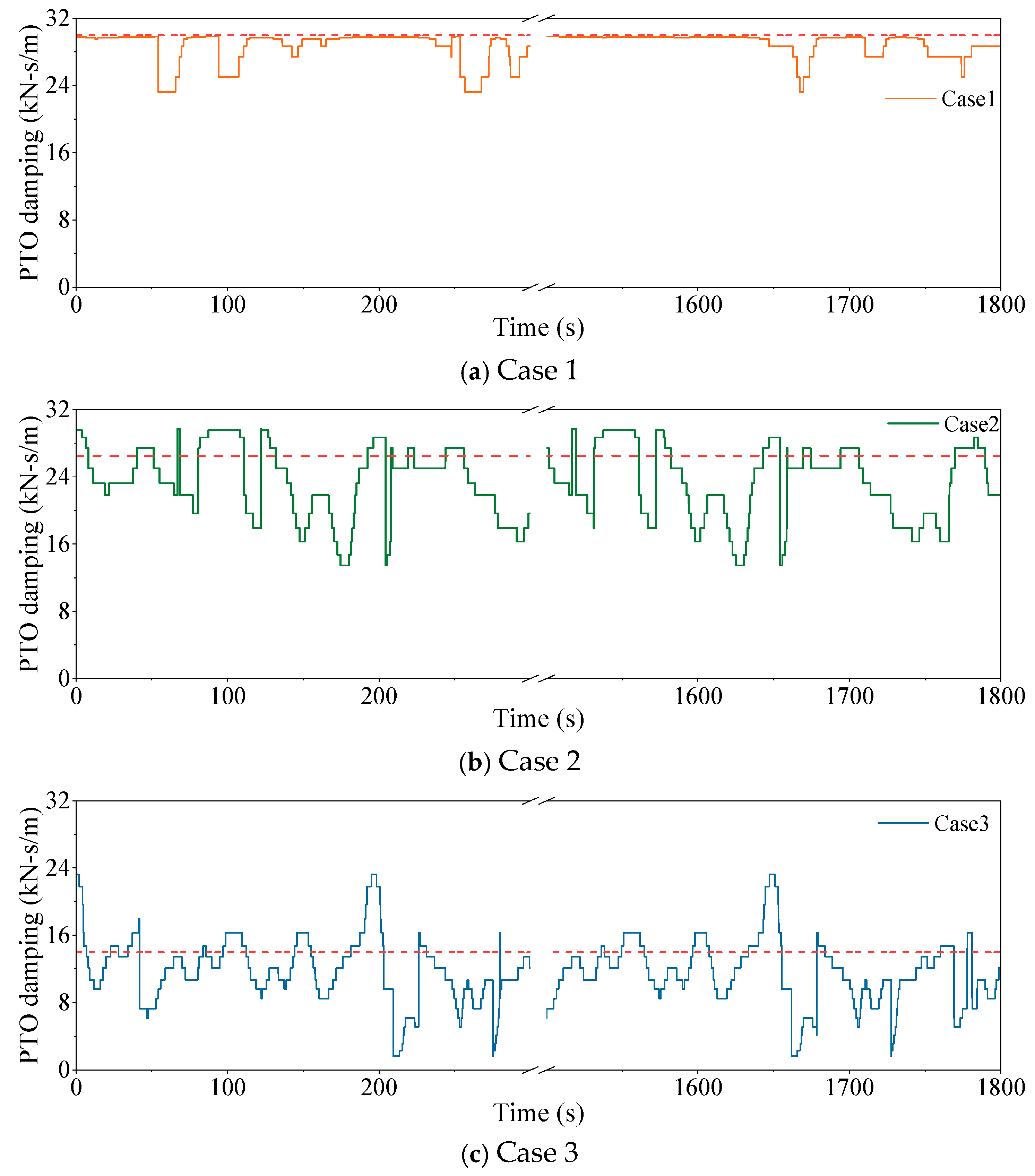
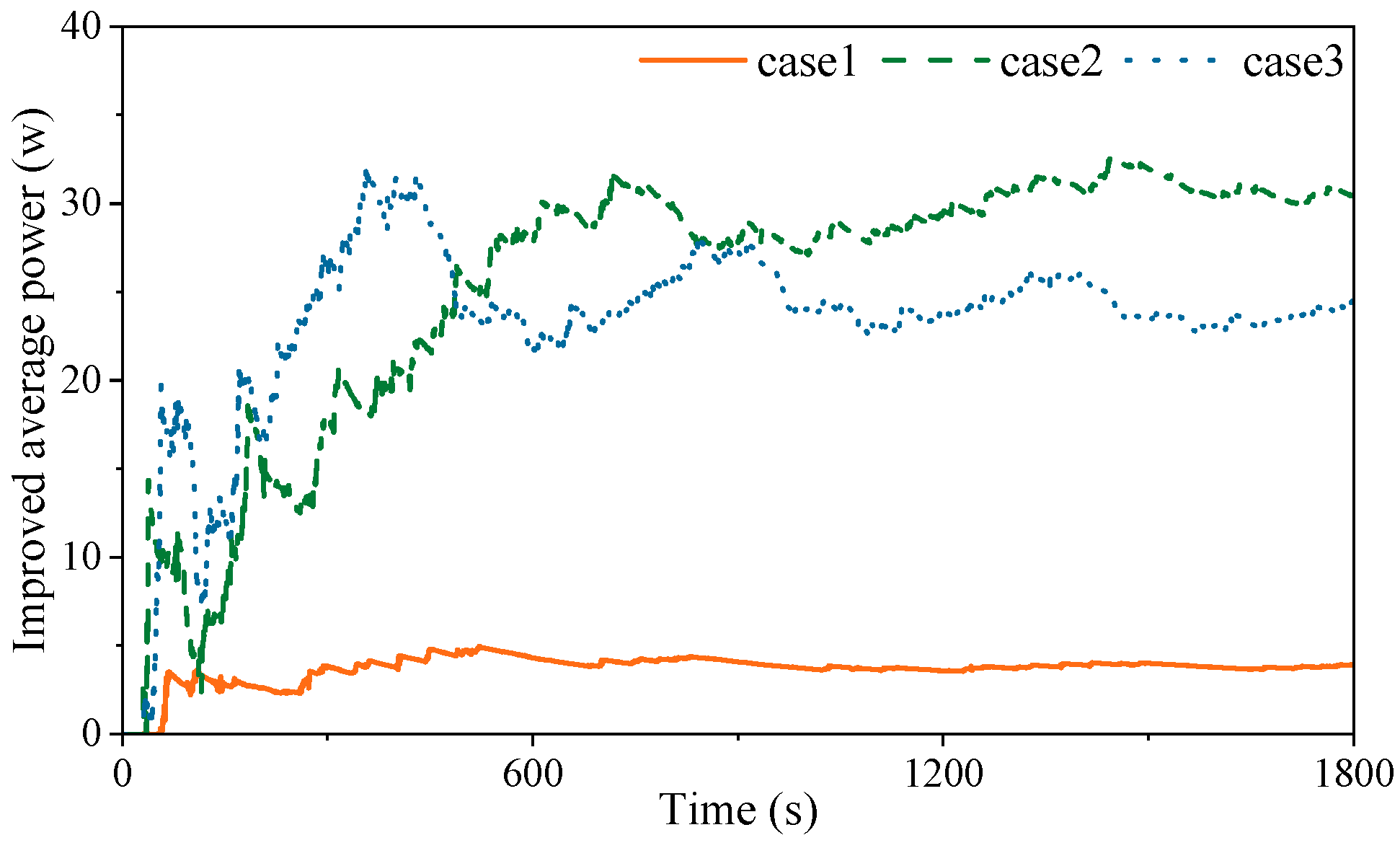
4.2. Calculation of Irregular Waves
5. Discussion
- (1)
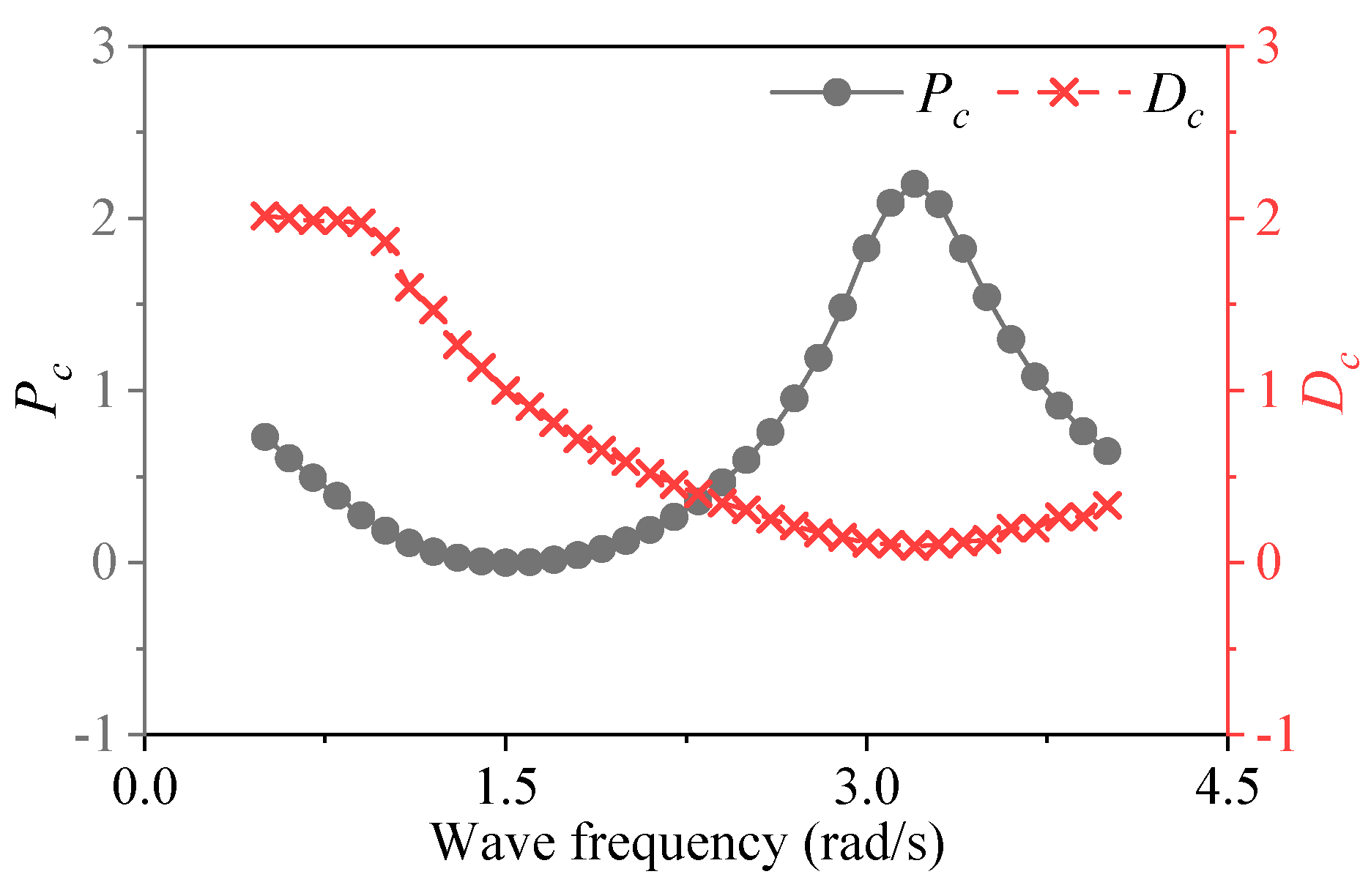
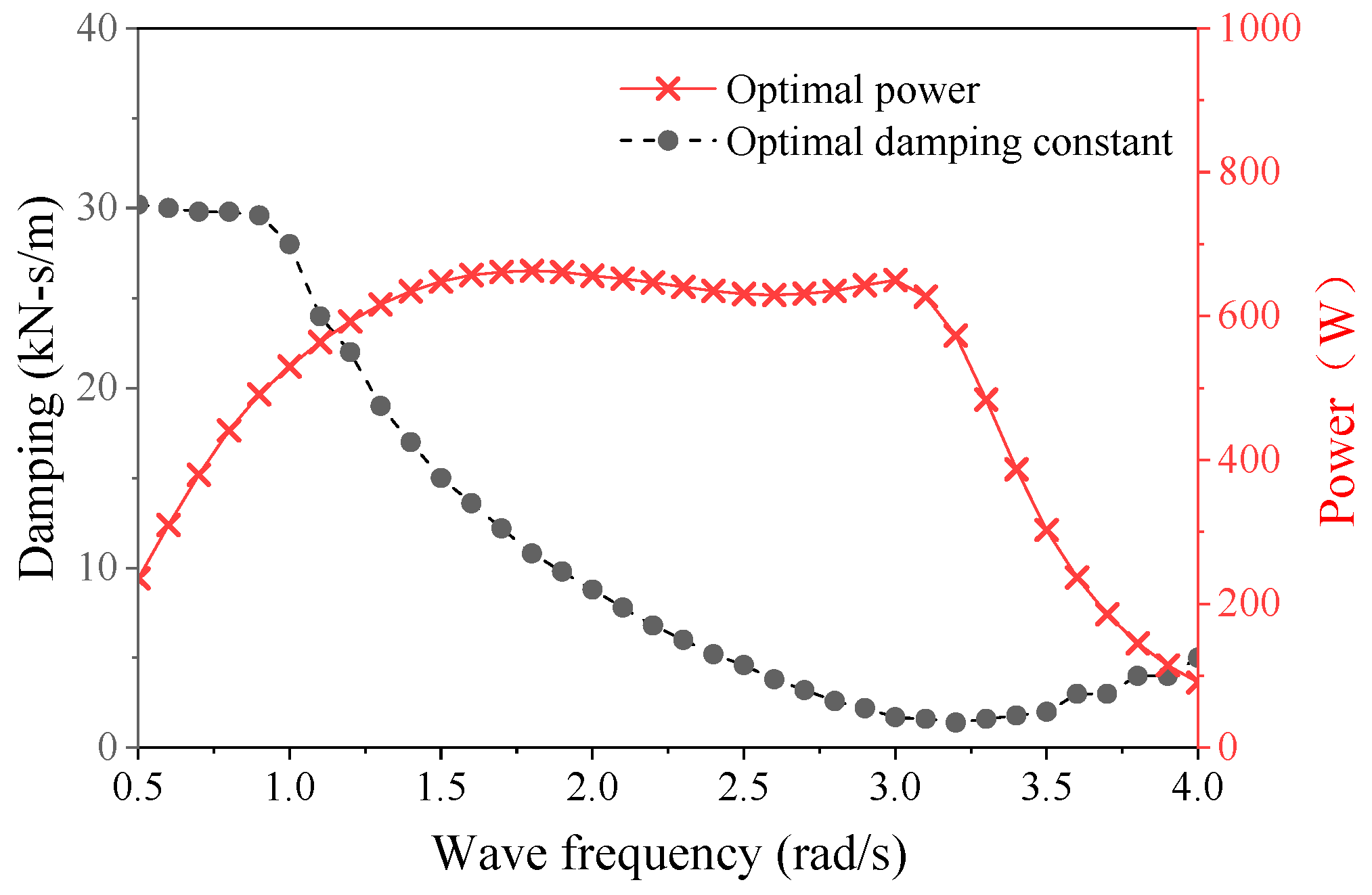
- The effect of the optimal PTO damping for different wave frequencies is analyzed. ω = 1.5–3.0 rad/s is the better working sea state, because it captures more wave energy in a limited wave frequency range and specific optimal PTO damping. The obtained wave energy is relatively stable and provides good protection for the power absorption device, despite the larger range of PTO damping.
- (2)
- The use of dimensionless numbers Pc and Dc shows that the result of power optimization is positive optimization. When the wave frequency is close to the WECs intrinsic frequency, Dc reaches the minimum value, and the Pc is most obvious.
- (3)
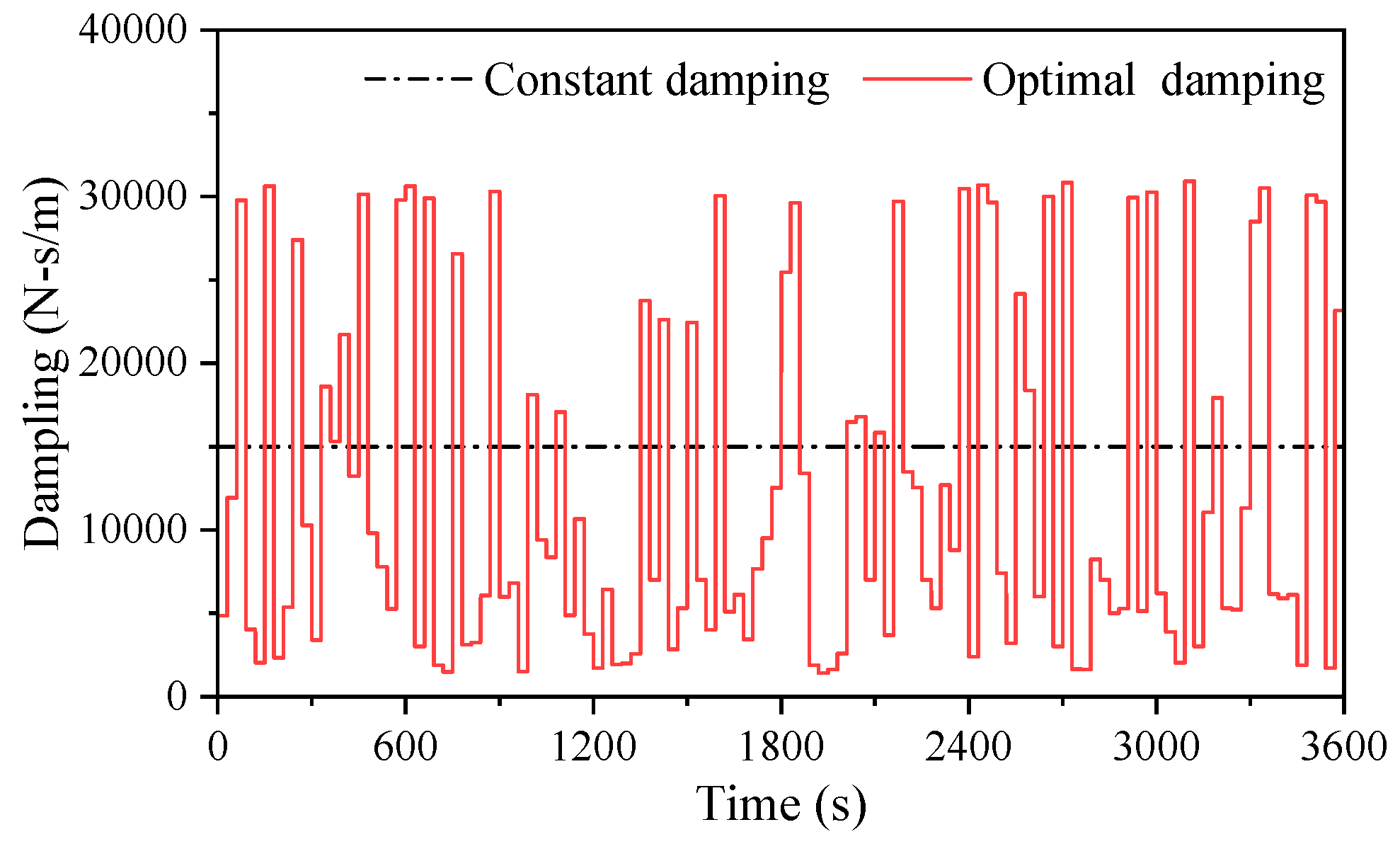
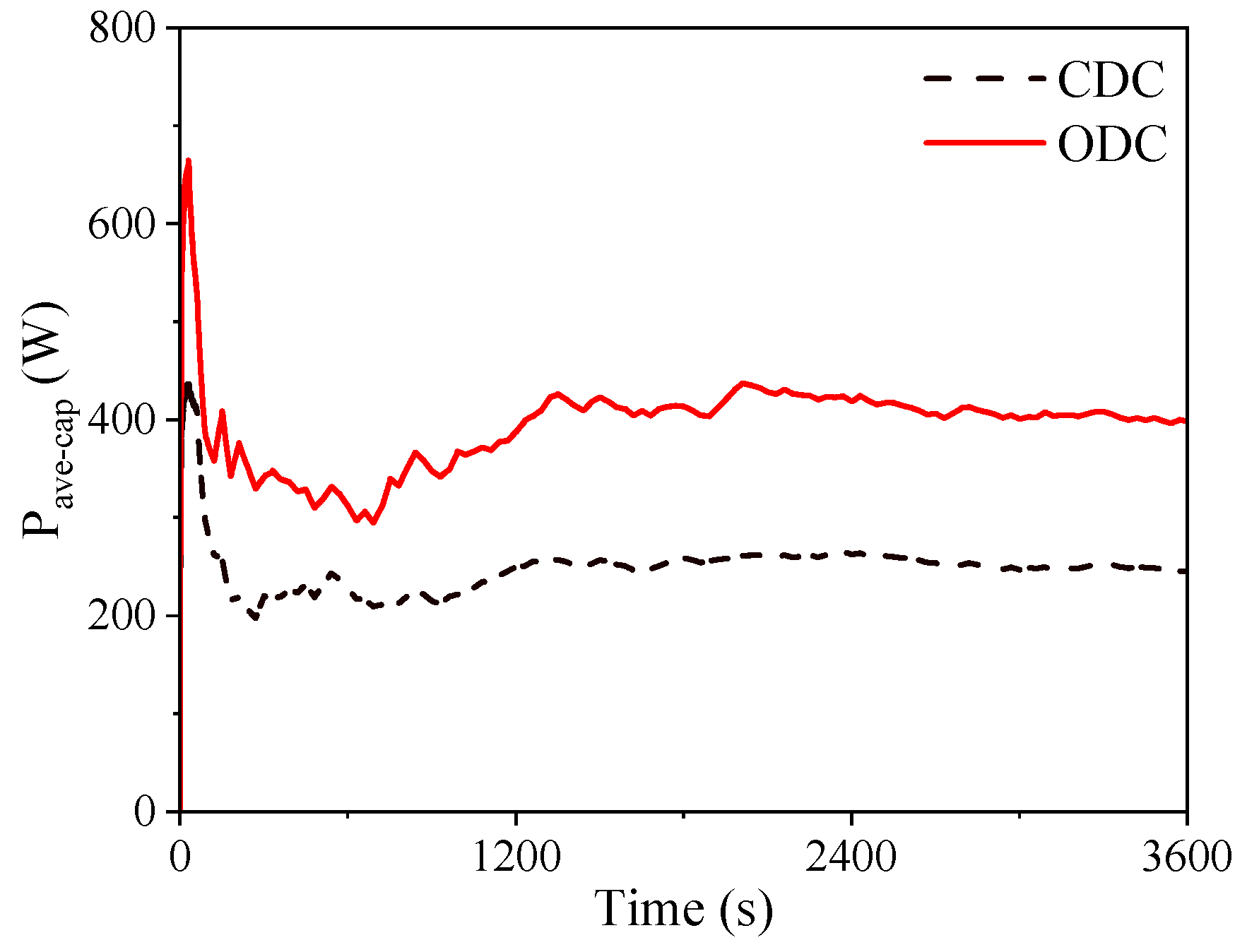
- The effects of constant damping control (CDC) PTO and ODC PTO on AMESIM were compared. The optimization effect increases in average power absorption for 1 h, is approximately 0.15 kWh, and the total increase in power absorption is 62.5%. It has a good improvement effect in the relatively slow-changing wave environment.
- (4)
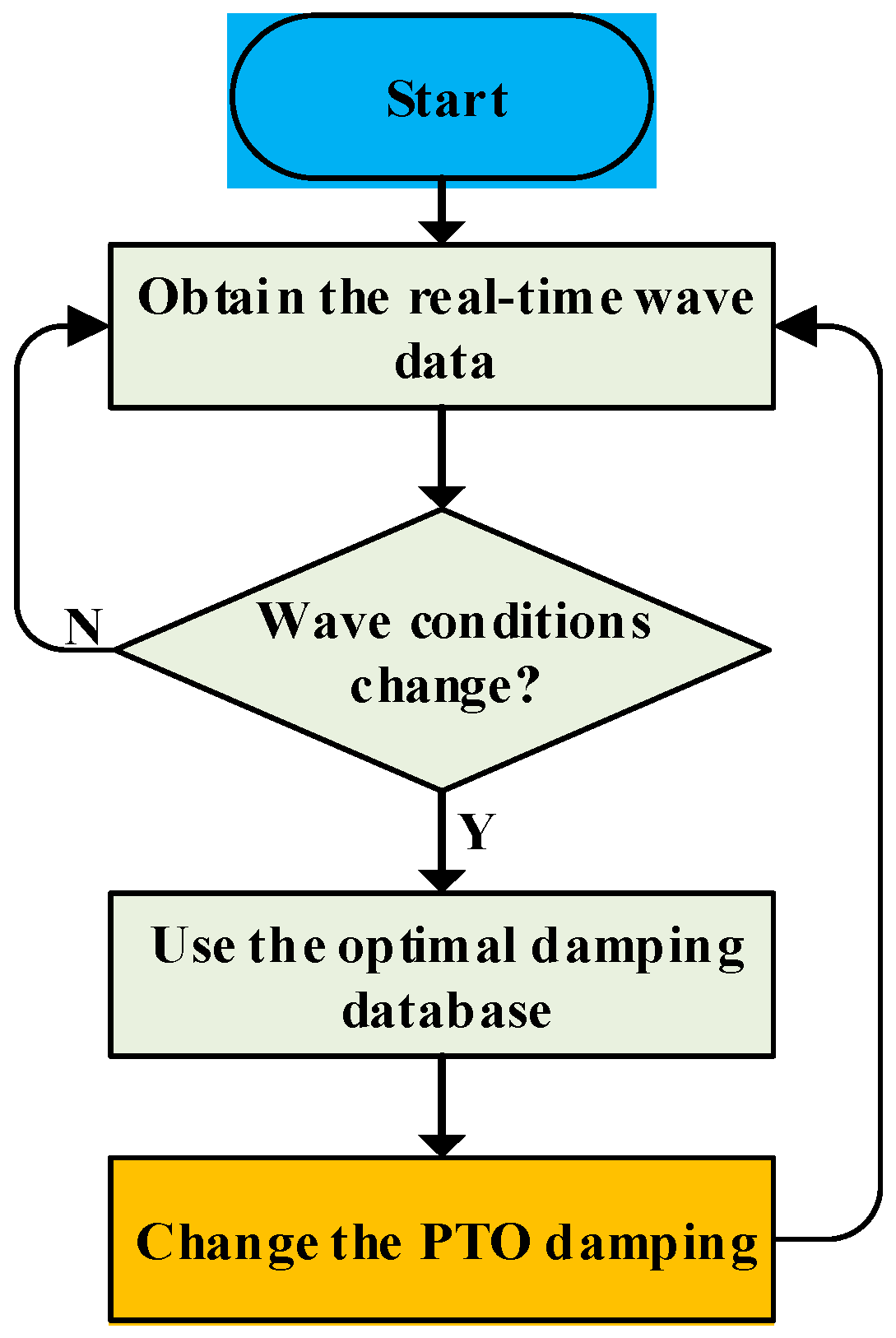
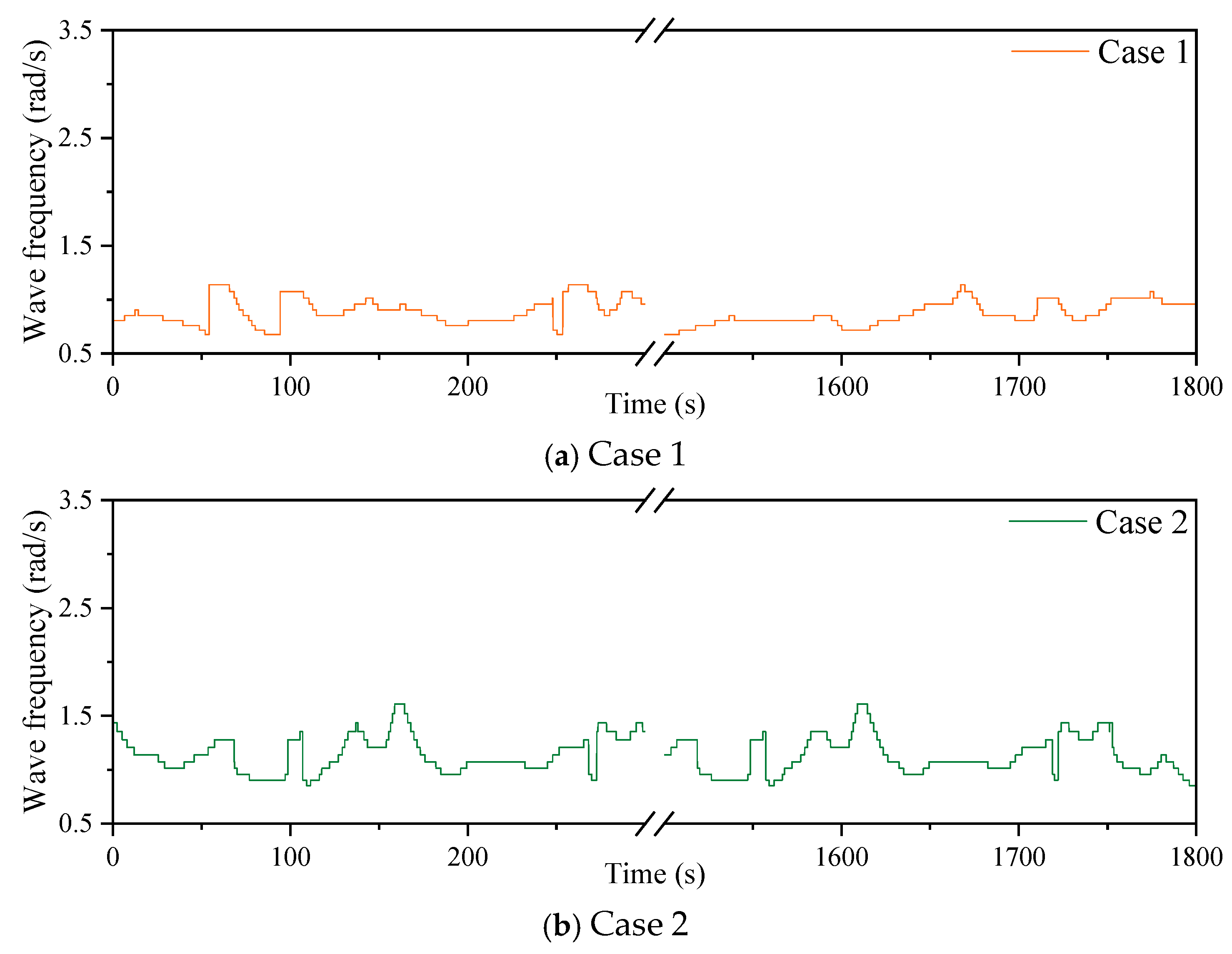
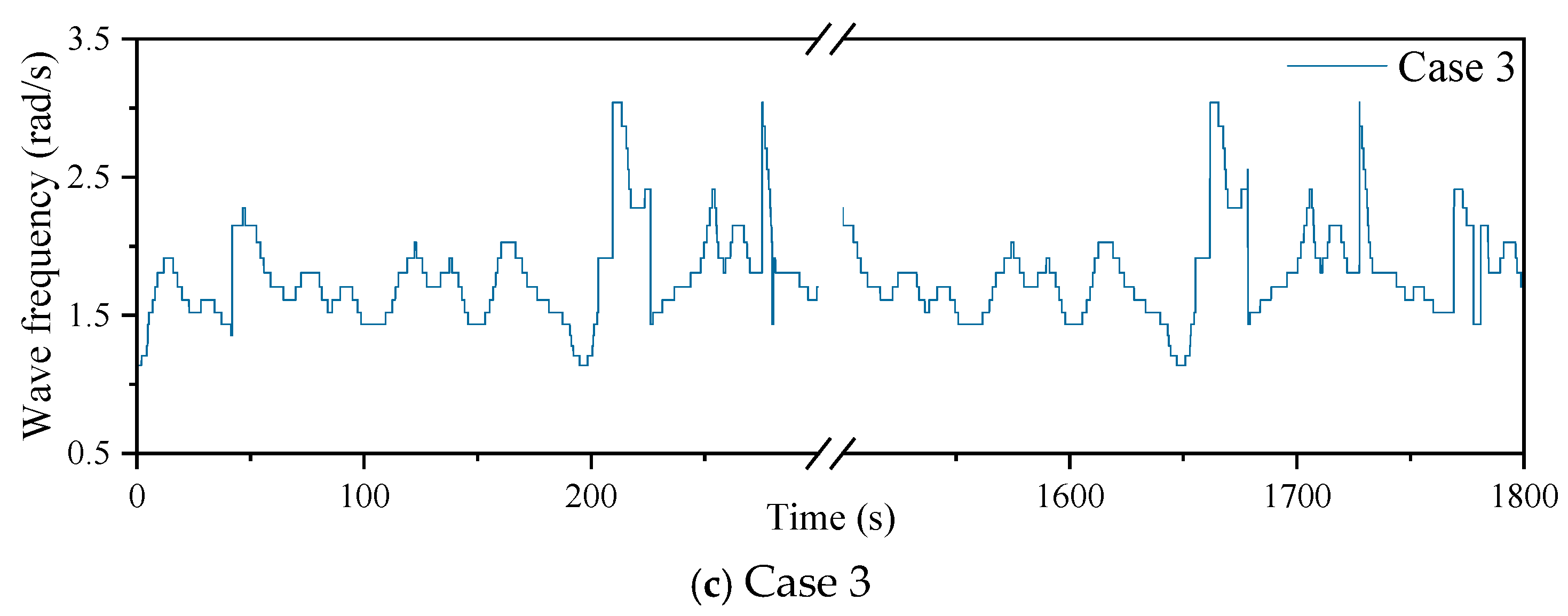
- The results of the PIMP algorithm are all positive, and they are not the same for the three spectral peak periods. The wave height recorder can be used to obtain the frequency in real time to achieve better optimization results under actual sea conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Wave amplitude | Fr | The added mass and radiation damping force |
| M33 | Added mass | Fs | The hydrostatic force |
| C33 | Radiation damping | Fe | Vertical wave excitation force |
| m | Mass of float | FPTO | PTO force |
| Ce | Excitation force coefficient | Pcap | Generated power |
| kw | Hydrostatic stiffness of float | H | Wave height |
| R | The radius of the float | Pc | Percentage of power optimization. |
| ρ | The density of sea water | Dc | Damping adjustment ratio |
| ω | wave frequency | t | time |
| CPTO | Load damping of PTO | PWT(τ,i) | Wavelet energy spectrum |
| kPTO | Stiffness of PTO | WT(τ,i) | Wavelet transform result |
References
- Yolcan, O.O. World energy outlook and state of renewable energy: 10-Year evaluation. Innov. Green Dev. 2023, 2, 100070. [Google Scholar] [CrossRef]
- He, G.; Zhao, C.; Liu, C.; He, R.; Luan, Z. Power absorption and dynamic response analysis of a hybrid system with a semi-submersible wind turbine and a Salter’s duck wave energy converter array. Energy 2024, 305, 132210. [Google Scholar] [CrossRef]
- Gaspar, J.F.; Pinheiro, R.F.; Mendes, M.J.C.; Kamarlouei, M.; Soares, C.G. Review on hardware-in-the-loop simulation of wave energy converters and power take-offs. Renew. Sustain. Energy Rev. 2024, 191, 114144. [Google Scholar] [CrossRef]
- Khojasteh, D.; Shamsipour, A.; Huang, L.; Tavakoli, S.; Haghani, M.; Flocard, F.; Farzadkhoo, M.; Iglesias, G.; Hemer, M.; Lewis, M.; et al. A large-scale review of wave and tidal energy research over the last 20 years. Ocean Eng. 2023, 282, 114995. [Google Scholar] [CrossRef]
- Barua, A.; Rasel, S. Advances and challenges in ocean wave energy harvesting. Sustain. Energy Technol. Assess. 2024, 61, 103599. [Google Scholar] [CrossRef]
- Gallutia, D.; Fard, M.T.; Soto, M.G.; He, J. Recent advances in wave energy conversion systems: From wave theory to devices and control strategies. Ocean. Eng. 2022, 252, 111105. [Google Scholar] [CrossRef]
- Ahamed, R.; McKee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) Systems: A review. Ocean Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Ghaedi, A.; Sedaghati, R.; Mahmoudian, M.; Bazyari, S. Reliability modeling of wave energy converters based on pelamis technology. Electr. Power Syst. Res. 2024, 227, 109977. [Google Scholar] [CrossRef]
- Yang, B.; Duan, J.; Chen, Y.; Wu, S.; Li, M.; Cao, P.; Jiang, L. A critical survey of power take-off systems based wave energy converters: Summaries. Ocean Eng. 2024, 298, 117149. [Google Scholar] [CrossRef]
- Xi, Y.; Wang, J.; Zi, Y.; Li, X.; Han, C.; Cao, X.; Hu, C.; Wang, Z. High efficient harvesting of underwater ultrasonic wave energy by triboelectric nanogenerator. Nano Energy 2017, 38, 101–108. [Google Scholar] [CrossRef]
- He, G.; Luan, Z.; Zhang, W.; He, R.; Liu, C.; Yang, K.; Yang, C.; Jing, P.; Zhang, Z. Review on research approaches for multi-point absorber Wave energy converters. Renew. Energy 2023, 218, 119237. [Google Scholar] [CrossRef]
- Gao, H.; He, K.; Guo, W.; Gao, X.; Li, B.; Zou, J.; Ding, S.; Song, Y. Response power of floating three-body wave energy converter with different shapes. Sustain. Energy Technol. Assess. 2023, 57, 103225. [Google Scholar] [CrossRef]
- He, G.; Liu, C.; Zhang, W.; Luan, Z.; Zhang, Z. Numerical study of the effect of central platform motion on the wave energy converter array. Ocean Eng. 2023, 286, 115483. [Google Scholar] [CrossRef]
- Amini, E.; Mehdipour, H.; Faraggiana, E.; Golbaz, D.; Mozaffari, S.; Bracco, G.; Neshat, M. Optimization of hydraulic power take-off system settings for point absorber wave energy converter. Renew. Energy 2022, 194, 938–954. [Google Scholar] [CrossRef]
- Çelik, A. An experimental investigation into the effects of front wall geometry on OWC performance for various levels of applied power take off dampings. Ocean. Eng. 2022, 248, 110761. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, Y.H.; Zhou, X.G. Power take-off mechanism analysis of oscillating-buoy wave energy converter. J. Vib. Shock. 2020, 39, 38–44. [Google Scholar]
- He, G.; Liu, C.; Chen, B.; Ghassemi, H.; Liu, L.; Yang, K.; Luan, Z. Effect of piecewise damping torques and coefficients on power absorption of a point-absorber wave energy converter. Renew. Energy 2023, 219, 119440. [Google Scholar] [CrossRef]
- Gadelho, J.; Rezanejad, K.; Soares, C.G.; Santos, J.; Anastas, G.; Fortes, C. Experimental study of an onshore dual chamber oscillating water column device. Ocean Eng. 2024, 300, 117240. [Google Scholar] [CrossRef]
- Khatri, P.; Liu, Z.; Rudolph, J.; Wang, X. A study of a modified design of dumbbell-shaped flux switching tubular linear generator for regular wave energy conversion. Renew. Energy 2023, 208, 287–300. [Google Scholar] [CrossRef]
- Xu, J.; Yang, Y.; Hu, Y.; Xu, T.; Zhan, Y. MPPT Control of Hydraulic Power Take-Off for Wave Energy Converter on Artificial Breakwater. J. Mar. Sci. Eng. 2020, 8, 304. [Google Scholar] [CrossRef]
- Ghafari, H.R.; Ghassemi, H.; Neisi, A. Power matrix and dynamic response of the hybrid Wavestar-DeepCwind platform under different diameters and regular wave conditions. Ocean Eng. 2022, 247, 110734. [Google Scholar] [CrossRef]
- Harms, J.; Hollm, M.; Dostal, L.; Kern, T.A.; Seifried, R. Design and optimization of a wave energy converter for drifting sensor platforms in realistic ocean waves. Appl. Energy 2022, 321, 119303. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, Y.-H.; Mizutani, N.; Nakamura, T. Simplified BEM-based mathematical model for bottom-hinged oscillating wave surge con-verters under large-amplitude regular waves. Ocean Eng. 2023, 272, 113893. [Google Scholar] [CrossRef]
- Grasberger, J.; Yang, L.; Bacelli, G.; Zuo, L. Control co-design and optimization of oscillating-surge wave energy converter. Renew. Energy 2024, 225, 120234. [Google Scholar] [CrossRef]
- Liang, H.; Qiao, D.; Wang, X.; Zhi, G.; Yan, J.; Ning, D.; Ou, J. Energy capture optimization of heave oscillating buoy wave energy converter based on model predictive control. Ocean Eng. 2023, 268, 113402. [Google Scholar] [CrossRef]
- Dong, F.; Pan, S.; Gong, J.; Cai, Y. Maximum power point tracking control strategy based on frequency and amplitude control for the wave energy conversion system. Renew. Energy 2023, 215, 118973. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Sun, W.; Li, J. Ocean wave energy converters: Technical principle. Renew. Sustain. Energy Rev. 2021, 141, 110764. [Google Scholar] [CrossRef]
- Zang, Z.; Zhang, Q.; Qi, Y.; Fu, X. Hydrodynamic responses and efficiency analyses of a heaving-buoy wave energy converter with PTO damping in regular and irregular waves. Renew. Energy 2018, 116, 527–542. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Yang, L.; Wu, X.; Huang, J.; Mi, J.; Zuo, L. Achieving optimum power extraction of wave energy converters through tunable mechanical com-ponents. Energy 2024, 291, 130322. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Y.; Zou, Q.; Zhang, J.; Li, H. Effect of varying PTO on a triple floater wave energy converter-breakwater hybrid system: An experimental study. Renew. Energy 2024, 224, 120100. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Xiao, L. Parametric study on power capture performance of an adaptive bistable point absorber wave energy converter in irregular waves. J. Ocean Eng. Sci. 2022, 7, 383–398. [Google Scholar] [CrossRef]
- Ni, W.; Zhang, X.; Zhang, W.; Liang, S. Numerical investigation of adaptive damping control for raft-type wave energy converters. Renew. Energy 2021, 175, 520–531. [Google Scholar] [CrossRef]
- Ali, R.; Meek, M.; Robertson, B. Submerged wave energy converter dynamics and the impact of PTO-mooring configuration on power performance. Renew. Energy 2025, 243, 122525. [Google Scholar] [CrossRef]
- Vakili, A.; Pourzangbar, A.; Ettefagh, M.M.; Haghghi, M.A. Optimal control strategy for enhancing energy efficiency of Pelamis wave energy converter: A Simulink-based simulation approach. Renew. Energy Focus 2025, 53, 100685. [Google Scholar] [CrossRef]
- Pourzangbar, A.; Vaezi, M. Optimal design of brace-viscous damper and pendulum tuned mass damper using Particle Swarm Optimization. Appl. Ocean Res. 2021, 112, 102706. [Google Scholar] [CrossRef]
- Pourzangbar, A.; Vaezi, M. Effects of pendulum tuned mass dampers on the dynamic response of jacket platforms. Ocean Eng. 2022, 249, 110895. [Google Scholar] [CrossRef]

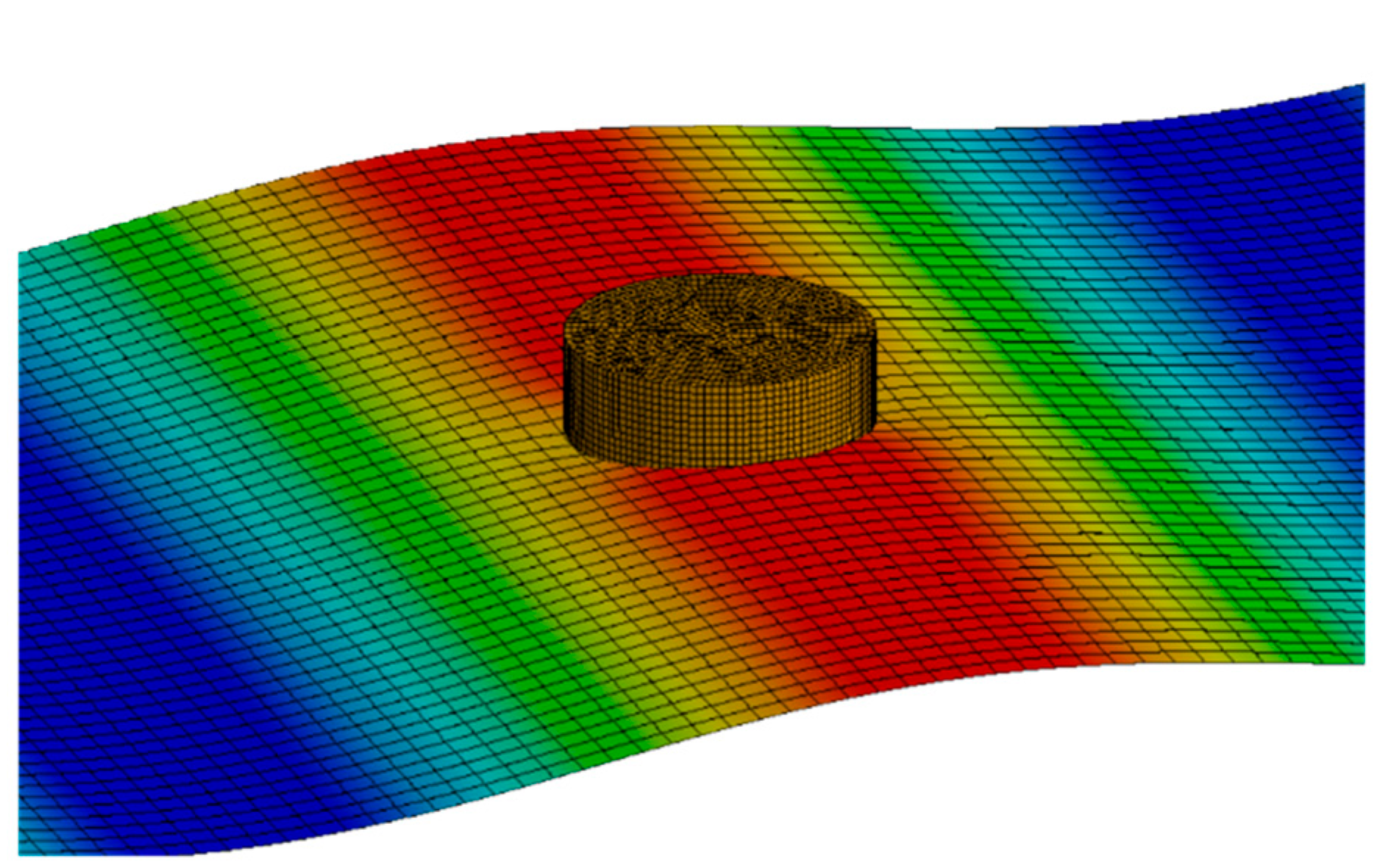
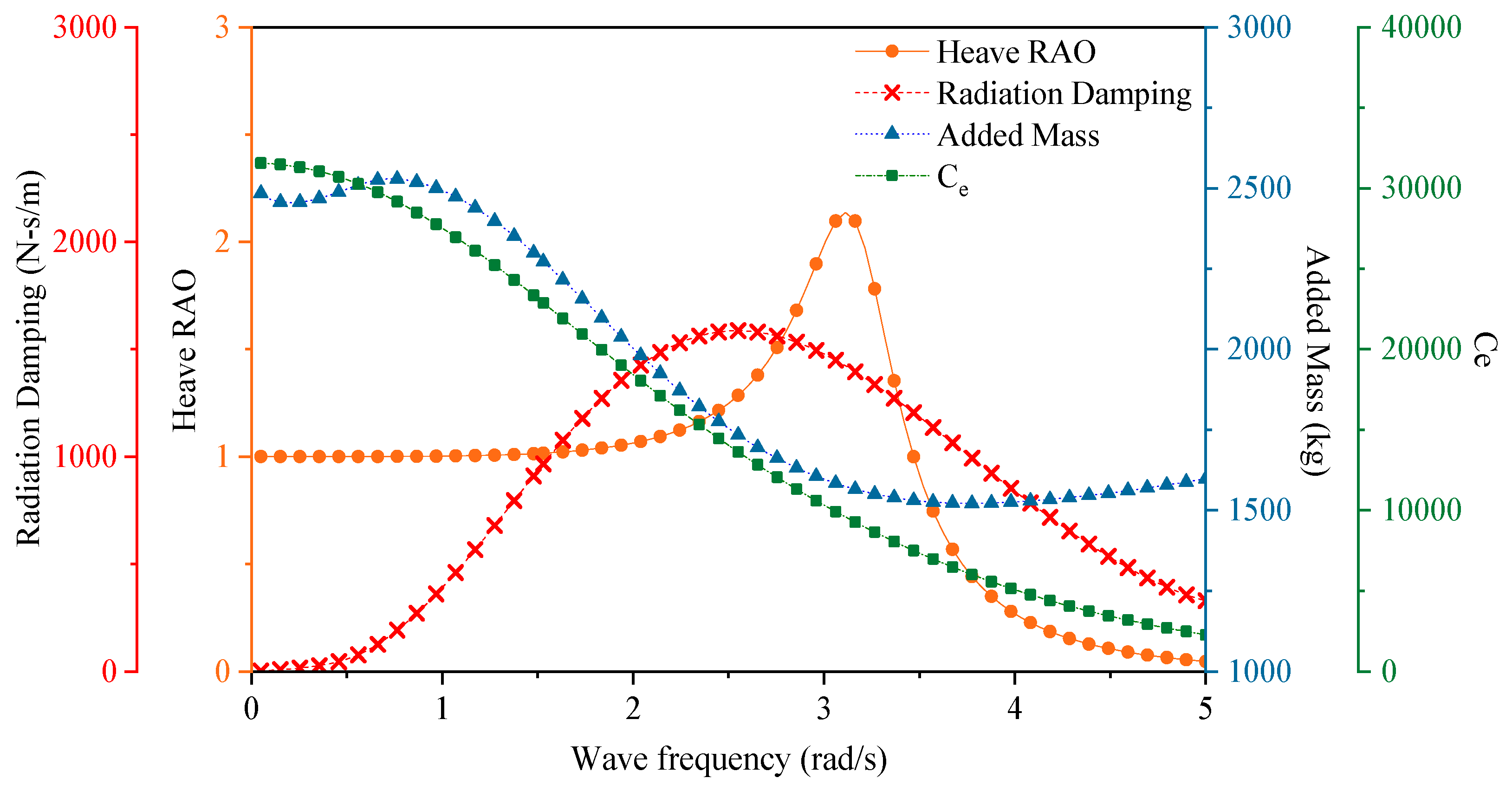






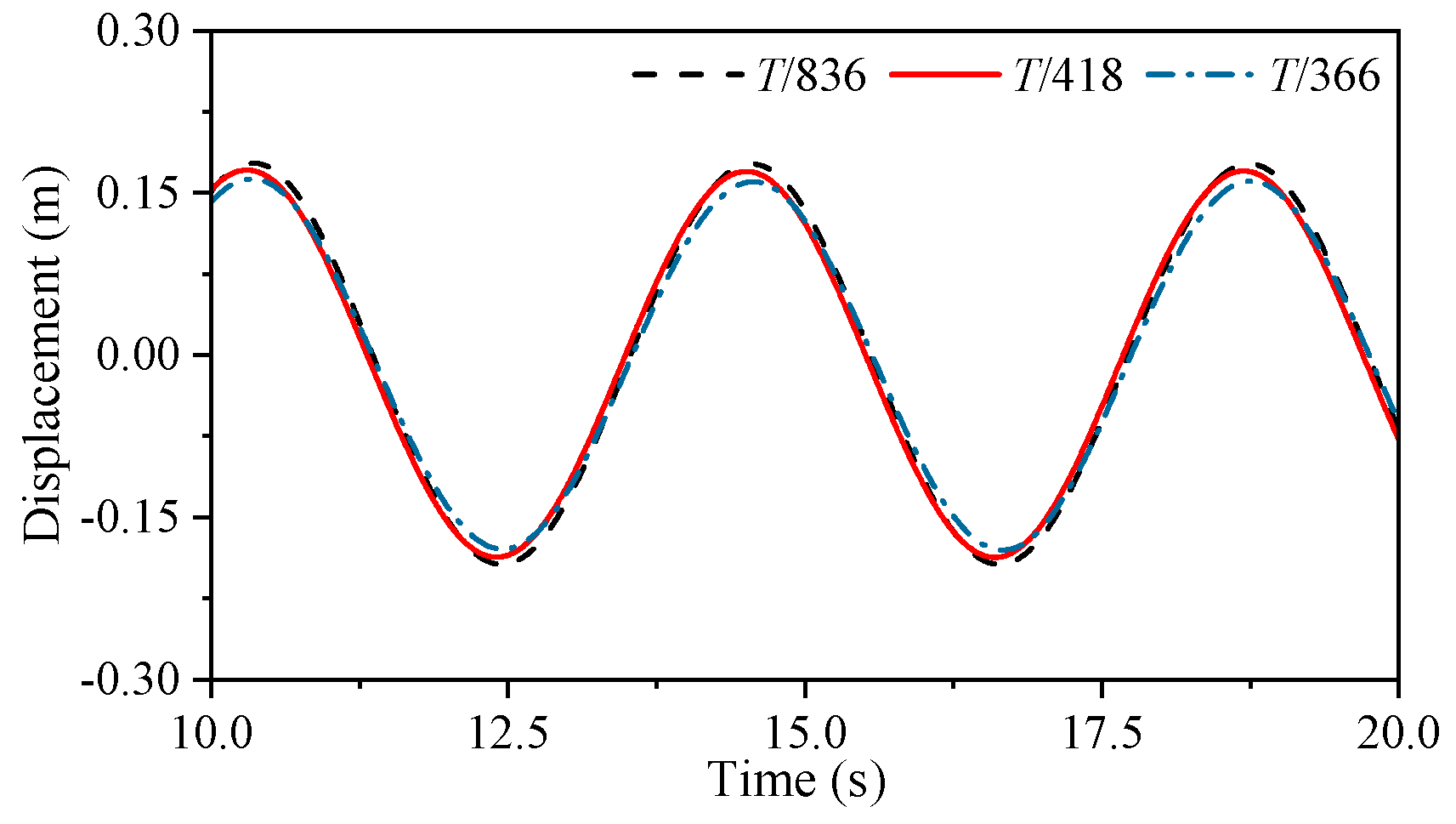





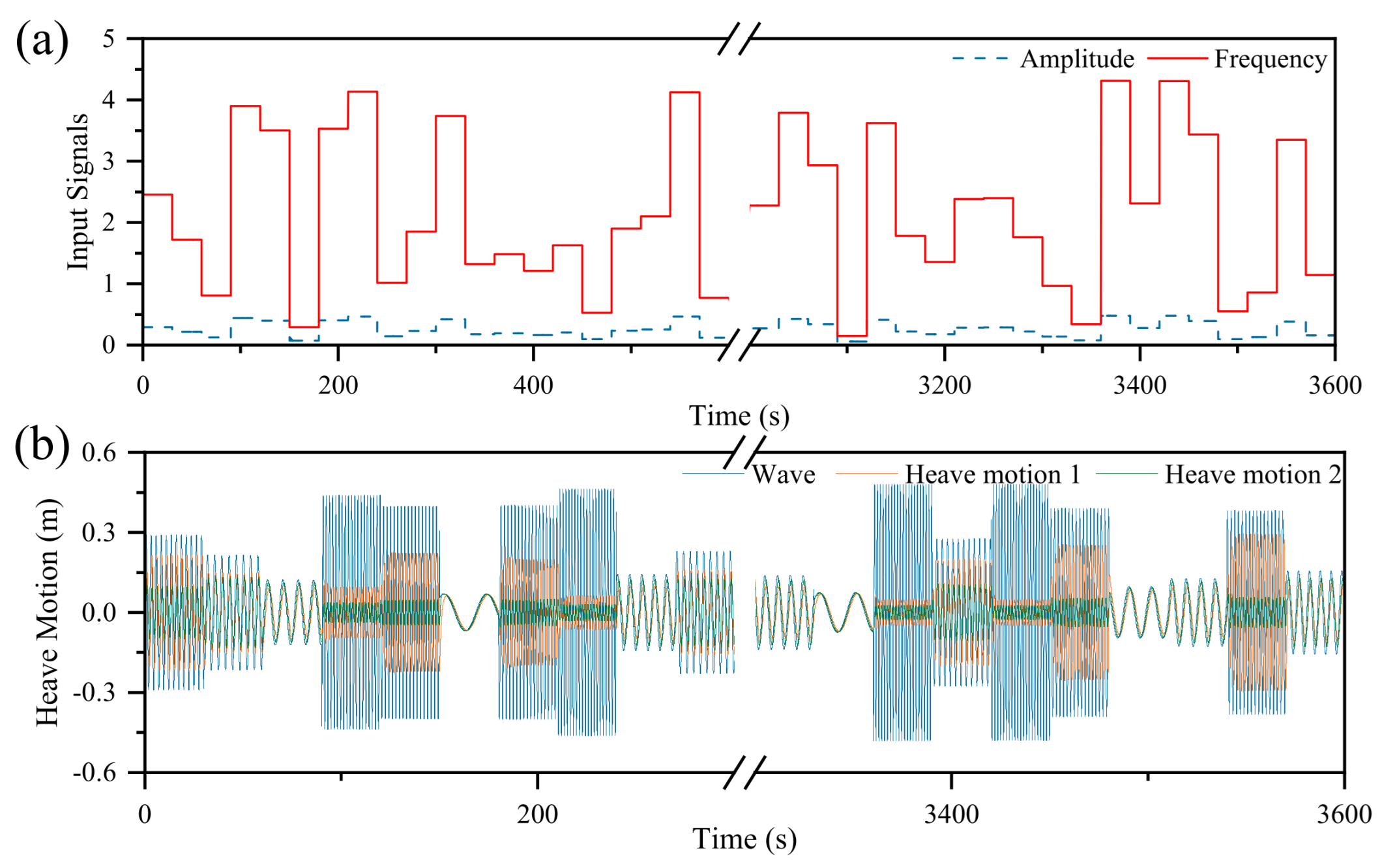

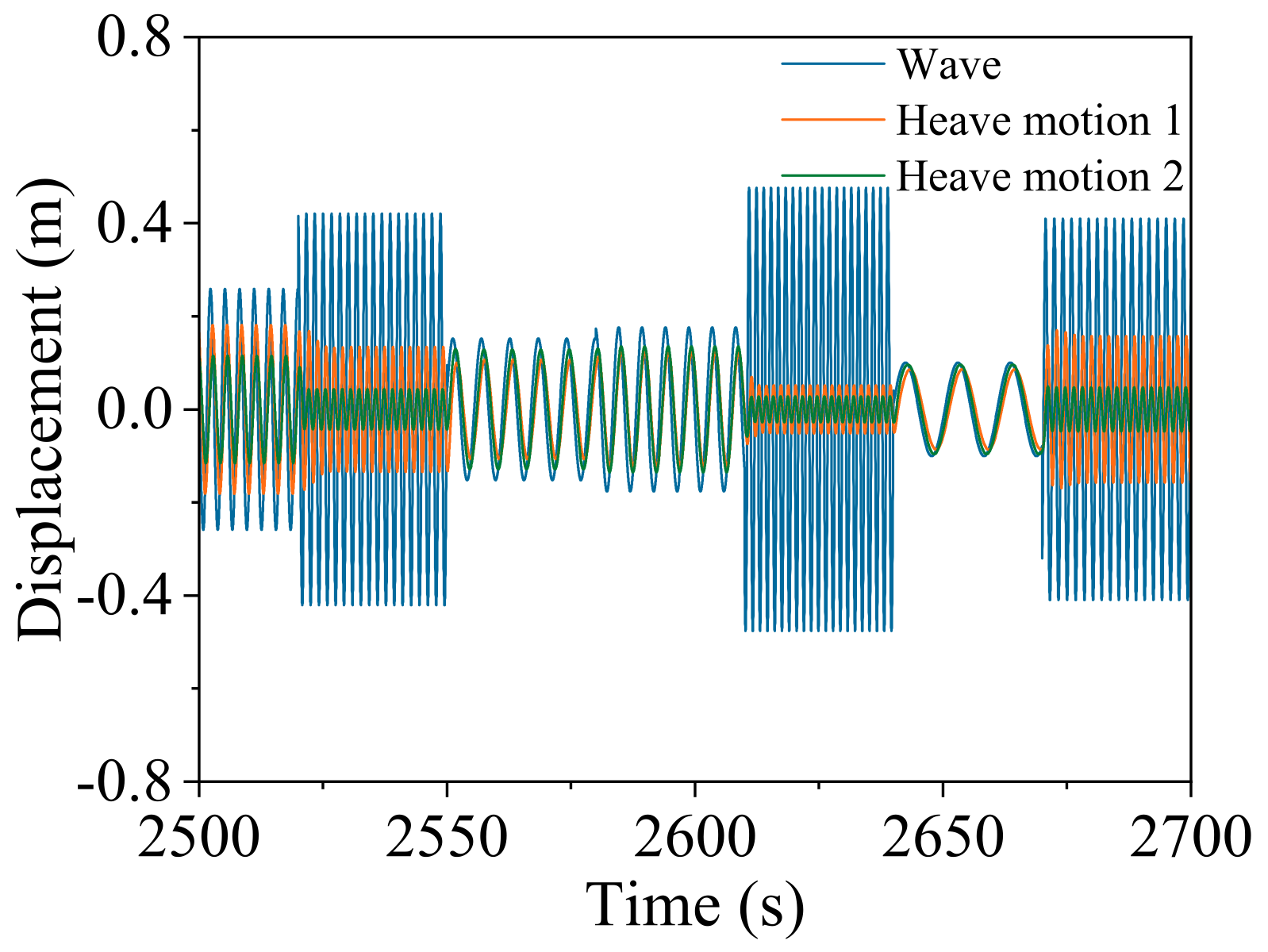
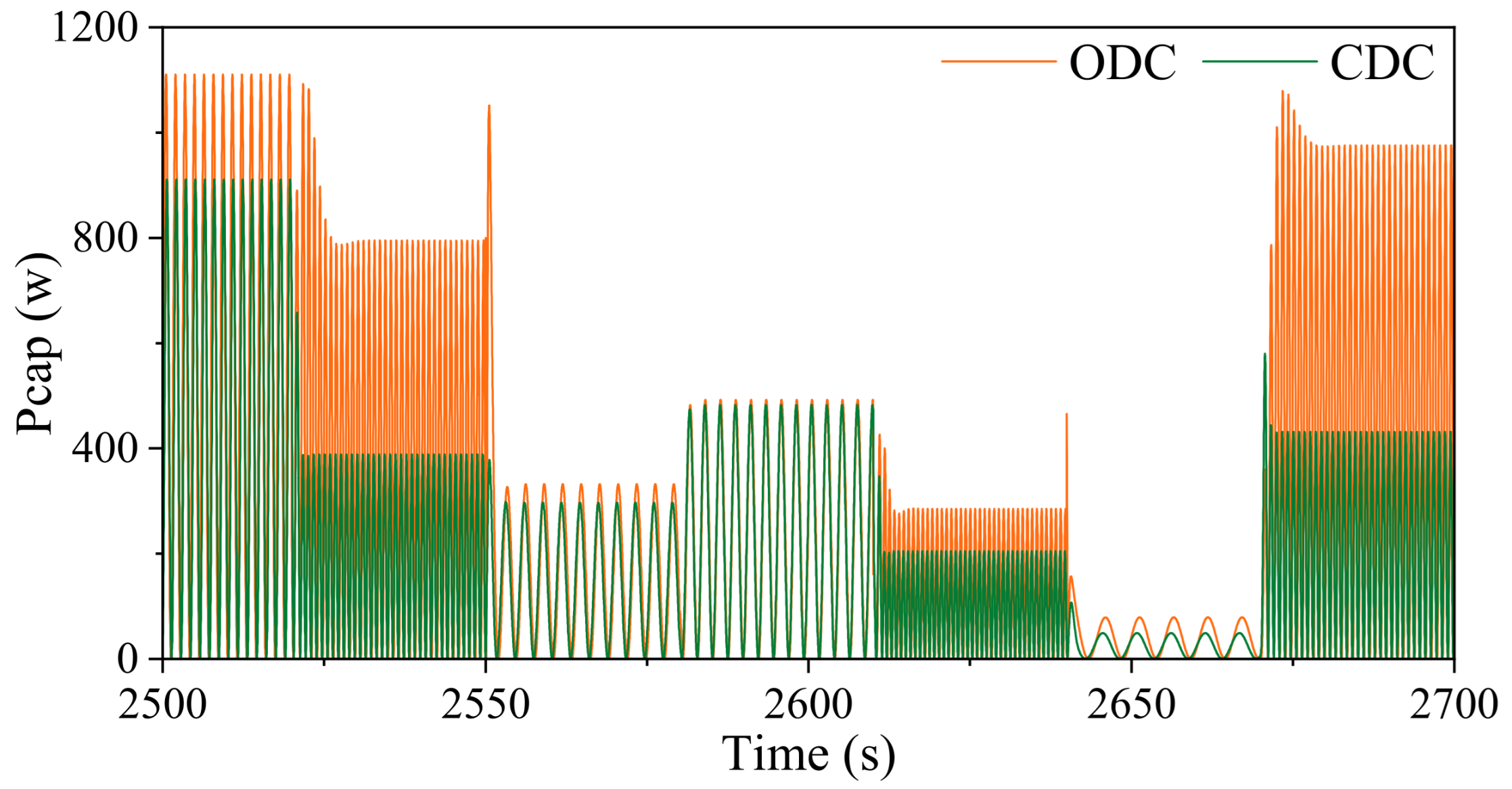




| Wave Height (m) | Frequency (rad/s) | H/L | M33 (kg) | C33 (N-s/m) | Fe (N) | Fh (N) | FPTO (N) |
|---|---|---|---|---|---|---|---|
| 0.56 | 1.5 | 0.02 | 2288.23 | 933.70 | 6487.04 | 31,541.3 | 0 |
| Mesh | Basic Size (m) | Number of Cells Per WAVELENGTH | Number of Cells for Wave Height | Total Number |
|---|---|---|---|---|
| A | 1.40 | 80 | 13 | 1,194,952 |
| B | 1.00 | 112 | 18 | 2,285,504 |
| C | 0.70 | 160 | 26 | 4,677,420 |
| Name | Lowest Value (rad/s) | Highest Value (rad/s) | Interval Time (s) | Total Duration (s) |
|---|---|---|---|---|
| Frequency | 0.1 | 5 | 60 | 1800 |
| Height | 0.05 | 1.0 | 60 | 1800 |
| Name | Peak Period (s) | Significant Height (m) | Frequency Range (rad/s) | Constant Damping (Nm-s) | Simulation Time (s) |
|---|---|---|---|---|---|
| Case 1 | 7.53 | 0.896 | 0.5–1.5 | 30,000 | 1800 |
| Case 2 | 5.64 | 0.896 | 0.75–2.0 | 26,500 | 1800 |
| Case 3 | 3.76 | 0.896 | 1.0–3.0 | 14,000 | 1800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; He, G.; Jing, P.; Luan, Z.; Liu, C. Adaptive Damping PTO Control of Wave Energy Converter for Irregular Waves Supported by Wavelet Transformation. Energies 2025, 18, 3328. https://doi.org/10.3390/en18133328
He R, He G, Jing P, Luan Z, Liu C. Adaptive Damping PTO Control of Wave Energy Converter for Irregular Waves Supported by Wavelet Transformation. Energies. 2025; 18(13):3328. https://doi.org/10.3390/en18133328
Chicago/Turabian StyleHe, Runhua, Guanghua He, Penglin Jing, Zhengxiao Luan, and Chaogang Liu. 2025. "Adaptive Damping PTO Control of Wave Energy Converter for Irregular Waves Supported by Wavelet Transformation" Energies 18, no. 13: 3328. https://doi.org/10.3390/en18133328
APA StyleHe, R., He, G., Jing, P., Luan, Z., & Liu, C. (2025). Adaptive Damping PTO Control of Wave Energy Converter for Irregular Waves Supported by Wavelet Transformation. Energies, 18(13), 3328. https://doi.org/10.3390/en18133328







