Abstract
Hydrogen is a potential source of imminent clean energy in the future, with its transportation playing a crucial role in allowing large-scale deployment. The challenge lies in selecting an effective, sustainable, and scalable transportation alternative. This study develops a multi-criteria decision-making (MCDM) framework based on the intuitionistic fuzzy analytic hierarchy process (IF-AHP) to evaluate land-based hydrogen transportation alternatives across Canada. The framework includes uncertainty and decision-maker hesitation through the application of triangular intuitionistic fuzzy numbers (TIFNs). Seven factors, their subsequent thirty-three subfactors, and three alternatives to hydrogen transportation were identified through a literature review. Pairwise comparison was aggregated among factors, subfactors, and alternatives from three decision makers using an intuitionistic fuzzy weighted average, and priority weights were computed using entropy-based weight. The results show that safety and economic efficiency emerged as the most influential factors in the evaluation of hydrogen transportation alternatives, followed by environmental impact, security, and social impact and public health in ascending order. Among the alternatives, tube truck transport obtained the highest overall weight (0.3551), followed by pipelines (0.3272) and rail lines (0.3251). The findings suggest that the tube ruck is currently the most feasible transport option for land-based hydrogen distribution that aims to provide a transition of Canada’s energy mix.
1. Introduction
1.1. Hydrogen Energy Transportation
The global transition to a hydrogen economy is underpinned by its potential to serve as a clean energy carrier, significantly reducing greenhouse gas emissions (GHGs) while addressing energy sustainability challenges [1,2]. The evolution of the hydrogen economy is pivotal in addressing climate change, with green hydrogen production and transportation identified as critical elements for achieving carbon neutrality by 2050 [3]. Recent studies emphasize the environmental and economic benefits of transitioning to hydrogen-based energy systems, showcasing their potential to drastically reduce greenhouse gas emissions while ensuring energy security [4]. Hydrogen is recognized as a clean energy carrier, and it is pivotal in reducing greenhouse gas emissions and decarbonizing heavy transport and industrial sectors [5]. However, the safety concerns associated with hydrogen’s flammability and leakage require robust regulatory frameworks and advanced detection technologies [6]. Hydrogen pipelines, a cornerstone of transportation infrastructure, face engineering challenges, such as material embrittlement and safety risks. Addressing these requires innovative solutions in pipeline coatings, maintenance technologies, and sensor integration [7]. Moreover, the deployment of hydrogen storage facilities, leveraging geological formations, like salt caverns, offers a cost-effective method for bridging the gap between variable renewable energy production and demand fluctuations, enhancing energy reliability [8].
Hydrogen transportation systems, including pipelines, rail, and trucks, are vital for linking production hubs to industrial sites and fueling stations, ensuring a seamless supply chain for end-users [9]. However, these systems face unique technical, regulatory, and logistical challenges, such as hydrogen embrittlement in pipelines and the need for optimized infrastructure to handle its low volumetric energy density [2]. The role of artificial intelligence in monitoring hydrogen transport systems has also emerged as a game changer. AI-driven systems enhance the predictive maintenance of hydrogen pipelines and vehicles, enabling real-time responses to potential failures and reducing risks [6]. Additionally, emergency response training tailored to hydrogen incidents has become a critical component in ensuring public safety and operational resilience in hydrogen transport systems [8]. These advancements underscore the need for comprehensive frameworks that integrate safety, efficiency, and resilience into hydrogen transportation systems. Such efforts are crucial not only for achieving net-zero emissions but also for fostering public confidence in hydrogen as a sustainable energy solution [5,7,10].
Hydrogen, hailed as the energy carrier of the future, offers a pivotal route for decarbonization across multiple sectors, but its transportation infrastructure, whether via pipelines or tube trailers, requires significant advancements to meet future energy demands [11]. The development of robust hydrogen storage and transportation systems is essential to transition toward a hydrogen-based economy, as they play a critical role in maintaining energy reliability while minimizing environmental impacts [12]. Recent studies emphasize that hydrogen transportation through liquid hydrogen and compressed gaseous methods offers distinct advantages in efficiency and scalability, despite the challenges associated with storage density and energy requirements for liquefaction [12]. Hydrogen logistics systems are expected to balance operational efficiency and environmental impact, as there are unintended consequences of logistics operations, such as pollutant emissions and noise. This transportation is a critical consideration for sustainable energy transition strategies [13]. Public acceptance and trust in hydrogen transportation systems play a pivotal role in their successful implementation [14]. Hazard evaluation in hydrogen storage and distribution systems, such as potential accidents from liquefied hydrogen spills, emphasizes the need for robust safety protocols and advanced dispersion models to prevent catastrophic incidents [15].
The integration of IoT and edge computing technologies in the hydrogen value chain can significantly enhance data collection and processing efficiency, ensuring real-time monitoring and improving operational security during transportation and storage phases [16]. Cybersecurity has become a critical element in the hydrogen economy, with advanced frameworks, like IoT-based systems, addressing vulnerabilities in hydrogen infrastructure to safeguard against potential threats [17]. One significant challenge in hydrogen transportation is its low energy density, which necessitates specialized containment and efficient logistics systems, particularly for long-distance and high-volume transport [4].
Research highlights the need for robust policies and collaborative frameworks to support the deployment of hydrogen transportation systems, ensuring alignment with global sustainability goals [4]. Pipeline transportation is particularly suitable for long-distance and high-volume transport, leveraging existing natural gas infrastructure to reduce costs and support the transition to a hydrogen economy [12]. Hydrogen transportation involves three primary methods, pipeline, road, and seaborne transport, with each offering unique advantages depending on the distance and volume of hydrogen transported [18]. Seaborne hydrogen transportation emerges as a cost-effective solution for large-scale, transoceanic deliveries, with cryogenic technologies minimizing boil-off losses during shipping [18].
1.2. Hydrogen Energy Landscape in Canada
Recent advancements in hydrogen transportation in Canada include Walmart Canada’s integration of hydrogen fuel cell-powered electric semi-trucks, marking a significant step towards achieving zero emissions in the retail supply chain. The development of hydrogen refueling stations by Air Products along Alberta’s Queen Elizabeth II Highway represents a pivotal initiative to support heavy-duty and light-duty hydrogen fuel cell vehicles, enhancing infrastructure readiness [19]. Moreover, Canada’s geological assets and renewable energy potential provide a robust foundation for scaling hydrogen storage and transportation, addressing both supply chain resilience and environmental objectives [1]. Advancements in transportation technology, such as salt cavern storage and dedicated pipelines, are crucial for hydrogen’s role as a sustainable energy carrier. Policy frameworks and financial incentives, including investment tax credits for hydrogen projects, further bolster the economic feasibility of these initiatives [20]. By addressing these challenges through comprehensive research and strategic infrastructure development, regions like Saskatchewan, Alberta, and British Columbia can position themselves as leaders in the global hydrogen economy [2]. These provinces, with their extensive renewable energy potential, are strategically positioned to lead in hydrogen infrastructure development, integrating hydrogen with their existing energy systems for a sustainable future [5]. Recent advances in hydrogen hub design, incorporating risk mitigation strategies and demand uncertainty modeling, are transforming the supply chain landscape, offering new possibilities for sustainable energy systems [21]. Metaheuristic optimization techniques have shown significant promise in overcoming the challenges of hydrogen storage and transportation, enabling efficient integration with renewable energy systems [21].
1.3. Transportation Pathways
The integration of liquid hydrogen and ammonia as alternative energy carriers is gaining attraction, driven by their ability to complement the existing energy infrastructure while addressing global supply chain limitations [4]. Hydrogen transportation systems are an important consideration for the transition from a conventional energy economy to an alternative sustainable energy economy in the recent advancement of hydrogen logistics for mitigating energy demand [4]. To optimize the logistical framework, the adoption of hydrogen as clean energy includes advanced infrastructure solutions, particularly for its special characteristics, like land transportation via trucks, railways, and pipelines [4]. Hydrogen production and handling are crucial for enhancing the efficiency and sustainability of hydrogen transport systems, paving the way for common acceptance in energy networks [4]. Blending hydrogen with natural gas in pipelines is an emerging strategy, though challenges such as material embrittlement and pressure management require technological solutions [18]. As hydrogen transportation technologies evolve, integrating advanced storage methods, like metal–organic frameworks and renewable energy-driven processes, will be key to achieving cost-efficient and sustainable solutions [18].
1.4. Objective of This Study
Hydrogen transportation includes three main methods, tube truck, railway, and pipeline transport, each presenting distinct benefits based on the distance and volume of hydrogen carried [18]. Hydrogen transportation networks are essential for facilitating the transition to a sustainable energy economy, with continuous improvements in hydrogen logistics providing walkable solutions to address global energy requirements [4]. The objectives of this study are as follows:
- To identify and categorize key factors and subfactors affecting the adoption of hydrogen-based land transportation in Canada.
- To establish a hierarchical structure among the identified factors, subfactors, and transportation alternatives.
- To apply the intuitionistic fuzzy analytic hierarchy process (IF-AHP) for prioritizing and evaluating hydrogen transportation alternatives under uncertainty.
1.5. Organization of This Study
In Section 2, a literature study of hydrogen land-based transportation systems is presented, specifically focusing on the identification of factors, subfactors, and alternatives. In Section 3, the intuitionistic fuzzy analytic hierarchy process (IF-AHP) utilized for factor prioritization is described, which provides an overview of the research methodology. In Section 4, the implementation of the IF-AHP framework is discussed. This includes the selection of decision makers, the factors, subfactors, alternatives, and the construction of the IF-AHP framework. The findings of the study are discussed in Section 5, which also includes an evaluation of alternative hydrogen transportation systems and a ranking of the most important alternatives under consideration. The conclusions of the study are summarized in Section 6, which includes recommendations for further research to improve hydrogen transportation networks, as well as critical insights and policy implications about the topic.
2. Literature Review
2.1. Hydrogen Transport Factors
A literature review has been performed to find the factors and subfactors involved in hydrogen land-based transportation. They are listed below to show the factors and subfactors in Table 1.

Table 1.
Factors and subfactors involved in hydrogen land-based transportation.
2.2. Hydrogen Transport Alternatives
2.2.1. Hydrogen Tube Truck
When hydrogen is transported in its gaseous state via trucks, it must first be compressed and stored in cylindrical containers at approximately 200 bar pressure [52]. Typically, these transport trucks are equipped with 12 to 20 cylinders, each ranging from 6 to 12 m in length. The transportation process is governed by federal regulations concerning vehicle weight limits and road safety [53]. In the United States, the standard pressure for hydrogen in each cylinder is around 165 bar, which directly impacts the quantity of hydrogen that can be transported. At this pressure, a truck can carry roughly 300 kg of gaseous hydrogen. Therefore, truck-based delivery of gaseous hydrogen is generally considered cost effective only for short-distance transportation and when the volume demand is relatively low. The estimated cost for a truck capable of carrying 300 kg of hydrogen is about USD 300,000 [54].
Although compressing hydrogen from 21 to 69 bar consumes approximately 0.66 kWh per kilogram, the bulk of energy consumption occurs during the transportation stage. Additionally, delivery costs are highly sensitive to distance, with gaseous hydrogen transport being more affected than its liquid counterpart [55]. Transporting hydrogen in its liquid form is generally considered low risk. Liquefaction significantly increases hydrogen’s volumetric density, enabling trucks to carry up to ten times more liquid hydrogen than their gaseous counterparts. A heavy-duty truck can transport approximately 4000 kg of liquid hydrogen [55]. This enhanced capacity reduces the number of delivery trips required to meet the needs of hydrogen refueling stations or facilities with high demand. However, the energy and capital expenditures for liquefaction and transport are considerably higher than those for gas compression—estimated at around USD 800,000, with liquefaction and onboard storage alone accounting for roughly USD 650,000 [55]. Liquid hydrogen must be transported at extremely low temperatures, specifically −252.8 °C. Investing in large-scale liquefiers can lower the per-unit cost of hydrogen. Over long distances, liquid hydrogen transport becomes more economically favorable. A study by [56] demonstrated that delivering liquefied hydrogen to 270 refueling stations across 2500 km was more cost effective than transporting gaseous hydrogen or using pipelines. Regulatory frameworks govern the weight and capacity limits of liquid hydrogen trucks to ensure public safety [52]. Additionally, the liquefaction process consumes a large amount of electricity—about 15 to 17.5 kWh/kg—which can lead to CO2 emissions, depending on the energy source used [53].
2.2.2. Distribution Through Canadian Rail
Hydrogen distribution by rail is emerging as a viable method for transporting compressed or liquefied hydrogen across Canada’s vast geography [57]. Custom-built or retrofitted railcars can carry high-pressure tanks or cryogenic vessels, allowing for efficient bulk transport. This mode complements trucks and pipelines, especially in remote or underserved regions [58]. Canada’s well-established freight rail network makes it an ideal candidate for hydrogen logistics expansion [59]. Industry experts and national agencies have explored rail as part of a broader hydrogen deployment strategy [60]. Pilot projects and risk assessments for hydrogen rail integration are already underway, including safety modeling and hydrail technology development [61]. Events such as the Smart Rail Innovation Conference emphasize rail’s role in decarbonizing hydrogen supply chains in Canada [62].
2.2.3. Hydrogen Pipeline Distribution
The primary capital expenditures for delivering hydrogen via pipelines include upfront construction costs, infrastructure investments, and ongoing expenses such as compression systems, storage, and pipeline maintenance [56]. Maintenance costs for hydrogen pipelines are generally comparable to those of natural gas pipelines [53]. Utilizing existing natural gas pipelines for transporting hydrogen either in pure form or mixed with natural gas can eliminate the need for new infrastructure, making it a cost-effective strategy. In 2020, the U.S. Department of Energy proposed repurposing the current natural gas network into a hydrogen-compatible system [2]. Existing compressors for natural gas can be reused for hydrogen transport without significant modifications [52]. Moreover, installing additional compressor stations can boost pipeline capacity, and the associated investment can be justified by the resulting efficiency gains.
Blending hydrogen at concentrations of up to 20% by volume with natural gas may allow for the continued use of current, nonmodified pipelines [63]. However, the integrity of pipeline materials under high-pressure hydrogen conditions must be assessed, particularly regarding their vulnerability to hydrogen embrittlement (HE), a phenomenon where hydrogen degrades steel, leading to cracking, blistering, or reduced fracture toughness [64,65]. Additionally, aged pipelines often have imperfections, such as corrosion, dents, or scratches, which can trap hydrogen atoms and trigger localized embrittlement and crack formation [66]. Constructing new, large-scale pipelines solely for hydrogen can cost approximately 1.5 to 1.8 times more than natural gas pipelines, depending on pipeline size and length [53]. For instance, a 12-inch hydrogen pipeline may cost around USD 500,000 per mile in rural Texas and up to USD 2 million per mile in urban areas, like California [53]. On average, new pipeline construction is estimated at USD 300,000/km in rural zones and USD 600,000/km in urban areas [54]. Pipelines are often more economical and efficient for transporting large volumes of hydrogen over long distances [2]. In Germany, converting existing gas pipelines for hydrogen use could reduce costs by 20 to 60% compared to new construction. A 10- or 12-inch pipeline operating at 41.38 bar can transport approximately 100,000 kg of hydrogen per hour [67]. However, hydrogen compressor costs must also be considered, as these units need to be installed at intervals to maintain pipeline pressure. Compared to the truck-based delivery of gaseous or liquid hydrogen, pipelines offer the lowest greenhouse gas emissions ranging from 0.7 to 1.0 kWh/kg [53].
3. Methodology
3.1. Intuitionistic Fuzzy Sets
This section outlines the fundamental concepts of fuzzy sets, intuitionistic fuzzy sets (IFSs), triangular fuzzy numbers (TFNs), and triangular intuitionistic fuzzy numbers (TIFNs). To address the imprecision and vagueness inherent in human reasoning, fuzzy set theory and fuzzy logic were introduced as powerful mathematical tools for modeling uncertainty within systems [68]. A fuzzy set A in a universe of discourse . For every element x in the set X, the fuzzy set A includes a pair the element x and its corresponding membership value . It assigns each element X a value between 0 and 1, which indicates how strongly that element belongs to the fuzzy set A.
The concept of intuitionistic fuzzy sets (IFSs) was introduced by [69] as an extension of traditional fuzzy sets. Let be a standard finite and nonempty set. An intuitionistic fuzzy set on can be represented as follows:
Here, the membership function and the non-membership function are subject to the constraint for every element . The values and , respectively, indicate the degree to which belongs or does not belong to the set . Additionally, the hesitation degree (also called the intuitionistic index or indeterminacy) for each element , denoted , is defined as follows:
This expression quantifies the hesitation level, also known as the intuitionistic index or degree of indeterminacy, associated with an element in the set . In the case of a traditional fuzzy set, this hesitation degree is zero, i.e., .
3.2. Triangular Fuzzy Numbers (TFNs) and Triangular Intuitionistic Fuzzy Numbers (TIFNs)
The fuzzy set theory was developed to extract the most plausible outcome from a range of imprecise and uncertain information. It interprets vague data as possibility distributions, using the concept of set membership to represent degrees of truth. Among various types of fuzzy numbers, the triangular fuzzy number (TFN) is widely used due to its simplicity and effective representation through membership functions.
According to [70], the TFN is defined as a fuzzy number on the real number line. is considered a TFN if its membership function is defined as follows:
3.3. Preference Scale of IF-AHP
When the values are expressed in natural language, it is known as a linguistic variable. This is useful for particularly intricate or unclear situations where traditional numerical approaches may be inadequate [71]. In this situation, all factors, subfactors, and alternatives have been evaluated using the AHP scale, which is subsequently translated into triangular intuitionistic fuzzy numbers (TIFNs) [72]. This conversion is stranded in the hesitation degree inherent to TIFNs. The conversion from AHP numeric values to TIFNs is accomplished by averaging each AHP rating in relation to the full scale. The process involves calculating the three TIFN component memberships (μx), non-memberships (νx), and hesitations (πx) through normalized averaging based on these expressions. The conversion reference used for this approach is adapted from and is summarized in Table 2 [73].

Table 2.
Conversion of consistency ratings into fuzzy membership scores [74].
The TIFN is calculated using Equation (7). The following example is given to understand the conversion:
where represents the AHP crisp value assigned and m denotes the total value of all preference scale measurements. The membership degree, non-membership degree, and hesitation degree are determined using Equations (8)–(10) as follows:
In this study, a revised approach within the IF-AHP framework was developed by introducing a new equation for calculating the consistency ratio (CR) of each pairwise comparison matrix. This formulation incorporates the hesitation degree embedded in the triangular intuitionistic fuzzy numbers (TIFNs), enhancing the representational power of the intuitionistic fuzzy matrix. Additionally, the standard intuitionistic fuzzy entropy method was modified by eliminating the summation component, enabling entropy calculation for each aggregated row individually rather than over the entire matrix. This adjustment aligns with the row-based structure of the aggregated intuitionistic fuzzy matrix and improves computational efficiency [72].
The intuitionistic fuzzy set (IFS) framework enhances Saaty’s traditional analytic hierarchy process (AHP) by integrating IFS theory. Like the fuzzy AHP, the proposed IF-AHP approach addresses the relative significance of factors and alternatives in multi-criteria decision-making (MCDM) scenarios. In this method, AHP crisp data are transformed into triangular intuitionistic fuzzy numbers (TIFNs) to form a judgment matrix for pairwise comparisons. The IF-AHP process can be outlined as follows.
Step 1: Develop the Hierarchical Structure of the MCDM Problem. Begin by identifying the factors and alternatives relevant to the decision-making context. These elements form the basis of the MCDM hierarchy. The IF-AHP scale was applied using the TIFN-based preference system. Decision makers (DMs) assessed the importance of factors through pairwise comparisons using a nine-point AHP linguistic scale, ranging from “equal importance” to “absolute importance.” These linguistic judgments were converted into TIFNs based on the revised preference scale shown in Table 3. This conversion enables a more nuanced representation of DM perceptions using degrees of membership, non-membership, and hesitation.

Table 3.
Mapping AHP preference numbers to triangular intuitionistic fuzzy numbers [73].
Step 2. The influence or importance of each DM was given the linguistic variables, which were then mapped to corresponding TIFNs, as outlined in Table 4.

Table 4.
Linguistic terms representing decision maker importance [74].
Let represent the intuitionistic fuzzy number assigned to the rating provided by the decision maker. In our study, we used Equation (11) to determine the importance of the decision makers [74].
Step 3. An aggregated intuitionistic fuzzy judgment matrix was developed. Let denote the intuitionistic fuzzy decision matrix provided by the decision maker. Let represent the set of weights assigned to each decision maker, such that , where each weight is . In group decision making, it is essential to consolidate the individual judgments of all decision makers into a single, unified assessment. This is achieved by constructing an aggregated intuitionistic fuzzy decision matrix using the intuitionistic fuzzy weighted averaging (IFWA) operator [75].
Here
Step 4: The consistency ratio (CR) for the aggregated intuitionistic fuzzy judgment matrix is calculated using the aggregated intuitionistic fuzzy (IF) matrix using the hesitation degree to evaluate the overall consistency using the consistency grading framework of TIFNs [72]. This method allows for a more comprehensive assessment of consistency within the IF context. The values of the Random Index (RI), originally established by Saaty (1980) [69], are referenced and presented in Table 5. The revised formula for calculating the consistency ratio (CR) is outlined in Equation (13).

Table 5.
Randomly generated consistency index (RI).
Step 5. The intuitionistic fuzzy weights of the aggregated judgment matrix were calculated. The factor weights are determined based on the highest preference indices assigned by the decision makers. For alternatives, the intuitionistic fuzzy (IF) matrix is evaluated in accordance with the sequence of weights attributed to each decision maker’s judgment. To derive the final weights, the intuitionistic fuzzy entropy method proposed by [76] is adapted. Specifically, the summation component in their original formulation is omitted to enable the calculation of entropy values for each individual row in the aggregated IF matrix. The revised intuitionistic fuzzy entropy for each aggregated row is defined in Equation (14).
Here, if , , and , then , , and , and if , , and , then , , and .
The ultimate entropy weights corresponding to each intuitionistic fuzzy (IF) matrix are recalculated as shown in Equation (15) below.
where .
Step 6. The final ranking of all alternatives was determined by calculating their relative weights using Equation (16).
4. Application of Framework
In this study, we engaged three subject-matter experts with professional experience in energy transportation systems, policy, and infrastructure development. Each expert possesses more than 10 years of domain-specific expertise.
Decision maker 1 is a senior systems engineer with more than 10 years of industry experience in energy pilot projects.
Decision maker 2 is a policy analyst at a provincial energy department with knowledge of energy infrastructure regulation and strategic planning.
Decision maker 3 is an academic researcher in sustainable transportation and clean energy transitions with over a decade of published research in system dynamic modeling.
The decision makers judged the relative comparison between the factors, subfactors, and alternatives using a pairwise comparison matrix. The relative preferences, abbreviations, and scale are mentioned in Table 3. The response “Equally Important” divides the IF-AHP preference and IF-AHP reciprocal responses in the table.
Step 1. The hierarchy structure of hydrogen transportation factors, subfactors, and alternatives is shown in Figure 1. The linguistic responses of the three decision makers are compiled in Table 6. For example, decision maker 1 had a preference for the F2 factor over F1 as VSMP (very strong more important) by 0.62, 0.18, and 0.20, and the reciprocal was VSLP (very strongly less important), with values of 0.20, 0.18, and 0.62.
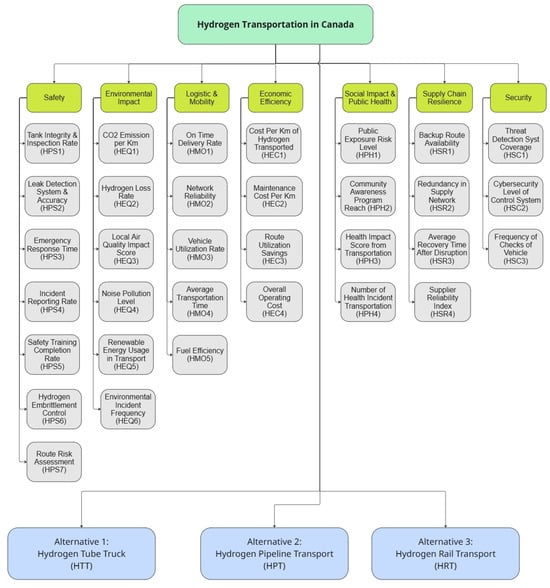
Figure 1.
Hierarchical diagram of factors and alternatives for hydrogen transportation in Canada.

Table 6.
Pairwise comparison factors.
Step 2: Determine the Weights of DM Calculations. The decision maker weight is evaluated using Equation (11). The levels of importance for the three decision makers are very important , important and medium .
Similarly, the importance of the other two was determined as and .
Step 3. An aggregated intuitionistic fuzzy judgment matrix has been developed using the input from decision makers using Equation (12) to combine all the converted intuitionistic fuzzy decision matrices for both factors, subfactors, and alternatives against each subfactor. Sample calculations for Factor 1 and Factor 2 for decision maker 1 have been shown here. Table 7 presents the values of the aggregated matrix, entropy weight, and final entropy weight of factors generated for decision maker 1.

Table 7.
Aggregated matrix and entropy weights of factors (decision maker 1).
Here, for , , , and , and then , , and . So, = (1, 0, 0). For a better understanding, the sample calculation for is shown below as follows:
Step 4: Consistency Ratio Calculation. The consistency ratio of the aggregated IF matrix has been calculated for all the factors, subfactors, and alternatives using Equation (13). A sample calculation for a consistency check of decision maker 1 has been shown among the factors below using Table 7. The ratio is 0.0489, which is less than 0.10, so the aggregated intuitionistic fuzzy judgment for the factors is consistent.
Step 5. In the next step, the intuitionistic fuzzy weights are calculated for aggregated intuitionistic fuzzy judgments. The entropy weights and final entropy weights have been calculated using Equations (14) and (15) simultaneously. In our case study, calculations for Factor 2 are shown below as an example as follows:
Similarly, intuitionistic fuzzy weights are calculated for aggregated intuitionistic fuzzy judgments. The values of the aggregated matrix, entropy weight, and final entropy weight for the subfactors of environmental impact, logistics and mobility, economic efficiency, social impact and public health, supply chain resilience, and security are shown in Table 8, Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14 simultaneously.

Table 8.
Safety subfactor entropy weights (decision maker 1).

Table 9.
Environmental impact subfactor entropy weights (decision maker 1).

Table 10.
Logistics and mobility subfactor entropy weights (decision maker 1).

Table 11.
Economic efficiency subfactor entropy weights (decision maker 1).

Table 12.
Social impact and public health subfactor entropy weights (decision maker 1).

Table 13.
Supply chain resilience subfactor entropy weights (decision maker 1).

Table 14.
Security subfactor entropy weights (decision maker 1).
Step 6. In the next step, the final entropy weight is multiplied by the respective factor weight to obtain the revised weight, which is shown in Appendix A Table A1.
The intuitionistic fuzzy weight of the aggregated intuitionistic fuzzy judgment matrix and its related entropy weights are calculated similarly for all three alternatives, HTT, HR, and HP, under their respective factors of safety (F1), environmental impact (F2), logistics and mobility (F3), economic efficiency (F4), social impact and public health (F5), supply chain resilience (F6), and security (F7). The values of entropy weights for alternatives for each subfactor are shown in Appendix A Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 simultaneously.
The final priority weights are calculated by multiplying each subfactor’s revised weight with the respective final entropy weight of each alternative using Equation (16). A sample calculation is shown below for the Hydrogen Tube Truck alternative. The priority weights are shown in Table 15 for DM1.

Table 15.
Final priority weight for alternatives (decision maker 1).
Finally, the priority weights of all decision makers are combined by taking the arithmetic mean of the weights of all three alternatives with respect to each subfactor. The final weights and rankings of the alternatives for hydrogen transportation in Canada are summarized in Table 16.

Table 16.
Weight of hydrogen energy transportation decision alternatives.
According to the IF-AHP framework, the Hydrogen Tube Truck is the best alternative solution, followed by hydrogen pipeline transportation and rail line transportation. Although Table 16 shows a relatively small numerical difference between the composite weights of the Hydrogen Tube Truck, pipeline, and rail alternatives, this slight variation can translate into noticeable differences in total transportation costs when scaled to industrial hydrogen supply levels. For example, even a little difference in preference weight may result in a significant annual cost difference, especially when transporting large volumes over long distances. Therefore, small rank differences should be carefully considered in policy and investment planning. The consistency ratio (CR) was computed for the pairwise comparison matrices, and the hesitation degree was incorporated using the triangular intuitionistic fuzzy numbers (TIFNs), which collectively improve the reliability of the ranking. The numerical differences appear modest, and the order of preference among the three transport modes is meaningful for decision making.
5. Findings and Discussion
In this study, the intuitionistic fuzzy analytical hierarchy process was applied for the evaluation and prioritization of the three land-based hydrogen transportation alternatives in Canada, which are tube trucks, pipelines, and rail lines. The factors that influence choosing these alternatives are safety, environmental impact, logistics and mobility, economic efficiency, social impact and public health, supply chain resilience, and security. There are also thirty-three subfactors under respective factors. Pairwise comparison was also performed among factors, subfactors, and alternatives. In the final aggregation results, the HTT (Hydrogen Tube Truck Transport) emerged as the ideal alternative, followed by pipeline transport and rail transport.
The consistency was checked for validation of the responses given by decision makers. For instance, all three decision makers consistently ranked the Hydrogen Tube Truck the highest, despite slight variations in their weighting contributions. On the other hand, safety, economic efficiency, and environmental impact were the most critical factors influencing hydrogen transportation, emphasizing the multidimensional nature of infrastructure ranking. The findings recommended that tube truck transport offers a satisfactory combination of flexibility, cost effectiveness, and manageable safety risks, making it a feasible near-term hydrogen delivery solution for the Canadian transport framework. Pipeline transport, while displaying durable performance on environmental and long-term scalability grounds, may face challenges related to infrastructure investment and regulatory endorsement. Some of the previous studies align with the study findings, where truck transport of hydrogen is preferable for relatively short distances and flexible supply locations or schedules [38,43,54]. Trucking provides decentralized refueling stations, cost effectiveness, and ease of deployment without large upfront investments, like pipelines and railways. The safety of regular commuters on the road, road congestion, and the long distance per unit transport cost are considerable limitations of truck-based transportation.
Rail transport, though moderately competitive in performance, ranks third due to concerns related to logistics intricacy and safety exposures in densely populated areas. This study shows that incorporating the IF-AHP into sustainable decision making improves the granularity of valuations by considering doubt and decision maker hesitation, which are particularly valuable when dealing with developing technologies like hydrogen energy systems.
6. Conclusions
The primary objective of this study was to apply an intuitionistic fuzzy analytic hierarchy process (IF-AHP) framework with a newly defined preference scale to support sustainable hydrogen transportation planning in Canada. Given the complex nature of hydrogen infrastructure, which demands consideration of both quantitative indicators and qualitative judgments, this enhanced the IF-AHP approach and incorporated a three-dimensional representation (membership, non-membership, and hesitation) of decision-maker uncertainty through triangular intuitionistic fuzzy numbers (TIFNs).
In the consistency calculation, the hesitation degree of the decision makers was taken into consideration to improve the robustness of pairwise comparison. The modified entropy method also enhanced the granularity and interpretability of decision-maker aggregation. The Hydrogen Tube Truck emerged as the preferred method with the highest composite weight, and it currently offers the best balance across safety, environmental impact, logistics, economic feasibility, and system resilience factors, followed by the hydrogen pipeline (HP) and hydrogen rail (HR).
While the proposed methodology demonstrated the integration of IF-AHP and sustainable transport planning, further research is needed to enhance its generalizability. Future investigations may explore validation through sensitivity analysis, cross-sector expert comparison, and integration with life cycle impact assessment (LCA) to capture environmental tradeoffs with greater accuracy. Additionally, expanding the framework to incorporate dynamic transportation demands or infrastructure evolution scenarios could increase the practical relevance of long-term hydrogen policy decisions in Canada.
The generalizability of the result of the study may be affected by a small number of decision makers. However, the decision makers were carefully selected based on their subject-specific expertise, practical experience, and policy and system modeling. Larger panels of decision makers will be considered in future studies for further validation and incorporation of the widespread expertise of panel members.
Author Contributions
Conceptualization, M.R. and G.K.; methodology, M.R. and G.K.; software, M.R.; validation, M.R. and G.K.; formal analysis, M.R.; investigation, M.R.; resources, G.K.; data curation, M.R.; writing—original draft preparation, M.R.; writing—review and editing, G.K.; visualization, M.R. and G.K.; supervision, G.K.; project administration, G.K.; funding acquisition, G.K. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge financial support through the Natural Sciences and Engineering Research Council of Canada Discovery Grant Program (RGPIN-2019–04704).
Data Availability Statement
Data will be made available upon request.
Acknowledgments
The authors acknowledge financial support through the Faculty of Graduate Studies and Research funding, University of Regina.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytic Hierarchy Process |
| IF | Intuitionistic Fuzzy |
| HTT | Hydrogen Tube Truck |
| HR | Hydrogen Railway |
| HP | Hydrogen Pipeline |
| ALP | Absolutely Less Important |
| IVALP | Intermediate Value Less Important |
| VSLP | Very Strong Less Important |
| IVVSLP | Intermediate Value Very Strong Less Important |
| SLI | Strongly Less Important |
| IVSLI | Intermediate Value Strongly Less Important |
| WLI | Weakly Less Important |
| IVWLI | Intermediate Value Weakly Less Important |
| E | Equally Important |
| IVWMI | Intermediate Value Weakly More Important |
| WMI | Weakly More Important |
| IVSMI | Intermediate value Strongly More Important |
| SMI | Strongly More Important |
| IVVSMI | Intermediate Value Very Strong More Important |
| VSMI | Very Strong More Important |
| IVAMI | Intermediate Value Absolutely More Important |
| AMI | Absolutely More Important |
| MCDM | Multi-Criteria Decision Making |
| TIFN | Triangular Intuitionistic Fuzzy Number |
Appendix A

Table A1.
Factor and subfactor e weights for decision maker 1).
Table A1.
Factor and subfactor e weights for decision maker 1).
| Factor Weight | Subfactors | Subfactor Weight | Revised Weight | |
|---|---|---|---|---|
| F1 | 0.1563 | HPS1 | 0.1521 | 0.0238 |
| HPS2 | 0.1451 | 0.0227 | ||
| HPS3 | 0.1419 | 0.0222 | ||
| HPS4 | 0.1408 | 0.0220 | ||
| HPS5 | 0.1400 | 0.0219 | ||
| HPS6 | 0.1407 | 0.0220 | ||
| HPS7 | 0.1395 | 0.0218 | ||
| F2 | 0.1524 | HEQ1 | 0.1729 | 0.0264 |
| HEQ2 | 0.1699 | 0.0259 | ||
| HEQ3 | 0.1655 | 0.0252 | ||
| HEQ4 | 0.1609 | 0.0245 | ||
| HEQ5 | 0.1602 | 0.0244 | ||
| HEQ6 | 0.1705 | 0.0260 | ||
| F3 | 0.1399 | HMO1 | 0.2073 | 0.0290 |
| HMO2 | 0.1974 | 0.0276 | ||
| HMO3 | 0.1997 | 0.0279 | ||
| HMO4 | 0.1994 | 0.0279 | ||
| HMO5 | 0.1962 | 0.0275 | ||
| F4 | 0.1406 | HEC1 | 0.2720 | 0.0382 |
| HEC2 | 0.2327 | 0.0327 | ||
| HEC3 | 0.2354 | 0.0331 | ||
| HEC4 | 0.2598 | 0.0365 | ||
| F5 | 0.1341 | HPH1 | 0.2719 | 0.0365 |
| HPH2 | 0.2307 | 0.0309 | ||
| HPH3 | 0.2376 | 0.0319 | ||
| HPH4 | 0.2598 | 0.0348 | ||
| F6 | 0.1428 | HSR1 | 0.2209 | 0.0315 |
| HSR2 | 0.2324 | 0.0332 | ||
| HSR3 | 0.2734 | 0.0390 | ||
| HSR4 | 0.2734 | 0.0390 | ||
| F7 | 0.1340 | HSC1 | 0.3387 | 0.0454 |
| HSC2 | 0.3227 | 0.0432 | ||
| HSC3 | 0.3387 | 0.0454 |

Table A2.
Alternative entropy weights for subfactors under safety.
Table A2.
Alternative entropy weights for subfactors under safety.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HPS1 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.367 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.317 | |
| HP | (0.181, 0.294, 0.525) | 0.327 | 0.316 | |
| HPS2 | HTT | (0.411, 0.147, 0.442) | 0.302 | 0.334 |
| HR | (0.417, 0.152, 0.431) | 0.303 | 0.333 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.333 | |
| HPS3 | HTT | (0.44, 0.139, 0.421) | 0.294 | 0.332 |
| HR | (0.552, 0.12, 0.328) | 0.261 | 0.347 | |
| HP | (0.15, 0.326, 0.524) | 0.317 | 0.321 | |
| HPS4 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.378 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.312 | |
| HP | (0.181, 0.294, 0.525) | 0.327 | 0.311 | |
| HPS5 | HTT | (0.375, 0.139, 0.486) | 0.306 | 0.333 |
| HR | (0.295, 0.221, 0.484) | 0.331 | 0.322 | |
| HP | (0.092, 0.407, 0.501) | 0.282 | 0.345 | |
| HPS6 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.354 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.321 | |
| HP | (0.092, 0.407, 0.501) | 0.282 | 0.325 | |
| HPS7 | HTT | (0.557, 0.117, 0.326) | 0.259 | 0.352 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |

Table A3.
Alternative entropy weights for subfactors under environmental impact.
Table A3.
Alternative entropy weights for subfactors under environmental impact.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HEQ1 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HEQ2 | HTT | (0.557, 0.117, 0.326) | 0.259 | 0.352 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |
| HEQ3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.53, 0.155, 0.314) | 0.281 | 0.341 | |
| HP | (0.181, 0.294, 0.525) | 0.327 | 0.320 | |
| HEQ4 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.157, 0.331, 0.512) | 0.318 | 0.324 | |
| HEQ5 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.249, 0.207, 0.544) | 0.332 | 0.317 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |
| HEQ6 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |

Table A4.
Alternative entropy weights for subfactors under logistics and mobility.
Table A4.
Alternative entropy weights for subfactors under logistics and mobility.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HMO1 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HMO2 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.321 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |
| HMO3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |
| HMO4 | HTT | (0.569, 0.11, 0.321) | 0.251 | 0.355 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.219, 0.227, 0.554) | 0.333 | 0.316 | |
| HMO5 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.417, 0.152, 0.431) | 0.303 | 0.331 | |
| HP | (0.171, 0.24, 0.589) | 0.331 | 0.318 | |

Table A5.
Alternative entropy weights for subfactors under economic efficiency.
Table A5.
Alternative entropy weights for subfactors under economic efficiency.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HEC1 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HEC2 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.512, 0.172, 0.315) | 0.291 | 0.337 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HEC3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.268, 0.245, 0.487) | 0.333 | 0.317 | |
| HP | (0.15, 0.326, 0.524) | 0.317 | 0.324 | |
| HEC4 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.321 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |

Table A6.
Alternative entropy weights for subfactors under social impact and public health.
Table A6.
Alternative entropy weights for subfactors under social impact and public health.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HPH1 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.321 | |
| HP | (0.166, 0.284, 0.551) | 0.326 | 0.320 | |
| HPH2 | HTT | (0.659, 0.093, 0.248) | 0.218 | 0.371 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.181, 0.294, 0.525) | 0.327 | 0.320 | |
| HPH3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.366, 0.219, 0.416) | 0.324 | 0.321 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HPH4 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.166, 0.284, 0.551) | 0.326 | 0.320 | |

Table A7.
Alternative entropy weights for subfactors under supply chain resilience.
Table A7.
Alternative entropy weights for subfactors under supply chain resilience.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HSR1 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HSR2 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.15, 0.326, 0.524) | 0.317 | 0.324 | |
| HSR3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.198, 0.259, 0.544) | 0.331 | 0.317 | |
| HP | (0.196, 0.256, 0.548) | 0.331 | 0.317 | |
| HSR4 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.389, 0.197, 0.414) | 0.318 | 0.324 | |
| HP | (0.092, 0.407, 0.501) | 0.282 | 0.341 | |

Table A8.
Alternative entropy weights for subfactors under security.
Table A8.
Alternative entropy weights for subfactors under security.
| Safety | Aggregated Matrix | Entropy Weights | Final Entropy Weights | |
|---|---|---|---|---|
| HSC1 | HTT | (0.557, 0.117, 0.326) | 0.259 | 0.352 |
| HR | (0.328, 0.17, 0.502) | 0.321 | 0.322 | |
| HP | (0.092, 0.407, 0.501) | 0.282 | 0.341 | |
| HSC2 | HTT | (0.557, 0.117, 0.326) | 0.259 | 0.352 |
| HR | (0.268, 0.245, 0.487) | 0.333 | 0.317 | |
| HP | (0.125, 0.367, 0.508) | 0.303 | 0.331 | |
| HSC3 | HTT | (0.738, 0.073, 0.189) | 0.181 | 0.389 |
| HR | (0.417, 0.152, 0.431) | 0.303 | 0.331 | |
| HP | (0.092, 0.407, 0.501) | 0.282 | 0.341 | |
References
- Anthony, D.; Pattison, D.; Sulatisky, M.; Razek, N. Hydrogen Hub Potential: A Feasibility Study for the Regina-Moose Jaw Industrial Corridor. Available online: https://transitionaccelerator.ca/reports/rmjic-hydrogen-hub-potential/ (accessed on 12 March 2025).
- Parfomak, P.W. Pipeline Transportation of Hydrogen: Regulation, Research, and Policy. Available online: https://crsreports.congress.gov/product/pdf/R/R46700 (accessed on 12 March 2025).
- Asghari, M.; Afshari, H.; Jaber, M.Y.; Searcy, C. Designing a Resilient Hydrogen Hub under Disruption Risks and Non-Stationary Demand Distribution. Int. J. Prod. Res. 2023, 63, 2780–2805. [Google Scholar] [CrossRef]
- Chen, L.; Qi, Z.; Zhang, S.; Su, J.; Somorjai, G.A. Catalytic Hydrogen Production from Methane: A Review on Recent Progress and Prospect. Catalysts 2020, 10, 858. [Google Scholar] [CrossRef]
- Qanbar, M.W.; Hong, Z. A Review of Hydrogen Leak Detection Regulations and Technologies. Energies 2024, 17, 4059. [Google Scholar] [CrossRef]
- Patil, R.R.; Calay, R.K.; Mustafa, M.Y.; Thakur, S. Artificial Intelligence-Driven Innovations in Hydrogen Safety. Hydrog. 2024, 5, 312–326. [Google Scholar] [CrossRef]
- Holohan, V. PHMSA Hydrogen Pipeline Safety and Challenges. In Proceedings of the 2024 DOE HFTO Workshop, Denver, CO, USA, 17–18 January 2024. [Google Scholar]
- Elmore, M.R. Hydrogen Emergency Response Training for First Responders. 2013; pp. 43–45. Available online: https://www.hydrogen.energy.gov/pdfs/review13/scs015_elmore_2013_o.pdf (accessed on 15 March 2025).
- Marahatta, S. A Hydrogen-Driven Sustainable Technology Mapping for Future Energy Hubs. Master’s Thesis, University of South-Eastern Norway, Notodden, Norway, 2024. Available online: https://hdl.handle.net/11250/3136684 (accessed on 25 March 2025).
- Calabrese, M.; Portarapillo, M.; Di Nardo, A.; Venezia, V.; Turco, M.; Luciani, G.; Di Benedetto, A. Hydrogen Safety Challenges: A Comprehensive Review on Production, Storage, Transport, Utilization, and CFD-Based Consequence and Risk Assessment. Energies 2024, 17, 1350. [Google Scholar] [CrossRef]
- Granovskii, M.; Dincer, I.; Rosen, M.A. Life Cycle Assessment of Hydrogen Fuel Cell and Gasoline Vehicles. Int. J. Hydrogen Energy 2006, 31, 337–352. [Google Scholar] [CrossRef]
- Yang, M.; Ralf, H.; Berrettoni, S.; Sprecher, B.; Wang, B. A Review of Hydrogen Storage and Transport Technologies. Oxf. Univ. Press Behalf Natl. Inst. Clean-Low-Carbon Energy 2023, 7, 190–216. [Google Scholar] [CrossRef]
- Sathaye, N.; Harley, R.; Madanat, S. Unintended Environmental Impacts of Nighttime Freight Logistics Activities. Transp. Res. Part A Policy Pract. 2010, 44, 642–659. [Google Scholar] [CrossRef]
- Ricci, M.; Bellaby, P.; Flynn, R. What Do We Know about Public Perceptions and Acceptance of Hydrogen? A Critical Review and New Case Study Evidence. Int. J. Hydrogen Energy 2008, 33, 5868–5880. [Google Scholar] [CrossRef]
- Rigas, F.; Sklavounos, S. Evaluation of Hazards Associated with Hydrogen Storage Facilities. Int. J. Hydrogen Energy 2005, 30, 1501–1510. [Google Scholar] [CrossRef]
- Department of Energy, USA. Cyber and Physical Security Best Practices; Department of Energy, USA: Washington, DC, USA, 2015; pp. 1–18. [Google Scholar]
- Alfasfos, R.; Ullah, M.; Sillman, J.; Nardelli, P.; Soukka, R. Recommendation on Cybersecurity and Safety in the Hydrogen Economy. In Proceedings of the 2024 47th ICT and Electronics Convention, MIPRO 2024—Proceedings, Opatija, Croatia, 20–24 May 2024; pp. 1837–1842. [Google Scholar]
- Xie, Z.; Jin, Q.; Su, G.; Lu, W. A Review of Hydrogen Storage and Transportation: Progresses and Challenges. Energies 2024, 17, 4070. [Google Scholar] [CrossRef]
- Reuters Hydrogen Fuel Cell-Powered Electric Semi-Truck to Fleet. Available online: https://www.reuters.com/sustainability/walmart-canada-adds-nikolas-hydrogen-fuel-cell-powered-electric-semi-truck-fleet-2024-06-27/?utm_source=chatgpt.com (accessed on 11 March 2025).
- Petroleum Technology Research Centre (PTRC). New Program to Investigate the Role of CCS in Canadas Blue Hydrogen Economy. Available online: https://ptrc.ca/pub/Blog/release-blue-hydrogen-u-of-r.pdf (accessed on 25 March 2025).
- Gorji, S.A. Challenges and Opportunities in Green Hydrogen Supply Chain through Metaheuristic Optimization. J. Comput. Des. Eng. 2023, 10, 1143–1157. [Google Scholar] [CrossRef]
- NASA-TM-112540; Safety Standard for Hydrogen and Hydrogen Systems: Guidelines for Hydrogen System Design, Materials Selection, Operations, Storage, and Transportation. National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1997.
- Post, M.B.; Buttner, W.J.; Pearman, D.E.; Hartmann, K.; Palin, I. The NREL Sensor Laboratory: Hydrogen Leak Detection for Large Scale Deployments: Preprint. Available online: https://docs.nrel.gov/docs/fy24osti/85816.pdf (accessed on 11 March 2025).
- Elmore, M.R.; Fassbender, L.L.; Hamilton, J.J.; Weiner, S.C. Hydrogen Emergency Response Training for First Responders; U.S. Department of Energy: Arlington, TX, USA, 2013. Available online: https://www.hydrogen.energy.gov/docs/hydrogenprogramlibraries/pdfs/review12/scs015_elmore_2012_o.pdf (accessed on 1 March 2025).
- Rivkin, C.; Burgess, R.; Buttner, W. Hydrogen Technologies Safety Guide. Available online: https://www.nrel.gov/docs/fy15osti/60948.pdf (accessed on 1 March 2025).
- Li, M.; Ming, P.; Jiao, H.; Huo, R. Techno-Economic, Energy, and Environmental Impact Assessment of Hydrogen Supply Chain: A Comparative Study of Large-Scale Production and Long-Distance Transportation. J. Renew. Sustain. Energy 2024, 16, 055905. [Google Scholar] [CrossRef]
- Keshri, S.; Sudha, S.; Saxena, A.K.S. State-of-the-Art Review on Hydrogen’s Production, Storage, and Potential as a Future Transportation Fuel. Environ. Sci. Pollut. Res. 2024, 31, 13361–13400. [Google Scholar] [CrossRef]
- Pederzoli, D.W.; Carnevali, C.; Genova, R.; Mazzucchelli, M.; Del Borghi, A.; Gallo, M.; Moreschi, L. Life Cycle Assessment of Hydrogen-Powered City Buses in the High V.LO-City Project: Integrating Vehicle Operation and Refuelling Infrastructure. SN Appl. Sci. 2022, 4, 57. [Google Scholar] [CrossRef]
- Stargardt, M.; Kress, D.; Heinrichs, H.; Meyer, J. Global Shipyard Capacities Limiting the Ramp-Up of Global Hydrogen-Based Transportation. Available online: https://arxiv.org/abs/2403.09272 (accessed on 25 March 2025).
- Chapman, A.; Nguyen, D.H.; Farabi-Asl, H.; Itaoka, K.; Hirose, K.; Fujii, Y. Hydrogen Penetration and Fuel Cell Vehicle Deployment in the Carbon Constrained Future Energy System. IET Electr. Syst. Transp. 2020, 10, 409–416. [Google Scholar] [CrossRef]
- Hasturk, U.; Schrotenboer, A.H.; Ursavas, E.; Roodbergen, K.J. Stochastic Cyclic Inventory Routing with Supply Uncertainty: A Case in Green-Hydrogen Logistics. Transp. Sci. 2024, 58, 315–339. [Google Scholar] [CrossRef]
- He, G.; Mallapragada, D.S.; Bose, A.; Heuberger, C.F.; Gençer, E. Hydrogen Supply Chain Planning with Flexible Transmission and Storage Scheduling. IEEE Trans. Sustain. Energy. 2021, 12, 1730–1740. [Google Scholar] [CrossRef]
- Robles, J.O.; Azzaro-Pantel, C.; Aguilar-Lasserre, A. Optimization of a Hydrogen Supply Chain Network Design under Demand Uncertainty by Multi-Objective Genetic Algorithms. Comput. Chem. Eng 2020, 140, 106853. [Google Scholar] [CrossRef]
- Riera, J.A.; Lima, R.M.; Knio, O.M. A Review of Hydrogen Production and Supply Chain Modeling and Optimization. Int. J. Hydrogen Energy 2023, 48, 13731–13755. [Google Scholar] [CrossRef]
- Nunes, P.; Oliveira, F.; Hamacher, S.; Almansoori, A. Design of a Hydrogen Supply Chain with Uncertainty. Int. J. Hydrogen Energy 2015, 40, 16408–16418. [Google Scholar] [CrossRef]
- De-León Almaraz, S.; Moustapha Mai, T.; Melendez, I.R.; Loganathan, M.K.; Azzaro-Pantel, C. A Holistic Approach to Assessing Reliability in Green Hydrogen Supply Chains Using Mixed Methods. Technol. Forecast. Soc. Change 2024, 209, 123816. [Google Scholar] [CrossRef]
- U.S. Department of Energy (DOE). Hydrogen Delivery and Dispensing Cost. In DOE Hydrogen and Fuel Cells Program Record 20003; U.S. Department of Energy (DOE): Washington, DC, USA, 2020; pp. 1–4. [Google Scholar]
- Solomon, M.D.; Heineken, W.; Scheffler, M.; Birth-Reichert, T. Cost Optimization of Compressed Hydrogen Gas Transport via Trucks and Pipelines. Energy Technol. 2024, 12, 2300785. [Google Scholar] [CrossRef]
- James, B.D.; Acevedo, Y.; Jensen, M.; Graham, M.; Watts, Z.; Prosser, J.; Huya-Kouadio, J.; Mcnamara, K.; Analysis, S. Hydrogen Production Cost and Performance Analysis DOE Hydrogen Program 2024 Annual Merit Review and Peer Evaluation. Available online: https://www.hydrogen.energy.gov/docs/hydrogenprogramlibraries/pdfs/review23/p204_james_2023_o-pdf.pdf (accessed on 20 March 2025).
- Rad, M.A.V.; Ghasempour, R.; Rahdan, P.; Mousavi, S.; Arastounia, M. Techno-Economic Analysis of a Hybrid Power System Based on the Cost-Effective Hydrogen Production Method for Rural Electrification, a Case Study in Iran. Energy 2020, 190, 116421. [Google Scholar] [CrossRef]
- Department for Energy Security & Net Zero (DESNZ). Hydrogen Transport and Storage Cost Report. Available online: https://assets.publishing.service.gov.uk/media/659e600b915e0b00135838a6/hydrogen-transport-and-storage-cost-report.pdf (accessed on 20 March 2025).
- Collis, J.; Schomäcker, R. Determining the Production and Transport Cost for H2 on a Global Scale. Front. Energy Res. 2022, 10, 888499. [Google Scholar] [CrossRef]
- Li, X.J.; Allen, J.D.; Stager, J.A.; Ku, A.Y. Paths to Low-Cost Hydrogen Energy at a Scale for Transportation Applications in the USA and China via Liquid-Hydrogen Distribution Networks. Clean Energy 2020, 4, 26–47. [Google Scholar] [CrossRef]
- Messaoudani, Z.L.; Rigas, F.; Binti Hamid, M.D.; Che Hassan, C.R. Hazards, Safety and Knowledge Gaps on Hydrogen Transmission via Natural Gas Grid: A Critical Review. Int. J. Hydrogen Energy 2016, 41, 17511–17525. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Colella, W.G.; Golden, D.M. Atmospheric Science: Cleaning the Air and Improving Health with Hydrogen Fuel-Cell Vehicles. Int. J. Hydrogen Energy 2005, 308, 1901–1905. [Google Scholar]
- Bicer, Y.; Dincer, I. Comparative Life Cycle Assessment of Hydrogen, Methanol and Electric Vehicles from Well to Wheel. Int. J. Hydrogen Energy 2017, 42, 3767–3777. [Google Scholar] [CrossRef]
- Liu, H.; Ma, J. Models and Methods for Planning Hydrogen Supply Chain Systems. CSEE J. Power Energy Syst. 2020, 10, 2517–2527. [Google Scholar]
- Haggi, H.; Sun, W.; Fenton, J.M.; Brooker, P. Proactive Rolling-Horizon-Based Scheduling of Hydrogen Systems for Resilient Power Grids. IEEE Trans. Ind. Appl. 2022, 58, 1737–1746. [Google Scholar] [CrossRef]
- Matošec, M. Cybersecurity in Hydrogen Production Plants. Available online: https://hydrogentechworld.com/cybersecurity-in-hydrogen-production-plants (accessed on 17 November 2024).
- U.S. Department of Energy. Hydrogen Strategy: Enabling a Low-Carbon Economy. Available online: https://www.energy.gov/sites/prod/files/2020/08/f77/Hydrogen%20Economy%20Strategy%20Fact%20Sheet.pdf (accessed on 11 March 2025).
- ISA Cybersecurity. Cybersecurity for the Transportation Sector. Available online: https://isacybersecurity.com/cybersecurity-for-the-transportation-sector/ (accessed on 17 November 2024).
- Sherif, S.A.; Barbir, F.; Veziroglu, T.N. Towards a Hydrogen Economy. Electr. J. 2005, 18, 143–180. [Google Scholar] [CrossRef]
- Nexant. Hydrogen Delivery Infrastructure Options Analysis, Task Report for Department of Energy; Nexant: San Francisco, CA, USA, 2008. [Google Scholar]
- Yang, C.; Ogden, J. Determining the Lowest-Cost Hydrogen Delivery Mode. Int. J. Hydrogen Energy 2007, 32, 268–286. [Google Scholar] [CrossRef]
- Razi, F.; Dincer, I. Challenges, Opportunities and Future Directions in Hydrogen Sector Development in Canada. Int. J. Hydrogen Energy 2022, 47, 9083–9102. [Google Scholar] [CrossRef]
- European Commission. Assessment of Hydrogen Delivery Options. Feasibility of Transport of Green Hydrogen within Europe. In Assessment of Hydrogen Delivery Options; EUR 31199 EN; Ortiz Cebolla, R., Dolci, F., Weidner Ronnefeld, E., Eds.; European Commission: Luxembourg; Publications Office of the European Union: Luxembourg, 2022; Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC130442 (accessed on 20 March 2025)ISBN 978-92-76-56421-8.
- Hydrogen Council. Hydrogen Insights 2021: A Perspective on Hydrogen Investment, Deployment and Cost Competitiveness; Hydrogen Council: Brussels, Belgium, 2021; Available online: https://hydrogencouncil.com/en/hydrogen-insights-2021/ (accessed on 20 March 2025).
- International Energy Agency (IEA). The Future of Hydrogen: Seizing Today’s Opportunities; Report Prepared by the IEA for the G20, Japan; IEA: Paris, France, 2019; Available online: https://www.iea.org/reports/the-future-of-hydrogen (accessed on 10 March 2025).
- Transport Canada. Rail Transportation in Canada; Transport Canada: Ottawa, ON, Canada, 2020; Available online: https://tc.canada.ca/en/corporate-services/transparency/corporate-management-reporting/transportation-canada-annual-reports/2020-2021/rail-transportation (accessed on 1 March 2025).
- National Research Council Canada (NRC). Towards a Net Zero Emission Railway System with Hydrogen Powered Trains; National Research Council Canada: Ottawa, ON, Canada, 2022; Available online: https://nrc.canada.ca/en/stories/towards-net-zero-emission-railway-system-hydrogen-powered-trains (accessed on 11 March 2025).
- Natural Resources Canada (NRCan). Hydrogen Strategy for Canada: Seizing the Opportunities; Natural Resources Canada: Ottawa, ON, Canada, 2020; Available online: https://natural-resources.canada.ca/sites/nrcan/files/environment/hydrogen/NRCan_Hydrogen-Strategy-Canada-na-en-v3.pdf (accessed on 15 March 2025).
- Canadian Urban Transit Research & Innovation Consortium (CUTRIC) Industry Experts Talk Hydrogen for Rail. Available online: https://www.powerprogress.com/news/industry-experts-talk-hydrogen-for-rail/8055622.article (accessed on 22 March 2025).
- British Columbia Bioenergy Network (BCBN). British Columbia Hydrogen Study; British Columbia Bioenergy Network: Victoria, BC, Canada, 2020; Available online: https://www.bcic.ca/wp-content/uploads/2021/01/BC-Hydrogen-Study-Final-2020.pdf (accessed on 2 March 2025).
- Ohaeri, E.G.; Szpunar, J.A. An Overview on Pipeline Steel Development for Cold Climate Applications. J. Pipeline Sci. Eng. 2022, 2, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Frank Cheng, Y. Hydrogen-Induced Degradation of High-Strength Steel Pipeline Welds: A Critical Review. Eng. Fail. Anal. 2022, 133, 105985. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Cheng, Y.F. A New Method for Assessment of Burst Pressure Capacity of Corroded X80 Steel Pipelines Containing a Dent. Int. J. Press. Vessel. Pip. 2022, 199, 104742. [Google Scholar] [CrossRef]
- Balat, M. Potential Importance of Hydrogen as a Future Solution to Environmental and Transportation Problems. Int. J. Hydrogen Energy 2008, 33, 4013–4029. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Laarhoven, P.J.M.; Pedrycz, W. A Fuzzy Extension of Saaty’s Priority Theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Zhang, S.F.; Liu, S.Y. A GRA-Based Intuitionistic Fuzzy Multi-Criteria Group Decision Making Method for Personnel Selection. Expert Syst. Appl. 2011, 38, 11401–11405. [Google Scholar] [CrossRef]
- Abdullah, L.; Najib, L. Sustainable Energy Planning Decision Using the Intuitionistic Fuzzy Analytic Hierarchy Process: Choosing Energy Technology in Malaysia. Int. J. Sustain. Energy 2014, 35, 360–377. [Google Scholar] [CrossRef]
- Hersh, M. Mathematical Modeling for Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-24216. [Google Scholar]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A Multi-Criteria Intuitionistic Fuzzy Group Decision Making for Supplier Selection with TOPSIS Method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic Fuzzy Information—Applications to Pattern Recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).