Designing a Waste Heat Recovery Heat Exchanger for Polymer Electrolyte Membrane Fuel Cell Operation in Medium-Altitude Unmanned Aerial Vehicles
Abstract
1. Introduction
2. Waste Heat Calculation of PEMFCs
2.1. Aircraft Specifications
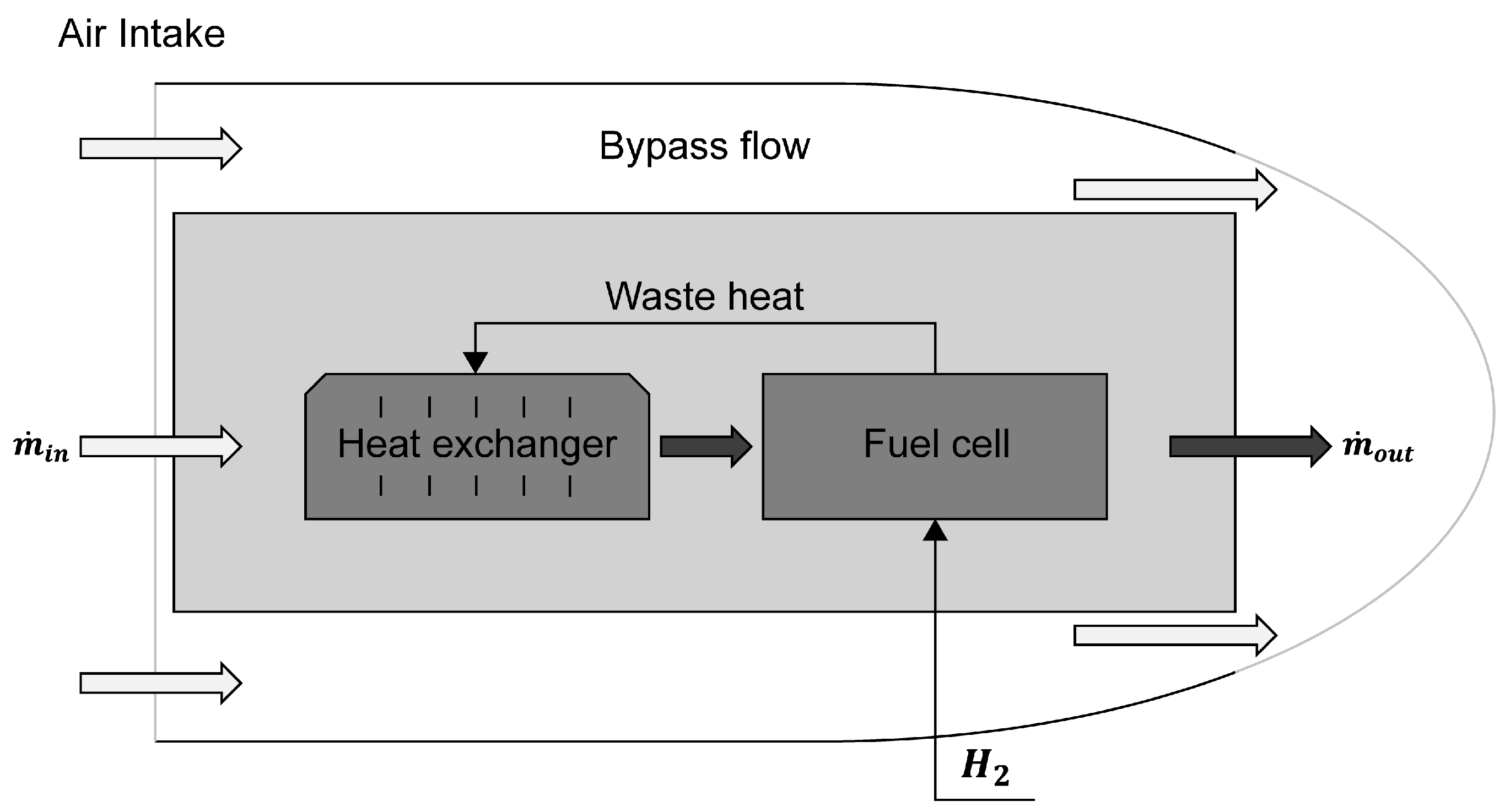
2.2. Heat Exchanger Selection
2.3. Air Properties
- is the air temperature by altitude;
- is the percentage decrease in temperature ();
- is the aircraft flight altitude.
- is the air pressure by altitude;
- is the standard atmospheric pressure (101,325 );
- is the standard atmosphere temperature (15 °C, 288.15 );
- is the gas constant (287.053 J/kg·K);
- is the gravitational acceleration (9.80665 ).
- is the air density.
- is air viscosity by altitude;
- is the standard atmospheric temperature (273.15 K);
- is the Sutherland temperature (111 K);
- is the reference air viscosity ( Pa s).
2.4. PEMFC Waste Heat
- is the power output of a single engine (691 );
- is the power output of the PEMFC;
- is the power output of the battery.
- is the degree of hybridization (0.47).
- is the reversible thermodynamic voltage of the PEMFC (1.23 );
- is the Gibbs free energy for the electrochemical reaction (−237 );
- is the number of electrons transferred in the electrochemical reaction in (2);
- is Faraday’s constant (96,485 ).
- is the reversible thermodynamic power output of the PEMFC;
- is the actual operating voltage of the PEMFC (0.6 ).
- is the waste heat generated from the PEMFC.
2.5. Air Consumption of PEMFCs
- is the oxygen mass flow rate required for a 369.41 kW PEMFC;
- is the stoichiometry of oxygen (2);
- is the oxygen fraction at altitude;
- is the molar mass of air (28.848 );
- is the current flowing in the PEMFC ();
- is the number of cells;
- is the power of the PEMFC (369.41 );
- is the voltage of the cell (0.6 ).
2.6. Required Preheating Energy
- is the convection heat transfer ();
- is the air mass flow rate required by the PEMFC;
- is the specific heat (1005 );
- is the air temperature after passing through the heat exchanger (−5 °C);
- is the outside air temperature.
3. Design of Shell-and-Tube Heat Exchangers
- Heat losses to the outside of the heat exchanger were ignored;
- Air and coolant were assumed to be incompressible fluids;
- Flow was assumed to be at steady-state operation and did not account for effects such as altitude changes or thrust variations;
- The specific heat was assumed to be constant;
- No phase changes were assumed to occur;
- No condensation or icing was assumed to occur in the heat exchanger.
3.1. Determination of Convective Heat Transfer Coefficient
- is the heat transfer coefficient ();
- is the Nusselt number;
- is the thermal conductivity ();
- is the heat exchanger shell diameter ().
- is the thermal conductivity at temperature ();
- is the temperature to be interpolated;
- is the temperature provided by experimental data
- is the temperature provided by experimental data );
- is the thermal conductivity at each temperature ;
- is the thermal conductivity at each temperature .
- is the volume flow rate of the air intake ();
- is the cross-section of air intake ();
- is the air velocity (86.67);
- is the air intake for outside air;
- is the heat exchanger diameter.
- is the Reynolds number;
- is the Prandtl number.
- is the hot fluid temperature (coolant);
- is the cold fluid temperature (air).
- is the shell-side temperature;
- is the tube-side temperature.
- is the heat transfer area without considering fouling ();
- is the area with a 10% additional area to account for fouling factors ().
3.2. Design of Tube
- is the heat exchanger tube’s outer diameter ();
- is the heat exchanger tube’s length (0.6 ).
- is the number of heat exchanger tubes.
- is the bundle diameter (0.21 );
- are constants determined by the array format and number of passes ();
- is the radial clearance (0.013 ).
- is the tube’s pitch length ().
3.3. Design of Baffles
- is the effective flow area between tubes ();
- is the tube’s pitch;
- is the baffle spacing ().
- is the equivalent diameter in the shells ().
- is the airflow velocity in the shells ().
- is the Nusselt number in the shell;
- is the Colburn j factor with a baffle cut of 0.25.
- is the heat transfer coefficient of the shell.
3.4. Pressure Drop
- is the pressure drop acting on the tube ();
- is the number of tube passes (1);
- is the friction factor of the tube;
- is the tube’s inner diameter ();
- is the tube’s flow rate ().
- is the pressure drop acting on the shell ();
- is the shell friction coefficient;
- is the shell flow rate ().
3.5. System Efficiency
- is the system power ();
- is the fluid mass flow rate ();
- is the system efficiency (0.75).
- is the available power for propulsion ();
- is the PEMFC’s power ();
- is the power required for heat exchange ();
- is the blower power ();
- is the coolant pump power ();
- is the additional electrical power ().
4. Results
4.1. Heat Transfer Rate According to Baffle Configuration
4.2. Calculation Results of Pressure Drop
4.3. Propulsion System Efficiency
- Figure 4a shows that varying has almost no effect on the available system power when waste heat recovery is employed. Even when is reduced stepwise, the power loss remains below 0.3%, and the highest efficiency is reached when is 1.0. A power saving of approximately 5% is confirmed when compared to preheating the air using external power.
- Figure 4b shows a similar trend: when the value of is between 0.5 and 1.0, the available power changes little, but when is 0.25, there is a power penalty of about 1% compared to 0.5. In this case, preheating the intake air using waste heat lowers total power consumption by 5% compared to external electric preheating.
- Figure 4c reveals that when is 0.75 or 1.0, the required convective heat transfer is not fully achieved, resulting in additional electrical energy consumption. A noteworthy observation is that is 0.75 performs slightly better than is 0.5, suggesting proximity to an optimal threshold. Further fine-tuning around this value is necessary to precisely determine the optimal . When is 0.25, a power penalty of approximately 4.3% occurs relative to is 0.5. Compared to external electric preheating, the maximum power consumption is reduced by 15.7%.
- As altitude increases, the improvement in heat transfer efficiency enhances the effectiveness of waste heat recovery; however, the resulting increase in pressure drop may lead to the potential damage or performance degradation of the heat exchanger. In addition, inefficient baffle design can reduce the overall efficiency of the system, making the optimization of baffle spacing according to the required convective heat transfer essential.
5. Conclusions
- As demonstrated in Reference [18], the incoming air to the PEMFC must be pre-heated to at least −5 °C to prevent MEA freezing and consequent performance degradation.
- The analysis showed that at 15,000 ft, the required heat transfer was achieved regardless of the presence of baffles; however, at altitudes of 20,000 ft and above, additional baffle design was necessary to compensate for insufficient heat transfer.
- The pressure drop was calculated by applying the minimum baffle configuration, and it was confirmed that the overall efficiency of the PEMFC system could be improved by up to 15.7%.
- As altitude increases, the required heat transfer also rises, necessitating a greater number of baffles. However, an increase in the number of baffles leads to higher pressure drop, which in turn reduces the efficiency of the power available for propulsion. To balance this trade-off, the waste heat recovery heat exchanger of a UAV-mounted PEMFC must be geometrically optimized for the altitude-dependent air properties required by the stack, ensuring that the preheated air remains above the freezing point and thereby preserving the efficiency of the MEA.
- Future work will focus on optimizing the heat exchanger geometry for each flight altitude, quantifying how waste heat recovery impacts PEMFC thermal management, and conducting three-dimensional simulations to obtain higher-fidelity thermal predictions. The analysis results will be used to quantify heat-transfer performance and pressure drop; icing tests will then be conducted, and the performance and reliability of the waste heat recovery system will be comprehensively evaluated.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, P.W.; Xu, G.; Latif, M.A.; Abbas, K.; Yasin, A. Uav’s Agricultural Image Segmentation Predicated by Clifford Geometric Algebra. IEEE Access 2019, 7, 38442–38450. [Google Scholar] [CrossRef]
- Panagiotou, P.; Tsavlidis, I.; Yakintkos, K. Conceptual design of a hybrid solar MALE UAV. Aerosp. Sci. Technol. 2016, 53, 207–219. [Google Scholar] [CrossRef]
- Gupta, P.; Pareek, B.; Singal, G.; Rao, D.V. Edge device based Military Vehicle Detection and Classification from UAV. Multimed. Tools Appl. 2022, 81, 19813–19834. [Google Scholar] [CrossRef]
- MQ-9 Reaper Specification. Available online: https://www.af.mil/About-Us/Fact-Sheets/Display/Article/104470/mq-9-reaper/ (accessed on 28 March 2025).
- KUS-FS Specification. Available online: https://aerospace.koreanair.com/business/uav/kusFs/ (accessed on 28 March 2025).
- Hermes 900 Specification. Available online: https://www.elbitsystems.com/autonomous/aerial/male-unmanned-aircraft-systems/hermes-900/ (accessed on 28 March 2025).
- RUSTOM-1 Specification. Available online: https://www.drdo.gov.in/drdo/rustom-1/ (accessed on 28 March 2025).
- Pan, Z.F.; An, L.; Wen, C.Y. Recent advances in fuel cells based propulsion systems for unmanned aerial vehicles. Appl. Energy 2019, 240, 473–485. [Google Scholar] [CrossRef]
- Hyun, D.; Han, H.; Hong, S. Development of hybrid-powered, sustainable multi-purpose drone system: An analysis model. Int. J. Hydrogen Energy 2024, 61, 762–773. [Google Scholar] [CrossRef]
- Cai, Q.; Brett, D.J.L.; Browing, D.; Brandon, N.P. A sizing-design methodology for hybrid fuel cell power systems and its application to an unmanned underwater vehicle. J. Power Sources 2010, 195, 6559–6569. [Google Scholar] [CrossRef]
- Donateo, T.; Ficarella, A.; Spedicato, L.; Arista, A.; Ferraro, M. A new approach to calculating endurance in electric flight and comparing fuel cells and batteries. Appl. Energy 2017, 187, 807–819. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, S. Development of optimal energy management strategy for proton exchange membrane fuel cell-battery hybrid system for drone propulsion. Appl. Therm. Eng. 2025, 258, 124646. [Google Scholar] [CrossRef]
- Shen, Z.; Liu, S.; Zhu, W.; Ren, D.; Xu, Q.; Feng, Y. A Review on Key Technologies and Developments of Hydrogen Fuel Cell Multi-Rotor Drones. Energies 2024, 17, 4193. [Google Scholar] [CrossRef]
- Zeng, Z.; Bao, C.; Li, C.; Ouyang, M. A Modeling Study on Water and Thermal Management and Cold Startup of Unmanned Aerial Vehicle Fuel Cell System. eTransportation 2023, 15, 100222. [Google Scholar] [CrossRef]
- Zeroavia Flight Test. Available online: https://zeroavia.com/flight-testing/ (accessed on 14 March 2025).
- H2FLY History. Available online: https://h2fly.uber.space/company/ (accessed on 17 March 2025).
- Rajbongshi, B.M.; Saneeth, M.; Verma, A. Investigation on sub-zero start-up of polymer electrolyte membrane fuel cell using un-assisted cold start strategy. Int. J. Hydrogen Energy 2020, 45, 34048–34057. [Google Scholar] [CrossRef]
- Zhan, Z.; Yuan, C.; Hu, Z.; Wang, H.; Sui, P.C.; Djilali, N.; Pan, M. Experimental study on different preheating methods for the cold-start of PEMFC stacks. Energy 2018, 162, 1029–1040. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Muhammad, I.; Alaswad, W.; Sayed, E.T.; Abo-Khalil, A.G.; Maghrabie, H.M.; Elsaid, K.; Abdelkareem, M.A. Recovery of waste heat from proton exchange membrane fuel cells—A review. Int. J. Hydrogen Energy 2024, 52, 933–972. [Google Scholar] [CrossRef]
- Sheshpoli, M.A.; Ajarostaghi, S.S.M.; Delavar, M.A. Waste heat recovery from a 1180 kW proton exchange membrane fuel cell (PEMFC) system by Recuperative organic Rankine cycle (RORC). Energy 2018, 157, 353–366. [Google Scholar] [CrossRef]
- Antonio, C.S.; Lusia, A.J.; Lorenzo, N.C. Residual heat use generated by a 12 kW fuel cell in an electric vehicle heating system. Energy 2014, 68, 182–190. [Google Scholar]
- Xu, Z.; Yan, Y.; Wei, W.; Sun, D.; Ni, Z. Supply system of cryo-compressed hydrogen for fuel cell stacks on heavy duty trucks. Int. J. Hydrogen Energy 2020, 45, 12921–12931. [Google Scholar] [CrossRef]
- Lu, D.; Yi, F.; Li, J. Optimization of the Adaptability of the Fuel Cell Vehicle Waste Heat Utilization Subsystem to Extreme Cold Environments. Sustainability 2022, 14, 11570. [Google Scholar] [CrossRef]
- TPE331 Turboprop Engine Specifications. Available online: https://aerospace.honeywell.com/us/en/products-and-services/products/power-and-propulsion/engines/turboprop-engines/tpe331-turboprop-engine (accessed on 17 March 2025).
- Hesselgreaves, J.E. Compact Heat Exchangers: Selection, Design and Operation; Pergamon: Oxford, UK, 2001. [Google Scholar]
- Jin, Y.; Tang, G.H.; He, Y.L.; Tao, W.Q. Numerical Study of the Solid Particle Erosion on H-Type Finned Circular/Elliptic Tube Surface. Commun. Comput. Phys. 2017, 21, 466–489. [Google Scholar] [CrossRef]
- Han, J.; Kim, S.-J.; Lee, Y.-K.; Hur, D.-H. Chemical Cleaning of Magnetite Deposits on the Flow Mini-Channels of a Printed Circuit Heat Exchanger in an EDTA-Based Solution. Materials 2022, 15, 1471. [Google Scholar] [CrossRef]
- Fetuga, I.A.; Olakoyejo, O.T.; Abolarin, S.M.; Gbegudu, J.K.; Onwuegbusi, A.; Adelaja, A.O. Numerical analysis of thermal performance of waste heat recovery shell and tube heat exchangers on counter-flow with different tube configurations. Alex. Eng. J. 2023, 64, 859–875. [Google Scholar] [CrossRef]
- Cavcar, M. The International Standard Atmosphere (ISA); Anadolu University: Eskisehir, Turkey, 2000; Available online: http://fisicaatmo.at.fcen.uba.ar/practicas/ISAweb.pdf (accessed on 7 May 2025).
- Sutherland, W. The viscosity of gases and molecular force. Philos. Mag. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Beyond Aero Prototypes. Available online: https://www.beyond-aero.com/prototypes (accessed on 16 March 2025).
- O’Hayre, R.; Cha, S.W.; Collela, W.G.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 25–46. [Google Scholar]
- Graf, T.; Fonk, R.; Bauer, C.; Kallo, J.; Willich, C. Optimal Sizing of Fuel Cell and Battery in a Direct-Hybrid for Electric Aircraft. Aerospace 2024, 11, 176. [Google Scholar] [CrossRef]
- Rostami, M.; Dehghan Manshadi, M.; Afshari, E. Performance evaluation of two proton exchange membrane and alkaline fuel cells for use in UAVs by investigating the effect of operating altitude. Int. J. Energy Res. 2022, 46, 1481–1496. [Google Scholar] [CrossRef]
- Kern, D.Q. Process Heat Transfer; McGraw-Hill Book Company: New York, NY, USA, 1950. [Google Scholar]
- Abd, A.A.; Naji, S.Z. Analysis study of shell and tube heat exchanger for clough company with reselect different parameters to improve the design. Case Stud. Therm. Eng. 2017, 10, 455–467. [Google Scholar] [CrossRef]
- Towler, G.; Sinnott, R. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Patel, V.K.; Rao, R.V. Design optimization of shell-and-tube heat exchanger using particle swarm optimization technique. Appl. Therm. Eng. 2010, 30, 1417–1425. [Google Scholar] [CrossRef]
- Abd, A.A.; Kareem, M.Q.; Naji, S.Z. Performance analysis of shell and tube heat exchanger: Parametric study. Case Stud. Therm. Eng. 2018, 12, 563–568. [Google Scholar] [CrossRef]
- Gnielinski, V. Neue Gleichungen für den Wärme-und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forsch. Im Ingenieurwesen 1976, 42, 145–153. [Google Scholar] [CrossRef]
- Lee, P.S.; Garimella, S.V.; Liu, D. Investigation of heat transfer in rectangular microchannels. Int. J. Heat Mass Transf. 2005, 48, 1688–1704. [Google Scholar] [CrossRef]
- Mya, N.S.; Thu, M.M.; Htwe, S.N.C.; Oo, M.P.S.; Htay, M.K.S.; Htet, M.N.L. Baffle Design of Shell And Tube Heat Exchanger. Int. J. Sci. Eng. Technol. Res. 2019, 8, 420–426. [Google Scholar]
- Azad, A.V.; Amidpour, M. Economic optimization of shell and tube heat exchanger based on constructal theory. Energy 2011, 36, 1087–1096. [Google Scholar] [CrossRef]
- Selbaş, R.; Kızılkan, Ö.; Reppich, M. A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem. Eng. Process. Process Intensif. 2006, 45, 268–275. [Google Scholar] [CrossRef]



| Aircraft | Country | Altitude (ft) | Power (hp) | Source |
|---|---|---|---|---|
| MQ-9 Reaper | USA | 25,000 | 900 | Air Force mil [4] |
| KUS-FS | South Korea | 45,000 | 1200 | Korea Air [5] |
| Elbit Hermes 900 | Israel | 30,000 | 210 | Elbit Systems [6] |
| DRDO Rustom-1 | India | 26,000 | 150 | DRDO [7] |
| Parameter | Value |
|---|---|
| Power (hp) | 900 (671 kW) |
| Maximum operating speed (mph) | 300 (482 km/h) |
| Cruising operating speed (mph) | 194 (312 km/h) |
| Maximum altitude (ft) | 50,000 (15,240 m) |
| Cruising altitude (ft) | 25,000 (7620 m) |
| Air mass flow () | 7.7 (3.5 ) |
| Altitude (ft) | T (°C) | P (Pa) | μ () | ||
|---|---|---|---|---|---|
| Parameter | Value () |
|---|---|
| 369.41 | |
| 757.29 | |
| 387.88 |
| Altitude () | Mass Flow Rate () |
|---|---|
| 15,000 | 0.78 |
| 20,000 | 0.95 |
| 25,000 | 1.14 |
| 30,000 | 1.46 |
| Altitude () | Convection Heat Transfer (kW) |
|---|---|
| 15,000 | 7.62 |
| 20,000 | 18.7 |
| 25,000 | 34.86 |
| 30,000 | 57.91 |
| Altitude (ft) | 15,000 | 20,000 | 25,000 | 30,000 |
|---|---|---|---|---|
| 0.023 | 0.022 | 0.021 | 0.02 | |
| 0.72 | 0.73 | 0.73 | 0.73 | |
| 0.0118 | 0.0121 | 0.0124 | 0.0127 | |
| 1069.08 | 953.79 | 860.41 | 763.82 | |
| 109.31 | 94.1 | 81.8 | 69.87 | |
| 81.75 | 86.42 | 91.08 | 95.36 | |
| 907,517.24 | 793,262.02 | 689,453.32 | 595,289.43 |
| Altitude (ft) | Heat Exchanger Area (m2) |
|---|---|
| 15,000 | 0.94 |
| 20,000 | 2.53 |
| 25,000 | 5.15 |
| 30,000 | 9.56 |
| Altitude (ft) | Number of Tubes Required |
|---|---|
| 15,000 | 27 |
| 20,000 | 71 |
| 25,000 | 144 |
| 30,000 | 267 |
| Altitude (ft) | ||||
|---|---|---|---|---|
| 20,000 | 46.94 | 31.85 | 25.15 | 20.96 |
| 25,000 | 87.71 | 59.49 | 47.41 | 40.34 |
| 30,000 | 103.77 | 69.56 | 54.57 | 46.25 |
| Altitude (ft) | Coolant Pressure Drop (Pa) |
|---|---|
| 20,000 | 32.56 |
| 25,000 | 113.45 |
| 30,000 | 306.2 |
| Altitude (ft) | ||||
|---|---|---|---|---|
| 20,000 | 217.67 | 108.84 | 72.56 | 54.42 |
| 25,000 | 316.75 | 158.38 | 105.58 | 79.18 |
| 30,000 | 587.98 | 293.99 | 195.99 | 146.99 |
| Altitude (ft) | Pumping Power (W) |
|---|---|
| 20,000 | 0.01 |
| 25,000 | 0.07 |
| 30,000 | 0.39 |
| Altitude (ft) | ||||
|---|---|---|---|---|
| 20,000 | 2132.82 | 1066.44 | 710.98 | 533.19 |
| 25,000 | 8310.47 | 4155.23 | 2770.11 | 2077.69 |
| 30,000 | 30,867.08 | 15,433.41 | 10,289.03 | 7716.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.; Choi, J.; Choi, S.-J.; Kim, S.-G. Designing a Waste Heat Recovery Heat Exchanger for Polymer Electrolyte Membrane Fuel Cell Operation in Medium-Altitude Unmanned Aerial Vehicles. Energies 2025, 18, 3262. https://doi.org/10.3390/en18133262
Jang J, Choi J, Choi S-J, Kim S-G. Designing a Waste Heat Recovery Heat Exchanger for Polymer Electrolyte Membrane Fuel Cell Operation in Medium-Altitude Unmanned Aerial Vehicles. Energies. 2025; 18(13):3262. https://doi.org/10.3390/en18133262
Chicago/Turabian StyleJang, Juwon, Jaehyung Choi, Seung-Jun Choi, and Seung-Gon Kim. 2025. "Designing a Waste Heat Recovery Heat Exchanger for Polymer Electrolyte Membrane Fuel Cell Operation in Medium-Altitude Unmanned Aerial Vehicles" Energies 18, no. 13: 3262. https://doi.org/10.3390/en18133262
APA StyleJang, J., Choi, J., Choi, S.-J., & Kim, S.-G. (2025). Designing a Waste Heat Recovery Heat Exchanger for Polymer Electrolyte Membrane Fuel Cell Operation in Medium-Altitude Unmanned Aerial Vehicles. Energies, 18(13), 3262. https://doi.org/10.3390/en18133262





