SOH and RUL Estimation for Lithium-Ion Batteries Based on Partial Charging Curve Features
Abstract
1. Introduction
- (1)
- A local health feature extraction strategy focusing on the constant voltage (CV) charging process and voltage relaxation is proposed. By extracting the key health characteristics of some stages in the battery charging process, and the charging data of these two stages are easy to obtain in the actual working condition, the dependence on the full charging curve is eliminated. Pearson correlation analysis and SHapley Additive exPlanations (SHAP) interpretability validation ensure the effectiveness and physical relevance of these features, enabling accurate SOH estimation under practical scenarios with incomplete data.
- (2)
- An estimation framework combining CatBoost and particle swarm optimization-support vector recognition (PSO-SVR) is developed. CatBoost achieves high-precision SOH estimation using partial charging features, leveraging its strengths with categorical data and gradient bias. Subsequently, PSO-SVR efficiently estimates RUL based on historical SOH sequences. This two-stage approach effectively couples SOH and RUL estimation.
- (3)
- The proposed method demonstrates superior performance when validated on two distinct battery datasets, outperforming mainstream models including long short-term memory (LSTM), temporal convolutional network (TCN), and Transformer by over 40% in SOH estimation accuracy while maintaining faster computational speeds. Ablation studies confirm the method’s robustness across critical parameters such as feature selection, window length, and optimization processes. SHapley Additive exPlanations (SHAP) analysis provides interpretable insights into the model’s decision-making process, enhancing its credibility for real-world BMS applications.
2. Data Analysis and Feature Extraction
2.1. Definition of SOH and RUL
2.2. Analysis of Battery Dataset
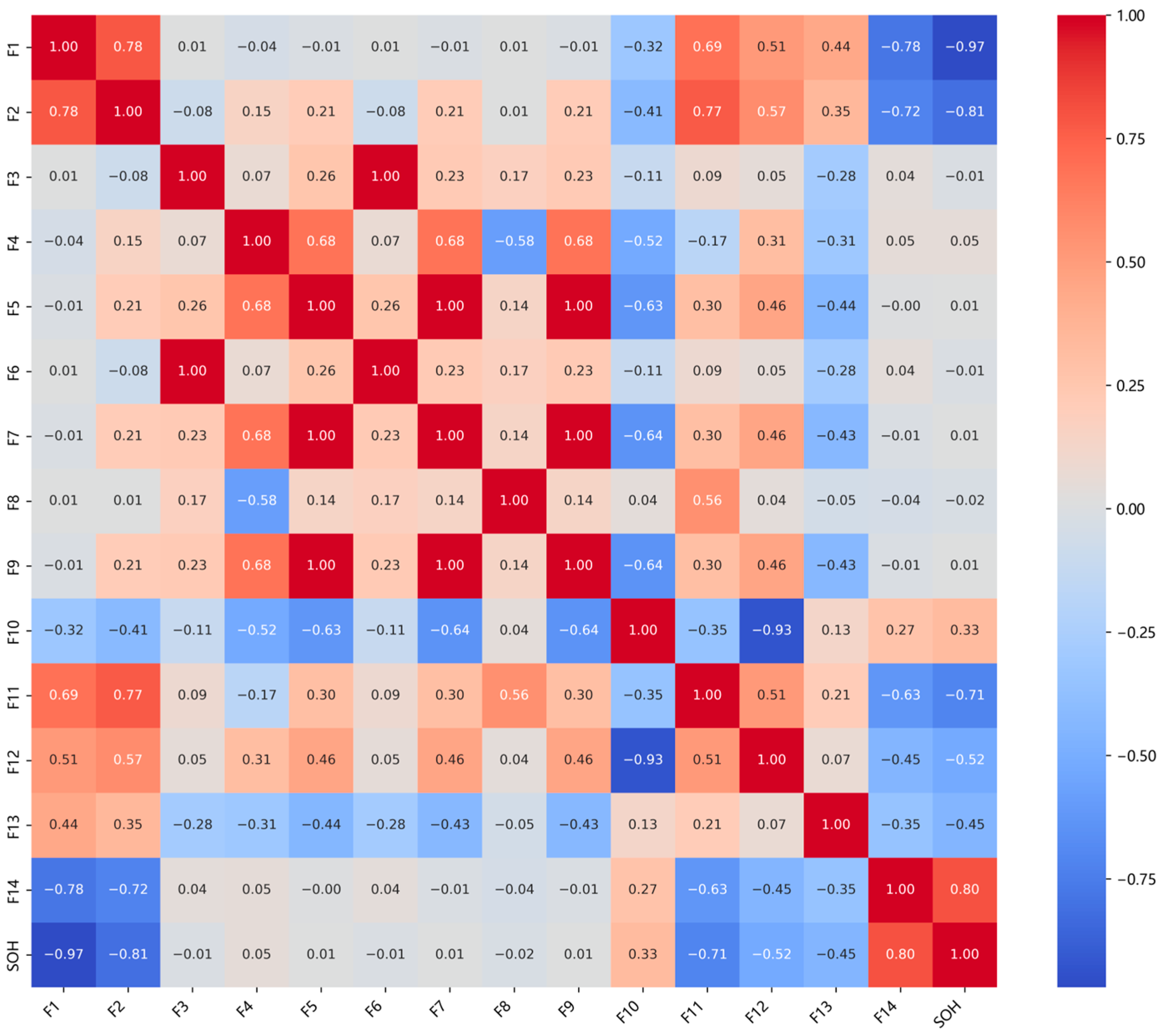
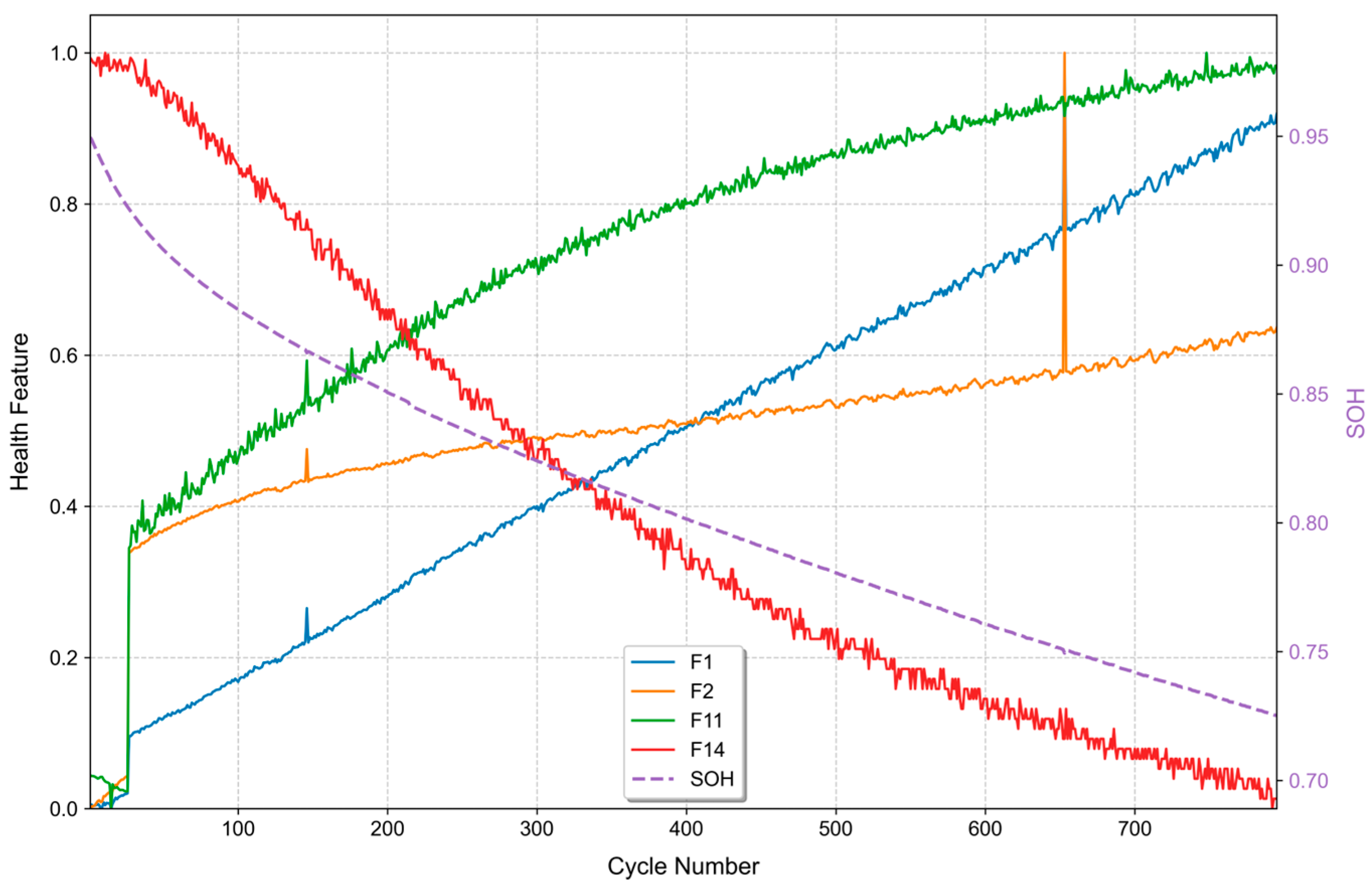
2.3. Health Feature Extraction and Analysis
3. Methodology
3.1. CatBoost
3.2. SHAP
3.3. PSO-SVR
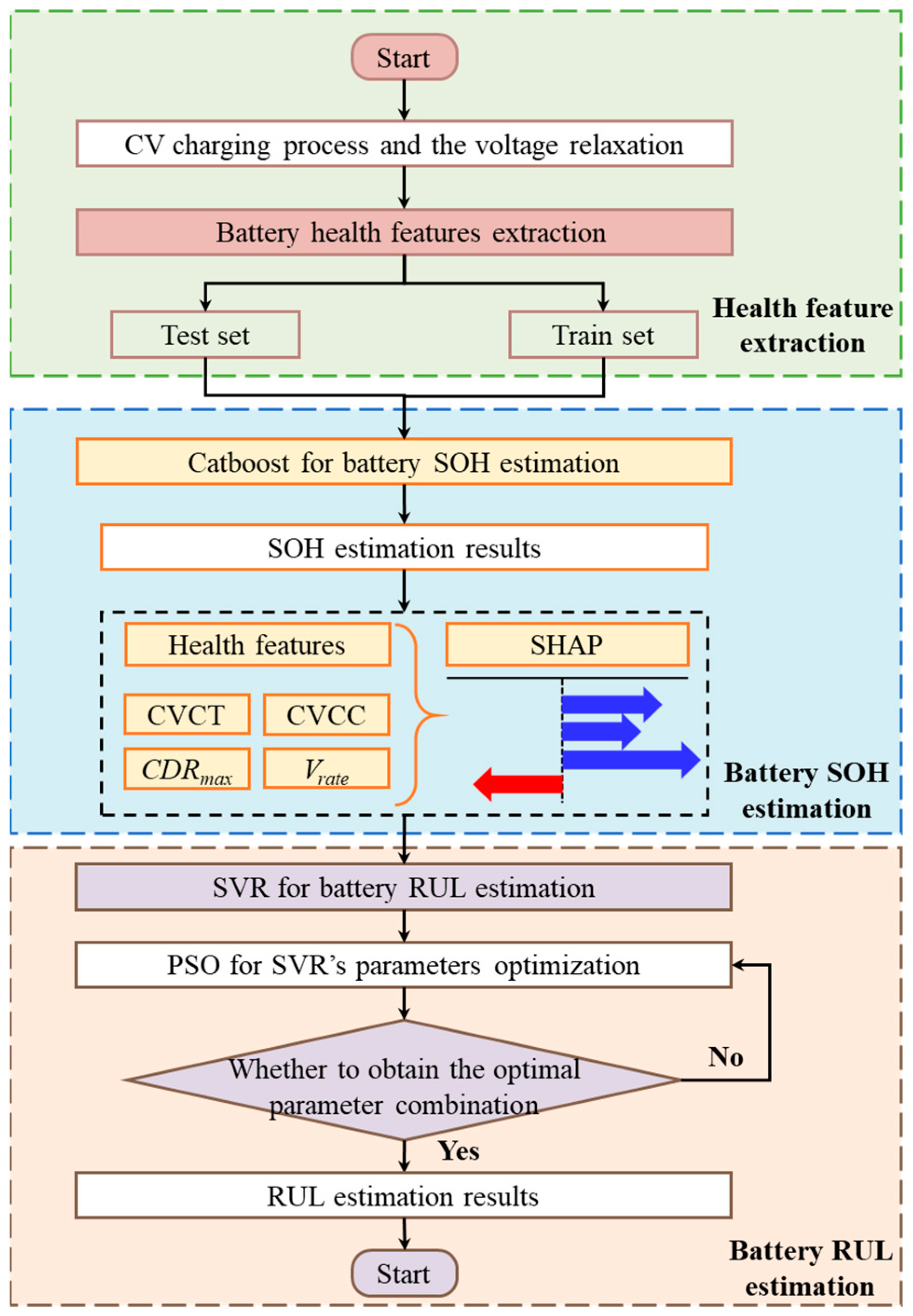
3.4. Proposed Method
4. Experiment and Discussion
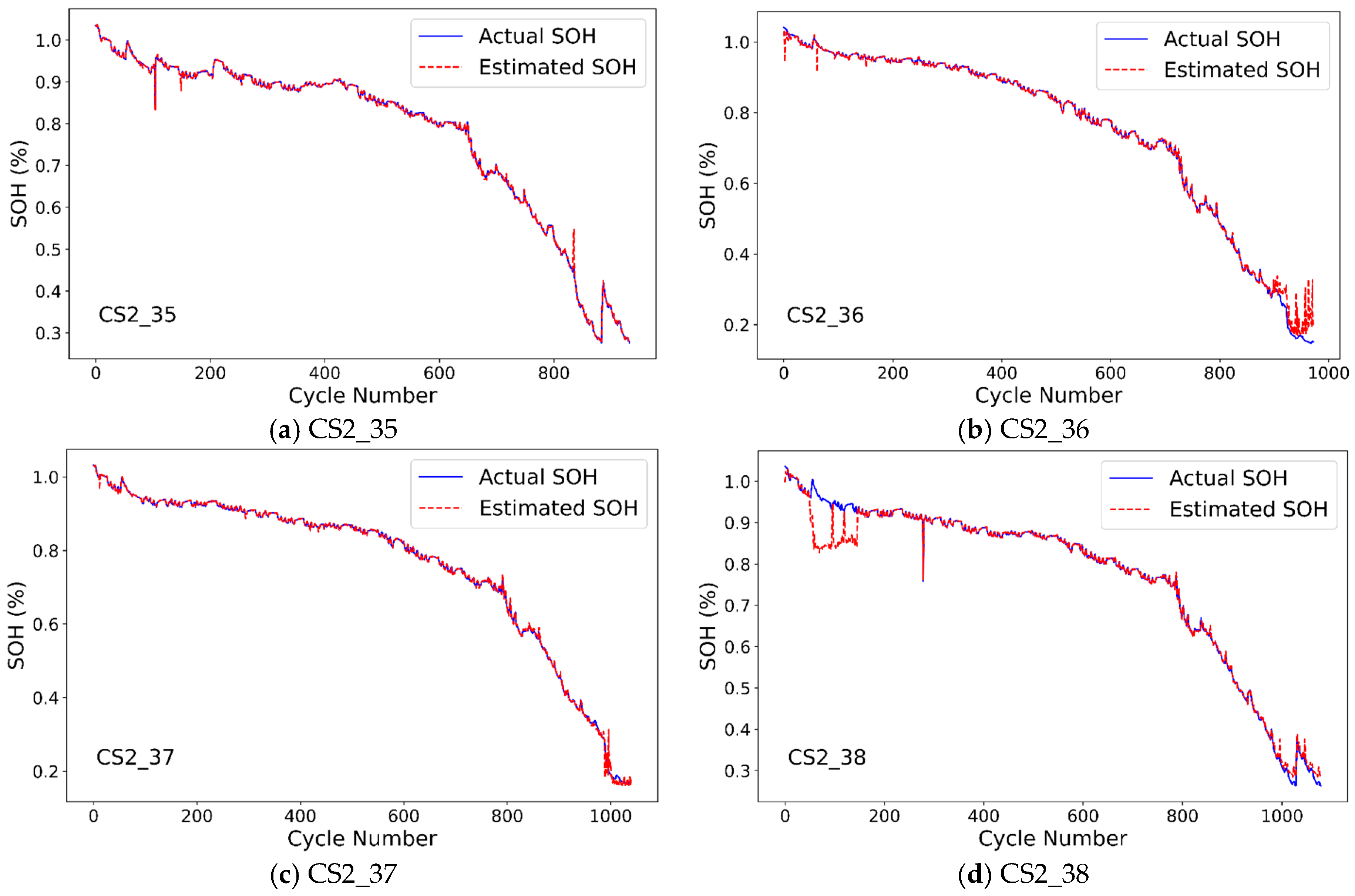
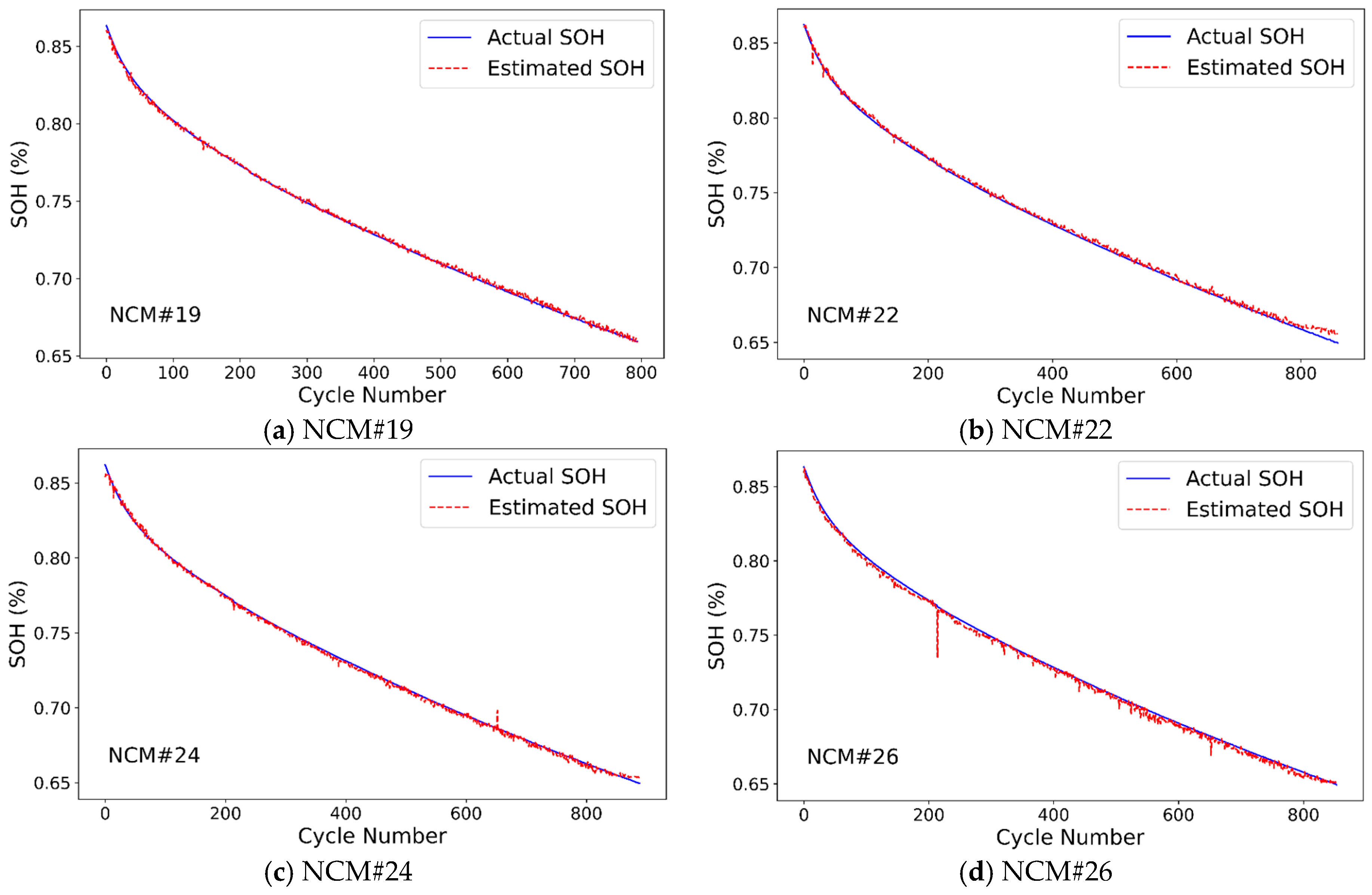
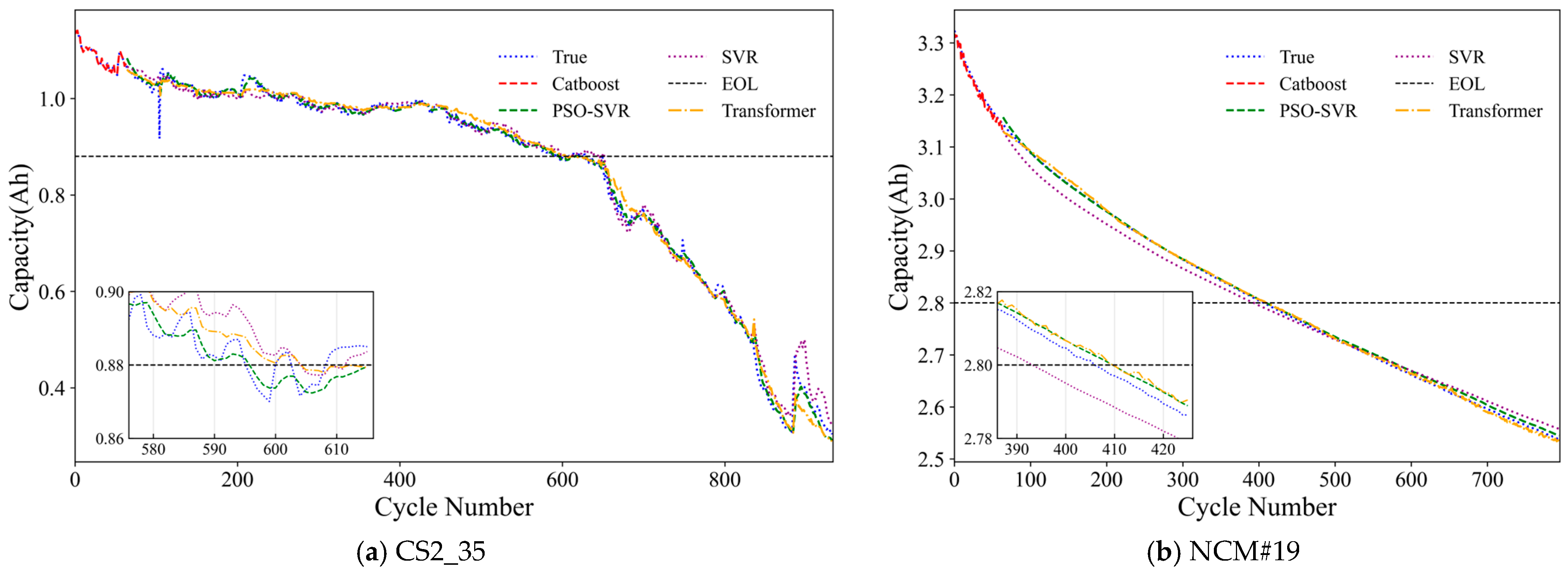
4.1. SOH Estimation Results
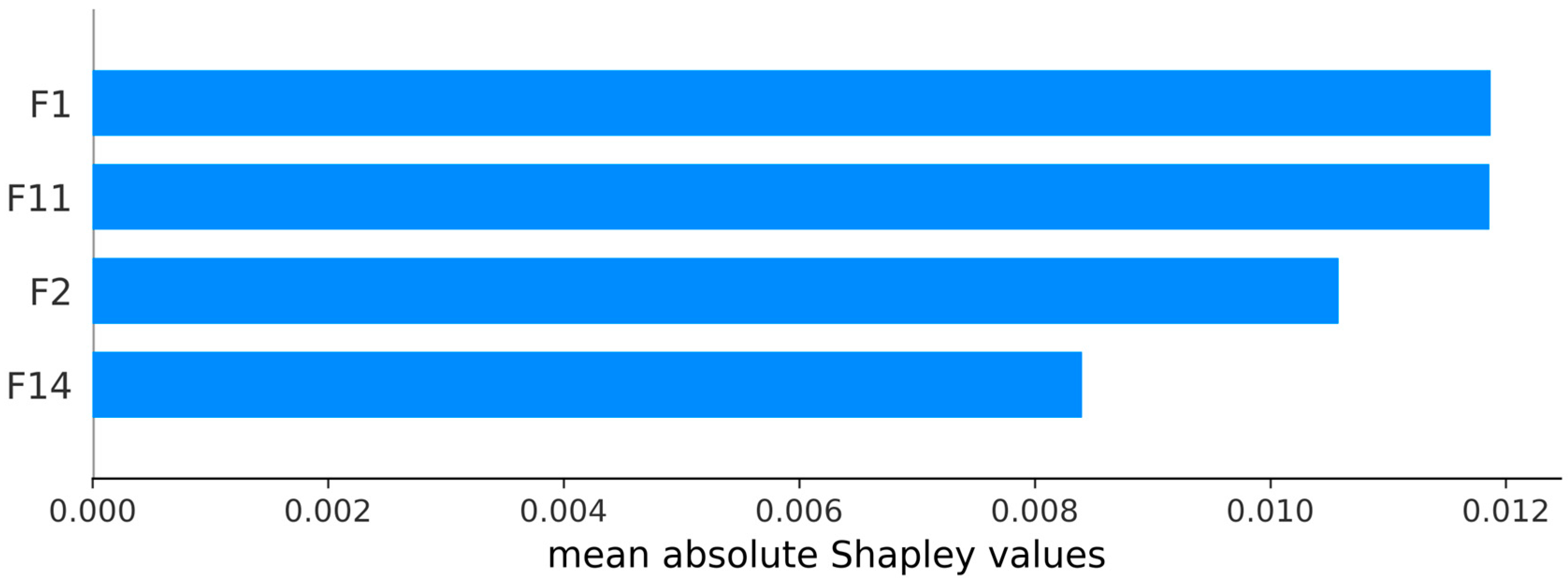
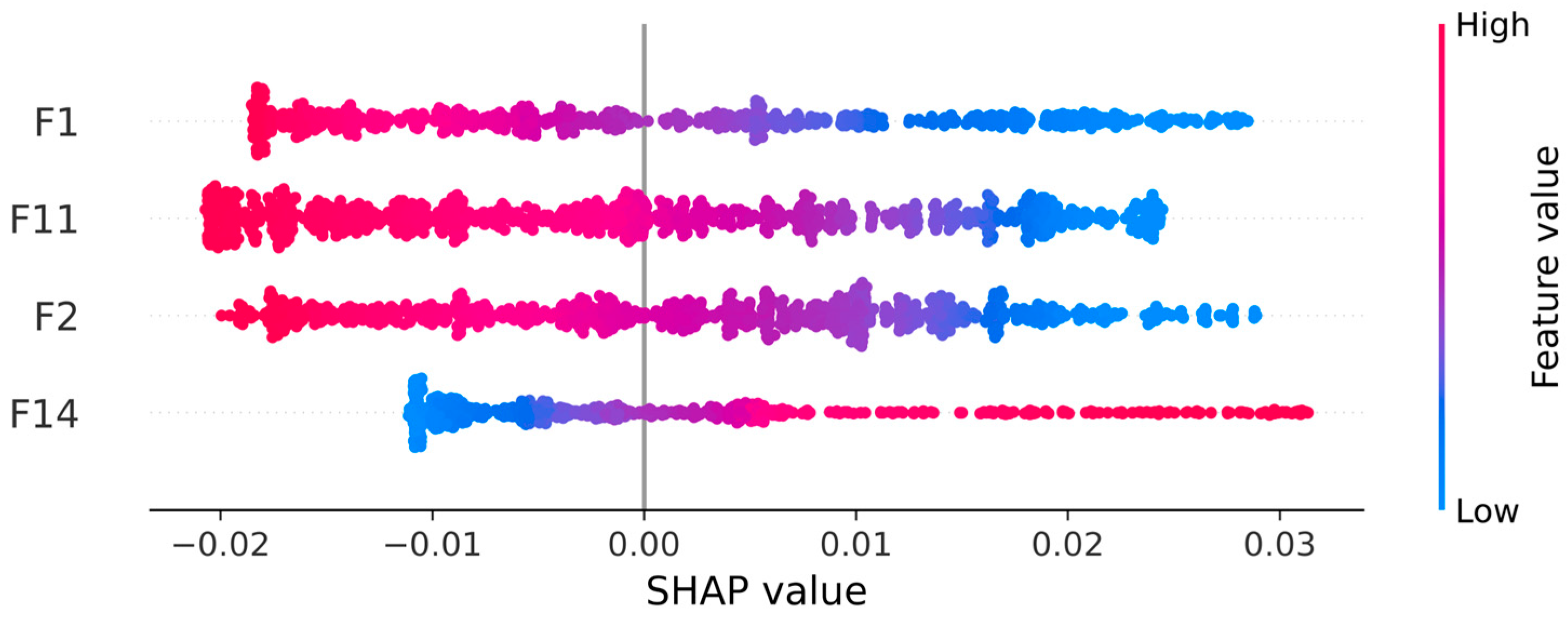
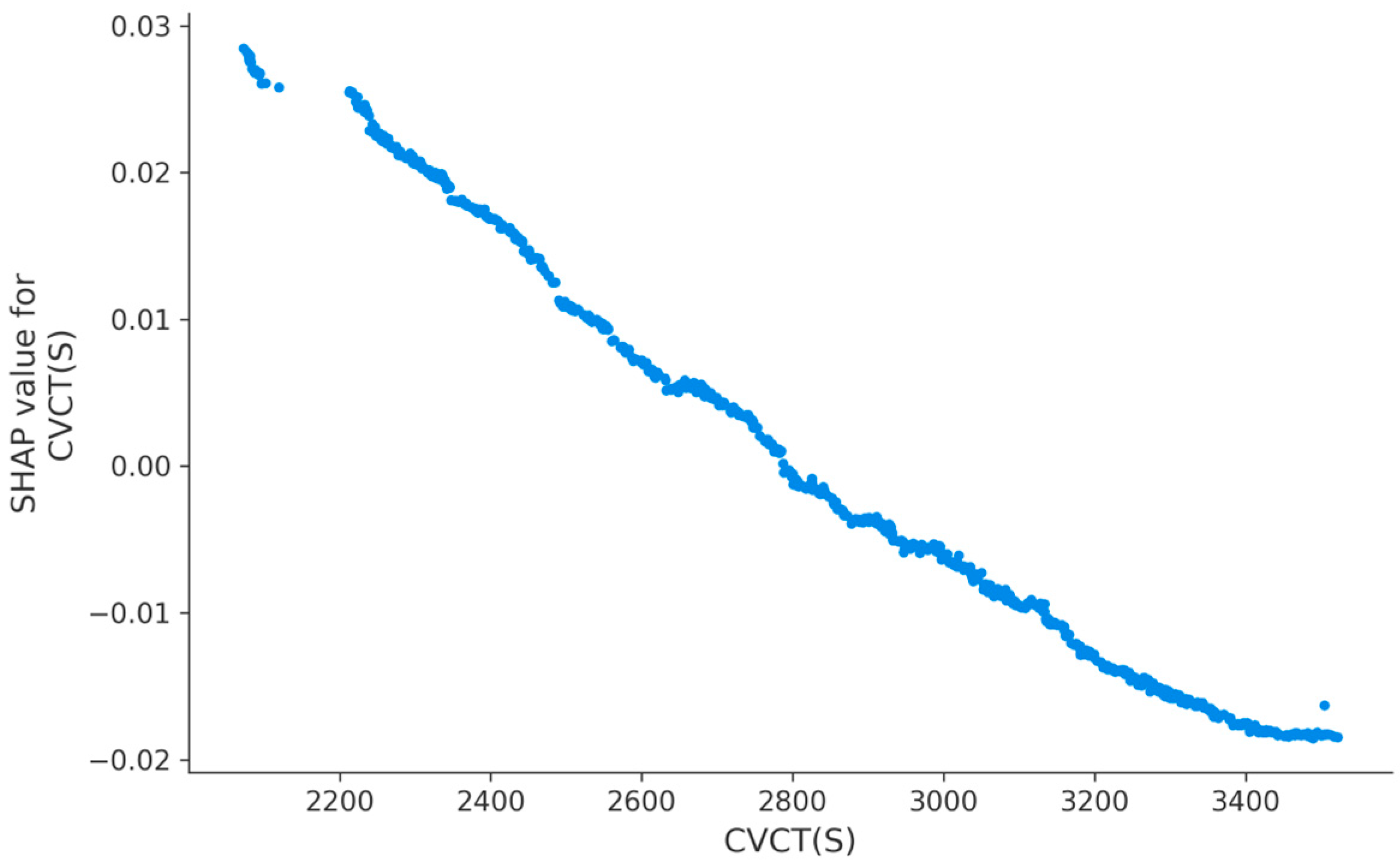
4.2. Interpretability Analysis
4.3. Features Effectiveness Analysis
4.4. RUL Estimation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Jin, S.; Deng, D.; Fernandez, C. A Critical Review of Online Battery Remaining Useful Lifetime Prediction Methods. Front. Mech. Eng. 2021, 7, 719718. [Google Scholar] [CrossRef]
- Kim, J.; Chun, H.; Kim, M.; Han, S.; Lee, J.W.; Lee, T.K. Effective and practical parameters of electrochemical Li-ion battery models for degradation diagnosis. J. Energy Storage 2021, 42, 103077. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, M.; Liu, H.; Tang, Z. State of health estimation and remaining useful life prediction for lithium-ion batteries by improved particle swarm optimization-back propagation neural network. J. Energy Storage 2022, 52, 104750. [Google Scholar] [CrossRef]
- Hallemans, N.; Widanage, W.D.; Zhu, X.; Moharana, S.; Rashid, M.; Hubin, A.; Lataire, J. Operando electrochemical impedance spectroscopy and its application to commercial Li-ion batteries. J. Power Sources 2022, 547, 2322005. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Z.; Qiu, Y.; Jing, B.; Yang, C. State of charge estimation for Li-ion batteries based on iterative Kalman filter with adaptive maximum correntropy criterion. J. Power Sources 2023, 580, 233282. [Google Scholar] [CrossRef]
- Song, Z.; Hou, J.; Li, X.; Wu, X.; Hu, X.; Hofmann, H.; Sun, J. The sequential algorithm for combined state of charge and state of health estimation of lithium-ion battery based on active current injection. Energy 2020, 193, 116732. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Sangiri, J.B.; Kulshreshtha, T.; Ghosh, S.; Maiti, S.; Chakraborty, C. A novel methodology to estimate the state-of-health and remaining-useful-life of a Li-ion battery using discrete Fourier transformation. J. Energy Storage 2022, 46, 103849. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, D.; Zhang, X.; Chen, Z. Probability based remaining capacity estimation using data-driven and neural network model. J. Power Sources 2016, 315, 199–208. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Berecibar, M.; Nanini-Maury, E.; van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Y.; Xiao, B. A novel hybrid neural network-based SOH and RUL estimation method for lithium-ion batteries. J. Energy Storage 2024, 98, 113074. [Google Scholar] [CrossRef]
- Tang, R.; Zhang, P.; Ning, S.; Zhang, Y. Prediction of battery SOH and RUL based on cooperative characteristics in voltage-temperature-time dimensions. J. Electrochem. Soc. 2023, 170, 060535. [Google Scholar] [CrossRef]
- Duan, W.; Song, S.; Xiao, F.; Chen, Y.; Peng, S.; Song, C. Battery SOH estimation and RUL prediction framework based on variable forgetting factor online sequential extreme learning machine and particle filter. J. Energy Storage 2023, 65, 107322. [Google Scholar] [CrossRef]
- Cai, N.; Que, X.; Zhang, X.; Feng, W.; Zhou, Y. A deep learning framework for the joint prediction of the SOH and RUL of lithium-ion batteries based on bimodal images. Energy 2024, 302, 131700. [Google Scholar] [CrossRef]
- Zhang, M.; Yin, J.; Chen, W. SOH estimation and RUL prediction of lithium batteries based on multidomain feature fusion and CatBoost model. Energy Sci. Eng. 2023, 11, 3082–3101. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z.; He, J.; Yu, S. Lithium battery state-of-health estimation and remaining useful lifetime prediction based on non-parametric aging model and particle filter algorithm. Etransportation 2022, 11, 100156. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, Y.; Lyu, Z. A SOH estimation method of lithium-ion batteries based on partial charging data. J. Energy Storage 2024, 103, 114309. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Yang, Z.; Du, B.; Zhou, Z.; Wu, J.; Chen, L. Flexible method for estimating the state of health of lithium-ion batteries using partial charging segments. Energy 2024, 295, 131009. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL prediction of lithium-ion batteries based on Gaussian process regression with indirect health indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Li, D.; Wang, K. State-of-health estimation of lithium-ion batteries based on electrochemical impedance spectroscopy: A review. Prot. Control Mod. Power Syst. 2023, 8, 1–17. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Osterman, M.; Pecht, M. Comparative analysis of features for determining state of health in lithium-ion batteries. Int. J. Progn. Health Manag. 2020, 4, 20–27. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Chen, Y.; Tao, Y. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction. J. Power Sources 2016, 321, 1–10. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Lin, B.; Bai, R. Machine learning approaches for explaining determinants of the debt financing in heavy-polluting enterprises. Financ. Res. Lett. 2022, 44, 102094. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Kong, C. Remaining useful life prediction of lithium-ion batteries based on a mixture of ensemble empirical mode decomposition and GWO-SVR model. IEEE Trans. Instrum. Meas. 2021, 70, 2517011. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Meng, H.; Geng, M.; Han, T. Long short-term memory network with Bayesian optimization for health prognostics of lithium-ion batteries based on partial incremental capacity analysis. Reliab. Eng. Syst. Saf. 2023, 236, 109288. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, S.; Park, K.; Kim, H. Machine learning-based lithium-ion battery capacity estimation exploiting multi-channel charging profiles. IEEE Access 2019, 7, 75143–75152. [Google Scholar] [CrossRef]
- Luo, K.; Zheng, H.; Shi, Z. A simple feature extraction method for estimating the whole life cycle state of health of lithium-ion batteries using transformer-based neural network. J. Power Sources 2023, 576, 233139. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, W.; Wang, L.; Chang, X.; Li, X.; Wu, P. Evaluation of the state of health of lithium-ion battery based on the temporal convolution network. Front. Energy Res. 2022, 10, 929235. [Google Scholar] [CrossRef]
- He, S.; Qin, W.; Yun, Z.; Wu, C.; Sun, C. SOH Estimation Method for Lithium-Ion Batteries Using Partial Discharge Curves Based on CGKAN. Batteries 2025, 11, 167. [Google Scholar] [CrossRef]
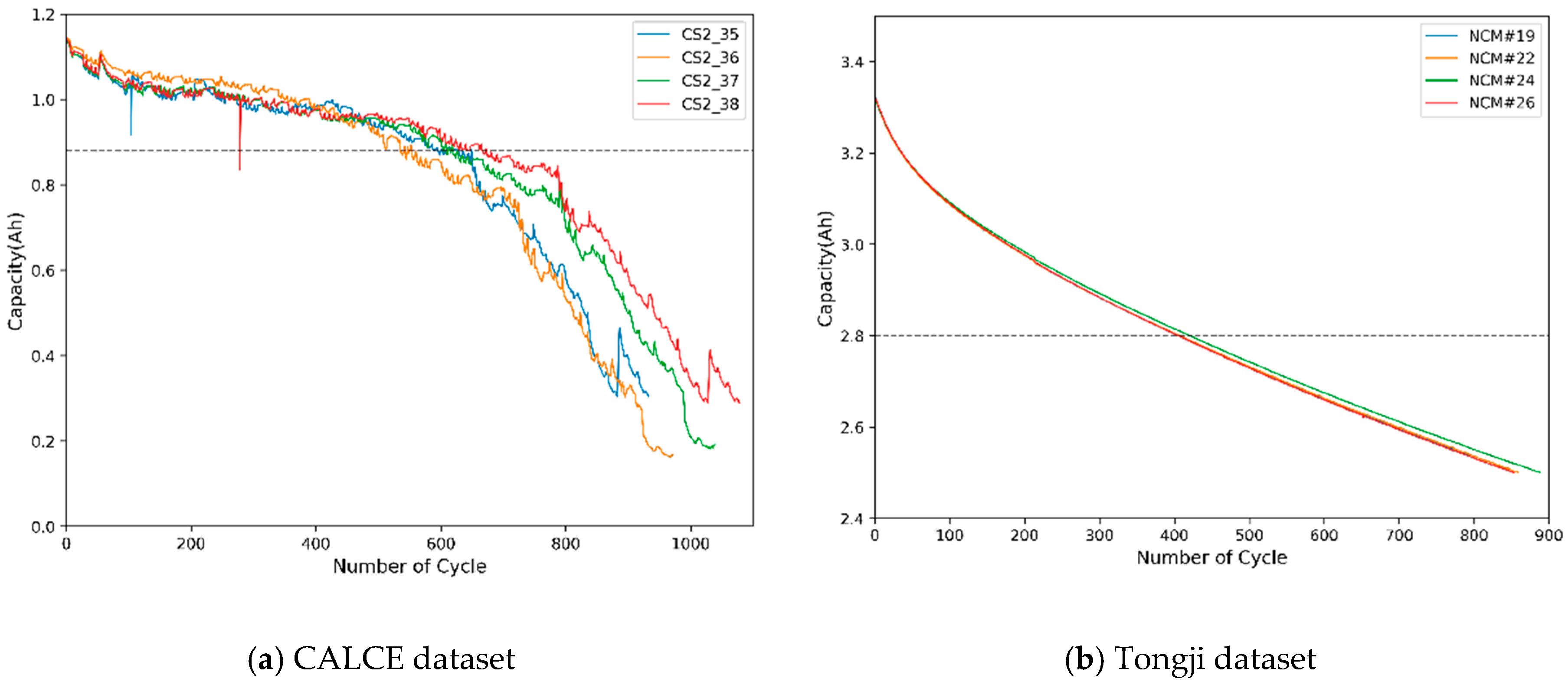
| Dataset | Battery Number | Ambient Temperature | Charge Cut-Off Voltage | Discharge Cut-Off Voltage | Constant Current Charging Current | Constant Current Discharge Current |
|---|---|---|---|---|---|---|
| CALCE | CS2_35 | 24 °C | 4.2 V | 2.7 V | 0.55 A | 1.1 A |
| CS2_36 | 24 °C | 4.2 V | 2.7 V | 0.55 A | 1.1 A | |
| CS2_37 | 24 °C | 4.2 V | 2.7 V | 0.55 A | 1.1 A | |
| CS2_38 | 24 °C | 4.2 V | 2.7 V | 0.55 A | 1.1 A | |
| Tongji | NCM#19 | 45 °C | 4.2 V | 2.5 V | 1.75 A | 3.5 A |
| NCM#22 | 45 °C | 4.2 V | 2.5 V | 1.75 A | 3.5 A | |
| NCM#24 | 45 °C | 4.2 V | 2.5 V | 1.75 A | 3.5 A | |
| NCM#26 | 45 °C | 4.2 V | 2.5 V | 1.75 A | 3.5 A |
| No. | Name | Definition | No. | Name | Definition |
|---|---|---|---|---|---|
| F1 | CVCT | CV charging time | F2 | CVCC | CV charging capacity |
| F3 | Iend | Current termination value in CV process | F4 | Iavg | average of CV charging current |
| F5 | Imax | Maximum CV charging current | F6 | Imin | Minimum CV charging current |
| F7 | Ivariance | F8 | Iskewness | ||
| F9 | ISD | F10 | CDRavg | ||
| F11 | CDRmax | Maximum decay rate of CV charging current | F12 | CDRinit | Initial decay rate of CV charging current |
| F13 | KI, avg | F14 | Vrate |
| SOH Estimation Method | RMSE (%) | MAE (%) | Time (s) |
|---|---|---|---|
| Health feature + CatBoost (ours) | 1.42 | 0.52 | 0.00319 |
| Health feature + XGBoost | 2.47 | 1.32 | 0.00551 |
| Health feature + MLP | 2.53 | 1.43 | 0.00735 |
| Complete voltage curve data + RNN | 2.77 | 1.35 | 0.02497 |
| Complete voltage curve data + GRU | 2.67 | 1.41 | 0.10013 |
| Complete voltage curve data + LSTM | 2.86 | 1.56 | 0.12075 |
| Bayesian-LSTM | 2.70 | 1.99 | 0.12268 |
| MC-LSTM | 2.51 | 2.31 | 0.17521 |
| Transformer | 2.46 | 1.41 | 0.0655 |
| TCN | 2.47 | 1.64 | 1.06052 |
| SOH Estimation Method | RMSE (%) | MAE (%) | Time (s) |
|---|---|---|---|
| Health feature + CatBoost (ours) | 0.21 | 0.16 | 0.00323 |
| Health feature + XGBoost | 0.24 | 0.17 | 0.00562 |
| Health feature + MLP | 0.73 | 0.49 | 0.00747 |
| Complete voltage curve data + RNN | 0.69 | 0.42 | 0.02501 |
| Complete voltage curve data + GRU | 0.55 | 0.35 | 0.10030 |
| Complete voltage curve data + LSTM | 0.58 | 0.33 | 0.12093 |
| Bayesian-LSTM | 0.53 | 0.36 | 0.12283 |
| MC-LSTM | 0.79 | 0.46 | 0.17503 |
| Transformer | 0.53 | 0.32 | 0.06588 |
| TCN | 0.57 | 0.33 | 1.06063 |
| Dataset | SOH Estimation Method | RMSE (%) | MAE (%) |
|---|---|---|---|
| CALCE | F1 + CatBoost | 2.36 | 1.24 |
| F2, F11, F14 + CatBoost | 2.13 | 1.08 | |
| F1, F2, F11, F14 + CatBoost | 1.42 | 0.52 | |
| Tongji | F1 + CatBoost | 0.41 | 0.26 |
| F2, F11, F14 + CatBoost | 0.38 | 0.21 | |
| F1, F2, F11, F14 + CatBoost | 0.21 | 0.16 |
| Dataset | SOH Estimation Method | RMSE (%) | MAE (%) | Time (s) |
|---|---|---|---|---|
| CALCE | Health feature + CatBoost | 1.42 | 0.52 | 0.00319 |
| Health feature + XGBoost | 2.47 | 1.32 | 0.00551 | |
| Health feature + MLP | 2.53 | 1.43 | 0.00735 | |
| Complete voltage curve data + CatBoost | 1.63 | 0.87 | 0.00915 | |
| Complete voltage curve data + XGBoost | 2.94 | 1.82 | 0.0127 | |
| Complete voltage curve data + MLP | 3.62 | 2.37 | 0.0167 | |
| Tongji | Health feature + CatBoost | 0.21 | 0.16 | 0.00323 |
| Health feature + XGBoost | 0.24 | 0.17 | 0.00562 | |
| Health feature + MLP | 0.73 | 0.49 | 0.00747 | |
| Complete voltage curve data + CatBoost | 0.26 | 0.22 | 0.00847 | |
| Complete voltage curve data + XGBoost | 0.31 | 0.24 | 0.0117 | |
| Complete voltage curve data + MLP | 1.3 | 1.19 | 0.01564 |
| SOH Estimation Method | RMSE (%) | MAE (%) |
|---|---|---|
| Health feature + CatBoost (ours) | 1.42 | 0.52 |
| Partial discharge curves + CGKAN [37] | 1.38 | 1.1 |
| Partial incremental capacity features + BO-LSTM [33] | 1.81 | 1.38 |
| Start Point | Battery Number | Rtrue (Cycle) | Rpred (Cycle) | RE (%) | Mean RE (%) |
|---|---|---|---|---|---|
| 64 | CS2_35 | 588 | 590 | 0.34 | 0.58 |
| CS2_36 | 537 | 539 | 0.37 | ||
| CS2_37 | 606 | 613 | 1.16 | ||
| CS2_38 | 668 | 671 | 0.45 | ||
| 128 | CS2_35 | 588 | 590 | 0.34 | 0.5 |
| CS2_36 | 537 | 539 | 0.37 | ||
| CS2_37 | 606 | 612 | 0.99 | ||
| CS2_38 | 668 | 670 | 0.3 |
| Start Point | Battery Number | Rtrue (Cycle) | Rpred (Cycle) | RE (%) | Mean RE (%) |
|---|---|---|---|---|---|
| 64 | NCM#19 | 407 | 411 | 0.98 | 1.865 |
| NCM#22 | 409 | 413 | 0.98 | ||
| NCM#24 | 423 | 409 | 3.3 | ||
| NCM#26 | 407 | 398 | 2.2 | ||
| 128 | NCM#19 | 407 | 411 | 0.98 | 1.8025 |
| NCM#22 | 409 | 412 | 0.73 | ||
| NCM#24 | 423 | 409 | 3.3 | ||
| NCM#26 | 407 | 398 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, K.; Li, Y.; Zou, Q.; Cao, K.; Li, Z. SOH and RUL Estimation for Lithium-Ion Batteries Based on Partial Charging Curve Features. Energies 2025, 18, 3248. https://doi.org/10.3390/en18133248
Qian K, Li Y, Zou Q, Cao K, Li Z. SOH and RUL Estimation for Lithium-Ion Batteries Based on Partial Charging Curve Features. Energies. 2025; 18(13):3248. https://doi.org/10.3390/en18133248
Chicago/Turabian StyleQian, Kejun, Yafei Li, Qiheng Zou, Kecai Cao, and Zhongpeng Li. 2025. "SOH and RUL Estimation for Lithium-Ion Batteries Based on Partial Charging Curve Features" Energies 18, no. 13: 3248. https://doi.org/10.3390/en18133248
APA StyleQian, K., Li, Y., Zou, Q., Cao, K., & Li, Z. (2025). SOH and RUL Estimation for Lithium-Ion Batteries Based on Partial Charging Curve Features. Energies, 18(13), 3248. https://doi.org/10.3390/en18133248





