Problems in Modeling Three-Phase Three-Wire Circuits in the Case of Non-Sinusoidal Periodic Waveforms and Unbalanced Load

Abstract

Asymmetry in the supply voltage in three-phase circuits disrupts the flow of currents. This worsens the efficiency of the distribution system and increases the problems in determining the mathematical model of the energy system. Among many power theories, the most accurate is the Currents’ Physical Components (CPC) power theory, which tries to justify the physical essence of each component. Such knowledge can be used to improve efficiency and reduce transmission losses in the power system. This article discusses the method of mathematical decomposition of current components in the case of a three-wire line connecting an asymmetric power source with linear time-invariant (LTI) loads. Special cases where irregularities appear in the results of calculations according to the CPC theory are discussed. The problem of equivalent conductance in the case of a non-zero value of the constant voltage component is discussed. The method of determining symmetrical components for periodic non-sinusoidal waveforms is also discussed. These considerations are supported by numerical examples.

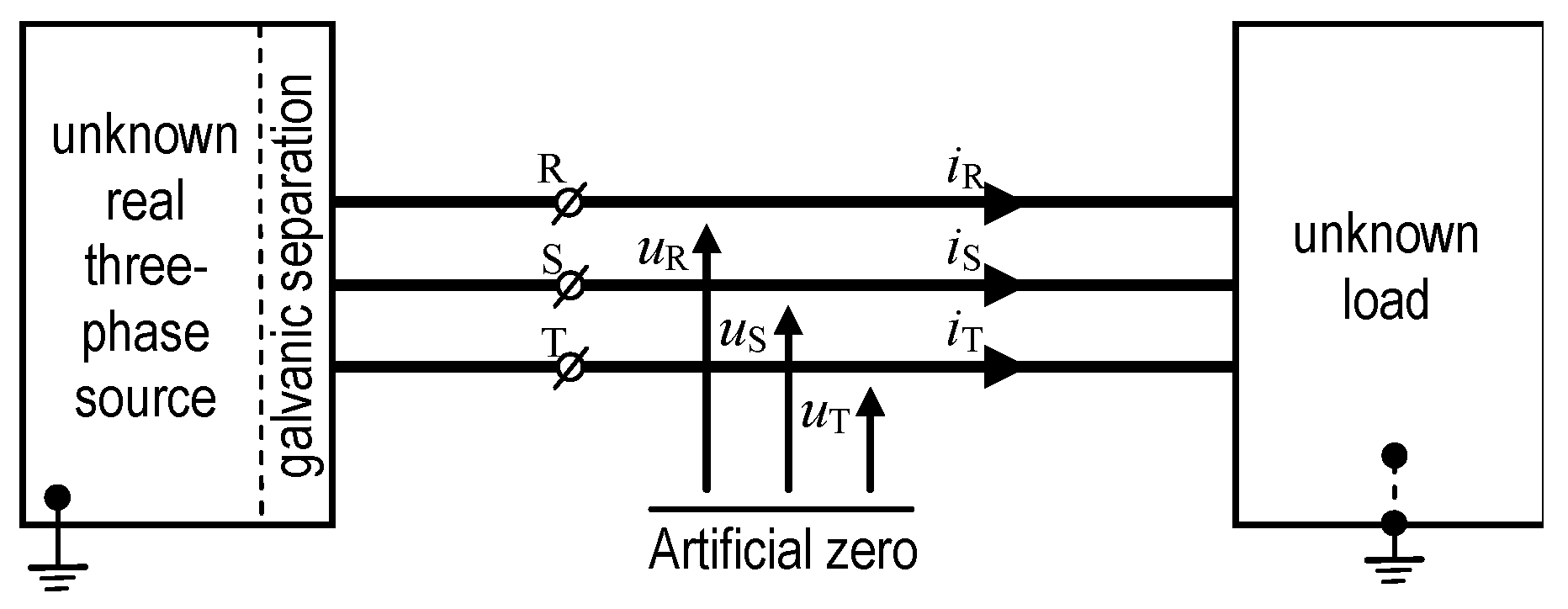
1. Introduction

Contemporary problems in the energy sector mainly focus on improving the efficiency of energy systems and improving energy quality [1,2,3]. These activities in the area of power engineering include, among others, monitoring the flow of current and actions to reduce transmission losses [4,5,6]. In this respect, developing methods to describe the mathematical model of the power system [7,8,9,10,11] and to determine the values of individual elements is crucial. Knowing the mathematical model of this system will make it possible to select the topology and parameters of the compensators [12,13,14,15,16,17,18,19,20,21,22,23,24].

In measurement practice, we most often only have data in the form of measured electrical quantities on the line connecting the load with the power source. This article focuses on the three-wire connection (Figure 1).

A linear time-invariant (LTI) load is supplied by a three-wire line with non-sinusoidal and asymmetrical voltage. The assumption of the LTI load is crucial here because in the case of a receiver generating harmonics [25,26,27,28,29,30,31,32,33,34,35], identifying all the parameters of the nonlinear load requires a more complicated measurement procedure [36,37,38,39,40,41]. The nonlinearity of the receiver causes a change in the direction of energy flow for some harmonics. This disrupts the operation of power systems operating on both micro and macro energy scales. The impact of a nonlinear receiver affects all receivers connected to a common power grid [37,38]. Disturbances in energy flow affect the measured active power and the control method in power electronic converters of electromechanical systems [39].

For easier presentation of the problems presented in this article, the case of harmonic generation by the load (Figure 1) is omitted. This means that the harmonics in the circuit were transferred from the outside to the tested measuring point of the power network using a real voltage source.

In the case of electromechanical systems, it should be borne in mind that under certain circumstances, an induction machine may cause the generation of energy in the opposite direction. Such generation may result from nonlinear magnetization characteristics (in motor operation) or the operation of a frequency converter, which results in the generation of energy with higher harmonics. A change in the direction of energy flow of the first harmonic will occur in generator operation. Such disturbances negatively affect the operation of the power grid and the service life of this machine [2]. The appearance of subharmonics and interharmonics in the current supplying an induction machine results in deformation of the rotating magnetic field. Improving the power factor in such a system is a big challenge.

There are several power theories that allow the description of an electric circuit in terms of energy [42,43,44,45,46,47,48,49,50,51,52,53,54,55]. The most important are two theories: the first is the IEEE Standard 1459 [56,57], which is treated as a standard for measurements in electric circuits, and the second is the CPC theory [58,59,60,61,62,63,64,65,66,67,68,69,70], which precisely recognizes the individual current components and allows for the parameters of compensators to be determined.

There is great conflict in the scientific community between several factions recognizing particular theories. When looking objectively at known power theories, it is necessary to emphasize the advantages of each.

The IEEE Standard 1459, due to its simplicity and simplification, is a good and sufficient way to describe the energy in an electric circuit for billing purposes. Due to the way in which components dependent on physical phenomena are determined, the CPC theory is an excellent tool for compensation purposes, design purposes, detailed mathematical analyses, and considerations for improving the efficiency of a power system.

The remarks on the CPC theory concerning the incorrectness of the considerations may be considered outdated over time as work on the detailed description is still in progress, and the results obtained bring us closer to honoring a universal power theory that does not arouse any controversy. Thanks to the way in which analyses are conducted in this theory, individual components of the current are added to the general mathematical description—analogously to puzzle pieces creating a unified graphic image. If at present day the CPC theory has not taken into account some electrical interaction in the circuit, one can be sure that in the future, an additional component will appear, which will be a new puzzle piece in the picture of power theory.

When performing circuit analysis using the CPC power theory, one may hit a dark area that has not yet been considered. This leads to misunderstandings and controversies regarding the entire CPC theory. So, it is important to find these unknown areas to learn the correct mathematical modeling of various electrical circuits.

The CPC theory is a method that allows for a broad view of all phenomena occurring in electrical circuits [71,72,73,74]. Thanks to continuous development, it provides the possibility of modeling various types of circuits. The first publications from the late 20th century provided insights into simple single-phase circuits. In subsequent stages, considerations took into account increasingly complex situations. Monitoring the progress of the CPC theory and pointing out ambiguities is beneficial because it allows for its development.

Is the current state of knowledge in CPC theory sufficient? Unfortunately not. During mathematical analyses of AC circuits, one can still come across problems that have not yet been solved. Therefore, it is important to continue research in this area. This article proposes a solution to several problems found. However, this does not mean that the topic is fully understood and that further research will no longer be needed.

The first few sections of this article point out several ambiguities that arise during mathematical analyses. Section 5 presents a revision of the CPC theory for a three-wire circuit connecting an asymmetric three-phase source to an unbalanced load.

2. Shift in Vectors by 90°

The voltage measurement [75,76,77,78] in a three-wire system is made with respect to an artificial zero (Figure 1). This circuit is designed in such a way that the three-phase voltage vector does not have a zero symmetrical component. This is possible when the three measuring channels of the voltmeters have the same internal impedances, Z_V. In practice, the Z_V value is many times greater than the source and receiver impedances in the tested system, i.e., the Z_V value does not affect the obtained measurements. The current is measured non-invasively using current transformers in the circuit powering a three-phase receiver. This means that the internal impedances Z_A of current meters are many times smaller than the source and receiver impedances. By measuring the instantaneous values of voltages and currents and using the FFT transform, amplitudes and phase shifts are separately obtained for each harmonic. The condition is that the current and voltage waveforms are periodic. When making measurements in a real measuring system, we only have access to the line connecting the source with the receiver (Figure 1). The source and receiver are unknown. As a result of measuring the instantaneous values of current and voltage and performing the FFT transformation, three-phase vectors are obtained in the form of

$$\begin{gathered} u_n=\left[\begin{array}{c}{u}_{\mathrm{R},n}\\ u_{\mathrm{S},n}\\ u_{\mathrm{T},n}\end{array}\right]=\sqrt{2}\Re e\left[\begin{array}{c}{\underset{¯}{U}}_{\mathrm{R},n}\\ {\underset{¯}{U}}_{\mathrm{S},n}\\ {\underset{¯}{U}}_{\mathrm{T},n}\end{array}\right]e^{jn{\omega }_{1}t}=\sqrt{2}\Re e\left\{{\underset{¯}{U}}_n{e}^{jn{\omega }_{1}t}\right\},u={\displaystyle \sum _n{u}_n}, \\ {i}_n=\left[\begin{array}{c}{i}_{\mathrm{R},n}\\ i_{\mathrm{S},n}\\ i_{\mathrm{T},n}\end{array}\right]=\sqrt{2}\Re e\left[\begin{array}{c}{\underset{¯}{I}}_{\mathrm{R},n}\\ {\underset{¯}{I}}_{\mathrm{S},n}\\ {\underset{¯}{I}}_{\mathrm{T},n}\end{array}\right]e^{jn{\omega }_{1}t}=\sqrt{2}\Re e\left\{{\underset{¯}{I}}_n{e}^{jn{\omega }_{1}t}\right\},i={\displaystyle \sum _n{i}_n}. \end{gathered}$$

(1)

Constant values of these elements can only be obtained in the case of continuous and periodic waveforms. So, this is the first and most important limitation that applies to most power theories.

When adopting the definitions of these vectors according to the CPC theory, it should be remembered that these vectors are shifted by 90° with respect to the other theories. In this case, the instantaneous values are based on the cosine function (2) and not the sine function. For example, for voltage, it would be

$$u=U_0+\sqrt{2}{\displaystyle \sum _{n=1}\left|{\underset{¯}{U}}_n\right|\cdot \cos \left(n{\omega }_{1}t+\arg \left\{{\underset{¯}{U}}_n\right\}\right)}.$$

(2)

It is known that the Fourier series coefficients a_n and b_n (3) determined in the period T are

$$a_n={\displaystyle \frac{2}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)\cos \left(n{\omega }_{1}t\right)dt},b_n={\displaystyle \frac{2}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)\sin \left(n{\omega }_{1}t\right)dt},$$

(3)

So, in CPC theory, these coefficients should be swapped as follows:

$$f\left(t\right)={\displaystyle \frac{a_0}{2}}+{\displaystyle \sum _{n=1}^{\infty }\left(b_n\cos \left(n{\omega }_{1}t\right)+a_n\sin \left(n{\omega }_{1}t\right)\right)}.$$

(4)

Phase shift is not a problem if it is taken into account in all results. In power systems, the cosine or sine function is used. Nevertheless, when comparing the results obtained between several theories, this should be kept in mind.

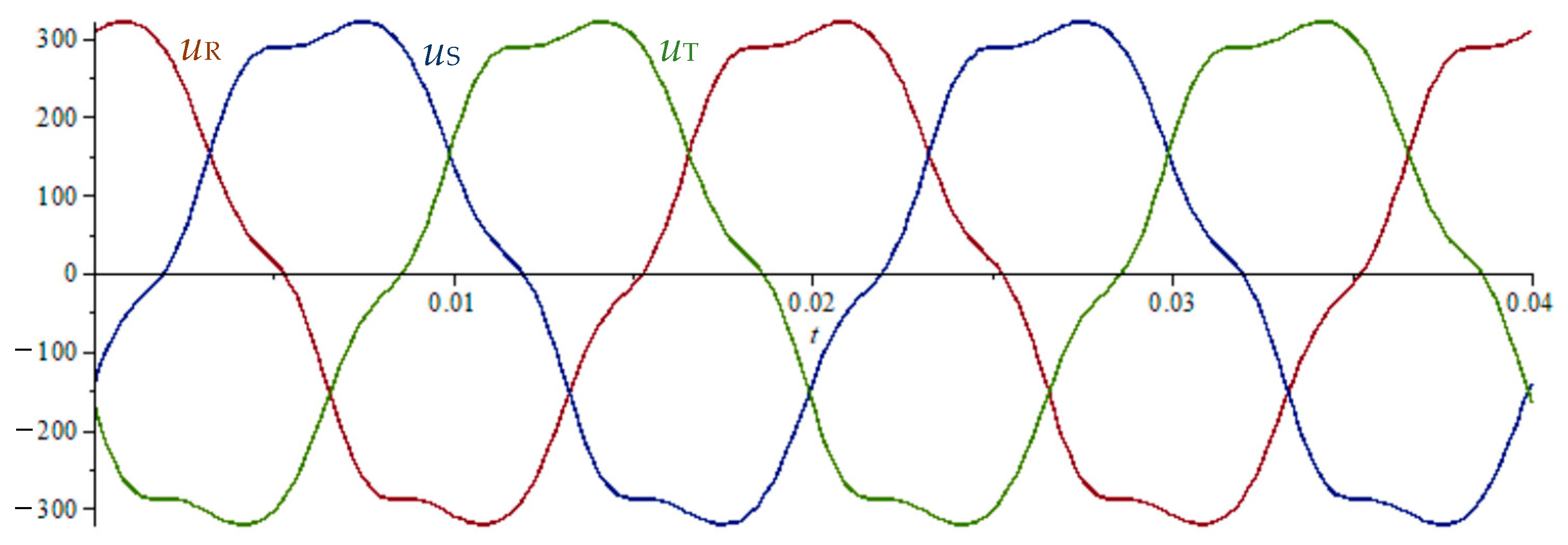
3. Problems with the Constant Voltage Component

The active component of current was proposed at the beginning of the 20th century by Prof. Fryze [79]. It makes physical sense for single- and three-phase circuits. As is known, the value of this component is related to the value of active power and the rms value of the voltage. For example, for single-phase circuits, the active component of the current is described by the following relations:

$$‖i_{\mathrm{a}}‖=‖u‖\cdot G_{\mathrm{e}}={\displaystyle \frac{P}{‖u‖}},i_{\mathrm{a}}=G_{\mathrm{e}}u=G_{\mathrm{e}}{U}_0+\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}^N{G}_{\mathrm{e}}{\underset{¯}{U}}_n{e}^{jn{\omega }_{1}t}}\right\}.$$

(5)

It can be seen in (5) that the value of the i_a component and the value of the power P depend on the equivalent conductance G_e. Therefore, G_e is a key parameter in determining the active component, and the value of this parameter is determined from the following relationship:

$$G_{\mathrm{e}}=P/{‖u‖}^2.$$

(6)

According to the accepted standards, in single-phase systems, the effective value of the voltage is equal:

$$‖u‖=\sqrt{U_0^2+{\displaystyle \sum _{n=1}{\left|{\underset{¯}{U}}_n\right|}^2}}.$$

(7)

Let us note that the rms value of voltage (7) is influenced by all components of this voltage that create the instantaneous value u(t) (e.g., for a three-phase system, it is expressed in Formula (2)). The effective value of the voltage depends on the subsequent harmonics and the constant voltage component. Therefore, all of these voltage components contribute to the power P and the equivalent conductance G_e (6).

Example 1.

Let us assume a single-phase receiver constructed from a series connection of a resistor R = 1 Ω and a capacitor C, which, for a pulsation of ω₁ = 1 rad/s, has a reactance of X_C = 1 Ω. This circuit is powered by voltage, $u=1+\sqrt{2}\left[\cos \left({\omega }_{1}t\right)+\cos \left(3{\omega }_{1}t\right)\right]\mathrm{V}.$

According to (7), the rms value of voltage is $‖u‖=\sqrt{U_0^2+U_1^2+U_3^2}=\sqrt{3}\mathrm{V}$. Active power is the power lost in the resistance R, where for the nth component, it is $P_n={\left|{\underset{¯}{I}}_n\right|}^{2}R$, while the current is ${\underset{¯}{I}}_n={\displaystyle \frac{U_n}{R-j\frac{X_C}{n{\omega }_1}}}$.

The current values are obtained, $\underset{¯}{I}=\left[0;0.5+j0.5;0.9+j0.3\right]\mathrm{A},$ and the powers are $P=\left[0;0.5;0.9\right]\mathrm{W}.$ The total active power is equal, $P={\displaystyle \sum _n{P}_n=1.4\mathrm{W}}$, i.e., the equivalent conductance (6) is G_e = 0.47 S.

In a series RC connection, the voltage component U₀ has no energetic effect and does not affect the value of the current flowing through these elements. The direct current component is equal to I₀ = 0 and does not depend on the value of R.

The definition of the effective value (7) is standardized and should not be modified. It corresponds to the value presented by measuring instruments. However, knowing that the product of the effective value of voltage and current is used for power calculations, when the effective value of voltage (7) is taken into account in the RC circuit, the result will be incorrect. The value of power in an RC circuit is influenced only by those voltage components that produce an energy effect. The numerator in Equation (6) can be easily determined as the sum of active powers for individual harmonics. However, the value of the denominator of this equation must depend only on those harmonics that affect the value of the power P.

The correct voltage value in Formula (6) must be defined as a parameter that produces a certain effect in the circuit, so in this example, it should be determined based on components U₁ and U₃ (8).

$$U_{eff}\stackrel{def}{=}\sqrt{{\displaystyle \sum _{n\in H}{U}_n^2}},$$

(8)

where H is the set of harmonics for which there is a plexus between the current I_H and the voltage U_H components, i.e., in this example, H = {1, 3}.

Equation (6) goes to the following notation:

$$G_{\mathrm{e}}=P/U_{eff}^2$$

(9)

The voltage value determined from (8) is $U_{eff}=\sqrt{2}\mathrm{V}$, which means that the equivalent conductance (9) is G_e = 0.7 S. By determining the rms value of the active current component according to (5) and using (7), we obtain $‖i_{\mathrm{a}}‖=1.4/\sqrt{3}=0.81\mathrm{A},$ and after using (8), the value of this current is $‖i_{\mathrm{a}}‖=1.4/\sqrt{2}=0.99\mathrm{A}$.

For three-phase circuits, the CPC theory also determines the equivalent conductance [13,14,15,16,17,18,19]. The DC component of voltage in three-phase circuits is practically non-existent. In three-phase circuits, the definition of the rms value of the three-phase voltage is

$$‖u‖=\sqrt{{‖u_{\mathrm{R}}‖}^2+{‖u_{\mathrm{S}}‖}^2+{‖u_{\mathrm{T}}‖}^2}.$$

(10)

The rms values of the L-phase voltages, where L = {R, S, T}, are also determined from (7). If there are components of the voltage vector that do not participate in the current flow, the equivalent conductance G_e and the active component of the three-phase current $‖i_{\mathrm{a}}‖$ will be determined incorrectly. Therefore, special attention should be paid to mathematical relationships.

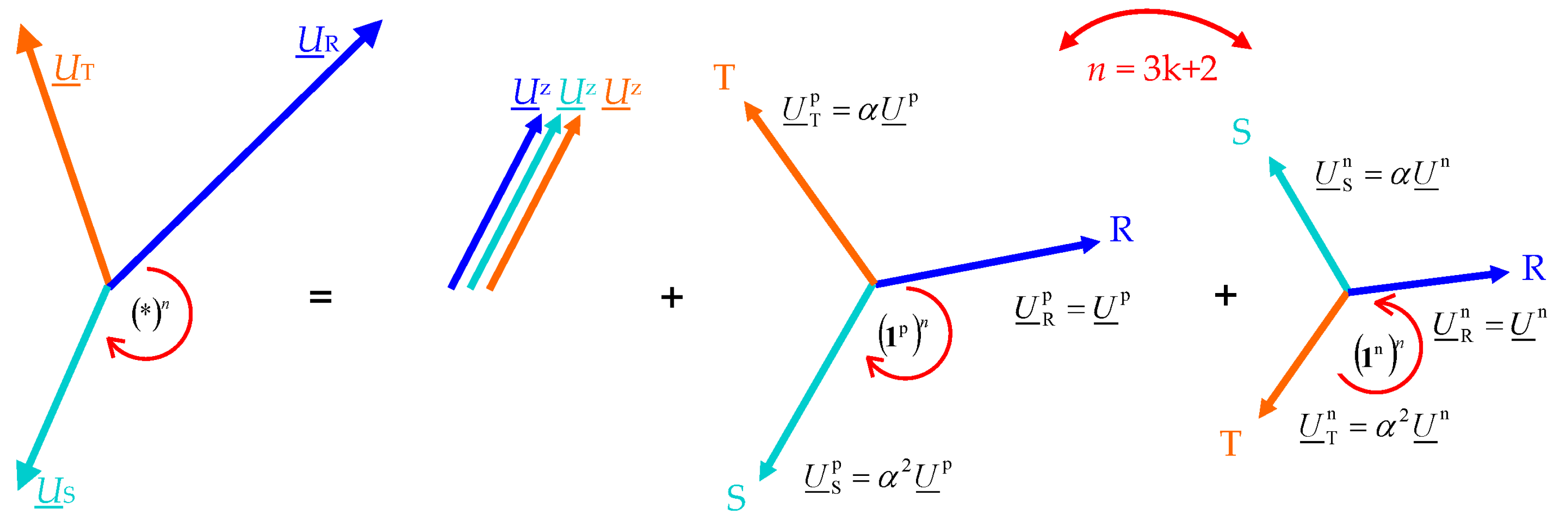
4. Notes on Three-Phase Current Components Using Fortescue Transformation

In three-phase systems, when there is no symmetry in the power source, symmetrical voltage components with positive U^p, negative Uⁿ, and zero U^z sequences are used to build mathematical relationships [80,81,82,83]. They are determined from (12), i.e., using three-phase symmetrical unit vectors of the positive 1^p, negative 1ⁿ, and zero 1^z sequences, defined as

$${\mathbf{1}}^{\mathrm{p}}=\left[\begin{array}{c}1\\ {\alpha }^2\\ \alpha \end{array}\right],{\mathbf{1}}^{\mathrm{n}}=\left[\begin{array}{c}1\\ \alpha \\ {\alpha }^2\end{array}\right],{\mathbf{1}}^{\mathrm{z}}=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].$$

(11)

where α is the rotation operator which is $\alpha =e^{j{120}^{\mathrm{o}}}=e^{j{\displaystyle \frac{2\pi }{3}}}$.

$$\left[\begin{array}{c}{\underset{¯}{U}}^{\mathrm{z}}\\ {\underset{¯}{U}}^{\mathrm{p}}\\ {\underset{¯}{U}}^{\mathrm{n}}\end{array}\right]={\displaystyle \frac{1}{3}}\left[\begin{array}{ccc}1& 1& 1\\ 1& \alpha & {\alpha }^2\\ 1& {\alpha }^2& \alpha \end{array}\right]\cdot \left[\begin{array}{c}{\underset{¯}{U}}_{\mathrm{R}}\\ {\underset{¯}{U}}_{\mathrm{S}}\\ {\underset{¯}{U}}_{\mathrm{T}}\end{array}\right].$$

(12)

From this point on, mathematical operations are performed individually on the crms values U^p, Uⁿ, and U^z as for a symmetric source. The transformation (12) is performed separately for each harmonic.

4.1. The Definition of Three-Phase Symmetrical Voltage in the Case of Multiple Harmonics

In three-phase unbalanced periodic and non-sinusoidal voltage waveforms for the nth harmonic (Figure 1), there is no symmetrical voltage component of zero sequence, and the following is true:

$${\underset{¯}{U}}_{\mathrm{R},n}+{\underset{¯}{U}}_{\mathrm{S},n}+{\underset{¯}{U}}_{\mathrm{T},n}=0,$$

(13)

In the case of symmetry, for each nth harmonic, the phase shift is equal to α or α². This can be written as an equation:

$$\begin{gathered} u_{\mathrm{L}}=\sqrt{2}{\displaystyle \sum _{n=1}\left|{\underset{¯}{U}}_{\mathrm{L},n}\right|\cdot \cos \left[n\left({\omega }_{1}t+s_{\mathrm{L}}+{\varphi }_n\right)\right]}=\sqrt{2}{\displaystyle \sum _{n=1}\left|{\underset{¯}{U}}_{\mathrm{L},n}\right|\cdot \cos \left(n{\omega }_{1}t+\arg \left\{{\underset{¯}{U}}_{\mathrm{L},n}\right\}\right)}, \\ {u}_{\mathrm{L}}=\sqrt{2}{\displaystyle \sum _{n=1}\Re e\left\{{\underset{¯}{U}}_{\mathrm{L},n}\cdot e^{jn{\omega }_{1}t}\right\}}, \end{gathered}$$

(14)

where L—the phase symbol, L = {R, S, T};

s_L—the phase shift equal to $s_{\mathrm{L}}=\left[0,{\displaystyle \frac{-2\pi }{3}},{\displaystyle \frac{2\pi }{3}}\right]$, meaning $s_{\mathrm{R}}=0$, $s_{\mathrm{S}}=\arg \left\{{\alpha }^2\right\}$, and $s_{\mathrm{T}}=\arg \left\{\alpha \right\}$;

φ_n—the phase shift between the current and voltage for the nth harmonic.

In (14) it can be seen that the argument of the complex number U_L,n contains the rotation vector α, the phase shift angle φ_n, and the nth harmonic order:

$$\arg \left\{{\underset{¯}{U}}_{\mathrm{L},n}\right\}\stackrel{\mathrm{def}}{=}n\left(s_{\mathrm{L}}+{\varphi }_n\right).$$

(15)

Example 2.

For the instantaneous voltage value in R phase, $u_{\mathrm{R}}=\sqrt{2}\cdot \Re e\left\{230e^{j{\omega }_{1}t}+\right.\left.20e^{j5\left({\omega }_{1}t+2\right)}+5e^{j7{\omega }_{1}t}\right\}\mathrm{V}$, it can be written in the time domain as follows: $u_{\mathrm{R}}=\sqrt{2}\cdot \left\{230\cos \left({\omega }_{1}t\right)+\right.\left.20\cos \left(5\left({\omega }_{1}t+2\right)\right)+5\cos \left(7{\omega }_{1}t\right)\right\}\mathrm{V}$.

In the case of symmetry, according to (14), the voltage curves in the remaining phases are

$$\begin{gathered} u_{\mathrm{S}}=\sqrt{2}\cdot \left\{230\cos \left({\omega }_{1}t-{\displaystyle \frac{2\pi }{3}}\right)+\right.\left.20\cos \left(5\left({\omega }_{1}t-{\displaystyle \frac{2\pi }{3}}+2\right)\right)+5\cos \left(7\left({\omega }_{1}t-{\displaystyle \frac{2\pi }{3}}\right)\right)\right\}\mathrm{V}, \\ {u}_{\mathrm{T}}=\sqrt{2}\cdot \left\{230\cos \left({\omega }_{1}t+{\displaystyle \frac{2\pi }{3}}\right)+\right.\left.20\cos \left(5\left({\omega }_{1}t+{\displaystyle \frac{2\pi }{3}}+2\right)\right)+5\cos \left(7\left({\omega }_{1}t+{\displaystyle \frac{2\pi }{3}}\right)\right)\right\}\mathrm{V}. \end{gathered}$$

The graphical waveforms of these voltages are presented in Figure 2.

In (14), the separation of the nth harmonic order and phase shifts, s_L and φ_n, simplifies the mathematical analysis of three-phase waveforms.

4.2. Using Fortescue Transformation in the Case of Multiple Harmonics

In the case of sinusoidal waveforms, the three-phase asymmetrical source is replaced by the sum of three symmetrical sources. Taking the phase R as the reference phase, from (12), we obtain

$$\underset{¯}{U}={\underset{¯}{U}}^{\mathrm{z}}+{\underset{¯}{U}}^{\mathrm{p}}+{\underset{¯}{U}}^{\mathrm{n}}=1^{\mathrm{z}}{\underset{¯}{U}}^{\mathrm{z}}+1^{\mathrm{p}}{\underset{¯}{U}}^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}^{\mathrm{n}}.$$

(16)

where $\underset{¯}{U}={\left[\begin{array}{ccc}{\underset{¯}{U}}_{\mathrm{R}}& {\underset{¯}{U}}_{\mathrm{S}}& {\underset{¯}{U}}_{\mathrm{T}}\end{array}\right]}^T$.

Similarly to (16), in reference [78], for non-sinusoidal periodic waveforms for the nth harmonic, the following relation is used:

$${\underset{¯}{U}}_n={\underset{¯}{U}}_n^{\mathrm{z}}+{\underset{¯}{U}}_n^{\mathrm{p}}+{\underset{¯}{U}}_n^{\mathrm{n}}=1^{\mathrm{z}}\cdot {\underset{¯}{U}}_n^{\mathrm{z}}+1^{\mathrm{p}}\cdot {\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}\cdot {\underset{¯}{U}}_n^{\mathrm{n}}.$$

(17)

So far, in the case of periodic non-sinusoidal waveforms, the values of symmetrical components have been determined in the same way as for sinusoidal circuits—i.e., using transformation (12). For waveforms consisting of many harmonics, Formula (15) is valid. It follows that the turnover factor α is multiplied n times. Therefore, Equation (12) for the nth harmonic should look like the below:

$$\left[\begin{array}{c}{\underset{¯}{U}}_n^{\mathrm{z}}\\ {\underset{¯}{U}}_n^{\mathrm{p}}\\ {\underset{¯}{U}}_n^{\mathrm{n}}\end{array}\right]\stackrel{\mathrm{def}}{=}{\displaystyle \frac{1}{3}}\left[\begin{array}{ccc}1& 1& 1\\ 1& {\alpha }^n& {\alpha }^{2n}\\ 1& {\alpha }^{2n}& {\alpha }^n\end{array}\right]\cdot \left[\begin{array}{c}{\underset{¯}{U}}_{\mathrm{R},n}\\ {\underset{¯}{U}}_{\mathrm{S},n}\\ {\underset{¯}{U}}_{\mathrm{T},n}\end{array}\right],$$

(18)

while the inverse transformation is described by the following relationship:

$$\left[\begin{array}{c}{\underset{¯}{U}}_{\mathrm{R},n}\\ {\underset{¯}{U}}_{\mathrm{S},n}\\ {\underset{¯}{U}}_{\mathrm{T},n}\end{array}\right]\stackrel{\mathrm{def}}{=}\left[\begin{array}{ccc}1& 1& 1\\ 1& {\alpha }^{2n}& {\alpha }^n\\ 1& {\alpha }^n& {\alpha }^{2n}\end{array}\right]\cdot \left[\begin{array}{c}{\underset{¯}{U}}_n^{\mathrm{z}}\\ {\underset{¯}{U}}_n^{\mathrm{p}}\\ {\underset{¯}{U}}_n^{\mathrm{n}}\end{array}\right].$$

(19)

The new vectors $1_n^{\mathrm{p}}$ and $1_n^{\mathrm{n}}$ arise after raising the vectors shown in (11) to the nth power:

$${\mathbf{1}}_n^{\mathrm{p}}\stackrel{\mathrm{def}}{=}{\left({\mathbf{1}}^{\mathrm{p}}\right)}^n=\left[\begin{array}{c}1\\ {\alpha }^{2\cdot n}\\ {\alpha }^n\end{array}\right],{\mathbf{1}}_n^{\mathrm{n}}\stackrel{\mathrm{def}}{=}{\left({\mathbf{1}}^{\mathrm{n}}\right)}^n=\left[\begin{array}{c}1\\ {\alpha }^n\\ {\alpha }^{2\cdot n}\end{array}\right].$$

(20)

The coefficients shown in (20) were called multiplied three-phase unit vectors.

When determining symmetric components using Fortescue transform in the presence of multiple harmonics, it is natural to raise the rotation factor α to the nth power. However, there is no formal note in the literature enabling such a transformation. Using the relationship between (18) and (19) is helpful in this case.

So far, the mathematical methods presented in [55] partially solved this problem by introducing additional vectors dependent on the nth harmonic. For example, the CPC theory [15,24] defines a coefficient β that depends on n and then multiplies it by the rotation vector α.

Example 3.

In the three-wire line from Figure 1, where the relationship ${\underset{¯}{U}}_{\mathrm{R},n}+{\underset{¯}{U}}_{\mathrm{S},n}+{\underset{¯}{U}}_{\mathrm{T},n}=0$ is valid, the following voltage values were measured:

$$\begin{array}{l}{u}_{\mathrm{R}}=\sqrt{2}\cdot \left\{300\sin \left({\omega }_{1}t\right)+\right.\left.30\sin \left(5{\omega }_{1}t\right)+3\sin \left(9{\omega }_{1}t\right)\right\}\mathrm{V},\\ u_{\mathrm{S}}=\sqrt{2}\cdot \left\{250\sin \left({\omega }_{1}t+s_{\mathrm{S}}\right)+\right.\left.25\sin \left(5\left({\omega }_{1}t+s_{\mathrm{S}}\right)\right)+2\sin \left(9\left({\omega }_{1}t+s_{\mathrm{S}}\right)\right)\right\}\mathrm{V},\\ u_{\mathrm{T}}=\sqrt{2}\cdot \left\{50\sqrt{31}\sin \left({\omega }_{1}t+{128.95}^{\mathrm{o}}\right)+\right.\left.5\sqrt{31}\sin \left(5{\omega }_{1}t-{128.95}^{\mathrm{o}}\right)+5\sin \left(9{\omega }_{1}t+{180}^{\mathrm{o}}\right)\right\}\mathrm{V}.\end{array}$$

(21)

The symmetric components (17) determined from (12) give the solution in the following form:

$$\begin{array}{l}{\underset{¯}{U}}_n^{\mathrm{z}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+{\underset{¯}{U}}_{\mathrm{S},n}+{\underset{¯}{U}}_{\mathrm{T},n}\right),\\ {\underset{¯}{U}}_n^{\mathrm{p}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+\alpha {\underset{¯}{U}}_{\mathrm{S},n}+{\alpha }^2{\underset{¯}{U}}_{\mathrm{T},n}\right),\\ {\underset{¯}{U}}_n^{\mathrm{n}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+{\alpha }^2{\underset{¯}{U}}_{\mathrm{S},n}+\alpha {\underset{¯}{U}}_{\mathrm{T},n}\right).\end{array}$$

(22)

After substituting the numerical data, we get

$$\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{p}}\\ {\underset{¯}{U}}_5^{\mathrm{p}}\\ {\underset{¯}{U}}_9^{\mathrm{p}}\end{array}\right]=\left[\begin{array}{c}275+j{\displaystyle \frac{25\sqrt{3}}{3}}\\ {\displaystyle \frac{5}{2}}+j{\displaystyle \frac{5\sqrt{3}}{6}}\\ {\displaystyle \frac{3}{2}}+j{\displaystyle \frac{7\sqrt{3}}{6}}\end{array}\right],\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{n}}\\ {\underset{¯}{U}}_5^{\mathrm{n}}\\ {\underset{¯}{U}}_9^{\mathrm{n}}\end{array}\right]=\left[\begin{array}{c}25-j{\displaystyle \frac{25\sqrt{3}}{3}}\\ {\displaystyle \frac{55}{2}}-j{\displaystyle \frac{5\sqrt{3}}{6}}\\ {\displaystyle \frac{3}{2}}-j{\displaystyle \frac{7\sqrt{3}}{6}}\end{array}\right],\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{z}}\\ {\underset{¯}{U}}_5^{\mathrm{z}}\\ {\underset{¯}{U}}_9^{\mathrm{z}}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right].$$

(23)

The same components determined from (19) give the following solution:

$$\begin{array}{l}{\underset{¯}{U}}_n^{\mathrm{z}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+{\underset{¯}{U}}_{\mathrm{S},n}+{\underset{¯}{U}}_{\mathrm{T},n}\right),\\ {\underset{¯}{U}}_n^{\mathrm{p}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+{\alpha }^n{\underset{¯}{U}}_{\mathrm{S},n}+{\alpha }^{2n}{\underset{¯}{U}}_{\mathrm{T},n}\right),\\ {\underset{¯}{U}}_n^{\mathrm{n}}={\displaystyle \frac{1}{3}}\left({\underset{¯}{U}}_{\mathrm{R},n}+{\alpha }^{2n}{\underset{¯}{U}}_{\mathrm{S},n}+{\alpha }^n{\underset{¯}{U}}_{\mathrm{T},n}\right),\end{array}$$

(24)

which, in this example, gives the following values:

$$\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{p}}\\ {\underset{¯}{U}}_5^{\mathrm{p}}\\ {\underset{¯}{U}}_9^{\mathrm{p}}\end{array}\right]=\left[\begin{array}{c}275+j{\displaystyle \frac{25\sqrt{3}}{3}}\\ {\displaystyle \frac{55}{2}}-j{\displaystyle \frac{5\sqrt{3}}{6}}\\ 0\end{array}\right],\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{n}}\\ {\underset{¯}{U}}_5^{\mathrm{n}}\\ {\underset{¯}{U}}_9^{\mathrm{n}}\end{array}\right]=\left[\begin{array}{c}25-j{\displaystyle \frac{25\sqrt{3}}{3}}\\ {\displaystyle \frac{5}{2}}+j{\displaystyle \frac{5\sqrt{3}}{6}}\\ 0\end{array}\right],\left[\begin{array}{c}{\underset{¯}{U}}_1^{\mathrm{z}}\\ {\underset{¯}{U}}_5^{\mathrm{z}}\\ {\underset{¯}{U}}_9^{\mathrm{z}}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right].$$

(25)

Comparing solutions (23) and (25), it should be noted that differences appear when n > 1. In practice, when n = 3k + 2 (where k is a natural number k ∈ {N₊}), the positive ${\underset{¯}{U}}_n^{\mathrm{p}}$ and negative ${\underset{¯}{U}}_n^{\mathrm{n}}$ symmetric components are swapped (Figure 3).

The appearance of non-zero ${\underset{¯}{U}}_9^{\mathrm{p}}$ and ${\underset{¯}{U}}_9^{\mathrm{n}}$ components in Equation (23) also indicates an incorrect transformation. When the equation ${\underset{¯}{U}}_{\mathrm{R},n}+{\underset{¯}{U}}_{\mathrm{S},n}+{\underset{¯}{U}}_{\mathrm{T},n}=0$ is satisfied, the appearance of zero-order harmonics (for n = 3k) is unnatural. In the functions shown in (21), in real systems, the amplitude of the ninth harmonic cannot be different from zero. This translates into zero values of a symmetrical component of the zero sequence ${\underset{¯}{U}}_n^{\mathrm{z}}$ for any nth harmonic.

5. Revised CPC Theory Definitions

The introduction of a correction to the decomposition into symmetrical components for periodic non-sinusoidal waveforms results in a different mathematical notation for electrical quantities for three-phase systems.

The vector of the supply voltage u as referenced to an artificial zero of the circuit (Figure 4) can be decomposed into symmetrical components of the positive and negative sequences:

$$u={\displaystyle \sum _n{u}_n}=\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}\left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}}\right\}=u^{\mathrm{p}}+u^{\mathrm{n}}.$$

(26)

Symbols ${\underset{¯}{U}}_n^{\mathrm{p}}$ and ${\underset{¯}{U}}_n^{\mathrm{n}}$ in (26) denote the crms values of the symmetrical components of the nth order supply voltage harmonic with positive and negative sequences, respectively. They are

$$\left[\begin{array}{c}{\underset{¯}{U}}_n^{\mathrm{p}}\\ {\underset{¯}{U}}_n^{\mathrm{n}}\end{array}\right]={\displaystyle \frac{1}{3}}\left[\begin{array}{ccc}1& {\alpha }^n& {\alpha }^{2n}\\ 1& {\alpha }^{2n}& {\alpha }^n\end{array}\right]\cdot \left[\begin{array}{c}{\underset{¯}{U}}_{\mathrm{R},n}\\ {\underset{¯}{U}}_{\mathrm{S},n}\\ {\underset{¯}{U}}_{\mathrm{T},n}\end{array}\right].$$

(27)

The three-phase rms value of the supply voltage, equal to the root of the sum of the squares of the effective values of the line voltages, is

$$‖u‖=\sqrt{{\displaystyle \sum _{\mathrm{L}=\mathrm{R},\mathrm{S},\mathrm{T}}{‖u_{\mathrm{L}}‖}^2}},\mathrm{where}‖u_{\mathrm{L}}‖=\sqrt{{\displaystyle \sum _{n=1}{\left|{\underset{¯}{U}}_{\mathrm{L},n}\right|}^2}}.$$

(28)

The load in Figure 5 is equivalent with respect to the active power P to a balanced resistive load of conductance G_b:

$$G_{\mathrm{b}}={\displaystyle \frac{P}{{‖u‖}^2}}.$$

(29)

The current flowing through such an equivalent load is called the active current and is as follows:

$$i_{\mathrm{a}}=\left[\begin{array}{c}{i}_{\mathrm{Ra}}\\ i_{\mathrm{Sa}}\\ i_{\mathrm{Ta}}\end{array}\right]=G_{\mathrm{b}}u=\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}{G}_{\mathrm{b}}\left(\underset{{\underset{¯}{U}}_n^{\mathrm{p}}}{\underbrace{1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}}}+\underset{{\underset{¯}{U}}_n^{\mathrm{n}}}{\underbrace{1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}}}\right)\cdot e^{jn{\omega }_{1}t}}\right\},‖i_{\mathrm{a}}‖=G_{\mathrm{b}}\cdot ‖u‖.$$

(30)

As a result of calculating Equation (30), we obtain the same form as in the previous articles that did not take into account the multiplied vector in (27) because the ${\underset{¯}{U}}_n^{\mathrm{p}}$ and ${\underset{¯}{U}}_n^{\mathrm{n}}$ components are swapped—which does not affect the result in the case of their sum. However, to improve readability, the elementary division between these components should be maintained.

The load for each harmonic has active and reactive powers. For the nth order harmonic, they are as follows:

$$\begin{gathered} P_n=\Re e\left\{{\underset{¯}{U}}_n^T\cdot {\underset{¯}{I}}_n^{*}\right\}=\Re e\left\{{\underset{¯}{U}}_{\mathrm{R},n}{\underset{¯}{I}}_{\mathrm{R},n}^{*}+{\underset{¯}{U}}_{\mathrm{S},n}{\underset{¯}{I}}_{\mathrm{S},n}^{*}+{\underset{¯}{U}}_{\mathrm{T},n}{\underset{¯}{I}}_{\mathrm{T},n}^{*}\right\}, \\ {Q}_n=\Im m\left\{{\underset{¯}{U}}_n^T\cdot {\underset{¯}{I}}_n^{*}\right\}. \end{gathered}$$

(31)

When for the nth order harmonic, the load is unbalanced, it is useful to define the balanced admittance Y_b. This admittance is already symmetrical and depends on the voltage u_n, the active powers P_n, and the reactive powers Q_n, and it is as follows:

$${\underset{¯}{Y}}_{\mathrm{b},n}=G_{\mathrm{b},n}+j{B}_{\mathrm{b},n}={\displaystyle \frac{P_n-j{Q}_n}{{‖u_n‖}^2}}={\displaystyle \frac{{\underset{¯}{C}}_n^{*}}{{\displaystyle \sum _{\mathrm{L}=\mathrm{R},\mathrm{S},\mathrm{T}}{\left|{\underset{¯}{U}}_{\mathrm{L},n}\right|}^2}}}.$$

(32)

In definition (32), the symbol “C” was used instead of the symbol “S”. This is an intentional action by the authors of [78] to avoid confusing the complex power P_n + jQ_n with the apparent power S_n, which may also contain components other than only active and reactive power. These powers are shown in Figure 6.

The supply current of such an equivalent load consists of the active current (33) and the reactive current (34):

$$i_{\mathrm{a},n}=G_{\mathrm{b},n}{u}_n=\sqrt{2}\Re e\left\{G_{\mathrm{b},n}\left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}\right\},$$

(33)

$$i_{\mathrm{r},n}=\sqrt{2}\Re e\left\{j{B}_{\mathrm{b},n}\left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}\right\}.$$

(34)

The i_r current component appears in the load current because of the phase shift in the load current harmonics relative to the supply voltage harmonics. It can be considered as a reactive current component on the load, whose value is

$$i_{\mathrm{r}}={\displaystyle \sum _n{i}_{\mathrm{r},n}}=\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}j{B}_{\mathrm{b},n}\left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}}\right\}.$$

(35)

Y_b,n is the admittance of the equivalent balanced load for the nth order harmonic. In practice, the load may be unbalanced, so the nth order harmonic of the load current i_n may contain the unbalanced current component:

$$\begin{gathered} i_{\mathrm{u},n}=i_n-i_{\mathrm{b},n}=i_n-\left(i_{\mathrm{a},n}+i_{\mathrm{r},n}\right)=\sqrt{2}\Re e\left\{{\underset{¯}{I}}_n-{\underset{¯}{Y}}_{\mathrm{b},n}\left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}\right\}, \\ {i}_{\mathrm{u}}={\displaystyle \sum _{n=1}{i}_{\mathrm{u},n}}. \end{gathered}$$

(36)

In the case of the (33) component, the relation holds:

$${\displaystyle \sum _{n=1}{i}_{\mathrm{a},n}}\ne i_{\mathrm{a}}=G_{\mathrm{b}}{\displaystyle \sum _{n=1}{u}_n}.$$

(37)

The inequality (37) occurs when the conductance G_b,n for harmonic frequencies is different from the conductance G_b of the equivalent balanced load. The difference between these components is

$${\displaystyle \sum _{n=1}{i}_{\mathrm{a},n}}-i_{\mathrm{a}}=\sqrt{2}\Re e\left\{\left(G_{\mathrm{b},n}-G_{\mathrm{b}}\right)\cdot \left(1^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}+1^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)\cdot e^{jn{\omega }_{1}t}\right\}=i_{\mathrm{s}}.$$

(38)

The current i_s is called a scattered current component because conductances at harmonic frequencies G_b,n are usually scattered around the balanced conductance G_b, and the current i_s is the effect of this scattering.

The current of the load is presented as the sum of the specific components:

$$i=i_{\mathrm{a}}+i_{\mathrm{s}}+i_{\mathrm{r}}+i_{\mathrm{u}}.$$

(39)

Because of the association of these load currents’ components with physical phenomena in the load, these currents are referred to as the Currents’ Physical Components (CPCs). However, this does not mean that these currents exist physically as they are mathematical entities, and not physical ones.

Each of these currents is associated with a different physical phenomenon in the load. The active current i_a is related to the phenomenon of supplying active power P to the load. The scattered current i_s is related to the phenomenon of changing the equivalent conductance G_b,n with the harmonic order n. The reactive current i_r is related to the phenomenon of phase shift in the current relative to the supply voltage for the nth harmonic. The unbalanced current i_u is related to the load imbalance for the nth harmonic.

The correction introduced to the definitions presented so far in this article does not change the rms values of these components. Only the equations defined in the time domain change.

The situation becomes more complicated when the unbalanced current component is decomposed and the values of the compensator parameters are determined. In reference [61], the unbalanced current component was decomposed into two elements:

$$i_{\mathrm{u}}=i_{\mathrm{u}}^{\mathrm{p}}+i_{\mathrm{u}}^{\mathrm{n}}.$$

(40)

The rms values of both components depend on the division into positive and negative sequence components. When Equation (17) is taken into account, these components can be represented in the following forms:

$$i_{\mathrm{u}}^{\mathrm{p}}=\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}\left({\underset{¯}{Y}}_{\mathrm{d},n}{\underset{¯}{U}}_n^{\mathrm{p}}+{\underset{¯}{Y}}_{\mathrm{u},n}^{\mathrm{n}}{\underset{¯}{U}}_n^{\mathrm{n}}\right)1^{\mathrm{p}}{e}^{jn{\omega }_{1}t}}\right\},$$

(41)

$$i_{\mathrm{u}}^{\mathrm{n}}=\sqrt{2}\Re e\left\{{\displaystyle \sum _{n=1}\left({\underset{¯}{Y}}_{\mathrm{d},n}{\underset{¯}{U}}_n^{\mathrm{n}}+{\underset{¯}{Y}}_{\mathrm{u},n}^{\mathrm{p}}{\underset{¯}{U}}_n^{\mathrm{p}}\right)1^{\mathrm{n}}{e}^{jn{\omega }_{1}t}}\right\},$$

(42)

where, according to [61], the voltage asymmetry dependent admittance is

$${\underset{¯}{Y}}_{\mathrm{d},n}={\underset{¯}{Y}}_{\mathrm{e},n}-{\underset{¯}{Y}}_{\mathrm{b},n},$$

(43)

the equivalent admittance is

$${\underset{¯}{Y}}_{\mathrm{e},n}={\underset{¯}{Y}}_{\mathrm{ST},n}+{\underset{¯}{Y}}_{\mathrm{TR},n}+{\underset{¯}{Y}}_{\mathrm{RS},n},$$

(44)

and the unbalanced admittances are

$$\begin{gathered} {\underset{¯}{Y}}_{\mathrm{u},n}^{\mathrm{p}}=-\left({\underset{¯}{Y}}_{\mathrm{ST},n}+\alpha {\underset{¯}{Y}}_{\mathrm{TR},n}+{\alpha }^2{\underset{¯}{Y}}_{\mathrm{RS},n}\right), \\ {\underset{¯}{Y}}_{\mathrm{u},n}^{\mathrm{n}}=-\left({\underset{¯}{Y}}_{\mathrm{ST},n}+{\alpha }^2{\underset{¯}{Y}}_{\mathrm{TR},n}+\alpha {\underset{¯}{Y}}_{\mathrm{RS},n}\right). \end{gathered}$$

(45)

Admittances (43), (44), (45), and (32) depend on the admittance values of the three-phase load, while the rotation vector α acts in the same direction of rotation regardless of the harmonic order.

As a result of changing the values of the symmetrical voltage components ${\underset{¯}{U}}_n^{\mathrm{p}}$ and ${\underset{¯}{U}}_n^{\mathrm{n}}$, which should be determined from (27), the values of the current unbalanced components (41) and (42) will change. Defining these variables in a different way causes the instantaneous and rms values of both components to change, and the formulas determining the reactive compensator parameters must be re-developed.

6. Conclusions

The computational problems revealed in this article are important when performing mathematical analyses in electrical systems powered by sources with periodic non-sinusoidal waveforms.

• The 90° shift in vectors discussed in point 2 is important in the case of time-domain notation and when comparing calculation results with oscilloscope measurements. To deal with this problem, one can use relationship (4), or each of the determined numerical values in the time domain can be shifted by a constant angle of −90°.
• The problem shown in point 3 concerns a special case when components that do not participate in the transmission of the energy appear. An example is a situation when the load has a series capacitance, which, as is known, does not carry a DC component. In such a situation, Formula (8) should only be used for harmonics that are related to energetic interactions.
• The method of notation of three-phase waveforms, discussed in point 4, revealed the need to change the definition of symmetrical components (18) when the instantaneous values are described by periodic non-sinusoidal functions. Determining the symmetric components using multiplied three-phase unit vectors (20) improves the mathematical notation. This observation revealed the need to improve the development of algorithms determining the unbalanced components and parameters of reactive compensators. These issues should be considered in further research.

The first problem may only occur when comparing the calculation results with the measurements and should instead be treated as a failure of the obligation to use a unified system for noting expressions in the time domain. This problem may arise when comparing power theories in the domain of instantaneous values.

The second problem concerns cases based on the CPC theory. Only in this theory is the equivalent conductance G_e determined. In other theories, the calculation for the DC component in a circuit connected in series with the capacitance is naturally omitted.

The third problem only applies to the case when Fortescue transformation is used. The degree of error committed cannot be determined in a general way. It depends on the degree of asymmetry of the three-phase voltage and current. Moreover, without knowledge of the equations determining the compensator parameters, based on (18) and (19), it is impossible to estimate the performance metric.

In summary, the remarks quoted cause imprecision in the description only in specific situations and do not affect the general relations between theories. A comparison of power theories with respect to the problems discussed is therefore pointless and would not contribute any cognitive information to this article.

It should be noted that this article discussed simple circuits and imperfections in power theory. However, the problems discussed here also affect the mathematical descriptions of power systems on a macro scale. Therefore, the significance of the presented results has great cognitive value.

In the case of cooperation between the power grid and power electronic converters, the problems occurring in the power description are still unclear. The CPC theory is based on the assumption that all harmonics are multiples of the fundamental harmonic. In practice, the switching frequency of the keys in a power electronic converter is not related to the frequency of the fundamental harmonic.

Future research should consider the correctness of analyses in the case of subharmonics and interharmonics [84].