Co-Optimization of Market and Grid Stability in High-Penetration Renewable Distribution Systems with Multi-Agent
Abstract
1. Introduction
- A dynamic electricity price-driven multi-agent transaction model is developed, embedding network loss costs and voltage sensitivity into market mechanisms. This establishes a collaborative mechanism between economic objectives and grid security boundaries through price-guided energy storage dispatch sequences.
- A spatiotemporal response matrix is constructed for four vehicle types (taxis, buses, official vehicles, and private cars), creating a dynamic matching model between charging behavior characteristics and grid flexibility demands, and overcoming the rigidity of conventional homogeneous scheduling methods.
- A deep coupling interface is designed to integrate market signals with physical regulation, enabling the self-organized optimization of “source–grid–load–storage” resources across temporal price incentives and spatial reactive power coordination.
2. Multi-Agent Operation Model
2.1. DG Output Model
2.2. EV Load Model
3. Multi-Agent Optimal Operation Model in the Market Environment
3.1. DG Optimal Output Model in Market Environment
3.2. Price-Responsive EV Ordered Charging Optimization Model
3.2.1. Dynamic Adjustment Mechanism for Charging Time Windows
3.2.2. Differentiated Scheduling Model for Multi-Class EVs
4. Multi-Objective Reactive Power Optimization Model
4.1. Objective Function
4.2. Constraint Conditions
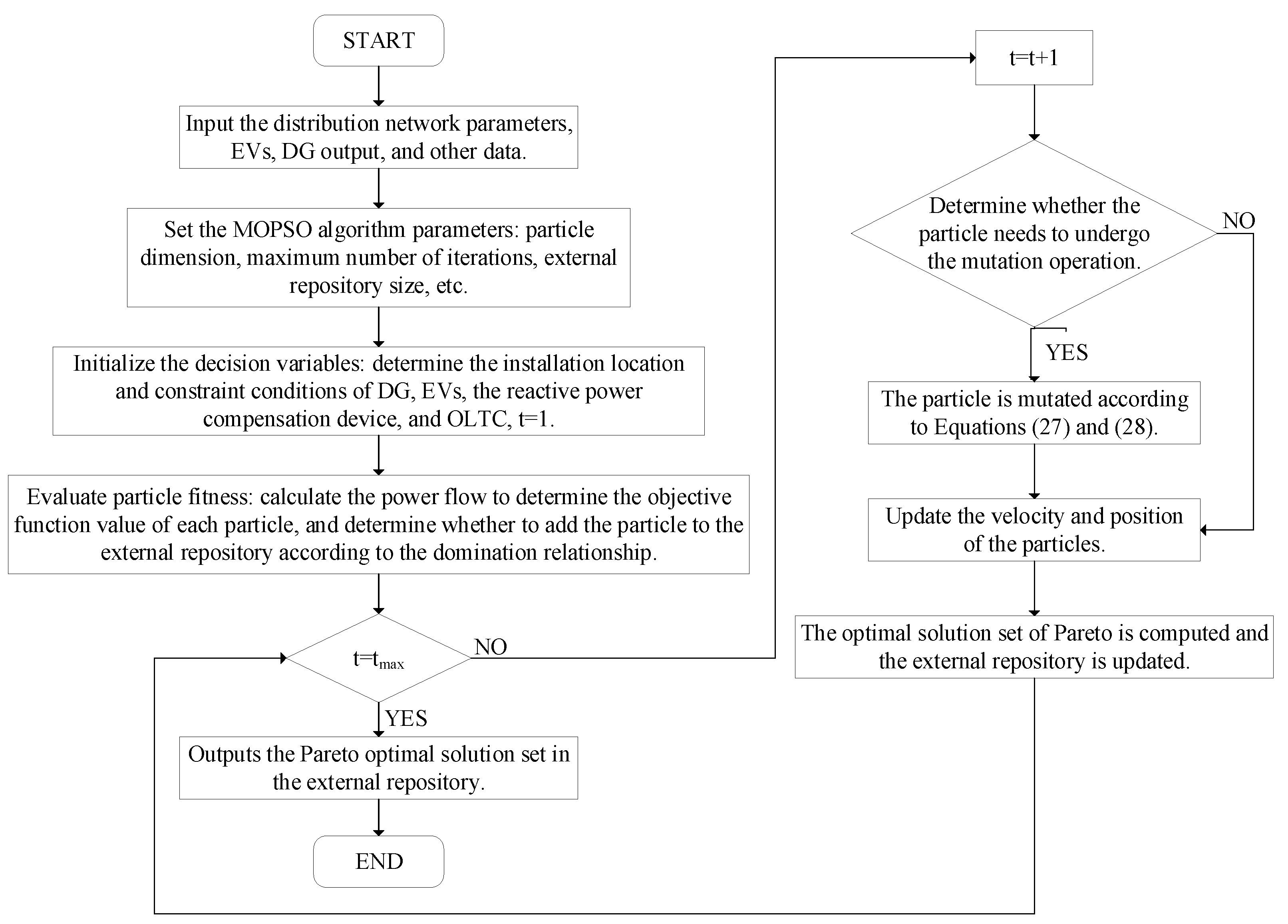
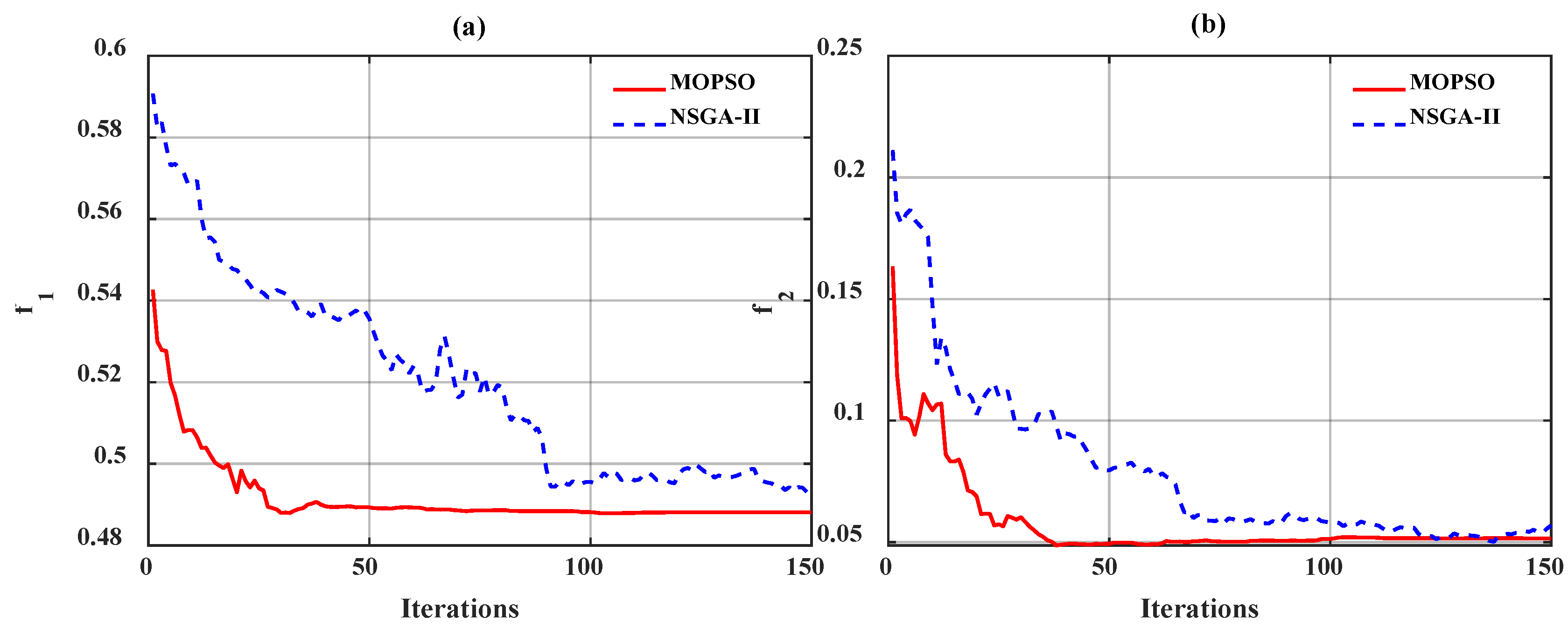
5. MOPSO Algorithm
5.1. Principle of the PSO Algorithm
5.2. Principle of the MOPSO Algorithm
6. Example Analysis
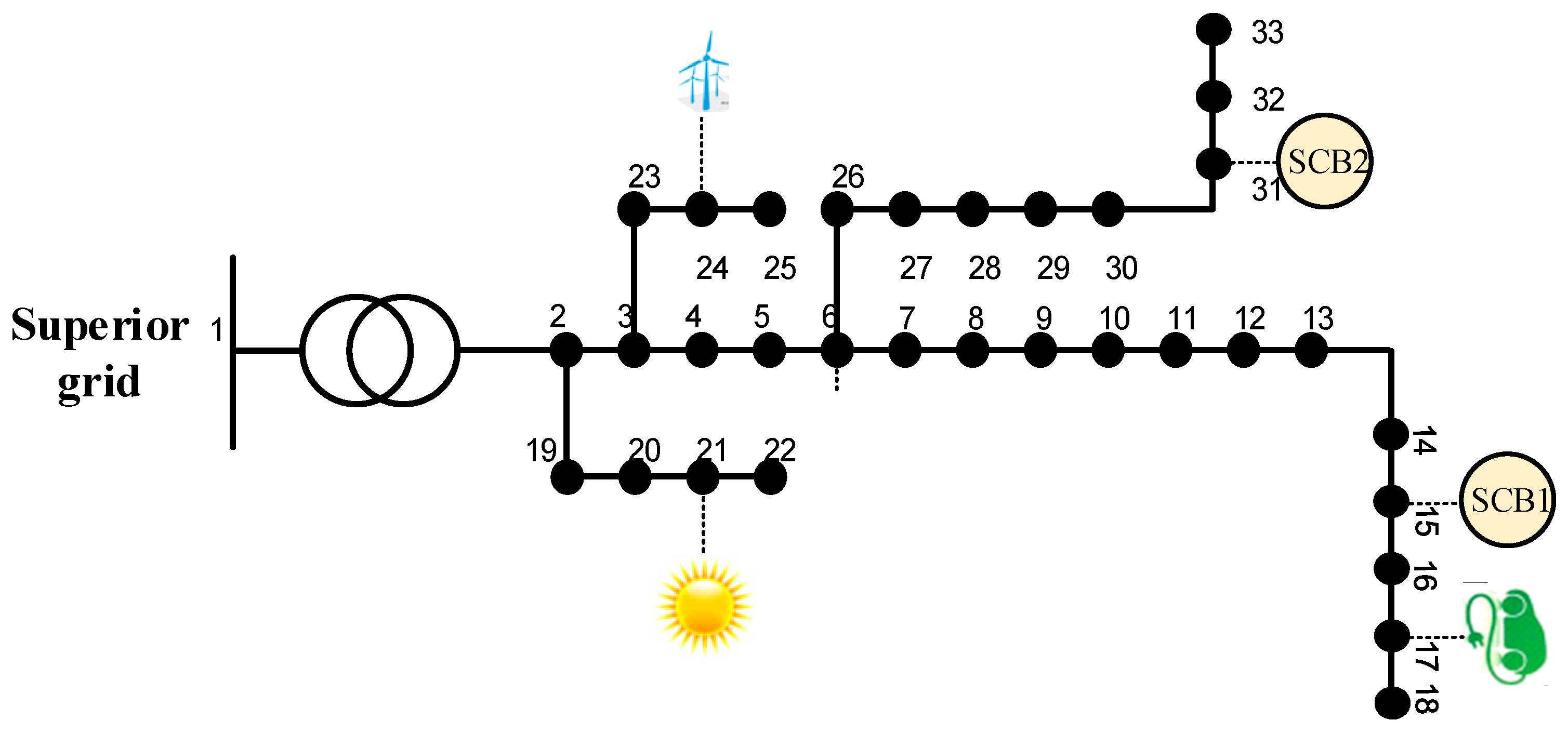
6.1. IEEE 33-Node Example
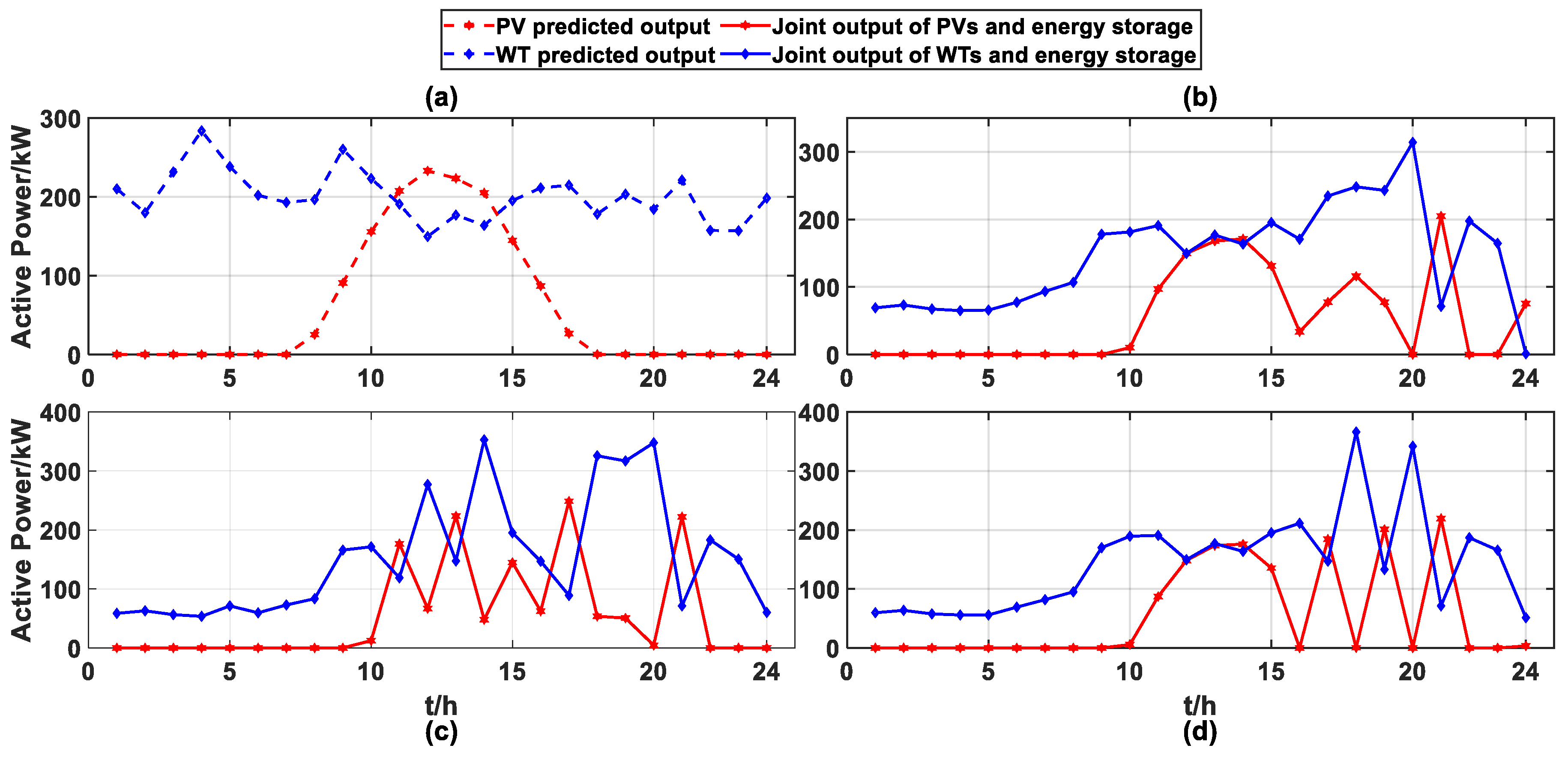
6.2. DG Output and EV Load Profiles
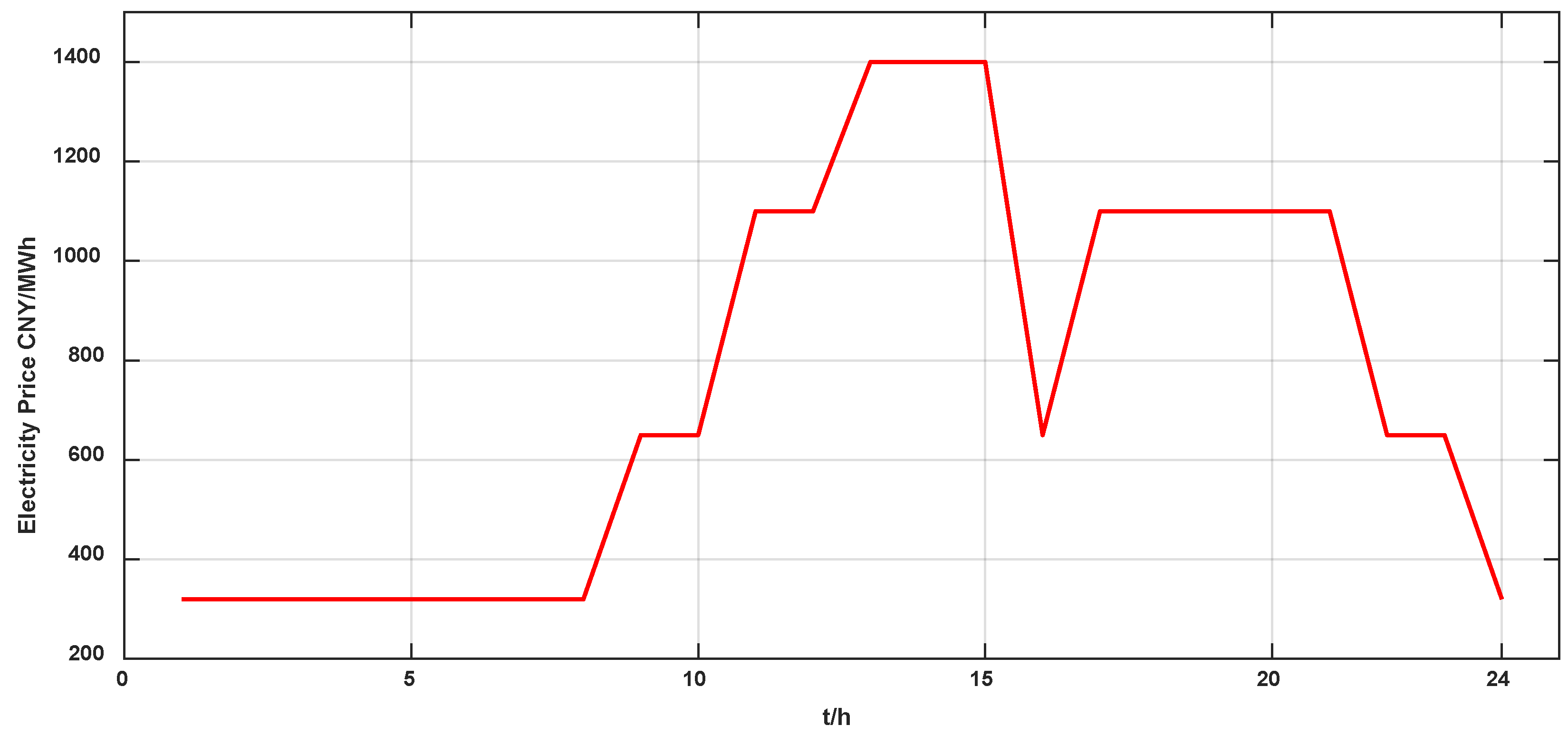
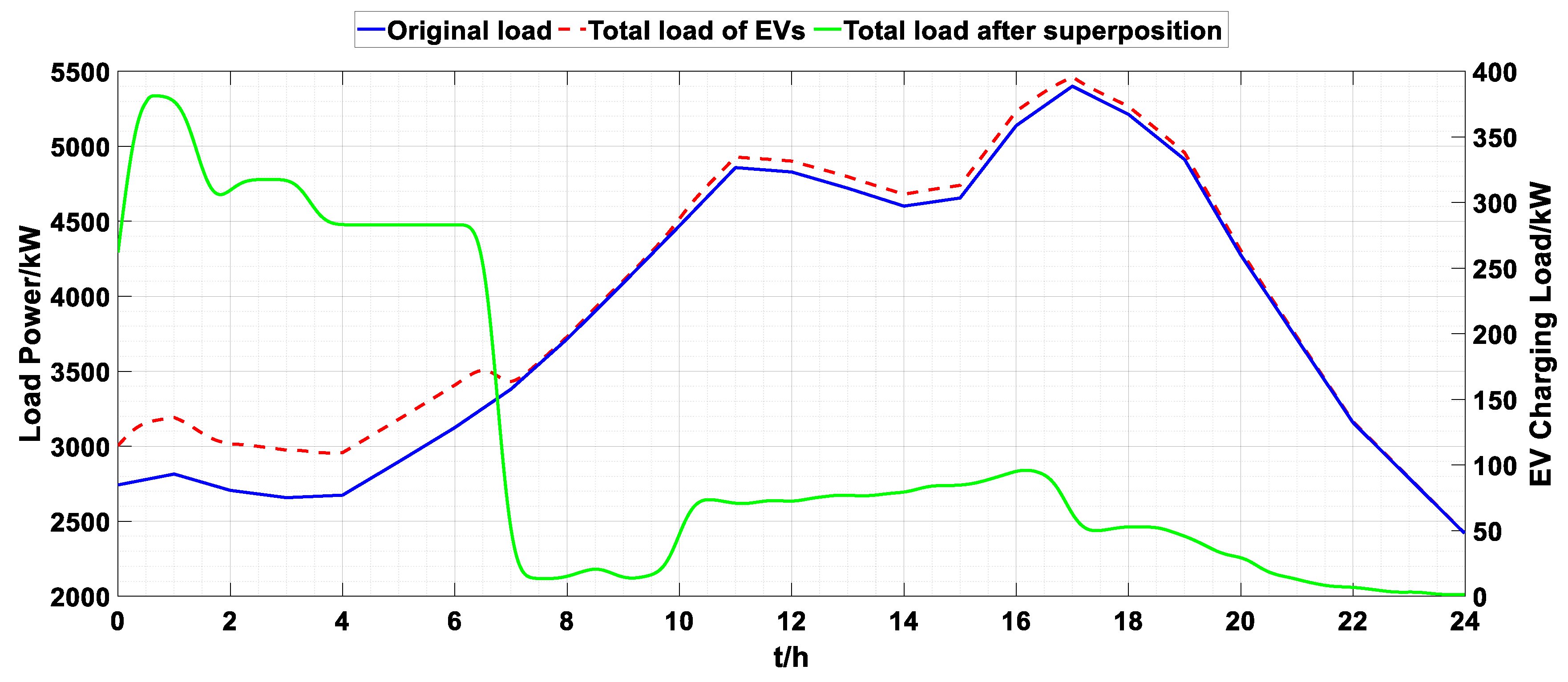
6.2.1. Load Profiles
6.2.2. DG Output Profiles
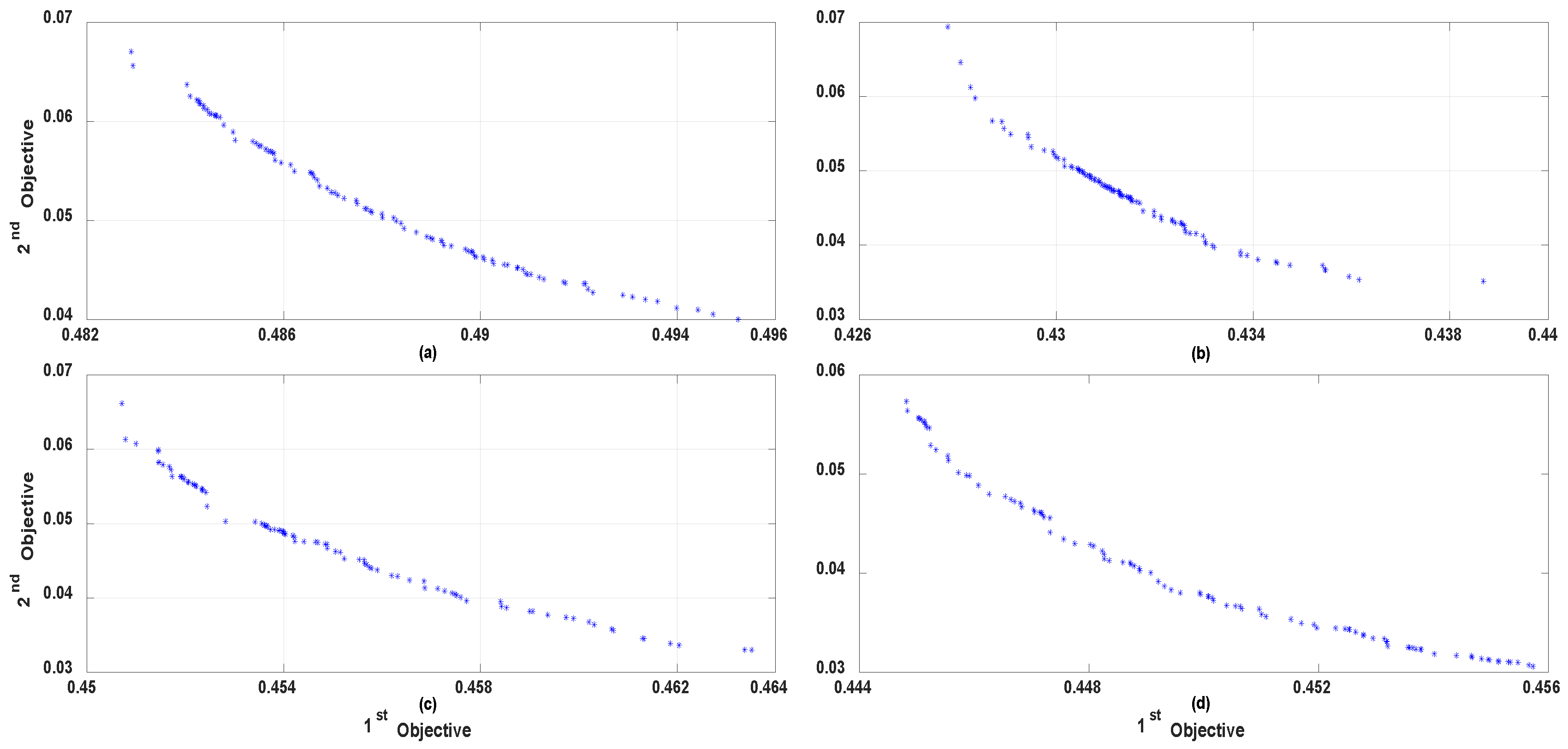
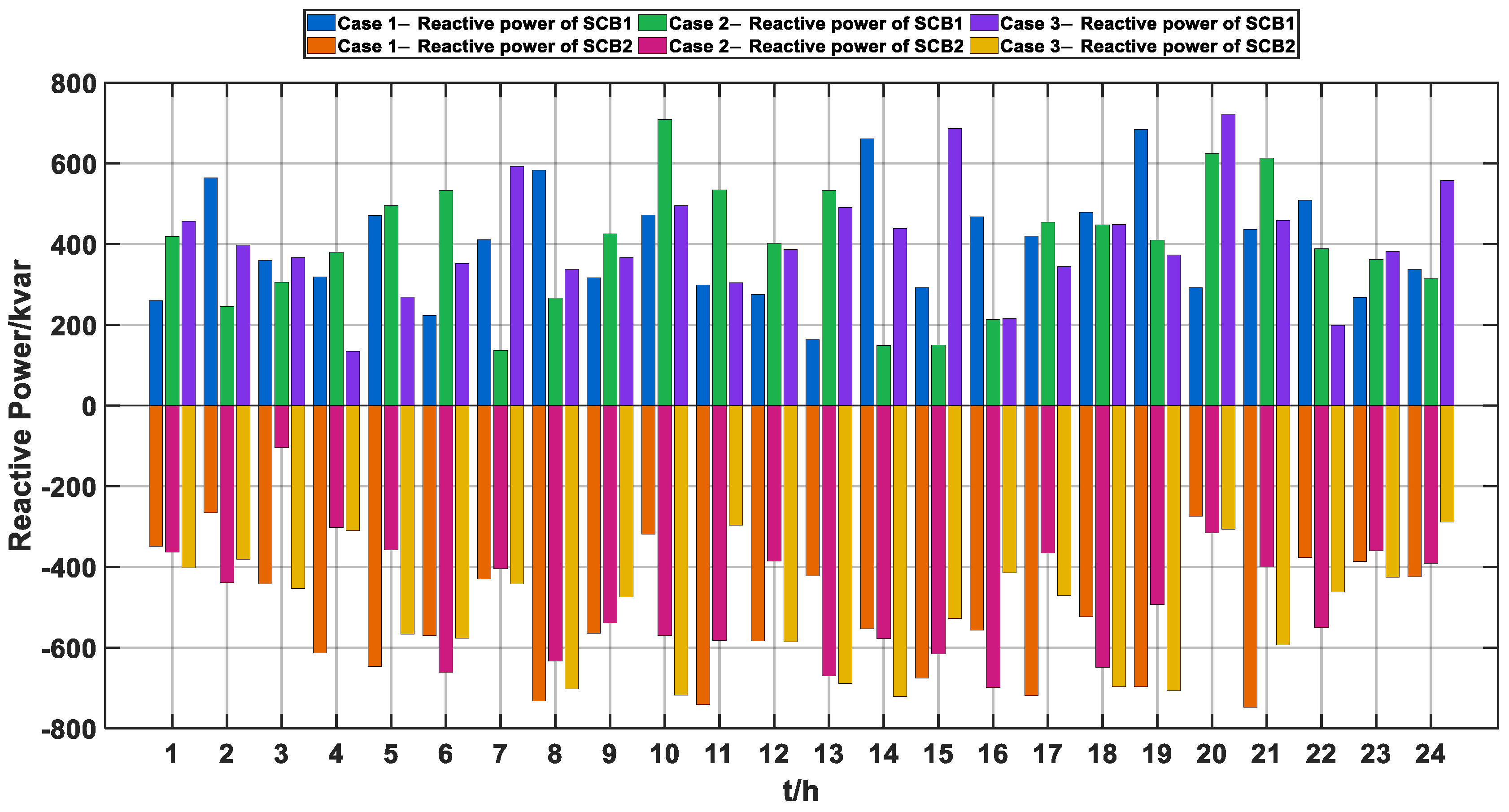
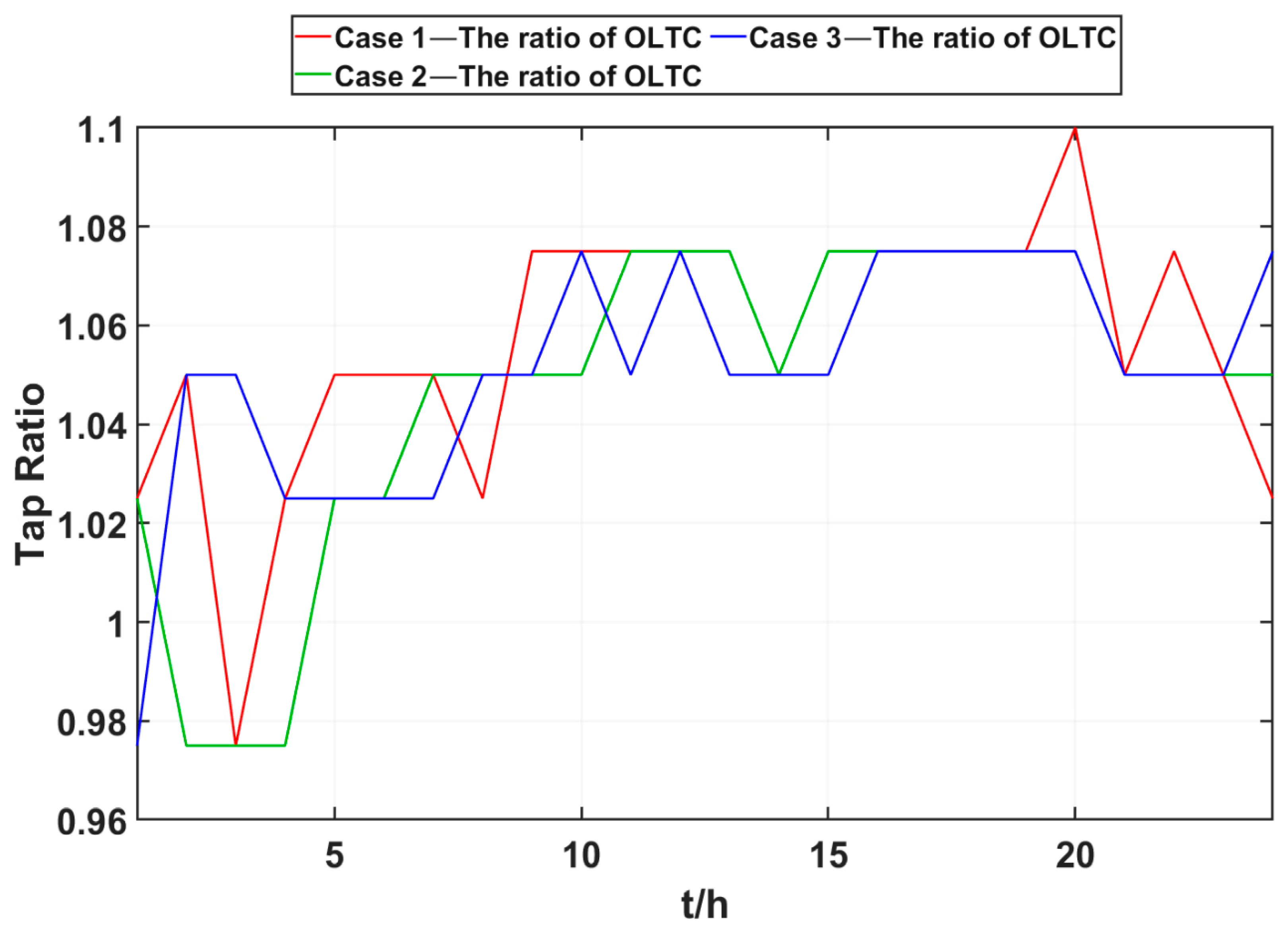
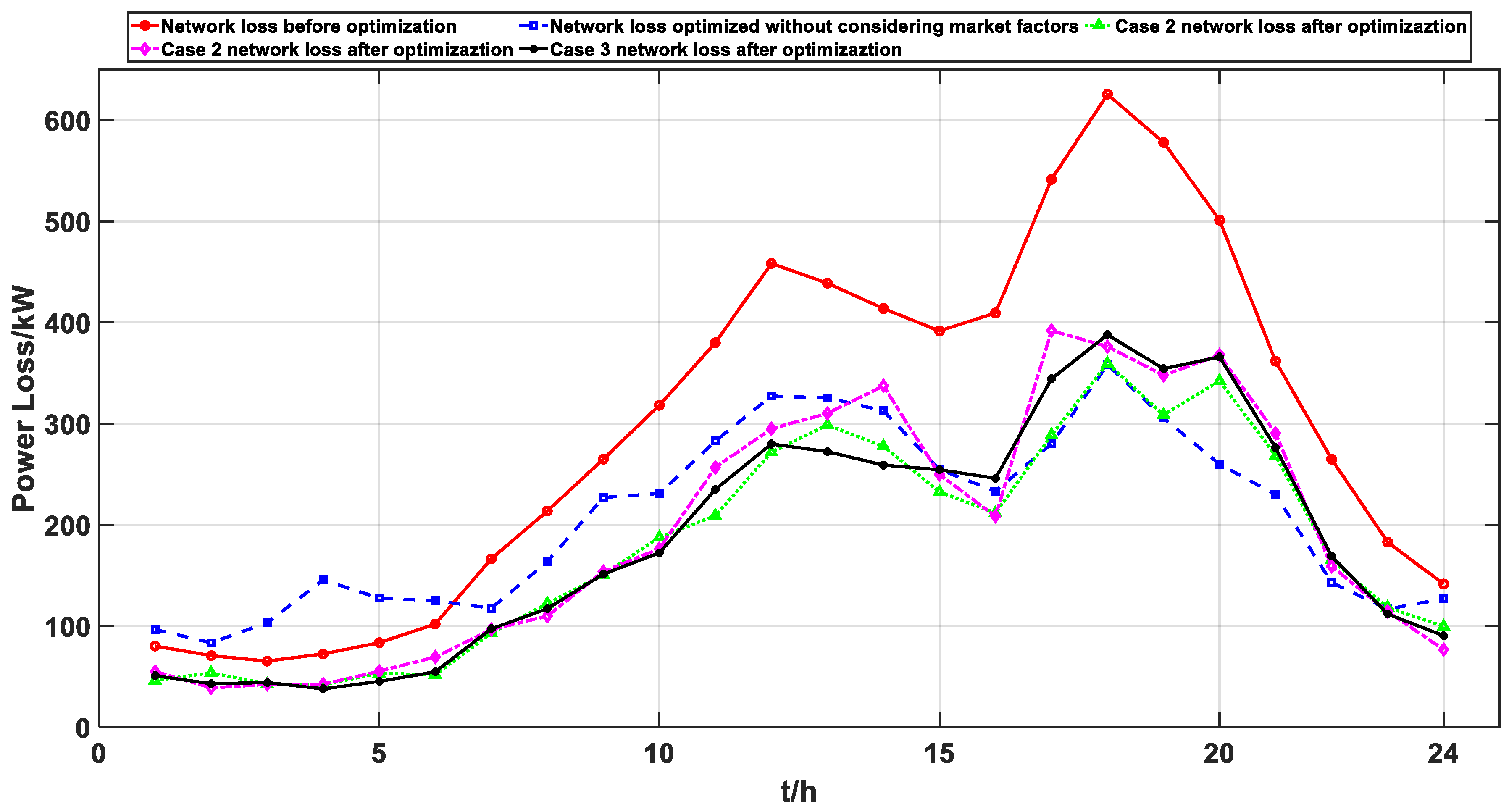
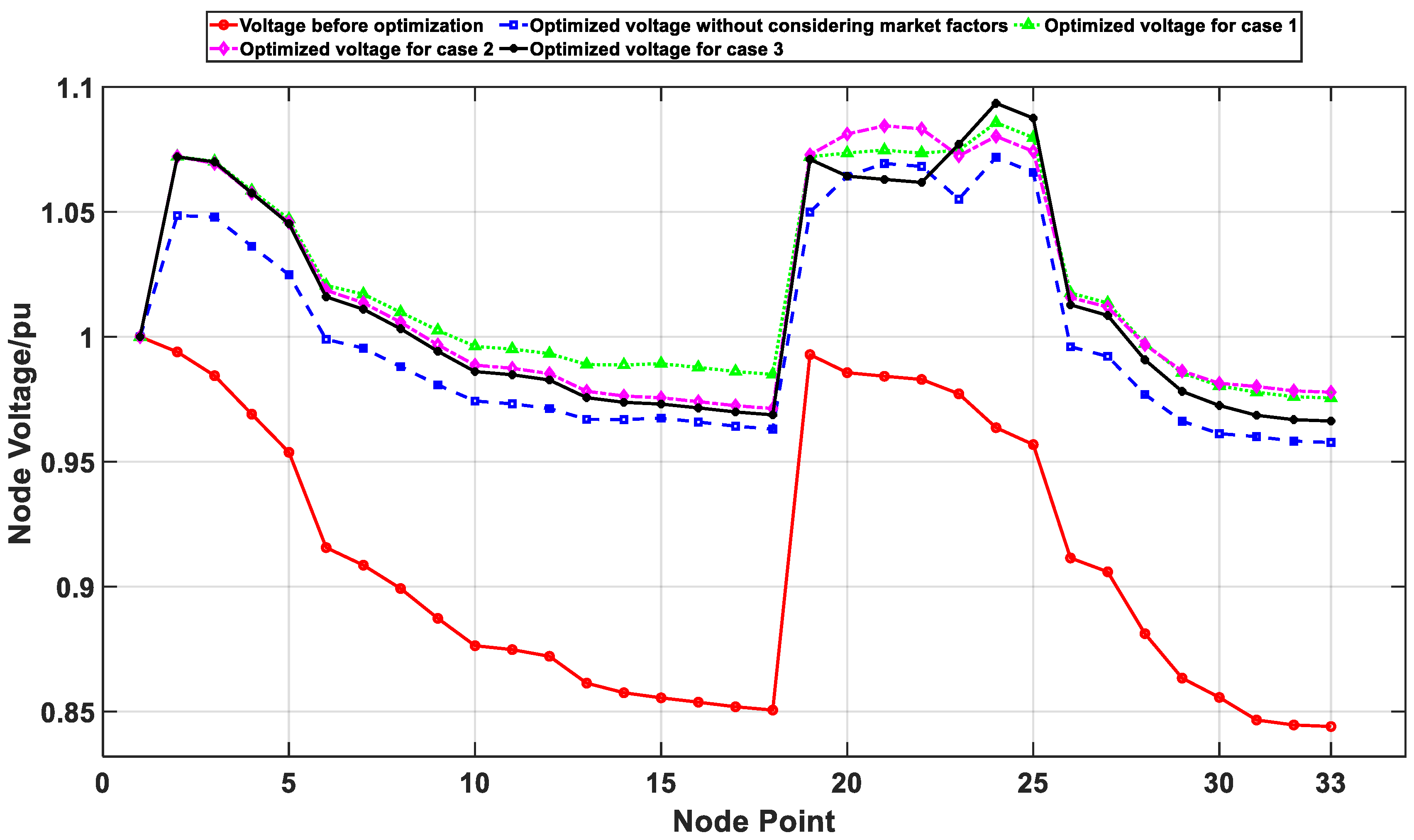
6.3. Optimization Analysis Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdel-Mawgoud, H.; Ali, A.; Kamel, S.; Rahmann, C.; Abdel-Moamen, M.A. A modified manta ray foraging optimizer for planning inverter-based photovoltaic with battery energy storage system and wind turbine in distribution networks. IEEE Access 2021, 9, 91062–91079. [Google Scholar] [CrossRef]
- Mathew, M.S.; Kolhe, M.L.; Kandukuri, S.T.; Omlin, C.W. Data driven approach for the management of wind and solar energy integrated electrical distribution network with high penetration of electric vehicles. J. Clean. Prod. 2023, 421, 138467. [Google Scholar] [CrossRef]
- Mu, Q.; Gao, Y.; Yang, Y.; Liang, H. Design of power supply package for electricity sales companies considering user side energy storage configuration. Energies 2019, 12, 3219. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Li, J.; Shao, L.; Zhang, D. Research on Smart Power Sales Strategy Considering Load Forecasting and Optimal Allocation of Energy Storage System in China. Energies 2023, 16, 3341. [Google Scholar] [CrossRef]
- Michalski, M.; Polański, J.; Nemś, M. Storing Electric Energy Generated by a Photovoltaic Installation to Increase Profit from Its Sale—Case Study in Poland. Sustainability 2024, 16, 5635. [Google Scholar] [CrossRef]
- Ren, Z.; Guo, H.; Yang, P.; Zuo, G.; Zhao, Z. Bi-level optimal allocation of flexible resources for distribution network considering different energy storage operation strategies in electricity market. IEEE Access 2020, 8, 58497–58508. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Coordinated investment planning of distributed multi-type stochastic generation and battery storage in active distribution networks. IEEE Trans. Sustain. Energy 2018, 10, 1813–1822. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Ge, S.; He, X.; Li, F.; Gu, C. Distributed day-ahead peer-to-peer trading for multi-microgrid systems in active distribution networks. IEEE Access 2020, 8, 66961–66976. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Guo, C. Hierarchical optimal configuration of multi-energy microgrids system considering energy management in electricity market environment. Int. J. Electr. Power Energy Syst. 2023, 144, 108572. [Google Scholar] [CrossRef]
- Vahidinasab, V. Optimal distributed energy resources planning in a competitive electricity market: Multiobjective optimization and probabilistic design. Renew. Energy 2014, 66, 354–363. [Google Scholar] [CrossRef]
- Wang, G.; Tan, Z.; Lin, H.; Tan, Q.; Yang, S.; Ju, L.; Ren, Z. Multi-level market transaction optimization model for electricity sales companies with energy storage plant. Energies 2019, 12, 145. [Google Scholar] [CrossRef]
- Jin, C.; Tang, J.; Ghosh, P. Optimizing electric vehicle charging with energy storage in the electricity market. IEEE Trans. Smart Grid 2013, 4, 311–320. [Google Scholar] [CrossRef]
- Yang, S.; Wang, X.; Yang, Y.; Li, J. Bi-level planning model of distributed PV-energy storage system connected to distribution network under the coordinated operation of electricity-carbon market. Sustain. Cities Soc. 2023, 89, 104347. [Google Scholar] [CrossRef]
- Filip, R.; Püvi, V.; Paar, M.; Lehtonen, M. Analyzing the impact of EV and BESS deployment on PV hosting capacity of distribution networks. Energies 2022, 15, 7921. [Google Scholar] [CrossRef]
- Manbachi, M.; Sadu, A.; Farhangi, H.; Monti, A.; Palizban, A.; Ponci, F.; Arzanpour, S. Impact of EV penetration on Volt–VAR Optimization of distribution networks using real-time co-simulation monitoring platform. Appl. Energy 2016, 169, 28–39. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, G.; Li, K.; Li, B.; Chi, H.; Yao, Y.; Fan, Z. Reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles. Prot. Control Mod. Power Syst. 2022, 7, 51. [Google Scholar] [CrossRef]
- Li, Z.; Xiong, J. Reactive Power Optimization in Distribution Networks of New Power Systems Based on Multi-Objective Particle Swarm Optimization. Energies 2024, 17, 2316. [Google Scholar] [CrossRef]
- Xia, L.; Lin, X.; Zhou, R.; Zhang, K. Research on Multi-Objective Reactive Power Optimization of Distribution Grid with Photovoltaics. World Electr. Veh. J. 2025, 16, 70. [Google Scholar] [CrossRef]
- Dharavat, N.; Sudabattula, S.K.; Velamuri, S.; Mishra, S.; Sharma, N.K.; Bajaj, M.; Elgamli, E.; Shouran, M.; Kamel, S. Optimal allocation of renewable distributed generators and electric vehicles in a distribution system using the political optimization algorithm. Energies 2022, 15, 6698. [Google Scholar] [CrossRef]
- Zhu, X.; Han, H.; Gao, S.; Shi, Q.; Cui, H.; Zu, G. A multi-stage optimization approach for active distribution network scheduling considering coordinated electrical vehicle charging strategy. IEEE Access 2018, 6, 50117–50130. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.; Du, Y.; Lu, Y.; Wang, Z. Multi-objective optimal peak load shaving strategy using coordinated scheduling of EVs and BESS with adoption of MORBHPSO. J. Energy Storage 2023, 64, 107121. [Google Scholar] [CrossRef]
- Gong, L.; Wang, X.; Tian, M.; Yao, H.; Long, J. Multi-objective optimal planning for distribution network considering the uncertainty of PV power and line-switch state. Sensors 2022, 22, 4927. [Google Scholar] [CrossRef]
- Barutcu, I.C. Examination of the chance constrained optimal wt penetration level in distorted distribution network with wind speed and load uncertainties. Eng. Technol. Appl. Sci. Res. 2021, 11, 7311–7320. [Google Scholar] [CrossRef]
- Ozay, C.; Celiktas, M.S. Statistical analysis of wind speed using two-parameter Weibull distribution in Alaçatı region. Energy Convers. Manag. 2016, 121, 49–54. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2010, 26, 802–810. [Google Scholar] [CrossRef]
- Eyer, J.; Corey, G. Energy storage for the electricity grid: Benefits and market potential assessment guide. Sandia Natl. Lab. 2010, 20, 5. [Google Scholar]
- Shi, Z.; Wang, W.; Huang, Y.; Li, P.; Dong, L. Simultaneous Optimization of Renewable Energy and Energy Storage Capacity with the Hierarchical Control. CSEE J. Power Energy Syst. 2020, 8, 95–104. [Google Scholar]
- Liu, H.; Ge, S. Optimization of TOU Price of Electricity Based on Electric Vehicle Orderly Charge. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting (PESGM 2013), Vancouver, BC, Canada, 21–25 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Yu, L.; Zhang, L.; Meng, G.; Zhang, F.; Liu, W. Research on Multi-Objective Reactive Power Optimization of Power Grid with High Proportion of New Energy. IEEE Access 2022, 10, 116443–116452. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling Multiple Objectives with Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Fu, C.; Liu, J.; Zeng, J.; Ma, M. Adaptive Reactive Power Optimization in Offshore Wind Farms Based on an Improved Particle Swarm Algorithm. Electronics 2024, 13, 1637. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation (CEC’02), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Niknam, T.; Meymand, H.Z.; Mojarrad, H.D. A practical multi-objective PSO algorithm for optimal operation management of distribution network with regard to fuel cell power plants. Renew. Energy 2011, 36, 1529–1544. [Google Scholar] [CrossRef]
- Adetunji, K.E.; Hofsajer, I.W.; Abu-Mahfouz, A.M.; Cheng, L. An optimization planning framework for allocating multiple distributed energy resources and electric vehicle charging stations in distribution networks. Appl. Energy 2022, 322, 119513. [Google Scholar] [CrossRef]
- Kuang, H.; Su, F.; Chang, Y.; Wang, K.; He, Z. Reactive power optimization for distribution network system with wind power based on improved multi-objective particle swarm optimization algorithm. Electr. Power Syst. Res. 2022, 213, 108731. [Google Scholar]



| Types of EVs | Charging Start Time | Initial SOC | ||
|---|---|---|---|---|
| Probability Distribution Type | Charging Period | Charging Ratio | ||
| Taxi | N(μ, σ2) | 0:00–8:00 | 0.1 V | N(μ, σ2) |
| Uniform distribution | 8:00–20:00 | 0.8 U | N(μ, σ2) | |
| N(μ, σ2) | 20:00–24:00 | 0.1 V | N(μ, σ2) | |
| Bus | Uniform distribution | 12:00–18:00 | 0.6 U | N(μ, σ2) |
| N(μ, σ2) | 23:00–24:00 | 0.4 V | N(μ, σ2) | |
| Official car | Uniform distribution | 10:00–20:00 | 0.7 V | N(μ, σ2) |
| Uniform distribution | 8:00–24:00 | 0.25 U | N(μ, σ2) | |
| N(μ, σ2) | 0:00–8:00 | 0.05 U | N(μ, σ2) | |
| Private car | N(μ, σ2) | 0:00–8:00 | 0.04 U | N(μ, σ2) |
| N(μ, σ2) | 8:00–12:00 | 0.08 U | N(μ, σ2) | |
| N(μ, σ2) | 15:00–19:00 | 0.08 U | N(μ, σ2) | |
| Uniform distribution | 0:00–24:00 | 0.8 V | N(μ, σ2) | |
| Contract Price of DG (CNY/MWh) | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| PVs | 850 | 850 | 800 |
| WTs | 800 | 850 | 850 |
| Scene | Average Voltage Amplitude/pu | Mean Voltage Standard Deviation |
|---|---|---|
| The DG is not connected | 0.9288 | 0.04455 |
| The unoptimized DG has been connected | 1.009 | 0.03492 |
| The case 1-optimized DG has been connected | 1.015 | 0.03153 |
| The case 2-optimized DG has been connected | 1.016 | 0.03206 |
| The case 3-optimized DG has been connected | 1.016 | 0.03156 |
| Scene | Network Loss/kW |
|---|---|
| The DG is not connected | 296.9 |
| The unoptimized DG has been connected | 207.3 |
| The case 1-optimized DG has been connected | 178.9 |
| The case 2-optimized DG has been connected | 192.5 |
| The case 3-optimized DG has been connected | 185.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Ren, Z.; Liu, K. Co-Optimization of Market and Grid Stability in High-Penetration Renewable Distribution Systems with Multi-Agent. Energies 2025, 18, 3209. https://doi.org/10.3390/en18123209
Jia D, Ren Z, Liu K. Co-Optimization of Market and Grid Stability in High-Penetration Renewable Distribution Systems with Multi-Agent. Energies. 2025; 18(12):3209. https://doi.org/10.3390/en18123209
Chicago/Turabian StyleJia, Dongli, Zhaoying Ren, and Keyan Liu. 2025. "Co-Optimization of Market and Grid Stability in High-Penetration Renewable Distribution Systems with Multi-Agent" Energies 18, no. 12: 3209. https://doi.org/10.3390/en18123209
APA StyleJia, D., Ren, Z., & Liu, K. (2025). Co-Optimization of Market and Grid Stability in High-Penetration Renewable Distribution Systems with Multi-Agent. Energies, 18(12), 3209. https://doi.org/10.3390/en18123209






