A Review of Agent-Based Models for Energy Commodity Markets and Their Natural Integration with RL Models
Abstract
1. Introduction
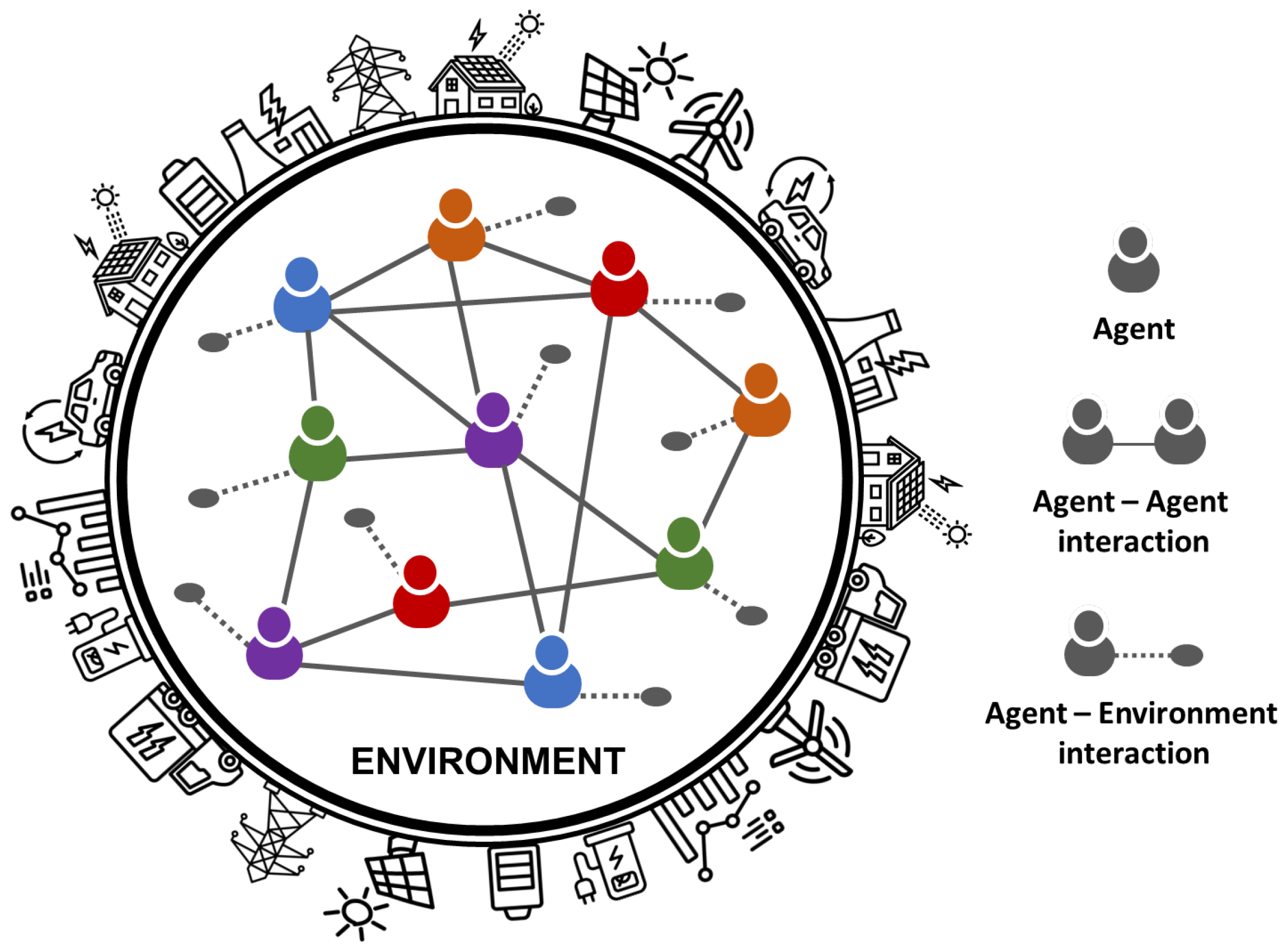
2. Foundations of Agent-Based Models in Energy Markets
3. Applications of ABMs in Energy Commodity Markets
- Definition of trading strategies;
- Generation of market scenarios;
- Evaluation of market designs.
3.1. Definition of Trading Strategies
3.2. Scenario Generation
3.3. Market Design Evaluation
4. Platforms and Tools for ABMs in Energy Markets
- Code language and software architecture (Java vs. Python; monolithic vs. modular);
- Agent design, including behavioral templates, decision trees, rule-based, and learning-enabled logic;
- Support for grid topology, load flow modeling, and stochastic demand/supply profiles;
- Coupling capabilities with external optimization solvers, ML libraries, or data streams;
- Flexibility in configuring market mechanisms, e.g., pay-as-clear vs. pay-as-bid auctions, and nodal vs. zonal pricing.
- Policy and regulation analysis: Some tools, such as AMES and ERCOT, are designed specifically to analyze policies, regulatory compliancies, and market structures. For example, AMES provides a flexible setting for assessing alternative market designs and bidding rules in wholesale electricity markets, allowing users to define complex market structures and observe emergent behavior. This tool has been employed to model the day-ahead and real-time US electricity markets, helping researchers and regulators to study how the locational marginal pricing is formed, how power grid congestion affects prices, and how electricity producers might behave strategically when placing their bids [57]. ERCOT focuses on dynamic modeling of wholesale power markets, with detailed representations of dispatchable and non-dispatchable generators and load-serving entities to evaluate specific market rules. It has been applied to the Texas wholesale energy market and employed in academic and transmission system operator (TSO) studies to test market rule changes [61].
- Trading strategies and price formation: Other tools are used to analyze various trading strategies, trader behaviors, and price formation mechanisms. MASCEM, for example, offers agents with adaptive learning capabilities to determine optimal bidding strategies based on market context, helping in the study of complex price formation dynamics. It has been applied in Iberian bidding studies, with agents using optimization, ML, and game theory, as a support tool in regulator decisions [64,73]. On the other hand, MATREM simulates day-ahead and futures electricity markets, enabling detailed analysis of generator and retailer interactions. This tool is mainly employed in research studies, focusing on feasibility assessments in energy markets [65].
- Renewable energy integration: The more recently developed tools, such as ASSUME, AMIRIS, and EMLab, focus on the effect that the integration of renewable energy sources is having and can have on the energy markets, enabling researchers and experts to cope with the energy transition, with its investment risks, and to ensure the necessary capacity within the power markets. For example, ASSUME is designed to analyze new electricity market designs under high-RES-penetration scenarios [59], while AMIRIS supports the modeling of dispatching and simulation of market prices with different energy actors, including policy providers. The latter has also been employed in real-world applications in Germany and Austria to simulate annual hourly dispatch under policy scenarios, and to analyze battery storage bidding, renewable subsidy impacts, and market price formation [58]. In addition, EMLab, used in multiple research studies, explores the long-term effects of interacting energy and climate policies, explicitly modeling power companies making investment decisions under imperfect information [60].
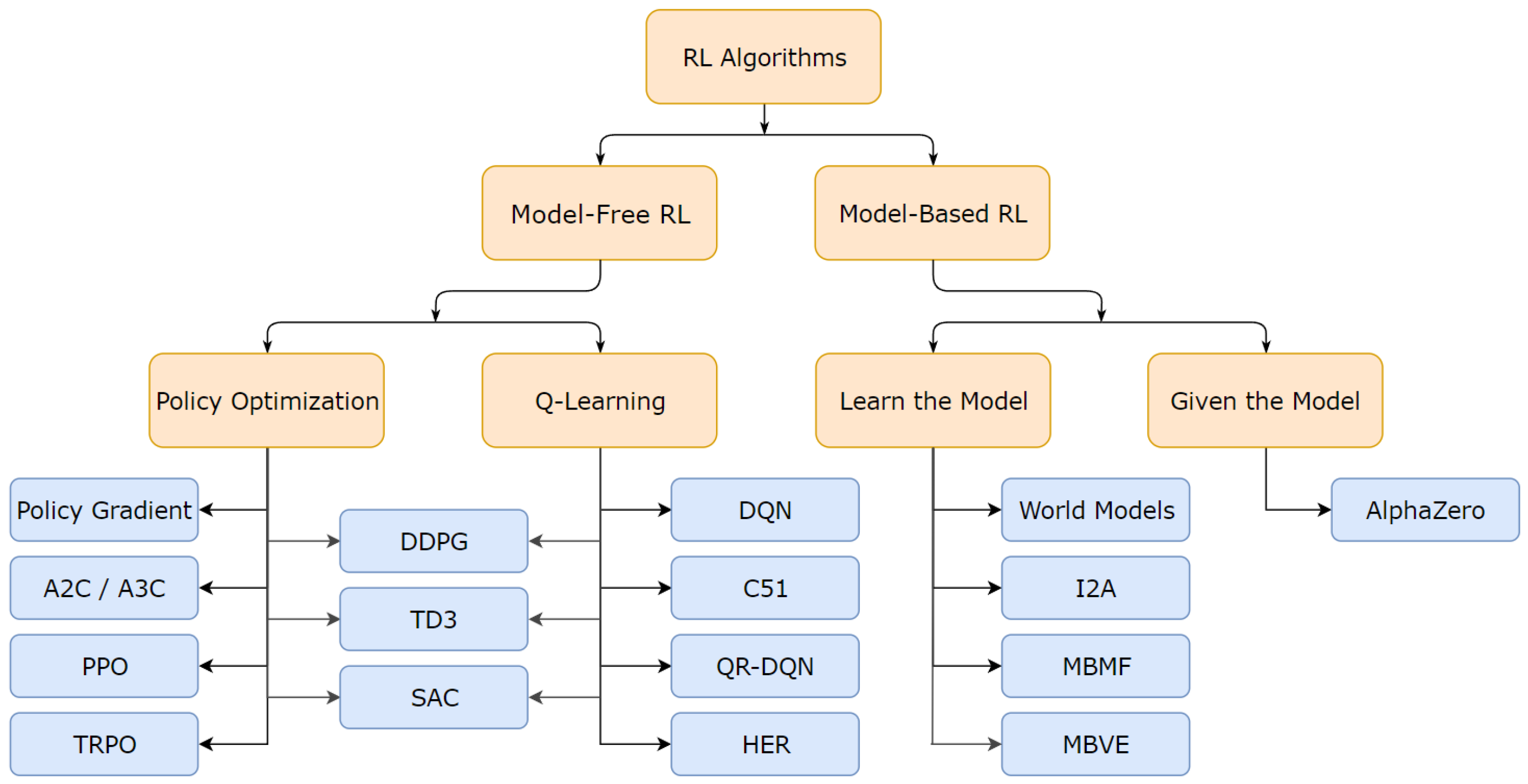
5. Machine Learning Integration with ABMs
6. Challenges and Limitations of ABMs for Energy Markets
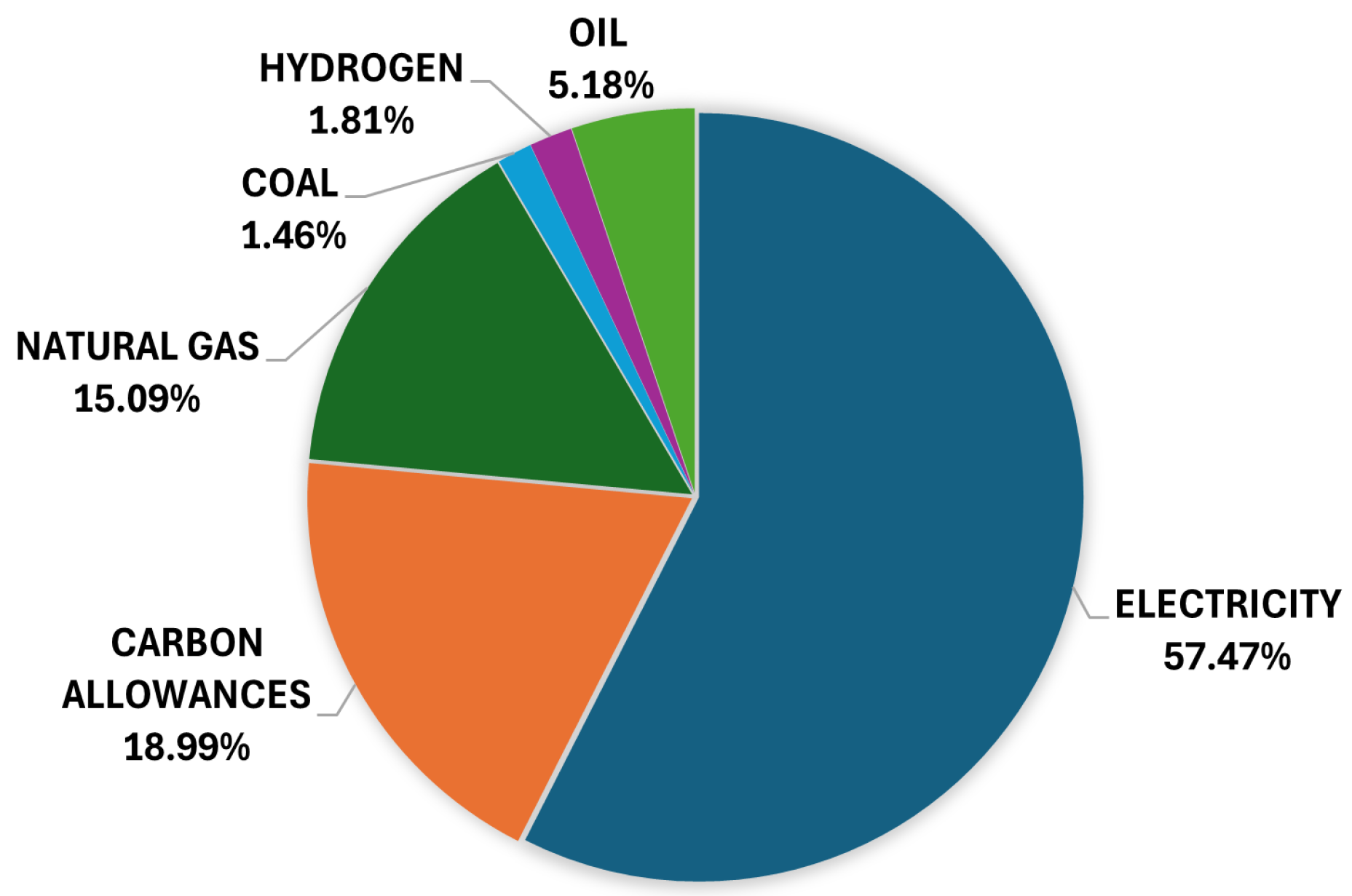
- Cross-relationships between energy commodities;
- Calibration and validation approaches;
- Scaling-up issue;
- Exploration–exploitation trade-off dilemma.
6.1. Cross-Relationships Between Energy Commodities
6.2. Calibration and Validation
6.3. Scaling Up
6.4. Exploration–Exploitation Trade-Off Dilemma
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A2C | Advantage Actor–Critic |
| ABM | Agent-based model |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| C51 | Categorical DQN—51 atom |
| DDPG | Deep Deterministic Policy Gradient |
| DL | Deep learning |
| DNN | Deep neural network |
| DQN | Deep Q-Network |
| DRL | Deep reinforcement learning |
| GPU | Graphics processing unit |
| HEM | Hierarchical Experience Management |
| HPC | High-performance computing |
| I2A | Imagination-Augmented Agents |
| ISO | Independent system operator |
| MADRL | Multi-agent deep reinforcement learning |
| MBMF | Model-Based Model-Free |
| MBVE | Model-based value expansion |
| MCDA | Multi-criteria decision analysis |
| MDP | Markov decision process |
| ML | Machine learning |
| POMDP | Partially observable Markov decision process |
| PPO | Proximal Policy Optimization |
| RES | Renewable energy source |
| RL | Reinforcement learning |
| SAC | Soft Actor–Critic |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient |
| TPO | Trust Region Policy Optimization |
| TSO | Transmission system operator |
References
- Axelrod, R. The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration: Agent-Based Models of Competition and Collaboration; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Epstein, J.M. Generative Social Science: Studies in Agent-Based Computational Modeling; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Axtell, R.L.; Farmer, J.D. Agent-based modeling in economics and finance: Past, present, and future. J. Econ. Lit. 2022, 63, 197–287. [Google Scholar] [CrossRef]
- Kapeller, M.L.; Jäger, G. Threat and anxiety in the climate debate—An agent-based model to investigate climate scepticism and pro-environmental behaviour. Sustainability 2020, 12, 1823. [Google Scholar] [CrossRef]
- Tesfatsion, L. Agent-based computational economics: Growing economies from the bottom up. Artif. Life 2002, 8, 55–82. [Google Scholar] [CrossRef]
- Weidlich, A.; Veit, D. A critical survey of agent-based wholesale electricity market models. Energy Econ. 2008, 30, 1728–1759. [Google Scholar] [CrossRef]
- Bjarghov, S.; Löschenbrand, M.; Saif, A.I.; Pedrero, R.A.; Pfeiffer, C.; Khadem, S.K.; Rabelhofer, M.; Revheim, F.; Farahmand, H. Developments and challenges in local electricity markets: A comprehensive review. IEEE Access 2021, 9, 58910–58943. [Google Scholar] [CrossRef]
- Wu, J.; Mohamed, R.; Wang, Z. An agent-based model to project China’s energy consumption and carbon emission peaks at multiple levels. Sustainability 2017, 9, 893. [Google Scholar] [CrossRef]
- Chen, P.; Wu, Y.; Zou, L. Distributive PV trading market in China: A design of multi-agent-based model and its forecast analysis. Energy 2019, 185, 423–436. [Google Scholar] [CrossRef]
- Ringler, P.; Keles, D.; Fichtner, W. Agent-based modelling and simulation of smart electricity grids and markets–a literature review. Renew. Sustain. Energy Rev. 2016, 57, 205–215. [Google Scholar] [CrossRef]
- Abar, S.; Theodoropoulos, G.K.; Lemarinier, P.; O’Hare, G.M. Agent Based Modelling and Simulation tools: A review of the state-of-art software. Comput. Sci. Rev. 2017, 24, 13–33. [Google Scholar] [CrossRef]
- Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Bellomo, M.; Trimarchi, S.; Niccolai, A.; Lorenzo, M.; Casamatta, F.; Grimaccia, F. A GAN Data Augmentation approach for trading applications in European Carbon Emission Allowances. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–5. [Google Scholar]
- Lin, B.; Su, T. Does COVID-19 open a Pandora’s box of changing the connectedness in energy commodities? Res. Int. Bus. Financ. 2021, 56, 101360. [Google Scholar] [CrossRef] [PubMed]
- Doumpos, M.; Zopounidis, C.; Gounopoulos, D.; Platanakis, E.; Zhang, W. Operational research and artificial intelligence methods in banking. Eur. J. Oper. Res. 2023, 306, 1–16. [Google Scholar] [CrossRef]
- Railsback, S.F.; Grimm, V. Agent-Based and Individual-Based Modeling: A Practical Introduction; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Cheng, S.F.; Lim, Y.P. Designing and Validating an Agent-Based Commodity Trading Simulation; Technical Report; Singapore Management University: Singapore, 2009. [Google Scholar]
- Vanfossan, S.; Dagli, C.H.; Kwasa, B. An agent-based approach to artificial stock market modeling. Procedia Comput. Sci. 2020, 168, 161–169. [Google Scholar] [CrossRef]
- Atkins, K.; Marathe, A.; Barrett, C. A computational approach to modeling commodity markets. Comput. Econ. 2007, 30, 125–142. [Google Scholar] [CrossRef]
- Reis, I.F.; Lopes, M.A.; Antunes, C.H. Energy transactions between energy community members: An agent-based modeling approach. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Cheng, S.F.; Lim, Y.P. An agent-based commodity trading simulation. In Proceedings of the Twenty-First IAAI Conference, Pasadena, CA, USA, 14–16 July 2009. [Google Scholar]
- Giulioni, G. An agent-based modeling and simulation approach to commodity markets. Soc. Sci. Comput. Rev. 2019, 37, 355–370. [Google Scholar] [CrossRef]
- Zhou, Y.; Lund, P.D. Peer-to-peer energy sharing and trading of renewable energy in smart communities: Trading pricing models, decision-making and agent-based collaboration. Renew. Energy 2023, 207, 177–193. [Google Scholar] [CrossRef]
- Kanzari, D.; Said, Y.R.B. A complex adaptive agent modeling to predict the stock market prices. Expert Syst. Appl. 2023, 222, 119783. [Google Scholar] [CrossRef]
- Castro, J.; Drews, S.; Exadaktylos, F.; Foramitti, J.; Klein, F.; Konc, T.; Savin, I.; van Den Bergh, J. A review of agent-based modeling of climate-energy policy. Wiley Interdiscip. Rev. Clim. Chang. 2020, 11, e647. [Google Scholar] [CrossRef]
- Mignot, S.; Vignes, A. The many faces of agent-based computational economics: Ecology of agents, bottom-up approaches and paradigm shift. OEconomia 2020, 10, 189–229. [Google Scholar] [CrossRef]
- Reis, I.F.; Gonçalves, I.; Lopes, M.A.; Antunes, C.H. A multi-agent system approach to exploit demand-side flexibility in an energy community. Util. Policy 2020, 67, 101114. [Google Scholar] [CrossRef]
- Ventosa, M.; Baıllo, A.; Ramos, A.; Rivier, M. Electricity market modeling trends. Energy Policy 2005, 33, 897–913. [Google Scholar] [CrossRef]
- Dai, T.; Qiao, W. Finding equilibria in the pool-based electricity market with strategic wind power producers and network constraints. IEEE Trans. Power Syst. 2016, 32, 389–399. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W.; Kelly, N.C. Agent-based modeling in electrical energy markets using dynamic Bayesian networks. IEEE Trans. Power Syst. 2016, 31, 4744–4754. [Google Scholar] [CrossRef]
- Gao, X.; Chan, K.W.; Xia, S.; Zhang, X.; Zhang, K.; Zhou, J. A multiagent competitive bidding strategy in a pool-based electricity market with price-maker participants of WPPs and EV aggregators. IEEE Trans. Ind. Inform. 2021, 17, 7256–7268. [Google Scholar] [CrossRef]
- Liang, Y.; Guo, C.; Ding, Z.; Hua, H. Agent-based modeling in electricity market using deep deterministic policy gradient algorithm. IEEE Trans. Power Syst. 2020, 35, 4180–4192. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Sun, M.; Papadaskalopoulos, D.; Strbac, G. Deep reinforcement learning for strategic bidding in electricity markets. IEEE Trans. Smart Grid 2019, 11, 1343–1355. [Google Scholar] [CrossRef]
- Jain, P.; Saxena, A. A Multi-Agent based simulator for strategic bidding in day-ahead energy market. Sustain. Energy Grids Netw. 2023, 33, 100979. [Google Scholar] [CrossRef]
- Nicolini, C.; Gopalan, M.; Lepri, B.; Staiano, J. Hopfield networks for asset allocation. In Proceedings of the 5th ACM International Conference on AI in Finance, Brooklyn, NY, USA, 14–17 November 2024; pp. 19–26. [Google Scholar]
- Gode, D.K.; Sunder, S. Allocative efficiency of markets with zero-intelligence traders: Market as a partial substitute for individual rationality. J. Political Econ. 1993, 101, 119–137. [Google Scholar] [CrossRef]
- Xu, S.; Chen, X.; Xie, J.; Rahman, S.; Wang, J.; Hui, H.; Chen, T. Agent-based modeling and simulation for the electricity market with residential demand response. CSEE J. Power Energy Syst. 2020, 7, 368–380. [Google Scholar]
- Fatras, N.; Ma, Z.; Jørgensen, B.N. An agent-based modelling framework for the simulation of large-scale consumer participation in electricity market ecosystems. Energy Inform. 2022, 5, 47. [Google Scholar] [CrossRef]
- Bose, S.; Kremers, E.; Mengelkamp, E.M.; Eberbach, J.; Weinhardt, C. Reinforcement learning in local energy markets. Energy Inform. 2021, 4, 7. [Google Scholar] [CrossRef]
- Osoba, O.A.; Vardavas, R.; Grana, J.; Zutshi, R.; Jaycocks, A. Modeling agent behaviors for policy analysis via reinforcement learning. In Proceedings of the 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 14–17 December 2020; pp. 213–219. [Google Scholar]
- Zheng, S.; Trott, A.; Srinivasa, S.; Parkes, D.C.; Socher, R. The AI Economist: Taxation policy design via two-level deep multiagent reinforcement learning. Sci. Adv. 2022, 8, eabk2607. [Google Scholar] [CrossRef] [PubMed]
- Harder, N.; Qussous, R.; Weidlich, A. Fit for purpose: Modeling wholesale electricity markets realistically with multi-agent deep reinforcement learning. Energy AI 2023, 14, 100295. [Google Scholar] [CrossRef]
- Miskiw, K.K.; Staudt, P. Explainable Deep Reinforcement Learning for Multi-Agent Electricity Market Simulations. In Proceedings of the 2024 20th International Conference on the European Energy Market (EEM), Istanbul, Turkey, 10–12 June 2024; pp. 1–9. [Google Scholar]
- Wu, Z.; Zhou, M.; Zhang, T.; Li, G.; Zhang, Y.; Liu, X. Imbalance settlement evaluation for China’s balancing market design via an agent-based model with a multiple criteria decision analysis method. Energy Policy 2020, 139, 111297. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Catalão, J.P. A stochastic multi-layer agent-based model to study electricity market participants behavior. IEEE Trans. Power Syst. 2014, 30, 867–881. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W.; Kelly, N.C. Agent-based modeling of retail electrical energy markets with demand response. IEEE Trans. Smart Grid 2016, 9, 3465–3475. [Google Scholar] [CrossRef]
- Tang, L.; Wu, J.; Yu, L.; Bao, Q. Carbon emissions trading scheme exploration in China: A multi-agent-based model. Energy Policy 2015, 81, 152–169. [Google Scholar] [CrossRef]
- Tang, L.; Wu, J.; Yu, L.; Bao, Q. Carbon allowance auction design of China’s emissions trading scheme: A multi-agent-based approach. Energy Policy 2017, 102, 30–40. [Google Scholar] [CrossRef]
- Allen, P.; Varga, L. Modelling sustainable energy futures for the UK. Futures 2014, 57, 28–40. [Google Scholar] [CrossRef][Green Version]
- D’Adamo, I.; Gastaldi, M.; Hachem-Vermette, C.; Olivieri, R. Sustainability, emission trading system and carbon leakage: An approach based on neural networks and multicriteria analysis. Sustain. Oper. Comput. 2023, 4, 147–157. [Google Scholar] [CrossRef]
- Wei, Y.; Liang, X.; Xu, L.; Kou, G.; Chevallier, J. Trading, storage, or penalty? Uncovering firms’ decision-making behavior in the Shanghai emissions trading scheme: Insights from agent-based modeling. Energy Econ. 2023, 117, 106463. [Google Scholar] [CrossRef]
- Peng, Z.S.; Zhang, Y.L.; Shi, G.M.; Chen, X.H. Cost and effectiveness of emissions trading considering exchange rates based on an agent-based model analysis. J. Clean. Prod. 2019, 219, 75–85. [Google Scholar] [CrossRef]
- Yu, S.m.; Fan, Y.; Zhu, L.; Eichhammer, W. Modeling the emission trading scheme from an agent-based perspective: System dynamics emerging from firms’ coordination among abatement options. Eur. J. Oper. Res. 2020, 286, 1113–1128. [Google Scholar] [CrossRef]
- Zhang, J.; Ge, J.; Wen, J. Agent-Based Modeling of Carbon Emission Trading Market With Heterogeneous Agents. SSRN Electron. J. 2021. [Google Scholar] [CrossRef]
- Shinde, P.; Amelin, M. Agent-based models in electricity markets: A literature review. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3026–3031. [Google Scholar]
- Tesfatsion, L. Software for Agent Based Computational Economics and Complex Adaptive Systems. 2024. Available online: https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/acecode.htm (accessed on 17 October 2024).
- El-adaway, I.H.; Sims, C.; Eid, M.S.; Liu, Y.; Ali, G.G. Preliminary attempt toward better understanding the impact of distributed energy generation: An agent-based computational economics approach. J. Infrastruct. Syst. 2020, 26, 04020002. [Google Scholar] [CrossRef]
- Schimeczek, C.; Nienhaus, K.; Frey, U.; Sperber, E.; Sarfarazi, S.; Nitsch, F.; Kochems, J.; El Ghazi, A.A. AMIRIS: Agent-based Market model for the Investigation of Renewable and Integrated energy Systems. J. Open Source Softw. 2023, 8, 5041. [Google Scholar] [CrossRef]
- Harder, N.; Miskiw, K.K.; Maurer, F.; Khanra, M.; Parag, P. ASSUME: Agent-Based Electricity Markets Simulation Toolbox. 2023. Available online: https://assume-project.de/ (accessed on 18 October 2024).
- Chappin, E.J.; de Vries, L.J.; Richstein, J.C.; Bhagwat, P.; Iychettira, K.; Khan, S. Simulating climate and energy policy with agent-based modelling: The Energy Modelling Laboratory (EMLab). Environ. Model. Softw. 2017, 96, 421–431. [Google Scholar] [CrossRef]
- Battula, S.; Tesfatsion, L.; McDermott, T.E. An ERCOT test system for market design studies. Appl. Energy 2020, 275, 115182. [Google Scholar] [CrossRef]
- Grid Singularity. 2024. Available online: https://gridsingularity.com/ (accessed on 17 October 2024).
- Pinto, T.; Vale, Z.; Sousa, T.M.; Praça, I.; Santos, G.; Morais, H. Adaptive learning in agents behaviour: A framework for electricity markets simulation. Integr. Comput.-Aided Eng. 2014, 21, 399–415. [Google Scholar] [CrossRef]
- Santos, G.; Pinto, T.; Praça, I.; Vale, Z. MASCEM: Optimizing the performance of a multi-agent system. Energy 2016, 111, 513–524. [Google Scholar] [CrossRef]
- Lopes, F. MATREM: An agent-based simulation tool for electricity markets. In Electricity Markets with Increasing Levels of Renewable Generation: Structure, Operation, Agent-Based Simulation, and Emerging Designs; Springer: Cham, Switzerland, 2018; pp. 189–225. [Google Scholar]
- Fraunholz, C.; Kraft, E.; Keles, D.; Fichtner, W. Advanced price forecasting in agent-based electricity market simulation. Appl. Energy 2021, 290, 116688. [Google Scholar] [CrossRef]
- Tesfatsion, L. The AMES Wholesale Power Market Test Bed. 2024. Available online: https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/AMESMarketHome.htm (accessed on 29 October 2024).
- GitHub. 2025. Available online: https://github.com/ (accessed on 8 January 2025).
- AMIRIS—The Open Agent-Based Electricity Market Model. 2024. Available online: https://www.dlr.de/en/ve/research-and-transfer/research-infrastructure/modelling-tools/amiris (accessed on 29 October 2024).
- Chappin, E. EMLab—Energy Modelling Laboratory. 2024. Available online: https://emlab.tudelft.nl/ (accessed on 29 October 2024).
- Mattsson, S.E.; Andersson, M.; Åström, K.J. Object-oriented modeling and simulation. In CAD for Control Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 31–69. [Google Scholar]
- Collier, N.T.; Ozik, J.; Tatara, E.R. Experiences in developing a distributed agent-based modeling toolkit with Python. In Proceedings of the 2020 IEEE/ACM 9th Workshop on Python for High-Performance and Scientific Computing (PyHPC), Atlanta, GA, USA, 13 November 2020; pp. 1–12. [Google Scholar]
- González-Briones, A.; De La Prieta, F.; Mohamad, M.S.; Omatu, S.; Corchado, J.M. Multi-agent systems applications in energy optimization problems: A state-of-the-art review. Energies 2018, 11, 1928. [Google Scholar] [CrossRef]
- Sutton, R.S. Reinforcement Learning: An Introduction; A Bradford Book; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Kell, A.J.; McGough, S.; Forshaw, M. Machine learning applications for electricity market agent-based models: A systematic literature review. arXiv 2022, arXiv:2206.02196. [Google Scholar]
- Ye, Y.; Papadaskalopoulos, D.; Yuan, Q.; Tang, Y.; Strbac, G. Multi-agent deep reinforcement learning for coordinated energy trading and flexibility services provision in local electricity markets. IEEE Trans. Smart Grid 2022, 14, 1541–1554. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, D.; Qiu, R.C. Deep reinforcement learning for power system applications: An overview. CSEE J. Power Energy Syst. 2019, 6, 213–225. [Google Scholar]
- Achiam, J. Spinning Up in Deep Reinforcement Learning. 2018. Available online: https://github.com/openai/spinningup (accessed on 5 November 2024).
- Klein, T. Autonomous algorithmic collusion: Q-learning under sequential pricing. RAND J. Econ. 2021, 52, 538–558. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. A survey and critique of multiagent deep reinforcement learning. Auton. Agents Multi-Agent Syst. 2019, 33, 750–797. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, T.; Jiang, C.; Ye, D.; Zhao, F. Prioritized experience replay based on multi-armed bandit. Expert Syst. Appl. 2022, 189, 116023. [Google Scholar] [CrossRef]
- Agostinelli, F.; Hocquet, G.; Singh, S.; Baldi, P. From reinforcement learning to deep reinforcement learning: An overview. In Proceedings of the Braverman Readings in Machine Learning, Key Ideas from Inception to Current State: International Conference Commemorating the 40th Anniversary of Emmanuil Braverman’s Decease, Boston, MA, USA, 28–30 April 2017; Invited Talks. Springer: Cham, Switzerland, 2018; pp. 298–328. [Google Scholar]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent cooperation and competition with deep reinforcement learning. PLoS ONE 2017, 12, e0172395. [Google Scholar] [CrossRef]
- Fang, Y.; Tang, Z.; Ren, K.; Liu, W.; Zhao, L.; Bian, J.; Li, D.; Zhang, W.; Yu, Y.; Liu, T.Y. Learning multi-agent intention-aware communication for optimal multi-order execution in finance. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 4003–4012. [Google Scholar]
- Lincoln, R.W.; Galloway, S.; Burt, G. Open source, agent-based energy market simulation with python. In Proceedings of the 2009 6th International Conference on the European Energy Market, Leuven, Belgium, 27–29 May 2009; pp. 1–5. [Google Scholar]
- Lussange, J.; Lazarevich, I.; Bourgeois-Gironde, S.; Palminteri, S.; Gutkin, B. Modelling stock markets by multi-agent reinforcement learning. Comput. Econ. 2021, 57, 113–147. [Google Scholar] [CrossRef]
- Harrold, D.J.; Cao, J.; Fan, Z. Renewable energy integration and microgrid energy trading using multi-agent deep reinforcement learning. Appl. Energy 2022, 318, 119151. [Google Scholar] [CrossRef]
- Aliabadi, D.E.; Chan, K. The emerging threat of artificial intelligence on competition in liberalized electricity markets: A deep Q-network approach. Appl. Energy 2022, 325, 119813. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Zhao, J.; Zhang, G.; Zhang, B.; Liu, Z.; Chen, Z.; Blaabjerg, F. Reinforcement learning and its applications in modern power and energy systems: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1029–1042. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6382–6393. [Google Scholar]
- Naeem, M.A.; Peng, Z.; Suleman, M.T.; Nepal, R.; Shahzad, S.J.H. Time and frequency connectedness among oil shocks, electricity and clean energy markets. Energy Econ. 2020, 91, 104914. [Google Scholar] [CrossRef]
- Rehman, M.U.; Naeem, M.A.; Ahmad, N.; Vo, X.V. Global energy markets connectedness: Evidence from time–frequency domain. Environ. Sci. Pollut. Res. 2023, 30, 34319–34337. [Google Scholar] [CrossRef]
- Avalos, F.; Huang, W.; Tracol, K. Margins and Liquidity in European Energy Markets in 2022; Technical Report; Bank for International Settlements: Basel, Switzerland, 2023. [Google Scholar]
- Bottecchia, L.; Lubello, P.; Zambelli, P.; Carcasci, C.; Kranzl, L. The potential of simulating energy systems: The multi energy systems simulator model. Energies 2021, 14, 5724. [Google Scholar] [CrossRef]
- Gao, X.; Knueven, B.; Siirola, J.D.; Miller, D.C.; Dowling, A.W. Multiscale simulation of integrated energy system and electricity market interactions. Appl. Energy 2022, 316, 119017. [Google Scholar] [CrossRef]
- Giorgi, F.; Herzel, S.; Pigato, P. A reinforcement learning algorithm for trading commodities. Appl. Stoch. Model. Bus. Ind. 2024, 40, 373–388. [Google Scholar] [CrossRef]
- Fagiolo, G.; Guerini, M.; Lamperti, F.; Moneta, A.; Roventini, A. Validation of agent-based models in economics and finance. In Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives; Springer: Cham, Switzerland, 2019; pp. 763–787. [Google Scholar]
- An, L.; Grimm, V.; Turner II, B.L. Meeting grand challenges in agent-based models. J. Artif. Soc. Soc. Simul. 2020, 23. [Google Scholar] [CrossRef]
- Collins, A.; Koehler, M.; Lynch, C. Methods that support the validation of agent-based models: An overview and discussion. J. Artif. Soc. Soc. Simul. 2024, 27, 11. [Google Scholar] [CrossRef]
- Barde, S.; van Der Hoog, S. An Empirical Validation Protocol for Large-Scale Agent-Based Models. In Bielefeld Working Papers in Economics and Management No. 04-2017; SSRN (Elsevier): Amsterdam, The Netherlands, 2017; Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2992473 (accessed on 25 November 2024).
- Lamperti, F. An information theoretic criterion for empirical validation of simulation models. Econom. Stat. 2018, 5, 83–106. [Google Scholar] [CrossRef]
- Williams, B.L.; Hooper, R.; Gnoth, D.; Chase, J. Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach. Energies 2025, 18, 1314. [Google Scholar] [CrossRef]
- Guerini, M.; Moneta, A. A method for agent-based models validation. J. Econ. Dyn. Control 2017, 82, 125–141. [Google Scholar] [CrossRef]
- Takahashi, S.; Chen, Y.; Tanaka-Ishii, K. Modeling financial time-series with generative adversarial networks. Phys. A Stat. Mech. Appl. 2019, 527, 121261. [Google Scholar] [CrossRef]
- Shinde, P.; Boukas, I.; Radu, D.; Manuel de Villena, M.; Amelin, M. Analyzing trade in continuous intra-day electricity market: An agent-based modeling approach. Energies 2021, 14, 3860. [Google Scholar] [CrossRef]
- An, L.; Grimm, V.; Sullivan, A.; Turner Ii, B.; Malleson, N.; Heppenstall, A.; Vincenot, C.; Robinson, D.; Ye, X.; Liu, J.; et al. Challenges, tasks, and opportunities in modeling agent-based complex systems. Ecol. Model. 2021, 457, 109685. [Google Scholar] [CrossRef]
- Richmond, P.; Chisholm, R.; Heywood, P.; Chimeh, M.K.; Leach, M. FLAME GPU 2: A framework for flexible and performant agent based simulation on GPUs. Softw. Pract. Exp. 2023, 53, 1659–1680. [Google Scholar] [CrossRef]
- Dong, D. Agent-based cloud simulation model for resource management. J. Cloud Comput. 2023, 12, 156. [Google Scholar] [CrossRef]
- Abbott, R.; Hadžikadić, M. Complex adaptive systems, systems thinking, and agent-based modeling. In Advanced Technologies, Systems, and Applications; Springer: Cham, Switzerland, 2017; pp. 1–8. [Google Scholar]
- Fruit, R. Exploration-Exploitation Dilemma in Reinforcement Learning Under Various Form of Prior Knowledge. Sciences et Technologies; CRIStAL UMR 9189. Ph.D. Thesis, Université de Lille 1, Villeneuve-d’Ascq, France, 2019. [Google Scholar]
- Guida, V.; Mittone, L.; Morreale, A. Innovative search and imitation heuristics: An agent-based simulation study. J. Econ. Interact. Coord. 2024, 19, 231–282. [Google Scholar] [CrossRef]
- Wei, P. Exploration-exploitation strategies in deep q-networks applied to route-finding problems. J. Phys. Conf. Ser. 2020, 1684, 012073. [Google Scholar] [CrossRef]
- Billinger, S.; Srikanth, K.; Stieglitz, N.; Schumacher, T.R. Exploration and exploitation in complex search tasks: How feedback influences whether and where human agents search. Strateg. Manag. J. 2021, 42, 361–385. [Google Scholar] [CrossRef]
| Tool Name | Code Language | Agents’ Properties | Scope | Year |
|---|---|---|---|---|
| AMES [57] | Java | Energy traders, transmission companies, and electrical grid | Analyze bidding of generating companies in wholesale markets | 2007–active |
| AMIRIS [58] | Java | Power plants, storage, traders, marketplaces, forecasters, and policy providers | Modeling of dispatching and simulation of market prices | 2017–active |
| ASSUME [59] | Python | Generation and demand-side agents | Analyze new market designs and dynamics in electricity markets | 2022–active |
| EMLab [60] | Java | Power companies with limited information that make imperfect investment decisions | Explore long-term effects of interacting energy and climate policies | 2010–active |
| ERCOT [61] | Java | Dispatchable and non-dispatchable generators, load-serving entities | Dynamic modeling of wholesale power markets | 2016–active |
| Grid Singularity [62] | Python | Scalable from individuals to nations | Simulate and optimize grid-aware energy markets | 2016–active |
| MASCEM [63,64] | Java | Emulate traders’ activity | Determine the best strategy depending on the context | 2012–active |
| MATREM [65] | Java | Generators, retailers, aggregators, consumers, market, and system operators | Simulate day-ahead and futures electricity markets | 2012–active |
| PowerACE [66] | Java | Utility companies, regulators, storage units, and consumers | Long-term analysis of EU day-ahead energy markets | 2013–active |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trimarchi, S.; Casamatta, F.; Gamba, L.; Grimaccia, F.; Lorenzo, M.; Niccolai, A. A Review of Agent-Based Models for Energy Commodity Markets and Their Natural Integration with RL Models. Energies 2025, 18, 3171. https://doi.org/10.3390/en18123171
Trimarchi S, Casamatta F, Gamba L, Grimaccia F, Lorenzo M, Niccolai A. A Review of Agent-Based Models for Energy Commodity Markets and Their Natural Integration with RL Models. Energies. 2025; 18(12):3171. https://doi.org/10.3390/en18123171
Chicago/Turabian StyleTrimarchi, Silvia, Fabio Casamatta, Laura Gamba, Francesco Grimaccia, Marco Lorenzo, and Alessandro Niccolai. 2025. "A Review of Agent-Based Models for Energy Commodity Markets and Their Natural Integration with RL Models" Energies 18, no. 12: 3171. https://doi.org/10.3390/en18123171
APA StyleTrimarchi, S., Casamatta, F., Gamba, L., Grimaccia, F., Lorenzo, M., & Niccolai, A. (2025). A Review of Agent-Based Models for Energy Commodity Markets and Their Natural Integration with RL Models. Energies, 18(12), 3171. https://doi.org/10.3390/en18123171








