Cable Aging State Diagnosis Adapted from Frequency-Domain Dielectric Spectroscopy and Polarization–Depolarization Current
Abstract
1. Introduction
2. Experimental Scheme
2.1. Thermal Aging Test
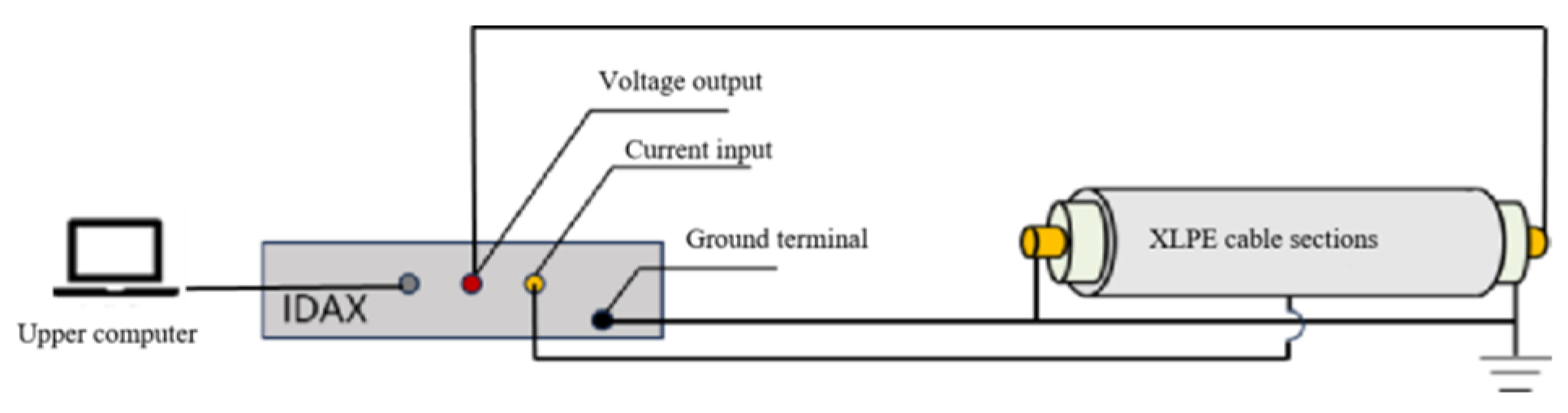
2.2. High-Voltage Dielectric Spectroscopy Test
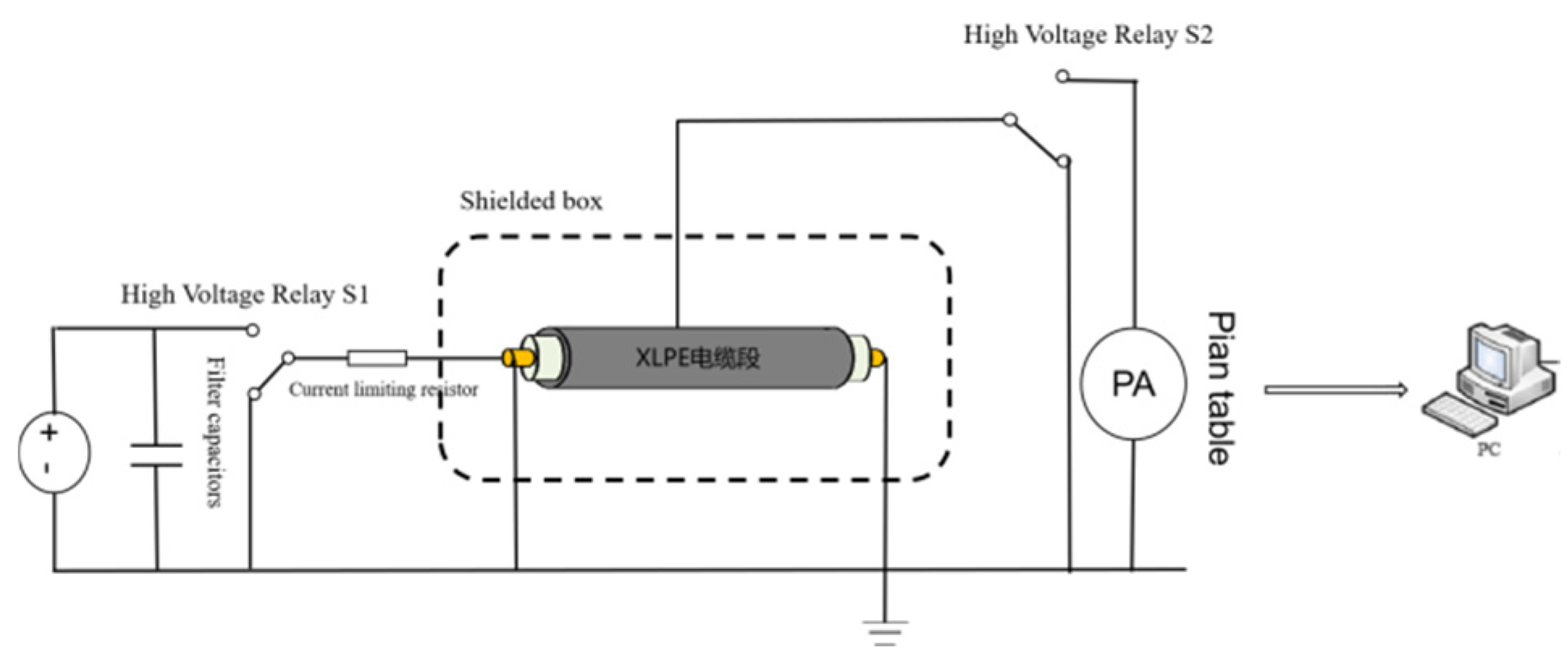
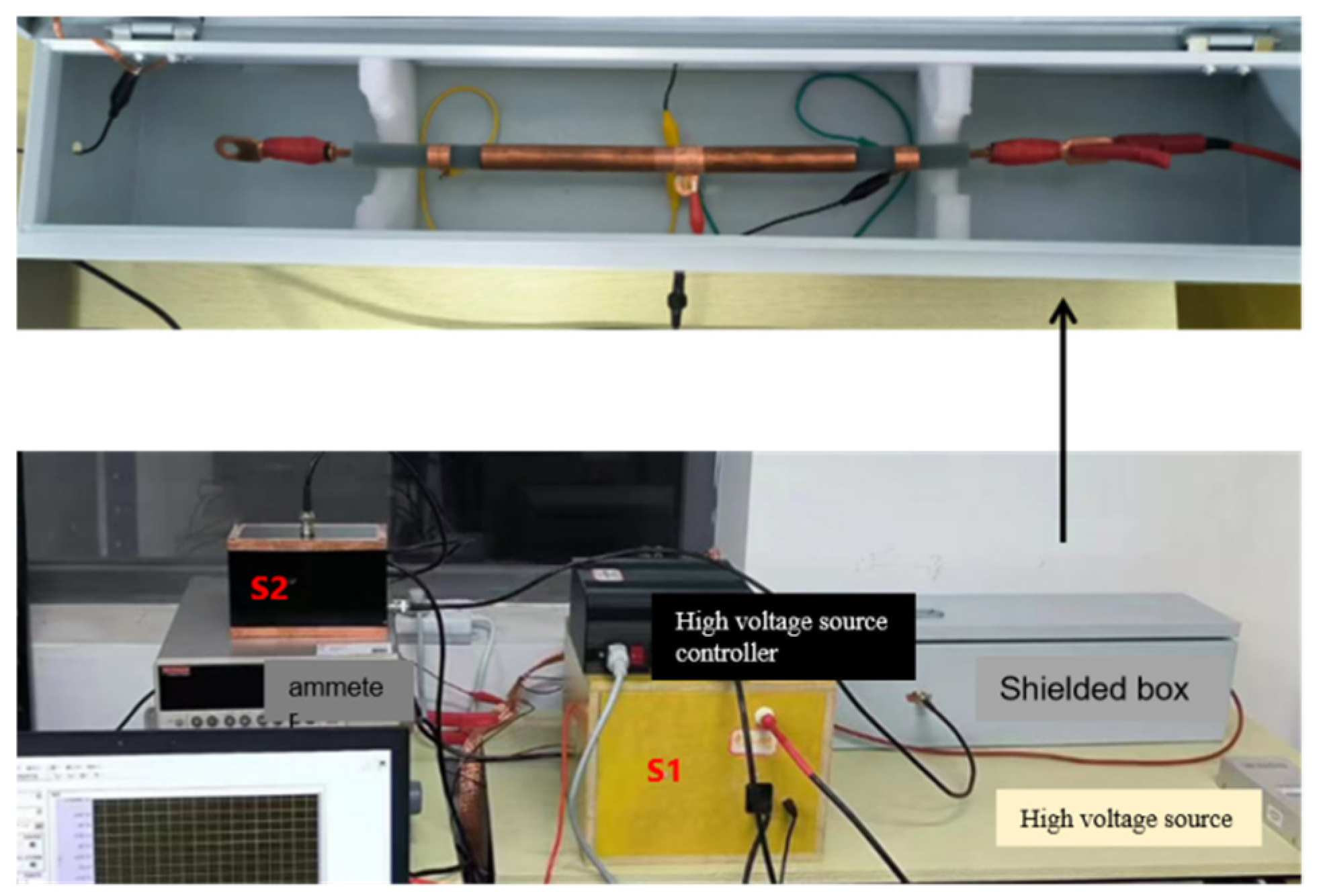
2.3. Polarization and Depolarization Current Test
3. Frequency-Domain Dielectric Spectrum Experimental Results and Analysis
3.1. Dielectric Spectrum Testing of Aged Cables
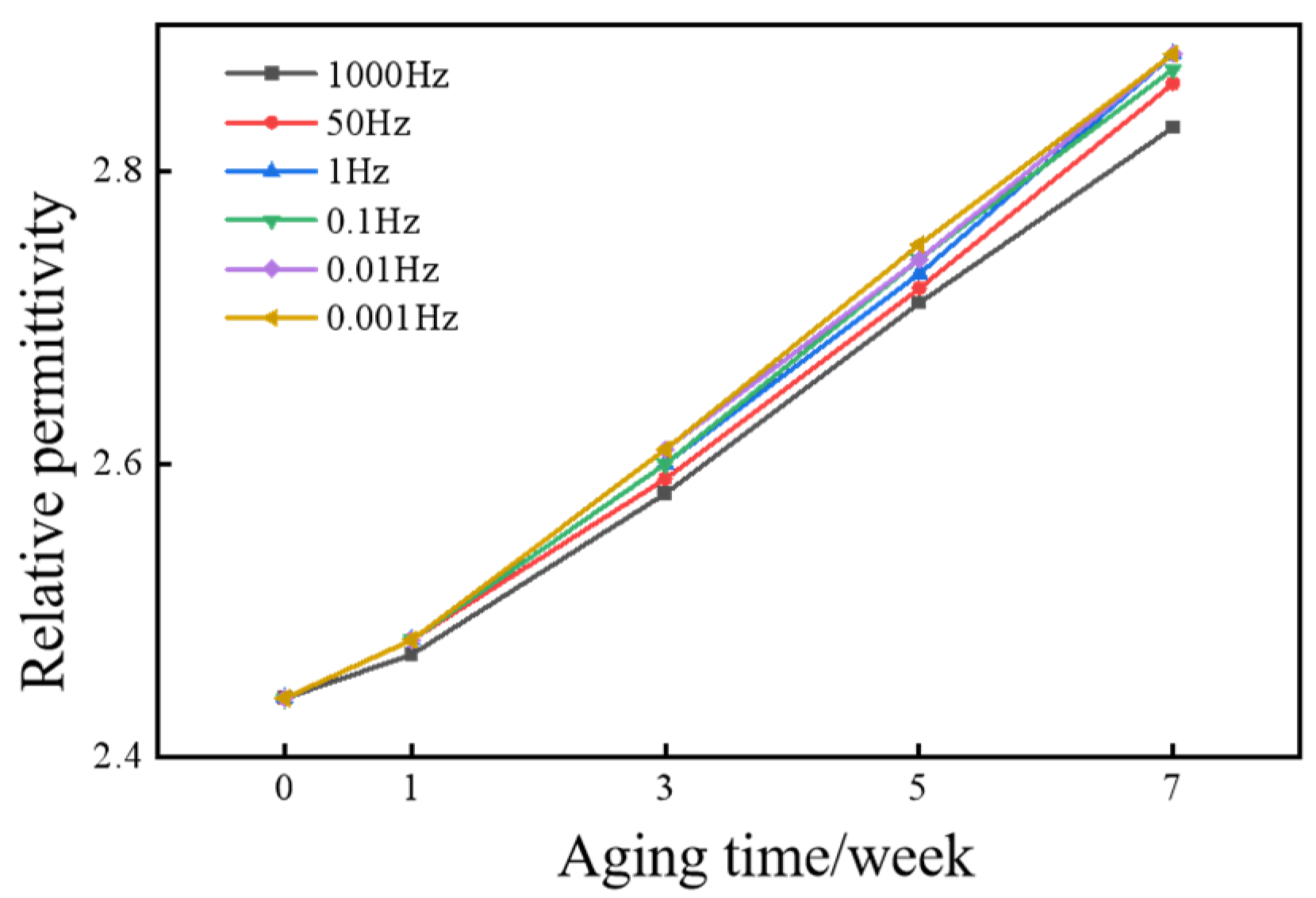
3.2. Relationship Between Cable Insulation Thermal Aging Time and High-Voltage Dielectric Spectrum
4. Polarization and Depolarization Current Testing
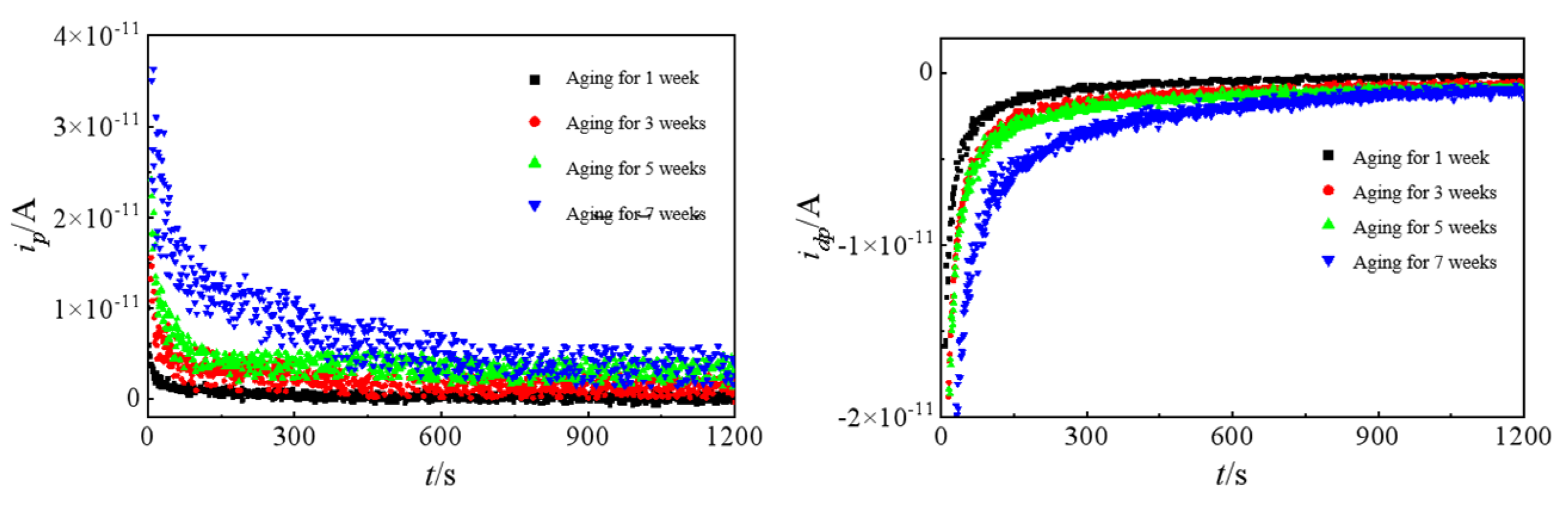
4.1. Polarization and Depolarization Current Tests on Cables
4.2. Relationship Between Thermal Aging Development and Polarization–Depolarization Current
5. Correlation Analysis of Cable Aging State Parameters
6. Conclusions
- (1)
- FDS measurement on aged cables reveals a general upward trend in dielectric loss. The low-frequency dielectric loss factor of XLPE increases with aging duration. The lower the frequency, the greater the increment in dielectric loss. The integral of the dielectric loss from FDS measurement also shows a monotonic increase with aging time, indicating that the integral value serves as an effective indicator for XLPE insulation aging state evaluation.
- (2)
- From the PDC tests, it can be seen that the decay rates of the polarization and depolarization currents significantly decrease after aging, while the steady-state values increase. DC conductivity, space charge density, and carrier mobility are calculated and adapted from the measurement results. Both conductivity and carrier mobility increase notably with aging duration, suggesting that these parameters can be used as reliable indicators of cable insulation aging.
- (3)
- Correlation analysis between aging time and parameters extracted from FDS and PDC tests, including conductivity, charge density (ρ), carrier mobility (μ), charge amount (Q), low-frequency integral, high-frequency integral, and aging parameter (A) shows the strongest correlation between the conductivity and the aging time (r = 0.9, p < 0.05). Outperforming charge density and mobility, the DC conductivity is better suited for aging assessment. In FDS tests, the high-frequency integral exhibits a non-significant correlation with a significance level p > 0.05, whereas the low-frequency integral demonstrates a strong correlation coefficient of 0.99 (p < 0.05), indicating a robust relationship with cable aging degradation. This establishes the low-frequency integral as a reliable metric for characterizing the insulation aging state of cables.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, B.X.; Li, Z.; Yang, Z.; Li, J. Application and research progress of HVDC XLPE cables. High Volt. Eng. 2017, 43, 14–24. [Google Scholar]
- Zhou, Y.; Zhao, J.; Liu, R.; Chen, Z.; Zhang, Y.X. Key technical analysis and prospect of high voltage and extra-high voltage power cable. High Volt. Eng. 2014, 40, 2593–2612. [Google Scholar]
- Werelius, P. Development and Application of High-Voltage Dielectric Spectroscopy for Diagnosis of Medium-Voltage XLPE Cables; Kungliga Tekniska Hogskolan: Stockholm, Sweden, 2001. [Google Scholar]
- Hvidsten, S.; Ildstad, E.; Sletbak, J.; Faremo, H. Understanding water treeing mechanisms in the development of diagnostic test methods. LEEE Trans. Dielectr. Electr. Insul. 2002, 5, 754–760. [Google Scholar] [CrossRef]
- He, D.; Gu, J.; Lu, J.; Wang, W. Electrical-thermal ageing test design of 10 kV XLPE cable. Insul. Mater. 2016, 49, 53–58. [Google Scholar]
- Xue, C. Research on Assessment Method for Insulation Aging State of XLPE Cables; Tianjin University: Tianjin, China, 2014. [Google Scholar]
- Bhumiwat, S.A. On-site non-destructive dielectric response diagnosis of rotating machines. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1453. [Google Scholar] [CrossRef]
- Abou Dakka, M.; Bulinski, A.; Bamji, S.S. On-site diagnostics of medium-voltage underground cross-linked polyethylene cables. IEEE Electr. Insul. Mag. 2011, 27, 34–44. [Google Scholar] [CrossRef]
- Yang, F.; Shen, Y.; Wang, Y.; Zhao, A.; Zhang, X.; Deng, J.; Zhang, G. Thermal Aging Status Diagnosis of XLPE Cable Using Polarization/Depolarization Current Method. High Volt. Eng. 2016, 42, 496–503. [Google Scholar]
- Cai, G.; Liu, X.; Pu, J.; Zhou, K.; Huang, M. Insulation diagnosis of water-treed cables based on polarization and depolarization current method. Insul. Mater. 2016, 49, 61–64+71. [Google Scholar]
- Lu, C.; Guangmao, L.; Sen, Y. Review of research on frequency domain response method and its application in defect location of power cables. South. Power Syst. Technol. 2023, 17, 53–64. [Google Scholar]
- Zhou, K.; Yuan, H.; Li, Y.; Li, M.; Li, Z.; Lin, S. Assessing aging status and type of XLPE cable insulation with a graphic approach based on PDC measurement. IEEE Trans. Power Deliv. 2022, 37, 5114–5123. [Google Scholar] [CrossRef]
- GB/T 11026.1-2012; Electrical Insulating Materials—Thermal Endurance—Part 1: Aging Procedures and Evaluation of Test Results. Jointly Issued by the General Administration of Quality Supervision, Inspection and Quarantine of the People’ Republic of China: Beijing, China, 2012.



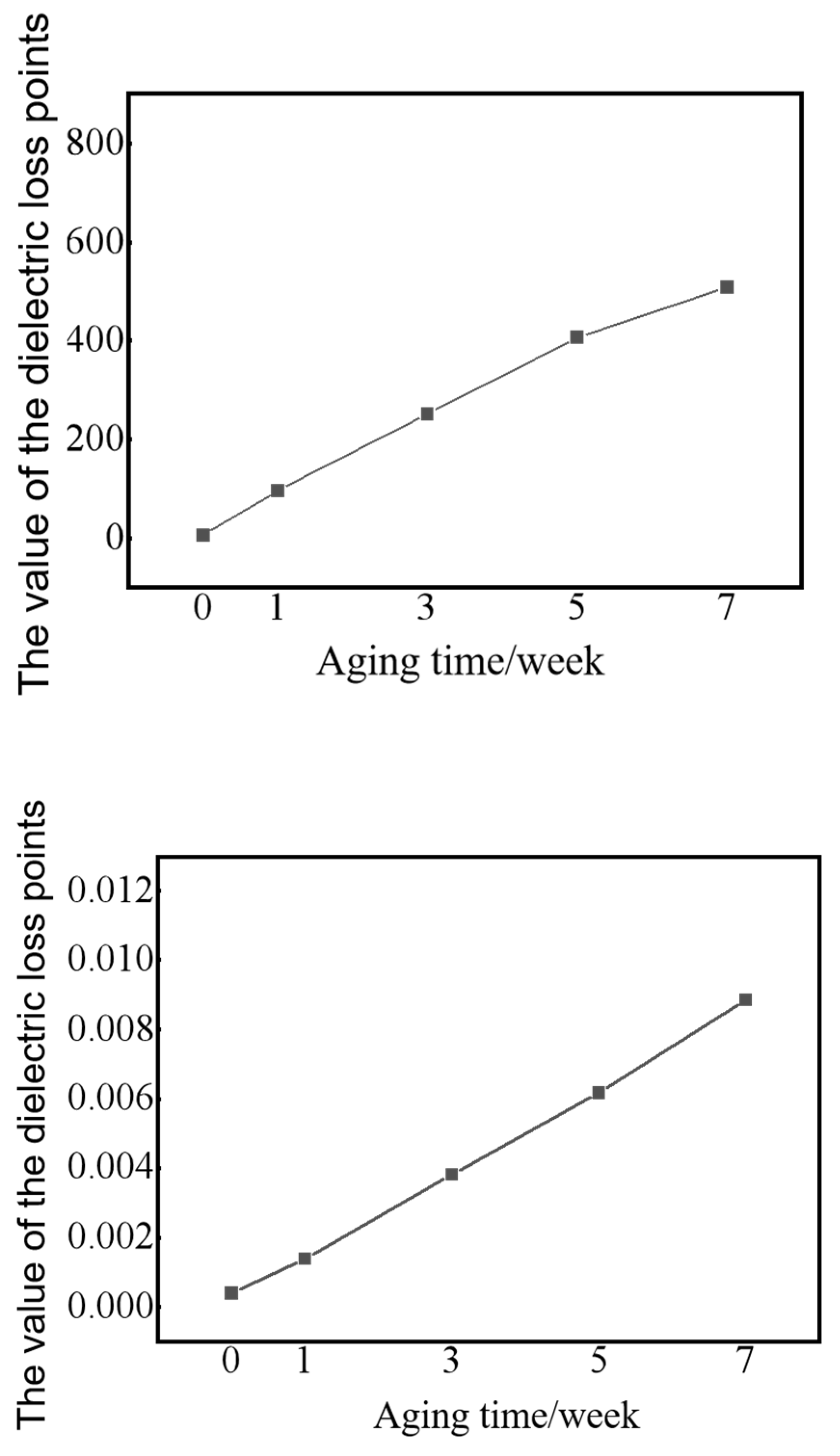

| Aging Time | No Aging | 1 Week Aging | 3 Week Aging | 5 Week Aging | 7 Week Aging |
|---|---|---|---|---|---|
| Low-frequency integration (10−4) | 3.8 | 13.9 | 38.1 | 61.8 | 88.6 |
| High-frequency integration | 6.457 | 97.28 | 251.96 | 406.25 | 508.87 |
| A2 | 1 | 9.36 | 24.52 | 39.59 | 51.06 |
| Aging Time | 1 Week | 3 Weeks | 5 Weeks | 7 Weeks |
|---|---|---|---|---|
| electrical conductivity/×10−17 S·m−1 | 1.86 | 7.31 | 8.81 | 11.9 |
| Aging Time | 1 Week | 3 Weeks | 5 Weeks | 7 Weeks |
|---|---|---|---|---|
| The total amount of charge/C | 1.5 × 10−9 | 2.6 × 10−9 | 2.8 × 10−9 | 3.3 × 10−9 |
| Charge density/C·m−3 | 8.74 × 10−6 | 1.52 × 10−5 | 1.63 × 10−5 | 1.92 × 10−5 |
| Charge mobility/m2·(V·s)−1 | 2.13 × 10−12 | 4.81 × 10−12 | 5.41 × 10−12 | 6.19 × 10−12 |
| Pearson Correlation Coefficient (r) | p | |
|---|---|---|
| Electrical conductivity σ | 0.972 | 0.0281 |
| Charge density ρ | 0.750 | 0.0250 |
| Carrier mobility μ | 0.803 | 0.0197 |
| The total amount of charge Q | 0.952 | 0.0479 |
| Low-frequency integration | 0.990 | 0.0157 |
| High-frequency integration | 0.992 | 0.1255 |
| Aging parameter A | 0.998 | 0.0438 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Zhao, Y.; Ji, H.; Ma, J.; Chen, J.; Li, Z.; Wang, K.; Lv, Z. Cable Aging State Diagnosis Adapted from Frequency-Domain Dielectric Spectroscopy and Polarization–Depolarization Current. Energies 2025, 18, 3169. https://doi.org/10.3390/en18123169
Shang Y, Zhao Y, Ji H, Ma J, Chen J, Li Z, Wang K, Lv Z. Cable Aging State Diagnosis Adapted from Frequency-Domain Dielectric Spectroscopy and Polarization–Depolarization Current. Energies. 2025; 18(12):3169. https://doi.org/10.3390/en18123169
Chicago/Turabian StyleShang, Yingqiang, Yang Zhao, Hongquan Ji, Jingyue Ma, Jiren Chen, Ziheng Li, Kejia Wang, and Zepeng Lv. 2025. "Cable Aging State Diagnosis Adapted from Frequency-Domain Dielectric Spectroscopy and Polarization–Depolarization Current" Energies 18, no. 12: 3169. https://doi.org/10.3390/en18123169
APA StyleShang, Y., Zhao, Y., Ji, H., Ma, J., Chen, J., Li, Z., Wang, K., & Lv, Z. (2025). Cable Aging State Diagnosis Adapted from Frequency-Domain Dielectric Spectroscopy and Polarization–Depolarization Current. Energies, 18(12), 3169. https://doi.org/10.3390/en18123169






