Characterization of Space Charge Accumulations in Alternative Gas-to-Liquid Oil-Immersed Paper Insulation Under Polarity Reversal Voltage Scenarios

Abstract

Due to its advantages, such as its corrosive sulfur-free property and high purity, gas-to-liquid (GTL) oil is regarded as an excellent alternative to conventional naphthenic mineral oil in the oil/paper composite insulation of UHV converter transformers. In such application scenarios, under the condition of voltage polarity reversal, charge accumulation is likely to occur along the liquid/solid interface, which leads to the distortion of the electric field, consequently reducing the breakdown voltage of the insulating material, and leading to flashover in the worst case. Therefore, understanding such space charge characteristics under polarity-reversed voltage is key for the insulation optimization of GTL oil-filled converter transformers. In this paper, a typical GTL oil is taken as the research object with naphthenic oil as the benchmark. Electroacoustic pulse measurement technology is used to study the space charge accumulation characteristics and electric field distribution of different oil-impregnated paper insulations under polarity-reversed conditions. The experimental results show that under positive–negative–positive polarity reversal voltage, the gas-impregnated pressboard exhibits significantly higher rates of space charge density variation and electric field distortion compared with mineral oil-impregnated paper. In stage B, the dissipation rate of negative charges at the grounded electrode in GTL oil-impregnated paper is 140% faster than that in mineral oil-impregnated paper. In stage C, the electric field distortion rate near the electrode of GTL oil-impregnated paper reaches 54.15%. Finally, based on the bipolar charge transport model, the microscopic processes responsible for the differences in two types of oil-immersed papers are discussed.

1. Introduction

High-voltage direct current (HVDC) transmission is a key technology to realize the west-to-east transmission of electricity under the dual-carbon strategy in China, and the converter transformer, as the core equipment for power transmission in the extra-high voltage system, mainly adopts oil–paper insulation structure [1]. In this application context, traditional naphthenic oil has many disadvantages, e.g., high corrosive sulfur content, large aromatic hydrocarbon proportion, and low fire resistance [2]. Therefore, the search for more environmentally friendly and stable insulating liquids has been a core issue that requires in-depth research for converter transformers in HVDC transmission scenarios. Gas-to-liquid (GTL) oil, derived from natural gas via Fischer–Tropsch conversion, has advantages such as low aromatic hydrocarbons and high purity, and has the potential to become an alternative to naphthenic oil in converter transformers. In practical operation, converter transformers would be subjected to direct current (DC), alternating current (AC), polarity-reversed, and other complex operating voltages, of which, polarity reversal voltage is likely to cause the space charge accumulations in insulation materials, consequently distorting the local electric field and causing flashover [3]. Therefore, understanding such space charge characteristics under polarity-reversed voltage is key for the insulation optimization of GTL oil-filled converter transformers.

For the space charge measurements in oil–paper insulation, the effects of variables, such as externally applied electric field, ambient temperature, and aging degree of the testing samples on space charge and electric field characteristics inside insulation materials, have been carefully studied in the previous literature. Katsumi [4] et al. used Kerr’s photoelectric technique to measure the electric field distribution of the oil–paper insulation, carried out an experimental study on 3 mm oil–paper insulation under 10 kV polarity reversal voltage, and found that the discharge was different under two polarity reversal cases, i.e., negative–positive and positive–negative voltage reversals, due to the different polarities of space charge accumulated on the surface of the oil–paper insulation. Zhang et al. measured the space charge distribution inside the oil–paper insulation at different temperatures using the pulsed electroacoustic (PEA) technique and found that the double-layer transient electric field conforms to be capacitive at room temperature, whereas the rapid change in charge density at the oil–paper interface at 60 °C leads to the double-layer transient electric field distribution to conform to be resistive [5]. Zhou et al. studied the effect of aged oil and paper on the space charge characteristics at the oil/paper interface through the PEA measurement technique, and found that, under the polarity reversal electric field, the aging state of the oil dominates the surface charge accumulation processes [6,7]. However, up to now, research on the differences between GTL oil and traditional naphthenic oils in terms of space charge accumulation and dissipation characteristics during polarity reversal is rare.

With the advances of computing technology, finite element simulation provides an effective supplement to the experimental work on space charge accumulations. He et al. used bipolar charge transport and hydrodynamic drift diffusion theory to establish a composite insulation model, and studied the impact of DC voltage amplitude, charge mobility, and other factors on spaces discharges at the oil/paper interface [8]. Based on the bipolar charge transport theory, Li et al. establishes a numerical model for calculating charge distributions along multi-layer liquid–solid insulation interfaces under AC and DC composed voltage stresses, as well as the influence of insulation board thickness and aging state on space charge accumulation rates [9].

Although a large amount of research has been conducted on the space charge characteristics of oil–paper insulation under polarity-reversed voltages, the space charge accumulation of GTL oil under voltage polarity reversal conditions and the corresponding mechanism is still unclear. In order to solve these problems, this paper builds a PEA testing system to measure the space charge and electric field distributions of GTL oil-impregnated paper under voltage polar reversal conditions, with a traditional naphthenic oil as the benchmark. The differences in space charge density, charge change rate, and electric field at the ground electrode are discussed. In addition, based on the bipolar charge transport model, a numerical model is built to calculate the differences in the charge mobilities of these two oils on space charge and electric field distributions.

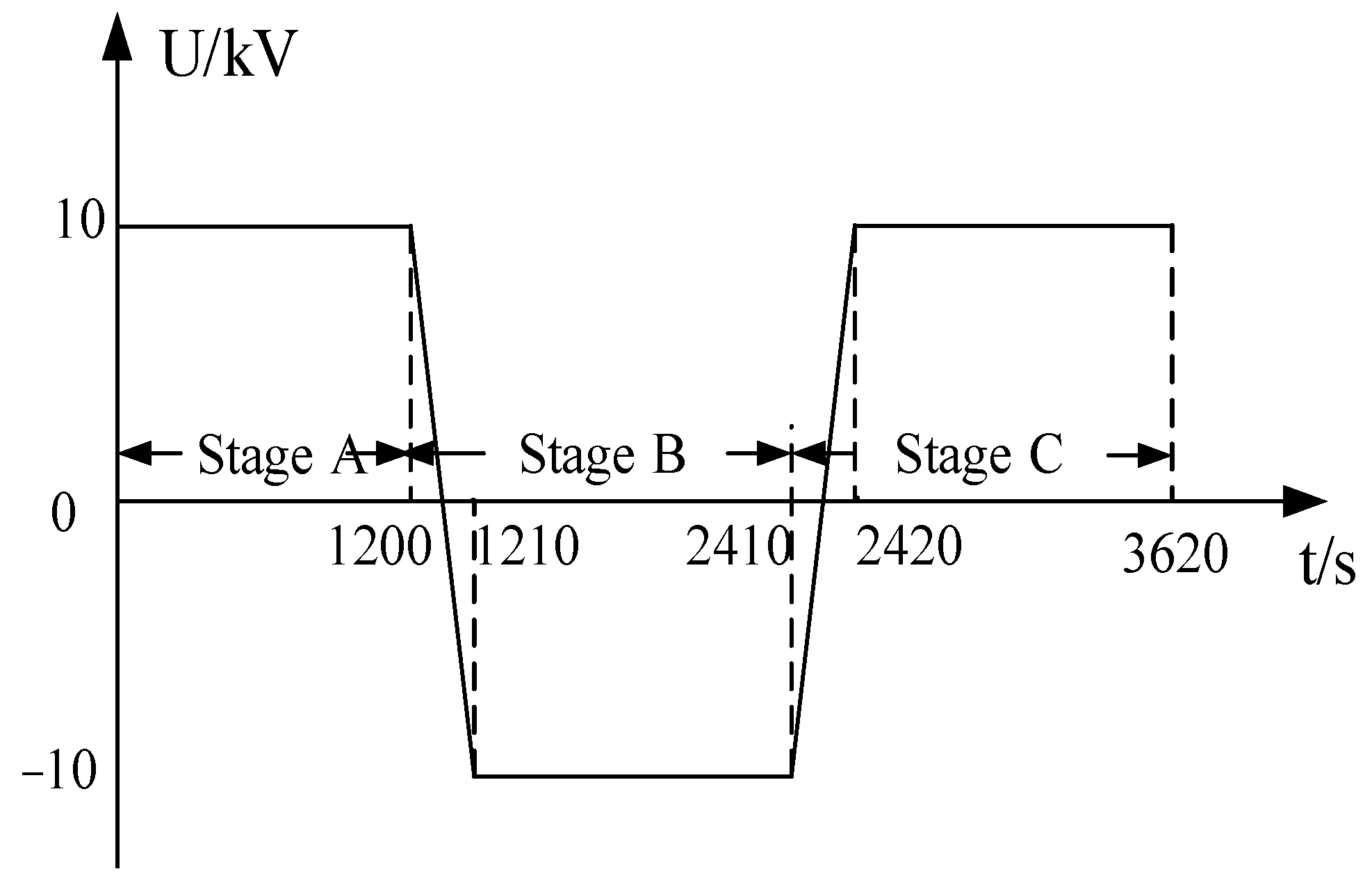
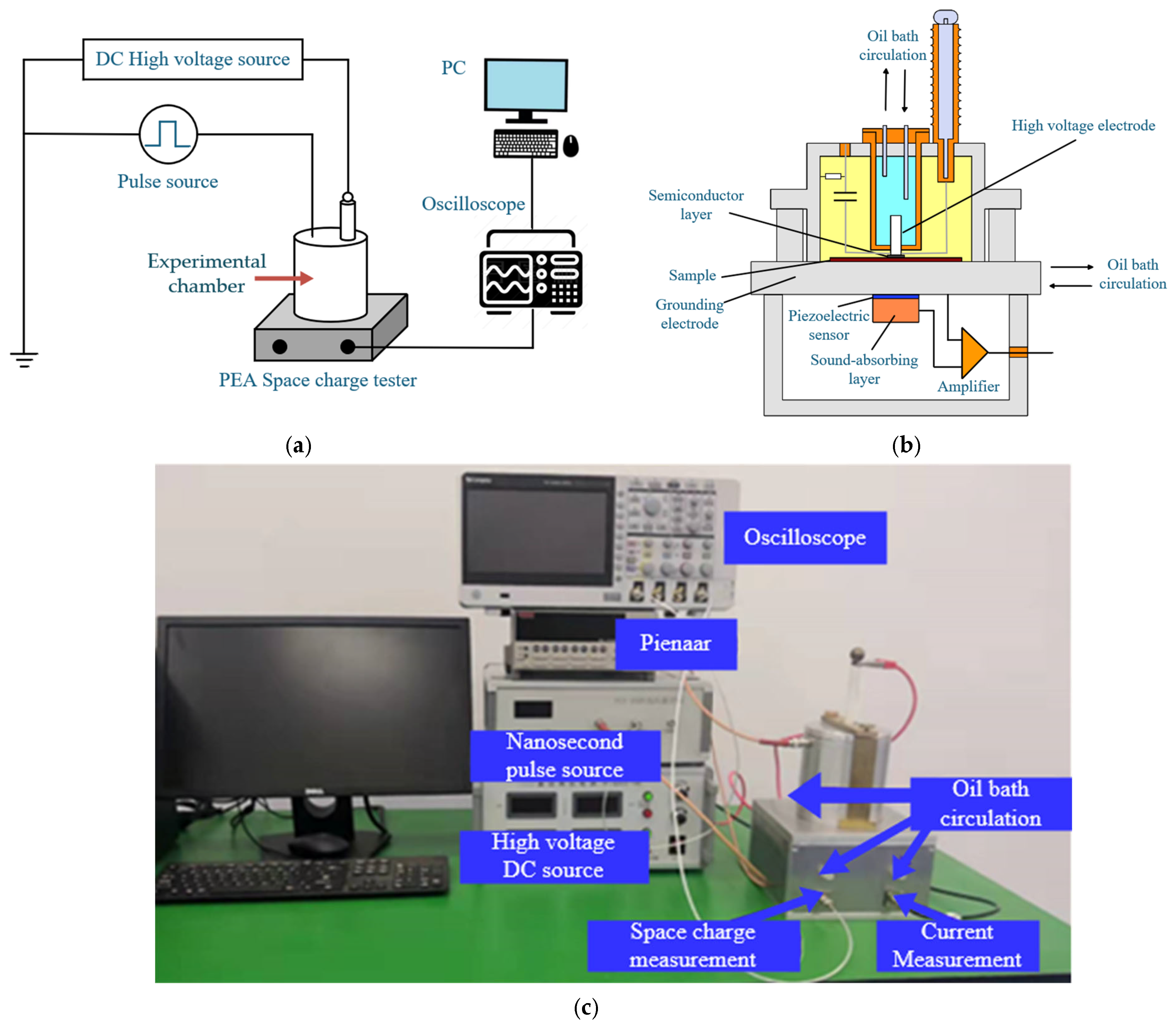
2. Experimental Methodology

The insulating oil samples used in this paper are isoparaffinic GTL oil (Shell Diala S4 ZX-I) and naphthenic oil (Shell Diala S3 ZX-I), and the insulating paper is a special paperboard for transformers that meets the requirements of IEC 60554-3-5-2020 [10]. The key parameters for the two oil samples in new conditions are shown in

Table 1. Key parameters for GTL oil and naphthenic oil.

Items	Experimental Methods	Shell Diala S3 ZX-IG	Shell Diala S4 ZX-I
Density/(kg/m3)	IEC 60867 [13]	878	805
Flash point/(°C)	ISO 2719 [14]	140	191
Pour point/(°C)	ISO 3016 [15]	−60	−42
Conductivity/(S/m)	IEC 60247 [16]	3.9 × 10−13	8.9 × 10−13
Dielectric loss factor	IEC 60247 [16]	0.00281	0.00053
Relative permittivity	IEC 60247 [16]	2.02	2.00
AC Breakdown voltage pretreatment/kV	IEC 60156 [17]	>30	70
AC Breakdown voltage after treatment/kV	IEC 60156 [17]	>70	78

[11,12].

Before the experiments, two types of insulating oils and paper cardboard were pretreated as follows. The insulating oils were heated at 85 °C by vacuum for 48 h to ensure the water content was less than 10 ppm.

The insulating cardboards were firstly cut into 60 × 60 × 0.5 mm slides with a total of 20. These small samples were then subjected to a drying treatment under 105 °C and 133 Pa with a duration of not less than 48 h, and then cooled down to room temperature and impregnated with dried oil samples in vacuum condition to obtain the desired oil-impregnated paper samples.

Two types of oil-immersed paper specimens were then applied with polarity reversal voltage as shown in Figure 1. The samples were first applied with +10 kV voltage for 1200 s. Then, the voltage polarity was reversed to −10 kV within 10 s and held for 1200 s. A second reversal within another 10 s restored the initial polarity voltage for 1200 s. In other words, the whole voltage polarity reversal test was divided into three stages, i.e., stage A (0–1200 s) for initial DC polarization; stage B (1200–2410 s) for the first polarity reversal to the end of negative polarity polarization; and stage C (2410–3620 s) for the second polarity reversal to the end of positive polarity polarization. The voltage reversal time met the voltage reversal time (<2 min) specified in the IEC 61378-2 standard [18] for the converter factory polarity reversal test [19]. The practical test platform is shown in Figure 2. The test temperature was controlled at 20 ± 0.1 °C by oil circulating bath, the polarity reversal voltage was applied to the semiconductor (SC) high-voltage electrode, where the specimen generated charge accumulation under the action of the applied electric field, and the grounded aluminum (Al) electrode’s PVDF thin film piezoelectric transducer received the vibration acoustic wave and converted the vibration acoustic wave into the electrical signal that is linear with the distribution of the space charge [5]. The test pulse width was 10 ns and the frequency was 1 kHz. Due to the inherent attenuation characteristics of the piezoelectric sensor for receiving sound signals, the experimental results focus on the charge data at the proximal end of the grounded electrode [20].

3. Experimental Results and Discussions

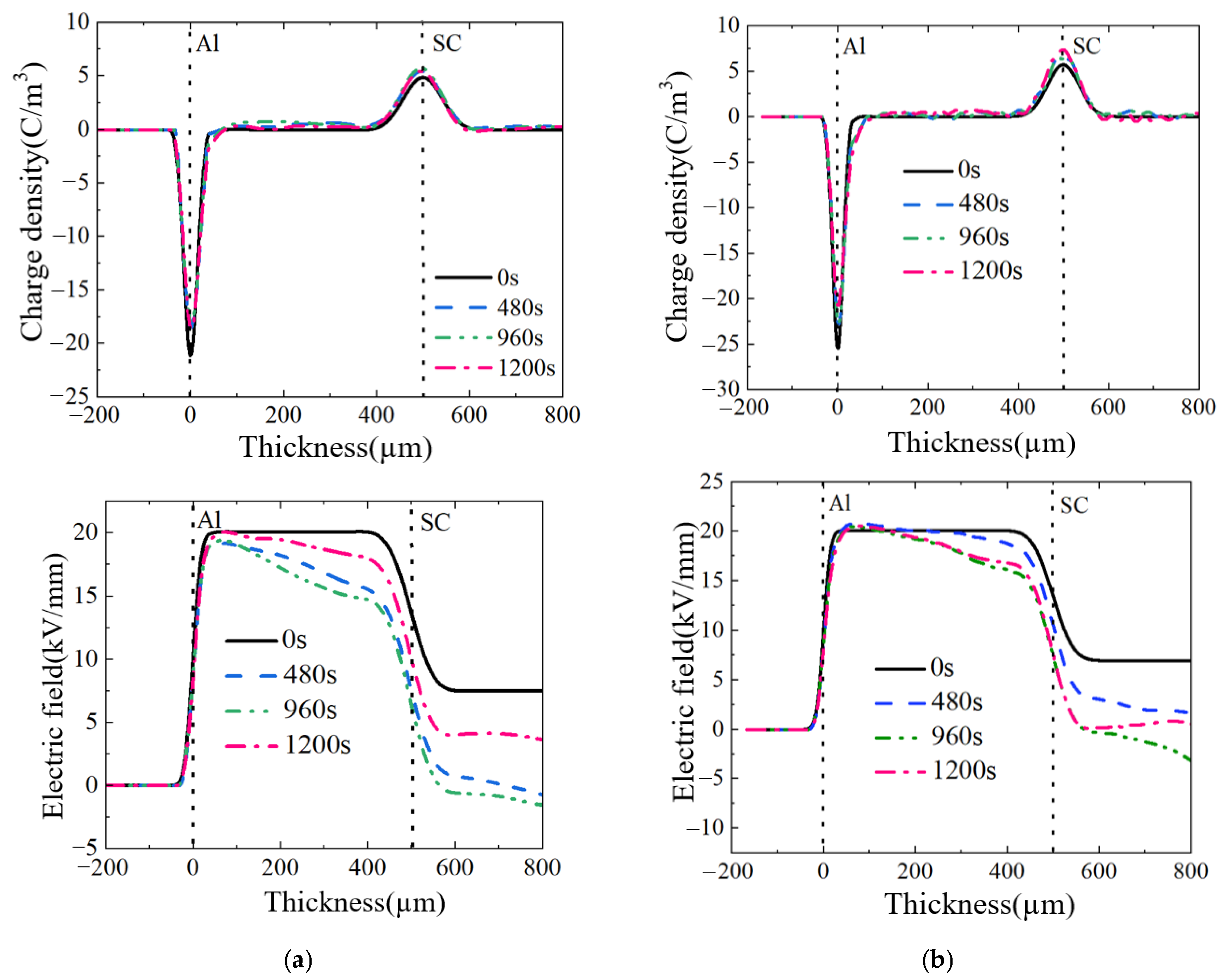
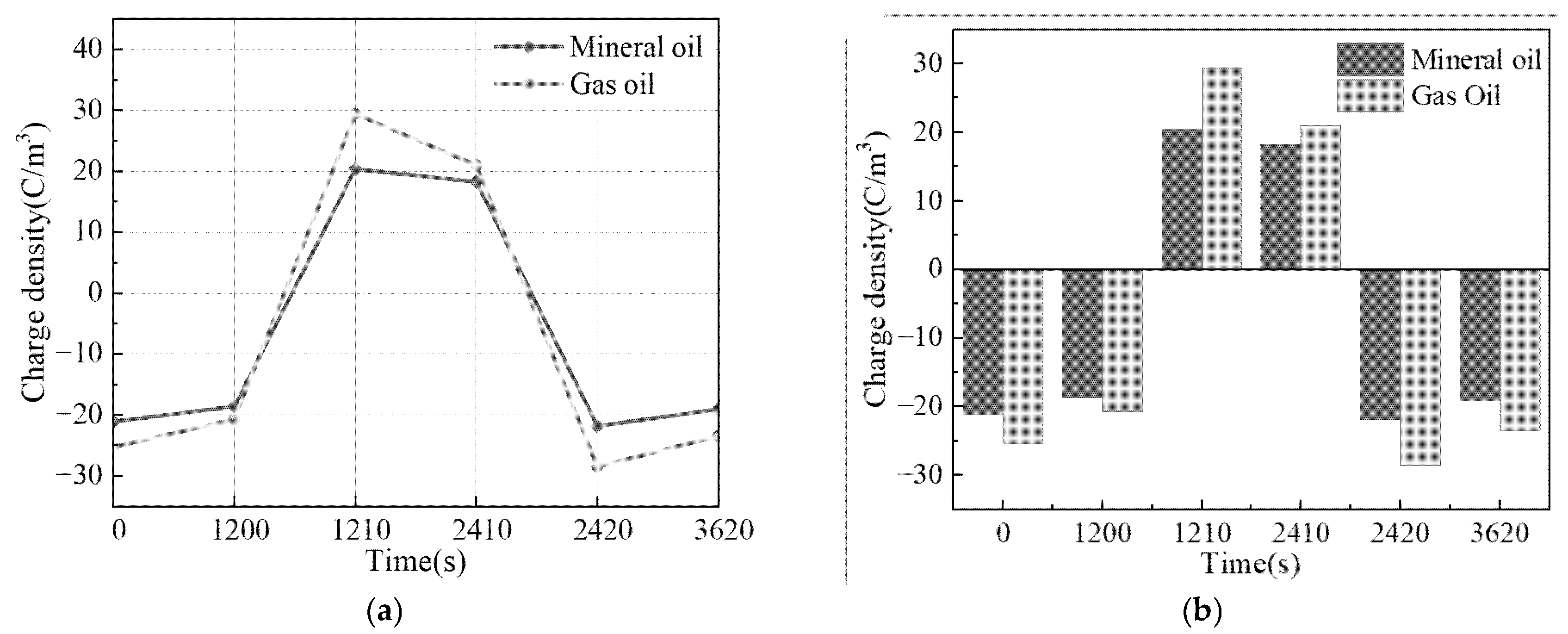
3.1. Stage A

The positive DC voltage, as shown in stage A of Figure 1, was applied to the high voltage electrode of the PEA test chamber. The internal charge distribution of the two specimens is shown in Figure 3. The space charge induced in the grounding electrode in the naphthenic oil-impregnated paper specimen decreases from −21.08 C/m³ to −18.71 C/m³, and the charge of the gas oil-impregnated paper specimen decreases from −25.27 C/m³ to −20.73 C/m³. The negative polar charge accumulated at the grounding electrode decreases gradually under the DC stresses.

At the initial energization time of 0 s, the space charge has not accumulated yet, the space electric field is equal to the applied electric field, with the increase in polarization time, and the uneven distribution of space charge accumulation leads to a space field strength more than 20 kV/mm. The field strength at the vicinity of the grounding electrode of the gas oil-impregnated paper is higher than that of the naphthenic oil-impregnated paper after the two specimens are polarized for 1200 s.

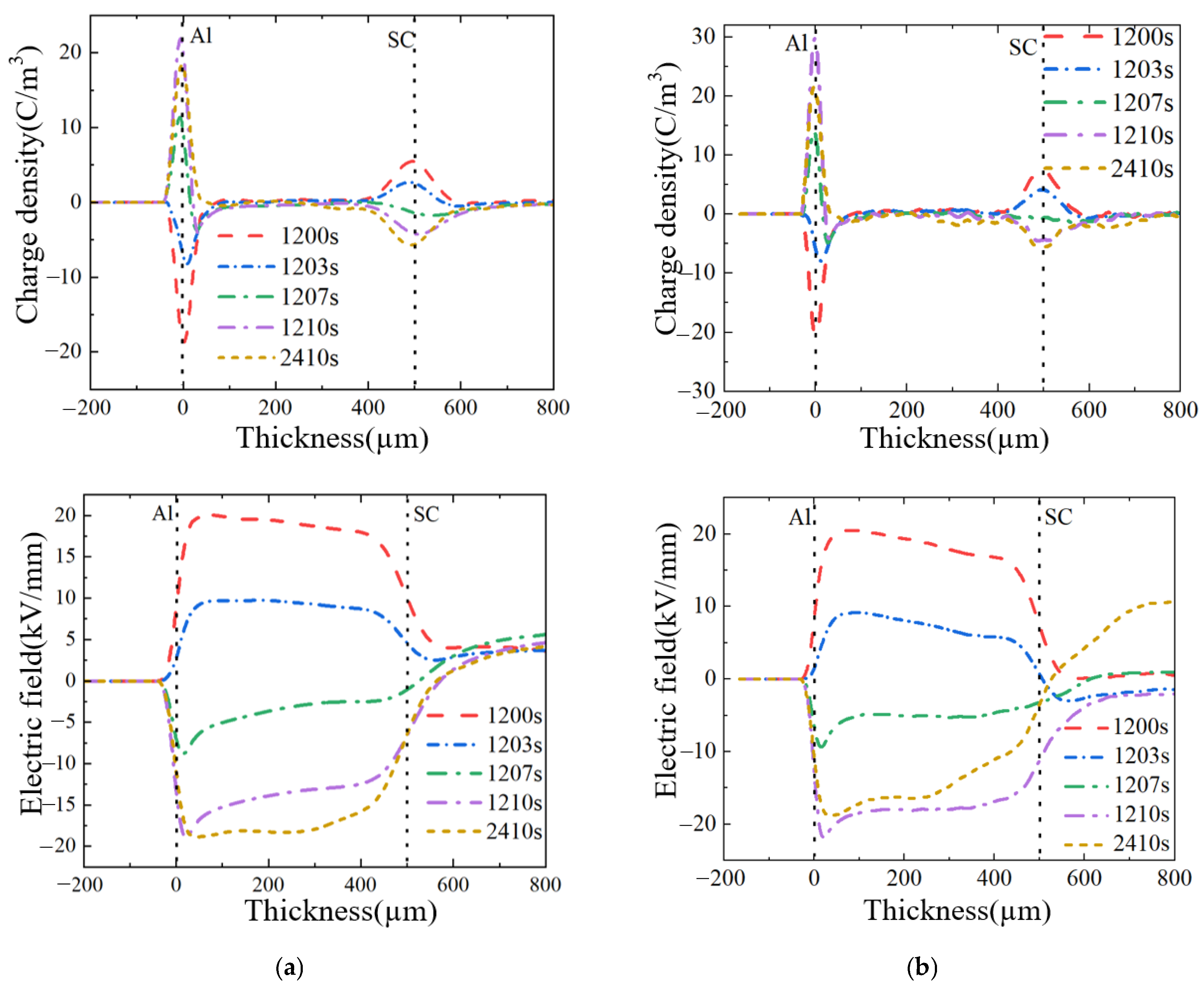
3.2. Stage B

Figure 4 shows the space charge accumulations of the two specimens in stage B. When the voltage polarity has not been reversed, the negative polar charge near the grounding electrode is dissipated more due to migration and recombination. At the end of the voltage polarity reversal, the space charge of the two samples at the grounding electrode reaches the maximum value, and the space charges at the grounding electrode of the naphthenic oil and GTL oil-impregnated papers are 21.9 C/m³ and 29.4 C/m³, respectively. The negative polar stagnant charge occurs near the grounding electrode, and the phenomenon is due to the hysteresis effect of the charge in the process of polarity reversal. The peak value of the density of the stagnant charge of the naphthenic oil- and the GTL oil-impregnated papers are −4.21 C/m³ and −4.16 C/m³, respectively. After 1200 s of negative DC field polarization, the space charge at the grounding electrode of GIL oil-immersed paper was reduced to 21.01 C/m³, and that at the grounding electrode of naphthenic oil-immersed paper was 18.41 C/m³. The field strengths of the two types of oil-impregnated paper samples are shown in Figure 4. The aberrant electric field of mineral oil reached a relatively smooth state after 1200 s of depolarization of the negative DC field, and has a high symmetry compared with the positive DC polarization for 1200 s. In contrast, the field intensity inside the specimen is lower than that before polarization after the GTL oil-impregnated paper is polarized under a negative DC field for 1200 s, whereas it does not have symmetry compared with the electric field after polarization for 1200 s under a positive polarity DC field.

3.3. Stage C

Figure 5 shows the space charge and space electric field changes in the specimens at stage C (2410–3620 s). At the end of the polarity reversal, the space charge density at the grounding electrode of naphthenic oil- and the GTL oil-impregnated papers reaches −22.2 C/m³ and −28.42 C/m³, respectively, whereas the stagnant positive polar charge densities at the electrodes reach the highest values of 1.7 C/m³ and 0.6 C/m³, respectively, with respect to the stagnant charge reductions by 2.51 C/m³ and 3.56 C/m³ at the polarity reversal in stage B, respectively.

After 1200 s of polarization by the positive polarity DC field, the charges at the grounding electrode of the naphthenic oil- and GTL oil-impregnated paper were reduced by −2.84 C/m³ and −4.59 C/m³, respectively. At the end of the applied voltage polarity reversal, there are still obvious electric field protrusions near the ground electrode in both oil–paper insulations. The peak electric field strength at the protrusion in mineral oil–paper reaches 20.45 kV/mm, whereas that in gas-to-liquid oil-impregnated paper reaches up to 23.52 kV/mm. At 3620 s, the maximum values near the grounding pole of the two specimens were 20.5 kV/mm and 26.11 kV/mm, respectively, and the field strength distortion rate in the gas-fed oil-immersed paper insulation reached 54.15%, which demonstrated easier insulation failure.

The differences in the variation in space charge at the grounding electrode between mineral insulating oil- and GTL oil-impregnated paper are shown in Figure 6, where there is a significant difference in the dynamic characteristics of the charge of the two oil-impregnated paper insulating specimens at the grounding electrode. In terms of the total amount of space charge density, space charge is injected more into the GTL oil-immersed paper. It can be seen by comparing the slope characteristics of the curves, that the rate of charge change in the naphthenic oil-impregnated paper specimens under the three electric field conditions (stage A, B, and C) is always lower than that of the GTL oil-impregnated paper specimens. The rate of space charge transport within the GTL oil-immersed paper is faster, especially in the negative polarity DC field (1210–2410 s), the charge decay characteristics of the space charge inside the gas oil-impregnated paper specimen are more obvious, and the rate of charge dissipation at the grounding electrode is about 140% higher than that of the conventional naphthenic oil-impregnated paper.

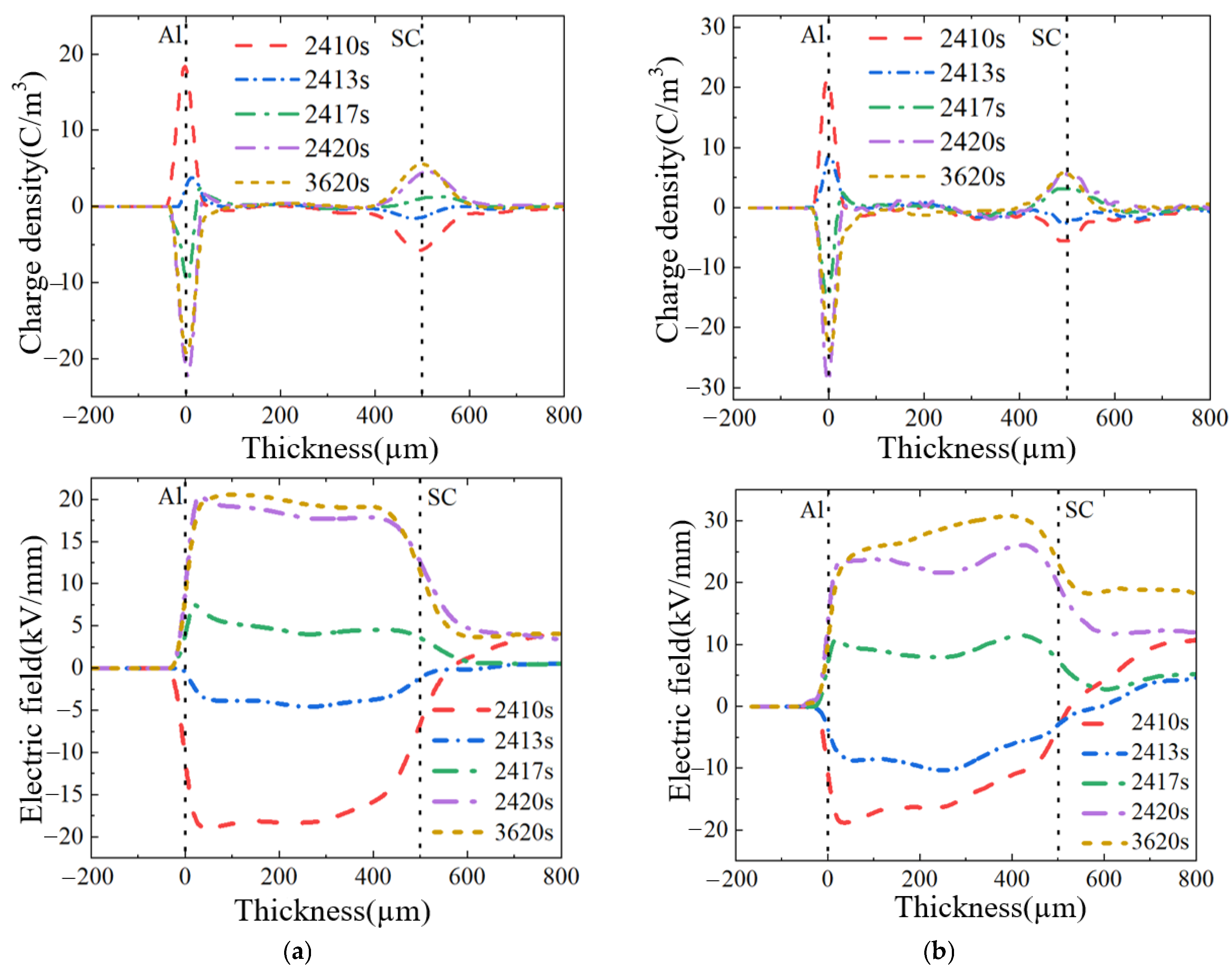
4. Numerical Calculations for Microscopic Analyses

In the experiment, it was found that the charge dynamic properties of the two oil-impregnated papers near the grounded electrode showed obvious differences, i.e., after the first voltage inversion, the charge dissipation rate and the amount of retained charge of the two have the largest difference. This suggests that the difference in charge transport ability within the material changes the equilibrium state of charge movement and complexity and affects the charge distribution. To verify this conjecture, a bipolar charge transport model is constructed using COMSOL 6.2, a multi-physics field coupling simulation platform, to study the dynamic process of different charge carriers’ mobilities during the electric field polarity reversal [21]. The right-hand side of Equations (1)–(4) describe the inter-charge carrier transitions among four morphology charge carriers, namely, free electrons (eμ), trapped electrons (et), free positive charge (hμ), and trapped positive charge (ht), as well as the effect on the space charge distribution, respectively. It is verified that the model can effectively reflect the characteristics of the charge behavior inside the solid medium:

$${\displaystyle \frac{\partial {\rho }_{e\mu }}{\partial t}}-\nabla \cdot \left({\rho }_{e\mu }{\mu }_{e\mu }E\right)=-S_1{\rho }_{ht}{\rho }_{e\mu }-S_3{\rho }_{h\mu }{\rho }_{e\mu }-B_e{\rho }_{e\mu }(1+{\displaystyle \frac{{\rho }_{e\mu }}{N_{et0}}})+D_e{\rho }_{et}$$

(1)

$${\displaystyle \frac{\partial {\rho }_{h\mu }}{\partial t}}+\nabla \cdot \left({\rho }_{h\mu }{\mu }_{h\mu }E\right)=+S_2{\rho }_{et}{\rho }_{h\mu }+S_3{\rho }_{e\mu }{\rho }_{h\mu }-B_h{\rho }_{h\mu }(1-{\displaystyle \frac{{\rho }_{h\mu }}{N_{ht0}}})+D_h{\rho }_{ht}$$

(2)

$${\displaystyle \frac{\partial {\rho }_{et}}{\partial t}}=-S_2{\rho }_{h\mu }{\rho }_{et}-S_0{\rho }_{ht}{\rho }_{et}+B_e{\rho }_{e\mu }(1+{\displaystyle \frac{{\rho }_{et}}{N_{et0}}})-D_e{\rho }_{et}$$

(3)

$${\displaystyle \frac{\partial {\rho }_{ht}}{\partial t}}=+S_1{\rho }_{e\mu }{\rho }_{ht}+S_0{\rho }_{et}{\rho }_{ht}+B_h{\rho }_{h\mu }(1-{\displaystyle \frac{{\rho }_{h\mu }}{N_{ht0}}})-D_h{\rho }_{ht}$$

(4)

where S₀, S₁, S₂, and S₃ are the composite coefficients, B_e and B_h are the trapped coefficients of free electrons and free positive charges, respectively, and D_e and D_h are the de-trapped coefficients of trapped electrons and positive charges, respectively [8].

The electron and positive charge injection densities satisfy the Schottky injection equation:

$$J_e=A{T}^2\exp (-{\displaystyle \frac{q{w}_{ei}}{K_{b}T}}+{\displaystyle \frac{q}{K_{b}T}}\sqrt{{\displaystyle \frac{qE}{4\pi {\epsilon }_0{\epsilon }_r}}})$$

(5)

$$J_h=A{T}^2\exp (-{\displaystyle \frac{q{w}_{hi}}{K_{b}T}}+{\displaystyle \frac{q}{K_{b}T}}\sqrt{{\displaystyle \frac{qE}{4\pi {\epsilon }_0{\epsilon }_r}}})$$

(6)

where $A$ is Richardson’s constant, $T$ is the temperature set by the simulation, and K_b is Boltzmann’s constant. The model is based on Poisson’s equation to establish the connection between the space charge and the transient space electric field in the oil–paper insulating medium:

$$-\nabla \cdot ({\epsilon }_{rp}{\epsilon }_0\nabla \phi )={\rho }_{e\mu }+{\rho }_{h\mu }+{\rho }_{et}+{\rho }_{ht}$$

(7)

For the simulation, the model sets the thickness of the insulating cardboard to 0.5 mm and takes the data of a truncated line in the direction of the thickness of the insulating cardboard as the object of analysis. The simulation parameters are listed in

Table 2. Simulation parameters for numerical calculations.

Parameters	Numerical Value	Unit	Meaning
ε0	8.854 × 10−12	F/m	Vacuum dielectric constant
εr	3.7	1	Relative dielectric constant of paperboard
Be	0.008	1/s	Entrapment factor of free electrons
Bh	0.007	1/s	Entrapment factor for free positive charge
ωei	1.18	eV	Injection barrier for free electrons
ωhi	1.20	eV	Injection barrier for a free positive charge
μeμ	5 × 10−15	m2/(V·s)	Small mobility of free electrons
μeμ	5 × 10−13	m2/(V·s)	Large mobility of free electrons
μhμ	4 × 10−15	m2/(V·s)	Small mobility of free positive charge
μhμ	4 × 10−13	m2/(V·s)	Large mobility of free positive charge
S0	0	m3/(s·C)	Composite coefficients of incoming electrons and incoming positive charges
S1	1 × 10−5	m3/(s·C)	Complexity factor of free electrons with incoming positive charge
S2	1 × 10−5	m3/(s·C)	Composite coefficient of free positive charge and incoming electrons
S3	1 × 10−5	m3/(s·C)	Composite coefficient of free electrons and free positive charges
A	1.2 × 106	A/(m·K)2	Richardson’s constant
Kb	1.3806 × 10−23	J/K	Boltzmann’s constant

. The mobility, as a core parameter, was reasonably configured based on the experimentally measured values from the tests in References [22,23]. The other parameter settings refer to References [8,9], where the polarity reversal voltage waveform is positive polarization voltage in 0–1200 s, polarity reversal time in 1200–1210 s, depolarization time ranges from 1210 to 3010 s, and the applied polarization field strength is 20 kV/mm. The principal model is shown in Figure 7.

Figure 8 shows the comparison between the experimental and simulated space charges before and after polarity reversal. The correlation coefficients between the experimental and simulation data reach 0.940 and 0.794 before and after polarity reversal, respectively. These results demonstrate that the simulation exhibits good consistency with the experimental observations in characterizing the dynamic evolution trends of space charges.

It is worth noting that the spatial internal charge density obtained from the simulation is lower than the experimental value, which mainly stems from the fact that the charge trap effect existing in the actual insulating paper has not been fully modeled. The narrower range of charge distribution near the electrodes in the simulation may be related to the fact that the actual specimen has a higher trap density near the electrodes. By tuning the parameters, it is possible to isolate the influence of a single physical factor on charge transport.

Figure 9 shows the space charge distribution curves inside the insulation for different mobilities. In the initial polarization stage, the charge polarity near the electrode is dominated by the field injection mechanism and the space charge at the electrode continues to accumulate with the increase in the pressurization time. Additionally, the charge at the grounded electrode under the large and small mobility is −0.62 C/m³ and −0.31 C/m³, respectively, at the time of 1210 s. With the increase in free charge carrier mobility, both the spatial charge density and distribution range within the insulating material exhibit significant enhancement. This phenomenon arises because charge carriers with lower mobility are more likely to be captured by traps near the electrodes during their migration through the dielectric medium, thereby reducing internal space charge density. In contrast, rapid carrier migration promotes the deeper trapping of charges along the material thickness direction, manifesting as extended spatial charge distribution characteristics toward the dielectric bulk. Poisson’s equation predicts that the maximum electric field intensity shifts to the material interior rather than remaining localized near the electrodes.

At 1810 s, under applied voltage, polarity reversal is observed: the ground electrode exhibits positive charges while the high-voltage electrode accumulates negative charges, marking the initiation of new charge accumulation. The simulation data show that at 2410 s, the peak stagnant charge density obtained from the full neutralization of the newly injected charge with the original charge in the low-mobility material is −0.01 C/m³. In contrast, high-mobility materials retain a higher stagnant charge density of −0.04 C/m³ due to greater internal charge accumulation during polarization. Space charges of the same polarity concentrate near electrodes, while opposite-polarity residual charges persist in the dielectric bulk. Consequently, the interfacial field strength at the ground electrode diminishes, and the field maximum shifts toward the material interior. By 3010 s, residual charges vanish in low-mobility dielectrics, whereas high-mobility dielectrics retain pronounced charge trapping near electrodes.

Polarity reversal leads to stagnant charge density not only related to the aforementioned mobility, but also to the formation of defects in the cardboard material. The traps formed by defects are categorized into deep traps and shallow traps [24,25]. Shallow traps give rise to the short-term capture of charges and space charges are prone to de-trapping motions. Charges in deep traps require a higher energy to break free from the confinement to become free charges that can migrate, which makes the charges in space continue to pile up and trigger an electric field distortion; a distorted electric field will further interfere with the shallow trajectory of the subsequent charges. The formation of charge distribution and electric field changes shows a dynamic coupling effect. Figure 10 shows the carrier transport process inside oil-impregnated paper [26]. During DC polarization, the whole process involves a complex balance of charge injection, trapping, de-trapping, migration, and composite behavior. The stagnant charge near the electrode and the increase in the trap density is due to the polarization process. The anisotropic charge is still difficult to dissipate after the electric field is reversed and the polarity of the charge near the electrode remains unchanged for a short period of time, presenting an obvious charge stagnation phenomenon. Traps near the electrodes induce the aggregation of same-polarity charges, which partially counteract the external electric field, leading to a relative reduction in field strength near the electrode regions. Conversely, in the bulk region of the specimen, the absence of such charge compensation results in an enhanced electric field intensity, with the peak field strength typically localized within the material interior. It reflects the regulatory effect of traps in the oil–paper medium on the electric field distribution of charges.

5. Conclusions

In this paper, both experiments and simulations on the space charge accumulations in a typical GTL oil-immersed paper insulation are taken as the research object with naphthenic oil-immersed paper insulation as the benchmark. The main research findings are as follows:

(1)

The experimental results demonstrate that under positive–negative–positive polarity reversal voltage, the gas-impregnated pressboard exhibits significantly higher rates of space charge density variation (140% faster negative charge dissipation at the ground electrode in stage B) and electric field distortion (54.15% distortion rate near electrodes in stage C) compared with mineral oil-impregnated paper.

(2)

A simulation model based on bipolar carrier theory was developed to investigate space charge accumulation and field distortion mechanisms in oil–paper insulation under polarity reversal. The simulation results indicate that enhanced mobility reduces space charge accumulation at the electrodes while increasing bulk charge density, thereby mitigating interfacial electric fields. However, excessive mobility may exacerbate post reversal residual charge retention, intensifying field distortion.

(3)

The analysis of carrier transport mechanisms in oil-impregnated paper reveals the critical regulatory role of traps in charge/field distribution. Future research should explore modifying transformer oil–paper composites with titanium dioxide nanoparticles. This modification strategy shows potential for accelerating space charge dissipation, optimizing trap energy distribution, and alleviating interfacial field distortion in gas-impregnated pressboard [27], though its practical feasibility requires systematic investigation.