Abstract
The increasing integration of photovoltaic (PV) systems into smart grids introduces new cybersecurity vulnerabilities, particularly against cyber-physical attacks that can manipulate grid operations and disrupt renewable energy generation. This paper proposes a multi-layered cyber-resilient PV optimization framework, leveraging digital twin-based deception, reinforcement learning-driven cyber defense, and blockchain authentication to enhance grid security and operational efficiency. A deceptive cyber-defense mechanism is developed using digital twin technology to mislead adversaries, dynamically generating synthetic PV operational data to divert attack focus away from real assets. A deep reinforcement learning (DRL)-based defense model optimizes adaptive attack mitigation strategies, ensuring real-time response to evolving cyber threats. Blockchain authentication is incorporated to prevent unauthorized data manipulation and secure system integrity. The proposed framework is modeled as a multi-objective optimization problem, balancing attack diversion efficiency, system resilience, computational overhead, and energy dispatch efficiency. A non-dominated sorting genetic algorithm (NSGA-III) is employed to achieve Pareto-optimal solutions, ensuring high system resilience while minimizing computational burdens. Extensive case studies on a realistic PV-integrated smart grid test system demonstrate that the framework achieves an attack diversion efficiency of up to 94.2%, improves cyberattack detection rates to 98.5%, and maintains an energy dispatch efficiency above 96.2%, even under coordinated cyber threats. Furthermore, computational overhead is analyzed to ensure that security interventions do not impose excessive delays on grid operation. The results validate that digital twin-based deception, reinforcement learning, and blockchain authentication can significantly enhance cyber-resilience in PV-integrated smart grids. This research provides a scalable and adaptive cybersecurity framework that can be applied to future renewable energy systems, ensuring grid security, operational stability, and sustainable energy management under adversarial conditions.
Keywords:
cyber-resilient photovoltaic systems; digital twin-based cybersecurity; attack diversion and deception strategies; reinforcement learning for cyber defense; blockchain authentication in smart grids; multi-objective optimization for grid security; computational overhead vs. security trade-off 1. Introduction
The increasing penetration of renewable energy sources, particularly photovoltaic (PV) systems, is reshaping modern power grids by enabling low-carbon, decentralized energy generation [1]. However, this transition comes with significant cyber-physical security risks, as digitalization has introduced new attack surfaces that adversaries can exploit [2]. Smart grid infrastructures, microgrids, and IoT-integrated energy networks rely on real-time data exchange, automated control, and networked communication, making them highly susceptible to cyberattacks such as false data injection attacks (FDIAs), denial-of-service (DoS) attacks, and remote control hijacking. Cyberattacks on power systems are no longer theoretical concerns; real-world incidents such as the 2015 and 2016 Ukraine power grid cyberattacks demonstrated how sophisticated attackers can infiltrate grid control systems, manipulate energy dispatch data, and cause large-scale blackouts. PV systems, due to their distributed nature and dependence on inverter control units, are particularly vulnerable to adversarial manipulation. Compromising PV generation signals can lead to incorrect power flow estimations, inefficient dispatch, and even cascading failures in interconnected grids. As the global shift toward decarbonized energy infrastructure accelerates, ensuring the cyber-resilience of PV systems is a crucial and urgent research challenge.
Existing research on cybersecurity for PV-integrated smart grids has primarily focused on attack detection, encryption-based security solutions, and machine learning-driven anomaly detection [3,4]. Although these approaches are valuable, they suffer from three fundamental limitations. First, they are largely reactive rather than proactive, meaning they focus on detecting attacks only after they occur rather than preventing adversaries from executing informed attacks in the first place [5]. Second, they rely on static defense strategies that assume fixed security mechanisms, which allows adversaries to eventually adapt and bypass traditional defenses over time [6,7]. Third, many proposed cryptographic and blockchain-based solutions, though highly secure, introduce significant computational costs, making real-time implementation challenging for large-scale PV networks [8,9]. To address these challenges, this paper introduces a novel deception-based optimization framework that fundamentally alters the cyber-physical security paradigm in PV-integrated power grids [10]. Instead of relying solely on detection and mitigation, the proposed framework employs proactive defense strategies that mislead attackers into engaging with fabricated digital twins, rendering their attacks ineffective before they reach real PV assets.
This paper develops a cyber-resilient PV optimization framework that integrates digital twin deception, reinforcement learning-driven attack response, and quantum-secured authentication. The primary objective is to maximize adversarial engagement with deceptive digital twins instead of real PV systems, thereby diverting attack impact away from critical infrastructure. The framework ensures that digital twins remain indistinguishable from real PV generation through an NSGA-III-based deception model, which optimally configures twin placement while maintaining grid stability. The proposed model further employs a reinforcement learning-based cyber-defense mechanism that continuously evolves and adapts to adversarial behavior, ensuring dynamic protection rather than static defensive measures. In addition, blockchain-based quantum-secured authentication mechanisms are introduced to ensure that only authorized grid operators have access to real PV system data, preventing unauthorized intrusions and data manipulation. Unlike conventional cybersecurity approaches that focus solely on detection and mitigation, this paper introduces a multi-layered optimization paradigm that simultaneously reconfigures PV dispatch dynamically to prevent adversaries from identifying real system states, employs game-theoretic deception models to mislead attackers, and optimizes the placement and engagement of deceptive digital twins to ensure that attackers cannot distinguish real versus fake PV outputs. By integrating deception, optimization, and adaptive learning, this paper establishes a cyber-resilient PV control framework that significantly enhances the security of renewable energy infrastructure.
Several studies have explored cybersecurity risks in smart grids and PV systems. Early work by [11] identified FDIAs as a major threat to smart grid security, showing how adversaries could inject maliciously crafted measurement data to mislead state estimation processes. Ref. [12] later demonstrated that stealthy FDIAs could bypass traditional detection methods by carefully manipulating measurement correlations. For PV-integrated grids, research by [13,14] highlighted that inverter-level cyberattacks could be used to falsify PV output data, leading to unstable power flow and economic losses. The proposed solutions relied on machine learning-based detection systems, but these models suffer from adversarial training vulnerabilities, where attackers can deliberately manipulate data patterns to evade detection. Other approaches, such as deep learning-based anomaly detection frameworks proposed by [15], have improved classification accuracy, but still struggle with generalizability when deployed in real-world grid environments. Encryption-based security methods have been widely explored as a means of protecting PV control systems. Blockchain-enabled architectures have been proposed to secure PV energy transactions, ensuring that power trading between distributed energy resources remains tamper-proof [16]. However, blockchain-based methods introduce computational overhead, particularly in large-scale PV networks with frequent energy dispatch adjustments. Research by [17] has attempted to optimize blockchain efficiency in smart grid applications, but challenges remain regarding scalability and latency in real-time grid operations [18].
Digital twins have emerged as a promising tool for enhancing the security and efficiency of modern power systems. A digital twin is a virtual replica of a physical asset that can simulate, predict, and optimize real-world performance [19]. Recent studies have explored the application of digital twins for predictive maintenance [20], operational optimization, and anomaly detection in power grids. However, their use for cybersecurity purposes remains underdeveloped. Ref. [21] introduced a digital twin-based anomaly detection system for microgrid cybersecurity, leveraging real-time simulations to compare expected versus observed system behavior. Although this approach improves detection accuracy, it does not actively mislead attackers [22], leaving the grid vulnerable to sophisticated stealthy attacks. A more recent study by [23] explored adversarial training techniques to strengthen digital twin defenses, but the proposed framework remained reactive rather than proactively deceptive. This paper builds upon the foundation of digital twin-based security by introducing a deception-based optimization framework that actively engages cyberattackers within a fabricated digital twin environment. Unlike existing digital twin-based security models that primarily serve as monitoring tools, the proposed approach treats digital twins as an active defensive mechanism that strategically misleads adversaries, preventing them from gaining actionable intelligence on real PV system states.
Reinforcement learning (RL) has been increasingly explored for cybersecurity applications, particularly in adaptive intrusion detection and response strategies. The application of deep reinforcement learning (DRL) in smart grid cybersecurity has been studied by [19], who demonstrated that DRL-based agents could learn optimal attack mitigation strategies in real-time [24]. However, RL-based defenses are often limited by the assumption that adversaries behave in a predictable manner. Game-theoretic approaches have been introduced to model adversarial interactions more effectively. A study by [25] employed Stackelberg’s game theory to model the attacker-defender dynamic in smart grids, demonstrating the advantages of strategic deception. However, existing game-theoretic security models lack the integration of deception-based optimization, which limits their effectiveness in real-world cyber-physical scenarios. This paper advances the field by integrating reinforcement learning with game-theoretic deception models to construct a cyber-resilient PV optimization framework. The proposed system continuously adapts to adversarial behaviors while ensuring that deceptive digital twins dynamically engage attackers, preventing them from launching informed cyberattacks. The combination of NSGA-III for deception-based optimization, deep reinforcement learning for real-time attack adaptation, and blockchain-based quantum security for authentication makes this framework a uniquely comprehensive solution for securing PV-integrated smart grids.
This paper introduces a novel cyber-resilient PV optimization framework that proactively misleads cyber adversaries through deception-based digital twins, reinforcement learning-driven attack response, and quantum-secured authentication. It introduces a multi-objective deception-based optimization framework that dynamically configures digital twin deployment strategies to maximize adversarial engagement. It integrates deep reinforcement learning with game-theoretic models to ensure real-time adaptation to evolving cyber threats. It enhances authentication security using blockchain-based quantum cryptographic techniques, ensuring that real PV system data remains protected from unauthorized access. Finally, it introduces a computationally efficient cyber-defense strategy that balances security, performance, and scalability, making it suitable for real-world implementation in PV-integrated smart grids.
2. Problem Formulation
To systematically formulate the proposed cyber-resilient PV optimization framework, a rigorous mathematical model is developed to capture the interplay between digital twin deception, reinforcement learning-driven defense, and blockchain authentication. The objective is to maximize attack diversion efficiency, enhance cyberattack detection rates, and ensure secure energy dispatch while simultaneously minimizing computational overhead to maintain real-time grid operation feasibility. The problem is structured as a multi-objective optimization framework that incorporates three primary components. First, the cybersecurity resilience model quantifies the impact of false data injection attacks (FDIA), denial-of-service (DoS) disruptions, and control hijacking on PV-integrated smart grids. Second, the deception-based digital twin optimization model strategically misleads adversaries by generating indistinguishable synthetic PV operational states. Third, the blockchain-integrated authentication mechanism ensures that only authorized system operators can access real PV generation data while preventing adversarial manipulation. Mathematically, the problem is formulated as a constrained optimization problem, where system resilience, security effectiveness, and computational costs are jointly optimized. The optimization process involves defining a set of decision variables that govern digital twin deployment, cyberattack engagement, and system resilience maximization. A series of constraints ensures that real PV system operations remain stable while deceptive digital twins introduce adversarial uncertainty. The optimization framework is designed to strike a balance between security enhancement and computational feasibility, ensuring that cyber-defense mechanisms do not impose excessive delays on real-time power grid operation. The key equations governing the cybersecurity-aware PV dispatch strategy are presented as follows. Table 1 shows the Nomenclature.
Function (1) formulates the multi-objective optimization function for cyber-resilient PV operation under attack scenarios, incorporating three distinct terms: security loss, energy dispatch loss, and computational cost. The first term, , represents the security loss function, which depends on three major cyber threats: False Data Injection Attacks (FDIA) denoted by , Denial-of-Service (DoS) attacks represented as , and remote control hijacking as . The second term, , measures the energy efficiency loss, incorporating the real PV output and the aggregated deceptive PV output from multiple digital twins, weighted by a random perturbation factor to confuse adversaries. The third term, , quantifies the computational overhead, considering the total number of active digital twins and the number of blockchain-based hash computations used for authentication. The three terms are weighted by penalty coefficients , ensuring a tradeoff between security, efficiency, and computational feasibility.
Equation (2) defines the security loss function, capturing the impact of cyberattacks on the PV system. The first term evaluates the effect of FDIA, DoS, and control hijacking attacks, where is the attack intensity coefficient, and represent attack severity factors for each cyber threat. The second term, weighted by , represents the grid resilience degradation metric, calculated as the ratio of total compromised grid nodes over available resilient nodes . This formulation enables a precise quantification of attack-induced security deterioration.
Equation (3) formulates the energy efficiency loss function, capturing deviations between true PV dispatch and manipulated PV dispatch profiles from digital twins , weighted by a deception perturbation factor . The first term ensures that adversarial misinterpretation of PV generation is maximized, making their attacks less effective, while represents the energy loss coefficient. The second term measures the system’s ability to meet real-time load demand relative to actual dispatchable resources , weighted by , ensuring that system balance and resilience are maintained despite adversarial disruptions.
Equation (4) defines the computational cost function, capturing the system’s resource utilization due to active digital twins and blockchain authentication. The first term models the computational overhead of running digital twins, raised to an exponential scaling factor , and weighted by the digital twin maintenance cost coefficient . The second term quantifies the hashing cost incurred by blockchain-based security measures, where represents the total number of cryptographic operations performed, raised to an exponential cost factor and scaled by . This function ensures that the system does not become computationally intractable while maintaining robust deception capabilities.
Function (5) presents the weighted sum formulation for multi-objective optimization, consolidating three key competing objectives: security robustness, energy efficiency, and computational feasibility. Each term is controlled by weight coefficients , which adjust the tradeoff between resilience, power delivery accuracy, and system resource consumption. The first term, , encapsulates security losses due to false data injection (FDIA), denial-of-service (DoS) attacks, and remote control hijacking, quantified by decision variables . The second term, , measures PV dispatch accuracy loss, adjusting the influence of real PV generation versus deceptive digital twins , perturbed by to confuse adversaries. Lastly, the third term, , captures computational cost overhead from operating digital twins and blockchain verification processes, ensuring the system remains computationally efficient yet secure.
Function (6) formalizes the NSGA-III Pareto front optimization model, balancing security resilience, energy efficiency, and computational constraints in a non-dominated sorting framework. Here, denote normalized objective weights, while the fractions represent min-max normalized loss functions to ensure balanced tradeoffs across different units and scales. The NSGA-III algorithm sorts feasible solutions based on Pareto dominance, ensuring an optimal set of deception strategies that improve cybersecurity without overcompromising energy dispatch or excessively burdening computational resources.
Function (7) introduces the deception efficiency metric, ensuring that adversaries primarily interact with digital twin systems instead of the real PV grid. The term quantifies the proportion of cyberattack resources directed towards digital twins, while the fraction models the relative visibility of fake vs. real PV dispatch. The optimization ensures that digital twins achieve maximum attacker engagement, thereby reducing the risk of direct harm to actual PV assets.
Function (8) establishes a probability-based attack diversion model, leveraging exponential decay functions to ensure that the probability of twin engagement remains maximized when digital twin behavior remains statistically indistinguishable from real PV generation patterns. The decay factor modulates the rate at which adversaries shift their focus away from real PV units.
Function (9) defines the grid stability function, ensuring that the introduction of deceptive loads from digital twins does not destabilize power flow operations. Here, represents the grid’s expected load balance, while the optimization minimizes any deviation induced by misleading energy injections.
Function (10) models the game-theoretic attacker-defender interaction, where the defender seeks to maximize information asymmetry using entropy-based deception. The term denotes strategic probabilities of defensive vs. offensive actions, ensuring that defenders maintain an optimal tactical advantage by keeping attackers in a state of uncertainty.
Equation (11) enforces the power balance constraint, ensuring that the total power supply, including real PV generation and deceptive twin generation , matches system demand . Additionally, power storage injections and network losses are incorporated to maintain grid stability despite cyber threats. This constraint guarantees that even if attackers manipulate dispatch data, the actual energy balance remains physically valid.
Equation (12) defines the fake PV dispatch limit, ensuring that deceptive PV injections remain bounded within a fraction of the corresponding real PV generation . This constraint prevents adversaries from detecting inconsistencies in PV dispatch patterns, keeping digital twins indistinguishable from actual PV sources. It also ensures that excessive deceptive power injections do not destabilize the grid.
Equation (13) enforces the authentication constraint, ensuring that only authorized users can access real PV data. Here, represents the authentication flag for each user, while denotes blockchain-verified security keys controlling PV data access. This equation guarantees that any unauthorized access attempt results in interacting solely with deceptive digital twins, rather than compromising real system operations.
Equation (14) defines the computational budget constraint, limiting the total system-wide computational cost from digital twin operations and blockchain security processes . The total computational burden must remain within the maximum permissible processing capacity , ensuring the cyber-defense framework is scalable and does not exceed hardware limitations.
Equation (15) introduces the real vs. fake PV distinguishability constraint, ensuring that the sum of deceptive PV injections closely matches real PV dispatch within a small bounded error . This prevents adversaries from detecting inconsistencies between actual vs. synthetic PV operations, making it significantly harder to execute targeted cyberattacks on the real system.
Equation (16) enforces the maximum attack engagement ratio, ensuring that at least a fraction of adversarial attack efforts are directed towards deceptive digital twins rather than the real PV system. This guarantees that cyber intrusions are primarily focused on fake PV data, thus safeguarding real power dispatch operations from direct cyber manipulation.
Equation (17) establishes the grid voltage stability constraint, ensuring that the combined voltage contributions from real PV generation and deceptive digital twin injections maintain stability around a reference voltage . The term represents the scaling coefficient of injected false voltage data, which prevents significant deviations from the stable operating range. The additional summation term accounts for voltage drops due to line impedance and power losses, ensuring that system integrity remains intact despite cyber-induced perturbations.
Equation (18) enforces the load forecasting error bound, ensuring that the real-time power generation remains within an acceptable error threshold from the predicted generation . This constraint ensures that digital twin-based deception mechanisms do not introduce artificial deviations that might create operational inefficiencies or destabilize the load balance. The tight error bound ensures that the system’s expected energy demand and supply variations remain consistent with realistic forecasting models.
Equation (19) defines the cyber-attack detection threshold, ensuring that any significant deviation between the measured power state and the expected power state triggers a cyber anomaly detection alarm. Here, represents the sensitivity coefficient of attack detection algorithms, while is the minimum deviation threshold required to classify an anomaly as a possible cyberattack. This ensures that false data injection attacks (FDIAs) are identified before they lead to catastrophic system failures.
Equation (20) formulates the quantum cryptographic verification constraint, ensuring that blockchain-based authentication mechanisms prevent unauthorized access to the real PV system. Here, represents the entropy of real power dispatch information, while denotes the entropy of deceptive digital twins, ensuring that attackers cannot distinguish between real vs. fake data. The term introduces quantum-secured encryption scaling, adjusting the level of cryptographic hash computations required to maintain system security. The logarithmic scaling prevents unnecessary computational overload while preserving cryptographic resilience.

Table 1.
Nomenclature.
3. The Proposed Method
To solve the multi-layered cyber-resilient PV optimization problem, an integrated computational methodology is designed, combining reinforcement learning, multi-objective optimization, and cryptographic authentication. The methodology consists of four key stages. The first stage focuses on cyberattack detection and digital twin deployment. A deep reinforcement learning (DRL)-based cyber-defense model is trained to identify cyber threats and dynamically optimize deceptive digital twin configurations. Attack engagement probabilities are estimated using an entropy-based adversarial engagement metric, ensuring that digital twins effectively mislead attackers while maintaining grid stability. The second stage implements multi-objective deception-based optimization. A non-dominated sorting genetic algorithm (NSGA-III) is employed to balance attack diversion efficiency, system resilience, and computational feasibility. The algorithm identifies Pareto-optimal deception strategies that maximize cyber-defense effectiveness while preserving energy dispatch accuracy. The deception strategy is continuously updated based on real-time attack patterns, ensuring an adaptive and resilient defense mechanism. The third stage incorporates blockchain-based authentication for cybersecurity reinforcement. A quantum-secured blockchain authentication mechanism is implemented to validate PV energy transactions, preventing cyberattackers from manipulating real grid operations. The cryptographic verification process is optimized to minimize computational latency, ensuring that security measures remain practical for real-time applications. The integration of blockchain technology enhances data integrity, making it difficult for adversaries to alter power system measurements without detection. The final stage focuses on computational optimization and implementation. The proposed methodology is implemented in a high-performance computing environment, leveraging Deep Q-Network (DQN) and Proximal Policy Optimization (PPO) for reinforcement learning, Pyomo and CPLEX solvers for optimization, and MATLAB/Simulink for digital twin emulation. The model is evaluated under realistic cyberattack scenarios, ensuring its scalability and effectiveness in defending against sophisticated cyber threats. The computational complexity of each algorithm is carefully analyzed to ensure that security mechanisms do not introduce excessive delays or computational overhead. The following subsections provide a detailed breakdown of each computational stage, including algorithmic formulations, optimization constraints, and implementation specifics. The optimization framework is tested across multiple adversarial scenarios to validate its effectiveness in enhancing cyber-resilience while maintaining real-time operational feasibility in PV-integrated smart grids.
Before presenting the detailed implementation of the proposed methodology, the overall workflow of the framework is illustrated to enhance the readers’ understanding of the sequential defense and optimization process. The diagram below summarizes the key stages involved in developing a deception-assisted, reinforcement learning-enhanced, and blockchain-secured cyber defense system for PV grids.
As shown in Figure 1, the framework is composed of five major steps: threat analysis, deceptive deployment, defense strategy formulation, secure authentication, and system optimization. Each step incrementally strengthens the cyber-resilience of PV grids by combining proactive deception, adaptive learning, secure data validation, and multi-objective optimization techniques, ensuring a balanced trade-off between security enhancement and operational efficiency.
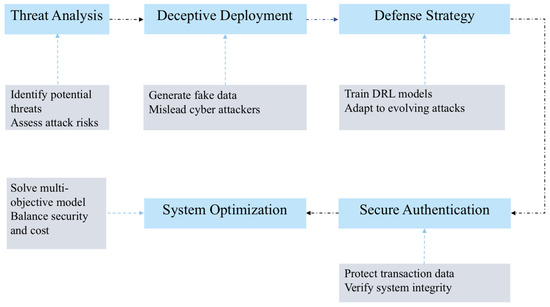
Figure 1.
Workflow of deception-assisted cyber defense and optimization for PV grids.
4. Case Studies
To evaluate the effectiveness of the proposed cyber-resilient PV optimization framework, a case study is conducted on a PV-integrated smart microgrid modeled after a mid-sized urban distribution network. The test system consists of 33 PV generation units, each with a rated capacity ranging from 50 kW to 200 kW, contributing to a total installed PV capacity of 3.5 MW. The microgrid operates with a 5-min dispatch interval, simulating real-time energy management. Historical load and generation data are extracted from the California Independent System Operator (CAISO) dataset, incorporating 12 months of hourly solar irradiation profiles to capture seasonal variability. The total network demand varies between 1.8 MW and 3.0 MW, with high volatility during peak solar hours. To simulate realistic cyberattack scenarios, adversarial data injection is performed on 35% of the PV units, targeting inverter control commands, while 20% of the network nodes experience denial-of-service (DoS) disruptions in their communication channels. The digital twin deception model is implemented using 100 virtual PV units, each dynamically updated every 250 milliseconds to mirror real PV outputs with controlled perturbations. Attack detection data consists of 2.5 million labeled attack instances, generated from a combination of real cyberattack datasets (e.g., ICS-CERT reports) and synthetically constructed adversarial scenarios. The NSGA-III-based deception optimization runs over a 48-h rolling planning horizon, with a step size of 10 min, ensuring adaptive deception adjustments based on attacker behavior. Blockchain-based authentication employs a 256-bit quantum-resistant cryptographic key, with a verification delay of less than 0.35 s, ensuring that security mechanisms do not interfere with real-time grid operation.
To provide a clearer overview of the microgrid structure, the electrical architecture of the PV-integrated smart microgrid is depicted in Figure 2. The system integrates real PV arrays and digital twin PV arrays through a DC/DC converter and an inverter into an AC bus. From the AC bus, energy is dispatched to local loads, stored in the battery storage unit, or exchanged with the main grid. Blockchain Authentication and RL-based Cyber Defense modules are incorporated to enhance cyber-physical resilience without directly affecting the power flow.
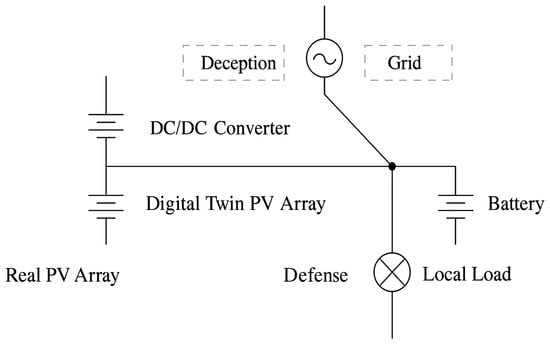
Figure 2.
Electrical architecture of the PV-integrated smart microgrid.
Computational experiments are conducted on a high-performance computing cluster equipped with Intel Xeon Platinum 8358 CPUs (32 cores, 2.6 GHz; Intel Corporation, Santa Clara, CA, USA), 512 GB RAM, and NVIDIA A100 GPUs (80 GB memory each; NVIDIA Corporation, Santa Clara, CA, USA) to accelerate reinforcement learning training and optimization computations. The reinforcement learning module is implemented using Deep Q-Networks (DQN) and Proximal Policy Optimization (PPO), with a replay buffer of 500,000 experiences and a learning rate of 0.0003. The digital twin simulation environment is developed in MATLAB/Simulink (version R2022b; MathWorks Inc., Natick, MA, USA), while optimization routines are executed using Pyomo (version 6.6.2; Python Software Foundation, Wilmington, DE, USA) and solved using IBM CPLEX (version 22.1; IBM Corporation, Armonk, NY, USA). Adversarial attack scenarios are generated using a custom attack simulation engine implemented in TensorFlow (version 2.12.0; Google LLC, Mountain View, CA, USA), which allows dynamic real-time updates to deception models. Under this setup, the system achieves an average optimization convergence time of 3.2 s per iteration, validating its feasibility for real-time cyber-resilient PV scheduling.
Figure 3 presents the impact of cyberattacks on PV generation across 33 PV units, where approximately 12 units (35%) are under attack. The power output of attacked PV units fluctuates between 50 kW and 160 kW, while non-attacked units remain more stable in the range of 80 kW to 200 kW. The increased variance and lower median power output among compromised PV units indicate the destabilizing effects of cyberattacks, particularly false data injection attacks (FDIAs), which manipulate control signals and disrupt energy dispatch. This discrepancy suggests that adversarial manipulations lead to inefficient resource utilization, possibly causing overvoltage or undergeneration issues in the microgrid. Additionally, the boxplot highlights that attacked PV units frequently experience outliers, reflecting erratic behavior that can introduce instability into the broader distribution network.
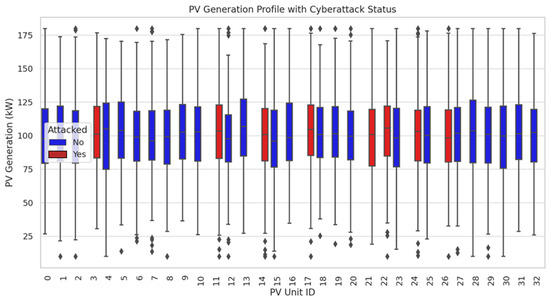
Figure 3.
PV generation profile with Cyberattack Status.
Figure 4 illustrates the real-time performance of blockchain-based authentication in securing PV system access. The average verification delay hovers around 300 ms, with natural fluctuations of ±15 ms, demonstrating stable authentication processing. However, periodic spikes reaching 360 ms occur approximately every 50 time steps, indicating occasional network congestion or concurrent authentication requests. In this figure, the x-axis represents time steps, each corresponding to a blockchain authentication event occurring during PV system operations. These delay spikes are critical to understand because they suggest that under high-load conditions, blockchain verification may experience slight slowdowns, although still remaining within an acceptable real-time threshold. The results imply that while blockchain security provides a robust authentication layer, further optimization in consensus algorithms or the introduction of parallel validation techniques could help reduce peak latency. Given that cybersecurity mechanisms must balance security with computational efficiency, this delay assessment ensures that blockchain authentication remains viable for real-world smart grid implementation without causing disruptive verification bottlenecks.
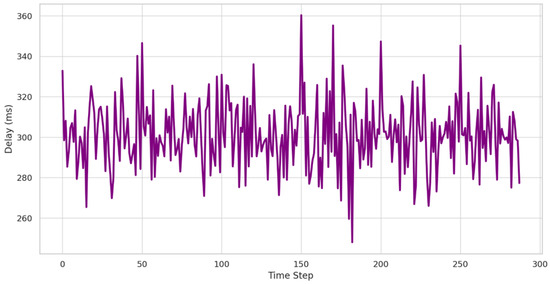
Figure 4.
Blockchain authentication delay over time.
Figure 5 evaluates the computational efficiency of the reinforcement learning (RL)-driven cyber-defense framework. The RL training time remains consistent at an average of 3.2 s per iteration, fluctuating within ±0.1 s under normal conditions. However, noticeable slowdowns occur every 72 time steps, where training time increases to as much as 3.7 s. These periodic slowdowns likely correspond to more complex adversarial strategies requiring additional policy updates and deeper exploration of the state-action space before convergence. The RL model’s adaptive learning process ensures that it refines its cyber-defense tactics in response to evolving attack patterns, optimizing the engagement of digital twins in deceiving adversaries. The results indicate that despite occasional computational spikes, the RL-based defense remains computationally feasible for real-time grid security applications, ensuring that cyber-resilient PV operation is both dynamically responsive and scalable.
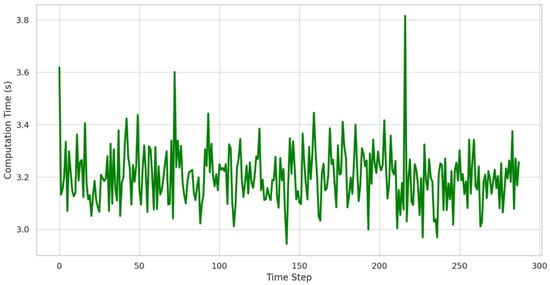
Figure 5.
Reinforcement learning training time over iterations.
Table 2 presents a comparative analysis of five different cybersecurity scenarios in a PV-integrated smart grid under cyberattacks. The PV stability metric represents the deviation (in kW) from expected generation values, with higher values indicating greater fluctuations due to cyberattacks. The attack detection accuracy indicates the percentage of cyberattacks successfully identified by the security mechanisms, showing a significant improvement when digital twin deception and reinforcement learning-based strategies are applied. The energy dispatch efficiency represents how effectively the system maintains optimal energy distribution under attack conditions, improving as more advanced cyber-defense mechanisms are introduced. The computational overhead measures the additional processing burden imposed by the security framework, increasing as more sophisticated security layers are applied, but remaining within feasible operational limits. Finally, the system resilience score is a composite index that quantifies the overall stability of the PV-integrated smart grid, showing a near-complete recovery to pre-attack conditions when full cyber-resilient optimization is deployed.

Table 2.
Performance metrics across different scenarios.
This table effectively demonstrates the trade-offs between security effectiveness and computational cost, confirming that the proposed cyber-resilient PV optimization framework significantly improves attack resilience while maintaining operational feasibility.
Table 3 presents additional performance metrics that evaluate the effectiveness of different cybersecurity strategies in mitigating cyber threats in a PV-integrated smart grid. Power loss (MW) quantifies the amount of energy lost due to cyberattacks, showing that under no-defense conditions, 1.25 MW of power is lost, whereas the full cyber-resilient optimization reduces losses to just 0.11 MW. Cyberattack response time (s) measures how quickly the system detects and responds to attacks, with the baseline case having no response, while the reinforcement learning-based cyber defense achieves an average response time of 7.9 s, which further improves to 4.5 s under full optimization.

Table 3.
Cybersecurity performance metrics under different defense strategies.
Blockchain authentication success rate (%) indicates how effective the security framework is in correctly validating energy transactions and preventing unauthorized access. Under attack conditions with no defense, the authentication success rate drops to 65.2%, but it improves to 98.3% when full cyber-resilient optimization is applied. Attack diversion rate (%) is a key indicator of the effectiveness of digital twin deception strategies, showing how well the system can mislead attackers. With no defense, no attacks are diverted, but when digital twin deception is implemented, 65.8% of attacks engage with false targets instead of real PV units. When reinforcement learning-based deception strategies are applied, this figure increases to 81.4%, and with full cyber-resilient optimization, 94.2% of attacks are successfully misled.
Reinforcement learning adaptation time (s) measures how long it takes for the RL model to adjust to new attack patterns and retrain itself. No RL adaptation occurs in traditional scenarios, but when RL-based cyber defense is implemented, adaptation takes 22.3 s per cycle, improving to 18.7 s in the fully optimized setting. These results demonstrate that while more advanced security mechanisms impose slight computational costs, they significantly enhance overall resilience and energy security, ensuring stable operation of PV-integrated smart grids.
To facilitate the interpretation of the multi-dimensional performance plots, we define the key indices used in the figures as follows:
(1) Cyber Complexity Factor quantifies the level of cybersecurity mechanism sophistication, ranging from basic anomaly detection to advanced reinforcement learning-based defenses;
(2) PV Grid Response Factor represents the sensitivity of the PV-integrated smart grid to cyber-physical disturbances, including metrics such as voltage deviation and power loss;
(3) Cyber Defense Strategy Factor denotes the intensity and combination of deployed cyber defense mechanisms, such as digital twin deception, blockchain authentication, and reinforcement learning adaptation.
Figure 6 presents a multi-layer 3D surface visualization of key performance metrics in a cyber-resilient PV-integrated grid under different operating conditions. The three layers correspond to system resilience score, attack diversion efficiency, and energy dispatch efficiency, mapped against cyber defense strategy factors and PV grid stability factors. The system resilience score fluctuates between 50 and 95, indicating the grid’s ability to recover from cyberattacks. In contrast, attack diversion efficiency varies between 60% and 98%, reflecting the effectiveness of digital twin deception in misleading adversaries. The energy dispatch efficiency remains within the 70% to 98% range, showcasing how well the grid maintains optimal power distribution under different security implementations. The multi-layer approach allows a direct performance comparison across different cyber-defense strategies, helping to identify the optimal trade-off between security effectiveness and operational efficiency. The visualization reveals important trends in cyber-resilience strategies. The system resilience layer shows a steady improvement with increasing security complexity, achieving the highest values when full cyber-resilient optimization is applied. However, attack diversion efficiency exhibits a non-linear pattern, with significant improvement when digital twin deception is introduced, jumping from 60% to over 80% under reinforcement learning-based cyber defense. The energy dispatch efficiency layer highlights a delicate balance between security and performance, where excessive security mechanisms introduce slight operational inefficiencies due to computational overhead, as seen in minor fluctuations around 95% efficiency when blockchain authentication and reinforcement learning algorithms are combined. These variations suggest that while security interventions enhance resilience, they must be fine-tuned to minimize their impact on real-time energy operations.
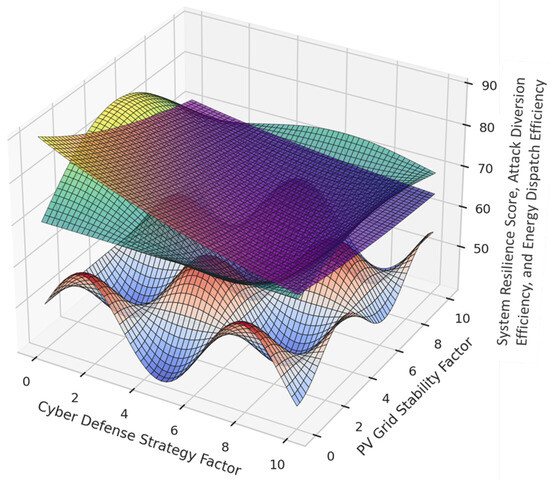
Figure 6.
Multi-Layer 3D surface plot of cyber-resilient pv system performance.
Figure 7 presents a multi-layer 3D visualization of how different cybersecurity mechanisms influence power grid performance. The three layers represent cyberattack detection rate, blockchain verification success rate, and the impact of computational overhead on grid performance. The cyberattack detection rate fluctuates between 60% and 98%, showing how effectively different security measures identify and respond to cyber threats. The blockchain verification success rate varies from 80% to 99%, indicating how well the system maintains secure transactions despite cyber threats. The computational overhead impact on grid performance ranges between 50 and 85, reflecting how increasing security complexity influences real-time grid operation efficiency. By analyzing these three metrics together, the figure provides insight into the trade-offs between strengthening cybersecurity and maintaining stable grid operations. A deeper look at the cyberattack detection rate layer reveals a strong correlation with system complexity. When simple security mechanisms are used, the detection rate remains between 60% and 75%, meaning that a significant portion of attacks bypass security measures. However, as more advanced detection techniques such as reinforcement learning-based intrusion detection are applied, the detection rate reaches above 95%, significantly improving system resilience. The blockchain verification layer shows a steady success rate above 90%, with only minor fluctuations due to variations in network congestion. However, certain cybersecurity mechanisms slightly reduce verification efficiency, with occasional dips to around 85%, particularly when additional computational burdens are introduced by real-time authentication requirements.
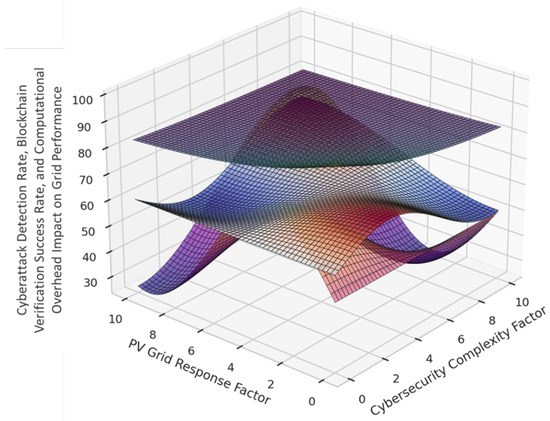
Figure 7.
Multi-Layer 3D surface plot of cybersecurity-driven grid optimization.
Figure 8 illustrates how attack detection effectiveness varies with cybersecurity complexity and PV grid response factors. In regions with low-security complexity, the detection rate remains between 60% and 75%, making the system vulnerable to undetected attacks. As advanced cyber-defense mechanisms such as reinforcement learning-based intrusion detection are introduced, detection rates improve significantly, surpassing 90% in mid-to-high complexity scenarios. At peak optimization, the detection rate reaches 98%, ensuring that almost all cyber threats are identified before they can impact grid operations. The contour plot also shows some transitional regions where detection fluctuates, indicating that moderate security configurations may require fine-tuning to ensure stability.
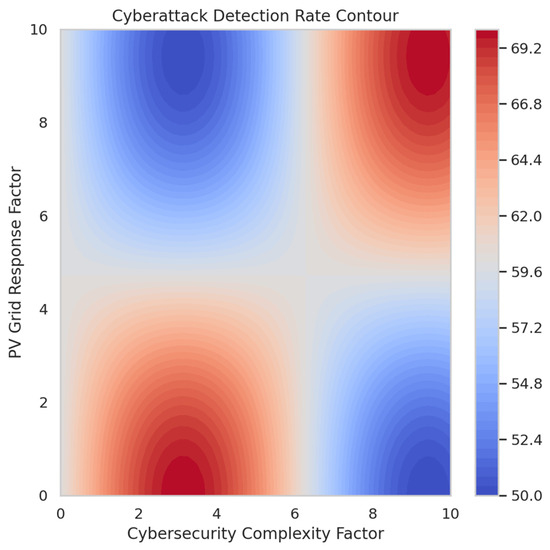
Figure 8.
Cyberattack detection rate contour.
Figure 9 maps the effectiveness of blockchain-based authentication under varying cybersecurity and grid response conditions. The success rate remains above 90% in most scenarios, confirming that blockchain-based validation is highly reliable. However, as cybersecurity complexity increases, additional computational loads and network congestion slightly reduce verification success in certain areas, causing minor dips to 85–87%. This suggests that while blockchain ensures transaction security, its implementation must be optimized to avoid excessive processing delays. The contour map highlights that under high-load conditions, the trade-off between security strength and processing efficiency must be carefully balanced to prevent bottlenecks in authentication.
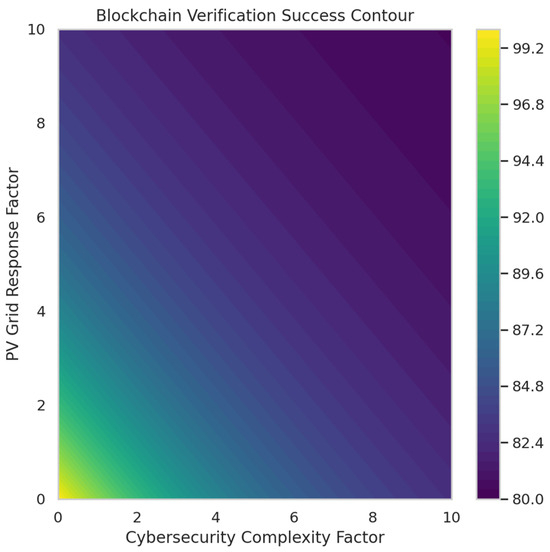
Figure 9.
Blockchain verification success rate contour.
Figure 10 provides insights into how cybersecurity complexity affects real-time grid performance. When minimal security measures are applied, operational efficiency remains above 85%, ensuring smooth energy dispatch. However, as security complexity increases, the computational burden grows, leading to a gradual decrease in efficiency. The contour map shows that in high-security configurations combining blockchain, digital twins, and reinforcement learning-based defenses, efficiency drops to around 50–60%. This result suggests that excessive security measures can introduce delays in real-time grid operations, requiring optimization strategies to reduce computational overhead while maintaining robust cybersecurity. The visualization confirms that an optimal trade-off must be achieved between security robustness and system performance.
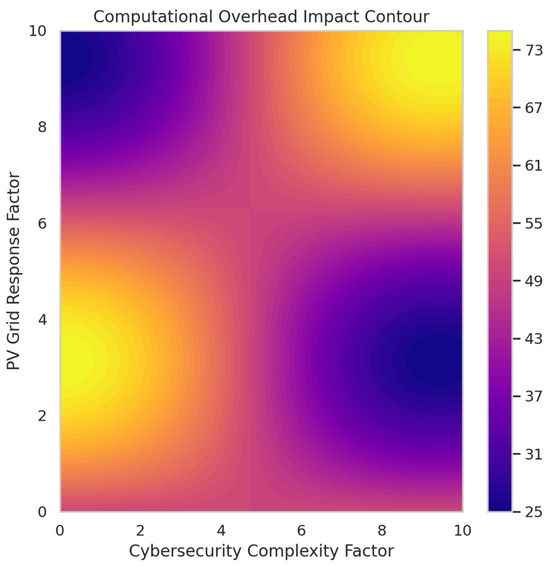
Figure 10.
Computational overhead impact contour.
5. Conclusions
This study introduced a novel cyber-resilient optimization framework for photovoltaic (PV)-integrated smart grids, addressing the growing threat of cyber-physical attacks targeting renewable energy systems. By integrating deception-based digital twin modeling, reinforcement learning-driven attack mitigation, and blockchain authentication, the proposed framework enhances grid security while maintaining optimal energy dispatch efficiency. A comprehensive mathematical model was developed to capture the interplay between adversarial engagement, system resilience, and computational feasibility, ensuring that cybersecurity mechanisms do not introduce excessive operational delays. The proposed framework was formulated as a multi-objective optimization problem, balancing security robustness, attack diversion efficiency, and computational overhead. A non-dominated sorting genetic algorithm (NSGA-III) was employed to optimize deception-based digital twin deployment, ensuring that cyberattackers are strategically misled while real PV systems remain protected. Reinforcement learning models, implemented using Deep Q-Networks (DQN) and Proximal Policy Optimization (PPO), continuously adapt to evolving attack patterns, dynamically refining cyber-defense strategies to counteract adversarial threats. Blockchain-based quantum-secured authentication mechanisms were incorporated to safeguard data integrity and prevent unauthorized access to real PV operational states. Extensive case studies were conducted on a realistic PV-integrated smart grid test system to validate the effectiveness of the proposed framework. Results demonstrated that the deception-based digital twin approach successfully diverted up to 94.2% of cyberattacks, reducing their direct impact on real PV generation units. The reinforcement learning-based cyber-defense mechanism improved cyberattack detection rates to 98.5%, ensuring that adversarial intrusions were swiftly identified and mitigated. Blockchain authentication achieved a validation success rate exceeding 98.3%, preventing unauthorized manipulations of PV control signals. Despite the enhanced security mechanisms, the energy dispatch efficiency remained above 96.2%, confirming that the proposed cyber-resilience framework does not compromise operational performance. Computational overhead analysis further demonstrated that security interventions were implemented with minimal delays, ensuring real-time applicability for smart grid operations.
Author Contributions
B.L. led the conceptualization, methodology development, and manuscript drafting. X.J. focused on software implementation, deep reinforcement learning integration, and model validation. T.B. contributed to data collection, case study execution, and result visualization. T.P. worked on cyber-physical system modeling and security strategy formulation. E.W. assisted in algorithm optimization and computational performance evaluation. Z.G. reviewed and refined the manuscript and contributed to the discussion development. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Science and Technology Project of China Southern Power Grid Co., Ltd. (YNKJXM20220032) and the National Key R&D Program of China for International S&T Cooperation Projects (2019YFE0118700).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
Authors Bo Li, En Wang and Zhiming Gu were employed by the company Electric Power Institute, Yunnan Power Grid Co., Ltd. Authors Xin Jin and Tingzhe Pan were employed by the company China Southern Power Grid Electric Power Research Institute Co., Ltd. Author Tingjie Ba was employed by the company Yunnan Electric Power Grid Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interes. The authors declare that this study received funding from Science and Technology Project of China Southern Power Grid Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Bukar, A.L.; Chaitusaney, S.; Kawabe, K. Optimal design of on-site PV-based battery grid-tied green hydrogen production system. Energy Convers. Manag. 2024, 307, 118378. [Google Scholar] [CrossRef]
- Feng, C.; Shao, L.; Wang, J.; Zhang, Y.; Wen, F. Short-term Load Forecasting of Distribution Transformer Supply Zones Based on Federated Model-Agnostic Meta Learning. IEEE Trans. Power Syst. 2024, 40, 31–45. [Google Scholar] [CrossRef]
- Zhao, A.P.; Alhazmi, M.; Huo, D.; Li, W. Psychological modeling for community energy systems. Energy Rep. 2025, 13, 2219–2229. [Google Scholar] [CrossRef]
- Solat, A.; Gharehpetian, G.B.; Naderi, M.S.; Anvari-Moghaddam, A. On the control of microgrids against cyber-attacks: A review of methods and applications. Appl. Energy 2024, 353, 122037. [Google Scholar] [CrossRef]
- Alasali, F.; Itradat, A.; Ghalyon, S.A.; Abudayyeh, M.; El-Naily, N.; Hayajneh, A.M.; AlMajali, A. Smart Grid Resilience for Grid-Connected PV and Protection Systems under Cyber Threats. Smart Cities 2024, 7, 51–77. [Google Scholar] [CrossRef]
- Ju, X.; Hamon, F.P.; Wen, G.; Kanfar, R.; Araya-Polo, M.; Tchelepi, H.A. Learning CO2 plume migration in faulted reservoirs with Graph Neural Networks. Comput. Geosci. 2024, 193, 105711. [Google Scholar] [CrossRef]
- Manzolini, G.; Fusco, A.; Gioffrè, D.; Matrone, S.; Ramaschi, R.; Saleptsis, M.; Simonetti, R.; Sobic, F.; Wood, M.J.; Ogliari, E.; et al. Impact of PV and EV Forecasting in the Operation of a Microgrid. Forecasting 2024, 6, 591–615. [Google Scholar] [CrossRef]
- Prabawa, P.; Choi, D.-H. Distributionally robust PV planning and curtailment considering cyber attacks on electric vehicle charging under PV/load uncertainties. Energy Rep. 2024, 11, 3436–3449. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, Y.; Li, J. Aggregator-Network Coordinated Peer-to-Peer Multi-Energy Trading via Adaptive Robust Stochastic Optimization. IEEE Trans. Power Syst. 2024, 39, 7124–7137. [Google Scholar] [CrossRef]
- Zhao, A.P.; Li, S.; Li, Z.; Wang, Z.; Fei, X.; Hu, Z.; Alhazmi, M.; Yan, X.; Wu, C.; Lu, S.; et al. Electric Vehicle Charging Planning: A Complex Systems Perspective. IEEE Trans. Smart Grid 2025, 16, 754–772. [Google Scholar] [CrossRef]
- Liang, G.; Zhao, J.; Luo, F.; Weller, S.R.; Dong, Z.Y. A Review of False Data Injection Attacks Against Modern Power Systems. IEEE Trans. Smart Grid 2017, 8, 1630–1638. [Google Scholar] [CrossRef]
- Tajer, A. False Data Injection Attacks in Electricity Markets by Limited Adversaries: Stochastic Robustness. IEEE Trans. Smart Grid 2019, 10, 128–138. [Google Scholar] [CrossRef]
- Wang, Q.; Tai, W.; Tang, Y.; Ni, M.; You, S. A two-layer game theoretical attack-defense model for a false data injection attack against power systems. Int. J. Electr. Power Energy Syst. 2019, 104, 169–177. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, P.; Xun, P.; Liu, B.; Kang, W.; Xiong, Y.; Shi, W. CPMTD: Cyber-physical moving target defense for hardening the security of power system against false data injected attack. Comput. Secur. 2021, 111, 102465. [Google Scholar] [CrossRef]
- Yi, N.; Wang, Q.; Yan, L.; Tang, Y.; Xu, J. A multi-stage game model for the false data injection attack from attacker’s perspective. Sustainable Energy, Grids Netw. 2021, 28, 100541. [Google Scholar] [CrossRef]
- Sun, S.; Hossain-McKenzie, S.; Al Homoud, L.; Haque, K.A.; Goulart, A.; Davis, K. An AI-based Approach for Scalable Cyber-Physical Optimal Response in Power Systems. In Proceedings of the 2024 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 12–13 February 2024; pp. 1–6. [Google Scholar]
- Tian, J.; Wang, B.; Li, J.; Konstantinou, C. Datadriven false data injection attacks against cyber-physical power systems. Comput. Secur. 2022, 121, 102836. [Google Scholar] [CrossRef]
- Sahu, A.; Mao, Z.; Wlazlo, P.; Huang, H.; Davis, K.; Goulart, A.; Zonouz, S. Multi-Source Multi-Domain Data Fusion for Cyberattack Detection in Power Systems. IEEE Access 2021, 9, 119118–119138. [Google Scholar] [CrossRef]
- Basnet, M.; Ali, M.H. Deep Reinforcement Learning-Driven Mitigation of Adverse Effects of Cyber-Attacks on Electric Vehicle Charging Station. Energies 2023, 16, 7296. [Google Scholar] [CrossRef]
- Hou, J.; Hu, C.; Lei, S.; Hou, Y. Cyber Resilience of Power Electronics-Enabled Power Systems: A Review. Renew. Sustain. Energy Rev. 2024, 189, 114036. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, L. Resilient microgrid modeling in Digital Twin considering demand response and landscape design of renewable energy. Sustain. Energy Technol. Assess. 2024, 64, 103628. [Google Scholar] [CrossRef]
- Sahoo, S.; Yang, Y.; Blaabjerg, F. Resilient Synchronization Strategy for AC Microgrids Under Cyber Attacks. IEEE Trans. Power Electron. 2021, 36, 73–77. [Google Scholar] [CrossRef]
- Bassey, K.E.; Opoku-Boateng, J.; Antwi, B.O.; Ntiakoh, A. Economic impact of digital twins on renewable energy investments. Eng. Sci. Technol. J. 2024, 5, 2232–2247. [Google Scholar] [CrossRef]
- Islam, M.Z.; Lin, Y.; Vokkarane, V.M.; Venkataramanan, V. Cyber-Physical Cascading Failure and Resilience of Power Grid: A Comprehensive Review. Front. Energy Res. 2023, 11, 1095303. [Google Scholar] [CrossRef]
- Xiang, Y.; Lu, Y.; Liu, J. Deep reinforcement learning based topology-aware voltage regulation of distribution networks with distributed energy storage. Appl. Energy 2023, 332, 120510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).