Space Vector Modulation Methods with Modified Zero Vector Distribution for Electrical Vehicle Drives with Six-Phase Induction Motor Operating Under Direct Field-Oriented Control
Abstract
1. Introduction
2. Mathematical Model of Six-Phase Squirrel-Cage Induction Motor
- -
- The stator and rotor voltage equations in the α–β coordinate system:
- -
- The stator voltage equations in the additional coordinate system z1–z2:
- -
- The stator voltage equations in the 01–02 coordinate system:
- -
- The equation of the electromagnetic torque:
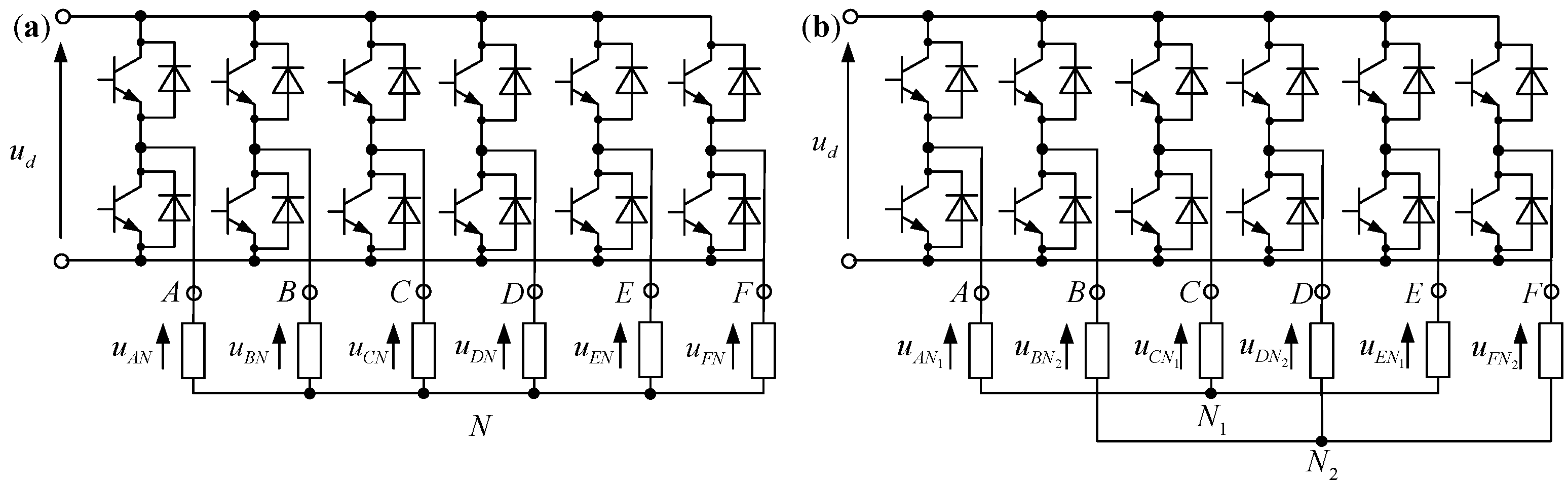
3. Mathematical Model of Six-Phase Voltage Source Inverter
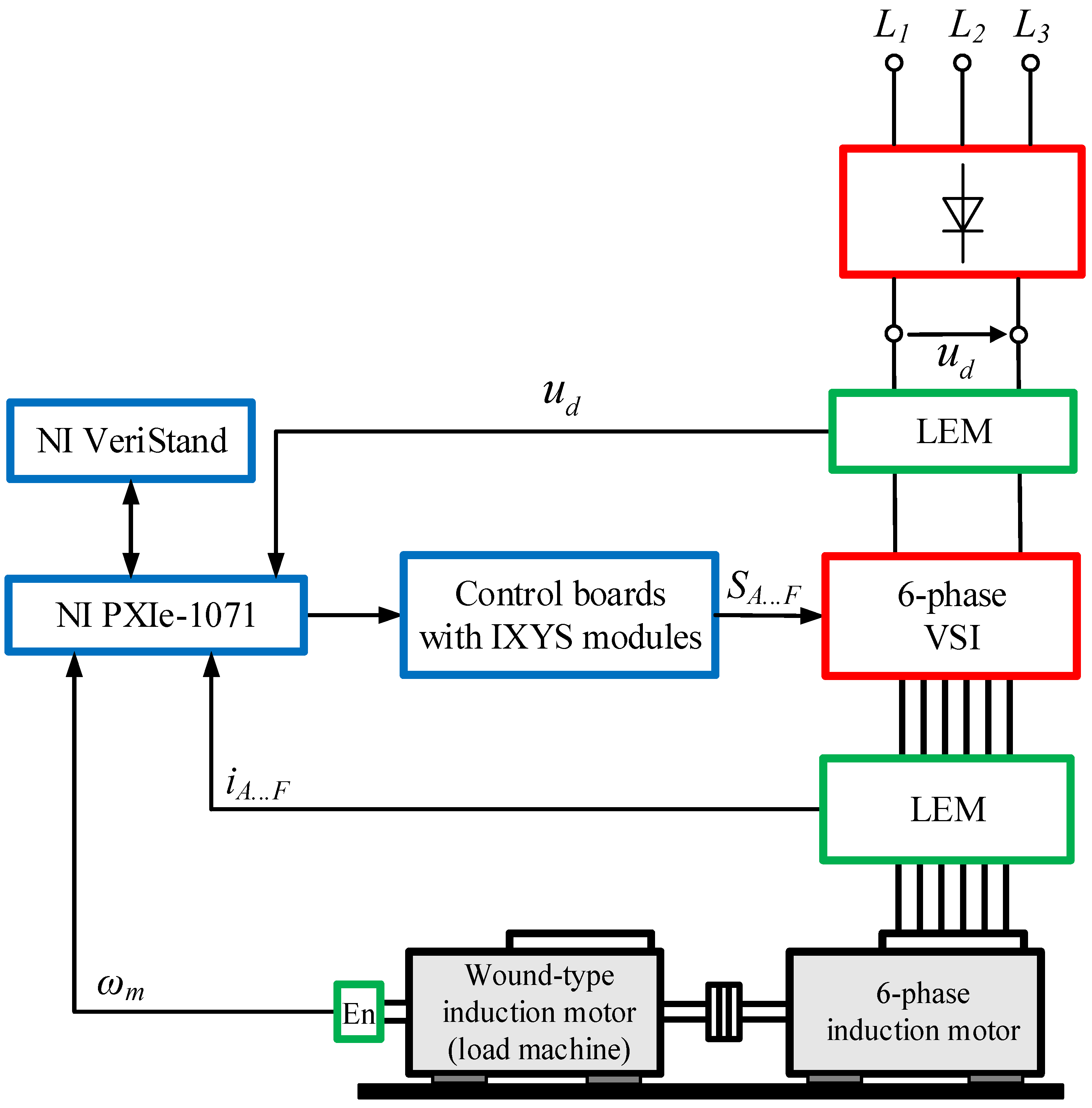
4. Experimental Setup
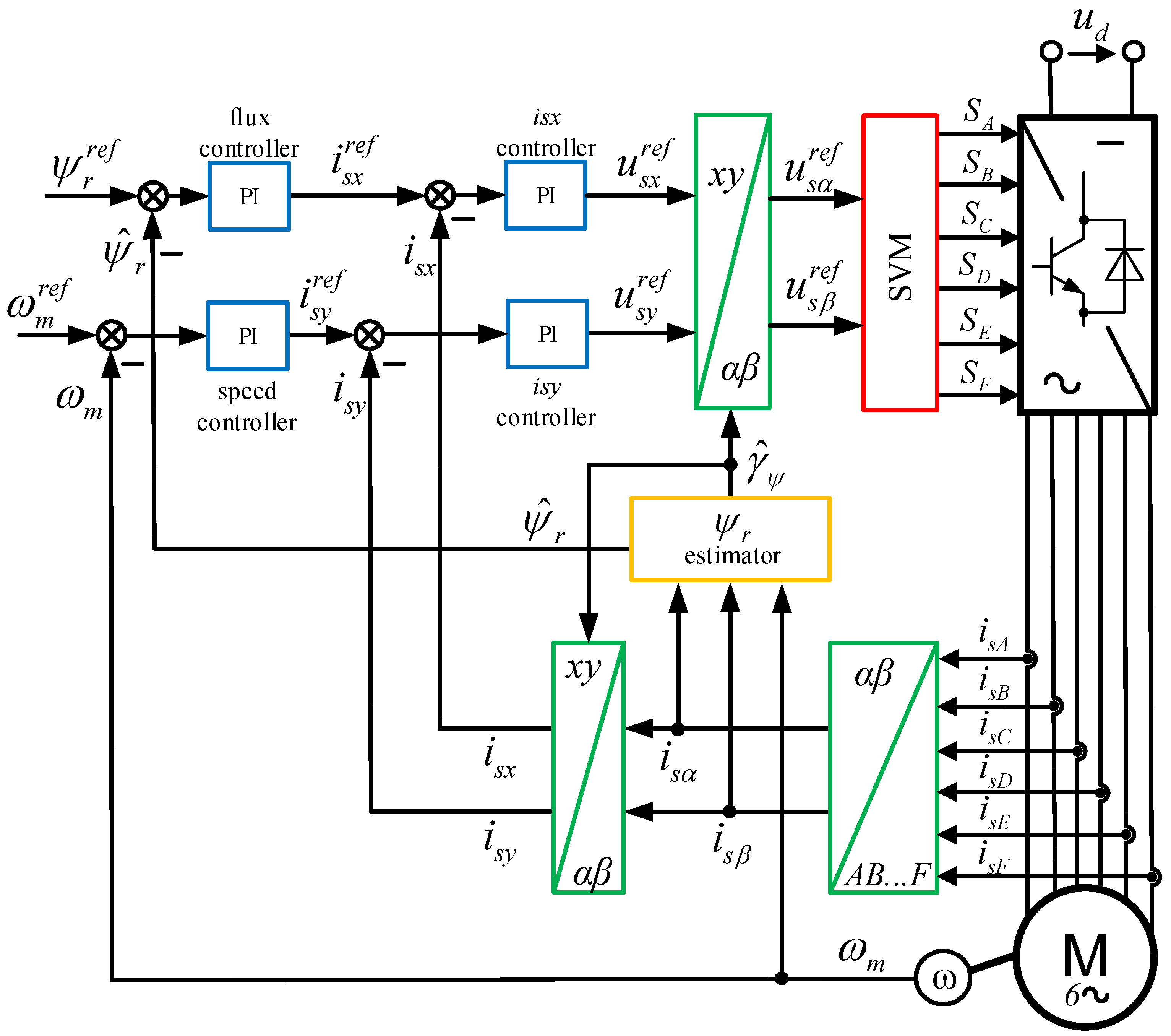
5. Direct Field-Oriented Control System
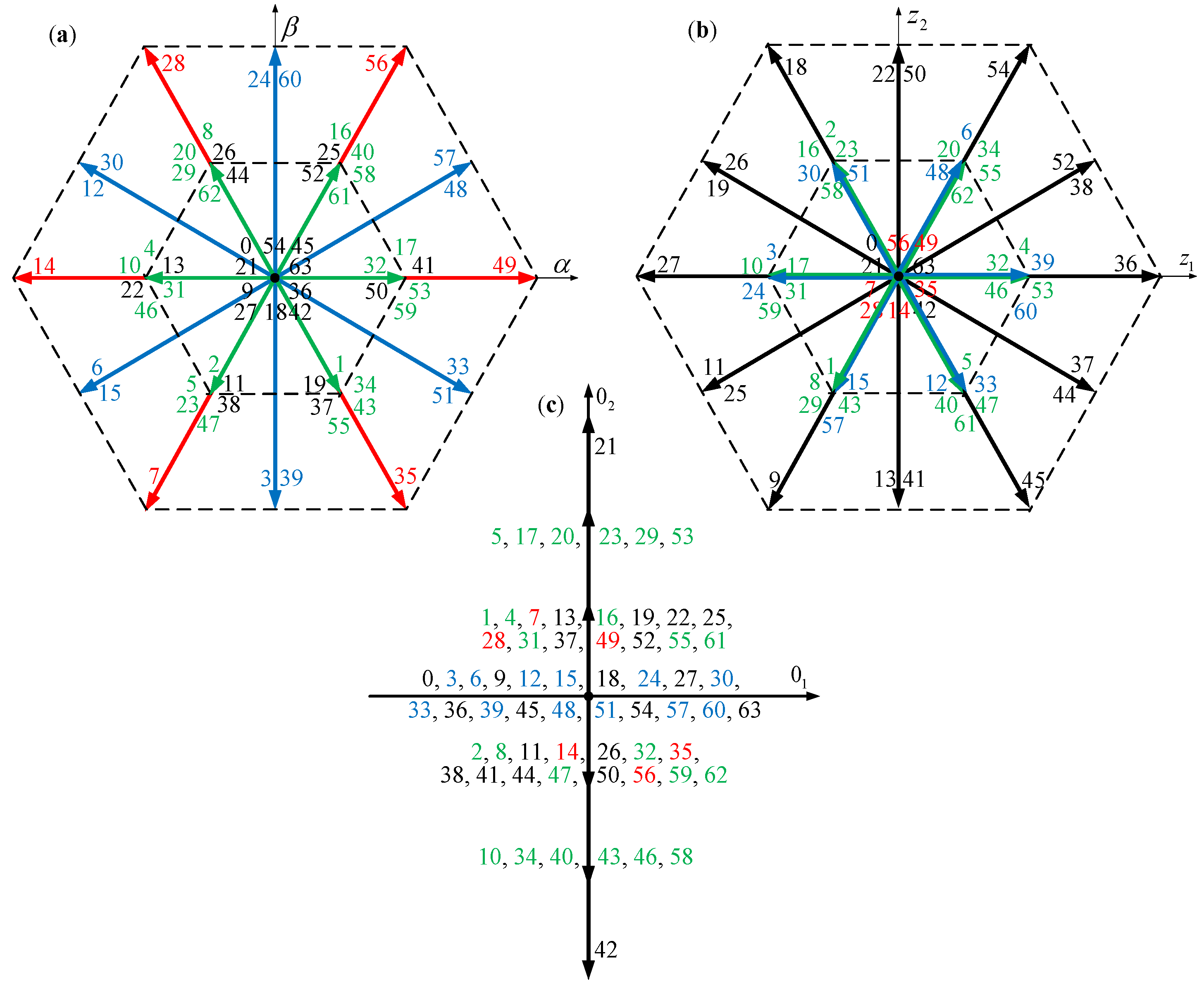
6. Space Vector Modulation Methods
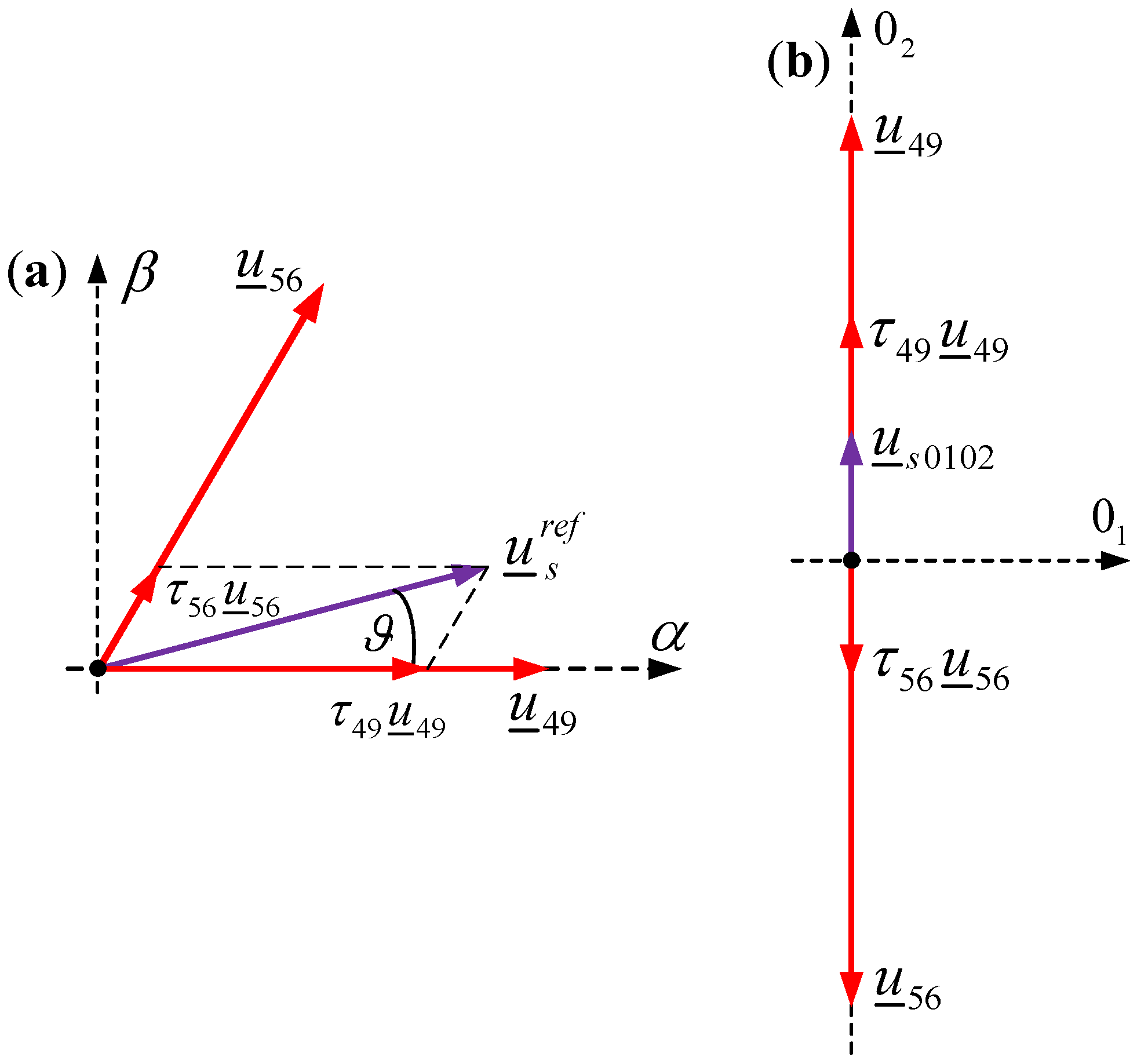
6.1. Classical Space Vector Modulation Method (Only Long Vectors and Two Different Zero Vectors)
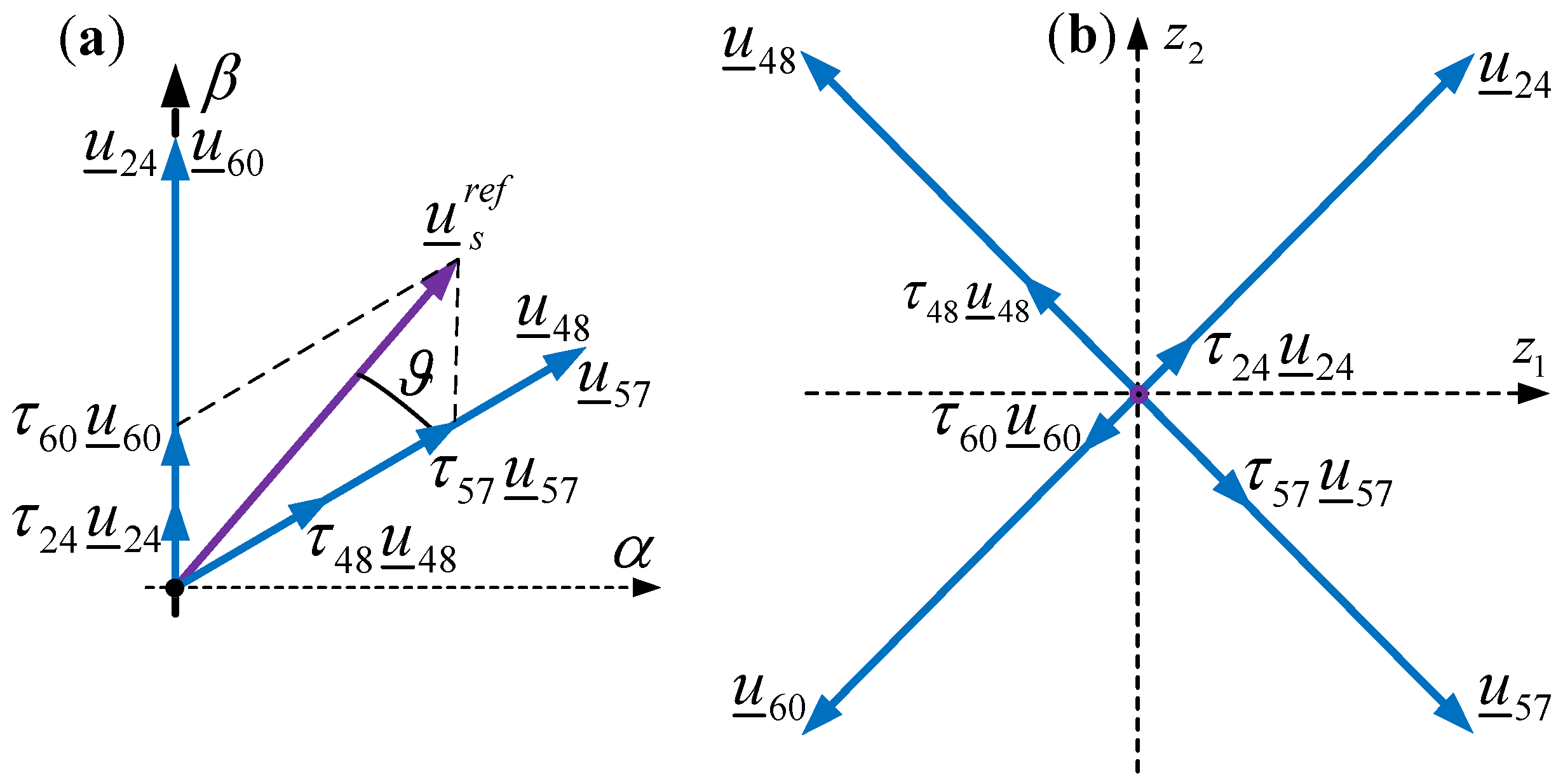
6.2. Vector Modulation Method for Six-Phase VSI Using Medium Vectors
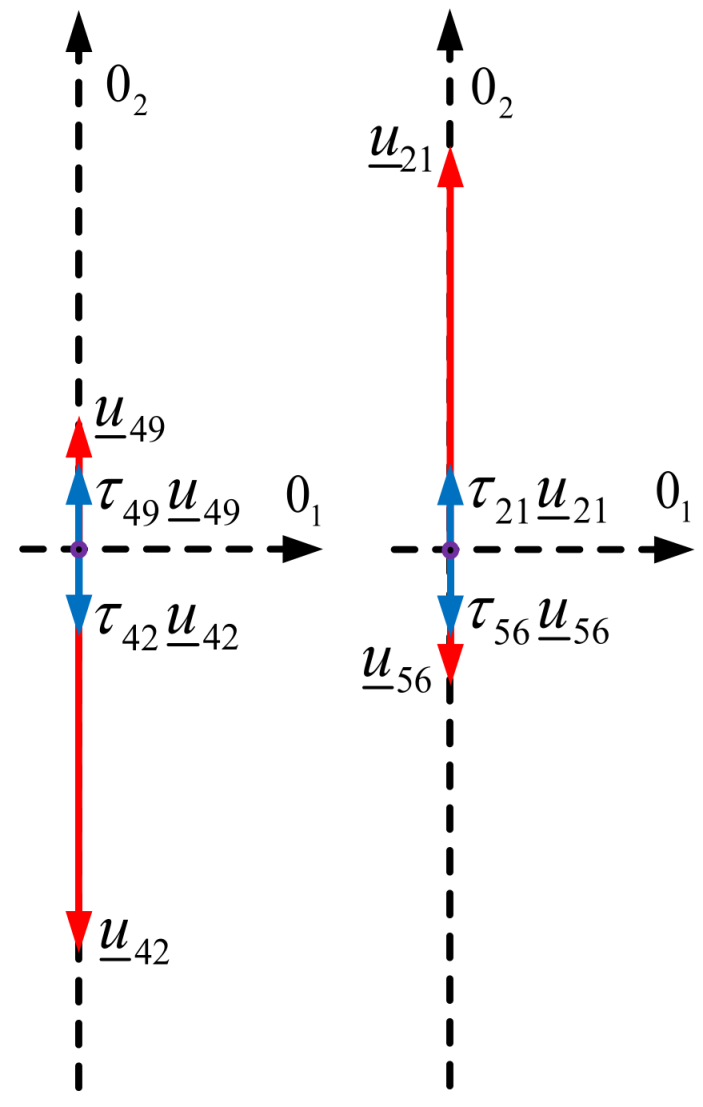
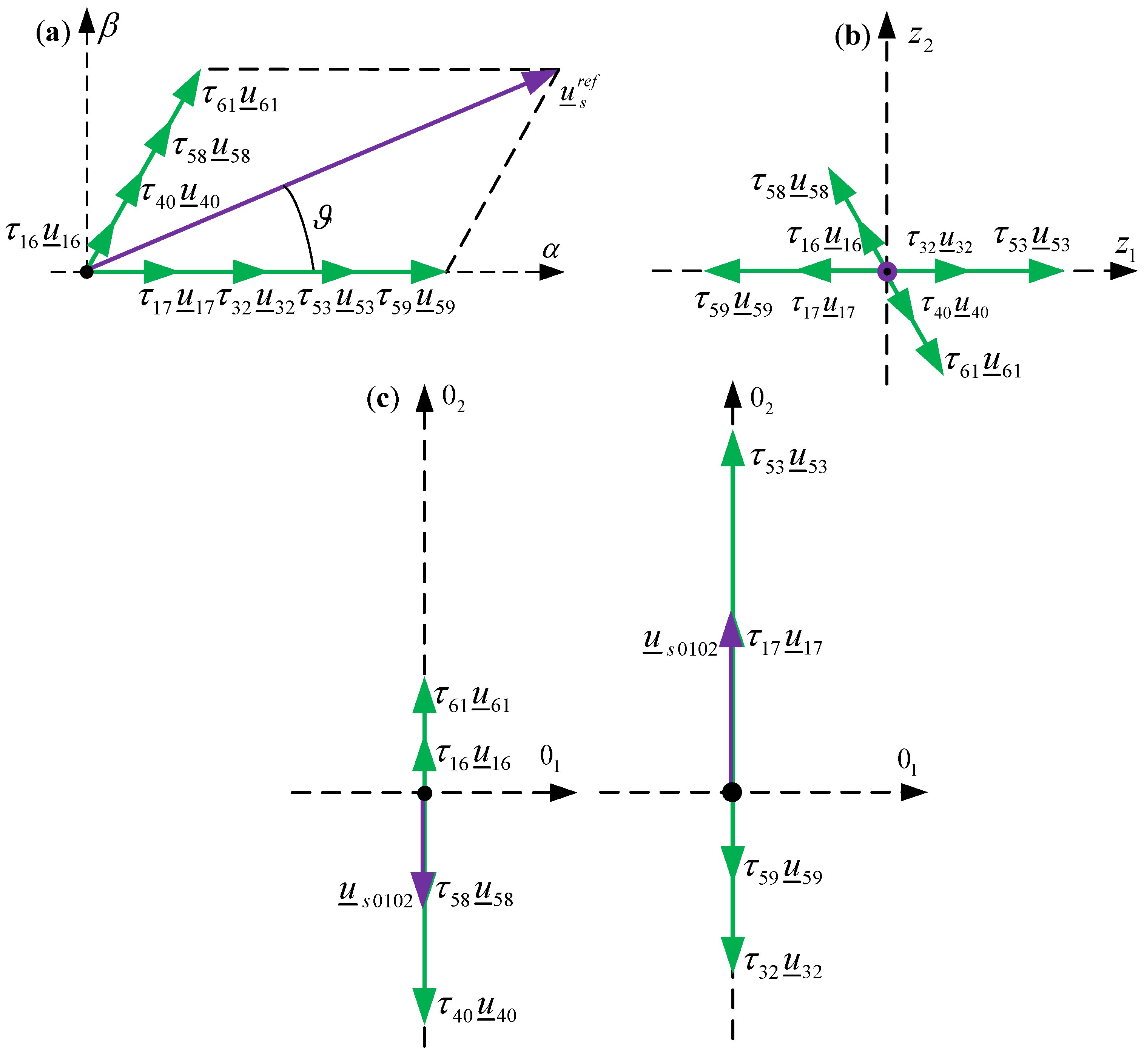
6.3. Modified Space Vector Modulation Method Using Long and Four Zero Voltage Vectors
6.4. Space Vector Modulation Method Using Short and Zero Voltage Vectors
7. Duty Cycles
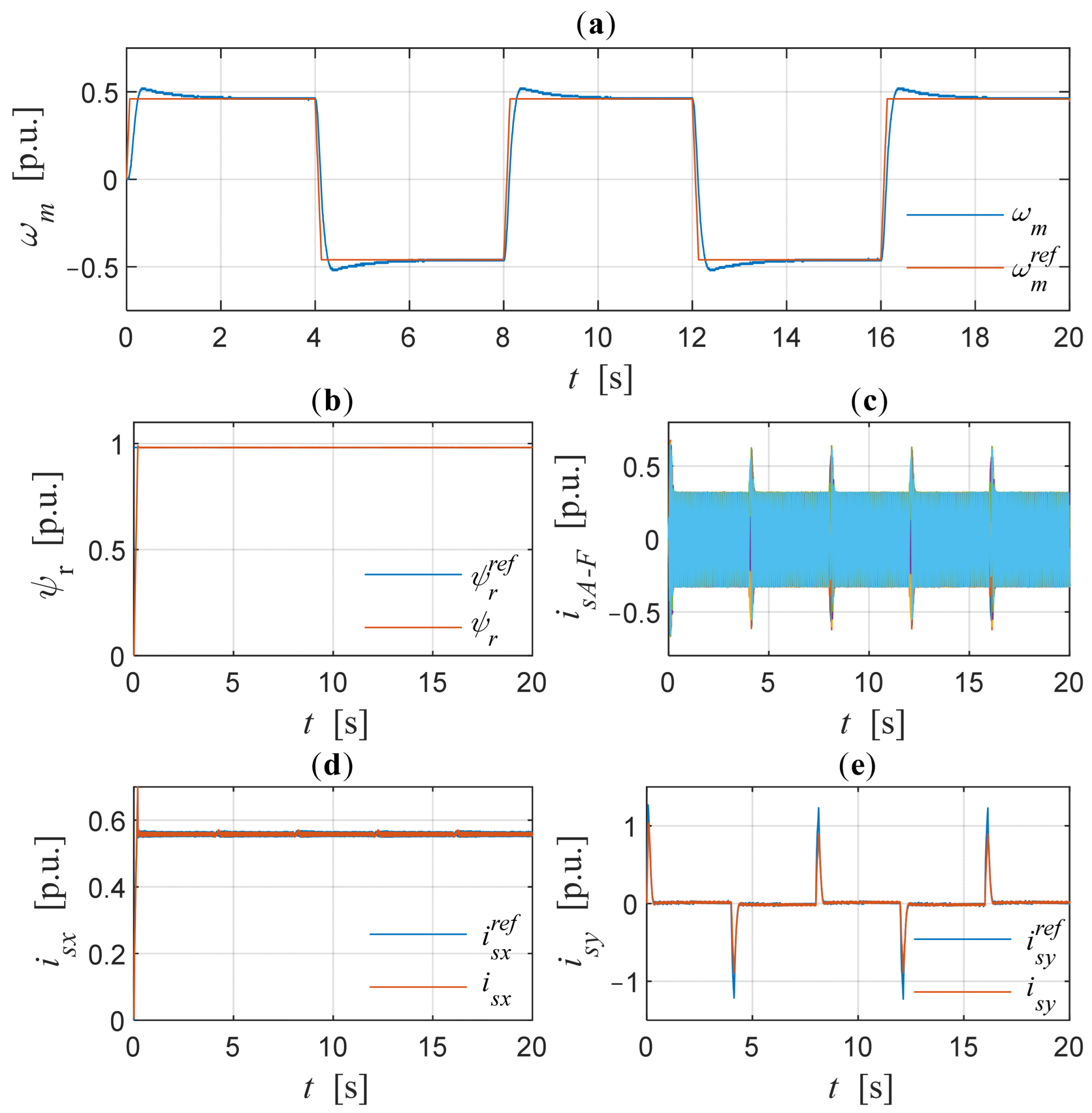
8. Experimental Test Results
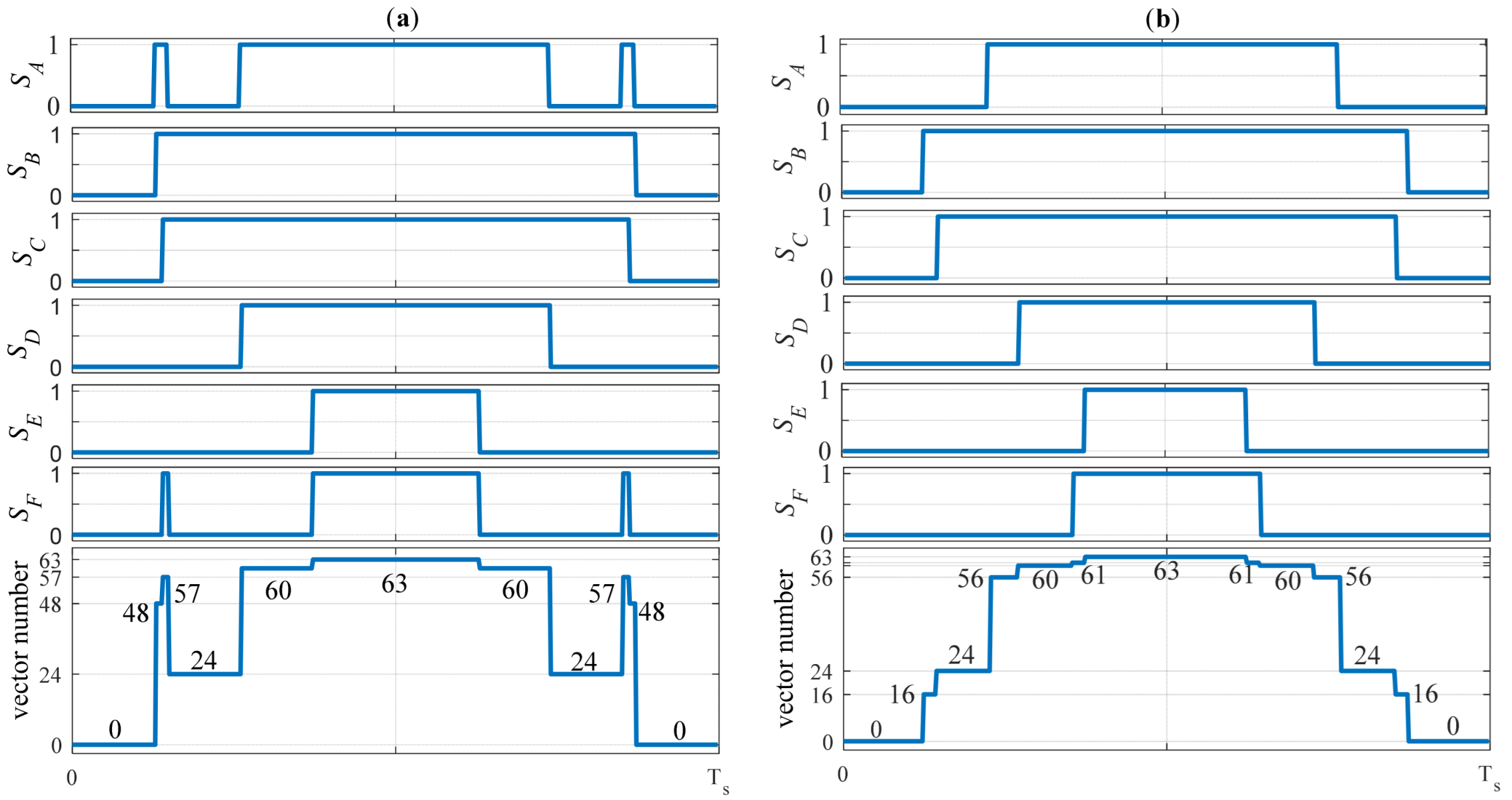
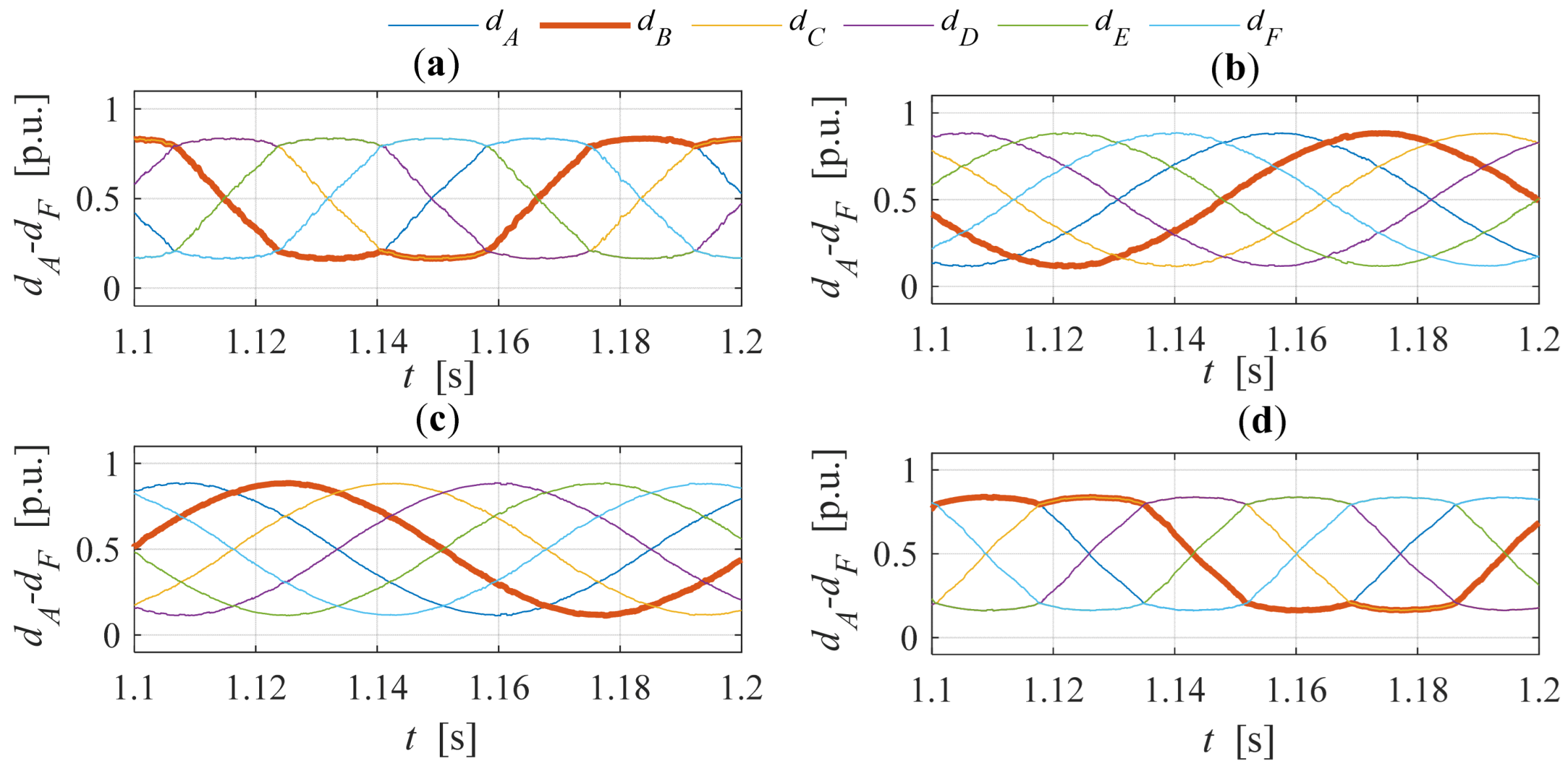
8.1. Duty Cycles in Experimental Tests
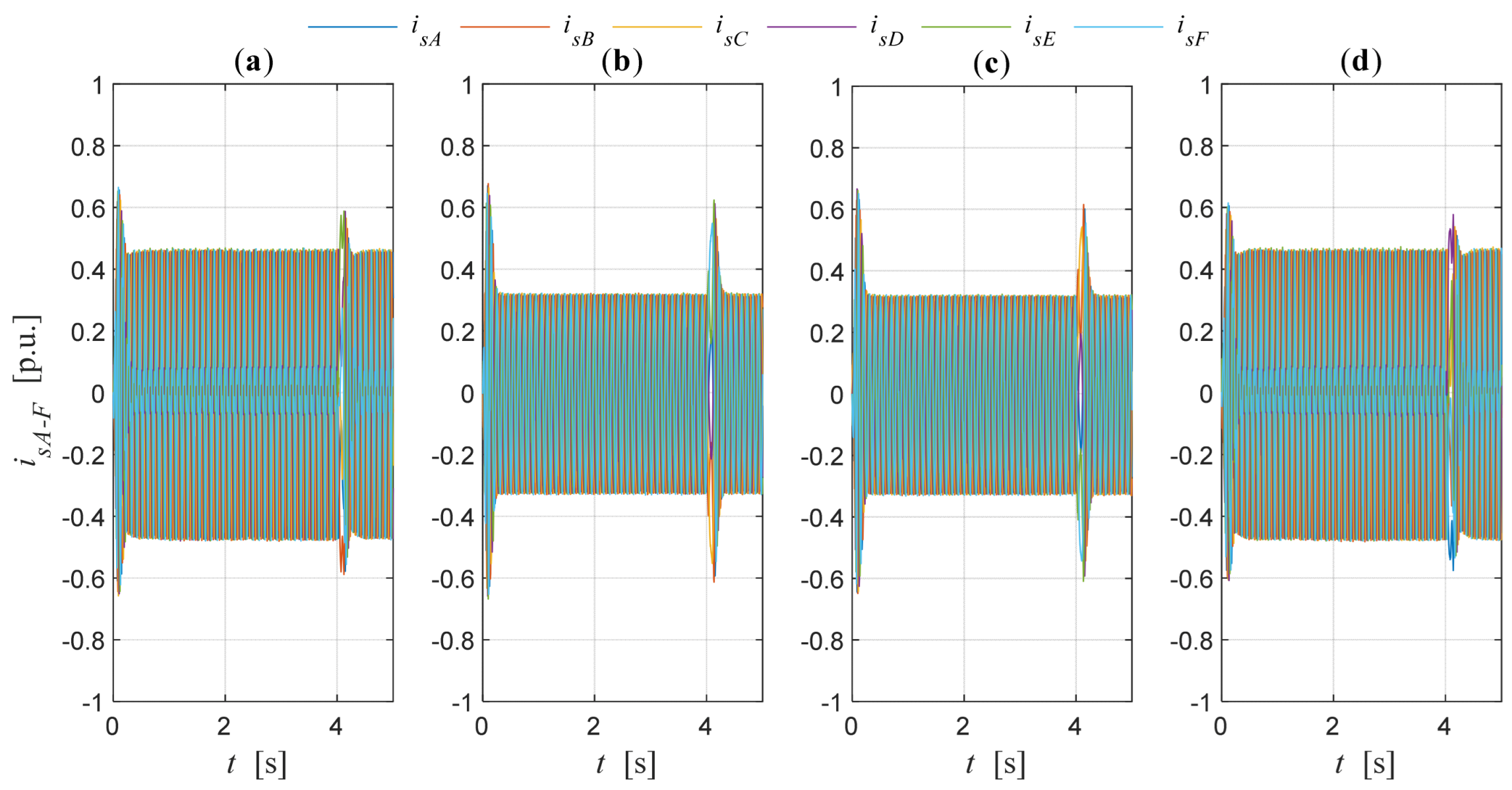
8.2. Effect of Modulation Type on Stator Currents of Induction Motor Operating Under DFOC
9. Modulation Characteristics
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power Electronics and Motor Drives in Electric, Hybrid Electric and Plug-In Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Faiz, J.; Sharifan, M.B.B.; Keyhani, A.; Proca, A.B. Sensorless Direct Torque Control of Induction Motors Used in Electric Vehicle. IEEE Trans. Energy Convers. 2003, 18, 1–10. [Google Scholar] [CrossRef]
- Hajary, A.; Kianinezhad, R.; Seifossadat, S.G.; Mortazavi, S.S.; Saffarian, A. Detection and Localization of Open-Phase Fault in Three-Phase Induction Motor Drives Using Second Order Rotational Park Transformation. IEEE Trans. Power Electron. 2019, 34, 11241–11252. [Google Scholar] [CrossRef]
- Wolkiewicz, M.; Tarchała, G.; Orłowska-Kowalska, T.; Kowalski Cz, T. Online Stator Interturn Short Circuits Monitoring in the DFOC Induction-Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 2517–2528. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Tenconi, A.; Tessarolo, A.; Vaschetto, S. Multiphase Electrical Machines and Drives in the Transportation Electrification. In Proceedings of the IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI), Turin, Italy, 16–18 September 2015. [Google Scholar]
- Frikha, M.A.; Croonen, J.; Deepak, K.; Benomar, Y.; El Baghdadi, M.; Hegazy, O. Multiphase Motors and Drive Systems for Electric Vehicle Powertrains: State of the Art Analysis and Future Trends. Energies 2023, 16, 768. [Google Scholar] [CrossRef]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase Induction Motor Drives—A Technology Status Review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Listwan, J.; Oleszczyszyn, P. Analysis of the Drive of the Electric Vehicle with Six-Phase Induction Motor. Power Electron. Drives 2023, 8, 252–274. [Google Scholar] [CrossRef]
- Nuca, I.; Cazac, V.; Turcanu, A.; Burduniuc, M. Development of Traction System with Six Phase Induction Motor for Urban Passenger Vehicle. In Proceedings of the 11th International Conference and Exposition on Electrical and Power Engineering (EPE 2020), Iasi, Romania, 22–23 October 2020. [Google Scholar]
- Salem, A.; Narimani, M. A Review on Multiphase Drives for Automotive Traction Applications. IEEE Trans. Transp. Electrif. 2019, 5, 1329–1348. [Google Scholar] [CrossRef]
- Iqbal, A.; Singh, G.K. PSO Based Controlled Six-phase Grid Connected Induction Generator for Wind Energy Generation. CES Trans. Electr. Mach. Syst. 2021, 5, 41–49. [Google Scholar] [CrossRef]
- Pantea, A.; Yazidi, A.; Betin, F.; Carriere, S.; Sivert, A.; Vacossin, B.; Henao, H.; Capolino, G.-A. Fault-Tolerant Control of a Low-Speed Six-Phase Induction Generator for Wind Turbines. IEEE Trans. Ind. Appl. 2019, 55, 426–436. [Google Scholar] [CrossRef]
- Bodo, N.; Levi, E.; Subotic, I.; Espina, J.; Empringham, L.; Johnson, C.M. Efficiency Evaluation of Fully Integrated On-Board EV Battery Chargers with Nine-Phase Machines. IEEE Trans. Energy Convers. 2017, 32, 257–266. [Google Scholar] [CrossRef]
- Diab, M.S.; Elserougi, A.A.; Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. A Nine-Switch-Converter-Based Integrated Motor Drive and Battery Charger System for EVs Using Symmetrical Six-Phase Machines. IEEE Trans. Ind. Electron. 2016, 63, 5326–5335. [Google Scholar] [CrossRef]
- Dujic, D.; Grandi, G.; Jones, M.; Levi, E. A Space Vector PWM Scheme for Multifrequency Output Voltage Generation with Multiphase Voltage-Source Inverters. IEEE Trans. Ind. Electron. 2008, 55, 1943–1955. [Google Scholar] [CrossRef]
- Iqbal, A.; Levi, E.; Jones, M.; Vukosavic, S.N. Generalised Sinusoidal PWM with Harmonic Injection for Multi-Phase VSIs. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006. [Google Scholar]
- Kianinezhad, R.; Nahid, B.; Betin, F.; Capolino, G.A. Multi-Vector SVM: A New Approach to Space Vector Modulation Control for Six-Phase Induction Machines. In Proceedings of the 31st Annual Conference of IEEE Industrial Society, IECON, Raleigh, NC, USA, 6–10 November 2005; pp. 1359–1364. [Google Scholar]
- Zandzadeh, M.J.; Saniei, M.; Kianinezhad, R. Space vector modulation with reduced common mode voltage for six-phase drives. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 395–411. [Google Scholar] [CrossRef]
- Listwan, J.; Pienkowski, K. Comparative Analysis of Control Methods with Model Reference Adaptive System Estimators of a Seven-Phase Induction Motor with Encoder Failure. Energies 2021, 14, 1147. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, L.; Yongdong, L.; Zheng, Z.; Wang, K. Modeling and Control of 15-Phase Induction Machine under One Phase Open Circuit Fault. In Proceedings of the International Conference on Electrical Machines and Systems, Busan, Republic of Korea, 26–29 October 2013. [Google Scholar]
- Bojoi, R.; Lazzari, M.; Profumo, F.; Tenconi, A. Digital Field-Oriented Control for Dual Three-Phase Induction Motor Drives. IEEE Trans. Ind. Appl. 2003, 39, 752–760. [Google Scholar] [CrossRef]
- Che, H.S.; Duran, M.J.; Levi, E.; Jones, M.; Hew, W.P.; Rahim, N.A. Postfault Operation of an Asymmetrical Six-Phase Induction Machine With Single and Two Isolated Neutral Points. IEEE Trans. Power Electron. 2014, 29, 5406–5416. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, M.; Jiang, J. A Comprehensive Review of the Multiphase Motor Drive Topologies for High-Power Electric Vehicle: Current Status, Research Challenges and Future Trends. IEEE Trans. Transp. Electrif. 2025, 11, 3631–3654. [Google Scholar] [CrossRef]
- Soares, E.L.; Jacobina, C.B.; de Freitas, N.B.; Rocha, N.; Maia, C.N.; Lima, M.N. A Multilevel Open-End Winding Six-Phase Induction Motor Drive Topology Based on Three Two-Level Three-Phase Inverters. IEEE Trans. Ind. Appl. 2023, 59, 6360–6372. [Google Scholar] [CrossRef]
- Moghadasian, M.; Kianinezhad, R.; Betin, F.; Capolino, G.A. Torque Ripple Minimization in Direct Torque Control of Six-Phase Induction Machines Using Fuzzy Inference Systems. In Proceedings of the XIX International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010. [Google Scholar]
- Lipinskis, T.; Baskys, A.; Rutkauskas, A. Six-Phase Voltage Forming Method Using the Largest Magnitude Space Vectors. Electron. Elektrotechnika 2013, 19, 99–102. [Google Scholar] [CrossRef][Green Version]
- Listwan, J. Analysis of Fauls States in Drive Systems with Multi-Phase Induction Motors. Arch. Electr. Eng. 2019, 68, 817–830. [Google Scholar]

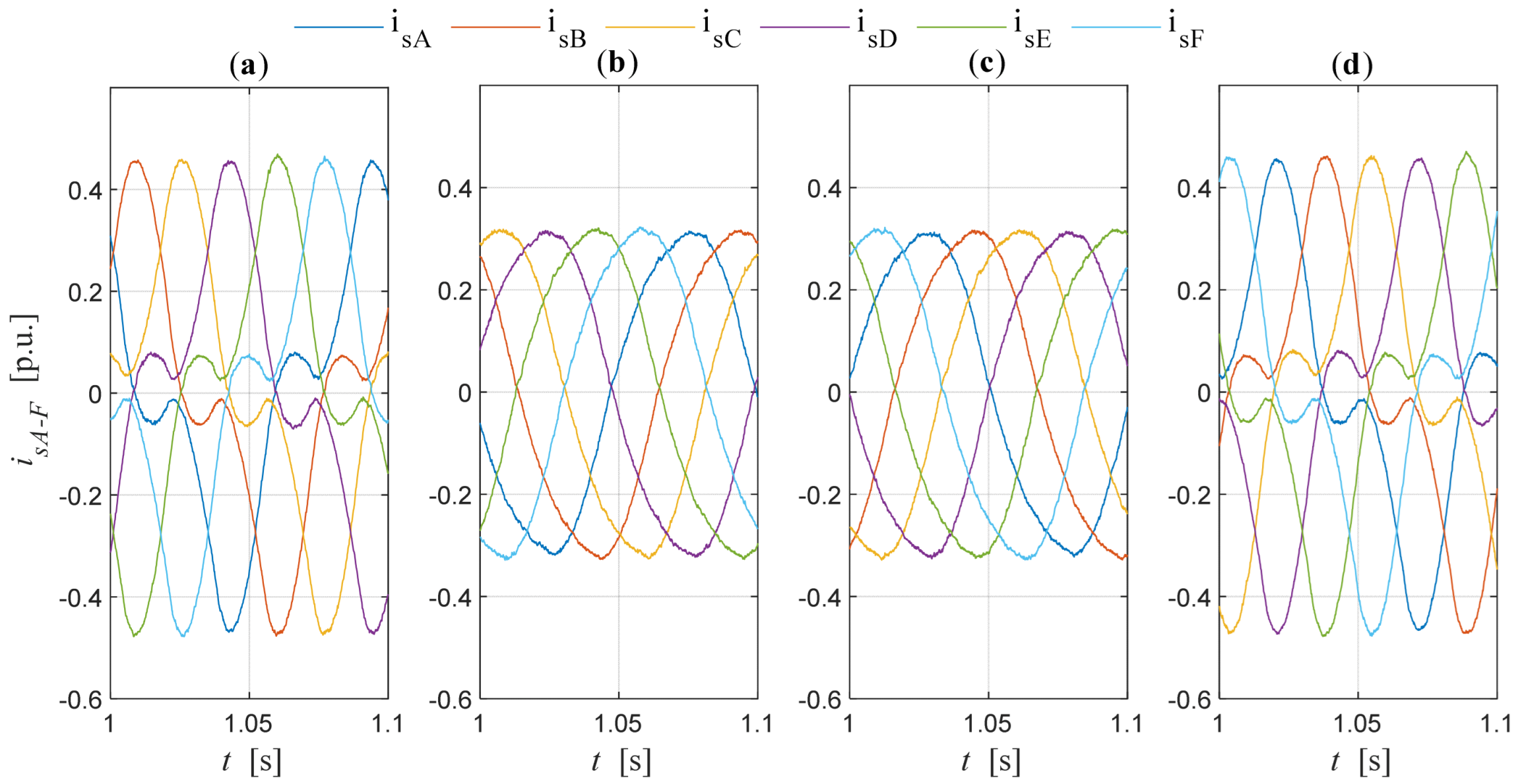
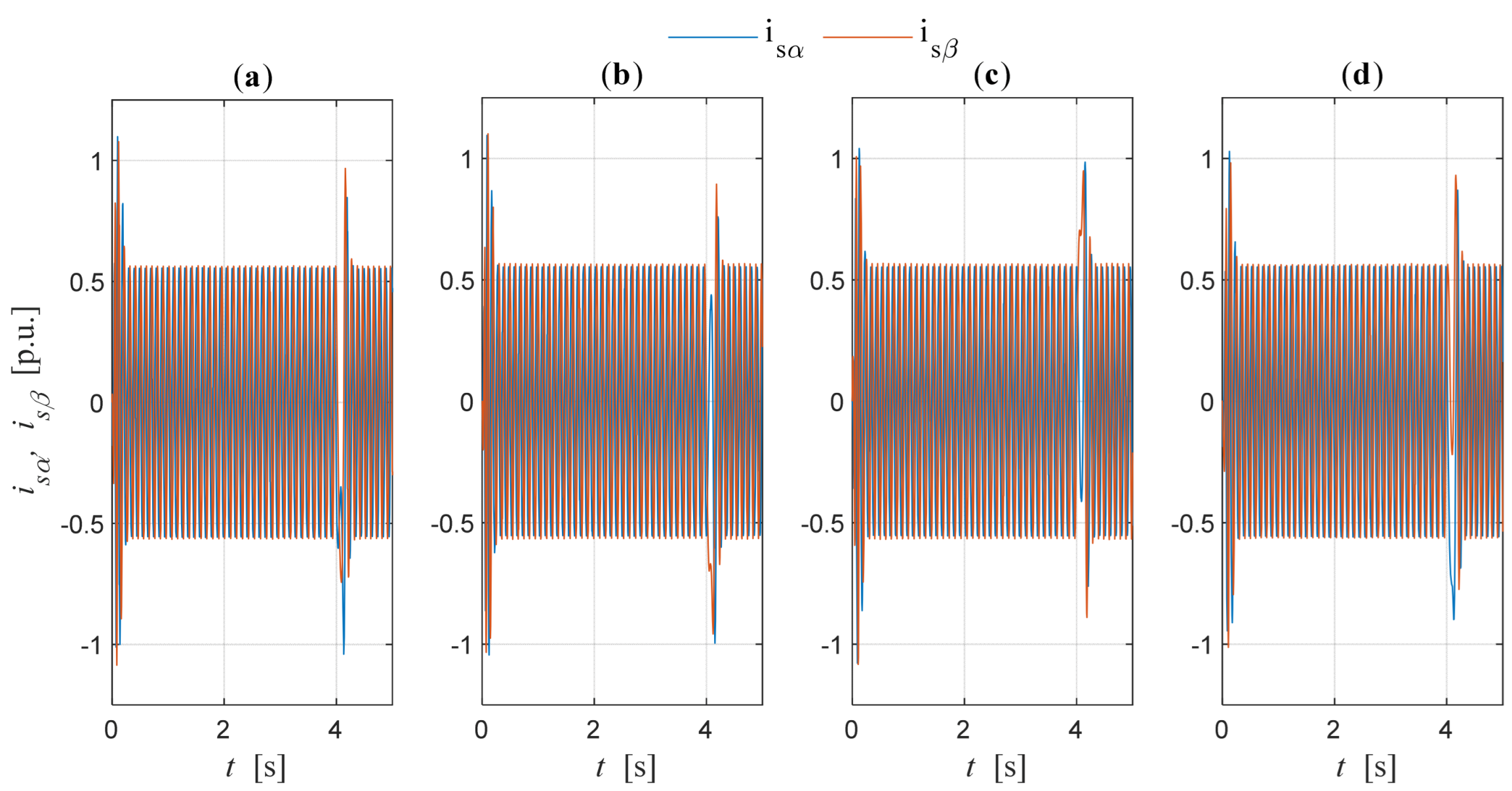
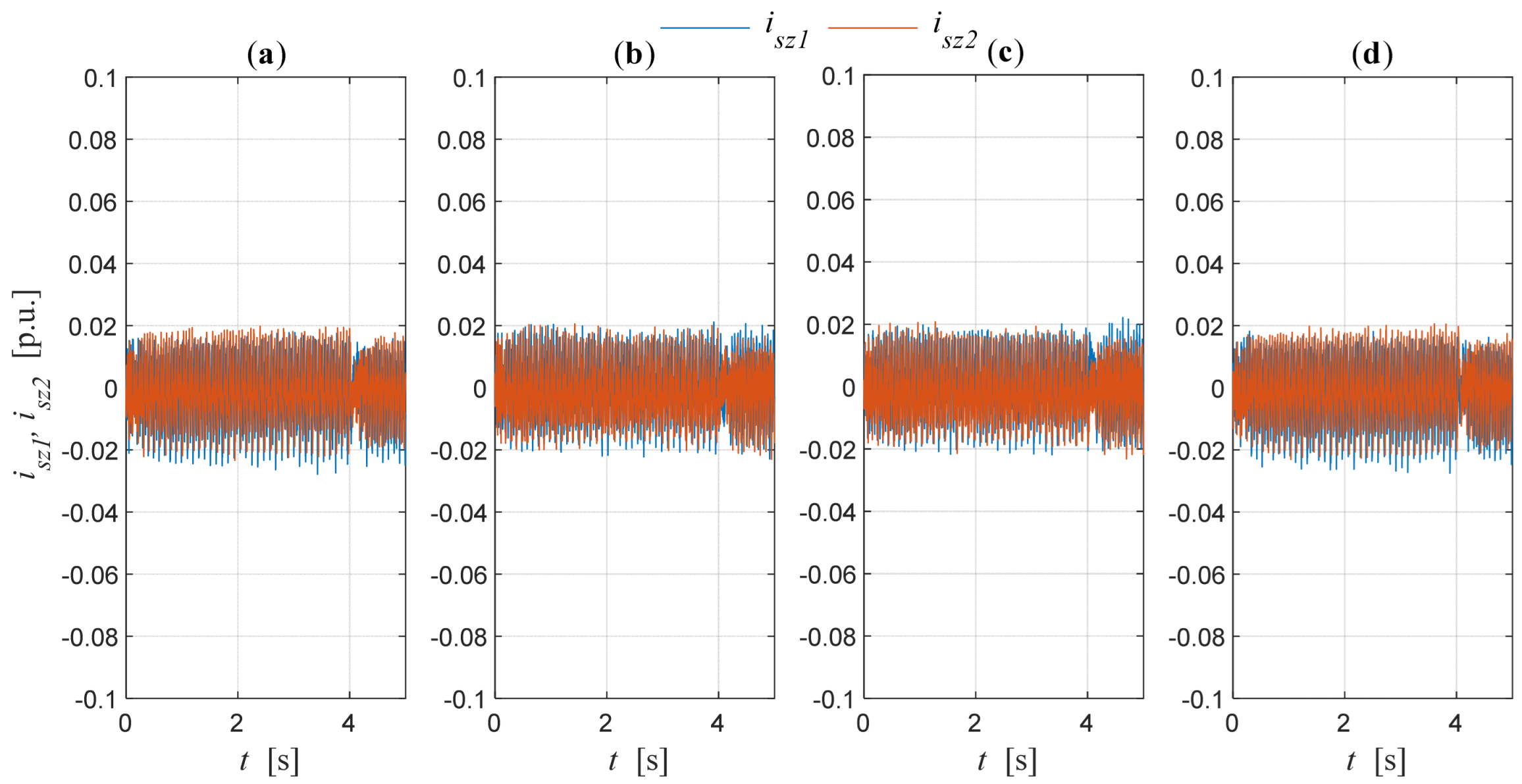
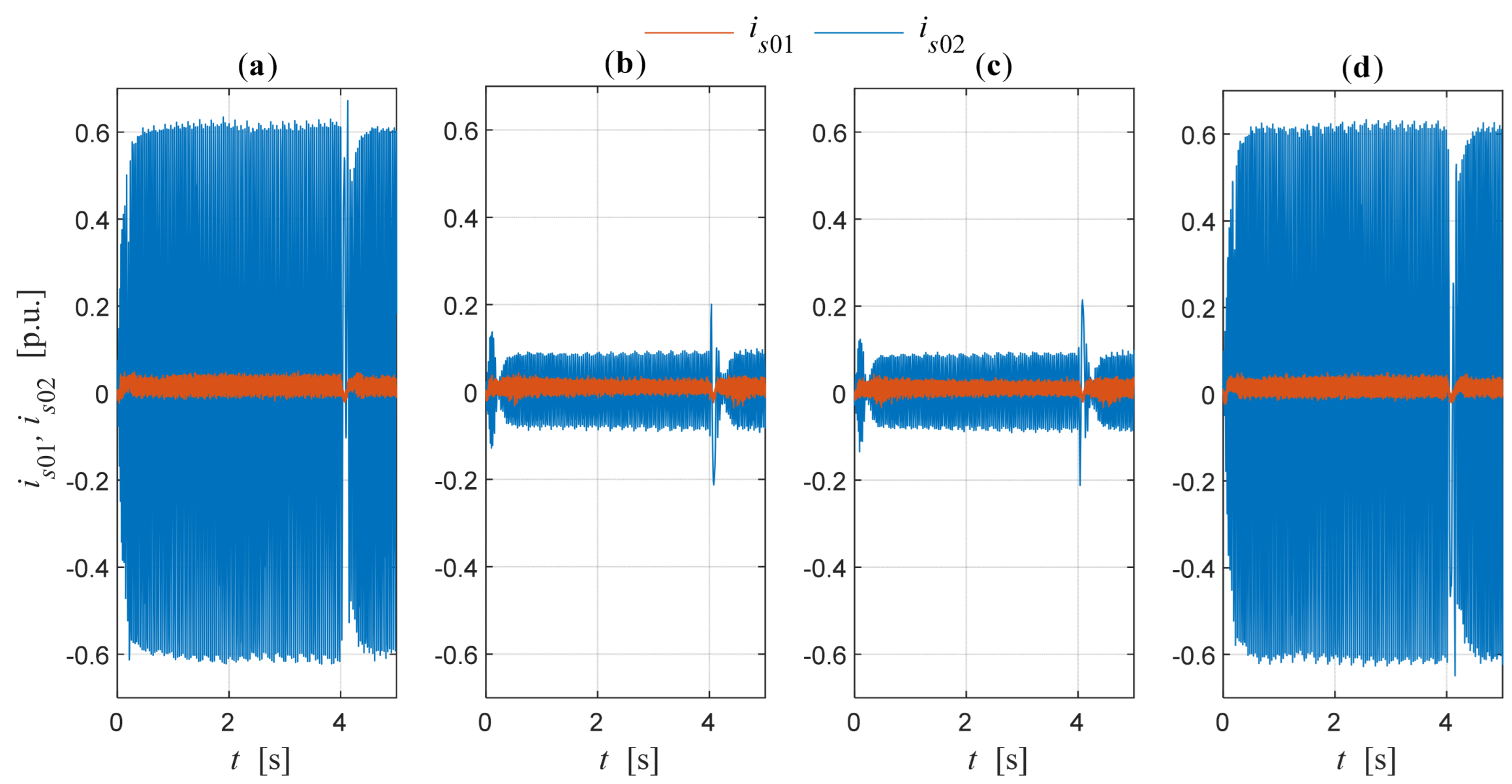

| Long Vectors | Medium Vectors | Short Vectors | Zero Vectors | ||
|---|---|---|---|---|---|
| 0 | |||||
| 0 | |||||
| single star | 0 | ||||
| double star | 0 | 0 | 0 | 0 | |
| Region | Modulation Index | 01–02 Component Compensation | Total Time for Zero Vectors | ||
|---|---|---|---|---|---|
| from | to | ||||
| I | 0 | always full compensation | never zero | never | |
| II | 1 | sometimes full compensation/sometimes partial compensation | never zero | sometimes | |
| III | 1 | always partial compensation | never zero | always | |
| IV | sometimes partial compensation/sometimes no compensation | sometimes zero | always | ||
| V | ∞ | no compensation | always zero | always | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarchała, G.; Listwan, J. Space Vector Modulation Methods with Modified Zero Vector Distribution for Electrical Vehicle Drives with Six-Phase Induction Motor Operating Under Direct Field-Oriented Control. Energies 2025, 18, 3122. https://doi.org/10.3390/en18123122
Tarchała G, Listwan J. Space Vector Modulation Methods with Modified Zero Vector Distribution for Electrical Vehicle Drives with Six-Phase Induction Motor Operating Under Direct Field-Oriented Control. Energies. 2025; 18(12):3122. https://doi.org/10.3390/en18123122
Chicago/Turabian StyleTarchała, Grzegorz, and Jacek Listwan. 2025. "Space Vector Modulation Methods with Modified Zero Vector Distribution for Electrical Vehicle Drives with Six-Phase Induction Motor Operating Under Direct Field-Oriented Control" Energies 18, no. 12: 3122. https://doi.org/10.3390/en18123122
APA StyleTarchała, G., & Listwan, J. (2025). Space Vector Modulation Methods with Modified Zero Vector Distribution for Electrical Vehicle Drives with Six-Phase Induction Motor Operating Under Direct Field-Oriented Control. Energies, 18(12), 3122. https://doi.org/10.3390/en18123122






