Determining Pilot Ignition Delay in Dual-Fuel Medium-Speed Marine Engines Using Methanol or Hydrogen
Abstract
1. Introduction
2. Experimental Setup
3. Numerical Methodology
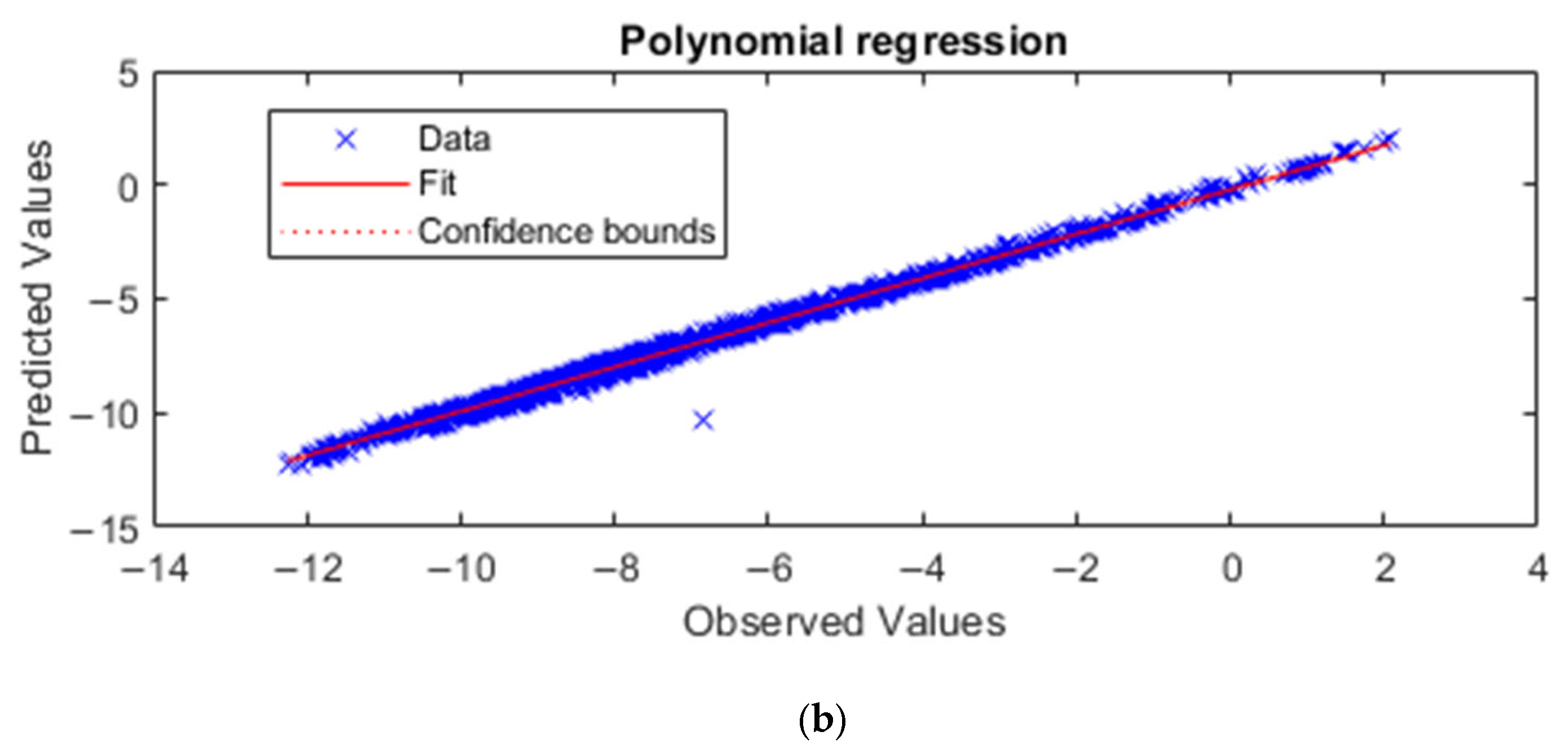
3.1. Dataset Generation Using Chemical Kinetic Mechanisms and Cantera
3.2. Machine Learning Method
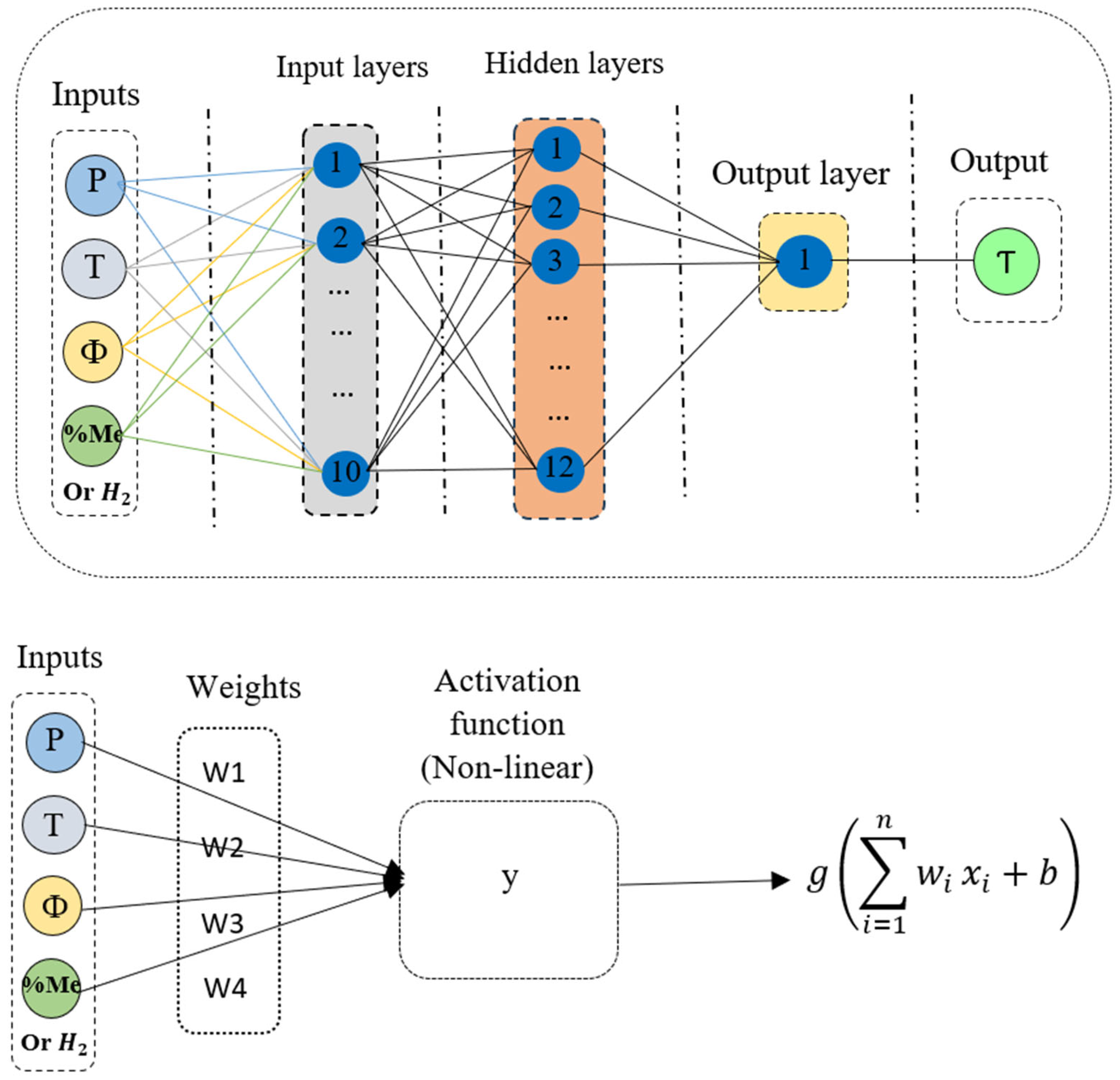
3.2.1. Artificial Neural Network (ANN)
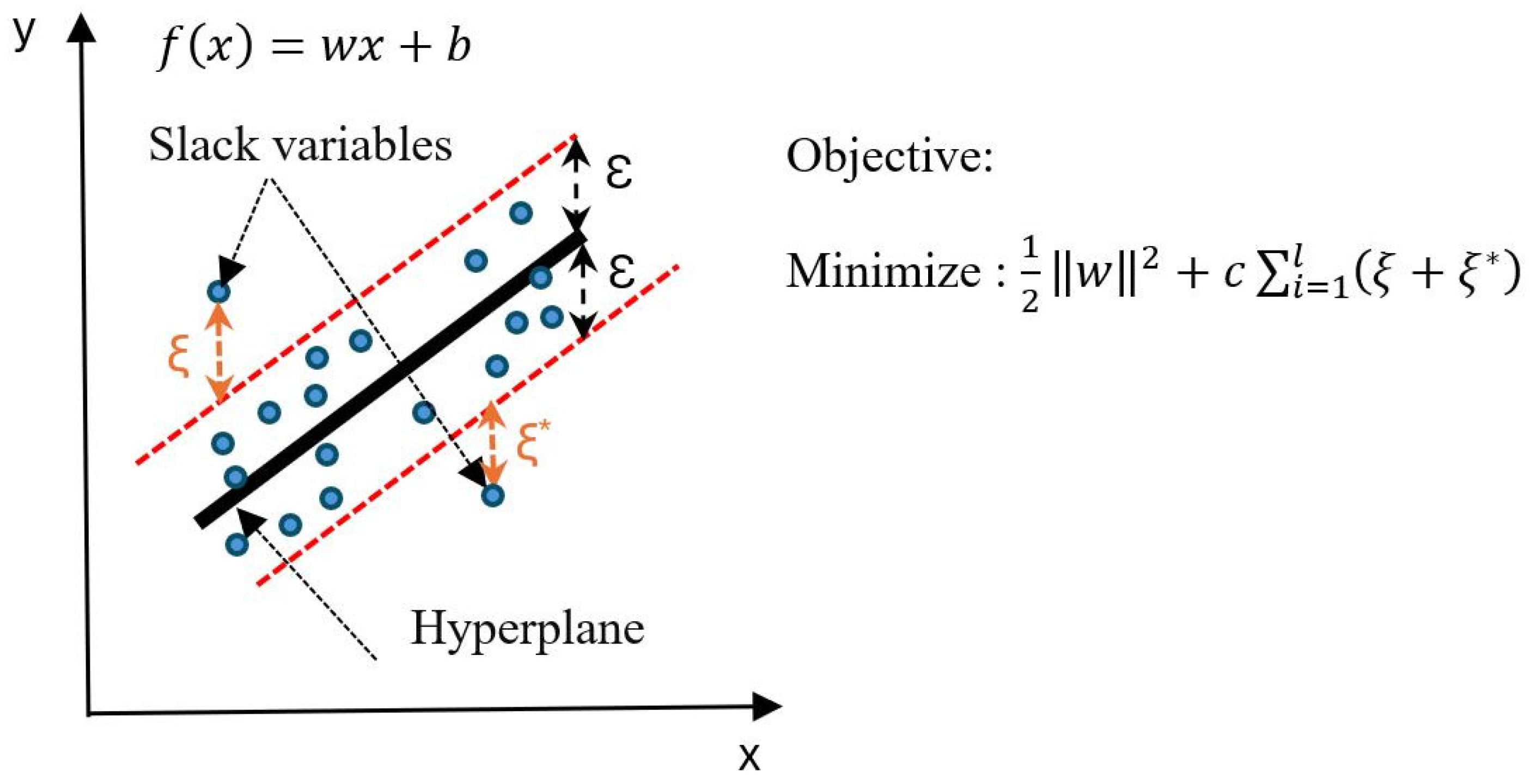
3.2.2. Support Vector Regression (SVR)
3.3. Multi-Zone Dual-Fuel Combustion Model in GT-Power
3.4. Integration of the ANN into the Multi-Zone Dual-Fuel Combustion Model in GT-Power
3.5. Look-Up Table and Correlation Methods
4. Results and Discussions
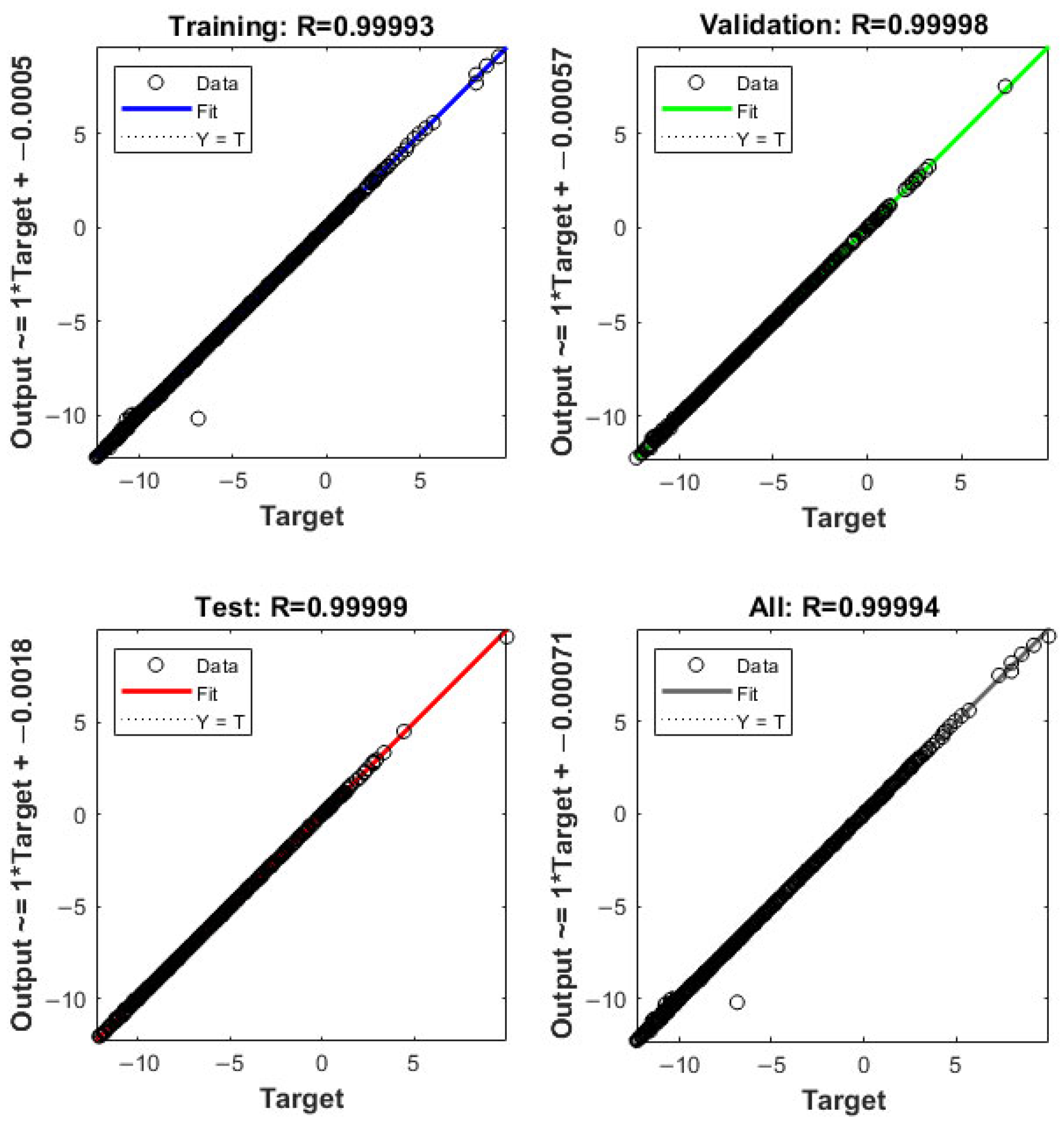
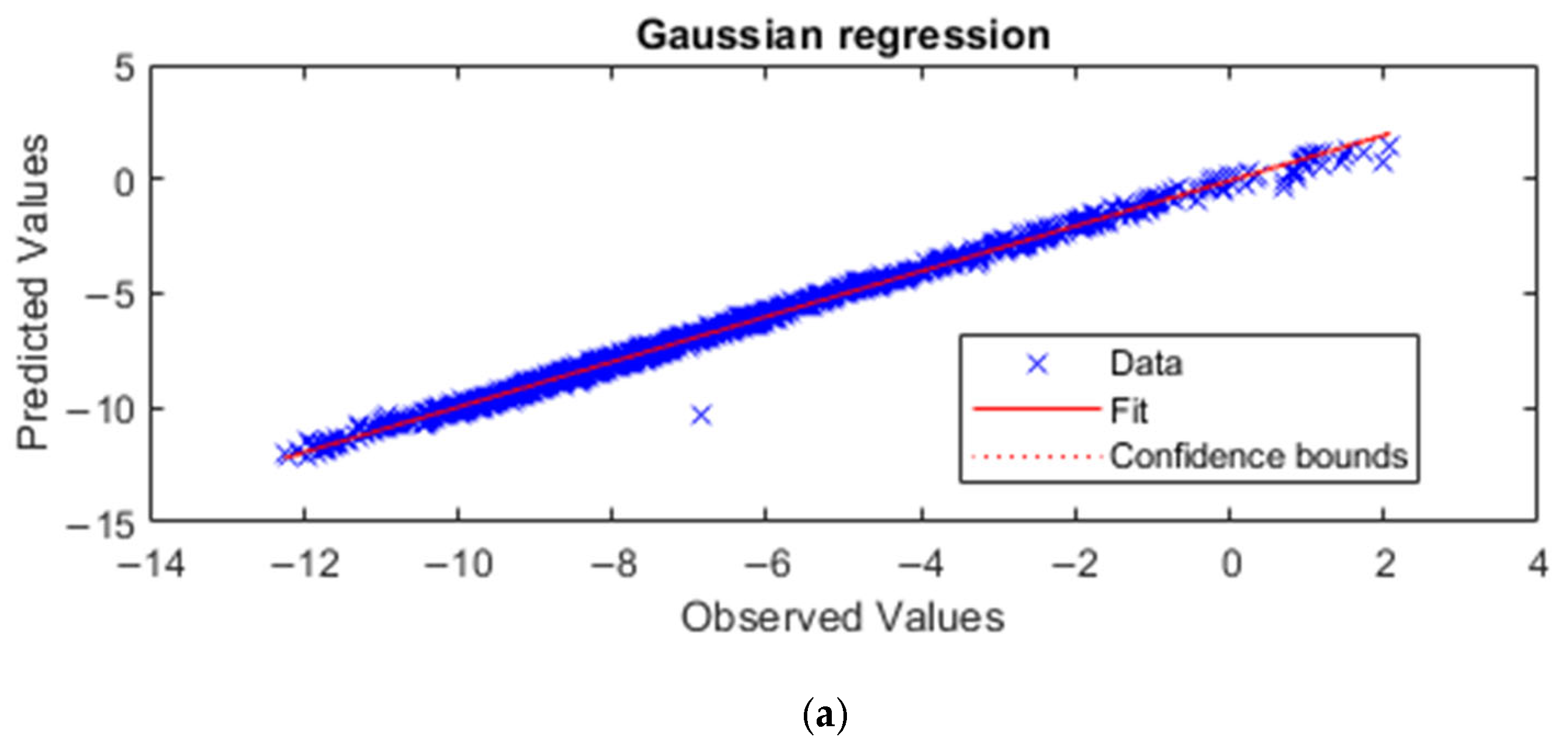
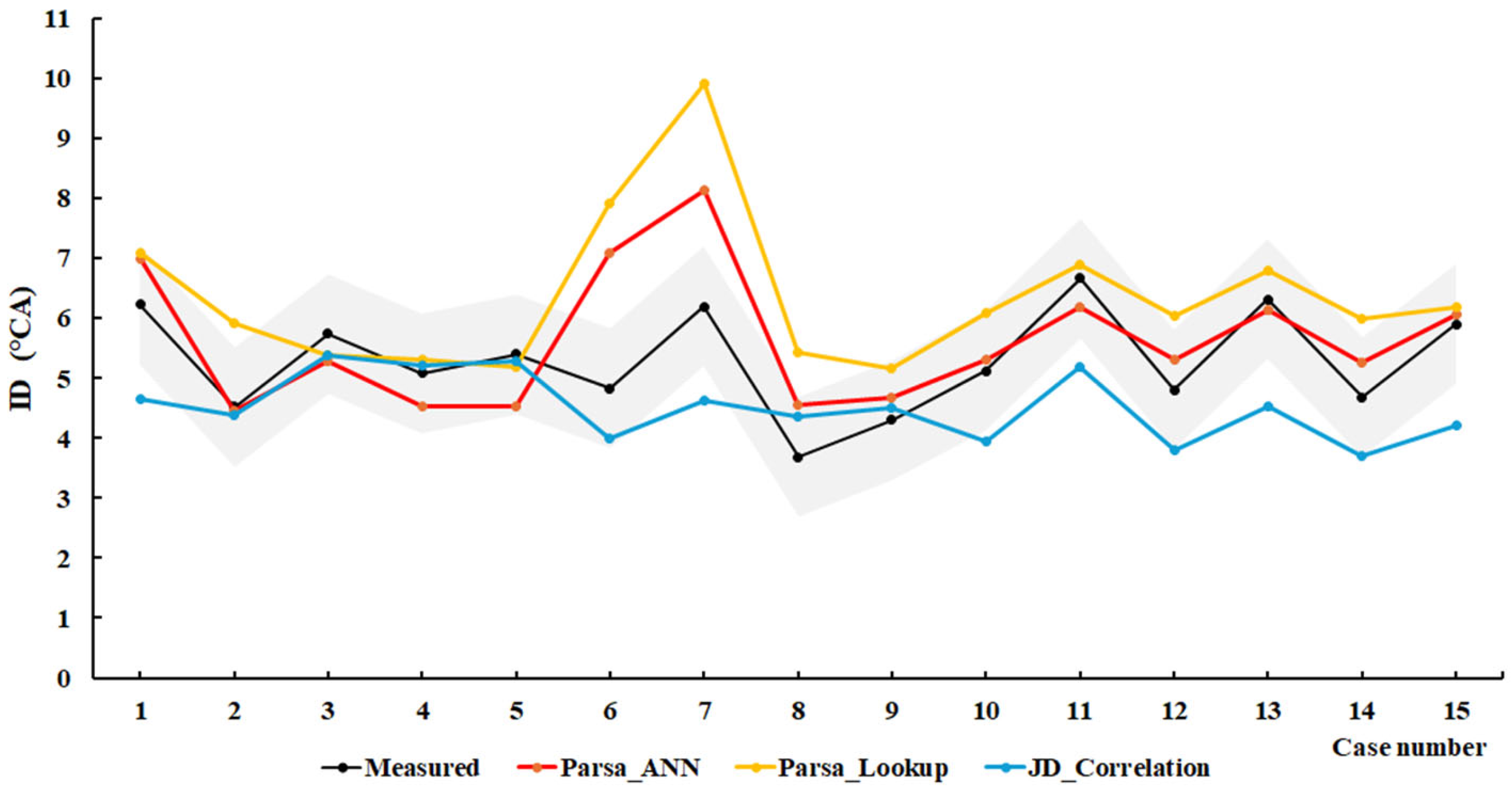
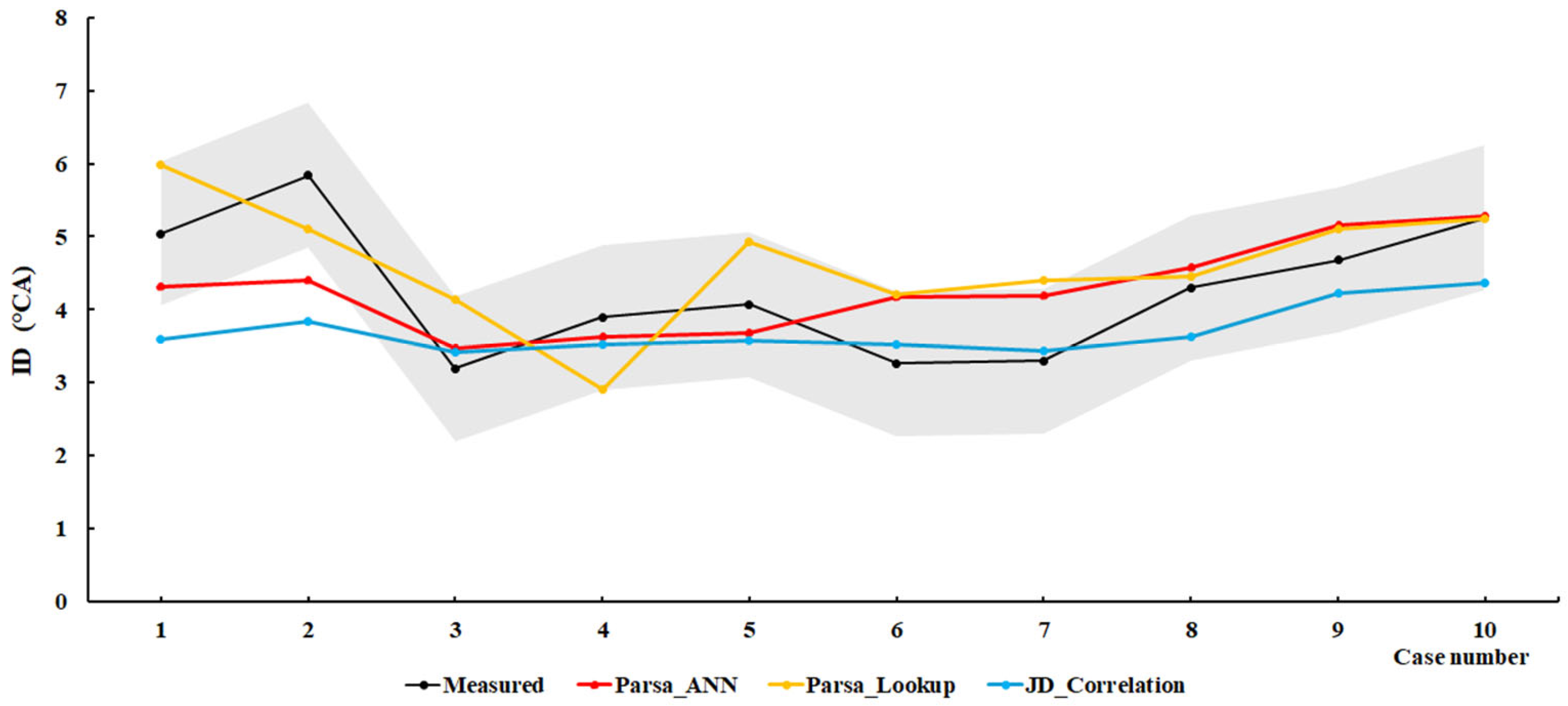
4.1. Methanol/Diesel
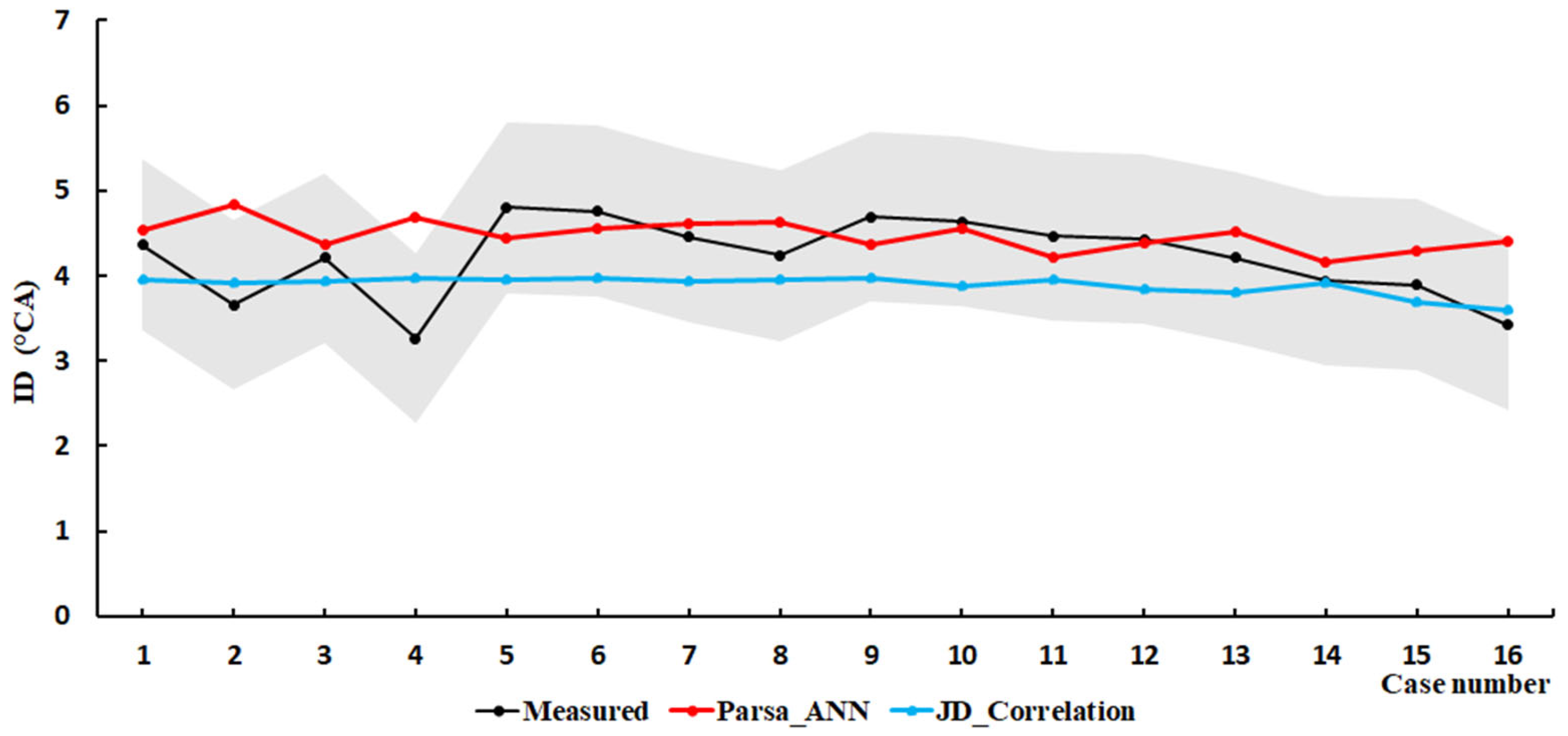
4.2. Hydrogen/Diesel
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faber, J.; Hanayama, S.; Zhang, S.; Pereda, P.; Comer, B.; Hauerhof, E.; van der Loeff, W.S.; Smith, T.; Zhang, Y.; Kosaka, H. Reduction of GHG emissions from ships—Fourth IMO GHG study 2020—Final report. IMO MEPC 2020, 75, 15. [Google Scholar]
- Dnv, G. Maritime Forecast to 2050, Energy Transition Outlook 2019; DNV GL: Høvik, Norway, 2019. [Google Scholar]
- Fetting, C. The European Green Deal; ESDN Report; ESDN Office: Vienna, Austria, 2020; p. 2. [Google Scholar]
- Hedberg, A. The European Green Deal: How to Turn Ambition into Action; EPC Discussion Paper 04 November 2021; EPC: Brussels, Belgium, 2021. [Google Scholar]
- Verhelst, S.; Turner, J.W.; Sileghem, L.; Vancoillie, J. Methanol as a fuel for internal combustion engines. Prog. Energy Combust. Sci. 2019, 70, 43–88. [Google Scholar] [CrossRef]
- Huang, Z. Fuel blend combustion for decarbonization. Proc. Combust. Inst. 2024, 40, 105776. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Tsolakis, A.; Alagumalai, A.; Mahian, O.; Lam, S.S.; Pan, J.; Peng, W.; Tabatabaei, M.; Aghbashlo, M. Use of hydrogen in dual-fuel diesel engines. Prog. Energy Combust. Sci. 2023, 98, 101100. [Google Scholar] [CrossRef]
- Verhelst, S. Recent progress in the use of hydrogen as a fuel for internal combustion engines. Int. J. Hydrogen Energy 2014, 39, 1071–1085. [Google Scholar] [CrossRef]
- Olah, G.A. After oil and gas: Methanol economy. Catal. Lett. 2004, 93, 1–2. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, Y.; Zhen, X.; Liu, Z. The effect of methanol production and application in internal combustion engines on emissions in the context of carbon neutrality: A review. Fuel 2022, 320, 123902. [Google Scholar] [CrossRef]
- Gautam, P.; Upadhyay, S.N.; Dubey, S. Bio-methanol as a renewable fuel from waste biomass: Current trends and future perspective. Fuel 2020, 273, 117783. [Google Scholar] [CrossRef]
- Lonis, F.; Tola, V.; Cau, G. Assessment of integrated energy systems for the production and use of renewable methanol by water electrolysis and CO2 hydrogenation. Fuel 2021, 285, 119160. [Google Scholar] [CrossRef]
- Geo, V.E.; Nagarajan, G.; Nagalingam, B. Experimental investigations to improve the performance of rubber seed oil–fueled diesel engine by dual fueling with hydrogen. Int. J. Green Energy 2009, 6, 343–358. [Google Scholar] [CrossRef]
- Parsa, S.; Jafarmadar, S.; Neshat, E. Application of waste heat in a novel trigeneration system integrated with an HCCI engine for power, heat and hydrogen production. Int. J. Hydrogen Energy 2022, 47, 26303–26315. [Google Scholar] [CrossRef]
- Basile, A.; Dalena, F. Methanol: Science and Engineering; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Agarwal, A.K.; Valera, H.; Pexa, M.; Čedík, J. Methanol: A Sustainable Transport Fuel for CI Engines; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, W.; Guo, L.; Zhang, H.; Jia, Z.; Qin, Z.; Zhu, G.; Yu, C.; Zhang, J. Numerical optimization of injector hole arrangement for marine methanol/diesel direct dual fuel stratification engines. Appl. Therm. Eng. 2024, 257, 124456. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Yin, Z.; Geng, H.; Zhu, R.; Zhen, X. Effect of injection strategy on a diesel/methanol dual-fuel direct-injection engine. Appl. Therm. Eng. 2021, 189, 116691. [Google Scholar] [CrossRef]
- Dierickx, J.; Verbiest, J.; Janvier, T.; Peeters, J.; Sileghem, L.; Verhelst, S. Retrofitting a high-speed marine engine to dual-fuel methanol-diesel operation: A comparison of multiple and single point methanol port injection. Fuel Commun. 2021, 7, 100010. [Google Scholar] [CrossRef]
- Yao, C.; Pan, W.; Yao, A. Methanol fumigation in compression-ignition engines: A critical review of recent academic and technological developments. Fuel 2017, 209, 713–732. [Google Scholar] [CrossRef]
- Saravanan, N.; Nagarajan, G. Performance and emission studies on port injection of hydrogen with varied flow rates with Diesel as an ignition source. Appl. Energy 2010, 87, 2218–2229. [Google Scholar] [CrossRef]
- Fayaz, H.; Saidur, R.; Razali, N.; Anuar, F.S.; Saleman, A.; Islam, M. An overview of hydrogen as a vehicle fuel. Renew. Sustain. Energy Rev. 2012, 16, 5511–5528. [Google Scholar] [CrossRef]
- Havemann, H.; Rao, M.; Natarajan, A.; Narasimhan, T. Alcohol in diesel engines. J. Indian Inst. Sci. 2008, 88, 820. [Google Scholar]
- Zhang, Z.; Tsang, K.; Cheung, C.S.; Chan, T.L.; Yao, C. Effect of fumigation methanol and ethanol on the gaseous and particulate emissions of a direct-injection diesel engine. Atmos. Environ. 2011, 45, 2001–2008. [Google Scholar] [CrossRef]
- Shi, M.; Wu, B.; Wang, J.; Jin, S.; Chen, T. Optimization of methanol/diesel dual-fuel engines at low load condition for heavy-duty vehicles to operated at high substitution ratio by using single-hole injector for direct injection of methanol. Appl. Therm. Eng. 2024, 246, 122854. [Google Scholar] [CrossRef]
- Imran, A.; Varman, M.; Masjuki, H.H.; Kalam, M.A. Review on alcohol fumigation on diesel engine: A viable alternative dual fuel technology for satisfactory engine performance and reduction of environment concerning emission. Renew. Sustain. Energy Rev. 2013, 26, 739–751. [Google Scholar] [CrossRef]
- Sun, Z.; Lian, Z.; Ma, J.; Wang, C.; Li, W.; Pan, J. Combustion and Emissions Optimization of Diesel–Methanol Dual-Fuel Engine: Emphasis on Valve Phasing and Injection Parameters. Processes 2025, 13, 1183. [Google Scholar] [CrossRef]
- Verhelst, S.; Wallner, T. Hydrogen-fueled internal combustion engines. Prog. Energy Combust. Sci. 2009, 35, 490–527. [Google Scholar] [CrossRef]
- Liew, C.; Li, H.; Nuszkowski, J.; Liu, S.; Gatts, T.; Atkinson, R.; Clark, N. An experimental investigation of the combustion process of a heavy-duty diesel engine enriched with H2. Int. J. Hydrogen Energy 2010, 35, 11357–11365. [Google Scholar] [CrossRef]
- Chintala, V.; Subramanian, K. A comprehensive review on utilization of hydrogen in a compression ignition engine under dual fuel mode. Renew. Sustain. Energy Rev. 2017, 70, 472–491. [Google Scholar] [CrossRef]
- Karagöz, Y.; Sandalcı, T.; Yüksek, L.; Dalkılıç, A.S.; Wongwises, S. Effect of hydrogen–diesel dual-fuel usage on performance, emissions and diesel combustion in diesel engines. Adv. Mech. Eng. 2016, 8, 1687814016664458. [Google Scholar] [CrossRef]
- Parsa, S.; Verhelst, S. Numerical Investigation of the Ignition Delay and Laminar Flame Speed for Pilot-Ignited Dual Fuel Engine Operation with Hydrogen or Methanol; 0148-7191; SAE Technical Paper; SAE: Warrendale, PA, USA, 2023. [Google Scholar]
- Coulier, J.; Verhelst, S. Using alcohol fuels in dual fuel operation of compression ignition engines: A review. In Proceedings of the 28th CIMAC World Congress on Combustion Engine, Helsinki, Finland, 6–10 June 2016; pp. 1–12. [Google Scholar]
- Yin, Z.; Yao, C.; Geng, P.; Hu, J. Visualization of combustion characteristic of diesel in premixed methanol–air mixture atmosphere of different ambient temperature in a constant volume chamber. Fuel 2016, 174, 242–250. [Google Scholar] [CrossRef]
- Dhole, A.; Yarasu, R.; Lata, D. Investigations on the combustion duration and ignition delay period of a dual fuel diesel engine with hydrogen and producer gas as secondary fuels. Appl. Therm. Eng. 2016, 107, 524–532. [Google Scholar] [CrossRef]
- Dierickx, J.; Mattheeuws, L.; Christianen, K.; Stenzel, K.; Verhelst, S. Evaluation and extension of ignition delay correlations for dual-fuel operation with hydrogen or methanol in a medium speed single cylinder engine. Fuel 2023, 345, 128254. [Google Scholar] [CrossRef]
- Zang, R.; Yao, C. Numerical study of combustion and emission characteristics of a diesel/methanol dual fuel (DMDF) engine. Energy Fuels 2015, 29, 3963–3971. [Google Scholar] [CrossRef]
- Xu, H.; Yao, C.; Xu, G. Chemical kinetic mechanism and a skeletal model for oxidation of n-heptane/methanol fuel blends. Fuel 2012, 93, 625–631. [Google Scholar] [CrossRef]
- Decan, G.; Lucchini, T.; D’Errico, G.; Verhelst, S. A novel technique for detailed and time-efficient combustion modeling of fumigated dual-fuel internal combustion engines. Appl. Therm. Eng. 2020, 174, 115224. [Google Scholar] [CrossRef]
- Andrae, J.C.; Head, R. HCCI experiments with gasoline surrogate fuels modeled by a semidetailed chemical kinetic model. Combust. Flame 2009, 156, 842–851. [Google Scholar] [CrossRef]
- Liu, S.; Sun, T.; Zhou, L.; Jia, M.; Zhao, W.; Wei, H. A new skeletal kinetic model for methanol/n-heptane dual fuels under engine-like conditions. Energy 2023, 263, 125648. [Google Scholar] [CrossRef]
- Lawal, A.I. An artificial neural network-based mathematical model for the prediction of blast-induced ground vibration in granite quarries in Ibadan, Oyo State, Nigeria. Sci. Afr. 2020, 8, e00413. [Google Scholar] [CrossRef]
- Shahpouri, S.; Norouzi, A.; Hayduk, C.; Fandakov, A.; Rezaei, R.; Koch, C.R.; Shahbakhti, M. Laminar flame speed modeling for low carbon fuels using methods of machine learning. Fuel 2023, 333, 126187. [Google Scholar] [CrossRef]
- Milojević, S.; Savić, S.; Mitrović, S.; Marić, D.; Krstić, B.; Stojanović, B.; Popović, V. Solving the problem of friction and wear in auxiliary devices of internal combustion engines on the example of reciprocating air compressor for vehicles. Teh. Vjesn. 2023, 30, 122–130. [Google Scholar]
- Wenig, M.; Roggendorf, K.; Fogla, N. Towards predictive dual-fuel combustion and prechamber modeling for large two-stroke engines in the scope of 0D/1D simulation. In Proceedings of the 29th CIMAC World Congress on Combustion Engine Technology, Vancouver, BC, Canada, 10–14 June 2019; pp. 10–14. [Google Scholar]
- Millo, F.; Accurso, F.; Piano, A.; Caputo, G.; Cafari, A.; Hyvönen, J. Experimental and numerical investigation of the ignition process in a large bore dual fuel engine. Fuel 2021, 290, 120073. [Google Scholar] [CrossRef]
- Livengood, J.; PC, W. Correlation of autoignition phenomena in internal combustion engines and rapid compression machines. Symp. (Int.) Combust. 1955, 5, 347–356. [Google Scholar] [CrossRef]




| Engine Model Name | FM24 |
|---|---|
| Cylinders | 1 |
| Compression ratio | 12.1:1 |
| Bore × stroke | 240 × 290 mm (SCE1) 256 × 290 mm (SCE2) |
| Displacement volume | 13.1 l (SCE1) and 14.9 l (SCE2) |
| Diesel injection system | Cam-driven Single Injection Pumps |
| Nominal power | 200 kW (SCE1), 224 kW (SCE2) |
| Nominal speed | 1000 rpm |
| Campaign | Samples | Parameter Variations |
|---|---|---|
| MEOH-SCE1 | 1 | |
| 2, 3 | ||
| 4, 5 | ||
| 6, 7 | ||
| 8, 9 | ||
| 10, 11 | ||
| 12, 13 | ||
| 14, 15 | ||
| MEOH-SCE2 | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6–8 | ||
| 9, 10 | ||
| H2-SCE1 | 1, 2 | |
| 3, 4 | ||
| 5–8 | ||
| 9, 10 | ||
| 11–13 | ||
| 14–16 |
| P (MPa) | T (K) | φ | Molar Percentage | Number of Datapoints | |
|---|---|---|---|---|---|
| Methanol/diesel | 7–13 | 625–1800 | 0.5–3.5 | 0–95 | 5240 |
| Hydrogen/diesel | 4–10 | 625–1100 | 0.5–3.0 | 0–95 | 3485 |
| Engine | Methodology | Root Mean Square Error (RMSE) | Mean Squared Relative Error (MSRE) |
|---|---|---|---|
| SCE1 | Parsa_ANN | 0.9127 | 0.0314 |
| Parsa_LookUP | 1.5192 | 0.0894 | |
| JD_Correlation | 1.0909 | 0.0366 | |
| SCE2 | Parsa_ANN | 0.6939 | 0.1640 |
| Parsa_LookUP | 0.7927 | 0.2115 | |
| JD_Correlation | 0.8996 | 0.1733 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parsa, S.; Verhelst, S. Determining Pilot Ignition Delay in Dual-Fuel Medium-Speed Marine Engines Using Methanol or Hydrogen. Energies 2025, 18, 3064. https://doi.org/10.3390/en18123064
Parsa S, Verhelst S. Determining Pilot Ignition Delay in Dual-Fuel Medium-Speed Marine Engines Using Methanol or Hydrogen. Energies. 2025; 18(12):3064. https://doi.org/10.3390/en18123064
Chicago/Turabian StyleParsa, Somayeh, and Sebastian Verhelst. 2025. "Determining Pilot Ignition Delay in Dual-Fuel Medium-Speed Marine Engines Using Methanol or Hydrogen" Energies 18, no. 12: 3064. https://doi.org/10.3390/en18123064
APA StyleParsa, S., & Verhelst, S. (2025). Determining Pilot Ignition Delay in Dual-Fuel Medium-Speed Marine Engines Using Methanol or Hydrogen. Energies, 18(12), 3064. https://doi.org/10.3390/en18123064






