Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer on CFD Simulation of Liquid Hydrogen Release
Abstract
1. Introduction
2. Experiment Description
3. Modeling Approaches
3.1. Mathematical Models
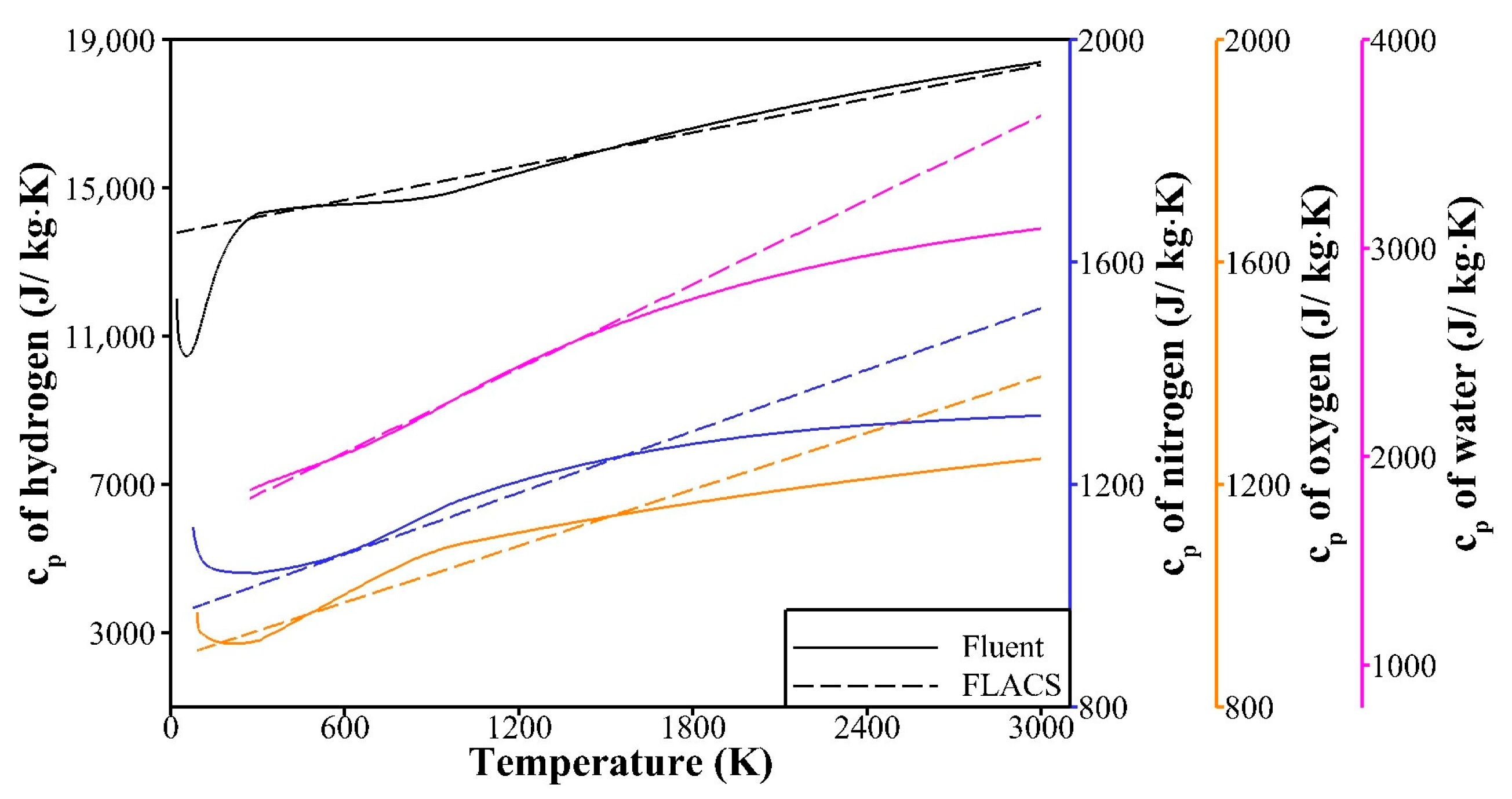
3.1.1. Models of Thermodynamic Properties of Species
3.1.2. Model of Liquid–Gas Mass Transfer in Fluent
3.1.3. Model of Liquid–Gas Mass Transfer in FLACS
3.2. Computational Domain and Boundary Conditions
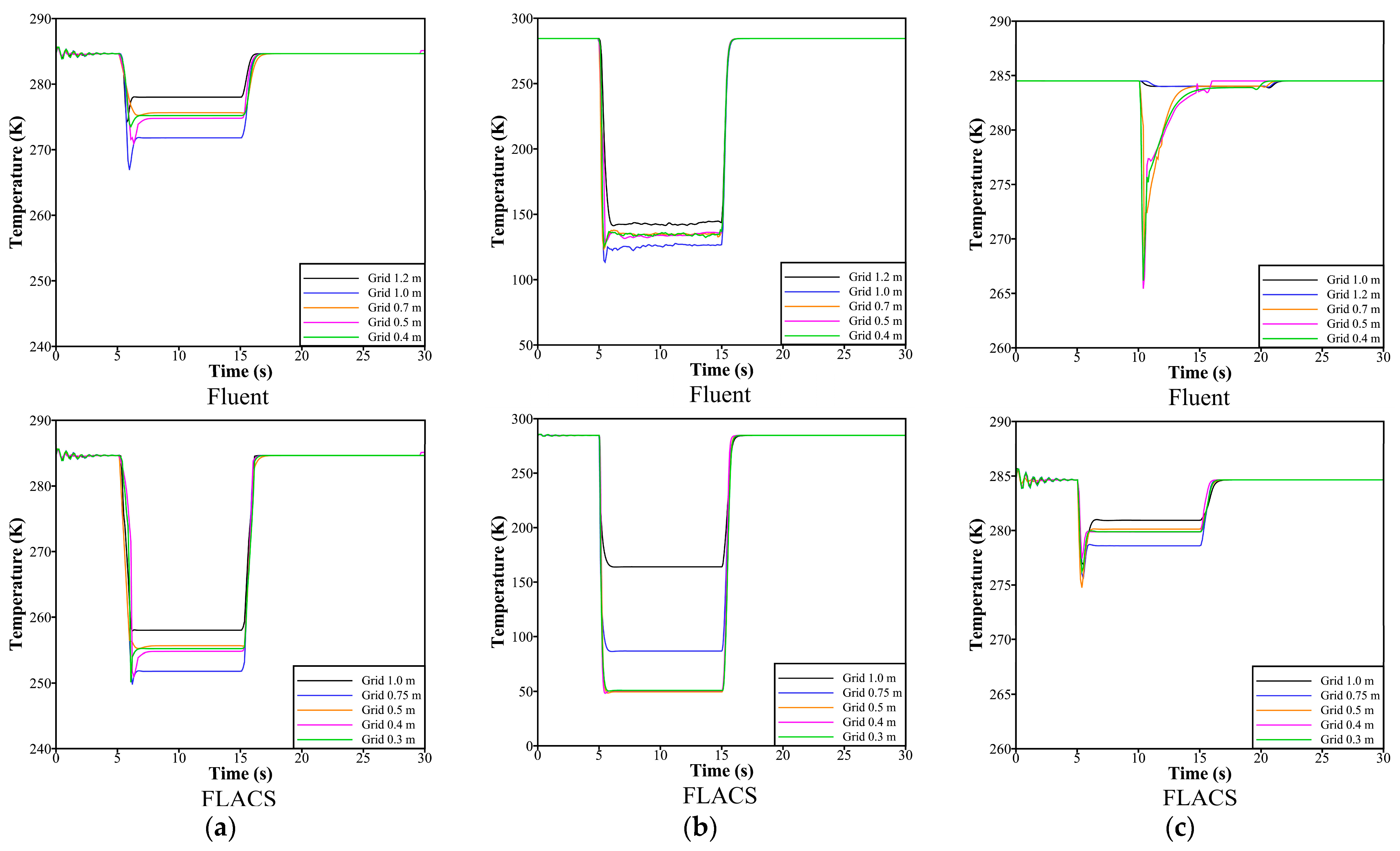
3.3. Mesh Information and Solution Method
4. Results and Discussion
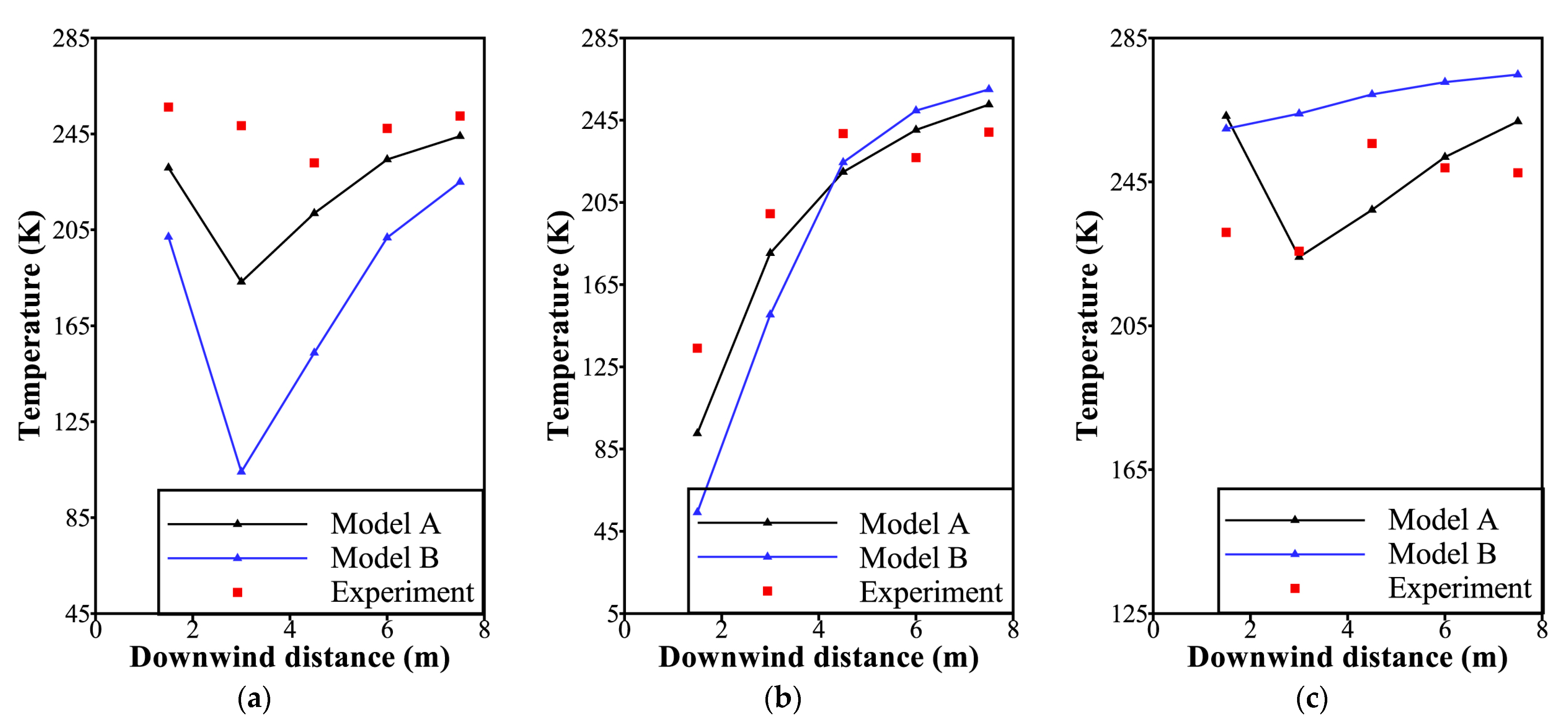
4.1. Model Validation
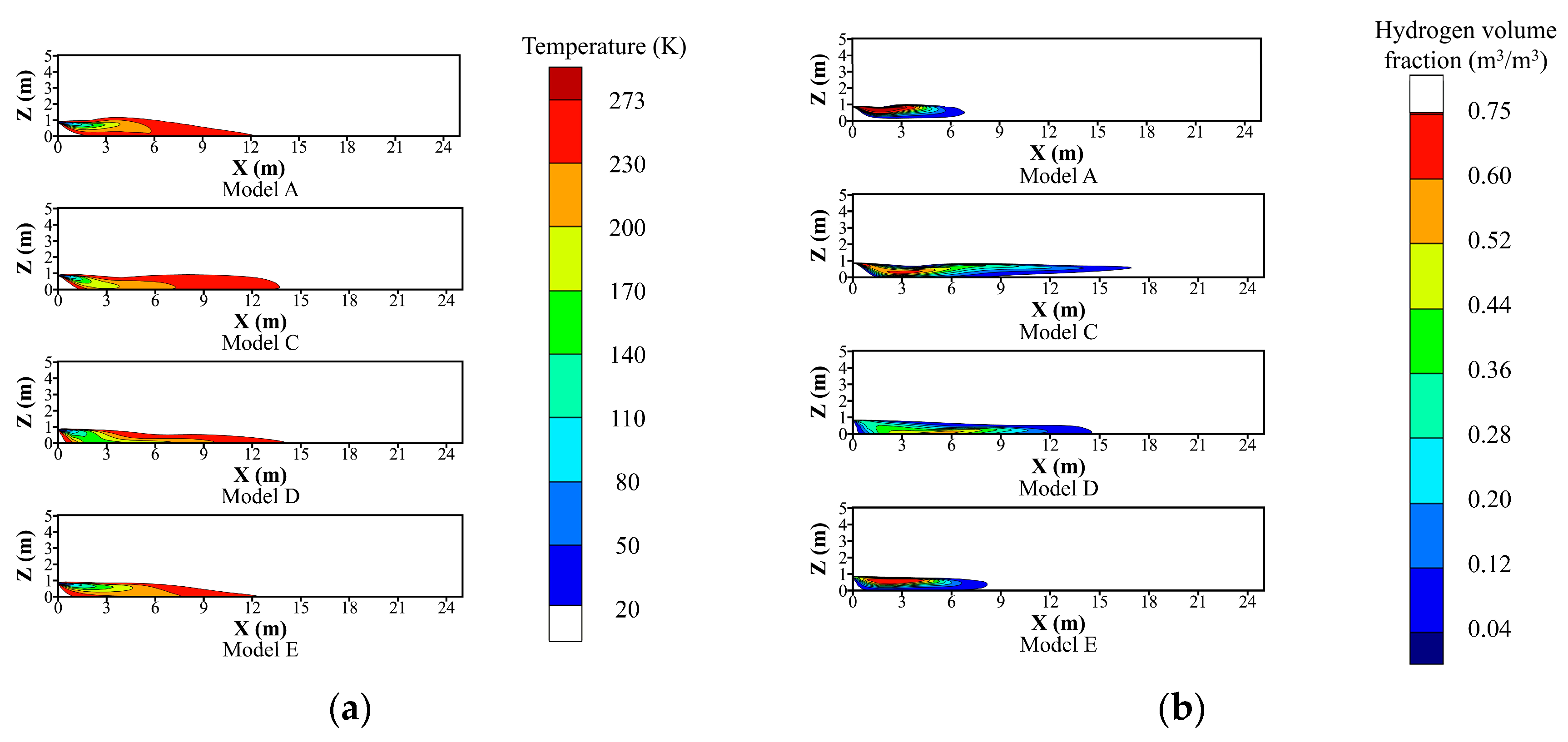
4.2. Comparison of Model Performance for Temperature and Hydrogen Volume Fraction
4.3. Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer
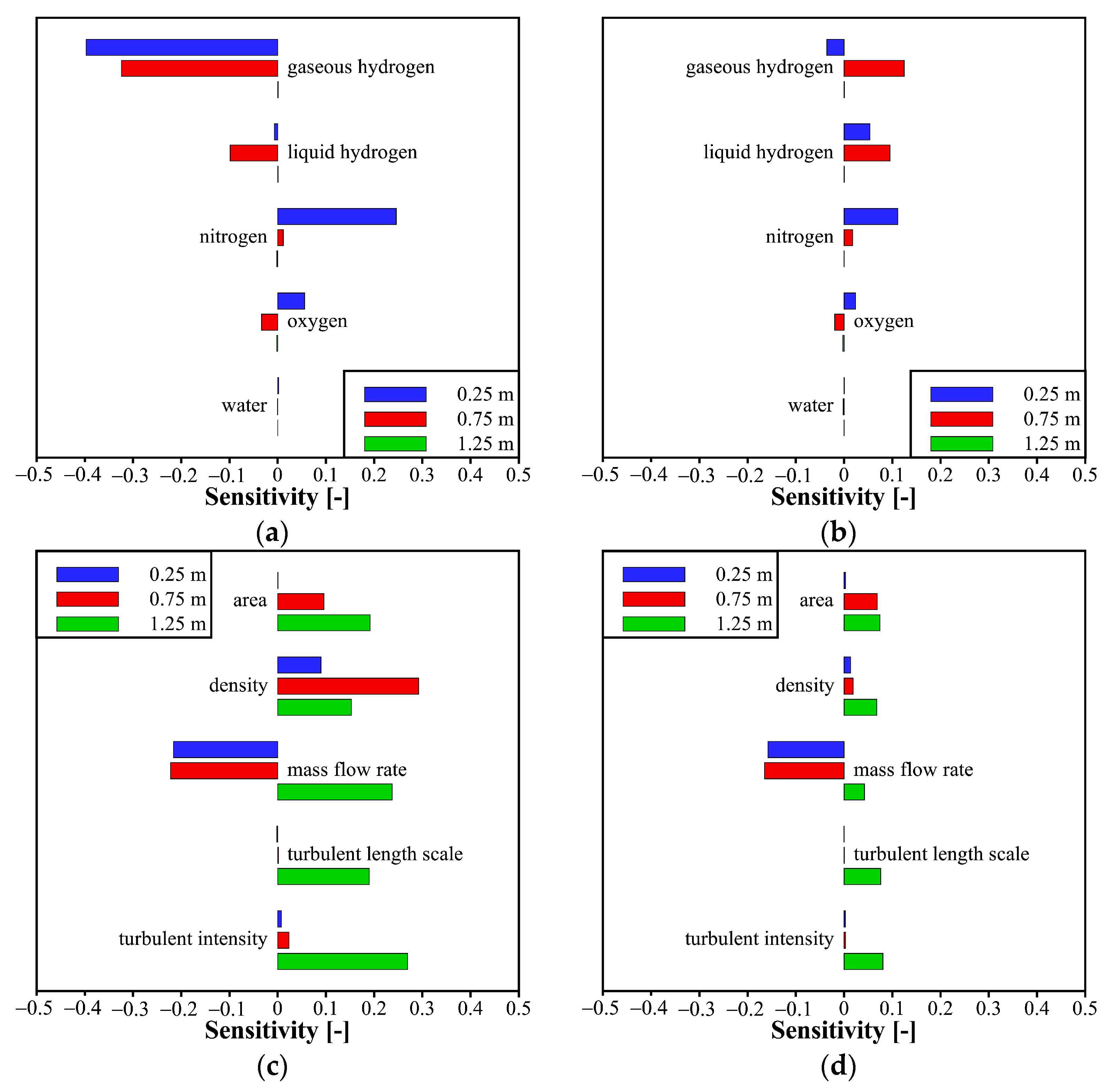
4.4. Sensitivity Analyses of Parameters in Models of Thermodynamic Properties and Liquid–Gas Mass Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Midilli, A.; Ay, M.; Dincer, I.; Rosen, M.A. On hydrogen and hydrogen energy strategies I: Current status and needs. Renew. Sustain. Energy Rev. 2005, 9, 255–271. [Google Scholar] [CrossRef]
- Aasadnia, M.; Mehrpooya, M. Large-scale liquid hydrogen production methods and approaches: A review. Appl. Energy 2018, 212, 57–83. [Google Scholar] [CrossRef]
- Sherif, S.A.; Zeytinoglu, N.; Veziroglu, T.N. Liquid hydrogen: Potential, problems, and a proposed research program. Int. J. Hydrogen Energy 1997, 22, 683–688. [Google Scholar] [CrossRef]
- Najjar, Y.S. Hydrogen safety: The road toward green technology. Int. J. Hydrogen Energy 2013, 38, 10716–10728. [Google Scholar] [CrossRef]
- Faye, O.; Szpunar, J.; Eduok, U. A critical review on the current technologies for the generation, storage, and transportation of hydrogen. Int. J. Hydrogen Energy 2022, 47, 13771–13802. [Google Scholar] [CrossRef]
- Kangwanpongpan, T.; Makarov, D.; Cirrone, D.; Molkov, V. LES model of flash-boiling and pressure recovery phenomena during release from large-scale pressurised liquid hydrogen storage tank. Int. J. Hydrogen Energy 2024, 50, 390–405. [Google Scholar] [CrossRef]
- Lowesmith, B.J.; Hankinson, G.; Chynoweth, S. Safety issues of the liquefaction, storage and transportation of liquid hydrogen: An analysis of incidents and HAZIDS. Int. J. Hydrogen Energy 2014, 39, 20516–20521. [Google Scholar] [CrossRef]
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies 2021, 14, 5917. [Google Scholar] [CrossRef]
- Alfarizi, M.G.; Ustolin, F.; Vatn, J.; Yin, S.; Paltrinieri, N. Towards accident prevention on liquid hydrogen: A data-driven approach for releases prediction. Reliab. Eng. Syst. Saf. 2023, 236, 109276. [Google Scholar] [CrossRef]
- Ikeuba, A.I.; Sonde, C.U.; Charlie, D.; Usibe, B.E.; Raimi, M.; Obike, A.I.; Magu, T.O. A review on exploring the potential of liquid hydrogen as a fuel for a sustainable future. Sust. Chem. One World 2024, 3, 100022. [Google Scholar] [CrossRef]
- Hall, J.E.; Hooker, P.; Willoughby, D. Ignited releases of liquid hydrogen: Safety considerations of thermal and overpressure effects. Int. J. Hydrogen Energy 2014, 39, 20547–20553. [Google Scholar] [CrossRef]
- Witcofski, R.D.; Chirivella, J.E. Experimental and analytical analyses of the mechanisms governing the dispersion of flammable clouds formed by liquid hydrogen spills. Int. J. Hydrogen Energy 1984, 9, 425–435. [Google Scholar] [CrossRef]
- Schmidtchen, U.; Marinescupasoi, L.; Verfondern, K.; Nickel, V.; Sturm, B.; Dienhart, B. Simulation of accidental spills of cryogenic hydrogen in a residential area. Cryogenics 1994, 34, 401–404. [Google Scholar] [CrossRef]
- Willoughby, D.B.; Royle, M. Experimental releases of liquid hydrogen. In Proceedings of 4th International Conference on Hydrogen Safety, San Francisco, CA, USA, 12–14 September 2011. [Google Scholar]
- ANSYS Inc. ANSYS Fluent 2022 R1, Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- GexCon. FLACS v21.3 User’s Manual; GexCon: Bergen, Norway, 2021. [Google Scholar]
- Venetsanos, A.G.; Baraldi, D.; Adams, P.; Heggem, P.S.; Wilkening, H. CFD modelling of hydrogen release, dispersion and combustion for automotive scenarios. J. Loss Prev. Process Ind. 2008, 21, 162–184. [Google Scholar] [CrossRef]
- Pashchenko, D. Comparative analysis of hydrogen/air combustion CFD-modeling for 3D and 2D computational domain of micro-cylindrical combustor. Int. J. Hydrogen Energy 2017, 42, 29545–29556. [Google Scholar] [CrossRef]
- Sun, H.J.; Yan, P.H.; Xu, Y.H. Numerical simulation on hydrogen combustion and flow characteristics of a jet-stabilized combustor. Int. J. Hydrogen Energy 2020, 45, 12604–12615. [Google Scholar] [CrossRef]
- Pu, L.; Shao, X.Y.; Zhang, S.Q.; Lei, G.; Li, Y.Z. Plume dispersion behaviour and hazard identification for large quantities of liquid hydrogen leakage. Asia-Pac. J. Chem. Eng. 2019, 14, e2299. [Google Scholar] [CrossRef]
- Jin, T.; Liu, Y.L.; Wei, J.J.; Wu, M.X.; Lei, G.; Chen, H.; Lan, Y.Q. Modeling and analysis of the flammable vapor cloud formed by liquid hydrogen spills. Int. J. Hydrogen Energy 2017, 42, 26762–26770. [Google Scholar] [CrossRef]
- Sklavounos, S.; Rigas, F. Fuel gas dispersion under cryogenic release conditions. Energy Fuels 2005, 19, 2535–2544. [Google Scholar] [CrossRef]
- Pu, L.; Tang, X.; Shao, X.Y.; Lei, G.; Li, Y.Z. Numerical investigation on the difference of dispersion behavior between cryogenic liquid hydrogen and methane. Int. J. Hydrogen Energy 2019, 44, 22368–22379. [Google Scholar] [CrossRef]
- Middha, P.; Ichard, M.; Arntzen, B.J. Validation of CFD modelling of LH2 spread and evaporation against large-scale spill experiments. Int. J. Hydrogen Energy 2011, 36, 2620–2627. [Google Scholar] [CrossRef]
- Shen, Y.H.; Wang, D.; Lv, H.; Zhang, C.M. Dispersion characteristics of large-scale liquid hydrogen spills in a real-world liquid hydrogen refueling station with various releasing and environmental conditions. Renew. Energy 2024, 236, 121327. [Google Scholar] [CrossRef]
- Hansen, O.R.; Hansen, E.S. CFD-modelling of large-scale LH2 release and explosion experiments. Process Saf. Environ. Prot. 2023, 174, 376–390. [Google Scholar] [CrossRef]
- Schmidt, D.; Krause, U.; Schmidtchen, U. Numerical simulation of hydrogen gas releases between buildings. Int. J. Hydrogen Energy 1999, 24, 479–488. [Google Scholar] [CrossRef]
- Ichard, M.; Hansen, O.R.; Middha, P.; Willoughby, D. CFD computations of liquid hydrogen releases. Int. J. Hydrogen Energy 2012, 37, 17380–17389. [Google Scholar] [CrossRef]
- Sun, R.F.; Pu, L.; Yu, H.S.; Dai, M.H.; Li, Y.Z. Modeling the diffusion of flammable hydrogen cloud under different liquid hydrogen leakage conditions in a hydrogen refueling station. Int. J. Hydrogen Energy 2022, 47, 25849–25863. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G. Study of key parameters in modeling liquid hydrogen release and dispersion in open environment. Int. J. Hydrogen Energy 2018, 43, 455–467. [Google Scholar] [CrossRef]
- Holborn, P.G.; Benson, C.M.; Ingram, J.M. Modelling hazardous distances for large-scale liquid hydrogen pool releases. Int. J. Hydrogen Energy 2020, 45, 23851–23871. [Google Scholar] [CrossRef]
- Liu, Y.L.; Wei, J.J.; Lei, G.; Chen, H.; Lan, Y.Q.; Gao, X.; Wang, T.X.; Jin, T. Spread of hydrogen vapor cloud during continuous liquid hydrogen spills. Cryogenics 2019, 103, 102975. [Google Scholar] [CrossRef]
- Jin, T.; Wu, M.X.; Liu, Y.L.; Lei, G.; Chen, H.; Lan, Y.Q. CFD modeling and analysis of the influence factors of liquid hydrogen spills in open environment. Int. J. Hydrogen Energy 2017, 42, 732–739. [Google Scholar] [CrossRef]
- Tang, X.; Pu, L.; Shao, X.Y.; Lei, G.; Li, Y.Z.; Wang, X.K. Dispersion behavior and safety study of liquid hydrogen leakage under different application situations. Int. J. Hydrogen Energy 2020, 45, 31278–31288. [Google Scholar] [CrossRef]
- Chen, W.; Gao, R.; Sun, J.F.; Lei, Y.F.; Fan, X.L. Modeling of an isolated liquid hydrogen droplet evaporation and combustion. Cryogenics 2018, 96, 151–158. [Google Scholar] [CrossRef]
- vom Lehn, F.; Cai, L.M.; Pitsch, H. Impact of thermochemistry on optimized kinetic model predictions: Auto-ignition of diethyl ether. Combust. Flame 2019, 210, 454–466. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G.; Markatos, N.; Bartzis, J.G. CFD modeling of hydrogen dispersion under cryogenic release conditions. Int. J. Hydrogen Energy 2014, 39, 15851–15863. [Google Scholar] [CrossRef]
- Hansen, O.R. Liquid hydrogen releases show dense gas behavior. Int. J. Hydrogen Energy 2020, 45, 1343–1358. [Google Scholar] [CrossRef]
- Venetsanos, A.G.; Papanikolaou, E.; Bartzis, J.G. The ADREA-HF CFD code for consequence assessment of hydrogen applications. Int. J. Hydrogen Energy 2010, 35, 3908–3918. [Google Scholar] [CrossRef]
- Visser, D.C.; Houkema, M.; Siccama, N.B.; Komen, E.M.J. Validation of a FLUENT CFD model for hydrogen distribution in a containment. Nucl. Eng. Des. 2012, 245, 161–171. [Google Scholar] [CrossRef]
- Yuan, W.H.; Li, J.F.; Zhang, R.P.; Li, X.K.; Xie, J.L.; Chen, J.Y. Numerical investigation of the leakage and explosion scenarios in China’s first liquid hydrogen refueling station. Int. J. Hydrogen Energy 2022, 47, 18786–18798. [Google Scholar] [CrossRef]
- Houf, W.G.; Winters, W.S. Simulation of high-pressure liquid hydrogen releases. Int. J. Hydrogen Energy 2013, 38, 8092–8099. [Google Scholar] [CrossRef]
- Eric, W.L.; Ian, H.B.; Marcia, L.H.; Mark, O.M. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2025. [Google Scholar]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Zhai, Z.J.; Chen, Q.Y. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part 2—Comparison with experimental data from literature. HVAC&R Res. 2007, 13, 871–886. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| Release conditions | Diameter (m) | 0.0266 |
| Height (m) | 0.86 | |
| Mass rate (kg/s) | 0.071 | |
| Direction | Horizontal | |
| Weather conditions | Wind speed at 2.5 m (m/s) | 2.9 |
| Ambient temperature (K) | 284.5 | |
| Relative humidity (%) | 64 | |
| 0.7 | 1 | 1.3 | 1.44 | 1.92 | 0.8 |
| CFD Models | Tools | Sub-Models | |
|---|---|---|---|
| Thermodynamic Properties | Liquid–Gas Mass Transfer | ||
| Model A | Fluent | Polynomial | Mixture model |
| Model B | FLACS | Linear | Pseudo source model |
| Model | Height | FB | MG | VG |
|---|---|---|---|---|
| Model A | H = 0.25 m | −0.127 | 0.879 | 1.024 |
| H = 0.75 m | −0.059 | 0.924 | 1.012 | |
| H = 1.25 m | 0.024 | 1.024 | 1.005 | |
| Sum | −0.052 | 0.940 | 1.014 | |
| Model B | H = 0.25 m | −0.330 | 0.692 | 1.231 |
| H = 0.75 m | −0.101 | 0.807 | 1.202 | |
| H = 1.25 m | 0.103 | 1.110 | 1.012 | |
| Sum | −0.096 | 0.853 | 1.144 |
| CFD Models | Tools | Sub-Models | |
|---|---|---|---|
| Thermodynamic Properties | Liquid–Gas Mass Transfer | ||
| Model C | Fluent | Linear | Mixture model |
| Model D | Fluent | Polynomial | Pseudo source model |
| Model E | Fluent | Linear | Pseudo source model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Yang, J.; Yuan, J.; Feng, L.; Li, W.; Zhang, C.; Cai, L.; Cao, J. Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer on CFD Simulation of Liquid Hydrogen Release. Energies 2025, 18, 3052. https://doi.org/10.3390/en18123052
Lu C, Yang J, Yuan J, Feng L, Li W, Zhang C, Cai L, Cao J. Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer on CFD Simulation of Liquid Hydrogen Release. Energies. 2025; 18(12):3052. https://doi.org/10.3390/en18123052
Chicago/Turabian StyleLu, Chenyu, Jianfei Yang, Jian Yuan, Luoyi Feng, Wenbo Li, Cunman Zhang, Liming Cai, and Jing Cao. 2025. "Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer on CFD Simulation of Liquid Hydrogen Release" Energies 18, no. 12: 3052. https://doi.org/10.3390/en18123052
APA StyleLu, C., Yang, J., Yuan, J., Feng, L., Li, W., Zhang, C., Cai, L., & Cao, J. (2025). Impact of Models of Thermodynamic Properties and Liquid–Gas Mass Transfer on CFD Simulation of Liquid Hydrogen Release. Energies, 18(12), 3052. https://doi.org/10.3390/en18123052





