Abstract
To address energy management challenges for intelligent connected automated range-extended electric vehicles under vehicle-road cooperative environments, a hierarchical energy management strategy (EMS) based on speed prediction is proposed from the perspective of multi-objective optimization (MOO), with comprehensive system performance being significantly enhanced. Focusing on connected car-following scenarios, acceleration sequence prediction is performed based on Kalman filtering and preceding vehicle acceleration. A dual-layer optimization strategy is subsequently developed: in the upper layer, optimal speed curves are planned based on road network topology and preceding vehicle trajectories, while in the lower layer, coordinated multi-power source allocation is achieved through EMSMPC-P, a Bayesian-optimized model predictive EMS based on Pontryagin’ s minimum principle (PMP). A MOO model is ultimately formulated to enhance comprehensive system performance. Simulation and bench test results demonstrate that with SoC0 = 0.4, 7.69% and 5.13% improvement in fuel economy is achieved by EMSMPC-P compared to the charge depleting-charge sustaining (CD-CS) method and the charge depleting-blend (CD-Blend) method. Travel time reductions of 62.2% and 58.7% are observed versus CD-CS and CD-Blend. Battery lifespan degradation is mitigated by 16.18% and 5.89% relative to CD-CS and CD-Blend, demonstrating the method’s marked advantages in improving traffic efficiency, safety, battery life maintenance, and fuel economy. This study not only establishes a technical paradigm with theoretical depth and engineering applicability for EMS, but also quantitatively reveals intrinsic mechanisms underlying long-term prediction accuracy enhancement through data analysis, providing critical guidance for future vehicle–road–cloud collaborative system development.
1. Introduction
Connected automated range-extended electric vehicle (CAR-EEV) energy management strategies (EMSs) are enhanced through the dynamic coordination of power source operational modes [1]. Although global optimization and real-time control advancements exist, their efficacy remains limited by operational uncertainty. Vehicle-to-everything (V2X) enables EMS optimization [2] but current strategies depend on full SPaT (signal phase and timing) data for green-wave passage, ignoring non-connected vehicle impacts. A real-time EMS is proposed for mixed traffic flows with limited information, balancing energy emissions, battery degradation, and traffic efficiency.
1.1. Literature Review
CAR-EEVs achieve energy savings through the coordinated operation of traction batteries and an auxiliary power unit (APU) [3], overcoming fixed state of charge (SoC) thresholds via external charging and enabling dynamic SoC regulation for flexible energy dispatch and range extension. The multi-power-source nonlinear coupling characteristics of CAR-EEVs render the fuel economy sensitive to engine efficiency, motor characteristics, drivetrain configurations, and dynamic conditions, positioning EMSs as core technologies for balancing performance and economy [4]. An EMS must consider the inputs for varying driving behaviors, road traffic, load, and environmental conditions to assure flexibility of EVs among different users across the globe [1]. Rule-based control strategies allocate power through preset thresholds (simple implementation and high reliability) but exhibit poor adaptability to operating conditions and lack global optimality. A rule-based fuel cell electric vehicle (FCEV) operating mode control strategy is presented and is validated through multiple tests with different driving cycles and battery SoC strategy points [5]. A real-time rule-based strategy is proposed to determine the torque distributions of the parallel electric-hydraulic hybrid powertrain, optimizing the electric motor operating points [6]. Global optimization strategies, such as dynamic programming (DP) and convex optimization, require complete driving cycle data to derive theoretical optimal solutions but are constrained by computational complexity and real-time feasibility [7]. DP is employed to solve the constrained optimal problem for travel time, distance, and speed limit by exploring all possible control options [8]. Instantaneous optimization strategies primarily include the equivalent consumption minimization strategy (ECMS) and Pontryagin’ s minimum principle (PMP). The disadvantage is that it is not possible to find a globally optimal solution. ECMS balances fuel and motor energy consumption through equivalence factors [9]. ECMS is combined to refine the algorithm to optimize fuel consumption and fuel cell lifespan, achieving high computation efficiency, lower power fluctuation of the fuel cell and optimal fuel economy of fuel cell hybrid electric vehicles (FCHEVs) [10]. A rolling convergent ECMS for energy management of plug-in hybrid electric vehicles (PHEVs) was proposed, gaining fuel economy better than that using a traditional adaptive ECMS under two real-world driving cycles, respectively [11]. An adaptive EMS is achieved by the selection of an optimal PMP co-state variable, utilizing the clustering driving patterns [12]. An adaptive co-state design approach was introduced aimed at improving the adaptability of PMP-based EMSs for real-time implementation in PHEVs, and its energy-saving effectiveness approaches that of DP solutions [13]. Model predictive control (MPC)-based EMSs balance real-time capability and quasi-global optimality through rolling optimization and short-term operational condition prediction [14]. A novel data-driven MPC-based EMS is proposed with a dual-model framework (DDMPC) for fuel cell electric vehicles (FCEVs) to substantially enhance economic performance while maintaining control robustness [15]. A switched model predictive control with a parametric weights-based mode transition strategy was proposed to significantly elevate the quality of mode transition for a specific parallel hybrid electric vehicle (HEV) configuration [16].
Global positioning system (GPS) technologies have driven hybrid vehicle energy management innovations [17]. Connected energy management frameworks can be categorized into single-vehicle and dual-vehicle scenarios. For single-vehicle scenarios, EMSs based on speed route prediction preplan SoC trajectories by integrating driving distance, gradient, and speed limit information but exhibit limited adaptability to dynamic traffic. A combined prediction model is proposed to improve the prediction accuracy [18]. A data-driven hierarchical control strategy is developed to optimize SoC trajectories in real-time, demonstrating significant energy savings compared to non-connected systems [19]. Eco-driving-based EMSs generate eco-speed profiles through global optimization and integrate them into EMS controllers, with core challenges lying in real-time solutions for complex traffic scenarios. Hierarchical control architectures decompose driving tasks into acceleration, constant-speed, deceleration, and braking modules, with the upper layer optimizing switching timing and the lower layer executing energy-optimal control [20]. Traffic flow prediction-based energy management systems dynamically optimize power allocation robustness by integrating ITS-predicted disturbances but remain sensitive to prediction accuracy. A Monte Carlo method is used to handle traffic light timing uncertainty combined with ECMS to improve fuel economy [21]; SoC trajectories are trained via PMP and neural networks to achieve fuel savings [19]. EMSs for two vehicles, in terms of adaptive cruise control (ACC)-based energy management strategies, include a target-decoupled hierarchical control architecture that is proposed for multi-objective synergy [22]. A novel co-optimization method is developed based on PMP, which reduces fuel consumption in two different scenarios incorporating the SPaT strategy [23]. A novel efficiency model of an HEV powertrain is proposed and is used to define the economic index for evaluation [24]. For predictive cruise control (PCC) strategies, an AI-MPC framework is proposed to synchronously plan speed-SoC trajectories while optimizing power allocation and inter-vehicle distance control [25]. Stochastic preceding vehicle speed prediction models are established using radar and SPaT data to enhance following efficiency [26]. A method is developed for fitting energy consumption and universal characteristics specific to commercial vehicles based on multi-operating condition data. The resulting dataset can then be leveraged to design and implement the PCC control system [27]. Both strategies must address dynamic traffic randomness.
To address existing limitations in EMS research concerning stochastic adaptation to dynamic traffic information and global optimality inadequacies, the real-time EMS resolution problem in connected car-following scenarios is investigated. With dynamic traffic information considered, a dynamic traffic scenario model is constructed, and acceleration sequence prediction is implemented based on Kalman filtering and preceding vehicle acceleration. A dual-layer optimization strategy is proposed: optimal speed curves are planned based on road network topology and preceding vehicle trajectories in the upper layer, while coordinated multi-power source allocation is achieved through a Bayesian-optimized PMP-based model predictive EMS (EMSMPC-P) in the lower layer. A multi-objective optimization model (MOO) is additionally formulated to achieve comprehensive system performance enhancement.
1.2. Motivation and Innovation
A multi-objective optimized control scheme integrating real-time traffic perception and hierarchical optimization is proposed to address energy management challenges in connected car-following scenarios for CAR-EEVs under vehicle-road cooperation. A dynamic traffic model with Kalman filtering-based acceleration prediction algorithms is established, involving a hierarchical framework where road topology-guided speed planning is executed in the upper layer and a Bayesian-optimized model predictive EMS based on the PMP (EMSMPC-P) is proposed to enable multi-power coordination in the lower layer. Finally, a MOO model for system performance enhancement is formulated to achieve the optimization of vehicle operating parameters. Innovations include the following: (1) Establishment of vehicle-road cooperative dynamic scenario models featuring Kalman filtering-based acceleration sequence prediction algorithms that improve traffic efficiency through analysis of preceding vehicle states and traffic light information; (2) An intelligent hierarchical architecture integrating topology-based speed planning with EMSMPC-P for power allocation; (3) A MOO model for comprehensive performance improvement. Through the deep integration of V2X perception and intelligent optimization technologies, enhancements of EMS in traffic efficiency, safety, and fuel economy are realized based on overcoming the limitations of conventional approaches, which provides a technical solution with both theoretical breakthroughs and engineering value for CAR-EEV.
2. Velocity Prediction Model Based on Acceleration Sequence
2.1. Acceleration Sequence Prediction Algorithm Based on Kalman Filtering
Under dynamic traffic conditions, CAR-EEV vehicles cannot rely solely on SPaT for speed planning to achieve green-wave passage. The timing of preceding vehicles passing through traffic signals is considered in the connected vehicle-following scenario. The traffic information framework of a CAR-EEV is shown in Figure 1a, while the velocity and acceleration selected as the testing set are shown in Figure 1b.
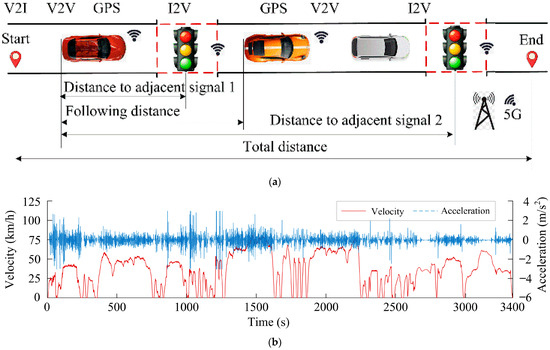
Figure 1.
Traffic information and testing set: (a) Traffic information framework diagram; (b) Velocity and acceleration testing set.
A Kalman filtering-based speed prediction algorithm utilizing preceding vehicle acceleration is developed for connected scenarios [28], where vehicle motion is assumed to remain almost unaffected by traffic variations. The optimal driving profile is selected from the maximum speed limit, acceleration profile, deceleration profile, and constant-speed profile, which are based on the acceleration magnitude, sign, and velocity values to plan instantaneous speed variations at time t. The instantaneous state xt at time t is defined as:
where vt is defined as the car-following speed at time t, and at is defined as the car-following acceleration at time t.
The state equation of the system is expressed as:
where at−1 denotes the preceding vehicle acceleration at time t − 1, with the state transition matrix , the control matrix . The process noise wt−1 follows a zero-mean Gaussian distribution, which can be represented as wt−1 ~ N (0, C).
The observation equation is defined as:
where zt represents the observed speed obtained from the wheel speed sensors at time t. W and vt are the observation matrix and measurement noise, which can be represented as W = [1 0] and vt ~ N (0, A), respectively.
The iterative updates for time and measurement states are subsequently performed as follows:
where xt−1*’ and xt*’ denote the posterior state estimates at time steps t − 1 and t, respectively, with xt* representing the prior state estimate at time t. While Pt−1’ and Pt’ are the posterior estimation covariance at time steps t − 1 and t, with Pt representing the prior estimation covariance at time t. C denotes the process noise covariance, kt is the Kalman gain matrix, and A is the measurement noise covariance.
Although the algorithm exhibits performance limitations under emergency conditions, during regular driving when system noise approximates a Gaussian distribution and vehicle dynamic models can be considered quasi-linear, it achieves high-precision prediction of preceding vehicle acceleration and velocity through iterative updates of state and observation equations. With low computational complexity, rapid prediction completion enables real-time response to vehicle state changes, delivering precise information for intelligent driving assistance systems. During continuous driving, the algorithm performance remains stable without degradation over time or mileage. Furthermore, the algorithm’s underlying assumptions generally hold approximately in real-world road environments, enabling adaptation to urban roads, highways, and various traffic flow scenarios.
Through the aforementioned Kalman filtering process, the state estimate xt at each time step can be obtained. This methodology enables long temporal interval prediction of vehicle arrival times at traffic signals based on current acceleration profiles. The pseudo-code of the speed prediction algorithm based on the acceleration of the front vehicle is shown in Algorithm 1.
| Algorithm 1: Vehicle speed prediction based on Kalman filtering |
| Input: Sensor measurement sequence {z1, z2, …, zN}, control input sequence {a1, a2, …, aN}, sampling interval dt Output: Followed vehicle speed estimation sequence 1: // Initialization parameters 2: Initialize x_t_minus_1 = [0; 0] // Initial state [Vehicle speed; Acceleration] 3: Initialize P_t_minus_1 = eye(2) // Initial covariance matrix 4: Define F = [1, dt; 0, 1], B = [0.5*dt^2; dt], H = [1, 0] // State transfer matrix, control matrix, observation matrix 5: Define Q = q_var * eye(2), R = r_var // Noise covariance 6: for t = 1 to N do // Time-based iteration 7: // Forecasting phase 8: u_t = a_t // The acceleration of the preceding vehicle at the current moment is used as a control input 9: x_t_hat_minus = F * x_t_minus_1 + B * u_t // Priori state estimation 10: P_t_minus = F * P_t_minus_1 * F′ + Q // Priori Estimated covariance 11: // Update phase 12: z_t = Get Wheel Speed Measurement(t) // Get the wheel speed sensor measurement value at the current moment 13: K_t = P_t_minus * H′ * inv(H * P_t_minus * H′ + R) // Filter gain matrix 14: x_t_hat = x_t_hat_minus + K_t * (z_t - H * x_t_hat_minus) // Posteriori estimated state update 15: P_t = (eye(2) - K_t * H) * P_t_minus // Posteriori estimated covariance update 16: x_t_minus_1 = x_t_hat, P_t_minus_1 = P_t // Save the result of the current moment for the next iteration 17: // Output current speed estimate 18: Output Or Record (x_t_hat(1)) // Following speed 19: end for 20: Function Output Or Record (value) // Output or record the estimated speed of the following vehicle (for plotting or subsequent processing) 21: end Function |
Based on this state estimation, the arrival time of vehicles can be predicted through combination with the location of traffic signals. This algorithm can comprehensively utilize the dynamic changes in acceleration and the uncertainty of observation data to achieve accurate prediction over a long time interval. By integrating dynamic acceleration information with observation data, effective reduction in noise interference and real-time prediction adjustment according to different acceleration changes can be achieved, which shows high adaptability to complex traffic scenarios and thus has strong fault tolerance for observation errors and model uncertainties. In summary, the velocity prediction results generated by the Kalman filtering are input to the EMSMPC-P through a rolling optimization mechanism. The predicted velocity profile vego(tk ~ tk + l) within the prediction horizon serves as an input for lower-layer energy management, combined with the cost function in Equation (30) to guide multi-objective weight allocation. Bayesian optimization dynamically adjusts the reference SoC curve, maps it to power allocation strategies, and employs MPC to update control variables for achieving optimal coordination.
2.2. Speed Predictions Results Based on the Acceleration Sequence
The speed prediction algorithm based on the acceleration sequence is simulated to compare the predicted speeds when the prediction domain is 8 s and 4 s. The fitting effect with the actual speed and simulation results are shown in Figure 2.
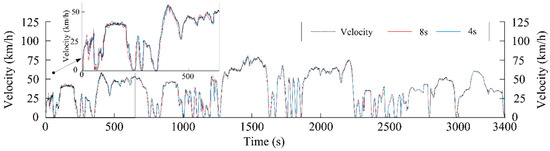
Figure 2.
Acceleration sequence-based speed prediction of two prediction domains.
It can be observed that during the initial simulation phase, velocity predictions in the 8 s prediction domain exhibited larger errors compared to that with a 4 s domain, where prediction deviations were reduced with alterations in the temporal window, demonstrating favorable tracking accuracy. Superior tracking performance of the 4 s domain velocity prediction curve was demonstrated compared to the 8 s domain implementation. Based on this prediction domain configuration, temporal predictions of the preceding vehicle’s arrival timing at traffic signals are generated, establishing informational foundations for subsequent eco-vehicle speed optimization.
Preceding vehicles are not equipped with vehicle-to-infrastructure (V2I) technology, so their operational information is transmitted to eco-vehicles (equipped with V2I technology) through vehicle-to-vehicle (V2V) communication, enabling prediction and computation within eco-vehicles. Using an acceleration sequence-based velocity prediction algorithm and signal/speed data, the arrival times of a preceding vehicle at two adjacent traffic signals are predicted in different time domains and time points.
The distance between the preceding vehicle and the signal is used to calculate the time t1-pre when it reaches the first approaching signal and to determine its corresponding signal phase (green or red). For the current instantaneous state, xt is in the acceleration case:
where tk is the current moment, t1-pre is the time at which the preceding vehicle arrives at Signal 1, t2-pre is the time at which the preceding vehicle arrives at signal 2, vpre is the predicted speed of the preceding vehicle, d1-pre is the distance from the preceding vehicle to Signal 1, and d2-pre is the distance from the preceding vehicle to Signal 2, which can be solved by the distance from the eco-vehicle to the signal and its following distance.
When the preceding vehicle decelerates to stop due to a red light, its final crossing time at the signal must account for the red-light waiting duration. Moreover, preceding vehicles do not accelerate immediately upon green light activation but exhibit a delayed response, potentially due to queued vehicles at the intersection. Thus, a Gaussian distribution model is established between the distance from the vehicle’s deceleration stop position (under a red light) to the traffic signal and the specific startup timing after green light activation. Consequently, the preceding vehicle’s arrival time at Signal 1 and 2 under deceleration conditions is calculated as:
where t1-inter is the red-light waiting duration at Signal 1, t2-inter is the red-light waiting duration at Signal 2, t1 is the moment when the preceding car slows down and stops at Signal 1, t2 is the moment when the preceding car slows down and stops at Signal 2, G is the Gaussian function equation, t1-pre’ is the final crossing time at signal 1, and t2-pre’ is the final crossing time at Signal 2.
SoC planning in the no-gradient scenario often uses an equidistant distribution method, where the total distance traveled is obtained by GPS. The SoC consumption is linearly correlated with the mileage and uniformly distributed over the whole road segment. The distance traveled in its prediction domain [tk, tf] at time tk is:
Then, its corresponding predicted optimal SoC value can be set by the scaling equation as follows:
Stotal is the total distance, Sk is the distance already traveled, SoCfinal is the final SoC after the total distance traveled, and SoCk is the SoC at the current tk time.
A Bayesian optimization-based dynamic SoC allocation strategy is proposed to reconstruct the SoC reference curve in the prediction domain. Bayesian optimization consists of a probabilistic agent model and an acquisition function. The acquisition function used in this paper is:
where x is the parameter to be updated, D1:t = {(m1, n1), (m2, n2), …, (mt, nt)} denotes the set of observations of the control variable mt and the corresponding state variable nt, μ(m*) denotes the optimal value in the current state set, Φ() denotes the standard normal distribution function, ξ is the balance parameter between global and local search, and σ(m) denotes the posterior standard deviation. The formula for the next evaluation point is:
The equation for the reference SoC under Bayesian optimization is updated as:
3. Hierarchical EMS Based on Speed Prediction
3.1. EMS for Eco-Vehicles in a Connected Scenario
The coexistence of connected and non-connected vehicles in mixed traffic flows is identified as a defining characteristic of early-stage intelligent connected driving environments. In connected car-following scenarios, preceding vehicle dynamics are perturbed by non-connected agent interactions and traffic signal variations, inducing operational complexities, including congestion-induced stationary states, emergency braking-triggered abrupt deceleration, and signal phase misinterpretation-driven red light violations. Such stochastic disturbances substantially escalate uncertainties in eco-vehicle velocity optimization. To address CAR-EEV control demands under dynamic traffic conditions, coordinated speed-energy management strategies are prioritized, integrating the MOO of traffic flow efficiency, safety distance compliance, and fuel economy enhancement. The implemented dual-layer energy management framework is architecturally shown in Figure 3.
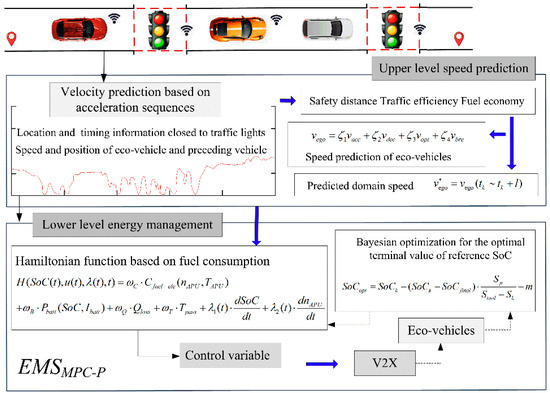
Figure 3.
EMS diagram for eco-vehicles in a connected scenario.
The upper layer of the architecture generates globally optimal speed trajectories through dynamic tracking of a preset optimal constant speed benchmark, with the objective of maximizing the stable cruising time window. In the lower-layer energy management module, a Bayesian-optimized model predictive EMS based on the PMP (EMSMPC-P) is proposed to solve MOO problems, achieving optimal allocation of the torque parameters and rotational speed operating points in the powertrain system. Numerical validation and algorithm performance evaluation are ultimately conducted through a MATLAB R2020a/Simulink co-simulation platform.
Cooperative passing strategies are proposed. The front vehicle is allowed to pass through Signal 1 quickly (and then wait at Signal 2), and the eco-vehicle is delayed to pass at Signal 1 until the next green period to achieve synchronization at Signal 2. By restricting the time deviation threshold for the two vehicles to reach the key nodes, the risk of cascading delays caused by a continuous green light for the front vehicle and a continuous red light for the rear vehicle can be effectively avoided. According to the above constraint principle of the following car scenario, the interval time Δts does not affect the pre-speed planning.
where tpre_end denotes the time used by the front vehicle to reach the end, and tego_end denotes the time used by the eco-vehicle to reach the end. This paper is based on the concept of MPC scrolling to improve the efficiency of the passage, so as to ensure in real-time that both vehicles arrive at the second signal from the target vehicle as simultaneously as possible.
where t2-egomin is defined as the eco-vehicle’s minimum arrival time at the second downstream signal, with t2-pre representing the preceding vehicle’s estimated arrival time at the same signal. Temporal traffic efficiency is ensured through rolling updates of the eco-vehicle’s real-time position calculations.
The minimum safety distance must consider rear-end collision risks and road access efficiency, where endpoint arrival time synchronization is already ensured by prior access efficiency constraints. Minimum safe spacing is determined via a time headway model, with the inter-vehicle safety distance defined as:
where spre is the real-time distance between the preceding vehicle and the starting point, sego is the real-time distance between the eco-vehicle and the starting point, smin indicates the minimum spacing between the vehicles, and h indicates the driver’s reaction time, whose specific value has less influence on the whole speed planning. The minimum spacing is set to 3 m, the reaction time is set to 0.5 s, and vego represents the speed of the eco-vehicle.
Optimal constant speeds of 5–15 m/s are set in this paper. The economy is optimized by maximizing the constant speed travel time of the eco-vehicle. For the optimal speed curve of the eco-vehicle, the planning steps are as follows:
- (1)
- The optimal constant-speed profile vopt is established as a stationary horizontal line. Derived from preceding vehicle historical driving data, the canonical acceleration profile vacc (standstill → maximum speed limit) and deceleration profile vdec (maximum speed limit → standstill) are extracted. These are systematically integrated with the emergency braking profile vbre to synthesize the optimal velocity trajectory.For the optimal constant speed curve, the influence of 11 constant speed plans in the interval of 5–15 m/s is considered in this paper. The emergency braking curve is dynamically generated based on the real-time acceleration demand to ensure that the distance from the front vehicle after braking satisfies the constraints of Equation (22).
- (2)
- The preceding vehicle’s speed prediction is based on its current speed vpre and SPaT information (remaining time tremain). An acceleration sequence model generates the speed sequence, which is combined with position data (d1-pre, d2-pre) to estimate its arrival times t1-pre and t2-pre at traffic signals (implemented in Section 2).
- (3)
- The temporal information from two adjacent signals and the predicted preceding vehicle arrival time is utilized to calculate the minimum allowable time and maximum allowable time for the eco-vehicle’s arrival at the first and second signal:where fix() is a rounding function, t1-remain indicates the remaining time of the current Signal 1 phase, t2-remain indicates the remaining time of the current Signal 2 phase, and tcir indicates the fixed cycle time of the signal.
- (4)
- The eco-vehicle’s arrival times (t1-acc/t1-opt/t1-dec for Signal 1, t2-acc/t2-opt/t2-dec for Signal 2) under three speed profiles (vacc, vopt, vdec) are computed. Prioritizing sustained travel duration maximization within the prediction horizon, the optimal speed profile vopt serves as the baseline velocity, formulated as:
The specific method of solving and analyzing can be followed in the following steps: eco-speed decision logic: If the eco-vehicle’s arrival time t2max at Signal 2 under speed vacc satisfies t2max < up_t2 + tb (up_t2 is the minimum allowable time to arrive at Signal 2, buffer threshold tb = 1 s), then vego = vopt; otherwise, vego = vacc. A secondary validation sets vego = vopt if t1-max < up_t1 + tb (up_t1 is the minimum allowable time to arrive at Signal 1), which compensates for the prediction error in the arrival time of the preceding vehicle to ensure near-synchronized passage through Signal 2. Speed control logic: if the eco-vehicle is stationary and can reach Signal 1 earlier via vopt, standstill is maintained; if it is in motion, it decides to accelerate or decelerate based on whether the following distance exceeds the safety threshold. The new speed vego is planned by validating if the vopt-based arrival time t1-opt falls within the window [up_t1, down_t1] (down_t1 is the maximum allowable time to arrive at Signal 1) at the signal. Then, under safety constraints, vego is iteratively updated, taking into account the dynamic parameters of the preceding vehicle (vpre, apre, dpre) and the stop line position. Finally, the optimal speed vego is updated again based on the last time down_t1 at which the eco-vehicle can cross the signal, ensuring that the eco-vehicle can cross the signal within the specified interval.
3.2. Multi-Objective Optimization Model
This study establishes a V2I-based car-following control framework employing an MPC rolling optimization mechanism. The speed prediction horizon is defined as [tk, t2-ego], where tk denotes the current timestep and t2-ego represents the predicted arrival time of the eco-vehicle at Signal 2. The initial segment [tk, tk + l] defines the prediction horizon with length l. Within this horizon, the traffic flow efficiency, fuel economy, and SoC are optimized simultaneously to generate the velocity prediction profile. The initial speed prediction segment is fed into the lower-layer EMS, where the optimal control variable for the next second is executed as the powertrain command, with real-time state updates and rolling solution enabled. The velocity trajectory optimization is formulated as a maximization problem:
The velocity in the prediction horizon is:
The predicted velocity profile within the prediction horizon is integrated into the lower-layer EMS, where the EMSMPC-P method presented solves the fuel consumption minimization problem. The lower-layer objective function is formulated as:
where J is the cost function, ωC is the unit fuel parameter, ωB is the unit battery parameter, ωQ is the unit battery life degradation parameter, ωT is the unit pass time parameter, nAPU is the APU system speed, TAPU is the APU system torque, Ibatt is the instantaneous battery current, Cfuel_ele is the oil-to-electric conversion loss rate, Qloss is the battery life degradation, Pbatt is the battery output power, and Tpass is the average pass time (sec) through traffic lights.
The Hamiltonian function is constructed as:
where λ1 is the covariate of the battery SoC, and λ2 is the covariate of the APU system speed.
The optimal EMS is transformed into a minimization problem:
In the CAR-EEV architecture, the internal combustion engine (ICE) serves as a vital energy conversion component, with fuel consumption being thoroughly evaluated. Fuel consumption assessment criteria and battery capacity degradation metrics are delineated. It demonstrates that battery longevity can be extended by stabilized SoC trajectories, which, in turn, improves the efficiency of energy exchange between the battery and engine. Functional synergy between the APU and batteries is achieved through hybrid energy storage system implementation, forming an effective strategy for battery service life extension. Electric motor efficiency considerations are integrated, with Cfuel_ele and Qloss being mathematically defined through Equation (33).
The power generation efficiency of the generator is represented by ηele, with ηfuel characterizing the fuel-to-effective power conversion efficiency of the engine. The gasoline calorific value (ρ) is quantified as 4.6 × 107 J/kg. The total cycle duration is designated as Tcyc. The depth of charge/discharge (DOD) is specified as 0.7, with Ncyc quantifying the total life cycles and Ahcell corresponding to the battery’s cumulative capacity. tj_pass is the passing time at the j-th traffic light, ntot is the number of traffic lights and Icom_ovp is the comprehensive performance evaluation index of the APU, taking into account the energy consumption and battery life. In practical considerations, the transit time weight coefficient is relatively lower than the energy consumption emission factors, being significantly influenced by external factors, such as road traffic conditions and traffic participant behaviors, that exhibit strong uncertainty and uncontrollability, while system control over the transit time remains limited. Furthermore, optimizing energy consumption emissions may involve sacrificing partial transit time but achieves enhanced energy efficiency and cost reduction. Comprehensively balancing the system control objectives with the controllability and importance of various factors, the weight parameters are adjusted to [ωC, ωQ, ωT]T = [0.4, 0.3, 0.3]T based on the developers’ understanding of the control requirements.
4. Verification and Results Analysis
4.1. Simulation Results and Analysis of Vehicle Speed Prediction of Eco-Vehicles
CAR-EEV is characterized as an electromechanical hybrid power system jointly driven by multiple energy sources, where precise modeling of its powertrain system and components is established as the fundamental basis for EMS research. Detailed component-level modeling of CAR-EEV powertrains is conducted utilizing AVL, encompassing dynamic system architectures, APU configurations, battery modules, DC/DC converters, and drive motor characteristics. The degradation mechanisms of the battery systems are analytically examined with corresponding lifespan deterioration models formulated. Traffic simulation scenario frameworks are constructed to enable subsequent traffic information-driven vehicle speed prediction studies. The topological structure of the powertrain system for a CAR-EEV is shown in Figure 4.
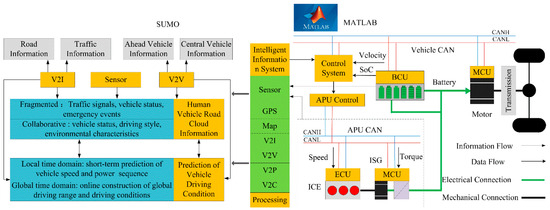
Figure 4.
Powertrain systems for CAR-EEV.
To validate the performance of the intelligent EMS proposed in terms of energy consumption economy and mitigating battery capacity degradation in a CAR-EEV, a traffic simulation framework based on SUMO with a co-simulation platform interfaced to MATLAB via Traci is utilized to obtain vehicle driving condition information, which is then applied to the EMSMPC-P within a continuous action space. Car-following and lane-changing behavioral models are implemented across all vehicular agents to enable route optimization for destination convergence. Real-world vehicular datasets are utilized to construct a SUMO traffic network model, ensuring full-scale roadway simulation across all segments.
The speed optimization analysis is carried out for the research scenario of this paper. The optimized simulated traffic trip is shown in Figure 5 (Where the red parts represent the red light time and the green parts represent the green light time):
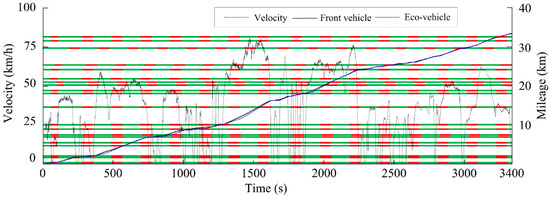
Figure 5.
The optimized simulated traffic trip.
It can be observed that during the car-following process, the trajectory curve of the eco-vehicle is maintained along the green line with synchronized arrival time relative to the preceding vehicle at 3400 s, satisfying trafficability requirements. At intersections, the trajectory of the preceding vehicle is precisely followed by the eco-vehicle, and no red light violations are observed throughout the process. When the preceding vehicle is halted by a red light, coordinated stopping is achieved with the eco-vehicle maintaining proximity to the preceding vehicle, where smooth traffic flow is ensured and the effectiveness of the speed planning strategy in maintaining following performance and traffic efficiency is validated.
4.2. Comparative Analysis and Verification of Experimental Results
A comparative analysis is performed to evaluate the energy consumption optimization and battery capacity degradation mitigation across four EMS for CAR-EEVs: Dynamic programming (DP)-based EMS, charge depleting-charge sustaining (CD-CS), charge depleting-blend (CD-Blend), and the proposed multi-objective intelligent EMS (EMSMPC-P). The effectiveness of EMSMPC-P in coordinated energy-battery optimization is verified through systematic benchmarking. The CD-CS strategy triggers APU activation at SoC = 30%, emulating conventional threshold control, whereas CD-Blend employs dynamic PI-controlled electric-oil power coupling. Comparative metrics reveal CD-CS reduces battery cycling by 42%, while CD-Blend decreases the APU start-stop frequency by 38%. Algorithmically, EMSMPC-P and DP share Q-value function frameworks but diverge in state-space treatment. DP utilizes 40 × 80 discretized grids versus EMSMPC-P’s four-layer fully connected network for continuous mapping, both maintaining a 0.95 discount factor. Experimental rigor is ensured through 100 Monte Carlo trials with 95% confidence intervals.
The energy storage system’s performance and fuel consumption were jointly assessed through simulation. The passage time Tpass and battery degradation metrics are tabulated in Table 1, with comparative results provided against DP-based EMS benchmarks. DP’s reliance on a priori information and its computationally intensive nature limits its applicability to real-time energy management, restricting its utilization to benchmark validation purposes.

Table 1.
Test results of simulation test.
The Cfuel_ele energy consumption values are measured as 0.76 and 0.71 for CD-CS-based EMSs and EMSMPC-P, respectively. Compared to CD-CS, a 6.58% reduction in equivalent energy consumption is achieved by the EMSMPC-P strategy, accompanied by a 7.89% deviation reduction from DP and energy efficiency reaching 80% of DP levels. In computational timeliness, CD-CS demonstrates optimal real-time performance with 0.15 s processing time, while EMSMPC-P requires 0.18 s, remaining feasible for online applications. With respect to reduction in pass time, the EMSMPC-P strategy has a ∆Tpass of −65.4%, which is close to the DP strategy’s −67.3%. Battery lifespan analysis reveals CD-Blend reduces degradation by 13.79% relative to CD-CS, with the DP strategy achieving 18.1% improvement. DP’s superiority is attributed to high-efficiency battery operation range maintenance, effectively mitigating degradation. EMSMPC-P exhibits 17.2% lower degradation than CD-CS, confirming its battery management efficacy. EMSMPC-P approaches optimality in degradation regulation and reduction in pass time.
The EMSMPC-P achieves energy consumption economy comparable to DP-based global optimization while demonstrating superior equilibrium in battery capacity degradation mitigation relative to DP and CD-CS strategies. This approach synergistically optimizes battery longevity and system economics through operational condition simulations, validating EMSMPC-P advantages in energy cost reduction, lifespan regulation, and control robustness across diverse driving scenarios (Figure 6). As the primary energy supply unit for hybrid electric vehicles, the APU system satisfies fundamental power demands. Battery-integrated APU configurations attenuate load power fluctuations through responsive energy buffering, thereby extending APU service life. The EMSMPC-P incorporates a battery SoC preservation coefficient within its reward function to explicitly address lifespan considerations. The EMSMPC-P framework defines four operational modes: (1) CD-EV Mode: Electric propulsion dominates, with the CD strategy managing battery charging during power surplus. (2) CD-Blend Mode: APU engagement balances dual-energy utilization, progressively increasing power contribution as reserves diminish while maintaining a certain percentage of power. (3) CS-Blend Mode: CS strategy stabilizes battery SoC via engine-dominant propulsion with concurrent charging. (4) DC Mode: Predictive congestion-triggered battery replenishment through dynamic charging during motion.
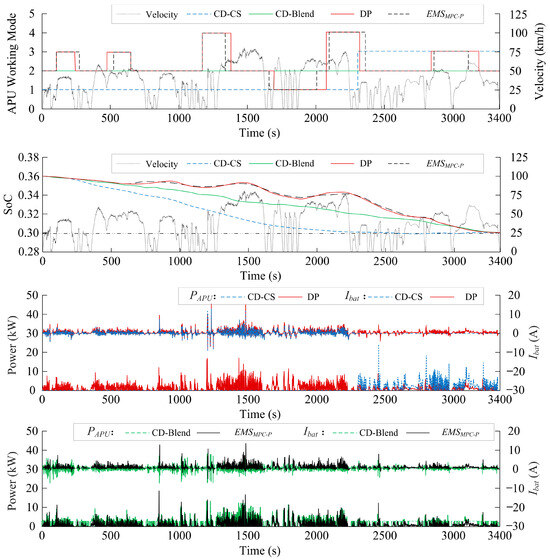
Figure 6.
Comparison of simulation results of different EMS.
The CD-CS strategy exhibits maximal SoC volatility, correlating with accelerated lifespan degradation. Battery current/power distributions under three EMS reveal EMSMPC-P’s operational point concentration in high-efficiency regions per strategic specifications, contrasting with fuel minimization-driven clustering in lower-efficiency zones. Comparative analysis demonstrates EMSMPC-P’s superiority in energy economy and lifespan preservation. The CD-CS strategy is characterized by the highest total equivalent energy consumption and maximal battery lifespan degradation, indicative of battery operation within minimally efficient ranges. A balance between energy consumption economy and capacity fade mitigation is achieved by the EMSMPC-P, where the global energy consumption economy is approximated, battery lifespan degradation is suppressed, and operational longevity is enhanced.
The developed control strategy demonstrates optimized energy consumption and battery longevity performance. DP is established as the offline optimal benchmark. Normalization parameters are computed for cross-strategy performance comparison due to dimensional heterogeneity among evaluation metrics, calculated as:
where ηik is defined as the normalized value of the j-th evaluation metric under the i-th strategy, and λij denotes the raw metric value, with λminij and λmaxij representing its theoretical minimum and maximum bounds.
Normalization analysis incorporates simulation outcomes from the implemented strategies, with the statistical results shown in Figure 7.
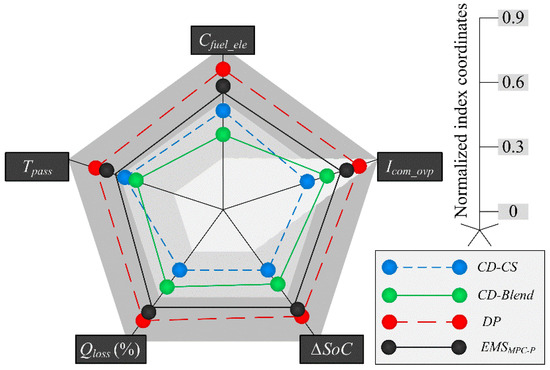
Figure 7.
Normalization performance comparison under different EMSs.
From the comparison of the normalization parameters, it can be seen that the CD-Blend strategy outperforms the CD-CS strategy in terms of Qloss and SoC, and the proposed EMSMPC-P is the closest to the DP-optimal solution in all the parameters.
4.3. Experimental Test Implementation and Its Results
EMSMPC-P was formulated and simulated offline, with adaptive control model recalibration required for real-world deployment to ensure real-time functionality. The experimental protocol comprises: (1) vehicle parameters and driving cycles conditions being loaded into road load simulation software; (2) AVL system emulation of road loads via closed-loop control of speed and torque of the motor/dynamometer; (3) real-time electric power calculation through DC bus voltage-current monitoring; (4) battery SoC-driven EMS execution generating engine/generator speed-torque commands; (5) APU power coordination determination. Four-strategy validation experiments were conducted with calculated APU power as tracking targets. The structure of the experimental platform is shown in Figure 8.
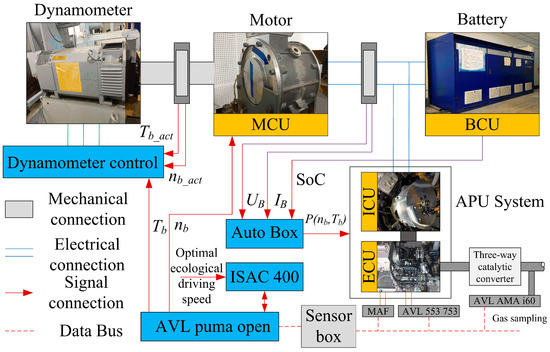
Figure 8.
Structure of the experimental platform.
The parameters of the components are provided in Table 2.

Table 2.
Parameters of the vehicle components of the experimental platform (Changchun, China).
The energy consumption economy outcomes from the simulations and bench tests are tabulated in Table 3. The consistency between the offline simulations and the bench testing results is demonstrated, confirming effective power tracking and dynamic performance compliance. A marginal increase in energy consumption is observed during bench testing compared to the simulations, with deviations remaining within acceptable thresholds. The proposed EMSMPC-P achieves real-time speed tracking with minimal errors, validating control precision. Simulation–experimental consistency is maintained despite minor discrepancies caused by signal accuracy and transmission latency, confirming EMS functional integrity.

Table 3.
Test results of experimental test.
Analysis of Table 3 reveals three conclusions: At SoC0 = 0.4, EMSMPC-P achieves the SoC control target, while CD-CS and CD-Blend exhibit poor performance. Fuel economy superiority is demonstrated by EMSMPC-P with Cfuel_ele = 0.72 (7.69% reduction vs. CD-CS, 5.13% reduction vs. CD-Blend). The pass time is reduced by EMSMPC-P with Tpass = 13.8 s (62.2% and 58.7% reduction vs. CD-CS and CD-Blend). The battery degradation is minimized under EMSMPC-P (16.18% and 5.89% reductions vs. CD-CS and CD-Blend). At SoC0 = 0.8, the energy consumption, pass time, and battery lifespan loss are also reduced. An enhancement in battery operating efficiency is demonstrated with the increase in SoC, accompanied by reductions in overall energy consumption and mitigation of battery lifespan degradation. Bench testing confirms the feasibility and effectiveness of the proposed EMSMPC-P.
5. Conclusions
To address energy management challenges for intelligent CAR-EEVs under vehicle-road cooperative environments, a hierarchical EMS based on speed prediction is proposed from the perspective of MOO, with comprehensive system performance being significantly enhanced. Focused on connected car-following scenarios, acceleration sequence prediction is performed based on Kalman filtering and preceding vehicle acceleration. A dual-layer architecture is designed: the upper layer plans optimal speed curves based on the road topology and preceding trajectories, while the lower layer enables coordinated multi-power allocation through EMSMPC-P. Finally, a MOO model for system performance enhancement is formulated to achieve the optimization of vehicle operating parameters. Simulations and bench tests validate the effectiveness of the proposed hierarchical energy management strategy. A vehicle-road cooperative dynamic scenario model was constructed, providing an extensible technical framework for real-time energy management of intelligent connected vehicles. The proposed EMSMPC-P achieves deep integration between MOO models and V2X perception, enhancing traffic efficiency and safety while reducing battery lifespan maintenance costs by over 16%. The research outcomes can be applied to on-board controller development in intelligent transportation systems, offering a theoretical foundation for standardized protocol design in vehicle–road–cloud cooperative systems. Considering the inherent robustness of Kalman filtering, future improvements could involve introducing extended Kalman filtering to handle nonlinear dynamics, integrating real-time sensor data (e.g., radar or camera) to enhance the environmental perception capabilities, and designing adaptive noise covariance update modules to improve the algorithm’s effectiveness and reliability in complex traffic scenarios.
Author Contributions
H.L. and Y.L. managed the project and conceptualized the scheme; H.L. and X.L. conceived the control method; X.L. and W.S. completed the modeling and performed the simulation experiments, and finished the manuscript; S.W., J.X. and Z.W. collected the data and reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support from Research on Collaborative Optimization of Optimal Speed Control and Energy Management for Connected Automated Range-Extended Electric Vehicle (No. 232699HJ0103108631), and the Design of Key Mechanical Components and Development of Intelligent Control System for Customized Material Handling Equipment (No. 2023220103000068).
Data Availability Statement
Data are provided within the manuscript.
Conflicts of Interest
The authors declare that there are no conflicts of interests regarding the publication of this paper.
Nomenclature
| CAR-EEV | connected automated range-extended electric vehicle | EMSMPC-P | Bayesian-optimized model predictive EMS based on PMP |
| EMS | energy management strategy | CD-CS | charge depleting-charge sustaining |
| MOO | multi-objective optimization | CD-Blend | charge depleting-blend |
| PMP | Pontryagin’s minimum principle | SoC | state of charge |
| DP | dynamic programming | MPC | model predictive control |
References
- Panaparambil, V.S.; Kashyap, Y.; Castelino, R.V. A review on hybrid source energy management strategies for electric vehicle. Int. J. Energy Res. 2021, 45, 19819–19850. [Google Scholar] [CrossRef]
- Mohan, A.; Manitha, P.V. Hybrid electric vehicles with V2X topology and smart energy management: An overview of their potential and limitations. In Proceedings of the 2nd IEEE International Conference on Futuristic Technologies, INCOFT 2023, Belagavi, Karnataka, India, 24–26 November 2023. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, H.; Jiang, S.; Tian, J.; Ai, Q. Study on coordinated control strategy for auxiliary power units in range-extended electric vehicles. Energy Rep. 2025, 13, 865–874. [Google Scholar] [CrossRef]
- Tran, D.-D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Uralde, J.; Barambones, O.; del Rio, A.; Calvo, I.; Artetxe, E. Rule-based operation mode control strategy for the energy management of a fuel cell electric vehicle. Batteries 2024, 10, 214. [Google Scholar] [CrossRef]
- Wang, F.; Wen, Q.Y.; Xu, B. An energy saving rule-based strategy for electric-hydraulic hybrid wheel loaders. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2023, 238, 4081–4092. [Google Scholar] [CrossRef]
- Hou, S.; Gao, J.; Zhang, Y.; Chen, M.; Shi, J.; Chen, H. A comparison study of battery size optimization and an energy management strategy for FCHEVs based on dynamic programming and convex programming. Int. J. Hydrog. Energy 2020, 45, 21858–21872. [Google Scholar] [CrossRef]
- Park, D.; Lee, W.; Jeong, J.; Karbowski, D.; Kim, N. Eco-driving profile optimization by dynamic programming for battery electric vehicles. Int. J. Automot. Technol. 2024, 25, 1309–1321. [Google Scholar] [CrossRef]
- Deng, T.; Wu, S.; Chen, Q.; Liu, P. Multi-objective energy management strategy for PHEVs based on working condition information prediction and time-varying equivalence factor ECMS. Automot. Innov. 2024, 7, 698–715. [Google Scholar] [CrossRef]
- Sun, H.; Fu, Z.; Tao, F.; Zhu, L.; Si, P. Data-driven reinforcement-learning-based hierarchical energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles. J. Power Sources 2020, 455, 227964. [Google Scholar] [CrossRef]
- Yang, C.; Du, X.; Wang, W.; Yang, L.; Zha, M. A rolling convergent equivalent consumption minimization strategy for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2023, 73, 1–13. [Google Scholar] [CrossRef]
- Wu, X.; Gu, Y.; Xu, M. Adaptive energy management strategy for extended-range electric vehicle based on micro-trip identification. IEEE Access 2020, 8, 176555–176564. [Google Scholar] [CrossRef]
- Liu, X.; Du, J.; Ma, J.; Liu, G.; Xiong, Y. An adaptive co-state design method for PMP-based energy management of plug-in hybrid electric vehicles based on fuzzy logical control. J. Energy Storage 2024, 102, 114118. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, F.; Shen, T. A real-time energy management strategy for parallel HEVs with MPC. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019. [Google Scholar] [CrossRef]
- Hou, Z.; Chu, L.; Du, W.; Hu, J.; Jiang, J.; Yang, J. A novel dual-model MPC-based energy management strategy for fuel cell electric vehicle. IEEE Trans. Transp. Electrif. 2024, 10, 8585–8604. [Google Scholar] [CrossRef]
- Hu, J.; He, H.; Wang, Z.; Ji, S.; Duan, Z. A switched model predictive control with parametric weights-based mode transition strategy for a novel parallel hybrid electric vehicle. Control. Eng. Pract. 2025, 155, 106161. [Google Scholar] [CrossRef]
- Thomas, J.; Thomas, A.; Biju, A.; Mathew, A.; Jose, C.P.; Haneesh, K.M. A GPS-gradient mapped database-based fuzzy energy management system for a Series—Parallel hybrid electric vehicle. In Advances in Electrical Control and Signal Systems; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, W.; Qi, B. Combined prediction for vehicle speed with fixed route. Chin. J. Mech. Eng. 2020, 33, 60. [Google Scholar] [CrossRef]
- Tian, H.; Wang, X.; Lu, Z.; Huang, Y.; Tian, G. Adaptive fuzzy logic energy management strategy based on reasonable SOC reference curve for online control of plug-in hybrid electric city bus. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1607–1617. [Google Scholar] [CrossRef]
- Chen, B.; Wang, M.; Hu, L.; Zhang, R.; Li, H.; Wen, X.; Gao, K. A hierarchical cooperative eco-driving and energy management strategy of hybrid electric vehicle based on improved TD3 with multi-experience. Energy Convers. Manag. 2025, 326, 119508. [Google Scholar] [CrossRef]
- Bouwman, K.R.; Pham, T.H.; Wilkins, S.; Hofman, T. Predictive energy management strategy including traffic flow data for hybrid electric vehicles. IFAC Pap. 2017, 50, 10046–10051. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, T.; Li, K. Multi-objective decoupling algorithm for active distance control of intelligent hybrid electric vehicle. Mech. Syst. Signal Process. 2015, 64–65, 29–45. [Google Scholar] [CrossRef]
- Zhang, F.; Qi, Z.; Xiao, L.; Coskun, S.; Xie, S.; Liu, Y.; Li, J.; Song, Z. Co-optimization on ecological adaptive cruise control and energy management of automated hybrid electric vehicles. Energy 2025, 314, 133542. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Li, L.; Shi, J.; An, Q. Modelling and control for economy-oriented car-following problem of hybrid electric vehicle. IET Intell. Transp. Syst. 2019, 13, 825–833. [Google Scholar] [CrossRef]
- Xie, S.; Liu, T.; Li, H.; Xin, Z. A study on predictive energy management strategy for a plug-in hybrid electric bus based on Markov Chain. Qiche Gongcheng/Automot. Eng. 2018, 40, 871–877+911. [Google Scholar] [CrossRef]
- Sakhdari, B.; Vajedi, M.; Azad, N.L. Ecological adaptive cruise control of a plug-in hybrid electric vehicle for urban driving. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Rio de Janeiro, Brazil, 1–4 November 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, K.; Gao, Y.; Hu, J.; Gao, B.; Hong, J. PCC energy-saving optimization based on historical driving data identification of energy consumption model. In Proceedings of the 2023 7th CAA International Conference on Vehicular Control and Intelligence (CVCI), Changsha, China, 27–29 October 2023. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoon, S.W. Dual Deep Neural Network Based Adaptive Filter for Estimating Absolute Longitudinal Speed of Vehicles. IEEE Access 2020, 8, 214616–214624. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).