Model Reference Adaptive Sensorless Control of Variable-Speed Pumped Storage Doubly Fed Induction Machine Under Reversible Operations
Abstract
1. Introduction
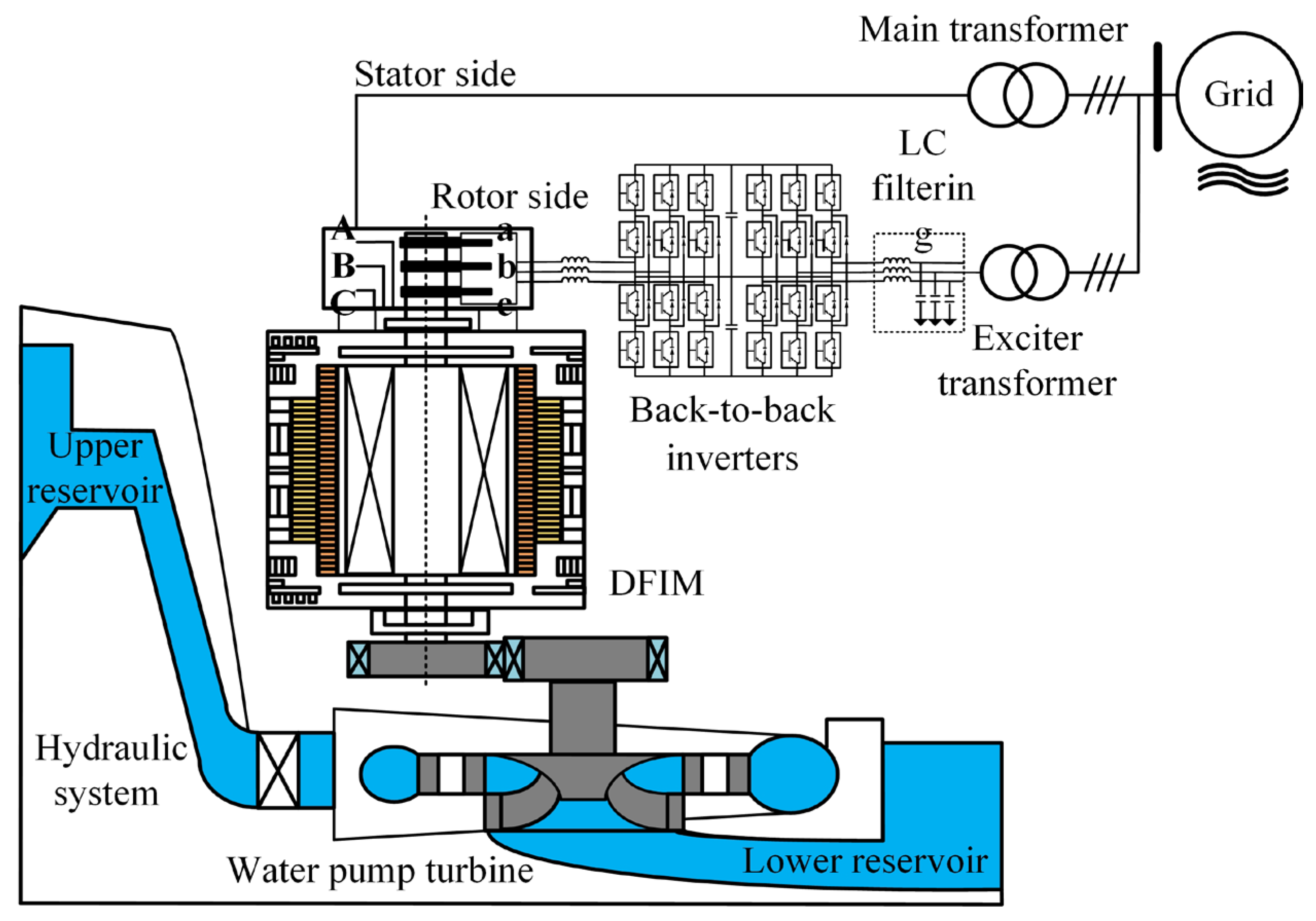
2. Model of DFIM for VSPS System
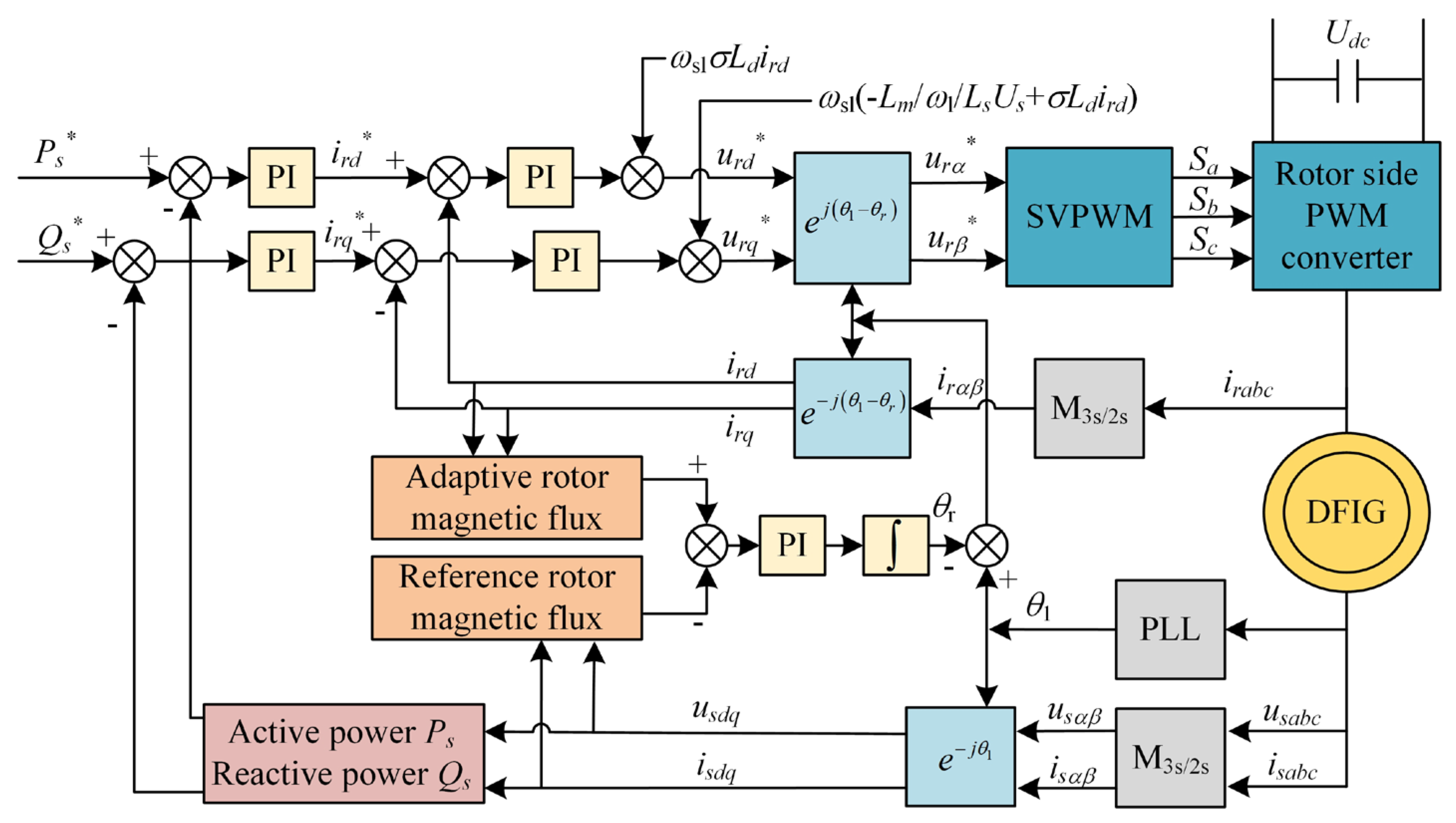
3. The Sensorless Closed-Loop Direct Detection Control
4. The Sensorless Control of Rotor Magnetic Flux Based on the MARS
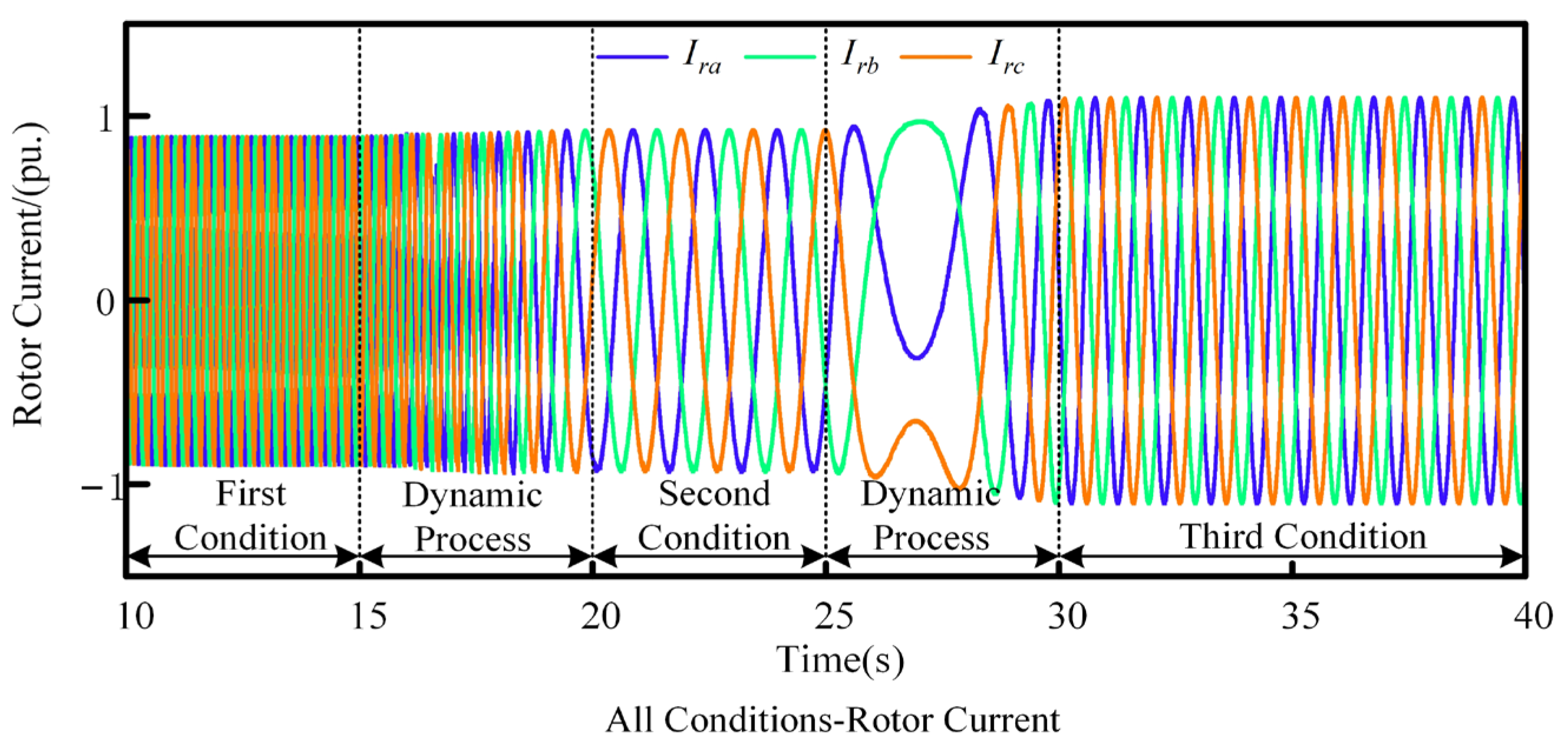
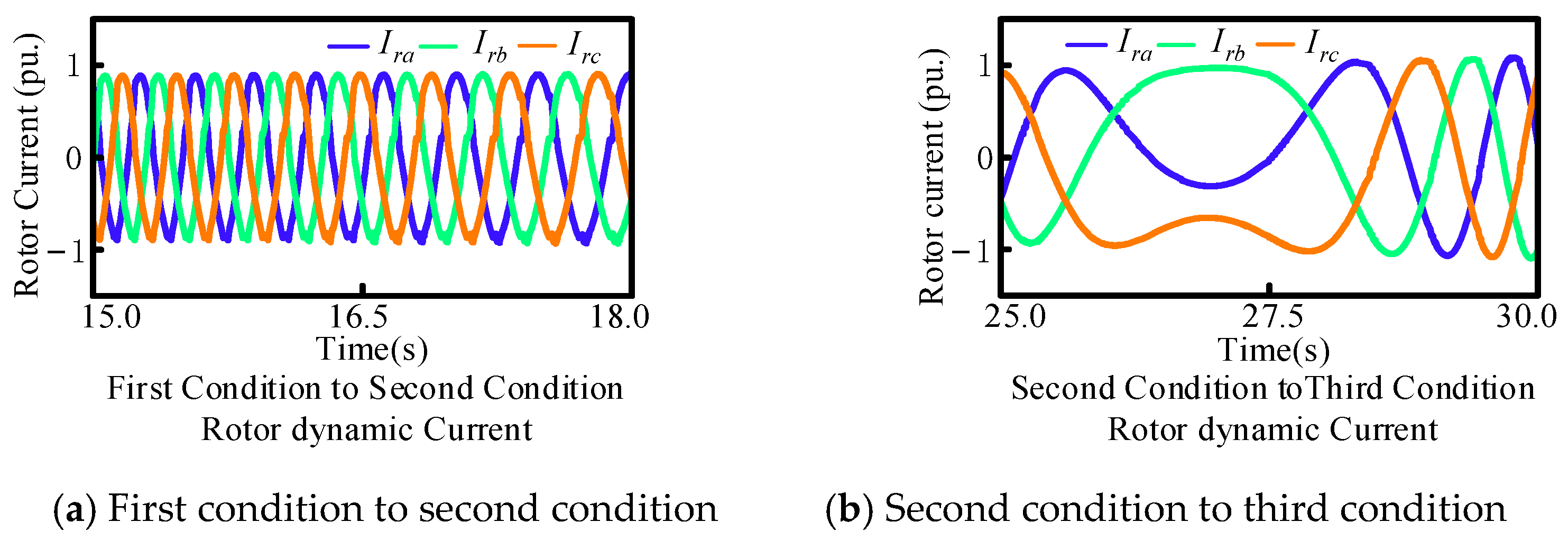
5. Simulation Verification
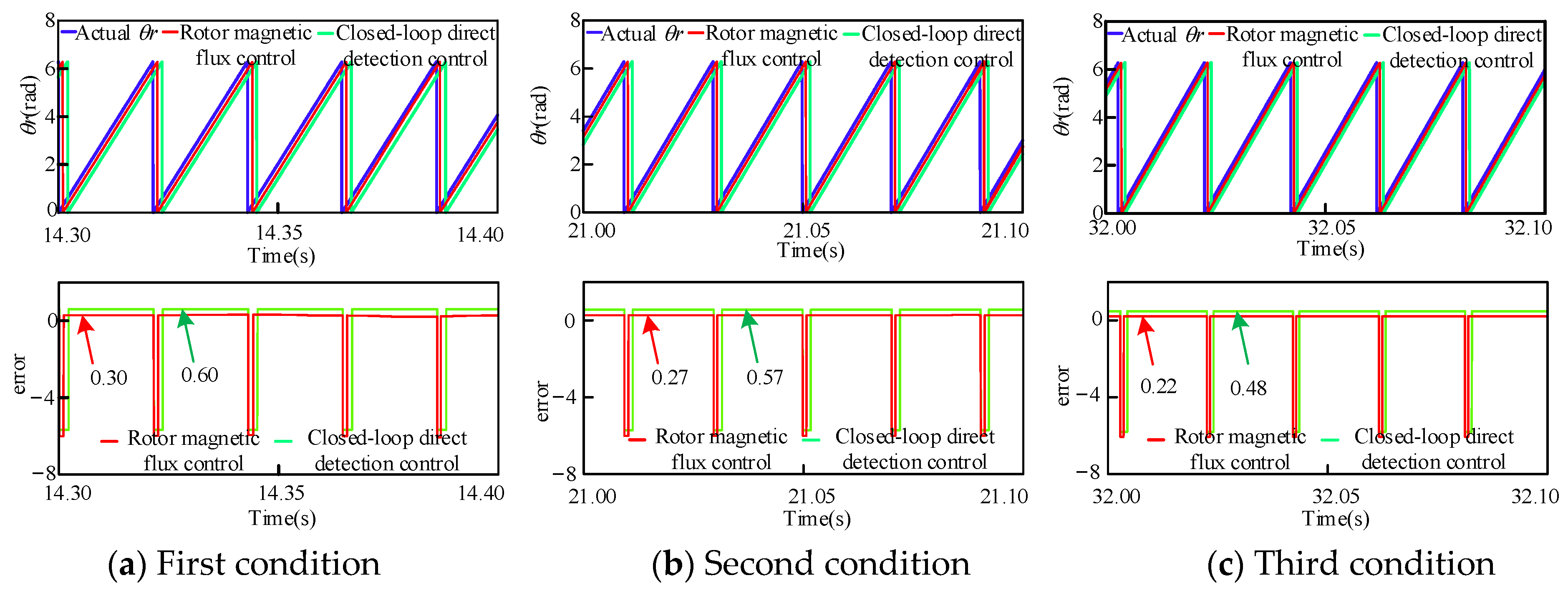
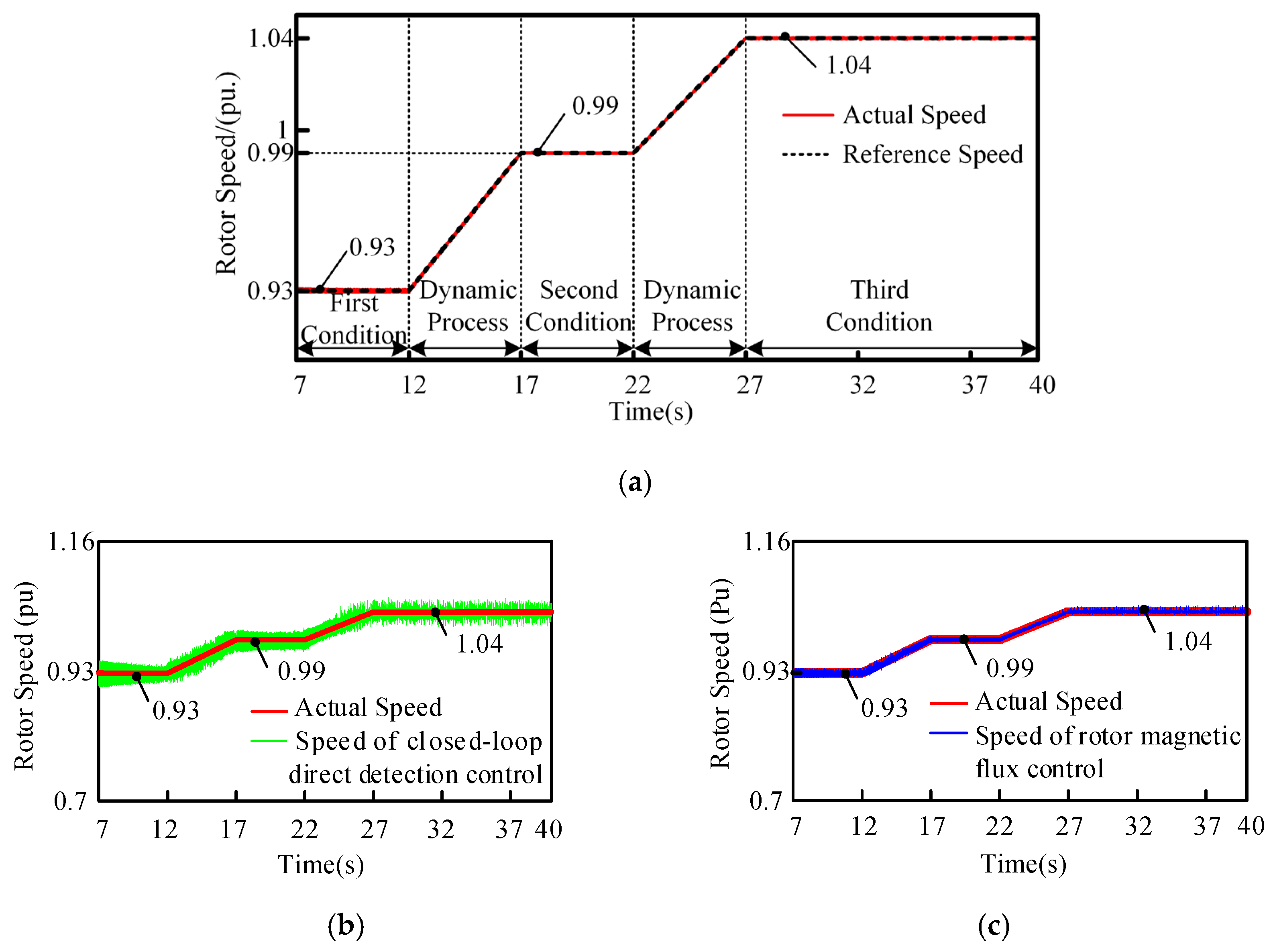
5.1. Power Generation State
5.2. Pumping State
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tiwari, R.; Nilsen, R.; Mo, O.; Nysveen, A. Control methods for operation of pumped storage plants with full-size back-to-back converter fed synchronous machines. IEEE Trans. Ind. Appl. 2023, 59, 6792–6803. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Liu, Y.; Bao, Z.; Mao, Z.; Rashad, E.M. Modeling and transient response analysis of doubly-fed variable speed pumped storage unit in pumping mode. IEEE Trans. Ind. Electron. 2023, 70, 9935–9947. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Liu, Y.; Mao, Z. Dynamical Response Comparison Between Variable Speed and Synchronous Speed Pumped-Storage Units in Turbine Mode. IEEE Trans. Energy Convers. 2024, 39, 2490–2503. [Google Scholar] [CrossRef]
- Munphal, S.; Suwankawin, S. A position-sensorless control of doubly fed induction machine by stator-equation-based adaptive reduced-order observer. IEEE Trans. Power Electron. 2022, 37, 15186–15208. [Google Scholar] [CrossRef]
- Krzeminski, Z. Sensorless multiscalar control of double fed machine for wind power generators. In Proceedings of the Power Conversion Conference-Osaka 2002, Osaka, Japan, 2–5 April 2002. [Google Scholar]
- Prystupa, D.; Huang, X.; Zhang, H.; Varvolik, V.; Buticchi, G.; Wang, S.; Zhang, X.; Li, J.; Gerada, C. Generalized high-frequency injection framework for sensorless control of synchronous reluctance machines. IEEE Open J. Ind. Electron. Soc. 2023, 4, 304–315. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, W.; Zhu, J.; Blaabjerg, F. Sensorless control of standalone brushless doubly fed induction generator feeding unbalanced loads in a ship shaft power generation system. IEEE Trans. Ind. Electron. 2019, 66, 739–749. [Google Scholar] [CrossRef]
- Mondal, P.; Malakar, M.K.; Tripathy, P.; Krishnaswamy, S.; Saha, U.K. Robust observer design for sensorless voltage and frequency control of a doubly fed induction generator in standalone mode. IEEE Trans. Energy Convers. 2022, 37, 844–854. [Google Scholar] [CrossRef]
- Yang, J.; Tang, W.; Zhang, G.; Sun, Y.; Ademi, S.; Blaabjerg, F.; Zhu, Q. Sensorless control of brushless doubly fed induction machine using a control winding current MRAS observer. IEEE Trans. Ind. Electron. 2019, 66, 728–738. [Google Scholar] [CrossRef]
- Rauth, S.S.; Kastha, D.; Bajpai, P. A Modified MRAS based Sensorless Control of DFIG in Wind Energy Conversion System. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022. [Google Scholar]
- Mbukani, M.W.K.; Gitau, M.N.; Naidoo, R.; Masike, L. A torque-based MRAS estimator for position/speed sensor-less control of DFIG systems. In Proceedings of the 2022 IEEE 1st Industrial Electronics Society Annual On-Line Conference (ONCON), Kharagpur, India, 9–11 December 2022. [Google Scholar]
- Zhou, Y.; Zhu, D.; Hu, J.; Zou, X.; Kang, Y. Phase Step Control in PLL of DFIG-Based Wind Turbines for Ultrafast Frequency Support. IEEE Trans. Power Electron. 2025, 40, 51–56. [Google Scholar] [CrossRef]
- Saihi, L.; Bakou, Y.; Ferroudji, F.; Tayebi, A.; Hadidi, A.; Ibrahim, O. A Novel Fuzzy-MRAS Observer of Wind Turbines Conversion Systems Based on DFIG. In Proceedings of the 2022 International Conference on Theoretical and Applied Computer Science and Engineering (ICTASCE), Ankara, Turkey, 29 September–1 October 2022. [Google Scholar]
- Lakhdar, S.; Ferroudji, F.; Roummani, K.; Koussa, K. Enhanced Sensor-Less Control of DFIG-Based Generators Using Hybrid MRAS-ANN Observer and PSO Parameter Optimization. In Proceedings of the 2023 14th International Renewable Energy Congress (IREC), Sousse, Tunisia, 16–18 December 2023. [Google Scholar]
- Gayen, P.K. An Enhanced Rotor Position/Speed Estimation Technique for Doubly Fed Induction Generator Using Stator-Side Reactive Current Variable in Model Reference Adaptive System. IEEE Trans. Ind. Electron. 2022, 69, 4409–4418. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Lee, D.-C. Sensorless Control of DFIG Wind Turbine Systems Based on SOGI and Rotor Position Correction. IEEE Trans. Power Electron. 2021, 36, 5486–5495. [Google Scholar] [CrossRef]
- Gayen, P.K. Stator Flux Producing Current-Based Promoted Rotor Angle Estimator of Doubly-Fed Induction Generator for Encoderless Operations. IEEE Sens. J. 2021, 21, 15133–15141. [Google Scholar] [CrossRef]
- Bose, S.; Singh, S.P. Sensor-less Vector Control of DFIG Based Micro Wind Energy Conversion System. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020. [Google Scholar]
- Wang, M.; Liu, J.; Jiang, L.; Tan, K.; Wang, Y. Position Sensorless Control of Permanent Magnet Synchronous Motor Based on Improved Model Reference Adaptive Systems. Energies 2025, 18, 2531. [Google Scholar] [CrossRef]
- Chakraborty, S.; Singh, B.; Panigrahi, B.K.; Das, S.; Roy, S. DMROGI-mEPLL Based Position Sensorless Disturbance Immune Control of a Wind and Solar Energy Driven Microgrid Amidst Abnormal Grid. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024. [Google Scholar]
- Shanming, W.; Fang, W.; Shenghua, H. A Position Sensorless Control Method of Brushless Doubly Fed Independent Generator System. China Electr. Eng. J. 2016, 36, 1705–1713. [Google Scholar]
- Liu, Y.; Ai, W.; Chen, B.; Chen, K.; Luo, G. Control design and experimental verification of the brushless doubly-fed machine for stand-alone power generation applications. IET Electr. Power Appl. 2016, 10, 25–35. [Google Scholar] [CrossRef]
- Prasad, R.M.; Mulla, M.A. Rotor Position-Sensorless Algorithms for Direct Power Control of Rotor-Tied DFIG. IEEE Trans. Power Electron. 2021, 36, 6213–6217. [Google Scholar] [CrossRef]














| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Grid voltage (kV) | 18 | Stator resistance (Ω) | 0.001113 |
| Rated power (MW) | 300 | Stator leakage reactance (Ω) | 0.119 |
| Rated frequency (Hz) | 50 | Rotor resistance (Ω) | 0.001225 |
| DC bus voltage (V) | 7000 | Rotor leakage reactance (Ω) | 0.141 |
| Variable ratio | 0.4287 | Excitation reactance (Ω) | 2.468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Man, Z.; Tan, S.; Yan, W.; Lu, Y.; Tian, J.; Liu, W.; Wang, X. Model Reference Adaptive Sensorless Control of Variable-Speed Pumped Storage Doubly Fed Induction Machine Under Reversible Operations. Energies 2025, 18, 2998. https://doi.org/10.3390/en18112998
Zheng Z, Man Z, Tan S, Yan W, Lu Y, Tian J, Liu W, Wang X. Model Reference Adaptive Sensorless Control of Variable-Speed Pumped Storage Doubly Fed Induction Machine Under Reversible Operations. Energies. 2025; 18(11):2998. https://doi.org/10.3390/en18112998
Chicago/Turabian StyleZheng, Zhi, Ziqiang Man, Shuxin Tan, Wei Yan, Yu Lu, Jie Tian, Weiqun Liu, and Xu Wang. 2025. "Model Reference Adaptive Sensorless Control of Variable-Speed Pumped Storage Doubly Fed Induction Machine Under Reversible Operations" Energies 18, no. 11: 2998. https://doi.org/10.3390/en18112998
APA StyleZheng, Z., Man, Z., Tan, S., Yan, W., Lu, Y., Tian, J., Liu, W., & Wang, X. (2025). Model Reference Adaptive Sensorless Control of Variable-Speed Pumped Storage Doubly Fed Induction Machine Under Reversible Operations. Energies, 18(11), 2998. https://doi.org/10.3390/en18112998







