Thermodynamic and Process Modeling of CO2 Chemical Absorption Process Using Aqueous Monoethanolamine and Enzymatic Potassium Carbonate Solvents: Validation and Comparative Analysis
Abstract
1. Introduction
2. Method
2.1. Thermodynamic Framework
2.1.1. Chemical Equilibrium
2.1.2. Vapor–Liquid Equilibrium
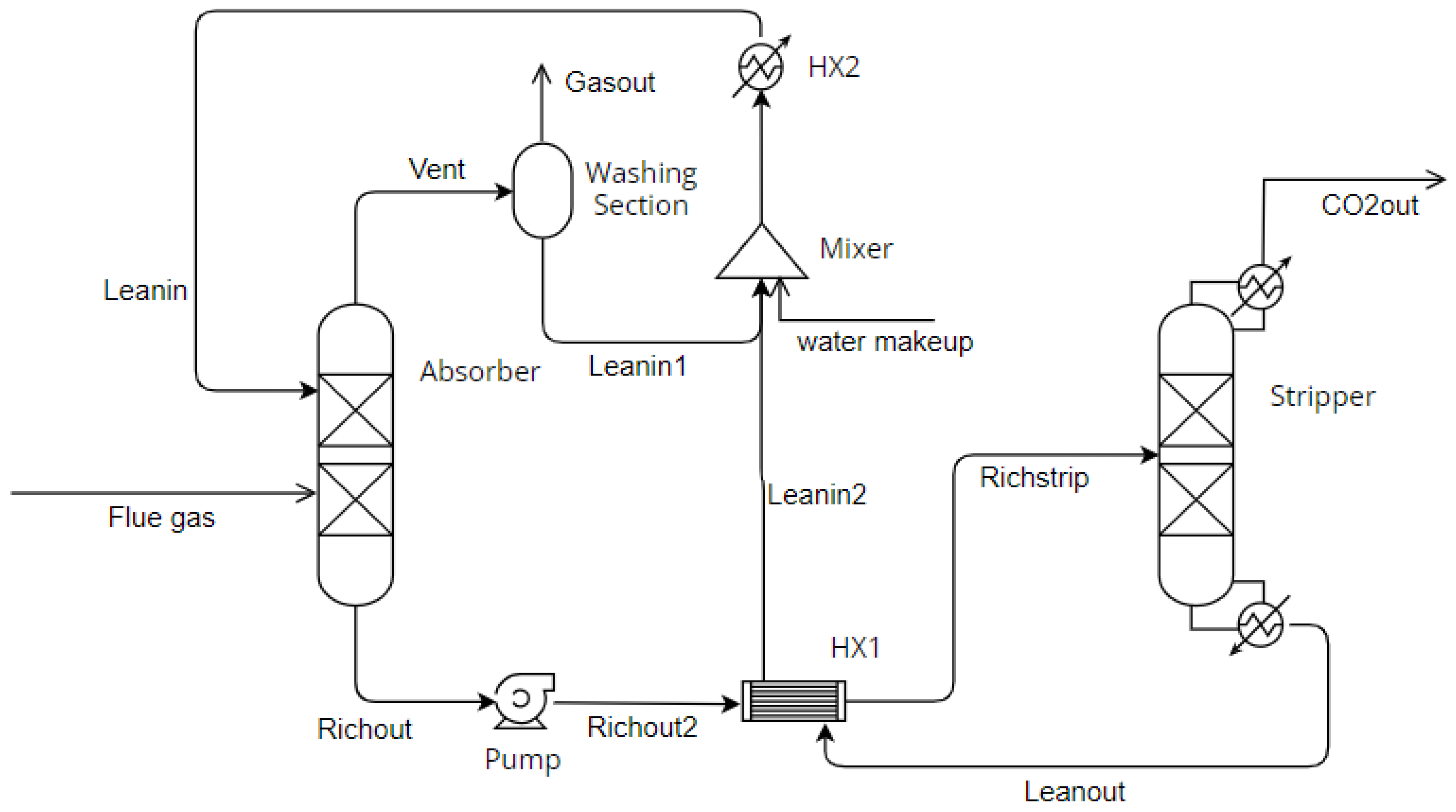
2.2. Process Simulation
3. Results and Discussion
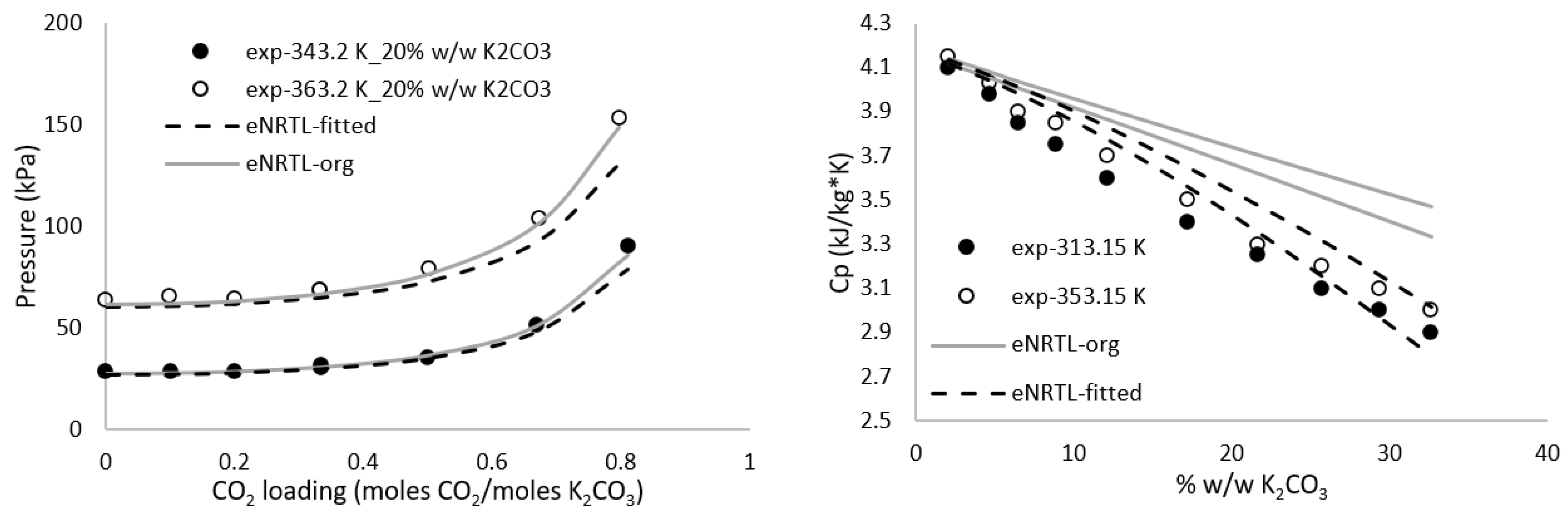
3.1. Thermodynamic Data Regression
| H2O-K2CO3 | ||||
|---|---|---|---|---|
| Reference | Data Type | Temperature (K) | Concentration (% w/w) | Average Absolute Deviation % |
| Roy et al. [63] | Osmotic coefficient | 298.15 | 0–30 | 4.2 |
| Mean ionic activity coefficient | 298.15 | 0–30 | 10.2 | |
| Hilliard et al. [37] | Heat capacity | 313.15–353.15 | 0–30 | 2.7 |
| H2O-KHCO3 | ||||
| Roy et al. [63] | Osmotic coefficient | 298.15 | 0–30 | 6.3 |
| Mean ionic activity coefficient | 298.15 | 0–30 | 31.2 | |
| Aseyev et al. [64] | Heat capacity | 283.15–378.15 | 0–30 | 13.9 |
| CO2-H2O-K2CO3 | ||||
| Kamps et al. [58] | TPxy | 313.2–353.1 | 5–20 | 21.6 |
| Tosh et al. [59] | TPxy | 343.15–383.15 | 20–30 | 10.5 |
| Jo et al. [65] | TPxy | 373.2 | 30 | 33.6 |
| Shen et al. [66] | TPxy | 313 | 30 | 15.6 |
| Endo et al. [67] | TPxy | 323.15–343.15 | 30 | 30.7 |
| Park et al. [68] | TPxy | 298.2–323.2 | 5–10 | 33.3 |
| MEA | ||||
|---|---|---|---|---|
| Reference | Data Type | Temperature (K) | Concentration (% w/w) | Average Absolute Deviation % |
| Kapteina et al. [69] | Heat of vaporization | 279–303.2 | 0.36 | |
| H2O-MEA | ||||
| Kim et al. [70] | TPxy | 313.15–373.15 | 0–78.9 | 0.95 |
| Hilliard et al. [37] | Heat capacity | 298.15–353.15 | 2.96–100 | 2.05 |
| CO2-H2O-MEA | ||||
| Jou et al. [61] | TPxy | 313.15–393.15 | 30 | 42.54 |
| Aronu et al. [25] | TPxy | 313.15–393.15 | 15–30 | 37.3 |
| Nakagaki et al. [24] | Heat capacity | 298.15–348.15 | 30 | 2.13 |
3.2. Process Model Validation
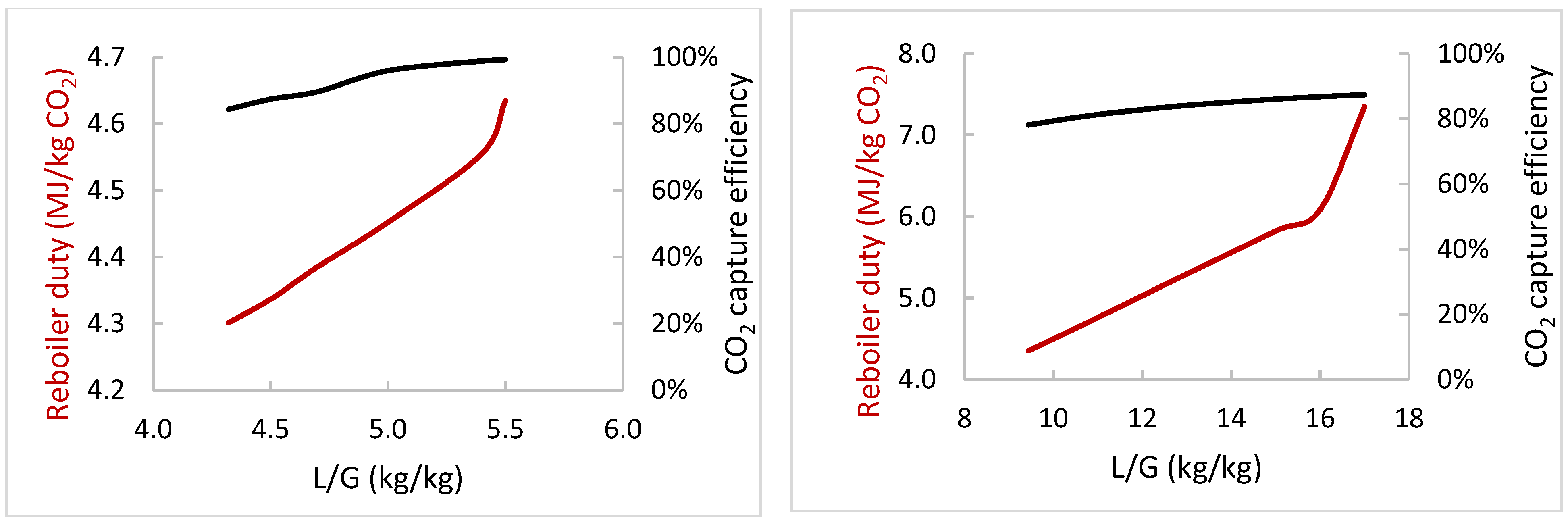
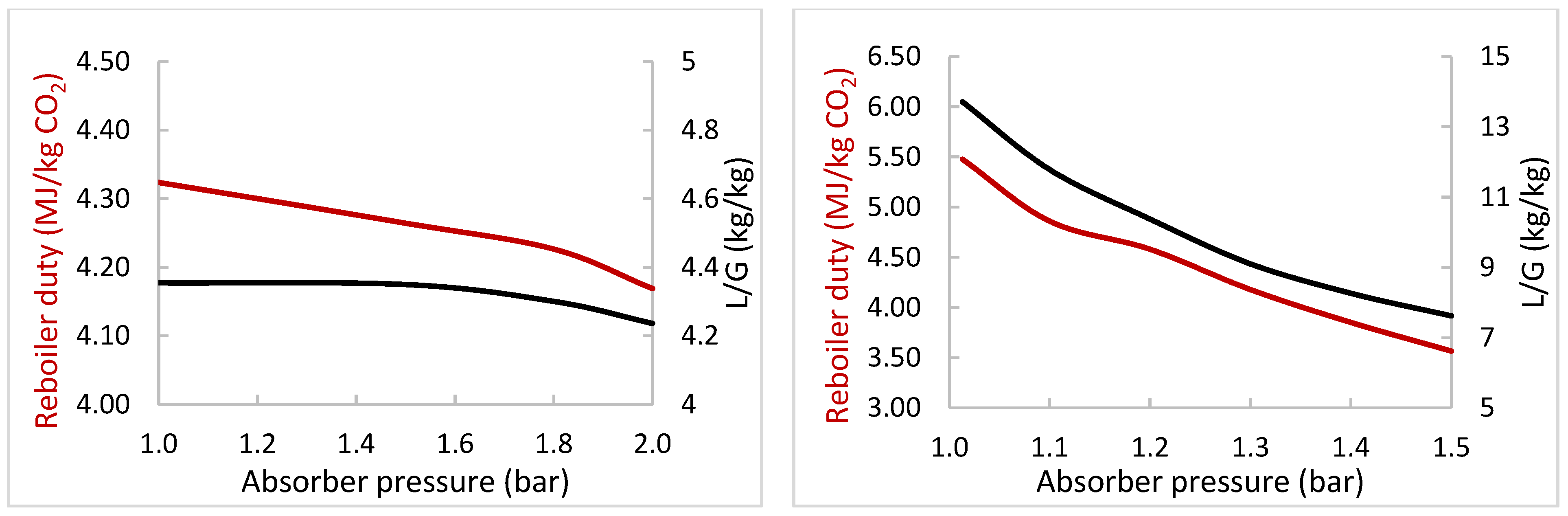
3.3. Comparison of Aqueous MEA and Enzymatic K2CO3 Solvents
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAD (%) | |
| CA | carbonic anhydrase |
| liquid phase fugacity | |
| excess Gibbs energy | |
| L/G | liquid to gas ratio (kg of solvent/kg of flue gas) |
| P | pressure |
| T | temperature |
| y | vapor phase mole fraction |
| x | liquid phase mole fraction |
| eNRTL | electrolyte Non-Random Two Liquid coefficient model |
| activity coefficient | |
| vapor phase fugacity coefficient |
References
- United Nations Climate Change. The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 2 April 2025).
- IPCC. Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [Google Scholar]
- European Commision. Energy Climate change, Environment, Causes of climate change. Available online: https://climate.ec.europa.eu/climate-change/causes-climate-change_en (accessed on 2 April 2025).
- Liu, H.; Lu, H.; Hu, H. CO2 capture and mineral storage: State of the art and future challenges. Renew. Sustain. Energy Rev. 2024, 189, 113908. [Google Scholar] [CrossRef]
- Li, B.-H.; Zhang, N.; Smith, R. Simulation and analysis of CO2 capture process with aqueous monoethanolamine solution. Appl. Energy 2016, 161, 707–717. [Google Scholar] [CrossRef]
- Mokhatab, S.; Poe, W.A.; Speight, J.G. Handbook of Natural Gas Transmission and Processing; Gulf Professional Publishing: Oxford, UK, 2012. [Google Scholar]
- Sadegh, N. Acid Gas Removal from Natural Gas with Alkanolamines: A Modeling and Experimental Study. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2013. [Google Scholar]
- Yang, H.; Xu, Z.; Fan, M.; Gupta, R.; Slimane, R.B.; Bland, A.E.; Wright, I. Progress in carbon dioxide separation and capture: A review. J. Environ. Sci. 2008, 20, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Nwaoha, C.; Saiwan, C.; Supap, T.; Idem, R.; Tontiwachwuthikul, P.; Rongwong, W.; Al-Marri, M.J.; Benamor, A. Carbon dioxide (CO2) capture performance of aqueous tri-solvent blends containing 2-amino-2-methyl-1-propanol (AMP) and methyldiethanolamine (MDEA) promoted by diethylenetriamine (DETA). Int. J. Greenh. Gas Control 2016, 53, 292–304. [Google Scholar] [CrossRef]
- Najafloo, A.; Zarei, S. Modeling solubility of CO2 in aqueous monoethanolamine (MEA) solution using SAFT-HR equation of state. Fluid Phase Equilib. 2018, 456, 25–32. [Google Scholar] [CrossRef]
- Gabrielsen, J.; Michelsen, M.L.; Stenby, E.H.; Kontogeorgis, G.M. Modeling of CO2 absorber using an AMP solution. AIChE J. 2006, 52, 3443–3451. [Google Scholar] [CrossRef]
- Qi, G.; Liu, K.; Frimpong, R.A.; House, A.; Salmon, S.; Liu, K. Integrated bench-scale parametric study on CO2 capture using a carbonic anhydrase promoted K2CO3 solvent with low temperature vacuum stripping. Ind. Eng. Chem. Res. 2016, 55, 12452–12459. [Google Scholar] [CrossRef]
- Business Analytiq. Price Trend Data & Tools to Create Benchmarks and Leading Indicators. Available online: https://businessanalytiq.com/ (accessed on 25 May 2025).
- Ghiat, I.; AlNouss, A.; Mckay, G.; Al-Ansari, T. Modelling and simulation of a biomass-based integrated gasification combined cycle with carbon capture: Comparison between monoethanolamine and potassium carbonate. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bangkok, Thailand, 11–14 December 2019; p. 012019. [Google Scholar]
- Kothandaraman, A.; Nord, L.; Bolland, O.; Herzog, H.J.; McRae, G.J. Comparison of solvents for post-combustion capture of CO2 by chemical absorption. Energy Procedia 2009, 1, 1373–1380. [Google Scholar] [CrossRef]
- Salmon, S.; House, A.; Liu, K.; Frimpong, R.; Liu, K.; Freeman, C.; Whyatt, G.; Slater, J.; Fitzgerald, D. Low-Energy Solvents for Carbon Dioxide Capture Enabled by a Combination of Enzymes and Vacuum Regeneration; Novozymes North America, Inc.: Franklinton, NC, USA, 2015. [Google Scholar]
- Zhang, S.; Lu, Y. Kinetic performance of CO2 absorption into a potassium carbonate solution promoted with the enzyme carbonic anhydrase: Comparison with a monoethanolamine solution. Chem. Eng. J. 2015, 279, 335–343. [Google Scholar] [CrossRef]
- Gabrielsen, J.; Michelsen, M.L.; Stenby, E.H.; Kontogeorgis, G.M. A Model for Estimating CO2 Solubility in Aqueous Alkanolamines. Ind. Eng. Chem. Res. 2005, 44, 3348–3354. [Google Scholar] [CrossRef]
- Kalatjari, H.R.; Haghtalab, A.; Nasr, M.R.J.; Heydarinasab, A. Experimental, simulation and thermodynamic modeling of an acid gas removal pilot plant for CO2 capturing by mono-ethanol amine solution. J. Nat. Gas Sci. Eng. 2019, 72, 103001. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M. Improving Prediction Accuracy of a Rate-Based Model of an MEA-Based Carbon Capture Process for Large-Scale Commercial Deployment. Engineering 2017, 3, 232–243. [Google Scholar] [CrossRef]
- Zhu, K.; Yue, C.; Wei, Z.; Huang, J.; Hu, M.; Ji, Y.; Liu, H.; Zhu, H.; Guo, W.; Zhou, F. Experimental and thermodynamic investigation on CO2 absorption in aqueous MEA solutions. Adv. Mater. Sci. Eng. 2022, 2022, 6278342. [Google Scholar] [CrossRef]
- Austgen, D.M.; Rochelle, G.T.; Peng, X.; Chen, C.C. Model of vapor-liquid equilibria for aqueous acid gas-alkanolamine systems using the electrolyte-NRTL equation. Ind. Eng. Chem. Res. 1989, 28, 1060–1073. [Google Scholar] [CrossRef]
- Zhang, Y.; Que, H.; Chen, C.-C. Thermodynamic modeling for CO2 absorption in aqueous MEA solution with electrolyte NRTL model. Fluid Phase Equilib. 2011, 311, 67–75. [Google Scholar] [CrossRef]
- Nakagaki, T.; Isogai, H.; Sato, H.; Arakawa, J. Updated e-NRTL model for high-concentration MEA aqueous solution by regressing thermodynamic experimental data at high temperatures. Int. J. Greenh. Gas Control 2019, 82, 117–126. [Google Scholar] [CrossRef]
- Aronu, U.E.; Gondal, S.; Hessen, E.T.; Haug-Warberg, T.; Hartono, A.; Hoff, K.A.; Svendsen, H.F. Solubility of CO2 in 15, 30, 45 and 60 mass% MEA from 40 to 120 °C and model representation using the extended UNIQUAC framework. Chem. Eng. Sci. 2011, 66, 6393–6406. [Google Scholar] [CrossRef]
- Darde, V.; Van Well, W.J.; Fosboel, P.L.; Stenby, E.H.; Thomsen, K. Experimental measurement and modeling of the rate of absorption of carbon dioxide by aqueous ammonia. Int. J. Greenh. Gas Control 2011, 5, 1149–1162. [Google Scholar] [CrossRef]
- Button, J.; Gubbins, K. SAFT prediction of vapour-liquid equilibria of mixtures containing carbon dioxide and aqueous monoethanolamine or diethanolamine. Fluid Phase Equilib. 1999, 158, 175–181. [Google Scholar] [CrossRef]
- Nasrifar, K.; Tafazzol, A. Vapor−Liquid Equilibria of Acid Gas−Aqueous Ethanolamine Solutions Using the PC-SAFT Equation of State. Ind. Eng. Chem. Res. 2010, 49, 7620–7630. [Google Scholar] [CrossRef]
- Téllez-Arredondo, P.; Medeiros, M. Modeling CO2 and H2S solubilities in aqueous alkanolamine solutions via an extension of the Cubic-Two-State equation of state. Fluid Phase Equilib. 2013, 344, 45–58. [Google Scholar] [CrossRef]
- Putta, K.R.; Svendsen, H.F.; Knuutila, H.K. CO2 absorption into loaded aqueous MEA solutions: Impact of different model parameter correlations and thermodynamic models on the absorption rate model predictions. Chem. Eng. J. 2017, 327, 868–880. [Google Scholar] [CrossRef]
- Moioli, S.; Nagy, T.; Langé, S.; Pellegrini, L.A.; Mizsey, P. Simulation model evaluation of CO2 capture by aqueous MEA scrubbing for heat requirement analyses. Energy Procedia 2017, 114, 1558–1566. [Google Scholar] [CrossRef]
- Borhani, T.N.G.; Akbari, V.; Hamid, M.K.A.; Manan, Z.A. Rate-based simulation and comparison of various promoters for CO2 capture in industrial DEA-promoted potassium carbonate absorption unit. J. Ind. Eng. Chem. 2015, 22, 306–316. [Google Scholar] [CrossRef]
- Imle, M.; Kumelan, J.; Speyer, D.; McCann, N.; Maurer, G.; Hasse, H. Solubility of carbon dioxide in activated potash solutions in the low and high gas loading regions. Ind. Eng. Chem. Res. 2013, 52, 13477–13489. [Google Scholar] [CrossRef]
- Bohloul, M.; Sadeghabadi, M.A.; Peyghambarzadeh, S.; Dehghani, M. CO2 absorption using aqueous solution of potassium carbonate: Experimental measurement and thermodynamic modeling. Fluid Phase Equilib. 2017, 447, 132–141. [Google Scholar] [CrossRef]
- Kaur, H.; Chen, C.-C. Thermodynamic modeling of CO2 absorption in aqueous potassium carbonate solution with electrolyte NRTL model. Fluid Phase Equilib. 2020, 505, 112339. [Google Scholar] [CrossRef]
- Lee, A.; Mumford, K.A.; Wu, Y.; Nicholas, N.; Stevens, G.W. Understanding the vapour–liquid equilibrium of CO2 in mixed solutions of potassium carbonate and potassium glycinate. Int. J. Greenh. Gas Control 2016, 47, 303–309. [Google Scholar] [CrossRef]
- Hilliard, M.D. A Predictive Thermodynamic Model for an Aqueous Blend of Potassium Carbonate, Piperazine, and Monoethanolamine for Carbon Dioxide Capture from Flue Gas. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Cullinane, J.T.; Rochelle, G.T. Thermodynamics of aqueous potassium carbonate, piperazine, and carbon dioxide. Fluid Phase Equilib. 2005, 227, 197–213. [Google Scholar] [CrossRef]
- Fosbøl, P.L.; Maribo-Mogensen, B.; Thomsen, K. Solids modelling and capture simulation of piperazine in potassium solvents. Energy Procedia 2013, 37, 844–859. [Google Scholar] [CrossRef]
- Rochelle, G.T.; Chen, E.; Oyenekan, B.; Sexton, A.; Davis, J.; Hilliard, M.; Veawab, A. CO2 Capture by Absorption with Potassium Carbonate; The University of Texas at Austin: Austin, TX, USA, 2003. [Google Scholar]
- Neveux, T.; Le Moullec, Y.; Corriou, J.-P.; Favre, E. Modeling CO2 capture in amine solvents: Prediction of performance and insights on limiting phenomena. Ind. Eng. Chem. Res. 2013, 52, 4266–4279. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.-C. Modeling CO2 absorption and desorption by aqueous monoethanolamine solution with Aspen rate-based model. Energy Procedia 2013, 37, 1584–1596. [Google Scholar] [CrossRef]
- Garcia, M.; Knuutila, H.K.; Gu, S. ASPEN PLUS simulation model for CO2 removal with MEA: Validation of desorption model with experimental data. J. Environ. Chem. Eng. 2017, 5, 4693–4701. [Google Scholar] [CrossRef]
- Smith, K.; Lee, A.; Mumford, K.; Li, S.; Thanumurthy, N.; Temple, N.; Anderson, C.; Hooper, B.; Kentish, S.; Stevens, G. Pilot plant results for a precipitating potassium carbonate solvent absorption process promoted with glycine for enhanced CO2 capture. Fuel Process. Technol. 2015, 135, 60–65. [Google Scholar] [CrossRef]
- Quyn, D.; Rayer, A.V.; Gouw, J.; Indrawan, I.; Mumford, K.A.; Anderson, C.J.; Hooper, B.; Stevens, G.W. Results from a pilot plant using un-promoted potassium carbonate for carbon capture. Energy Procedia 2013, 37, 448–454. [Google Scholar] [CrossRef]
- Mumford, K.A.; Smith, K.H.; Anderson, C.J.; Shen, S.; Tao, W.; Suryaputradinata, Y.A.; Qader, A.; Hooper, B.; Innocenzi, R.A.; Kentish, S.E. Post-combustion capture of CO2: Results from the solvent absorption capture plant at Hazelwood power station using potassium carbonate solvent. Energy Fuels 2012, 26, 138–146. [Google Scholar] [CrossRef]
- Aspen Technology Inc. Aspen Plus V11; Aspen Technology Inc.: Cambridge, MA, USA, 2020. [Google Scholar]
- Hilliard, M.D.; Rochelle, G.T. Thermodynamics of aqueous piperazine/potassium carbonate/carbon dioxide chare cterized by the electrolyte non-random two-liquid model in aspen plus. In Greenhouse Gas Control Technologies 7; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1975–1978. [Google Scholar]
- Arshad, M.; Wukovits, W.; Friedl, A. Simulation of CO2 absorption using the system K2CO3-piperazine. Chem. Eng. 2014, 39, 577–582. [Google Scholar]
- Redlich, O.; Kwong, J.N. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Chen, C.C.; Evans, L.B. A local composition model for the excess Gibbs energy of aqueous electrolyte systems. AIChE J. 1986, 32, 444–454. [Google Scholar] [CrossRef]
- Mangalapally, H.P.; Hasse, H. Pilot plant study of post-combustion carbon dioxide capture by reactive absorption: Methodology, comparison of different structured packings, and comprehensive results for monoethanolamine. Chem. Eng. Res. Des. 2011, 89, 1216–1228. [Google Scholar] [CrossRef]
- Frailie, P.T.; Rochelle, G.T. Kinetics of Aqueous Methyldiethanolamine/Piperazine for CO2 Capture. In Process Systems and Materials for CO2 Capture: Modelling, Design, Control and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 137–152. [Google Scholar]
- Ye, X.; Lu, Y. CO2 absorption into catalyzed potassium carbonate–bicarbonate solutions: Kinetics and stability of the enzyme carbonic anhydrase as a biocatalyst. Chem. Eng. Sci. 2014, 116, 567–575. [Google Scholar] [CrossRef]
- Zaks, A.; Reardon, J. Advanced Low Energy Enzyme Catalyzed Solvent for CO2 Capture; Akermin Inc.: St. Louis, MO, USA, 2013. [Google Scholar]
- Hikita, H.; Asai, S.; Ishikawa, H.; Honda, M. The kinetics of reactions of carbon dioxide with monoethanolamine, diethanolamine and triethanolamine by a rapid mixing method. Chem. Eng. J. 1977, 13, 7–12. [Google Scholar] [CrossRef]
- Pinsent, B.; Pearson, L.; Roughton, F. The kinetics of combination of carbon dioxide with hydroxide ions. Trans. Faraday Society 1956, 52, 1512–1520. [Google Scholar] [CrossRef]
- Pérez-Salado Kamps, Á.; Meyer, E.; Rumpf, B.; Maurer, G. Solubility of CO2 in aqueous solutions of KCl and in aqueous solutions of K2CO3. J. Chem. Eng. Data 2007, 52, 817–832. [Google Scholar] [CrossRef]
- Tosh, J.S.; Field, J.H.; Benson, H.E.; Anderson, R.B. Equilibrium Pressures of Hydrogen Sulfide and Carbon Dioxide over Solutions of Potassium Carbonate; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1960; Volume 5622.
- Lee, J.I.; Otto, F.D.; Mather, A.E. Equilibrium between carbon dioxide and aqueous monoethanolamine solutions. J. Appl. Chem. Biotechnol. 1976, 26, 541–549. [Google Scholar] [CrossRef]
- Jou, F.Y.; Mather, A.E.; Otto, F.D. The solubility of CO2 in a 30 mass percent monoethanolamine solution. Can. J. Chem. Eng. 1995, 73, 140–147. [Google Scholar] [CrossRef]
- de Oliveira Maciel, A.; Christakopoulos, P.; Rova, U.; Antonopoulou, I. Carbonic anhydrase to boost CO2 sequestration: Improving carbon capture utilization and storage (CCUS). Chemosphere 2022, 299, 134419. [Google Scholar] [CrossRef]
- Roy, R.N.; Gibbons, J.J.; Williams, R.; Godwin, L.; Baker, G.; Simonson, J.M.; Pitzer, K.S. The thermodynamics of aqueous carbonate solutions II. Mixtures of potassium carbonate, bicarbonate, and chloride. J. Chem. Thermodyn. 1984, 16, 303–315. [Google Scholar] [CrossRef]
- Aseyev, G. Electrolytes: Equilibria in Solutions and Phase Equilibria; Begell House: Danbury, CT, USA, 1999. [Google Scholar]
- Jo, H.; Lee, M.-g.; Kim, B.; Song, H.-J.; Gil, H.; Park, J. Density and solubility of CO2 in aqueous solutions of (potassium carbonate + sarcosine) and (potassium carbonate + pipecolic acid). J. Chem. Eng. Data 2012, 57, 3624–3627. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Y.-n.; Wang, Y.; Ren, S.; Han, J.; Chen, A. CO2 absorption into aqueous potassium salts of lysine and proline: Density, viscosity and solubility of CO2. Fluid Phase Equilib. 2015, 399, 40–49. [Google Scholar] [CrossRef]
- Endo, K.; Nguyen, Q.S.; Kentish, S.E.; Stevens, G.W. The effect of boric acid on the vapour liquid equilibrium of aqueous potassium carbonate. Fluid Phase Equilib. 2011, 309, 109–113. [Google Scholar] [CrossRef]
- Park, S.-B.; Shim, C.-S.; Lee, H.; Lee, K.-H. Solubilities of carbon dioxide in the aqueous potassium carbonate and potassium carbonate poly (ethylene glycol) solutions. Fluid Phase Equilib. 1997, 134, 141–149. [Google Scholar] [CrossRef]
- Kapteina, S.; Slowik, K.; Verevkin, S.P.; Heintz, A. Vapor pressures and vaporization enthalpies of a series of ethanolamines. J. Chem. Eng. Data 2005, 50, 398–402. [Google Scholar] [CrossRef]
- Kim, I.; Svendsen, H.F.; Børresen, E. Ebulliometric determination of vapor− liquid equilibria for pure water, monoethanolamine, n-methyldiethanolamine, 3-(methylamino)-propylamine, and their binary and ternary solutions. J. Chem. Eng. Data 2008, 53, 2521–2531. [Google Scholar] [CrossRef]
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1993; Volume 2. [Google Scholar]
- Onda, K.; Takeuchi, H.; Okumoto, Y. Mass transfer coefficients between gas and liquid phases in packed columns. J. Chem. Eng. Japan 1968, 1, 56–62. [Google Scholar] [CrossRef]
- Stichlmair, J.; Bravo, J.; Fair, J. General model for prediction of pressure drop and capacity of countercurrent gas/liquid packed columns. Gas Sep. Purif. 1989, 3, 19–28. [Google Scholar] [CrossRef]
- Pinto, D.; Monteiro, J.; Skylogianni, E.; Moser, P.; Wiechers, G. Validation of process simulator with new plant data for MEA and CESAR1. In Proceedings of the 16th Greenhouse Gas Control Technologies Conference (GHGT-16), Lyon, France, 23–27 October 2022; pp. 23–24. [Google Scholar]
- Plus, A. Rate Based Model of the CO2 Capture Process by MEA Using Aspen Plus; Aspen Technology Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
- Zhang, Y.; Chen, H.; Chen, C.-C.; Plaza, J.M.; Dugas, R.; Rochelle, G.T. Rate-based process modeling study of CO2 capture with aqueous monoethanolamine solution. Ind. Eng. Chem. Res. 2009, 48, 9233–9246. [Google Scholar] [CrossRef]
- Bravo, J.e.L.; Rocha, J.A.; Fair, J.R. Mass transfer in gauze packings. Hydrocarbon Process. 1985, 64, 91–95. [Google Scholar]
- Flø, N.E.; Knuutila, H.; Kvamsdal, H.M.; Hillestad, M. Dynamic model validation of the post-combustion CO2 absorption process. Int. J. Greenh. Gas Control 2015, 41, 127–141. [Google Scholar]
- Chuenphan, T.; Yurata, T.; Sema, T.; Chalermsinsuwan, B. Techno-economic sensitivity analysis for optimization of carbon dioxide capture process by potassium carbonate solution. Energy 2022, 254, 124290. [Google Scholar] [CrossRef]
- Kothandaraman, A. Carbon Dioxide Capture by Chemical Absorption: A Solvent Comparison Study. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]


| Reaction | k | n | E (cal/mol) | CA (g/L) |
|---|---|---|---|---|
| 19 | 4.32 × 1013 | 0 | 13249 | 0 |
| 20 | 2.38 × 1017 | 0 | 29451 | 0 |
| 19 | 4.23 × 1013 | 0 | 8737 | 1 |
| 20 | 2.1744 × 109 | 3.0638 | 24937 | 1 |
| 19 | 4.32 × 1013 | 0 | 7950 | 4 |
| 20 | 3.57 × 1018 | 0 | 26473 | 4 |
| Reaction | k | E (cal/mol) |
|---|---|---|
| 21 | 9.77 × 1010 | 9855.8 |
| 22 | 3.23 × 1019 | 15655 |
| 23 | 4.32 × 1013 | 13249 |
| 24 | 2.38 × 1017 | 29451 |
| Exp | Ref. | CA (g/L) | Lean Loading (mol CO2/mol K2CO3) | L/G (kg/kg) | Exp_CO2 Absorption (%) | Exp_Reboiler Duty (MJ/kg) | AAD_CO2 Absorption (%) | AAD_Reboiler Duty (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | [45] | 0 | 0.08 | 4 | 10.9 | - | 25.1 | |
| 2 | [45] | 0 | 0.09 | 6 | 14.1 | - | 3.1 | |
| 3 | [45] | 0 | 0.08 | 4 | 11.4 | - | 35.4 | |
| 4 | [45] | 0 | 0.10 | 4 | 11.0 | - | 13.1 | |
| 5 | [45] | 0 | 0.14 | 4 | 12.7 | - | 7.5 | |
| 6 | [16] | 1 | 0.32 | 9.4 | 69.0 | 6.8 | 10.5 | 28.3 |
| 7 | [16] | 1 | 0.32 | 15.8 | 72.0 | 7.3 | 0.8 | 12.1 |
| 8 | [16] | 4 | 0.30 | 9.4 | 84.0 | 6.2 | 6.8 | 31.0 |
| 9 | [16] | 4 | 0.30 | 15.7 | 83.0 | 6.5 | 4.4 | 8.3 |
| Average | 11.8 | 19.9 |
| Exp | Ref. | Lean Loading (mol_CO2/mol MEA) | L/G (kg/kg) | Exp_CO2 Absorption (%) | Exp Reboiler Duty (MJ/kg) | AAD_CO2 Absorption (%) | AAD_Reboiler Duty (%) |
|---|---|---|---|---|---|---|---|
| 1 | [16] | 0.300 | 7.79 | 93.6 | 5.9 | 6.4 | 17.0 |
| 2 | [52] | 0.205 | 1.31 | 90.5 | 4.7 | 0.4 | 21.0 |
| 3 | [52] | 0.259 | 1.97 | 90.5 | 5.1 | 0.4 | 5.1 |
| 4 | [52] | 0.25 | 2.64 | 89.7 | 5.7 | 2.7 | 13.0 |
| 5 | [52] | 0.276 | 2.61 | 89.9 | 5.6 | 1.0 | 3.8 |
| 6 | [52] | 0.23 | 3.49 | 87.9 | 5.0 | 6.4 | 24.4 |
| 7 | [52] | 0.23 | 2.46 | 93.0 | 4.4 | 0.2 | 14.4 |
| 8 | [52] | 0.208 | 2.49 | 90.7 | 4.4 | 5.2 | 3.6 |
| 9 | [52] | 0.222 | 1.30 | 87.9 | 5.1 | 5.6 | 16.1 |
| 10 | [52] | 0.204 | 1.30 | 91.4 | 4.7 | 3.0 | 12.5 |
| Average | 3.1 | 13.1 |
| Parameter | Value |
|---|---|
| Flue gas flow rate (kg/h) | 2.31 |
| CO2 flue gas (vol%) | 14.8 |
| Flue gas temperature (°C) | 41.3 |
| Solvent temperature (°C) | 39.4 |
| MEA Solvent | |
| MEA wt% in solvent | 30 |
| Lean loading (mol CO2/kg MEA) | 0.005 |
| Absorber pressure (bar) | 1 |
| Stripper pressure (bar) | 1.22 |
| Stripper temperature (°C) | 100 |
| K2CO3 Solvent | |
| K2CO3 wt% in solvent | 23.5 |
| Lean loading (mol CO2/kg K2CO3) | 0.002 |
| Absorber pressure (bar) | 1 |
| Stripper pressure (bar) | 0.35 |
| Stripper temperature (°C) | 65 |
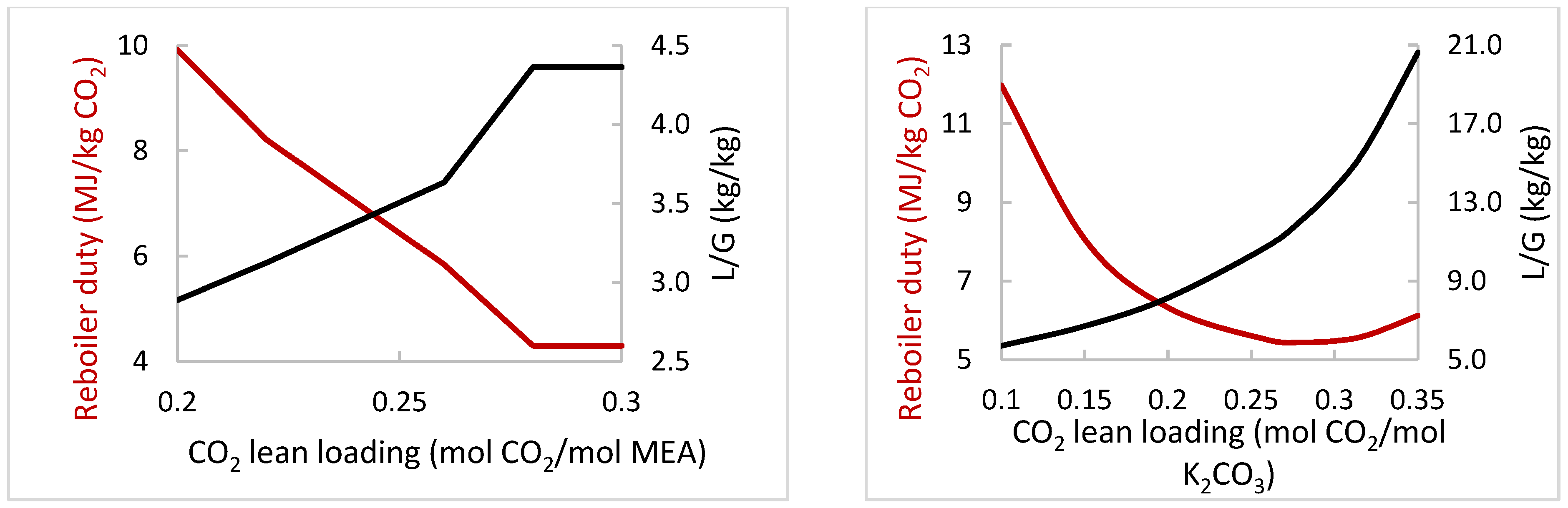
| Variation Study | Varied Operating Parameter | Range of Variation for the Two Solvents | Key Performance Indicators | Most Important Constant Parameters |
|---|---|---|---|---|
| A | L/G (kg/kg) | MEA: 4.3–5.5, K2CO3: 9.4–17 | % CO2 capture, Qreb | Flue gas flow and composition, flue gas and lean solvent temperature, CO2 lean loading, Pabs/strip |
| B | Pabs (bar) | MEA: 1–2, K2CO3: 1–1.5 | Qreb | % CO2 capture, flue gas flow and composition, flue gas and lean solvent temperature, CO2 lean loading, Pstrip |
| C | Pstrip (bar) | MEA: 1–1.5, K2CO3: 0.25–0.5 | Qreb | % CO2 capture, flue gas flow and composition, flue gas and lean solvent temperature, CO2 lean loading, Pabs |
| D | Lean loading (mol CO2/mol Solvent) | MEA: 0.2–0.3, K2CO3: 0.1–0.35 | Qreb | % CO2 capture, flue gas flow and composition, flue gas and lean solvent temperature, Pabs/strip |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plakia, A.; Papaioannou, C.; Grammelis, P. Thermodynamic and Process Modeling of CO2 Chemical Absorption Process Using Aqueous Monoethanolamine and Enzymatic Potassium Carbonate Solvents: Validation and Comparative Analysis. Energies 2025, 18, 2981. https://doi.org/10.3390/en18112981
Plakia A, Papaioannou C, Grammelis P. Thermodynamic and Process Modeling of CO2 Chemical Absorption Process Using Aqueous Monoethanolamine and Enzymatic Potassium Carbonate Solvents: Validation and Comparative Analysis. Energies. 2025; 18(11):2981. https://doi.org/10.3390/en18112981
Chicago/Turabian StylePlakia, Anthoula, Christina Papaioannou, and Panagiotis Grammelis. 2025. "Thermodynamic and Process Modeling of CO2 Chemical Absorption Process Using Aqueous Monoethanolamine and Enzymatic Potassium Carbonate Solvents: Validation and Comparative Analysis" Energies 18, no. 11: 2981. https://doi.org/10.3390/en18112981
APA StylePlakia, A., Papaioannou, C., & Grammelis, P. (2025). Thermodynamic and Process Modeling of CO2 Chemical Absorption Process Using Aqueous Monoethanolamine and Enzymatic Potassium Carbonate Solvents: Validation and Comparative Analysis. Energies, 18(11), 2981. https://doi.org/10.3390/en18112981







