Experiment and Simulation of the Non-Catalytic Reforming of Biomass Gasification Producer Gas for Syngas Production
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Setup and Procedure
2.3. Modeling and Numerical Methods
2.3.1. Ideal Plug Flow Reactor Modeling and Optimization
- (1)
- Within the reactor, there is no axial back-mixing, and the state (temperature, composition, flow rate, etc.) is a function of the axial position alone, with no radial distribution;
- (2)
- All gaseous compounds have ideal gas behavior;
- (3)
- The thermal effect of the reactions has a negligible effect on the temperature profile along the reactor depth;
- (4)
- Pressure was uniform inside the reactor;
- (5)
- Soot is considered a gas-phase component in the reaction;
- (6)
- The process was in a steady state;
- (7)
- Tar composition was assumed to be C6H6, C6H6O, C7H8, and C10H8;
- (8)
- Arrhenius kinetics were considered for each reaction.
2.3.2. Data Evaluation
2.3.3. Sensitivity Analysis
3. Results and Discussion
3.1. Effect of Reaction Temperature on the Model Producer Gas Reforming
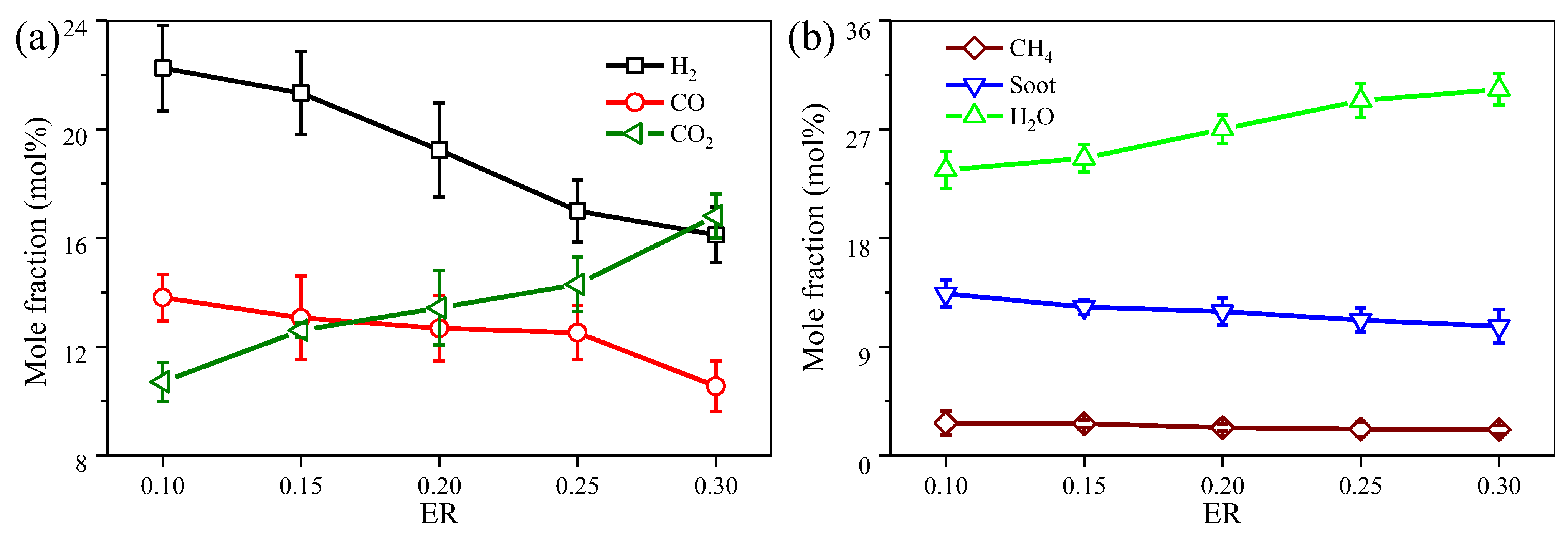
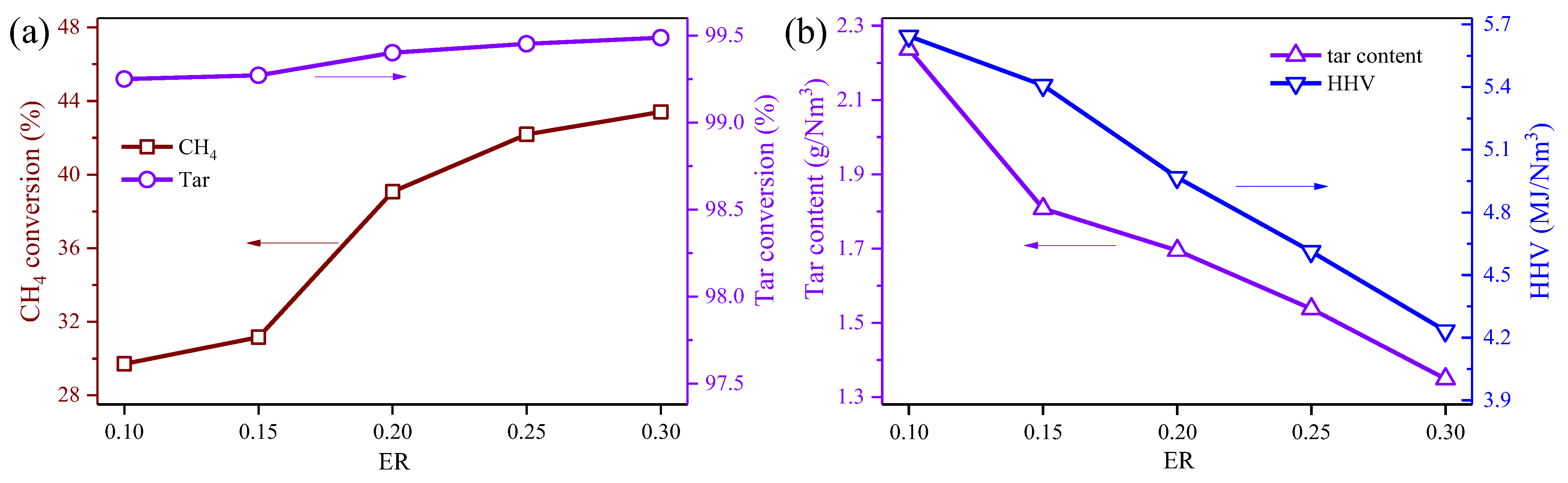
3.2. Effect of ER on the Medel Producer Gas Reforming
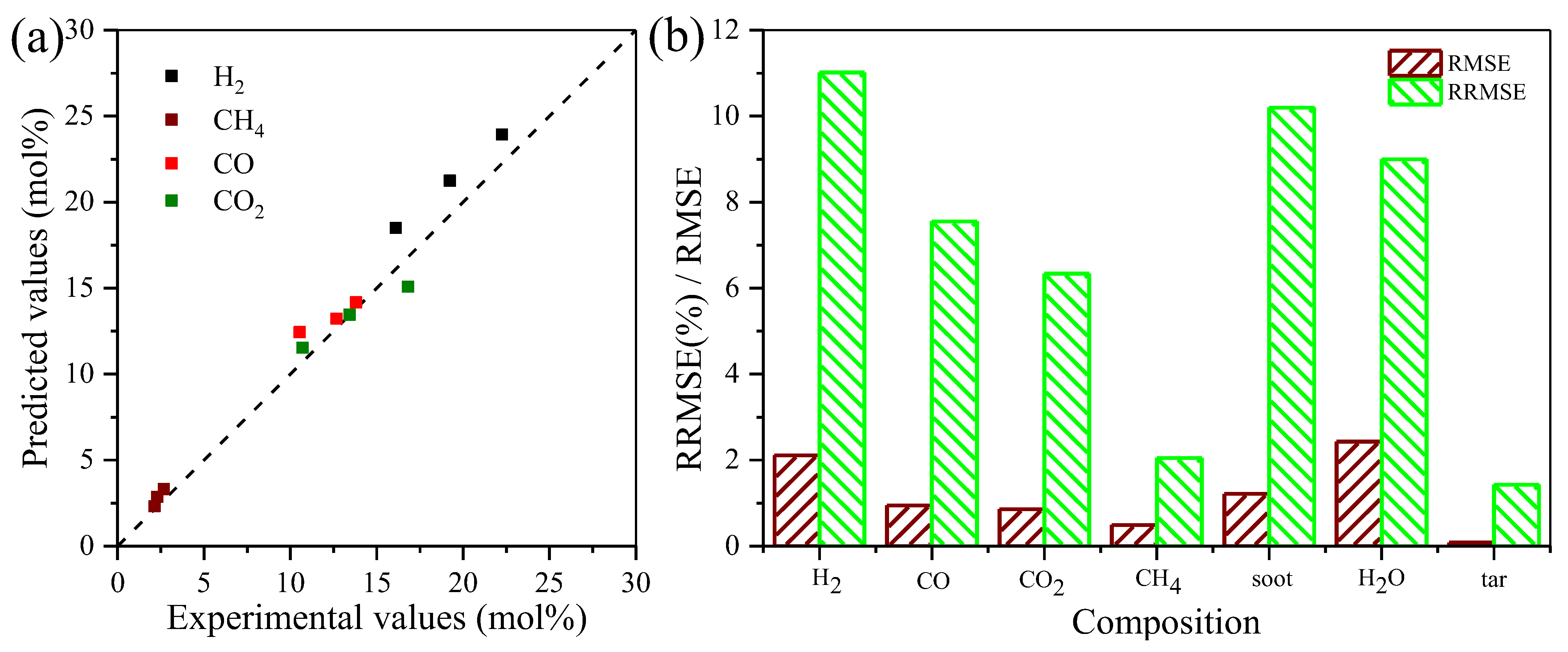
3.3. Calibration and Evaluation of the Kinetic Model
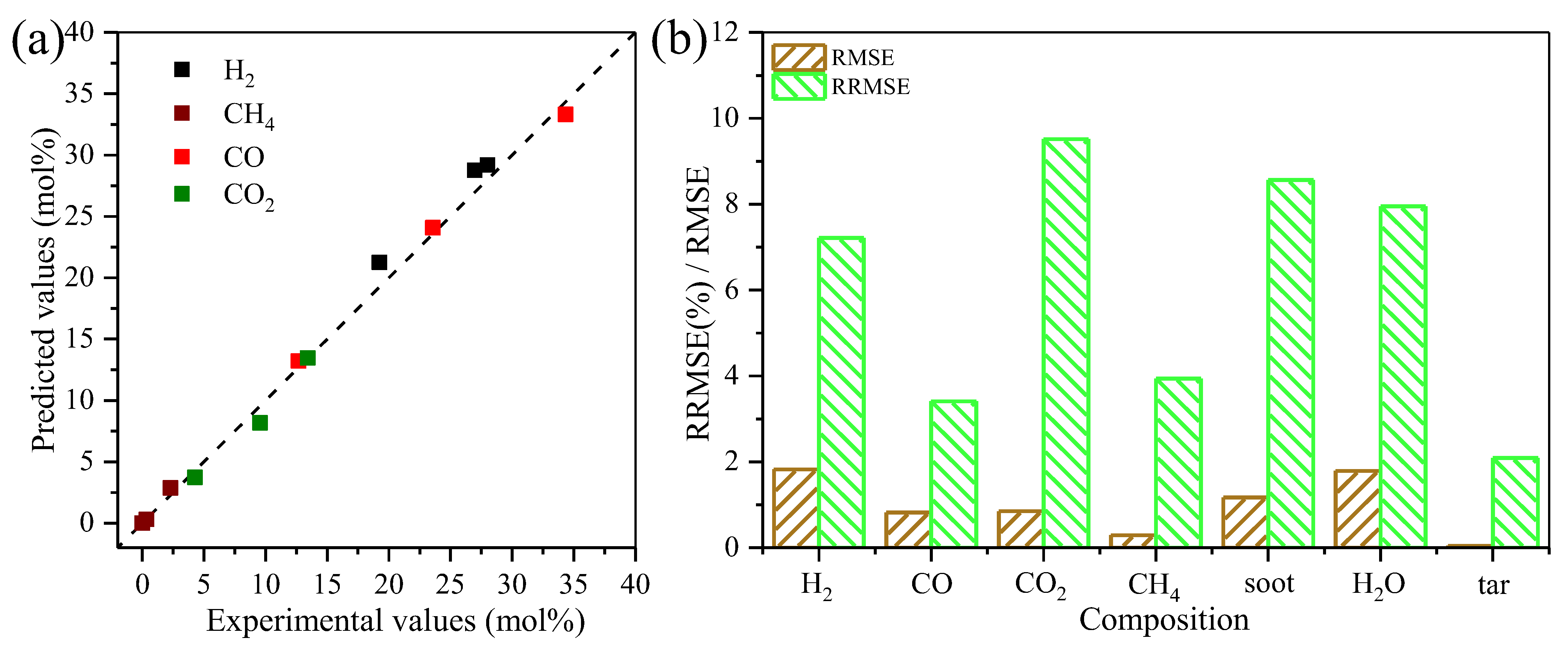
3.3.1. Kinetic Model Calibration and Validation
3.3.2. Evaluation of the Effect of Temperature on the Model Producer Gas Reforming
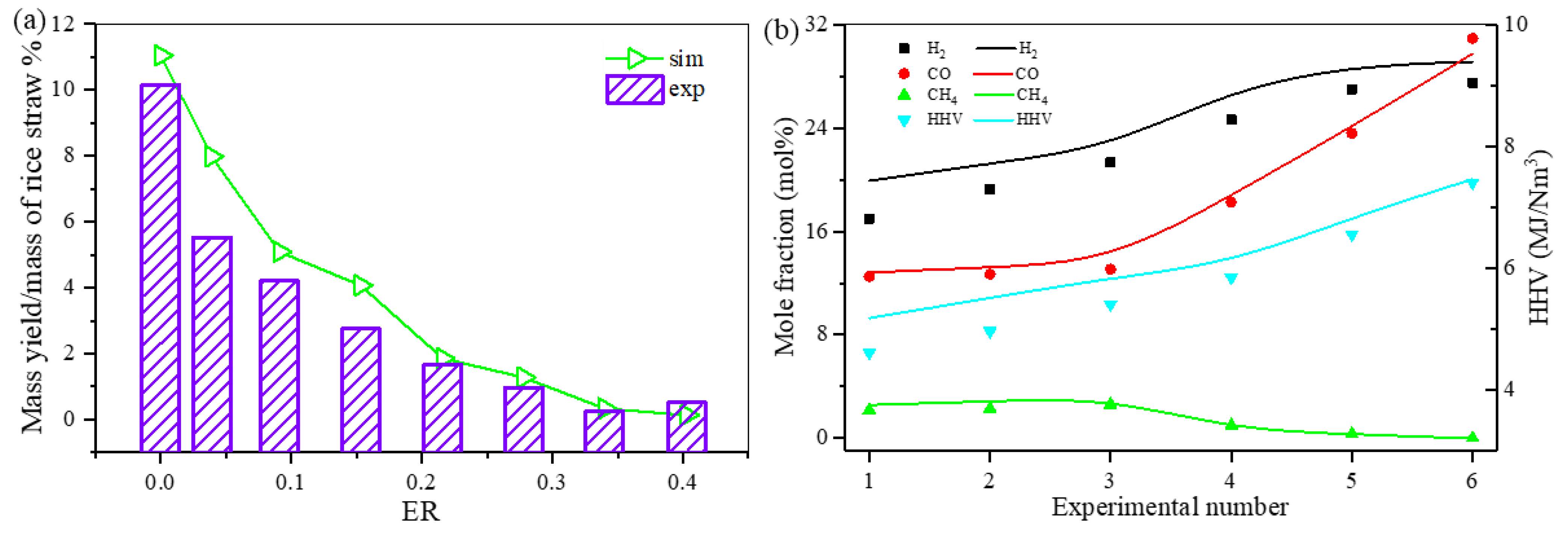
3.3.3. Evaluation of the Effect of ER on the Model Producer Gas Reforming
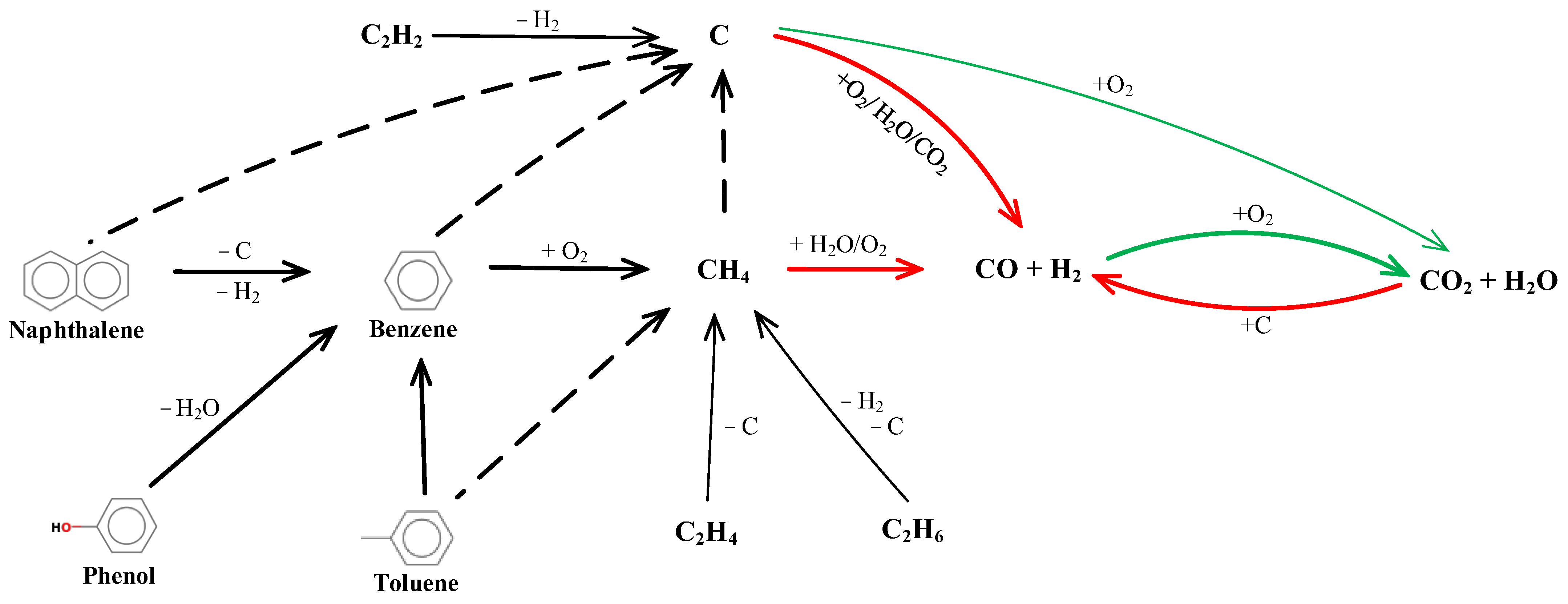
3.4. Proposed Reaction Pathways
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Renewable Energy Agency. Available online: https://www.irena.org/Publications/2024/Jul/Renewable-energy-statistics-2024 (accessed on 7 May 2025).
- Mtshali, B.; Kassim, A.; Sibanda, S.; Workneh, T. Characterization of South African Woody and Non-Woody Invasive Alien Plant Species for Sustainable Bio-Oil Production. Energies 2025, 18, 1919. [Google Scholar] [CrossRef]
- Kim, S.; Yoon, S.; Zulqarnain; Yoo, J.; Im, H.; Kim, S.; Chun, D.; Choi, H.; Lim, J. Steam Reforming of High-Concentration Toluene as a Model Biomass Tar Using a Nickel Catalyst Supported on Carbon Black. Energies 2025, 18, 327. [Google Scholar] [CrossRef]
- Talero, G.; Kansha, Y. Atom economy or product yield to determine optimal gasification conditions in biomass-to-olefins biorefinery. Chem. Eng. Res. Des. 2023, 199, 689–699. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Liang, W.; Cao, G.; Li, C.; Zhao, J.; Fang, Y. Kinetic Analysis of Biomass Gasification Coupled with Non-Catalytic Reforming to Syngas Production. J. Fuel Chem. Technol. 2023, 51, 921–929. [Google Scholar]
- Errekatxo, A.; Ibarra, A.; Gutierrez, A.; Bilbao, J.; Arandes, J.M.; Castaño, P. Catalytic deactivation pathways during the cracking of glycerol and glycerol/VGO blends under FCC unit conditions. Chem. Eng. J. 2017, 307, 955–965. [Google Scholar] [CrossRef]
- Anis, S.; Zainal, Z.A. Tar reduction in biomass producer gas via mechanical, catalytic and thermal methods: A review. Renew. Sustain. Energy Rev. 2011, 15, 2355–2377. [Google Scholar] [CrossRef]
- Tian, Y.; Du, J.; Luo, Z.; He, D.; Ma, W.; Zhou, X.; Liang, S.; Yuan, L. Kinetic study on biomass gasification coupled with tar reforming for syngas production. Biomass Convers. Biorefinery 2023, 14, 28377–28385. [Google Scholar] [CrossRef]
- Su, Y.; Luo, Y.; Chen, Y.; Wu, W.; Zhang, Y. Experimental and numerical investigation of tar destruction under partial oxidation environment. Fuel Process. Technol. 2011, 92, 1513–1524. [Google Scholar] [CrossRef]
- Demol, R.; Ruiz, M.; Schnitzer, A.; Herbinet, O.; Mauviel, G. Experimental and modeling investigation of partial oxidation of gasification tars. Fuel 2023, 351, 128990. [Google Scholar] [CrossRef]
- Wongchang, T.; Patumsawad, S.; Fungtammasan, B. An analysis of wood pyrolysis tar from high temperature thermal cracking process. Energy Sources Part A Recovery Util. Environ. Eff. 2013, 35, 926–935. [Google Scholar] [CrossRef]
- Qin, K.; Lin, W.; Jensen, P.A.; Jensen, A.D. High-temperature entrained flow gasification of biomass. Fuel 2012, 93, 589–600. [Google Scholar] [CrossRef]
- Ahrenfeldt, J.; Egsgaard, H.; Stelte, W.; Thomsen, T.; Henriksen, U.B. The influence of partial oxidation mechanisms on tar destruction in TwoStage biomass gasification. Fuel 2013, 112, 662–680. [Google Scholar] [CrossRef]
- Lapuerta, M.; Hernández, J.J.; Pazo, A.; López, J. Gasification and co-gasification of biomass wastes: Effect of the biomass origin and the gasifier operating conditions. Fuel Process. Technol. 2008, 89, 828–837. [Google Scholar] [CrossRef]
- Sittisun, P.; Tippayawong, N.; Pang, S. Biomass gasification in a fixed bed downdraft reactor with oxygen enriched air: A modified equilibrium modeling study. Energy Procedia 2019, 160, 317–323. [Google Scholar] [CrossRef]
- Martínez, J.D.; Silva Lora, E.E.; Andrade, R.V.; Jaén, R.L. Experimental study on biomass gasification in a double air stage downdraft reactor. Biomass Bioenergy 2011, 35, 3465–3480. [Google Scholar] [CrossRef]
- Jaojaruek, K.; Jarungthammachote, S.; Gratuito, M.K.; Wongsuwan, H.; Homhual, S. Experimental study of wood downdraft gasification for an improved producer gas quality through an innovative two-stage air and premixed air/gas supply approach. Bioresour. Technol. 2011, 102, 4834–4840. [Google Scholar] [CrossRef]
- Puig-Gamero, M.; Pio, D.T.; Tarelho, L.A.C.; Sánchez, P.; Sanchez-Silva, L. Simulation of biomass gasification in bubbling fluidized bed reactor using aspen plus®. Energy Convers. Manag. 2021, 235, 113981. [Google Scholar] [CrossRef]
- Martínez González, A.; Silva Lora, E.E.; Escobar Palacio, J.C.; Almazán del Olmo, O.A. Hydrogen production from oil sludge gasification/biomass mixtures and potential use in hydrotreatment processes. Int. J. Hydrogen Energy 2018, 43, 7808–7822. [Google Scholar] [CrossRef]
- Champion, W.M.; Cooper, C.D.; Mackie, K.R.; Cairney, P. Development of a chemical kinetic model for a biosolids fluidized-bed gasifier and the effects of operating parameters on syngas quality. J. Air Waste Manag. Assoc. 2013, 64, 160–174. [Google Scholar] [CrossRef]
- Eri, Q.; Peng, J.; Zhao, X. CFD simulation of biomass steam gasification in a fluidized bed based on a multi-composition multi-step kinetic model. Appl. Therm. Eng. 2018, 129, 1358–1368. [Google Scholar] [CrossRef]
- Milne, T.A.; Evans, R.J.; Abatzaglou, N. Biomass Gasifier “Tars”: Their Nature, Formation, and Conversion; National Renewable Energy Laboratory: Golden, CO, USA, 1998. [Google Scholar]
- Srinivas, S.; Field, R.P.; Herzog, H.J. Modeling Tar Handling Options in Biomass Gasification. Energy Fuels 2013, 27, 2859–2873. [Google Scholar] [CrossRef]
- Evans, R.; Knight, R.; Onischak, M.; Babu, S. Development of Biomass Gasification to Produce Substitute Fuels; Pacific Northwest Lab.: Richland, WA, USA, 1988. [Google Scholar]
- Kondratiev, V. Determination of the rate constant for thermal cracking of methane by means of adiabatic compression and expansion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1965; pp. 319–322. [Google Scholar]
- Schulz, G.; Klotz, H.D.; Spangenberg, H.J. Reaktionsmodell zur Bruttokinetik der Pyrolyse von Methan im Stoßwellenrohr bei Temperaturen von 1800 K bis 2500 K. Z. Für Chemie 1985, 25, 88–92. [Google Scholar] [CrossRef]
- Niu, B.; Jia, M.; Xu, G.; Chang, Y.; Xie, M. Efficient Approach for the Optimization of Skeletal Chemical Mechanisms with Multiobjective Genetic Algorithm. Energy Fuels 2018, 32, 7086–7102. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Jess, A. Mechanisms and kinetics of thermal reactions of aromatic hydrocarbons from pyrolysis of solid fuels. Fuel 1996, 75, 1441–1448. [Google Scholar] [CrossRef]
- Zubair Yahaya, A.; Rao Somalu, M.; Muchtar, A.; Anwar Sulaiman, S.; Ramli Wan Daud, W. Effects of temperature on the chemical composition of tars produced from the gasification of coconut and palm kernel shells using downdraft fixed-bed reactor. Fuel 2020, 265, 116910. [Google Scholar] [CrossRef]
- Yahaya, A.Z.; Somalu, M.R.; Muchtar, A.; Sulaiman, S.A.; Wan Daud, W.R. Effect of particle size and temperature on gasification performance of coconut and palm kernel shells in downdraft fixed-bed reactor. Energy 2019, 175, 931–940. [Google Scholar] [CrossRef]
- Kuo, P.-C.; Wu, W.; Chen, W.-H. Gasification performances of raw and torrefied biomass in a downdraft fixed bed gasifier using thermodynamic analysis. Fuel 2014, 117, 1231–1241. [Google Scholar] [CrossRef]
- Harris, S.; Elliott, L.; Ingham, D.; Pourkashanian, M.; Wilson, C. The optimisation of reaction rate parameters for chemical kinetic modelling of combustion using genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 190, 1065–1090. [Google Scholar] [CrossRef]
- Elliott, L.; Ingham, D.; Kyne, A.; Mera, N.; Pourkashanian, M.; Wilson, C. A novel approach to mechanism reduction optimization for an aviation fuel/air reaction mechanism using a genetic algorithm. J. Eng. Gas Turbines Power 2006, 128, 255–263. [Google Scholar] [CrossRef]
- Pio, D.; Tarelho, L. Empirical and chemical equilibrium modelling for prediction of biomass gasification products in bubbling fluidized beds. Energy 2020, 202, 117654. [Google Scholar] [CrossRef]
- Gao, N.; Salisu, J.; Quan, C.; Williams, P. Modified nickel-based catalysts for improved steam reforming of biomass tar: A critical review. Renew. Sustain. Energy Rev. 2021, 145, 111023. [Google Scholar] [CrossRef]
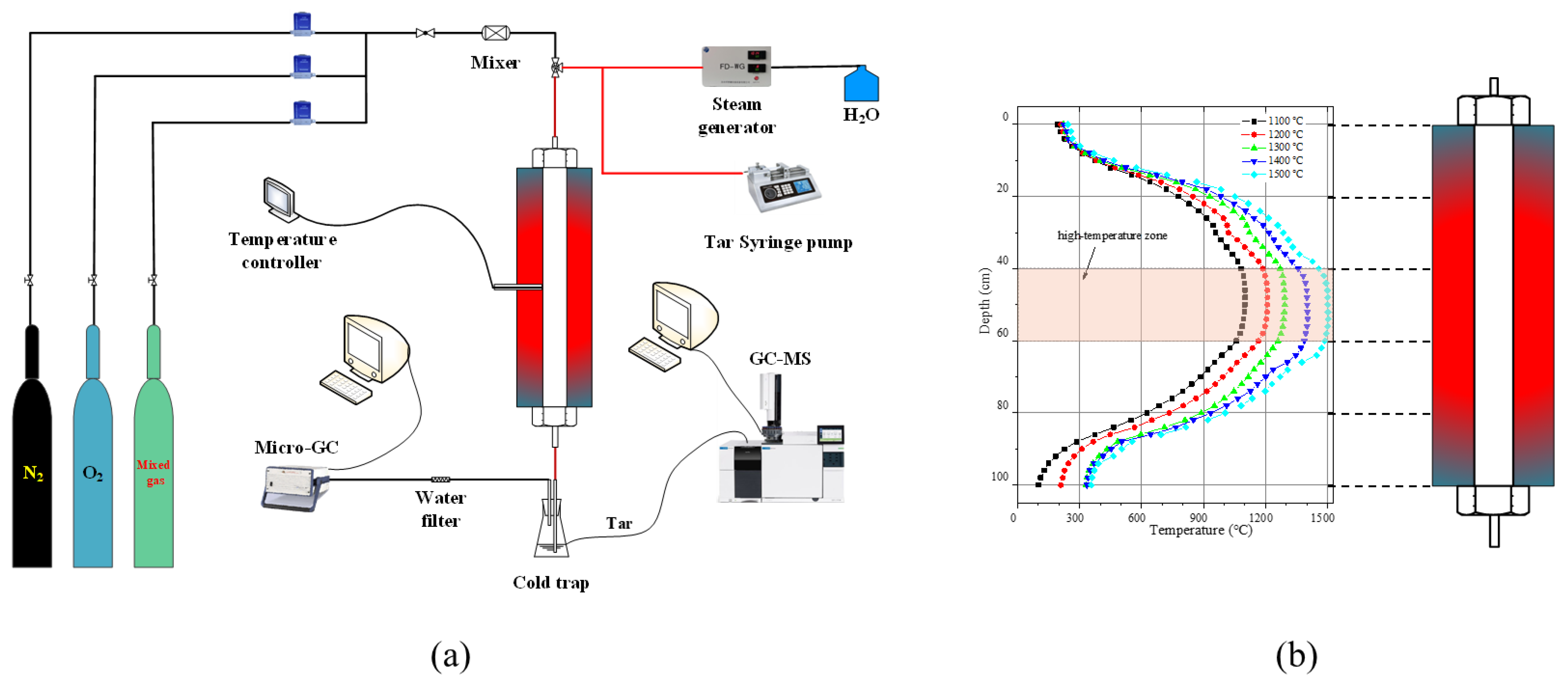
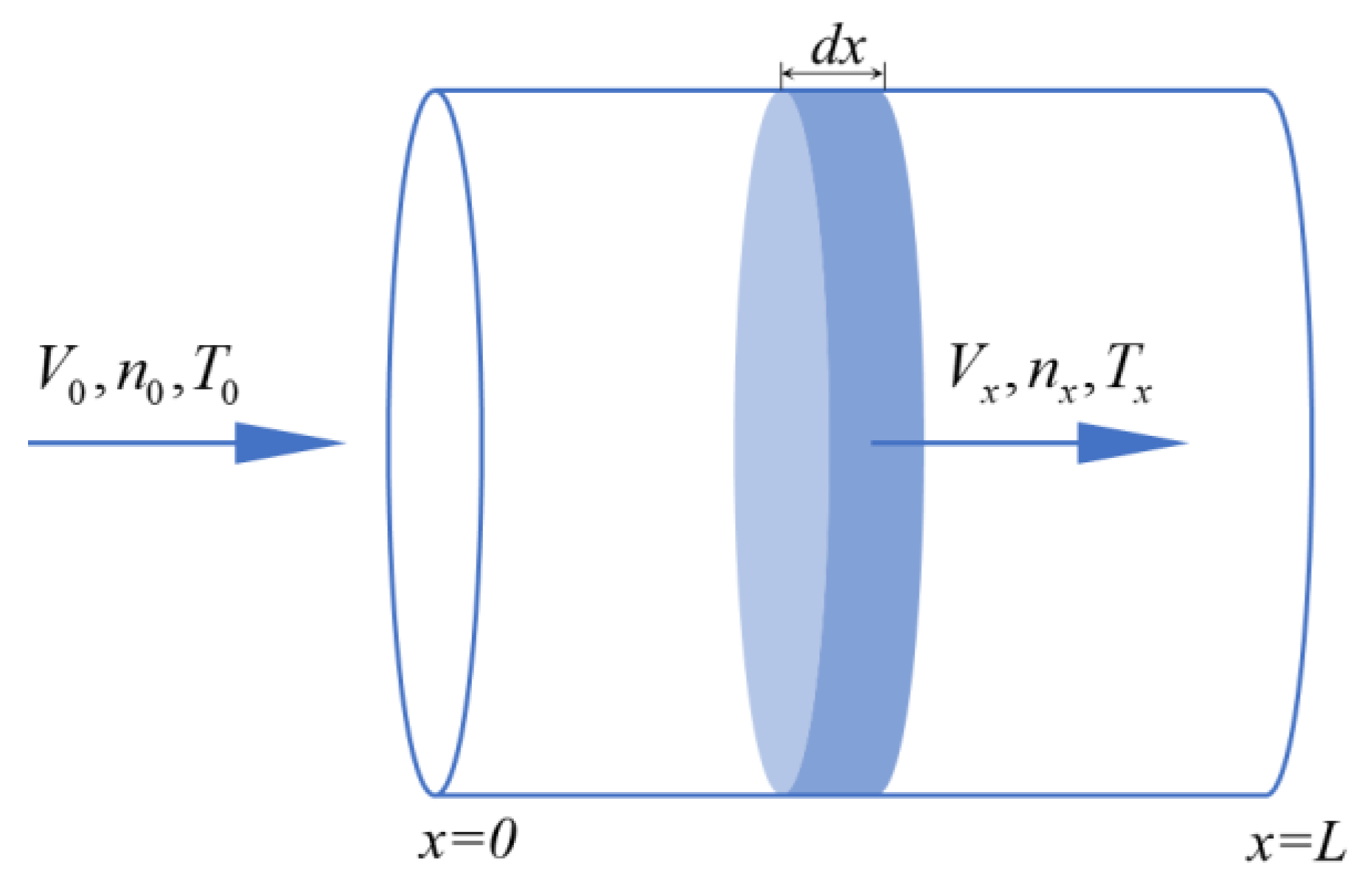
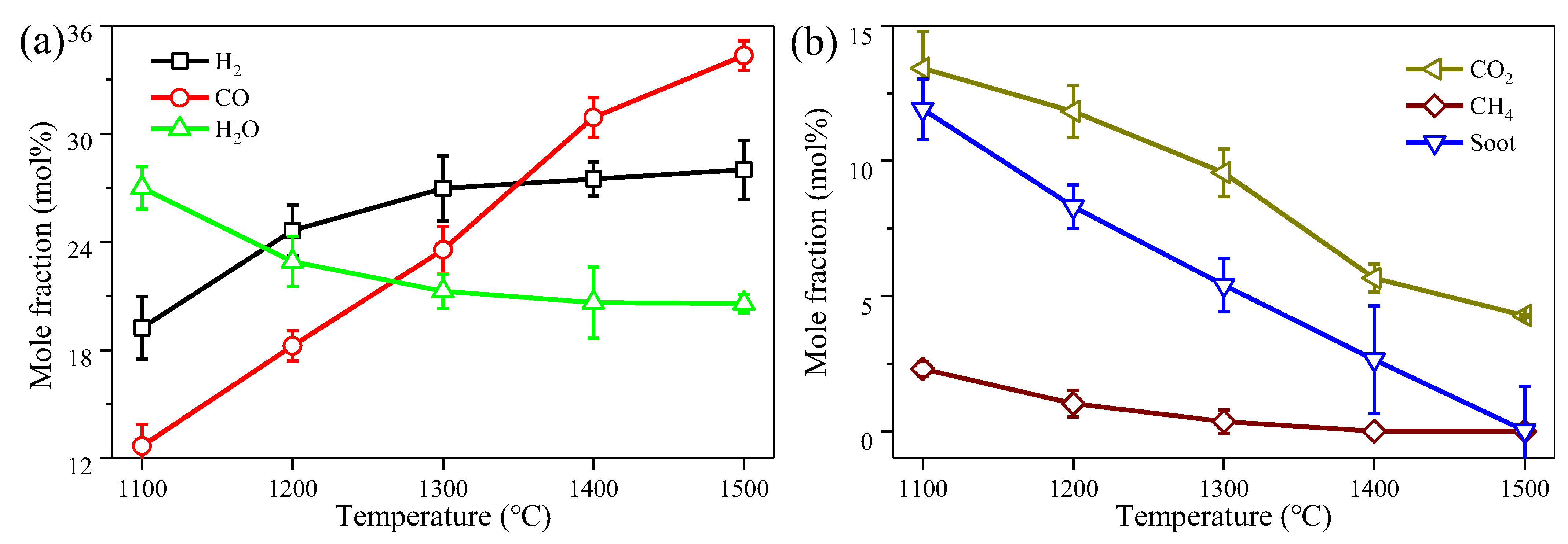
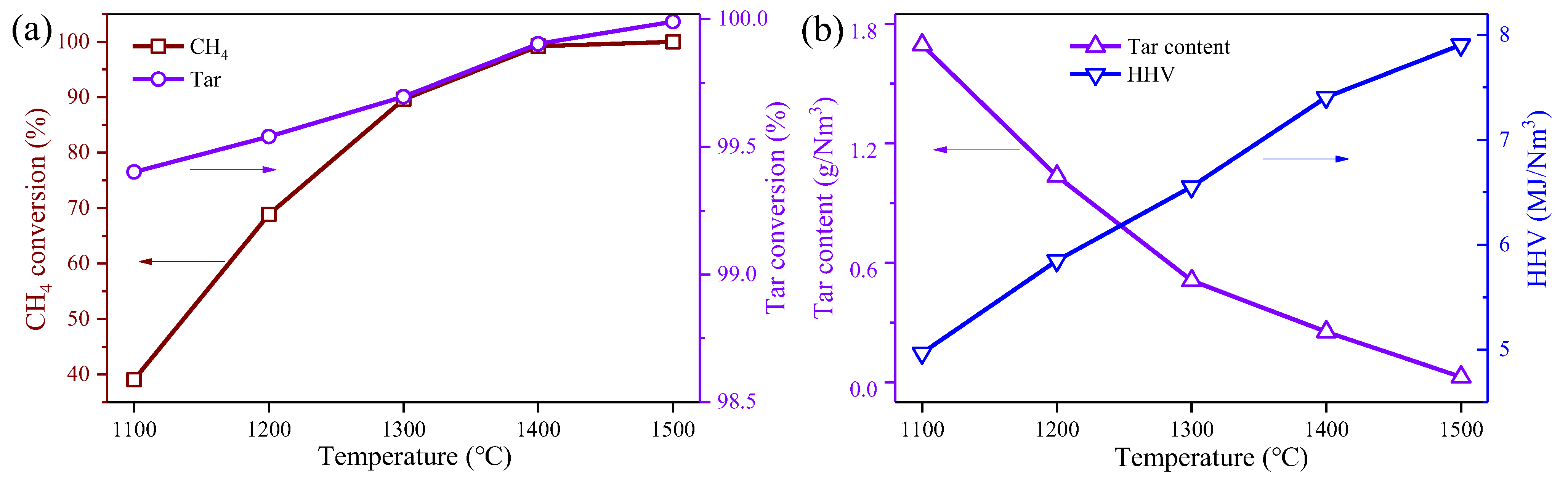


| Composition | Content/mol.% | Composition | Content/mol.% |
|---|---|---|---|
| CO | 6.83 | C2H6 | 0.38 |
| CO2 | 15.29 | C2H4 | 0.20 |
| H2 | 10.01 | C6H6 | 1.67 |
| H2O | 40.02 | C7H8 | 0.15 |
| N2 | 20.68 | C10H8 | 2.15 |
| CH4 | 6.22 | C6H5OH | 0.10 |
| Reaction | Rate Expression (mol‧m−3·s−1) | Ref. | Reaction Number |
|---|---|---|---|
| [18] | (1) | ||
| Hydrogen oxidation: | [18] | (2) | |
| [19] | (3) | ||
| [18] | (4) | ||
| [19] | (5) | ||
| [20] | (6) | ||
| [19] | (7) | ||
| [18] | (8) | ||
| [25] | (9) | ||
| [26] | (10) | ||
| [25] | (11) | ||
| [25] | (12) | ||
| [23] | (13) | ||
| [18] | (14) | ||
| [18] | (15) | ||
| [23] | (16) |
| Reaction | Optimized Value | |
|---|---|---|
| k | Ea (J/mol) | |
| R1 | 1.40 × 1012 | 1.80 × 105 |
| R2 | 5.20 × 1013 | 1.25 × 105 |
| R3 | 2.26 × 1012 | 1.50 × 106 |
| R4 | 1.11 × 1014 | 2.02 × 105 |
| R5 | 4.32 × 106 | 1.59 × 105 |
| R6 | 2.28 × 103 | 1.26 × 104 |
| R7 | 5.94 × 108 | 1.25 × 105 |
| R8 | 2.08 × 107 | 1.35 × 105 |
| R9 | 3.27 × 109 | 2.63 × 105 |
| R10 | 4.57 × 1010 | 1.72 × 105 |
| R11 | 1.92 × 1010 | 1.59 × 105 |
| R12 | 3.07 × 1015 | 3.00 × 105 |
| R13 | 6.20 × 1015 | 3.50 × 105 |
| R14 | 1.05 × 109 | 1.00 × 105 |
| R15 | 2.71 × 1015 | 2.47 × 105 |
| R16 | 6.97 × 1022 | 3.28 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cao, G.; Ba, Z.; Cheng, H.; Hu, D.; Baltrusaitis, J.; Li, C.; Zhao, J.; Fang, Y. Experiment and Simulation of the Non-Catalytic Reforming of Biomass Gasification Producer Gas for Syngas Production. Energies 2025, 18, 2945. https://doi.org/10.3390/en18112945
Wang Y, Cao G, Ba Z, Cheng H, Hu D, Baltrusaitis J, Li C, Zhao J, Fang Y. Experiment and Simulation of the Non-Catalytic Reforming of Biomass Gasification Producer Gas for Syngas Production. Energies. 2025; 18(11):2945. https://doi.org/10.3390/en18112945
Chicago/Turabian StyleWang, Yongbin, Guoqiang Cao, Zhongren Ba, Hao Cheng, Donghai Hu, Jonas Baltrusaitis, Chunyu Li, Jiantao Zhao, and Yitian Fang. 2025. "Experiment and Simulation of the Non-Catalytic Reforming of Biomass Gasification Producer Gas for Syngas Production" Energies 18, no. 11: 2945. https://doi.org/10.3390/en18112945
APA StyleWang, Y., Cao, G., Ba, Z., Cheng, H., Hu, D., Baltrusaitis, J., Li, C., Zhao, J., & Fang, Y. (2025). Experiment and Simulation of the Non-Catalytic Reforming of Biomass Gasification Producer Gas for Syngas Production. Energies, 18(11), 2945. https://doi.org/10.3390/en18112945






