ARIMA Markov Model and Its Application of China’s Total Energy Consumption
Abstract
1. Introduction
- (1)
- An ARIMA model was established based on time series data. The stationarity of the original time series was evaluated, and the sequence after -order difference was tested using the ADF test. During the model selection process, AIC and BIC criteria were used to determine the values of the model;
- (2)
- Based on the Markov transition probability matrix and state division, concrete expressions for the estimated and predicted values of the ARIMAMKM model were constructed;
- (3)
- The validity of the model was verified through numerical examples, and the model was used to predict energy consumption. The proposed model and four comparison models were analyzed, with the validity and robustness of each model expressed using and STD statistics;
- (4)
- To verify the validity and applicability of our model, the ARIMAMKM model was applied to study Guangdong Province’s permanent population data. This model proved more effective than ARIMA, GM, NAR, and FGM models in the application of Guangdong Province’s permanent population data.
2. ARIMAMKM Model
2.1. ARIMA Model
2.2. Markov Model and Markov Correction
2.2.1. Partitioning Prediction States
2.2.2. Construct the State Transition Probability Matrix
2.2.3. Confirmation of Forecast Values
2.3. Model Error Validation and Flow Chart
3. Forecasting China’s Total Energy Consumption
3.1. Selection and Testing of ARIMA() Model
3.1.1. Stationarity Assessment of ARIMA() Model
3.1.2. Stationarity Test of the Difference ARIMA() Model
3.1.3. Determination of ARIMA() Model
3.1.4. Test of ARIMA()
3.2. Estimation and Forecasting Using the ARIMA(0,4,2) Model
3.3. Markov Model Prediction
3.3.1. Determination of Predicted Values
3.3.2. Total Energy Consumption Forecasting
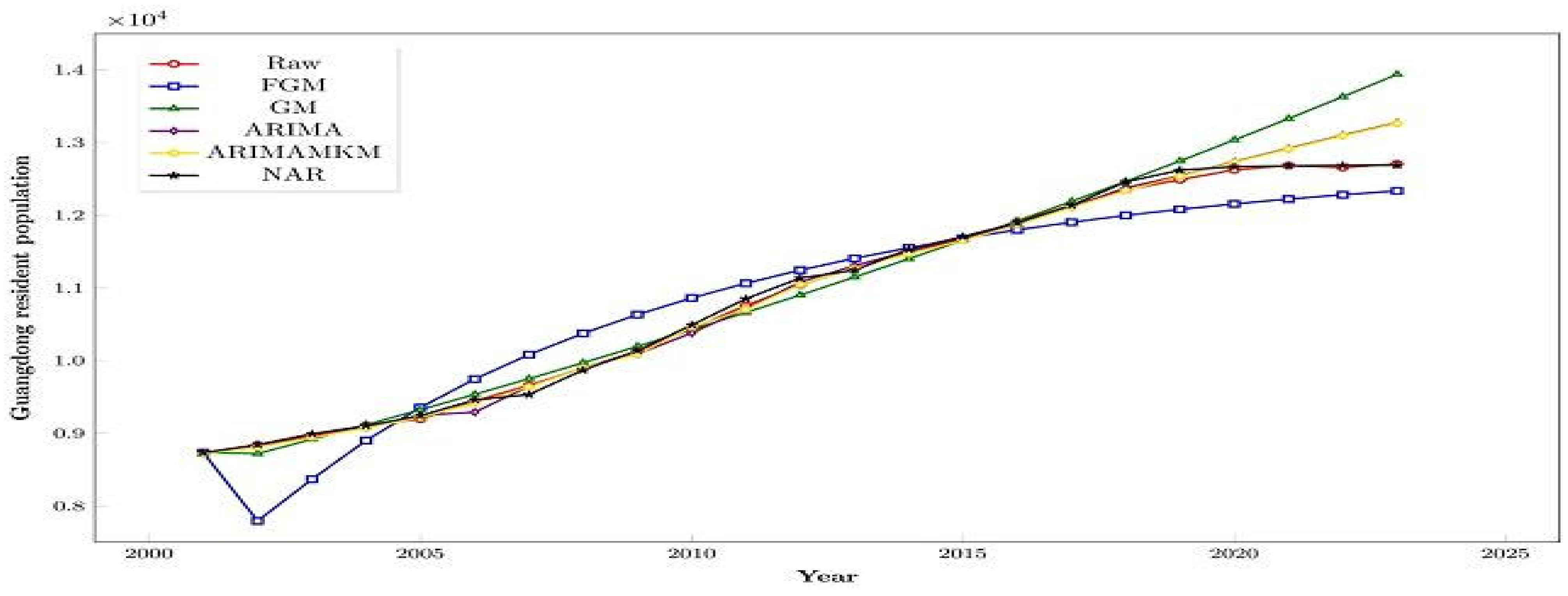
4. Research on the Prediction of Permanent Resident Population in Guangdong
5. Research Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shu, Y.B.; Wang, Z.; Long, L.; Wang, L.-J.; Ju, X.-P. Simulation on China’s Economy and Prediction on Energy Consumption and Carbon Emission under Optimal Growth Path. Acta Geogr. Sin. 2009, 64, 935–944. [Google Scholar] [CrossRef]
- Li, S.; Li, W.D. Analysis of Influencing factors and Short-term forecast of energy consumption in Beijing. China Econ. Trade Guide 2018, 29, 20–21. Available online: https://link.cnki.net/urlid/11.3876.F.20181025.1006.014 (accessed on 30 May 2025).
- Wu, W.Q.; Ma, X.; Zeng, B.; Wang, Y.; Cai, W. Forecasting short-term renewable energy consumption of China using a novel fractional nonlinear grey Bernoulli model. Renew. Energy 2019, 140, 70–87. [Google Scholar] [CrossRef]
- He, Z.Q.; Dong, Y.J. Prediction of China’s total energy consumption based on improved GM(1,1) model. Energy Conserv. 2024, 43, 89–91. [Google Scholar] [CrossRef]
- Shan, B.G.; Yao, L.; Zhang, C.L.; Tan, X.D. Carbon Peak Prediction of Energy Consumption in China: Based on STIRPAT Extended Model (OL). Environ. Sci. 2025, 1–15. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef] [PubMed]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT:analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z.B. Application of a novel time-delayed polynomial grey model to predict thenatural gas consumption in China. J. Comput. Appl. Math. 2017, 324, 17–24. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, W.G. Forecast of China’s natural gas consumption using mathematical models. Energy Sources Part B 2018, 13, 246–250. [Google Scholar] [CrossRef]
- Cai, Y.B.; Ma, X. A novel ensemble learning-based grey model for electricity supply forecasting in China. AIMS Math. 2021, 6, 12339–12358. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, X.; Li, W.P.; Wu, W.Q.; Tu, D.X. Forecasting manufacturing industrial natural gas consumption of China using a novel time-delayed fractional grey model with multiple fractional order. Comput. Appl. Math. 2020, 39, 263. [Google Scholar] [CrossRef]
- Wu, W.Q.; Ma, X.; Zeng, B.; Lv, W.Y.; Wang, Y.; Li, W.P. A novel Grey Bernoulli model forshort-term natural gas consumption forecasting. Appl. Math. Model. 2020, 84, 393–404. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Li, S.Z.; Gu, S.B. A novel fractional Hausdorff discrete Grey model for forecasting the renewable energy consumption. J. Math. 2022, 2022, 8443619. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Guo, H.; Xiong, X. Forecasting Chinese carbon emissions from fossil energy based on the fractional order cumulative multivariate Grey model. J. Math. 2022, 2022, 5623519. [Google Scholar] [CrossRef]
- Li, Z.H.; Zou, Z.H.; Yu, Y. Forecasting of wastewater discharge and the energy consumption in China based on Grey. Math. Probl. Eng. 2019, 2019, 4141085. [Google Scholar] [CrossRef]
- Nong, H.; Guan, Y.T.; Jiang, Y.Y. Identifying the volatility spillover risks between crude oil prices and China’s clean energy market. Electron. Res. Arch. 2022, 30, 4593–4618. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, J.; Kan, C.; He, Y.; Ao, X.; Li, B.; Gu, T.; Liu, Y. Multivariate load forecasting for integrated energy systems based on variational modal decomposition and combined deep neural networks. Power Syst. Technol. 2024, 1–12. [Google Scholar] [CrossRef]
- Zhao, H.R.; Guo, S. Uncertain interval forecasting for combined electricity-heat-cooling-gas loads in the integrated energy system based on multi-task learning and multi-kernel extreme learning machine. Mathematics 2021, 9, 1645. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhang, Z.S. Short-term multiple load forecasting model of regional integrated energy system based on QWGRU-MTL. Energies 2021, 14, 6555. [Google Scholar] [CrossRef]
- Tan, Z.F.; De, G.; Li, M.L.; Lin, H.; Yang, S.; Huang, L.; Tan, Q. Combined electricity-heat-cooling-gas load forecasting model for integrated energy system based on multi-task learning and least square support vector machine. J. Clean. Prod. 2020, 248, 119252. [Google Scholar] [CrossRef]
- Abid, F.; Alam, M.; Alamri, F.S.; Siddique, I. Multi-directional gated recurrent unit and convolutional neural network for load and energy forecasting: A novel hybridization. AIMS Math. 2023, 8, 19993–20017. [Google Scholar] [CrossRef]
- Alrashidi, M. Ultra-short-term solar forecasting with reduced pre-acquired data considering optimal heuristic configurations of deep neural networks. AIMS Math. 2024, 9, 12323–12356. [Google Scholar] [CrossRef]
- Xu, N.; Dang, Y.; Gong, Y. Novel grey prediction model with nonlinear optimized time response method for forecasting of electricity consumption in China. Energy 2017, 118, 473–480. [Google Scholar] [CrossRef]
- Wang, J.; Du, P.; Lu, H.; Yang, W.; Niu, T. An improved grey model optimized by multi-objective ant lion optimization algorithm for annual electricity consumption forecasting. Appl. Soft Comput. 2018, 72, 321–337. [Google Scholar] [CrossRef]
- Ding, S.; Hipel, K.W.; Dang, Y. Forecasting China’s electricity consumption using a new grey prediction model. Energy 2018, 149, 314–328. [Google Scholar] [CrossRef]
- Liu, L.; Cao, J.H.; Xiang, X.W.; Zhang, P. Forecasting China’s per capita energy consumption using dynamic grey model based on ARIMA model. In Proceedings of the 2019 5th International Conference on Advances in Energy Resources and Environment Engineering (ICAESEE 2019) (VOL.1), Chongqing, China, 6–8 December 2019; IOP Publishing: Bristol, UK, 2019; Volume 7. [Google Scholar] [CrossRef]
- Miao, J.W. The Energy Consumption Forecasting in China Based on ARIMA Model, International Society for Information Technology and Engineering. In Proceedings of the 2015 International Conference on Materials Engineering and Information Technology Applications (MEITA 2015), Guilin, China, 30–31 August 2015; Department of Economic Management, North China Electric Power University: Beijing, China, 2015; Volume 5. [Google Scholar] [CrossRef][Green Version]
- Liu, J.B.; Yuan, X.Y. Prediction of the air quality index of Hefei based on an improved ARIMA model. AIMS Math. 2023, 8, 18717–18733. [Google Scholar] [CrossRef]
- Kulkarni, G.E.; Muley, A.A.; Deshmukh, N.K.; Bhalchandra, P.U. Modeling Eart Autoregressive integrated moving average time series model for forecasting air pollution in Nanded city, Maharashtra, India. Model. Earth Syst. Environ. 2018, 4, 1435–1444. [Google Scholar] [CrossRef]
- Naveen, V.; Anu, N. Time Series Analysis to Forecast Air Quality Indices in Thiruvananthapuram District, Kerala, India. Int. J. Eng. Res. Appl. 2017, 7, 66–84. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Wang, P.; Qin, Y.; Wang, H. Forecasting of particulate matter time series using wavelet analysis and wavelet-ARMA/ARIMA model in Taiyuan. J. Air Waste Manag. Assoc. 2017, 67, 776–788. [Google Scholar] [CrossRef]
- Aladag, E. Forecasting of particulate matter with a hybrid ARIMA model based on wavelet transformation and seasonal adjustment. Urban Climb 2021, 39, 100930. [Google Scholar] [CrossRef]
- Wibawa, A.P.; Utama, A.B.P.; Elmunsyah, H.; Pujianto, U.; Dwiyanto, F.A.; Hernandez, L. Timeseries analysis with smoothed convolutional neural network. J. Big Data 2022, 9, 44. [Google Scholar] [CrossRef] [PubMed]
- Alfadda, A.; Rahman, S.; Pipattanasomporn, M. Solar irradiance forecast using aerosols measurements: A data driven approach. Sol. Energy 2018, 170, 924–939. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term photovoltaic power forecasting using an LSTM neural network and synthetic weather forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]






| Model | Autocorrelation Coefficient | Partial Autocorrelation Coefficient |
|---|---|---|
| AR() | Dragging tail | -th order dragging tail |
| MA() | -th order chop off the tail | Dragging tail |
| ARMA() | Dragging tail | Dragging tail |
| t-Statistics | Prob | |
|---|---|---|
| Augmented Dickey—Fuller test statistics | –0.270605 | 0.9846 |
| Test critical values: 1% level | –4.57159 | |
| 5% level | –3.690814 | |
| 10% level | –3.286906 |
| Augmented Dickey–Fuller Test | Ljung-Box Test | ||||
|---|---|---|---|---|---|
| Lag order | Dickey—Fuller Test | -value | df | -squared | -value |
| 2 | –4.4732 | 0.01 | 1 | 4.9408 | 0.02632 |
| Model | AR(1) | MA(1) | MA(2) | MA(6) | ARMA(1,1) | ARMA(1,2) | ARMA(1,6) |
|---|---|---|---|---|---|---|---|
| AIC | 333.6152 | 327.0116 | 323.9768 | 327.1382 | 327.4539 | 325.7543 | 328.9624 |
| BIC | 335.7394 | 329.1358 | 326.809 | 332.8026 | 330.2861 | 329.2945 | 335.3348 |
| Ljung-Box Test | ||
|---|---|---|
| df | -squared | -value |
| 1 | 1.4155 | 0.2342 |
| ARIMA | GM | FGM | NAR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Raw | Predicted Value | Relative Error | Predicted Value | Relative Error | Predicted Value | Relative Error | Predicted Value | Relative Error |
| 2000 | 146,964 | 146,946.3 | –0.01% | 146,964 | 0.00% | 146,964 | 0.00% | 146,964 | 0.00% |
| 2001 | 155,547 | 155,633.5 | 0.06% | 209,642 | 34.78% | 193,540 | 24.43% | 155,547 | 0.00% |
| 2002 | 169,577 | 169,418.9 | –0.09% | 220,954 | 30.30% | 212,861 | 25.52% | 157,982.51 | –6.84% |
| 2003 | 197,083 | 197,147.1 | 0.03% | 232,876 | 18.16% | 229,490 | 16.44% | 180,992.56 | –8.16% |
| 2004 | 230,281 | 241,228.8 | 4.75% | 245,442 | 6.58% | 245,178 | 6.47% | 208,834.34 | –9.31% |
| 2005 | 261,369 | 268,180.5 | 2.61% | 258,685 | –1.03% | 260,563 | –0.31% | 242,588.14 | –7.19% |
| 2006 | 286,467 | 287,843.8 | 0.48% | 272,643 | –4.83% | 275,966 | –3.67% | 274,962.32 | –4.02% |
| 2007 | 311,442 | 303,532.1 | –2.54% | 287,355 | –7.73% | 291,577 | –6.38% | 300,552.97 | –3.50% |
| 2008 | 320,611 | 333,451.8 | 4.01% | 302,860 | –5.54% | 307,523 | –4.08% | 321,490.82 | 0.27% |
| 2009 | 336,126 | 312,804.3 | –6.94% | 319,201 | –5.04% | 323,899 | –3.64% | 349,782.65 | 4.06% |
| 2010 | 360,648 | 356,869.1 | –1.05% | 336,425 | –6.72% | 340,780 | –5.51% | 367,549.22 | 1.91% |
| 2011 | 387,043 | 393,983.9 | 1.79% | 354,577 | –8.39% | 358,230 | –7.44% | 385,573.73 | –0.38% |
| 2012 | 402,138 | 414,705.6 | 3.13% | 373,710 | –7.07% | 376,304 | –6.42% | 397,313.35 | –1.20% |
| 2013 | 416,913 | 405,425.0 | –2.76% | 393,874 | –5.53% | 395,055 | –5.24% | 418,340.43 | 0.34% |
| 2014 | 428,334 | 430,052.1 | 0.40% | 415,127 | –3.08% | 414,533 | –3.22% | 434,273.92 | 1.39% |
| 2015 | 434,113 | 435,680.9 | 0.36% | 437,526 | 0.79% | 434,784 | 0.15% | 444,207.63 | 2.33% |
| 2016 | 441,492 | 433,686.3 | –1.77% | 461,134 | 4.45% | 455,856 | 3.25% | 448,919.26 | 1.68% |
| 2017 | 455,827 | 449,869.9 | –1.31% | 486,015 | 6.62% | 477,797 | 4.82% | 451,886.75 | –0.86% |
| 2018 | 471,925 | 476,731.9 | 1.02% | 512,240 | 8.54% | 500,653 | 6.09% | 456,046.63 | –3.36% |
| RMSE | 8635.4 | RMSE | 27,668.4 | RMSE | 22,349.85 | RMSE | 10,709.85 | ||
| MAPE | 1.85% | MAPE | 8.69% | MAPE | 7.00% | MAPE | 2.98% | ||
| STD | 1.82% | STD | 9.03% | STD | 7.06% | STD | 2.85% | ||
| 99.32% | 92.26% | 94.87% | 99.04% | ||||||
| 2019 | 487,488 | 489,822.2 | 0.48% | 539,879 | 10.75% | 524,474 | 7.59% | 461,968.45 | –5.23% |
| 2020 | 498,314 | 509,285.9 | 2.20% | 569,010 | 14.19% | 549,309 | 10.23% | 470,947.09 | –5.49% |
| 2021 | 525,896 | 530,083.6 | 0.80% | 599,712 | 14.04% | 575,208 | 9.38% | 482,537.05 | –8.24% |
| 2022 | 540,956 | 551,982.6 | 2.04% | 632,071 | 16.84% | 602,225 | 11.33% | 505,342.54 | –6.58% |
| 2023 | 572,000 | 574,750.3 | 0.48% | 666,176 | 16.46% | 630,414 | 10.21% | 530,118.52 | –7.32% |
| RMSE | 7382.6 | RMSE | 77,926.46 | RMSE | 52,088.79 | RMSE | 35,503.71 | ||
| MAPE | 1.20% | MAPE | 14.46% | MAPE | 9.75% | MAPE | 6.57% | ||
| STD | 0.76% | STD | 2.18% | STD | 1.24% | STD | 1.12% | ||
| 94.22% | 22.52% | 32.92% | 30.63% |
| Year | Initial State | Transferring Steps | |||||
|---|---|---|---|---|---|---|---|
| 2018 | 3 | 1 | 0 | 0.25 | 0.5 | 0.25 | |
| 2017 | 2 | 2 | 0.5 | 0.2375 | 0.4250 | 0.2875 | |
| 2016 | 2 | 3 | 0.0575 | 0.2231 | 0.4387 | 0.2806 | |
| 2015 | 3 | 4 | 0.0561 | 0.2216 | 0.4446 | 0.2777 | |
| Total | 0.6136 | 0.9322 | 1.8083 | 1.0958 |
| Year | Raw | QFM | ARIMA | ARIMAMKM | ||||
|---|---|---|---|---|---|---|---|---|
| Predicted Value | Relative Error | Predicted Value | Relative Error | Station Value | Predicted Value | Relative Error | ||
| 2000 | 146,964 | 128,263.95 | –12.72% | 146,946.3 | –0.01% | 3 | 146,601.78 | –0.25% |
| 2001 | 155,547 | 156,619.24 | 0.69% | 155,633.5 | 0.06% | 3 | 155,268.62 | –0.18% |
| 2002 | 169,577 | 183,868.37 | 8.43% | 169,418.9 | –0.09% | 3 | 169,021.69 | –0.33% |
| 2003 | 197,083 | 210,011.34 | 6.56% | 197,147.1 | 0.03% | 3 | 196,684.89 | –0.20% |
| 2004 | 230,281 | 235,048.15 | 2.07% | 241,228.8 | 4.75% | 4 | 233,522.55 | 1.41% |
| 2005 | 261,369 | 258,978.79 | –0.91% | 268,180.5 | 2.61% | 4 | 259,613.26 | –0.67% |
| 2006 | 286,467 | 281,803.28 | –1.63% | 287,843.8 | 0.48% | 3 | 297,168.95 | 3.74% |
| 2007 | 311,442 | 303,521.61 | –2.54% | 303,532.1 | –2.54% | 2 | 311,458.72 | 0.01% |
| 2008 | 320,611 | 324,133.77 | 1.10% | 333,451.8 | 4.01% | 4 | 322,799.41 | 0.68% |
| 2009 | 336,126 | 343,639.78 | 2.24% | 312,804.3 | –6.94% | 1 | 330,922.29 | –1.55% |
| 2010 | 360,648 | 362,039.62 | 0.39% | 356,869.1 | –1.05% | 3 | 356,032.42 | –1.28% |
| 2011 | 387,043 | 379,333.30 | –1.99% | 393,983.9 | 1.79% | 4 | 381,397.77 | –1.46% |
| 2012 | 402,138 | 395,520.83 | –1.65% | 414,705.6 | 3.13% | 4 | 401,457.50 | –0.17% |
| 2013 | 416,913 | 410,602.19 | –1.51% | 405,425.0 | –2.76% | 2 | 416,012.51 | –0.22% |
| 2014 | 428,334 | 424,577.39 | –0.88% | 430,052.1 | 0.40% | 3 | 429,043.84 | 0.17% |
| 2015 | 434,113 | 437,446.43 | 0.77% | 435,680.9 | 0.36% | 3 | 434,659.45 | 0.13% |
| 2016 | 441,492 | 449,209.32 | 1.75% | 433,686.3 | –1.77% | 2 | 445,011.85 | 0.80% |
| 2017 | 455,827 | 459,866.04 | 0.89% | 449,869.9 | –1.31% | 2 | 461,618.08 | 1.27% |
| 2018 | 471,925 | 469,416.60 | –0.53% | 476,731.9 | 1.02% | 3 | 475,614.20 | 0.78% |
| RMSE | 7801.5 | RMSE | 8635.4 | RMSE | 3807.5 | |||
| MAPE | 2.59% | MAPE | 1.85% | MAPE | 0.80% | |||
| STD | 3.11% | STD | 1.82% | STD | 0.86% | |||
| 99.45% | 99.32% | 99.87% | ||||||
| 2019 | 487,488 | 477,860.99 | –1.97% | 489,822.2 | 0.48% | 3 | 488,673.81 | 0.24% |
| 2020 | 498,314 | 485,199.23 | –2.63% | 509,285.9 | 2.20% | 4 | 508,091.88 | 1.96% |
| 2021 | 525,896 | 491,431.31 | –6.55% | 530,083.6 | 0.80% | 3 | 528,840.82 | 0.56% |
| 2022 | 540,956 | 496,557.23 | –8.21% | 551,982.6 | 2.04% | 4 | 550,688.48 | 1.80% |
| 2023 | 572,000 | 500,576.99 | –12.49% | 574,750.3 | 0.48% | 3 | 573,402.80 | 0.25% |
| RMSE | 41,292.6 | RMSE | 7382.6 | RMSE | 6362.0 | |||
| MAPE | 6.37% | MAPE | 1.20% | MAPE | 0.96% | |||
| STD | 3.85% | STD | 0.76% | STD | 0.76% | |||
| 35.01% | 94.22% | 95.63% | ||||||
| ARIMA | NAR | GM | FGM | ARIMAMKM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Raw | Predicted Value | Relative Error | Station Value | Predicted Value | Relative Error | Predicted Value | Relative Error | Predicted Value | Relative Error | Predicted Value | Relative Error |
| 2001 | 8733.18 | 8724.45 | –0.10% | 3 | 8733.18 | 0.00% | 8733.18 | 0.00% | 8733.18 | 0.00% | 8718.78 | –0.16% |
| 2002 | 8842.08 | 8812.97 | –0.33% | 3 | 8842.08 | 0.00% | 8719.83 | –1.38% | 7793.29 | –11.86% | 8807.24 | –0.39% |
| 2003 | 8962.69 | 8947.45 | –0.17% | 3 | 8992.16 | 0.33% | 8916.77 | –0.51% | 8367.22 | –6.64% | 8941.63 | –0.23% |
| 2004 | 9110.66 | 9077.85 | –0.36% | 3 | 9102.76 | –0.09% | 9118.16 | 0.08% | 8899.98 | –2.31% | 9071.95 | –0.42% |
| 2005 | 9194 | 9248.87 | 0.60% | 4 | 9242.68 | 0.53% | 9324.11 | 1.42% | 9355.25 | 1.75% | 9219.36 | 0.28% |
| 2006 | 9442.07 | 9289.95 | –1.61% | 1 | 9459.41 | 0.18% | 9534.7 | 0.98% | 9744.78 | 3.21% | 9415.61 | –0.28% |
| 2007 | 9659.52 | 9645.07 | –0.15% | 3 | 9532.94 | –1.31% | 9750.05 | 0.94% | 10,081.33 | 4.37% | 9638.8 | –0.21% |
| 2008 | 9893.48 | 9902.23 | 0.09% | 4 | 9869.17 | –0.25% | 9970.26 | 0.78% | 10,374.85 | 4.87% | 9899.06 | 0.06% |
| 2009 | 10,130.19 | 10,092.1 | –0.38% | 3 | 10,137.34 | 0.07% | 10,195.45 | 0.64% | 10,632.86 | 4.96% | 10,085.54 | –0.44% |
| 2010 | 10,440.94 | 10,379.71 | –0.59% | 2 | 10,490.13 | 0.47% | 10,425.72 | –0.15% | 10,861.06 | 4.02% | 10,461.83 | 0.20% |
| 2011 | 10,756 | 10,714.49 | –0.39% | 3 | 10,850.3 | 0.88% | 10,661.2 | –0.88% | 11,063.88 | 2.86% | 10,707.53 | –0.45% |
| 2012 | 11,041 | 11,080.37 | 0.36% | 4 | 11,136.08 | 0.86% | 10,901.99 | –1.26% | 11,244.8 | 1.85% | 11,045.02 | 0.04% |
| 2013 | 11,270 | 11,305.26 | 0.31% | 4 | 11,242.36 | –0.25% | 11,148.22 | –1.08% | 11,406.61 | 1.21% | 11,269.19 | –0.01% |
| 2014 | 11,489 | 11,507.86 | 0.16% | 4 | 11,533.14 | 0.38% | 11,400.01 | –0.77% | 11,551.61 | 0.54% | 11,471.15 | –0.16% |
| 2015 | 11,678 | 11,689.21 | 0.10% | 4 | 11,706.54 | 0.24% | 11,657.49 | –0.18% | 11,681.69 | 0.03% | 11,651.92 | –0.22% |
| 2016 | 11,908 | 11,873.7 | –0.29% | 3 | 11,895.01 | –0.11% | 11,920.79 | 0.11% | 11,798.44 | –0.92% | 11,865.98 | –0.35% |
| 2017 | 12,141 | 12,114.25 | –0.22% | 3 | 12,136.02 | –0.04% | 12,190.03 | 0.40% | 11,903.19 | –1.96% | 12,106.38 | –0.29% |
| 2018 | 12,348 | 12,378.04 | 0.24% | 4 | 12,459.88 | 0.91% | 12,465.35 | 0.95% | 11,997.1 | –2.84% | 12,338.55 | –0.08% |
| RMSE | 48.1 | RMSE | 52.2 | RMSE | 84.66 | RMSE | 394.71 | RMSE | 27.9 | |||
| MAPE | 0.0036 | MAPE | 0.0038 | MAPE | 0.0069 | MAPE | 0.0312 | MAPE | 0.0024 | |||
| STD | 0.0034 | STD | 0.0037 | STD | 0.0045 | STD | 0.0277 | STD | 0.0014 | |||
| 0.9984 | 0.9978 | 0.9949 | 0.9057 | 0.9994 | ||||||||
| 2019 | 12,489 | 12,542.53 | 0.43% | 4 | 12,619.88 | 1.05% | 12,746.89 | 2.06% | 12,081.16 | –3.27% | 12,534.38 | 0.36% |
| 2020 | 12,624 | 12,736.49 | 0.89% | 4 | 12,667.62 | 0.35% | 13,034.79 | 3.25% | 12,156.23 | –3.71% | 12,728.21 | 0.83% |
| 2021 | 12,684 | 12,919.34 | 1.86% | 4 | 12,680.12 | –0.03% | 13,329.19 | 5.09% | 12,223.08 | –3.63% | 12,910.94 | 1.79% |
| 2022 | 12,656.8 | 13,101.12 | 3.51% | 4 | 12,685.88 | 0.23% | 13,630.24 | 7.69% | 12,282.37 | –2.96% | 13,092.6 | 3.44% |
| 2023 | 12706 | 13,272.96 | 4.46% | 4 | 12,687.49 | –0.15% | 13,938.09 | 9.70% | 12,334.7 | –2.92% | 13,264.33 | 4.39% |
| RMSE | 343.44 | RMSE | 63.62 | RMSE | 789.57 | RMSE | 418.48 | RMSE | 336.47 | |||
| MAPE | 0.0223 | MAPE | 0.0036 | MAPE | 0.0556 | MAPE | 0.033 | MAPE | 0.0216 | |||
| STD | 0.0154 | STD | 0.0036 | STD | 0.0281 | STD | 0.0033 | STD | 0.0154 | |||
| 0.1949 | 0.0802 | 0.0734 | 0.0351 | 0.2012 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Liu, C.; Huang, C.; Qiu, M.; Li, D. ARIMA Markov Model and Its Application of China’s Total Energy Consumption. Energies 2025, 18, 2914. https://doi.org/10.3390/en18112914
Luo C, Liu C, Huang C, Qiu M, Li D. ARIMA Markov Model and Its Application of China’s Total Energy Consumption. Energies. 2025; 18(11):2914. https://doi.org/10.3390/en18112914
Chicago/Turabian StyleLuo, Chingfei, Chenzi Liu, Chen Huang, Meilan Qiu, and Dewang Li. 2025. "ARIMA Markov Model and Its Application of China’s Total Energy Consumption" Energies 18, no. 11: 2914. https://doi.org/10.3390/en18112914
APA StyleLuo, C., Liu, C., Huang, C., Qiu, M., & Li, D. (2025). ARIMA Markov Model and Its Application of China’s Total Energy Consumption. Energies, 18(11), 2914. https://doi.org/10.3390/en18112914






