A Study on the Hydrodynamic Excitation Characteristics of Pump and Pipeline Systems Considering the Weakly Compressible Fluid During the Pump Start-Up Condition
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. Model Introduction
2.2. Boundary Condition Acquisition
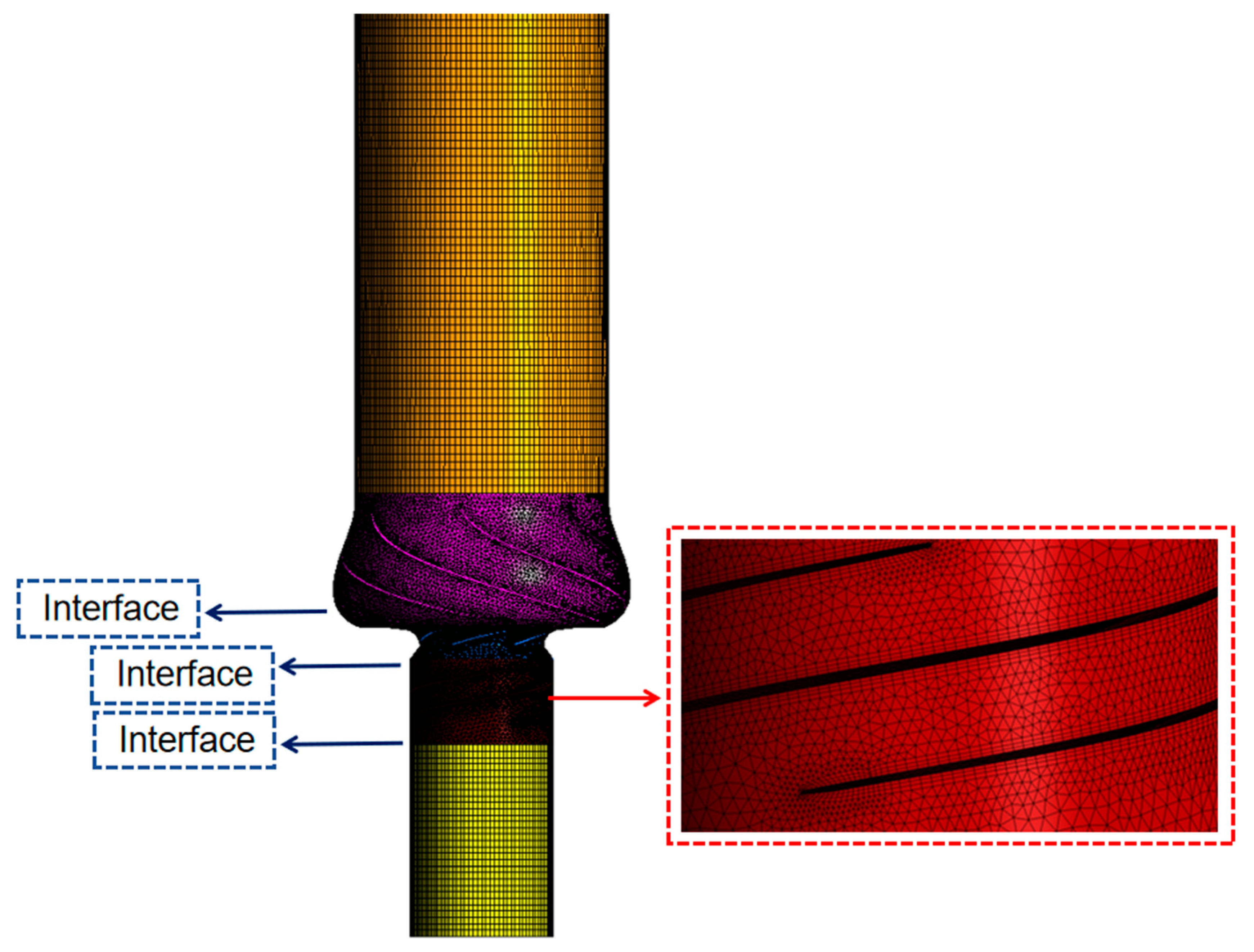
2.3. Grid and Boundary Conditions
3. Results and Discussion
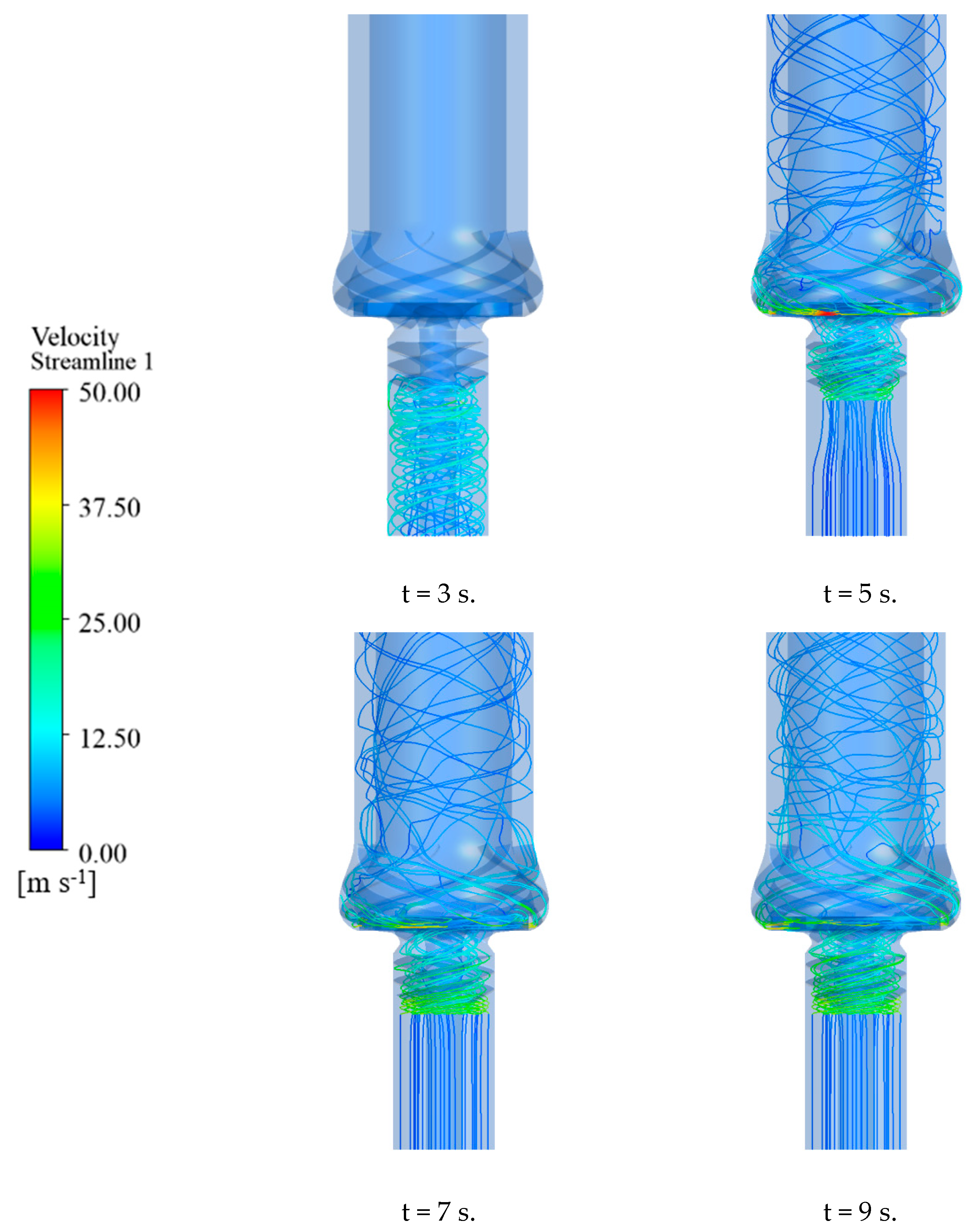
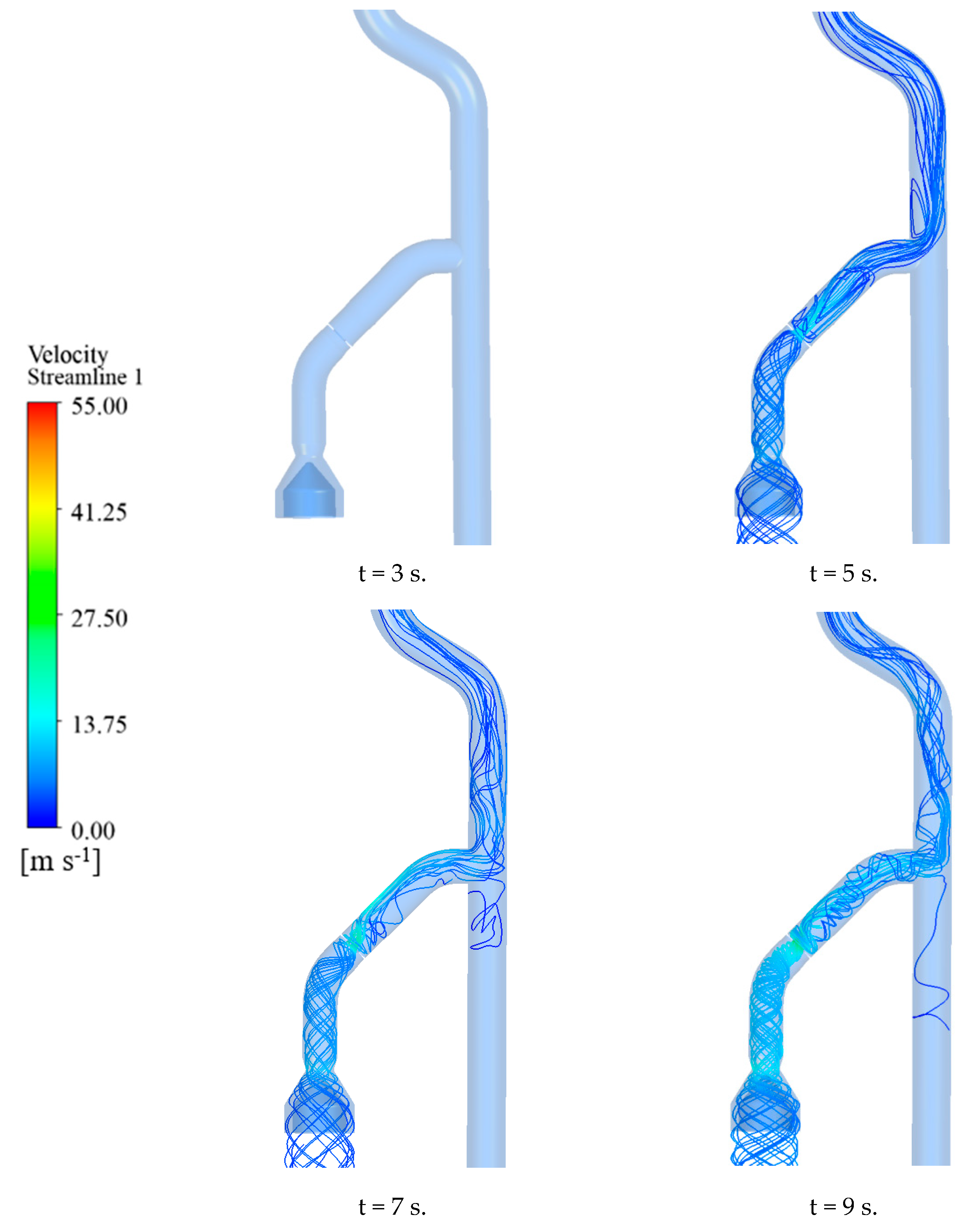
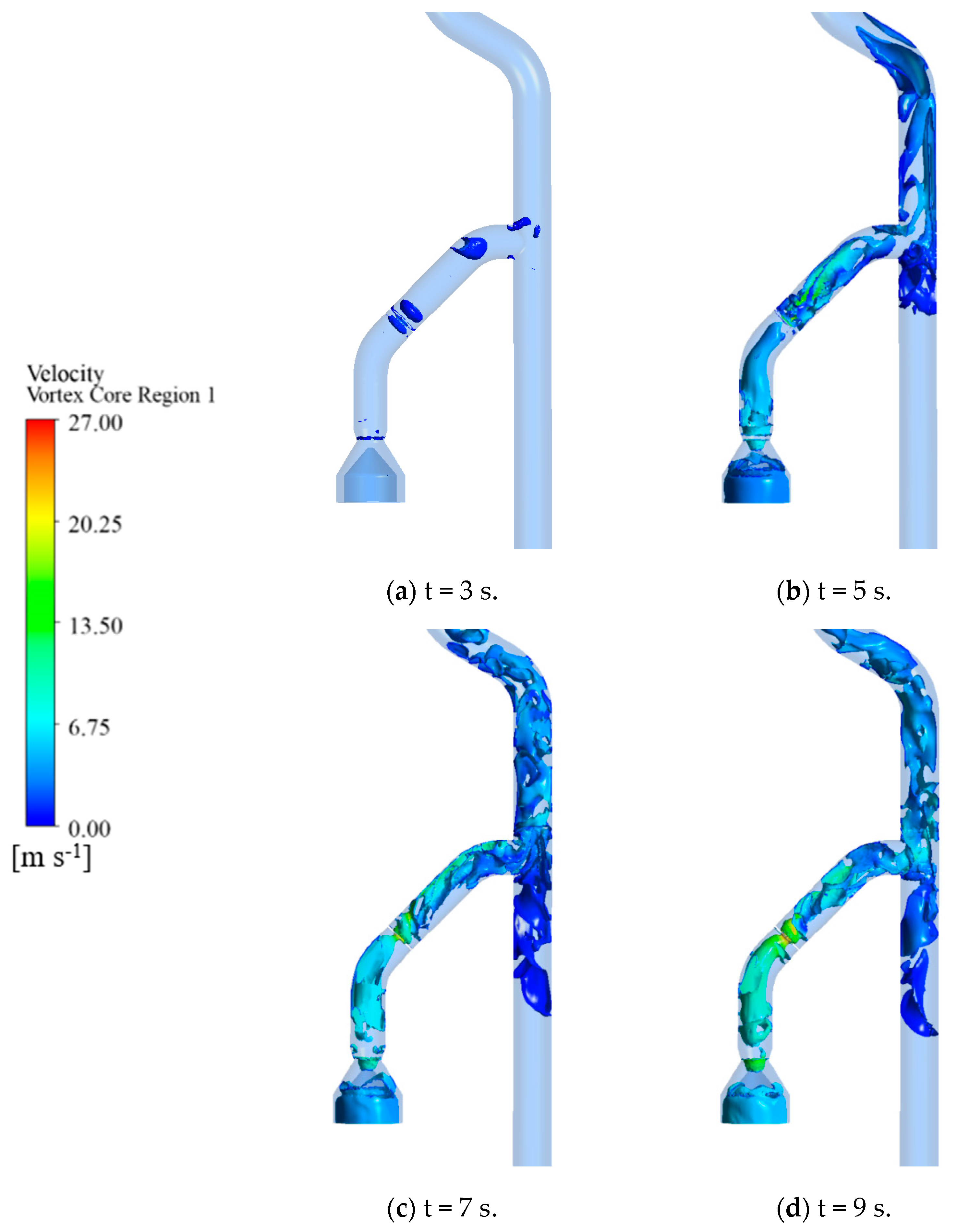
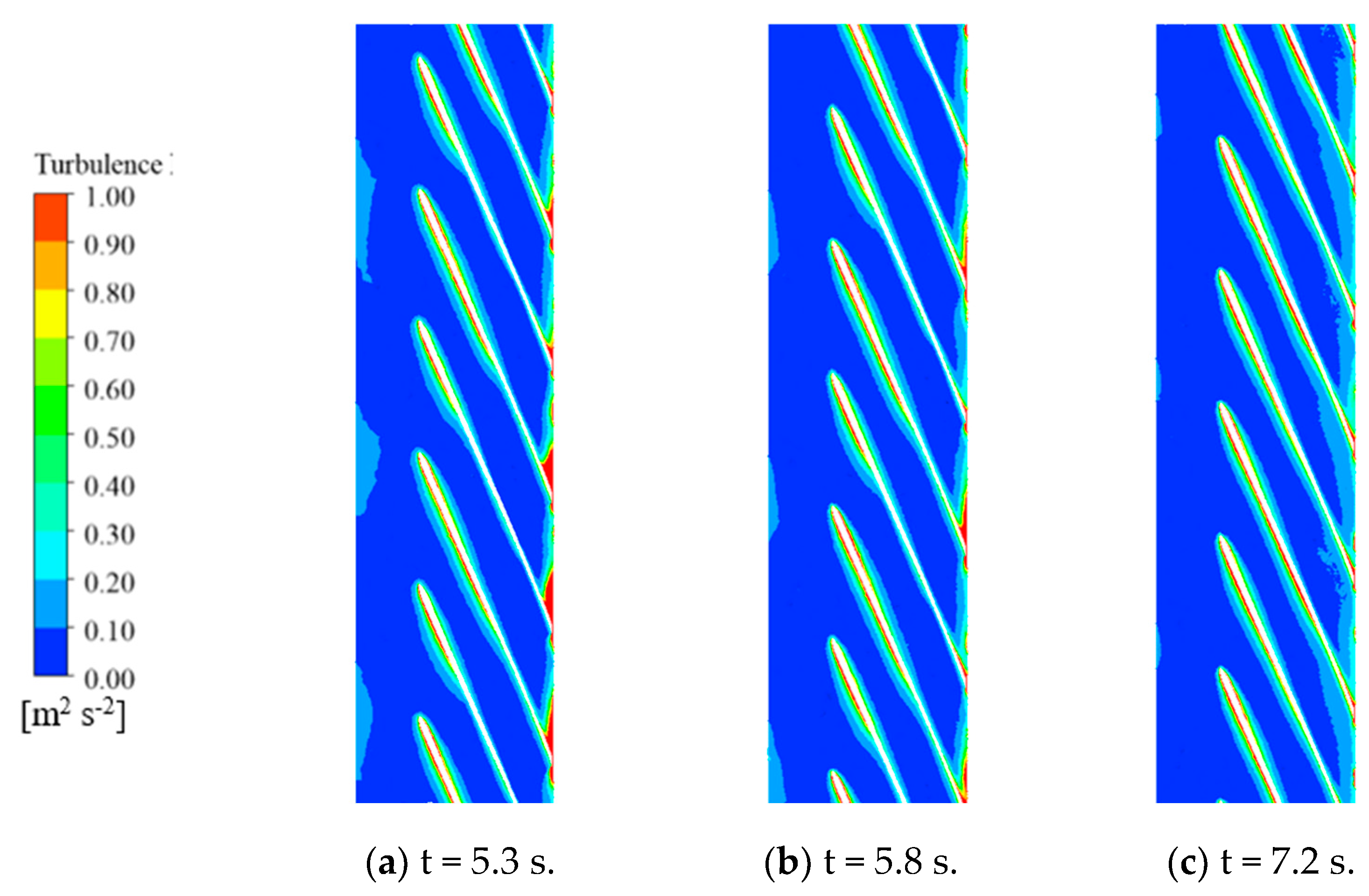
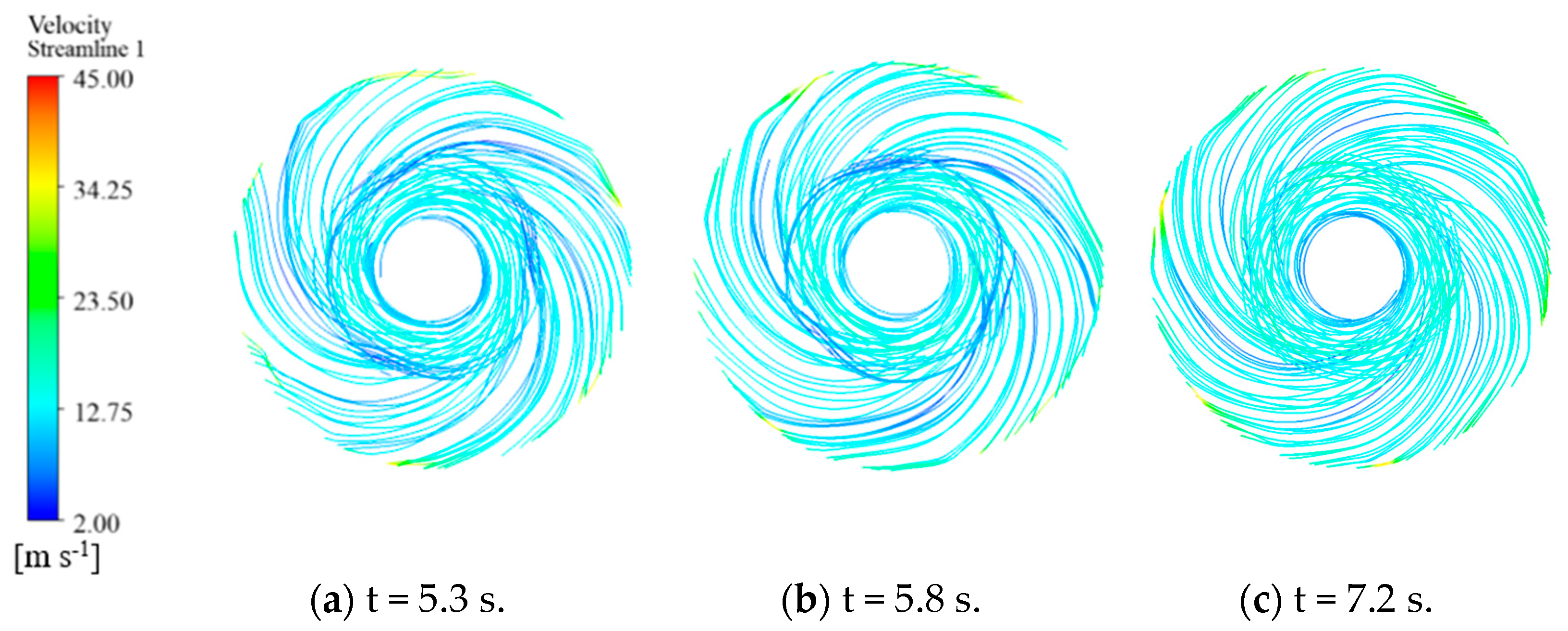
3.1. External and Internal Flow Characteristics of LNG Pump
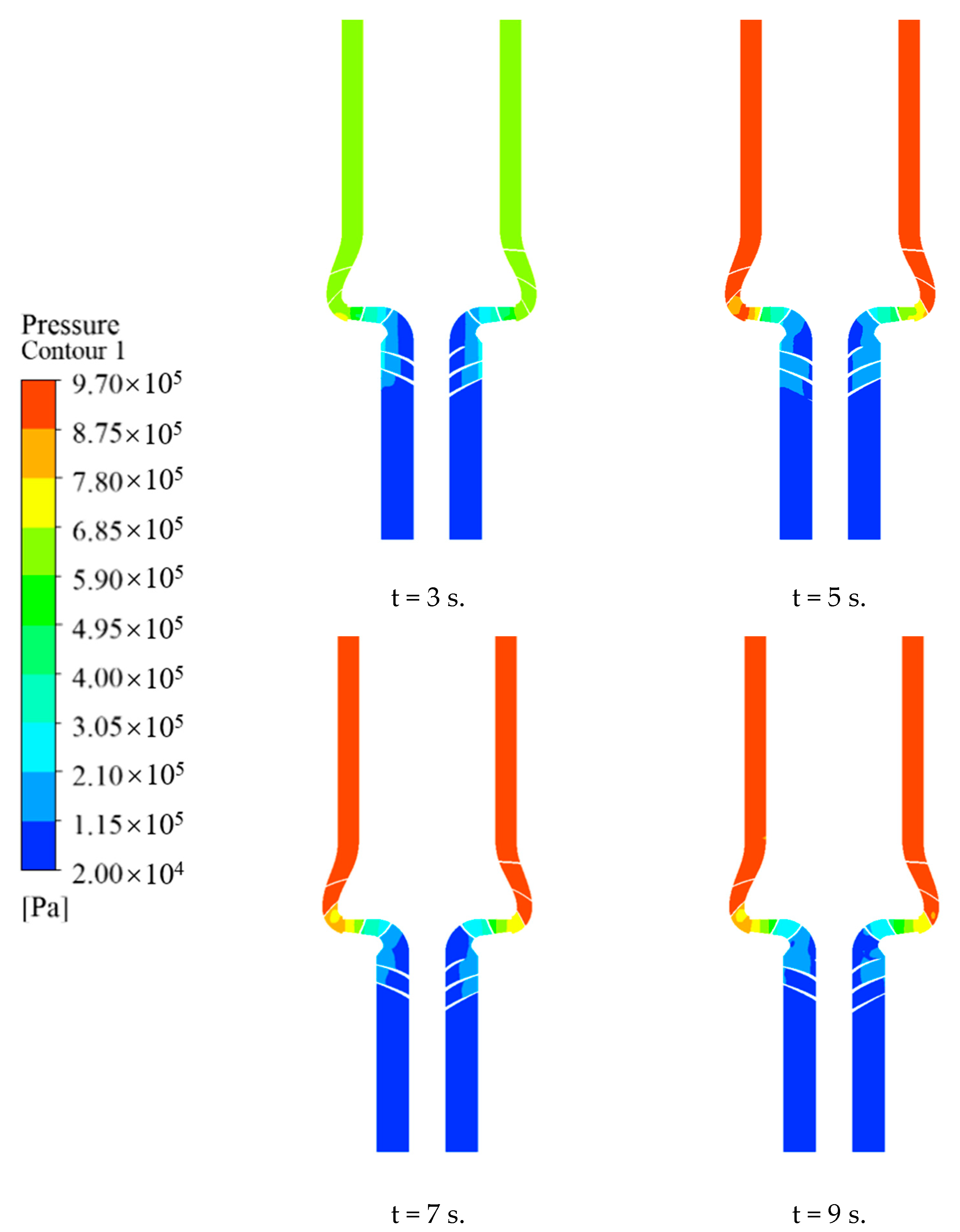
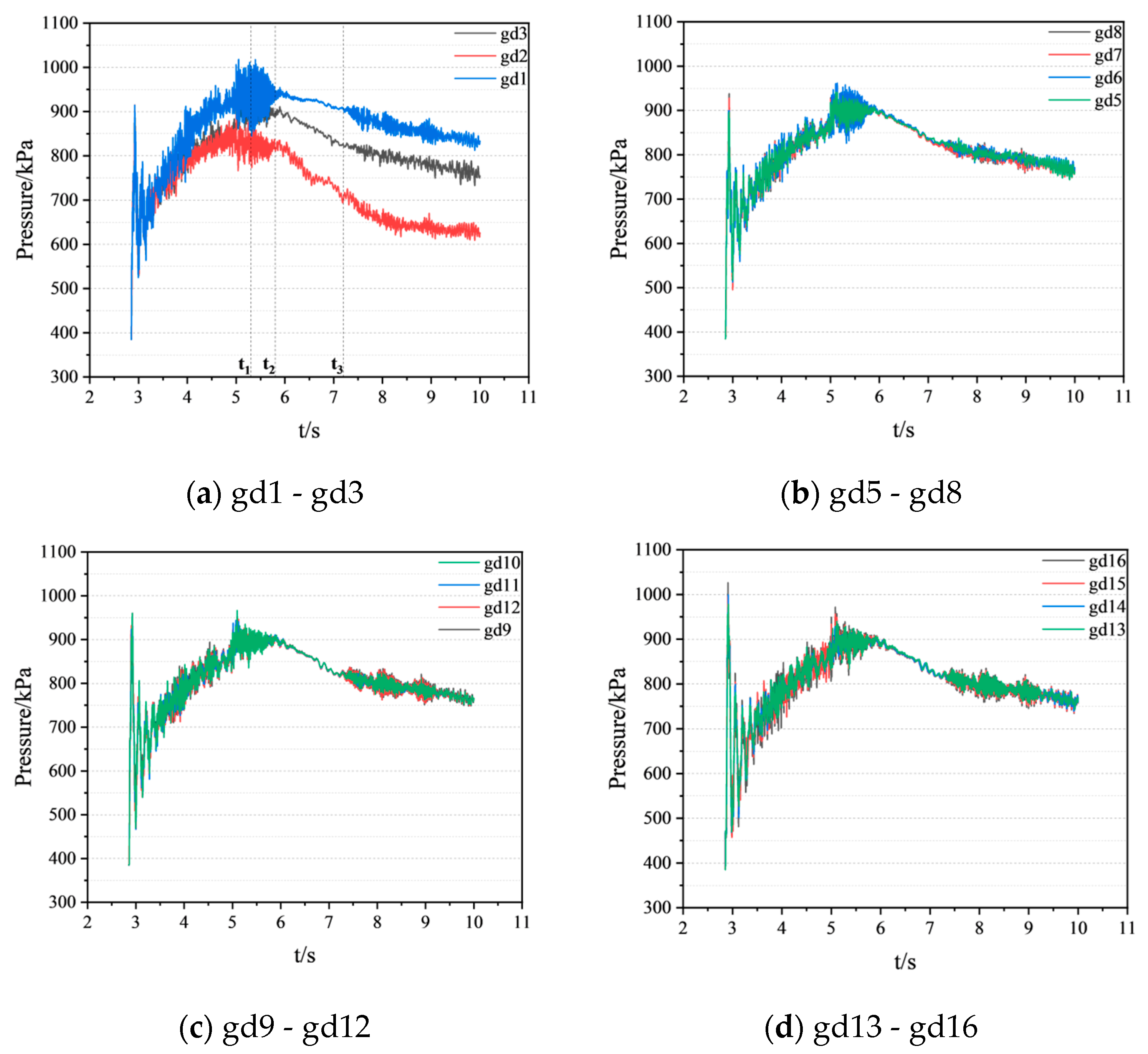
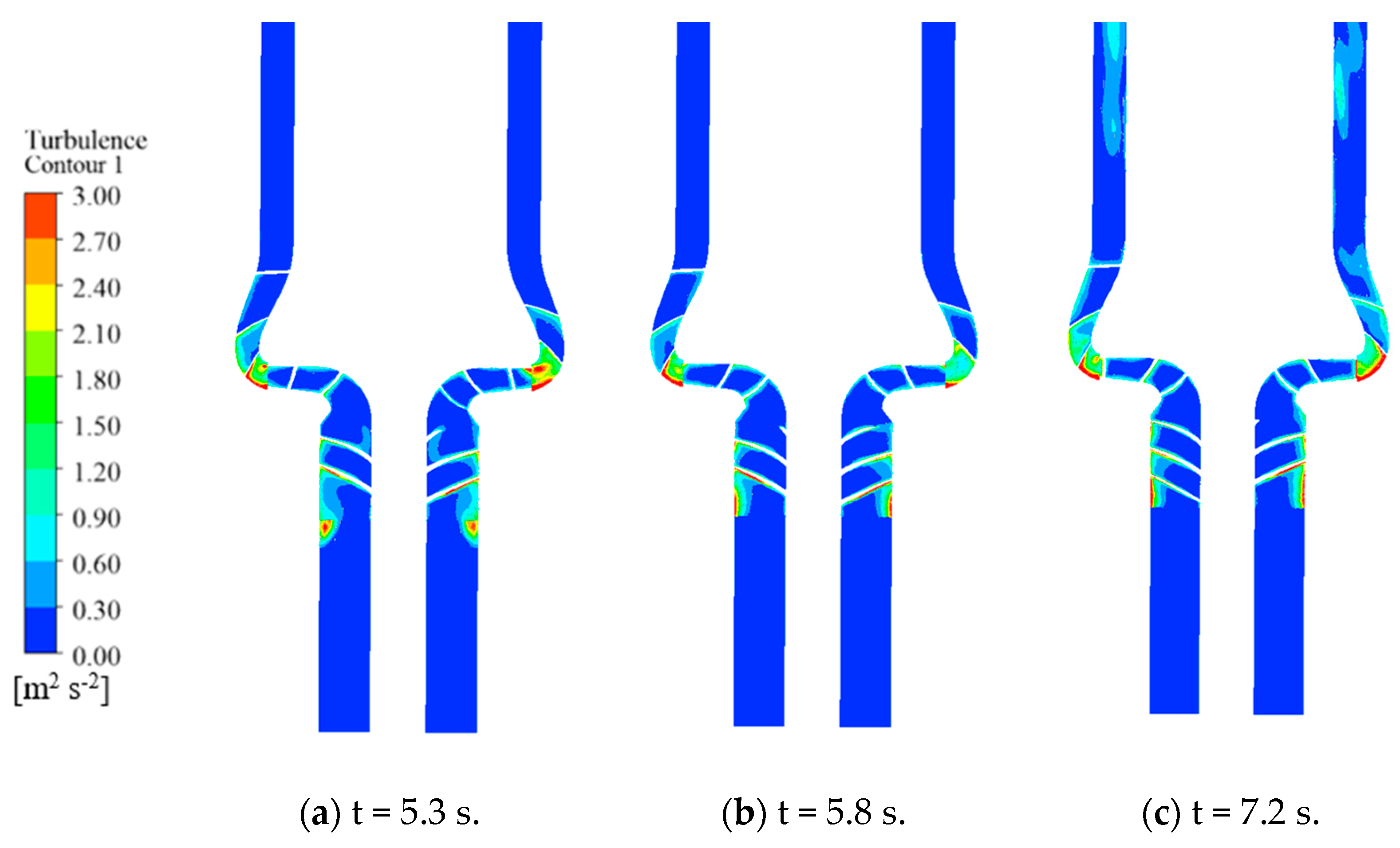
3.2. Flow Characteristics and Pressure Attenuation Within the Pipeline
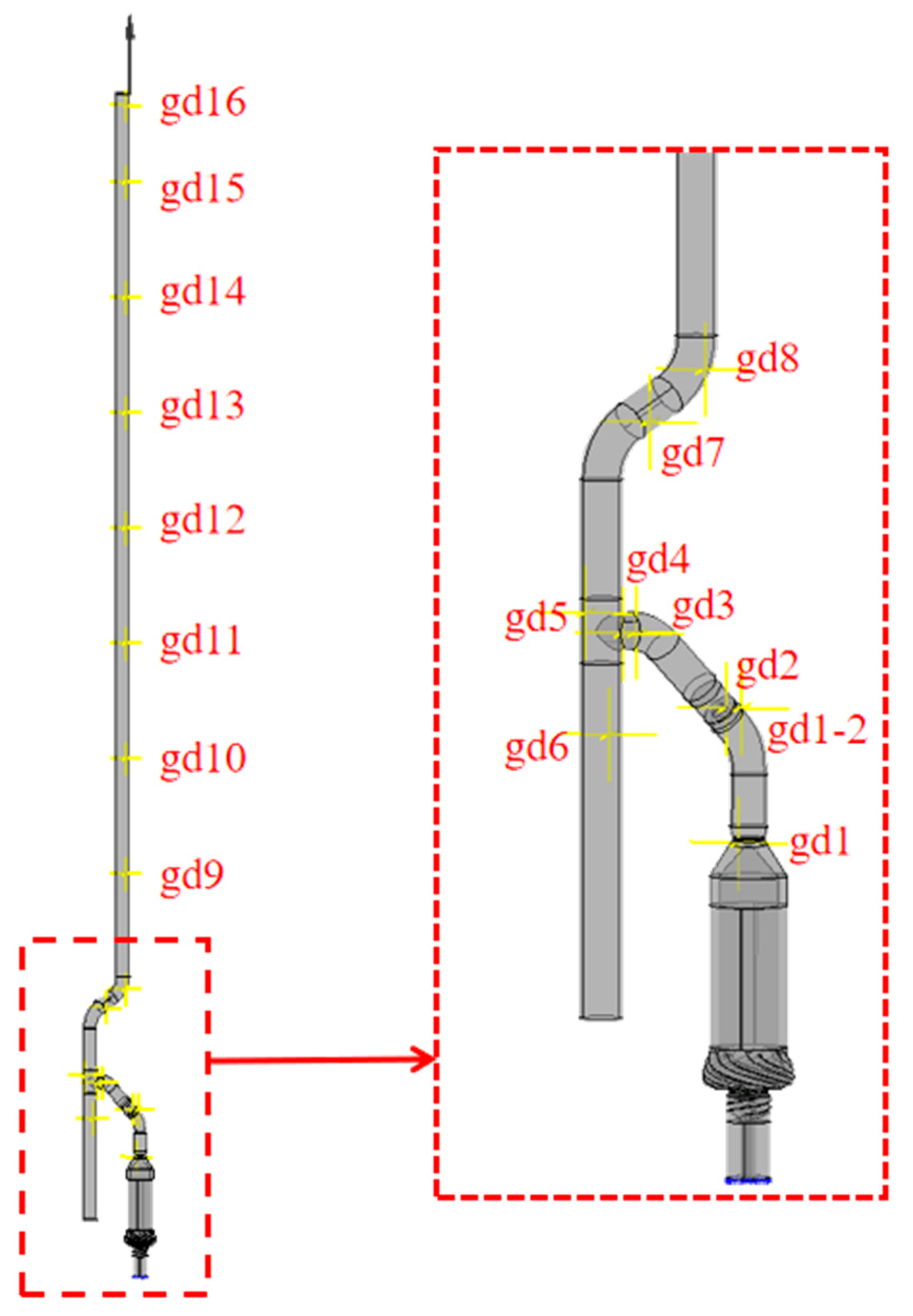
3.2.1. Monitoring Point Setup
3.2.2. Flow Analysis at the Pipeline Tee Junctions
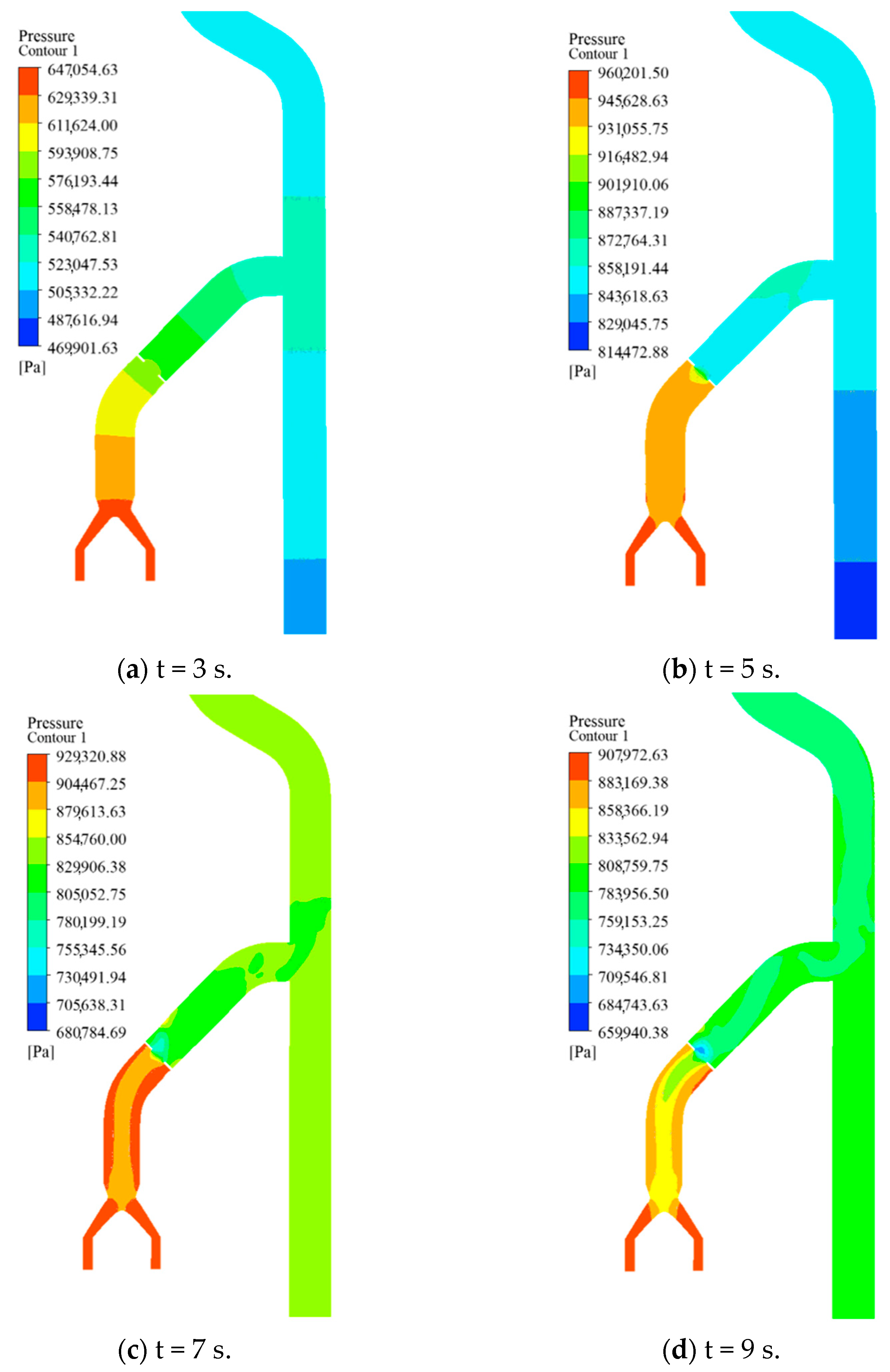
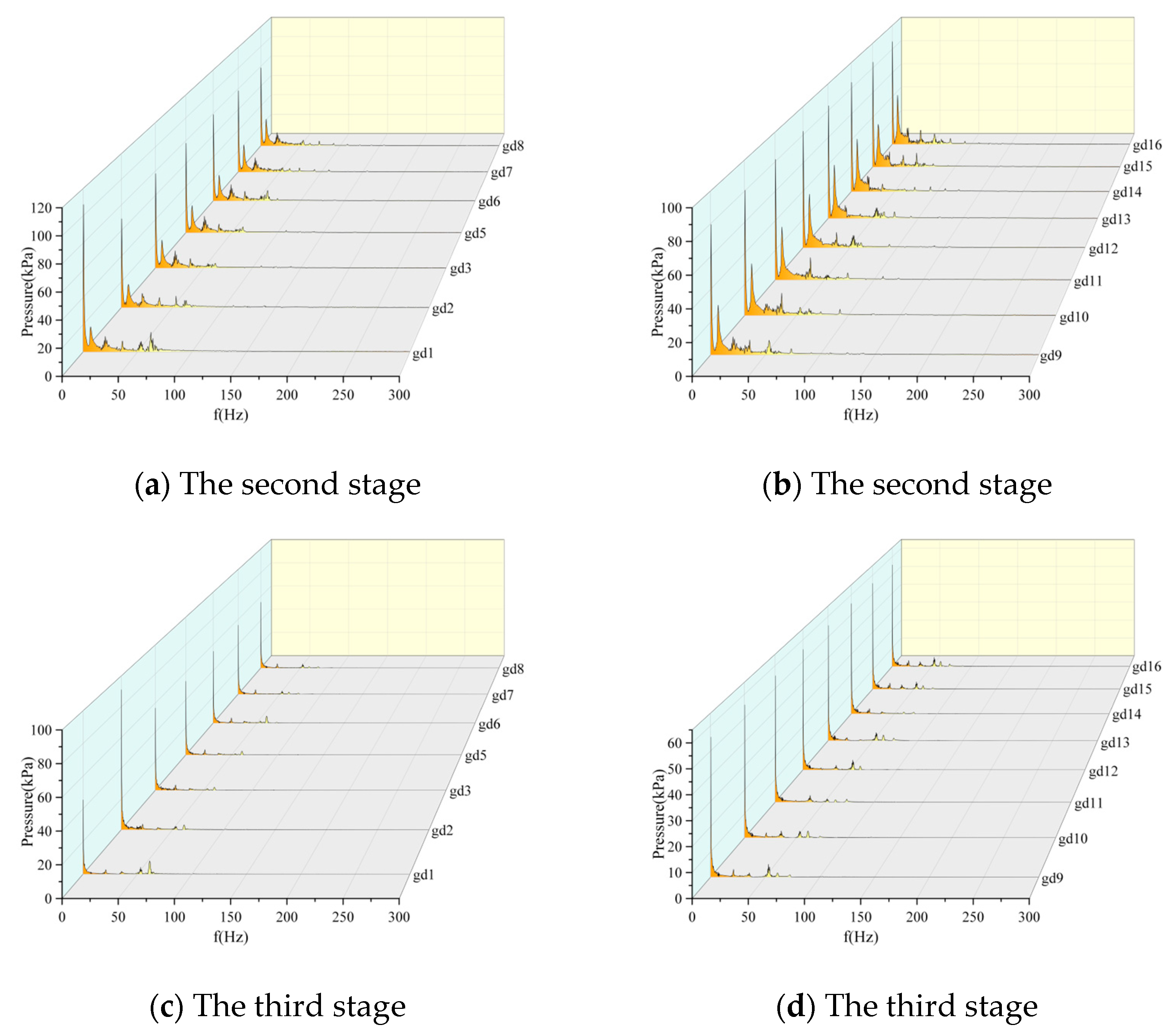
3.2.3. Pressure Wave Attenuation Within the Pipeline
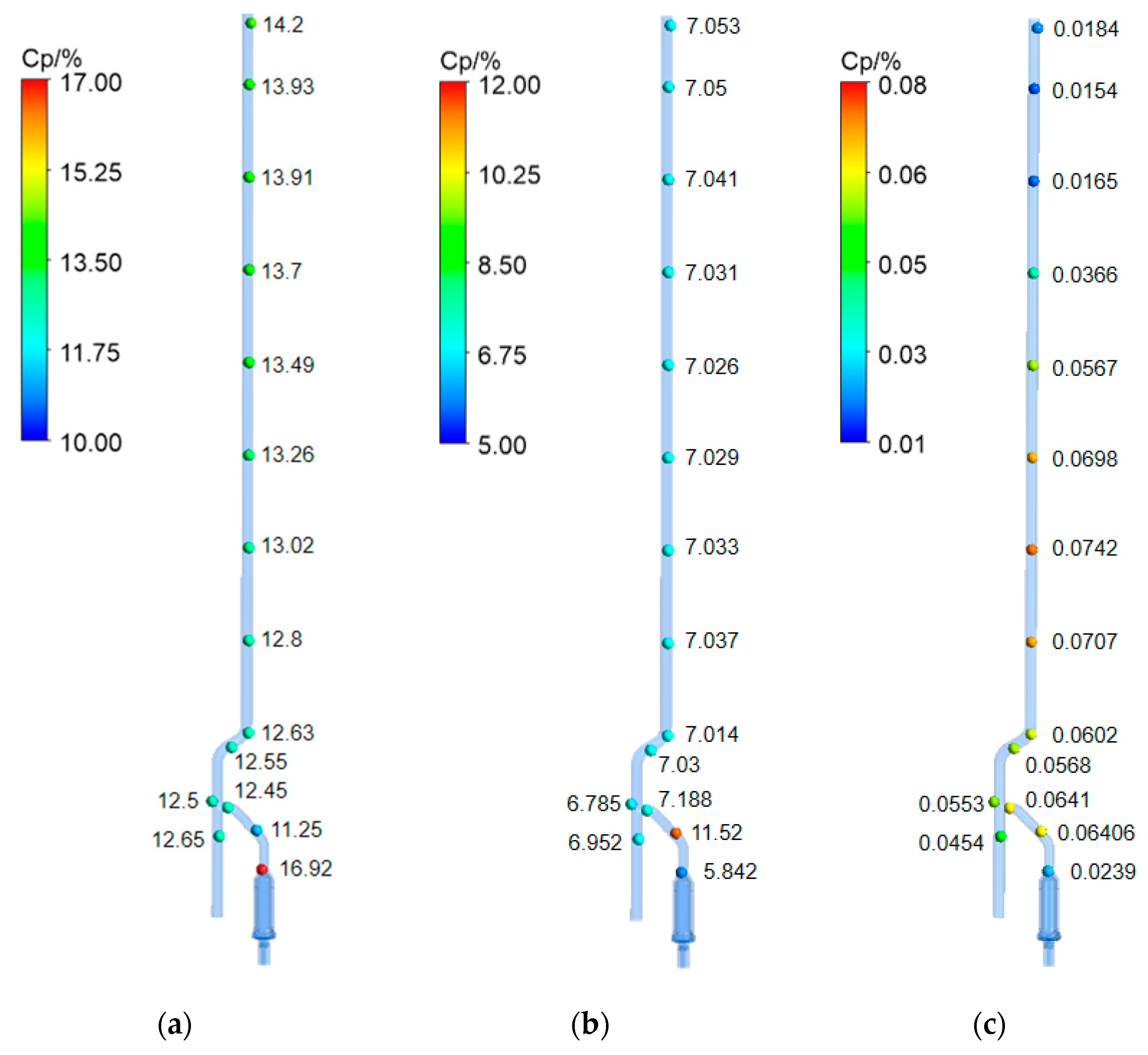
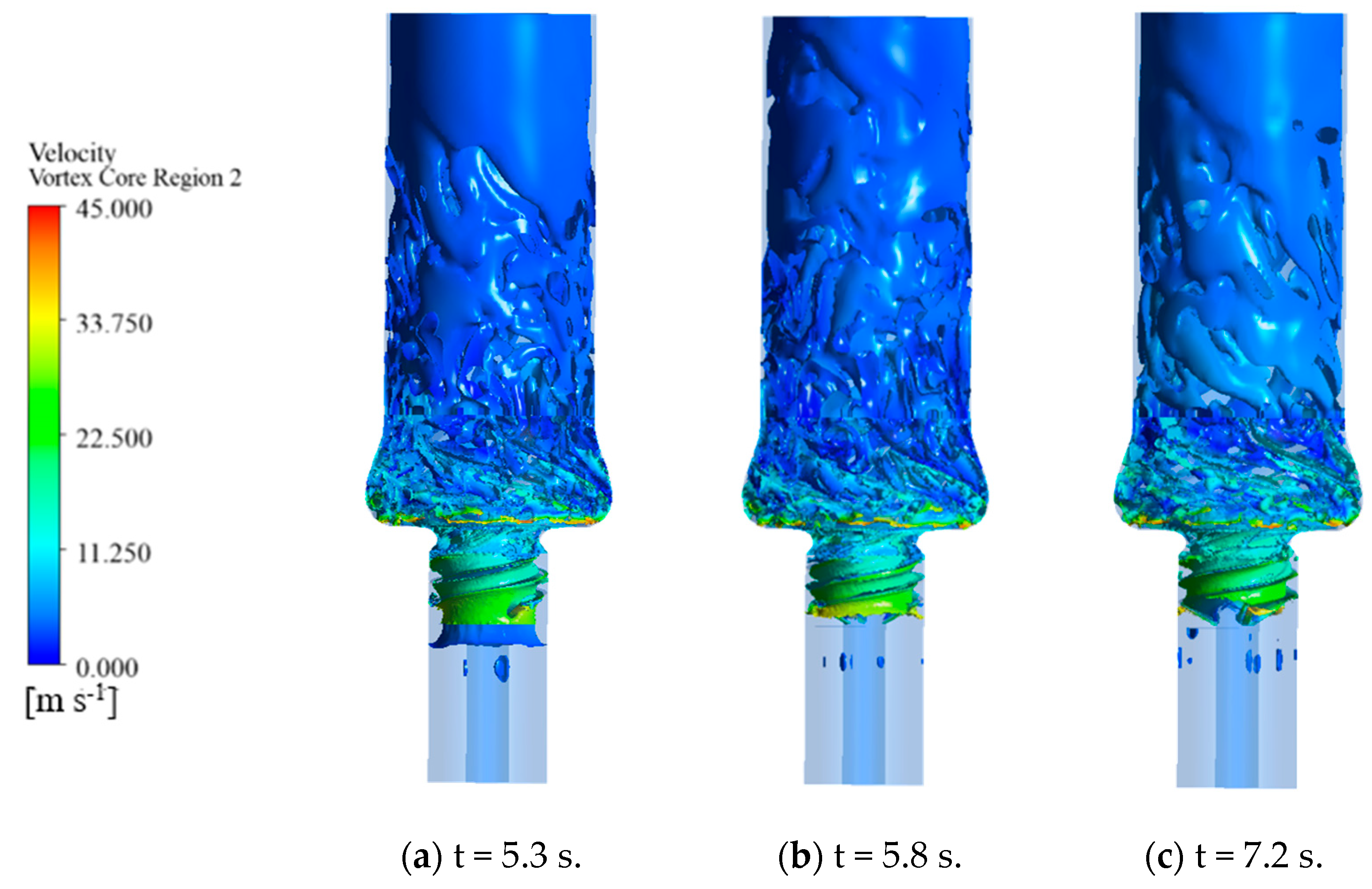
3.3. Influence of Pump Internal Flow Field on Pipeline Pressure
4. Conclusions
- During the start-up phase, significant fluctuations in head and torque were observed, particularly in the initial stages. The mass flow rate increased rapidly in the second stage and stabilized in the third stage. The internal flow patterns within the pump were visualized through streamlines and pressure contours. Complex flow structures, including vortices and recirculation zones, were identified during the early stages of start-up, which gradually stabilized as the flow rate and speed increased.
- Pressure pulsations within the pipeline were monitored at various locations. The pressure pulsation coefficients were found to vary significantly along the pipeline, with higher values near the pump outlet and lower values in the downstream sections. The pressure attenuation characteristics were analyzed in both time and frequency domains. The pressure pulsation coefficients in the straight pipe section (gd9–gd16) increased toward the pipeline outlet.
- The internal flow field of the LNG pump at three critical time points was examined to understand its impact on pipeline pressure fluctuations. High turbulent kinetic energy regions were identified in the inducer and impeller, which correlated with pressure pulsations in the pipeline. This study revealed that the initial transient flow conditions within the pump, which are characterized by high turbulence and flow separation, significantly influenced the pressure pulsations in the pipeline. As the flow stabilized, the pressure pulsations in the pipeline also decreased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Long, Y.; Wu, Z.G.; Zhang, M.Y.; Xu, Y. Research on the transient flow and vortex structure evolution mechanism of reactor coolant pump under non-uniform inflow. Ann. Nucl. Energy 2025, 217, 111346. [Google Scholar]
- Liu, M.; Tan, L.; Zhao, X.C.; Ma, C.; Gou, J.L. Theoretical model on transient performance of a centrifugal pump under start-up conditions in pumped-storage system. Energy 2024, 299, 131452. [Google Scholar] [CrossRef]
- Chai, B.D.; Yan, J.H.; Wang, X.H. Force characteristics of centrifugal pump as turbine during start-up process under gas-liquid two-phase conditions. Actuators 2022, 11, 370. [Google Scholar] [CrossRef]
- Farhadi, K.; Bousbia-Salah, A.; D’Auria, F. A model for the analysis of pump start-up transients in Tehran Research Reactor. Prog. Nucl. Energy 2007, 49, 499–510. [Google Scholar] [CrossRef]
- Fu, S.F.; Zheng, Y.; Kan, K.; Chen, H.X.; Han, X.X.; Liang, X.L.; Liu, H.W.; Tian, X.Q. Numerical simulation and experimental study of transient characteristics in an axial flow pump during start-up. Renew. Energy 2020, 146, 1879–1887. [Google Scholar] [CrossRef]
- Elaoud, S.; Hadj-Taïeb, E. Influence of pump starting times on transient flows in pipes. Nucl. Eng. Des. 2011, 241, 3624–3631. [Google Scholar] [CrossRef]
- Kittredge, C.P. Hydraulic transients in centrifugal pump systems. J. Fluids Eng. 1956, 78, 1307–1320. [Google Scholar] [CrossRef]
- Cao, J.W.; Luo, Y.Y.; Shi, Y.S.; Liu, X.; Xu, D.X.; Wang, Y.H.; Zhai, L.M.; Wang, Z.W. A review of hydro-turbine unit rotor system dynamic behavior: Multi-field coupling of a three-dimensional model. Phys. Fluids 2024, 36, 121304. [Google Scholar] [CrossRef]
- Zhou, D.B.; Zhang, N.; Zheng, F.K.; Gad, M.; Gao, B. Experimental investigation on the effect of the rotor-stator matching mode on velocity pulsation in the centrifugal pump with a vaned diffuser. Nucl. Eng. Technol. 2025, 57, 103255. [Google Scholar] [CrossRef]
- Li, D.L.; Zhang, N.; Jiang, J.X.; Gao, B.; Akurugo Alubokin, A.; Zhou, W.J.; Shi, J.L. Numerical investigation on the unsteady vortical structure and pressure pulsations of a centrifugal pump with the vaned diffuser. Int. J. Heat Fluid Flow 2022, 98, 109050. [Google Scholar] [CrossRef]
- Wang, W.J.; Liu, S.; Pei, J.; Sun, J.; Sun, Q. Efficiency improvement and pressure pulsation reduction of volute centrifugal pump through diffuser design optimization. J. Energy Storage 2024, 102, 114184. [Google Scholar] [CrossRef]
- Yan, J.; Koutnik, J.; Seidel, U.; Hübner, B. Compressible simulation of rotor-stator interaction in pump-turbines. Int. J. Fluid Mach. Syst. 2010, 3, 315–323. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Hua, L.; Zhang, D.M. Three-dimensional flow breakup characteristics of a circular jet with different nozzle geometries. Biosyst. Eng. 2020, 193, 216–231. [Google Scholar] [CrossRef]
- Xu, L.Z.; Hansen, A.C.; Li, Y.M.; Liang, Z.W.; Yu, L.J. Numerical and experimental analysis of airflow in a multi-duct cleaning system for a rice combine harvester. Trans. ASABE 2016, 59, 1101–1110. [Google Scholar]
- Long, Y.; Xu, Y.; Guo, X.A.; Zhang, M.Y. Analysis of internal flow excitation characteristics of reactor coolant pump based on POD. Ann. Nucl. Energy 2025, 216, 111286. [Google Scholar]
- Lu, Y.G.; Xin, L.C.; Hu, N.M.; Zhu, Z.X.; Xia, W.X. Influences of floating ice on the water entry process of slender body on the cavity evolution and hydrodynamic characteristic. Phys. Fluids 2025, 37, 042103. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, Y.Y.; Liu, J.P.; Zhao, Y.X.; Hussain, Z.; Xie, R.J. Numerical simulation of the flow field stabilization of a pressure-regulating device. Agriculture 2024, 14, 1873. [Google Scholar] [CrossRef]
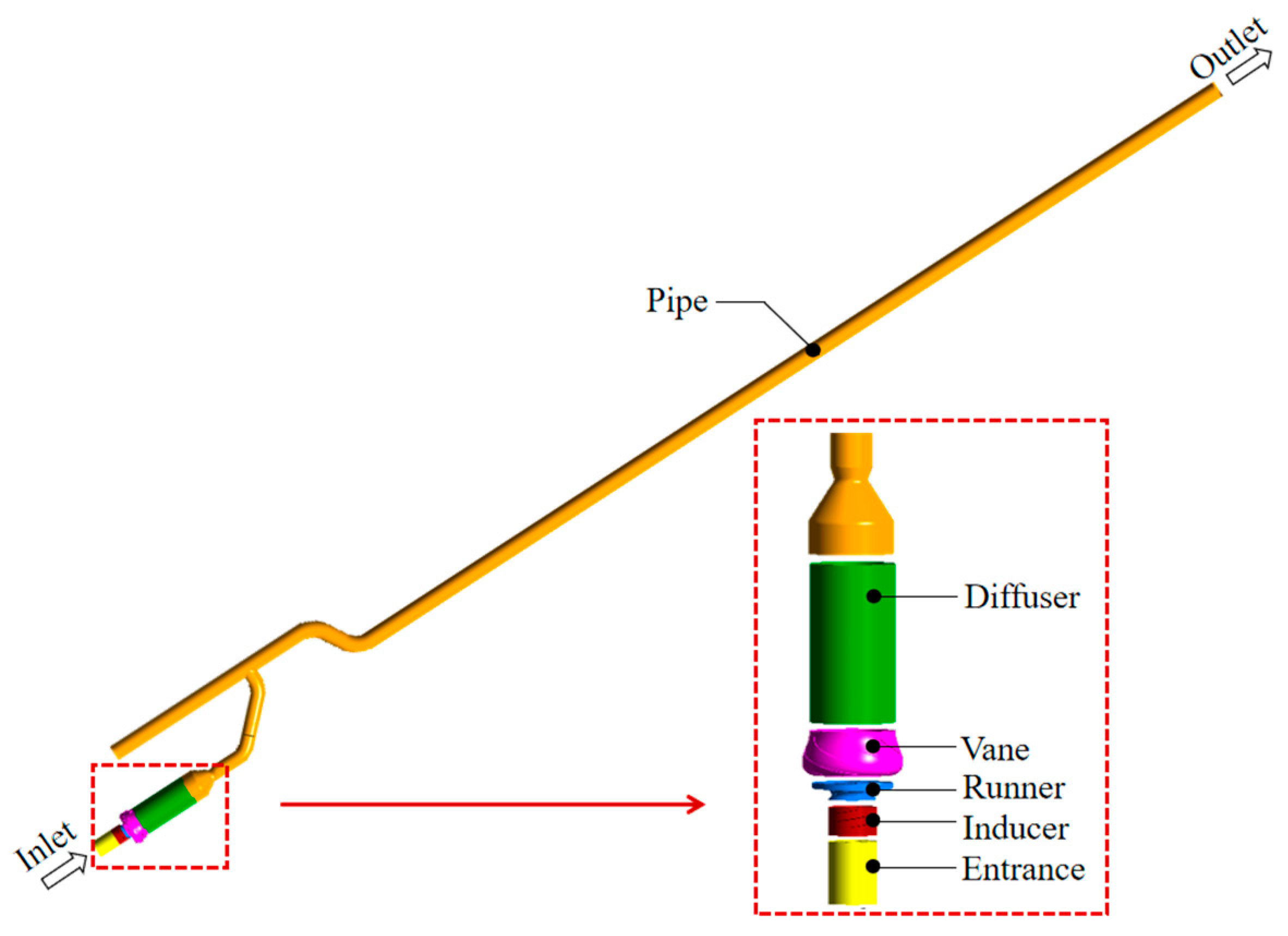
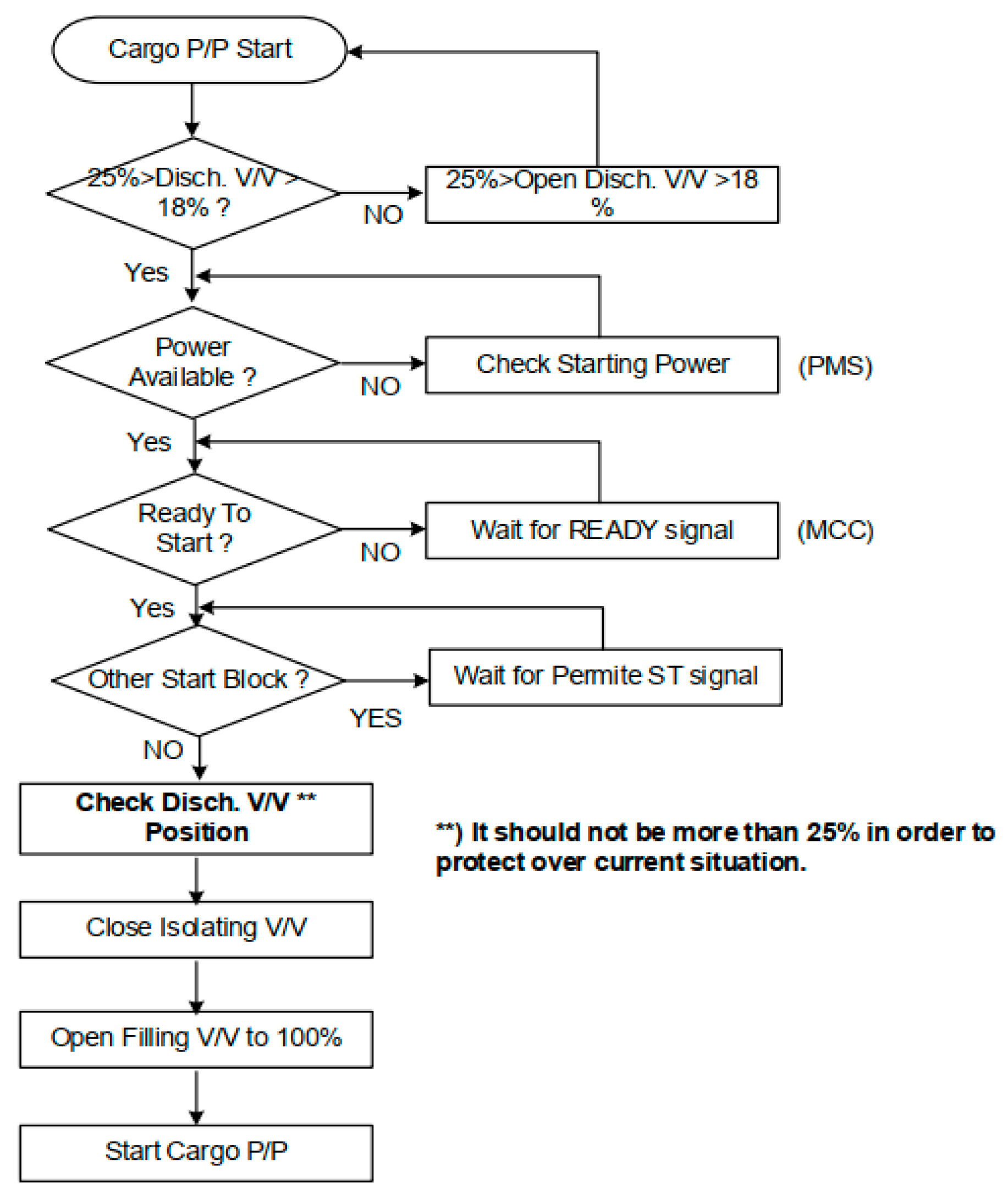
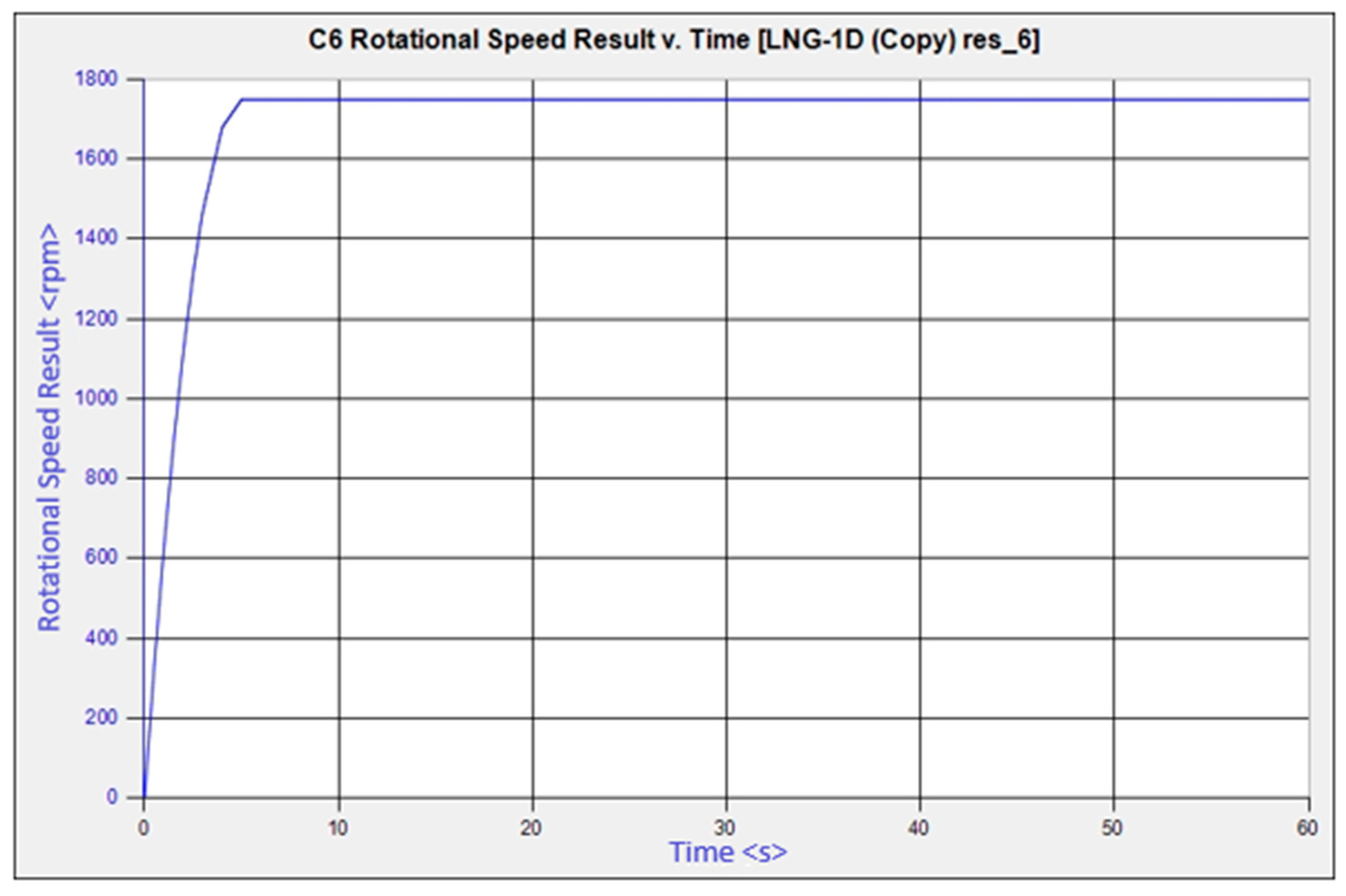
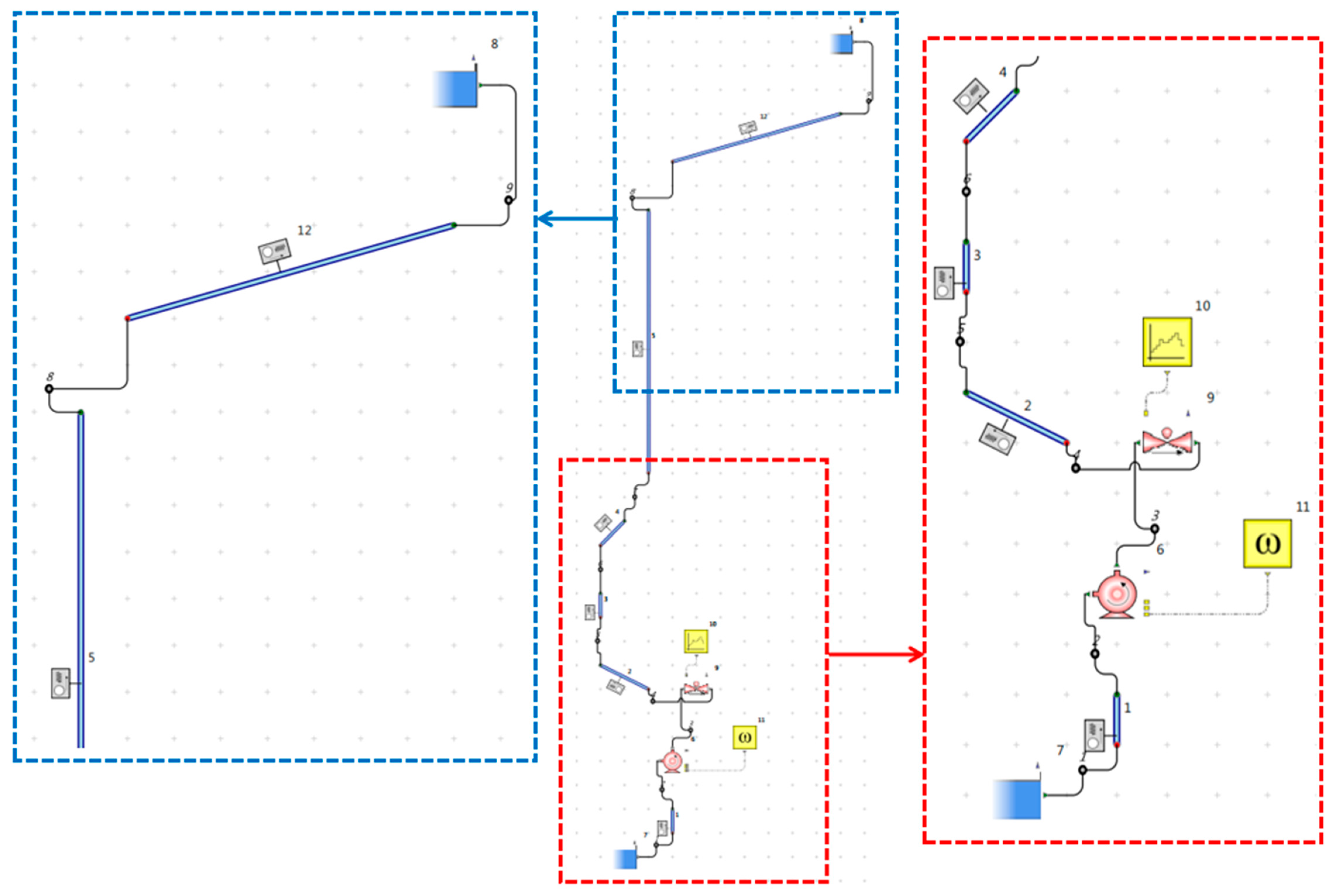
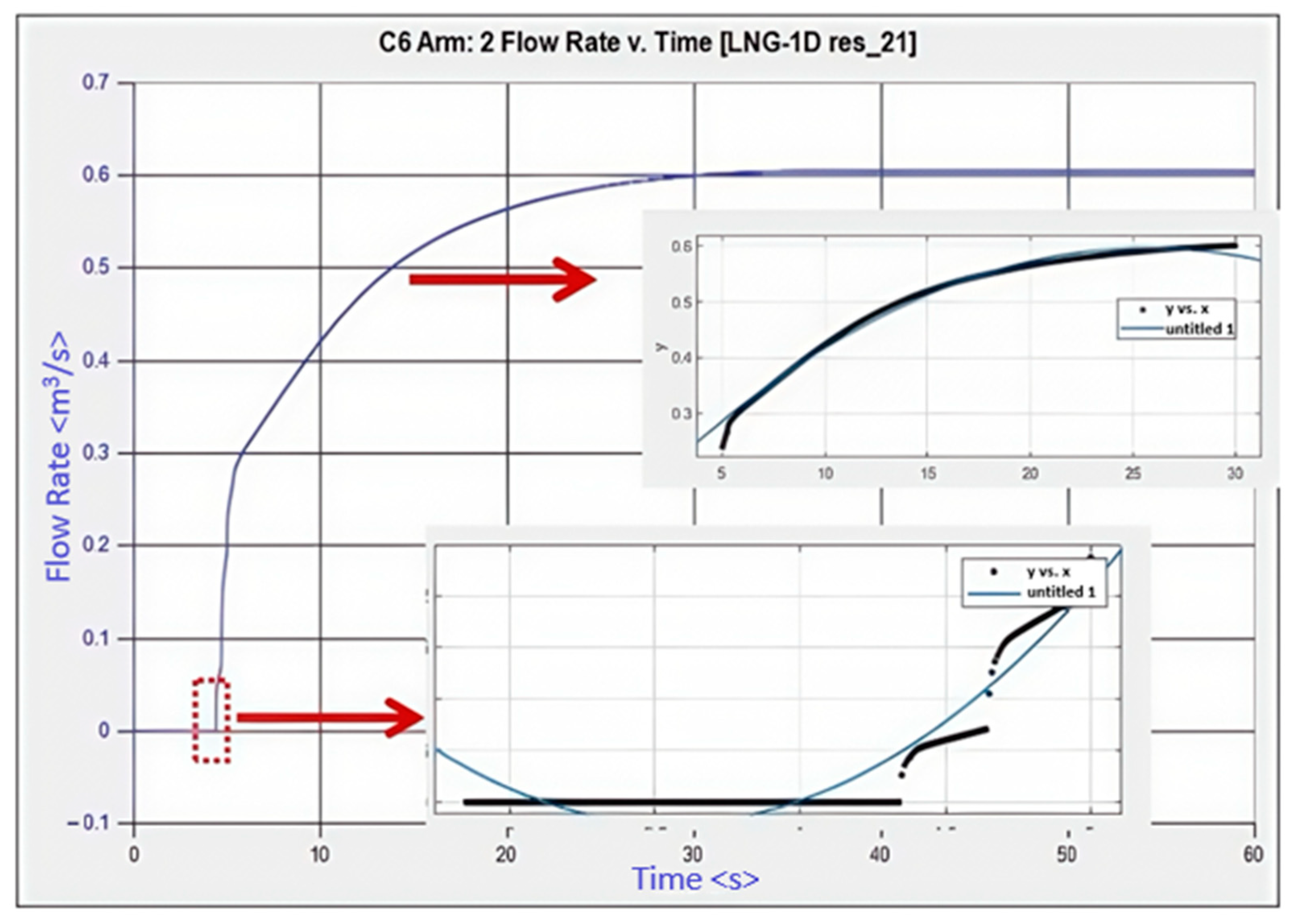
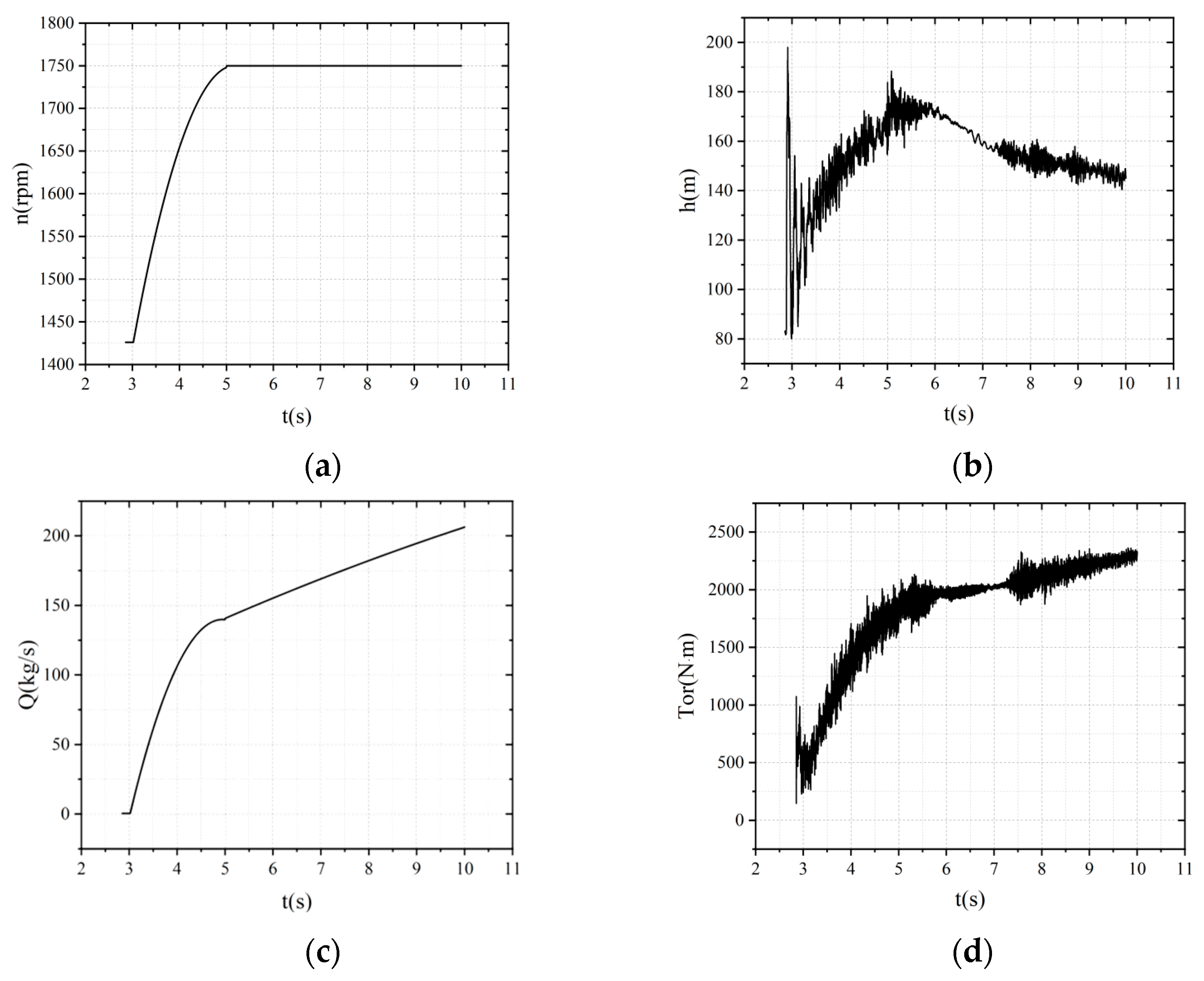
| Stage | Valve Opening | Flow Rate Q (kg/s) | Rotational Speed n (r/min) |
|---|---|---|---|
| 1: 0 s < t < 2.85 s | 0% | 0 | −0.06899 × t2+ 350.5 × t − 0.1542 |
| 2: 2.85 s < t < 5 s | 20% | 0.1094 × t2 − 0.7775 × t + 1.361 | −0.06899 × t2+ 350.5 × t − 0.1542 |
| 3: 5 s < t < 10 s | 20% | −0.0007175 × t2 + 0.037 × t + 0.1183 | 1750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Min, M.; Song, W.; Zhao, Y.; Wang, Z. A Study on the Hydrodynamic Excitation Characteristics of Pump and Pipeline Systems Considering the Weakly Compressible Fluid During the Pump Start-Up Condition. Energies 2025, 18, 2911. https://doi.org/10.3390/en18112911
Lu Y, Min M, Song W, Zhao Y, Wang Z. A Study on the Hydrodynamic Excitation Characteristics of Pump and Pipeline Systems Considering the Weakly Compressible Fluid During the Pump Start-Up Condition. Energies. 2025; 18(11):2911. https://doi.org/10.3390/en18112911
Chicago/Turabian StyleLu, Yonggang, Mengjiao Min, Wei Song, Yun Zhao, and Zhengwei Wang. 2025. "A Study on the Hydrodynamic Excitation Characteristics of Pump and Pipeline Systems Considering the Weakly Compressible Fluid During the Pump Start-Up Condition" Energies 18, no. 11: 2911. https://doi.org/10.3390/en18112911
APA StyleLu, Y., Min, M., Song, W., Zhao, Y., & Wang, Z. (2025). A Study on the Hydrodynamic Excitation Characteristics of Pump and Pipeline Systems Considering the Weakly Compressible Fluid During the Pump Start-Up Condition. Energies, 18(11), 2911. https://doi.org/10.3390/en18112911








