A Two-Stage Planning Method for Rural Photovoltaic Inspection Path Planning Based on the Crested Porcupine Algorithm
Abstract
1. Introduction
2. Multi-Regional PV Inspection Planning Model
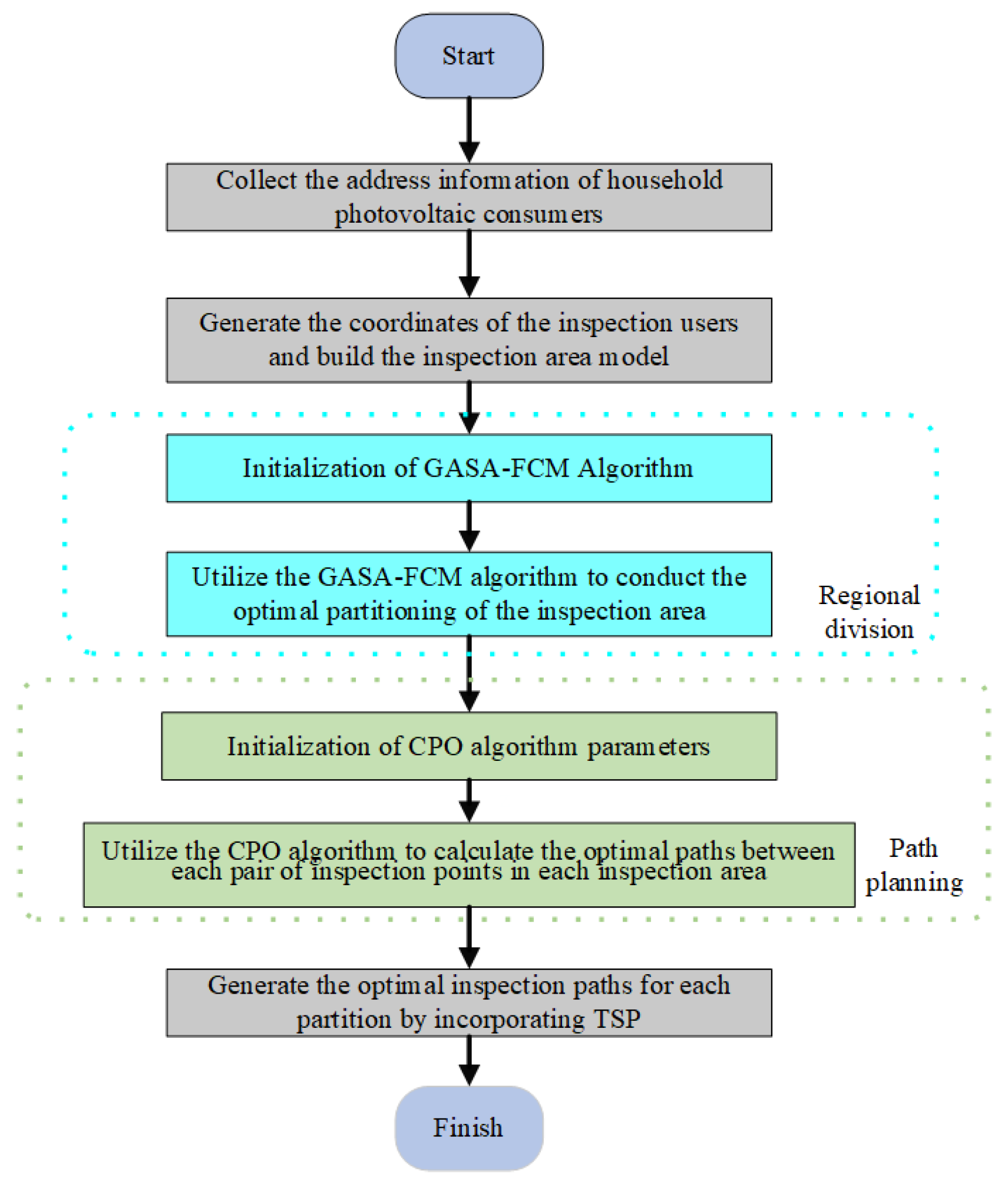
2.1. Overall Process
2.2. Regional Division Model Based on the GASA-FCM Algorithm
Fuzzy C-Means Clustering
2.3. Clustering Validity Evaluation Metrics
Silhouette Coefficient
2.4. Path Planning Algorithm Model
2.4.1. Initialization
2.4.2. Cyclic Population Reduction Technique
2.4.3. Exploration Phase
2.4.4. Development Phase
3. Simulation Results and Analysis
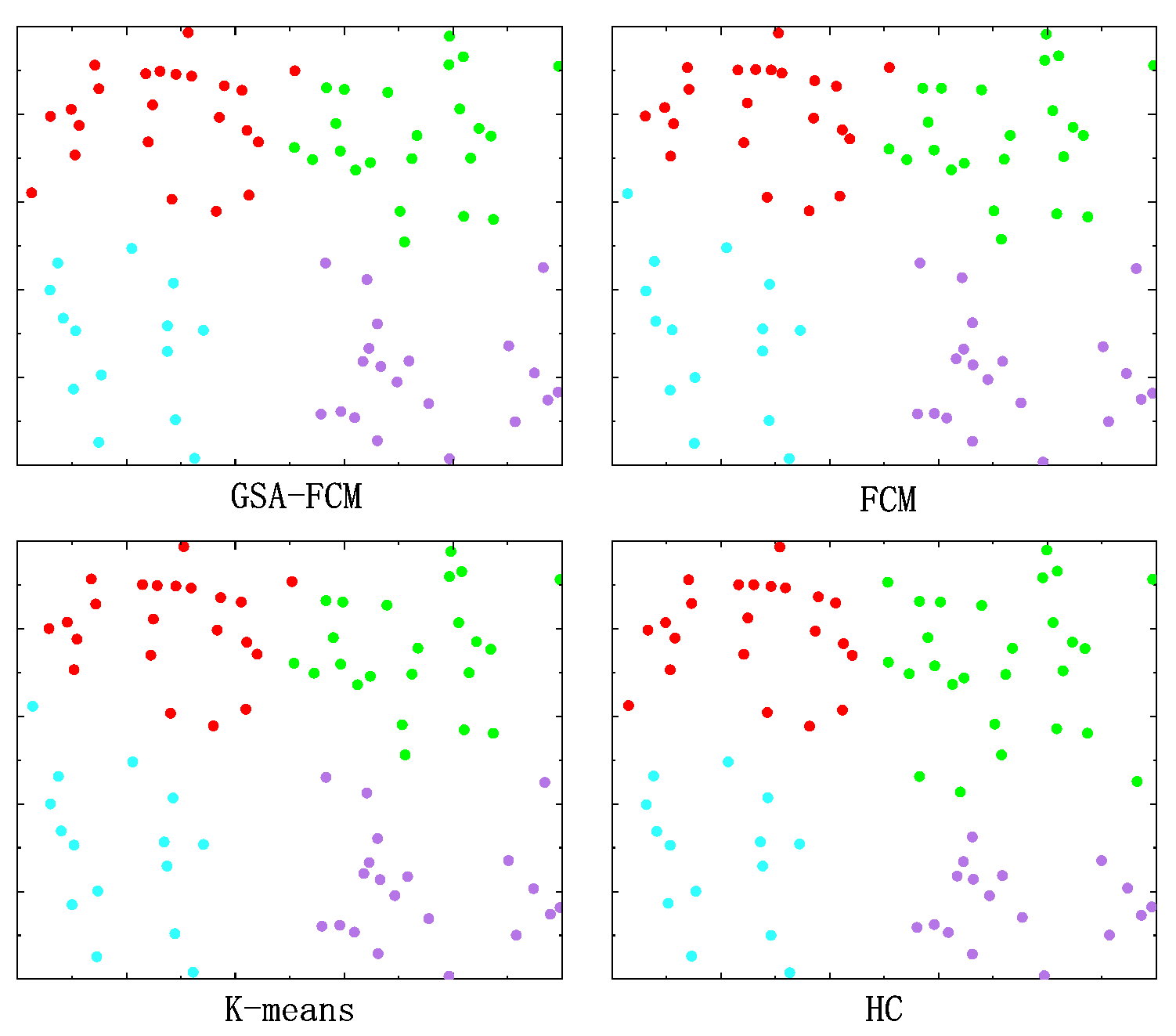
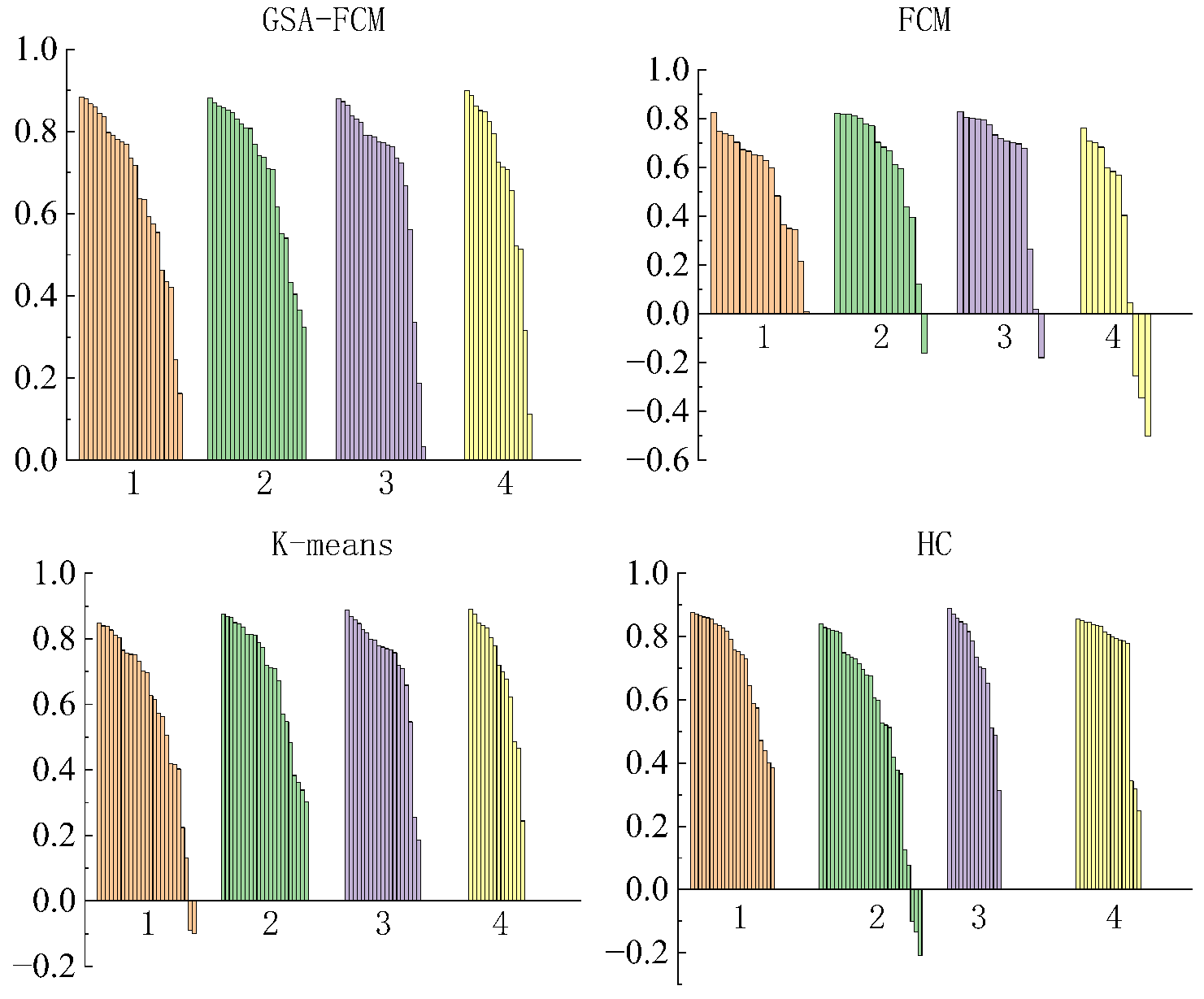
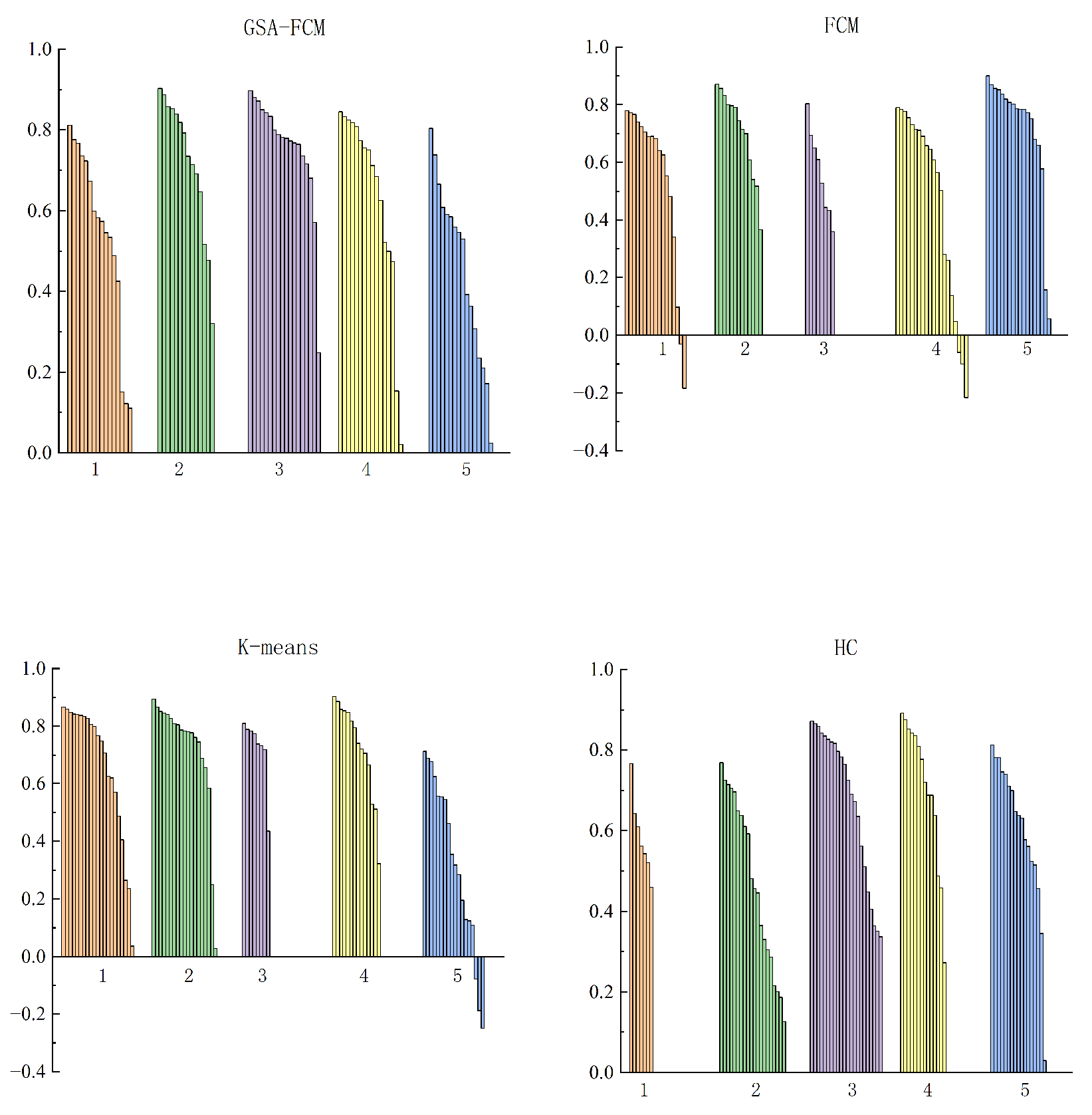
3.1. Clustering Algorithm Simulation Experiments
Comparison of Average Silhouette Values of Four Clustering Algorithms
3.2. Path Planning Simulation Experiments
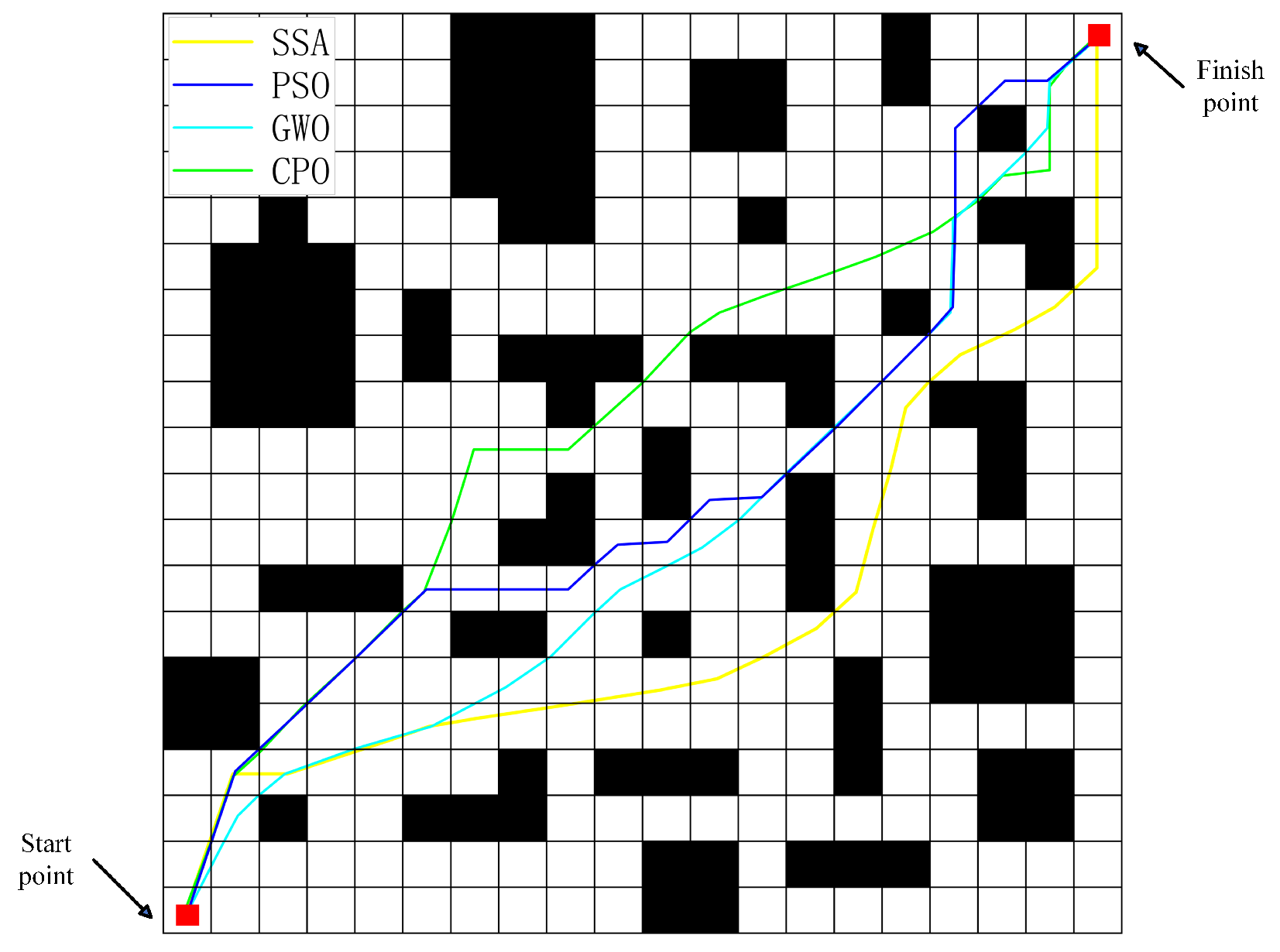
3.2.1. The 20 × 20 Simulation Environment
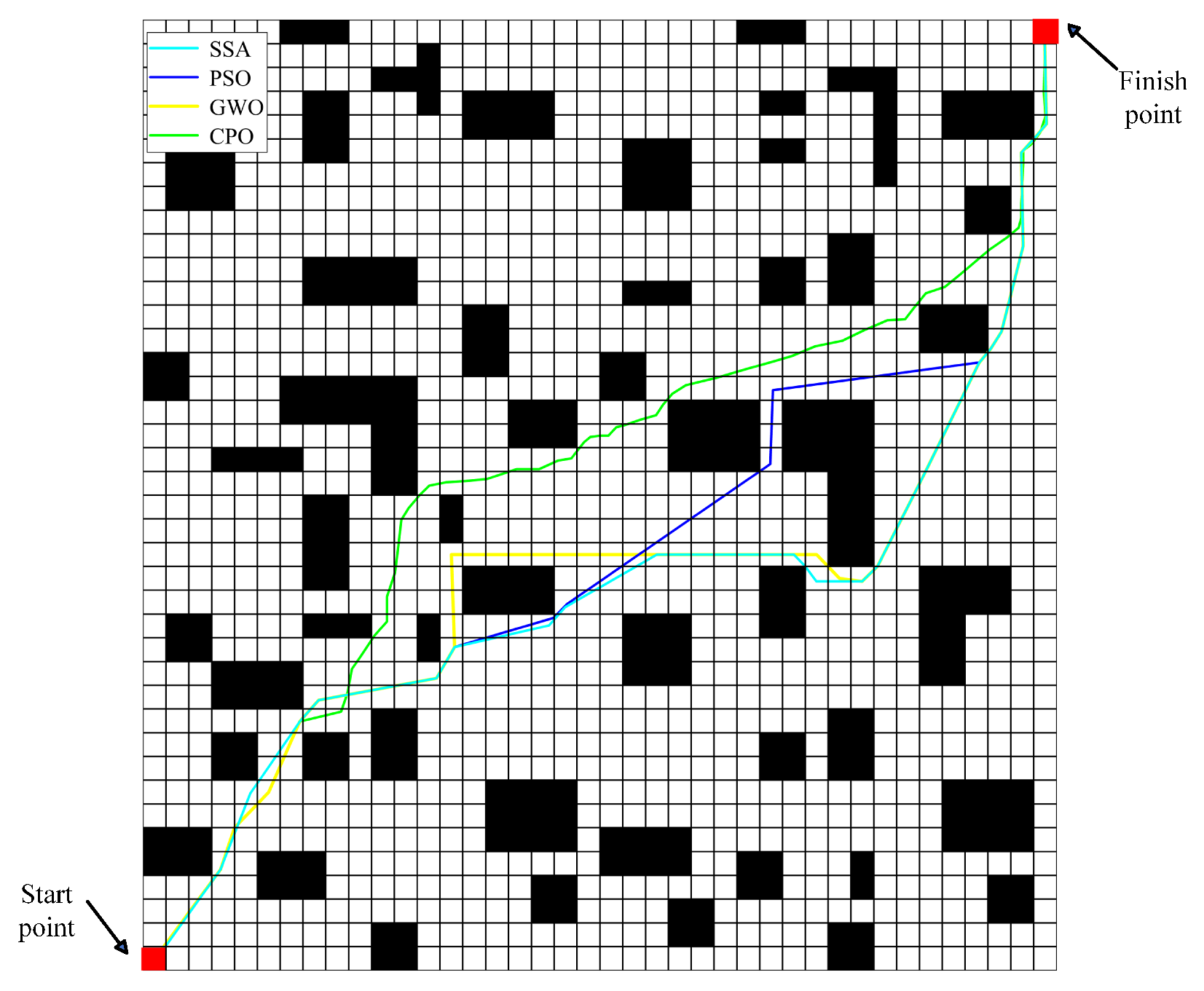
3.2.2. The 40 × 40 Simulation Environment
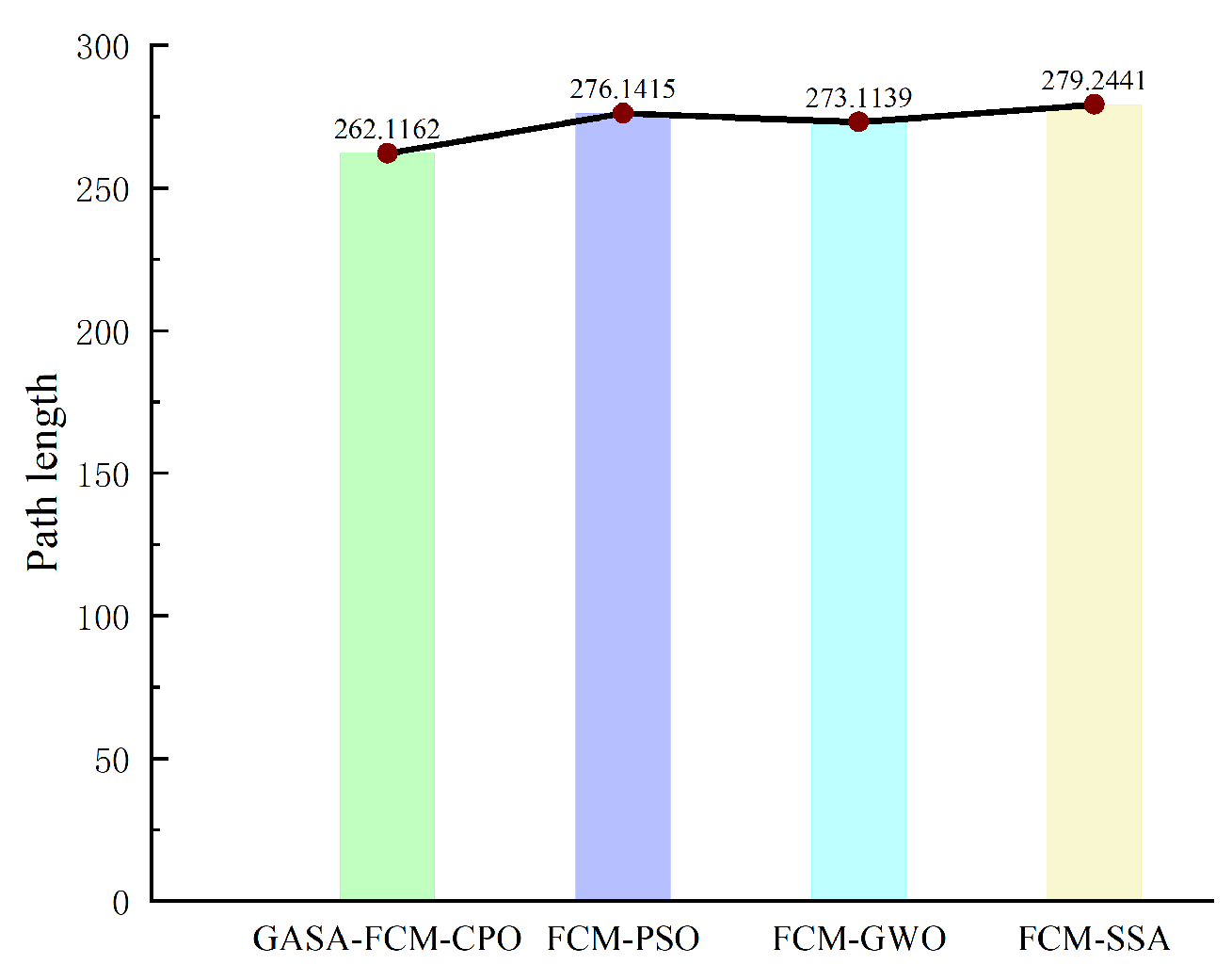
3.3. Comprehensive Simulation Experiments
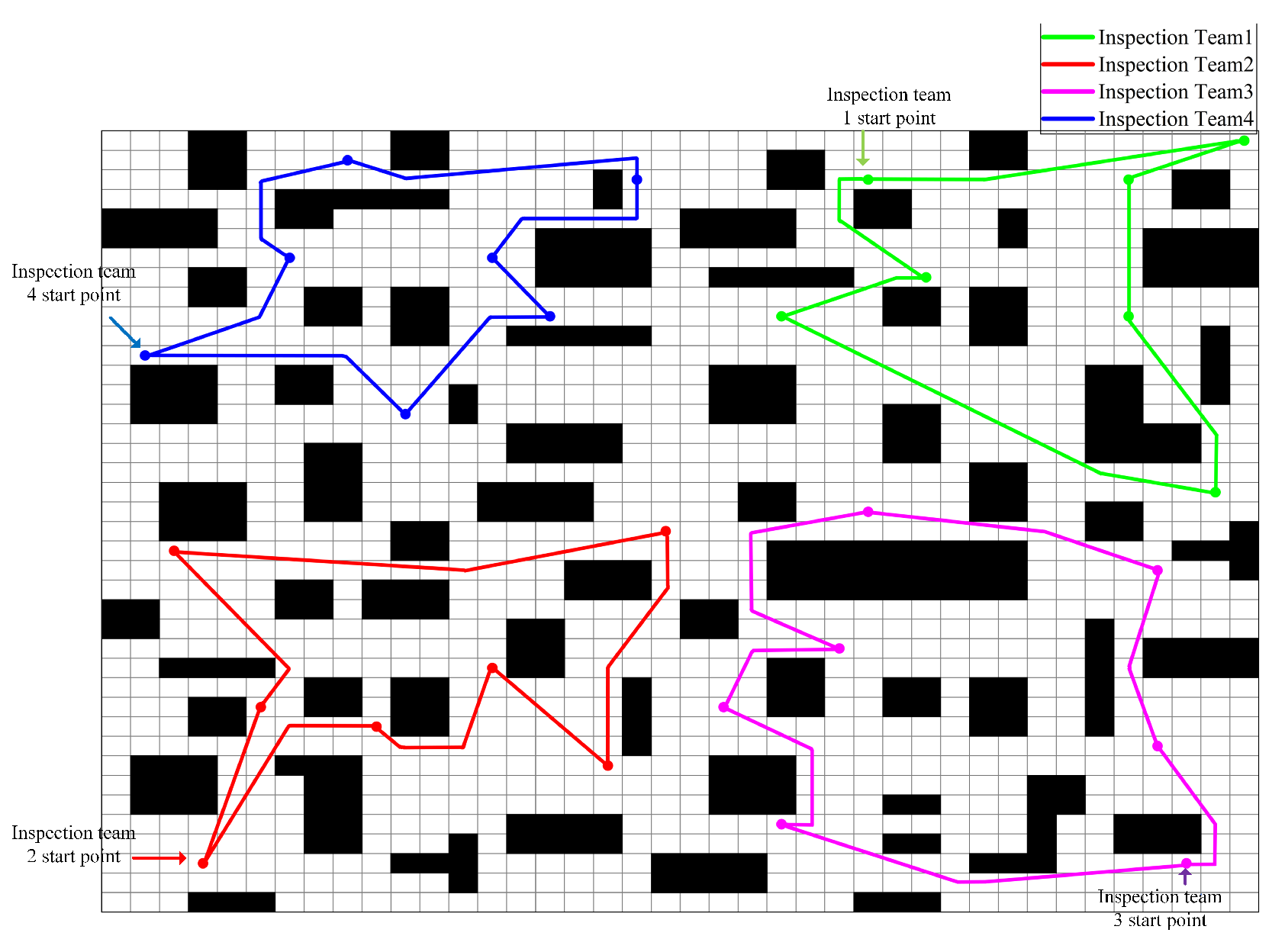
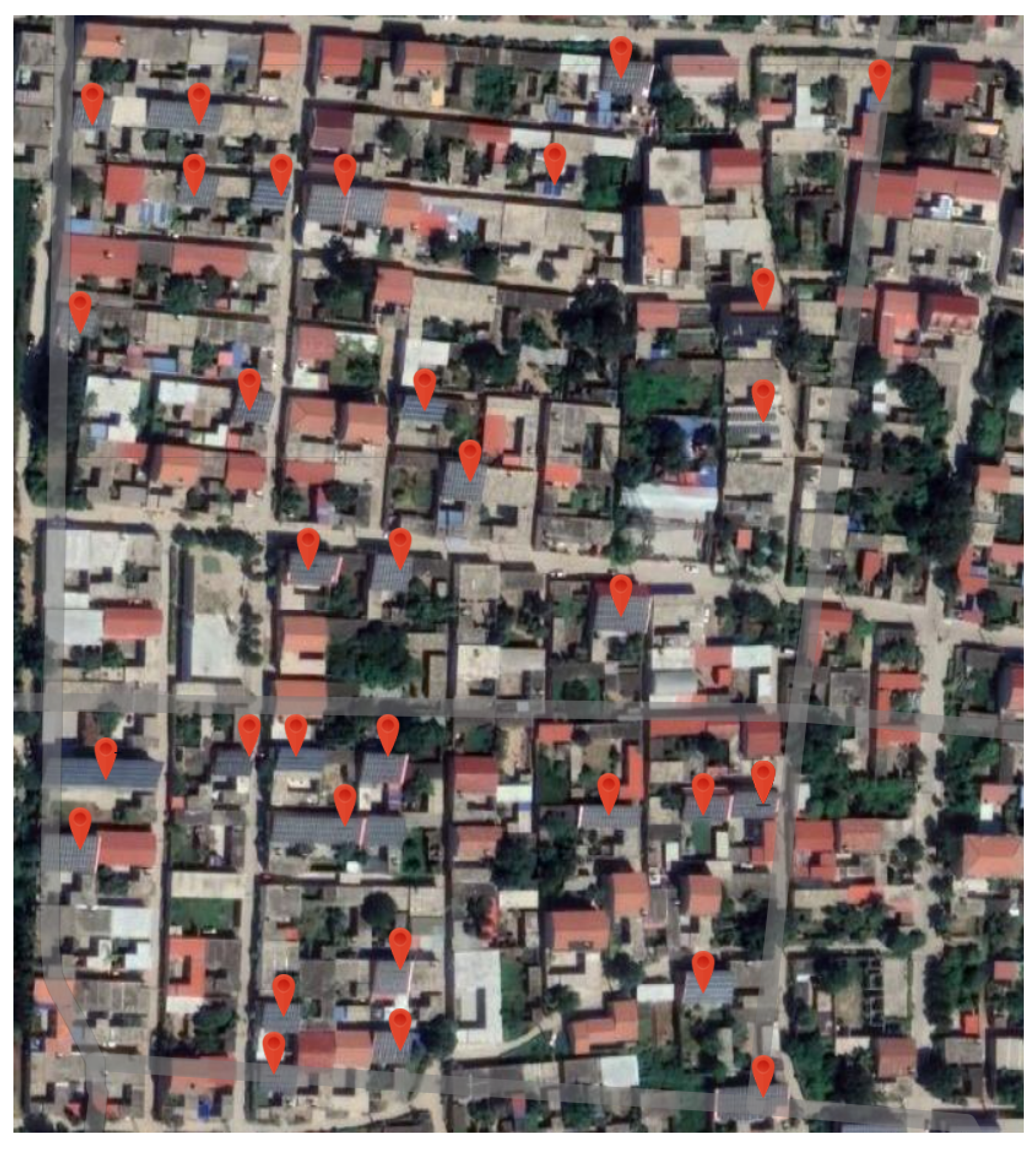
3.4. Practical Case Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, L.; Geng, Y.; Zhang, Y.; Zhang, Y.; Wang, H. Testing the effectiveness of deploying distributed photovoltaic power systems in residential buildings: Evidence from rural China. Environ. Impact Assess. Rev. 2024, 104, 107300. [Google Scholar] [CrossRef]
- Zhu, T.; Chang, X.; Zhu, F.; Shen, Y.; Zhu, L.; Xu, C. Empirical study on sustainable energy development goals: Analysis of rural roof distributed photovoltaic systems in Jiangsu, China. Phys. Chem. Earth 2024, 136, 103711–103720. [Google Scholar] [CrossRef]
- Su, X.; Liu, P.; Mei, Y.; Chen, J. The role of rural cooperatives in the development of rural household photovoltaics: An evolutionary game study. Energy Econ. 2023, 126, 106962. [Google Scholar] [CrossRef]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Li, Z. Two stage stochastic Energy scheduling for multi energy rural microgrids with irrigation systems and biomass fermentation. Energy Econ. 2025, 16, 1075–1087. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling Salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 4, 100369–100380. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Chen, Z.; Huang, Z. Coverage path planning of bridge inspection with Unmanned aerial vehicle. Eng. Appl. Artif. Intell. 2025, 156, 111253. [Google Scholar] [CrossRef]
- Thongpiem, J.; Punkong, N.; Ratanavilisagul, C.; Kosolsombat, S. Hybrid Genetic Algorithm and Ant Colony Algorithm for Solving Travelling Salesman Problem. In Proceedings of the 2024 IEEE 9th International Conference on Computational Intelligence and Applications (ICCIA), Haikou, China, 9–11 August 2024. [Google Scholar]
- Daoqing, Z.; Mingyan, J. Parallel discrete lion swarm optimization algorithm for solving traveling salesman problem. J. Syst. Eng. Electron. 2020, 31, 751–760. [Google Scholar] [CrossRef]
- Wu, C.; Fu, S.; Pei, J.; Dong, Z. A novel sparrow search algorithm for the traveling salesman problem. IEEE Access 2021, 9, 153456–153471. [Google Scholar] [CrossRef]
- Tao, Q.; Zhang, T.; Han, J. An approximate parallel annealing Ising machine for solving traveling salesman problems. IEEE Embed. Syst. Lett. 2023, 15, 226–229. [Google Scholar] [CrossRef]
- Liu, M.; Li, Y.; Li, A.; Huo, Q.; Zhang, N.; Qu, N.; Zhu, M.; Chen, L. A slime mold-ant colony fusion algorithm for solving traveling salesman problem. IEEE Access 2020, 8, 202508–202521. [Google Scholar] [CrossRef]
- Kerschke, P.; Kotthoff, L.; Bossek, J.; Hoos, H.H.; Trautmann, H. Leveraging TSP solver complementarity through machine learning. Evol. Comput. 2018, 26, 597–620. [Google Scholar] [CrossRef] [PubMed]
- Arslan, H.; Manguoglu, M. A parallel bio-inspired shortest path algorithm. Computing 2019, 101, 969–988. [Google Scholar] [CrossRef]
- Nand, R.; Chaudhary, K.; Sharma, B. Single depot multiple travelling salesman problem solved with preference-based step ahead firefly algorithm. IEEE Access 2024, 12, 26655–26666. [Google Scholar] [CrossRef]
- Zheng, J.; Hong, Y.; Xu, W.; Li, W.; Chen, Y. An effective iterated two-stage heuristic algorithm for the multiple Traveling Salesmen Problem. Comput. Oper. Res. 2022, 143, 105772. [Google Scholar] [CrossRef]
- Tong, M.; Peng, Z.; Wang, Q. A hybrid artificial bee colony algorithm with high robustness for the multiple traveling salesman problem with multiple depots. Expert Syst. Appl. 2025, 260, 125446. [Google Scholar] [CrossRef]
- Hamza, A.; Darwish, A.H.; Rihawi, O. A new local search for the bees algorithm to optimize multiple traveling salesman problem. Intell. Syst. Appl. 2023, 18, 200242. [Google Scholar] [CrossRef]
- Cunha, C.B.; Massarotto, D.F.; Fornazza, S.L.; Mendes, A.B. An ALNS metaheuristic for the family multiple traveling salesman problem. Comput. Oper. Res. 2024, 169, 106750. [Google Scholar] [CrossRef]
- Tong, S.; Qu, H.; Xue, J. K-DSA for the multiple traveling salesman problem. J. Syst. Eng. Electron. 2023, 34, 1614–1625. [Google Scholar] [CrossRef]
- Sanyal, S.; Roy, K. Neuro-ising: Accelerating large-scale traveling salesman problems via graph neural network guided localized ising solvers. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 5408–5420. [Google Scholar] [CrossRef]
- Yang, Z.; Nai, W.; Li, D.; Liu, L.; Chen, Z. A Mixed Generative Adversarial Imitation Learning Based Vehicle Path Planning Algorithm. IEEE Access 2024, in press. [CrossRef]


| Dataset | Number of Data Points | Data | Feature Type |
|---|---|---|---|
| BLERSSI | 6611 | 6 | Integer |
| Number of Clusters | GASA-FCM | FCM | k-Means | HC |
|---|---|---|---|---|
| 4 | 0.682671 | 0.61261 | 0.659822 | 0.6717 |
| 5 | 0.621103 | 0.577799 | 0.614267 | 0.605279 |
| Scenario | Simulation Environment | SSA | PSO | GWO | CPO |
|---|---|---|---|---|---|
| 1.1 | 20 × 20 | √ | |||
| 1.2 | 20 × 20 | √ | |||
| 1.3 | 20 × 20 | √ | |||
| 1.4 | 20 × 20 | √ | |||
| 2.1 | 40 × 40 | √ | |||
| 2.2 | 40 × 40 | √ | |||
| 2.3 | 40 × 40 | √ | |||
| 2.4 | 40 × 40 | √ |
| Scenario | Algorithm | Average Path Length | Average Path Points | Average Runtime (s) | Shortest Path | Path Standard Deviation |
|---|---|---|---|---|---|---|
| 1.1 | SSA | 30.08012 | 16.95 | 2.968242 | 28.605 | 0.92838 |
| 1.2 | PSO | 29.63031 | 17.85 | 1.889432 | 27.5668 | 1.118081 |
| 1.3 | GWO | 29.49351 | 16.6 | 1.301083 | 27.9007 | 0.714452 |
| 1.4 | CPO | 29.22382 | 16.5 | 1.163811 | 28.4865 | 0.372128 |
| Scenario | Algorithm | Average Path Length | Average Path Points | Average Runtime (s) | Shortest Path | Path Standard Deviation |
|---|---|---|---|---|---|---|
| 2.1 | SSA | 62.19886 | 22.6 | 12.94032 | 58.6576 | 2.440526 |
| 2.2 | PSO | 63.21584 | 22.3 | 7.37224 | 57.0243 | 4.447651 |
| 2.3 | GWO | 62.59868 | 21.05 | 7.378058 | 59.0857 | 2.285714 |
| 2.4 | CPO | 61.15182 | 21.65 | 5.879644 | 58.9176 | 0.953437 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Yang, X.; Chen, S.; Wu, Z.; Kuang, X.; Zhou, Q. A Two-Stage Planning Method for Rural Photovoltaic Inspection Path Planning Based on the Crested Porcupine Algorithm. Energies 2025, 18, 2909. https://doi.org/10.3390/en18112909
He X, Yang X, Chen S, Wu Z, Kuang X, Zhou Q. A Two-Stage Planning Method for Rural Photovoltaic Inspection Path Planning Based on the Crested Porcupine Algorithm. Energies. 2025; 18(11):2909. https://doi.org/10.3390/en18112909
Chicago/Turabian StyleHe, Xinyu, Xiaohui Yang, Shaoyang Chen, Zihao Wu, Xianglin Kuang, and Qi Zhou. 2025. "A Two-Stage Planning Method for Rural Photovoltaic Inspection Path Planning Based on the Crested Porcupine Algorithm" Energies 18, no. 11: 2909. https://doi.org/10.3390/en18112909
APA StyleHe, X., Yang, X., Chen, S., Wu, Z., Kuang, X., & Zhou, Q. (2025). A Two-Stage Planning Method for Rural Photovoltaic Inspection Path Planning Based on the Crested Porcupine Algorithm. Energies, 18(11), 2909. https://doi.org/10.3390/en18112909






